小学奥数数图形练习题

合集下载

小学奥数题—数复杂图形

• 先是单个单个的数
• 再是2个2个组合的
• 然Байду номын сангаас3个3个组合的数
• 数一数，下面图形中有多少个三角形？
3+2+1=6(个)
• 练习
下图中有几个三角形？
• 练习下图中有几个三角形？
问题2
• 数一数，下面图形中有多少个长方形？
• 数长方形的个数：采用数线段的方法如果所有长方形的边在同一条直线上，就可以采用数长边上总共有多
• 有层次的图形，可以把它分成不同的层数。 • 先数上面一层，再数中间一层，最后数下面一层，然后把多层合
在一起。
第一层：5 ×4 ÷2=10
第二层：5 ×4 ÷2=10
第三层：5 ×4 ÷2=10
总共：10 ×3=30个三角形
• 练习，下面图形中有多少个长方形？
第一层：5 ×4 ÷2=10
第二层：5 ×4 ÷2=10
少条线段，就有多少个长方形。
• 数线段
我发现了一个秘密，下图中
的三角形也可以用数线段的方法来数有共几个三角形。
如果所有三角形有一个顶点在同一点上，边在同一条直线上，就可以数线上总共有多少条线段，就有多少个三角形。
我又发现了一个秘密！
线段总数=端点数× 基本线段数÷ 2
问题3
• 数一数，下面图形中有多少个三角形？
小学三年级奥数
数复杂图形
• 问题1 数三角形 • 问题2 数长方形 • 问题3 数多层图形
• 问题4 数复杂图形
问题1
• 数一数，下面图形中有多少个三角形？
• 数三角形的个数：采用分类法
先是单个单个的数，再是2个2个组合的数，然后3个3个组合的数……
为了便于观察，给各部分编上号,就可以把每个三角形都简单表示出来。

六年级奥数题图形题

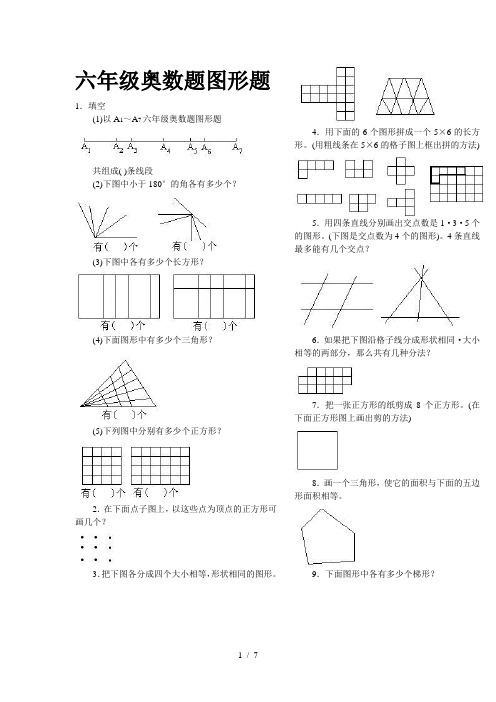
六年级奥数题图形题1．填空(1)以A1～A7六年级奥数题图形题共组成( )条线段(2)下图中小于180°的角各有多少个？(3)下图中各有多少个长方形？(4)下面图形中有多少个三角形？(5)下列图中分别有多少个正方形？2．在下面点子图上，以这些点为顶点的正方形可画几个？3．把下图各分成四个大小相等，形状相同的图形。

4．用下面的6个图形拼成一个5×6的长方形。

(用粗线条在5×6的格子图上框出拼的方法)5．用四条直线分别画出交点数是1·3·5个的图形。

(下图是交点数为4个的图形)。

4条直线最多能有几个交点？6．如果把下图沿格子线分成形状相同·大小相等的两部分，那么共有几种分法？7．把一张正方形的纸剪成8个正方形。

(在下面正方形图上画出剪的方法)8．画一个三角形，使它的面积与下面的五边形面积相等。

9．下面图形中各有多少个梯形？10．下面图形中各有多少个三角形？11．下图中正四棱锥的底面和正方体的面是同样大小的正方形，将这两个面对齐粘合后，这多面体有多少个面？多少条棱？多少个顶点？12．一个正方形把平面分成两部分(如下图中的A ·B 两部分)，那么两个正方形最多能把平面分成几部分？答案A 卷 1．（1）6×7÷2=21（条）（2）4×5÷2=10（个）（3）5×6÷2=15（个）（4）5×6÷2=15 15×4=60（个）（5）左图;42+32+22+12=30（个）右图;6×4＋5×3＋4×2＋3×1=50（个） 2．6个 3．4，5，6，运用中心对称的原理，可以得到九种分法 7，可分成下图所示的8个正方形8，运用等底等高的两个三角形面积相等的知识，把图形变换如下。

9，36个，90个 10，27个，180个11，9个面，16条棱，9个顶点 12，分成10部分应用题1·电影票原价每张若干元,现在每张降低3元出售,观众增加一半,收入增加五分之一,一张电影票原价多少元？2·甲乙在银行存款共9600元，如果两人分别取出自己存款的40%，再从甲存款中提120元给乙。

五年级奥数专题：图形的计数

五年级奥数专题：图形的计数A 3A 1OA 2A 4A 5A 7A 6A 8A 9A 10A 11 A 12九图形的计数(A)年级班姓名得分⼀、填空题1．下图中⼀共有（）条线段.2. 如右上图,O 为三⾓形A 1A 6A 12的边A 1A 12上的⼀点,分别连结OA 2,OA 3,…OA 11，这样图中共有_____个三⾓形.3. 下图中有_____4. 右上图中共有_____个梯形.5.数⼀数(1)⼀共有( )个长⽅形. (2)6. 在下图中,所有正⽅形的个数是______.AC E7. 在⼀块画有4?4⽅格⽹⽊板上钉上了25颗铁钉(如下图),如果⽤线绳围正⽅形,最多可以围出_____个.8. ⼀块相邻的横竖两排距离都相等的钉板,上⾯有4?4个钉(如右图).以每个钉为顶点,你能⽤⽪筋套出正⽅形和长⽅形共_____个.9. 如下图,⽅格纸上放了20枚棋⼦,以棋⼦为顶点的正⽅形共有_____个.10. 数⼀数,下图是由_____个⼩⽴⽅体堆成的.要注意那些看不见的.⼆、解答题11. 右图中共有7层⼩三⾓形，求⽩⾊⼩三⾓形的个数与⿊⾊⼩三⾓形的个数之⽐.12. 下图中,AB 、CD 、EF 、MN 互相平⾏，则图中梯形个数与三⾓形个数的差是多少？13．现在都是由边长为1厘⽶的红⾊、⽩⾊两种正⽅形分别组成边长为2厘⽶、4厘⽶、8厘⽶、9厘⽶的⼤⼩不同的正⽅形、它们的特点都是正⽅形的四边的⼩正⽅形都是涂有红颜⾊的⼩正⽅形，除此以外，都是涂有⽩⾊的⼩正⽅形，要组成这样4个⼤⼩不同的正⽅形，总共需要红⾊正⽅形多少个？⽩⾊正⽅形多少个？14ABC的每⼀边4等分，过各分点作边的平⾏线，在所得下图中有多少个平⾏四边形？九图形的计数（B）年级班姓名得分⼀、填空题1. 下图中长⽅形（包括正⽅形）总个数是_____.2. 右上图中有正⽅形_____个,三⾓形_____个,平⾏四边形_____个,梯形_____个.3. 下图中共出现了_____个长⽅形.4. 先把正⽅形平均分成8个三⾓形.再数⼀数,它⼀共有_____个⼤⼩不同的三⾓形.5. 图形中有_____个三⾓形.6．如右上图,⼀个三⾓形分成36个⼩三⾓形.把每个⼩三⾓形涂上红⾊或蓝⾊,两个有公共边的⼩三⾓形要涂上不同的颜⾊,已知涂成红⾊的三⾓形⽐涂成蓝⾊的三⾓形多,那么多_____个.7. 下图是由⼩⽴⽅体码放起来的,其中有⼀些⼩⽅体看不见.图中共有_____个⼩⽴⽅体.8. 右上图中共有_____个正⽅形.9. 有九张同样⼤⼩的圆形纸⽚,其中标有数码“1”的有1张；标有数码“2”的有2张；标有数码“3”的有3张，标有数码“4”的也有3张。

五年级奥数数图形

数三角形的个数
数长方形的个数
解决了车票设计问题
解决了比赛场次安排问题
下面图形中有多少个正方形，多少个三角形？有1个正方形。8个三角形。有1正方形。8个三角形。
下面二图形叠加后有多少个正方形，多少个三角形？
+
二图形共有2个正方形，16个三角形
二图叠加后新增8个正方形，新增三角形：16+12=28个二图叠加后总共有2+8=10个正方形，16+28=44个三角形。
或 52 4个2 32 22 11 55
拓展17. 数一数，图中有多少个长方形？
15 6
总共15+6-1= 20个（6+5+4+2+1）× （3+2+1）= 126个
问题4：综合应用探索之旅
解决问题（一）：售票员需要准备几种车票？
钟楼易初莲唐兴
花
路
学校
解决问题（二）：一年级有六个班,每两个班之间要进行一场比赛,一共需要几场比赛?
15 15
5
15+5+15= 35 个
拓展6. 数一数，下图有多少个三角形？
1 3
7 16
16+7+3+1= 27个
6+6+3=15个
拓展7. 数一数，下图中有多少个三角形？
4
24
12
32
8 16
4
24+16+12+4=56个 32+24+16+8+4=84个
拓展8:数一数，下图中共有多少个三角形？
总共有：3+2= 5 个

小学奥数图形题

小学奥数图形题（一）例题精选例1、图中的甲和乙都是正方形，求阴影部分的面积。

（单位：厘米）例2、计算图形的面积。

（单位：厘米）例3、如图，已知四条线段的长分别是：AB=2厘米，CE=6厘米，CD=5厘米，AF=4厘米，并且有两个直角。

求四边形ABCD的面积。

例4、下图是两个相同的直角三角形叠在一起，求阴影部分的面积。

（单位：分米）例5、如图，EC把平行四边形ABCD分成两部分，它们的面积差是18.6平方厘米，问梯形的上底AE 是多少厘米？例6、一个长方体，如果长减少2厘米，宽、高都不变，它的体积减少48立方厘米，如果宽增加3厘米，长、高都不变，它的体积增加99立方厘米；如果高增加4厘米，长、宽都不变，它的体积增加352立方厘米，原长方体的表面积是多少立方厘米？例7、把一个长、宽、高分别是7厘米、6厘米、5厘米的长方体截成两个长方体，使这两个长方体的表面积之和最大，这时表面积之和是多少平方厘米？例8、将高都是1厘米，底面积半径分别是1.5米、1米、和0.5米的三个圆柱体正叠放组成一个新物体，求这个物体的表面积。

例9、用长是9厘米、宽是6厘米、高是7厘米的长方体木块叠成一个正方体，至少需要这种长方体木块多少块？练习题1、求图中阴影部分的面积（单位：米）2、求图中阴影部分的面积（单位：分米）3、下图的长方形中，三角形ADE与四边形DEBF和三角形CDF的面积都相等，求三角形DEF的面积。

（AD=12厘米，CD=9厘米）4、图中平行四边形ABCD的边BC长10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。

5、如图，平行四边形ABCD的面积为54平方厘米，E、F分别为AC和BC边上的三等分点，求阴影部分的面积。

6、从一个长方体上截下一个体积是32立方厘米的小长方体后剩下的部分正好是棱长4厘米的正方体，原来这个长方体的表面积是多少平方厘米？7、一个长方体的表面积是30平方厘米，把它平均切开，正好成为两个相同的小正方体，求每个小正方体的表面积是多少平方厘米？8、有一个立方体，边长是5，如果它的左上方截去一个边长分别是5、3、2的长方体（如图），那么，它的表面积减少了百分之几？9、一块长24厘米的长方形铁皮，在四角上剪去边长为3厘米的正方形，将它焊接成一个盒子，已知盒子的容积是486立方厘米，求这块铁皮原来的宽是多少厘米？10、如图，是一个零件的直观图，下部是一个棱长为5厘米的正方体，上部正好是圆柱体的一半，求这个零件的表面积和体积。

小学数学六年级奥数《立体图形(1)》练习题(含答案)

小学数学六年级奥数《立体图形（1）》练习题（含答案）一、填空题1.一个正方体的表面积是384平方分米，体积是512立方分米，这个正方体棱长的总和是 .2.如图,在一块平坦的水泥地上,用砖和水泥砌成一个长方体的水泥池,墙厚为10厘米(底面利用原有的水泥地).这个水泥池的体积是 .3.一个边长为4分米的正方形,以它的一条边为轴,把正方形旋转一周后,得到一个 ,这个形体的体积是 .4.把19个边长为2厘米的正方体重叠起来堆成如右图所示的立方体,这个立方体的表面积是平方厘米.5.图中是一个圆柱和一个圆锥(尺寸如图).问:柱锥V V 等于 .6.一个长方体的表面积是67.92平方分米.底面的面积是19平方分米.底面周长是17.6分米,这个长方体的体积是 .2 单位:米7.一块长方体木块长2.7米,宽1.8分米,高1.5分米.要把它裁成大小相等的正方体小木块,不许有剩余,小正方体的棱长最大是分米.8.王师傅将木方刨成横截面如右图(单位:厘米)那样高40厘米的一根棱柱.虚线把横截面分成大小两部分,较大的那部分的面积占整个底面的60%.这个棱柱的体积是立方厘米.9.小玲有两种不同形状的纸板.一种是正方形的,一种是长方形的(如下图).正方形纸板的总数与长方形纸板的总数之比是1:2.她用这些纸板做成一些竖式和横式的无盖纸盒,正好将纸板用完.在小玲所做的纸盒中,坚式纸盒的总数与横式纸盒的总数之比是 .10.在桌面上摆有一些大小一样的正方体木块,从正南方向看如下图(1),从正东方向看如下图(2),要摆出这样的图形至多能用块正方体木块,至少需要块正方体木块.二、解答题11.一个长方形水箱,从里面量长40厘米,宽30厘米,深35厘米.原来水深10厘米,放进一个棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,这时水面高多少厘米?12.如图表示一个正方体,它的棱长为4厘米,在它的上下、前后、左右的正中位置各挖去一个棱长为1厘米的正方体,问此图的表面积是多少?8 28 2412（图1）（图2）13.下图是正方体,四边形APQC 是表示用平面截正方体的截面,截面的线表现在展开图的哪里呢?把大致的图形在右面展开图里画出来.14.雨哗哗地不停地下着,如在雨地里放一个如图1那样的长方形的容器,雨水将它下满要用1小时.有下列(A )-(E )不同的容器(图2),雨水下满各需多少时间(注面是朝上的敞口部分.)PF2cm 2cm （A ）（B ）（C ）（D ）（E ）雨———————————————答案——————————————————————1. 96分米.正方体的底面积为384÷6=64(平方分米).故它的棱长为512÷64=8(分米),棱长的总和为8×12=96(分米).2. 8.96立方米.(3-0.1×2)×(1.8-0.1×2)×2=8.96(立米米).3. 圆柱体,200.96立方分米.(3.14×42)×4=200.96(立方分米).4. 216.这个立方体的表面由3×3×2+8×2+10×2=54个小正方形组成,故表面积为4×54=216(平方厘米).5. 241. ππππ816828,3164243122⨯=⨯⎪⎭⎫ ⎝⎛⨯==⨯⎪⎭⎫ ⎝⎛⨯⨯=柱锥V V ,故241=柱锥V V .6. 32.3立方分米.长方体的侧面积是67.92-19×2=29.92(平方分米),长方体的高为29.92÷17.6=1.7(分米),故长方体的体积为19×1.7=32.3(立方分米).7. 0.3长、宽、高分别是270厘米、18厘米和15厘米,而270、18和15的最大公约数为3(厘米),这就是小正方体棱长的最大值.8. 17200.设较大部分梯形高为x 厘米,则较小部分高为(28- x )厘米.依题意有: 4:6)28()824(21:)2412(21=⎥⎦⎤⎢⎣⎡-⨯+⨯⎥⎦⎤⎢⎣⎡+⨯x x 解得x =16,故这棱柱的体积为 1920040)1628()824(2116)2412(21=⨯⎥⎦⎤⎢⎣⎡-⨯+⨯+⨯+⨯(立方厘米).9. 3:1.一个竖式的无盖纸盒要用一个正方形纸板和4个长方形纸板,一个横式的无盖纸盒要用2个正方形纸板和3个长方形纸板.设小玲做的纸盒中,有x 个竖式的, y 个横式的,则共用正方形纸板(x +2 y )个,用长方形纸板(4 x +3 y )个,依题意有: (x +2 y ):(4 x +3 y )=1:3.解得x : y =3:1.10. 20,6.至多要20块(左下图),至少需要6块(右下图).11. 若铁块完全浸入水中,则水面将提高326)3040(203=⨯÷(厘米).此时水面的高小于20厘米,与铁块完全浸入水中矛盾,所以铁块顶面仍然高于水面.设放入铁块后,水深为x 厘米.因水深与容器底面积的乘积应等于原有水体积与铁块浸入水中体积之和,故有:x x 20201030403040⨯+⨯⨯=⨯解得x =15,即放进铁块后,水深15厘米.12. 大正方体的表面还剩的面积为()9014622=-⨯(厘米2),六个小孔的表面积为()305162=⨯⨯(厘米2),因此所求的表面积为90+30=120(厘米2).13. 截面的线在展开图中如右图的A -C -Q -P -A .14. 在例图所示的容器中,容积:按水面积=(10×10×30):(10×30)=10:1,需1小时接满,所以容器(A):容积:接水面积=(10×10×10):(10×10)=10:1,需1小时接满; 容器(B):容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满; 容器(C):容积:接水面积=(20×20×10-10×10×10):(10×10)=30:1,需32 1 2 1 2 2 1 2 1 1 1 1 1 1 1 1 1 2 1 1A小时接满;容器(D):容积:接水面积=(20×20×10-10×10×10):(20×10)=15:1,需1.5小时接满;容器(E):容积:接水面积=20×S:S=20:1(S为底面积),接水时间为2小时.。

小学一年级奥数题：图形计数练习题【五篇】

小学一年级奥数题：图形计数练习题【五篇】2.小敏到商店买文具用品。

她用所带钱的一半买了1支铅笔，剩下的一半买了1支圆珠笔，还剩下1元钱。

小敏原来有多少钱?3.有两篮苹果，第一篮25个，第二篮19个，从第一篮中拿几个放入第二篮，两篮的苹果数相等?4.小明从家到学校跑步来回要10分钟，如果去时步行，回来时跑步一共需要12分钟，那么小明来回都是步行需要几分钟?5.小红和小绿都有10块橡皮，小兰给小绿2块后，现在小绿比小兰多几块橡皮?【第二篇】1.有一本书，小华第一天看了2页，以后每一天都比前一天多看2页，第4天看了多少页?2.妈妈从家里到工厂要走3千米，一次，她上班走了2千米，又回家取一很重要工具，再到工厂。

这次妈妈上班一共走了多少千米?3.像18+81这样十位数字与个位数字顺序颠倒的一对两位数是好朋友，它们相加和是99，请问像这样的相加和是99的好朋友有几对?4.桌子上有三盘桃子，第一盘比第三盘多3只，第三盘比第二盘少5只。

问：哪盘桃子最少?5.13个小朋友玩"老鹰抓小鸡"的游戏，已经抓住了5只"小鸡"，还有几只没抓住?6.修花坛要用94块砖，第一次搬来36块，第二次搬来38块，还要搬多少块?(用两种方法计算)7.海盗抓小孩去无人岛，一共抓了15个小孩，他让小孩排队报数，第一次把报单数的孩子都送去了无人岛，接着让剩下的孩子报数，又把报单数的孩子送去了无人岛，把其他孩子放回了家。

问强盗放多少个孩子回家?8.懒羊羊一次买来了30个苹果，它第一天吃了一些，第二天又吃了一些，这时还剩下12个苹果，懒羊羊两天一共吃了多少个苹果?9.5只兔子和4只猫一样重，那么一只兔重还是一只猫重?10.一只井底的蜗牛，白天能够爬2米，晚上下滑1米，已知井深5米，蜗牛多久能够爬到井外?【第三篇】1.小明把一根木棍锯成2段需要2分钟，那么依照这样的速度，把一根木棍据成3段需要多少分钟?2.一个猴子吃3个桃子多出一个，一个猴子吃4个桃子就少2个。

小学奥数[图形推理]练习题集与答案解析

word 格式小学奥数《图形推理》练习题及答案（B）一、填空1.观察下面这组图形的变化规律，在标号处画出相应的图形.2.下图是由9个小人排列的方阵，但有一个小人没有到位，请你从右面的6个小人中选一位小人放到问号的位置你认为最合适的人选是_______ 号.654•一-3■- 21V 1丁？AftAAA Tx XX②①3•下图是用几何图形组成的小房子，请你根据组成的规律在标号处画出相应应变为变成那么③7.请观察下图中已有图形的规律，并按这一规律在空白处填出图形△□O□ 0△2变成应变成6.观察给出图形的变化规律，按照这种规律，在空格中填上应有的图形9.下图的排列规律你发现了吗？请你根据这一规律，把第3幅图填出来. 10•下图的变化很多，请你认真仔细地观察，画出第四幅图的答案涉E a△0㊉<1区1V D38.观察下图的变化规律，在空白处填上适当的图1、2、3、4四个数字.现在有三个四面体，请问哪一个和其它两个不同？图(1) 图(2) 图(3)12.兵”、马”、卒”如图所示占田”字的四个小格，把它们不停的变换位置第一次上下两排交换，第二次在第一次交换后左右两列交换，第三次再上下两排交换，第四次再左右两列交换••…这样交换二十次位置后，马”在几号小格内？⑴（2）⑶（4）⑸二、解答题11.正四面体分别写有13.在下面图形中找出一个与众不同的14.依照下面图中所给图形的变化规律，在空格中填图.---------------------------- 答案----------------------------------------------1.这道题中的每一个图形是由里外两部分组成的，我们分开来看•先看外面的图形•外面的图形都是由△、口、0组成，并每一横行（或每一竖行）中都没有重复的图形•这样我们可以先确定①、②、③外面的图形.通过题目中给出的图形我们不能确定出③的外部图形，因为不论③所在的横行还是③所在的竖行都只给出1个图形，所以我们应先确定出①和②的外部图形.①所在的横行中只有O和△，所以①的外部图形是□,②所在的竖行只有△和O,所以②的外部图形也是□, ③所在的横行只有□和O所以③的外部图形是△.然后按照这种方法确定内部图形,可知①的内部图形是□，②的内部图形是△,③的内部图形是O,形状确定好以后，我们还要注意各个图形的内部图形是有不同颜色的，分别由点状、斜线和空白三种组成，确定的方法和确定形状是完全相同的，请你自己把三个图的颜色确定出来最后①、②、③应分别为：①② ③2. 仔细观察，可发现图中小人的排列规律：即每行例）的小人手臂”向上、水平、向下）.身腰”（三角形矩形、半圆），及脚”圆脚、方脚、平脚）各不相同.从中可知问号处的小人应是向上伸臂.矩形腰圆脚的小人即最合适的人选是6 号.3. 这道题同（1）卷解答题第4题分析完全相同.①、②、③图形分别如下：4. 第1行图形由左向右变化的规律是左右颠倒，上下颠倒.（或旋转180 ），然①③后将移到上面的图形以中线为对称轴做出另一半图形.根据这个变化规律，请你做出要求的图形•答案应为:5. 分析:先应找出变化的规律，然后再依规律，在空白处填画所缺的图形•从题图的第一行可以看到，当左边的图形变化成右边的图形时，图形外部的圆变为图形的下半部分，且圆变成半圆，白色变成灰色（画有斜线）.也就是说，在变化过程中,原来图形的外部部分有形状、位置、颜色这三个方面的变化•再看原图形的内部部分：中间的灰色正方形变到了上半部分（位置变）成了白色的（颜色变化）斜放着的正方形（角度变化）.根据这些规律可以知道，空白处的图形其下部分是由左边图形的外部大正方形变化而成的，半个大正方形，颜色为灰色；上半部分是由左边图形的中间部分变化而成的一个白色、正放着的小正方形，如图•解在空白处的图形如图所示6. 观察这道题给出的八个图，形状都是箭，这使我们可以肯定空格处的图形也是箭•在这组图中，发生变化的有两点：一是箭的方向，二是箭尾的羽毛”首先我们看横行（从左到右）,箭的方向是顺时针依次旋转90得到的,所以空格处的箭应向上.再看箭尾的羽毛”，每一行也是依次减少一对，所以空格处的箭箭笔没有羽毛”所以空格的图形为：7. 在这幅图中，都是△、。

六年级奥数《平面图形》练习题

第十一讲平面图形（必做与选做）1.在一张长12厘米、宽6厘米的长方形纸上剪下一个最大的半圆，这个半圆的周长是多少厘米？A. 24.84B. 30.84C. 43.68D. 49.68解析：最大的半圆以长方形长为直径，宽为半径。

这个半圆的周长C＝3.14×6＋12＝30.84（厘米）。

所以选B。

2.在一张长12厘米、宽5厘米的长方形纸上剪下一个最大的半圆，这个半圆的周长是多少厘米？A. 20.7B. 25.7C. 27.5D. 41.4解析：最大的半圆以长方形的宽为半径，宽的两倍为直径。

这个半圆的周长C＝3.14×5＋5×2＝25.7（厘米）。

所以选B。

3.在一张长12厘米、宽7厘米的长方形纸上剪下一个最大的半圆，剩下纸的周长是多少厘米？A. 32.84B. 30.84C. 44.84D. 63.68解析：最大的半圆是以长方形的长为直径，长的一半为半径。

剩下的纸的周长C＝12＋7×2＋3.14×（12÷2）＝44.84（厘米）。

所以选C。

4.有2根直径都是3分米的圆柱形木头，现用绳子分别在两处把它们捆在一起，至少需要绳子多少分米？（接头处不计）A. 15.42B. 24.84C. 30.84D. 49.68解析：需计算两部分的长度，一部分是两条线段的长度，都是直径的长度；另一部分是两段圆弧的长度，一共是一个圆的周长。

因此一共需要绳子：（3.14×3＋3×2）×2＝30.84（分米）。

所以选C。

5.有3根直径都是5分米的圆柱体木头，现用绳子分别在三处把它们捆在一起，至少需要绳子多少分米？（接头处不计）A. 30.7B. 61.4C. 77.1D. 92.1解析：需计算两部分的长度，一部分是三条线段的长度，都是直径的长度；另一部分是三段圆弧的长度，一共是一个圆的周长。

因此一共需要绳子：（3.14×5＋5×3）×3＝92.1（分米）。

六年级奥数图形问题精选

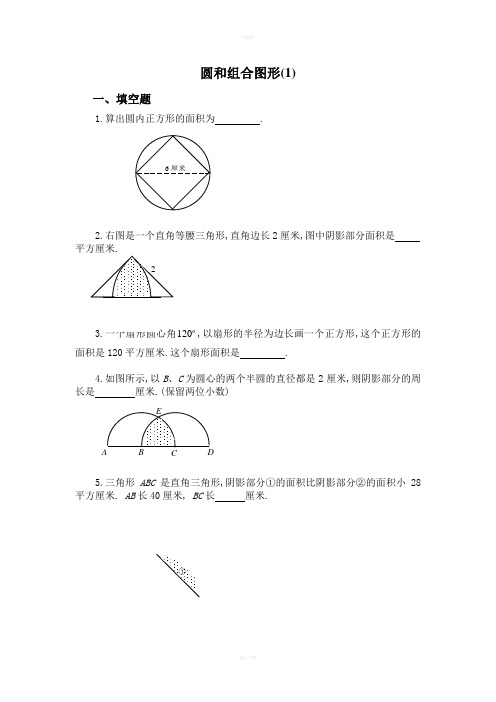
圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=（平方厘米）.12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC . 扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).十二、圆和组合图形（2）一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是平方厘米.8.已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是平方厘米.(π取3.14)2二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22)取12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、CD 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为⌒61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ,解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r,则①的面积为:72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯,②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:)420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).D面积计算（三）专题简析：对于一些比较复杂的组合图形，有时直接分解有一定的困难，这时，可以通过把其中的部分图形进行平移、翻折或旋转，化难为易。

小学奥数思维训练-几何(三)立体图形(拓展训练)(通用,含答案)

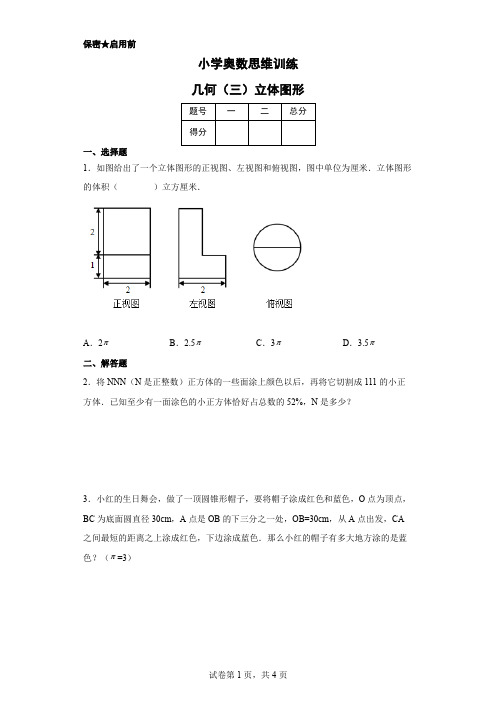
保密★启用前小学奥数思维训练几何（三）立体图形一、选择题1．如图给出了一个立体图形的正视图、左视图和俯视图，图中单位为厘米．立体图形的体积（）立方厘米．A．2πB．2.5πC．3πD．3.5π二、解答题2．将NNN（N是正整数）正方体的一些面涂上颜色以后，再将它切割成111的小正方体．已知至少有一面涂色的小正方体恰好占总数的52%，N是多少？3．小红的生日舞会，做了一顶圆锥形帽子，要将帽子涂成红色和蓝色，O点为顶点，BC为底面圆直径30cm，A点是OB的下三分之一处，OB=30cm，从A点出发，CA 之间最短的距离之上涂成红色，下边涂成蓝色．那么小红的帽子有多大地方涂的是蓝色？（π=3）4．一个正方体纸盒中恰好能放入一个体积为628立方厘米的圆柱，纸盒的容积有多大？（π=3.14）5．图中的立体图形是由14个棱长为5cm的立方体组成的，求这个立体图形的表面积？6．圆柱形的售报亭的高和底面直径相等（如图），开一个边长等于底面半径的正方形售报窗口．问窗口处挖去的圆柱部分的面积占圆柱形侧面积的几分之几？7．一个正方体木块，棱长是15．从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体．这个木块剩下部分的表面积最少是多少？8．如图，一个正方体形状的木块，棱长1米，沿水平方向将它锯成3片，每片又锯成4长条，每条又锯成5小块，共得到大大小小的长方体60块．那么这60块长方体表面积的和是多少平方米？9．如图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞，第三个正方形小洞的挖法和前两个相同，棱长为1/4厘米，那么最后得到的立体图形的表面积是多少平方厘米？10．把一个棱长为2cm正方体在同一平面的边的中点用线段连接起来，如图．然后把正方体顶点上的三角锥锯掉，请问最后所得的立体图形的表面积的多少平方厘米？（1.732×1.732=3）参考答案：1．A【解析】【详解】首先确定此图形为“不完整的圆柱”，先求出圆柱体积，再求出缺失的半个小圆柱，最后作差．如图，从给定的正视图、左视图和俯视图可以看出，该立体图形由一个半径为1厘米、高为1厘米的圆柱和一个半径为1厘米、高为2厘米的半圆柱组成．．π×1×1×（1+2）-12π×1×1×2=2π，选A【点睛】这里的要点在于还原，还原的技巧在于先补全，再细雕刻2．5【解析】【详解】一个正整数×52%=另一个正整数,那么这个正整数必须能被25整除1352%25⎛⎫=⎪⎝⎭因为．那么N必须能被5整除．当N取最小N=5 正方体有5×5×5=125个小正方体涂色的小正方体5×5×5×52%=65（个）不可能被涂色的小正方体3×3×3=27（个）27+65小于125成立当N=2×5=10时，正方体有10×10×10=1000个小正方体涂色的小正方体10×10×10×52%=520（个）不可能被涂色的小正方体 8×8×8=512（个） 512+520大于1000 不成立同理N 大于10都不成立所以 N=53．750平方厘米【解析】【详解】底面周长为圆锥展开后扇形的弧长蓝色面积=圆锥侧面积-红色面积底面周长=30×π=30×3=90侧面展开后扇形所在圆的周长=2×π×30=1809011802= 所以侧面展开图为半圆蓝色面积=π×30×30×12-12×（20+20） ×30 =1350-600=750（平方厘米）4．800cm 3【解析】【详解】设纸盒棱长为x圆柱体积=22x x x π⨯⨯⨯=628 整理上边式子得x 3=800(cm 3) 即为纸盒容积．5．1050平方厘米【解析】【详解】用透视法观察上、下两个面的面积相等4个侧面的每个侧面面积为6个小正方形面积底面棱长5×3=15 上、下两个面的面积=15×15×2=4504个侧面面积=4×6×5×5=600总面积=450+600=1050（平方厘米）6．1 12【解析】【详解】窗口上下的弧长为底面圆周长的六分之一窗口的高为圆柱的高的二分之一挖去的圆柱部分的面积占圆柱形侧面积的16×12=1127．1252【解析】【详解】截去一个小正方体，表面积不变．只有在截去的小正方体的面相重合时，表面积才会减少．所以要使木块剩下部分的表面积尽可能小，应该在同一条棱的两端各截去棱长7与8的小正方体（如图所示），这时剩下部分的表面积比原正方体的表面积减少最多．剩下部分的表面积最小是：15×15×6-7×7×2=1252．想想为什么不是15×15×6-7×7-8×8.8．24平方米【解析】【详解】我们知道每切一刀，多出的表面积恰好是原正方体的2个面的面积．现在一共切了（3-1）+（4-1）+（5-1）=9刀，而原正方体一个面的面积1×1=1（平方米），所以表面积增加了9×2×1=18（平方米）．原来正方体的表面积为6×1=6（平方米）．所以现在的这些小长方体的表积之和为6+18=24（平方米）．9．29.25平方厘米【解析】【详解】俯视图发现上表面积就是大正方体的一个面的面积表面积为大正方体表面积加上3个小正方体的侧面积2×2×6+1×1×4+12×12×4+14×14×4=24+4+1+1 4=29.25（平方厘米）10．18.928cm2【解析】【详解】所得立体图形表面为6个正方形和8个等边三角形勾股定理等边三角形的高的平方=底边的平方-半个底边的平方=34底边的平方6个正方形面积=6×（1×1+1×1）=6×2=12等边三角形的高的平方=34×2=32等边三角形的高的平方×底边的平方=32×2=3所以等边三角形的高×底边=1.732，等边三角形的面积=1/2×1.732=0.866立体图形的表面积=12+8×0.866=18.928(cm2)。

小学二年级奥数题《图形的平移题目大全及答案》题库大全

小学二年级奥数题《图形的平移题目大全及答案》题库大全姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分评卷人得分1、下面的图形，平移哪些线段，就可以变成长方形，用笔画出来。

答案与解析：2、飞禽馆长颈鹿馆大象馆熊猫馆猴山（1）从入口向右平移5格是猴山。

（2）从猴山向上平移4格是熊猫馆。

（3）从熊猫馆向右平移3格是飞禽馆，再向右平移3格是长颈鹿馆。

（4）从长颈鹿馆向下平移6格是大象馆。

答案与解析：“略”3、电梯上下移动是（）现象。

水龙头开关的转动是（）现象。

（平移或旋转）答案与解析：平移；旋转4、画出平移后的图形。

答案与解析：5；5、请在（）里填上“平移”或“旋转”（1）（2）（3）答案与解析：（1）平移；旋转；旋转（2）旋转；平移（3）旋转；旋转；平移；平移6、分别画出将向下平移3格和向右平移5格后得到的图形。

答案与解析：7、画出下图向左平移6格后的图形。

答案与解析：“略”8、画出下图向右平移8格得到的图形。

答案与解析：9、钟面上的指针是（）现象。

（填“平移”或“旋转”）答案与解析：旋转10、把图案平移后的图形画出来。

答案与解析：“略”11、连线旋转平移答案与解析：旋转；平移12、把向左平移6格后得到的涂上颜色。

答案与解析：“略”13、下面的图形是平移的填“”，是旋转的填“○”。

（1）（2）（3）（）（）（）（4）（5）（6）（）（）（）（7）（8）（9）（）（）（）答案与解析：（1）○；（2）；（3）○；（4）；（5）○；（6）○；（7）；（8）；（9）14、分别画出将凸向右平移5格，向下平移3格后得到的图形。

答案与解析：“略”15、下面现象中是平移的在（）里打“”，是旋转的画“○”。

（1）建筑工地的升降机。

（2）直升机的螺旋桨。

（）（）（3）工作中的排气扇。

（4）行进中的滑雪板。

（）（）答案与解析：（1）；（2）○；（3）○；（4）16、把可以平移到1号小鱼位置的小鱼涂上颜色。

小学一年级奥数题及答案 - 认识图形题及答案

小学一年级奥数题及答案 - 认识图形题及答案1.如何用两个同样大小的直角三角形拼成一个平行四边形？答案：一个平行四边形的两组对角相等、两组对边平行且相等。

通过试验，我们可以用两个直角三角形拼成如下的平行四边形。

2.在下面的五个图形中，哪一个与其他四个不同？答案：图(2)与其他四个不同。

其他图形都是由正方形和圆形构成，而第(2)个图形是由三角形和圆形构成。

3.计算规则图形中三角形的数量。

答案：这个图形中有6个三角形。

4.你能用一笔画出下面的图形吗？答案：5.数一数下列各图中有多少个三角形。

答案：分别为3、8、5.6.下面是一个倒着的缺一条腿的椅子，请你移动2根火柴棒，把它正过来，并看起来没有缺腿，你会吗？答案：这道题考察大家的应变能力，通过移动一至三根火柴棒对之前的图案有小小的变化，成为另一个图案。

7.移动3根火柴棒，使桌子在两把椅子的中间。

答案：8.如果想让下图的小鱼头朝右，尾向左，最少需要移动几根火柴？答案：需要移动3根火柴，具体操作如下：9.在空格中应填什么样的图形？答案：10.按照图形变化的规律，在空格处应画什么样的图形？答案：11.空白处应填什么样的图形？答案：12.在空格中应填什么样子的图形？答案：13.下面的一组图形的“?”中，应填什么样的图形？答案：14.你能把下面的平面图形分分类吗？答案：⑴、⑷、⑾为一类——三角形；⑵、⑺为一类——圆，因为它们没有角，边是弯曲的；⑶、⑸、⑻、⑼、⑽、⑿为一类——四边形，因为它们有四条边，四个角；剩下的图形⑹为六边形。

15.答案：16.答案：17.按照图形的变化规律，在“?”处画出相符的图形。

答案：这组图形的变化只在于正方形中阴影部分的位置。

通过观察，我们可以发现阴影部分是按照逆时针方向依次旋转得到的。

所以“?”处的图形应为：18.在下面的图中，哪个图形与其他四个不同？答案：这五辆汽车车窗一致，车轮一致，车底一致，差异就只能在车头、车身部分去寻找。

3 小学奥数——几何图形试题及解析

小学奥数——几何图形一.选择题（共50小题）1.图中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道()条线段的长度，才可以计算出这个八边形的周长.A.4B.3C.5D.102.如图中阴影部分是正方形，最大长方形的周长是()厘米.A.22B.26C.36D.无法确定3.如图，由6个边长为3厘米的小正方形拼成的图形，它的周长是()厘米.A.36B.39C.42D.454.把一个直径是4厘米的圆分成两个完全相等的半圆，这两个半圆的周长之和是()A.12.56厘米B.16.56厘米C.20.56厘米D.24.56厘米5.如图，有8条线段，至少要分别测量编号为()的三条线段的长度，才能求出这个图形的周长.A.①②⑤B.①②③C.①②⑦D.②③⑦6.如图，是一个台阶的侧面（线段AC，BC，AB的长依次为5米、12米、13米）要在台阶上面铺上红地毯，且上下各多铺出两米，需要地毯的长度是()米.A.17B.18C.20D.217.如图，正方形被一条曲线分成了A、B两部分，下面第()种说法不正确？A.如果a b>，那么A的周长大于B的周长B.如果a b<，那么A的周长小于B的周长C.如果a b=，那么A的周长等于B的周长D.不管a、b哪个大，A、B的周长总是相等8.如图是用3个长8厘米、宽3厘米的长方形拼成的，这个图形的周长是()A.66厘米B.48厘米C.45厘米9.图中多边形每相邻两条边都互相垂直，若要计算起其周长，那么至少要知道()边长.A.6B.5C.4D.310.一个长方形花园长是30米，宽是10米，沿着花园走两圈，共走了()A.45米B.90米C.160米D.200米11.把如图的长方形用一条曲线分成甲、乙两个图形，甲图与乙图的周长相比，()A.甲图的长B.乙图的长C.甲图与乙图同样长12.如图，在由11⨯的正方形组成的网格中写有2015四个数字（阴影部分），其边线要么是水平或竖直的直线段，要么是连接11⨯的正方形相邻两边中点的线段，或者是11⨯的正方形的对角线，则图中2015四个数字（阴影部分）的面积是()A.47B.1472C.48D.148213.如图中，正八边形ABCDEFGH的面积为1，其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积()A.12B.23C.35D.5814.如图，大正方形的边长为14，小正方形的边长为10，阴影部分的面积之和是( )A.25B.40C.49D.5015.大、中、小三个正方形，边长都是整数厘米，小正方形的周长比中正方形的边长小，把这两个正方形放在大正方形上（如图），大正方形露出的部分的面积是10平方厘米（图中阴影部分）.那么，大正方形的面积是( )平方厘米.A.25B.36C.49D.6416.如图，大正六边形内部有7个完全一样的小正六边形，已知阴影部分的面积是180平方厘米.那么大正六边形的面积是( )平方厘米.A.240B.270C.300D.36017.如图所示，在58 的方格中，阴影部分的面积为237cm .则非阴影部分的面积为( 2)cm .A.43B.74C.80D.11118.图中，将两个正方形放在一起，大、小正方形的边长分别为0l，6，则图中阴影部分面积为()A.42B.40C.38D.3619.下图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB、BC、CD、DA的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn，那么，m n的值等于()A.5B.7C.8D.1220.有5个长方形，它们的长和宽都是整数，且5个长和5个宽恰好是1~10这10个整数；现在用这5个长方形拼成1个大正方形，那么，大正方形面积的最小值为()A.169B.144C.121D.10021.一个梯形的上底增加2厘米，下底减少2厘米，高不变，它的面积与原面积相比()A.变大了B.变小了C.不变D.高不知道，所以无法比较22.已知图中正方形的两个顶点正好是两个等腰直角三角形斜边上的中点，小等腰直角三角形与正方形中的圆面积相等，请问正方形中的阴影面积与大等腰直角三角形面积的比值A.13B.12C.1D.3223.如图，梯形ABCD 中，//AB DC ，90ADC BCD ∠+∠=︒，且2DC AB =，分别以DA 、AB 、BC 为边向梯形外作正方形，其面积分别为1S ，2S ，3S ，则1S ，2S ，3S 之间的关系是下列选项中的( )A.123S S S +>；B.132S S S +=；C.132S S S +<；D.无法确定.24.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片；第二次在这个小正三角形纸片四周再放三张纸片；第三次在第二次摆好的图形四周再摆放纸片；⋯摆放要求是：每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合，且纸片之间除边之外，无重合（见图）.第20次摆放后，该图形共用了正三角形纸片( )张.A.571B.572C.573D.57425.在88⨯网格的所有方格中放入黑白两种围棋子，每个方格放一枚棋子，要求每行中的白色棋子的数目互不相同，每列中的白色棋子的数目相等，那么这个88⨯网格中共有( )枚黑色棋子.A.42B.32C.22D.1226.在66⨯网格的所有方格中放入围棋子，每个方格放1枚棋子，要求每行中的白色棋子的数目互不相等，每列中的白色棋子的数目都相等，那么这个66⨯网格中共有( )枚黑A.18B.14C.12D.1027.一块木板上有13枚钉子（如图1所示）.用橡皮筋套住其中的几枚钉子，可以构成三角形，正方形，梯形等等（如图2).请回答：可以构成()个正方形.A.9B.10C.11D.1228.在如图中，一共能数出()个含有“☆”的长方形.A.8B.10C.12D.1429.如图，木板上有10根钉子，任意相邻的两根钉子距离都相等，以这些钉子为顶点，用橡皮筋可套出()个正三角形.A.6B.10C.13D.1530.以平面上任意4个点为顶点的三角形中，钝角三角形最多有()个.A.5B.2C.4D.331.图中，有()个三角形.A.13B.15C.14D.1632.图中共有()个三角形.A.10B.9C.19D.1833.两个小三角形不重叠放置可以拼成一个大三角形，那么这个大三角形不可能由()拼成.A.两个锐角三角形B.两个直角三角形C.两个钝角三角形D.一个锐角三角形和一个钝角三角形34.将长方形ABCD对角线平均分成12段，连接成如图，长方形ABCD内部空白部分面积总和是10平方厘米，那么阴影部分面积总和是()平方厘米.A.14B.16C.18D.2035.在桌面上，将一个边长为1 的正六边形纸片与一个边长为1的正三角形纸片拼接，要求无重叠，且拼接的边完全重合，则得到的新图形的边数为()A.8B.7C.6D.536.用210个大小相同的正方形拼成一个长方形，不同的拼法有()种.A.2B.4C.6D.837.一个长方形由15个小正方形拼成，如图所示，若这个长方形的周长是64cm，则它的面)cm.积为(2A.960B.256C.240D.12838.如图，每条边都相等，每个角都是直角，则根据信息，求下图的面积为()平方厘米.A.16B.20C.24D.3239.如图，四边形ABCD为长方形，四边形CDEF为平行四边形.下面四种说法中正确的是()A.甲的面积比乙的面积大B.甲的面积比乙的面积小C.只有当丙、丁两部分面积相等时，甲、乙两部分面积才相等D.甲、乙两部分面积总是相等的，与丙、丁两部分面积的大小无关40.如图，正方形ABCD的边长是10厘米，长方形EFGH的长为8厘米，宽为5厘米.则阴影部分的甲与阴影部分乙面积的差是()平方厘米.A.40B.50C.60D.8041.如图，线段BE将长方形ABCD分成M、N两个部分，如果M部分比N部分的面积小80l 平方厘米，那么AE的长是()A.24厘米B.21厘米C.20厘米D.14厘米42.如图，一个33的正方形网格，如果小正方形边长是1，那么阴影部分的面积是()A.5B.4C.3D.243.如图所示，四边形BCDE 为平行四边形，AOE ∆的面积为6，求BOC ∆的面积.( )A.3B.4C.5D.644.如图，M 为平行四边形ABCD 的边BC 上的一点，且:2:3BM MC =，已知三角形CMN的面积为245cm ，则平行四边形ABCD 的面积为( 2)cm .A.30B.45C.90D.10045.如图，长方形ABCD 中的AE 、AF 、AG 、AH 四条线段把此长方形面积五等分，又长方形长20厘米、宽12厘米，那么三角形AFG 的面积AFG S ∆等于( )平方厘米.A.41.2B.43.2C.43.1D.42.346.在等腰梯形ABCD 中，AB 平行于CD ，6AB =，14CD =，AEC ∠是直角，CE CB =，则2AE 等于( )A.84B.80C.75D.6447.下面的四个图形中，第()幅图只有2条对称轴.A. B.C. D.48.下面图形中，恰有2条对称轴()A. B. C. D.49.在如图的阴影三角形中，不能由右图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B.C. D.50.在下面的阴影三角形中，不能由图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B. C. D.参考答案与试题解析一.选择题（共50小题）1.图中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道()条线段的长度，才可以计算出这个八边形的周长.A.4B.3C.5D.10【解析】如上图，把线段①平移到②的位置可以组成一个大长方形，大长方形的4条边，对边相等，所以只需知道相邻两条边的长度，③=④，所以只需知道1条线段的长度，所以求八边形的周长需要知道：213+=条线段的长度.故选：B.2.如图中阴影部分是正方形，最大长方形的周长是()厘米.A.22B.26C.36D.无法确定【解析】+⨯=(94)226答：最大长方形的周长是26厘米.3.如图，由6个边长为3厘米的小正方形拼成的图形，它的周长是()厘米.A.36B.39C.42D.45【解析】3412⨯=（厘米）326⨯=（厘米）+⨯+(126)26366=+=（厘米）42答：它的周长是42厘米.故选：C.4.把一个直径是4厘米的圆分成两个完全相等的半圆，这两个半圆的周长之和是()A.12.56厘米B.16.56厘米C.20.56厘米D.24.56厘米【解析】(3.14424)2⨯÷+⨯=+⨯(6.284)210.282=⨯=（厘米）20.56答：这两个半圆周长之和是20.56厘米.故选：C.5.如图，有8条线段，至少要分别测量编号为()的三条线段的长度，才能求出这个图形的周长.A.①②⑤B.①②③C.①②⑦D.②③⑦【解析】由图形可知，④+⑥的线段补给⑧所在的长方形边的虚线部分，⑦-⑤等长线段的补给③所在边的虚线部分，这样就构成了一个完整的长方形，原图形的周长就是答长方形的周长2+个⑤的线段总长，所以图形的周长只要知道①②⑤即可求得.故选：A.6.如图，是一个台阶的侧面（线段AC，BC，AB的长依次为5米、12米、13米）要在台阶上面铺上红地毯，且上下各多铺出两米，需要地毯的长度是()米.A.17B.18C.20D.21【解析】12522++⨯=++1254=（米)21答：需要地毯的长度是21米.故选：D.7.如图，正方形被一条曲线分成了A、B两部分，下面第()种说法不正确？A.如果a b>，那么A的周长大于B的周长B.如果a b<，那么A的周长小于B的周长C.如果a b=，那么A的周长等于B的周长D.不管a、b哪个大，A、B的周长总是相等【解析】A的周长=曲线长+正方形边长2b a⨯+-B的周长=曲线长+正方形边长2a b⨯+-所以A、B、C选项都是正确的，错误的是D.8.如图是用3个长8厘米、宽3厘米的长方形拼成的，这个图形的周长是()A.66厘米B.48厘米C.45厘米【解析】8631⨯-⨯483=-=（厘米）45答：这个图形的周长是45厘米.故选：C.9.图中多边形每相邻两条边都互相垂直，若要计算起其周长，那么至少要知道()边长.A.6B.5C.4D.3【解析】根据题干分析可得：这个图形的横着的边长之和是：2b；竖着的边长之和是：22+；a c所以这个图形的周长是：2222()++=++，故计算这个图形的周长至少需要知道3a b c a b c条边，故选：D.10.一个长方形花园长是30米，宽是10米，沿着花园走两圈，共走了()A.45米B.90米C.160米D.200米【解析】(3010)22160+⨯⨯=（米)故选：C.11.把如图的长方形用一条曲线分成甲、乙两个图形，甲图与乙图的周长相比，()A.甲图的长B.乙图的长C.甲图与乙图同样长【解析】因为，甲图形的周长是：AB BC AC++，乙图形的周长是：DC AD AC++，而AB CD=，AD BC=，所以，甲、乙两个图形的周长相等；故选：C.12.如图，在由11⨯的正方形组成的网格中写有2015四个数字（阴影部分），其边线要么是水平或竖直的直线段，要么是连接11⨯的正方形相邻两边中点的线段，或者是11⨯的正方形的对角线，则图中2015四个数字（阴影部分）的面积是()A.47B.1472C.48D.1482【解析】据分析可知：将小三角形移到空白处补全完整正方形，共47.5个，所以阴影部分的面积是1 472；故选：B.13.如图中，正八边形ABCDEFGH的面积为1，其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积()A.12B.23C.35D.58【解析】根据分析，将图中阴影部分进行等积变形，由图不难发现，阴影部分和空白部分的面积刚好相等，正八边形中阴影部分的面积占：1 2故选：A.14.如图，大正方形的边长为14，小正方形的边长为10，阴影部分的面积之和是()A.25B.40C.49D.50【解析】根据分析，如下图所示，图①逆时针旋转90︒，阴影部分可拼成一等腰直角三角形，214449S=÷=故选：C.15.大、中、小三个正方形，边长都是整数厘米，小正方形的周长比中正方形的边长小，把这两个正方形放在大正方形上（如图），大正方形露出的部分的面积是10平方厘米（图中阴影部分）.那么，大正方形的面积是()平方厘米.A.25B.36C.49D.64【解析】根据分析，一条阴影部分的面积为1025÷=平方厘米.因为都是整数，所以只能为15⨯.故，大正方形面积(15)(15)6636=+⨯+=⨯=平方厘米.故选：B.16.如图，大正六边形内部有7个完全一样的小正六边形，已知阴影部分的面积是180平方厘米.那么大正六边形的面积是()平方厘米.A.240B.270C.300D.360【解析】如图所示，将图分割成面积相等的小正三角形，显然，图中的空白部分的面积和等于3个小正六边形.而阴影部分由6个小正六边形组成，所以，大正六边形是由9个小正六边形组成的.一个小正六边形的面积为：180630÷=（平方厘米），大正六边形的面积为：309270⨯=（平方厘米），故选：B.17.如图所示，在58⨯的方格中，阴影部分的面积为237cm .则非阴影部分的面积为( 2)cm .A.43B.74C.80D.111【解析】如图，阴影部分占了18.5个格，面积为237cm ，每格的面积是：23718.52()cm ÷=；非阴影就分占21.5格，其面积是：221.5243()cm ⨯=；答：则非阴影部分的面积为243cm ；故选：A .18.图中，将两个正方形放在一起，大、小正方形的边长分别为0l ，6，则图中阴影部分面积为( )A.42B.40C.38D.36【解析】1010666(106)210102⨯+⨯-⨯+÷-⨯÷ 100364850=+--38=答：阴影部分的面积是38.故选：C.19.下图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB、BC、CD、DA的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn，那么，m n+的值等于()A.5B.7C.8D.12【解析】由以上可知，两个阴影面积比为11:3:2 23=，325+=.故选：A.20.有5个长方形，它们的长和宽都是整数，且5个长和5个宽恰好是1~10这10个整数；现在用这5个长方形拼成1个大正方形，那么，大正方形面积的最小值为()A.169B.144C.121D.100【解析】如图所示，，于是可得：正方形的边长为11，则其面积为1111121⨯=.答：大正方形面积的最小值为121.故选：C.21.一个梯形的上底增加2厘米，下底减少2厘米，高不变，它的面积与原面积相比( ) A.变大了 B.变小了C.不变D.高不知道，所以无法比较【解析】因为梯形的面积=（上底+下底）⨯高2÷，若“上底增加2厘米，下底减少2厘米，高不变”则（上底+下底）的和不变，且高不变，所以梯形的面积不变. 故选：C .22.已知图中正方形的两个顶点正好是两个等腰直角三角形斜边上的中点，小等腰直角三角形与正方形中的圆面积相等，请问正方形中的阴影面积与大等腰直角三角形面积的比值是( )A.13B.12C.1D.32【解析】设小等腰三角形的边长是a ，大等腰三角形的边长为b ， 2a 2b 则正方形的面积是22222222()(222a b a b a b ++=+=小等腰三角形与大等腰三角形的面积和：2222222a b a b ++=又因小等腰直角三角形与正方形中的圆面积相等，所以正方形中的阴影面积与大等腰直角三角形面积相等. 所以它们的比值是1. 故选：C .23.如图，梯形ABCD 中，//AB DC ，90ADC BCD ∠+∠=︒，且2DC AB =，分别以DA 、AB 、BC 为边向梯形外作正方形，其面积分别为1S ，2S ，3S ，则1S ，2S ，3S 之间的关系是下列选项中的( )A.123S S S +>；B.132S S S +=；C.132S S S +<；D.无法确定.【解析】过点A 作//AE BC 交CD 于点E ，因为//AB DC ，所以四边形AECB 是平行四边形，所以AB CE =，BC AE =，BCD AED ∠=∠，因为90ADC BCD ∠+∠=︒，2DC AB =，所以AB DE =，90ADC AED ∠+∠=︒，所以90DAE ∠=︒那么222AD AE DE +=，因为21S AD =，222S AB DE ==，223S BC AE ==，所以213S S S =+. 故选：B .24.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片；第二次在这个小正三角形纸片四周再放三张纸片；第三次在第二次摆好的图形四周再摆放纸片；⋯摆放要求是：每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合，且纸片之间除边之外，无重合（见图）.第20次摆放后，该图形共用了正三角形纸片( )张.A.571B.572C.573D.574【解析】根据分析可得，第20次摆放后，该图形共用：++++⋯+⨯-13693(201)=++++⋯+136957=+⨯-÷+(357)(201)21=+5701=（个)571答：第20次摆放后，该图形共用了正三角形纸片571张.故选：A.25.在88⨯网格的所有方格中放入黑白两种围棋子，每个方格放一枚棋子，要求每行中的白色棋子的数目互不相同，每列中的白色棋子的数目相等，那么这个88⨯网格中共有( )枚黑色棋子.A.42B.32C.22D.12【解析】由分析得+++++++=（枚)0123567832⨯-=（枚)883232故选：B.26.在66⨯网格的所有方格中放入围棋子，每个方格放1枚棋子，要求每行中的白色棋子的数目互不相等，每列中的白色棋子的数目都相等，那么这个66⨯网格中共有()枚黑色围棋子.A.18B.14C.12D.10【解析】每行的数目可以为0~6个，每列都相等，所以一定是6的倍数，++++++=，012345621如果去掉3，那么剩下的数：21318-=正好是6的倍数，所以，白棋子有18个，则，黑色围棋子有：661818⨯-=（个)故选：A.27.一块木板上有13枚钉子（如图1所示）.用橡皮筋套住其中的几枚钉子，可以构成三角形，正方形，梯形等等（如图2).请回答：可以构成()个正方形.A.9B.10C.11D.12【解析】第一种正方形有5个，第二种正方形有4个，第三个正方形有1个，第四种正方形有1个，共11个.故选：C.28.在如图中，一共能数出()个含有“☆”的长方形.A.8B.10C.12D.14【解析】根据分析可得，共有：6612+=（个)；答：图中，一共能数出12个含有“☆”的长方形.故选：C.29.如图，木板上有10根钉子，任意相邻的两根钉子距离都相等，以这些钉子为顶点，用橡皮筋可套出()个正三角形.A.6B.10C.13D.15【解析】单个的三角形有9个，4个三角形组成的大三角形3个，最外面的最大的三角形1个，共有：93113++=（个)答：用橡皮筋可套出13个正三角形. 故选：C .30.以平面上任意4个点为顶点的三角形中，钝角三角形最多有( )个. A.5B.2C.4D.3【解析】如图，平面上任意4点构成了4个钝角三角形： ABC ∆、ABD ∆、ACD ∆、BCD ∆，所以以平面上任意4个点为顶点的三角形中，钝角三角形最多有4个. 故选：C .31.图中，有( )个三角形.A.13B.15C.14D.16【解析】由题意，由一个小三角形构成的，有6个；由两个小三角形构成的，有3个；由三个小三角形构成的，有6个；大三角形1个，所以三角形的个数为636116+++=个，故选：D .32.图中共有( )个三角形.A.10B.9C.19D.18【解析】根据题干分析可得：88218++=（个)，答：图中一共有18个三角形.故选：D.33.两个小三角形不重叠放置可以拼成一个大三角形，那么这个大三角形不可能由()拼成.A.两个锐角三角形B.两个直角三角形C.两个钝角三角形D.一个锐角三角形和一个钝角三角形【解析】因为拼在一起的两个小三角形一定有两条边共线，这时能组成一个平角，A、因为两个锐角的和小于180度，所以，两个锐角三角形不可能拼成一个大三角形；B、因为9090180︒+︒=︒，所以两个直角三角形能拼成一个大三角形；C、因为钝角+锐角有可能等于180︒，所以两个钝角三角形可能拼成一个大三角形；D、因为钝角+锐角有可能等于180︒，所以两个钝角三角形可能拼成一个大三角形；故选：A.34.将长方形ABCD对角线平均分成12段，连接成如图，长方形ABCD内部空白部分面积总和是10平方厘米，那么阴影部分面积总和是()平方厘米.A.14B.16C.18D.20【解析】设把中间最小的空白长方形的面积看作单位1ab=，那么与它相邻的阴影部分的面积就是2233a b ab ab⨯-==，同理，相邻的空白部分的面积就是55ab=，依此规律，面积依次下去为7，9，11，则空白部分的面积总和是15915++=，而实际空白部分面积总和是10平方厘米，可得单位1的实际面积是210153÷=（平方厘米）；那么阴影部分面积总和是：371121++=，则实际面积是：221143⨯=（平方厘米）；答：阴影部分面积总和是14平方厘米.故选：A.35.在桌面上，将一个边长为1 的正六边形纸片与一个边长为1的正三角形纸片拼接，要求无重叠，且拼接的边完全重合，则得到的新图形的边数为()A.8B.7C.6D.5【解析】180(62)6︒⨯-÷18046=︒⨯÷120=︒180660︒÷=︒12060180︒+︒=︒所以，拼接后的图形是：6345+-=（条)答：得到的新图形的边数为5.故选：D.36.用210个大小相同的正方形拼成一个长方形，不同的拼法有()种.A.2B.4C.6D.8【解析】2102357=⨯⨯⨯因数的总个数：(11)(11)(11)(11)16+⨯+⨯+⨯+=（个)不同的拼法有：1628÷=（种)答：不同的拼法有8种.故选：D.37.一个长方形由15个小正方形拼成，如图所示，若这个长方形的周长是64cm，则它的面积为(2)cm.A.960B.256C.240D.128【解析】64[(53)2]÷+⨯=÷6416=（厘米）4⨯⨯=（平方厘米）4415240答：它的面积为2240cm.故选：C.38.如图，每条边都相等，每个角都是直角，则根据信息，求下图的面积为()平方厘米.A.16B.20C.24D.32【解析】如右图进行分割，把图形分成了8个边长是2厘米的小正方形⨯⨯=（平方厘米）22832答：这个图形的面积是32平方厘米.故选：D.39.如图，四边形ABCD为长方形，四边形CDEF为平行四边形.下面四种说法中正确的是()A.甲的面积比乙的面积大B.甲的面积比乙的面积小C.只有当丙、丁两部分面积相等时，甲、乙两部分面积才相等D.甲、乙两部分面积总是相等的，与丙、丁两部分面积的大小无关【解析】四边形ABCD为长方形，所以BC AD=，AB CD=，因为四边形CDEF为平行四边形，所以CD EF=，=，所以AB EF两边同时加上BE，所以BF AE=；根据等底等高的三角形的面积相等，所以得出三角形CBF的面积=三角形DAE的面积，则：三角形CBF的面积-丁的面积=三角形DAE的面积-丁的面积，所以甲、乙两部分面积总是相等，与与丙、丁两部分面积的大小无关；故选：D.40.如图，正方形ABCD的边长是10厘米，长方形EFGH的长为8厘米，宽为5厘米.则阴影部分的甲与阴影部分乙面积的差是()平方厘米.A.40B.50C.60D.80【解析】⨯-⨯=（平方厘米）10108560故选：C.41.如图，线段BE将长方形ABCD分成M、N两个部分，如果M部分比N部分的面积小80l 平方厘米，那么AE的长是()A.24厘米B.21厘米C.20厘米D.14厘米【解析】设N部分的面积为x，那么M部分的面积为180x-，+-=⨯(180)3020x xx-=2180600x=+2600180x=2780x=；390N部分的面积是390平方厘米.设梯形的上底为y，1y+⨯⨯=(30)203902y+=10300390y=1090y=；9AE=-=（厘米）；30921故选：B.42.如图，一个33⨯的正方形网格，如果小正方形边长是1，那么阴影部分的面积是()A.5B.4C.3D.2【解析】通过观察可知，阴影部分的面积=长是3宽是1的长方形的面积-中间边长是1的正方形的面积.⨯-⨯=31112故选：D.43.如图所示，四边形BCDE为平行四边形，AOE∆的面积.()∆的面积为6，求BOCA.3B.4C.5D.6【解析】连接BD，因为，//BE CD ，OB OB =，所以，BOC ∆的面积等于BOD ∆的面积，又因为，//DE AC ，AB AB =，所以，ABE ∆的面积等于ABD ∆的面积，又因为，ABO ∆是ABE ∆和ABD ∆的公共部分，所以，BOD ∆的面积等于AOE ∆的面积，即，BOD ∆的面积AOE =∆的面积6=.答：BOC ∆的面积是6.故选：D .44.如图，M 为平行四边形ABCD 的边BC 上的一点，且:2:3BM MC =，已知三角形CMN的面积为245cm ，则平行四边形ABCD 的面积为( 2)cm .A.30B.45C.90D.100【解析】如图，连接AC .Q 四边形ABCD 是平行四边形，//AD BN ∴，ADM NCM ∴∆∆∽，∴24()9ADM MNC S DM S CM ∆∆==， 45MNC S ∆=Q ，20ADM S ∆∴=，:3:2CM DM =Q ，30ACM S ∆∴=，50ADC S ∆∴=，2100ADC ABCD S S ∆∴==平行四边形，故选：D .45.如图，长方形ABCD 中的AE 、AF 、AG 、AH 四条线段把此长方形面积五等分，又长方形长20厘米、宽12厘米，那么三角形AFG 的面积AFG S ∆等于( )平方厘米.A.41.2B.43.2C.43.1D.42.3【解析】由题意可知2012485ABE AEF AGH ADH AFCG S S S S S ∆∆∆∆⨯======四边形， BE EF ∴=，DH HG =，Q 1482BE AB =g g ， 8BE EF ∴==，20164CF =-=，Q 1482DH AD =g g ， 4.8DH HG ∴==， 2.4CG =，14 2.4 4.82FGC S ∆∴=⨯⨯=， 48 4.843.2AFG S ∆∴=-=，故选：B .46.在等腰梯形ABCD 中，AB 平行于CD ，6AB =，14CD =，AEC ∠是直角，CE CB =，则2AE 等于( )A.84B.80C.75D.64【解析】如图，连接AC ，过点A 作AF CD ⊥于点F ，过点B 作BG CD ⊥于点G ，则AF BG =，6AB FG ==，4DF CG ==.在直角AFC ∆中，22222210100AC AF FC AF AF =+=+=+，在直角BGC ∆中，222222416BC BG GC AF AF =+=+=+，又CE CB =Q ，90AEC ∠=︒，22222100(16)84AE AC EC AF AF ∴=-=+-+=，即284AE =.故选：A .47.下面的四个图形中，第( )幅图只有2条对称轴. A. B. C. D.【解析】如果沿某条直线对折，对折的两部分是完全重合的，那么就称这样的图形为轴对称图形，这条直线叫做这个图形的对称轴.观察易知，符合题意的是C.故选：C.48.下面图形中，恰有2条对称轴()A. B. C. D.【解析】根据轴对称图形的定义，可得：A有4条对称轴，B没有对称轴，C有2条对称轴，D有1条对称轴.故选：C.49.在如图的阴影三角形中，不能由右图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B.C. D.【解析】根据分析，可以逆向思维，可以将题中的阴影三角形经过旋转、平移，长直角边旋转和短直角边旋转后得到的图形，不难看出，只有A选项是不可能出现的.图中图中①、②、③三边应为顺时针关系，A不合要求.故选：A.50.在下面的阴影三角形中，不能由图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B. C. D.【解析】解析：由图可知：A、C、D都可由原三角形经过旋转和平移得到，而B选项必须经过对称才能与原三角形重合，故选：B.。