圆单元知识结构图
圆的认识知识结构图

《圆的认识》单元知识点1、圆的认识(1) 直径是圆中所有线段中最长的一条。
(2) 半径和直径的关系:同一个圆里,直径是半径的两倍,半径 是直径的一半。
(3) 在同一个圆里,有无数条半径,所有半径的长度都相等。
(4) 在同一个圆里,有无数条直径,所有直径的长度都相等。
(5) 画圆时,圆规针尖固定的一点是圆心,圆规两脚之间距离是 半径。
圆心确定圆的位置,半径确定圆的大小、知识结构图广 圆各部分名称(圆心、直径、半径) 圆的认识 < 圆的画法、对称轴 圆的周长圆的认识r推导过程(渗透转化思想)圆的面积2 . . 2圆面积=n r X r= n r 。
即:S=n r 与圆相关的计算二、核心知识点半圆的周长、面积计算圆的周长=圆周率x 直径=圆周率x 半 径 X 2 (C =n d 或 C = 2 n r ) 组合图形求面积(6) 圆是轴对称图形,有无数条对称轴,对称轴就是直径所在的直线(7) 正方形里最大的圆:圆心是对角线交点,半径是正方形边长的一半。
(8) 长方形里最大的圆:圆心是对角线交点,半径是长方形宽的一半。
2、圆的周长(1) 圆周率:任何一个圆的周长除以它直径的商都是一个固定的数,我们把它叫做圆周率,用字母n表示。
n是一个无限不循环小数,n~ 3.14。
(2) 圆的周长二圆周率X直径二圆周率x半径X 2 (C=n d或C= 2(3) 半圆的周长二圆周长的一半+直径(C半圆二n d宁2+ d, C半圆二n r + 2r (4)常用数据(略,自己背诵)(5)同一个圆里,圆的周长是直径的n倍,圆的周长是半径的2 n倍。
3、圆的面积(1) 圆面积公式的推导过程把圆分成若干等份,剪开后,拼成了一个近似的长方形。
长方形的面积与圆的面积相等;长方形的长相当于圆周长的一半,宽相当于圆的半径。
因为:长方形面积二长X宽,所以:圆面积二n r X r= n r2。
即:S=n r2。
要求圆的面积只要知道圆的半径或者知道圆的半径的平方。
24--圆复习

于P点,交AB、BC于E、F,则△BEF的周长是_2_c_m__.
G E
FH
三.正多边形:
A
B
1叫.做中这心个:正一多个边正形多的边中形心外.接圆的圆心F O
2.半径:正多边形外接圆的半径叫做这
个正多边形的半径.
直线与这个圆相离. (2) 相切: 一条直线与一个圆只有一个公共点,叫
做直线与这个圆相切. (3) 相交: 一条直线与一个圆有两个公共点,叫
做直线与这个圆相交.
切线长定理:
从圆外一点引圆的两条切线,它们 的切线长相等;这点与圆心的连线平分 这两条切线的夹角。
.A
. O . B
∵PA、PB为⊙O的切线 ∴PA=PB, P ∠APO= ∠BPO
三角形的内心就是三角形各角平分线的交点.
不在同一直线上的三点确定一个圆.
3.如图,是某机械厂的一种零件平面图.
(1)请你根据所学的知识找出该零件所在圆的 圆心(要求正确画图,不写做法,保留痕迹).
(2)若弦AB=80cm,AB的中点C到AB的距离是 20cm,求该零件所在的半径长.
基础题:
1.既有外接圆,又内切圆的平行四边形是正__方__形__. 2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
角的计算常要连, 遇到直径想直角,
构成等腰解疑难; 灵活应用才方便。
熟练掌握以下的结论
设a、b、c分别为ABC中A、B、C的对边,面积为S,
则内切圆半径(1)r s ,其中p 1(a b c);
p
2
(2)C 90,则r 1(a b c) 2
r
圆知识结构
《圆》知识结构.圆周角定理
圆周角定理:
C O A B C D O A B C
如左图: AB AB ACB 1 AOB 2
1同弧所对的圆周角等于
所对圆心角的一半 .
圆周角定理
2同弧(等弧)所对的
圆周角相等 .
如左图: AB AB ACB ADB
如左图:
A
B
相交圆定理: 相交两弦的连心线 垂直平分公共弦
O1
如左图:
O2
两圆相交于AB两点 则O1 , O2垂直平分AB
B A B
平行弦定理: 夹在平行弦间 的弧相等
C
如左图:
D
若弦AB // CD 则 AC BD
O
弦切角定理: 弦切角等于所夹弧 所对的圆周角 .
A
E
D
如左图 若AB为O的切线且 C为切点
C
B
则BCD CED
《圆》知识结构.补充的几个定理
切线长定理: 过圆外一点作圆的 两条切线, 这一点到 两个切点之间的 距离相等
A P
如左图: 若PA, PB为O的 两条切线, 切点为 A, B 则PA PB
B
O
圆周角定理
3直径所对的圆周角是直 角 A
直角所对的弦是圆的直 径.
AB为O的直径 ACB 9线垂直于经过 切点的直径(半径)
A O
如左图: 若AB为O的切线 且C为切点
C B
则OC AB
切线的判定定理: 经过直径的一端且垂直 于直径的直线是圆的切 线
1垂直于弦的直径平分弦 ,
A
E D
并且平分弦所对的弧 .
B
圆中知识结构图

关于《圆》的知识结构整理一.主要定理及其作用:1.圆心角,弧,弦,弦心距之间的关系定理:在同圆或等圆中,如果①两个圆心角②两条弧,③两条弦④两条弦心距中,有一组量相等, 那么它们所对应的其余各组量都分别相等:(等弧一等角-一等弦……)用的最多的依据:①在同圆或等圆中,如果两个圆心角相等,那么它们所对的两条弧相等②等弧所对的圆心角相等:③在同圆或等圆中,如果两条弦相等,那么它们所对的两条弧相等④等弧所对的两条弦相等2.垂径定理:如果一条直线①过圆心;②垂直于弦:③平分弦:④平分劣弧:⑤平分优弧•只要具备其中两个条件,就可推岀其余三个结论. (直角三角形一等弧……)用的最多的依据:①垂直于弦的直径平分弦,并且平分弦所的两条弧②平分弦(非直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧.③一条弦的垂直平分线I I经过圆心,并且平分这条弦所对的两条弧④平分弧的直径过圆心的直线垂直平分这条弧所对的弦.3.圆周角定理:(1)直径所对的圆周角是直角:(2) 90°的圆周角所对的弦是直径。
(3)—条弧所对的圆周角等于它所对的圆心角的一半:(4)同弧所对的圆周角相等:(5)等弧所对的圆周角相等:(6)在同圆或等圆中,相等的圆周角所对的弧相等:(等弧——等角——直角三角形)4.切线的性质定理:圆的切线垂直于经过切点的半径(直径)。
(垂直关系)5.切线的判定定理:经过半径的外端,并且垂直于这条半径的直线是圆的切线O6.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
(等弦一-等弧一-等角)7.相切和相交两圆的性质定理:如果两圆相切,连心线必过切点。
如果两圆相交,连心线垂直平分公共弦二.主要辅助线及其作用:1.作弦心距:弦的中点.弧的中点。
2.过某一点作弦:构造相等的圆周角。
3.作直径:构造直角三角形和同弧所对的圆周角。
4.连结过切点的半径:“题中若有圆切线圆心切点连一连”。
(完整版)圆知识结构图

第二十四章《圆》小结一、本章知识结构框图二、本章知识点概括(一)圆的有关概念1、圆(两种定义)、圆心、半径;2、圆的确定条件:①圆心确定圆的位置,半径确定圆的大小;②不在同一直线上的三个点确定一个圆。
3、弦、直径;4、圆弧(弧)、半圆、优弧、劣弧;5、等圆、等弧,同心圆;6、圆心角、圆周角;7、圆内接多边形、多边形的外接圆;8、割线、切线、切点、切线长;9、反证法:假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立。
(二)圆的基本性质1、圆的对称性①圆是轴对称图形,任何一条直径所在的直线都是它的对称轴。
*②圆是中心对称图形,圆心是对称中心。
2、圆的弦、弧、直径的关系①垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
* [引申] 一条直线若具有:Ⅰ、经过圆心;Ⅱ、垂直于弦;Ⅲ、平分弦;Ⅳ、平分弦所对的劣弧;Ⅴ、平分弦所对的优弧,这五个性质中的任何两条,必具有其余三条性质,即“知二推三”。
(注意:具有Ⅰ和Ⅲ时,应除去弦为直径的情况)3、弧、弦、圆心角的关系①在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
②在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等。
③在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等。
归纳:在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量也相等。
4、圆周角的性质①定理:在同圆或等圆中,同弧或等弧所对圆周角相等,都等于这条弧所对的圆心角的一半。
②在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等。
③推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
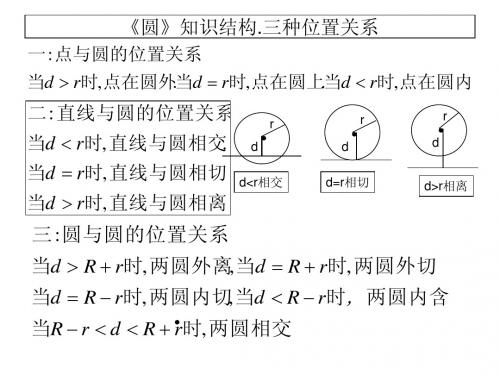
(三)与圆有关的位置关系1、点与圆的位置关系设⊙O的半径为r,OP=d则:点P在圆内d<r;点P在圆上d=r;点P在圆外d>r.2、直线与圆的位置关系设⊙O的半径为r,圆心O到l的距离为d则:直线l与⊙O相交d<r直线和圆有两个公共点;直线l与⊙O相切d=r直线和圆只有一个公共点;直线l与⊙O相离d>r直线和圆没有公共点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形面积长方形面积=长×宽
数方格圆面积÷正方形面积=3倍多一些S=πr²等积变形
圆的面积圆的面积=圆周长一半×半径
完整性各部分面积之和
圆的组合图形面积组合图形面积大面积-小面积大圆面积-小圆面积
圆环面积(R²-r²)π
方法的迁移应用
完善特征
基本特征:曲线围成的平面图形
平面图形特征圆的特征圆心:决定圆的大小
组成半径
定扇形是圆的几分之几
一部分圆心角
圆扇形半径决定扇形的大小
弧
完善对圆的认识
正方形:周长÷直径=4
平面图形周长圆:周长圆周长÷直径圆周长÷直径=πC=dπ或C=2πr
六边形:周长÷直径=3
“化曲为直”,曲线图形与直线图形周长的探索
