信号与系统自测题(第3章 参考答案)
信号与系统课后习题与解答第三章
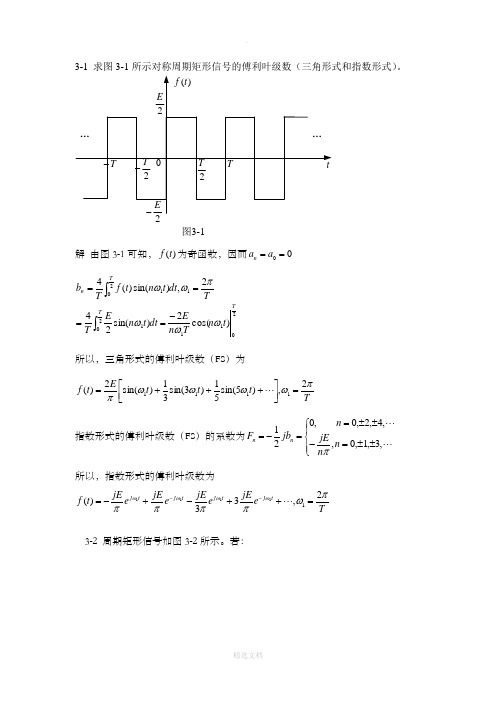
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为Te jE e jE e jEe jEt f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20= 幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
<信号与系统学习指导>第三章自测题(参考答案)

∞
∞
y (t ) = c0 + ∑ [ck cos(kω 0t ) + d k sin( kω 0t )]
k =1
求三角形式傅里叶级数的系数; (2) 如 z (t ) = a0 + c0 + x(t)
∑
k =1
∞
[ck cos(kω 0t ) + d k sin( kω 0t )] ,求信号 z(t)。
y1 (t ) = ∑ a1k e jkω0t
k = −∞ ∞
t
-T
, 则 有 k≠0 时 ,
-4/T -T 图(b’)4/T
T
a1k =
Eω 0 T 4
π
Sa(kω 0
T E kπ E ) = Sa ( ) , a10 = 2 4 2 2
设 y (t ) = ∑ a k e jkω0t ,则有 a k = a1k =
<信号与系统学习指导> P69 第三章自测题
3.1 选择题 (1)连续时间周期信号的傅里叶变换是( C ) A.连续的; B. 周期性的; C. 离散的; D. 与非周期的相同 (2)连续时间信号 x(t ) = [sin(100t ) / 50t ] cos(1000t ) ,该信号的频带为( B ) ;
2 0
(5)满足狄里赫利收敛条件时,傅里叶变换与原周期信号 x(t ) 之间(
C )
A. 处处相等;
B. 只能保证傅里叶级数系数有界;
C. 除 x(t ) 不连续的 t 值外,处处相等; D. 处处不相等,但能量相同。
(6)满足傅里叶级数收敛条件时,周期信号 x(t ) 的平均功率(
D )
A. 大于各谐波分量平均功率之和; B. 不等于各谐波分量平均功率之和; C. 小于各谐波分量平均功率之和; D. 等于各谐波分量平均功率之和。
信号与系统第3章 习题答案

第3章 傅里叶变换与连续系统的频域分析3.1 证明函数集{}0cos ,0,1,2,n t n ω=在区间()00,2πω内是正交函数集。
证明: 对任意的自然数n,m (n ≠m),有220000011cos cos [cos()+cos()]22n t m tdt n m t n m t dt ππωωωωωω=+-⎰⎰=0证毕 3.2 一个由正弦信号合成的信号由下面的等式给出:()10cos(800)7cos(1200)5cos(1600)43x t t t t πππππ=++-- (1)画出这个信号的频谱图,表明每个频率成分的复数值。
对于每个频率的复振幅,将其实部和虚部分开或者将其幅度和相位分开来画。
(2)()x t 是周期信号吗?如果是,周期是什么?(提示:按照最小公倍数计算) (3)现在考虑一个新的信号:()()5cos(1000)2y t x t t ππ=++,请问,频谱如何变化?()y t 是周期信号吗?如果是,周期是什么?解:(1)频谱图如下ωX(j ω) 05107 800π 1600π1200π107 -5振幅图(2)()x t 三项都是周期信号,周期分别为1/400、1/600、1/800,所以()x t 是周期信号,周期为为1/400、1/600、1/800的最小公倍数为1/200。
(3)根据频谱的分析()y t 比()x t 多了一个频谱分量,频率为1/500,所以()y t 还是周期信号,周期为1/200和1/500的最小公倍数1/100。
3.3 求下列每个信号的傅里叶级数表示式。
(1)200j te; (2)(1)cos 4t π-⎡⎤⎢⎥⎣⎦; (3)cos 4sin 8t t +;(4)()x t 是周期为2的周期信号,且(),11t x t e t -=-<<(5)()x t ,如题图3.3所示。
题图3.3(6)()x t 是周期为4的周期信号,且sin 02()024t t x t t π≤≤⎧=⎨≤≤⎩(7)2sin tω)(ωϕ800π1200π4π-3π相位图解(1)该信号为虚指数信号,自身就是指数级数,频0200ω=,周期100T π=三角级数为200cos(200)sin(200)j t e t j t =+ (2)基频04πω=,周期8T = 三角级数(1)2cos cos sin 4244t t t πππ-⎡⎤⎡⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦指数级数44444422()cos sin 24422222(1)(1)44t t t tj j j j t tj j t t e e j e e j e j e ππππππππ---⎡⎤⎡⎤+-⎛⎫⎛⎫⎢⎥+=+⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎢⎥⎣⎦=-++ (3)自身为三角级数cos 4sin 8t t +,基频04ω=,周期2T π=指数级数44888448()cos 4sin8222222j t j t j t j t j t j t j t j t e e j e e je e e je t t -----+-+=+=++-(4)周期T=2;基频0ωπ=11011 1.17522t e e a e dt ----===⎰11212(1)()cos()21()n t n e e a e n t dt n ππ----+==+⎰ 11212()(1)sin()21()n t n e e n b e n t dt n πππ-----==+⎰ 三角级数:1() 1.175[cos()sin()]nn n x t an t b n t ππ∞-=++∑1(1)11111(1)()22(1)2(1)jn jn k t jn t n e e e e F e e dt jn jn πππππ+-+-------===++⎰ 指数级数:11(1)()()2(1)k jntjn tnn n e e x t F ee jn ππ-∞∞=-∞=-∞--==+∑∑(5)由图可知,周期T=2;基频0ωπ=,且该信号为奇信号00n a a ==11022sin()(1)n n b t n t dt n ππ-==-⎰三角级数:111122(1)()(1)sin()sin()n n n n x t n t n t n n ππππ-∞∞-==-=-=∑∑111(1)2n n n F jb n π-=-=- 指数级数:11()(1)jntn jn t n n n x t F ee n ππ∞∞-=-∞=-∞==-∑∑ (6)周期T=4;基频02πω=2001sin()04a t dt π==⎰ 21sin()cos(/2)2n a t n t dt ππ==⎰⎪⎩⎪⎨⎧-为偶数为奇数n 0n ,)n 4(42π201sin()sin(/2)2n b t n t dt ππ==⎰0 三角级数:11()[cos(/2)n n x t a n t ππ∞==+∑/22/2202sin(/2)21sin()(4)402jn jn t n j n e n F t e dt n n πππππ--⎧≠±⎪==-⎨⎪=±⎩⎰指数级数: ()jntnn x t F e∞=-∞=∑(7)21cos(2)sin 2t t -=2211()24j tj t e e -=-+三角级数为0211,22a a ==-,其他系数为0 指数级数: x(t)=2211()24j tj t e e --+ 3.4 给定周期方波()x t 如图题图3.4所示,求该信号的傅里叶级数(包括三角形式和指数形式)。
《信号与系统》第三章习题解答

Chapter 3 3.15
Problem Solution
1 ω ≤ 100 H ( jω ) = 0 ω > 100
x(t ) , T = π/ 6 S y (t ) = x(t ) →
For what values of k is guaranteed that ak = 0 ?
k =−∞
分别如图2和图3 两个子系统的频率响应 H1 ( jω)和 H2 ( jω)分别如图2和图3 所示。 所示。试求该系统的输出信号 y ( t ) 。
x( t )
1
0
H1 ( jω)
+
−
H1 ( jω)
H2 ( jω)
y( t )
ω
H1 ( jω)
2
图1
H2 ( jω)
0 −1
ω
图2
+π / 2
Chapter 3 3.13 Consider a continuous-time LTI system
Problem Solution
H ( jω ) =
sin (4ω )
ω
1 0 ≤ t < 4 x(t ) = −1 4 ≤ t < 8
T =8
y (t ) =
k = −∞
∑
∞
ak H ( jkω 0 )e jkω 0t = 0
+∞
sin πt πt
n = −∞
∑ x (t − 3n )
1
Suppose we are given
1 -1 < t < 1 x1 (t ) = 0 others
2π 2 sin 2 3 cos 2π t y (t ) = + π 3 3
北理工-信号与系统-第三版-第三章-作业参考答案
k
| u[k ] | ,有界
是非稳定系统
(e) 显然n<0时,h[n]=0,所以是因果系统;
k
| h[k ] | | u[k ] / n | ,无界
k
是非稳定系统
(f) 显然n<0时,h[n]=0,所以是因果系统;
| h[k ] |
(d)
y[n] x[n] h[n]
k
[k n ] [n k n ]
1 2
[n n1 n2 ]
3.11在LTI离散时间系统中 已知x[n]=u[n]时的零状态响应(单位阶跃响应)为s[n],求单位抽样响应h[n]; 已知h[n],求s[n].
y[n] - 4y[n-1] =2x[n]+3x[n-1];
令x[n]=δ[n],则有 h[n] – 4h[n-1] =2 δ[n]+3 δ[n-1];当n<0时,h[n]=0,得h[0]=2,h[1]=11,
特征方程为 λ-4=0, 得λ=4,
h[n]=c(4)nu[n],由h[1]=4c=11,c=11/4得 h[n]=(11/4)(4)nu[n-1]=11 (4)n-1u[n-1],考虑h[0]=2=2 δ[n],得 h[n]=2 δ[n]+11 (4)n-1u[n-1]。(n>0的解) (b).据图有同(a)一样的结果…。 (c).据图 y[n]=3y[n-1]- 2y[n-2]+ x[n]+2x[n-1]+x[n-2] ,即差分方程为 y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求
信号与系统课后习题与解答第三章
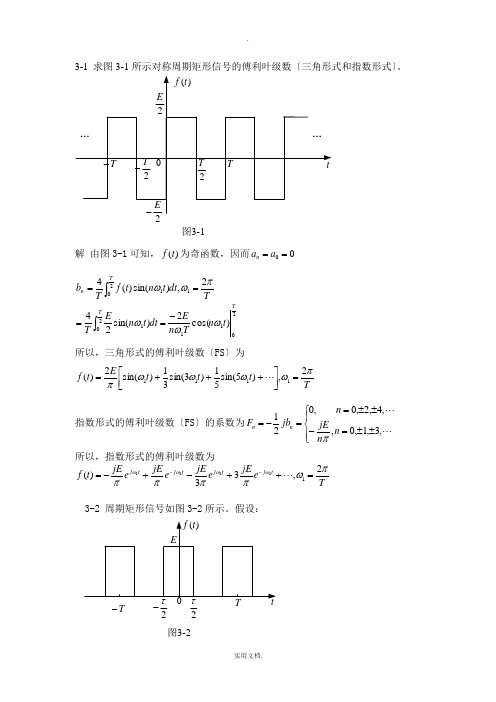
3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
假设:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕,频率单位以kHz 表示; 〔2〕)(2t f 的谱线间隔和带宽; 〔3〕)(1t f 与)(2t f 的基波幅度之比; 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。
西交版信号与系统习题答案-第三章

第三章习题答案3.1 计算下列各对信号的卷积积分()()()y t x t h t =*:(a)()()()()t t x t e u t h t e u t αβ==(对αβ≠和αβ=两种情况都做)。
(b)2()()2(2)(5)()t x t u t u t u t h t e =--+-=(c)()3()()()1t x t e u t h t u t -==-(d)5,0()()()(1),0t t te t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e)[]()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f)()x t 和()h t 如图P3.1(a)所示。
(g)()x t 和()h t 如图P3.1(b)所示。
图P3.1解:(a)()()0()()()(0)t ttt y t x t h t e ed e e d t βτατβαβτττ------=*==>⎰⎰当αβ≠时,()1()()t te y t e u t αβββα----=-当αβ=时,()()t y t te u t α-=(b) 由图PS3.1(a)知,当1t ≤时,252()2()22(2)2(5)021()22t t tt t y t e d e d e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰当13t ≤≤时,252()2()22(2)2(5)121()22t t t t t y t ed e d e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时,52()2(5)211()2t t t y t e d e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时,()0y t =(c) 由图PS3.1(b)知,当1t ≤时,()0y t =当1t >时,133(1)1()13t t y t e d e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知:当0t ≤时,11()tt t t y t e d e e ττ--==-⎰当01t <≤时,055(1)1014()(2)255t t t t t y t e d e e d e e e τττττ-----=+-=+--⎰⎰当1t >时,555(1)(1)111()(2)2255t t t t t t y t e e d e e e e τττ------=-=-+-⎰ (e) 如下图所示:(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦,则11()()()(2)3y t x t h t x t =*--由图PS3.1(h)知,11424()()()()(21)333tt y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g)()x t 是周期信号,由此可推知()()()y t x t h t =*也是周期的,且周期也为2。
信号与系统第三章习题部分参考答案

(w)
(14) f (t)u(t) ↔ 1 F ( jw) *[ 1 + πδ (w)]
2π
jw
(15) df (1 − t) ↔ jwF (−w)e− jw
dt t df (1 − t) ↔ jwF (−w)e− jw − F (−w)e− jw − wF ′(−w)e− jw
dt
(16) (t − 2) f (t)e j2(t−3) ↔ e− j6[F ′(w − 2) − 2F (w − 2)]
−τ τ
w
方法二 利用时域微分性质
对 f(t)求一阶导数得到
f
′(t)
=
1 τ
G2τ
(t)
−
δ
(t
+
τ
)
−
δ
(t
−
δ
)
F1 (w) = 2sa(wτ ) − 2 cos(wτ )
F1 (0) = 0
F (w) =
F1 (w) jw
+
πF1
(0)δ
(w)
=
j
2 [cos(wτ ) − sa(wτ )] w
1
− F(
jw )]
−∞
−∞
j2w 2
(12) df (t) ↔ jwF (w)
dt
df (t) + f (3t − 2)e− jt ↔ jwF (w) + 1 F ( w + 1)e j2(w+1) / 3
dt
33
(13) sa(t) ↔ πG4 (w) / 2
f
(t)
*
sa(t)
↔
π 2
F (w)G4
↔ 2π e−a⎜−ω⎜
信号与系统第三章习题答案

d (t - 1) « e- jw
\ e-2( t -1)d (t - 1) « e- jw
(8) U (t ) - U (t - 3) Q 根据傅里叶变换的线性性质可得: 1 U (t ) « p d (w ) + jw 1 U (t - 3) « e - j 3w (p d (w ) + ) jw \ U (t ) - U (t - 3) « ( 1- e - j 3w )(p d (w ) + 1 ) jw
U (t - 1) « e - jw (pd (w ) +
t 1 U ( - 1) « 2e - j 2w (pd (2w ) + ) 2 j 2w Q d (aw ) = 1 d (w ) a
\ 2e- j 2wpd (2w ) = 2pd (2w )w =0 = pd (w ) \ 2e - j 2w (pd (2w ) +
e - jtd (t - 2 ) « e - j 2(w +1)
(6) e -2( t -1)d (t - 1) Q 根据傅里叶变换的性质 f (t ± t0 ) « e ± jwt0 F ( jw ) 可得: e -2( t -1)d (t - 1) = d (t - 1) d (t ) « 1 (t = 1)
d F ( jw ) - 2 F ( jw ) dw
y ''(t ) + 4 y '(t ) + 3 y (t ) = f (t ) y ''(t ) + 5 y '(t ) + 6 y (t ) = f '(t ) + f (t )
(1) 求系统的频率响应 H(jw)和冲激响应 h(t) ; (2) 若激励 f (t ) = e-2tU (t ) ,求系统的零状态响应 y f (t ) 。 解: 方程 1:
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集? 解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
郑君里信号与系统第3章 习题解

第3章 习题解3-1. 求下列周期信号的基波角频率0ω和周期T 。
(1)()t B t A t f 6sin 4cos +=;(3)()65sin 4cost B t A t f +=; (2)()t C t B t A t f πππ5sin 3sin 2cos +-=; (4)()()2sin t t f π=;(5)()tj et f 10=;(6)()()25sin 2cos t B t A t f -=; (7)()t B eA t f tj 6sin +=-;31-3-2:已知连续时间周期信号()⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛+=35sin 432cos 2t t t f ππ。
将其表示成复指数傅立叶级数形式,求n F ,并画出双边幅度谱和相位谱。
解:由于()t f 为连续的时间周期信号。
由于题易知 T=6 1ω=3π又 ()⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛+=35sin 432cos 2t t t f ππ 即有 20=a 12=a 45=b200==a F ()2121222=-=jb a F ()221555j jb a F -=-=431F F F ==故 ()53322212t jt jjeet f ππ-+=又 n n F F -= 其双边幅度谱如图 3-2-1所示易知 43210ϕϕϕϕϕ====25πϕ-= 25πϕ=-其相位谱如图 3-2-2所示 3-3已知周期电压()⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++=33cos 42sin 4cos 22πππt t t t f ,试画其单边,双边幅度谱和相位谱。
解:由题易知 11=w π2=T210==a a 132==a b故 210==c c 132==c c 其单边幅度谱如图 3-3-120=F 11=F 22j F -= 213=Fn n F F -=故双边幅度谱如图3-3-2所示图 3-2-1图3-2-2 相位谱图 3-3-2 双边幅度谱()3cos()42cos()4cos(22ππ+-+++=tttf故有41πϕ=42πϕ-=33πϕ=其相位谱如图3-3-3所示3-4 如题图3-4所示信号,求指数形式和三角形式的傅里叶级数。
信号与系统第三章习题答案

T 0
−
T 0
e−
jnω0t dt
( ) =
1 − jnω0T
e− jnω0T
+
1 jnω0T
+
1 jnω0T 2
Te
−
jnω0
T
−1 − jnω0
e− jnω0t T 0
=
1 jnω0T
+
1 j2 n 2ω02T 2
e− jnω0T
−1 =
1 j2nπ
+
1 n 2π
2
1−
e− j2 nπ
=1 j2 nπ
n = ±1, ±2,L
∫ ∫ F0
=
1 T
T f (t ) dt = 1
0
T
T 0
1−
1 T
t
dt
=
1 2
该信号的指数型傅里叶级数为
( ) ∑∞
ft =
1 e jnω0t
n=−∞ j 2nπ
98
其频谱图如图 3.2(b)所示。
(2)由图 3.1(b)可知,其周期为T = 2π ,其频ω0 = 1,信号的解析式为:
2πn
100
即
bn
=
−
2E nπ
n为奇数
0
n为偶数
故得信号的傅里叶级数展开式为
f
(t )
=
−
2E π
sin
ω0t
+
1 sin 3
3ω 0t
+
1 sin 5
5ω 0t
+
L
+
1 n
sin
nω0 t
+
信号与系统第三章习题解答

⎧0 ⎪ = ⎨ 2E ⎪ ⎩ nπ
d F (ω ) = − jA ⎡ ⎣δ (ω + ω0 ) − δ (ω ) ⎤ ⎦ + jA ⎡ ⎣δ (ω ) − δ (ω − ω0 ) ⎤ ⎦ dω
另 f1 ( t ) = F
−1
jA − jω0t jA ⎧ d ⎫ ⎡ ⎡ F (ω ) ⎬ = − e − 1⎤ + 1 − e jω0t ⎤ ⎨ ⎣ ⎦ ⎣ ⎦ 2π 2π ⎩ dω ⎭
其频谱图如下图所示:
3-19 分析:本题意在说明:对于两频域信号,如果其幅频特性相同,但是相频特性不同则 它们对应的时域信号是不一样的。 解题过程: (a) F ( ω ) = A ⎡ ⎣ u ( ω + ω0 ) − u ( ω − ω0 ) ⎤ ⎦ ⎣ u ( ω + ω0 ) − u ( ω − ω0 ) ⎤ ⎦ , ϕ ( ω ) = ω t0 ⎡ 所以, F (ω ) = F (ω ) e
⎞ ⎡ ⎛ τ ⎞ ⎛ τ ⎞⎤ t ⎟ ⎢u ⎜ t + ⎟ − u ⎜ t − ⎟ ⎥ ⎠ ⎣ ⎝ 2 ⎠ ⎝ 2 ⎠⎦
⎛π F (ω ) = ∫ 2τ E cos ⎜ − ⎝τ 2
τ
⎞ t ⎟ e − jωt dt ⎠
⎛π ⎞ ⎛π ⎞ −ω ⎟t − j ⎜ +ω ⎟ t ⎤ E τ2 ⎡ j ⎜ ⎝τ ⎠ ⎝τ ⎠ = ∫ τ ⎢e +e ⎥ dt 2 −2 ⎢ ⎥ ⎣ ⎦
信号与系统第一、二、三章自测题解答

第一章自测题答案1.已知)()4()(2t u t t f +=,则)(''t f =(t)4δ2u(t)'+ 2.2(2)1()t t d t t δ∞-∞+⋅+-=⎰3=-⋅+⎰∞∞-dt t t t )1()2(2δ。
3.=-⎰∞∞-dt t t e tj )(0δωoj ωet 。
4.试画出下列各函数式表示的信号图形: (1)0 ),()(001>-=t t t u t f(2))]4()([3cos )(2--=t u t u t t f π在0到4区间内的6个周期的余弦波,余弦波的周期为2/3。
(3)][sin )(3t u t f π=5.已知f (t )的波形如图1.1所示,求f (2-t )与f (6-2t )的表达式,并画出波形。
答:函数表达式:f(2-t) = [u(t)-u(t-1)]+2[u(t-1)-u(t-2)] f(6-2t)=[u(t-2)-u(t-2.5)]+2[u(t-2.5)-u(t-3)]6.信号f (5-3t )的波形如图1.2所示,试画出f (t )的波形。
答:f(5-3t)左移5/3得到f(-3t),然后再扩展3倍得到f(-t),最后反褶可得到f(t)7.对于下述的系统,输入为e (t ), 输出为r (t ),T [e (t )]表示系统对e (t )的响应,试判定下述系统是否为: (1) 线性系统;(2)非时变系统;(3)因果系统;(4)稳定系统:(a) r (t )=T [e (t )]=e (t -2)线性、非时变、因果、稳定系统 (b) r (t )=T [e (t )]=e (-t )线性、时变、非因果、稳定系统 (c) r (t )=T [e (t )]=e (t )cos t 线性、时变、因果、稳定系统 (d) r (t )=T [e (t )]=a e (t )非线性、时不变、因果、稳定系统9. 一线性非时变系统,当输入为单位阶跃信号u (t )时,输出r (t )为 )1()()(t u t u e t r t --+=-,试求该系统对图1.3所示输入e (t )的响应。
信号与线性系统第三章答案(简)

3-9 求图题3-9所示各信号的傅里叶变换。
解:()()()()()()()1 222j j j ja j 1Sa e e 12b j 1j e T F E F T Tττττ---=⋅=-=--ωωωωωωωωω3-10 试求下列信号的频谱函数。
()()()()()()()()sgn()()()()t t f t e t f t t G t f t t f t e t εδε () -=--=-+=-=312234j212122113 4 2解:()()()()()()()j j e F F e Sa j ωωπδωω -+-=-=++3 121j 4 2j 223ωωω ()()()()()()F F j πδ ==-+- 34113 j j 4 j 22ωωωωω3-11 利用傅里叶变换的对称性求下列信号的频谱函数。
(1))2(π)2(π2sin )(1--=t t t f (2)()()f t G t =22解:()()()()()()F G e F Sa ω-==j2 124π1 j 2 j 2ωωωω3-12 已知信号f (t )的频谱函数F (j )如下,求信号f (t )的表达式。
()()();()()()(). 0001 j 3 j F F δεε =-=+--ωωωωωωωω解:()()()()().000j 11 3 Sa 2ππtf t e f t t == ωωω△3-13 利用傅立叶变换的微积分性质求图所示信号的频谱函数F (j )。
解:()[()cos()] 2j 2j F Sa =-ωωωω3-15 已知f (t )* f '(t ) (1-t )e -t ε(t ),求信号f (t )。
解:()()e t f t t ε-=±(b)3-17 利用频域卷积定理求下列信号的频谱函数。
()()cos ()f t t t ε=101 ω △()()()cos f t Sa t t π=22 22解:()()[()()] 00220j π1 j 2F δδ=++-+-ωωωωωωωω △()()F G G ππωω=-+ 2222 j (2)+(2)ω3-20 设f (t )为限带信号,频带宽度为 m ,其频谱F ( j )如图所示。
信号与系统(上海理工大学)智慧树知到答案章节测试2023年

第一章测试1.已知 f(t),为求 f(5-3t)则下列运算正确的是f ( -3t )右移5/3A:对B:错答案:A2. [e -2t u(t)]’ = δ(t)A:错B:对答案:A3.x(t)δ(t) = x(0),等式恒成立。
A:错B:对答案:A4.[δ(t +π)+δ(t -π)]cost在-∞到+∞区间积分值为A:0B:-2C:2D:1答案:B5.(t + 2)δ(1 - 2t )在-∞到+∞区间积分值为A:3B:1.25C:2.5D:5答案:B6.线性性质包括均匀性和稳定性两个方面A:对B:错答案:B第二章测试1.微分方程经典解的基本形式是多项式函数A:对B:错答案:B2.零状态响应是指输入为零时系统的响应A:对B:错答案:B3.当系统的初始状态为零时,LTI系统的冲激响应是指系统输入为单位冲激函数时得到的响应A:对B:错答案:A4.卷积积分满足交换律A:对B:错答案:A5.卷积积分不满足分配律A:对B:错答案:B6.描述某系统的微分方程y”(t) + 5y’(t) + 6y(t) = f(t) 的特征根为A: –2,-3B: –2,3C: 2,-3D: 2,3答案:A7.一个零状态的线性时不变系统,单位冲激响应为 h0(t),当系统激励为 f0(t)时,响应为 y0(t),且 h0(t),f0(t) 都是实函数,则当 f(t) = f0(t) – f0(t-1),h(t) = h0(t) 时的零状态响应为()。
A:f0(t) – f0(t-1)B: f0(t)* h0(t)– f0(t-1)* h0(t)C:h0(t) – h0(t-1)D:y0(t) – y0(t-1)答案:BD第三章测试1.已知f(t)<–> F(jw), 则函数tf(t)的频谱为A:dF(jw)/dwB:j·dF(jw)/jwC:-jdF(jw)/jwD:jwF(jw)答案:B2.已知f(t)<–> F(jw), 则函数(1-t)f(1-t)的频谱为-jejwdF(-jw)/dwA:对B:错答案:A3.实偶函数的频谱描述正确的是A:实部非0,虚部非0B:实部为0,虚部为0C:实部为0,虚部非0D:实部非0,虚部0答案:D4.狄利赫里条件是周期信号傅里叶级数存在的充要条件A:对B:错答案:B5.实奇函数的频谱描述正确的是A:实部非0,虚部0B:实部为0,虚部非0C:实部为0,虚部为0D:实部非0,虚部非0答案:B6.已知f(t)<–> F(jw), 则函数f(n)(t)的频谱为(jw)nF(jw)A:错B:对答案:B7.已知f(t)<–> F(jw), 则函数F(n)(jw)在n>0时的时域为(-jt)fn(t)A:错B:对答案:A8.函数sin(t)的频谱函数为A:jΠ[δ(w+1)+δ(w-1)]B:Π[δ(w+1)-δ(w-1)]C:Π[δ(w+1)+δ(w-1)]D:jΠ[δ(w+1)-δ(w-1)]答案:D9.函数jsint/t的频谱为jΠg2(w)A:错B:对答案:B10.群时延时常数的传输系统一定是无失真传输A:对B:错答案:B第四章测试1.u(t)、u(t+2)单边拉普拉斯变换之间的关系是:前者的拉普拉斯变换乘以复指数e2s可得后者A:对B:错答案:B2.已知时域函数f(t)对应的拉普拉斯变换F(s)=(s+1)/[(s+2)2(s+3)2],则f(t)当t趋向于∞时,f(t)的极限为:A:1/36B:0C:都不对D:F(s)不符合使用终值定理的条件答案:B3.F(s)=(s2+s+1)/(s2+3s+2)的拉普拉斯反变换为A:δ(t)+(e-t-3e-2t)u(t)B:(e-t-3e-2t)u(t)C:δ(t)+(-e-t+3e-2t)u(t)D:(-e-t+3e-2t)u(t)答案:A4.给出任何拉普拉斯表达式,可以直接用部分分式展开法求出其时域对应的函数A:对B:错答案:B5.二个并联电路其系统函数分别为H1(S)、H2(S),则系统总的传输函数为H1(S)H2(S)A:错B:对答案:A第五章测试1.如果系统函数H(s)有一个极点在复平面的右半平面,则可知该系统。
3信号与系统,每章课后答案第三章作业

CC43
5 -4
则 yf (t) f (t)h(t) u(t)[5etu(t) - 4e2tu(t)] 3u(t) 5etu(t) 2e2tu(t)
(3)全响应 y(t) yx (t)
2019/5/22
(2)该系统的阶跃响应 g(t)
解:设 系统的零输入相应为 yx (t)
输入为 f1(t) u(t) 系统的零状态相应为 y f (t) g(t)
y1(t) y2 (t)
yx (t) yx (t)
y f (t 3yf
) (t)
2e t u (t ) 3etu(t
C3 4 2 C3 2 y(t) yc (t) yp (t) 2e3t 4e2t t 0
2019/5/22
6
<Signal & System>By 谢睿
3-2 描述某LTI系统的微分方程为
d
2 y(t) dt 2
3
dy(t) dt
2 y(t)
h(t)
1
Rt
e L u(t)
L
(3)零状态响应
y
f
(t
)
v(t
)
h(t
)
e
t 2
[u
(t
)
u(t
2)]
1 L
e
R L
t
u(t
)
(若假设L=1,R=1)
e
t 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《信号与系统》自测题
第3章 连续时间信号与系统的的频域分析
一、填空题
1、周期信号的傅里叶级数的两种表示形式是 三角函数形式 和 指数形式 。
2、信号的频谱包括两部分,他们分别是 幅度 谱和 相位 谱。
3、从信号频谱的连续性和离散型来考虑,非周期信号的频谱是 连续 的。
4、周期信号的频谱是 离散 的。
5、时域为1的信号傅里叶变换是2()πδω。
6、已知()x t 的傅里叶变换为()X j ω,则1()(3)x t x t =的傅里叶变换为 1()33
X j ω 7、频谱函数1()[(2)(2)]2F u u ωωω=+--的原函数()f t =1(2)Sa t π。
8、频谱函数()(2)(2)F ωδωδω=-++的傅里叶反变换()f t =cos(2)t π。
9、已知()f t 的频谱函数为()F j ω,则函数
0()j t df t e dt
ω-的频谱函数为0()j F ωωω+。
10、若()f t 的频谱函数为()F j ω,则0()j t f t e ω-的傅里叶变换为0()F ωω+,()df t dt 的傅里叶变换为()j F ωω。
11、()t δ的傅里叶变换是 1 。
12、已知()x t 的傅里叶变换为()X j ω,则1()()3y t x t =的傅里叶变换为3(3)X j ω 。
13、常见的滤波器有 低通 、 高通 和 帯通 。
14、对带宽为20kHz 的信号()f t 进行抽样,其奈奎斯特间隔N T = 25 s μ;信号(2)f t 的带宽为 40 kHz ,其奈奎斯特频率N f = 80 kHz 。
15、人的声音频率为3003400Hz ,若对其无失真采样,则最低采样频率应为6800Hz 。
16、对频带为020kHz 的信号进行抽样,最低抽样频率为40kHz 。
17、无失真传输系统的频率响应函数为0()j t H j Ke
ωω-=。
二、单项选择题
1、狄里赫利条件是傅里叶级数存在的( B )。
A 、充分条件
B 、必要条件
C 、充要条件
D 、以上均否
2、当周期信号的周期增大时,频谱图中谱线的间隔( B )。
A 、增大
B 、减小
C 、不变
D 、无法确定
3、当周期信号的持续时间减少时,频谱图中谱线的幅度( B )。
A 、增大
B 、减小
C 、不变
D 、无法确定
4、当信号()f t 的带宽为ω∆,则信号(2)f t 的带宽为( C )。
A 、ω∆
B 、2ω∆
C 、12
ω∆ D 、4ω∆ 5、信号经过时移后,其频谱函数的变化为( A )。
A 、幅度频谱不变,相位频谱变化
B 、幅度频谱变化,相位频谱不变
C 、幅度频谱、相位频谱均不变
D 、幅度频谱、相位频谱均变化
6、已知信号()f t 刚好无失真通过某一系统,则信号1()2f t 能否无失真通过该系统
( A )。
A 、不能
B 、能
C 、不一定
D 、无法回答
7、信号的频带宽度与信号的持续时间成( A )。
A 、反比
B 、正比
C 、不变
D 、无法回答
8、频谱搬移后,信号的带宽( C )。
A 、增大
B 、减小
C 、不变
D 、无法回答
9、在卷积12()()*()f t f t f t =中,当1()f t 和2()f t 都是从0-开始的函数时,积分限应为
( C )。
A 、+∞
-∞⎰ B 、0-+∞⎰ C 、 0t -⎰ D 、0-∞⎰
10、系统频域分析的基础是( C )。
A 、线性特性
B 、频域卷积特性
C 、时域卷积特性
D 、频移特性
11、无失真传输系统的含义是( B )。
A 、输出信号与输入信号完全一样
B 、输出信号与输入信号相比,波形相同,起始位置不同
C 、输出信号与输入信号相比,波形不同,起始位置相同
D 、输出信号与输入信号相比,波形和起始位置都不同
12、无失真传输系统的频率特性是( B )。
A 、幅度特性和相频特性均为常数
B 、幅频特性为常数,相频特性为ω的线性函数
C 、幅度特性和相频特性均为ω的线性函数
D 、幅度特性为ω的线性函数,相频特性为常数
13、信号2(1)(1)t e t ε---的频谱为( C )。
A 、22e j ω-+
B 、22e j ω--+
C 、2j e j ωω-+
D 、2
2e j ω
--+ 14、信号(25)()j t e t ε-+的频谱为( C )。
A 、25j e j ω-
B 、25j e j ω
+ C 、12(5)
j ω++ D 、12(5)j ω-++ 15、函数2[()]t d
e t dt ε-的傅里叶变换为( C )。
A 、1
2j ω+ B 、1
2j ω-+ C 、2j j ω
ω+
D 、2j j ωω-+ 16、周期信号1
()12cos sin(3)2f t t t =++的傅里叶变换为( C
)。
A 、1
()2(3)(3)3δωδωδω+++-
B 、2()[(3)(3)]2j
πδωπδωδω++--
C 、2()2[(1)(1)][(3)(3)]2j
πδωπδωδωπδωδω+++-++--
D 、()2[(1)(1)][(3)(3)]2j
δωδωδωδωδω+++-++--
17、若()()f t F j ω↔,则()f at b -的傅里叶变换为( A )。
A 、1()b
j a F j e a a ωω- B 、1()b
j a
F ja e a ωω-
C 、1()b
j a F j e a a ωω D 、1()j b
F j e a a ωω-
18、信号2()()2()t f t t e t δε-=-的频谱为( C )。
A 、2j j ωω-
B 、212j ω--
C 、2j
j ω
ω+
D 、22j ω- 19、信号()2g t ττ
-的频谱为( B )。
A 、2()2j Sa e τ
ω
τω- B 、2()2j Sa e τ
ωτ
τω-
C 、()2j Sa e ωτ
ττω- D 、()2j Sa e ωτ
ττω
20、信号经微分后,频谱中高频分量的比重( D )。
A 、增大
B 、减小
C 、不变
D 、无法回答
21、理想低通滤波器(LPF )的频率特性为2()()H j G πωω=,输入信号为()()f t Sa t π=,输出信号()y t =( C )。
A 、2()G t π
B 、2()Sa t ππ
C 、 ()Sa t π
D 、22()G t ππ
22、如果12()()f t g t =,2()cos(4)f t t π=。
则12()()f t f t 的频谱为( D )。
A 、(4)*(4)Sa Sa ωπωπ+-
B 、2(4)Sa ωπ-
C 、2(4)Sa ωπ+
D 、(4)(4)Sa Sa ωπωπ++-
23、如下图所示系统,当输入信号为1
()1cos sin(3)2e t t t =++时的响应为(
B )。
A 、1
()12cos sin(3)2y t t t =++ B 、()12cos y t t =+
C 、1
()1cos sin(3)4y t t t =++ D 、()24cos ()y t t H j ω=+。
