趣味数学一笔画
趣味数学300题 第三章 画来画去。移来移去……
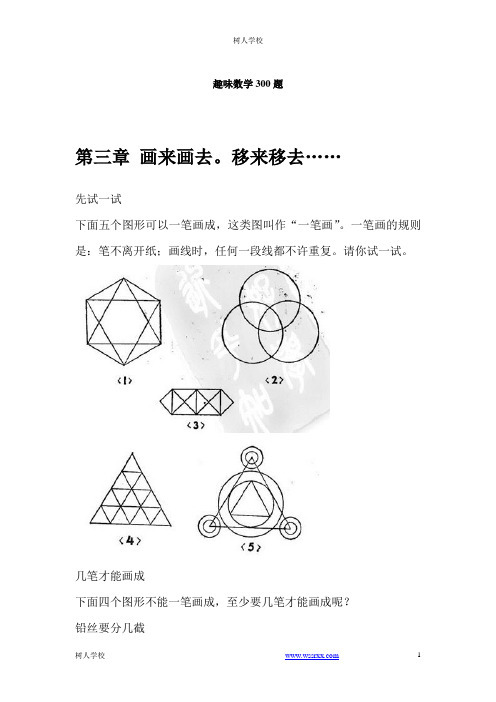
趣味数学300题第三章画来画去。
移来移去……先试一试下面五个图形可以一笔画成,这类图叫作“一笔画”。
一笔画的规则是:笔不离开纸;画线时,任何一段线都不许重复。
请你试一试。
几笔才能画成下面四个图形不能一笔画成,至少要几笔才能画成呢?铅丝要分几截在下面三个架子中,有一个只用一根铅丝就可以构成,而另外两个,要把铅丝分成几段才能构成。
请在每一个架子下注明,是用几根铅丝构成的。
擦掉哪一根线下图不能一笔画,可是,只要擦去一根线,图形就可以一笔画成。
应该擦掉哪一根线,你知道吗?走遍所有的门下图是一座房屋的平面图。
每两个相邻房间之间,都有一个门相通;除中间两个房间E和F 以外,每个房间都有门通向室外。
你能够不重复地穿过每一道门吗?提示:把每一个房间设想成一个点,室外也用一个点表示。
如果两个房间这间有门相通,设想相应的两点之间有线段连接。
画出这个图,上述问题就相当于一个“一笔画”。
十五座桥下图中有A、B、C、D、E、F六个小岛,各岛之间共有十五座桥(桥已编号)。
现在要从A 岛出发,不重复地走遍十五座桥,该怎么走呢?你是不是已经看出,这也是一笔画问题?十八世纪伟大的数学家欧拉从哥尼斯堡城的七桥入手,研究了“一笔画”问题。
因此,现代的图论著作和书籍中,都把“一笔画”称为欧拉问题,把能不重复走遍的路,称为欧拉路。
别致的画廊公园里布置了一个很别致的画廊(请看图)。
画廊分为25段,每段画廊两头的圆圈是休息处。
A处为入口,B处是出口,H处设有小吃部。
现在有一个人要不重复地看遍所有画廊,并且打算在看了8段画廊后恰好到小吃部(H处),吃点东西后,再看9段,又恰好回到小吃部(H处),最后看完剩下的8段画廊,从B处出来。
请你替这个人安排一条参观的路线。
最短路线下图是一些街道的平面图,中间九个方格是一些建筑物。
有一辆洒水车从A点出发,要往每一条街道上洒水最后仍回到A点。
洒水车在街道上必然有重复行驶,可是精心地选择行驶路线,能使重复行驶的路程尽可能少。
小学奥数一笔画课件

单击此处添加正文,文字是您思想的提炼,为了演示发布的良好效果,请言简意赅地阐述您的观点。您的内容已经简明扼要,字字珠玑,但信息却千丝万缕、错综复杂,需要用更多的文字来表述;但请您尽可能提炼思想的精髓,否则容易造成观者的阅读压力,适得其反。正如我们都希望改变世界,希望给别人带去光明,但更多时候我们只需要播下一颗种子,自然有微风吹拂,雨露滋养。恰如其分地表达观点,往往事半功倍。当您的内容到达这个限度时,或许已经不纯粹作用于演示,极大可能运用于阅读领域;无论是传播观点、知识分享还是汇报工作,内容的详尽固然重要,但请一定注意信息框架的清晰,这样才能使内容层次分明,页面简洁易读。如果您的内容确实非常重要又难以精简,也请使用分段处理,对内容进行简单的梳理和提炼,这样会使逻辑框架相对清晰。为了能让您有更直观的字数感受,并进一步方便使用,我们设置了文本的最大限度,当您输入的文字到这里时,已濒临页面容纳内容的上限,若还有更多内容,请酌情缩小字号,但我们不建议您的文本字号小于14磅,请您务必注意。单击此处添加正文,文字是您思想的提炼,为了演示发布的良好效果,请言简意赅地阐述您的观点。您的内容已经简明扼要,字字珠玑,但信息却千丝万缕、错综复杂,需要用更多的文字来表述;但请您尽可能提炼思想的精髓,否则容易造成观者的阅读压力,适得其反。正如我们都希望改变世界,希望给别人带去光明,但更多时候我们只需要播下一颗种子,自然有微风吹拂,雨露滋养。恰如其分地表达观点,往往事半功倍。当您的内容到达这个限度时,或许已经不纯粹作用于演示,极大可能运用于阅读领域;无论是传播观点、知识分享还是汇报工作,内容的详尽固然重要,但请一定注意信息框架的清晰,这样才能使内容层次分明,页面简洁易读。如果您的内容确实非常重要又难以精简,也请使用分段处理,对内容进行简单的梳理和提炼,这样会使逻辑框架相对清晰。为了能让您有更直观的字数感受,并进一步方便使用,我们设置了文本的最大限度,当您输入的文字到这里时,已濒临页面容纳内容的上限,若还有更多内容,请酌情缩小字号,但我们不建议您的文本字号小于14磅,请您务必注意。单击此处添加正文,
四年级趣味数学思维训练题50道及答案

四年级趣味数学思维训练题50道及答案(1) 【一笔画】如图所示,某小区花园的道路为一个长480米,宽200米的长方形;一个边长为260米的菱形和十字交叉的两条道路组成.一天,王大爷A 处进入花园,走遍花园的所有道路并从A 处离开.如果他每分钟走60米,那么他从进入花园到走出花园最少要用______分.(2) 【三角形】周长是12,各边长都是整数的等腰三角形有几种?长方形有几种?(3) 【一笔画】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?(4) 【图形面积】7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?(5) 【图形拼接】用“四连块”拼成一个正方形,按编号画入右边图中.A(6) 【还原问题】桃园里来了第一群猴子,吃去桃子总数的一半又半个;第二群猴子又来吃掉剩下桃子的一半又半个;第三群猴子又来吃掉剩下桃子数的一半又半个.这时桃园里还只有100个桃了.那么园中原有多少桃?(7) 【图形面积】两个正方形的面积相差29cm ,边长相差1cm .求两个正方形的面积和.(8) 【还原问题】小丽用4元买了一本《童话大王》,又用剩下的钱的一半买了一本《儿童时代》,买钢笔又用去第二次剩下的钱的一半多1元,最后还剩4元,问:小丽原有多少钱?(9) 【等比数列】从前,有一位樵夫,整天幻想着遇见神仙,求得一种不花气力就能发财的窍门.一天,有一位老人突然来到樵夫面前,对他说:“你不是想见到神仙吗?”樵夫苦苦哀求:“我在山里砍了三天柴,累的要死要活,才卖的这么几个钱.您老人家神通广大,恳求您指点,使我可以不费力气就能得到钱吧!”老人指着东边的一座石头桥说:“好吧!从现在开始,你只要从那座桥上每走一个来回,口袋里的钱都会增长一倍,但是每次回来都要付给我24个钱作为报酬.”④③②①CB A樵夫高兴的在桥上走了一个来回,他数一数口袋里的钱,果然增长了一倍.他拿出24个钱交给神仙,然后又向桥上走去,等到他第三次回来,把24个钱交给神仙后,摸一摸口袋,里面竟然一个钱都没有了.正当他焦急不安的时候,神仙按原数把钱留下飘然而去,并留下一句话:“年轻人,不劳而获可不行啊!”故事读完了,小朋友们,你能不能算出,樵夫原来有多少钱呢?(10)【鸡兔同笼】一张数学试卷,只有25道选择题.做对一题得4分,做错一题倒扣1分;如不做,不得分也不扣分.若小明得了78分,那么他做对______题,做错________题,没做__________题.(11)【正方形】把一个正方形分割为三种面积不同的小正方形,并且小正方形的个数是8.如何分?(12)【图形拼接】试将一个49 的长方形分割成两个大小相等,形状相同的图形,然后拼成一个正方形.(13)【图形分割】在一块长方形的地里有一正方形的水池(如下图).试画一条直线把除开水池外的这块地平分成两块.OA(14) 【盈亏问题】猴王带领一群猴子去摘桃,下午收工后,猴王开始分配,若大猴分5个,小猴分3个,猴王可以留10个,若大,小猴都分4个,猴王能留下20个。
小学奥数 奇妙的一笔画 精选例题练习习题(含知识点拨)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【例 3】 判断下列图a 、图b 、图c 能否一笔画.图aNML KF DECBA 图bODCBA图cGFEDCBA例题精讲知识点拨4-1-5.奇妙的一笔画【例 4】 下面图形能不能一笔画成?若果能,应该怎样画?(1)(2)(3)【例 5】 下面的图形,哪些能一笔画出?哪些不能一笔画出?【例 6】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?E CDB A【例 7】 下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?乙甲【例 8】 能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?【例 9】 下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?IHGFEDC BA【例 10】 邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【例 11】 观察下面的图,看各至少用几笔画成?(1)A ED HCF G B (2)(3)【例 12】 在3×3的方阵中每个小正方形的边长都是100 米.小明沿线段从A 点到B 点,不许走重复路,他最多能走多少米?【例 13】 有16个点排成的44 方阵。
趣味一笔画知识

一笔画知识点:1.一笔画概念:(用自己的话:一笔画出图)“”由画圆引入“一笔画”的特点:①一笔画成②笔不离纸③不重复(已画成不需重复)。
下面这三个图,同学们先尝试画一下,请3位同学上来画(要求尽量一笔画出)。
①②③大家发现这两个图都可以一笔画出来,可是这些图都比较简单,如果是复杂的图怎么画呢?也是一一尝试吗?所以今天我们学习怎么快速方便的判断图形能否一笔画。
接下来一起观察,大家有没有发现每一个图都是由点和线组成的。
那么我们想要找办法一笔画图肯定跟图中的点和线有关系的。
首先呢,老师要告诉你们这些点都是有名字的,而且呢,这个名字还是由线来命名的哦。
大家是不是很好奇呢?老师把这个点叫做双数点,这边这个叫做单数点,你们知道为什么吗?每个小朋友都有自己的想法,你们听听老师是怎么命名的。
从该点出发,有2条线画出,其实呢,就是从该点出发,发出双数条线的点叫做双数点。
那么谁可以告诉老师,为什么这个点是单数点吗?对了,因为这个图里从这个点出发,发出了3条线。
单数点的概念就是:从该点出发,发出单数条线的点叫做单数点。
到底一笔画跟双数点和单数点有什么关系呢?回过头来我们看看刚刚的图。
首先请同学们迅速的把图中的点找出来,请你在每一个点旁边写上发出线的条数。
仔细观察,谁能告诉老师这些点都是什么点?大家学的都非常快,这些点都是双数点,因为从点出发发出的线都是双数条。
这些图没有单数点,但是大家尝试过,虽然尝试的画法不一样,但是大家都一笔画出来了。
原来没有单数点的图一定可以一笔画。
而且,画时,任意一个双数点既是起点,又是终点。
刚刚讨论的3个图都没有单数点,下面我们看看有单数点的图:④这个图能不能一笔画出呢?同样的,先请同学们找出图上的点,在每一个点旁边写上线的条数。
都写好了吗?那么请个小助手上来告诉老师,哪些点是单数点,用红笔把它圈出来。
这个图上一共有几个单数点?刚刚大家尝试了,这个图可以一笔画的。
那么总结一下:只有两个单数点的图,也可以一笔画。
小学数学《一笔画》练习题(含答案)

小学数学《一笔画》练习题(含答案)什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.所谓一笔画,就是从图形上的某点出发,笔不离开纸,而且每条线都只画一次不准重复.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.判断图形能否一笔画的规律:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点.以另一个奇点作为终点;(4)奇点个数超过两个的图形,一定不能一笔画.(一) 一笔画以及多笔画【例1】 观察下面的图形,说明哪些图可以一笔画完,哪些不能,为什么?对于可以一笔画的图形,指明画法.(f)(e)(d)JIH G F ED C BAJ K IHGFED CB A分析:(a )图:可以一笔画,因为只有两个奇点A 、B ;画法为A →头部→翅膀→尾部→翅膀→嘴. (b )图:不能一笔画,因为此图不是连通图.(c )图:不能一笔画,因图中有四个奇点:A 、B 、C 、D.(d )图:可以一笔画,因为只有两个奇点;画法为:A →C →D →A →B →E →F →G →H →I →J →K →B. (e )图:可以一笔画,因为没有奇点;画法可以是:A →B →C →D →E →F →G →H →I →J →B →D →F →H →J →A.(f )图:不能一笔画出,因为图中有八个奇点.[注意]在上面能够一笔画出的图中,画法并不是惟一的.事实上,对于有两个奇点的图来说,任一个奇点都可以作为起点,以另一个奇点作为终点;对于没有奇点的图来说,任一个偶点都可以作为起点,最后仍以这点作为终点.[巩固]判断下列图a 、图b 、图c 能否一笔画.E分析:图a是一个连通的图形,图中只有点A和点F两个奇点,所以它能一笔画,其中一种画法如下:A —M—N—A—F—B—C—B—K—C—D—E—D—L—E—F.‘图b是一个不连通的图形,所以不能一笔画.图c是连通图,图中所有点都是偶点,所以能一笔画.其中一种画法如下:A—B—C—D—E—F—D—A—F —C—A.【例2】右图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达 C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析:本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C.容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和.仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C.[巩固]在六面体的顶点B和E处各有一只蚂蚁(见右图),它们比赛看谁能爬过所有的棱线,最终到达终点D.已知它们的爬速相同,哪只蚂蚁能获胜?分析:许多同学看不出这是一笔画问题,但利用一笔画的知识,能非常巧妙地解答这道题.这道题只要求爬过所有的棱,没要求不能重复.可是两只蚂蚁爬速相同,如果一只不重复地爬遍所有的棱,而另一只必须重复爬某些棱,那么前一只蚂蚁爬的路程短,自然先到达D点,因而获胜.问题变为从B到D与从E到D哪个是一笔画问题.图中只有E,D两个奇点,所以从E到D可以一笔画出,而从B到D却不能,因此E点的蚂蚁获胜.[数学小游戏] 用一笔画成四条线段把所有的点连起来,怎样画?分析:通过试画,似乎不可以画,但通过仔细观察,对照一笔画的规律,便可发现,若添上两个辅助点,就可画成.如右图:FE DCB AEDCBA我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.公式如下: 奇点数÷2=笔画数,即2n ÷2=n.【例3】 判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.IH G FED CBA 图aH G I KLJ F EDCBA 图b DC HG EFBA图c分析:图a :原图有四个奇点,所以不能一笔画,在B,D 两点之间加一条线后,图中只有两个奇点,故可以一笔画出,如图d 所示.画法:H →A →B →C →D →E →F →I →D →B →I →H →G →F .图b :原图有四个奇点,所以不能用一笔画.去掉K ,L 两点之间的连线,图中只有两个奇点,故 可以一笔画出,如图e 所示.画法:B →C →D →E →F →→J →H →G →I →A →B →K →I →L →E .图c :原图有四个奇点,所以不能用一笔画.在B ,C 两点之间加一条线后,图中只有两个奇点, 故可以一笔画出,如图f 所示.画法:A →E →D →H →A →B →F →C →G →B →C →D注意:a 、b 、c 三个图都是连通的图形,但由于每个图的奇点个数均超过两个,所以都不能一笔画.图dA BCD EFG H IH GI KLJ F EDCB A 图eDC HG EFBA图f[前铺]观察下面的图,看各至少用几笔画成?分析:(1)图中有8个奇点,因此需用4笔画成. (2)图中有12个奇点,需6笔画成. (3)图是无奇点的连通图,可一笔画成.【例4】 将下图改为一笔画.DC BA(2)(1)FEC DB A分析:图(1)中有6个奇点,因此可添上两条(或3条)边后可改为一笔画;又因为这个图中,把这6个奇点任意分为3对后,最多只有两对奇点间有边相连,因此,可去掉两条边后改为一笔画,举例如图(3)~(6).图(2)中有4个奇点,因此,可添上2条(或1条)边后改为一笔画;又因为把奇点按A 与B ,C 与D (或A 与D ,B 与C )分为两对后,每对间均有边相连,因此,可去掉两条(或1条)边后改为一笔画.举例如图(7)~(8).说明:图(6)运用了两种方法,去掉边BC ,添上边AD 与EF.(二)一笔画的实际应用【例5】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?:这个有趣的问题引起了著名数学家欧拉的注意,他证明了七桥问题中提到的走法根本不存在. 下面,我们考虑如下两个问题:(1)如果再架一座桥,游人能否走遍所有这八座桥?若能,这座桥应架在何处?若不能,请说明理由. (2)架设几座桥可以使游人走遍所有的桥回到出发地?而得到一个由四个点和七条线组成的图形(如图b).在图b 中,点A ,B ,C ,D 四个点均为奇点,显然不能一笔画出这个图形.若将其中的两个奇点改成偶点,即在某两个奇点之间连一条线,这样奇点个数由四个变为两个,此时,图形可以一笔画出.如我们可以选择奇点B ,D ,在B ,D 之间连一条线(架一座桥),如图c .在图c 中只有点A 和C 两个奇点,那么我们可以以A 为起点,C 为终点将图形一笔画出.其中一种画法为:A →C →A →B →A →D →B →D →C所以,如果在河岸B 与小岛D 之间架一座桥,游人就可以不重复地走遍所有的桥.(2)在(1)的基础上,再在另外两个奇点A 与C 之间连一条线(即架一座桥),使这两个奇点也变成偶点,如图d .那么A ,B ,C ,D 四个点均为偶点,所以图d 可以一笔画出,并且可以以任意点为起点,最后 仍回到这个点.其中一种画法为:A →C →A →C →D →A →B →D →B →A这表明:在河岸B 与小岛D 之间架一座桥后,再在小岛A 与河岸C 之间架一座桥,共架设两座桥,就可以使游人不重复地走遍所有的桥并回到出发地.[巩固]如图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?分析:用点表示小岛与河岸,用连接两点的线表示连接相应两地的桥,如图,有2个奇点,所以该图可以一笔画,即可以一次不重复地走遍这七座桥.例如右下图的走法.EDCBA【例6】 有一个邮局,负责21个村庄的投递工作,右图中的点表示村庄,线段表示道路.邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?分析:图中有两个奇点,所以该图可以一笔画,但因为邮局所在点为奇点,所以要一笔画就不可能回到邮局.又图中A,B,C,D,E,F,G,H,I,J十点均有4条线段与之相连,如果我们将上图一笔画的话,就要经过以上十点各两次,这也不满足题目的要求,所以要将这些点相连的线段去掉一些,使得与这些点相连的线段均只有两条,并且将两个奇点也变成只有两条线段与之相连,这样得到的图形即可一笔画,又只经过每个点一次,并且可以回到邮局,一种可行路线如下:邮局I JHGF E D C B A 邮局邮局【例7】 右图是某博物馆的平面图,相邻两个展厅之间有一扇门相通,每一个展厅都有一门通往馆外.问参观者能否不重复地一次穿过每一扇门?若能,请找出一条可行路径;若不能,请说明理由.如果允许关闭某一扇门,问参观者能否不重复地穿过每一扇开着的门?分析:我们把展厅A,B,C,D,E 及馆外F 看成某个图中的点,把两个展厅之间的门看作是连接表示这两个展厅的点的线.根据题中条件知,馆外F 与A ,B ,C ,D ,E 各展厅相通,这样将点F 与点A ,B ,C ,D ,E 用线连接;展厅A 与展厅B ,C ,D 相通,将点A 与点B ,C ,D 用线连接;展厅B 除与A 相通外,它还与D ,E 展厅相通,将B 与D ,E 连接;除此之外,展厅C ,D 相通,展厅D ,E 相通,将点C ,D 连接,再将点D ,E 连接(如图a).于是本题要解决的问题就变成了能否将图a 一笔画的问题.可以看出:图a 中共有六个点,其中有四个奇点,它们分别为C ,D ,E ,F ,由一笔画的规律可知,图a 不能一笔画.也就是说,参观者不能够不重复地一次穿过每一扇门.如果允许关闭某一扇门,这相当于在图a 中去掉一条线,那么参观者就有可能不重复地一次穿过每一扇门.我们知道,在图a 中有四个奇点C ,D ,E ,F 为了把图a 改成一笔画图形,我们设法减少奇点个数,使奇点数变为两个.为此,我们可以去掉一条连接两个奇点的线,如去掉E 与F 间的连线,相应的图a 就变成了图b .在图b 中,除了原来的C 和D 是奇点外,其余点全部是偶点,故图b 可以一笔画.其中一种画法为:C →F →D →E →B →F →A →B →D →A →C →D .上面的分析表明,如果关闭连接E 、F 两展厅之间的门,参观者就可以不重复地一次穿过每一扇开着的门. 本题与七桥问题类似,只是将行人过桥换成了参观者穿过每一扇门.我们将这个问题转化为一笔画问题来研究.[前铺]右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走? FFF F E C D BA EB A分析:我们将每个展室看成一个点,室外看成点E ,将每扇门看成一条线段,两个展室间有门相通表示两个点间有线段相连,于是得到下图.能否不重复地穿过每扇门的问题,变为下图是否一笔画问题.EDC BA图中只有A ,D 两个奇点,是一笔画,所以答案是肯定的,应该从A 或D 展室开始走. 【例8】 已知长方体木块的长是80厘米,宽40厘米,高80厘米(如右图),并且要求蜘蛛在爬行过程中只能前进,不能后退,同一条棱不能爬两次.请问这只蜘蛛最多要爬行多少厘米?分析:图中八个顶点均为奇点,所以不能一笔画,要使其能一笔画,至少要去掉三条棱,使上图只有两个奇点,就可以满足一笔画的条件.长方体的棱长总和一定,(80+80+40)×4=800(厘米),因此去掉的三条棱越短,蜘蛛爬过的距离就越远.所以我们去掉三条棱长为40厘米的棱,于是可知,蜘蛛爬行的最远距离为: 800-40×3=680(厘米).蜘蛛的爬行路径为:G →F →C →D →G →H →A →B →E →H(如右图).[注意]这是一个立体图形,它有八个顶点,我们把长方体的棱看作顶点与顶点之间的连线,蜘蛛只能前进不能后退,并且每一条棱不能爬两次,这实质上是一个一笔画问题.【例9】 右图是某小区的街道分布图,街道长度如图所示(单位:公里),图中各点表示不同楼的代号.一辆垃圾清扫车从垃圾站(垃圾站位于C 楼与D 楼之间的P 处)出发要清扫完所有街道后仍回到垃圾站,问怎样走路线最短,最短路线是多少公里?分析:为了少走冤枉路和节省时间,题目中要求最短路线,根据一笔画原理,我们知道一笔画路线就是最短路线.本题要求清扫车从P点出发,仍回到P 点.通过观察上图可知,图中有六个奇点,根据一笔画规律可知,清扫车想清扫完所有街道而又不走重复的路是不可能的.要使清扫车从P 点出发,最后仍回到P 点,就必须把图中所有的奇点都变成偶点,即在两奇点之间添加一条线.在实际问题中,就是清扫车在哪些街道上重复走的问题,由于每条街道的长度不同,因此需要我们考虑清扫车重复走哪条街道才使总路线最短.为使六个奇点都变成偶点,我们可以有下图中的四种方法表示清扫车所走的重复路线,其中填虚线的地方表示的是重复路线.重复的路程分别为:图a :2×2+3=7;图b :3+4×2=11;图C :3×3=9; 图d :3+6×2=15.显然,重复走的路线最短,总路程就最短.从上述计算中就可找到最短路线图,即下面四个图中的图a .408080H G F ED C BA804080H GFED CBA图b 图a图d图c在图a 中,所有点均为偶点,是一笔画图形.清扫车可按如下路径走:P →D →G →D →E →F →G →H →L →H →C →B →L →M →A →B →C →P ,全程为:(1+2+4+2)×2+3×5+2×2+3=40(公里).【例10】 邮递员李文投送邮件的街道以及街道的长度如右图所示(单位:千米),每天小李要从邮局出发,走遍所有街道后回到邮局.请你帮他设计一条最短路线,并计算出这条路线有多少千米?分析:本题仍可以用一笔画图形的方法来解决.在图a 中共有六个奇点E ,F ,G ,H ,I ,J ,把这些奇点配对,每对之间用虚线连接(如图a),其中要用到D 点,这样图中就没有奇点了,从而可以不重复地走遍所有的街道.由于邮递员李文要重复走一些路段,因此重复走的路越短越好,即添上去的重复线段的总长度越短越好.在图a 中H 与E 之间有重叠,这样势必会增加李文所走路程的长度,应作调整.经调整后,将重叠部分去掉便得图b .在图b 的圈形闭路IHGJI 中,I ,J ,G ,H 各点没有连线时是奇点,连线后变成偶点,增加长度为50×2=100千米.而如果连IJ 和HG ,增加的长度仅为10×2=20,由此可知图b 需继续作调整,改成图c ,这种连接方法是最好的,它使李文行走的路线最短.根据以上分析,为了保证添上去的线段之和最短,应遵循下面的两条原则:(1)连线不能有重叠的线段;(2)在每一个圈形闭路上,连线长度之和不能超过 这个闭路总圈长的一半.经过分析可以知道,图c 的连接方法能使邮递员李文行走路线最短,而且能保证李文从邮局出发又回到邮局.这时他的行走路线为:邮局→A →I →J →I →H →G →H →E →D →F →D →G →J →B →C →D →E →邮局 他行走的全程为: (50+15)×4+20×4+10×6+20×2=440(千米).图a图b图c[小结]本题中采用的方法叫做“奇偶点图上作业法”,用这种方法来确定最短路线比较简便实用.此方法可以用下面的口诀来描述:画出路线图,确定奇偶点;奇点对对连,连线不重叠;闭路添连线.不得过半圈.[巩固]右图是某地区街道的平面图,图上的数字表示那条街道的长度.清晨,洒水车从A 出发,要洒遍所有的街道,最后再回到A.问:如何设计洒水路线最合理? 分析:这又是一个最短路线的问题.通过分析可以知道:在洒水路线中,K 是中间点,因此必须成为偶点,这样洒水车必须重复走KC 这条边(如下左图).至此,奇点的个数并未减少,仍是6个.容易得出,洒水车必须重复走的路线有:GF 、IJ 、BC.即洒水路线如下右图.全程45+3+6=54(里).1. (例1)判断下列各图能否一笔画.图aG I H F ECD BA图bF ED CBA分析:图a 中九个点全是偶点,因此可以一笔画,其中一种画法为:A →F →B →G →C →H →D →E →H →l →→F →G →l →E →A .图b 中A ,B ,C ,D 四个点均为奇点,故不可以一笔画.图c 中,只有A,C 为奇点,故可一笔画.其中一种画法为:A →D →E →C →H →N →G →M →F →A →B →C .2. (例3)下列各图至少要用几笔画完?分析:(1)4笔;(2)4笔;(3)2笔;(4)1笔;(5)1笔;(6)1笔.3.(例6)右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析:把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A.上图(b)中,所有的结点都是偶点,因此,一定可以以A作为起点和终点而一笔画完此图.也即游人可以从入口进,一次不重复地穿过所有的门,最后从出口出来.下面仅给出一种参观路线:A→E→B→C→E→F→C→D→F→A.4.(例7)一辆清洁车清扫街道,每段街道长1公里,清洁车由A出发,走遍所有的街道再回到A.怎样走路程最短,全程多少公里?分析:清洁车走的路径为: ABCNPBCDEFMNEFGHOLMHOIJKPLJKA. 即:清洁车必须至少重复走4段1公里的街道,如下图.最短路线全程为28公里.5.(例10)一个邮递员的投递范围如右图,图上的数字表示各段街道的长度.请你设计一条最短的投递路线,并求出全程是多少?分析:邮递员的投递路线如下图,即:路线为:ABCDEDOBOMNLKLGLNEFGHIMOJIJA.最短路线的全程为39+9=48.。
二年级奥数:《有趣的一笔画》

二年级奥数:《有趣的一笔画》(预热)前铺知识一、认识单双数单数:1、3、5、7、9、11……双数:0、2、4、6、8、10……(注意:0是最小的双数)二、了解一笔画的初步概念对于一笔画的具体条件,我们上课的时候会加以说明,但是一笔画出的意义,可以让孩子提前有所认识:笔不离开纸,不来来回回重复画,一笔画成.比如:乙日十这三个字中,前两个是可以用一笔写出来的,而第三个则不可以.三、找规律品川这两个字显然都不能用一笔画画出,它们之间有什么共同点呢?尝试可以发现要想画完整笔都得离开纸,也就是说是断开的,没有连通,也叫不连通.所以一笔画的要求是首先得是连通图.本讲重点这一讲的知识实际上是比较特别的,是否能够一笔画用数学知识来概括的非常的复杂,但是同学们却能够通过找规律发现本堂课的知识并很好的掌握.同时可以培养孩子平时找规律的习惯,这也是数学题目中常见的一种方法,也是一种非常科学的思维习惯——归纳与演绎.三年级的时候我们会进一步教同学们多笔画的知识,对奇点偶点的判断也是学习这类型问题的基础.如何预习?为了保护孩子课前的好奇心和学习兴趣,以及保证课堂效果,家长在给孩子预习的时候,一定要把握好度.预习,切忌给孩子讲解书本上的例题和知识点,因为孩子容易先入为主,如果家长选取的方式方法不当,那么孩子很难转换思路了;另外,家长给孩子讲过例题后,孩子可能会觉得自己已经学会了,上课的时候就不愿意认真听了.我们预习的目的是回顾这一讲课前的铺垫知识,以及引起孩子的思考,因此家长可以把我们的这份预习资料打印出来,让孩子自己看一看,如果孩子有不明白的,您可以适当点拨.《有趣的一笔画》【知识点总结】一、什么是一笔画?特点:笔不离纸,不重复,一笔画成.前提:能一笔画的图形必须是连通图.【例】:下面的图形能不能一笔画成?都不能,因为都不是连通图.二、单数点和双数点1. 单数点:从该点出发一共有单数条线的点;2. 双数点:从该点出发一共有双数条线的点.判断小技巧:可以想象自己站在那个点有几条路可以走.(上,下,左,右)三、一笔画的判定1. 图形是连通图2. 有0个或2个单数点的能一笔画3. 超过2个单数点的不能一笔画【例】下面的图形哪些可以一笔画成?2个单数点4个单数点0个单数点可以一笔画不能一笔画可以一笔画四、如何一笔画1.有0个单数点的:同进同出.意思是从哪一个点开始画就哪一个点结束.2.有2个单数点的:单进单出.意思是从一个单数点开始画,另一个单数点结束.五、多笔画变一笔画方法:添(去)单数点之间的线【例】下面的图形都不能一笔画,想办法给每个图形添加一条线段让它变成可以一笔画的图形.(1)(2)(1)(2)本来的图形都有4个单数点不能一笔画,单数点多了,至少得变成2个单数点才能一笔画,那就想办法让其中两个单数点变成双数点,只要在任意两个单数点间添上一条线就可以了.六、一笔画的应用方法:画点线图画法:区域成点,通道成线.【例】下图是一幅简易地图,能不能一次性不重复地走完所有的路.乙村甲村丙村首先要明白题意,把人看成笔,就变成了一次性不重复地画完所有的路,其实就是一笔画!先画出点线图:甲村,乙村,丙村看成点,道路看成线.再判断:有两个单数点,可以一笔画.甲→乙→丙→甲→乙【学习建议】本讲讲的是一笔画,首先要了解什么是一笔画,再学会如何判断能不能一笔画,怎么画?问清楚自己这几个问题简单的一笔画就没问题了.然后再去拓展一笔画的应用,以及初步掌握多笔画如何变成一笔画,更多关于多笔画的内容我们在三年级还会遇到.最后,学习这讲的内容还需要同学们勤标记,多尝试,记规律.《有趣的一笔画》练习1. 判断下面的图形能不能一笔画?为什么?A B C D2. 下面的图形都是不能一笔画成的,你能不能去掉一条线,使他们变成一笔画?3. 下面是一座公园的道路设计图,问能不能一次不重复的把所有小路都走遍?要从哪里开始?HGA D FE CB4、小明要把四个三角形和一个正方形一次性从纸上剪下来,他能做到吗?5、平安小镇上有两个邮递员,甲邮递员喜欢从A 点出发开始送信,乙邮递员喜欢从B点出发开始送信,他们俩都选择最优路线,谁能更快的跑遍多有的街道呢?6. 幸福乡有四个村庄,幸福河从村庄间流过,村民们在河上一共建了5 座桥,问来到幸福乡的人能不能一次不重复地走遍所有的桥.答案解析1.①0个单数点,可以一笔画;②0个单数点,可以一笔画;③4个单数点,不可以一笔画;④2个单数点,可以一笔画2. 答案不唯一.3.图中有两个单数点A和H,从A或H开始就能一笔画.4.有两个单数点,可以一次性剪下所有的图形.5.图中有两个单数点A和E,从单数点出发可以不重复地跑遍所有街道,从B点出发必须要重复才能跑遍多有街道,所以从A点出发的甲邮递员更快.6. 画点线图如下,有两个单数点,所以可以一次不重复走遍所有的桥.。
一笔画(奥数)

一笔画【知识要点】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。
2 下列图形中各有几个单数点?能一笔画成吗?3 判断下面图形能不能一笔画成?如果能,应该怎样画?A4下面图形能不能一笔画成?这什么?5 如图是一个大型花池中小路的平面图,你能否不重复地一次走完所有的小路?进出口应设在什么地方?6 将下图加上最少的线改成一笔画的图形。
7.将下图去掉最少的线改成一笔画图形。
8.下图中的线段代表小路,请小朋友想一想,能够不重复地爬遍小路的甲蚂蚁还是乙蚂蚁?该怎么爬?9.为迎接2008年奥运会在北京召开,你能一笔画出奥运会的五环图案吗?10.下图是一个公园的平面图,应怎样走才能使游客走通每条路而不重复,设计一条最佳路线。
11 一个公园的平面图如下,请你设计好入口、出口,并给出一条浏览路线,要求走遍每一条路且不重复。
12.如图,是一个公园的平面图,请你设计好入口、出口,并给出一种游玩路线,要求走遍每一条路且不重复。
13.如图,是一个名画展厅的平面图,要使参观者不重复地走遍每一条画廊,问:出口、入口应设在哪里?14.黑色的鱼与白色的鱼所能游动的河道如下图所示。
黑色的鱼在A点位置,白色的鱼在B点位置。
哪条鱼能不重复地游遍所有的河道?15.能用一根铁丝弯成下面的图形吗?16.一个邮递员投递信件要走的街道如图,为节约时间,他想自己设计一条线路,可以不重复的走遍每一条街道,你能帮帮他吗?17.一只蚂蚁要想不重复的爬遍每一条线路,应从哪里出发,到哪里结束?18.你能用一笔画成4条线段把下图的9个点都连起来吗?19.下图能否一笔画成?如果能,应怎样画?20.如图,在一个六面体的顶点A和B处各有一只蜗牛,它们比赛看谁能不重复地爬遍每一棱线到达C点。
有趣一笔画问题

有趣的一笔画问题一笔画问题的提出:一笔画是一个大问题,为了更好的解决这个问题,我们从生活提出一笔画问题。
我们先看一个公路检查员的问题:他为了检查几个城市之间的假设干公路,希望在这些城市和公路组成的公路系统中找出一条路线,使他能不重复地恰好通过每条公路一次,而经过每个城市的次数不限。
这就是拓扑学中的数学问题。
一笔画的含义如果用笔在纸上连续不断又不重复,一笔画成某种图形,这种图形就叫一笔画。
下面的画能一笔画成,你也试着描一描,画一画吧!那么是不是所有的图形都能一笔画成呢那我们就要一起学习一笔画的规律。
其实一笔画是一个几何问题,一个图形由一笔构成叫一笔画。
传统意义上的几何学是研究图形的形状大小等性质,而对于平面图形的一笔画与多笔画问题,通常的几何方法是无能为力的,因为一个图形能否一笔画,与图形的大小、形状和线段的长短等几何概念都没有关系,而是与图形中线段的数目及连接关系有关,我们可以随意地将图形拉伸、压缩或弯曲,甚至在保持端点不动的前提下,还可以将某些线段“搬家〞,只要图形的整体结构不变,能否一笔画的性质也就不会改变。
一笔画问题是一个简单的数学游戏,即平面上由曲线段构成的一个图形能不能一笔画成,使得在每条线段上都不重复例如汉字‘日’和‘中’字都可以一笔画的,而‘田’和‘目’那么不能。
(在日本动画片一休中,是采用对折纸张的方法画出‘田’和‘目’的一笔画〕也是可取之处。
一笔画图形的规律和判别:着名的哥尼斯堡七桥问题实质上就是一个一笔画问题。
欧拉最终证明了这个图形是不能一笔画成的,并在关于七桥问题的报告中得到了任一网络图能否一笔画的判别法那么。
欧拉认为,能一笔画的图形必须是连通图。
连通图就是指一个图形各局部总是有边相连的.但是,不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
数学家欧拉找到一笔画的规律是:1.但凡由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
一年级一笔画数学题

一年级一笔画数学题
题目1:
下面这些图形,哪些可以一笔画成?(人教版一年级数学一笔画相关)
(1)正方形。
(2)圆形。
(3)“十”字形状。
解析:
对于正方形,它有4个顶点,都是偶数条线相连(每个顶点连接2条线),所以可以一笔画成。
圆形没有顶点这种概念,但它是一个封闭的曲线,我们可以从圆上任意一点开始,沿着圆周画一圈就能一笔画成。
对于“十”字形状,中间的交点连接了4条线,是偶数条线相连,所以也可以一笔画成。
题目2:
观察下面的图形,能一笔画成的在()里打“√”,不能的打“×”。
(人教版一年级数学一笔画相关)
图形1:三角形()
图形2:两个不相连的圆形()
图形3:“Z”字形()
解析:
三角形有3个顶点,每个顶点连接2条线,都是偶数条线相连,所以能一笔画成,(√)。
两个不相连的圆形,因为是两个独立的图形,不能一笔同时画出这两个不相连的图形,所以(×)。
“Z”字形有2个端点和2个转折点,端点连接1条线(可视为奇数条线相连),所以不能一笔画成,(×)。
四年级奥数:一笔画问题

四年级奥数:一笔画问题小朋友们,你们能把下面的图形一笔画出来吗?如果用笔在纸上连续不断又不重复,一笔画成某种图形,这种图形就叫一笔画.那么是不是所有的图形都能一笔画成呢?这一讲我们就一起来学习一笔画的规律.典型例题例【1】下面这些图形,哪个能一笔画?哪个不能一笔画?(1)(2)(3)(4)分析图(1)一笔画出,可以从图中任意一点开始画该图,画到同一点结束.经过尝试后,可以发现图(2)不能一笔画出.图(3)不是连通的,显然也不能一笔画出.图(4)也可以一笔画出,且从任何一点出发都可以.通过观察,我们可以发现一个几何图形中和一点相连通的线的条数不同.由一点发出有偶数条线,那么这个点叫做偶点.相应的,由一点出发有奇数条数,则这个点叫做奇点.再看图(1)、(4),其中每一点都是偶点,都可以一笔画,且可以从任意一点画起.而图(2)有4个奇点,2个偶点,不能一笔画成.这样我们发现,一个图形能否一笔画和这个图形奇点,偶点的个数有某种联系,到底存在什么样的关系呢,我们再看一个例题.例【2】下面各图能否一笔画成?(1)(2)(3)分析图(1)从任意一点出都可以一笔画成,因为它的每一个点都是与两条线相连的偶点.关于图(2),经过反复试验,也可找到画法:由A B C AD C.图中B、D为偶点,A、C为奇点,即图中有两个奇点,两个偶点.要想一笔画,需从奇点出发,回到奇点.经过尝试,图(3)无法一笔画成,而图中有4个奇点,5个偶点.解图(1)、(2这样我们可以发现能否一笔画和奇点、偶点的数目有着紧密的关系.如果图形只有偶点,可以以任意一点为起点,一笔画出.如果只有两个奇点,也可以一笔画出,但必须从奇点出发,由另一点结束.如果图形的奇点个数超过两个,则图形不能一笔画出.例【3】 下面的图形,哪些能一笔画出?哪些不能一笔画出?分析 图(1)有两个奇点,两个偶点,可以一笔画,须由A 开始或由B 开始到B 结束或到A 结束.图(2)有10个奇点,大于2,不能一笔画成.图(3)有4个奇点,1个偶点,因此也不能一笔画成.解 图(1)的画法见下图.例【4】 下图中,图(1)至少要画几笔才能画成?分析 图(1)有4个奇点,所以不能一笔画出.如果把它分成几个部分,而每个部分是一笔画图形,则我们就可以用最少的几笔画出这个图形.按照这样的要D (1)求,每个部分最多含有两个奇点,可以采用再两个奇点之间增加一条或者去掉一条线的方法,该奇点就变成偶点.经观察,图(1)可以切分成图(A )、(B )两个图形.这两部分都可以一笔画出,所以图(1)至少用两笔画出.解 将图(1)分成图(A )、(B ),则图(A )可由A-B-O-D-A-C-D 一笔画成,图(B )由B-C 一笔画成,所以图(1)至少要两笔画完.小结 能否一笔画成,关键在于判别奇点、偶点的个数.一、 只有偶点,可以一笔画,并且可以以任意一点作为起点.二、 只有两个奇点,可以一笔画,但必须以这两个奇点分别作为起点和终点.三、 奇点超过两个,则不能一笔画.对于一些比较复杂的路线问题,可以先转化为简单的几何图形,然后根据判定是否能一笔画的方法进行解答.D (1) A O B C D(A ) B C (B )。
有趣的一笔画

有趣的一笔画(一)※效能训练 ※姓名:1、口算39+48= 58+17= 78+59= 56+44=67+29= 48+76= 57+48= 72+68=67-18= 39+64= 68+72= 47+57= 24×2= 20×4= 60×5= 36÷4=58+27= 63-28= 59+68= 92-48=81-19+35= 48+67-94= 48+25-9= 35+28-37= 57+29-18= 68+46-26= 80+14-18= 47+19+53=2、看谁算得又对又快9 3 8 8 7 5 7 6 5 4 6 8+ 7 8 + 2 3 5 + 1 9 6 + 1 5 25 0 8 5 9 46 57 1 6 4+ 2 6 8 + 6 8 7 + 3 8 6 + 6 8 93、接力赛【要点提示】“一笔画”是一种有名的数字游戏,是指在笔不离开纸的前提下,每条线只能画一次而且不能重复的平面图形。
能不能一笔画成?该怎样画?我们知道任何图形都是由点和线组成的,图形中的点可以分为两大类(1 (2) (3)开心一练:下面图形能否一笔画成?(1)(2)(3)(4)(5)(6)例2、下图能不能一笔画成,如能,应该如何画?(1)(2)开心一练:下图能不能一笔画成,如能,应该如何画?(1)(2)(3)例3、下面图形能一笔画成吗?为什么?(1)(2)开心一练:下面图形能一笔画成吗?为什么?(1(2)(3)课外冲浪,你是最棒的!☺1、下面图形能一笔画成吗?为什么?(1(2)(3)2、下面图形能一笔画成吗?如果能,请你试一试。
(1(2(3)3、下面图形能一笔画成吗?为什么?(1(2)(3)4、下面图形能一笔画成吗?为什么?(1)(2(35、下面图形能一笔画成吗?为什么?(1)(23)6、下面图形能一笔画成吗?为什么?(1(2)(3)(4(5)(7、下图是国际奥林匹克运动会的会微,你能把它一笔画出来吗?8、一块菜地共生产黄瓜870筐,第一次运走284筐,第二次运走290筐,还剩下多少筐?有趣的一笔画(二)※效能训练 ※姓名:1、口算39+45= 56+47= 38+59= 58+44=67+49= 45+76= 57+38= 76+28=91-18= 39+68= 69+22= 48+57= 58+37= 83-28= 49+68= 92-45=81-29+37= 38+65-24= 48+25-19= 65+28-37= 47+59-18= 48+56-27= 80+14-38= 67+19+28=2、看谁算得又对又快3、接力赛4、四年级种树106棵,三年级比四年级少种29棵。
一笔画完的规律

一笔画完的规律
【实用版】
目录
1.一笔画完的定义与特点
2.一笔画完的规律
3.一笔画完的应用实例
4.结论
正文
一笔画完的定义与特点
一笔画完,又称连通图,是指在一个平面内,通过一笔连续的线段将所有点连接起来,并且线段不能重复经过已经连接过的点。
一笔画完是一个具有挑战性和趣味性的数学问题,它涉及到图论的知识,具有广泛的应用。
一笔画完的规律
一笔画完的规律可以归纳为以下几点:
1.所有点必须处于连通状态,即从一个点出发,可以通过线段到达所有其他点。
2.奇数点时,必须有一个点是起点或终点,否则无法连接所有点。
3.偶数点时,起点和终点必须相邻,否则无法连接所有点。
4.所有线段不能相交,否则会导致无法通过一笔画完连接所有点。
一笔画完的应用实例
一笔画完在实际生活中有很多应用,例如:
1.旅行商问题(TSP 问题):在给定的城市之间选择最短路径,使得
一辆卡车能够一次性地经过所有城市并返回起点。
2.电子电路设计:在印刷电路板上设计线路,使得所有元件能够通过一笔画完连接。
3.物流配送:在一定区域内设置仓库和配送点,使得所有客户能够通过一笔画完的方式接收货物。
结论
一笔画完问题不仅是图论领域的一个有趣问题,同时也具有广泛的实际应用。
了解一笔画完的规律和特点,有助于解决实际生活中的许多问题。
一笔画问题例题加解析

一笔画问题例题加解析一、什么是一笔画问题。
一笔画问题呀,就像是一个超有趣的小谜题呢。
简单来说,就是在一个图形里,能不能一笔就把这个图形画出来,而且笔不能离开纸,也不能重复画已经画过的线。
这就像是在走迷宫,但是这个迷宫是用线条画出来的。
比如说,一个圆形,那肯定能一笔画出来,就顺着圆的边画一圈就好啦,简单得很。
二、一笔画问题的小规则。
这里面可是有小秘密的哦。
有个叫欧拉的超级聪明的人发现了一些规律。
对于一个连通图(就是这个图里的各个部分都是连着的,没有分开的小块),如果这个图里的奇点(就是从这个点出发的线的数量是奇数条的点)个数是0或者2的时候,这个图就能一笔画出来。
要是奇点个数是0呢,就可以从任何一个点开始画,最后还能回到这个点;要是奇点个数是2呢,就得从其中一个奇点开始画,然后到另一个奇点结束。
三、例题来啦。
1. 比如说这个三角形,我们来看看它能不能一笔画出来呢。
三角形的每个顶点,都有两条线连着,那就是说,它的奇点个数是0。
按照我们刚刚说的规则,它肯定能一笔画出来啦。
怎么画呢?就从三角形的一个顶点开始,顺着边画,绕一圈就画好啦,是不是很容易呢?2. 再看这个正方形加上一条对角线的图形。
这个图形的四个顶点本来都是有两条线连着的,但是加上对角线之后呢,对角线的两个端点就变成了奇点,这时候奇点个数是2。
那按照规则,我们从其中一个奇点开始,沿着边画,就能一笔画出来啦。
四、解析例题。
1. 对于三角形那个例子,因为每个顶点都是偶点(从这个点出发的线的数量是偶数条的点),所以我们在画的时候,就可以很顺畅地绕着图形走一圈,不会出现画不下去或者必须重复的情况。
这就像是在一个没有障碍的小路上散步,一路畅通无阻。
2. 在正方形加对角线的例子里,由于有两个奇点,这就像是两个特殊的出入口。
我们从一个奇点这个特殊的入口进去,然后沿着图形的边和线走,最后到达另一个奇点这个出口,就刚好把整个图形一笔画完了。
如果我们不按照这个规则,从别的点开始画,就会发现画到一半就会走不下去,或者必须要重复画某些线了。
四年级数学思维拓展:一笔画问题

【四年级数学思维拓展】趣味入门—神奇的森林王国(一)
------白猫侦探一笔画问题
知道能否一笔画的判断法则,明白0个奇点和2个奇点图形的一笔画区别。
1.简单图形的一笔画。
2.一笔画的规则。
3.0奇点和2奇点一笔画出发点的区别。
例题1:小白猫有天问他爸爸白猫侦探,这个图形能不重复一笔画出来么?白猫侦探一看,这有何难!然后直接一笔画出来了。
大家知道怎么画么?
例题2小白猫又拿出一些形状,这些图形能不重复一笔画出来么?
例题3:白猫侦探要巡视一遍街道,街道平面图如图所示,问白猫侦探能否不重复的巡视完所有街道?
例题4:河马邮递员要给一个村子的每户送信,村庄街道形状如下图,请为河马设计一条路线能够不重复的走完每条路。
例题5:一条河中有两个小岛,一共有7座桥负责交通。
问能否一口气不重复走完所有的桥?
(即是该课程的课后测试)
1、尝试把下图不重复的一笔画出。
2、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
3、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
4、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
5、先根据一笔画规则判断下图能否一笔画出,如果可以,就一笔画出。
1、略。
2、没有奇点,所以可以一笔画出。
3、有4个奇点,所以不能一笔画出。
4、没有奇点,所以可以一笔画出。
5、有4个奇点,所以不能一笔画出。
