一笔画趣味数学
浅谈一笔画问题

浅谈一笔画问题公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]浅谈一笔画问题摘要:一笔画问题是一个几何问题,传统意义上的几何学是研究图形的形状大小等性质,而存在一些几何问题,它们所研究的对象与图形的形状和线段的长短没关系,而只和线段的数目和它们之间的连接关系有关,比如一笔画问题就是如此。
一笔画问题是一个简单的数学游戏,即平面上由曲线段构成的一个图形能不能一笔画成,使得在每条线段上都不重复例如汉字‘日’和‘中’字都可以一笔画的,而‘田’和‘目’则不能。
关键词:一笔画规律原理早在18世纪,瑞士的着名数学家欧拉就找到了一笔画的规律。
欧拉认为,能一笔画的图形必须是连通图。
连通图就是指一个图形各部分总是有边相连的.但是,不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
一笔画问题是图论中一个着名的问题。
一笔画问题起源于柯尼斯堡七桥问题。
数学家欧拉在他1736年发表的论文《柯尼斯堡的七桥》中不仅解决了七桥问题,也提出了一笔画定理,顺带解决了一笔画问题。
一般认为,欧拉的研究是图论的开端。
与一笔画问题相对应的一个图论问题是哈密顿问题。
一、一笔画规律数学家欧拉找到一笔画的规律是:(一)凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
(二)凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起,,另一个奇点终点。
(三)其他情况的图都不能一笔画出。
(有偶数个奇点除以二便可算出此图需几笔画成)比如附图:(a)为(1)情况,因此可以一笔画成;(b)(c)(d)则没有符合以上两种情况,所以不能一笔画成。
补充:相关名词的含义◎顶点与指数:设一个平面图形是由有限个点及有限条弧组成的,这些点称为图形的顶点,从任一顶点引出的该图形的弧的条数,称为这个顶点的指数。
◎奇顶点:指数为奇数的顶点。
◎偶顶点:指数为偶数的顶点。
趣味数学300题 第三章 画来画去。移来移去……
趣味数学300题第三章画来画去。
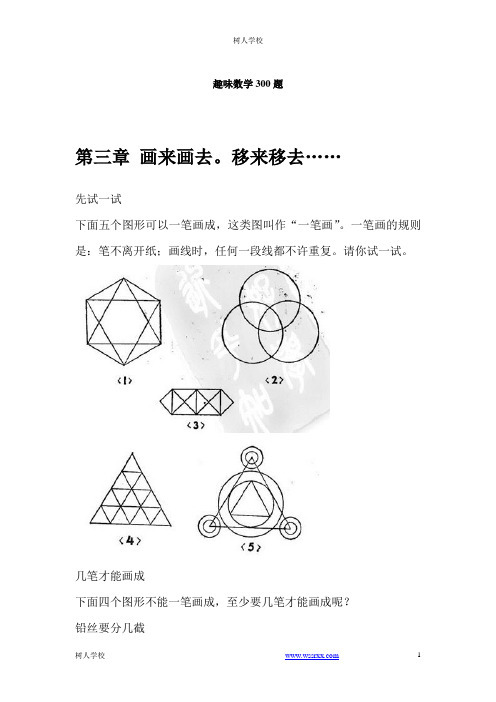
移来移去……先试一试下面五个图形可以一笔画成,这类图叫作“一笔画”。
一笔画的规则是:笔不离开纸;画线时,任何一段线都不许重复。
请你试一试。
几笔才能画成下面四个图形不能一笔画成,至少要几笔才能画成呢?铅丝要分几截在下面三个架子中,有一个只用一根铅丝就可以构成,而另外两个,要把铅丝分成几段才能构成。
请在每一个架子下注明,是用几根铅丝构成的。
擦掉哪一根线下图不能一笔画,可是,只要擦去一根线,图形就可以一笔画成。
应该擦掉哪一根线,你知道吗?走遍所有的门下图是一座房屋的平面图。
每两个相邻房间之间,都有一个门相通;除中间两个房间E和F 以外,每个房间都有门通向室外。
你能够不重复地穿过每一道门吗?提示:把每一个房间设想成一个点,室外也用一个点表示。
如果两个房间这间有门相通,设想相应的两点之间有线段连接。
画出这个图,上述问题就相当于一个“一笔画”。
十五座桥下图中有A、B、C、D、E、F六个小岛,各岛之间共有十五座桥(桥已编号)。
现在要从A 岛出发,不重复地走遍十五座桥,该怎么走呢?你是不是已经看出,这也是一笔画问题?十八世纪伟大的数学家欧拉从哥尼斯堡城的七桥入手,研究了“一笔画”问题。
因此,现代的图论著作和书籍中,都把“一笔画”称为欧拉问题,把能不重复走遍的路,称为欧拉路。
别致的画廊公园里布置了一个很别致的画廊(请看图)。
画廊分为25段,每段画廊两头的圆圈是休息处。
A处为入口,B处是出口,H处设有小吃部。
现在有一个人要不重复地看遍所有画廊,并且打算在看了8段画廊后恰好到小吃部(H处),吃点东西后,再看9段,又恰好回到小吃部(H处),最后看完剩下的8段画廊,从B处出来。
请你替这个人安排一条参观的路线。
最短路线下图是一些街道的平面图,中间九个方格是一些建筑物。
有一辆洒水车从A点出发,要往每一条街道上洒水最后仍回到A点。
洒水车在街道上必然有重复行驶,可是精心地选择行驶路线,能使重复行驶的路程尽可能少。
一笔画完园的三个扇形

一笔画完园的三个扇形
(原创版)
目录
1.引言:一笔画完园的三个扇形的趣味数学问题
2.分析:通过数学原理解析一笔画完园的三个扇形的可能性
3.解答:如何一笔画完园的三个扇形
4.结论:总结解答过程,强调数学的美妙与趣味
正文
一笔画完园的三个扇形是一个有趣的数学问题,它涉及到图论和几何学的知识。
在这个问题中,我们要求通过一笔画出三个扇形,使得它们共享一个公共的顶点,并且每个扇形的圆心角大小相等。
首先,让我们从数学原理的角度来分析这个问题。
根据图论,一个图形可以被分为若干个顶点和边。
在这个问题中,每个扇形可以被视为一个顶点,而连接三个扇形的公共顶点则是一个边。
因此,我们的目标是找到一种方法,使得这个边可以被一笔画出,并且三个扇形的圆心角大小相等。
接下来,我们来解答这个问题。
实际上,一笔画完园的三个扇形是可行的,但需要满足一定的条件。
首先,三个扇形的圆心角大小必须相等,也就是说,它们的圆心角都应该是 120 度。
其次,三个扇形之间应该共享一个公共的顶点,这个顶点是三个扇形的圆心角的公共端点。
最后,三个扇形应该两两相邻,即它们的边缘应该相连,形成一个封闭的图形。
在满足上述条件的情况下,我们可以通过一笔画出三个扇形。
具体来说,我们可以先画出一个 120 度的扇形,然后再从这个扇形的边缘出发,画出另外两个 120 度的扇形,使得它们的边缘与第一个扇形的边缘相连。
这样,我们就成功地一笔画出了三个扇形,它们共享一个公共的顶点,并且每个扇形的圆心角大小相等。
综上所述,一笔画完园的三个扇形是可行的,但需要满足一定的条件。
二年级奥数第10讲 学习一笔画带答案

第10讲学习一笔画【专题简析】一笔画,就是从图形某点出发,笔不离开纸,而且每条线段都只画一次不重复.它是一种有趣的数学游戏.那么,哪些图形不能一笔画成,哪些图形可以一笔画成呢?一个图形能否一笔画成,关键在于单数点的多少,有2个或0个单数点的图形就能够一笔画成,单数点在一笔画中只能作为起点和终点.【例题1】一些平面图形是由点和线构成的,这里的“线”可以是线段,也可以是一段曲线,请自己画一些图研究每个点和线的连接情况.思路导航:请小朋友仔细观察下列各图中的点,他们分别与几条线相连.①②③④(1)与一条线段相连的点有:(2)与两条线段相连的点有:(3)与三条线段相连的点有:(4)与四条线段相连的点有:归纳:把和一条、三条、五条等单数条线连得点叫做单数点;把和两条、四条、六条、八条等双数条线连的点叫双数点,每个图中的点要么是单数点,要么是双数点.练习11.任意找一个平面图形,数一数图中有几个单数点,几个双数点.2.下面图形中有哪几个单数点?B答案:A D3.数一数下面图形中有几个双数点,分别是哪些点?B 答案:A BCDE F【例题2】下面的图形能不能一笔画成?如果能,应该怎样画?AC C(1) O (2)B DF(3)D【思路导航】图(1)中A 、B 、C 、D 、O 五个点都是双数点,所以这个图形可以一笔画成.画时可以从任意一点出发.图(2)中A 、C 、D 、F 四个点都是双数点,B 和E 两个点是单数点,所以这个图形也可以一笔画成.画时要从单数点出发,最后回到另一个单数点.图(3)中A 、D 是双数点,B 、C 、E 和F 四个点是单数点,单数点的个数超过了两个,这个图形不能一笔画成.练习21.下面的图形能不能一笔画成,如果能,请说明画法,如果不能,请说明理由(1)(2)答案:图(1)可以一笔画成,因为单数点有两个图(2)不能一笔画成,因为单数点大于两个2.下列图形能一笔画成吗?为什么?答:图(1)可以一笔画成,因为单数点个数为零图(2)不可以画成,因为单数点只有一个图(3)不可以画成,单数点个数大于两个3.观察下列图形,哪个图形可以一笔画成?怎么画?图(1)单数点个数为0,可以一笔画出图(2)单数点个数为4个,不可以一笔画出图(3)单数点2个,可以画出【例题3】下图是某地区所有街道的平面图,甲、乙两人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.那么两人谁先到达?AC思路导航:题中要求两人必须走遍所有街道,最后到达C.仔细观察,可以发现图中有两个单数点:A 、C.这就是说:甲可以从A 点出发,不重复地走遍所有街道,最后到达C.而B 点是双数点,从B 点出发的乙则不行.因此,甲所走的路程正好等于所有街道的总和,而乙所走的路程一定比这个总和多,所以甲最先到达C.解:甲最先到达C.练习31.下图是某新村小区主干道平面图.甲、乙两人同时分别从A 、B 出发,以相同的速度走遍所有的主干道,最后到达C.问谁能最先到达C?答:A 先到达,因为A 是单数点,可以不重复走遍所有街道.2. 甲、乙两辆车同时以相同的速度分别从A 、B 出发,哪辆车能最先行驶完所有的路程?B答:A 先到达,因为A 是单数点.3.一只蚂蚁分别从A 点和B 点出发,爬遍所有的小路.如果每次爬行的速度相同,那么从哪一点出发所用的时间少?答:从A 点出发用时最少【例题4】下图(图1)能否一笔画成,若不能,你能用什么方法把它改成能够一笔画成的图形?(1)(2)思路导航:此图共有9个点,其中5个点是双数点,4个点是单数点,由于超过两个单数点,因此不能一笔画成.要想改为一笔画成,关键在于减少单数点数目(把单数点的个数减少到0或2),所以只要在任意两个单数点间连上线,就可以一笔画,有时也可以将多余的两个单数点间的连线去掉,改成一笔画. 解:图(1)有4个单数点,不能一笔画成.要改成一笔画成,如图(2)练习41.将下图改成一笔画.1. 2.3.在一个小区中有一些路,每个圆柱表示邮筒(如下图),邮递员叔叔每次送信时,总是没法走过每一条路而又不重复,你知道为什么吗?如果请你给小区加一条路来解决这个问题,你准备把这条路加在哪儿?请你动手画一画.【例题5】邮递员叔叔要给一个居民小区送信(如图),怎么走才能少走重复路,使每天走的路尽可能短?A G HD B思路导航:图中一共有九个点,其中单数点有2个(点D 和点F ),因此能一次不重复走过所有的路,但必须从这两个单数点中的一个出发,再回到另一个单数点.解:邮递员叔叔只能从点D (或点F )出发,走过所有的路后,再回到点F(或点D) .练习51.下图是以个小区的中心花园的平面图,你能一次不重复地走完所有的路吗?入口和出口应该设在哪儿呢?答:可以从任一点出发.2.园林工人在花园里浇花,怎样才能不重复地走遍每条小路?答:从A点出发,终止于B点.或从B点出发,终止于A点.3. 下图是“儿童乐园”平面图,出、入口应分别设在哪里才能不重复地走遍每条路?可以怎么走?D CAB答案:从A点出发,终止于C点或从C点出发,终止于A点【拓展提高】1、下面的图形能不能一笔画成?为什么?如果能,应该怎样画?答:从A点出发,终止于B点;或从B点出发,终止于A点2、给下面的图形添一条线,使它能够一笔画成.3、小明和玲玲玩“过木桥”的游戏(如下图),他们谁能不走重复的路?小明玲玲答:小明,因为他处于奇数点4、在王大爷家的花园中有一些路(如下图),王大爷每次给花浇水时,总是没法走过每一条路而又不重复,你知道为什么吗?如果请你给花园加一条路来解决这个问题,你准备把这条路加在哪儿?请你动手画一画.。
小学数学《一笔画》练习题(含答案)精选全文

可编辑修改精选全文完整版小学数学《一笔画》练习题(含答案)什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.所谓一笔画,就是从图形上的某点出发,笔不离开纸,而且每条线都只画一次不准重复.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.判断图形能否一笔画的规律:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点.以另一个奇点作为终点;(4)奇点个数超过两个的图形,一定不能一笔画.(一) 一笔画以及多笔画【例1】 观察下面的图形,说明哪些图可以一笔画完,哪些不能,为什么?对于可以一笔画的图形,指明画法.(f)(e)(d)JIH G F ED C BAJ K IHGFED CB A分析:(a )图:可以一笔画,因为只有两个奇点A 、B ;画法为A →头部→翅膀→尾部→翅膀→嘴. (b )图:不能一笔画,因为此图不是连通图.(c )图:不能一笔画,因图中有四个奇点:A 、B 、C 、D.(d )图:可以一笔画,因为只有两个奇点;画法为:A →C →D →A →B →E →F →G →H →I →J →K →B. (e )图:可以一笔画,因为没有奇点;画法可以是:A →B →C →D →E →F →G →H →I →J →B →D →F →H →J →A.(f )图:不能一笔画出,因为图中有八个奇点.[注意]在上面能够一笔画出的图中,画法并不是惟一的.事实上,对于有两个奇点的图来说,任一个奇点都可以作为起点,以另一个奇点作为终点;对于没有奇点的图来说,任一个偶点都可以作为起点,最后仍以这点作为终点.[巩固]判断下列图a、图b、图c能否一笔画.E分析:图a是一个连通的图形,图中只有点A和点F两个奇点,所以它能一笔画,其中一种画法如下:A —M—N—A—F—B—C—B—K—C—D—E—D—L—E—F.‘图b是一个不连通的图形,所以不能一笔画.图c是连通图,图中所有点都是偶点,所以能一笔画.其中一种画法如下:A—B—C—D—E—F—D—A—F —C—A.【例2】右图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达 C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析:本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C.容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和.仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C.[巩固]在六面体的顶点B和E处各有一只蚂蚁(见右图),它们比赛看谁能爬过所有的棱线,最终到达终点D.已知它们的爬速相同,哪只蚂蚁能获胜?分析:许多同学看不出这是一笔画问题,但利用一笔画的知识,能非常巧妙地解答这道题.这道题只要求爬过所有的棱,没要求不能重复.可是两只蚂蚁爬速相同,如果一只不重复地爬遍所有的棱,而另一只必须重复爬某些棱,那么前一只蚂蚁爬的路程短,自然先到达D点,因而获胜.问题变为从B到D与从E到D哪个是一笔画问题.图中只有E,D两个奇点,所以从E到D可以一笔画出,而从B到D却不能,因此E点的蚂蚁获胜.[数学小游戏] 用一笔画成四条线段把所有的点连起来,怎样画?分析:通过试画,似乎不可以画,但通过仔细观察,对照一笔画的规律,便可发现,若添上两个辅助点,就可画成.如右图:FE DCB ADCBA我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.公式如下: 奇点数÷2=笔画数,即2n ÷2=n.【例3】 判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.IH G FED CBA 图aH G I KLJ F EDCBA 图b DC HG EFBA图c分析:图a :原图有四个奇点,所以不能一笔画,在B,D 两点之间加一条线后,图中只有两个奇点,故可以一笔画出,如图d 所示.画法:H →A →B →C →D →E →F →I →D →B →I →H →G →F .图b :原图有四个奇点,所以不能用一笔画.去掉K ,L 两点之间的连线,图中只有两个奇点,故 可以一笔画出,如图e 所示.画法:B →C →D →E →F →→J →H →G →I →A →B →K →I →L →E .图c :原图有四个奇点,所以不能用一笔画.在B ,C 两点之间加一条线后,图中只有两个奇点, 故可以一笔画出,如图f 所示.画法:A →E →D →H →A →B →F →C →G →B →C →D注意:a 、b 、c 三个图都是连通的图形,但由于每个图的奇点个数均超过两个,所以都不能一笔画.图dA BCD EFG H IH GI KLJ F EDCB A 图eDC HG EFBA图f[前铺]观察下面的图,看各至少用几笔画成?分析:(1)图中有8个奇点,因此需用4笔画成. (2)图中有12个奇点,需6笔画成. (3)图是无奇点的连通图,可一笔画成.DC BA(2)(1)FEC DB A分析:图(1)中有6个奇点,因此可添上两条(或3条)边后可改为一笔画;又因为这个图中,把这6个奇点任意分为3对后,最多只有两对奇点间有边相连,因此,可去掉两条边后改为一笔画,举例如图(3)~(6).图(2)中有4个奇点,因此,可添上2条(或1条)边后改为一笔画;又因为把奇点按A 与B ,C 与D (或A 与D ,B 与C )分为两对后,每对间均有边相连,因此,可去掉两条(或1条)边后改为一笔画.举例如图(7)~(8).说明:图(6)运用了两种方法,去掉边BC ,添上边AD 与EF.(二)一笔画的实际应用【例5】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?:这个有趣的问题引起了著名数学家欧拉的注意,他证明了七桥问题中提到的走法根本不存在. 下面,我们考虑如下两个问题:(1)如果再架一座桥,游人能否走遍所有这八座桥?若能,这座桥应架在何处?若不能,请说明理由. (2)架设几座桥可以使游人走遍所有的桥回到出发地?而得到一个由四个点和七条线组成的图形(如图b).在图b 中,点A ,B ,C ,D 四个点均为奇点,显然不能一笔画出这个图形.若将其中的两个奇点改成偶点,即在某两个奇点之间连一条线,这样奇点个数由四个变为两个,此时,图形可以一笔画出.如我们可以选择奇点B ,D ,在B ,D 之间连一条线(架一座桥),如图c .在图c 中只有点A 和C 两个奇点,那么我们可以以A 为起点,C 为终点将图形一笔画出.其中一种画法为:A →C →A →B →A →D →B →D →C所以,如果在河岸B 与小岛D 之间架一座桥,游人就可以不重复地走遍所有的桥.(2)在(1)的基础上,再在另外两个奇点A 与C 之间连一条线(即架一座桥),使这两个奇点也变成偶点,如图d .那么A ,B ,C ,D 四个点均为偶点,所以图d 可以一笔画出,并且可以以任意点为起点,最后 仍回到这个点.其中一种画法为:A →C →A →C →D →A →B →D →B →A这表明:在河岸B 与小岛D 之间架一座桥后,再在小岛A 与河岸C 之间架一座桥,共架设两座桥,就可以使游人不重复地走遍所有的桥并回到出发地.[巩固]如图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?分析:用点表示小岛与河岸,用连接两点的线表示连接相应两地的桥,如图,有2个奇点,所以该图可以一笔画,即可以一次不重复地走遍这七座桥.例如右下图的走法.EDCBA【例6】 有一个邮局,负责21个村庄的投递工作,右图中的点表示村庄,线段表示道路.邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?分析:图中有两个奇点,所以该图可以一笔画,但因为邮局所在点为奇点,所以要一笔画就不可能回到邮局.又图中A,B,C,D,E,F,G,H,I,J十点均有4条线段与之相连,如果我们将上图一笔画的话,就要经过以上十点各两次,这也不满足题目的要求,所以要将这些点相连的线段去掉一些,使得与这些点相连的线段均只有两条,并且将两个奇点也变成只有两条线段与之相连,这样得到的图形即可一笔画,又只经过每个点一次,并且可以回到邮局,一种可行路线如下:邮局I JHGF E D C B A 邮局邮局【例7】 右图是某博物馆的平面图,相邻两个展厅之间有一扇门相通,每一个展厅都有一门通往馆外.问参观者能否不重复地一次穿过每一扇门?若能,请找出一条可行路径;若不能,请说明理由.如果允许关闭某一扇门,问参观者能否不重复地穿过每一扇开着的门?分析:我们把展厅A,B,C,D,E 及馆外F 看成某个图中的点,把两个展厅之间的门看作是连接表示这两个展厅的点的线.根据题中条件知,馆外F 与A ,B ,C ,D ,E 各展厅相通,这样将点F 与点A ,B ,C ,D ,E 用线连接;展厅A 与展厅B ,C ,D 相通,将点A 与点B ,C ,D 用线连接;展厅B 除与A 相通外,它还与D ,E 展厅相通,将B 与D ,E 连接;除此之外,展厅C ,D 相通,展厅D ,E 相通,将点C ,D 连接,再将点D ,E 连接(如图a).于是本题要解决的问题就变成了能否将图a 一笔画的问题.可以看出:图a 中共有六个点,其中有四个奇点,它们分别为C ,D ,E ,F ,由一笔画的规律可知,图a 不能一笔画.也就是说,参观者不能够不重复地一次穿过每一扇门.如果允许关闭某一扇门,这相当于在图a 中去掉一条线,那么参观者就有可能不重复地一次穿过每一扇门.我们知道,在图a 中有四个奇点C ,D ,E ,F 为了把图a 改成一笔画图形,我们设法减少奇点个数,使奇点数变为两个.为此,我们可以去掉一条连接两个奇点的线,如去掉E 与F 间的连线,相应的图a 就变成了图b .在图b 中,除了原来的C 和D 是奇点外,其余点全部是偶点,故图b 可以一笔画.其中一种画法为:C →F →D →E →B →F →A →B →D →A →C →D .上面的分析表明,如果关闭连接E 、F 两展厅之间的门,参观者就可以不重复地一次穿过每一扇开着的门. 本题与七桥问题类似,只是将行人过桥换成了参观者穿过每一扇门.我们将这个问题转化为一笔画问题来研究.[前铺]右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走? FFF F E C D BA EB A分析:我们将每个展室看成一个点,室外看成点E ,将每扇门看成一条线段,两个展室间有门相通表示两个点间有线段相连,于是得到下图.能否不重复地穿过每扇门的问题,变为下图是否一笔画问题.EDC BA图中只有A ,D 两个奇点,是一笔画,所以答案是肯定的,应该从A 或D 展室开始走. 【例8】 已知长方体木块的长是80厘米,宽40厘米,高80厘米(如右图),并且要求蜘蛛在爬行过程中只能前进,不能后退,同一条棱不能爬两次.请问这只蜘蛛最多要爬行多少厘米?分析:图中八个顶点均为奇点,所以不能一笔画,要使其能一笔画,至少要去掉三条棱,使上图只有两个奇点,就可以满足一笔画的条件.长方体的棱长总和一定,(80+80+40)×4=800(厘米),因此去掉的三条棱越短,蜘蛛爬过的距离就越远.所以我们去掉三条棱长为40厘米的棱,于是可知,蜘蛛爬行的最远距离为: 800-40×3=680(厘米).蜘蛛的爬行路径为:G →F →C →D →G →H →A →B →E →H(如右图).[注意]这是一个立体图形,它有八个顶点,我们把长方体的棱看作顶点与顶点之间的连线,蜘蛛只能前进不能后退,并且每一条棱不能爬两次,这实质上是一个一笔画问题.【例9】 右图是某小区的街道分布图,街道长度如图所示(单位:公里),图中各点表示不同楼的代号.一辆垃圾清扫车从垃圾站(垃圾站位于C 楼与D 楼之间的P 处)出发要清扫完所有街道后仍回到垃圾站,问怎样走路线最短,最短路线是多少公里?分析:为了少走冤枉路和节省时间,题目中要求最短路线,根据一笔画原理,我们知道一笔画路线就是最短路线.本题要求清扫车从P点出发,仍回到P 点.通过观察上图可知,图中有六个奇点,根据一笔画规律可知,清扫车想清扫完所有街道而又不走重复的路是不可能的.要使清扫车从P 点出发,最后仍回到P 点,就必须把图中所有的奇点都变成偶点,即在两奇点之间添加一条线.在实际问题中,就是清扫车在哪些街道上重复走的问题,由于每条街道的长度不同,因此需要我们考虑清扫车重复走哪条街道才使总路线最短.为使六个奇点都变成偶点,我们可以有下图中的四种方法表示清扫车所走的重复路线,其中填虚线的地方表示的是重复路线.重复的路程分别为:图a :2×2+3=7;图b :3+4×2=11;图C :3×3=9; 图d :3+6×2=15.显然,重复走的路线最短,总路程就最短.从上述计算中就可找到最短路线图,即下面四个图中的图a .408080H G F ED C BA804080H GFED CBA图b 图a图d图c在图a 中,所有点均为偶点,是一笔画图形.清扫车可按如下路径走:P →D →G →D →E →F →G →H →L →H →C →B →L →M →A →B →C →P ,全程为:(1+2+4+2)×2+3×5+2×2+3=40(公里).【例10】 邮递员李文投送邮件的街道以及街道的长度如右图所示(单位:千米),每天小李要从邮局出发,走遍所有街道后回到邮局.请你帮他设计一条最短路线,并计算出这条路线有多少千米?分析:本题仍可以用一笔画图形的方法来解决.在图a 中共有六个奇点E ,F ,G ,H ,I ,J ,把这些奇点配对,每对之间用虚线连接(如图a),其中要用到D 点,这样图中就没有奇点了,从而可以不重复地走遍所有的街道.由于邮递员李文要重复走一些路段,因此重复走的路越短越好,即添上去的重复线段的总长度越短越好.在图a 中H 与E 之间有重叠,这样势必会增加李文所走路程的长度,应作调整.经调整后,将重叠部分去掉便得图b .在图b 的圈形闭路IHGJI 中,I ,J ,G ,H 各点没有连线时是奇点,连线后变成偶点,增加长度为50×2=100千米.而如果连IJ 和HG ,增加的长度仅为10×2=20,由此可知图b 需继续作调整,改成图c ,这种连接方法是最好的,它使李文行走的路线最短.根据以上分析,为了保证添上去的线段之和最短,应遵循下面的两条原则:(1)连线不能有重叠的线段;(2)在每一个圈形闭路上,连线长度之和不能超过 这个闭路总圈长的一半.经过分析可以知道,图c 的连接方法能使邮递员李文行走路线最短,而且能保证李文从邮局出发又回到邮局.这时他的行走路线为:邮局→A →I →J →I →H →G →H →E →D →F →D →G →J →B →C →D →E →邮局 他行走的全程为: (50+15)×4+20×4+10×6+20×2=440(千米).图a图b图c[小结]本题中采用的方法叫做“奇偶点图上作业法”,用这种方法来确定最短路线比较简便实用.此方法可以用下面的口诀来描述:画出路线图,确定奇偶点;奇点对对连,连线不重叠;闭路添连线.不得过半圈.[巩固]右图是某地区街道的平面图,图上的数字表示那条街道的长度.清晨,洒水车从A 出发,要洒遍所有的街道,最后再回到A.问:如何设计洒水路线最合理? 分析:这又是一个最短路线的问题.通过分析可以知道:在洒水路线中,K 是中间点,因此必须成为偶点,这样洒水车必须重复走KC 这条边(如下左图).至此,奇点的个数并未减少,仍是6个.容易得出,洒水车必须重复走的路线有:GF 、IJ 、BC.即洒水路线如下右图.全程45+3+6=54(里).1. (例1)判断下列各图能否一笔画.图aG I H F ECD BA图bF ED CBA分析:图a 中九个点全是偶点,因此可以一笔画,其中一种画法为:A →F →B →G →C →H →D →E →H →l →→F →G →l →E →A .图b 中A ,B ,C ,D 四个点均为奇点,故不可以一笔画.图c 中,只有A,C 为奇点,故可一笔画.其中一种画法为:A →D →E →C →H →N →G →M →F →A →B →C .2. (例3)下列各图至少要用几笔画完?分析:(1)4笔;(2)4笔;(3)2笔;(4)1笔;(5)1笔;(6)1笔.3.(例6)右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析:把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A.上图(b)中,所有的结点都是偶点,因此,一定可以以A作为起点和终点而一笔画完此图.也即游人可以从入口进,一次不重复地穿过所有的门,最后从出口出来.下面仅给出一种参观路线:A→E→B→C→E→F→C→D→F→A.4.(例7)一辆清洁车清扫街道,每段街道长1公里,清洁车由A出发,走遍所有的街道再回到A.怎样走路程最短,全程多少公里?分析:清洁车走的路径为: ABCNPBCDEFMNEFGHOLMHOIJKPLJKA. 即:清洁车必须至少重复走4段1公里的街道,如下图.最短路线全程为28公里.5.(例10)一个邮递员的投递范围如右图,图上的数字表示各段街道的长度.请你设计一条最短的投递路线,并求出全程是多少?分析:邮递员的投递路线如下图,即:路线为:ABCDEDOBOMNLKLGLNEFGHIMOJIJA.最短路线的全程为39+9=48.。
一笔画完的规律

一笔画完的规律摘要:一、引言1.一笔画完的概念2.一笔画完的趣味性和挑战性二、一笔画完的规律1.基本规律a.起点和终点相同b.只能向一个方向画线c.不可重复经过已画过的线段2.特殊情况a.多边形b.连续相同线段c.转折点三、应用和挑战1.实际应用a.设计游戏b.益智类玩具2.挑战与研究a.寻找更复杂的一笔画完图形b.探究一笔画完与其他数学领域的关联四、总结1.一笔画完规律的重要性2.未来研究方向正文:一、引言在闲暇时光,你是否曾经尝试过一些有趣的涂鸦游戏,例如一笔画完?这个游戏看似简单,只需一根连续的线条,却充满了趣味性和挑战性。
那么,你是否了解一笔画完背后的规律呢?本文将为你揭示这笔画完的神秘规律。
二、一笔画完的规律要了解一笔画完的规律,首先我们要明确其基本概念。
一笔画完是指用一根连续的线条,不离开纸面,不重复经过已画过的线段,将图形中所有的点连接起来。
根据这个定义,我们可以总结出一笔画完的三条基本规律:1.起点和终点相同2.只能向一个方向画线3.不可重复经过已画过的线段在遵循这三条基本规律的前提下,我们可以尝试解决一些特殊情况。
1.特殊情况a.多边形对于一个多边形,我们可以从一个角点出发,连接到与之相邻的另一个角点,这样就能保证一笔画完。
b.连续相同线段当遇到连续相同的线段时,我们可以选择从其中一段开始,沿着这个方向画线,直到遇到不同的线段。
c.转折点在转折点处,我们需要判断哪个方向是符合规律的。
一般来说,从较长的线段转向较短的线段是符合规律的。
三、应用和挑战了解了一笔画完的规律,我们可以将其应用到实际生活中。
例如,设计一款基于一笔画完的游戏,或者制作一些具有益智功能的玩具。
此外,我们还可以挑战自己,寻找更复杂的一笔画完图形,或者探究一笔画完与其他数学领域的关联。
四、总结总的来说,一笔画完的规律为我们提供了一个理解这个趣味游戏的理论基础。
通过掌握这些规律,我们可以更好地享受这个游戏带来的乐趣,同时也可以挑战自己的智慧。
二年级奥数:《有趣的一笔画》

二年级奥数:《有趣的一笔画》(预热)前铺知识一、认识单双数单数:1、3、5、7、9、11……双数:0、2、4、6、8、10……(注意:0是最小的双数)二、了解一笔画的初步概念对于一笔画的具体条件,我们上课的时候会加以说明,但是一笔画出的意义,可以让孩子提前有所认识:笔不离开纸,不来来回回重复画,一笔画成.比如:乙日十这三个字中,前两个是可以用一笔写出来的,而第三个则不可以.三、找规律品川这两个字显然都不能用一笔画画出,它们之间有什么共同点呢?尝试可以发现要想画完整笔都得离开纸,也就是说是断开的,没有连通,也叫不连通.所以一笔画的要求是首先得是连通图.本讲重点这一讲的知识实际上是比较特别的,是否能够一笔画用数学知识来概括的非常的复杂,但是同学们却能够通过找规律发现本堂课的知识并很好的掌握.同时可以培养孩子平时找规律的习惯,这也是数学题目中常见的一种方法,也是一种非常科学的思维习惯——归纳与演绎.三年级的时候我们会进一步教同学们多笔画的知识,对奇点偶点的判断也是学习这类型问题的基础.如何预习?为了保护孩子课前的好奇心和学习兴趣,以及保证课堂效果,家长在给孩子预习的时候,一定要把握好度.预习,切忌给孩子讲解书本上的例题和知识点,因为孩子容易先入为主,如果家长选取的方式方法不当,那么孩子很难转换思路了;另外,家长给孩子讲过例题后,孩子可能会觉得自己已经学会了,上课的时候就不愿意认真听了.我们预习的目的是回顾这一讲课前的铺垫知识,以及引起孩子的思考,因此家长可以把我们的这份预习资料打印出来,让孩子自己看一看,如果孩子有不明白的,您可以适当点拨.《有趣的一笔画》【知识点总结】一、什么是一笔画?特点:笔不离纸,不重复,一笔画成.前提:能一笔画的图形必须是连通图.【例】:下面的图形能不能一笔画成?都不能,因为都不是连通图.二、单数点和双数点1. 单数点:从该点出发一共有单数条线的点;2. 双数点:从该点出发一共有双数条线的点.判断小技巧:可以想象自己站在那个点有几条路可以走.(上,下,左,右)三、一笔画的判定1. 图形是连通图2. 有0个或2个单数点的能一笔画3. 超过2个单数点的不能一笔画【例】下面的图形哪些可以一笔画成?2个单数点4个单数点0个单数点可以一笔画不能一笔画可以一笔画四、如何一笔画1.有0个单数点的:同进同出.意思是从哪一个点开始画就哪一个点结束.2.有2个单数点的:单进单出.意思是从一个单数点开始画,另一个单数点结束.五、多笔画变一笔画方法:添(去)单数点之间的线【例】下面的图形都不能一笔画,想办法给每个图形添加一条线段让它变成可以一笔画的图形.(1)(2)(1)(2)本来的图形都有4个单数点不能一笔画,单数点多了,至少得变成2个单数点才能一笔画,那就想办法让其中两个单数点变成双数点,只要在任意两个单数点间添上一条线就可以了.六、一笔画的应用方法:画点线图画法:区域成点,通道成线.【例】下图是一幅简易地图,能不能一次性不重复地走完所有的路.乙村甲村丙村首先要明白题意,把人看成笔,就变成了一次性不重复地画完所有的路,其实就是一笔画!先画出点线图:甲村,乙村,丙村看成点,道路看成线.再判断:有两个单数点,可以一笔画.甲→乙→丙→甲→乙【学习建议】本讲讲的是一笔画,首先要了解什么是一笔画,再学会如何判断能不能一笔画,怎么画?问清楚自己这几个问题简单的一笔画就没问题了.然后再去拓展一笔画的应用,以及初步掌握多笔画如何变成一笔画,更多关于多笔画的内容我们在三年级还会遇到.最后,学习这讲的内容还需要同学们勤标记,多尝试,记规律.《有趣的一笔画》练习1. 判断下面的图形能不能一笔画?为什么?A B C D2. 下面的图形都是不能一笔画成的,你能不能去掉一条线,使他们变成一笔画?3. 下面是一座公园的道路设计图,问能不能一次不重复的把所有小路都走遍?要从哪里开始?HGA D FE CB4、小明要把四个三角形和一个正方形一次性从纸上剪下来,他能做到吗?5、平安小镇上有两个邮递员,甲邮递员喜欢从A 点出发开始送信,乙邮递员喜欢从B点出发开始送信,他们俩都选择最优路线,谁能更快的跑遍多有的街道呢?6. 幸福乡有四个村庄,幸福河从村庄间流过,村民们在河上一共建了5 座桥,问来到幸福乡的人能不能一次不重复地走遍所有的桥.答案解析1.①0个单数点,可以一笔画;②0个单数点,可以一笔画;③4个单数点,不可以一笔画;④2个单数点,可以一笔画2. 答案不唯一.3.图中有两个单数点A和H,从A或H开始就能一笔画.4.有两个单数点,可以一次性剪下所有的图形.5.图中有两个单数点A和E,从单数点出发可以不重复地跑遍所有街道,从B点出发必须要重复才能跑遍多有街道,所以从A点出发的甲邮递员更快.6. 画点线图如下,有两个单数点,所以可以一次不重复走遍所有的桥.。
(小学一年级作文)趣味数学-笔画和欧拉的七桥问题

趣味数学-笔画和欧拉的七桥问题老师要求一笔要画完,左边的这三个,很简单啊,多好看的飞机、大树和鱼儿呀!
老师给我们讲了一个故事:在德国的有个人提出一个问题:一个步行者从这四块陆地的任何一块出发,怎样才能不重复、不遗漏地一次走完七座桥?很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决这个问题。
直到____年,数学家欧拉研究并解决了此问题,他把这个问题归结为“一笔画”问题,证明上述走法是根本不可能的。
1、凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
2、凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起点,另一个奇点终点。
3、其他情况的图都不能一笔画出。
以后,一笔画一个图形的问题再也难不倒我了!欧拉的故事告诉我,做任何事情都需要认真细致的去观察,除了多次的尝试去做,也需在反复做的过程中去总结,才会发现真理!
老师通过一个画画小游戏,给我们讲解了数学家欧拉七桥故事,让我们明白了做任何事情都需要认真细致的去观察,除了多次的尝试去做,也需在反复做的过程中去总结,才会发现真理!。
小学奥数奇妙的一笔画题库教师版

奇妙的一笔画例题精讲所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画.多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n个奇点(n为自然数),那么这个图一定可以用n笔画成.【例 1】我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点哪些点是奇点【解析】奇点:J D H F偶点:A E B C G I【例 2】判断下列图a、图b、图c能否一笔画.【解析】图a能,因为有2个奇点,图b不能,因为图形不是连通的,图c能,因为因为图中全是奇点【例 3】下面图形能不能一笔画成若果能,应该怎样画【解析】图1能因为图中全是偶点,图2能因为图中全是偶点,图3不能因为有4个奇点.【例 4】下面的图形,哪些能一笔画出哪些不能一笔画出【解析】第1个能,2、3不能【例 5】下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.【解析】不能一笔画出,因为图中有E H G F四个奇点,连结EH就可以使图形一笔画出.【例 6】下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁该怎样爬【解析】要想不重复爬出,需要图形能一笔画出,由于图中有两个奇点,所以应该从奇点出发才能一笔画出图形,所以甲蚂蚁能够.【例 7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形【解析】可以.【例 8】下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里【解析】要想不重复,需要路线能一笔画出,由于图中有两个奇点,所以入口和出口应该分别放在两个奇点出,即F和I点.【例 9】邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适【解析】不走重复路,一笔能画出路线图,图中有2个奇点,应该从奇点处出发,下面有一种参考路线:4-1-2-5-8-9-6-【例 10】观察下面的图,看各至少用几笔画成【解析】图(1)有8个奇点,所以要4笔画出,图(2)有12个奇点,所以要一笔画出,图(3)能一笔画出.【例 11】判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.【解析】图(1)不能一笔画出,因为图中有4个奇点,连结BD,或者去掉BF都可以使图形能一笔画出.图(2)不能一笔画出,因为图中有4个奇点,去掉KL,或者BK都可以使图形能一笔画出.图(3)不能一笔画出,因为图中有4个奇点,去掉AB可以使图形能一笔画出.一个K(K>1)笔画最少要添加几条连线才能变成一笔画呢我们知道K笔画有2K个奇点,如果在任意两个奇点之间添加一条连线,那么这两个奇点同时变成了偶点.如左下图中的B,C两个奇点在右下图中都变成了偶点.所以只要在K笔画的2K个奇点间添加(K-1)笔就可以使奇点数目减少为2个,从而变成一笔画.【例 12】18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A和一座半岛D,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功【解析】欧拉解决这个问题的方法非常巧妙.他认为:人们关心的只是一次不重复地走遍这七座桥,而并不关心桥的长短和岛的大小,因此,岛和岸都可以看作一个点,而桥则可以看成是连接这些点的一条线.这样,一个实际问题就转化为一个几何图形(如下图)能否一笔画出的问题了.而图B中有4个奇点显然不能一笔画出.【巩固】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥【解析】能【例 13】右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出【解析】将图形中的6个区域看成6个点,每个门看成连结他们的线段,显然6个点都是偶点,所以有人能一次不重复的走过所有的门.【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门如果不能,请说明理由.如果能,应从哪开始走【解析】不能【例 14】一条小虫沿长6分米,宽4分米,高5分米的长方体的棱爬行.如果它只能进不能退,并且同一条棱不能爬两次,那么它最多能爬多少分米【解析】8个定点都是奇点,所以至少需要4笔.多画长和高能保证总路程最长,为A-B-G-H-A-D-C-F-E-D总长为6×4+5×4 +4×1=48分米.【巩固】一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A点时,最多能爬行多少厘米【解析】最多34厘米【例 15】如图是某餐厅的平面图,共有五个小厅,相邻两厅之间有门相通,并且设有入口.请问你能否从入口进入一次不重复地穿过所有的门.如果可以,请指明穿行路线,如果不能,应关闭哪个门就可以办到【解析】可以将图中的五个小厅以及厅外的部分都抽象成点,为方便解题,给它们分别编号.这时,连通厅与厅之间的门就相当于各点之间的连线.于是题目中餐厅的平面图就抽象成为一个连通的图形,求穿形路线的问题就转化成一笔画的问题.在抽象出的图形中,我们可以找到四个奇点,即①、④、③和厅外,所以图形不能一笔画出也就是说,从入口进入不可能一次不重复的穿过所有的门.但根据一笔画问题的知识,只要关闭门,把③、④变为偶点,就可以办到,可行路线如下图:B【例 16】在3×3的方阵中每个小正方形的边长都是100米.小明沿线段从A点到B 点,不许走重复路,他最多能走多少米【解析】这道题大多数同学都采用试画的方法,实际上可以用一笔画原理求解.首先,图中有8 个奇点,在8 个奇点之间至少要去掉4 条线段,才能使这8 个奇点变成偶点;其次,从A点出发到B 点,A,B 两点必须是奇点,现在A,B 都是偶点,必须在与A,B 连接的线段中各去掉1 条线段,使A,B 成为奇点.所以至少要去掉6 条线段,也就是最多能走1800 米,走法如图【例 17】一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发,要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短全程多少千米【解析】图中共有8 个奇点,必须在8 个奇点间添加4 条线,才能消除所有奇点,成为能从邮局出发最后返回邮局的一笔画.在距离最近的两个奇点间添加一条连线,如左下图中虚线所示,共添加4 条连线,这4 条连线表示要重复走的路,显然,这样重复走的路程最短,全程30 千米.走法参考右下图(走法不唯一).。
一笔画完的规律

一笔画完的规律
【实用版】
目录
1.一笔画完的定义与特点
2.一笔画完的规律
3.一笔画完的应用实例
4.结论
正文
一笔画完的定义与特点
一笔画完,又称连通图,是指在一个平面内,通过一笔连续的线段将所有点连接起来,并且线段不能重复经过已经连接过的点。
一笔画完是一个具有挑战性和趣味性的数学问题,它涉及到图论的知识,具有广泛的应用。
一笔画完的规律
一笔画完的规律可以归纳为以下几点:
1.所有点必须处于连通状态,即从一个点出发,可以通过线段到达所有其他点。
2.奇数点时,必须有一个点是起点或终点,否则无法连接所有点。
3.偶数点时,起点和终点必须相邻,否则无法连接所有点。
4.所有线段不能相交,否则会导致无法通过一笔画完连接所有点。
一笔画完的应用实例
一笔画完在实际生活中有很多应用,例如:
1.旅行商问题(TSP 问题):在给定的城市之间选择最短路径,使得
一辆卡车能够一次性地经过所有城市并返回起点。
2.电子电路设计:在印刷电路板上设计线路,使得所有元件能够通过一笔画完连接。
3.物流配送:在一定区域内设置仓库和配送点,使得所有客户能够通过一笔画完的方式接收货物。
结论
一笔画完问题不仅是图论领域的一个有趣问题,同时也具有广泛的实际应用。
了解一笔画完的规律和特点,有助于解决实际生活中的许多问题。
数学新思维一笔画

$
我能用一笔画出 下面这些图形。
$
例1:判断下列图形是否能一笔画成,并说明理由。
我发现这些图形中都有好多点。 这些点对我们的判断有帮助吗?
这些点叫做线段的端点。
$
(1)从一个端点引出的线段条数是双数的,叫 做双数点(偶点)。 (2)从一个端点引出的线段条数是单数的,叫 做单数点(奇点)。
$
端点数
$
例3:下图是一个公园的道路平面图,要使游客走遍每条路而 又不重复,出、入口应该设在哪里?
分析
这个图形中有2个单数点(I、E),7个 双数点。怎样才能一笔画这个图形呢?
一笔画的要求是,以一个单数点为起点,以另 一个单数点为终点。所以出、入口应该分别设在I 点、E点。
$
例4:下面的图形能不能一笔画成?如果不能,请你加一条线 使这个图形能一笔画成。
分析
这个图形中有4个单数点,4个双数点。怎样才 能一笔画这个图形呢?
这个图形要想一笔画成, 就得全是双数点或只有 两个单数点,怎么办呢?
$
在两个单数点之间 添上一条线就能使这两个 单数点变成双数点了!
$
例5:下面的图形能不能一笔画成?如果不能,请你添加线段 使其能一笔画成。
•
分析
这个图形中有4个单数点,5个双数点。怎样才能一笔画这个图 形呢?
1、参观博物馆
——一笔画
$
程程和朋朋要参观完博物馆的每个角落,但是他们又不想走 重复的路线。
你能帮他们制定出合理的参观路线吗?
$
不走重复路线,就是数学中一笔画的问题。
“一笔画”是指笔不离开纸, 而且每条线都只画一次不准
重复而画成的图形。
“一笔画”是一种有趣的数学游戏,什么样的图形可以一笔画成呢? 试一试,画一画,发挥你的想象力,发现一笔画的规律。
兴趣 七桥问题与一笔画

仔细观察并找出规律
①可以一笔画成的图形,与偶点个数无关,与奇点个数有关. 其个数是0或2. ②其中若奇点个数为0,可选任一个点做起点,且一笔画后可 以回到出发点。若奇点个数为2,可选其中一个奇点做起点, 而终点一定是另一个奇点,即一笔画后不可以回到出发点。图 形中任何端点根据所连接线条数被分为奇点、偶点。只有所有 点为偶点的图形和只有两个奇点的图形可以一笔画。只有偶点 的图形不限出发点,只有两个奇点必然从其中一点出发到另一 点结束。在任何图形中,奇点都是成对出现的,没有奇数个奇 点的图形。
仔 细 观 察 并填写
下列图形中。请找出每个图的奇点个数,偶点个数。试一 试哪些可以一笔画出,请填表,从中你能发现什么规律? 对于图①②③⑥⑦有什么共 同的特点?如果它们能一笔 画,必须从什么样的点出发 ?你得到了那些结论? 对于图①②③④⑤⑥⑨有什 么共同的特点?如果它们能 一笔画,必须从什么样的点 出发?你得到了哪些结论?
我们是个设计规划师
知识来源于生活,通过学以致用,把在探究活动中学到的 知识又服务日常生活之中。在此设置三道练习题,让学生 分析问题及解决问题的能力在此得到升华,同时也增强数 学的趣味性。 一辆洒水车要给某 城市的街道洒水, 街道地图如下:你 能否设计一条洒水 车洒水的路线,使 洒水车不重复地走 过所有的街道,再 回到出发点?
1、今天你学到了你想要的只是了吗? 2、所学的知识能够对你解题有帮助吗? 3、有没有你想学但是没有学到的知识。 4、...... . . . . . .
同学们,下节课再见!
聪明在于学习,天才在于积累。
哥尼斯堡问题
用你发现的规律,说一说七桥问题的答案?
答:因为奇点个数为4,所以七桥问题不能一笔画,也就 是说,不能不重复地走过所有的七座桥,再回到出发点 。
一笔画出的数学题

一笔画出的数学题
今天数学课老师给我们出了一道很有趣的数学题目,让我们用一笔画出一个图形,使得图形上每个点都只被画一次,最后得到的图形可以分解成若干个三角形。
我们思考了一会儿,尝试了几次,发现好像不太容易完成这个任务。
但是,我们并没有放弃,而是继续尝试。
我们发现,要想一笔画出图形,并且满足上述条件,就必须先找到一些规律。
我们发现,所有的三角形都是由三个点组成的,而且这三个点之间的连线不会相交。
于是我们开始寻找这些点,不断尝试,最终找到了一组符合要求的点序列。
然后,我们就开始画图了。
画图的过程中,我们需要依次连接这些点,但是不能出现交叉的情况。
这个过程中,我们需要不断调整方向和角度,才能最终完成任务。
最终,我们成功地用一笔画出了这个数学题,得到了一个可以分解成若干个三角形的图形。
这个过程虽然有些困难,但是我们也学到了很多。
我们明白了,只有不断尝试,才能发现问题的规律,并最终解决问题。
- 1 -。
一笔画练习题

一笔画练习题一笔画练习题是一种有趣而具有挑战性的智力游戏。
它要求玩家在不抬笔、不重复线段,且必须将所有点连接起来的条件下来画出一个特定的图形。
这种练习题既可以锻炼我们的空间想象力,又能提高我们的逻辑思维和解决问题的能力。
本文将对一笔画练习题的原理进行解析,并提供一些经典的练习题供读者挑战。
一笔画练习题的原理是利用图论中的欧拉图和哈密顿图的概念。
欧拉图是指一种只有0个或2个奇数度顶点的连通图。
换言之,如果一个图中存在奇数度顶点的个数大于2,那么这个图就不可能被一笔画出。
相反,如果一个图中所有顶点的度数都是偶数,那么这个图就可以被一笔画出。
哈密顿图是指一种包含每个顶点且不重复经过每条边的图。
如果在一笔画的过程中,我们能够遍历每个点恰好一次,并且每条线段都恰好被经过一次,那么这个题目就可以被正确解答。
接下来,我们来看几个经典的一笔画练习题。
1. 五个点的一笔画题目题目要求:画出一个正五边形,五个顶点依次为A、B、C、D、E。
解答:根据欧拉图的原理,五个顶点都是偶数度,因此可以一笔画出。
首先,我们可以从A点开始,按照顺时针或逆时针的方向连接四个线段分别到达B、C、D、E五个顶点,最终回到A点,形成一个正五边形。
2. 六个点的一笔画题目题目要求:画出一个六边形,六个顶点依次为F、G、H、I、J、K。
解答:根据欧拉图的原理,六个顶点中有两个顶点的度数为奇数,所以不可能一笔画出。
这也是六个点的一笔画题目中常见的例子,可以提醒我们在做一笔画题时要注意图的结构。
3. 七个点的一笔画题目题目要求:画出一个正方形,七个顶点依次为L、M、N、O、P、Q、R。
解答:根据欧拉图的原理,七个顶点中有一个顶点的度数为奇数,所以不可能一笔画出。
我们可以设想,从任意一个顶点开始,我们无法回到这个顶点,因为每次画线段都必须经过一个未访问的点,而这个未访问的点最后不能回到起点。
因此,无论从哪个点开始,都无法满足条件。
通过以上的例子,我们可以看出在一笔画练习题中,图的结构对是否能够一笔画出影响很大。
一笔画趣味数学

甲乙两个邮递员去送信,两人同时出发
以同样的速度走遍所有的街道,甲从A点出 发,乙从B点出发,最后都回到邮局(C点)。 如果要选择最短的线路,谁先回到邮局?
一笔画图片欣赏
一笔画图片欣赏
课后作业
请你观察生活,设计一个运用“一笔 画”的数学知识来解决的实际问题,并与 同伴交流。
谢谢!
A
B
C
D
欧拉:“一笔画图”的规 规律律3:
如果没有奇点,那么每个点都能作为起点;
如果有两个奇点,那其中一个必为起点,另 一个必为终点。
怎样走才能不重复不遗漏地逛完整个超市?
零食区
服
文
装家电区具区区日常用品区课堂练习
下面是一公园的平面图,要使游客走 遍每一条路,且不重复,问出入口应设在 哪里?
让我们先来了解两个新概念
1、奇点:有奇数条边相连的点 2、偶点:有偶数条边相连的点
探究“一笔画”与奇偶点个数之间的关系
图形 能否一笔画成 奇点个数 偶点个数
能
2个
2个
能
2个
4个
能
0个
6个
能
0个 10个
能
0个
8个
能
0个
9个
欧拉:“一笔画图”的规
规律律1:凡能一笔画的图形必须是一个连通图;
规律2:凡能一笔画的图形,与偶点个数无关, 与奇点个数有关,其个数是0或2.
把与奇数条边相连的结点叫做奇点, 把与偶数条边相连的点称为偶点.
①凡是由偶点组成的连通图,一定可以一笔画成; 画时可以任一偶点为起点,最后一定能以这个点为 终点画完此图。
②凡是只有两个奇点(其余均为偶点)的连通图, 一定可以一笔画完;画时必须以一个奇点为起点, 另一个奇点为终点。
小学奥数著名问题之——一笔画问题习题集

一笔画问题(教师必备)一、欧拉的一笔画原理是:(1)一笔画必须是连通的(图形的各部分之间连接在一起);(2)没有奇点的连通图形是一笔画,画时可以以任一偶点为起点,最后仍回到这点;(3)只有两个奇点的连通图形是一笔画,画时必须以一个奇点为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形不是一笔画。
利用一笔画原理,七桥问题很容易解决。
因为图中A,B,C,D都是奇点,有四个奇点的图形不是一笔画,所以一个散步者不可能不重复地一次走遍这七座桥。
二、顺便补充两点:(1)一个图形的奇点数目一定是偶数。
因为图形中的每条线都有两个端点,所以图形中所有端点的总数必然是偶数。
如果一个图形中奇点的数目是奇数,那么这个图形中与奇点相连接的端点数之和是奇数(奇数个奇数之和是奇数),与偶点相连的线的端点数之和是偶数(任意个偶数之和是偶数),于是得到所有端点的总数是奇数,这与前面的结论矛盾。
所以一个图形的奇点数目一定是偶数。
(2)有K个奇点的图形要K÷2笔才能画成。
例如:下页左上图中的房子共有B,E,F,G,I,J六个奇点,所以不是一笔画。
如果我们将其中的两个奇点间的连线去掉一条,那么这两个奇点都变成了偶点,如果能去掉两条这样的连线,使图中的六个奇点变成两个,那么新图形就是一笔画了。
将线段GF和BJ去掉,剩下I和E两个奇点(见右下图),这个图形是一笔画,再添上线段GF和BJ,共需三笔,即(6÷2)笔画成。
一个K(K>1)笔画最少要添加几条连线才能变成一笔画呢?我们知道K笔画有2K个奇点,如果在任意两个奇点之间添加一条连线,那么这两个奇点同时变成了偶点。
如左下图中的B,C两个奇点在右下图中都变成了偶点。
所以只要在K笔画的2K个奇点间添加(K-1)笔就可以使奇点数目减少为2个,从而变成一笔画。
三、到现在为止,我们已经学会了如何判断一笔画和多笔画,以及怎样添加连线将多笔画变成一笔画,看下面的例题:1.下列图形分别是几笔画?怎样画?2.能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?3.从A点出发,走遍右上图中所有的线段,再回到A点,怎样走才能使重复走的路程最短?4.下图是国际奥林匹克运动会的会标,能一笔画吗?如果能,请你把它画出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探究“一笔画”与奇偶点个数之间的关系
图形
能否一笔画成 奇点个数 偶点个数
能
能 能 能 能
2个
ቤተ መጻሕፍቲ ባይዱ2个 0个
2个 4个
6个 10个
8个
0个
0个 0个
能
9个
欧拉:“一笔画图”的规 规律律 1:凡能一笔画的图形必须是一个连通图;
规律2:凡能一笔画的图形,与偶点个数无关, 与奇点个数有关,其个数是0或2.
从哥尼斯堡 七桥问题谈起
故事发生在18世纪的哥尼斯堡城.流经那里的一条 河中有两个小岛,还有七座桥把这两个小岛与河岸 联系起来,
那里风景优美,游人众多.在这美丽的地方, 人们议论着一个有趣的问题:一个游人怎样 才能不重复地一次走遍七座桥,最后又回到 出发点呢?
直到1836年,瑞士著名的数学家欧拉才证明了这个 问题的不可能性。 欧拉解决这个问题的方法非常巧妙.他认为: 人们关心的只是一次不重复地走遍这七座桥,而 并不关心桥的长短和岛的大小,因此,岛和岸都 可以看作一个点,而桥则可以看成是连接这些点 的一条线.这样,一个实际问题就转化为一个几何 图形(如下图)能否一笔画出的问题了.
课前小游戏——科学家的生日都有此规律
按照以下方法计算其结果都能等于“9”,你 也用你的生日来试试吧!看看你有成为科学家的 潜质吗?
将生日日期组成一个八位数 如:爱因斯坦的生日1879年3月14日,即18790314 任意重新排列这些数字 如:37140819 用大数减去小数 如:37140819-18790314 =18350505 把差的各位上的数字加起来 如果加起来会等于9;或将得到的两位数相加 能等于9(如1+8+3+5+0+5+0+5=27 2+7=9) 你能等于“9”吗?
A
B
①凡是由偶点组成的连通图,一定可以一笔画成; 画时可以任一偶点为起点,最后一定能以这个点为 终点画完此图。 ②凡是只有两个奇点(其余均为偶点)的连通图, 一定可以一笔画完;画时必须以一个奇点为起点, 另一个奇点为终点。 ③其他情况的图,都不能一笔画出。
让我们先来了解两个新概念
1、奇点:有奇数条边相连的点 2、偶点:有偶数条边相连的点
欢迎您多提宝贵意见!
甲乙两个邮递员去送信,两人同时出发 以同样的速度走遍所有的街道,甲从A点出 发,乙从B点出发,最后都回到邮局(C点)。 如果要选择最短的线路,谁先回到邮局?
一笔画图片欣赏
一笔画图片欣赏
课后作业
请你观察生活,设计一个运用“一笔 画”的数学知识来解决的实际问题,并与 同伴交流。
世界是美的, 只要有一双发现美的眼睛; 数学是美的, 只要有一颗发现美的心灵。
A
B
C
D
欧拉:“一笔画图”的规 规律律 3:
如果没有奇点,那么每个点都能作为起点; 如果有两个奇点,那其中一个必为起点,另 一个必为终点。
怎样走才能不重复不遗漏地逛完整个超市?
零食区 服 装 区 家电区 日常用品区 文 具 区
课堂练习
下面是一公园的平面图,要使游客走 遍每一条路,且不重复,问出入口应设在 哪里?
