必修四任意角附答案

合集下载

人教a版必修4学案：1.1.1任意角(含答案)

第一章三角函数§1.1任意角和弧度制1.1.1任意角自主学习知识梳理1．角的概念(1)角的概念：角可以看成平面内________________绕着________从一个位置________到另一个位置所成的图形．(2)角的分类：按旋转方向可将角分为如下三类：类型定义图示正角按______________________形成的角负角按________________形成的角零角一条射线________________，称它形成了一个零角2.象限角角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，那么，角的终边(除端点外)在第几象限，就说这个角是______________．如果角的终边在坐标轴上，就认为这个角不属于任何一个象限．3．终边相同的角所有与角α终边相同的角，连同角α在内，可构成一个集合S＝{β|β＝____________}，即任一与角α终边相同的角，都可以表示成角α与____________的和．4．终边落在坐标轴上角的集合终边所在的位置角的集合x轴正半轴x轴负半轴x轴y轴正半轴y轴负半轴y轴自主探究终边落在各个象限的角的集合.α终边所在的象限角α的集合第一象限第二象限第三象限第四象限对点讲练知识点一终边相同的角与象限角例1在0°～360°范围内，找出与下列各角终边相同的角，并判定它们是第几象限角．(1)－150°；(2)650°；(3)－950°15′.回顾归纳解答本题可先利用终边相同的角的关系：β＝α＋k ·360°，k ∈Z ，把所给的角化归到0°～360°范围内，然后利用0°～360°范围内的角分析该角是第几象限角．变式训练1 判断下列角的终边落在第几象限内： (1)1 400°； (2)－2 010°.知识点二终边相同的角的应用例2 已知，如图所示，(1)写出终边落在射线OA ，OB 上的角的集合； (2)写出终边落在阴影部分(包括边界)的角的集合．回顾归纳解答此类题目应先在0°～360°上写出角的集合，再利用终边相同的角写出符合条件的所有角的集合，如果集合能化简的还要化成最简．变式训练2 如图所示，写出终边落在阴影部分的角的集合．知识点三角的象限的判断例3 已知α是第二象限角，试确定2α，α2的终边所在的位置．回顾归纳若已知角α是第几象限角，判断α2，α3等是第几象限角，主要方法是解不等式并对k 进行分类讨论．考查角的终边的位置．变式训练3 已知α为第三象限角，则α2所在的象限是( )A ．第一或第二象限B ．第二或第三象限C ．第一或第三象限D ．第二或第四象限1．对角的理解，初中阶段是以“静止”的眼光看，高中阶段应用“运动”的观点下定义，理解这一概念时，要注意“旋转方向”决定角的“正负”，“旋转幅度”决定角的“绝对值大小”．2．关于终边相同角的认识一般地，所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋k ·360°，k ∈Z }，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．注意：(1)α为任意角．(2)k ·360°与α之间是“＋”号，k ·360°－α可理解为k ·360°＋(－α)．(3)相等的角，终边一定相同；终边相同的角不一定相等，终边相同的角有无数多个，它们相差360°的整数倍．(4)k ∈Z 这一条件不能少.课时作业一、选择题 1．与405°角终边相同的角是( ) A ．k ·360°－45°，k ∈Z B ．k ·180°－45°，k ∈Z C ．k ·360°＋45°，k ∈Z D ．k ·180°＋45°，k ∈Z 2．若α＝45°＋k ·180° (k ∈Z )，则α的终边在( ) A ．第一或第三象限 B ．第二或第三象限 C ．第二或第四象限 D ．第三或第四象限 3．若角α与β的终边相同，则α－β的终边落在( ) A ．x 轴的正半轴 B ．x 轴的负半轴 C ．y 轴的正半轴 D ．y 轴的负半轴 4．若α是第四象限角，则180°－α是( ) A ．第一象限角 B ．第二象限角 C ．第三象限角 D ．第四象限角 5. 如图，终边落在阴影部分(含边界)的角的集合是( )A ．{α|－45°≤α≤120°}B ．{α|120°≤α≤315°}C ．{α|k ·360°－45°≤α≤k ·360°＋120°，k ∈Z }D ．{α|k ·360°＋120°≤α≤k ·360°＋315°，k ∈Z }二、填空题6．经过10分钟，分针转了________度．7．下列命题：①第一象限角都是锐角；②锐角都是第一象限角；③第一象限角一定不是负角；④第二象限角大于第一象限角；⑤第二象限角是钝角；⑥小于180°的角是钝角、直角或锐角．其中判断错误的是______．(把有关命题的序号写上即可)8．若α＝1 690°，角θ与α终边相同，且－360°<θ<360°，则θ＝________.三、解答题9．在与角－2 010°终边相同的角中，求满足下列条件的角．(1)最小的正角；(2)最大的负角；(3)－720°～720°内的角．10．已知角x的终边落在图示阴影部分区域，写出角x组成的集合．第一章三角函数§1.1任意角和弧度制1．1.1任意角知识梳理1．(1)一条射线端点旋转(2)类型定义图示正角按逆时针方向旋转形成的角负角按顺时针方向旋转形成的角零角一条射线没有作任何旋转，称它形成了一个零角3．α＋k·360°，k∈Z整数个周角4.终边所在的位置角的集合x轴正半轴{α|α＝k·360°，k∈Z}x轴负半轴{α|α＝k·360°＋180°，k∈Z}x轴{α|α＝k·180°，k∈Z}y轴正半轴{α|α＝k·360°＋90°，k∈Z}y轴负半轴{α|α＝k·360°＋270°，k∈Z}y轴{α|α＝k·180°＋90°，k∈Z}自主探究α终边所在的象角α的集合限第一{α|k·360°<α<k·360°＋90°，k∈Z}象限第二{α|k·360°＋90°<α<k·360°＋180°，k∈Z}象限第三{α|k·360°＋180°<α<k·360°＋270°，k∈Z}象限第四{α|k·360°－90°<α<k·360°，k∈Z}象限对点讲练例1解(1)因为－150°＝－360°＋210°，所以在0°～360°范围内，与－150°角终边相同的角是210°角，它是第三象限角．(2)因为650°＝360°＋290°，所以在0°～360°范围内，与650°角终边相同的角是290°角，它是第四象限角．(3)因为－950°15′＝－3×360°＋129°45′，所以在0°～360°范围内，与－950°15′角终边相同的角是129°45′角，它是第二象限角．变式训练1解(1)1 400°＝3×360°＋320°，∵320°是第四象限角，∴1 400°也是第四象限角．(2)－2 010°＝－6×360°＋150°，∴－2 010°与150°终边相同．∴－2 010°是第二象限角．例2解(1)终边落在射线OA上的角的集合是{α|α＝k·360°＋210°，k∈Z}．终边落在射线OB上的角的集合是{α|α＝k·360°＋300°，k∈Z}．(2)终边落在阴影部分(含边界)角的集合是{α|k·360°＋210°≤α≤k·360°＋300°，k∈Z}．变式训练2解设终边落在阴影部分的角为α，角α的集合由两部分组成．(1){α|k·360°＋30°≤α<k·360°＋105°，k∈Z}．(2){α|k·360°＋210°≤α<k·360°＋285°，k∈Z}．∴角α的集合应当是集合(1)与(2)的并集：{α|k·360°＋30°≤α<k·360°＋105°，k∈Z}∪{α|k·360°＋210°≤α<k·360°＋285°，k∈Z}＝{α|2k·180°＋30°≤α<2k·180°＋105°，k∈Z}∪{α|(2k＋1)·180°＋30°≤α<(2k＋1)·180°＋105°，k∈Z}＝{α|2k·180°＋30°≤α<2k·180°＋105°或(2k＋1)·180°＋30°≤α<(2k＋1)·180°＋105°，k∈Z}＝{α|k ·180°＋30°≤α<k ·180°＋105°，k ∈Z }．例3 解因为α是第二象限角，所以k ·360°＋90°<α<k ·360°＋180°，k ∈Z . 所以2k ·360°＋180°<2α<2k ·360°＋360°，k ∈Z ，所以2α的终边在第三或第四象限或终边在y 轴的非正半轴上．因为k ·360°＋90°<α<k ·360°＋180°，k ∈Z ，所以k ·180°＋45°<α2<k ·180°＋90°，k ∈Z ，所以当k ＝2n ，n ∈Z 时，n ·360°＋45°<α2<n ·360°＋90°，即α2的终边在第一象限；当k ＝2n ＋1，n ∈Z 时，n ·360°＋225°<α2<n ·360°＋270°，即α2的终边在第三象限．所以α2的终边在第一或第三象限．变式训练3 D [由于k ·360°＋180°<α<k ·360°＋270°，k ∈Z ，得k 2·360°＋90°<α2<k 2·360°＋135°. 当k 为偶数时，α2为第二象限角；当k 为奇数时，α2为第四象限角．]课时作业 1．C 2.A3．A [∵α＝β＋k ·360°，k ∈Z ， ∴α－β＝k ·360°，k ∈Z .]4．C [可以给α赋一特殊值－60°，则180°－α＝240°，故180°－α是第三象限角．]5．C [与边界终边相同的角为k ·360°＋120°或k ·360°－45°.故阴影部分的角为k ·360°－45°≤α≤k ·360°＋120°，k ∈Z .] 6．－607．①③④⑤⑥解析 ①390°角是第一象限角，可它不是锐角，所以①不正确．②锐角是大于0°且小于90°的角，终边落在第一象限，故是第一象限角，所以②正确． ③－330°角是第一象限角，但它是负角，所以③不正确．④120°角是第二象限角，390°是第一象限角，显然390°>120°，所以④不正确． ⑤480°角是第二象限角，但它不是钝角，所以⑤不正确．⑥0°角小于180°，但它既不是钝角，也不是直角或锐角，故⑥不正确． 8．－110°或250°解析 ∵α＝1 690°＝4×360°＋250°，∴θ＝k ·360°＋250°，k ∈Z .∵－360°<θ<360°， ∴k ＝－1或0. ∴θ＝－110°或250°.9．解(1)∵－2 010°＝－6×360°＋150°，∴与角－2 010°终边相同的最小正角是150°.(2)∵－2 010°＝－5×360°＋(－210°)，∴与角－2 010°终边相同的最大负角是－210°.(3)∵－2 010°＝－6×360°＋150°，∴与－2 010°终边相同也就是与150°终边相同．由－720°≤k·360°＋150°<720°，k∈Z，解得：k＝－2，－1,0,1.代入k·360°＋150°依次得：－570°，－210°，150°，510°.10．解(1){x|k·360°－135°≤x≤k·360°＋135°，k∈Z}．(2){x|k·360°＋30°≤x≤k·360°＋60°，k∈Z}∪{x|k·360°＋210°≤x≤k·360°＋240°，k∈Z}＝{x|2k·180°＋30°≤x≤2k·180°＋60°或(2k＋1)·180°＋30°≤x≤(2k＋1)·180°＋60°，k∈Z}＝{x|k·180°＋30°≤x≤k·180°＋60°，k∈Z}．。

高一数苏教必修四讲义：第1章 1.1 1.1.1 任意角 Word含答案

任意角、弧度1．1.1任意角预习课本P5～7，思考并完成下列问题1．在初中，角是怎样定义的？2．如果角按旋转的方向来进行分类，可分为哪三类？3．如果把角放入平面直角坐标系中，象限角和轴线角的规定是怎样的？4．如何表示终边相同的角？[新知初探]1．任意角(1)角的概念一个角可以看做平面内一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形．射线的端点称为角的顶点，射线旋转的开始位置和终止位置称为角的始边和终边．(2)角的分类正角：按逆时针方向旋转所形成的角；负角：按顺时针方向旋转所形成的角；零角：射线没有作任何旋转所形成的角．[点睛]对角的理解关键是抓住旋转二字(1)要明确旋转的方向；(2)要明确旋转量的大小；(3)要明确旋转的开始位置．2．象限角、轴线角以角的顶点为坐标原点，角的始边为x轴正半轴，建立平面直角坐标系．这样，角的终边(除端点外)在第几象限，就说这个角是第几象限角．如果角的终边在坐标轴上，称这个角为轴线角．[点睛](1)角的顶点要与坐标原点重合；(2)角的始边要与x轴的正半轴重合.3．终边相同的角一般地，与角α终边相同的角的集合为{β|β＝k·360°＋α，k∈Z}．[点睛]终边相同的角与相等的角是两个不同的概念，两角相等，终边一定相同，但是两角终边相同时，两角不一定相等，它们相差360°的整数倍．[小试身手]1．下列命题正确的是____________(填序号)．①－30°是第一象限角；②750°是第四象限角；③终边相同的角一定相等；④－950°12′是第二象限的角．★答案★：④2．－1 120°角所在象限是____________．★答案★：第四象限3．与405°角终边相同的角的集合是____________．★答案★：{α|α＝k·360°＋45°，k∈Z}4．在－180°到360°范围内，与2 000°角终边相同的角为____________．★答案★：－160°，200°角的概念辨析[典例]有下列说法：①相差360°整数倍的两个角，其终边不一定相同；②{α|α是锐角}{β|0°≤β<90°}；③第一象限角都是锐角；④小于180°的角是钝角、直角或锐角．其中正确说法的序号是________．[解析]①不正确．终边相同的两个角一定相差360°的整数倍，反之也成立；②∵α是锐角，即0°<α<90°，故{α|0°<α<90°}{β|0°≤β<90°}，故②正确；③第一象限角不一定都是锐角，如380°是第一象限角，但它不是锐角，故③不正确；④0°角小于180°，但它既不是钝角，也不是直角或锐角，故④不正确．[★答案★]②有关角的概念辨析的解题策略(1)正确理解象限角及锐角、直角、钝角、平角、周角等概念．(2)可通过举出反例来进行判断．下列命题是真命题的序号是________．①三角形的内角必是一、二象限内的角；②第二象限角是钝角； ③不相等的角终边一定不同；④{α|α＝k ·360°±90°，k ∈Z}＝{α|α＝k ·180°＋90°，k ∈Z}．解析：①90°不是象限角；②如－240°是第二象限角，但不是钝角； ③如0°和360°不相等，但终边相同；④k ·360°±90°＝2k ·180°±90°＝2k ·180°＋90°或(2k －1)·180°＋90°，k ∈Z. ★答案★：④象限角及终边相同的角[典例] 在0°到360°的范围内，求出与下列各角终边相同的角，并判断是第几象限角． (1)－736°；(2)904°18′.[解] (1)－736°＝－3×360°＋344°，344°是第四象限角． ∴344°与－736°是终边相同的角，且－736°为第四象限角． (2)904°18′＝2×360°＋184°18′，184°18′是第三象限角． ∴184°18′与904°18′是终边相同的角，且904°18′为第三象限角．(1)把任意角化为α＋k ·360°(k ∈Z 且0°≤α<360°)的形式，关键是确定k .可以用观察法(α的绝对值较小)，也可用除法．要注意：正角除以360°，按通常的除法进行；负角除以360°，商是负数，其绝对值比被除数为其相反数时的商大1，使余数为正值．(2)要求适合某种条件且与已知角终边相同的角，其方法是先求出与已知角终边相同的角的一般形式，再依条件构建不等式求出k 的值．[活学活用]写出－720°到720°之间与－1 068°终边相同的角的集合为______________．解析：与－1 068°终边相同的角为－1 068°＋k ·360°，要落在－720°到720°之间，则取k ＝1,2,3,4.★答案★：{－708°，－348°，12°，372°}已知角α所在象限，判断αn 或nα(n ∈Z)所在象限[解] ∵α是第二象限角，∴90°＋k ·360°＜α＜180°＋k ·360°，k ∈Z. ∴180°＋2k ·360°＜2α＜360°＋2k ·360°，k ∈Z.∴2α是第三或第四象限角，或是终边落在y 轴的非正半轴上的角． [一题多变]1．[变设问]若本例条件不变，求α2是第几象限角？解：45°＋k 2 ·360°＜α2＜90°＋k2·360°，k ∈Z.当k 为偶数时，不妨令k ＝2n ，n ∈Z ，则45°＋n ·360°＜α2＜90°＋n ·360°，此时，α2为第一象限角；当k 为奇数时，令k ＝2n ＋1，n ∈Z ，则225°＋n ·360°＜α2＜270°＋n ·360°，此时，α2为第三象限角．∴α2为第一或第三象限角．2．[变设问]若本例条件不变，求α3是第几象限角？解：∵k ·120°＋30°<α3<k ·120°＋60°(k ∈Z)，当k ＝3n (n ∈Z)时， n ·360°＋30°＜α3＜n ·360°＋60°；当k ＝3n ＋1(n ∈Z)时， n ·360°＋150°＜α3＜n ·360°＋180°；当k ＝3n ＋2(n ∈Z)时， n ·360°＋270°＜α3＜n ·360°＋300°.∴α3是第一或第二或第四象限的角. 3．[变条件]已知α是第二象限角，且8α与2α的终边相同，判断2α是第几象限角．解：8α＝2α＋k ·360°(k ∈Z)，所以α＝k ·60°(k ∈Z)，所以，2α＝k ·120°(k ∈Z)，当k 为偶数时， 2α的终边分别落在x 轴的正半轴和第二、第三象限．当k 为奇数时，2α的终边分别落在x 轴的正半轴和第二、第三象限，所以，2α为第二或第三象限角，或是终边落在x 轴正半轴上的角．已知角α终边所在象限，(1)确定nα终边所在的象限，直接转化为终边相同的角即可． (2)确定αn 终边所在象限常用的步骤如下：①求出αn 的范围；②对n 的取值分情况讨论：被n 整除；被n 除余1；被n 除余2；…；被n 除余n －1； ③下结论．层级一学业水平达标1．在0°到360°范围内，与－950°角终边相同的角是________．解析：－950°＝130°－3×360°，所以在0°～360°的范围内，与－950°角终边相同的角是130°.★答案★：130°2．在－390°，－885°，1 351°，2 016°这四个角中，其中第四象限角的个数为________．解析：－390°＝－360°－30°是第四象限角；－885°＝－2×360°－165°是第三角限角；1 351°＝3×360°＋271°是第四象限角；2 016°＝5×360°＋216°是第三象限角．故有2个．★答案★：23．钟表经过2小时，时针转过的度数为________．解析：时针均按顺时针方向旋转，2小时时针转过16周，所以时针转过了－60°.★答案★：－60°4．已知角α，β的终边相同，那么α－β的终边在________．解析：∵角α，β的终边相同， ∴α＝k ·360°＋β，k ∈Z.作差α－β＝k ·360°＋β－β＝k ·360°，k ∈Z. ∴α－β的终边在x 轴的正半轴上． ★答案★：x 轴的正半轴上5. 设集合A ＝{α|α＝90°·k ＋30°，k ∈Z}，B ＝{α|0°≤α<360°}，则A ∩B ＝________. 解析：由0°≤90°·k ＋30°<360°，k ∈Z ，得－13≤k <113，k ∈Z ，所以k ＝0,1,2,3，所以A ∩B ＝{30°，120°，210°，300°}． ★答案★：{30°，120°，210°，300°}6．若α＝45°＋k·180° (k∈Z)，则α的终边在第________象限．解析：由题意知α＝k·180°＋45°，k∈Z，当k＝2n＋1，n∈Z时，α＝2n·180°＋180°＋45°＝n·360°＋225°，在第三象限，当k＝2n，n∈Z时，α＝2n·180°＋45°＝n·360°＋45°，在第一象限．∴α是第一或第三象限的角．★答案★：一或三7．已知α与β均为正角，且α＋β＝180°，若0°<α≤90°，则角β的终边位于_______________．解析：若0°<α<90°，则90°<β＝180°－α<180°，即角β的终边在第二象限；若α＝β＝90°，则角β的终边位于y轴正半轴上．★答案★：第二象限或y轴正半轴上8．若角α满足180°＜α＜360°，角5α与角α有相同的始边，且又有相同的终边，那么角α＝______________.解析：∵5α与α的始边和终边相同，∴这两角的差应是360°的整数倍．即5α－α＝4α＝k·360°，k∈Z.即α＝k·90°.又180°<α<360°，∴180°<k·90°<360°.∴2<k<4.∴k＝3，故α＝270°.★答案★：270°9．已知角x的终边落在图示阴影部分区域，写出角x组成的集合．解：(1){x|k·360°－135°≤x≤k·360°＋135°，k∈Z}．(2){x|k·360°＋30°≤x≤k·360°＋60°，k∈Z}∪{x|k·360°＋210°≤x≤k·360°＋240°，k∈Z}＝{x|2k·180°＋30°≤x≤2k·180°＋60°或(2k＋1)·180°＋30°≤x≤(2k＋1)·180°＋60°，k∈Z}＝{x|k·180°＋30°≤x≤k·180°＋60°，k∈Z}．10．已知α＝－1 910°，(1)把α写成β＋k·360°(k∈Z,0°≤β＜360°)的形式，指出它是第几象限的角；(2)求θ，使θ与α的终边相同，且－720°≤θ＜0°.解：(1)设α＝β＋k·360°(k∈Z)，则β＝－1 910°－k·360°(k∈Z)．令－1 910°－k·360°≥0，解得k≤－1 910 360.所以k的最大整数解为k＝－6，求出相应的β＝250°，于是α＝250°－6×360°，它是第三象限的角．(2)令θ＝250°＋k·360°(k∈Z)，取k＝－1，－2就得到符合－720°≤θ＜0°的角：250°－360°＝－110°，250°－720°＝－470°.故θ＝－110°或－470°.层级二应试能力达标1．在0°到360°范围内，与角－60°的终边在同一条直线上的角为___________．解析：与角－60°的终边在同一条直线上的角为－60°＋k·180°，k∈Z，取k＝1,2.★答案★：120°与300°2．射线OA绕端点O逆时针旋转120°到达OB位置，再顺时针旋转270°到达OC位置，则∠AOC＝________.解析：根据任意角的定义可得∠AOC＝120°＋(－270°)＝－150°.★答案★：－150°3．若α是第三象限角，则180°－α是第________象限角．解析：因为α是第三象限角，所以k·360°＋180°<α<k·360°＋270°，k∈Z.所以k·360°－90°<180°－α<k·360°，k∈Z.所以180°－α为第四象限角．★答案★：四4．与1 991°终边相同的最小正角是________，绝对值最小的角是________．解析：与1 991°终边相同的角为1 991°＋k·360°，取k＝－5，－6.★答案★：191°，－169°5．角α，β的终边关于y轴对称，若α＝30°，则β＝________________.★答案★：150°＋k·360°，k∈Z6．已知角2α的终边落在x 轴上方，那么α是第________象限角．解析：由题知k ·360°＜2α＜180°＋k ·360°，k ∈Z ， ∴k ·180°＜α＜90°＋k ·180°，k ∈Z.当k 为偶数时，α是第一象限角；当k 为奇数时，α为第三象限角，∴α为第一或第三象限角．★答案★：一或三7．若θ是第一象限角，判断θ2所在的象限．解：∵θ是第一象限角， ∴k ·360°<θ<k ·360°＋90°(k ∈Z)． k ·180°<θ2<k ·180°＋45°(k ∈Z)．当k ＝2n ，n ∈Z 时，n ·360°<θ2<n ·360°＋45°，∴θ2为第一象限角；当k ＝2n ＋1，n ∈Z 时， n ·360°＋180°<θ2<n ·360°＋225°，∴θ2为第三象限角．综上，θ2为第一或第三象限角．8．已知角β的终边在直线3x －y ＝0上． (1)写出角β的集合S ；(2)写出S 中适合不等式－360°<β<720°的元素．解：(1)如图，直线3x －y ＝0过原点，倾斜角为60°，在0°～360°范围内，终边落在射线OA 上的角是60°，终边落在射线OB 上的角是240°，所以以射线OA ，OB 为终边的角的集合为： S 1＝{β|β＝60°＋k ·360°，k ∈Z}， S 2＝{β|β＝240°＋k ·360°，k ∈Z}，所以角β的集合S ＝S 1∪S 2＝{β|β＝60°＋k ·360°，k ∈Z}∪{β|β＝60°＋180°＋k ·360°，k ∈Z} ＝{β|β＝60°＋2k ·180°，k ∈Z}∪{β|β＝60°＋(2k ＋1)·180°，k ∈Z} ＝{β|β＝60°＋k ·180°，k ∈Z}．(2)由于－360°<β<720°，即－360°<60°＋k·180°<720°，k∈Z.解得－73<k<113，k∈Z，所以k＝－2，－1,0,1,2,3.所以S中适合不等式－360°<β<720°的元素为：60°－2×180°＝－300°；60°－1×180°＝－120°；60°＋0×180°＝60°；60°＋1×180°＝240°；60°＋2×180°＝420°；60°＋3×180°＝600°.。

人教版高中数学必修四教材用书第一章三角函数 1.1.1 任意角 Word版含答案

．任意角和弧度制．任意角[提出问题]问题：当钟表慢了(或快了)，我们会将分针按某个方向转动，把时间调整准确．在调整的过程中，分针转动的角度有什么不同？提示：旋转方向不同．问题：在体操或跳水比赛中，运动员会做出“转体两周”“向前翻腾两周半”等动作，做上述动作时，运动员分别转体多少度？提示：顺时针方向旋转了°或逆时针方向旋转了°，顺时针方向旋转了°.[导入新知]角的分类．按旋转方向.()角的终边在第几象限，则称此角为第几象限角；()角的终边在坐标轴上，则此角不属于任何一个象限．[化解疑难]．任意角的概念认识任意角的概念应注意三个要素：顶点、始边、终边．()用旋转的观点来定义角，就可以把角的概念推广到任意角，包括任意大小的正角、负角和零角．()对角的概念的认识关键是抓住“旋转”二字．①要明确旋转方向；②要明确旋转角度的大小；③要明确射线未作任何旋转时的位置．．象限角的前提条件角的顶点与坐标原点重合，角的始边与轴的非负半轴重合.[提出问题]在条件“角的顶点与坐标原点重合，始边与轴非负半轴重合”下，研究下列角：°，°，－°.问题：这三个角的终边位置相同吗？提示：相同．问题：如何用含°的式子表示°和－°？提示：°＝×°＋°，－°＝－×°＋°.问题：确定一条射线，以它为终边的角是否唯一？提示：不唯一．[导入新知]终边相同的角所有与角α终边相同的角，连同角α在内，可构成一个集合＝，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．[化解疑难]所有与角α终边相同的角，连同角α在内可以用式子·°＋α，∈表示，在运用时需注意以下几点．()是整数，这个条件不能漏掉．()α是任意角．()·°，∈与α之间用“＋”连接，如·°－°，∈应看成·°＋(－°)，∈.()终边相同的角不一定相等，终边相同的角有无数个，它们相差周角的整数倍；相等的角终边一定相同．[例] 已知角的顶点与坐标原点重合，始边落在轴的非负半轴上，作出下列各角，并指出它们是第几象限角．()－°；()°；()－°.。

人教版高中数学必修四1.2任意角的三角函数1.2.1二含答案

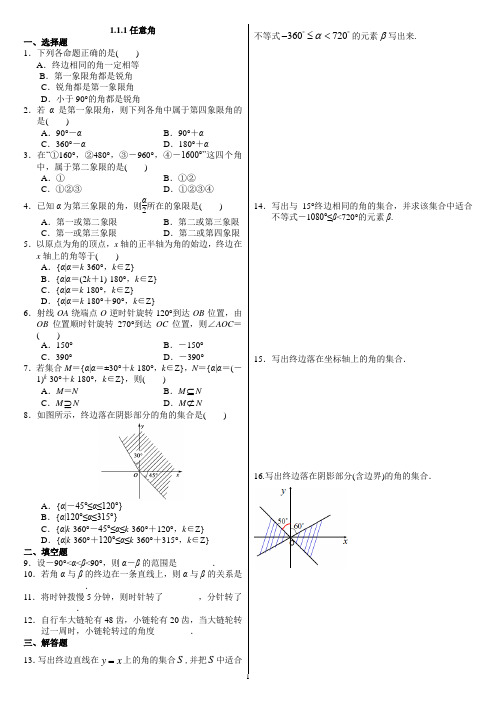
1.2.1 任意角的三角函数(二) 课时目标 1.掌握正弦、余弦、正切函数的定义域.2.了解三角函数线的意义，能用三角函数线表示一个角的正弦、余弦和正切．1．三角函数的定义域正弦函数y ＝sin x 的定义域是______；余弦函数y ＝cos x 的定义域是______；正切函数y ＝tan x 的定义域是_____________________________________________________________．2．三角函数线如图，设单位圆与x 轴的正半轴交于点A ，与角α的终边交于P 点．过点P 作x 轴的垂线PM ，垂足为M ，过A 作单位圆的切线交OP 的延长线(或反向延长线)于T 点．单位圆中的有向线段______、______、________分别叫做角α的正弦线、余弦线、正切线．记作：sin α＝______，cos α＝______，tan α＝______.一、选择题1. 如图在单位圆中角α的正弦线、正切线完全正确的是( )A ．正弦线PM ，正切线A ′T ′B ．正弦线MP ，正切线A ′T ′C ．正弦线MP ，正切线ATD ．正弦线PM ，正切线AT2．角α(0<α<2π)的正、余弦线的长度相等，且正、余弦符号相异，那么α的值为( ) A.π4 B.3π4 C.7π4 D.3π4或7π43．若α是第一象限角，则sin α＋cos α的值与1的大小关系是( )A ．sin α＋cos α>1B ．sin α＋cos α＝1C ．sin α＋cos α<1D ．不能确定4．利用正弦线比较sin 1，sin 1.2，sin 1.5的大小关系是( )A ．sin 1>sin 1.2>sin 1.5B ．sin 1>sin 1.5>sin 1.2C ．sin 1.5>sin 1.2>sin 1D ．sin 1.2>sin 1>sin 1.5 5．若0<α<2π，且sin α<32，cos α>12，则角α的取值范围是( ) A.⎝⎛⎭⎫－π3，π3 B.⎝⎛⎭⎫0，π3 C.⎝⎛⎭⎫5π3，2π D.⎝⎛⎭⎫0，π3∪⎝⎛⎭⎫5π3，2π 6．如果π4<α<π2，那么下列不等式成立的是( ) A ．cos α<sin α<tan α B ．tan α<sin α<cos αC ．sin α<cos α<tan αD ．cos α<tan α<sin α二、填空题7．在[0,2π]上满足sin x ≥12的x 的取值范围为________． 8．集合A ＝[0,2π]，B ＝{α|sin α<cos α}，则A ∩B ＝________________.9．不等式tan α＋33>0的解集是______________． 10．求函数f (x )＝lg(3－4sin 2x )的定义域为________．三、解答题11．在单位圆中画出适合下列条件的角α终边的范围，并由此写出角α的集合．(1)sin α≥32； (2)cos α≤－12.12．设θ是第二象限角，试比较sin θ2，cos θ2，tan θ2的大小．能力提升13．求函数f (x )＝1－2cos x ＋ln ⎝⎛⎭⎫sin x －22的定义域．14．如何利用三角函数线证明下面的不等式？当α∈⎝⎛⎭⎫0，π2时，求证：sin α<α<tan α.1．三角函数线的意义三角函数线是用单位圆中某些特定的有向线段的长度和方向表示三角函数的值，三角函数线的长度等于三角函数值的绝对值，方向表示三角函数值的正负，具体地说，正弦线、正切线的方向同纵坐标轴一致，向上为正，向下为负；余弦线的方向同横坐标轴一致，向右为正，向左为负，三角函数线将抽象的数用几何图形表示出来了，使得问题更形象直观，为从几何途径解决问题提供了方便．2．三角函数的画法定义中不仅定义了什么是正弦线、余弦线、正切线，同时也给出了角α的三角函数线的画法即先找到P 、M 、T 点，再画出MP 、OM 、AT .注意三角函数线是有向线段，要分清始点和终点，字母的书写顺序不能颠倒．1．2.1 任意角的三角函数(二)答案知识梳理1．R R {x |x ∈R 且x ≠k π＋π2，k ∈Z } 2．MP OM AT MP OM AT作业设计1．C2．D [角α终边落在第二、四象限角平分线上．]3．A [设α终边与单位圆交于点P ，sin α＝MP ，cos α＝OM ，则|OM |＋|MP |>|OP |＝1，即sin α＋cos α>1.]4．C [∵1,1.2,1.5均在⎝⎛⎭⎫0，π2内，正弦线在⎝⎛⎭⎫0，π2内随α的增大而逐渐增大， ∴sin 1.5>sin 1.2>sin 1.]5．D [在同一单位圆中，利用三角函数线可得D 正确．]6．A [如图所示，在单位圆中分别作出α的正弦线MP 、余弦线OM 、正切线AT ，很容易地观察出OM <MP <AT ，即cos α<sin α<tan α.] 7.⎣⎡⎦⎤π6，5π6 8.⎣⎡⎭⎫0，π4∪⎝⎛⎦⎤54π，2π 9.⎩⎨⎧⎭⎬⎫α|k π－π6<α<k π＋π2，k ∈Z 解析不等式的解集如图所示(阴影部分)，∴⎩⎨⎧⎭⎬⎫α|k π－π6<α<k π＋π2，k ∈Z . 10.⎝⎛⎭⎫k π－π3，k π＋π3，k ∈Z 解析如图所示．∵3－4sin 2x >0，∴sin 2x <34，∴－32<sin x <32.∴x ∈⎝⎛⎭⎫2k π－π3，2k π＋π3∪⎝⎛⎭⎫2k π＋2π3，2k π＋4π3 (k ∈Z )．即x ∈⎝⎛⎭⎫k π－π3，k π＋π3 (k ∈Z )． 11．解 (1) 图1作直线y ＝32交单位圆于A 、B ，连结OA 、OB ，则OA 与OB 围成的区域(图1阴影部分)，即为角α的终边的范围．故满足条件的角α的集合为{α|2k π＋π3≤α≤2k π＋2π3，k ∈Z }． (2)图2 作直线x ＝－12交单位圆于C 、D ，连结OC 、OD ，则OC 与OD 围成的区域(图2阴影部分)，即为角α的终边的范围．故满足条件的角α的集合为{α|2k π＋2π3≤α≤2k π＋4π3，k ∈Z }． 12．解 ∵θ是第二象限角，∴2k π＋π2<θ<2k π＋π (k ∈Z )，故k π＋π4<θ2<k π＋π2(k ∈Z )．作出θ2所在范围如图所示．当2k π＋π4<θ2<2k π＋π2 (k ∈Z )时，cos θ2<sin θ2<tan θ2. 当2k π＋5π4<θ2<2k π＋32π (k ∈Z )时，sin θ2<cos θ2<tan θ2. 13．解由题意，自变量x 应满足不等式组⎩⎪⎨⎪⎧ 1－2cos x ≥0，sin x －22>0. 即⎩⎨⎧ sin x >22，cos x ≤12.则不等式组的解的集合如图(阴影部分)所示，∴⎩⎨⎧⎭⎬⎫x |2k π＋π3≤x <2k π＋34π，k ∈Z . 14．证明如图所示，在直角坐标系中作出单位圆，α的终边与单位圆交于P ，α的正弦线、正切线为有向线段MP ，AT ，则MP ＝sin α，AT ＝tan α.因为S △AOP ＝12OA ·MP ＝12sin α，S 扇形AOP ＝12αOA 2＝12α，S △AOT ＝12OA ·AT ＝12tan α，又S △AOP <S 扇形AOP <S △AOT ，所以12sin α<12α<12tan α，即sin α<α<tan α.附赠材料答题六注意：规范答题不丢分提高考分的另一个有效方法是减少或避免不规范答题等非智力因素造成的失分,具体来说考场答题要注意以下六点:第一,考前做好准备工作。

高一数学人教A版必修4学案：111任意角含答案1.doc

THE FIRST CHAPTER第一章三角函数1. 1任意角和弧度制1. 1.1任意角［学习目标］1•了解角的概念2掌握正角、负角和零角的概念，理解任意角的意义.3.熟练掌握象限角、终边相同的角的概念，会用集合符号表示这些角.尹预习导学全挑战自我•点点落实________________________________________________ ［知识链接］1.手表慢了5分钟，如何校准？手表快了1.5小吋，又如何校准？答可将分针顺时针方向旋转30。

；可将时针逆时针方向旋转45。

.2.在初中角是如何定义的？答定义1：有公共端点的两条射线组成的儿何图形叫做角.定义2：平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形叫做角.3.初中所学角的范围是什么？答角的范围是［0。

，360°］.［预习导引］1.角的概念(1)角的概念：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.(2)角的表示方法：①常用大写字母儿3, C等表示:②也可以用希腊字母$、匸匕等表示；③特别是当角作为变量时，常用字母丄表示.(3)角的分类：按旋转方向可将角分为如下三类：2.象限角角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，那么，角的终边（除端点外）在第儿象限，就说这个角是第儿象限角.如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.3.终边相同的角所有与角a终边相同的角，连同角a在内，可构成一个集合S=｛0|0=a+E36O。

，MZ｝, 即任一与角a终边相同的角，都可以表示成角a与整数个周角的和.戸课堂讲义/ 重点难点，个个击破 ____________________________________________________________要点一任意角概念的辨析例1在下列说法中：①0。

〜90。

的角是第一象限角；②第二象限角大于第一象限角；③钝角都是第二象限角；④小于90。

人教A版高中数学必修4课后习题第一章 1.1.1 任意角

第一章三角函数1.1 任意角和弧度制1.1.1 任意角课后篇巩固探究1.200°角是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角180°<200°<270°,第三象限角α的取值范围为k·360°+180°<α<k·360°+270°,k∈Z,所以200°角是第三象限角.2.在-360°≤α<0°范围内与60°角终边相同的角为( )A.-300°B.-300°,60°C.60°D.420°60°角终边相同的角α可表示为α=60°+k·360°,当k=-1时,α=-300°,故在-360°≤α<0°范围内与60°角终边相同的角为-300°.3.若角θ是第四象限角,则90°+θ是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角,将θ的终边按逆时针方向旋转90°得90°+θ的终边,则90°+θ是第一象限角.4.角α=45°+k×180°(k∈Z)的终边落在( )A.第一或第三象限B.第一或第二象限C.第二或第四象限D.第三或第四象限k是偶数时,角α是第一象限角,当k是奇数时,角α是第三象限角.5.如图,终边在阴影部分(含边界)的角的集合是( )A.{α|-45°≤α≤120°}B.{α|120°≤α≤315°}C.{α|-45°+k·360°≤α≤120°+k·360°,k∈Z}D.{α|120°+k·360°≤α≤315°+k·360°,k∈Z},终边落在阴影部分(含边界)的角的集合是{α|-45°+k·360°≤α≤120°+k·360°,k∈Z}.故选C.±45°,k∈Z},P=,P之间的关系为( ) 6.已知集合M={x|x=k·180°2A.M=PB.M⊆PC.M⊇PD.M∩P=⌀±45°=k·90°±45°=(2k±1)·45°,k∈Z, M,x=k·180°2对于集合P,x=k·180°±90°=k·45°±90°=(k±2)·45°,k∈Z.∴4M⊆P.7.已知角α,β的终边关于直线x+y=0对称,且α=-60°,则β=.-90°到0°的范围内,-60°角的终边关于直线y=-x对称的射线的对应角为-45°+15°=-30°,所以β=-30°+k·360°,k∈Z.30°+k·360°,k∈Z8.若角α与角288°终边相同,则在0°~360°内终边与角α4终边相同的角是.,得α=288°+k·360°(k∈Z),α4=72°+k·90°(k∈Z).又α4在0°~360°内,所以k=0,1,2,3,相应地有α4=72°,162°,252°,342°.9.终边落在图中阴影部分所示的区域内(包括边界)的角的集合为.由图易知在0°~360°范围内,终边落在阴影区域内(包括边界)的角为45°≤α≤90°与225°≤α≤270°,故终边落在阴影部分所示的区域内(包括边界)的角的集合为{α|k·360°+45°≤α≤k·360°+90°,k ∈Z}∪{α|k·360°+225°≤α≤k·360°+270°,k∈Z}={α|k·180°+45°≤α≤k·180°+90°,k∈Z}.Z}10.已知α=-1 910°.(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,并指出它是第几象限角;(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.设α=β+k·360°(k∈Z),则β=-1910°-k·360°(k∈Z).令-1910°-k·360°≥0,解得k≤-1910360=-51136.k的最大整数解为k=-6,求出相应的β=250°,于是α=250°-6×360°,它是第三象限角.(2)令θ=250°+n·360°(n∈Z),取n=-1,-2就得到符合-720°≤θ<0°的角. 250°-360°=-110°,250°-720°=-470°.故θ=-110°或θ=-470°.11.已知角α的终边在图中阴影部分所表示的范围内(不包括边界),写出角α的集合.0°~360°范围内,终边落在阴影部分内的角为30°<α<150°与210°<α<330°,故所有满足题意的角α的集合为{α|k·360°+30°<α<k·360°+150°,k∈Z}∪{α|k·360°+210°<α<k·360°+330°,k∈Z}={α|n·180°+30°<α<n·180°+150°,n∈Z}.12.已知α,β都是锐角,且α+β的终边与-280°角的终边相同,α-β的终边与670°角的终边相同,求角α,β的大小.-280°+k·360°,k∈Z.∵α,β都是锐角,∴0°<α+β<180°.取k=1,得α+β=80°.①α-β=670°+k·360°,k∈Z.∵α,β都是锐角,∴-90°<α-β<90°.取k=-2,得α-β=-50°.②由①②,得α=15°,β=65°.。

人教版高中数学必修四1.1任意角和弧度制1.1.2含答案

1.1.2 弧度制课时目标 1.理解角度制与弧度制的概念，掌握角的不同度量制度，能对弧度和角度进行正确的变换.2.掌握并会应用弧度制下的弧长公式和扇形面积公式．1．角的单位制(1)角度制：规定周角的________为1度的角，用度作为单位来度量角的单位制叫做角度制．(2)弧度制：把长度等于________的弧所对的圆心角叫做1弧度的角，记作________．(3)角的弧度数求法：如果半径为r 的圆的圆心角α所对的弧长为l ，那么l ，α，r 之间存在的关系是：____________；这里α的正负由角α的________________决定．正角的弧度数是一个________，负角的弧度数是一个________，零角的弧度数是________．2．角度制与弧度制的换算角度化弧度弧度化角度360°＝________ rad 2π rad ＝________180°＝______ rad π rad ＝________1°＝______rad ≈ 0.017 45 rad1 rad ＝______≈57°18′ 3.扇形的弧长及面积公式设扇形的半径为R ，弧长为l ，α (0<α<2π)为其圆心角，则度量单位类别α为角度制 α为弧度制扇形的弧长 l ＝________ l ＝______扇形的面积 S ＝________ S ＝______＝______一、选择题1．集合A ＝⎩⎨⎧⎭⎬⎫α|α＝k π＋π2，k ∈Z 与集合B ＝⎩⎨⎧⎭⎬⎫α|α＝2k π±π2，k ∈Z 的关系是( ) A ．A ＝B B ．A ⊆BC ．B ⊆AD ．以上都不对2．已知2弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长是( )A ．2B ．sin 2 C.2sin 1D ．2sin 1 3．扇形周长为6 cm ，面积为2 cm 2，则其中心角的弧度数是( ) A ．1或4 B ．1或2 C ．2或4 D ．1或54．已知集合A ＝{α|2k π≤α≤(2k ＋1)π，k ∈Z }，B ＝{α|－4≤α≤4}，则A ∩B 等于( )A ．∅B ．{α|－4≤α≤π}C ．{α|0≤α≤π}D ．{α|－4≤α≤－π，或0≤α≤π}5．把－114π表示成θ＋2k π(k ∈Z )的形式，使|θ|最小的θ值是( ) A.π4 B ．－π4 C.34π D ．－34π 6．扇形圆心角为π3，半径长为a ，则扇形内切圆的圆面积与扇形面积之比为( ) A ．1∶3 B ．2∶3 C ．4∶3 D ．4∶9二、填空题7．将－1 485°化为2k π＋α (0≤α<2π，k ∈Z )的形式是________．8．若扇形圆心角为216°，弧长为30π，则扇形半径为____．9．若2π<α<4π，且α与－7π6角的终边垂直，则α＝______. 10．若角α的终边与角π6的终边关于直线y ＝x 对称，且α∈(－4π，4π)，则α＝________________.三、解答题11．把下列各角化成2k π＋α (0≤α<2π，k ∈Z )的形式，并指出是第几象限角：(1)－1 500°；(2)236π；(3)－4.12．已知一扇形的周长为40 cm ，当它的半径和圆心角取什么值时，才能使扇形的面积最大？最大面积是多少？能力提升13．已知一圆弧长等于其所在圆的内接正方形的周长，那么其圆心角的弧度数的绝对值为________．14．已知一扇形的中心角是α，所在圆的半径是R .(1)若α＝60°，R ＝10 cm ，求扇形的弧长及该弧所在的弓形面积；(2)若扇形的周长是一定值c (c >0)，当α为多少弧度时，该扇形有最大面积？1．角的概念推广后，在弧度制下，角的集合与实数集R 之间建立起一一对应的关系：每一个角都有唯一的一个实数(即这个角的弧度数)与它对应；反过来，每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应． 2．解答角度与弧度的互化问题的关键在于充分利用“180°＝π”这一关系式．易知：度数×π180＝弧度数，弧度数×⎝⎛⎭⎫180π＝度数． 3．在弧度制下，扇形的弧长公式及面积公式都得到了简化，具体应用时，要注意角的单位取弧度．1.1.2 弧度制答案知识梳理1．(1)1360 (2)半径长 1 rad (3)|α|＝l r终边的旋转方向正数负数 0 2．2π 360° π 180° π180 ⎝⎛⎭⎫180π° 3.απR 180 αR απR 2360 12αR 2 12lR 作业设计1．A2．C [r ＝1sin 1，∴l ＝|α|r ＝2sin 1.] 3．A [设扇形半径为r ，圆心角为α，则⎩⎪⎨⎪⎧2r ＋αr ＝612αr 2＝2，解得⎩⎪⎨⎪⎧ r ＝1α＝4或⎩⎪⎨⎪⎧r ＝2α＝1.] 4．C [集合A 限制了角α终边只能落在x 轴上方或x 轴上．] 5．D [∵－114π＝－2π＋⎝⎛⎭⎫－34π，∴θ＝－34π.] 6．B [设扇形内切圆半径为r ，则r ＋r sin π6＝r ＋2r ＝a .∴a ＝3r ，∴S 内切＝πr 2. S 扇形＝12αr 2＝12×π3×a 2＝12×π3×9r 2＝32πr 2. ∴S 内切∶S 扇形＝2∶3.]7．－10π＋74π 解析 ∵－1 485°＝－5×360°＋315°，∴－1 485°可以表示为－10π＋74π. 8．25解析 216°＝216×π180＝6π5，l ＝α·r ＝6π5r ＝30π，∴r ＝25. 9.73π或103π 解析－76π＋72π＝146π＝73π，－76π＋92π＝206π＝103π. 10．－11π3，－5π3，π3，7π3解析由题意，角α与π3终边相同，则π3＋2π＝73π， π3－2π＝－53π，π3－4π＝－113π. 11．解 (1)－1 500°＝－1 800°＋300°＝－10π＋5π3， ∴－1 500°与53π终边相同，是第四象限角． (2)236π＝2π＋116π，∴236π与116π终边相同，是第四象限角． (3)－4＝－2π＋(2π－4)，∴－4与2π－4终边相同，是第二象限角．12．解设扇形的圆心角为θ，半径为r ，弧长为l ，面积为S ，则l ＋2r ＝40，∴l ＝40－2r .∴S ＝12lr ＝12×(40－2r )r ＝20r －r 2＝－(r －10)2＋100. ∴当半径r ＝10 cm 时，扇形的面积最大，最大值为100 cm 2，此时θ＝l r ＝40－2×1010＝2 rad. 13．4 2解析设圆半径为r ，则内接正方形的边长为2r ，圆弧长为42r .∴圆弧所对圆心角|θ|＝42r r＝4 2. 14．解 (1)设弧长为l ，弓形面积为S 弓， ∵α＝60°＝π3，R ＝10，∴l ＝αR ＝10π3(cm)． S 弓＝S 扇－S △＝12×10π3×10－12×102×sin 60°＝50⎝⎛⎭⎫π3－32 (cm 2)． (2)扇形周长c ＝2R ＋l ＝2R ＋αR ，∴α＝c －2R R， ∴S 扇＝12αR 2＝12·c －2R R ·R 2＝12(c －2R )R ＝－R 2＋12cR ＝－(R －c 4)2＋c 216. 当且仅当R ＝c 4，即α＝2时，扇形面积最大，且最大面积是c 216.附赠材料答题六注意：规范答题不丢分提高考分的另一个有效方法是减少或避免不规范答题等非智力因素造成的失分,具体来说考场答题要注意以下六点:第一,考前做好准备工作。

高一数学人教A版必修4练习1.1.1 任意角 Word版含解析

第一章三角函数三角函数
．任意角和弧度制
．任意角
．理解任意角的概念，特别是象限角、区间角、终边相同的角的概念及其表示方法．
．了解正角、负角、零角的概念．
．注意数形结合思想的应用．
一、任意角
．任意角的概念：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．射线的起始位置是角的始边，射线的终止位置是角的终边，射线的端点是角的顶点．
练习：下列说法正确的是()
．最大角是°．最大角是°
．角不可以是负的．角可以任意大小
解析：由角的定义，角可以是任意大小的．故选.
．正角、零角、负角概念：按旋转方向，角可以分为以下三类：
()正角——按逆时针方向旋转所形成的角；
()零角—射线没有作任何旋转形成的角；
()负角——按顺时针方向旋转所形成的角．
练习：时钟的分针经过分钟旋转的角为()
．°．°．－°．－°
解析：时针的分针是按顺时针旋转形成的角，所以为负角．故选.。

数学人教A版必修4习题：111任意角含解析.doc

1. -215°是（）A. 第一象限角C.第三象限角解析：选 B.由于一215°=-360°+145°,而145。

是第二象限角，则一215。

也是第二象限角. 2.与1 303。

终边相同的角是（）A. 763°B. 493°C. -137°D. 一47。

解析：选C.因为1 303。

=4><360。

一 137。

，所以与1 303。

终边相同的角是一137。

.3・集合 ^ = {a|a=^90°-36°, kWZ\, 3={0|—180°V“<180。

},则 AQB 等于（）A. {-36°, 54°}B. {-126°, 144°}C. {-126°, -36°, 54°, 144°}D. {-126°, 54°}解析：选 C.令 k=T, 0, 1, 2,则B 的公共元素有一126。

，-36°, 54°, 144°. 4.若角a 满足a=45°+Z:-180o , kWZ,则角a 的终边落在（）A.第一或第三象限B.第一或第二象限C.第二或第四象限D.第三或第四象限解析：选A.当&为奇数时，角a 与225。

角终边相同，在第三象限；当£为偶数时，角 a 与45。

角终边相同，在第一象限.5・把一 1 485。

转化为 a+A:-360o （0o ^«<360o , *WZ ）的形式是（）A. 45°-4X360°B. -45°-4X360°C. -45°-5X360°D. 315°-5X360°解析：选D.B, C 选项中a 不在0。

必修四任意角的三角函数(附规范标准答案)

任意角的三角函数(一)[学习目标] 1.借助单位圆理解任意角的三角函数定义.2.掌握正弦、余弦、正切函数在各象限内的符号.3.通过对任意角的三角函数的定义理解终边相同角的同一三角函数值相等．知识点一三角函数的概念1．利用单位圆定义任意角的三角函数如图，在平面直角坐标系中，设α是一个任意角，它的终边与单位圆交于点P (x ，y )，那么：(1)y 叫做α的正弦，记作sin α，即sin α＝y ；(2)x 叫做α的余弦，记作cos α，即cos α＝x ； (3)y x叫做α的正切，记作tan α，即tan α＝y x(x ≠0)．对于确定的角α，上述三个值都是唯一确定的．故正弦、余弦、正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，统称为三角函数．2．一般地，设角α终边上任意一点的坐标为(x ，y )，它与原点的距离为r ，则sin α＝y r，cosα＝x r ，tan α＝yx.思考角α三角函数值的大小与角α终边上的点P 离原点距离的远近有关吗？答案角α的三角函数值是比值，是一个实数，这个实数的大小与点P (x ，y )在终边上的位置无关，只由角α的终边位置决定，即三角函数值的大小只与角有关．知识点二正弦、余弦、正切函数值在各象限的符号口诀概括为：一全正、二正弦、三正切、四余弦(如图)．思考三角函数在各象限的符号由什么决定？答案三角函数值的符号是根据三角函数定义和各象限内坐标符号推导出的．从原点到角的终边上任意一点的距离r总是正值．因此，三角函数在各象限的符号由角α的终边所在象限决定．知识点三诱导公式一终边相同的角的同一三角函数的值相等，即：sin(α＋k·2π)＝sin α，cos(α＋k·2π)＝cos α，tan(α＋k·2π)＝tan α，其中k∈Z.题型一三角函数定义的应用例1 已知θ终边上一点P(x,3)(x≠0)，且cos θ＝1010x，求sin θ，tan θ.解由题意知r＝|OP|＝x2＋9，由三角函数定义得cos θ＝xr＝xx2＋9.又∵cos θ＝1010x，∴xx2＋9＝1010x.∵x≠0，∴x＝±1.当x＝1时，P(1,3)，此时sin θ＝312＋32＝31010，tan θ＝31＝3.当x＝－1时，P(－1,3)，此时sin θ＝3－12＋32＝31010，tan θ＝3－1＝－3.跟踪训练1 (1)已知角α的终边经过点P (－4a,3a )(a ≠0)，求sin α，cos α，tan α的值； (2)已知角α的终边在直线y ＝3x 上，求sin α，cos α，tan α的值．解 (1)r ＝－4a2＋3a2＝5|a |.若a >0，则r ＝5a ，α是第二象限角，则 sin α＝y r ＝3a 5a ＝35，cos α＝x r ＝－4a5a ＝－45，tan α＝y x ＝3a－4a ＝－34，若a <0，则r ＝－5a ，α是第四象限角，则 sin α＝－35，cos α＝45，tan α＝－34.(2)因为角α的终边在直线y ＝3x 上，所以可设P (a ，3a )(a ≠0)为角α终边上任意一点．则r ＝a 2＋3a2＝2|a |(a ≠0)．若a >0，则α为第一象限角，r ＝2a ，所以sin α＝3a 2a ＝32，cos α＝a2a ＝12，tan α＝3a a＝3.若a <0，则α为第三象限，r ＝－2a ，所以sin α＝3a －2a ＝－32，cos α＝－a 2a ＝－12，tan α＝3a a＝3.题型二三角函数值符号的判断例2 判断下列三角函数值的符号： (1)sin 3，cos 4，tan 5； (2)sin(cos θ)(θ为第二象限角)．解 (1)∵π2<3<π<4<3π2<5<2π，∴3,4,5分别在第二、三、四象限， ∴sin 3>0，cos 4<0，tan 5<0. (2)∵θ是第二象限角， ∴－π2<－1<cos θ<0，∴sin(cos θ)<0.跟踪训练2 若sin θ<0且tan θ<0，则θ是第象限的角．答案四解析 ∵sin θ<0，∴θ是第三或第四象限或终边在y 轴的非正半轴上的角，又tan θ<0，∴θ是第四象限的角．题型三诱导公式一的应用例3 求下列各式的值：(1)sin(－1 395°)cos 1 110°＋cos(－1 020°)sin 750°；(2)sin ⎝ ⎛⎭⎪⎫－11π6＋cos 12π5·tan 4π. 解 (1)原式＝sin(－4×360°＋45°)cos(3×360°＋30°)＋cos(－3×360°＋60°)sin(2×360°＋30°)＝sin 45°cos 30°＋cos 60°sin 30°＝22×32＋12×12＝64＋14＝1＋64.(2)原式＝sin ⎝ ⎛⎭⎪⎫－2π＋π6＋cos ⎝⎛⎭⎪⎫2π＋2π5·tan(4π＋0)＝sin π6＋cos 2π5×0＝12.跟踪训练3 求下列各式的值：(1)cos 25π3＋tan ⎝ ⎛⎭⎪⎫－15π4； (2)sin 810°＋tan 765°－cos 360°.解 (1)原式＝cos ⎝ ⎛⎭⎪⎫8π＋π3＋tan ⎝⎛⎭⎪⎫－4π＋π4＝cos π3＋tan π4＝12＋1＝32；(2)原式＝sin(90°＋2×360°)＋tan(45°＋2×360°)－cos 360°＝sin 90°＋tan 45°－1＝1＋1－1＝1.利用任意角的三角函数的定义求值，忽略对参数的讨论而致错例4 已知角α的终边上有一点P (24k,7k )，k ≠0，求sin α，cos α，tan α的值．错解令x ＝24k ，y ＝7k ，则有r ＝24k 2＋7k 2＝25k ，∴sin α＝y r ＝725，cos α＝x r ＝2425，tan α＝y x ＝724.错因分析点P (24k,7k )中参数k 只告诉了k ≠0，而没有告诉k 的符号，需分k >0与k <0讨论，而上述解法错在默认为k >0. 正解当k >0时，令x ＝24k ，y ＝7k ，则有r ＝24k2＋7k 2＝25k ，∴sin α＝y r ＝725，cos α＝x r ＝2425，tan α＝y x ＝724. 当k <0时，令x ＝24k ，y ＝7k ，则有r ＝－25k ， ∴sin α＝y r ＝－725，cos α＝xr ＝－2425，tan α＝y x ＝724.1．cos(－11π6)等于( )A.12 B ．－12 C.32 D ．－32 2．当α为第二象限角时，|sin α|sin α－cos α|cos α|的值是( )A ．1B ．0C ．2D ．－2 3．如果角α的终边过点P (2sin 30°，－2cos 30°)，则cos α的值等于( ) A.12 B ．－12 C ．－32 D.324．若点P (3，y )是角α终边上的一点，且满足y <0，cos α＝35，则tan α＝ .5．已知角α的终边经过点P (2，－3)，求α的三个函数值．一、选择题1．若sin θcos θ>0，则θ在( ) A ．第一、二象限 B ．第一、三象限 C ．第一、四象限D ．第二、四象限2．sin(－1 380°)的值为( )A ．－12 B.12 C ．－32 D.323．设角α终边上一点P (－4a,3a )(a <0)，则2sin α＋cos α的值为( ) A.25 B.25或－25 C ．－25D ．与a 有关 4．若tan x <0，且sin x －cos x <0，则角x 的终边在( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限5．已知角α的终边上一点的坐标为⎝ ⎛⎭⎪⎫sin 2π3，cos 2π3，则角α的最小正值为( ) A.5π6 B.2π3 C.5π6 D.11π6 6．角α的终边经过点P (－b,4)且cos α＝－35，则b 的值为( )A ．3B ．－3C ．±3D ．5 二、填空题7．使得lg(cos αtan α)有意义的角α是第象限角．8．已知α终边经过点(3a －9，a ＋2)，且sin α>0，cos α≤0，则a 的取值范围为． 9．若角α的终边与直线y ＝3x 重合且sin α<0，又P (m ，n )是α终边上一点，且|OP |＝10，则m －n ＝ .10．函数y ＝|sin x |sin x ＋|cos x |cos x －2|sin x cos x |sin x cos x 的值域是．三、解答题11．已知角α的终边落在直线y ＝2x 上，求sin α，cos α，tan α的值．12．求下列各式的值．(1)a 2sin(－1 350°)＋b 2tan 405°－2ab cos(－1 080°)； (2)tan 405°－sin 450°＋cos 750°.当堂检测答案1．答案 C解析 cos(－116π)＝cos(－2π＋π6)＝cos π6＝32.2．答案 C解析 ∵α为第二象限角，∴sin α>0，cos α<0， ∴|sin α|sin α－cos α|cos α|＝sin αsin α－cos α－cos α＝2. 3．答案 A解析 ∵2sin 30°＝1，－2cos 30°＝－3，∴r ＝2，∴cos α＝12.4．答案－43解析 ∵cos α＝332＋y 2＝35，∴32＋y 2＝5，∴y 2＝16，∵y <0，∴y ＝－4，∴tan α＝－43. 5．解因为x ＝2，y ＝－3，所以r ＝22＋－32＝13.于是sin α＝y r＝－313＝－31313，cos α＝x r＝213＝21313，tan α＝y x ＝－32.课时精练答案一、选择题 1．答案 B 2．答案 D解析 sin(－1 380°)＝sin(－360°×4＋60°)＝sin 60°＝32.3．答案 C 解析 ∵a <0，∴r ＝－4a2＋3a 2＝5|a |＝－5a ，∴cos α＝x r ＝45，sin α＝yr ＝－35，∴2sin α＋cos α＝－25.4．答案 D解析 ∵tan x <0，∴角x 的终边在第二、四象限，又sin x －cos x <0，∴角x 的终边在第四象限．故选D. 5．答案 D解析 ∵sin 2π3＝32，cos 2π3＝－12.∴角α的终边在第四象限，且tan α＝cos 2π3sin 2π3＝－33， ∴角α的最小正角为2π－π6＝11π6. 6．答案 A解析 ∵r ＝b 2＋16，cos α＝－b r ＝－b b 2＋16＝－35. ∴b ＝3.二、填空题7．答案一或二解析要使原式有意义，必须cos αtan α>0，即需cos α，tan α同号，所以α是第一或第二象限角．8．答案－2<a ≤3解析 ∵sin α>0，cos α≤0，∴α位于第二象限或y 轴正半轴上，∴3a －9≤0，a ＋2>0，∴－2<a ≤3.9．答案 2解析 ∵y ＝3x ，sin α<0，∴点P (m ，n )位于y ＝3x 在第三象限的图象上，且m <0，n <0，n ＝3m .∵|OP |＝m 2＋n 2＝10|m |＝－10m ＝10.∴m ＝－1，n ＝－3，∴m －n ＝2.10．答案 {－4,0,2}解析由sin x ≠0，cos x ≠0知x 的终边不能落在坐标轴上，当x 为第一象限角时，sin x >0，cos x >0，sin x cos x >0，y ＝0；当x 为第二象限角时，sin x >0，cos x <0，sin x cos x <0，y ＝2；当x 为第三象限角时，sin x <0，cos x <0， sin x cos x >0，y ＝－4；当x 为第四象限角时，sin x <0，cos x >0，sin x cos x <0，y ＝2，故函数y ＝|sin x |cos x ＋|cos x |cos x －2|sin x cos x |sin x cos x的值域为{－4,0,2}．三、解答题11．解当角α的终边在第一象限时，在角α的终边上取点P (1,2)，由r ＝|OP |＝12＋22＝5，得sin α＝25＝255，cos α＝15＝55，tan α＝2；当角α的终边在第三象限时，在角α的终边上取点Q (－1，－2)，由r ＝|OQ |＝－12＋－22＝5，得sin α＝－25＝－255， cos α＝－15＝－55， tan α＝2.12．解 (1)原式＝a 2sin(－4×360°＋90°)＋b 2tan(360°＋45°)－2ab cos(－3×360°)＝a 2sin 90°＋b 2tan 45°－2ab cos 0°＝a 2＋b 2－2ab ＝(a －b )2.(2)tan 405°－sin 450°＋cos 750°＝tan(360°＋45°)－sin(360°＋90°)＋cos(720°＋30°)＝tan 45°－sin 90°＋cos 30°＝1－1＋32＝32.。

必修四任意角和弧度制课时练习含答案

必修四§1.1任意角和弧度制第一课时：§1.1.1任意角1. 下列命题中正确的是( )A ．终边在y 轴非负半轴上的角是直角B ．第二象限角一定是钝角C ．第四象限角一定是负角 D.若β＝α＋ｋ·360°（ｋ∈Ｚ），则α与β终边相同2.将-885化为360k α+⋅ (0360α≤<k ,∈Z )的形式是 ( ) A.-165(2)360+-⨯ B.195(3)360+-⨯ C.195(2)360+-⨯ D.165(3)360+-⨯3．在［360°，1440°］中与－21°16′终边相同的角有( )A ．1个B ．2个C ．3个D ．4个4．终边落在X 轴上的角的集合是（）A.{ α|α=k ·360°,K ∈Z }B.{ α|α=(2k+1)·180°,K ∈Z }C.{ α|α=k ·180°,K ∈Z }D.{ α|α=k ·180°+90°,K ∈Z }5．角α＝45°＋ｋ·180°，ｋ∈Ｚ的终边落在 ( )A ．第一或第三象限B ．第一或第二象限C ．第二或第四象限D ．第三或第四象限6.设,,,,那么( ) A ．B C A B ．B A C C ．D (A ∩C) D ．C ∩D=B7.下列各组角中终边相同的是( )A. +90与Z B.与ZC. +30与+30Z D.与+60Z 8.若角和的终边关于y 轴对称,则有 ( ) A. B.Z C.Z D.Zo {90A =小于的角｝{B =锐角｝{C ＝第一象限的角｝00{900}D =小于而不小于的角180k ⋅90k ⋅k ,∈(21)180k +⋅(41)180k ±⋅k ,∈180k ⋅360k ⋅k ,∈60k ⋅180k ⋅k ,∈αβ90αβ+=90αβ+=360k +⋅k ,∈360k αβ+=⋅k ,∈180αβ+=360k +⋅k ,∈9.若β是第四象限角,则180β-是第象限角。

新人教A版必修四第一章1.1.1任意角知识梳理及重难点题型(含解析版)

1.1.1任意角重难点题型【举一反三系列】知识链接【知识点1 任意角的概念】1.任意角2.角的分类【知识点2 象限角与非象限角】1.象限角当角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，则角的终边（除端点外）在第几象限，就称这个角为第几象限角.2.象限角的集合表示3.非象限角当角的顶点与坐标原点重合，角的始边与x 轴的非负半轴重合，如果角的终边落在坐标轴上，就认为这个角不属于任何一个象限.4.非象限角的集合表示【知识点3 终边相同的角】一般地，所有与角α终边相同的角，连同角α在内，可构成一个集合，即任一与角α终边相同的角，都可以表示成角α与整个周角的和. 举一反三【考点1 象限角与集合间的基本关系】【例1】（2019春•杜集区校级月考）设A ＝{小于90°的角}，B ＝{第一象限角}，则A ∩B 等于（）A ．{锐角}B ．{小于90°的角}C ．{第一象限角}D ．{α|k •360°＜α＜k •360°+90°（k ∈Z ，k ≤0）} {}Z k k S ∈⋅+==,360| αββ【变式1-1】（2019秋•钦南区校级月考）已知A ＝{第一象限角}，B ＝{锐角}，C ＝{小于90°的角}，那么A 、B 、C 关系是（）A ．A ∩C ＝CB ．B ⊆C C ．B ∪A ＝CD ．A ＝B ＝C【变式1-2】（2019秋•黄陵县校级月考）设A ＝{θ|θ为锐角}，B ＝{θ|θ为小于90°的角}，C ＝{θ|θ为第一象限的角}，D ＝{θ|θ为小于90°的正角}，则下列等式中成立的是（）A ．A ＝B B ．B ＝C C ．A ＝CD ．A ＝D【变式1-3】（2019秋•宜昌月考）设M ＝{α|α＝k •90°，k ∈Z }∪{α|α＝k •180°+45°，k ∈Z }，N ＝{α|α＝k •45°，k ∈Z }，则（）A ．M ⊆NB ．M ⊇NC ．M ＝ND ．M ∩N ＝∅【考点2 求终边相同的角】【例2】（2019春•娄底期末）下列各角中与225°角终边相同的是（）A ．585°B ．315°C ．135°D ．45°【变式2-1】（2018春•武功县期中）下列各组角中，终边相同的角是（）A ．﹣398°，1042°B ．﹣398°，142°C ．﹣398°，38°D ．142°，1042°【变式2-2】（2018春•武邑县校级期末）与﹣457°角终边相同角的集合是（）A ．{α|α＝k •360°+457°，k ∈Z }B ．{α|α＝k •360°+97°，k ∈Z }C ．{α|α＝k •360°+263°，k ∈Z }D ．{α|α＝k •360°﹣263°，k ∈Z } 【变式2-3】（2018春•林州市校级月考）在0°～360°范围内，与﹣853°18'终边相同的角为（）A ．136°18'B ．136°42'C ．226°18'D ．226°42'【考点3 已知α终边所在象限求2α，2α，3α】【例3】（2018秋•宜昌期末）已知α为锐角，则2α为（）A ．第一象限角B ．第二象限角C ．第一或第二象限角D ．小于180°的角【变式3-1】（2018•徐汇区校级模拟）若α是第二象限的角，则3α的终边所在位置不可能是（） A ．第一象限 B ．第二象限 C ．第三象限D ．笫象限【变式3-2】（2019春•北碚区校级期中）已知α为第二象限角，则2α所在的象限是（） A ．第一或第二象限B ．第二或第三象限C ．第一或第三象限D ．第二或第四象限【变式3-3】（2019秋•宜城市校级月考）如果α是第三象限角，则2α-是（）A ．第一象限角B ．第一或第二象限角C ．第一或第三象限角D ．第二或第四象限角【考点4 终边对称的角的表示法】【例4】（2019春•南京期中）若角α＝m •360°+60°，β＝k •360°+120°，（m ，k ∈Z ），则角α与β的终边的位置关系是（）A ．重合B ．关于原点对称C ．关于x 轴对称D ．关于y 轴对称【变式4-1】若角α的终边与45°角的终边关于原点对称，则α＝．【变式4-2】若角α和β的终边关于直线x +y ＝0对称，且α＝﹣60°，则角β的集合是．【变式4-3】已知α＝﹣30°，若α与β的终边关于直线x ﹣y ＝0对称，则β＝；若α与β的终边关于y 轴对称，则β＝；若α与β的终边关于x 轴对称，则β＝．【考点5 已知终边求角】【例5】（2019春•凉州区校级月考）已知α＝﹣1910°．（1）把角α写成β+k •360°（k ∈Z ，0°≤β＜360°）的形式，指出它是第几象限的角；（2）求出θ的值，使θ与α的终边相同，且﹣720°≤θ＜0°．【变式5-1】若角α的终边落在直线x +y ＝0上，求在[﹣360°，360°]内的所有满足条件的角α．【变式5-2】已知α、β都是锐角，且α+β的终边与﹣280°角的终边相同，α﹣β的终边与670°角的终边相同，求∠α、∠β的大小．【变式5-3】（2018春•武功县期中）已知角α＝45°；（1）在区间[﹣720°，0°]内找出所有与角α有相同终边的角β；（2）集合|18045,2k M x x k Z ⎧⎫==⨯︒+︒∈⎨⎬⎩⎭，|18045,4k N x x k Z ⎧⎫==⨯︒+︒∈⎨⎬⎩⎭那么两集合的关系是什么？【考点6 已知角终边的区域确定角】【例6】写出角的终边在阴影中的角的集合．【变式6-1】如图所示；（1）分别写出终边落在0A ，0B 位置上的角的集合；（2）写出终边落在阴影部分（包括边界）的角的集合．【变式6-2】用集合表示顶点在原点，始边重合于x轴非负半轴，终边落在阴影部分内的角（不含边界）．【变式6-3】已知角x的终边落在图示阴影部分区域，写出角x组成的集合．1.1.1任意角重难点题型【举一反三系列】知识链接【知识点1 任意角的概念】1.任意角2.角的分类【知识点2 象限角与非象限角】1.象限角当角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，则角的终边（除端点外）在第几象限，就称这个角为第几象限角.2.象限角的集合表示3.非象限角当角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，如果角的终边落在坐标轴上，就认为这个角不属于任何一个象限.4.非象限角的集合表示【知识点3 终边相同的角】一般地，所有与角α终边相同的角，连同角α在内，可构成一个集合，即任一与角α终边相同的角，都可以表示成角α与整个周角的和. 举一反三【考点1 象限角与集合间的基本关系】【例1】（2019春•杜集区校级月考）设A ＝{小于90°的角}，B ＝{第一象限角}，则A ∩B 等于（）A ．{锐角}B ．{小于90°的角}C ．{第一象限角}D ．{α|k •360°＜α＜k •360°+90°（k ∈Z ，k ≤0）}【分析】先求出A ＝{锐角和负角}，B ＝{α|k •360°＜α＜k •360°+90°，k ∈Z }，由此利用交集的定义给求出A ∩B ．【答案】解：∵A ＝{小于90°的角}＝{锐角和负角}，B ＝{第一象限角}＝{α|k •360°＜α＜k •360°+90°，k ∈Z }，∴A ∩B ＝{α|k •360°＜α＜k •360°+90°（k ∈Z ，k ≤0）}． {}Z k k S ∈⋅+==,360| αββ故选：D．【点睛】本题考查交集的求法，是基础题，解题时要认真审题，注意任意角的概念的合理运用．【变式1-1】（2019秋•钦南区校级月考）已知A＝{第一象限角}，B＝{锐角}，C＝{小于90°的角}，那么A、B、C关系是（）A．A∩C＝C B．B⊆C C．B∪A＝C D．A＝B＝C【分析】分别判断，A，B，C的范围即可求出【答案】解解：∵A＝{第一象限角}＝（k•360°，90°+k•360°），k∈Z；B＝{锐角}＝（0，90°），C＝{小于90°的角}＝（﹣∞，90°）∴B⊆C，故选：B．【点睛】本题考查了任意角的概念和角的范围，属于基础题．【变式1-2】（2019秋•黄陵县校级月考）设A＝{θ|θ为锐角}，B＝{θ|θ为小于90°的角}，C＝{θ|θ为第一象限的角}，D＝{θ|θ为小于90°的正角}，则下列等式中成立的是（）A．A＝B B．B＝C C．A＝C D．A＝D【分析】根据A＝{θ|θ为锐角}＝{θ|0°＜θ＜90°}，D＝{θ|θ为小于90°的正角}＝{θ|0°＜θ＜90°}，可得结论．【答案】解：根据A＝{θ|θ为锐角}＝{θ|0°＜θ＜90°}，D＝{θ|θ为小于90°的正角}＝{θ|0°＜θ＜90°}，可得A＝D．故选：D．【点睛】本题考查象限角和任意角，考查学生对概念的理解，比较基础．【变式1-3】（2019秋•宜昌月考）设M＝{α|α＝k•90°，k∈Z}∪{α|α＝k•180°+45°，k∈Z}，N＝{α|α＝k •45°，k∈Z}，则（）A．M⊆N B．M⊇N C．M＝N D．M∩N＝∅【分析】讨论k为偶数和k为奇数时，结合N的表示，从而确定N与M的关系．【答案】解：∵N＝{α|α＝k•45°，k∈Z}，∴当k为偶数，即k＝2n时，n∈Z，α＝k•45°＝2n•45°＝n•90°，∴当k为奇数，即k＝2n+1时，n∈Z，α＝k•45°＝（2n+1）•45°＝n•90°+45°，又M＝{α|α＝k•90°，k∈Z}∪{α|α＝k•180°+45°，k∈Z}，∴M⊆N．故选：A．【点睛】本题主要考查了集合之间的关系与应用问题，是基础题．【考点2 求终边相同的角】【例2】（2019春•娄底期末）下列各角中与225°角终边相同的是（）A．585°B．315°C．135°D．45°【分析】写出与225°终边相同的角，取k值得答案．【答案】解：与225°终边相同的角为α＝225°+k•360°，k∈Z，取k＝1，得α＝585°，∴585°与225°终边相同．故选：A．【点睛】本题考查终边相同角的表示法，是基础题．【变式2-1】（2018春•武功县期中）下列各组角中，终边相同的角是（）A．﹣398°，1042°B．﹣398°，142°C．﹣398°，38°D．142°，1042°【分析】根据终边相同的角的定义，化﹣398°和1042°为α+k•360°，k∈Z的形式，再判断即可．【答案】解：由题意，﹣398°＝322°﹣2×360°，1042°＝322°+2×360°，142°，38°；这四个角中，终边相同的角是﹣398°和1042°．故选：A．【点睛】本题考查了终边相同角的概念与应用问题，是基础题．【变式2-2】（2018春•武邑县校级期末）与﹣457°角终边相同角的集合是（）A．{α|α＝k•360°+457°，k∈Z}B．{α|α＝k•360°+97°，k∈Z}C．{α|α＝k•360°+263°，k∈Z}D．{α|α＝k•360°﹣263°，k∈Z}【分析】终边相同的角相差了360°的整数倍，又263°与﹣457°终边相同．【答案】解：终边相同的角相差了360°的整数倍，设与﹣457°角的终边相同的角是α，则α＝﹣457°+k•360°，k∈Z，又263°与﹣457°终边相同，∴{α|α＝263°+k•360°，k∈Z}，故选：C．【点睛】本题考查终边相同的角的概念及终边相同的角的表示形式．【变式2-3】（2018春•林州市校级月考）在0°～360°范围内，与﹣853°18'终边相同的角为（）A．136°18'B．136°42'C．226°18'D．226°42'【分析】直接由﹣853°18'＝﹣3×360°+226°42′得答案．【答案】解：由﹣853°18'＝﹣3×360°+226°42′，可得，在0°～360°范围内，与﹣853°18'终边相同的角为226°42′，故选：D ．【点睛】本题考查终边相同的角的表示法，是基础题．【考点3 已知α终边所在象限求2α，2α，3α】【例3】（2018秋•宜昌期末）已知α为锐角，则2α为（）A ．第一象限角B ．第二象限角C ．第一或第二象限角D ．小于180°的角【分析】写出α的范围，直接求出2α的范围，即可得到选项．【答案】解：α为锐角，所以α∈（0°，90°），则2α∈（0°，180°），故选：D ．【点睛】本题考查象限角与轴线角，基本知识的考查，送分题．【变式3-1】（2018•徐汇区校级模拟）若α是第二象限的角，则3α的终边所在位置不可能是（）A ．第一象限B ．第二象限C ．第三象限D ．笫象限【分析】写出第二象限的角的集合，得到的范围，分别取k 值得答案．【答案】解：∵α是第二象限角，∴90°+k •360°＜α＜180°+k •360°，k ∈Z ．则30°+k •120°＜＜60°+k •120°，k ∈Z ．当k ＝0时，30°＜＜60°，α为第一象限角；当k ＝1时，150°＜＜180°，α为第二象限角；当k ＝2时，270°＜＜300°，α为第四象限角．由上可知，的终边所在位置不可能是第三象限角．故选：C ．【点睛】本题考查象限角及轴线角，考查终边相同角的集合，是基础题．【变式3-2】（2019春•北碚区校级期中）已知α为第二象限角，则2α所在的象限是（） A ．第一或第二象限B ．第二或第三象限C ．第一或第三象限D ．第二或第四象限【分析】用不等式表示第二象限角α，再利用不等式的性质求出满足的不等式，从而确定角的终边在的象限．【答案】解：∵α是第二象限角，∴k •360°+90°＜α＜k •360°+180°，k ∈Z ，则k •180°+45°＜＜k •180°+90°，k ∈Z ，令k ＝2n ，n ∈Z有n •360°+45°＜＜n •360°+90°，n ∈Z ；在一象限；k ＝2n +1，n ∈z ，有n •360°+225°＜＜n •360°+270°，n ∈Z ；在三象限；故选：C ．【点睛】本题考查象限角的表示方法，不等式性质的应用，通过角满足的不等式，判断角的终边所在的象限【变式3-3】（2019秋•宜城市校级月考）如果α是第三象限角，则2α-是（）A ．第一象限角B ．第一或第二象限角C．第一或第三象限角D．第二或第四象限角【分析】由α是第三象限角，得到180°+k•360°＜α＜270°+k•360°，k∈Z，从而能求出﹣的取值范围，由此能求出﹣所在象限．【答案】解：∵α是第三象限角，∴180°+k•360°＜α＜270°+k•360°，k∈Z，∴﹣135°﹣k•180°＜﹣＜﹣90°﹣k•180°，∴﹣是第一或第三象限角．故选：C．【点睛】本题考查角所在象限的判断，是基础题，解题时要认真审题，注意第三象限角的取值范围的合理运用．【考点4 终边对称的角的表示法】【例4】（2019春•南京期中）若角α＝m•360°+60°，β＝k•360°+120°，（m，k∈Z），则角α与β的终边的位置关系是（）A．重合B．关于原点对称C．关于x轴对称D．关于y轴对称【分析】结合角的终边相同的定义进行判断即可．【答案】解：α的终边和60°的终边相同，β的终边与120°终边相同，∵180°﹣120°＝60°，∴角α与β的终边的位置关系是关于y轴对称，故选：D．【点睛】本题主要考查角的终边位置关系的判断，结合角的关系是解决本题的关键．【变式4-1】若角α的终边与45°角的终边关于原点对称，则α＝．【分析】角α的终边与45°角的终边关于原点对称，可得α＝k•360°+225°，（k∈Z）．【答案】解：∵角α的终边与45°角的终边关于原点对称，∴α＝k•360°+225°，（k∈Z）．故答案为：α＝k•360°+225°，（k∈Z）．【点睛】本题考查了终边相同的角，属于基础题．【变式4-2】若角α和β的终边关于直线x+y＝0对称，且α＝﹣60°，则角β的集合是．【分析】求出β∈[0°，360°）时角β的终边与角α的终边关于直线y＝﹣x对称的值，再根据终边相同的角写出角β的取值集合．【答案】解：若β∈[0°，360°），则由角α＝﹣60°，且角β的终边与角α的终边关于直线y＝﹣x对称，可得β＝330°，所以当β∈R时，角β的取值集合是{β|β＝330°+k•360°，k∈Z}．故答案为：{β|β＝330°+k•360°，k∈Z}．【点睛】本题主要考查了终边相同的角的定义和表示方法，是基础题．【变式4-3】已知α＝﹣30°，若α与β的终边关于直线x﹣y＝0对称，则β＝；若α与β的终边关于y轴对称，则β＝；若α与β的终边关于x轴对称，则β＝．【分析】由题意画出图形，然后利用终边相同角的表示法得答案．【答案】解：如图，设α＝﹣30°所在终边为OA，则关于直线x﹣y＝0对称的角β的终边为OB，终边在OB上的最小正角为120°，故β＝120°+k•360°，k∈Z；关于y轴对称的角β的终边为OC，终边在OC上的最小正角为210°，故β＝210°+k•360°，k∈Z；关于x轴对称的角β的终边为OD，终边在OD上的最小正角为30°，故β＝30°+k•360°，k∈Z．故答案为：120°+k•360°，k∈Z；210°+k•360°，k∈Z；30°+k•360°，k∈Z．【点睛】本题考查终边相同角的表示法，数形结合使问题更加直观，是基础题．【考点5 已知终边求角】【例5】（2019春•凉州区校级月考）已知α＝﹣1910°．（1）把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式，指出它是第几象限的角；（2）求出θ的值，使θ与α的终边相同，且﹣720°≤θ＜0°．【分析】（1）利用终边相同的假的表示方法，把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式，然后指出它是第几象限的角；（2）利用终边相同的角的表示方法，通过k的取值，求出θ，且﹣720°≤θ＜0°．【答案】解：（1）∵﹣1910°＝﹣6×360°+250°，180°＜250°＜270°，∴把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式为：﹣1910°＝﹣6×360°+250°，它是第三象限的角．（2）∵θ与α的终边相同，∴令θ＝k•360°+250°，k∈Z，k＝﹣1，k＝﹣2满足题意，得到θ＝﹣110°，﹣470°．【点睛】本题考查终边相同角的表示方法，基本知识的考查．【变式5-1】若角α的终边落在直线x+y＝0上，求在[﹣360°，360°]内的所有满足条件的角α．【分析】求出角α的终边相同的角，然后求解在[﹣360°，360°]内的所有满足条件的角α．【答案】解：角α的终边落在直线x+y＝0上，则直线的倾斜角为：45°，角α的终边的集合为：{α|α＝k•180°+45°，k∈Z}．当k＝﹣2时，α＝﹣315°，k＝﹣1时，α＝﹣135°，k＝0时，α＝45°，k＝1时，α＝225°，在[﹣360°，360°]内的所有满足条件的角α：﹣315°，135°，45°，225°．【点睛】本题考查终边相同角的表示，考查计算能力．【变式5-2】已知α、β都是锐角，且α+β的终边与﹣280°角的终边相同，α﹣β的终边与670°角的终边相同，求∠α、∠β的大小．【分析】按照终边相同角的表示方法将α+β、α﹣β表示出来，然后解出α、β，由α、β都是锐角得到所求．【答案】解：因为α+β的终边与﹣280°角的终边相同，α﹣β的终边与670°角的终边相同，所以α+β＝﹣280°+360°k；α﹣β＝670°+360°k；k∈Z；两式相加，2α＝390°+720°k ＝360°+30°+720°k ＝30°+720°k ；α＝15°+360°k ；因为α，β是锐角，所以α＝15°；β＝65°．【点睛】本题考查了终边相同角的表示，利用方程组的思想求两角，属于基础题．【变式5-3】（2018春•武功县期中）已知角α＝45°；（1）在区间[﹣720°，0°]内找出所有与角α有相同终边的角β；（2）集合|18045,2k M x x k Z ⎧⎫==⨯︒+︒∈⎨⎬⎩⎭，|18045,4k N x x k Z ⎧⎫==⨯︒+︒∈⎨⎬⎩⎭那么两集合的关系是什么？【分析】（1）所有与角α有相同终边的角可表示为45°+k ×360°（k ∈Z ），列出不等式解出整数k ，即得所求的角．（2）先化简两个集合，分整数k 是奇数和偶数两种情况进行讨论，从而确定两个集合的关系．【答案】解析：（1）由题意知：β＝45°+k ×360°（k ∈Z ），则令﹣720°≤45°+k ×360°≤0°，得﹣765°≤k ×360°≤﹣45°，解得，从而k ＝﹣2或k ＝﹣1，代回β＝﹣675°或 β＝﹣315°．（2）因为M ＝{x |x ＝（2k +1）×45°，k ∈Z }表示的是终边落在四个象限的平分线上的角的集合；而集合N ＝{x |x ＝（k +1）×45°，k ∈Z }表示终边落在坐标轴或四个象限平分线上的角的集合，从而：M ⊊N ．【点睛】（1）从终边相同的角的表示入手分析问题，先表示出所有与角α有相同终边的角，然后列出一个关于k的不等式，找出相应的整数k，代回求出所求解；（2）可对整数k的奇、偶数情况展开讨论．【考点6 已知角终边的区域确定角】【例6】写出角的终边在阴影中的角的集合．【分析】利用象限角的表示方法、终边相同的角的集合性质即可得出．【答案】解：图1：角的集合为{α|30°+k×360°≤α≤120°+k•360°，k∈Z}；图2：角的集合为{α|﹣210°+k•360°≤α≤30°+k•360°，k∈Z}；图3：角的集合为{α|﹣45°+k•360°≤α≤30°+k•360°，k∈Z}；图4：角的集合为{α|60°+k•360°≤α≤120°+k•360°，k∈Z}∪{α|240°+k•360°≤α≤300°+k•360°，k∈Z}．【点睛】本题考查了象限角的表示方法、终边相同的角的集合性质，考查了推理能力与计算能力，属于中档题．【变式6-1】如图所示；（1）分别写出终边落在0A，0B位置上的角的集合；（2）写出终边落在阴影部分（包括边界）的角的集合．【分析】（1）直接由终边相同角的表示法写出终边落在0A，0B位置上的角的集合；（2）结合（1）中写出的终边落在0A，0B位置上的角的集合，利用不等式表示出终边落在阴影部分（包括边界）的角的集合．【答案】解：（1）如图，终边落在OA上的角的集合为{α|α＝150°+k•360°，k∈Z}．终边落在OB上的角的集合为{α|α＝﹣45°+k•360°，k∈Z}；（2）如图，终边落在阴影部分（包括边界）的角的集合为{β|﹣45°+k•360°≤β≤150°+k•360°，k∈Z}．【点睛】本题考查象限角和轴线角，考查了终边相同角的概念，是基础题．【变式6-2】用集合表示顶点在原点，始边重合于x轴非负半轴，终边落在阴影部分内的角（不含边界）．【分析】直接利用所给角，表示角的范围即可．【答案】解：图1所表示的角的集合：{α|k•360°﹣30°＜α＜k•360°+75°，k∈Z}．图2终边落在阴影部分的角的集合．{α|k•360°﹣135°＜α＜k•360°+135°，k∈Z}【点睛】本题考查角的表示方法，是基础题．【变式6-3】已知角x的终边落在图示阴影部分区域，写出角x组成的集合．【分析】直接利用所给角，表示角的范围即可．【答案】解：图（1）所表示的角的集合：{α|k•360°﹣135°≤α≤k•360°+135°，k∈Z}．图2终边落在阴影部分的角的集合{α|k•180°+30°≤α≤k•180°+60°，k∈Z【点睛】本题考查角的表示方法，是基础题．。

高中数学人教版必修四课后练习(含解析)：1.1.1任意角

1.1.1任意角班级:__________姓名:__________设计人:__________日期:__________课后练习基础过关1．下列说法中，正确的是A.第二象限角为钝角B.第三象限角必大于第二象限角C.是第二象限角D.−95020′,984040′,264040′是终边相同的角2．若角2α与240°角的终边相同,则α=( )A.120°+k·360°,k∈ZB.120°+k·180°,k∈ZC.240°+k·360°,k∈ZD.240°+k·180°,k∈Z3．如图所示,终边落在阴影部分的角的集合是信达信达A .{α|-45°≤α≤120°}B .{α|120°≤α≤315°}C .{α|k ·360°-45°≤α≤k ·360°+120°,k ∈Z }D .{α|k ·360°+120°≤α≤k ·360°+315°,k ∈Z }4．集合A ={α|α=k ⋅360∘+120∘,k ∈Z}中属于区间(−360°，360°)的角是____.5．如图所示，终边落在直线y =√3x 上的角的集合为______．6．在角的集合{α|α=45°+k ⋅90°，k ∈Z}中：(1)有几种终边不相同的角？(2)在−360°∼360°范围内的角有几个？7．(1)已知角α =45°，在区间[―720°，0°]内找出所有与角α有相同终边的角β.(2)集合M ={x|x =k 2×180°+45°,k ∈Z}，N ={x|x =k4×180°+45°,k ∈Z}，那么两集合的关系是什么？8．已知−900<α<900,−900<β<900,求α−β2的范围. 能力提升1．已知角α是第二象限角,试确定角2α,α2是第几象限角..2．写出终边在如图所示阴影部分内的角的集合信达信达1.1.1任意角【基础过关】1．D；【解析】本题考查象限角的判定.对A，第二象限也有负角；对B；第三象限角可能为负，第二象限取正；对C，为第三象限，故错误，选D.【备注】无2．B【解析】角2α与240°角的终边相同,则2α=240°+k·360°,k∈Z,则α=120°+k·180°,k ∈Z.选B.【备注】无3．C【解析】由图可知,终边落在阴影部分的角的取值范围为k·360°-45°≤α≤k·360°+120°,k ∈Z,故选C.【备注】该题易出现的问题是忽略角的方向,不能准确表示两个边界角.4．−240°，120°【解析】无【备注】无5．{α|α=60°+n⋅180°，n∈Z}【解析】本题主要考查角的概念.终边落在射线y=√3x(x≥0)上的角的集合是S1={α|α=60°+k⋅360°，k∈Z}，终边落在射线y=√3x(x≤0)上的角的集合是S2={α|α=240°+k⋅360°，k∈Z}，于是终边落在直线y=√3x上的角的集合是S={α|α=60°+k⋅360°，k∈Z}∪{α|α=240°+k⋅360°，k∈Z}={α|α=60°+2k⋅180°，k∈Z}∪{α|α= 60°+(2k+1)⋅180°，k∈Z}={α|α=60°+n⋅180°，n∈Z}．【备注】无6．解：(1)在给定的角的集合中，终边不相同的角共有四种．(2)由−360°<45°+k⋅90°<360°，得−92<k<72．又k∈Z，故k=−4，−3，−2，−1，0，1，2，3．信达信达∴给定的集合中在−360°∼360°范围内的角共有8个．【解析】本题主要考查角的概念。

高中数学必修四练习册(后含答案)

C．{α|α＝k·180°，k∈Z}
D．{α|α＝k·180°＋90°，k∈Z}
6．射线 OA 绕端点 O 逆时针旋转 120°到达 OB 位置，由
OB 位置顺时针旋转 270°到达 OC 位置，则∠AOC＝
()
A．150°
B．－150°
C．390°
D．－390°
7．若集合 M＝{α|α＝±30°＋k·180°，k∈Z}，N＝{α|α＝(－
D.α|α＝2kπ＋53π，k∈Z
3．已知集合 A＝{α|2kπ≤α≤(2k＋1)π，k∈Z}，B＝{α|－
4≤α≤4}，则 A∩B＝( )
A．
B．{α|0≤α≤π|
C．{α|－4≤α≤4|
D．{α|－4≤α≤－π 或 0≤α≤π}
4．一条弦的长等于半径，则这条弦所对的圆心角是____
弧度 ( )
1.1.1 任意角
一、选择题
1．下列各命题正确的是( )
A．终边相同的角一定相等
B．第一象限角都是锐角
C．锐角都是第一象限角
D．小于 90°的角都是锐角
2．若 α 是第一象限角，则下列各角中属于第四象限角的
是( )
A．90°－α
B．90°＋α
C．360°－α
D．180°＋α
3．在“①160°，②480°，③－960°，④－1600°”这四个角
A．sinα＋cosα<0
B．tanα－sinα<0
π
π
π
A.π
B.2
C.3
D.4
5．如图中，圆的半径为 5，圆内阴影部分的面积是( )
175π A. 36
125π B. 18
75π C. 18

2024年新高一数学初升高衔接《任意角》含答案解析

第21讲任意角模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．了解任意角的概念，能正确区分正角、零角和负角；2．理解象限角的意义，掌握终边相同的角的意义与表示；3．通过正角和负角理解角的大小、旋转方向，通过角的终边所在的象限的讨论，培养数学抽象与逻辑推理核心素养.知识点 1 角的概念1、角的概念：角可以看成平面内一条射线绕其端点从一个位置旋转到另一个位置形成的图形。

2、角的表示：（1）始边：射线的起始位置OA ．（2）终边：射线的终止位置OB ．（3）顶点：射线的端点O ．（4）记法：图中的角α可记为“角α”或“α∠”或“AOB ∠”．3、角的分类：（1）正角：按逆时针方向旋转形成的角；（2）负角：按顺时针方向旋转形成的角；（3）零角：一条射线没有作任何旋转形成的角。

知识点 2 相等角与角的加减1、相等角：设角α由射线OA 绕端点O 旋转而成，角β由射线O'A'绕端点O'旋转而成，如果他们的旋转方向相同且旋转量相等，那么就称αβ=.2、相反角：把射线OA 绕端点O 按不同方向旋转相同的量所成的两个角叫做互为相反角，角α的相反角记为α-.3、角的加减：记α，β是任意两个角，我们规定：把角α的终边按逆时针旋转角β，这时终边所对应的角是αβ+；按顺时针旋转角β，这时终边所对应的角是αβ-知识点 3 终边相同的角1、终边相同的角的表示：所有与角α终边相同的角，连同角α在内，可构成一个集合S ，它们彼此相差360()k k Z ⋅∈，即{}360,S k k Z ββα==+⋅∈.【要点辨析】相等的角终边一定相同，但终边相同的角却不一定相等，终边相同的角有无数个，它们之间相差360°的整数倍，要注意角的集合的表示形式不是唯一的。

1、象限角：当角的顶点与坐标原点重合，角的始边与x 轴的非负半轴重合，那么角的终边（除端点外）在第几象限，就说这个角是第几象限；象限角集合表示第一象限角{}36036090,⋅<<⋅+∈x k k k Z α第二象限角{}36090360180,⋅+<<⋅+∈x k k k Z α第三象限角{}360180360270,⋅+<<⋅+∈x k k k Z α第四象限角{}360270360360,⋅+<<⋅+∈x k k k Z α3、轴线角：当角的顶点与坐标原点重合，角的始边与x 轴的非负半轴重合，并且角的终边落在坐标轴上时，称这个角为轴线角，这时，这个角不属于任何象限。

新课标数学必修4第1章三角函数练习(含答案)

1.1.1任意角一、情景导入： 1．角的概念的推广(1)任意角的形成：角可以看成是由一条射线绕着它的端点旋转而成的，射线的端点叫做角的顶点，旋转开始时的射线叫做角的始边，终止时的射线叫做角的终边．(2)正角、负角和零角：按逆时针方向旋转而成的角叫做正角．按顺时针方向旋转而成的角叫做负角．当射线没有作任何旋转时，形成的角叫做零角．(3)象限角：角的顶点与坐标原点重合，角的始边与x 轴的正半轴重合，角的终边落在第几象限，就把这个角称为第几象限的角．如果角的终边落在坐标轴上,则称这个角称为轴上角. ２．象限角及终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合{|360,}S k k Z ββα==+⋅︒∈，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和；二、感受理解：１．设{}90E =︒小于的角，{}F =锐角，{}G =第一象限的角，{}90M =︒︒小于的角,但不小于0的角，你能分清这几个有关角的集合之间的包含关系吗？2．在～间，求出与下列各角终边相同的角，并判定它们分别是哪一个象限的角．（1）；（2）．3．分别写出： ①终边在轴负半轴上的角的集合； ②终边在轴上的角的集合；③终边在第一、三象限角平分线上的角的集合； ④终边在四象限角平分线上的角的集合．４．如图，终边落在位置时的角的集合是____________；线边落在位置，且在[]360,360-︒︒内的角的集合是_________；终边落在阴影部分（含边界）的角的集合是______________．５．探究等分角所在的象限我们都知道，60︒是锐角，60︒角的一半30︒也是锐角．60360k ︒+⋅︒,k Z ∈是第一象限角，它的一半30180,k k Z ︒+⋅︒∈是否仍在第一象限呢？三、迁移拓展：6．下列命题中，正确的是（）．A ．始边和终边都相同的两个角一定相等B ．是第二象限的角C ．若，则4α是第一象限角 D ．相等的两个角终边一定相同7．在“①160°②480°③-960°④-1600°”这四个角中，属于第二象限的角是( )A ．①B ．①②C ．①②③D ．①②③④8．经过3小时35分钟，时针与分针转过的度数之差是（）．A ．B ．C ．D ．9．下列结论中正确的是( )A.小于90°的角是锐角B.第二象限的角是钝角C.相等的角终边一定相同D.终边相同的角一定相等10．若α是第一象限的角，则-2α是( )A.第一象限的角B.第一或第四象限的角C.第二或第三象限的角D.第二或第四象限的角11．与终边相同的角的集合是___________，它们是第____________象限的角，其中最小的正角是___________，最大负角是___________．12．已知的终边在轴上的上方，那么是第__________象限的角．13．设，，，则相等的角集合为____________．14．若角与的终边关于轴对称，则与的关系是__________；若角与的终边互相垂直，则与的关系是___________．提示：可结合图形分析 15．给出下列命题：①和的角的终边方向相反； ②和的角的终边相同；③第一象限的角和锐角终边相同； ④ (21)180k α=+⋅︒与(41)180,()k k Z β=±⋅︒∈终边相同；其中所有正确命题的序号是______________．16．求所有与所给角终边相同的角的集合，并求出其中的最小正角，最大负角：（1）；（2）．17．已知{}9036045360,90360225360,A k k k k k Z ααα=-︒+⋅︒<<︒+⋅︒︒+⋅︒<<︒+⋅︒∈或{}360150360,B k k k Z ββ=⋅︒<<︒+⋅︒∈，求与提示：可根据图形分析两集合间的关系18．如图所示，写出图中阴影部分（包括边界）的角的集合，并指出是否是该集合中的角．19．已知是第二象限的角，你能结合图示分别找到以下问题的答案吗？（1）2α角所在的象限（2）角所在的象限20．若角的终边经过点，试写出角的集合，并求出集合中绝对值最小的角．四、实践应用：21．α是一个任意角，则α与-α的终边是( )A ．关于坐标原点对称B ．关于x 轴对称C ．关于直线y=x 对称D ．关于y 轴对称 22．若α与β的终边互为反向延长线，则有( )A ．α＝β＋180°B ．α＝β－180°C ．α＝－βD ．α＝β＋（2ｋ＋1）180°，ｋ∈Ｚ参考答案： 1.1.1任意角二、感受理解 1．略２．（1），三（2），三３．①；② ；③；④．４．{}120k k Zαα=︒+⋅︒∈；{}45,315-︒︒{}45360120360,k k k Z ββ-︒+⋅︒≤≤︒+⋅︒∈．５．一、三三、迁移拓展：6．D 7．C 8．C 9．Ｃ 10．Ｄ11．，三，，12．一、三13．，14．(21)180,k k Z αβ+=+⋅︒∈,90360,k k Z αβ-=±︒+⋅︒∈15．②、④16．（1）{}120360,k k Z αα=-︒+⋅︒∈，，；（2），31523'︒，4437'-︒．17． {}90360150360,36045360,A B k k k k k Z ααα=︒+⋅︒<<︒+⋅︒⋅︒<<︒+⋅︒∈或 {}90360225360,A B k k k Z αα=︒+⋅︒<<︒+⋅︒∈-18．，是19．（１）一、三，（２）三，四，或轴负半轴上的角20．，．四、实践应用： 21．Ｂ 22．Ｄ1.1.2弧度制一、情景导入：1. 弧度制(1)1弧度的角：等于半径长的圆弧所对的圆心角叫做１弧度的角，这种用弧度来度量的制度称弧度制(2)正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零，任一已知角α的弧度数都满足lr α=，其中l 为以角α作为圆心角时所对圆弧的长，r 为圆的半径．2．度数与弧度数的换算：180rad π︒=10.01745180rad rad π︒=≈, 1801()57.35718'rad π=︒≈︒=︒请写出下列特殊角的弧度数与角度数．3．相关计算公式（１）圆心角α，半径r ，弧长l 之间的关系：l r α=＝180n r π（２）扇形面积公式：221122360n r S r lr πα===二、感受理解：１．请你用弧度制表示下列特殊位置的角，这些内容对今后的学习很重要．（1）终边在x 轴上的角（2）终边在y 轴上的角（3）终边在坐标轴上的角（4）终边在第一、三象限角平分线上的角。

高中数学必修4讲义：第一章 1.1 1.1.1 任意角 Word版含答案

1．1.1任意角预习课本P2～5，思考并完成以下问题(1)角是如何定义的？角的概念推广后，分类的标准是什么？(2)象限角的含义是什么？判断角所在的象限时，要注意哪些问题？(3)终边相同的角一定相等吗？如何表示终边相同的角？[新知初探]1．任意角(1)角的概念：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)角的表示：如图，OA是角α的始边，OB是角α的终边，O是角的顶点．角α可记为“角α”或“∠α”或简记为“α”．(3)角的分类：[点睛]对角的概念的理解的关键是抓住“旋转”二字：①要明确旋转的方向；②要明确旋转量的大小；③要明确射线未作任何旋转时的位置．2．象限角把角放在平面直角坐标系中，使角的顶点与原点重合，角的始边与x轴的非负半轴重合，那么，角的终边在第几象限，就说这个角是第几象限角；如果角的终边在坐标轴上，就认为这个角不属于任何一个象限．[点睛]象限角的条件是：角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合．3．终边相同的角所有与角α终边相同的角，连同角α在内，可构成一个集合S＝{β|β＝α＋k·360°，k ∈Z}，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．[点睛]对终边相同的角的理解(1)终边相同的角不一定相等，但相等的角终边一定相同；(2)k∈Z，即k为整数这一条件不可少；(3)终边相同的角的表示不唯一．[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)(1)－30°是第四象限角．()(2)钝角是第二象限的角．()(3)终边相同的角一定相等．()答案：(1)√(2)√(3)×2．与45°角终边相同的角是()A．－45°B．225°C．395°D．－315°答案：D3．下列说法正确的是()A．锐角是第一象限角B．第二象限角是钝角C．第一象限角是锐角D．第四象限角是负角答案：A4．将35°角的终边按顺时针方向旋转60°所得的角度数为________，将35°角的终边按逆时针方向旋转一周后的角度数________．答案：－25°395°[典例]下列命题正确的是()A．终边与始边重合的角是零角B．终边和始边都相同的两个角一定相等C．在90°≤β<180°范围内的角β不一定是钝角D．小于90°的角是锐角[解析] 终边与始边重合的角还可能是360°，720°，…，故A 错；终边和始边都相同的两个角可能相差360°的整数倍，如30°与－330°，故B 错；由于在90°≤β<180°范围内的角β包含90°角，所以不一定是钝角，C 正确；小于90°的角可以是0°，也可以是负角，故D 错误．[答案] C[活学活用]如图，射线OA 绕端点O 旋转90°到射线OB 的位置，接着再旋转－30°到OC 的位置，则∠AOC 的度数为________．解析：∠AOC ＝∠AOB ＋∠BOC ＝90°＋(－30°)＝60°. 答案：60°[典例] 写出与75°角终边相同的角β的集合，并求在360°≤β<1 080°范围内与75°角终边相同的角．[解] 与75°角终边相同的角的集合为S ＝{β|β＝k ·360°＋75°，k ∈Z}．当360°≤β<1 080°时，即360°≤k ·360°＋75°<1 080°，解得1924≤k <21924.又k ∈Z ，所以k ＝1或k ＝2. 当k ＝1时，β＝435°；当k ＝2时，β＝795°.综上所述，与75°角终边相同且在360°≤β<1 080°范围内的角为435°角和795°角．分别写出终边在下列各图所示的直线上的角的集合．解：(1)在0°～360°范围内，终边在直线y＝0上的角有两个，即0°和180°，因此，所有与0°角终边相同的角构成集合S1＝{β|β＝0°＋k·360°，k∈Z}，而所有与180°角终边相同的角构成集合S2＝{β|β＝180°＋k·360°，k∈Z}，于是，终边在直线y＝0上的角的集合为S＝S1∪S2＝{β|β＝k·180°，k∈Z}．(2)由图形易知，在0°～360°范围内，终边在直线y＝－x上的角有两个，即135°和315°，因此，终边在直线y＝－x上的角的集合为S＝{β|β＝135°＋k·360°，k∈Z}∪{β|β＝315°＋k·360，k∈Z}＝{β|β＝135°＋k·180°，k∈Z}.[典例]并指出它们是第几象限角．(1)－75°；(2)855°；(3)－510°.[解]作出各角，其对应的终边如图所示：(1)由图①可知：－75°是第四象限角．(2)由图②可知：855°是第二象限角．(3)由图③可知：－510°是第三象限角．若α是第四象限角，则180°－α一定在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析：选C ∵α与－α的终边关于x 轴对称，且α是第四象限角，∴－α是第一象限角．而180°－α可看成－α按逆时针旋转180°得到，∴180°－α是第三象限角.[典例] 已知α是第二象限角，求角α2所在的象限． [解] 法一：∵α是第二象限角，∴k ·360°＋90°<α<k ·360°＋180°(k ∈Z)．∴k 2·360°＋45°<α2<k 2·360°＋90°(k ∈Z)．当k 为偶数时，令k ＝2n (n ∈Z)，得n ·360°＋45°<α2<n ·360°＋90°，这表明α2是第一象限角；当k 为奇数时，令k ＝2n ＋1(n ∈Z)，得n ·360°＋225°<α2<n ·360°＋270°，这表明α2是第三象限角． ∴α2为第一或第三象限角．法二：如图，先将各象限分成2等份，再从x 轴正向的上方起，依次将各区域标上一、二、三、四，则标有二的区域即为α2的终边所在的区域，故α2为第一或第三象限角． [一题多变]1．[变设问]在本例条件下，求角2α的终边的位置．解：∵α是第二象限角，∴k ·360°＋90°<α<k ·360°＋180°(k ∈Z)．∴k ·720°＋180°<2α<k ·720°＋360°(k ∈Z)．∴角2α的终边在第三或第四象限或在y 轴的非正半轴上．2．[变条件]若角α变为第三象限角，则角α2是第几象限角？解：如图所示，先将各象限分成2等份，再从x 轴正半轴的上方起，按逆时针方向，依次将各区域标上一、二、三、四，则标有三的区域即为角α2的终边所在的区域，故角α2为第二或第四象限角．层级一学业水平达标1．－215°是()A．第一象限角B．第二象限角C．第三象限角D．第四象限角解析：选B由于－215°＝－360°＋145°，而145°是第二象限角，则－215°也是第二象限角．2．下面各组角中，终边相同的是()A．390°，690°B．－330°，750°C．480°，－420°D．3 000°，－840°解析：选B∵－330°＝－360°＋30°，750°＝720°＋30°，∴－330°与750°终边相同．3．若α＝k·180°＋45°，k∈Z，则α所在的象限是()A．第一、三象限B．第一、二象限C．第二、四象限D．第三、四象限解析：选A由题意知α＝k·180°＋45°，k∈Z，当k＝2n＋1，n∈Z，α＝2n·180°＋180°＋45°＝n·360°＋225°，在第三象限，当k＝2n，n∈Z，α＝2n·180°＋45°＝n·360°＋45°，在第一象限．∴α是第一或第三象限的角．4．终边在第二象限的角的集合可以表示为()A．{α|90°<α<180°}B．{α|90°＋k·180°<α<180°＋k·180°，k∈Z}C．{α|－270°＋k·180°<α<－180°＋k·180°，k∈Z}D．{α|－270°＋k·360°<α<－180°＋k·360°，k∈Z}解析：选D终边在第二象限的角的集合可表示为{α|90°＋k·360°<α<180°＋k·360°，k∈Z}，而选项D是从顺时针方向来看的，故选项D正确．5．将－885°化为α＋k·360°(0°≤α＜360°，k∈Z)的形式是()A．－165°＋(－2)×360°B．195°＋(－3)×360°C．195°＋(－2)×360°D．165°＋(－3)×360°解析：选B－885°＝195°＋(－3)×360°，0°≤195°<360°，故选B.6．在下列说法中：①时钟经过两个小时，时针转过的角是60°；②钝角一定大于锐角；③射线OA绕端点O按逆时针旋转一周所成的角是0°；④－2 000°是第二象限角．其中错误说法的序号为______(错误说法的序号都写上)．解析：①时钟经过两个小时，时针按顺时针方向旋转60°，因而转过的角为－60°，所以①不正确．②钝角α的取值范围为90°<α<180°，锐角θ的取值范围为0°<θ<90°，因此钝角一定大于锐角，所以②正确．③射线OA按逆时针旋转一周所成的角是360°，所以③不正确．④－2 000°＝－6×360°＋160°与160°终边相同，是第二象限角，所以④正确．答案：①③7．α满足180°<α<360°，5α与α有相同的始边，且又有相同的终边，那么α＝________.解析：5α＝α＋k·360°，k∈Z，∴α＝k·90°，k∈Z.又∵180°<α<360°，∴α＝270°.答案：270°8．若角α＝2 016°，则与角α具有相同终边的最小正角为________，最大负角为________．解析：∵2 016°＝5×360°＋216°，∴与角α终边相同的角的集合为{α|α＝216°＋k·360°，k∈Z}，∴最小正角是216°，最大负角是－144°.答案：216°－144°9．在0°～360°范围内，找出与下列各角终边相同的角，并指出它们是第几象限角：(1)549°；(2)－60°；(3)－503°36′.解：(1)549°＝189°＋360°，而180°<189°<270°，因此，549°角为第三象限角，且在0°～360°范围内，与189°角有相同的终边．(2)－60°＝300°－360°，而270°<300°<360°，因此，－60°角为第四象限角，且在0°～360°范围内，与300°角有相同的终边．(3)－503°36′＝216°24′－2×360°，而180°<216°24′<270°，因此，－503°36′角是第三象限角，且在0°～360°范围内，与216°24′角有相同的终边．10．已知角的集合M ＝{α|α＝30°＋k ·90°，k ∈Z}，回答下列问题：(1)集合M 中大于－360°且小于360°的角是哪几个？(2)写出集合M 中的第二象限角β的一般表达式．解：(1)令－360°<30°＋k ·90°<360°，则－133<k <113，又∵k ∈Z ，∴k ＝－4，－3，－2，－1,0,1,2,3，∴集合M 中大于－360°且小于360°的角共有8个，分别是－330°，－240°，－150°，－60°，30°，120°，210°，300°.(2)集合M 中的第二象限角与120°角的终边相同，∴β＝120°＋k ·360°，k ∈Z.层级二应试能力达标1．给出下列四个结论：①－15°是第四象限角；②185°是第三象限角；③475°是第二象限角；④－350°是第一象限角．其中正确的个数为( )A ．1B ．2C ．3D ．4解析：选D ①－15°是第四象限角；②180°<185°<270°是第三象限角；③475°＝360°＋115°，而90°<115°<180°，所以475°是第二象限角；④－350°＝－360°＋10°是第一象限角，所以四个结论都是正确的．2．若角2α与240°角的终边相同，则α＝( )A ．120°＋k ·360°，k ∈ZB ．120°＋k ·180°，k ∈ZC ．240°＋k ·360°，k ∈ZD ．240°＋k ·180°，k ∈Z解析：选B角2α与240°角的终边相同，则2α＝240°＋k·360°，k∈Z，则α＝120°＋k·180°，k∈Z.选B.3．若α与β终边相同，则α－β的终边落在()A．x轴的非负半轴上B．x轴的非正半轴上C．y轴的非负半轴上D．y轴的非正半轴上解析：选A∵α＝β＋k·360°，k∈Z，∴α－β＝k·360°，k∈Z，∴其终边在x轴的非负半轴上．4．设集合M＝{α|α＝45°＋k·90°，k∈Z}，N＝{α|α＝90°＋k·45°，k∈Z}，则集合M与N的关系是()A．M∩N＝∅B．M NC．N M D．M＝N解析：选C对于集合M，α＝45°＋k·90°＝45°＋2k·45°＝(2k＋1)·45°，即M＝{α|α＝(2k＋1)·45°，k∈Z}；对于集合N，α＝90°＋k·45°＝2×45°＋k·45°＝(k＋2)·45°，即N＝{α|α＝(k＋2)·45°，k∈Z}＝{α|α＝n·45°，n∈Z}．∵2k＋1表示所有的奇数，而n 表示所有的整数，∴N M，故选C.5．从13：00到14：00，时针转过的角为________，分针转过的角为________．解析：经过一小时，时针顺时针旋转30°，分针顺时针旋转360°，结合负角的定义可知时针转过的角为－30°，分针转过的角为－360°.答案：－30°－360°6．已知角2α的终边在x轴的上方，那么α是第______象限角．解析：由题意知k·360°<2α<180°＋k·360°(k∈Z)，故k·180°<α<90°＋k·180°(k ∈Z)，按照k的奇偶性进行讨论．当k＝2n(n∈Z)时，n·360°<α<90°＋n·360°(n∈Z)，∴α在第一象限；当k＝2n＋1(n∈Z)时，180°＋n·360°<α<270°＋n·360°(n∈Z)，∴α在第三象限．故α是第一或第三象限角．答案：一或三7．试写出终边在直线y＝－3x上的角的集合S，并把S中适合不等式－180°≤α<180°的元素α写出来．解：终边在直线y＝－3x上的角的集合S＝{α|α＝k·360°＋120°，k∈Z}∪{α|α＝k·360°＋300°，k∈Z}＝{α|α＝k·180°＋120°，k∈Z}，其中适合不等式－180°≤α<180°的元素α为－60°，120°.8.如图，分别写出适合下列条件的角的集合：(1)终边落在射线OB上；(2)终边落在直线OA上；(3)终边落在阴影区域内(含边界)．解：(1)终边落在射线OB上的角的集合为S1＝{α|α＝60°＋k·360°，k∈Z}．(2)终边落在直线OA上的角的集合为S2＝{α|α＝30°＋k·180°，k∈Z}．(3)终边落在阴影区域内(含边界)的角的集合为S3＝{α|30°＋k·180°≤α≤60°＋k·180°，k∈Z}．。