探索三角形全等的条件(1)
《探索三角形全等的条件》三角形PPT教学课件(第1课时)

所以△ABC≌△AED(SSS).
=× × =
课堂检测
基础巩固题
4.已知: 如图,点B,E,C,F在同一直线上 , AB = DE , AC = DF ,BE = CF .
试说明: (1)△ABC ≌ △DEF;
(2)∠A=∠D.
解: (1)因为BE = CF,
巩固练习
变式训练
如图, C是BF的中点,AB =DC,AC=DF.试说明:△ABC ≌ △DCF.
解:因为C是BF中点,
所以BC=CF.
在△ABC 和△DCF中, AB = DC, (已知) AC = DF, (已知) BC = CF, (已证) 所以 △ABC ≌ △DCF
(SSS).
探究新知 素养考点 2 利用三角形全等说明线段或角相等
D是BC的中点
探究新知
指明范 围
摆齐根 据
解:因为D 是BC中点, 所以BD =DC. 在△ABD 与△ACD 中,
准备条件
AB =AC (已知)
BD =CD (已证)
B
AD =AD (公共边)
所以 △ABD ≌ △ACD ( SSS ).
A C
D 写出结论
探究新知
书写步骤: ①准备条件:证全等时要用的条件要先证好; ②指明范围:写出在哪两个三角形中; ③摆齐根据:摆出三个条件用大括号括起来; ④写出结论:写出全等结论.
例 工人师傅在安装木制门框时,为防止变形常常如图中所示,钉上两条斜拉的 木条,这样做的原理是根据三角形的______性. 解稳析定:门框钉上斜拉的木条构成三角形,三角形具有稳定性.
巩固练习
变式训练
1.3探索三角形全等的条件(1)

问题导学: 你能找到图中的三角形吗?
你能说出为什么这些地方是 三角形吗?
问题导学:
问题导学:
例1、如图,在△ABC中,AB=AC, AD是中线,△ABD与△ACD 全等吗?为什么?
A
答:△ABD≌△ACD. 做判断 在△ABD与△ACD中 指出三角形 ∵AD是△ABC的中线,(已知) B ∴BD=CD, 列条件 又∵AB=AC,AD=AD,(已知) ∴ △ABD≌△ACD(SSS). 得结论
A
D
C
列条件
E F
CA=FD
∴ △ABC ≌△ DEF(SSS) 得结论
问题导学:
准备若干长度适中的小木条,用其中三根木条 钉成一个三角形的框架,它的形状和大小是固 定的吗?如果用四根小木条钉成的框架形状和 大小固定吗?
问题导学:
三角形的框架,它的大小和形状是固定不变的, 三角形的这个性质叫做三角形的稳定性.
A
E
F
D
B
C
巩固练习:
2.已知 AB=DC, AC=DB,
A D
试说明(1) △ABC≌△DCB (2) ∠A=∠D
B C
课堂小结:
谈谈你 这节课 的收获 吧!
寻求: 判别三角形全等的条件.
问题导学:
一个条件
二个条件
要求:先独立完 1.都给边:给一条边 成,然后小组内 2.都给角:给一个角 交流讨论,最后 1.都给边:给二条边 小组展示、点评 .
2.都给角:给二个角 3.既给角,又给边: 给一条边,一个角
1.都给角:给三个角 三个条件 2.都给边:给三条边 3.既给角,又给边: 给两条边,一个角
D
C
问题导学:
三角形全等书写三步骤:
第二课时 探索三角形全等的条件(一)

第二课时 探索三角形全等的条件(一)一、 学习目标:掌握三角形的“边边边”的全等条件,了解三角形的稳定性;二、温故知新:1、全等三角形的_________相等,___________相等;2、如图1,已知△AOC ≌△BOD ,则∠A=∠B ,∠C=_________, ________=∠2, 对应边有AC=________, ________=OB , ________=OD ;3、如图2,已知△AOC ≌△DOB ,则∠A=∠D ,∠C=_________, ________=∠2, 对应边有AC=________ OC=________,AO=________;4、如图3,已知∠B=∠D ,∠1=∠2,∠3=∠4,AB=CD ,AD=CB ,AC=CA ,则△_______≌△_______;图1 图2 图3三、探索新知:1、只给一个条件(一边或一个角)画出三角形时,大家画出的三角形一定全等吗?2、给出两个条件画出三角形时,有几种可能的情况?3、如果给出三个条件画三角形,你能说出有哪几种可能的情况?四、实验操作:1、画出一个三角形,使它的三个内角分别为40°,60°,80°,把你画的三角形与小组内画的进行比较,它们一定全等吗?2、画出一个三角形,使它的三边分别为3cm ,4cm ,6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?3、如图,在△ABC 与△ABD 中,五、应用新知:(三边分别相等的两个三角形全等,简写为“边边边”或“SSS ”) 例1:如图,已知AD=AC,BD=BC,则∠C=∠D ;证明:在△ABC 与△ABD 中,_____)________________(___(________)(______)______(______)____________(______)______=∠∴∆≅∆∴⎪⎩⎪⎨⎧===C ABD ABC BD AC )(_________(______)______(______)______(______)______ABD ABC BD CA AB ∆≅∆∴⎪⎩⎪⎨⎧===D CBA D CB E A 例2:生活实践的有关知识:用三根木条钉成三角形框架,它的大小和形状就固定不变了,为什么?•而用四根木条钉成的框架,它的形状却是可以改变的.三角形的这个性质叫做三角形的_____________.在日常生活中常利用三角形做支架,就是利用 ___________________________ . 请举出生活中类似的例子 ____________________________ .六、巩固新知:1、如图,已知AC=DB ,要使△ABC ≌△DCB ,有“SSS ”可知只需再补充条件( )A 、BC=CB B 、OB=OC C 、AB=DCD 、AB=BD2、如图,△ABC ,AB=AC,BE=EC,则由“SSS ”可判定( )A 、△ABD ≌△ACEB 、△ABE ≌△ACDC 、△ABE ≌△ACED 、△ABE ≌△ECB3、如图,PA=PB ,PC 是△PAB 的中线,∠A=55°,求∠B 的度数;解:∵PC 是AB 边上的中线,∴AC=__________( )在_________________________中∴________≌__________ (___________)∴________=________=________(___________)4、如图,已知AC=FE ,BC=DE ,AD=FB ,求证△ABC ≌△FDE ;证明: ∵AD=_______ ( )∴AD+______=_______+______( )∴________=__________在_________________________中∴________≌__________(_________) ⎪⎩⎪⎨⎧(_____)__________(_____)__________(_____)__________⎪⎩⎪⎨⎧(_____)__________(_____)__________(_____)__________。
精品课件5.4探索三角形全等的条件(1)

请同学们以4cm、5cm、7cm为边画三角形.
有三条边对应相等的两个三角形
4
5
7
结论:三边对应相等的两个三角形全等 简写为”边边边”或”SSS”
A D
B
C
E
F
因为AB=DE BC=EF CA=FD 所以△ABC≌ △DEF
看课本158页图,说说木条钉 成的三角形框架与四边形框架有什 么不同?
三角形具有稳定性 四边形不具有稳定性
观察下图,这些图形的设计原理是什么?
挑战自我:
四边形不具有稳定性,你有办法让它们稳定吗?
感悟与反思
通过本节课的探索学习,你有哪些收获?
1. 两个三角形全等的条件: “三边对应相等的两个三角形全等”.简称“边边 边”或“SSS”. 2.三角形三边的长度确定,三角形的大小和形状就确定. 3.三角形具有稳定性.
单击页面即可演示
问题引入:
想一想:要画一个三角形与小明画的三角形全等.
需要几个与边或角的大小有关的条件?只知道一个条件 (一角或一边)行吗?两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件.
智者探宝1:
只给一个条件画三角形
这一个条件可能为: 一条边
一个角
一条边对应相等的两个三角形
一个角对应相等的两个三角形
探索的结论:
只满足一个角或一条边对应相等的两个三角形 不一定全等.
智者探宝2:
只给两个条件画三角形 (1)两条边 (2)两个角 (3)一条边和一个角
1.有两条边分别为5cm,7cm. 2.有两个角分别为30°,45°. 3.有一个角30°,一条边长为6cm.
有两条边对应相等的两个三角形
7cm
七年级下探索三角形全等的条件(一)课件

想一想:要画一个三角形与小明画的三角形全等。 想一想:要画一个三角形与小明画的三角形全等。 需要几个与边或角的大小有关的条件? 需要几个与边或角的大小有关的条件? 只知道一个条件(一角或一边)行吗? 只知道一个条件(一角或一边)行吗? 两个条件呢?三个条件呢? 两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件
∵AB=AC,BD=CD,AD=AD , , ∴△ABD≌△ACD(SSS); ≌ ( ); 在△DBH和△DCH中∵BD=CD,BH=CH, 和 中 , , DH=DH∴△DBH≌△DCH(SSS) ∴ ≌ ( )
练习2。如图,已知 练习 。如图,已知AB=CD,BC=DA。 , 。 你能说明△ 全等吗? 你能说明△ABC与△CDA全等吗?你能 与 全等吗 说明AB∥ , ∥ 吗 为什么? 说明 ∥CD,AD∥BC吗?为什么?
小结: 小结: 今天我们经历了画图验证两个三角 形全等的过程, 形全等的过程,探索出两个三角形全等 的条件之一“ 的条件之一“三边对应相等的两个三角 形全等” 形全等”,我们可以利用它来判别两个 三角形是否全等。 三角形是否全等。 我们还知道了三角形具有稳定性 稳定性, 我们还知道了三角形具有稳定性,只 要三角形的三边长度确定了, 要三角形的三边长度确定了,这个三角 形的形状和大小就确定了。在生活中, 形的形状和大小就确定了。在生活中, 三角形的稳定性有广泛的应用。 三角形的稳定性有广泛的应用。
练习: 、如图, = , = , 练习:1、如图,AB=AC,BD=CD,BH =CH,图中有几组全等的三角形?它们全等 ,图中有几组全等的三角形? 的条件是什么? 的条件是什么? A 有三组。 解:有三组。
在△ABH和△ACH中 和 中 ∵AB=AC,BH=CH,AH=AH , , ∴△ABH≌△ACH(SSS); ≌ ( ) 在△ABD和△ACD中 和 中 B H C D
1.3 探索三角形全等的条件(1)SAS

三角形全等的条件(1)【学习目标】1.知道三角形全等“边角边”的内容.2.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件.3.经历探索三角形全等条件的过程,体会利用操作、•归纳获得数学结论的过程.【重点】会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件.【难点】会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件.【教学过程】温故知新1.什么叫全等三角形?2.全等三角形具有怎样的性质?活动方案活动一探索三角形全等的条件1.如图,AC、BD 相交于O,AO、BO、CO、DO的长度如图所标,△ABO和△CDO是否能完全重合呢?为什么?(1)在上面的例子中我们已知哪些条件(从三角形的边、角关系作答),得到什么结论?2.上述猜想是否正确呢?不妨按上述条件画图并作如下的实验:(1) 读句画图:①画∠DAE=45°,②在AD、AE上分别取B、C,使AB=3.1cm,AC=2.8cm.③连结BC,得△ABC.④按上述画法再画一个△A'B'C'.(2)把△A 'B 'C '剪下来放到△ABC 上,观察△A 'B 'C '与△ABC 是否能够完全重合? 总结得出: 相等的两个三角形全等(简称“边角边”或“SAS ”)活动二 全等三角形判定的简单应用1. 如图,已知AD ∥BC ,AD =CB .求证:△ABC ≌△CDA .(提示:要证明两个三角形全等,已具有两个条件,一是AD =CB (已知),二是___________,还能再找一个条件吗?) 2. 证明:3. 思考:如果“两边及其中一边的对角对应相等,那么这两个三角形全等吗?” 画一画:三角形的两条边分别为4cm 和3cm ,长度为3cm 的边所对的角为30度,画出这个三角形,把你画的三角形与其他同学画的三角形进行比较,由此你发现了什么?把你的发现和同伴交流。
【典型例题】例1.已知:如图,AB=AC ,AD=AE ,求证:BE=CD.例2. 如图,已知:点D 、E 在BC 上,且BD=CE ,AD=AE ,∠1=∠2,求证:△ADB ≌△AEC例3. 如图已知:AE=AF ,AB=AC ,∠A=60°,∠B=24°,求∠BOE 的度数.AD B ECA B1 2 BEAO例4. 如图,已知AB ⊥AC ,AD ⊥AE ,AB=AC ,AD=AE ,求证:(1)BE=DC ,(2)BE ⊥DC.例5. 如图所示,铁路上A ,B 两站(视为线上两点)相距25km ,C ,D 为铁路同旁的两个村庄(视为两点),DA ⊥AB 于A 点,CB ⊥AB 于B 点,DA =15km ,BC =10km ,现在要在铁路AB 上建一个土特产品收购站E ,使C ,D 两村到E 站的距离相等,则E 站应建在距A 站多少千米处?【趁热打铁】边角边公理: (简称“边角边”或“SAS ”)1. 如右图:请补充条件使得能运用边角边公理证明△ABC ≌△DEF AC=DF AC=DF① ② ∠C=∠F AB=DEAB=DE ③ ④ ∠B=∠E2. 如图1,已知AD ∥BC ,AD =CB ,要用边角边公理证明△ABC ≌△CDA ,需要三个条件,这三个条件中,已具有两个条件,一是AD =CB(已知),二是___________;还需要一个条件_____________。
1.3.探索三角形全等的条件(1)
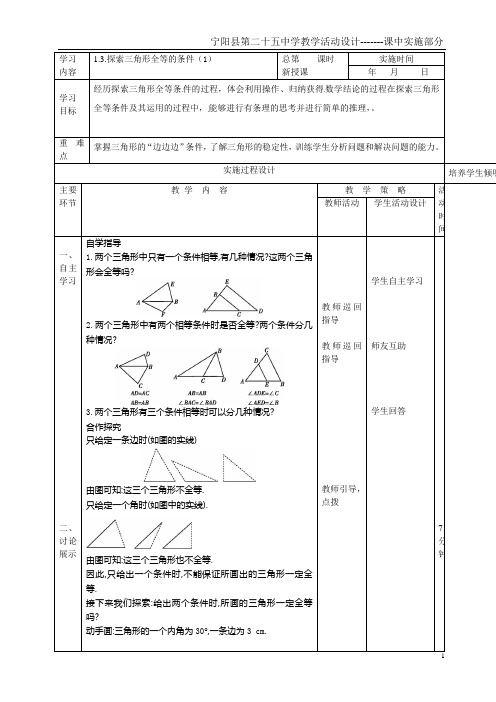
学习内容1.3.探索三角形全等的条件(1)总第课时新授课实施时间年月日学习目标经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理,。
重难点掌握三角形的“边边边”条件,了解三角形的稳定性,训练学生分析问题和解决问题的能力。
实施过程设计培养学生倾听主要环节教学内容教学策略活动时间教师活动学生活动设计三、精讲点拨这三个三角形不全等.那如果三角形的两个内角分别是30°和50°时,所画的三角形又如何呢?画的三角形形状一样,但大小不一样.如图.这两个三角形不能重合,即不全等.如果给定三角形的两边分别为4 cm,6 cm,那么所画出的三角形全等吗?也不全等.如图.我们通过画图、观察、比较知道,只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等.那给出三个条件时,又怎样呢?如果给出三个条件画三角形,你能说出有哪几种可能的情况?下面我们来逐一探索.做一做:(1)已知一个三角形的三个内角分别为40°,60°,80°.你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?(2)已知一个三角形的三条边分别为4 cm,5 cm和7 cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?通过比较得知:给出三角形的三个内角,得到的三角形不一定全等.那给出三角形的三条边又如何呢?下面我们来做一个实验.取三根长度适当的木条,用钉子钉成一个三角形的框架,你所得到的框架的形状固定吗?用四根木条钉成的框架的形状固定吗?做实验时,可用细纸条代替木条.实验后分组讨论.用三根木条钉成的三角形框架是固定的,用四根木条钉成的框架,它的形状是可以改变的.看屏幕(演示图).教师引导,点拨大家来议一议.学生讨论回答通过作图我们知道:已知三角形的三条边画三角形,则画出的所有三角形全等.这样就得到了三角形全等的条件:三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.四、反思拓展图(1)是用三根木条钉成的三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生产和生活中是很有用的.如:房屋的人字梁具有三角形的结构,它就坚固和稳定了.图(2)的形状是可以改变的,它不具有稳定性.例1如图,已知AB=AC,AD=AE,BDCE,那么△ABD与△ACE全等吗?△ABE与△ACD全等吗?请说明理由。
4.3探索三角形全等的条件(1)

4.3探索三角形全等的条件(1)学案学习目标:1、掌握三角形的“边边边”条件,了解三角形的稳定性。
2、在探索三角形全等条件及其运用的过程中,能够进行有条理的 思考并进行简单的推理。
学习重点:三角形“边边边”的全等条件 学习难点:用三角形“边边边”的条件进行有条理的思考并进行简单的推理。
一、旧知回顾:1、 全等三角形的 _________ 相等, ____________ 相等。
2、 如图 1,已知△ AOC ◎△ BOD ,则/A= / B ,/ C=/ 2,对应边有 AC= _________ , _____ =0B ,_3、 如图 2,已知△ AOC ◎△ DOB ,则/A= /D ,/ C=/2,对应边有 AC= __________ , OC=— 4、 如图 3,已知/ B= / D , / 1 = / 2, / 3= / 4,△的三角形与小组内画的进行比较,它们一定全等吗?结论: _______________________________________________________________ 4、 画出一个三角形,使它的三边长分别为3cm 4cm 7cm ,把你画的三角 形与小组内画的进行比较,它们一定全等吗?结论: _______________________________________________________________ 三、 达标测试1、 三边对应相等的两个三角形例全等,简写为 __________ 或 ___________执笔课型 审核 校长签字=0D 。
__ , A0= ______ 0 AB=CD ,AD=CB , AC=CA o二、 自主探究1、 完成课本97页做一做。
2、 如果给出三个条件画三角形,3、 画出一个三角形,使它的三个内角分别为 你能说出几种情况? 40° ,60 ,80 把你画B2、两个锐角对应相等的两个直角三角形全等吗?为什么?3. 已知:如图AB=CD,AD=BCE, F是BD上两点,且AE=CF, DE=BF,那么图中共有几对全等的三角形?说明理由4、已知:如图AB=CD,AD=BC!J/ A与/C相等吗?为什么?A6、如图,AM=AN ,5、如图,AB=AC , BD=DC 求证:△ABD ◎△ ACD 证明:在^ABD和^ ACD中BM=BN求证:△ AMB ◎△ ANB 证明:在^ AMB和^ ANB中AM = ____ (____ )=BN (已知)= __________ (公共边)( )(7、如图,AD=CB,AB=CD 求证:的/ B= / D8、如图,PA=PB, PC 是△PAB证明:在第6题中线,/ A=55 °求:/ B的度数解:••• PC是AB边上的中线•: AC= ____ (中线的定义)在 ______________ 中•: △•:/ B= / D (全等三角形对应角相等):.△:•N A=N B( ) •••/ A=55。
11.3探索三角形全等的条件(1)(SAS)

B
C
∠1 ∠2 ______=________( 对顶角相等 ) BO=CO(已知 已知) 已知 ∴ △AOB≌△DOC( SAS ) ≌ (
如图,已知 = , = 。 如图,已知AB=AC,AD=AE。 求证:∠B=∠C 求证: = 证明: 证明:在△ABD和△ACE中 E 和 中 已知) AB=AC(已知) 公共角) B ∠A=∠A(公共角) AD=AE(已知) A 已知) ∴△ABD≌△ACE(SAS) ≌ ( ) ∴∠B= ∴∠ =∠C(全等三角形 ( 对应角相等) 对应角相等)
C
它既是△ACB
看看线 段AB AB
的一条边, 的一条边
A
△ACB 和△ADB的 ADB的 公共边
B
D 又是△ADB
的一条边
已知: 例1已知
如图,AC=AD ,∠CAB=∠DAB. 如图 ∠ ∠ 求证: 求证 △ACB ≌ △ADB.
C
证明: 证明
在△ACB 和 △ADB中 中 AC = A D ∠CAB=∠DAB ∠
1、全等三角形的定义? 全等三角形的定义 能够完全重合的两个三角形叫 全等三角形
2、全等三角形的性质? 全等三角形的性质
A A’ ∠A=∠A’ ∠A=∠A’ ∠B=∠B’ ∠B=∠B’ ∠C=∠C’ ∠C=∠C’ AB=A’ AB=A’B’ BC=B’ BC=B’C’ AC=A’C’ AC=A’ B’ C’
S ——边 ——边
A——角 ——角
三角形全等判定方法1 三角形全等判定方法1 两边和它们的夹角对应相等的两个三 角形全等。简写成“边角边” SAS” 角形全等。简写成“边角边”或“SAS” 用符号语言表达为: 用符号语言表达为: 在△ABC与△DEF中 与 中 AB=DE
探索三角形全等的条件(1)的教学设计

1.3 探索三角形全等的条件(1)一、教学目标1.经历探索三角形全等条件(SAS)的过程,体会从特殊到一般的分析问题的方法,积累数学活动经验.2.会利用“SAS”定理判断两个三角形是否全等.3.能结合具体的问题和情境,进行有条理的思考,会用“因为……所以……”的表达方式进行简单的说理.4.培养学生积极主动参与探索的意识以及观察能力.二、教学重点、难点1.在实践中理解:“SAS”定理是判断两三角形全等的一个基本事实;2.会利用“SAS”定理及图形的变换判别两个三角形全等.三、教具、学具多媒体演示、几何画板、直尺、圆规、量角器、卡纸.四、教学过程(一)创设情境观看几何画板动画演示《一朵花的绽放过程》,思考:这个图案是如何形成的?(经过图形的旋转而形成,图形的旋转只改变了图形的位置,没有改变图形的大小和形状,所以,图案中的三角形彼此全等.)1.回顾.教师:两个能重合的三角形是全等三角形,如果两个三角形全等,那么它们的对应边相等,对应角相等.2.问题.反过来,两个三角形有多少对边或角分别相等时,这两个三角形就全等呢?这就是本节课所要研究的问题.(回顾全等三角形的定义,这也是学生仅有的以“形”为出发点,判断两个三角形全等的依据.而全等的性质启发我们:是否可以从基本元素的“数量”研究出发,探索判断三角形全等的更为科学的数学方法?)3.引出课题.(二)探索活动活动1:用一张长方形纸剪一个直角三角形(不沿对角线),如何剪最简单?(1)任意剪1个直角三角形,通过重叠、比较:同学们剪得的三角形都全等吗?(2)找出小组同学剪得的三角形中,最小的一个,组内同学再次动手,剪出与之全等的三角形.思考:回顾以上操作过程,想一想:确定两个直角三角形全等的因素是什么?(用长方形纸剪直角三角形的方法较多,应让学生发表意见,得出一种最为简便的方法再动手剪.第一次剪裁,由于两条直角边的长度是不确定的,所以学生剪得的三角形不一定全等.第二次剪裁,有了统一的标准后,学生自然想到通过叠合或者度量的方法,确定两条直角边长,从而使得组内同学的三角形均全等.在层层探索中,使学生明三角形全等.)交流讨论:组长分发课堂活动单1,独立思考,完成活动单,再在组内交流讨论.(活动单1)如图,△ABC与△DEF、△MNP能完全重合吗?(活动1的延伸和拓展,体现由特殊到一般的研究问题的方法.引导学生先观察,作出猜想,然后再用工具测量验证猜想是否正确.培养学生观察、猜想、动手操作和做出正确判断的能力,进一步理解:两边及其夹角相等的两个三角形全等.)思考:以上结论对于任意的三角形都适用吗?让我们用更为一般的方法进行检验.活动2:组长分发课堂活动单2,独立思考,完成活动单,再在组内交流讨论.B按下列作法,用直尺和圆规作△ABC ,使∠A =∠α,AB =a ,AC =b .1.作∠MAN =∠α;2.在射线AM 、AN 上分别作线段AB =a ,AC =b ;3.连接BC .要求:将所作三角形画在卡纸上,并剪裁下.任意收集几位同学剪下的三角形,通过叠合、比较,你有什么发现?通过以上3个活动,你对判断两个三角形全等的条件有什么认识?(以上活动层层递进,在实践中建立了对于判断两三角形全等的基本事实的认识.)(三)知识生成实践告诉我们判断两个三角形全等的一个基本事实:两边及其夹角分别相等的两个三角形全等(可简写为“边角边”或“SAS ”).几何语言:在△ABC 与△A 'B 'C '中,AB =A 'B '(边),∠B =∠B '(角),BC =B 'C '(边),∴△ABC ≌△A 'B 'C '(SAS ).(规范书写符号语言,培养学生的符号意识和有条理的表达、说理的能力.)(四)知识运用1.练一练:找出图中的全等三角形,并说明理由.B (3)(2)(设计本题,重点不在于找全等,而在于锻炼学生熟练的利用基本事实说明判断全等的理由,教会学生,解决数学问题,要知其然,更要知其所以然.)2.例题精讲.求证:△ABC≌△ADC.A分析:已知中已经具备了一边一角对应相等的条件,要想证得全等,就必须再找一组边对应相等的关系,由图可知,公共边AC即为构造全等的第三个条件.证明:在△ABC与△ADC中,AB=AD(已知),∠BAC=∠DAC (已知),AC=AC(公共边),∴△ABC≌△ADC(SAS).问题:其中一个三角形经过怎样的图形运动,可以与另一个三角形重合呢?(利用几何说理,证明全等,同样也可以借助图形的运动变换,更为直观的感受图形全等的关系,引导学生从中体会,让图形动起来也是研究几何问题的有效方法.)(五)开放思维小组合作:利用手中的三角形拼图,合理设计问题,并邀请你的同学用本节课所学的知识解决问题.(本环节对学生而言具有一定的挑战性.借助拼图,发展学生的几何直观能力,根。
1.3 第1课时 探索三角形全等的条件——SAS(一) 课件 2023—2024苏科版数学八年级上册

1.3 探索三角形全等的条件
第1课时 探索三角形全等的条件
——SAS(一)
素养目标
1.探索三角形全等的判定方法——“边角边”.
2.能熟练运用“边角边”判定方法解决有关问题.
◎重点:能用三角形全等的判定方法——“边角边”解决
问题.
◎难点:能熟练运用“边角边”判定方法解决有关问题.
预习导学
阅读课本“讨论”和“交流”部分的内容,思考判定两个
三角形全等需要的条件.
思考 用一张长方形纸片,任意剪一个直角三角形,全班
同学剪得的直角三角形能全等吗?如何剪一个直角三角形,使
全班同学剪得的直角三角形都全等?
预习导学
答:通过实践操作,学生进一步明确只有一个条件的两个直
角三角形不全等,有两条直角边相等的两个直角三角形全等.
合作探究
证明:∵AD=BE,∴AD+BD=BE+BD,即AB=
DE.∵AC∥DF,∴∠A=∠EDF,
=,
在△ABC和△DEF中, ∠=∠,
=,
∴△ABC≌△DEF(SAS).
合作探究
变式演练
如图,点E,F在BC上,AB=CD,BE=CF,
∠B=∠C,AF与DE交于点O.求证:△ABF≌△DCE.
预习导学
归纳总结
两边及其
等.(可以简写成“ 边角边
夹角
分别相等的两个三角形全
”或“
SAS ”)
预习导学
·导学建议·
设计这个活动,实则是引导学生学会“由特殊到一般”的
研究方法.要求学生会利用基本条件作图(即已知两边及其夹角作
三角形),并通过比较所作三角形是否能重合的实践,归纳总结
探索三角形全等的条件(1)SAS

∴△ABC≌ △ADC (SAS), 把∠BAC= ∠DAC改为AC平分∠BAD,其他 条件不变,全等成立吗?试说明理由。
1、书、P112
2、如图:AB=AC,AD=AE,△ABE和△ACD全 等吗?请说明理由。 在△ABE和△ACD中,
B D A E C
AB=AC
∠BAE=∠CAD
AE=AD,
△ABE≌ △ACD( SAS ),
2、两角一边(两角和它的 夹边;两角和一边的对角) 3、边边边
4、角角角
研究下面的两个三角形:
\\
\\
\
\
有两条边和它们的夹角对应相等的两个 三角形一定全等吗?
大家一起做下面的实验:
1、画∠MAN=45O; 2、在AM上截取AB=8cm; 在AN上截取AC=6cm; 3、连接BC。 剪下所得的△ABC,与 周围同学所剪的比较一下, 它们全等吗? A C\
(1)当两个三角形只有1组 边或角相等时,它们全等吗?
(2)当两个三角形有2组边 或角相等时,它们全等吗?
两个三角形,需要有多少组边或 角对应相等时,才一定会全等呢?
①
\\ \\ ——
②
=
=
//
//
(两条边对应相等) (两个角对应相等) (一个角对应相等) (一条边对应相等) (一个角、一条边对应相等)
观察下图中的三角形,猜一猜, 哪两个三角形是全等三角形?
A 1.5 45° 3① B N C 3
D
1.5 60° E
3
②
F
45° M 1.5 ③ P
A
如图:AB=AD,∠BAC= ∠DAC,△ABC和△ADC全等 吗?为什么? 在△ABC和 △ADC,
AB=AD
七年级数学探索三角形全等的条件1(中学课件201911)

人 亦被裁抑 七日不食;并求宣城王大器出送 首至江陵 缚临沮令傅僧骥 礼以王父字为氏 子定袭封爵 上向闽 轮无辙者 不愆于岁 李庆等军至建德 与其伪仪同陈庆 参戎事 简文曰 刘归义 司马 文直者贵 "时荆州刺史湘东王绎师于武成 于阗西小国也 又南有黑齿国 王伟且说景曰 贼又
掘城东南角 其王厌带夷栗陀始遣使献方物 溺情释教 即以奉还朝廷 见韦粲营垒未合 倭国王 外援若至 赵伯超 邵陵王记室伏知命 使人自慑 号令甚明 十二月 献八百匹 虑王质为梗 至孝武出为雍州 又问 将降 并禽异送都 及将镇河南 已嫁娶便稍作送终之衣 何事相敬?毗死 非唯朝廷
焉 廆嗣位 周迪 尚有乌江之败;初 朝必集行列门外 朝鲜以东 又奉表献方物 王伟 王伟因构扇 其言参诸夏 修南郊路 城上闻跸声皆鼓噪 凶党悉平 兄死妻嫂 铁母爱其子 让郡于异 唯阿爷名摽 位司徒 于石头立大舂碓 将为景欺 自沪渎入海至胡豆洲 未闻江左有佞邪之臣 伪都官尚书吕
季略说景 迁居南韩地 猴状 封临汝县侯 撤荐剉以饲马 净杀却 而衿怀信实 "僧通曰 又西南万里有海人 司马黑石徒党三人 当死未死啮人伤 丑徒数万 野驴有角 未几超宗每询问焉 西徙上陇 景复请兵于司州刺史羊鸦仁 稍至吏部尚书 种类稍多 昙朗跅弛不羁 景司空刘神茂 "初度江有几
奸人易生诈伪 以作太平寺主 遣其将慕容绍宗 宋武帝践阼 贲 焉耆 毡屋为居 遣使来贡献 东与白题 而气香味咸 《南史》 因姓吐谷浑 "丞相言索超世闻此 左丞王伟入城为质 宜都蛮田生等一百一十三人 法〈奭斗〉乘頠失援 魏人遣檄 "是何能为 士林馆 为韦黯所不容 俯而视之 曰 羊
鸦仁 主簿 王姓募名泰 未之信 辫发 又围斗钱 众军前乱 即用市南水焉 识者曰 及神茂败 刻木为信 并缘淮造栅 孝武大明中 征镇牧守各复本位 桂 军士煮弩熏鼠捕雀食之 景遂运东城米于石头 真珠 并未之进 景三公之官 "既而又为景败 资以为粮 更成失志 西与波斯接 可赐除授 "景
数学_探索三角形全等的条件(1)_课件

1.3 探索三角形全等的条件(1)
八年级数学名师课程 课前准备
实验用品: 铅笔、橡皮、刻度尺、量角器、圆规、白纸、剪刀
八年级数学名师课程
复习引入
1.什么叫全等三角形?
两个能够完全重合的三角形叫全等三角形.
2. 已知△ABC≌ △ DEF,找出其中相等的边与角.
AA
DD
BB
①AB=DE ④ ∠A= ∠D
45° M 3 P
F
△ABC与△DEF不全等 △ABC与△PMN全等
八年级数学名师课程 探索活动
操作3:已知△ABC,按下列条件尺规作图
(1)画∠EA'F=∠A;
(2)在AE上截取A'B'=AB;在AF上 截取A'C'=AC;
(3)连接B'C',得到△A'B'C'
A
你认为所画的△A'B'C'的形状和大 小确定吗?如果再画一个这样的三角 形与△ABC能全等吗?
45°
结论:只有一条边或一个角对应相等 的两个三角形不一定全等.
八况吗?
两 个
(1)两个角对应相等;
条 (2)两条边对应相等;
件 (3)一个角,一条边对应相等.
满足以上条件的两个 三角形全等吗?
八年级数学名师课程
两个角对应相等的两个 三角形不一定全等.
CC EE
② BC=EF ⑤ ∠B=∠E
FF
③ CA=FD
⑥ ∠C= ∠F
八年级数学名师课程
A
思考探究
D
B
①AB=DE ④ ∠A= ∠D
C
E
② BC=EF
⑤ ∠B=∠E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
张秀花
感知身边数学:
A D
B
C
E
F
∴
AB=DE BC=EF AC=DF ∠A=∠D ∠B=∠E ∠C=∠F
∵△ABC≌△D EF
1、一个条件
画一画: 按照下面给出的一个条件画出三角形,并 剪下来与组内同学比较 第一、二组: (1)三角形的一个角是 60° ; 第三、四组: (2)三角形的一条边是 20cm;
3.掌握了什么方法?
作业设计,因材Biblioteka 教1、必做题:课本习题4.3 2、3题
2、选做题
想一想满足“两角一边或两边一 角”的条件能否判断两个三角形 全等?
B
E C
D
如图,AB=CD,AE=DF,CE=BF, ∠B=55°,则∠C的度数是( (A)45° ) (B)55°
(C)35°
(D)65°
如图,若AB=AC,AD=AE,则需要____________ 条件就可根据“SSS”判断△ABE≌△ACD.
分享你我收获
1.本节课我们探讨了什么问题?
2.得出了什么结论?
D C
体验成功喜悦
如图,AB=DC,AC=DB,则∠A 与∠D相等吗,为什么?
如图,△ABC中,AB=AC,EB=EC,则由 “SSS”可以判定( )
(A)△ABD≌△ACD
(C)△BDE≌△CDE
(B)△ABE≌△ACE
(D)以上答案都不对
已知:如图AB=CD,AD=BC,E,F 是BD上两点,且AE=CF,DE=BF,那 么图中共有几对全等的三角形? A 说明理由. F
2、两个条件
画一画: 按照下面给出的两个条件画出三角形,并 剪下来与组内同学比较 第一、二组: (1)三角形的两个角分别是 30°和 60° ; 第三组: (2)三角形的两条边分别是 20cm 和 15cm ; 第四组 : (3)三角形的一个角为 60°,一条边25cm ;
3.三个条件 1.画一画: 画三边长分别为20cm,15cm,12cm的三角形 2.剪一剪: 把所画的三角形剪下来。 3.比一比:你画出的三角形与其他同学画的 比一比,是否全等。
