第七讲:椭圆焦点三角形面积问题
椭圆焦点三角形的面积公式

椭圆焦点三角形的面积公式
椭圆焦点三角形也叫椭圆酉三角形,三角形一般由椭圆上两个焦
点O1和O2以及椭圆周上一点P构成。
椭圆焦点三角形的面积公式为:S = |OO1 × OO2 × a| / 6,其中OO1和OO2分别表示椭圆上两个焦
点之间的距离,a表示椭圆的长轴半径。
椭圆焦点三角形的形成有很多种情况:
一、当椭圆上的三点共线时,椭圆焦点三角形的面积为零,因为
在此情况下三点重合,没有三角形的形成。
二、当三点不共线时,根据椭圆焦点三角形的面积公式,可以计
算出这三角形的面积。
三、如果椭圆的两个焦点落在三点的延长线上时,椭圆焦点三角
形的面积也为零,因为此时三角形边长小于椭圆两个焦点間的距离,
因此不存在三角形,即三角形面积为零。
四、如果椭圆的两个焦点分别落在三角形的三条边上,则椭圆焦
点三角形的面积等于三角形的面积。
椭圆焦点三角形的面积公式是求解椭圆焦点三角形面积的有效工具,可用于几何分析和图形计算。
该公式既适用于共线的情况,也适
用于不共线的情况,可以让我们准确求得椭圆焦点三角形的面积,这
在几何图形分析中非常有用。
理解椭圆焦点三角形的特性并应用面积
公式可以让我们更好地分析几何图形。
高中数学破题致胜微方法(椭圆的进阶性质):椭圆焦点三角形的面积

今天我们研究椭圆焦点三角形的面积。
椭圆上一点和两个焦点构成的三角形,称之为椭圆焦点三角形。
其中,我们把椭圆的两个焦点和其短轴的一个端点构成的等腰三角形称为椭圆的一个特征焦点三角形。
先看例题:例:已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).求椭圆C的方程.解:依题意,设椭圆C的方程为22221x ya b+=(a>b>0)焦距为2c,由题设焦点和短轴的两个端点围成正方形且面积为8可知:b=c, a2=8,进而22142b a==,故椭圆C的方程为22184x y+=.归纳整理:12焦点三角形的面积求法:2211||,||r PF r PF ==,12F PF θ∠=;122r r a += 22212122cos (2)r r r r c θ+-= ∴222122()21cos 1cos a c b r r θθ-==++ 122121sin sin 21cos FP F Sr r b θθθ==+;再看一个例题,加深印象: 例:若P 是椭圆16410022=+y x 上的一点,1F 、2F 是其焦点,且︒=∠6021PF F ,求△21PF F 的面积. 解:可以直接用焦点三角形面积公式计算,即122121sin 643sin 21cos FP F S r r b θθθ===+ 注意:不必死记硬背公式,也可以求解,我们只需要记住求解思路,具体问题具体分析即可。
在椭圆16410022=+y x 中,,6,8,10===c b a 而.60︒=θ 记.||,||2211r PF r PF ==3点P 在椭圆上,∴由椭圆的第一定义得:.20221==+a r r在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ 配方,得:.1443)(21221=-+r r r r .144340021=-∴r r 从而.325621=rr .336423325621sin 212121=⨯⨯==∆θr r S PF F总结:1.椭圆焦点三角形是一个很重要的三角形,相关的知识有椭圆的定义、余弦定理等.2.掌握椭圆焦点三角形的面积公式,根据已知条件合理选择面积公式计算.练习:1.已知点P 是椭圆2216251600x y +=上一点,且在x 轴上方,F 1,F 2分别是椭圆的左、右焦点,直线PF 2的斜率为43-,求12PF F ∆的面积.2.曲线C 是平面内与两个顶点F 1(-1,0)和F 2(1,0)的距离的积等于常数a 2(a >1)的点的轨迹.4给出下列三个结论:①曲线C 过坐标原点;②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则△F 1PF 2的面积不大于212a . 其中,所有正确结论的序号是________. 3. 已知F 1,F 2是椭圆C:22221x y a b+=(a>b>0)的两个焦点,P 为椭圆C 上一点,且12PF PF ⊥ .若△PF 1F 2的面积为9,则b=________.答案:1. 解:椭圆即22110064x y +=,所以右焦点()26,0F 直线PF 2为)6y x =--,代入椭圆方程,消去x得2197680y --= 因为0y >,所以y =P的纵坐标P y =,所以12122PF F P S c y ∆=⨯⨯=。
椭圆焦点三角形面积公式几种推导

椭圆焦点三角形面积公式几种推导说到椭圆焦点三角形面积公式,不得不提它那一段“曲折”的历史。
哈哈,别误会啊,椭圆可不是弯弯的像个弓弦的什么奇怪东西。
它就是那种看起来圆圆的,其实两头被拉长了的形状。
想象一下,咱们常见的篮球,稍微压了一下两边,球的中间依然饱满,圆滚滚的。
但要是你把它再拉长一点,那个形状就变得有点像橄榄球,懂吗?这就是椭圆——拉长了的圆,简直就是“圆的亲戚”。
焦点嘛,你可以理解成椭圆“眼睛”的位置,站在那儿的点,看的都能不偏不倚地收获椭圆的全部信息。
搞清楚了椭圆是啥,接下来就是焦点三角形的事儿了。
这个三角形,不是你随便画个三条边就能搞定的那种;它是椭圆内部的一种特殊几何形状——三个点形成的三角形,这三个点分别就是椭圆的两个焦点,还有椭圆的一个点。
具体来讲呢,焦点分别在椭圆的左右两侧,而第三个点嘛,得是椭圆上任何一个点。
怎么样,这个三角形有点意思吧?好啦,咱们先来说说如何推导椭圆焦点三角形的面积。
这个面积公式怎么来呢?你可能会说,哎,这不就跟常见的三角形面积一样吗?其实不然。
你得知道,椭圆的焦点位置可不是随便找的,它们满足一个条件,就是椭圆上任意一点到两个焦点的距离之和是个常数。
这个常数,咱们叫它“椭圆的长轴”。
这就是椭圆的一个“宝贝”特性,简直是“心机”满满,搞得你总是捉摸不透。
好,既然大家都明白了椭圆的形状与焦点的关系,咱们来聊聊推导公式的步骤。
假设椭圆的长轴是2a,短轴是2b。
你可以把椭圆看作是圆的一个“伸长版”。
焦点之间的距离是2c,c就是个固定值,跟a、b都有关系。
更重要的是,这个c满足这样的关系:c² = a² b²。
也就是说,焦点的位置不是随便“摆”的,它和椭圆的长短轴息息相关。
然后,椭圆的焦点三角形面积公式是怎么来的呢?嘿,数学就是这么个“有趣”的东西,公式看上去简单,实际推导过程一波三折。
首先咱们通过坐标系来搞定它。
设定坐标,假设椭圆的中心在原点,焦点分别位于(c, 0)和(c, 0)这两个位置。
椭圆中焦点三角形面积公式

2023年高考数学椭圆焦点三角形的面积问题【考点梳理】焦点三角形:椭圆上的点P (x 0,y 0)与两焦点构成的△PF 1F 2叫做焦点三角形.r 1=|PF 1|,r 2=|PF 2|,∠F 1PF 2=θ,△PF 1F 2的面积为S ,则在椭圆x 2a 2+y 2b2=1(a >b >0)中:①焦点三角形的周长为2(a +c );②4c 2=r 21+r 22-2r 1r 2cos θ;③当r 1=r 2时,即点P 的位置为短轴端点时,θ最大;④S =12r 1r 2sin θ=b 2tan θ2=c |y 0|,当|y 0|=b 时,即点P 的位置为短轴端点时,S 取最大值,最大值为bc .【题型归纳】一、求椭圆焦点三角的面积1.已知点P 是椭圆22:1259x y C +=上一点,12,F F 是其左右焦点,且1260F PF ∠=,则三角形12F PF △的面积为_________2.已知点P 是椭圆221259x y +=上的点,点12,F F 是椭圆的两个焦点,若12F PF △中有一个角的大小为3π,则12F PF △的面积为______.3.设12,F F 是椭圆2241496x y +=的两个焦点,P 是椭圆上的点,且12||:||4:3PF PF =,则12PF F △的面积为()A .22B .42C .4D .64.设12,F F 是椭圆2211224x y +=的两个焦点,P 是椭圆上一点,且1213cos F PF ∠=.则12PF F △的面积为()A .6B .62C .8D .825.已知点F 1,F 2分别是椭圆22:14x C y +=的左右焦点,点M 在椭圆C 上,且满足1223MF MF += ,则12MF F △的面积为___________.6.已知椭圆()2222:10x y C a b a b+=>>的焦点为1F ,2F ,若椭圆C 上存在一点P ,使得120PF PF ⋅= ,且△12F PF 的面积等于4.则实数b 的值为___________.二、椭圆焦点三角形面积的最值问题7.已知1F 、2F 为椭圆22:14xy Γ+=的左、右焦点,M 为Γ上的点,则12MF F △面积的最大值为()A .3B .2C .23D .4三、已知椭圆焦点三角形面积求边8.设1F 、2F 是椭圆22:110x C y +=的两个焦点,O 为坐标原点,点P 在C 上,且12PF F △的面积为7,则OP =()A .3B .73C .83D .39.已知12,F F 分别是椭圆2222:1(0)x y C a b a b+=>>的左,右焦点,点M 是椭圆C 上的一点,且1212,2F MF F MF π∠= 的面积为1,则椭圆C 的短轴长为()A .1B .2C .22D .4四、与内切圆相结合10.已知椭圆2212516x y +=两焦点1F 、2F ,P 为椭圆上一点,若123F PF π∠=,则12F PF △的内切圆半径为______五、与平面向量相结合11.已知P 是椭圆221259x y +=上的点,1F 、2F 分别是椭圆的左、右焦点,若1212PF PF PF PF ⋅=⋅12,则12F PF △的面积为()A .33B .93C .3D .912.已知1F 、2F 是椭圆()2222:10x y C a b a b+=>>的两个焦点,P 为椭圆C 上一点,且12PF PF ⊥ .若12PF F △的面积为9,求实数b 的值.【巩固训练】一、单选题13.已知点P 在椭圆221164x y +=上,1F 与2F 分别为左、右焦点,若1223F PF π∠=,则12F PF △的面积为()A .43B .63C .83D .13314.已知椭圆C :221259x y +=,1F ,2F 分别为它的左右焦点,A ,B 分别为它的左右顶点,点P 是椭圆上的一个动点,下列结论中错误的是()A .离心率45e =B .12F PF △的周长为18C .直线PA 与直线PB 斜率乘积为定值925-D .若1290F PF ︒∠=,则12F PF △的面积为815.已知椭圆2221(10)y x b b +=>>的左、右焦点分别为1F ,2F ,点M 是椭圆上一点,点A 是线段12F F 上一点,且121223F MF F MA π∠=∠=,3||2MA =,则该椭圆的离心率为()A .32B .12C .223D .33二、多选题16.椭圆22:143x y C +=的左、右焦点分别为1F ,2F ,点P 在椭圆C 上,若方程340mx y m ++-=所表示的直线恒过定点M ,点Q 在以点M 为圆心,C 的长轴长为直径的圆上,则下列说法正确的是()A .椭圆C 的离心率为12B .12PF PF ⋅的最大值为4C .12PF F △的面积可能为2D .2PQ PF -的最小值为256-17.已知椭圆22:14x M y +=,若P 在椭圆M 上,1F 、2F 是椭圆M 的左、右焦点,则下列说法正确的有()A .若12PF PF =,则1230PF F ∠=B .12F PF △面积的最大值为3C .12PF PF -的最大值为23D .满足12F PF △是直角三角形的点P 有4个18.已知椭圆22:143x y C +=的左、右焦点分别是1F ,2F ,04,3M y ⎛⎫ ⎪⎝⎭为椭圆C 上一点,则下列结论正确的是()A .12MF F △的周长为6B .12MF F △的面积为153C .12MF F △的内切圆的半径为159D .12MF F △的外接圆的直径为321119.双曲线22:1124x y C -=的左,右焦点分别为1F ,2F ,点P 在C 上.若12PF F △是直角三角形,则12PF F △的面积为()A .833B .433C .4D .220.已知P 是椭圆C :2216x y +=上的动点,过11,4Q ⎛⎫ ⎪⎝⎭直线与椭圆交于,M N 两点,则()A .C 的焦距为5B .当Q 为MN 中点时,直线MN 的斜率为3-C .C 的离心率为306D .若1290F PF ︒∠=,则12F PF △的面积为121.设椭圆22:12x C y +=的左右焦点为1F ,2F ,P 是C 上的动点,则下列结论正确的是()A .离心率62e =B .12PF F △面积的最大值为2C .以线段12F F 为直径的圆与直线20x y +-=相切D .12PF PF ⋅的最小值为0三、填空题22.设12F F ,是椭圆22196x y +=的两个焦点,P 是椭圆上的点,且1221PF PF =::,则12F PF △的面积等于_______.23.已知F 1,F 2是椭圆2214x y +=的两个焦点,点P 在椭圆上,2PF ⊥x 轴,则12PF F 的面积为_________.四、解答题24.设椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F 、2F ,点P ,Q 为椭圆C 上任意两点,且()110PF QF λλ=< ,若2PQF 的周长为8,12PF F △面积的最大值为2.(1)求椭圆C 的方程;(2)设椭圆C 内切于矩形ABCD (椭圆与矩形四条边均相切),求矩形ABCD 面积的最大值.25.已知椭圆C 的两焦点分别为()11,0F -、()21,0F ,P 为椭圆上一点,且12122F F PF PF =+.(1)求椭圆C 的标准方程;(2)若点P 在第二象限,12120F PF ∠=︒,求△12PF F 的面积.26.已知圆22:(3)64M x y ++=圆心为M ,定点(3,0)N ,动点A 在圆M 上,线段AN 的垂直平分线交线段MA 于点P(1)求动点P 的轨迹C 的方程;(2)若点Q 是曲线C 上一点,且60QMN ∠=︒,求 QMN 的面积.参考答案1.33【分析】由椭圆方程可得,,a b c ,利用椭圆定义和余弦定理可构造方程求得12PF PF ⋅,由三角形面积公式可求得结果.【详解】由椭圆方程知:5a =,3b =,则22216c a b =-=;由椭圆定义知:12210PF PF a +==,由余弦定理得:222121212122cos F F PF PF PF PF F PF =+-⋅∠,()2212121243100364c PF PF PF PF PF PF ∴=+-⋅=-⋅=,解得:1212PF PF ⋅=,12121213sin 63322F PF S PF PF F PF ∴=⋅∠=⨯= .故答案为:33.2.33或63##63或33【分析】由椭圆方程可求得,,a b c ;当123F PF π∠=时,由焦点三角形面积公式可求得12F PF S ;当123PF F π∠=时,利用余弦定理可构造方程求得1PF ,由三角形面积公式可得结果.【详解】由椭圆方程知:5a =,3b =,则224c a b =-=;若123F PF π∠=,则12212tan9tan 3326F PF F PF S b π∠=== ;若123PF F π∠=,设1PF m =,则2210PF a m m =-=-,由余弦定理得:22222112112122cos 648PF PF F F PF F F PF F mm =+-⋅∠=+-=()210m -,解得:3m =,1211212113sin 3863222F PF S PF F F PF F ∴=⋅∠=⨯⨯⨯= ;同理可得:当21π3PF F Ð=时,1263F PF S = .综上所述:12F PF △的面积为33或63.故答案为:33或63.3.D【分析】根据椭圆的定义求出12||4,||3PF PF ==,从而判断出12PF F △为直角三角形,然后即可求出12PF F △的面积.【详解】易知2494a =,26b =,所以222254c a b =-=,72a =,即52c =,由椭圆的定义,知12||||27PF PF a +==,又因为12||:||4:3PF PF =,所以12||4,||3PF PF ==,又1225F F c ==,所以12PF F △为直角三角形,所以13462ABC S =⨯⨯=△.故选:D.4.B【分析】利用椭圆的几何性质,得到12246PF PF a +==,12243F F c ==,进而利用1213cos F PF ∠=得出1218PF PF ⋅=,进而可求出12S PF F 【详解】解:由椭圆2211224x y +=的方程可得2224,12a b ==,所以22212c a b =-=,得26,23a c ==且12246PF PF a +==,12243F F c ==,在12PF F △中,由余弦定理可得222221212121212121212||||||(||||)2||||||cos 2||||2||||PF PF F F PF PF PF PF F F F PF PF PF PF PF +-+--∠==22212121212442||||42||||2||||2||||a c PF PF b PF PF PF PF PF PF ---==12124122||||2||||PF PF PF PF ⨯-=,而121cos 3F PF ∠=,所以,1218PF PF ⋅=,又因为,121cos 3F PF ∠=,所以1222sin 3F PF ∠=,所以,1212121122sin 1862223S PF F PF PF F PF =⋅∠=⨯⨯= 故选:B 5.1【分析】设00(,)M x y ,则可得1200(2,2)MF MF x y +=-- ,再由1223MF MF += 可得22003x y +=,而点00(,)M x y 在椭圆上,则有220014x y +=,求出0y ,从而可求出12MF F △的面积【详解】由题意可得2,1,3a b c ===,则12(3,0),(3,0)F F -,设00(,)M x y ,则12000000(3,)(3,)(2,2)MF MF x y x y x y +=---+--=--,因为1223MF MF +=,所以22004412x y +=,所以22003x y +=,因为点00(,)M x y 在椭圆上,所以220014x y +=,解得033y =,所以12MF F △的面积为1323123⨯⨯=,故答案为:16.2【分析】由三角形面积公式、向量数量积的坐标表示及P 在椭圆上列方程可得||4P c y =、2||P b y c=,即可求参数b .【详解】由题设,12||||42P P c y c y ⨯⨯==,且(,)(,)0P P P P c x y c x y ---⋅--=,可得222P P x c y =-,又222222222:1P P P Px y c y y C a b a b-+=+=,则2||P b y c =,综上,24b =,又0b >,则2b =.故答案为:27.A【分析】由于12F F 为定值,所以当点M 到12F F 的距离最大时,12MF F △面积取得最大值,即当M 与短轴的一个端点重合时,12MF F △面积的最大【详解】由2214x y +=,得224,1a b ==,所以222,1,3a b c a b ===-=,由椭圆的性质可知当M 与短轴的一个端点重合时,12MF F △面积的最大,所以12MF F △面积的最大值为1211231322F F b =⨯⨯=,故选:A 8.A【分析】根据三角形12PF F △的面积可求得点P 的坐标,由此可求得OP 的值.【详解】在椭圆C 中,10a =,1b =,则223c a b =-=,所以,1226F F c ==,12121372PF F P P S F F y y =⋅==△,所以73P y =,所以253P x =,则223P P OP x y =+=,故选:A.9.B【分析】首先分别设1MF x =,2MF y =,再根据椭圆的定义和性质列出等式,即可求解椭圆的短轴长.【详解】设1MF x =,2MF y =,所以22221124x y a xy x y c+=⎧⎪⎪=⎨⎪+=⎪⎩,即()222222244x y x y xy x y a +=++=++=,即22444c a +=,得2221b a c =-=,短轴长为22b =.故选:B 10.233##233【分析】根据椭圆的方程求得c ,得12||F F ,设出11||PF t =,22||PF t =,利用余弦定理可求得12t t 的值,得到△12F PF 的面积,再由等面积法求出△12F PF 内切圆的半径.【详解】由题意方程可得,5a =,4b =,223c a b ∴=-=,即12||6F F =,设11||PF t =,22||PF t =,则根据椭圆的定义可得:1210t t +=,①在12F PF △中,123F PF π∠=,∴根据余弦定理可得:22212122cos 63t t t t π+-⋅=,②联立①②得12643t t ⋅=,∴121211643163sin 232323F PF S t t π=⋅=⨯⨯= ,设△12F PF 内切圆半径为r ,△12F PF 的周长为10616L =+=,面积为1633S =,则1112F PF S Lr =,2233S r L ∴==,故答案为:23311.A【分析】由已知可得12F PF ∠,然后利用余弦定理和椭圆定义列方程组可解.【详解】因为121212121212cos 1cos 2PF PF F PF PF PF F PF PF PF PF PF ⋅∠⋅==∠=⋅⋅,120F PF π∠≤≤所以123F PF π∠=,又224c a b =-=记12,PF m PF n ==,则222464210m n mn c m n a ⎧+-==⋅⋅⋅⎨+==⋅⋅⋅⎩①②,②2-①整理得:12mn =,所以12113sin 12332322F PF S mn π==⨯⨯= 故选:A12.3b =【分析】由题意以及椭圆的几何性质列方程即可求解.【详解】因为12PF PF ⊥,所以1290F PF ∠=︒,所以12F PF △为直角三角形,22212(2)PF PF c +=,122PF PF a +=,()2221212122PF PF PF PF PF PF +=+-⋅,即()()221212242c a PF PF =-⨯⋅,1212192F PF S PF PF =⋅=△,所以2244490c a =-⨯=,所以2449b =⨯.所以3b =;综上,b =3.13.A【分析】由椭圆的定义结合余弦定理解得1216PF PF =,通过三角形面积公式即可求得答案.【详解】由12222121212128cos 2PF PF PF PF F F F PF PF PF ⎧+=⎪+-⎨∠=⎪⎩,,又1243F F =,解得1216PF PF =,1212121sin 313422162F PF S PF P PF F F =⨯⨯==∠△.故选:A.14.D【分析】根据离心率的定义可判断A ;利用椭圆的定义可判断B ;求出PA PB k k ⋅可判断C ;利用勾股定理以及椭圆的定义求出12PF PF 可判断D.【详解】由221259x y +=,可得5a =,3b =,224c a b =-=,A ,离心率45c e a ==,故A 正确;B ,12F PF △的周长为12122218PF PF F F a c ++=+=,故B 正确.C ,设()00,P x y ,2020002200009125955252525PA PBx y y y k k x x x x ⎛⎫- ⎪⎝⎭⋅=⋅===-+---,故C 正确;D ,1290F PF ︒∠= ,222121264PF PF F F ∴+==,又因为12210PF PF a +==,所以()212100PF PF +=,即2212122100PF PF PF PF ∴++=,解得1218PF PF =,所以1212192F PF S PF PF ==△,故D 错误.故选:D 15.B【分析】由椭圆定义得12MF MF +,由余弦定理可得12MF MF ,再由三角形面积公式得12MF MF +和12MF MF 的关系,从而求得c ,然后可得离心率.【详解】解:设11||MF r =,22||MF r =,则1222r r a +==,由余弦定理得2221212122||||||2||||cos3F F MF MF MF MF π=+-,即222212*********()4c r r r r r r r r r r =++=+-=-,所以21244r r c =-,因为1212F MF F MA AMF S S S =+ ,所以12121211sin ||sin ||sin 232323r r r MA r MA πππ=⋅⋅+⋅⋅,整理得1212()||r r r r MA =+⋅,即234422c -=⨯,整理得214c =,所以12c =,1a =,12c e a ==,故选:B.16.ABD【分析】A :根据椭圆方程可直接求得2a =,3b =,1c =,和离心率ce a=;B :由椭圆的定义可得124PF PF +=,结合不等式22a b ab +⎛⎫≤ ⎪⎝⎭代入运算;C :点P 位于椭圆的上、下顶点时,12PF F △的面积取得最大,计算判断;D :利用椭圆定义和圆的性质转化处理.【详解】对于选项A ,由椭圆C 的方程知2a =,3b =,1c =,所以离心率12c e a ==,故选项A 正确;对于选项B ,由椭圆的定义可得124PF PF +=,所以2121242PF PF PF PF ⎛+⎫⋅≤= ⎪⎝⎭,即12PF PF ⋅的最大值为4,故选项B 正确;对于选项C ,当点P 位于椭圆的上、下顶点时,12PF F △的面积取得最大值123322⨯⨯=<,故选项C 错误;对于选项D ,易知()3,4M -,则圆()()22:344M x y ++-=,所以()21114424256PQ PF PQ PF QF MF -=--≥-≥--=-,故选项D 正确,故选:ABD .17.ABC【分析】利用余弦定理可判断A 选项;利用三角形的面积公式可判断B 选项;利用椭圆的定义可判断C 选项;利用平面向量的数量积可判断D 选项.【详解】在椭圆M 中,2a =,1b =,3c =,且1223F F =,对于A 选项,当12PF PF =时,则122PF PF a ===,由余弦定理可得2221122121123cos 22PF F F PF PF F PF F F +-∠==⋅,因为120180PF F <∠<,所以,1230PF F ∠= ,A 对;对于B 选项,当点P 为椭圆M 的短轴顶点时,点P 到x 轴的距离最大,所以,12F PF △面积的最大值为1232c b bc ⨯⨯==,B 对;对于C 选项,因为2a c PF a c -≤≤+,即22323PF -≤≤+,所以,()1222222223PF PF a PF a a c c -=-≤--==,C 对;对于D 选项,当112PF F F ⊥或212PF F F ⊥时,12PF F 为直角三角形,此时满足条件的点P 有4个,当P 为直角顶点时,设点()00,P x y ,则220044x y =-,()1003,F P x y =+ ,()2003,F P x y =- ,222120003130F P F P x y y ⋅=-+=-= ,所以,033y =±,0263x =±,此时,满足条件的点P 有4个,综上所述,满足12F PF △是直角三角形的点P 有8个,D 错.故选:ABC.18.ABC【分析】求得0y ,进而求得12,MF MF ,由此对选项进行分析,从而确定正确选项.【详解】椭圆22:143x y C +=的左、右焦点分别是()11,0F -,()21,0F ,04,3M y ⎛⎫ ⎪⎝⎭为椭圆C 上一点,220041531,433y y ⎛⎫ ⎪⎝⎭+==,所以2212715884,433333MF MF ⎛⎫⎛⎫=+==-= ⎪ ⎪ ⎪⎝⎭⎝⎭.所以12MF F △的周长为22426a c +=+=,A 正确.12MF F △的面积为001151521233c y c y ⨯⨯=⨯=⨯=,B 正确.设12MF F △的内切圆的半径为r ,则115156,239r r ⨯⨯==,C 选项正确.1212641641199cos 0,8416233F MF F MF +-∠==>∠⨯⨯为锐角,12121135315sin 12561616F MF ∠=-==,所以12MF F △的外接圆的直径为12122323215sin 4531531516F F F MF ===∠,D 选项错误.故选:ABC 19.AC【分析】根据双曲线方程求出c ,再根据对称性只需考虑112PF F F ⊥或12PF PF ⊥.当12PF PF ⊥时,将4x =-代入双曲线方程,求出y ,即可求出三角形面积,当12PF PF ⊥时,由双曲线的定义可知1243PF PF -=,再由勾股定理求出12PF PF ,即可得解;【详解】解:由双曲线22:1124x y C -=可得221244c a b =+=+=.根据双曲线的对称性只需考虑112PF F F ⊥或12PF PF ⊥.当12PF PF ⊥时,将4x =-代入221124x y -=可得233y =±,所以12PF F △的面积为12118323F F PF =.当12PF PF ⊥时,由双曲线的定义可知,12243PF PF a -==,由勾股定理可得()22221212264PF PF F F c +===.因为()222121212264PF PF PF PF PF PF +=-+⋅=,所以128PF PF =,此时12PF F △的面积为12142PF PF ⋅=综上所述,12PF F △的面积为4或833.故选:AC .20.CD【分析】由题知226,1a b ==,25c =,进而根据离心率公式和焦距可判断A ,C ;对于B ,利用中点弦的直线的斜率公式直接计算即可判断;对于D 选项,结合椭圆定义得122PF PF =,进而计算面积即可判断.【详解】解:由题知226,1a b ==,所以2615c =-=,故焦距为225c =,故A 选项错误;对于B 选项,当Q 为MN 中点时,由中点弦公式得2020121364MNb x k a y =-=-=-⨯,故B 选项错误;对于C 选项,椭圆的离心率为53066c e a ===,故C 选项正确;对于D 选项,1290F PF ︒∠=,则12222121226PF PF PF PF F F ⎧+=⎪⎨+=⎪⎩,即()1222121212262PF PF PF PF PF PF F F ⎧+=⎪⎨+-=⎪⎩,代入数据得122PF PF =,所以12F PF △的面积为12112S PF PF ==,故D 选项正确;故选:CD 21.CD【分析】求出离心率可判断A ;计算12PF F △面积的最大值1212F F b ⋅可判断B ;求出圆的方程,再判断圆心到直线的距离与半径的关系可判断C ;设(),P x y 进行数量积的坐标运算结合2212x y +=可判断D ,进而可得正确选项.【详解】对于A :由椭圆22:12x C y +=可知,2a =,1b =,1c =,所以左、右焦点分别为()11,0F -,()21,0F ,离心率22c e a ==,故选项A 错误;对于B :122F F =,当P 点与椭圆的上下顶点重合时,12PF F △面积的最大,所以12PF F △面积的最大值为11221122b ⨯⨯=⨯⨯=,故选项B 错误;对于C :以线段12F F 为直径的圆的圆心()0,0,半径为1,由圆心()0,0到直线20x y +-=的距离222111d c ===+,所以以线段12F F 为直径的圆与直线20x y +-=相切,故选项C 正确;对于D :设(),P x y ,()()121,,1,PF x y PF x y =---=--,2222212111022x x PF PF x y x ⋅=+-=+--=≥ ,则12PF PF ⋅ 的最小值为0,故选项D 正确;故选:CD .22.23【分析】先利用定义求出12F PF △的各边,再求出123sin 2F PF ∠=,即可求出12F PF △的面积.【详解】由126PF PF +=,且1221PF PF =::,12124229623PF PF F F ∴===-=,,又在12PF F △中,cos ∠2221242(23)12422F PF +-==⨯⨯,123sin 2F PF ∴∠=12121S sin 232PF PF F PF ∴=∠=.故答案为:2323.32##132【分析】2PF ⊥x 轴可得P 点横坐标,再根据点P 在椭圆上,求出P 的纵坐标,代入三角形面积公式即可求解.【详解】由题意不妨设1(F ﹣3,0),2(F 3,0),∵P 2F ⊥x 轴,∴P (3,±12),∵△P 12F F 的面积=12|P 2F ||12F F |=12⨯12⨯23=32,故答案为:32.24.(1)22142x y +=(2)12【分析】(1)根据椭圆的定义可知24PQF C a = ,即可求出a ,再根据()12max122PF F S c b =⨯⨯ 及a 、b 、c 的关系计算可得;(2)当矩形ABCD 中有一条边与坐标轴平行时,直接求出矩形的面积,当矩形ABCD 的边都不与坐标轴平行时,设出直线方程,联立直线与椭圆方程,消元、根据0∆=求出2242m k =+,同理得2242n k =+,再由平行线之间的距离公式求出AD ,AB ,即可求出ABCD S ,最后利用基本不等式计算可得;(1)解:由()110PF QF λλ=<得P 、1F 、Q 三点共线,因为三角形2PQF 的周长为8,即22211224PQF C PQ PF QF PF QF PF QF a =++=+++=,所以48a =,则2a =.当P 点为椭圆上或下顶点时12PF F △的面积最大,即121222=⨯⨯== PF F S c b bc ,由222244=-=-b ac b,解得22b =,所以椭圆C 的方程为22142x y +=.(2)解:当矩形ABCD 中有一条边与坐标轴平行时,则另外三条边也与坐标轴平行,矩形ABCD 的两条边长分别为24a =,222b =,此时42282ABCD S =⨯=.当矩形ABCD 的边都不与坐标轴平行时,由对称性,不妨设直线AB 的方程为:y kx m =+,则CD 的方程为:y kx m =-,AD 的方程为:1y x n k =-+,BC 的方程为:1y x n k =--.由22142y kx mx y =+⎧⎪⎨+=⎪⎩,得()()222124220k x kmx m +++-=,令0∆=得2242m k =+,同理得2242n k =+,矩形ABCD 的边长分别为221m AD k =+,2211n AB k =+,∴()22222222821122411111ABCD kk m n mnk k S k kk k⎛⎫++ ⎪⎝⎭=⨯==++++,2211828212142k k=+≤+=++,当且仅当1k =±时取等号,所以矩形ABCD 面积的最大值是12.综上所述,矩形ABCD 面积的最大值是12.25.(1)22143x y +=(2)33【分析】(1)根据椭圆的定义得1,2c a ==,进而得答案;(2)根据余弦定理,结合椭圆定义,解决焦点三角形的面积问题即可.(1)解:∵椭圆C 的两焦点分别为()11,0F -、()21,0F ,∴设椭圆C 的方程为()222210x y a b a b+=>>,1c =,12||||42PF PF a ∴+==,2a ∴=.222413b a c ∴=-=-=,∴椭圆的标准方程为22143x y +=.(2)解:在△12PF F 中,由余弦定理得222121212||||||2||||cos F F PF PF PF PF =+-120︒,即212124(||||)||||PF PF PF PF =+-,212124(2)||||16||||a PF PF PF PF ∴=-=-,12||||12PF PF ∴=,1212113||||sin1201233222PF F S PF PF ∴=︒=⨯⨯= .26.(1)221167x y +=;(2)213.5【分析】(1)根据题意中的几何关系,判断动点P 的轨迹为椭圆,写出其方程即可;(2)利用椭圆定义结合余弦定理,即可求得MQ ,再求三角形面积即可.(1)由已知PN PA =,故8PM PN PM PA AM MN +=+==>,所以P 点轨迹是以M 、N 为焦点的椭圆,设P 点轨迹方程为22221(0)x y a b a b+=>>,则228,3,7a c b ===,所以P 点轨迹方程为221167x y +=.(2)不妨设MQ m =,由椭圆定义可得28QN a m m =-=-,又26MN c ==,则在MNQ 中,由余弦定理可得:()222681cos 212m m QMN m+--∠==,解得145m =.故 QMN 的面积13314213sin 2322255S QMN m c c m =⨯∠⨯⨯=⨯=⨯⨯=.。
椭圆焦点三角形面积公式

求解运用公式设P为椭圆上的任意一点,角F1F2P=α ,F2F1P=β,F1PF2=θ,则有离心率e=sin(α+β) / (sinα+sinβ),焦点三角形面积S=b^2*tan(θ/2)。
证明方法一设F1P=m ,F2P=n ,2a=m+n,由射影定理得2c=mcosβ+ncosα,e=c/a=2c/2a=mcosβ+ncosα / (m+n),由正弦定理e=sinαcosβ+sinβcosα/ (sinβ+sinα)=sin(α+β)/ (sinα + sinβ)。
证明方法二对于焦点△F1PF2,设PF1=m,PF2=n则m+n=2a在△F1PF2中,由余弦定理:(F1F2)^2=m^2+n^2-2mncosθ即4c^2=(m+n)^2-2mn-2mncosθ=4a^2-2mn(1+cosθ)所以mn(1+cosθ)=2a^2-2c^2=2b^2所以mn=2b^2/(1+cosθ)例题F1,F2是椭圆x^2/a^2+y^2/b^2=1(a>b>0)的焦点,PQ是过F1的一条弦,求三角形PQF2面积的最大值【解】S△PQF2=S△QF1F2+S△QF1F2=1/2 * |y2-y1| * 2c=c*|y2-y1|△QF1F2与△QF1F2底边均为F1F2=2c,之后是联立直线方程与椭圆方程,利用韦达定理表示出|y2-y1|进行分析即可【|y1-y2| = √(1+1/k^2)[(y1+y2)^2 - 4y1y2] 】请你看下面的一个具体例题,会对你有所启发的。
设点F1是x^2/3+y^2/2=1的左焦点,弦AB过椭圆的右焦点,求三角形F1AB的面积的最大值。
【解】a^2=3,b^2=2,c^2=3-2=1→→c=1 ∴F1F2=2c=2假设A在x上方,B在下方直线过(1,0)设直线是x-1=m(y-0)x=my+1代入2x^2+3y^2=6(2m^2+3)y^2+4my-4=0→→y1+y2=-4m/(2m^2+3),y1y2=-4/(2m^2+3) △F1AB=△F1F2A+△F1F2B 他们底边都是F1F2=2 则面积和最小就是高的和最小(即|y1|+|y2|最小[1])∵AB在x轴两侧,∴一正一负→→|y1|+|y2|=|y1-y2|(y1-y2)^2=(y1+y2)^2-4y1y2=16m^2/(2m^2+3)2+16/(2m^2+3)→→|y1-y2|=4√[m2+(2m2+3)]/(2m2+3)=4√3*√(m2+1)]/(2m2+3)令√(m^2+1)=p^2m^2+3=2p^2+1且p>=1则p/(2p^2+1)=1/(2p+1/p) (分母是对勾函数) ∴p=√(1/2)=√2/2时最小这里p>=1→→p=1,2p+1/p最小=3此时p/(2p2+1)最大=1/3→→|y1-y2|最大=4√3*1/3∴最大值=2*4√3/3÷2=4√3/3在椭圆中,我们通常把焦点与过另一个焦点的弦所围成的三角形叫做焦点三角形,类似地,我们也把顶点与过另一个顶点所对应的焦点弦围成的三角形叫顶焦点三角形.在椭圆的顶焦点三角形中有许多与椭圆焦点三角形相类似的几何特征,蕴涵着椭圆很多几何性质,在全国各地的高考模拟试卷及高考试题中,都曾出现过以“顶焦点三角形”为载体的问题.本文对椭圆的顶焦点三角形的性质加以归纳与剖析.。
如何解答与椭圆有关的面积问题

与椭圆有关的面积问题,侧重于考查椭圆的方程、定义、几何性质,三角形的面积公式,弦长公式,以及直线与椭圆的位置关系.而求解与椭圆有关的面积问题主要用到两种三角形的面积公式:(1)S =12ab ⋅sin θ;(2)S =12×底×高.在解题时,需要根据图形的形状来选择合适的公式进行求解.一、焦点三角形的面积问题若P 为椭圆x 2a 2+y 2b2=1(a >b >0)上异于长轴端点的点,F 1F 2为两个焦点,则ΔF 1PF 2称作焦点三角形.(1)若∠F 1PF 2=θ,由椭圆的定义知||F 1F 2=2c ,||PF 1+||PF 2=2a ,可得||PF 12+2||PF 1||PF 2+||PF 22=4a 2①,由余弦定理可得||PF 12+||PF 22-2||PF 1||PF 2cos θ=4c 2②.由①②可得:||PF 1||PF 2=2b 21+cos θ,则S ΔPF F =12|PF 1||PF 2|sin θ=12×2b 21+cos θsin θ=b 2tan θ2.(2)若∠F 1PF 2=θ是未知或不可求的,则需先根据椭圆的定义求得||F 1F 2=2c ;然后将P 点的纵坐标的绝对值看作焦点三角形的高,根据公式S =12×底×高,求焦点三角形的面积.例1.已知P 为椭圆x 2a 2+y 264=1上的一点,F 1和F 2是椭圆的左右焦点.若∠F 1PF 2=60°,则△F 1PF 2的面积为______.解:因为∠F 1PF 2=60°,即α=60°,b 2=64,由S △F 1PF 2=b 2tan α2知,△F 1PF 2的面积为6433.对于本题,由于∠F 1PF 2=60°,且椭圆的方程已知,所以可以直接运用焦点三角形面积公式S △F 1PF 2=b 2tanα2进行求解.例2.已知F 1,F 2分别为椭圆x 29+y 2b2=1(0<b <3)的左右焦点,点P 在椭圆上,点I 为△PF 1F 2的内心,若PI =29PF 1+49 PF 2,则△PF 1F 2的面积为______.解:延长PI ,交x 轴于点Q ,设 PI =xPQ ,则 PI =x PQ =29 PF 1+49 PF 2,PQ =29x PF 1+49xPF 2,因此29x +49x =1,得x =23,因此 PI =23PQ .设P ()x 0,y 0,y 0≠0,则△PF 1F 2内切圆的半径r =13||y 0.又S △P F 1F 2=12||F 1F 2||y 0=12r ()||PF 1+||PF 2+||F 1F 2,所以c ||y 0=r (a +c )=13(a +c )||y 0,即a =2c .因为a =3,所以||PF 1+||PF 2=6,由 PQ =13 PF 1+23PF 2可得 PQ - PF 1=2() PF 2- PQ ,即 F 1Q =2 QF 2,所以||F 1Q =2||F 2Q ,由角平分线的性质可得||PF 1=2||PF 2,因此||PF 1=2||PF 2=4,||F 1F 2=3,由余弦定理得cos∠F 1PF 2=||PF 12+||PF 22-||F 1F 222||PF 1||PF 2=1116,因此sin∠F 1PF 2=1-cos 2∠F 1PF 2=31516,所以S △PF F =12||PF 1⋅||PF 2⋅sin∠F 1PF 2=3154,故△PF 1F 2的面积为3154.本题较为复杂,需先根据三角形内心的性质以及角平分线的性质得出a 、c 的值;然后利用椭圆的定义、余弦定理求得||PF 1⋅||PF 2以及sin∠F 1PF 2,即可根据三角形的面积公式S =12ab ⋅sin θ求得问题的答案.二、非焦点三角形的面积问题非焦点三角形的面积问题往往可以通过分割,将转化为三角形的面积问题.主要有两种情形:(1)若三角形的一个顶点在坐标轴上,则可用该坐标轴将三角形分为两部分,分别将该坐标轴上的线段看作两个三角形的底边,另外两个定点的横(纵)坐标的绝对值看作高线长,利用S =12×底×高求三角形的面积;(2)若三角形的三个顶点均不在坐标轴上,需先求出三角形一条边AB 所在直线的方程;然后根据点到直线的距离公式求得另一个顶点到AB 的距离d ,则三角形的面积为S =12×||AB×d .例3.如图1,已知椭圆x 2a 2+y2b2=1()a >b >0的离心率左右顶点分别为A ,B ,上顶点为D ,坐标原点O 到考点透视38直线AD 的距离为255.(1)求椭圆的方程;(2)过A 点作两条互相垂直的直线AP ,AQ ,分别与椭圆交于P ,Q 两点,求△BPQ 面积的最大值.解:(1)椭圆的方程为x 24+y 2=1.(过程略)(2)设PQ 的直线方程为x =ty +m ,P ()x 1,y 1,Q ()x 2,y 2,联立方程得ìíîx =ty +m ,x 2+4y 2-4=0,得()t 2+4y 2+2mty +m 2-4=0,所以y 1+y 2=-2mt t 2+4,y 1y 2=m 2-4t 2+4,因为AP ⊥AQ ,则A ()-2,0,所以()x 1+2()x 2+2+y 1y 2=0,得x 1x 2+2()x 1+x 2+4+y 1y 2=0,即()t 2+1y 1y 2+()mt +2t ()y 1+y 2+(m +2)2=0.所以()t 2+1⋅m 2-4t 2+4+()mt +2t ⋅-2mt t 2+4+(m +2)2=0.整理得5m 2+16m +12=0,解得m =-65或m =-2(舍去),故y 1+y 2=12t 5()t 2+4,y 1y 2=-6425()t 2+4,则S △BPQ =12⋅()2+65||y 1-y 253225令25t 2+64=u ()u ≥8,则S △BPQ =3225⋅u u 2-6425+4=32u +36u ≤328+368=6425,此时△BPQ 最大值为6425.我们需先将直线与椭圆的方程联立,构造一元二次方程,根据韦达定理求得y 1+y 2、y 1y 2的表达式;然后用x轴将△BPQ 拆分为两部分,以x 轴上的线段为底边,P 、Q的纵坐标的绝对值为高线长,利用S =12×底×高求三角形的面积.图1图2例4.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个顶点为A (0,1),(1)求椭圆C 的方程;(2)如图2,过点P (-2,1)的直线与椭圆C 交于不同的两点D ,E ,点D 在第二象限,直线AD ,AE 分别与x 轴交于M ,N ,求四边形DMEN 面积的最大值.解:(1)椭圆方程为x 24+y 2=1;(过程略)(2)由题意可知直线DE 的斜率存在,设直线DE 的方程为y -1=k (x +2),k <0,D ()x 1,y 1,x 1<0,y 1>0,则E ()x 2,y 2,y 2<y 1,y 1=kx 1+2k +1,y 2=kx 2+2k +1,联立方程得ìíîy =kx +2k +1,x 2+4y 2-4=0,可得()1+4k 2x 2+8k (2k +1)x +16k 2+16k =0,需满足Δ>0,可得x 1+x 2=-8k (2k +1)1+4k 2,x 1⋅x 2=16k (k +1)1+4k 2,又l AD :y =y 1-1x 1x +1,则x M =x 11-y 1,同理可得x N =x 21-y 2,故S DMEN =12||x N -x M ×()y 1-y 2=12||||||||x 21-y 2-x 11-y 1×()y1-y 2=16k 2(2k +1)2-16k (k +1)()4k 2+14k 2+1=-164k +1k=16-4k +()-1k≤1624=4,当且仅当-4k =()-1k ,即k =-12时等号成立,故四边形DMEN 面积的最大值为4.对于四边形面积问题,通常可将四边形合理拆分为两个易于求面积的三角形.对于本题,我们将四边形DMEN 拆分为三角形NMD 与三角形MNE ,并以MN 为底,D 、E 两点的纵坐标的绝对值为高线长,即可运用S =12×底×高求三角形的面积.由此可见,求解与椭圆有关的面积问题,关键是根据图形的形状,选择合适的三角形面积公式,并利用弦长公式、点到直线的距离公式、韦达定理、余弦定理求三角形的边长、底边长、高线长、夹角.(作者单位:贵州省遵义市绥阳中学)考点透视39。
椭圆中焦点三角形的面积问题

椭圆中焦点三角形的面积问题
椭圆中焦点三角形的面积问题可以通过以下步骤来解决:
步骤1:确定椭圆的焦点和顶点。
椭圆有两个焦点,分别记为F1和F2,以及两个顶点,分别记为A和B。
步骤2:连接焦点F1和F2与顶点A和B,得到两条线段AF1、AF2和BF1、BF2。
步骤3:计算三角形AF1F2的面积。
根据三角形面积公式,可以使用以下公式计算三角形面积:面积= 底边长度×高÷2。
在这种情况下,底边是线段F1F2的长度,高是从线段F1F2到顶点A的垂直距离。
步骤4:计算三角形BF1F2的面积。
同样地,使用相同的面积公式计算三角形BF1F2的面积,其中底边是线段F1F2的长度,高是从线段F1F2到顶点B的垂直距离。
步骤5:将步骤3和步骤4得到的两个三角形的面积相加,即可得到椭圆中焦点三角形的总面积。
请注意,以上步骤是基于椭圆的简化模型,假设椭圆的焦点和顶点已知,并且椭圆是对称的。
实际情况可能更为复杂,需要更多的几何计算和测量才能得到准确的结果。
高中数学椭圆焦点三角形面积公式的应用

椭圆焦点三角形面积公式的应用定理 在椭圆12222=+by a x (a >b >0)中,焦点分别为1F 、2F ,点P 是椭圆上任意一点,θ=∠21PF F ,则2tan 221θb S PF F =∆证明:记2211||,||r PF r PF ==.4)(,2222121a r r a r r =+∴=+在△21PF F 中,由余弦定理得:cos 2212221r r r r -+θ配方得:.4cos 22)(22121221c r r r r r r =--+θ 即.4)cos 1(242212c r r a =+-θ.cos 12cos 1)(222221θθ+=+-=∴b c a r r由任意三角形的面积公式得:2tan 2cos 22cos2sin2cos 1sin sin 2122222121θθθθθθθ⋅=⋅=+⋅==∆b b b r r S PF F ..2tan 221θb S PF F =∴∆同理可证,在椭圆12222=+bx a y (a >b >0)中,公式仍然成立.典题妙解例 1 若P 是椭圆16410022=+y x 上的一点,1F 、2F 是其焦点,且︒=∠6021PF F ,求△21PF F 的面积.解法一:在椭圆16410022=+y x 中,,6,8,10===c b a 而.60︒=θ记.||,||2211r PF r PF ==点P 在椭圆上,∴由椭圆的第一定义得:.20221==+a r r在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ 配方,得:.1443)(21221=-+r r r r.144340021=-∴r r 从而.325621=r r .336423325621sin 212121=⨯⨯==∆θr r S PF F 解法二:在椭圆16410022=+y x 中,642=b ,而.60︒=θ .336430tan 642tan221=︒==∴∆θb S PF F 解法一复杂繁冗,运算量大,解法二简捷明了,两个解法的优劣立现!例2 已知P 是椭圆192522=+y x 上的点,1F 、2F 分别是椭圆的左、右焦212121=,则△21PF F 的面积为( ) A. 33 B. 32 C. 3D.33 解:设θ=∠21PF F ,则21||||cos 2121=⋅=PF PF θ,.60︒=∴θ .3330tan 92tan221=︒==∴∆θb S PF F故选答案A.例3(04湖北)已知椭圆191622=+y x 的左、右焦点分别是1F 、2F ,点P在椭圆上. 若P 、1F 、2F 是一个直角三角形的三个顶点,则点P 到x 轴的距离为( )A. 59B. 779C. 49D.49或779解:若1F 或2F 是直角顶点,则点P 到x 轴的距离为半通径的长492=a b ;若P 是直角顶点,设点P 到x 轴的距离为h ,则945tan 92tan 221=︒==∆θb S PF F ,又,7)2(2121h h c S PF F =⋅⋅=∆97=∴h ,.779=h 故答案选D. 金指点睛1. 椭圆1244922=+x y 上一点P 与椭圆两个焦点1F 、2F 的连线互相垂直,则△21PF F 的面积为( )A. 20B. 22C. 28D. 242. 椭圆1422=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积为1时,21PF ⋅的值为( )A. 0B. 1C. 3D. 63. 椭圆1422=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积最大时,21PF ⋅的值为( )A. 0B. 2C. 4D. 2-4.已知椭圆1222=+y ax (a >1)的两个焦点为1F 、2F ,P 为椭圆上一点,且︒=∠6021PF F ,则||||21PF PF ⋅的值为( )A .1B .31C .34D .325. 已知椭圆的中心在原点,对称轴为坐标轴,1F 、2F 为焦点,点P 在椭圆上,直线1PF 与2PF 倾斜角的差为︒90,△21PF F 的面积是20,离心率为35,求椭圆的标准方程.6.已知椭圆的中心在原点,1F 、2F 为左右焦点,P 为椭圆上一点,且21||||2121-=⋅PF PF ,△21PF F 的面积是3,准线方程为334±=x ,求椭圆的标准方程.参考答案1. 解:24,90221=︒==∠b PF F θ,∴2445tan 242tan 221=︒==∆θb S PF F .故答案选D.2. 解:设θ=∠21PF F , 12tan 2tan 221===∆θθb S PF F ,∴︒=︒=90,452θθ,021=⋅PF PF .故答案选A.3. 解:3,1,2===c b a ,设θ=∠21PF F , 2tan 2tan 221θθ==∆b S PF F ,∴当△21PF F 的面积最大时,θ为最大,这时点P 为椭圆短轴的端点,︒=120θ,∴2120cos cos ||||22121-=︒=⋅=⋅a PF PF PF θ.故答案选D.4. 解:︒==∠6021θPF F ,1=b ,3330tan 2tan 221=︒==∆θb S PF F , 又 ||||43sin ||||21212121PF PF PF PF S PF F ⋅=⋅=∆θ, ∴33||||4321=⋅PF PF ,从而34||||21=⋅PF PF . 故答案选C.5. 解:设θ=∠21PF F ,则︒=90θ. 2045tan 2tan 22221==︒==∆b b b S PF F θ,又 3522=-==a b a ac e , ∴95122=-a b ,即952012=-a.解得:452=a .∴所求椭圆的标准方程为1204522=+y x 或1204522=+x y . 6.解:设θ=∠21PF F ,∴︒=-=⋅=120,21||||cos 2121θθPF PF . 3360tan 2tan22221==︒==∆b b b S PF F θ,∴1=b .又 3342=c a ,即33333411222+==+=+=+c c c c c b c . ∴3=c 或33=c . 当3=c 时,222=+=c b a ,这时椭圆的标准方程为1422=+y x ;当33=c 时,33222=+=c b a ,这时椭圆的标准方程为13422=+y x ;但是,此时点P 为椭圆短轴的端点时,θ为最大,︒=60θ,不合题意.故所求的椭圆的标准方程为1422=+y x .仰望天空时,什么都比你高,你会自卑; 俯视大地时,什么都比你低,你会自负; 只有放宽视野,把天空和大地尽收眼底, 才能在苍穹泛土之间找准你真正的位置。
椭圆的焦点三角形面积公式推导过程

椭圆的焦点三角形面积公式推导过程好嘞,今天咱们来聊聊椭圆的焦点三角形面积公式的推导过程。
说实话,听起来可能有点高深,但其实也没那么复杂,慢慢来就好了。
咱们先说说椭圆。
想象一下,一个完美的椭圆,就像一个被压扁的圆,边缘光滑,形状优雅。
椭圆有两个焦点,听起来是不是很神秘?其实这两个焦点就像是一对小伙伴,默默地在椭圆内部守护着,构成了椭圆的灵魂。
要想理解焦点三角形的面积,咱们得先搞清楚这个三角形是怎么来的。
椭圆的每一个点都和这两个焦点有关系,啥意思呢?举个例子,当你在椭圆上选一个点,连接这个点和两个焦点,形成的那个三角形就出现了。
想象一下,就像你在海滩上挖沙子,两个小伙伴在一边帮你拿水桶,而你在开心地挖沙。
这个三角形的面积可大可小,完全取决于你选择的那个点。
咱们得了解一下如何计算这个三角形的面积。
最常见的三角形面积公式是底乘高再除以二。
这里的底,就是两个焦点之间的距离,哎呀,距离可不小哦,咱们用个符号“2c”表示。
而高呢,咱们用“h”来代表,它就是从选择的那个点到这条底边的垂直距离。
想象一下,站在一个大树下,你伸直手臂,试图把手放到地上,这就是你和树之间的高度。
咱们得把这些元素结合起来。
把底和高代入面积公式,得出的结果就是:面积等于(2c乘以h)除以2,这简直就是数学界的“简化王”嘛!结果得出是:c乘以h,哇,这个公式看上去简单得多了,是不是有种“水到渠成”的感觉?但咱们还没完呢。
现在,咱们再深入一点,来看看这个高h是如何得到的。
想象一下,如果你在椭圆上找那个点的时候,你其实是在考量两个焦点到这个点的距离。
记得吗?椭圆的定义就是到两个焦点的距离之和是个定值。
这样一来,咱们可以通过几何关系,把h转化成其他的变量,这就是数学的美妙之处了。
经过一番推理,咱们会发现,h其实可以用椭圆的标准方程来表示。
椭圆的标准方程是这样的:(frac{x^2{a^2 + frac{y^2{b^2 = 1),其中a和b分别是椭圆的长短轴半径。
椭圆焦点三角形的面积

综上所述,点 P 到 x 轴的距离 9 或 9
45
课堂总结
椭圆
C:
x2 a2
y2 b2
1( a
b
0 )的焦点三角形的面积为:
S△PF1F2
1 2
PF1
PF2
sin
S△PF1F2
b2
tan
2
S△PF1F2 c y0 .( y0 为 P 点的纵坐标)
作业:
椭圆的焦点三角形练习(二)
谢 谢!
椭圆焦点三角形的面积:
在椭圆
C: x2
a2
y2 b2
1( a
b
0 )中,F1 和
F2 是椭圆的两个焦点,
P 是椭圆上任意一点, F1PF2 ,则焦点三角形的面积为
S△PF1F2
b2
tan
2
证明:
记 | PF1 | m, | PF2 | n
m
n
在 F1PF2 中,由余弦定理有:
m2 n2 2mn cos | F1F2 |2 4c2
|
1 2
,求
F1PF2 的面积。
PF1 . PF2 | PF1 | . | PF2
|
cos
1 2
60
,
tan
2
tan 30
3 3
SPF1F2
b2
tan
2
3
3
例 3:已知椭圆 x2 y2 1的左、右焦点分别是
25 9
F1, F2 ,点 P 在椭圆上,若 P、F1、F2 是一个直
角三角形的三个顶点,求点 P 到 x 轴的距离。
椭圆的焦点三角形
(第二课时)
关于椭圆焦点三角形的常见问题:
椭圆中三角形面积公式
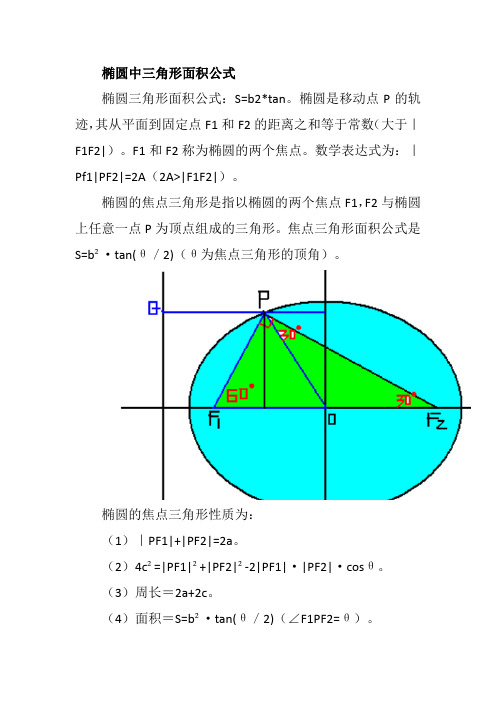
椭圆中三角形面积公式椭圆三角形面积公式:S=b2*tan。
椭圆是移动点P的轨迹,其从平面到固定点F1和F2的距离之和等于常数(大于|F1F2|)。
F1和F2称为椭圆的两个焦点。
数学表达式为:|Pf1|PF2|=2A(2A>|F1F2|)。
椭圆的焦点三角形是指以椭圆的两个焦点F1,F2与椭圆上任意一点P为顶点组成的三角形。
焦点三角形面积公式是S=b²·tan(θ/2)(θ为焦点三角形的顶角)。
椭圆的焦点三角形性质为:(1)|PF1|+|PF2|=2a。
(2)4c²=|PF1|²+|PF2|²-2|PF1|·|PF2|·cosθ。
(3)周长=2a+2c。
(4)面积=S=b²·tan(θ/2)(∠F1PF2=θ)。
椭圆三角形面积公式:S=b^2*tan(θ/2)。
1、离心率由正弦公式推导:F1P/sinα=F2P/sinβ=F1F2/sin θ,sinθ=sin(α+β),F1P+F2P=2a,F1F2=2c,e=c/a。
2、已知tan(θ/2)=sinα/(cosα+1)。
3、焦点三角形面积由余弦公式推导:∠F1PF2=θ,PF1=m,PF2=n。
4、则m+n=2a,在△F1PF2中,由余弦定理:(F1F2)^2=m^2+n^2-2mncosθ。
5、即4c^2=(m+n)^2-2mn-2mncosθ=4a^2-2mn(1+cosθ)。
6、所以mn=2b^2/(1+cosθ)。
7、S=(mnsinθ)/2=b^2*sinθ/(1+cosθ)=b^2*tan(θ/2)。
椭圆三角形表达椭圆是移动点P的轨迹,其从平面到固定点F1和F2的距离之和等于常数(大于|F1F2|)。
F1和F2称为椭圆的两个焦点。
数学表达式为:Pf1|PF2|=2A(2A>|F1F2|)。
焦点三角形面积公式是S=b²·tan(θ/2)(θ为焦点三角形的顶角)。
椭圆焦点三角形的面积

椭圆焦点三角形的面积椭圆焦点三角形是椭圆中的一个重要几何图形,它由椭圆上的一点与椭圆的两个焦点所构成。
而椭圆焦点三角形的面积是一个具有特定计算公式和重要性质的量,理解和掌握它对于解决与椭圆相关的问题具有重要意义。
我们先来明确一下椭圆焦点三角形的定义。
椭圆焦点三角形是指以椭圆的两个焦点以及椭圆上的任意一点为顶点所构成的三角形。
要探讨椭圆焦点三角形的面积,就不得不提到椭圆的基本性质。
对于椭圆标准方程:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\)(\(a > b > 0\)),其中\(a\)为椭圆的长半轴,\(b\)为椭圆的短半轴,两个焦点之间的距离\(2c\)(\(c\)为椭圆的半焦距)满足\(c^2 = a^2 b^2\)。
接下来,我们推导椭圆焦点三角形的面积公式。
假设椭圆上一点\(P\)的坐标为\((x_0, y_0)\),两个焦点分别为\(F_1\)、\(F_2\),且\(\angle F_1PF_2 =\theta\)。
根据余弦定理,在\(\triangle F_1PF_2\)中,\(|F_1F_2|^2 =|PF_1|^2 +|PF_2|^2 2|PF_1|\cdot|PF_2|\cos\theta\)又因为\(|PF_1| +|PF_2| = 2a\)(椭圆的定义),将其平方可得:\\begin{align}|PF_1|^2 +|PF_2|^2 + 2|PF_1|\cdot|PF_2|&=4a^2\\|PF_1|^2 +|PF_2|^2&=4a^2 2|PF_1|\cdot|PF_2|\end{align}\将其代入余弦定理的式子中可得:\\begin{align}4c^2&=4a^2 2|PF_1|\cdot|PF_2| 2|PF_1|\cdot|PF_2|\cos\theta\\2|PF_1|\cdot|PF_2|(1 +\cos\theta)&=4(a^2 c^2)\\2|PF_1|\cdot|PF_2|(1 +\cos\theta)&=4b^2\\|PF_1|\cdot|PF_2|&=\frac{2b^2}{1 +\cos\theta}\end{align}\那么椭圆焦点三角形的面积\(S =\frac{1}{2}|PF_1|\cdot|PF_2|\sin\theta\)\\begin{align}S&=\frac{1}{2}\cdot\frac{2b^2}{1 +\cos\theta}\cdot\sin\theta\\&=b^2\cdot\frac{\sin\theta}{1 +\cos\theta}\\&=b^2\cdot\tan\frac{\theta}{2}\end{align}\这就是椭圆焦点三角形面积的重要公式。
椭圆焦点三角形面积公式的推导过程

椭圆焦点三角形面积公式的推导过程嘿,大家好!今天咱们聊聊一个挺有意思的数学话题,那就是椭圆的焦点三角形面积公式。
听起来可能有点晦涩,其实一点也不难,咱们用轻松的方式来捋一捋这个内容,让你也能轻松掌握哦。
咱们得搞清楚椭圆是什么。
想象一下,像个被压扁的圆,长长的,宽宽的。
这个椭圆有两个特别的点,叫做焦点,分别用 F1 和 F2 表示。
就像爱情中的两个焦点,彼此牵挂,永不分离。
这两个焦点在椭圆的中轴线上,离中心有一定的距离,具体的距离跟椭圆的形状有关。
说到这里,你可能会问,这个椭圆跟三角形有什么关系呢?咱们可以在椭圆的焦点之间画一个三角形,想象一下 F1、F2 和椭圆上一个任意点 P 组成的三角形。
嘿,光听名字就有点意思,是吧?这个三角形的面积就成了咱们要探讨的重点了。
在数学上,咱们知道焦点到椭圆上任何一点的距离是有关系的。
这种关系可以用一个公式来表达,虽然听起来有点复杂,但放轻松,其实就像做一道菜,按步骤来就行。
椭圆的方程一般是这样的:( frac{x^2{a^2 + frac{y^2{b^2 = 1 ),其中 a 和 b 分别是椭圆的半长轴和半短轴。
焦点的距离就可以用公式 ( c = sqrt{a^2 b^2 ) 来计算,F1 和 F2 的位置就是 (c, 0) 和 (c, 0)。
好啦,咱们把这些信息整理整理,接下来就是要找这个三角形的面积啦。
三角形的面积公式大家应该都知道,底乘高再除以二,没错吧?这时候,F1 和 F2 之间的距离就是三角形的底,而从点 P 到这条底边的垂直距离就是高。
听起来是不是有点学术?别担心,接下来我们让这个过程变得简单点。
假设咱们在椭圆上选了一个点 P,那么用直线连接 F1 和 F2 的距离就是 ( 2c ),也就是 ( 2sqrt{a^2 b^2 )。
咱们需要计算点 P 到这条底边的距离。
通过一些几何的推导,可以得出这个距离与椭圆的参数有关系,虽然这里的公式不说也罢,但大体上就是根据位置来定的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题型七:焦点三角形的面积有关问题
定理在椭圆(>>0)中,焦点分别为、,点P是椭圆上任意一点,,则.
y
F1 O F2 x
P
P
例1 若P是椭圆上的一点,、是其焦点,且,求△的面积.
例2 已知P是椭圆上的点,、分别是椭圆的左、右焦点,
若,则△的面积为()A. B. C. D.
例3已知椭圆的左、右焦点分别是、,点P在椭圆上. 若P、、是一个直角三角形的三个顶点,则点P到轴的距离为()A. B. C. D. 或
例4:已知椭圆:的右顶点为,过的焦点且垂直长轴的弦长为.求椭圆的方程;点评:过椭圆焦点的所有弦中通径最短,通径为。
练习:1、椭圆上一点P与椭圆个焦点、的连线互相垂直,则△的面积为()A. 20 B. 22 C. 28 D. 24
. 椭圆的左右焦点为、,P是椭圆上一点,当△的面积最大时,的值为() A. 0 B. 2 C. 4 D.
3.已知
是椭圆
的两个焦点,
为椭圆
上的一点,且。
若
的面积为9,则
.
4.已知椭圆的两个焦点分别为,,为椭圆上一点,且,则的值等于 .。
