第六章 函数逼近
《数学函数逼近》PPT课件

---------(2)
a0 * 0(x) a1 * 1(x) an * n(x)
使得 * 2 2
m
(S * ( xi ) yi )2
i0
m
min S ( x)
2 2
min
S ( x)
i0
( S ( xi
)
yi
)2
n
其中S(x) a j j (x)为中的任意函数。
j0
---------(3)
EAST CHINA INSTITUTE OF TECHNOLOGY
理学院
n
称满足条件(3)的求函数S *(x) a*j j (x)的方法为 j0
数据拟合的最小二乘法.
n
S *(x) a*j j (x)为最小二乘解. j0 n
S(x) a j j (x)为拟合函数, a j ( j 0,1, , n)为拟合系数. j0 * 2 称为最小二乘解的平方误差. 2
解: 从数据的散点图可以看出
y与x之间具有三角函数关系 cos x y与x之间还具有指数函数关 系ex
y与x之间还具有对数函数关 系ln x 因此假设拟合函数与基函数分别为
设x, y的关系为
y S(x)
其中S(x)来自函数类 如(1)中y(x)来自线性函数类
设函数类 的基函数为 i(x)(i 0,1,,n) 一般要求n m
也称是由i(x)(i 0,1,, n)生成的函数集 ,即
span{0(x),1(x),,n(x)}
n
i0
k 0,1,,n 即
m
m
m
a0 0(xi )k (xi ) a1 1(xi )k (xi ) an n(xi )k (xi )
函数逼近基本概念

如 果 存 在 不 全 为 零 的 数 1,2,L,nP,使 得
1x12x2Lnxn0,
( 1.1)
则 称 x1,x2,L,xn线 性 相 关 . 否 则 ,称 x1,x2,L,xn线 性 无 关 .
若 x1,x2,L,xn线 性 无 关 , 且 对 任 意 xS,都 有
x1x12x2Lnxn
则 记 Sspan{x1,x2, L,xn}
(2)(u,v)(u,v), R;
(3) (uv,w)(u,w)(v,w), u,v,wX; (4) (u,u)0,当且仅u当 0时(, u,u)0. 则称 (u,v)为X上的 u与v的内积 . 定义了内积的 称线 为内积空 . (v,间 u )为 (u)的 ,v 共 K 轭 R 时 (v,, u ) (u当 ),.v
并x称 1,x2,,xn为空 S的 间 一组基 S为 , n维 称 空 空 间
有 序 1,数 2,,组 n称 为 x在 元 x1,x2,素 ,xn这 个 基,下 的 并 记 1,作 2,,( n)
如S 果 中有无限个素 线, 性S 则 无 为称 关 无元 限维线性空
例 p ( x ) : H n { a n x n 设 a 1 x a 0 |a n R } 则p(x)anxna1xa0 又1,x, ,xn线性无关
故 H n sp, ax , n, { x n } 1H ,n 维n 数 1 . 为
对连续函数f(x)∈C[a, b],它不能用有限个线性无关的 函 数 表 示 , 故 C[a, b] 是 无 限 维 的 , 但 它 的 任 一 元 素
f(x)∈C[a, b]均可用有限维的p(x)∈ H n 逼近,使误差
函数类 B 通常是 n 次多项式,有理函数或分段低次多项式。
数值分析06函数逼近

函数逼近的历史与发展
早期发展
早在古希腊时期,数学家就开始研究用简单的几何图形来近 似表示复杂的曲线。随着数学的发展,函数逼近的理论和方 法不断完善和丰富。
现代进展
随着计算机科学和数值分析的兴起,函数逼近在数值计算、 信号处理、图像处理等领域的应用越来越广泛。现代的逼近 方法不仅追求形式简单,还注重逼近的精度和计算效率。
数据拟合
在数据分析和机器学习中,利用数值逼近方法对数据进行拟合, 以提高预测精度。
图像处理
在图像处理中,利用数值逼近方法对图像进行平滑、去噪等处理, 以提高图像质量。
工程计算
在工程计算中,利用数值逼近方法对复杂函数进行近似计算,以简 化计算过程和提高计算效率。
05
结论与展望
总结与评价
总结
数值分析06函数逼近课程是一门重要的数学课程,它涉及到许多实际问题的求解,如插值、拟合、最小二乘法等。 通过学习这门课程,学生可以掌握如何使用数学工具来近似描述和分析函数,从而更好地理解和解决实际问题。
数。
稳定性分析
稳定性定义
稳定性是指在逼近过程中,对于小的扰动或误差,逼近结果的变 化程度。
不稳定性影响
不稳定的逼近可能导致结果出现较大的偏差,影响数值计算的精 度和可靠性。
稳定性判据
根据稳定性判据,判断逼近函数的稳定性以及如何提高稳定性。
04
数值实例与应用
一元函数逼近实例
01
线性逼近
通过多项式逼近方法,将一元函 数在某点附近展开成线性形式, 如泰勒级数展开。
评价
这门课程的内容非常实用,对于数学专业的学生来说是一门必修课程。它不仅有助于提高学生的数学素养,还可 以为学生提供解决实际问题的能力。然而,该课程难度较大,需要学生具备较高的数学基础和思维能力。
第6章 函数逼近与函数插值

第六章 函数逼近与函数插值本章介绍函数逼近与插值的有关理论和算法. 函数逼近问题与插值问题两者既有联系又有区别,它们都是用较简单的函数来近似未知的、或表达式较复杂的函数. 一般来说,函数逼近是要在整个区间、或一系列离散点上整体逼近被近似函数,而在进行插值时,则须保证在若干自变量点上的函数值与被近似函数相等.6.1 函数逼近的基本概念进行函数逼近一般是在较简单的函数类Φ中找一个函数p(x)来近似给定的函数f(x),以使得在某种度量意义下误差函数p (x )−f(x)最小. 被逼近函数f(x)可能是较复杂的连续函数,也可能是只在一些离散点上定义的表格函数,而函数类Φ可以是多项式、分段多项式、三角函数、有理函数,等等. 函数逼近问题中度量误差的手段主要是函数空间的范数,下面先介绍函数空间的范数、内积等有关概念,然后讨论函数逼近问题的不同类型.6.1.1 函数空间线性空间的概念大家都很熟悉,其定义中包括一个元素集合和一个数域,以及满足一定运算规则的“加法”和“数乘”运算. 简单说,若这个元素集合对于“加法”和“数乘”运算封闭,则为一线性空间. 线性空间的元素之间存在线性相关和线性无关两种关系,进而又有空间的基和维数的概念.在这里我们先考虑连续函数形成的线性空间. 例如C [a,b ]按函数加法、以及函数与实数乘法,构成一个线性空间. 对于[a,b]区间上所有k 阶导数连续的函数全体C k [a,b ],也类似地构成一个线性空间. 我们一般讨论实数函数,因此对应的是实数域ℝ,若讨论复数函数,则相应的是复数域ℂ. 另外,与线性代数中讨论的向量空间ℝn 不同,连续函数空间是无限维的.对线性空间可以定义范数的概念(见3.1.2节). 针对实连续函数空间C [a,b ],与向量空间类似,可定义如下三种函数的范数(function norm):1) ∞-范数 设f (x )∈C [a,b ],则‖f (x )‖∞=max x∈[a,b ]|f (x )| .其几何意义如图6-1所示,即函数值绝对值的最大值.2) 1-范数‖f (x )‖1=∫|f (x )|dx b a .其几何意义如图6-2所示,即函数曲线与横轴之间的面积总和.3) 2-范数‖f (x )‖2=[∫f 2(x )dx b a ]1/2. 2-范数也常称为平方范数,其几何意义与1-范数类似. 线性空间还有一个重要概念是内积,它定义了空间中两个元素的一种运算. 下面给出一般的复数域上线性空间内积的定义.定义6.1:设S为实数域ℝ上的线性空间,∀u,v∈S,定义值域为ℝ的二元运算〈u,v〉,若满足1)〈u,v〉=〈v,u〉, (可交换性)2)〈αu,v〉=α〈u,v〉, ∀α∈ℂ(线性性1)3)〈u+v,w〉=〈u,w〉+〈v,w〉, ∀w∈S(线性性2)4)〈u,u〉≥0,当且仅当u=O时①,〈u,u〉=0, (非负性)则称〈u,v〉为一种实内积运算(inner product). 定义了内积的线性空间称为实内积空间.应说明的是,将定义6.1加以扩展可在更一般的实数域ℂ上定义内积,区别只是将第1条性质改为共轭可交换性:〈u,v〉=〈v,u〉 .例如复向量的内积为: 〈u,v〉=u T v̅,可以验证它满足上述共轭可交换性. 下面只考虑实内积,但得到的结果都可以类似地推广到复内积空间. 另外,定义6.1的条件2还说明零元素与任意元素的内积均等于0.根据内积的线性性可推出:〈α1u1+α2u2,v〉=α1〈u1,v〉+α2〈u2,v〉,∀α1,α2∈ℂ,(6.1) 更一般地有:〈∑αj u j nj=1,v〉=∑αj〈u j,v〉nj=1,∀α1,⋯,αn∈ℂ.(6.2)这里主要考虑函数空间,则(6.2)式表明,线性组合函数(与另一函数作)内积等于(相应各个函数)内积的线性组合.可以规定一种依赖于内积运算的范数:‖u‖≡√〈u,u〉 .易知这种内积导出的范数满足范数定义的三个条件(见3.1.2节),详细证明过程留给读者思考. 应注意,在向量空间中,由内积导出的范数等同于向量的2-范数. 在实函数空间C[a,b]中,一般定义内积为〈u(x),v(x)〉=∫u(x)v(x)dxba,(6.3) 因此,由它导出的范数也等同于函数空间的2-范数.下面介绍与内积有关的两个重要定理.定理6.1:设S为实内积空间,∀u,v∈S,有:|〈u,v〉|2≤〈u,u〉∙〈v,v〉 .(6.4) 这是著名的柯西-施瓦茨不等式(Cauchy-Schwarz inequality).定理6.1的证明留给读者思考,若u,v为三维向量,也请思考该定理有什么几何含义?定理6.2:设S为实内积空间,u1,…,u n∈S,则格莱姆矩阵(Gram matrix)G=[〈u1,u1〉〈u2,u1〉⋯〈u n,u1〉〈u1,u2〉〈u2,u2〉⋯〈u n,u2〉⋮⋮⋱⋮〈u1,u n〉〈u2,u n〉⋯〈u n,u n〉](6.5)非奇异的充要条件是u1,…,u n线性无关.[证明] 首先要用到线性代数中的一个基本结论:矩阵G非奇异⟺det(G)≠0⟺齐次线性方程组Ga=0只有全零解.设向量a=[a1,…,a n]T,则方程Ga=0可写成:①这里用正体的字母O表示线性空间的零元素.∑a j 〈u j ,u k 〉nj=1=0,k =1,2,⋯,n (6.6)下面证明方程组(6.6)只有恒零解的充分必要条件是u 1,…,u n 线性无关. 先证必要性,即已知方程组(6.6)只有恒零解,要证u 1,…,u n 线性无关. 采用反证法,若u 1,…,u n 线性相关,即存在不全为0的一组系数{αj ,j =1,⋯,n}使∑αj u j n j=1=O ,则∑αj 〈u j ,u k 〉n j=1=〈∑αj u j nj=1,u k 〉=〈O,u k 〉=0,(k =1,…,n ),即这组{αj }是方程组(6.6)的解,与已知条件矛盾!再证明充分性,即已知u 1,…,u n 线性无关,要证方程组(6.6)只有全零解. 仍采用反证法,若方程组(6.6)存在不全为零的一组解{αj },则∑αj 〈u j ,u k 〉n j=1=〈∑αj u j nj=1,u k 〉=0,k =1,…,n将上述方程中第k 个方程乘以αk ,累加所有方程得到,〈∑αj u j n j=1,∑αj u j nj=1〉=0 ,根据内积的定义,必有∑αj u j n j=1=O , 也就是说存在不全为0的一组{αj }j=1n 使∑αj u j n j=1=O ,这与u 1,…,u n 线性无关的已知条件矛盾!综上所述,完成了定理的证明.应注意,格莱姆矩阵是实对称矩阵,并且当u 1,…,u n 线性无关时,它是对称正定矩阵. 针对实函数空间C[a, b],常常有权函数、加权内积的概念.定义6.2:若函数ρ(x )≥0,∀x ∈[a,b],且满足1) ∫x k ρ(x )dx ba 存在,(k =0,1,…),2) 对非负连续函数g (x ),若∫g (x )ρ(x )dx =0b a 可推出g (x )≡0,则称ρ(x)为区间[a,b]上的权函数(weight function).关于权函数的定义,说明几点:● 定义中对连续性没有要求,即ρ(x )可能不是连续函数;第1个条件要求的是ρ(x )与多项式乘积为可积函数.● 定义中第2条件的意义不是很直观,较直观的一种等价形式为:不存在子区间(c,d )⊆[a,b],使ρ(x )=0,∀x ∈(c,d ),即“权函数在[a,b]中任一子区间不恒为零”. ● 一般遇到的C [a,b ]中非负函数(一定有界、可积),若不在某一子区间恒为零,则都可作权函数.定义6.3:若ρ(x )为区间[a,b]上的权函数,则可定义C [a,b ]上的内积为:〈u (x ),v (x )〉=∫ρ(x )u (x )v (x )dx b a ,(6.7)并称其为加权内积(weighted inner product).容易验证加权内积满足一般内积的定义,并且常用的函数内积(6.3)式是加权内积的特例,其对应于权函数ρ(x )≡1的情况. 根据加权内积,也可以导出范数,这种范数可看成是广义的2-范数,其公式为:‖f(x)‖=[∫ρ(x )f 2(x )dx b a ]12⁄ .6.1.2 函数逼近的不同类型在函数逼近问题中,用简单函数p(x)来近似f(x),并要求误差最小. 这里度量误差大小的标准是范数,采用不同范数时其问题的性质是不同的. 下面分两种情况作些讨论.1) ∞-范数考虑误差函数p (x )−f (x )的∞-范数,假设函数的定义域为[a, b],则可设ε=‖p (x )−f (x )‖∞=max x∈[a,b ]|p (x )−f (x )| , 因此有−ε≤p (x )−f (x )≤ε,∀x ∈[a,b ],即p (x )−ε≤f (x )≤p (x )+ε, ∀x ∈[a,b ]图6-3显示了函数p (x ),f (x ), 以及‖p (x )−f (x )‖∞之间的关系,从中可以看出,在∞-范数意义下的逼近要求使ε尽量小,也就是要p (x )在整个区间上“一致地”接近f (x ). 因此,采用∞-范数的函数逼近问题常称为最佳一致逼近.2) 1-范数和2-范数先看看误差函数p (x )−f (x )的1-范数,‖p (x )−f (x )‖1=∫|p (x )−f (x )|dx ba令A =‖p (x )−f (x )‖1,则它表示p (x )和f (x )两个函数曲线之间的面积(如图6-4所示). 在1-范数意义下的逼近,要求使A 尽量小,也就是要p (x )与f (x )曲线之间的总面积尽量小,反映出这种逼近有整个区间上“平均”误差尽量小的含义(在某个子区间上误差可能很大).2-范数的意义与1-范数大体上类似,由于它更容易处理,在实际的逼近问题中一般采用图6-3 函数p (x ),f (x ), 以及‖p (x )−f (x )‖∞之间的关系.图6-4 函数p (x ),f (x ), 以及‖p (x )−f (x )‖1之间的关系.2-范数. 这种逼近称为最佳平方逼近或最小二乘逼近(least squares fitting).从直观上看,采用∞-范数的最佳一致逼近效果更好一些,而最佳平方逼近具有平均误差最小的含义.除了度量误差函数可采用不同的范数,被逼近函数也可分为连续函数和表格函数两种情况. 表格函数就是仅在一系列离散自变量点上已知函数值的函数,可通过函数值组成的向量来刻画,有关逼近问题的求解有特殊的处理方法. 而在逼近函数类方面,多项式函数是最常用的一种. 下面给出魏尔斯特拉斯定理(Weierstrass Theorem ),它是用多项式函数进行逼近的一个重要依据.定理6.3:设f (x )∈C[a,b],则对任何ϵ>0,总存在一个多项式P (x ),使‖P (x )−f (x )‖∞<ϵ在[a, b]上一致成立.该定理的证明已超出了本书的要求,因此不做讨论. 值得一提的是,若f (x )∈C[0,1],伯恩斯坦多项式(Bernstein polynomial)②B n (f,x )=∑f (k )Q k (x )nk=0 , 其中Q k (x )=(n k)x k (1−x )n−k , 就是满足定理要求的多项式P (x ). 注意B n (f,x )为n 次多项式,并且可以证明,lim n→∞B n (f,x )=f(x)在[0, 1]上一致成立. 因此,C[0,1]中的任意函数都可以用伯恩斯坦多项式(一致)逼近到任意好的程度. 应注意,它一般不是多项式函数类ℙn 中的最佳一致逼近.最后说明一点,求最佳一致逼近多项式的方法比较复杂,感兴趣的读者请参考[4, 9]. 本章后面主要介绍求最佳平方逼近的方法,它有很广泛的应用.6.2 连续函数的最佳平方逼近为了记号的方便,在6.2节和6.3节的介绍中记函数的自变量为t.6.2.1 一般的法方程方法一. 问题描述假设对f (t )∈C [a,b ]进行函数逼近,逼近函数类Φ应是形式简单的函数类,比如多项式函数、三角函数、有理函数,等等,并且它是有限维的线性子空间. 设Φ=span {φ1(t ),…,φn (t )},则Φ的任一元素可表示为:S (t )=Σj=1n x j φj (t ), (6.8)其中x 1,…,x n ∈ℝ.连续函数的最佳平方逼近问题就是求S (t )∈Φ,使 ‖S (t )−f (t )‖2达到最小值. 利用公式(6.8)以及2-范数的定义,上述问题等价于最小化F =‖S (t )−f (t )‖22=∫[Σj=1n x j φj (t )−f (t )]2dt b a .(6.9)F 是关于实系数x 1,x 2,…,x n 的多元函数,需求出F 的最小值对应的那组系数x 1,x 2,…,x n .二. 法方程方法下面推导如何求(6.9)式的最小值点. 为了记号简便,省略函数记号中的“(t )”,即直接② 由原苏联数学家伯恩斯坦(1880—1968)于1912年提出.f ̃=f (3)=f (2)−2v 2T f (2)v 2T v 2v 2=[ −4.2061330.399807−0.004750130.0009512830.00195269], 此时矩阵A 经变换为: R =A (3)=[ −2.236068−3.35410200.790569000000] . 根据算法6.3,需求解方程R 1x =b ,其中R 1=[−2.236068−3.35410200.790569],b =[−4.2061330.399807]. 解得:x =[1.12250.5057]T ,即拟合公式为y ̃=1.1225+0.5057t ,它与例6.6, 6.7得到的结果是一样的.根据表格函数与其函数值向量的对应关系可证明,算法6.3与通过Gram-Schmidt 正交化过程求最佳逼近函数的方法在数学上是等价的. 不同之处在于:前者不涉及正交函数族,直接得到原基函数对应的拟合系数;前者的主要计算是矩阵的QR 分解,它可通过Householder 变换或Givens 旋转变换等不同方法实现. 由于算法6.3直接利用矩阵的QR 分解的特点,它更易于实现和应用,而且稳定性比算法6.2好. 最后说明一点,若初始的表格函数φ1(t ),…,φn (t )线性相关,矩阵A 不是列满秩的,QR 分解也能进行,但得到的上三角阵R 1奇异. 可以证明,这种情况下有无穷多个最小二乘解,详细的讨论请参考[6].一. 问题背景1945年7月16日,美国科学家在新墨西哥州Los Alamos沙漠试爆了世界上第一颗原子弹,这一事件令全球震惊. 但在当时有关原子弹爆炸的任何资料都是保密的,而很多其他国家的科学家非常想知道这次爆炸的威力有多大.两年之后,美国政府首次公开了这次爆炸的录像带,而其他数据和资料仍然不被外界所知. 英国物理学家G. I. Taylor(1886 ~ 1975)通过研究原子弹爆炸的录像带,建立数学模型对爆炸所释放出的能量进行了估计,得到估计值与若干年后正式公布的爆炸能量21 kt 相当接近(1 kt 为1千吨TNT 炸药的爆炸能量). Taylor 是如何根据爆炸录像估计的呢?主要是通过测量爆炸形成的“蘑菇云”半径来进行估计的(如图(A)). 因为爆炸产生的冲击波从中心点向外传播,爆炸的能量越大,在相同时间内冲击波传播得越远、蘑菇云的半径就越大. Taylor 通过图(A) 原子弹爆炸的蘑菇云.*t 的单位为ms, r 的单位为m.然后通过量纲分析法建立了蘑菇云半径r 与时间t 和爆炸能量E 的关系式,利用上述数据最后求出了爆炸的能量.二. 数学模型考虑到原子弹爆炸在极短的时间内释放出巨大的能量,蘑菇云半径r 主要与时间t 、爆炸能量E 、以及空气密度ρ等几个参数有关. 通过仔细分析这几个量的单位,采用量纲分析法得到如下的蘑菇云半径的近似表达式:r =(t 2E )15. 其中r , t , E 的单位分别为米(m), 秒(s)和焦耳,而空气密度ρ的值为1.25 (kg m 3⁄). 对这次原子弹爆炸来说,E 为一固定值,因此r 与t 2成正比. 图(B)是根据蘑菇云半径与对应时刻的数据画出的散点图,它大体反映了这个趋势. 接下来的问题是如何求未知的参数E .三. 求解过程首先,改写蘑菇云半径的公式为r =at b 的形式,通过测量数据拟合出参数a 和b ,来验证量纲分析法得到的公式. 要作线性最小二乘拟合,进一步改写公式为:lnr =lna +blnt . 根据测量数据我们得到lnr 和lnt 的数据,将它们的函数关系拟合为1次多项式,得到系数b =0.4094,其值与前面分析的结果2/5非常接近,从而验证了量纲分析得到的公式.为了更为准确地计算爆炸能量E ,将蘑菇云半径公式改写为:5lnr −2lnt =ln (E ) . 此时可根据测量数据得到5lnr −2lnt 对应的一组数据,将它拟合为0次多项式(常数),设得到拟合系数为c ,则E ≈ρ∙e c .根据此方法算出E ≈8.6418×1013,单位为焦耳,查表得知1kt=4.184×1012焦耳,因此爆炸能量约等于20.65 kt.6.4函数插值与拉格朗日插值法函数插值可看作一种“特殊”的函数逼近问题,其逼近采用的“度量”准则是要求在插值节点处误差函数的值为0. 本节先介绍关于插值(interpolation)的一些基本概念,然后讨论最简单的一种多项式插值——拉格朗日插值法.图(B) 蘑菇云半径与对应时刻的数据 rt个节点:x 0<x 1<⋯<x n 进行插值,只需将B −k k (x ),B −k+1k (x ),⋯,B n−1k (x )这n+k 个k 次B-样条函数进行组合. 可以证明,它们在区间[x 0,x n ]上的部分组成n+k 个线性无关的基函数. 因此,对于满足额外边界条件的[x 0,x n ]上的k 次样条函数,可唯一地用这些基函数的线性组合表示. 感兴趣地读者可以推导B i 3(x )的表达式,然后利用插值条件和边界条件列方程求这些基函数对应的系数,进而推导出三次样条插值函数的表达式. 这个计算过程将与上一小节的方法得到相同的结果.利用B-样条基函数,可得到确定和计算各阶样条插值的有效而稳定的方法. 此外,它在计算机图形学、几何建模,以及数值求解微分方程等领域都有广泛的应用.评述关于多项式逼近和插值问题的研究历史悠久,应用面也很广. 本章只讨论了一元函数的最佳平方逼近,更多的相关内容,包括多元函数的逼近、正交多项式等,可参考下述文献:● P . J. Davis, Interpolation and Approximation , Dover, 1975.● W. Cheney, Introduction to Approximation Theory , AMS Chelsea Publishing, 2nd edition,1998.● G. A. Baker, and P . R. Graves-Morris, Pade Approximations , Cambridge University Press,2nd edition, 1996.● W. Gautschi, “Orthogonal polynomials: Applications and computation,” Acta Numerica ,Vol. 5, pp. 45-119, 1996.最佳平方逼近的法方程方法在1795年由高斯提出. 格莱姆-斯密特正交化方法在1883年由格莱姆提出,1907年斯密特给出了现代算法. 在求解最小二乘问题中使用QR 分解方法,特别是使用Householder 变换的方法是在1965年由G. Golub ⑥提出的. 最小二乘方法是统计学的重要工具,也称为回归分析,很多常用的数据处理软件(比如微软公司的Excel 软件)都具有这个功能. 本章讨论的线性最小二乘问题实际上是一种最简化的形式,即假设待逼近函数是基函数的线性组合. 在实际应用中还常遇到非线性最小二乘问题,它属于非线性优化问题,见参考文献[6]及其中给出的更多文献. 另外,若考虑所有参量都带有随机误差的情形,则成为完全最小二乘问题,有关详细讨论见文献:● S. Van Huffel and J. Vandewalle, The Total Least Squares Problem , SIAM Press, 1991. 本章也没有讨论拟合的基函数可能线性相关的情况,这在实际中可能由于拟合模型的不合理或数值误差造成,它使得矩阵A 列不满秩. 此时最佳平方逼近解不唯一,要得到实际有用的一个逼近解,需采用列重排的QR 分解等技术,更多讨论参见文献[6]及其他文献.多项式插值问题历史非常悠久,牛顿、拉格朗日等都在这方法做出了很多贡献. 除了将函数值作为条件的插值问题,插值条件中包括各阶导数值的情况也常见于各种工程应用中. 目前,常用的文档编辑软件都已使用保形分段插值来绘制曲线,例如微软公司的Word 和Power Point 软件. 样条函数是1946年由Schoenberg 首先提出的,本章只讨论了一维数据的样条插值和B-样条函数,实际问题中还有高维的插值问题,尤其在计算机图形学中二维B-样条是一个重要的工具. 关于样条的参考文献主要有:● C. de Boor, A Practical Guide to Splines , Springer-Verlag, 2nd edition, 1984.● E. V. Shikin and A. I. Plis, Handbook on Splines for the User , CRC Press, 1995.最后,列表说明Matlab 中与本章讨论的函数逼近与插值有关的命令和功能.⑥ Gene H. Golub (1932-2007), 美国斯坦福大学计算机系教授,美国科学院、工程院、艺术与科学院三院院士,著名的数值计算专家,1996年出版的著作”Matrix Computations ” [21]被奉为矩阵计算领域的经典.线拟合与样条插值的功能.[本章知识点]: 连续函数的范数;内积及其性质;内积空间的格莱姆矩阵、及其非奇异的充要条件;权函数与加权内积;最佳一致逼近与最佳平方逼近的概念;法方程方法求连续函数的最佳平方逼近;最佳平方逼近的误差;正交函数族与Gram-Schimdit正交化过程;勒让德多项式;用正交函数族作最佳平方逼近;曲线拟合的线性最小二乘问题;线性最小二乘问题的矩阵描述;法方程方法解线性最小二乘问题;表格函数的线性无关性与相关性;利用矩阵的QR分解解线性最小二乘问题;插值的基本概念;范德蒙矩阵与多项式插值的存在唯一性;拉格朗日插值公式;拉格朗日插值余项公式;牛顿插值公式;差商的计算;牛顿插值余项公式;高次多项式插值的问题;分段线性插值;埃尔米特插值;分段三次埃尔米特插值;保形分段插值;三次样条插值及边界条件;三次样条插值的构造方法;三弯矩方程;几种插值的比较;B-样条函数的基本概念与性质.算法背后的历史:拉格朗日与插值法约瑟夫·路易斯·拉格朗日(Joseph-Louis Lagrange,1736年1月25日—1813年4月10日)是法国数学家、物理学家. 他在数学、力学和天文学三个领域中都有巨大的贡献,其中尤以数学方面的成就最为突出. 拉格朗日与同时代的勒让德(Legendre)、拉普拉斯(Laplace)并称为法国的3L.拉格朗日于1736年生于意大利西北部的都灵. 17岁时,开始专攻当时迅速发展的数学分析. 1756年,受欧拉的举荐,拉格朗日被任命为普鲁士科学院通讯院士. 1766年赴柏林任普鲁士科学院数学部主任,居住柏林达20年之久,这是他一生科学研究的鼎盛时期. 在此期间,他完成了著作《分析力学》. 1786年加入了巴黎科学院成立的研究法国度量衡统一问题的委员会,并出任法国米制委员会主任. 1795年建立了法国最高学术机构——法兰西研究院后,拉格朗。
正交多项式

(Function Approximation and Interpolation)
❖ 主要内容:
❖ 正交多项式的构造; ❖ 常用的多项式; ❖ 一致逼近的基本概念; ❖ 最佳一致逼近多项式; ❖ 均方逼近的基本概念; ❖ 最佳均方逼近多项式; ❖ 最小二乘曲线拟合的基本概念; ❖ 用正交多项式作最小二乘曲线拟合。
5 )( x 8
5) 8
3 64
x2
5 4
x
11 32
Qj (x) 为 j 次多项式
1. 正交多项式(Orthogonal Multinomial)
切比雪夫多项式:设 x cos , 0 则称 Tn (x) cos(n ) cos(n arccos x)
为(第一类)n 阶切比雪夫多项式。
x)m
(
x)n
(
x)dx
0, 0,
m n,(x) > 0
mn
则称此函数系为在此区间上关于权函数 ( x)的正交函数系。
当
b a
(
x)n
(
x)n
(
x)dx
1时称之为规范的正交函数系;
当此函数系中的每一个函数均为多项式时称之为正交多项式(系)。
6. 1正交多项式(Orthogonal Multinomial)
b a
x(
x
0
)2
dx
,
d1
d0
b a
Q02
(
x)dx
பைடு நூலகம்
b dx,
a
d1
b a
Q12
( x)dx
b a
(
x
0
)2
dx
Example 6.1
计算方法讲义:六 函数逼近

第六章 函数逼近用简单的函数近似代替复杂函数,是计算数学中最基本的方法之一。
近似又称为逼近,被逼近的函数与逼近函数之差)()()(x p x f x R -=称为逼近的误差或余项。
简单函数:仅用加、减、乘、除。
多项式是简单函数。
插值也可以理解为一种逼近形式。
用Taylor展开:10)1(00)(000)()!1()()(!)())(()()(++-++-+-'+=n n nn x x n f x x n x fx x x f x f x f ξ 的部分和逼近f (x )也是一种逼近方法,其特点是:x 越接近于x 0,误差就越小。
如何在给定精度下求出计算量最小的近似式,这就是函数逼近要解决的问题。
逼近的度量标准有:一致逼近和平方逼近。
6.1 函数内积本节介绍几个基本定义:权函数、内积、正交、正交函数系。
定义1 设ρ (x )定义在有限或无限区间[a , b ]上,若具有下列性质:(1) ρ(3) 对非负的连续函数g (x ),若⎰=ba dx x x g 0)()(ρ,则在(a ,b )上g (x ) ≡ 0,称ρ (x )为[a , b ]上的权函数。
常用权函数有:211)(],1,1[xx -=-ρ;x e x -=∞)(],,0[ρ;2)(],,[x e x -=∞+-∞ρ;1)(],1,1[=-x ρ等。
定义2 设f (x ),g (x ) ∈ C [a , b ],ρ (x )是[a , b ]上的权函数,则称⎰=ba dx x g x f x g f )()()(),(ρ为f (x )与g (x )在[a ,b ]上以ρ (x )为权函数的内积。
内积有如下性质:(1) (f , f )≥0,且(f , f )=0 ⇔ f = 0;(2) (f , g ) = (g , f );(3) (f 1 + f 2, g ) = (f 1, g ) + (f 2,g );(4)对任意实数k ,(kf , g ) = k (f , g )。
函数逼近论

函数逼近论函数逼近论是函数论的一个重要组成部分,涉及的基本问题是函数的近似表示问题。
在数学的理论研究和实际应用中经常遇到下类问题:在选定的一类函数中寻找某个函数g,使它是已知函数ƒ在一定意义下的近似表示,并求出用g近似表示ƒ而产生的误差。
这就是函数逼近问题。
在函数逼近问题中,用来逼近已知函数ƒ的函数类可以有不同的选择;即使函数类选定了,在该类函数中用作ƒ的近似表示的函数g的确定方式仍然是各式各样的;g对ƒ的近似程度(误差)也可以有各种不同的含义。
所以函数逼近问题的提法具有多样的形式,其内容十分丰富。
从18世纪到19世纪初期,在L.欧拉、P.-S.拉普拉斯、J.-B.-J.傅里叶、J.-V.彭赛列等数学家的研究工作中已涉及一些个别的具体函数的最佳逼近问题。
这些问题是从诸如绘图学、测地学、机械设计等方面的实际需要中提出的。
在当时没有可能形成深刻的概念和统一的方法。
切比雪夫提出了最佳逼近概念,研究了逼近函数类是n次多项式时最佳逼近元的性质,建立了能够据以判断多项式为最佳逼近元的特征定理。
他和他的学生们研究了与零的偏差最小的多项式的问题,得到了许多重要结果。
已知[α,b]区间上的连续函数ƒ(x),(n≥0),叫做ƒ(x)的n阶最佳一致逼近值,简称为最佳逼近值,简记为En(ƒ)。
能使极小值实现的多项叫做ƒ(x)的n阶最佳逼近多项式。
切比雪夫证明了,在区间[-1,1]上函数xn+1的n阶最佳逼近多项式必满足关系式。
多项式就是著名的切比雪夫多项式。
切比雪夫还证明了ƒ(x)在[α,b]上的n 阶最佳逼近多项式的充分必要条件是:在[α,b]上存在着n+2个点:α≤x1<x2<…xn+2≤b,在这些点上依照i=1,2,…,n+2的次序交错变号,像这样的点组{x1,x2,…,xn+2} 便是著名的切比雪夫交错组。
1885年德国数学家K.(T.W.)外尔斯特拉斯在研究用多项式来一致逼近连续函数的问题时证明了一条定理,这条定理在原则上肯定了任何连续函数都可以用多项式以任何预先指定的精确度在函数的定义区间上一致地近似表示,但是没有指出应该如何选择多项式才能逼近得最好。
数值分析06-一致逼近

Y
在度量标准 max ri
i
(达到最小),这就是最佳一致逼近(不要产生最大误差, 均匀一些),通常仍 然取 (x)为多项式,即求多项式 (x) 使残差: r f (x ) (x )
i i i
绝对值的最大值 达到最小。或可写为:在H中求满足 (x) (f 的逼近函数 (x) ):
a xb
max
即在H中 (x)与f(x)之差的绝对值的最大值是最小的,H中 任一ψ (x)与f(x)之差的绝对值的最大值都比它大,这样的 6-3 阜师院数科院第六章 函数逼近 (x)为f(x)在H中的最佳一致逼近函数。
W Y
§5 最佳一致逼近多项式
下,求 (x) ,使
max ri max f ( x ) ( x ) min
例如:要求区间[0,1]上y=arctgx的一次近似式 可以有多种方法: (1)Talor公式:tg-1x x,误差R(x)= tg-1x- x,在 x=0附近很小,x=1时误差最大,R(x)|x=1=0.2146; (2)插值: x=0,1作节点=>L1(x)=πx/4,tg-1x πx/4, 4 其误差在 x 1 1 . 12 处,即在1附近较大为0.0711;
定理6.6 P (x)H 是f(x)C[a,b]的最佳一致逼近多项式的 n n 充要条件是Pn(x)在[a,b]上至少有n+2个不同的依次轮流为 正,负的偏差点(这些点称为切比雪夫交错点组)。 切比雪夫定理给出了最佳一致逼近多项式的特征,性质, 在最佳一致逼近理论中起着重要作用。 推论1 如果f(x)C[a,b],则在Hn中存在唯一的最佳一致 逼近多项式。 推论2
(3)最小二乘法(例10 §4中)
tg
阜师院数科院第六章 函数逼近
数值分析第六章函数逼近

2 i 2
拟合 函数
st . ,∑ δ = ∑[ yi −ϕ(xi )] = ∑⎡ yi −∑j=1ajϕj (xi )⎤ →min = F(a0, a1,⋯, am) ⎣ ⎦ i=1 i=1 i=1
拟合条件
n
m
2
该方法称为拟合曲线方法
适当选取函数类
{ϕ0 ( x), ϕ1 ( x),⋯, ϕn ( x)}
(*)有最小二乘解
Φ Φ ⋅a = Φ ⋅ y
⎡ (ϕ0 , ϕ0 ) (ϕ0, ϕ1) ⎢ (ϕ , ϕ ) (ϕ , ϕ ) 1 1 ΦT Φa = ⎢ 1 0 ⎢ ⋯ ⎢ ⎣(ϕm , ϕ0 ) (ϕm , ϕ1) ⎡ ϕ0 ( x1 ) ϕ1 ( x1 ) ⎢ϕ ( x ) ϕ ( x ) 1 2 ΦT y = ⎢ 0 2 ⎢ ⋯ ⎢ ⎣ϕ0 ( xn ) ϕ1 (xn ) ⋯ (ϕ0, ϕm ) ⎤ ⎡a0 ⎤ ⎢a ⎥ ⋯ (ϕ1, ϕm ) ⎥ ⎥ ⎢ 1 ⎥, ⎥ ⎢⋮ ⎥ ⋯ ⎥⎢ ⎥ ⋯ (ϕm , ϕm ) ⎦ ⎣an ⎦
T
T
T
⋯ ϕ m xn )⎦
⎡ y1 ⎤ ⎢y ⎥ ⎢ 2 ⎥, ⎢⋮ ⎥ ⎢ ⎥ ⎣ yn ⎦
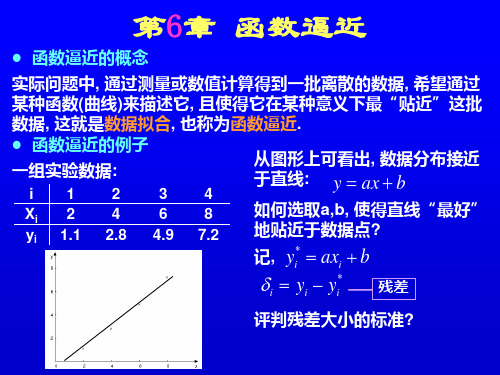
例:已知一组实验数据 求拟合曲线。
X Y
1 4
2 4.5
3 6
4 8
5 9
解:观察数据特征,各点的变化接近一条二次曲线。 选用 ϕ ( x) = a0ϕ 0 ( x) + a1ϕ1( x) + a2ϕ 2 ( x), ϕ ( x) = p2( x)
主要问题的提出和解决
�
一、给出函数表
x Y x1,x2,---,xn
f(x)
P(x) y1,y2,---,yn O x1, x2,--,xj,--, xn 求拟合函数 ϕ ( x) = a0ϕ0 ( x) + a1ϕ1 ( x ) + ⋯ + amϕ m ( x ), ϕ ( x ) = p ( x )
函数逼近

上海理工大学理学院
University of Shanghai for Science and Technology
College of Science
计算方法与数值计算
函数逼近问题的一般提法: 对于函数类A(如连续函数类)中给定的函数f (x),要求在另 一类较简单的且便于计算的函数类B(如多项式、三角函数类等)
b
a
g ( x) ( x)dx 0
上海理工大学理学院
University of Shanghai for Science and Technology
College of Science
计算方法与数值计算
2.内积
则称
定义2 设f (x),g (x) C [a, b], (x)是[a, b]上的权函数,
1
1
0, 1 Tm ( x)Tn ( x)dx , 1 x2 2 ,
mn mn0 mn0
上海理工大学理学院
University of Shanghai for Science and Technology
College of Science
计算方法与数值计算
S ( x) a 0 0 ( x) a11 ( x) a n n ( x)
的全体是C[a, b]的一个子集,记为
Span{ 0 , 1 , , n }
并称
0 ( x), 1 ( x), , n ( x) 是生成集合的一个基底。
上海理工大学理学院
a
b
则称f (x)与g (x)在[a, b]上带权 (x)正交。 定义4 设在[a, b]上给定函数系{k(x)} ,若满足条件
函数逼近
m次多项式: Pm ( x ) a0 a1 x
i 1 2 i n i 1
am x m ( m n )
F 要求F(a0,…,am) 极小 0 ( j 0,1, a j
2 [ y P ( x )] i m i
, m)
n
2 [ yi Pm ( xi )]xi 0
1 当数据点分布接近于函数 y 时 ax b 1 1 作变换: z ax b 对数据点 ( xi , zi ) 进行线性最小二乘拟合. yi y 1 1 参数a, b y 拟合曲线 z ax b z ax b t 当数据点分布接近于函数 y 时 a bt 1 1 1 1 作变换: x , z ax b 对数据点 ( xi , zi ) 进行线性最 ti yi y t 小二乘拟合. 1 1 t 参数a, b y 拟合曲线 z ax b z ax b a bt 上面两种拟合中, 参数a, b 满足以下正则方程:
2 i
x
3 i
n x y i i 1 a0 i 1 n n yx 3 x a i 1 i i i 1 i 1 a 2 n n 4 2 xi yi xi i 1 i 1
例 : 已知一组数据 i xi yi 1 1.0 0.931 2 1.4 0.473 3 1.8 0.297 4 2.2 0.224 5 2.6 0.168
求形如y
1 的拟合函数( 保留四位小数) ax b
1 1 , 令Y , 则有Y ax b. ax b y
1.4 1.8 2.2 2.6
k 0
)ak yi xij
傅里叶级数 函数逼近

傅里叶级数函数逼近傅里叶级数是一种将周期函数表示为正弦和余弦函数的无穷级数的方法,它在数学和工程领域中具有广泛的应用。
函数逼近则是利用傅里叶级数或其他逼近方法来近似表示一个给定的函数。
傅里叶级数的基本思想是将一个周期为T的函数f(x)表示为一组正弦和余弦函数的线性组合。
具体而言,傅里叶级数可以表示为以下形式的级数:f(x) = a0 + Σ(ancos(nωt) + bnsin(nωt))。
其中,a0、an和bn是系数,ω是角频率,t是时间。
这个级数包含了无穷多个谐波分量,每个分量对应一个正弦或余弦函数。
系数an和bn决定了每个分量的振幅,而角频率则决定了每个分量的频率。
通过求解函数f(x)与正弦和余弦函数的内积,可以得到傅里叶级数的系数。
这样,我们就可以用有限项级数来逼近原始函数f(x)。
通常情况下,选择足够多的项,级数的逼近效果会更好。
函数逼近是利用傅里叶级数或其他逼近方法来近似表示一个给定函数的过程。
除了傅里叶级数,还有其他的逼近方法,如泰勒级数、插值法等。
这些方法的选择取决于所要逼近的函数的性质和所需的逼近精度。
函数逼近的应用非常广泛。
在信号处理领域,傅里叶级数可以用于信号的频谱分析和滤波,可以将复杂的信号分解成一系列简单的谐波分量。
在数值计算和数值分析中,函数逼近可以用于数值积分、数值解微分方程等问题。
在图像处理中,函数逼近可以用于图像的压缩和降噪等。
总结起来,傅里叶级数和函数逼近是一种将周期函数表示为正弦和余弦函数的无穷级数的方法,通过选择适当的系数和项数,可以用有限项级数来逼近原始函数。
函数逼近在数学和工程领域具有广泛的应用。
函数逼近与曲线拟合PPT课件

例 已知点集 {xi} i=0,1,…,4 ={0,0.25,0.5,0.75,1} 和 权数{ i}i=0,…4 ={1,1,1,1,1}.试用三项递推公式求关于
该点集的正交多项式 P0(x),P1(x),P2(x)
解 先令 P0(x)=1 ,由此得
4
(P0, P0 ) iP02 (xi ) 5 i0
)
k
(x)
k
k
(x), k 1, 2,
k 1
n 1
给出的多项式序列
n
Pk(x)
(n
k 0
m)
是正交多项式序列
,其中
(x , )
(,
P P P P
k k,
k
a b k ( , ) k ( ,
P P P P k k
k 1
) k.
)
k 1
(5)
三项递推公式(4)是构造正交多项式的简单公 式,此外,还有其他的特殊的情形,这里,不进一 步讨论。
有了内积,就可以定义正交性。若函数 f (x) 和 g (x) 的内积 (f , g)=0,则称两者正交。
第12页/共81页
若多项式组{k(x)}k=0,…n 在离散意义下的内积满足
(i , j )
0,i j ai 0,i
j
(3)
则称多项式组{k(x)}k=0,…n为在离散点集 {xi} i=0,1,…,m 上的带权 { i}i=0,…m的正交多项式序列.
第8页/共81页
更一般函数逼近的概念:
可用一
组
在C
a,
b上线
性
无
关
的函数
集
合
i
x
n i0
函数逼近

我 们 将 定 义 在 区 间, b]上 的 全 体 连 续 函 数 构 成 [a 的 集 合 记 作 [a , b]。 显 然 , [a , b]可 以 构 成 一 个 C C 线 性 空 间 ( 连 续 函 数 间 ) 。 设 0 ( x ),1 ( x ), , 空
n ( x ) C [a , b], 当 且 仅 当 0 a1 a n 0时 , a
pn ( x ) H n
min max | f ( x ) p
a xb
n
( x) |
称 为f ( x )在[a , b]上 的 最 小 偏 差 。 如 果 存 在 ( x) H n使 得 p
max | f ( x ) p( x ) | E
a xb
n
,
那 么p( x )称 为f ( x )在[a , b]上 的 最 佳 一 致 逼 近 多项式。
2 3 , i 0, 1 ( i , f ) x i x 1 / 2 dx 0 2 , i 1. 5 相应的法方程为 1 2 a 0 a1 , 2 3 1 a 1 a 2 , 2 0 3 1 5 解得 4 4 ( x) x. 15 5
近似最佳一致逼近
Lagrange插 值 余 项 的 极 小 化 f ( n1) ( ) rn ( x ) f ( x ) p n ( x ) w n1 ( x ) ( n 1)! 其 中w n1 ( x ) ( x x 0 )( x x1 )( x x n )。 余 项 的 大 小 与 插 值 基 点 有 关若 选 去 。 Chebyshev多 项 式 的 零 点 作 为 插 值 基 点则 可 使 余 项 极 小 化 。 设 , f ( x )定 义 在 1,1]上 , [ x j cos 有 m inmax | w n1 ( x ) | max |
函数逼近与曲线拟合

函数逼近与曲线拟合3.1函数逼近的基本概念3.1.1 函数逼近与函数空间在数值计算中常要计算函数值,如计算机中计算基本初等函数及其他特殊函数;当函数只在有限点集上给定函数值,要在包含该点集的区间上用公式给出函数的简单表达式,这些都涉及到在区间上用简单函数逼近已知复杂函数的问题,这就是函数逼近问题.上章讨论的插值法就是函数逼近问题的一种.本章讨论的函数逼近,是指“对函数类A中给定的函数,记作,要求在另一类简单的便于计算的函数类B中求函数,使与的误差在某种度量意义下最小”.函数类A通常是区间上的连续函数,记作,称为连续函数空间,而函数类B通常为n次多项式,有理函数或分段低次多项式等.函数逼近是数值分析的基础,为了在数学上描述更精确,先要介绍代数和分析中一些基本概念及预备知识.数学上常把在各种集合中引入某些不同的确定关系称为赋予集合以某种空间结构,并将为样的集合称为空间.例如将所有实n维向量组成集合,按向量加法及向量与数的乘法构成实数域上的线性空间,记作,称为n维向量空间.类似地,对次数不超过n(n为正整数)的实系数多项式全体,按通常多项式与多项式加法及数与多项式乘法也构成数域上的一个线性空间,用表示,称为多项式空间.所有定义在上的连续函数集合,按函数加法和数与函数乘法构成数域上的线性空间,记作.类似地,记为具有p阶的连续导数的函数空间.定义1设集合S是数域P上的线性空间,元素,如果存在不全为零的数,使得, (3.1.1)则称线性相关.否则,若等式(3.1.1)只对成立,则称线性无关.若线性空间S是由n个线性无关元素生成的,即对都有则称为空间S的一组基,记为,并称空间S为n维空间,系数称为x在基下的坐标,记作,如果S中有无限个线性无关元素,…,则称S为无限维线性空间.下面考察次数不超过n次的多项式集合,其元素表示为, (3.1.2)它由个系数唯一确定.线性无关,它是的一组基,故,且是的坐标向量,是维的.对连续函数,它不能用有限个线性无关的函数表示,故是无限维的,但它的任一元素均可用有限维的逼近,使误差(为任给的小正数),这就是著名的Weierstrass定理.定理1(Weierstrass)设,则对任何,总存在一个代数多项式,使在上一致成立.这个定理已在“数学分析”中证明过.这里需要说明的是在许多证明方法中,伯恩斯坦1912年给出的证明是一种构造性证明.他根据函数整体逼近的特性构造出伯恩斯坦多项式, (3.1.3)其中,其中,并证明了在上一致成立;若在上阶导数连续,则.这不但证明了定理1,而且由(3.1.3)给出了的一个逼近多项式.它与拉格朗日插值多项式很相似,对,当=1时也有关系式. (3.1.4)这只要在恒等式中令就可得到.但这里当时还有,于是是有界的,因而只要对任意成立,则有界,故是稳定的.至于拉格朗日多项式,由于无界,因而不能保证高阶插值的稳定性与收敛性.相比之下,多项式有良好的逼近性质,但它收敛太慢,比三次样条插值效果差得多,实际中很少被使用.更一般地,可用一组在上线性无关的函数集合来逼近,元素,表示为. (3.1.5) 函数逼近问题就是对任何,在子空间中找一个元素,使在某种意义下最小.3.1.2 范数与赋范线性空间为了对线性空间中元素大小进行衡量,需要引进范数定义,它是空间中向量长度概念的直接推广.定义2.1.2 设为线性空间,,若存在唯一实数,满足条件:(1)正定性:,(2)当且仅当时,(3);(4)齐次性:,(5);(6)三角不(7)等式:,(8).则称为线性空间上的范数,与一起称为赋范线性空间,记为.例如,在上的向量,三种常用范数为类似地对连续函数空间,若可定义三种常用范数如下:可以验证这样定义的范数均满足定义3.1.2中的三个条件.3.1.3 内积与内积空间在线性代数中,中两个向量及的内积定义为.若将它推广到一般的线性空间,则有下面的定义.定义3.1.3设是数域上的线性空间,对,有中一个数与之对应,记为,它满足以下条件:(1);(2);(3);(4),当且仅当时,.则称为上与的内积.定义了内积的线性空间称为内积空间.定义中(1)的右端称为的共轭,当为实数域时.如果=0,则称与正交,这是向量相互垂直的概念的推广.关于内积空间性质有以下重要定理.定理3.1.2设为一个内积空间,对,有(3.1.6) 称为Cauchy-Schwarz不等式.[证明]当时(3.1.6)式显然成立.现设,则,且对任何数有.取,代入上式右端,得,即得时.定理证毕定理3.1.2设为一个内积空间,,矩阵(3.1.7)称为Gram矩阵,则G非奇异的充分必要条件是线性无关.[证明]G非奇异等价于,其充分必要条件是齐次方程组(3.1.8) 只有零解.而(3.1.9) 从以上的等价关系可知,等价于从(3.1.8)推出.而后者等价于从(3.1.9)推出,即线性无关.定理证毕在内积空间上可以由内积导出一种范数,即对于,记(3.1.10) 容易验证它满足范数定义的三条性质,其中三角不等式(3.1.11)可由定理3.1.2直接得出,即两端开方即得(3.1.11).例1与的内积.设,,,则其内积定义为(3.1.12)由此导出的向量2-范数为.若给定实数,称为权系数,则在上可定义加权内积为(3.1.13)相应的范数为.不难验证(3.1.13)给出的满足内积定义的4条性质,当时,(3.1.13)就是(3.1.12).如果,带权内积定义为(3.1.14) 这里仍为正实数序列,为的共轭.在上也可以类似定义带权内积,为此先给出权函数的定义.定义3.1.4 设是有限或无限区间,在上的非负函数满足条件:(1)存在且为有限值;(2)对上的非负连续函数,如果,则.则称为上的一个权函数.例2上的内积.设,是上给定的权函数,则可定义内积. (3.1.15)容易验证它满足内积定义的4条性质,由此内积导出的范数为. (3.1.16)称(3.1.15)和(3.1.16)为带权的内积和范数.特别常用的是的情形,即若是中的线性无关函数族,记,它的Gram矩阵为(3.1.17)根据定理3.1.3可知线性无关的充分必要条件是.3.2 正交多项式正交多项式是函数逼近的重要工具,在数值积分中也有着重要的应用.3.2.1 正交函数族与正交多项式定义3.2.1 若,为上的权函数且满足, (3.2.1)则称与在上带权正交.若函数族满足关系(3.2.2)则称是上带权的正交函数族;若,则称之为标准正交函数族.例如,三角函数族就是在区间上的正交函数族.因为对有,而对,当时有定义3.2.2 设是上首项系数的次多项式,为上权函数,如果多项式序列满足关系式(3.2.2),则称多项式序列为在上带权正交,称为上带权的次正交多项式.只要给定区间及权函数,均可由一族线性无关的幂函数,利用逐个正交化手续构造出正交多项式序列;,(3.2.3) 这样得到的正交多项式序列有以下性质:(1)是具有最高次项系数为1的次多项式.(2)任何次多项式均可表示为的线性组合.(3)当时,,且与任一次数小于的多项式正交.(4)成立递推关系.其中这里.(5)设是在上带权的正交多项式序列,则的个根都是在区间内的单重实根.3.2.2 勒让德多项式当区间为[-1,1],权函数时,由正交化得到的多项式就称为勒让德(Legendre)多项式,并用表示.这是勒让德于1785年引进的,1814年罗德利克(Rodrigul)给出了简单的表达式由于是2次的多项式,求阶导数后得,于是得首项系数为,显然最高项系数为1的勒让德多项式为.(3.2.6) 勒让德多项式有下述几个性质:性质1正交性(3.2.7) [证明]令,则.设是在区间[-1,1]上的阶连续可微的函数,由分部积分知下面分两种情况讨论:(1)若是次数小于的多项式,则,故得(2)若,则,于是由于,故,于是(3.2.7)得证.性质2奇偶性(3.2.8)[证明]由于是偶次多项式,经过偶次求导仍为偶次多项式,经过奇次求导则为奇次多项式,故为偶数时为偶函数,为奇数时为奇函数,于是(3.2.8)成立.性质3递推关系(3.2.9) [证明]考虑+1次多项式,它可表示为两边乘以,并从-1到1积分,得.当时,的次数小于-1,上式左端积分为0,故得.当时.为奇函数,左端积分仍为0,故.于是.其中,代入上式整理可得(3.2.9).例1由利用性质3可得性质4在区间[-1,1]内有个不同的实零点.3.2.3 切比雪夫多项式当权函数,区间为[-1,1]时,由序列正交化得到的多项式就称为切比雪夫(Chebyshev)多项式,它可表示为(3.2.10)若令,则.切比雪夫多项式有很多重要性质:性质1递推关系(3.2.11) 这只要由三角不等式.令即得.由(3.2.11)就可推出由递推关系(3.2.11)还可得到的最高次项系数是.性质6切比雪夫多项式在区间[-1,1]上带权正交,且(3.2.12) 事实上,令,则,于是性质7只含的偶次幂,只含有的奇次幂.这性质由递推关系直接得到.性质8在区间[-1,1]上的个零点此外,实际计算中时常要求用的线性组合,其公式为. (3.2.13) 例如:结果如下:3.2.4 其他常用的正交多项式一般说,如果区间及权函数不同,则得到的正交多项式也不同.除上述两种最重要的正交多项式外,下面再给出三种较常用的正交多项式.第二类切比雪夫多项式在区间[-1,1]上带权的正交多项式称为第二类切比雪夫多项式,其表达式为. (3.2.14)令,可得即是[-1,1]上带权的正交多项式族.还可得到递推关系式.拉盖尔多项式在区间上带权的正交多项式称为拉盖尔(Laguerre)多项式,其表达式为. (3.2.15)其正交性为和递推关系.3. 埃尔米特多项式在区间上带权的正交多项式称为埃尔米特多项式.其表达式为, (3.2.16)其正交性为递推关系为.3.3 最佳一致逼近多项式3.3.1 基本概念及其理论本节讨论,在中求多项式,使其误差.这就是通常所谓最佳一致逼近或切比雪夫逼近问题.为了说明这一概念,先给出以下定义.定义3.3.1 设,,称. (3.3.1) 为与在上的偏差.显然,的全体组成一个集合,记为{},它有下界0.若记集合的下确界为(3.3.2)则称之为在上的最小偏差.定义3.3.2 假定,若存在,使得, (3.3.3)则称是在上的最佳一致逼近多项式或最小偏差逼近多项式,简称最佳逼近多项式.注意,定义并未说明最佳逼近多项式是否存在,但可证明下面的存在定理.定理4若,则总存在,使.为了研究最佳逼近多项式的特性,先引进偏差点的定义.定义3.3.3设,,若在上有,就称是的偏差点.若,称为“正”偏差点.若,称为“负”偏差点.由于函数在上连续,因此,至少存在一个点,使,也就是说的偏差点总是存在的.下面给出反映最佳逼近多项式特征的切比雪夫定理.定理3.3.2是的最佳逼近多项式的充分必要条件是在上至少有个轮流为“正”、“负”的偏差点,即有个点,使. (3.3.4) 这样的点组称为切比雪夫交错点组.[证明]只证充分性.假定在上有个点使(3.3.4)成立,要证明是在上的最佳逼近多项式.用反证法,若存在,使.由于在点上的符号与一致,故也在个点上轮流取“+”、“-”号.由连续性质,它在内有个零点,但因是不超过次的多项式,它的零点不超过.这矛盾说明假设不对,故就是所求最佳逼近多项式.充分性得证,必要性证明略,可参看[5].定理5说明用逼近的误差曲线是均匀分布的.由这定理还可得以下重要推论.推论1若,则在中存在唯一的最佳逼近多项式.证明略.利用定理5可直接得到切比雪夫多项式的一个重要性质,即定理3.3.3 在区间[-1,1]上所有最高次项系数为1的次多项式中与零的偏差最小,其偏差为.[证明]由于,且点是的切比雪夫交错点组,由定理5可知,区间[-1,1]上在中最佳逼近多项式为,即是与零的偏差最小的多项式.定理证毕例3求在[-1,1]上的最佳2次逼近多项式.解由题意,所求最佳逼近多项式应满足由定理3.3.3可知,当时,多项式与零偏差最小,故就是在[-1,1]上的最佳2次逼近多项式.3.3.2 最佳一次逼近多项式定理3.3.2给出了最佳逼近多项式的特性,但要求出却相当困难.下面讨论的情形.假定,且在内不变号,我们要求最佳一次逼近多项式.根据定理3.3.2可知至少有3个点,使由于在内不变号,故单调,在内只有一个零点,记为,于是,即.另外两个偏差点必是区间端点,即,且满足由此得到(3.3.5) 解出, (3.3.6) 代入(3.3.5)得. (3.3.7)这就得到了最佳一次逼近多项式,其几何意义如图3-3所示.直线与弦MN平行,且通过MQ的中点D,其方程为.图3-3一次最佳一致逼近多项式几何意义例4 求在上的最佳一次逼近多项式。
函数逼近基本概念

加权内积
(x, y)
n
i xi yi;
加 权 范 数 || x ||2
n
1/2
i xi2
i1
i1
n
若x, y C n, 则 定 义 加 权 内 积 ( x, y) i xi yi .
i 1
定 义 4 设 ( x)是 区 间[a, b(] 有 限 的 或 无 限 的 ) 上的 非 负 函 数,
(2) (u,v) (u,v), R;
(3) (u v, w) (u,w) (v,w), u,v,w X ; (4) (u, u) 0,当且仅当u 0时,(u, u) 0. 则称(u,v)为X上的u与v的内积. 定义了内积的线性空间称 为内积空间. (v,u)为(u,v)的共轭,当K R时 (v,u) (u,v).
三、内积与内积空间
Rn中向量x及y的内积定义为 : ( x, y) x1 y1 L , xn yn.
将其推广有如下定义 .
定义3 设X是数域K(R或C)上的线性空间,对u,v X, 有K中一个数与之对应,记为( u, v ),并满足条件: (1) (u,v) (v, u), u,v X ;
1,||
f ( x) ||2
b a
1/2
f 2( x)dx .
设0, ,n C[a,b],则Gram矩阵为
G G(0 , ,n )
(0 ,0 ) (0 ,1 )
(1
,0
)
(1,1 )
(n ,0 ) (n ,1 )
(0 ,n )
(1
,
n
)
(n ,n )
根据定理3,0, ,n线性无关 det(G) 0.
(u1, un ) (u2, un )
研究生数值分析(20)函数的最佳平方逼近

中寻求对f(x)的最佳平方逼近元素 pn (x)
现对该 Hn另取一组基底,即
H n Span L0 , L1 , L2 , , Ln } {
其中 Lj (x) 是 j 次Legendre多项式。此时,
法方程的解可直接得到,就是
( f , Lk ) 2k 1 1 c 1 Lk ( x) f ( x)dx ( Lk , Lk ) 2
以此为基底,生成空间 C[a,b] 的一个子空间
H n Span 0 , 1 ,, n } {
则 Hn中的任一个元素为
p ( x ) c j j ( x )
j 0 n
对空间C[a , b] 中的任意两个函数 f 和 g, 定义内积
( f , g ) ( x) f ( x) g ( x)dx
0
1 2 1 t dt , 3 2 t 6 1 t dt 15 2
可知
2 6 2 6 q1 (t ) L0 ( x) L1 ( x) t , 3 15 3 15 1 t 1
把 t =2x-1代人 q1 (t )
得
x
在区间[0,1]上的一次最佳平方
逼近多项式
n
这是一个以 c , c , , c 为未知数的 n+1 元线性方程组,称该式为法方程组和正规方程。 它的系数矩阵为
(0 , 0 ) (1 , 0 ) ( n , 0 ) ( , ) ( , ) ( , ) 1 1 n 1 0 1 G (0 , n ) (1 , n ) ( n , n )
( x) 的形式;
* ( x) (2)求最小二乘解,即求满足条件的近似解
[ ( xi ) yi ] min
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章函数逼近/shuzhifenxi/index.htm 第一节曲线拟合的最小二乘法问题的背景通过观测、测量或试验得到某一函数在x1 ,x2,…,x n的函数值. 我们可以用插值的方法对这一函数进行近似,而插值方法要求所得到的插值多项式经过已知的这n个插值结点;在n比较大的情况下, 插值多项式往往是高次多项式, 这也就容易出现振荡现象:虽然在插值结点上没有误差,但在插值结点之外插值误差变得很,从“整体”上看,插值逼近效果将变得“很差”. 于是, 我们采用数据拟合的方法.定义1 数据拟合就是求一个简单的函数φ(x), 例如是一个低次多项式,不要求通过已知的这n个点,而是要求在整体上“尽量好”的逼近原函数,这时在每个已知点上就会有误差y k -φ(x k),(k=1,2,…,n),数据拟合就是从整体上使误差y k -φ(x k),(k=1,2,…,n), 尽量的小一些.如果要求: 达到最小,因误差y k -φ(x k)可正可负本来很大的误差可能会正负抵消,这样的提法不合理,为防止正负抵消,可以要求:达到最小,但是由于绝对值函数不可以求导,分析起来不方便,求解也很难. 为了既能防止正负抵消,又能便于我们分析、求解,提出如下问题:求一个低次多项式φ(x) ,使得: 达到最小,此问题便是一个数据拟合的最小二乘问题.一、直线拟合(一次函数)通过观测、测量或试验得到某一函数在x1 ,x2,…,x n的函数值:y1 ,y2,…,y n ,即得到n组数据(x1 ,y1 ),(x2 ,y2),…,(x n ,y n ),如果这些数据在直角坐标系中近似地分布在一条直线上,我们可以用直线拟合的方法.已知数据(x1 ,y1 ),(x2 ,y2),…,(x n ,y n ),求一次多项式φ(x)=a+bx(实际上,就是求a,b), 使得:(1)达到最小.注意到Q(a,b)中,x k ,y k均是已知的,而a,b是未知量,Q(a,b)是未知量a,b的二元函数,利用高等数学求二元函数极小值(最小值)的方法,上述问题转化为求解下列方程组:的解.由得因为得到如下的正则方程组:(3)这是个关于a,b的二元一次方程组,称其为最小二乘问题的正则方程组解得a,b,便得到最小二乘问题的拟合函数.例1 已知10对数据如下表,利用最小二乘法求拟合曲线y=a+bx .解:先列表来计算四个形成所谓正则方程组:解得a=6.4383,b=-0.7877于是,最小二乘拟合一次函数为y=6.4383-0.7877x二、多项式拟合已知一组数据对(x i ,y i),(i=1,2,…,n),求一个m次多项式(m<n-1): P m (x)=a0 +a1x+…+a m x m ,使得误差的平方和达到最小. 即求待定参数a0 ,a1,…,a m使得(4)达到最小.如果m=n-1, 过这n个点可以决定一个n-1次多项式, 此时说明:P m(x)正好可以过这n个点,Q=0时达到最小,这就成为一个插值问题.如果m>n-1,此时过这n个点的m次多项式不仅存在,而且有无穷多个,解是不确定的. 因而, 对于拟合问题,一般总是针对大量的数据对而选用低次多项式.类似直线拟合方法,可找a0 ,a1,…,a m满足的所谓正则方程组, 令整理得到下面的正则方程组(法方程组):这是一个m+1阶的线性方程组. 例如m=2, 法方程组为这是一个三元一次方程组.例2 给定数据如下表, 求最小二乘拟合多项式P2(x) .解:设P2(x)=a0 +a1 x+a2 x2,列表计算:于是,法方程组为:解得故所求的二次多项式为:y = -1.7143 + 3.8690x - 0.4881x2三、指数拟合和一些非线性拟合有些数据(x k ,y k),(k=1,2,…,n),在直角坐标系中的分布近似于指数曲线, 则可以用指数函数进行拟合.已知一组数据对(x k ,y k),(i=1,2,…,n),求一个指数函数y=be ax,使得误差的平方和:(6)达到最小.指数函数y=be ax ,两边取对数,得:lny=lnb+ax,作变换y* =lny,得y* =lnb+ax这是一个一次函数,lnb和a是待定系数. 指数拟合的具体步骤:(1) 我们可以将数据对(x k ,y k)转化为数据对(x k ,lny k) ;(2) 用最小二乘法求出拟合曲线y* =a0 +a1 x (即解出a0 ,a1 );(3) 由lnb=a0=m,故b=e m,而a=a1 ,从而得到拟合的指数函数y=be ax例3 设一个发射源的发射公式为I=I0 e-αt ,通过实验得如下数据:利用最小二乘法确定I0和α.解 lnI=lnI0 -αt* ,设I =a0 +a1 t ,将数据对(t k ,I k)转化为数据对:(t k ,lnI k), 然后进行直线拟合.于是得到法方程组:解得m=a 0 =1.728288,a 1 =-2.888282,则α= -a 1 =2.89, 由lnI 0 =a 0 ,I 0 = e m = 5.631006于是得到拟合指数函数I=5.63e -2.89t .其它一些非线性拟合(1) 双曲线 (2) 对数函数 (3) S 型曲线(1) 双曲线先变形为: 令得到:y * = a + bx * 我们可以将数据对(x k ,y k ) 转化为数据对然后进行直线拟合.(2) 对数函数 y=a+blnx *令x =lnx , 变形为y=a+bx *(3) S型曲线先变形为,令, x* =e-x, 得到y* =a+bx* .四、函数逼近的相关概念1. 函数空间定义1 设集合S是数域P上的线性空间,元素x1 ,x2,…,x n∈S,如果存在不全为零的数a1 ,a2,…,a n∈P, 使得a1 x1 +a2 x2+ … + a n x n =0 (7)称x1 ,x2,…,x n线性相关,否则,称x1 ,x2,…,x n线性无相关。
如果x1 ,x2,…,x n线性无关,它们可生成S的n维线性子空间span{x1 ,x2,…,x n}={x|x=a1 x1 +a2 x2+ … + a n x n , a ∈P,i=1,2,…,n}函数f(x)的n次多项式逼近就是在多项式空间span{1,x,…,x n }中找出元素P(x)=a0 +a1x +…+a n x n与f(x)“最接近”. 函数的多项式逼近有下面的重要定理.定理(Weierstrass)1 设f(x)∈C[a,b], 对任意ε>0,总存在一个代数多项式P(x),使得‖f(x)-P(x)‖<ε在[a,b]上一致成立。
2. 范数与赋范线性空间定义2 设集合S是线性空间,x∈S, 如果存在函数ρ(x), 满足1) ρ(x)≥0, 且ρ(x)=0 <==>x=0(正定性)2) ρ(αx)=|α| ρ(x), α∈R (齐次性)3) ρ(x+y)≤ρ(x)+ρ(y), x,y∈S(三角不等式)则称ρ(x)为线性空间上的范数,通常记作‖·‖, 即‖x‖=ρ(x).范数S与‖·‖一起称为赋范线性空间, 记作X.赋范线性空间向量范数见第二章第五节,主要有: 对x=(x1 ,x2,…,x n)a. 向量的∞-范数(最大范数):b. 向量的1-范数:c. 向量的2-范数:类似地对连续函数空间C[a,b],若f∈C[a,b],可定义三种范数a. 向量的∞-范数(最大范数):b. 向量的1-范数:c. 向量的2-范数:3. 内积与内积空间定义3 设X是数域K(R或C)上的线性空间,对u,v ∈X,由K中一个数与之对应,记为(u,v),它满足一下条件则称(u,v)为X上u与v的内积. 定义了内积的线性空间称为内积空间.如果(u,v)=0, 则称u与v正交.定理2 设X为内积空间,对u,v∈X,有称为Cauchy-Schwarz不等式.证明对任一数λ∈K(u+λv,u+λv)=(u,u)+2(u,v)λ+(v,v)λ2≥0由一元二次方程根的判别定理可知定理的结论成立.定理3 设X为内积空间,u1 ,u2,…,u n∈X,矩阵称为(Gram)矩阵,则G为奇异的充分条件是,u1 ,u2,…,u n线性无关. 证明首先指出,定理中奇异可改成正定.对α=(α1,α2,…,αn)≠0,由以及线性代数的理论可知,定理的结论成立.最常见的内积有,1) 对x,y∈C n , x=(x1 ,x2,…,x n ), y=(y1 ,y2,…,y n )2) 对f(x),g(x)∈C[a,b],上面的两种内即可推广到所谓带权的内积,即称为权系数;称为权函数.一般对ρ(x)有如下要求四、线性最小二乘法的一般形式一般地,设给定数据组(x i ,y i)(i=1,2,…,n),φ1(x),…,φn(x)为已知的一组[a,b]上线性无关的函数,选取近似函数为:φ(x)=a0φ0 (x)+a1φ1(x)+…+a mφm (x)使得:其中ωi>0(i=1,2,…,n)为权函数,H为φ0(x),φ1(x),…,φm(x)的线性组合的全体,这就是线性最小二乘法的一般形式. 与多项式拟合的讨论相类似,上述问题的正则方程组为:即:(9)如果引入内积:方程组(9)可表示成矩阵形式:(10)定理4 设a0 ,a1, …,a m为方程组(9)的解,则函数满足关系式(8),即它是数据组(x i ,y i)(i=1,2, …,n)的最小二乘解. 证明(略)定义4 称满足的函数族φ0(x),φ1(x),…,φm(x)为以{ωi}(i=1,2, …,n)为权关于点集{x1 ,x2, …,x n}的正交函数族. 容易推出下列多项式系:是以{ωi}(i=1,2, …,n)为权关于点集{x1 ,x2, …,x n}的正交函数族. 其中于是,求数据组(x i ,y i)(i=1,2,...,n)带权{ωi}(i=1,2,…,n)的最小二乘拟和多项式可按以下过程进行.(1) 按式(12),(13)构造正交函数族φ0(x),φ1(x),…,φm(x)(2) 求出正则方程组(9)的解:(3) 写出最小二乘m次拟合多项式:。
