信号检测与理论(复习)

合集下载

信号检测与估计理论(复习题解)-精选文档

a ba 0 图 2. 1 (b)
ab y

2 b y x
2 2 y 4 x
第2章信号检测与估计理论的基础知识例题解答
例 2 . 3 设连续随机信号 x ( t ) a cos( t ), 其振幅 a 和频率已知相位在 [ , ) 范围内均匀分布。分析该信号的广义平稳并求其自差函数。解：分析该信号是否满足广义平稳的条件。信号的均值 ( t ) E a cos( t ) a cos( t ) p ( ) d x
2 1 ( y b ) / 2 1 x p ( y ) exp 2 2 2 2 2 x x 1 2
2 1 y ( 2 b ) x exp 2 2 8 8 x x 1 2
二. 离散随机信号矢量
1. 概率密度函数描述。 2. 统计平均量：均值矢量 , 协方差, 协方差矩阵。 3. 各分量之间的互不相关性和相互统计独立性及关系。 4. 高斯离散随机信号矢量的概率密度函数及特点： x ~ N ( μ , C ), 互不相关等价于相互统计独立 , 独立同分布 x x

E ( x b ) b
y
2 y
2 2 22 E ( y b ) E ( x b b ) E ( x 0 ) a / 6
第2章信号检测与估计理论的基础知识例题解答
当 a b 2 a 时, p ( y ) 的函数曲线如图 2 . 1 (b)所示。 p ( x) p( y ) 1/ a 1/ a
第 1章
信号检测与估计概论

信号检测期末考试题及答案

信号检测期末考试题及答案一、选择题（每题2分，共20分）1. 在信号检测理论中，信号检测的两个主要参数是：A. 信号强度和噪声大小B. 信号频率和信号幅度C. 信号到噪声比和信号的信噪比D. 信号的信噪比和信号的频率带宽2. 信号检测中的ROC曲线表示的是：A. 信号的频率响应曲线B. 信号的幅度响应曲线C. 接收者操作特征曲线D. 信号的时域特性曲线3. 信号检测理论中，d'值表示的是：A. 信号的信噪比B. 信号的幅度C. 信号的频率D. 信号与噪声的区分能力4. 以下哪个不是信号检测理论中常用的指标：A. 灵敏度B. 特异性C. 准确率D. 信噪比5. 信号检测理论中的β错误是指：A. 漏检B. 误报C. 假阳性D. 假阴性...（此处省略剩余选择题）二、简答题（每题10分，共30分）1. 简述信号检测理论中的信号到噪声比（SNR）的概念及其重要性。

2. 解释ROC曲线在信号检测中的应用及其优势。

3. 什么是d'值？它在信号检测中的作用是什么？三、计算题（每题15分，共30分）1. 假设一个信号检测系统接收到的信号强度为10，噪声强度为5，请计算该系统的信号到噪声比（SNR）。

2. 给定一个信号检测系统的ROC曲线数据，计算其d'值和β错误。

四、论述题（每题20分，共20分）1. 论述信号检测理论在实际工程中的应用及其重要性。

答案一、选择题1. D2. C3. D4. D5. A...（此处省略剩余选择题答案）二、简答题1. 信号到噪声比（SNR）是信号检测理论中衡量信号在噪声中可检测性的一个重要参数。

它表示信号强度与背景噪声强度的比值。

高SNR意味着信号更容易被检测和识别，而低SNR则意味着信号可能被噪声淹没，难以检测。

2. ROC曲线是接收者操作特征曲线的简称，它用于描述信号检测系统的性能。

通过绘制不同阈值下系统的正确检测率（真阳性率）与错误检测率（假阳性率）的关系，ROC曲线可以直观地展示系统在不同灵敏度水平下的表现。

第三章信号检测与估计理论3

判决的代价因子cij （i , j 0,1,,M 1）赋定的条件下，使平均代价
最小的准则，就是M元信号检测的贝叶斯准则。平均代价 C 的分析表示式
根据判决域Ri的划分3.6.1式，将3.6.2式写为3.6.3式
M 1
因为判决域Ri可表示为 Ri R Rj ,
jj0i
平均代价C的分析表示式为
其中, s0 1,
s1 2 ,
s2 3 ,
s3

4;
nk
~
N
0,
2 n
,相互统计独
立;先验概率 PH j 相等; cij 1 ij。设计最佳检测系统。
解由题意得各假设下的似然函数为
p x | H j

1
2
2 n
N
2 exp
p l | H j

N
2
2 n
1
2

exp

N
l sj
2
2 n
2
，j 0,1,2,3
于是各判决概率为
P Hi | H j Li p l | H j dl
其中，Li 是各假设成立的判决域。最小平均错误概率为
Ii x 0
于是应当满足Ii x＝MinI0 x, I1 x..., IM 1 x
的x划归R i 域，判决假设Hi 成立，即当满足
Ii x I j x ，j 0,1, , M 1, j i
时，判决假设Hi成立。这意味着判决假设Hi成立的判决域是通过求解M-1个不等式组成的联立不等式获得的。
Pe

13

3

信号检测理论

信号检测论
雷玉菊
测量阈限的三种方法的比较
• 测量阈限的三种方法各有自己的特点
–最小变化法的实验程序和计算过程都具体地说明了感觉阈限的含义，但它会因其渐增和渐减的刺激系列而产生习惯误差与期望误差。 –恒定刺激法的实验结果可以应用各种数学方法加以处理，因而便于与其它测定感受性的方法进行比较。在应用3类反应的实验程序时，被试的态度会对差别阈限值有较大影响。 –平均差误法的特点是求等值，它的实验程序容易引起被试的兴趣，但对不能连续变化的刺激则不能用平均差误法来测其差别阈限。
MN
MSN
MSN-MN MSN MN d’= ——— = — - — = Z击中-Z虚惊
σ
σ
σ
99%击中？
d’=Z击中-Z虚惊=2.326-(-2.326)=4.63
95%击中？
d’=Z击中-Z虚惊=1.645-(-1.645)=3.29
93%击中
d’=Z击中-Z虚惊=1.476-(-1.476)=2.95
2.评价法-1
• 有无法仅采用二级计分（有或无），评价法则允许多级计分
确信程度第6等第5等第4等第3等第2等第1等含义十分肯定有信号出现肯定有信号出现可能有信号出现可能没信号出现肯定没信号出现十分肯定没信号出现相应的概率判断 100%有信号出现 80%有信号出现 60%有信号出现 40%有信号出现 20%有信号出现 0%有信号出现
?判断结果的奖惩价值多少来源于噪声的收益来源于信号的收益pnpsvcrcfavhcmpnps正确拒绝的奖励数虚报的惩罚数报准的奖励数漏报的惩罚数支付矩阵sn1n111刺激yn反应刺激sn2020n11sn11n3030反应刺激支付代价小支付代价大影响的因素?信号和噪声的先验概率?判断结果的奖惩价值多少?被试要达到的目追求准确率报准率虚报等?其它一些有关因素影响的因素的其它因素?速度于准确性权衡随可利用信息变化而不断变化?有关试验的知识于经验基于被试对基础感觉强度分布性质的判断基于被试对基础感觉强度分布性质的判断?主观预期概率根据前一测查情况预测下一测查为哪一刺激的概率?系列跟随效应当前判断受前面多次反应和的反应和的影响二反应偏向指标?似然比值决策标准?报告标准c是被试选择的反应标准相对应的物理强度cz1i1i2i1di2i1dd二反应偏向指标?似然比值决策标准?报告标准c是被试选择的反应标准相对应的物理强度iii2i1di2ccz1i1i2i1di2i1dz1i2i1dci1ci2z2ci1i2i1dz2z1i2i1i2cz2d?c躁声强度d正确拒斥率z值?c信号强度d报准率z值cz1i1i2i1dci2z2i2i1d二择一的刺激情境一定范围内的模糊感觉弱强判断为sn的概率判断为n的概率辨别能力判断标准nnsnsnxcnsnnsn三操作者特性曲线?虚报率作为横坐标击中率作为纵坐标随着标准的变化击中率与虚报率的关系?这个曲线上各点代表在特?这个曲线上各点代表在特定刺激条件下被试所采用的各种反应方式所以叫做接受者操作特点特征曲线receiveroperatingcharacteristiccurveroc

信号检测与估计理论(复习题解)

优缺点
最大似然估计法具有一致性和渐近无偏性等优点，但在小样本情况下可能存在偏差。此外，该方法对模型的假设较为敏感，不同的模型假设可能导致不同的估计结果。
最小二乘法
01
原理
最小二乘法是一种基于误差平方和最小的参数估计方法，它通过最小化预测值与观测值之间的误差平方和来估计模型参数。
02 03
步骤
首先，构建包含未知参数的预测模型；然后，根据观测数据计算预测值与观测值之间的误差平方和；接着，对误差平方和求导并令其为零，得到参数的估计值；最后，通过求解方程组得到参数的最小二乘估计值。
优缺点
最小二乘法具有计算简单、易于实现等优点，但在处理非线性问题时可能效果不佳。此外，该方法对异常值和噪声较为敏感，可能导致估计结果的偏差。
01
小波变换基本原理
小波变换是一种时频分析方法，通过伸缩和平移等运算对信号进行多尺
度细化分析，能够同时提供信号的时域和频域信息。
02
小波变换在信号去噪中的应用
小波变换具有良好的时频局部化特性，可以用于信号的去噪处理。通过
对小波系数进行阈值处理等操作，可以有效去除信号中的噪声成分。
03
小波变换在信号特征提取中的应用
3. 观察相关函数的峰值，判断是否超过预设门限。
实现步骤
2. 将待检测信号与本地参考信号进行相关运算。
优缺点：相关接收法不需要严格的信号同步，但要求参考信号与待检测信号具有较高的相关性，且容易受到多径效应和干扰的影响。
能量检测法
原理：能量检测法通过计算接收信号的能量来判断信号是否存在。在噪声功率已知的情况下，可以通过比较接收信号的能量与预设门限来判断信号是否存在。 1. 计算接收信号的能量。
经典参数估计方法

信号检测与估计复习纲要与习题参考答案_2012

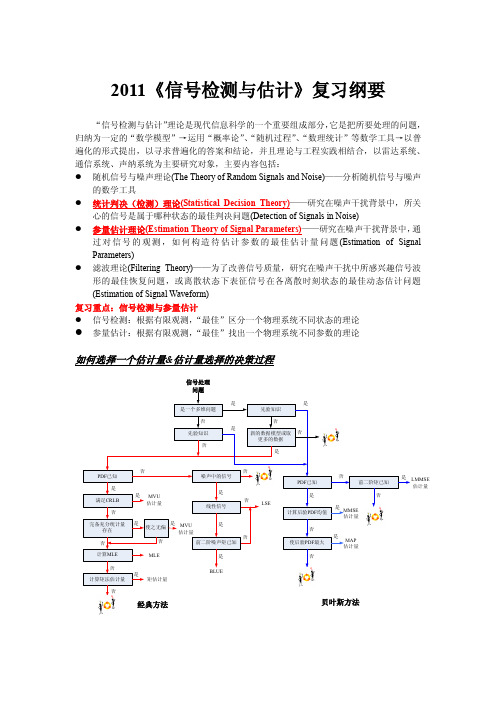
2011《信号检测与估计》复习纲要“信号检测与估计”理论是现代信息科学的一个重要组成部分，它是把所要处理的问题，归纳为一定的“数学模型”→运用“概率论”、“随机过程”、“数理统计”等数学工具→以普遍化的形式提出，以寻求普遍化的答案和结论，并且理论与工程实践相结合，以雷达系统、通信系统、声纳系统为主要研究对象，主要内容包括：● 随机信号与噪声理论(The Theory of Random Signals and Noise)——分析随机信号与噪声的数学工具● 统计判决（检测）理论(Statistical Decision Theory)——研究在噪声干扰背景中，所关心的信号是属于哪种状态的最佳判决问题(Detection of Signals in Noise)● 参量估计理论(Estimation Theory of Signal Parameters)——研究在噪声干扰背景中，通过对信号的观测，如何构造待估计参数的最佳估计量问题(Estimation of Signal Parameters)● 滤波理论(Filtering Theory)——为了改善信号质量，研究在噪声干扰中所感兴趣信号波形的最佳恢复问题，或离散状态下表征信号在各离散时刻状态的最佳动态估计问题(Estimation of Signal Waveform) 复习重点：信号检测与参量估计 ● 信号检测：根据有限观测，“最佳”区分一个物理系统不同状态的理论 ● 参量估计：根据有限观测，“最佳”找出一个物理系统不同参数的理论如何选择一个估计量&估计量选择的决策过程信号处理否估计量LSE经典方法贝叶斯方法如何选择一个检测器－二元信号检测如何选择一个检测器－多元信号检测*注：ARMA：自回归滑动平均BLUE：最佳线性无偏估计CFAR：恒虚警率CRLB ：Cramer-Rao下限EM：数学期望最大化GLRT：广义似然比检验IID：独立同分布LLR：对数似然比LMMSE：线性最小均方误差LMP：局部最大势LRT：似然比检验LSE：最小二乘估计LSI：线性时不变MAP：最大后验概率MLE：最大似然估计MMSE：最小均方误差估计MVU：最小方差无偏NP：Neyman-Pearson准则PRN：伪随机噪声RBLS：Rao-Blackwell-Lehmann-Scheffe定理ROC:接收机工作特性UMP：一致最大势WGN：白色高斯噪声WSS：广义平稳2011《信号检测与估计》复习参考题参数估计部分：1.基本概念理解：最小方差无偏估计，最佳线性无偏估计，最大似然估计，最小二乘估计，矩方法估计，最小均方误差估计，最大似然估计，线性最小均方误差估计，一般（经典）线性模型和贝叶斯线性模型。

第三章信号检测的基本理论

j 0 i 0
1
1

R0

R1
C 00 P ( H 0 ) C 01 P ( H 1 )
固定平均代价
R0
P x | H 0 dx C10 P ( H 0 ) P x | H 0 dx
R1
P x | H 1 dx C11 P ( H 1 ) P x | H 1 dx
H1： x A n +A、-A均为确定信号，n为随机信号，因此x也为随机信号，仅仅是均值发生偏移，即有：
x H ~ A， x H ~ A，
0 2 n 1 2 n
5/83
第三章
信号检测的基本理论 3.2 假设检测的基本概念
P(n)
主讲:刘颖 2009年秋
H 0 或H 1
概率转移机构
观测空间R 基本检测理论模型
判决准则
H 0或H 1
观测空间R：在信源不同输出下，观测空间R是由概率转移机构所形成的可能观测的集合。观测量可以是一维的，也可以是N 维矢量。
8/83
主讲:刘颖 2009年秋
信源
H0或H1
概率转移机构
观测空间R 基本检测理论模型
3.2.2 统计检测的结果和判决概率
信号统计检测就是统计学中的假设检验。
给信号的每种可能状态一个假设 Hj(j=0,1,2,…,M)，检验就是信号检测系统对信号属于哪个状态的统计判决。一维观测信号是N维观测矢量信号的特例，因此下面按N维观测矢量信号来讨论信号的统计检测问题，也就是假设检验结果和判决概率问题。
12/83
第三章
信号检测的基本理论 3.2 假设检测的基本概念
主讲:刘颖 2009年秋

信号检测与估计知识点总结（2）

信号检测与估计知识点总结（2）第三章估计理论1. 估计的分类矩估计：直接对观测样本的统计特征作出估计。

参数估计：对观测样本中的信号的未知参数作出估计。

待定参数可以是未知的确定量，也可以是随机量。

点估计：对待定参量只给出单个估计值。

区间估计：给出待定参数的可能取值范围及置信度。

(置信度、置信区间) 波形估计：根据观测样本对被噪声污染的信号波形进行估计。

预测、滤波、平滑三种基本方式。

已知分布的估计分布未知或不需要分布的估计。

估计方法取决于采用的估计准则。

2. 估计器的性能评价无偏性：估计的统计均值等于真值。

渐进无偏性：随着样本量的增大估计值收敛于真值。

有效性：最小方差与实际估计方差的比值。

有效估计：最小方差无偏估计。

达到方差下限。

渐进有效估计：样本量趋近于无穷大时方差趋近于最小方差的无偏估计。

? 一致性：随着样本量的增大依概率收敛于真值。

Cramer-Rao 界：其中为Fisher 信息量。

3. 最小均方误差准则模型：假定：是观测样本，它包含了有用信号及干扰信号，其中是待估计的信号随机参数。

根据观测样本对待测参数作出估计。

最小均方误差准则：估计的误差平方在统计平均的意义上是最小的。

即使达到最小值。

此时从而得到的最小均方误差估计为：即最小均方误差准则应是观测样本Y 一定前提下的条件均值。

需借助于条)()(1αα-≥F V =????????-=2212122);,(ln );,(ln )(αααααm m y y y p E y y y p E F )(),()(t n t s t y +=θ)(t n T N ),,,(21θθθθ=),(θts {}{})?()?()?,(2θθθθθθ--=T E e E {}0)?,(?2==MSE e E d d θθθθθθθθθd Y f Y MSE )|()(??=件概率密度求解，是无偏估计。

4. 线性最小均方误差准则线性最小均方误差准则：限定参数估计结果与观测样本间满足线性关系。

《信号检测与估计》复习纲要与复习题参考答案-2012

否
ML（4）
多元假设检验的最佳贝叶斯方法
*注：
ARMA：自回归滑动平均 BLUE：最佳线性无偏估计 CFAR：恒虚警率 CRLB ：Cramer-Rao 下限 EM：数学期望最大化 GLRT：广义似然比检验 IID：独立同分布 LLR：对数似然比 LMMSE：线性最小均方误差 LMP：局部最大势 LRT：似然比检验 LSE：最小二乘估计 LSI：线性时不变 MAP：最大后验概率 MLE：最大似然估计 MMSE：最小均方误差估计 MVU：最小方差无偏 NP：Neyman-Pearson 准则 PRN：伪随机噪声 RBLS：Rao-Blackwell-Lehmann-Scheffe 定理 ROC:接收机工作特性 UMP：一致最大势 WGN：白色高斯噪声 WSS：广义平稳
ˆ2 1 N 1 2 x [ n] N n 0
ˆ 2 的方差，并考察当 N 时会发生什么情况？这是无偏估计吗？求
3. 如果观测到数据 x[n] A w[n], n 0,1,, N 1 ，其中噪声数据
w [w[0], w[1],, w[ N 1]]T N (0, C) ，求 A 的 CRLB。有效估计量存在吗？如果
N
充分统计量为
N 1 x[n]cos 2 f 0 n n 0 T ( X ) N 1 x[n]2 n 0
由（1）已经知道 A
x[n]cos 2 f n
n 0 N 1 n0 0
N 1
cos
2
2 f 0 n
并且，
N 1 N 1 2 E ( x[n]2 ) E A cos 2 f 0 n w[n] n 0 n 0
S T C 1 X 1 S T C 1S N

信号检测与估计理论-第四章-信号波形检测

6. 充分统计量的分析方法
利用充分统计量 x1构造似然比检验 x1 是高斯随机变量，有
返回
一般二元信号波形的检测
1. 信号模型
2. 判决表示式
用正交级数展开系数表示接收信号：
一般二元信号波形的检测
2. 判决表示式
取展开系数的前N项
一般二元信号波形的检测
2. 判决表示式
一般二元信号波形的检测
3. 检测系统的结构
图4.15 判决域划分示意图
一般二元信号波形的检测
7. 二元信号波形检测归纳
（3）分界线：直线的斜率：原信号差矢量的斜率：
有：判决域分界线是垂直于信号间连线的直线！
一般二元信号波形的检测
7. 二元信号波形检测归纳
（4）若二元信号假设的先验概率相等，采用最小平均错误概率准则，则判决域分界线满足：
输出功率信噪比
利用Schwarz不等式，满足式（4.2.12）
，等号成立。
匹配滤波器的设计
令
由
有当式（4.2.16）中的等号成立。
匹配滤波器的设计
噪声为有色噪声时，广义滤波器：
当滤波器输入为白噪声时，
，
有
匹配滤波器的主要特点
1. 匹配滤波器的脉冲响应与时刻的选择
图4.4 匹配滤波器的脉冲响应特性
简单二元信号的波形检测
4. 检测性能分析
检验统计量
在假设H0或假设H1下，都是高斯随机变量。
通过分析两种假设下的均值和方差，计算判决概率，
并据此分析检测性能。
可以得到，
，
，
简单二元信号的波形检测
偏移系数：
简单二元信号的波形检测
5. 最佳信号波形设计
在高斯白噪声条件下，简单二元确知信号波形的检测性能由偏移系数d2决定，d2取决于信号的能量Es，与信号波形无关。

信号检测与估计理论统计检测理论PPT

率都是最大得,称为一致最大势检验。
4、 M元参量信号得统计检测
参量信号得统计检测
图3、17 m为正值时得判决域图3、18 m为负值时得判决域图3、19 双边检验得判决域
信号得序列检测
信号序列检测得基本概念
若观测到k次还不能作出满意得判决, 则先不作判决,继续进行第k+1次判决。在给定得检测性能指标要求下, 平均检测时间最短。
信号得序列检测
信号序列检测得基本概念
信号得序列检测
信号序列检测得基本概念
满足判决假设H1成立。满足判决假设H0成立。
若
则需要进行下一次观测后,根据 xN 1再进行检验。
信号得序列检测
信号得序列检测
信号序列检测得平均观测次数
若序列检测到第 N 次观测终止,即满足
或者
(判决假设H1成立) (判决假设H0成立)
派生贝叶斯准则
极小化极大准则
先验概率未知,使极大可能代价极小化
由于先验概率未知,在无法选择最优解得情况下,设计算法, 选择不是“最坏”得结果！
若 c10 c00 c01 c11 ,极小化极大准则与等先验概率结果相同。
派生贝叶斯准则
极小化极大准则
例题 3、4、2
派生贝叶斯准则
奈曼-皮尔逊准则(N-P准则)
统计检测理论得基本概念
统计检测得结果和判决概率
1、二元信号得情况——例3、2、1
x0 P(H0 | H0 )
x0 P(H1 | H1)
统计检测理论得基本概念
统计检测得结果和判决概率
2、 M元信号得情况
P(H i | H j ) Ri p(x | H j )dx
i, j 0,1,..., M 1

信号检测与估计理论(2)

第2章基础知识 2.2 离散随机信号的统计特性描述－高斯离随信矢量
2.2.7 高斯离散随机信号矢量的统计特性
1. 定义
设 N 维离散随机信号矢量 x ( x1
x2 xN )T，
对于任意 N 维非零常值矢量 a (a1 a2 aN )T，当且仅当满足
a x ak xk
T k 1
2 设高斯离散随机信号 x1 ~ N( x1 , x )，x2 ~ N( x2 , x2 )。 1 2
若 x1 x2 , 请在同一个坐标上分别画出：
2 2 x x 时，p( x1 ) 和 p( x2 ) 的图形；
1 2
2 2 x x 时，p( x1 ) 和 p( x2 ) 的图形。
(2.2.4) (2.2.5)
x 的方差
2 2 x E x x 2 x x p( x)dx

(2.2.6)
(2.2.7)
并有关系式
x2 x2 x2
统计平均量是离散随机信号主要统计特性的描述。
第2章基础知识
2.2 离散随机信号的统计特性描述－常用离随信号
k
2 1 N （xk x） p( x ) (2.2.27) 2 2 2 exp k 1 2 x x (5) 高斯离散随机信号矢量 x 的线性变换，仍然是高斯离散随机信号矢量。设N维高斯离散随机信号矢量 x ~ N( μ x ,C x )，对于
12
第2章基础知识
2.2 离散随机信号的统计特性描述－高斯离随信号
高斯离散随机信号的概率密度函数如图 2.2.5所示。
p( x)
o
x
( x 0)

信号测试技术复习题资料

一、是非题（对的打√，错的打×）（每题2分，共20分）1.分析周期信号的频谱的工具是傅立叶级数。

( T )2.所有周期信号都是功率信号。

(√)3.电阻应变式传感器只用于测定结构的应力或应变。

（×）4.瞬态信号的频谱一定是连续的。

( T )5.凡频谱是离散的信号必然是周期信号。

( F )6.信号x(t)=sin(2t+1)+cos(t/3)是瞬态信号。

（ F ）7.频响函数反映了系统响应的稳态过程。

（√）8.已知信号x(t)与信号y(t)完全不相关，则该二信号的互相关系数满足ρxy(τ)=1( F )9.一阶系统的时间常数τ越小越好。

( T )10.单自由度系统的刚度越大，其固有频率就越低。

( F )11.具有质量为M，刚度为K的振动体的固有频率为 0=MK。

( F )12.传感器与被测量的对应程度可用其灵敏度表示（ T ）。

13.对传感器进行动态标定的主要目的是检测传感器的动态性能指标（ T ）。

14.系统的不失真测试条件要求测试系统的幅频特性和相频特性均保持恒定。

( F )15.稳态响应法不能用于一阶系统的动态特性测试。

（×）16.直流信号具有无限的频谱。

（×）17.表示测量装置的静态输入与输出之间关系的实验曲线称为幅频曲线。

（ F ）18.电桥测量电路的作用是把传感器的参数变化转为电荷的输出。

（ F ）19.一选频装置，其幅频特性在f1～f2区间急剧衰减(f2>f1)，在0～f1和f2～∞之间近乎平直，这叫低通滤波器。

（ F ）20.半桥联接中要求两个桥臂阻值变化大小相等，极性相反。

（√）21.电桥电路是一个很好的幅度调制器。

( T )22.从信号运算的角度看，调幅过程就是将调制信号与载波信号相乘。

( T )23.相敏检波是一种能鉴别信号的相位和极性却无放大能力的检波电路。

( T )24.压电式传感器不一定要配接前置放大器。

（×）25.电荷放大器使压电加速度计输出的电荷量得到放大，由此而得电荷放大器的名称。

第四章信号检测与估计理论(2)概要

ii
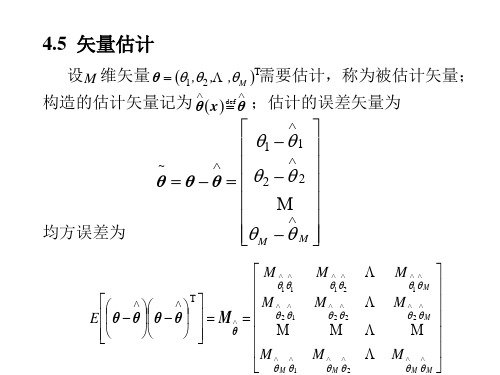
2. 随机矢量情况
如果被估计矢量是M维随机矢量，下面分析其性质。 a. 无偏性对于随机矢量，其估计量为满足下式，则为无偏估计量
(4.5.17)

则称为的无偏估计量。

估计量的误差矢量为
1 1 ~ θ θ θ 2 2 M M
矩阵J通常称为费希尔信息矩阵，它表示从观测数据中获得的信息。对所有的x和，当且仅当下式成立时， (4.5.14)式取等号成立，
(4.5.16)
(4.5.14)
如果对于M维非随机矢量的任意无偏估计矢量 ˆ ,(4.5.14)式中的等号均成立，中的每个参量
i
则这种估计称为联合有效估计。 ˆ的均方误差的下界，即克拉美－罗界。是

5.7.7 (4.7.7)
联立解这两个方程,求得a1和B1
将a1和B1代入(4.7.7)式,得
4.7.3 线性最小均方误差估计量的性质
性质1 性质2
θ lmse 是 x 的线性函数(又是最佳估计)。 θ lmse 是无偏估计量，即
E θ lmse μθ E θ
写成矩阵形式的观测方程为 x Hθ n
假定n是均值矢量为0，协方差矩阵为Cn的高斯随机矢量，其概率密度函数为
(4.6.3)
协方差矩阵为Cn E (n j nk ), 它是N N维的对称矩阵，其元素为 cn j nk E (n j nk )
4.6.2 高斯噪声中非随机矢量的最大似然估计
若被估计矢量 θ 为非随机矢量,则其最大似然估计量
θ ml , 是使似然函数 p x | θ 为最大的 θ 作为估计量。因

现代信号处理技术-4信号检测与估计理论(基础知识)

F(x)
0, x 0.
p(x)≥0,
p(x)dx
exdx
0
[ex ]0
1.
其均值和方差分别为
x
1
2 x
1
2
若 r.v X具有概率密度
p(x) e|x| 0
2 则称 X 服从参数为的双边带指数分布.
p(x)
ab
则称x服从区间[ a, b ]上的均匀分布，记作：
X ～ U(a, b)
分布函数为:
0,
F
( x)
x b
a a
,
1,
x a, a x b,
x b.
p(x)≥0,
b
p(x)dx
1
dx 1
a ba
若X~U [a, b], (x1, x2)为[a, b]的任意子区间，则
(iii) 若事件An F，n=1,2...,则 An F
则称F为事件域。
c. 对于随机事件A，如果满足如下三条，则称P（A）为定义在二元组上的概率（i）P( A) 0, 对一切A F；
(ii) P（）＝1；
(iii) 若事件Ai F, i 1, 2,...，且两两互不相容，则P（ Ai）= P(Ai)
4 信号检测与估计理论的基础知识
4.1 引言
x(t) s(t) n(t)
x(t) s(t, ) n(t), 0 t T [1, 2 , ... ,M ]T
信号不可预测，但是其统计特性都非常有规律，因此选择用概率论、数理统计、随机过程等工具来描述.
4.2 随机变量、随机矢量及其统计描述
p(x)
1
(x )2
e 2 2 , x
2
用求导的方法可以证明，

信号检测与估计理论

信号检测与估计理论介绍信号检测与估计理论是数字通信和统计信号处理中的一个重要领域。

它研究的是如何准确地检测到信号的存在以及对信号进行估计。

该理论在许多实际应用中具有重要意义，包括雷达系统、通信系统、生物医学信号处理等。

信号检测在信号检测中，我们的目标是从观测到的信号中确定是否存在某个特定的信号。

通常情况下，我们将信号检测问题建模为一个假设检验问题，其中有两个假设：零假设H0表示没有信号存在，备择假设H1表示信号存在。

在信号检测中，我们通过设计一个检测器来根据观测到的信号样本进行决策。

常用的检测器包括最大似然检测器、贝叶斯检测器等。

这些检测器利用观测到的信号样本的统计特性，通过最大化某个准则函数（如似然比）来做出决策。

信号估计信号估计是根据观测到的信号样本，估计出信号的参数或者信号本身的过程。

信号估计有多种方法，包括参数估计和非参数估计。

在参数估计中，我们假设信号遵循某个已知的参数化模型，并通过观测到的信号样本去估计这些参数。

常用的参数估计方法有极大似然估计、最小二乘估计等。

这些方法基于最优准则来选择最优参数估计。

非参数估计不需要对信号满足某个特定的参数化模型的假设，它们通常利用样本的统计特性来进行估计。

常用的非参数估计方法有最小二乘法、核方法等。

检测与估计的性能评价在信号检测与估计中，我们需要对检测与估计的性能进行评价。

通常情况下，我们使用概率误差、均方误差等作为评价指标。

在信号检测中，我们常用的评价指标有误报概率和漏报概率。

误报概率指当信号不存在时，检测器判定信号存在的概率；漏报概率指当信号存在时，检测器未能正确判定信号存在的概率。

在信号估计中，我们常用的评价指标有均方误差和偏差方差平衡等。

均方误差指估计值和真实值之间的平均平方误差；偏差方差平衡则是指在估计和真实值之间平衡偏差和方差。

应用领域信号检测与估计理论在许多领域都有广泛的应用。

其中，雷达系统是一个重要的应用领域。

在雷达系统中，我们需要通过检测和估计来实现目标检测、目标定位等功能。

第四章信号检测与估计理论(3)

d
t
xI 0T
2 T
xt
sin0
t
d
t
则整理得判决式
4.6.10a
4.6.10b
xt
1
2
exp
2
Es N0
xR cos
xIsin
d
exp
Es N0
H1
H0
进行变量代换,即令
4.6.11
l
x
2
R
x
2
I
1
2 ，l 0
arctg
xI xR
，
4.6.12a 4.6.12b
18
则有
xR lcos ，l 0 xI lsin ， l 0
；H1 ；H1
p xR
, xI
|
；H1
pl ,
|
；H1
pl
|
；H1
pl | H1
PHi | H1
Es 0 pl | H0
PHi | H0
33
根据xR和xI的定义：
xR 0T
2 T
xt
cos0t
dt
xI 0T
2 T
xt
sin0t
d
t
在假设H1下，x(t)是高斯随机变量，xR和xI都是高斯随机
p[(x(t)|Hj )
7
这样，似然比检验表示为下式，其中就不含随机参量了。
8
对于先验概率密度函数未知的情况，或先验概率密度函数未知的随机参量，通常采用参量的最大似然估计方法，求得参量的最大似然估计量
ˆjml，然后用该估计量代替信号的随机参量或未知
参量，构成广义似然比检验，完成对信号的检测。

信号检测与估计理论 (复习题解)

概率密度函数。
第2章信号检测与估计理论的基础知识内容提要
五. 线性时不变系统对平稳连续随机信号的响应
1. 输入平稳连续随机信号x(t),响应y(t)也是平稳的。
2. 响应y(t)均值 y H (0)x，自相关函数ry ( ) h( ) h( ) rx ( )，功率谱密度Py () | H () |2 Px ()。
第2章信号检测与估计理论的基础知识内容提要
三. 离散随机信号的函数
1. 一维雅可比变换,特别是简单线性函数时的变换。 2. N维雅可比变换。
四. 连续随机信号
1. 任意tk时刻采样所得样本x(tk ) (xk；tk )(k 1,2, , N )的概率密度函数描述。
2. 统计平均量：均值,均方值,方差,自相关函数,协方差函数及关系。
图2.1(a)
图2.1(b)
ab y
例2.2
设x ~
N(x
,
2 x
)。若y
2
x
b,
求p(
y)及
y和
2。
y
解：y
2x
b是线性变换,所以y
~
N(
y
,
2 y
)。
反函数 x ( y b) / 2, 雅可比 J d[(y b) / 2]/ dy 1/ 2。所以
p(
y)
1
2
2 x
1
2
exp
(
y
b) / 2
a x a 其他
(a 0)
如图2.1(a )所示。已知x的均值和方差分别为 x
0,
2 x
a2
/ 6。
设y x b,求p( y)及y的均值和方差；当a b 2a时,画出p( y)的函数

第二章信号检测与估计理论(2)

[
]
随机过程的平均统计量之间的关系随机过程的平均统计量之间的关系: 关系
2 ϕx (t ) = rx (t ,t )
σ2 (t ) = cx (t ,t ) x
cx (t j ,tk ) = rx (t j ,tk ) − µx (t j )µx (tk )
2 σ2 (t ) = ϕx (t ) - µ2 (t ) x x
rxy(t j ,tk ) = E x(t j ) y(tk )
[
]
随机过程的互协方差函数：随机过程的互协方差函数：互协方差函数随机过程 x(t)和 y(t) ，其互协方差函数为
cxy(t j ,tk ) = E ( x(t j ) - µx (t j ))( y(tk ) - µy (tk ))
2.3.5 随机过程的正交性、不相关性和统计独立性随机过程的正交性、正交性
设随机过程 x(t) 的任意不同时刻的随机变量为
x(tk ) ， k = 1,2,L N ,
1. 定义：定义： (1) 相互正交性
rx (t j ,tk ) = 0 ， j ≠k
j ≠k
(2) 互不相关性
cx (t j ,tk ) = 0 ，
随机过程用其概率密度函数进行统计描述。随机过程用其概率密度函数进行统计描述。
一维pdf：一维：
Fx ( x1 , t1 ) = P [ x(t1 ) ≤ x1 ]
∂Fx ( x1 , t1 ) Px ( x1 , t1 ) = ∂x1 Fx ( x1 , x2 ; t1 , t2 ) = P [ x(t1 ) ≤ x1 , x(t2 ) ≤ x2 ]
cx y (t j ,tk ) = rx y (t j ,tk ) − µx (t j )µy (tk )