6-4.2弯曲梁的剪应力计算及强度计算解析
弯曲应力及强计算

中性轴
正应力沿截面高度呈线性分布,
中性轴上为零,其最大值发生
在截面的上下边缘处。
横力弯曲正应力
横力弯曲时的正应力,用纯弯曲正应力公式计算 不会引起很大的误差,能够满足工程问题所需的 精度。
等直梁 max
Mmax所在横截面 离中性轴最远处
max
Mmax IZ
ymax
等直梁的最大弯曲正应力公式
8 hb 2
12MPa
6
【例2】一矩形截面的简支梁,梁上作用有均布荷载,已
知:l=4m,b=140mm,h=210mm,q=2kN/m,弯曲时木
材的容许正应力 10MPa ,试校核该梁的强度。
解:作梁的弯矩图
q
h
M max
ql 2 8
2 42 8
4kN.m
l
b
WZ
bh 2 6
z
横截面
(1)中性层是对整个截面而言的,中性轴是对某 个截面而言的。
(2)中性轴通过横截面的形心,是截面的 形心主惯性轴。
三、 弯曲正应力公式
My z
I z
M
M
中性轴
z
m
n
y
o
o
dA
z
mn
y
dx
MZ: 横截面上的弯矩
y: 所求应力点到中性轴的距离 M
M
IZ: 截面对中性轴的惯性矩
上式表面:弯曲横截面上的
M max W
M max h3
9
取 h=300mm 则:b=200mm
小结:
一、 弯曲正应力公式
梁的剪应力及其强度条件梁的弯曲应力与强度计算剪应力计算公式

8.1 梁弯曲时横截面上的正应力 8.2 弯曲正应力的强度条件 8.3 梁的剪应力及其强度条件 8.4 提高弯曲强度的措施
8.1 梁弯曲时横截面上的正应力
横截面上有弯矩又有剪力。 例如:AC和DB段。 称为横力弯曲(剪切弯曲)。 横截面上有弯矩没有剪力。 例如:CD段。 称为纯弯曲。
力 max 发生在弯矩最大的截面上,且离中性轴最远处。即
引用记号 则
max
M max ymax Iz
Wz
Iz ymax
max
M max Wz
Wz 称为弯曲截面模量。它与截面的几何形状有关,单位为m3。
8.2 弯曲正应力的强度条件
对于宽为 b ,高为 h 的矩形截面
Wz
Iz ymax
bh3 /12 h/2
A
A
M
E
Iz
式中1/ρ为梁弯曲后轴线的曲率。
EIz 称为梁的弯曲刚度。
8.1 梁弯曲时横截面上的正应力
E y
(b)
由上面两式,得纯弯曲时正应力的计算公式:
将弯矩 M 和坐标 y 按规定的正负代入,所得到的正应力若为 正,即为拉应力,若为负则为压应力。
一点的应力是拉应力或压应力,也可由弯曲变形直接判定。 以中性层为界,梁在凸出的一侧受拉,凹入的一侧受压。
8.1 梁弯曲时横截面上的正应力
E y
(b)
将式(b)代入式(d),得
M y
z dA 0
A
(d)
M z
y dA M
A
(e)
z dA E y z dA 0
A
A
A y z dA I yz 0
(自然满足)
y 轴为对称轴,必然有Iyz=0。
弯曲应力(剪应力6月9日)(1)

[1 12
16
283
16
28
(14
13)2 ]
[1 12
8 103
18 10
(19
13)2 ]
26200cm4
Wz
Iz ym a x
26200 (28 13)
1748cm3
(3)正应力校核
max
M Wz
1.2 105 1748 106
1.0 1.04 1.12 1.57 2.30
(四)切应力强度条件
max
(
FQ Sz,max
I z
)max
[
]
对于等宽度截面, m ax发生在中性轴上;对于宽度变化的截面,
m ax不一定发生在中性轴上。
在进行梁的强度计算时,需注意以下问题: (1)对于细长梁的弯曲变形,正应力的强度条件是主要的,剪应
S
* z
:y以外面积对中性轴的静矩
I z :整个截面对中性轴的惯性矩
b:y处的宽度
c
yc
y
z h
b
对于矩形:
S* z
A*
yc
b(h 2
y) [ y
h 2
2
y
]
b (h2 24
y2)
弯曲应力/弯曲时的剪应力
而
Iz
1 bh3 12
6FQ bh3
( h2 4
y2)
力的强度条件是次要的。但对于较粗短的梁,当集中力较大 时,截面上的剪力较大而弯矩较小,或是薄壁截面梁时,也 需要较核剪应力强度。
学习任务6 弯曲强度计算
例2 已知悬臂梁如图,l 1.5m ,P=32kN,梁由22a工字
钢制成,自重按 q 0.33kN / m ,材料的 160 MPa
140 MPa 校核粱强度。
q
p
A
B
z
l
例3 矩形截面松木梁如图,已知 q 3.6kN / m ,材料的
10MPa 2MPa l 4m
计算:1)若截面高宽比h/b=2,设计木梁尺寸b、h。 2)若木梁采用b=140mm,h=210mm的矩形截面,计算
z
Wz1
D13
32
max
1.33 m
4Q 3A
D1
As D12 a2 , a
4
R; (R D1 / 2)
a
z
Wz 2
bh2 6
(
R)3
6
1.18Wz1
a
max 1.5 m
当 D12
4
[D2
(0.8D)2 ]时, D 4
1.67 D1
Wz3
D3
32
(1 -
0.8
4
)
2.75Wz1
z
max 2 m
0.8D D
2a1
当 D12
4
2a12时, a1
2 D1 / 4
Wz 4
bh2 6
4a13 6
1.67Wz1
max 1.5 m
z a1
2a2 1.6a2
当 D12
4
2a22
0.81.6a22时, a2
1.05D1
z 0.8a2
a2
Wz5 4.57Wz1
max 2.3 m (= Q Af )
求最大应力并校核强度
max
梁的弯曲应力和强度计算
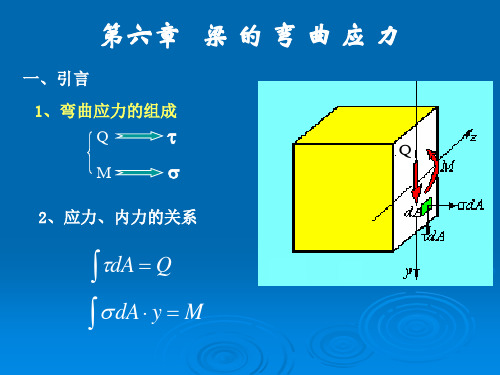
88
7.5 106 7.6 106
88 86.8MPa
弯曲正应力计算
三、计算题
27.一矩形截面简支梁,梁上荷载如图所示.已知P=6kN、 l=4m、b=0.1m、h=0.2m,试画出梁的剪力图和弯矩图并求 梁中的最大正应力. 解:(1) 作剪力图、弯矩图
(2)求最大正应力
Mmax 6kN m
横向线:仍为直线,仍与纵向线正交,相对转动了一个角度 纵向线:曲线,下部伸长,上部缩短
(2)假设 平面假设:横截面在变形前为平面,变形后仍为平面,且仍
垂直于变形后梁的轴线,只是绕横截面上某个轴 旋转了一个角度。 单向受力假设:梁由无数根纵向纤维组成,之间无横向挤压,
只受轴向拉伸与压缩。
中性层
3、正应力计算公式 〖1〗几何变形关系
内容回顾
弯曲正应力 1. 基本假设:
(1)平面假设:变形前为平面的横截面,变形后仍为平面,但转动了一角度。 (2)单向受力假设:杆件的纵截面(与杆轴平行的截面)上无正应力。
2.中性轴Z:
中性层与横截面的交线,平面弯曲时中性轴过形心且与对称轴垂直。
3.正应力计算公式:
中性层
4.正应力分布规律:沿截面高度呈线性分布。
4、正负号确定 1)M、y 符号代入公式
2)直接观察变形
5、适用范围及推广
〖1〗适用范围: 平面弯曲(平面假设、单向受力假设基础上)、 线弹性材料
〖2〗推广: ① 至少有一个对称轴的截面; ② 细长梁 (l/h>5);
6、最大正应力
工程上关心的是极值应力:
只与截面形状、尺寸有关
抗弯截面模量
对剪切(横力)弯曲: 矩形:
解:(1)作弯矩图,
求最大弯矩
六弯曲应力专业知识

= 0.045m
2.计算截面对中性轴旳惯性矩
I1z
=
(0.120m)(0.020m3 ) 12
+ (0.120×0.020m2 )(0.045m
- 0.010m)2
=
3.02×10-6 m4
I2z
=
(0.020m)(0.120m3 ) 12
+ (0.120×0.020m2 )(0.080m - 0.045m)2
3、推论
梁在弯曲变形时, 接近凹边旳纵向纤维 缩短,接近凸边旳纤 维伸长,根据变形旳 连续性,其中必有一 层纵向纤维既不伸长 也不缩短,即保持原来 旳长度,这一纵向纤 维层称为中性层。
中性层与横截面旳交线称为中性轴。
4、几何分析
ρ :变形后中性层旳曲率半径。
4、几何分析 ρ :变形后中性层旳曲率半径。
例:图示钢制矩形截面简支梁,已知:P =6kN,
截面宽度 b =30mm,高度 h =60 mm,试求梁竖放
和横放时梁内最大正应力,并分别画出应力沿截面
高度旳分布图。
RA
解:求支承反力,作弯矩图;
M
RA
RB
P 2
3kN
Mmax 900N m
竖放时:
max
M max W
M max bh2 / 6
Iz = I1z + I2z = 3.02×10-6 m4 + 5.82×10-6 m4 = 8.84×10-6 m4
3.计算最大弯曲正应力
截面B-B旳弯矩大小为:
M B = F ×0.400m = (15×103 N)(0.400m) = 6000N • m
在截面B旳上下边沿处,分别作用有最大拉应力与最大压应力
第6章梁的应力分析与强度计算

第6章梁的应力分析与强度计算梁是一种常见的结构构件,在建筑、桥梁、机械等领域都有广泛的运用。
在使用梁时,需要对其进行应力分析与强度计算,以确保其安全运行。
本章将介绍梁的应力分析与强度计算的基本原理和方法。
1.梁的应力分析梁的应力分析是指对梁内部各点的应力状态进行分析。
应力是指单位截面上受力的大小,常用的应力有轴力、弯矩和剪力。
对于梁的应力分析,主要有两个基本的方程:平衡方程和应变-位移关系。
1.1平衡方程平衡方程是指在梁内力平衡的条件下,梁内部各点的受力平衡。
对于梁来说,平衡方程可以表示为:∑Fx=0∑Fy=0∑M=0其中,∑Fx和∑Fy分别表示横截面上各点受力在X和Y方向的合力,∑M表示横截面上各点受力对横截面上其中一点产生的力矩。
通过求解平衡方程可以得到梁内力的分布情况。
1.2应变-位移关系应变-位移关系是指梁内部各点的应变与位移之间的关系。
梁的应变可以分为轴向应变、横向应变和剪应变三种,位移则可以分为平移位移和旋转位移。
应变-位移关系可以表示为:εx = du/dxεy = dv/dyγxy = (dudv + dvdx)/2其中,εx和εy分别表示横截面上各点的轴向应变,γxy表示横截面上各点的剪应变,du和dv分别表示横截面上各点的位移在X和Y方向上的微分。
2.梁的强度计算梁的强度计算是指根据应力分析的结果,对梁的强度进行评估。
梁的强度主要包括弯曲强度、剪切强度和扭转强度。
2.1弯曲强度弯曲强度是指梁在受到弯矩作用时的抗弯承载能力。
根据弯曲的理论,可以得到梁的最大正应力和最大剪应力。
对于矩形截面的梁来说,最大正应力和最大剪应力可以分别表示为:σmax = M * y / Iτmax = T * Q / It其中,M表示弯矩,y表示梁离中性轴的距离,I表示梁的惯性矩,T表示剪力,Q表示横截面的剪力传递量,It表示横截面的扭转惯性矩。
2.2剪切强度剪切强度是指梁在受到剪力作用时的抗剪承载能力。
6-4.2弯曲梁的剪应力计算及强度计算

要求梁内的最大弯曲正应力σmax不超过材料在 单向受力时的许用应力[σ]
利用上述强度条件,可以对梁进行三方面的计算: 正应力强度校核、截面选择和确定容许荷载。
2、 弯曲剪应力强度条件
最大弯曲剪应力作用点处于纯剪切状态, 相应的强度条件为:
FQ S z m ax m ax I zb m ax
细长等值梁
Hale Waihona Puke L 5 h max 10 max
二、 梁的强度条件
为了保证梁的安全工作,梁最大应力不能超出一 定的限度,也即,梁必须要同时满足正应力强度 条件和剪应力强度条件。
1、 弯曲正应力强度条件
弯曲正应力强度条件为:
max
M W z max
C
3m 3m
解:该梁C截面的弯矩最大,
F=20kN B C 3m 3m
Mmax=10×3=30kN.m
⑴矩形截面:
A
1 3 bh bh 2 Wz 12 32.67 10 4 mm 3 1 6 h 2
max
M max 30 103 91.8MPa 5 Wz 32.67 10
⑵圆形截面
A
d2
4
bh
d = 133.5mm
Wz 64 d 2
d4
d3
32
23.36 103 mm 3
max
M max 30 103 128.4MPa 6 Wz 23.36 10
⑶ 工字形截面。
选用50C号工字钢,其截面面积为139000mm2。
SZ (20mm 120 mm 35mm) 8.40 10 4 mm3
梁的弯曲计算—弯曲切应力及强度计算(工程力学课件)

(3)几种特殊情况下必须进行梁的切应力强度计算。
短粗梁 自行焊接 木梁
梁的合理截面
max
M max Wz
(1) 将材料配置于离中性轴较远处
(2) 采用不对称于中性轴的截面
脆性材料
(3) 采用变截面梁
弯曲切应力及强度计算
弯曲
(内力图)
外力 —— 内力 —— 应力
弯曲变形 的条件
求约束反力
弯矩M 剪力Fs
My
Iz
Fs
S
* z
bI z
梁横截面上的切应力 矩形截面梁
S
* z
bI z
x
σ 分布规律 τ 分布规律
Fs
S
* z
不同形状截面梁的最大剪应力
bI z
矩形截面梁
B
A
C
A
C
B
max l max h
梁内的主要应力是正应力!
危险截面、危险点
E右到B左
z
y
危险点
危险截面 24
D右 28
24
My
Iz
Fs
S
* z
bI z
危险截面上的危险点
max ≤[ ]
max ≤[ ]
正应力强度条件 切应力强度条件
三类计算:①强度校核、②截面设计、③确定许用荷载
(1)在进行梁的强度计算时,必须同时满足正应力 和切应力两种强度条件。
“等强度梁”
Wz (x)
M ( x)
[ ]
工字形截面梁
max
3 2
Fs A
max
工程力学弯曲强度2(应力分析与强度计算

max
y
2
当中性轴是横截面的对称轴时:
IZ
max
IZ
y
y1 y2 y max
1
即对称截 面梁
max max max
y
Iz 简单截面的抗弯截面系数 Wz= ymax y
h z
y z
bh Iz bh 2 Wz= 12 h h 6 2 2
3
max - max -
i max
M z max max i = Wz i
一般非等直梁
M z x y x max = max x = I z x max
可利用函数求导的方法得到最大正应力数值
固定端处梁截面上的弯矩: M=Me 。 且这一梁的所有横截面上的弯矩都 等于外加力偶的力偶矩Me
中性轴通过 截面形心,因此z 轴就是中性轴。 据弯矩方向可知中性 轴以上均受压应力,以下 均受拉应力。 根据正应力公式,横截面上正应力沿截面高度(y) 按直线分布,在上、下边缘正应力最大。可画出固定 端截面上的正应力分布图。
M max y 2 0.253N m 10 3 15 10 3 m 2 0.842 10 3 Pa 84.2MPa Iz 4.5 10 -8 m 4
例题
C
FRA FRB
T形截面简支梁在中点承受集中力 FP =32kN, l=2m。 T形截面的形心坐标yC=96.4mm,横截面对于z 轴的惯性矩Iz =1.02108 mm4。求:弯矩最大截面上的 最大拉应力和最大压应力。 解: 根据静力学平衡可求得支座A和B处的约束力分别 为FRA=FRB=16 kN。据内力分析,知梁中点截面 上弯矩最大
梁的应力及强度计算

Q图
-
2KN
y2=32.8mm由弯矩图可知上部受拉,下部受压
最大拉应力在上边缘
1KNm
s l max
M maxy1 IZ
1106 15.2 25.6 104
59.4MPa 拉
M图
最大压应力在下边缘
s ymax
M maxy2 IZ
1106 32.8 25.6 104
128.1MPa压
23
9 104
:3
144 104
:
4
3
642
2
104
3 72 : 3 144 : 3 64
结论:矩形截面最省料;圆形截面用料最多。
Z
Z
习题8-44
2、横截面上:在与中性轴平行的一条直线上的各点应力相 等。
3、截面上与中性轴距离最远的点应力最大。
横截面上正应力的画法:
M 0
M 0
M
M
smax
smax
第九章 梁的应力及强度计算
公式适用范围: ①弹性范围—正应力小于比例极限; ②精确适用于纯弯曲梁; ③对于横力弯曲的细长梁(跨度与截面高度比L/h>5),上述公 式的误差不大。
20kNm
20kNm
-
-
50 2003 50 200 94.6 1502
12 102106 mm4
+
20kNm
10kN/m
CA 2m
40kN
D 2m 2m
10kN/m
BE 2m
Q图
20kN
20kN
+
+
-
20kN
(完整版)梁横截面上的剪应力及其强度计算

梁横截面上的剪应力及其强度计算在一般情况下,剪应力是影响梁的次要因素。
在弯曲应力满足的前提下,剪应力一般都满足要求。
一、矩形截面梁的剪应力 利用静力平衡条件可得到剪应力的大小为:*z Z QS I b τ=; 公式中:Q ——为横截面上的剪力;*z S ——为横截面上所求剪应力处的水平线以下(或以上)部分面积A*对中性轴的静矩;I Z ——为横截面对中性轴的惯性矩;b ——矩形截面宽度。
计算时Q 、*z S 均为绝对值代入公式。
当横截面给定时,Q 、I Z 、b 均为确定值,只有静矩*z S 随剪应力计算点在横截面上的位置而变化。
222**2214()[()]()(1)222248z h h h h bh y S A y b y y y y h =⨯=-⨯+-=-=- 把上式及312z bh I =代入*z Z QS I bτ=中得到:2234(1)2Q y bh h τ=- 可见,剪应力的大小沿着横截面的高度按二次抛物线规律分布的。
在截面上、下边缘处(y=±0.5h ),剪应力为零;在中性轴处(y=0)处,剪应力最大,其值为:33 1.522Q Q Q bh A A τ=⨯=⨯= 由此可见,矩形截面梁横截面上的最大剪应力值为平均剪应力值的1.5倍,发生在中性轴上。
二、工字形截面梁的剪应力在腹板上距离中性轴任一点K 处剪应力为:*1z Z QS I b τ=; 公式中:b 1——腹板的宽度(材料表中工字钢腹板厚度使用字母d 标注的);*z S ——为横截面上阴影部分面积A*对中性轴的静矩;工字形截面梁的最大剪应力发生在截面的中性轴处,其值为:*max max1z Z QS I b τ=; 公式中:*max z S ——为半个截面(包括翼缘部分)对中性轴的静矩。
三、梁的剪应力强度计算梁的剪应力强度条件为:*max max max max *[](/)z Z Z Z Q S Q I b b I S ττ==≤。
第九章第六节梁弯曲时的应力及强度计算(上课用)

m n
变形后变成弧线,且凹边纤维缩 短、凸边纤维伸长。
2、变形前垂直于纵向线的横向
m
n
线,变形后仍为直线,且仍与弯曲 了的纵向线正交,但两条横向线 间相对转动了一个角度。
所以,可作出如下 假设和推断:
1、平面假设:
2.单向受力假设: 各纵向纤维之间互不挤压,纵向纤维均处于单向受拉或受压的状态。 因此梁横截面上只有正应力σ而无剪应力τ
b 0
1 h FL 2 3 3 1.65MPa bh 12 1 h FL M B yc 2 2 c bh 3 IZ 12
1 M B FL 2
bh3 IZ 12
2.47MPa
(压)
例2:图示T形截面简支梁在中点承受集中力F=32kN,梁的长度L=2m。yc
=96.4mm,横截面对于z轴的惯性矩Iz=1.02×108mm4。求弯矩最大截面上的 最大拉应力和最大压应力。 y
P1
1 2 3 4 5 x m
P2
q x
m
m
3 1 3
1
3
2
3
x x
1
3
1 3 1 3 1
3 1 3 1
x
4
x x
m
5
1
§9-5
二向应力状态下的强度条件——强度理论
各种材料因强度不足而引起的失效现象是不同的。塑料材料, 如普通碳钢,以发生屈服现象、出现塑性变形为失效的标志。 脆性材料,如铸铁,失效现象是突然断裂。在单向受力情况下, 出现塑性变形时的屈服极限σs和发生断裂时的强度极限σb,可 由实验测定。σS和σb可统称为失效应力。失效应力除以安全 因数,便得到许用应力[σ],于是建立强度条件 可见,在单向应力状态下,失效状态或强度条件以实验为基础 是容易建立的。因为一方面构件内的应力状态比较简单,另一 方面要用σ≤[σ]接近这类构件受力情况的试验装置求失效应力值 比较容易实现。
(完整版)梁横截面上的剪应力及其强度计算

梁横截面上的剪应力及其强度计算在一般情况下,剪应力是影响梁的次要因素。
在弯曲应力满足的 前提下,剪应力一般都满足要求一、矩形截面梁的剪应力利用静力平衡条件可得到剪应力的大小为:公式中:Q ――为横截面上的剪力;S ;――为横截面上所求剪应力处的水平线以下(或以上)部分面积A*对中性轴的静矩;I Z ――为横截面对中性轴的惯性矩;b ――矩形截面宽度。
计算时Q S ;均为绝对值代入公式。
当横截面给定时,Q l z 、b 均为确定值,只有静矩S ;随剪应力计算点在横截面上的位置而变化* *h1 h h h2 2bh 2 4y 2S ; A yb(- y) [y (- y)]-(-y )(1 2 )2 2 22 48h 把上式及I ;bh 3 代入虫 中得到:3Q(1 4^)12I Z b2bhh 2可见,剪应力的大小沿着横截面的高度按二次抛物线规律分布的。
在截面上、下边缘 处(y=± 0.5h ),剪应力为零;在中性轴处(y=0)处,剪应力最大,其值为:由此可见,矩形截面梁横截面上的最大剪应力值为平均剪应力值的1.5倍,发生在中性轴上。
二、工字形截面梁的剪应力在腹板上距离中性轴任一点K处剪应力为:公式中:b i――腹板的宽度(材料表中工字钢腹板厚度使用字母S z ――为横截面上阴影部分面积A对中性轴的静矩;公式中:S zmax ――为半个截面(包括翼缘部分)对中性轴的静矩。
Cb)图皐工字卑梁横苗面的应力计算图三、梁的剪应力强度计算梁的剪应力强度条件为:*QmaxSzmax Zmaxmax I z b b(l z/S;)[]d标注的);工字形截面梁的最大剪应力发生在截面的中性轴处,其值为:max* QS z max .;I Z b1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
要求梁内的最大弯曲正应力σmax不超过材料在 单向受力时的许用应力[σ]
利用上述强度条件,可以对梁进行三方面的计算: 正应力强度校核、截面选择和确定容许荷载。
2、 弯曲剪应力强度条件
最大弯曲剪应力作用点处于纯剪切状态, 相应的强度条件为:
FQ S z max I zb max
⑵圆形截面
A
d2
4
bh
d = 133.5mm
Wz 64 d 2
d4
d3
32
23.36 103 mm3
max
M max 30 103 128.4MPa 6 Wz 23.36 10
⑶ 工字形截面。
选用50C号工字钢,其截面面积为139000mm2。
Wz 2080 10 mm
3
3
max
结论如下:
M max 30 103 14.4MPa 6 Wz 2080 10
在承受相同荷载和截面面积相同时,工字梁所产生的最大拉应力最小。反 过来说,如果使三种截面所产生的最大拉应力相同时,工字梁所承受的荷载 最大。因此,工字形截面最为合理,矩形截面次之,圆形截面最差。
细长等值梁
L 5 h
max 10 max
二、 梁的强度条件
为了保证梁的安全工作,梁最大应力不能超出一 定的限度,也即,梁必须要同时满足正应力强度 条件和剪应力强度条件。
1、 弯曲正应力强度条件
弯曲正应力强度条件为:
max
M W z max
V max 1.5 1.5 A
工字形截面梁
d
h
h0
z
t
b
横截面上的切应力(95--97)%由腹板承担,而 翼缘仅承担了(3--5) %,且翼缘上的切应力情 况又比较复杂.为了满足实际工程中计算和设计 的需要仅分析腹板上的切应力。
(二)、工字形(T字型)截面梁的剪应力
V S I zd
C
3m 3m
解:该梁C截面的弯矩最大,
F=20kN B C 3m 3m
Mmax=10×3=30kN.m
⑴矩形截面:
A
1 3 bh 2 bh Wz 12 32.67 104 mm3 1 6 h 2
max
M max 30 103 91.8MPa 5 Wz 32.67 10
例题
矩形截面简支梁,加载于梁中点C,如图示。 求σmax , τmax 。
F
h
M max
FL 4
bh 2 WZ 6
l 2
l 2
Fs max
max
F 3 2 3 Fs 3 F 2 bh 2 A 4 bh
F 2
FL b M 3FL max max 4 2 1 2 WZ 2 bh bh 6 3 FL 2 2L max 2 bh 3 F h max 4 bh
Z
腹板上的剪应力沿腹板高度按抛物 线规律变化(翼板上的剪应力很小 )
最大剪应力发生在中性轴上,工字形截面翼缘上承担了绝大部分弯矩,腹板 上承担绝大部分剪力。
最大剪应力实用计算公式
腹板 面积
(三 )、圆截面梁的最大剪应力
近似均匀分布
max
4V 3A
最大剪应力发生在中性轴上
例 梁截面如图所示,横截面上剪力V=15KN。 试计算该截面的最大弯曲剪应力,以及腹板与 翼缘交接处的弯曲剪应力。截面的惯性矩 Iz=8.84×10-6m4。
一、梁的弯曲剪应力
(一)、矩形截面梁的弯曲剪应力
1.横截面上剪应力分布规律的假设 (1)横截面上各点处的剪应力方向与剪 力的方向一致(此处剪应力没规定正负 号); (2)横截面上至中性轴等距离各点的剪 应力相等,既沿截面宽度均匀分布。
V
2 .横截面上任一点处的剪应力计算公式(推导略)
V S
Z
SZ (20mm120mm 35mm) 8.40104 mm3
近似均匀分布
例 一简支梁及其所受荷载如图所示。若分别采用 截面面积相同的矩形截面,圆形截面和工字形截面, 试求以三种截面的最大拉应力。设矩形截面高为 140mm,宽为100mm,面积为14000mm2。
F=20kN A B
解: 1.最大弯曲剪应力。
最大弯曲剪应力发生 在中性轴上。中性轴 一侧的部分截面对中 性轴的静矩为:
Sz yc A
2 ( 20 mm 120 mm 45 mm ) 20mm S z , max 9.025 104 mm3 2
最大弯曲剪应力:
(2).腹板、翼缘交接处的弯曲剪应力
V——横截面上的剪力
Iz——整个横截面对中性轴的惯性矩
I zb
3V 4 y2 (1 2 ) 2bh h
b——需求剪应力处横截面的宽度 S*Z——横截面上需求剪应力处的水平线 以下(或以上)部分面积A*(如图 )对 中性轴的静矩 3 .剪应力分布规律 剪应力沿截面高度按二次抛物 线规律分布 。上下边缘处 剪应力为零,中性轴上剪应力 最大。 4 .最大剪应力
6-4.2梁的剪应 力及强度计算
湖北省工业建筑学校建筑工程建筑力学多媒体课件
任课 授课 授课 洪单平 12建筑工程 2013/3 教师 班级 时间 梁的弯曲应力(剪应力) 课 强度计算 课型 题 学 时 面授 2
教学 讲练结合 方法 教学 掌握梁弯曲时横截面剪应力分布规律;掌握剪应力的计 目的 算.掌握强度计算 教学 重点 剪应力分布规律;剪应力的计算.强度计算
教学 难点
横截面上剪应力的计算、强度计算。
问题的引出
荷载靠近支座,剪力如何?
短梁上剪力如何?
I z1 I z a A
2
前面我们学习了,梁弯曲时横截面 正应力分布规律及计算,在工程中,一 般正应力是梁破坏的主要因素。但是, 当梁的跨度很小或在支座附近有很大的 集中力作用,这时梁的最大弯矩比较小, 而剪力却很大,如果梁截面窄且高,这 时剪应力可达到相当大的数值,剪应力 就不能忽略了。
max
要求梁内的最大弯曲剪应力τmax不超过 材料在纯剪切时的许用剪应力[τ]
在一般细长的非薄壁截面梁中,最大弯曲正 应力远大于最大弯曲剪应力。
但是,对于薄壁截面梁与弯矩较小而剪力却较 大的梁,后者如短而粗的梁、集中荷载作用在支座 附近的梁等,则不仅应考虑弯曲正应力强度条件, 而且弯曲剪应力强度条件也可能起控制作用。 例6.4 图所示外伸梁,用铸铁制成,横截面为T字 形,并承受均布荷载q作用。试校该梁的强度。已 知荷载集度q=25N/mm,截面形心离底边与顶边的 距离分别为y1=95mm和y2=95mm,惯性矩Iz =8.84×力[σc]=140Mpa。
