简易逻辑导学案(带答案)
高中物理 2.11《简单的逻辑电路》导学案 新人教版选修

高中物理 2.11《简单的逻辑电路》导学案新人教版选修2、10 简单的逻辑电路1、初步了解简单的逻辑电路及表示符号。
2、通过实验,理解“与”“或”和“非”逻辑电路中结果与条件的逻辑关系。
3、知道真值表,会用真值表来表示一些简单的逻辑关系。
4、通过简单的逻辑电路的设计,体会逻辑电路在现实生活中的意义。
5、初步了解集成电路,关注我国集成电路的发展情况。
1、数字电路(1)数字信号:数字信号在变化中只有两个对立的状态:“①有”或者“②没有”。
(2)数字电路:处理数字信号的电路叫作数字电路,具有③逻辑功能的数字电路叫作逻辑电路。
2、“与”门 (1)门:所谓“门”,就是一种开关,在一定的条件下它允许信号通过,如果条件不满足,信号就被④阻止在“门”外。
(2)“与”门:如果一个事件的几个条件⑤都满足后,该事件才能发生,这种逻辑关系叫作“与”逻辑关系。
具有“与”逻辑关系的电路称为⑥“与”门电路。
简称⑦“与”门。
(3)“与”门的符号:⑧。
(4)真值表:记录用数字“1”和“0”表示的各种控制⑨条件和控制⑩结果的表格叫作真值表。
3、“或”门(1)“或”门:如果几个条件当中,只要有一个条件得到满足,该事件就会发生,这种关系叫作“或”逻辑关系;具有“或”逻辑关系的电路叫作“或”门。
(2)“或”门的符号:。
4、“非”门(1)“非”门:输出状态与输入状态相反的逻辑关系叫作“非”逻辑关系,具有“非”逻辑关系的电路叫作“非”门。
(2)“非”门的符号:。
主题1:“与”门电路阅读教材中“‘与’门”标题下的相关内容,回答下列问题。
(1)商品房楼道中的路灯什么条件下才会发光?此种“条件”与“结果”之间的关系是什么逻辑关系?(2)如果用数字“1”来表示声控、光控开关的接通,用数字“0”来表示声控、光控开关的断开,路灯接通定义为“1”,断开定义为“0”,试完成以下状态表和真值表:条件结果声控开关A光控开关B路灯L 输入输出ABY主题2:“或”门电路阅读教材中“‘或’门”标题下的内容,回答下列问题。
高中数学《简单的逻辑联结词》导学案 北师大版选修1-1

第5课时简单的逻辑联结词1.理解逻辑联结词“且”“或”“非”的含义.2.会判断含“且”“或”“非”的命题的真假及相关应用.歌德是18世纪德国的一位著名文艺大师,一天,他与一位文艺批评家“狭路相逢”.这位批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,一边高傲地往前走,一边大声说道:“我从来不给傻子让路!”面对如此尴尬局面,只见歌德笑容可掬,谦恭地闪在一旁,一边有礼貌地回答道:“呵呵,我可恰恰相反.”问题1: 歌德表达的意思是,对一个命题p的结论的否定 ,就得到一个新命题,记作,读作“非p”,即是“p的否定”.问题2: 常见的逻辑联结词有“或”“且”“非”.不含逻辑联结词的命题叫,含有逻辑联结词的命题叫.(1)用联结词“或”把命题p和命题q联结起来,就得到一个新命题“p或q”.(2)用联结词“且”把命题p和命题q联结起来,就得到一个新命题“p且q”.问题3: 命题的否定与否命题的区别(1)命题的否定是否定命题的,而命题的否命题是对原命题的和同时进行否定.(2)命题的否定的真假与原命题的真假总是的,即一真一假;而否命题的真假与原命题的真假无必然的联系.问题4: (1)复合命题是由简单命题与逻辑联结词构成的,简单命题的真假决定了复合命题的真假,(2)常见关键词及其否定形式附表如下:1.命题:“方程x2-1=0的解是x=±1”,其使用逻辑联结词的情况是().A.使用了逻辑联结词“且”B.使用了逻辑联结词“或”C.使用了逻辑联结词“非”D.没有使用逻辑联结词2.有下列命题:①2是偶数,又是素数;②10的倍数一定是5的倍数;③梯形不是矩形;④明天早餐吃面包或鸡蛋.其中可使用逻辑联结词的命题有( ).A.1个B.2个C.3个D.4个3.命题p:方向相同的两个向量共线,q:方向相反的两个向量共线,则命题“p或q”为.4.分别写出由下列各组命题构成的“p且q”“p或q”“p”形式的命题:(1)p:π是无理数,q:e是有理数;(2)p:三角形的外角等于与它不相邻的两个内角的和,q:三角形的外角大于与它不相邻的任一个内角.含有逻辑联结词命题的构成指出下列命题的形式及构成它的简单命题.(1)48是16与12的倍数.(2)方程x2+x+3=0没有实数根.(3)属于集合Q或属于集合R.判断含逻辑联结词命题的真假分别指出由下列各组命题构成的“p或q”“p且q”“p”形式的命题的真假.(1)p:3>3,q:3=3;(2)p:⌀⫋{0},q:0∈⌀;(3)p:A⊆A,q:A∩A=A;(4)p:函数x2+3x+4=0的图像与x轴有公共点,q:方程x2+3x-4=0没有实根.命题的否定写出下列命题的否定:(1)正方形的四条边都相等;(2)已知a,b∈N,若ab能被5整除,则a,b中至少有一个不能被5整除;(3)若x2-x-2≠0,则x=-1且x=2.指出下列命题的形式及构成它的简单命题.(1)方程x2+x+1=0没有实数根;(2)他是运动员,又是教练;(3)这些文学作品不仅艺术上有缺点,而且政治上有错误.已知命题p、q,试写出p或q、p且q、p形式的命题并判断真假.(1)p:平行四边形的一组对边平行,q:平行四边形的一组对边相等;(2)p:2∈{1,3,5,7},q:2∈{2,4,6,8};(3)p:1∈{1,2}, q:{1}⫋{1,2}.写出下列命题的否定和否命题,并判定其真假.(1)p:若x2+y2=0,则x,y全为零;(2)p:若x=3且y=5,则x+y=8.1.已知命题p:2+2=5,命题q:3>2,则下列判断正确的是( ).A.“p或q”为假,“q”为假B.“p或q”为真,“q”为假C.“p且q”为假,“p”为假D.“p且q”为真,“p或q”为假2.已知p:⌀⊆{0},q:{1}∈{1,2}.由它们构成的新命题“p且q”“p或q”“p”中,真命题有().A.1个B.2个C.3个D.0个3.命题“若a<b,则2a<2b”的否命题为,命题的否定为.4.分别指出由下列各组命题构成的“p或q”“p且q”形式的复合命题的真假.(1)p:在集合{x|0<x<2}中,q:在集合{x|x>1.5}中.(2)p:方程x2-3x-1=0有两正根,q:方程x2-3=0有两实数根.(3)p:集合{x|1<x<2}是集合{x|x>0}的子集,q:集合{x|1≤x<2}是集合{x|1<x<4}的子集.(2013年·湖北卷)在一次跳伞训练中,甲、乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为().A.(p)或(q)B.p或(q)C.(p)且(q)D.p或q考题变式(我来改编):第5课时简单的逻辑联结词知识体系梳理问题1:我会给傻子让路p问题2:简单命题复合命题问题3:(1)结论条件结论(2)相对立问题4:(1)真真假假假假基础学习交流1.B“x=±1”可以写成“x=1或x=-1”,故选B.2.C①中可用“且”,②中没,③中可用“ ,④中可用“或”,故选C.3.方向相同或相反的两个向量共线方向相同的两个向量共线或方向相反的两个向量共线,即“方向相同或相反的两个向量共线”.4.解:(1)“p且q”:π是无理数且e是有理数.“p或q”:π是无理数或e是有理数.“p”:π不是无理数.(2)“p且q”:三角形的外角等于与它不相邻的两个内角的和且大于与它不相邻的任一个内角.“p或q”:三角形的外角等于与它不相邻的两个内角的和或大于与它不相邻的任一个内角.“p”:三角形的外角不等于与它不相邻的两个内角的和.重点难点探究探究一:【解析】(1)这个命题是“p且q”的形式,其中p:48是16的倍数;q:48是12的倍数.(2)这个命题是“p”的形式,其中p:方程x2+x+3=0有实数根.(3)这个命题是“p或q”的形式,其中p: ∈Q,q:∈R.【小结】①在“p或q”“p且q”“p”中,p,q都是命题,但在“若p,则q”中,p,q 可以是命题,也可以是含有变量的陈述句.②正确理解逻辑联结词“或”“且”“非”是解题的关键,有些命题并不一定包含“或”“且”“非”这些逻辑联结词,要结合命题的具体含义进行命题构成的判定.探究二:【解析】(1)∵p假q真,∴“p或q”为真,“p且q”为假,“p”为真.(2)∵p真q假,∴“p或q”为真,“p且q”为假,“p”为假.(3)∵p真q真,∴“p或q”为真,“p且q”为真,“p”为假.(4)∵p假q假,∴“p或q”为假,“p且q”为假,“p”为真.【小结】为了正确判断复合命题的真假,首先要确定复合命题的构成形式,然后指出其中简单命题的真假,再根据有关结论判断这个复合命题的真假.探究三:【解析】(1)正方形的四条边都不相等.(2)已知a,b∈N,若ab不能被5整除,则a,b中至少有一个不能被5整除.(3)若x2-x-2≠0,则x≠-1且x≠2.[问题]上述解法中逻辑词的否定词用得正确吗?[结论]不正确.上面错解的主要原因是不能正确理解“p”的含义,错用逻辑词的否定词.一般地,写出否定,往往需要对正面叙述的词语进行否定.一个命题的否定不仅要否定结论,还要否定逻辑联结词.于是,正确解答如下:(1)正方形的四条边不都相等;(2)已知a,b∈N,若ab能被5整除,则a,b都能被5整除;(3)若x2-x-2≠0,则x≠-1或x≠2.【小结】p不是命题p的否命题,而是命题p的否定形式.对命题“若p则q”来说,命题的否定是“若p则非q”;命题的否命题是“若非p则非q”.思维拓展应用应用一:(1)这个命题是“p”的形式,其中p: 方程x2+x+1=0有实数根.(2)这个命题是“p且q”的形式,其中p:他是运动员;q:他是教练.(3)这个命题是“p且q”的形式,其中p:这些文学作品艺术上有缺点,q:这些文学作品政治上有错误.应用二:(1)p或q:平行四边形的一组对边平行或相等(真命题).p且q:平行四边形的一组对边平行且相等(真命题).p:平行四边形的一组对边不平行(假命题).(2)p或q:2∈{1,3,5,7}或2∈{2,4,6,8},即2∈{1,2,3,4,5,6,7,8}(真命题).p且q:2∈{1,3,5,7}且2∈{2,4,6,8}(假命题).p:2∉{1,3,5,7}(真命题).(3)p或q:1∈{1,2}或{1}⫋{1,2}(真命题).p且q:1∈{1,2}且{1}⫋{1,2}(真命题).p:1∉{1,2}(假命题).应用三:(1)p的否定:若x2+y2=0,则x,y不全为零(假命题);p的否命题:若x2+y2≠0,则x,y不全为零(真命题).(2)p的否定:若x=3且y=5,则x+y≠8(假命题);p的否命题:若x≠3或y≠5,则x+y≠8(假命题).基础智能检测1.B显然p假q真,故“p或q”为真,“p且q”为假,“p”为真,“q”为假,故选B.2.A容易判断命题p:⌀⊆{0}是真命题,命题q:{1}∈{1,2}是假命题,所以p且q是假命题,p或q是真命题,p是假命题,故选A.3.若a≥b,则2a≥2b若a<b,则2a≥2b命题“若a<b,则2a<2b”的否命题为“若a≥b,则2a≥2b”,命题的否定为“若a<b,则2a≥2b”.4.解:(1)因为p为真,而<1.5,q为假,所以p或q为真,p且q为假.(2)因为方程x2-3x-1=0中两根之积为负,所以p为假.又q为真,所以p或q为真,p且q为假.(3)因为p为真,而1∉{x|1<x<4},所以{x|1≤x<2}⊈{x|1<x<4},即q为假,所以p或q为真,p 且q为假.全新视角拓展A“至少有一位学员没有降落在指定范围”表示甲没有降落在指定范围或者乙没有降落在指定范围或者甲乙都没有降落在指定范围.又命题p是“甲降落在指定范围”,可知命题p是“甲没有降落在指定范围”;同理,命题q是“乙没有降落在指定范围”,所以“至少有一位学员没有降落在指定范围”可表示为(p)或(q).故选A.。
《简易逻辑()学案优秀教案

《简易逻辑》学案1.什么是命题________________。
命题的结构是“假设A则B〞其中A是题设,B是结论。
请举例。
2.举不是命题的例子:〔没有作出判断的如:不能判断真假的如:〕3.什么是真命题、假命题,请举例〔说明:“成立〞的命题称真命题;反之,称假命题。
成立的标志是什么呢?是指满足了它的题设,一定得到它所说的结果,得不到或者不一定得到〔有时得到,有时得不到〕,都谓之不成立。
例如,“锐角和钝角相等〞是假命题,“互补的两个角,是一个锐角一个钝角〞也是假命题。
所以,判定命题的真假时,是否满足“一定〞,是唯一标准,只要有一个反例,就是假命题。
请说明“SSA〞不能判断三角形全等的道理。
4.什么是假命题,请举例。
〔说明:假命题也是命题,要有“一分为二〞的思想〕5逻辑连接词有“或〞、“且〞、“非〞6什么是简单命题7什么是复合命题8常用的复合命题有:〔其中p、q是简单命题〕,请举例。
9.“非命题〞的真值表p 非p真假假真10.“且命题〞的真值表P q p且q真真真真假假假真假假假假11.“或命题〞的真值表P q p或q真真真真假真假真真假假假P 非p是不是= ≠≥<> ≤〔不大于〕∈∉⊂⊄A且A或B BA或A且B B都是不都是任意x……存在x……至少n个至多〔n-1〕个有无…………13.复合命题的非命题.写复合命题的“非命题〞时,假设原来命题是用“或〞字连接的复合命题,应把每个根本命题否认后再用“且〞字连接;假设原来命题是用“且〞字连接的复合命题,应把每个根本命题否认后,用“或〞字连接。
你知道为什么吗? 〔B A B A ⋃=⋂,B A B A ⋂=⋃〕14.四种命题原命题 〔假设A 则B 〕逆命题 〔假设B 则A 〕否命题 〔假设A 则B 〕逆否命题〔假设B 则A 〕 说明:原命题具有相对性。
“假设A 则B 〞并不是命中注定的原命题,以上四种命题中的任何一个都可以做原命题。
15.重要结论:〔1〕原命题真,它的逆命题不一定真。
简易逻辑教学案(老师篇)

简易逻辑〖课标要求〗了解命题的概念和命题的构成;掌握简单逻辑连接词“或”“且”“非”的含义;、能判断简单命题与复合命题的真假(由真值表判断复合命题的真假)、掌握四种命题的关系、掌握充要条件的判断、理解反证法的理论依据并且会用反证法证明数学命题一定需要注意〖知识梳理〗命题与逻辑连接词;1.用语言、符号或式子表达的,可以判断真假、的陈述句称为命题. 其中判断为真的语句称为真命题,判断为假的语句称为假命题 2.逻辑联结词“或”“且”“非”与集合中的并集、交集、补集有着密切的关系,解题时注意类比; 3.不含逻辑联结词的命题称为简单命题_;有时一个命题的叙述方式比较的简略,此时应先分清条件和结论,该写成“若p ,则q ”的形式; 4.含有逻辑联结词的命题称为__复合命题,复合命题有三种形式p 且q 、p 或q 、非p对一个命题p 的全盘否定, 就得到一个新的命题, 记作__⌝p _,读作非p __通常复合命题的否定“p 或q ”的否定为“p ⌝且q ⌝”、 “p 且q ”的否定为“p ⌝或q ⌝”、“全为”的否定是“不全为”、 “都是”的否定为“不都是”等等5.三种复合命题的真值表:(1)“p 且q ”: 一假即假(2)“p 或q ”: 一真即真(3)“非p ”: 真假相反6.短语“_对所有的”、“对任意一个” 逻辑中称为全称量词,并用符号“___∀__” 表示。
7.短语“存在一个”、“_至少有一个” 逻辑中称为存在量词,并用符号“∃” 表示。
8.含有全称量词的命题称为全称命题__;含有存在量词的命题称为__特称命题__.9.全称命题形式:,()x M p x ∀∈;特称命题形式:,()x M p x ∃∈。
其中M 为给定的集合,特别提醒:全称命题p :,()x M p x ∀∈的否定⌝p :,()x M p x ∃∈⌝;全称命题的否定为特称命题特称命题p :,()x M p x ∃∈的否定⌝p :,()x M p x ∀∈⌝;特称命题的否定为全称命题其中p(x)是一个关于x 的命题。
2020高考数学理科大一轮复习导学案:第一章 集合及简易逻辑1.2 Word版含解析

姓名,年级:时间:错误!错误!知识点一命题及四种命题1.命题的概念用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.2.四种命题及其关系(1)四种命题间的相互关系(2)四种命题的真假关系①两个命题互为逆否命题,它们有相同的真假性;②两个命题互为逆命题或互为否命题,它们的真假性没有关系.1.对于命题“单调函数不是周期函数",下列陈述正确的是( D )A.逆命题为“周期函数不是单调函数"B.否命题为“单调函数是周期函数”C.逆否命题为“周期函数是单调函数”D.以上三者都不正确解析:原命题可以改写为“若函数是单调函数,则函数不是周期函数”.其逆命题为“若函数不是周期函数,则函数是单调函数”,故选项A不正确;其否命题为“若函数不是单调函数,则函数是周期函数",故选项B不正确;其逆否命题为“若函数是周期函数,则函数不是单调函数”,故选项C不正确.2.“若a,b都是偶数,则ab是偶数"的逆否命题为若ab不是偶数,则a,b不都是偶数.解析:“a,b都是偶数”的否定为“a,b不都是偶数”,“ab是偶数”的否定为“ab不是偶数",故其逆否命题为“若ab不是偶数,则a,b不都是偶数”.3.在命题“若m>-n,则m2>n2”的逆命题、否命题、逆否命题中,假命题的个数是3。
解析:原命题为假命题,则逆否命题也为假命题,逆命题也是假命题,则否命题也是假命题.故假命题的个数为3。
知识点二充分条件与必要条件1.若p⇒q且q错误!p,则p是q的充分不必要条件,q是p的必要不充分条件;若p⇒q且q⇒p,则p是q的充分必要条件,q也是p的充分必要条件.2.若A、B为两个集合,满足A B,则A是B的充分不必要条件,B是A的必要不充分条件;若A=B,则A是B的充分必要条件.4.(2018·天津卷)设x∈R,则“|x-12|〈错误!"是“x3〈1”的( A )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解析:解法1:由|x-错误!|〈错误!,得0<x〈1,所以0<x3〈1;由x3<1,得x〈1,不能推出0<x〈1.所以“|x-错误!|<错误!”是“x3〈1”的充分而不必要条件.故选A.解法2:由|x-错误!|<错误!,得0<x<1,所以0〈x3〈1,所以充分性成立;取x=-错误!,则|-错误!-错误!|=错误!〉错误!,(-错误!)3=-164〈1,所以必要性不成立.故选A。
简易逻辑复习导学案 (1)

第一章常用逻辑用语(复习)学习目标1. 命题及其关系(1)了解命题的逆命题、否命题与逆否命题,会分析四种命题间的相互关系;(2)理解必要条件、充分条件与充要条件的意义.2. 简单的逻辑联结词了解逻辑联结词“或”“且”“非”的含义.3. 全称量词与存在量词(1) 理解全称量词与存在量词的意义;(2)能正确地对含有一个量词的命题进行否定.学习过程一、课前准备复习2:1.什么是命题?其常见的形式是什么?什么是真命题?什么是假命题?2.有哪四种命题?他们之间的关系是怎样的?3.什么是充分条件、必要条件和充要条件?4你学过哪些逻辑联结词?四逻辑联结词联结而成的命题的真假性怎样?5.否命题与命题的否定有什么不同?6.什么是全称量词和存在量词?7.怎样否定含有一个量词的命题?二、新课导学典型例题例1 命题“若21x<,则11x-<<”的逆否命题是()A.若21x≥,则1x≥或1x≤- B.若11x-<<,则21x<C.若1x>或1x<-,则21x> D.若1x≥或1x≤-,则21x≥变式:命题“若1x ≥或1x ≤-,则21x ≥”的逆否命题是 .小结:弄清四种命题之间的关系是解决此类问题的关键.例2 下列各小题中,p 是q 的充要条件的是( ).(1)p :2m <-或6m >;q :23y x mx m =+++有两个不同的零点 (2)p :()1()f x f x -=;q :()y f x =是偶函数 (3)p :cos cos αβ=;q :tan tan αβ= (4)p :A B A = ;q :B ⊂AA.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)变式:设命题p :|43|1x -≤,命题q :2(21)(1)0x a x a a -+++≤,若p ⌝是q ⌝的必要不充分条件,求实数a 的取值范围.小结:处理充分、必要条件的问题首先要分清条件和结论,有时利用逆否命题与原命题等价的性对解题很有帮助.例3 给出下列命题:p :关于x 的不等式22(1)0x a x a --+>的解集是R ,q :函数2lg(2)x y a a =-是增函数. (1) 若p q ∨为真命题,求a 的取值范围. (2) 若p q ∧为真命题,求a 的取值范围.练一练:练1. 如果命题“p 且q ”与命题“p 或q ”都是假命题,那么 ( ) A.命题“非p ”与命题“非q ”的真值不同 B.命题p 与命题“非q ”的真值相同 C.命题q 与命题“非p ”的真值相同 D.命题“非p 且非q ”是真命题 练2. 若命题p 的逆命题是q ,命题p 的否命题是r ,则q 是r 的( ) A.逆命题 B.否命题 C.逆否命题 D.以上结论都不正确练 3.已知函数22()42(2)21f x x p x p p =----+在区间[1,1]-的所有的x ,都有()0f x ≤恒成立,求p 的取值范围.学习小结这节课你学到了一些什么?当堂检测:1. 下列语句不是命题的有( ).①230x -=;②与一条直线相交的两直线平行吗? ③315+=;④536x ->A.①③④B.①②③C.①②④D.②③④2. 给出命题:p :31>,q :4{2,3}∈,则在下列三个复合命题:“p 且q” “p 或q” “非p”中,真命题的个数为( ).A.0B.3C.2D.13. 若a b c 、、是常数,则“2040a b ac >-<且”是“对任意x R ∈,有20ax bx c ++>”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.即不充分也不必要条件4. 已知a ,b 是两个命题,如果a 是b 的充分条件,那么a ⌝是b ⌝的 条件.5. “tan tan αβ≠”的 条件是“αβ≠”6. 写出命题“若2780x x +-=,则8x =-或1x =”的逆命题、否命题、逆否命题,并分别判断它们的真假。
简单的推理题及答案.doc

简单的推理题及答案【篇一:小学简单推理题】、知识要点数学课上,老师布置了一道题:□+△=28□=△+△+△□=()△=()要得出正确的结论,就要进行分析、推理。
学会了推理,能使你变得更聪明,头脑更灵活。
数学上有许多重大的发现和疑难问题的解决都离不开推理。
解答这类推理题时,要求小朋友仔细观察,认真分析等式中几个图形之间的关系,寻找解题的突破口,然后再利用等量代换、消去等方法来进行解答。
二、精讲精练【例题1】下式中,□和△各代表几?□+△=28□=△+△+△□=()△=()练习1:1.☆+○=18☆=○+○☆=()○=()2.△+○=25△=○+○+○+○△=()○=()3.○+□=36 ○=+□□+□+□+□○(=)□=()【例题2】下式中,□和△各代表几?练习2:1.○和□各表示几?2.想想,填填。
3.□和○各代表几?【例题3】下式中,□和△各代表几?□+□+△=16 □+△+△=14□=()△=()练习3:1.□+□+○+○=38□+□+○=22 □(=)○=()2.□+□+□+△+△=52□+□+△+△+△=48□=()△=()3.○+△+□+□=10△+□+△+□=12△+○+□+○=12○=()□=()△=()【例题4】下式中,□和○各代表几?□+□+○+○+○=34○+○+○+○+□+□+□=48 □(=)○=()练习4:1.☆+☆+△+△+△=24 △+△+△+△+☆+☆+☆ =36 ☆=()△=()2.○+○+○+△+△=54 △+△+△+○+○+○+○=76 ○(=)△=()3.□+□+□+△+△+△+△=96 △+△+△+△+△+□+□+□+□=123□=()△=()【例题5】下式中,□、☆和△各代表几?☆+☆=□+□+□+□□+□=△+△+△+△☆+□+△+△=80☆=()□=()△=()【思路导航】因为2个☆等于3 个□,3 个□又等于 4 个△,所以 2个☆等于4 个△,那么1 个☆等于2 个△。
高中数学 第一章第26课时“简易逻辑”教师专用教案 新人教A版

第二十六教时“简易逻辑”习题课目的:通过习题的讲解与练习,努力达到熟练技巧。
过程:一、分别写出由下列各种命题构成的“p或q”“p且q”“非p”形式的复合命题: 1.p:李明是高中一年级学生q:李明是共青团员解:p或q:李明是高中一年级学生或是共青团员p且q:李明是高中一年级学生且是共青团员非p:李明不是高中一年级学生2.p:25>q:5是无理数解:p或q:5是大于2或是无理数p且q:5是大于2且是无理数非p:5不大于23.p:平行四边形对角线相等q:平行四边形对角线互相平分解:p或q:平行四边形对角线相等或互相平分p且q:平行四边形对角线相等且互相平分非p:平行四边形对角线不一定相等4.p:10是自然数q:10是偶数解:p或q:10是自然数或是偶数p且q:10是自然数且是偶数非p:10不是自然数二、分别指出下列复合命题的构成形式及构成它的简单命题:1.x=2或x=3是方程x2-5x+6=0的根解:p:x=2是方程x2-5x+6=0的根q:x=3是方程x2-5x+6=0的根是p或q的形式2.π既大于3又是无理数解:p:π大于3 q:π是无理数是p且q的形式 3.直角不等于90︒解:p:直角等于90︒是非p形式4.x+1≥x-3解:p:x+1>x-3 q:x+1=x-3 是p或q的形式5.垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧。
解:p:垂直于弦的直径平分这条弦q:垂直于弦的直径平分这条弦所对的两条弧是p且q的形式三、分别写出由下列各种命题构成的“p或q”“p且q”“非p”形式的复合命题,并判断它们的真假:1.p:末位数字是0的自然数能被5整除q:5∈{x|x2+3x-10=0}解:p或q:末位数字是0的自然数能被5整除或5∈{x|x2+3x-10=0}p且q:末位数字是0的自然数能被5整除且5∈{x|x2+3x-10=0}非p:末位数字是0的自然数不能被5整除∵p真q假∴“p或q”为真,“p且q”为假,“非p”为假。
简单的逻辑联结词导学案(二)

班级:姓名:学号:评价:课题选修1-1简单的逻辑联结词导学案(二)教学目标1、通过教学实例,了解逻辑联结词“且”、“或”、“非”的含义,使学生能正确地表述相关数学内容,能判断”p q∧”、“p q∨”、“p⌝”的真假性2、重点:正确理解逻辑联结词“且”、“或”“非”的含义,并能正确表述这“p q∧”、“p q∨”、“p⌝”这些新命题.3、简洁、准确地表述新命题“p q∧”、“p q∨”“p⌝”.并能判断其真假性课型新授课时 2【学法指导】:探究、讨论、归纳、类比【教学过程及内容】1.上节回顾1.逻辑联结词命题中的或,且,非叫做逻辑联结词.“p且q”记作_____“p或q”记作_______“非p”记作._______ 自我升华:2.命题p∧q,p∨q,非p的真假判断p q p∧q p∨q 非p真真真假假真假假注意:1. 对有逻辑联结词的命题真假性的判断当p、q都为真,p∧q才为真;当p、q有一个为真,p∨q即为真;p与p的真假性相反且一定有一个为真.2..含有逻辑联结词的命题否定(1)“x=0或x=1”的否定是“x≠0且x≠1”而不是“x≠0或x ≠1”;(2)“x、y全为0”的否定是“x、y不全为0”,而不是“x、y 全不为0”;(3)“全等三角形一定是相似三角形”的否定是“全等三角形一定不是相似三角形”而不是“全等三角形不一定是相似三角形”2.自主探究3.典例讲析例1.将下列命题写成“p∧q”“p∨q”和“綈p”的形式:(1)p:菱形的对角线互相垂直,q:菱形的对角线互相平分;(2)p:能被5整除的整数的个位数一定为5,q:能被5整除的整数的个位数一定为0.知识点二从复合命题中找出简单命题例2.指出下列复合命题的形式及构成它的简单命题.(1)96是48与16的倍数;(2)方程x2-3=0没有有理数解;(3)不等式x2-x-2>0的解集是{x|x<-1或x>2};(4)他是运动员兼教练员.知识点三判断含有逻辑联结词的命题的真假例3.分别指出下列命题的形式及构成它的命题,并判断真假:(1)相似三角形周长相等或对应角相等;(2)9的算术平方根不是-3;(知识点四非命题与否命题例4.写出下列命题的否定及命题的否命题:(1)菱形的对角线互相垂直;(2)面积相等的三角形是全等三角形.知识点五.简单的逻辑联结词的综合应用例5.已知p:函数y=x2+mx+1在(-1,+∞)上单调递增,q:函数y=4x2+4(m-2)x+1大于零恒成立.若p或q为真,p且q为假,求m的取值范围.4.变式练习判断下列命题是否是复合命题并说明理由.(1)2是4和6的约数;(2)不等式x2-5x+6>0的解为x>3或x<2.已知p:方程x2+mx+1=0有两个不等负根.q:方程4x2+4(m-2)x+1=0无实根.(1)当m为何值时,p或q为真?(2)当m为何值时,p且q为真?课后反思:【反馈习题】一、选择题1.p:点P在直线y=2x-3上,q:点P在抛物线y=-x2上,则使“p∧q”为真命题的一个点P(x,y)是()A.(0,-3) B.(1,2)C.(1,-1) D.(-1,1)2.条件p:x∈A∪B,则綈p是()A.x∉A或x∉B B.x∉A且x∉BC.x∈A∩B D.x∉A或x∈B3.命题p:函数y=log a(ax+2a)(a>0且a≠1)的图象必过定点(-1,1);命题q:如果函数y=f(x)的图象关于(3,0)对称,那么函数y=f(x-3)的图象关于原点对称,则有() A.“p且q”为真B.“p或q”为假C.p真q假D.p假q真4.若p、q是两个简单命题,p或q的否定是真命题,则必有()A.p真q真B.p假q假C.p真q假D.p假q真5.下列命题中既是p∧q形式的命题,又是真命题的是()A.10或15是5的倍数B.方程x2-3x-4=0的两根是-4和1C.方程x2+1=0没有实数根D.有两个角为45°的三角形是等腰直角三角形二、填空题6.由命题p:6是12的约数,命题q:6是24的约数.构成的“p∨q”形式的命题是______________________________,“p∧q”形式的命题是______________________________,“綈p”形式的命题是________________________________.7.若“x∈[2,5]或x∈{x|x<1或x>4}”是假命题,则x的范围是________.8.已知a、b∈R,设p:|a|+|b|>|a+b|,q:函数y=x2-x+1在(0,+∞)上是增函数,那么命题:p∨q、p∧q、綈p中的真命题是________.三、解答题9.判断下列复合命题的真假:(1)等腰三角形顶角的平分线平分底边并且垂直于底边;(2)x=±1是方程x2+3x+2=0的根;(3)A⃘(A∪B).【课堂小结】【作业布置】已知p:x2+4mx+1=0有两个不等的负数根,q:函数f(x)=-(m2-m+1)x在(-∞,+∞)上是增函数.若p或q为真,p且q为假,求实数m的取值范围.备用题库详解答案例1.解(1)p∧q:菱形的对角线互相垂直且平分.p∨q:菱形的对角线互相垂直或平分.綈p:菱形的对角线不互相垂直.(2)p∧q:能被5整除的整数的个位数一定为5且一定为0;p∨q:能被5整除的整数的个位数一定为5或一定为0;綈p:能被5整除的整数的个位数一定不为5.【反思感悟】简单命题用联结词“或”、“且”、“非”联结得到的新命题是复合命题,联结后可以综合起来叙述,但综合叙述不能叙述成条件复合的简单命题或叙述成结论复合的简单命题.如(2)中的p∨q不能叙述成:能被5整除的整数的个位数一定为5或0,因为p、q都是假命题,则p∨q也为假命题.变式迁移1.解(1)是“p且q”形式的复合命题,其中p:2是4的约数;q:2是6的约数.(2)是简单命题,而不是用“或”联结的复合命题,因不等式x2-5x+6>0的解为x>3是假命题,不等式x2-5x+6>0的解为x<2也是假命题,而命题(2)是真命题,这与p、q都假,则p∨q一定假矛盾.命题“不等式x2-5x+6>0的解为x>3或解为x<2”是p∨q的形式.例2.解(1)“p且q”形式,其中p:96是48的倍数,q:96是16的倍数.(2)“非p”形式,其中p:方程x2-3=0有有理数解.(3)“p或q”形式,其中p:不等式x2-x-2>0的解集是{x|x<-1},q:不等式x2-x-2>0的解集是{x|x>2}.(4)“p且q”形式,其中p:他是运动员,q:他是教练员.例3.解(1)这个命题是p∨q的形式,其中p:相似三角形周长相等,q:相似三角形对应角相等,因为p假q真,所以p∨q为真.(2)这个命题是綈p的形式,其中p:9的算术平方根是-3,因为p假,所以綈p为真.(3)这个命题是p∧q的形式,其中p:垂直于弦的直径平分这条弦,q:垂直于弦的直径平分这条弦所对的两段弧,因为p真q真,所以p∧q为真.【反思感悟】判断含逻辑联结词的命题的真假,关键是对应p、q的真假及“p∧q”“p∨q”为真时的判定依据,至于“綈p”的真假,可就p的真假判断,也可就“綈p”直接判断.变式迁移2.解(1)此命题为“p∨q”的形式,其中p:-1是偶数,q:-1是奇数,因为p为假命题,q为真命题,所以“p∨q”为真命题,故原命题为真命题.(2)此命题为“p∧q”的形式,其中p:2属于Q,q:2属于R,因为p为假命题,q为真命题,所以“p∧q”为假命题,故原命题为假命题.(3)此命题为“綈p”的形式,其中p:A⊆(A∪B).因为p为真命题,所以“綈p”为假命题,故原命题为假命题.例4.解(1)命题的否定:存在一个菱形,其对角线不互相垂直.否命题:不是菱形的四边形,其对角线不互相垂直.(2)命题的否定:存在面积相等的三角形不是全等三角形.否命题:面积不相等的三角形不是全等三角形.例5.解若函数y=x2+mx+1在(-1,+∞)上单调递增,则-m2≤-1,∴m≥2,即p:m≥2;若函数y=4x2+4(m-2)x+1恒大于零,则Δ=16(m-2)2-16<0,解得1<m <3,即q :1<m <3.因为p 或q 为真,p 且q 为假,所以p 、q 一真一假,当p 真q 假时,由⎩⎨⎧ m ≥2m ≥3或m ≤1,得m ≥3, 当p 假q 真时,由⎩⎨⎧m <21<m <3,得1<m <2. 综上,m 的取值范围是{m |m ≥3或1<m <2}.【反思感悟】 由p 、q 的真假,可以判断“p ∨q ”“p ∧q ”“綈p ”的真假.反之,由“p ∧q ”“p ∨q ”“綈p ”的真假,也能推断p 、q 的真假,如“p ∧q ”为假,则包括“p 真q 假”“p 假q 真”“p 假q 假”三种情况.变式迁移3.解 由已知可知:p 真时m >2,q 真时1<m <3,(1)若p 或q 为真,只需m ∈{m |m >2}∪{m |1<m <3}={m |m >1}.(2)若p 且q 为真,只需m ∈{m |m >2}∩{m |1<m <3}={m |2<m <3}课堂检测1.答案 C解析 点P (x ,y )满足⎩⎪⎨⎪⎧y =2x -3,y =-x 2. 可验证各选项中,只有C 正确.2.答案 B解析 因x ∈A ∪B ⇔x ∈A 或x ∈B ,所以綈p 为x ∉A 且x ∉B ,故选B.3.答案 C解析 由于将点(-1,1)代入y =log a (ax +2a )成立,故p 真;由y =f (x )的图象关于(3,0)对称,知y =f (x -3)的图象关于(6,0)对称,故q 假.4.答案 B解析 因为p 或q 的否定綈p 且綈q 为真命题,所以綈p 与綈q 都是真命题,所以p 与q 都为假命题.所以选B.5.答案 D解析 A 中的命题是条件复合的简单命题,B 中的命题是结论复合的简单命题,C 中的命题是綈p 的形式,D 中的命题为p ∧q 型.二、填空题6.答案 6是12或24的约数 6是12和24的约数 6不是12的约数7.答案 [1,2)解析 x ∈[2,5]或x ∈(-∞,1)∪(4,+∞),即x ∈(-∞,1)∪[2,+∞),由于命题是假命题,所以1≤x <2,即x ∈[1,2).8.答案 綈p解析 对于p 当a >0,b >0时,|a |+|b |=|a +b |,故p 假,綈p 为真;对于q ,抛物线y =x 2-x +1的对称轴为x =12,故q 假,所以p ∨q 假,p ∧q 假.这里綈p 应理解成|a |+|b |>|a +b |不恒成立,而不是|a |+|b |≤|a+b |.三、解答题9.解 (1)这个命题是“p 且q ”的形式,其中p :等腰三角形顶角的平分线平分底边,q :等腰三角形顶角的平分线垂直于底边,因为p 真q 真,则“p 且q ”真,所以该命题是真命题.(2)这个命题是“p 或q ”的形式,其中p :1是方程x 2+3x +2=0的根,q :-1是方程x 2+3x +2=0的根,因为p 假q 真,则“p 或q ”真,所以该命题是真命题.(3)这个命题是“非p ”的形式,其中p :A ⊆(A ∪B ),因为p 真,则“非p ”假,所以该命题是假命题.10.解 p :x 2+4mx +1=0有两个不等的负根⇔⎩⎪⎨⎪⎧ Δ=16m 2-4>0-4m <0⇔m >12. q :函数f (x )=-(m 2-m +1)x 在(-∞,+∞)上是增函数⇔0<m 2-m +1<1⇔0<m <1.(1)若p 真,q 假,则⎩⎪⎨⎪⎧m >12,m ≤0或m ≥1.⇒m ≥1.(2)若p 假,q 真,则⎩⎪⎨⎪⎧ m ≤120<m <1⇒0<m ≤12综上,得m ≥1或0<m ≤12.。
1.2简易逻辑学案(高考一轮复习)

2014年高中数学一轮复习教学案第一章集合与常用逻辑用语第2节命题及其关系、充分条件与必要条件一.学习目标:1.理解命题的概念.2.了解“若p,则q”形式的命题的逆命题、否命题与逆否命题,会分析四种命题的相互关系.3.理解必要条件、充分条件与充要条件的意义.二.学习重、难点:1.学习重点:理解必要条件、充分条件与充要条件的意义;2.学习难点:能够判断必要条件、充分条件与充要条件.三.学习方法:讲练结合四.自主复习:1.命题用语言、符号或式子表达的,可以判断真假的_______叫做命题,其中__________的语句叫做真命题,__________的语句叫做假命题.2.四种命题及其关系(1)四种命题间的相互关系(2)四种命题的真假关系①两个命题互为逆否命题,它们有_______的真假性;②两个命题为互逆命题或互否命题,它们的真假性_____________.3.充分条件、必要条件与充要条件(1)“若p,则q”为真命题,记p⇒q,则p是q的_______,q是p的____________.(2)如果既有p⇒q,又有q⇒p,记作:p⇔q,则p是q的充要条件,q也是p的____________.五.复习前测:1.已知a∈R,则“a=2”是“(a-1)(a-2)=0”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件2.命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是( )A.若f(x)是偶函数,则f(-x)是偶函数B.若f(x)不是奇函数,则f(-x)不是奇函数C.若f(-x)是奇函数,则f(x)是奇函数D.若f(-x)不是奇函数,则f(x)不是奇函数3.命题“若a>b,则ac2>bc2”(这里a,b,c都是实数)与它的逆命题、否命题、逆否命题中,真命题的个数为( )A.4 B.3C.2 D.14.已知P:x+y≠2011;Q:x≠2000且y≠11,则P是Q的__________条件.5.设a ,b 是两个单位向量,命题“(2a +b )⊥b ”是命题“a ,b 的夹角等于2π3”成立的__________条件.要点点拨:1.逆命题、否命题及逆否命题的写法及真假判断写出一个命题的逆命题、否命题及逆否命题的关键是分清原命题的条件和结论,然后按定义来写;在判断原命题及其逆命题、否命题以及逆否命题的真假时,要借助原命题与其逆否命题同真或同假,逆命题与否命题同真或同假来判定.2.判断命题的充要条件的三种方法(1)定义法:判断B 是A 的什么条件,实际上就是判断B ⇒A 或A ⇒B 是否成立,只要把题目中所给条件按逻辑关系画出箭头示意图,再利用定义即可判断.(2)转换法:当所给命题的充要条件不易判定时,可对命题进行等价转换,例如改用其逆否命题进行判断.(3)集合法:在命题的条件和结论间的关系判断有困难时,有时可以从集合的角度来考虑,记条件p 、q 对应的集合分别为A 、B ,则若A ⊆B ,则p 是q 的充分条件;若A B ,则p 是q 的充分不必要条件;若A ⊇B ,则p 是q 的必要条件;若A B ,则p 是q 的必要不充分条件;若A =B ,则p 是q 的充要条件.六.复习过程:题型一:四种命题及其关系[例1](1)(2013·德州模拟)命题“若一个数是负数,则它的平方是正数”的逆命题是__________.(2)(2013·岳阳模拟)命题“若a>b,则a-1>b-1”的否命题是__________.[思路点拨] 先分清原命题的条件和结论,再根据四种命题的概念,写出逆命题、否命题.[规律总结]1.对于四种命题真假的判断,关键是分清命题的条件和结论,然后再结合相关的知识进行判断;2.因为互为逆否命题的两个命题具有相同的真假性,可利用判断逆否命题的真假,得原命题的真假.变式训练1(1)(2012·湖南)命题“若α=π4,则tanα=1”的逆否命题是( )A.若α≠π4,则tanα≠1B.若α=π4,则tanα≠1C.若tanα≠1,则α≠π4D.若tanα≠1,则α=π4(2)已知命题“若函数f(x)=e x-mx在(0,+∞)上是增函数,则m≤1”,则下列结论正确的是( )A.否命题是“若函数f(x)=e x-mx在(0,+∞)上是减函数,则m>1”,是真命题B.逆命题是“若m≤1,则函数f(x)=e x-mx在(0,+∞)上是增函数”,是假命题C.逆否命题是“若m>1,则函数f(x)=e x-mx在(0,+∞)上是减函数”是真命题D.逆否命题是“若m>1,则函数f(x)=e x-mx在(0,+∞)上不是增函数”,是真命题。
高考数学第一轮《简易逻辑》复习导学案

简易逻辑备案[开课一分钟]逻辑是研究思维形式及其规律的一门科学,是人们认识和研究问题不可缺少的工具,是为了培养学生的推理技能,发展学生的思维能力.要求正确理解逻辑联结词“或、且、非”的含义.理解四种命题及其相互关系,掌握充要条件的意义及判定.[课堂链接]1.逻辑联结词:或(∨),且(∧),非(⌝).2.命题:(1)命题:可以判断真假的语句叫命题.一个命题由题设和结论两部分构成,命题有真假之分.(2)简单命题:不含逻辑联结词的命题.(3)复合命题:是由简单命题和逻辑联结词构成的命题,构成形式有三种:“p或q”,“p 且q”,“非p”.判断复合命题的真假可以用真值表.3.命题的四种形式及相互关系:4.反证法:假设命题结论不成立(反设);从这个假设出发,经过正确的逻辑推理,得出矛盾(归缪);由矛盾判断假设不成立,从而肯定命题结论成立(结论).5.充要条件:如果p⇒q,则称p是q的充分条件,同时也称q是p的必要条件.如果p⇒q,且q⇒p,称p与q互为充要条件,记为p⇔q,也称p与q等价.如果p⇒q且q⇒p,称p是q的既不充分也不必要条件,同时易知q也是p的既不充分又不必要条件.[知识释点]1.要正确认识一个命题,首先一定要找出命题的条件和结论.2.原命题与逆否命题,逆命题与否命题都是等价的.这一点可以用来判断命题真假,特别是当一个命题的真假不易判断时,通过这种等价转化的思想,往往可以化难为易.3.反证法的应用:结论本身是否定形式的命题;结论中是以“至多”、“至少”形式出现的命题;关于惟一性、存在性的问题;结论的反面是比原结论更具体更容易研究的命题.4.根据反证法的原理,我们可以明白,要推翻一个命题,只需找到一个反例就够了.举反例是一种很重要的数学方法和解题技巧.5.对充要条件的判定,注意以下步骤:认清条件与结论→摆好位置→打对箭头→给出正确判定6.证明p是q的充要条件通常要分两个层次:(1)p⇒q,即证p的充分性;(2)q⇒p,即证p的必要性;由(1)(2)可知条件p的充要性,即说p是q的充要条件.在这里要注意的是认清谁是条件,谁是结论,切不可混淆.当然,如果在证明过程中能始终保证任意前后两步的等价性,则可以不必分开证明.[结尾两分钟]逻辑是新增内容,高考只对其基本内容进行考查,特别是条件问题每年必考.一般难度不大,主要集中在考查命题的四种形式和充要条件的判定.要注意的是充要条件涉及知识面广,综合性强,能与高中数学任何知识结合.。
第5讲.简易逻辑.(答案版)

当前形势简易逻辑在近五年北京卷(理)考查5分高考 要求内容要求层次 具体要求A B C “若p ,则q ”形式的命题及其逆命题、否命题与逆否命题 √了解命题的逆命题、否命题与逆否命题.四种命题的相互关系;简单的逻辑联结词;全称量词与存在量词√ 会分析四种命题的相互关系;了解“或”、“且”、“非”逻辑联结词的含义;理解全称量词与存在量词的意义;能正确地对含有一个量词的命题进行否定.充要条件√理解必要条件、充分条件与充要条件的意义.北京 高考 解读 2009年 2010年(新课标)2012年(新课标)2013年(新课标)第5题5分第6题5分第3题5分第3题5分1.下列命题中是真命题的是( )A .x ∀∈R ,21x x <+B .x ∀∈R ,21x x +≥C .x ∃∈R ,y ∀∈R ,22xy y =D .x ∃∈R ,y ∀∈R ,2x y >【解析】 C2.命题“x ∀∈R ,3210x x -+≤”的否定是( )A .不存在x ∈R ,3210x x -+≤B .存在x ∈R ,3210x x -+≤C .存在x ∈R ,3210x x -+>D .对任意的x ∈R ,3210x x -+> 【解析】 C3.已知命题p :()0x ∃∈-∞,,23x x <;命题q :π02x ⎛⎫∀∈ ⎪⎝⎭,,cos 1x <,则下列命题为真命题的是( )A .p q ∧B .()p q ∨⌝C .()p q ⌝∧D .()p q ∧⌝【解析】 C4.已知函数()f x 是R 上的增函数,a b ∈R ,,对命题“若0a b +≥,则 ()()()()f a f b f a f b +-+-≥”,写出其逆命题和逆否命题,并判断其真假.暑期知识回顾新课标剖析第5讲简易逻辑【解析】 逆命题:若()()()()f a f b f a f b +-+-≥,则0a b +≥,是真命题;逆否命题:若()()()()f a f b f a f b +<-+-,则0a b +<,是真命题.5.下列说法中,正确的是( )A .命题“若22am bm <,则a b <”的逆命题是真命题B .命题“若2320x x -+=,则1x =”的逆否命题为:“若1x ≠,则2320x x -+≠”C .命题“p q ∨”为真命题,则命题p 和命题q 均为真命题D .已知x ∈R ,则“1x >”是“2x >”的充分不必要条件 【解析】 B6.(2013陕西)设a ,b 为向量,则“a b a b ⋅=”是“a b ∥”的( ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【解析】 C 7.(2013北京)“πϕ=”是“曲线()sin 2y x ϕ=+过坐标原点”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】 A 8.(2013上海)钱大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的( ) A .充分条件 B .必要条件 C .充分必要条件 D .即不充分也不必要条件 【解析】 B<教师备案>暑期简易逻辑知识的回顾,1~5为逻辑联结词与命题,6~8为充要条件.考点1:命题的判断命题与量词:1.命题:用语言、符号或式子表达的,能够判断真假的语句叫做命题,一般可以用一个小写英文字母表示,如p q r,,,. 其中判断为真的命题叫做真命题,判断为假的命题叫做假命题.2.全称量词:短语“所有”、“一切”、“每一个”,在陈述中表示所述事物的全体,逻辑中通常叫做全称量词,并用符号“∀”表示.全称命题:含有全称量词的命题.全称命题就是陈述某集合所有元素都具有某种性质的命题. 知识点睛5.1逻辑联结词与四种命题一般地,设()p x 是某集合M 的所有元素都具有的性质,那么全称命题就是形如“对M 中所有x ,()p x ”的命题,用符号简记为:x M ∀∈,()p x .3.存在量词:短语“有一个”、“有些”、“至少有一个”在陈述中表示所述事件的个体或部分,逻辑中通常叫做存在量词,并用符号“∃”表示.存在性命题:含有存在量词的命题就叫做存在性命题,又叫特称命题. 存在性命题就是陈述在集合中有(存在)一些元素具有某性质的命题.一般地,设()q x 是某集合M 的有些元素x 具有的某种性质,那么存在性命题就是形如“存在集合M 中的元素x ,()q x ”的命题,用符号简记为:x M ∃∈,()q x .<教师备案>命题的“真”或“假”是唯一确定的,在证明一个命题为真时,要由条件通过严密的逻辑推理得到结论,而确定一个命题为假时,一般只需要举一个反例即可.【例1】 ⑴命题p :奇函数一定有(0)0f =;命题q :函数1y x x=+的单调递减区间是[10)(01]-,,. 则下列四个判断中正确的是( )A .p 真q 真B .p 真q 假C .p 假q 真D .p 假q 假⑵给出下列三个命题 ①若1a b >-≥,则11a ba b++≥. ②若正整数m 和n 满足m n ≤2n.③设()11,P x y 是圆221:9O x y +=上的任意一点,圆2O 以(),Q a b 为圆心,且半径为1.当()()22111a x b y -+-=时,圆1O 与圆2O 相切.其中假命题的个数为( )A .0B .1C .2D .3⑶(2013湖南)设函数()x x x f x a b c =+-,其中0c a >>,0c b >>.若a b c ,,是ABC △ 的三边长,则下列结论正确的是 .(写出所有正确结论的序号)①()1x ∀∈-∞,,()0f x >; ②x ∃∈R ,使x x x a b c ,,不能构成一个三角形的三条边长;③若ABC △为钝角三角形,则()12x ∃∈,,使()0f x =.【解析】 ⑴ D ⑵ B⑶ ①②③提高班学案1【拓1】 命题p :在锐角三角形ABC △中,sin cos A B >成立.p 是______命题(填“真”或“假”). 【解析】 真;经典精讲尖子班学案1【拓2】 对于四面体ABCD ,下列命题正确的是___________(写出所有正确命题的编号).①相对棱AB 与CD 所在的直线是异面直线;②由顶点A 作四面体的高,其垂足是BCD △的三条高线的交点;③若分别作ABC △和ABD △的边AB 上的高,则这两条高所在的直线异面; ④分别作三组相对棱中点的连线,所得的三条线段相交于一点;⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱. 【解析】 ①④⑤;目标班学案1【拓3】 设直线系:cos (2)sin 1(02π)M x y θθθ+-=≤≤,对于下列四个命题:A .M 中所有直线均经过一个定点B .存在定点P 不在M 中的任一条直线上C .对于任意整数(3)n n ≥,存在正n 边形,其所有边均在M 中的直线上D .M 中的直线所能围成的正三角形面积都相等,其中真命题的代号是__________(写出所有真命题的代号). 【解析】 B 、C ;考点2:逻辑联结词基本逻辑联结词:1.且:一般地,用逻辑联结词“且”把命题p 和q 联结起来,就得到一个新命题,记作p q ∧,读作“p 且q ”.可以用“且”定义集合的交集:{|()()}A B x x A x B =∈∧∈.2.或:一般地,用逻辑联结词“或”把命题p 和q 联结起来,就得到一个新命题,记作p q ∨,读作“p 或q ”.可以用“或”定义集合的并集:{|()()}A B x x A x B =∈∨∈.3.非:一般地,对命题p 加以否定,就得到一个新的命题,记作p ⌝,读作“非p ”或“p 的否定”.可以用“非”来定义集合A 在全集U 中的补集:{|()}{|}U A x U x A x U x A =∈⌝∈=∈∉ð. 4.不含逻辑联结词的命题称为简单命题,含有逻辑联结词的命题称为复合命题.知识点睛5.存在性命题的否定:存在性命题 p :x A ∃∈,()p x ;它的否定是 p ⌝:x A ∀∈,()p x ⌝. 6.全称命题的否定:全称命题 q :x A ∀∈,()q x ;它的否定是 q ⌝:x A ∃∈,()q x ⌝.<教师备案>1.在判断一个命题是简单命题还是复合命题时,不能只从字面上来看有没有“或”、“且”、“非”.例如命题“等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合”,此命题字面上无“且”;命题“5的倍数的末位数字不是0就是5”的字面上无“或”,但它们都是复合命题.2.对联言命题与选言命题的否定比较容易出错,它符合德摩根定律:()()()p q p q ⌝∧=⌝∨⌝,()()()p q p q ⌝∨=⌝∧⌝.即:⑴ 联言命题p q ∧:(0)(0)a b =∧=;否定()p q ⌝∧:(0)(0)a b ≠∨≠; ⑵ 选言命题p q ∨:(0)(0)a b =∨=;否定()p q ⌝∨:(0)(0)a b ≠∧≠.如:1x =或2x =的否定是:1x ≠且2x ≠;x y ,全为零的否定是:0x ≠且0y ≠. 对于“至少有”,“至多有”类型的命题的否定:“至少有两个解”的否定是“至多有一个解”,注意有些命题的否定容易出错,需要考虑全面一些,如方程220x x a -+=有且只有一根的否定为:方程220x x a -+=无根或至少有两根.3.存在性命题和全称命题的否定比较公式化,在暑假已经学过,本讲不再放例题. 我们一般不研究“若…,则…”形式的命题的否定,只研究这类命题的四种命题形式. 因为“若…,则…”命题的否定比较复杂,有两类问题:⑴ 命题p :若实数0x =,则2x x =.它的否定p ⌝:若0x =,则2x x ≠. 这类命题的否定就是直接否定结论即可.⑵命题p :若实数0x >,则2x x >.这是一个假命题,它的否定p ⌝是:若实数0x >,则2x x ≤吗?显然不是,因为这也是一个假命题,而一个命题与它的否定的真假一定相反.问题出在哪里?命题p 其实是一个全称命题,它想表达的意思是:对任意的实数0x >,有2x x >,所以它的否定是:存在0x >,2x x ≤.对于程度比较好的学生,可以对此进行介绍,但一般来说,我们不需要研究“若…则…”类命题的否定,只研究这类问题的否命题.如果出现对这类问题的否定的真假的判断,我们也更倾向于通过原来的命题的真假来推导它的否定的真假,如例2后面的拓1.【例2】 ⑴已知全集U =R ,A U ⊆,B U ⊆,如果命题pA B ,则命题“p ⌝”是( )AABU B ðCA B D()()U U A B 痧 ⑵(2013湖北)在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p 是“甲降落在指经典精讲定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为( )A .()()p q ⌝∨⌝B .()p q ∨⌝C .()()p q ⌝∧⌝D .p q ∨⑶若:p 关于x 的不等式1x a >的解集是()0-∞,;q :函数()2lg y ax x a =-+的定义域为R .如果p q ∧为假,p q ∨为真,求实数a 的取值范围.【追问】如果()p q ∧⌝为假,p q ∨为真,求实数a 的取值范围.【解析】 ⑴ D⑵A⑶a 的取值范围是102a <≤或1a ≥.【追问】等价于q 真,故12a >.提高班学案2【拓1】 已知命题p :若实数x y ,满足220x y +=,则x y ,全为0;命题q :若a b >,则11a b<,给 出下列四个复合命题:①p 且q ,②p 或q ,③p ⌝,④q ⌝,其中真命题的个数为( ) A .1 B .2 C .3 D .4【解析】 B尖子班学案2【拓2】 判断下面对结论的否定是否正确,如果不正确,请写出正确的否定结论:⑴至少有一个S 是P ;否定:至少有两个或两个以上S 是P ; ⑵最多有一个S 是P .否定:最少有一个S 是P ; ⑶全部S 都是P .否定:全部的S 都不是P .【解析】 对结论的否定都不正确,正确的否定为:⑴没有一个S 是P . ⑵至少有两个S 是P . ⑶存在一个S 不是P .考点3:四种命题知识点睛命题的四种形式命题“如果p ,则q ”是由条件p 和结论q 组成的,对p q ,进行“换位”和“换质(否定)”后,可以构成四种不同形式的命题. ⑴原命题:如果p ,则q ;⑵原命题的逆命题:如果q ,则p ; ⑶原命题的否命题:如果非p ,则非q ; ⑷原命题的逆否命题:如果非q ,则非p .<教师备案> 注意命题的否定与否命题之间的区别命题的否定是命题的反面,只否定命题的结论,不改变命题的条件,且与命题的真假恰好相反;命题的否定通常是对简单命题而言的,特别是全称命题与存在性命题.否命题是对条件与结论同时进行否定,它的真假与原命题的真假没有绝对的联系.否命题通常是对“若…则…”形式的命题进行的,所以通常遇不到同时写出否命题与命题的否定的问题,下面给出两个同时写出否命题与命题的否定例子,供老师选用.(对于这类命题的否定,前面的教师备案有详细讲解说明)例:写出下列命题的否命题及命题的否定形式,并判断其真假. ⑴ 若0m >,则关于x 的方程20x x m +-=有实数根. ⑵ 若x ,y 都是奇数,则x y +是奇数.【解析】 ⑴ 否命题:若0m >,则关于x 的方程20x x m +-=无实数根,是假命题;命题的否定:存在0m >,关于x 的方程20x x m +-=无实数根,假命题. ⑵ 否命题:若x 、y 不都是奇数,则x y +不是奇数,是假命题;命题的否定:存在x 、y 都是奇数,x y +不是奇数,是真命题.【例3】 ⑴下列命题中,真命题有_________.①“若1xy =,则x 、y 互为倒数”的逆命题 ②“面积相等的三角形一定全等”的否命题③“若1m ≤,则方程220x x m -+=有实根”的逆否命题 ④“若A B B =,则A B ⊆”的逆否命题⑤“若220x y +=,则x ,y 全为0”的否命题;⑥“全等三角形是相似三角形”的逆命题; ⑦“圆内接四边形对角互补”的逆否命题.⑵已知命题“如果1a ≤,那么关于x 的不等式22(4)(2)10a x a x -++-≥的解集为∅”.它的逆命题、否命题、逆否命题及原命题中是假命题的共有( ) A .0个 B .2个 C .3个 D .4个【解析】 ⑴ ①②③⑤⑦;⑵ B ;经典精讲目标班学案2【拓3】 已知等比数列{}n a 的前n 项和为n S .⑴若m S ,2m S +,1m S +成等差数列,证明m a ,2m a +,1m a +成等差数列; ⑵写出⑴的逆命题,判断它的真伪,并给出证明.【解析】 ⑴ ∵11m m m S S a ++=+,212m m m m S S a a +++=++.由已知212m m m S S S ++=+,∴1212()()m m m m m m S a a S S a +++++=++,∴2112m m a a ++=-,即数列{}n a 的公比12q =-.∴112m m a a +=-,214m m a a +=,∴212m m m a a a ++=+,∴m a ,2m a +,1m a +成等差数列.⑵ ⑴的逆命题是:若m a ,2m a +,1m a +成等差数列,则m S ,2m S +,1m S +成等差数列. 设数列{}n a 的公比为q ,∵1m m a a q +=,22m m a a q +=.由题设,212m m m a a a ++=+,即22m m m a q a a q =+,即2210q q --=,∴1q =或12q =-.当1q =时,∴1m S ma =,21(2)m S m a +=+,11(1)m S m a +=+不成等差数列. 故逆命题为假.考点4:充分必要条件1.对于“如果p ,则q ”形式的命题,p 称为命题的条件,q 称为命题的结论.当命题“如果p ,则q ”经过推理证明断定是真命题时,我们就说则p 可以推出q ,记作p q ⇒,读作“p 推出q ”.2.如果p 可推出q ,则称p 是q 的充分条件,q 是p 的必要条件. 一般地,如果p q ⇒,且q p ⇒,则称p 是q 的充分且必要条件,简称p 是q 的充要条件,记作p q ⇔,显然q 也是p 的充要条件,此时又常说“当且仅当p ”或“p 与q 等价”.如果p q ⇒,且q p ¿,则称p 是q 的充分不必要条件,称q 为p 的必要不充分条件.<教师备案> 在数学上,找到一个“事物”的充分必要条件是特别重要的一件事情,它可以帮助我们从不同的角度,全面地反映同一个“事物”的面貌.在数学上有很多非常重要的充分必要条件的结果.一个事物的充分必要条件会给我们讨论问题带来很大的方便,给我们提供了全面刻画事物的另外一个角度,甚至可以帮助我们开拓新的研究方向. ①勾股定理.勾股定理中222a b c +=就是直角三角形的充分必要条件,有了这个条件,我们就可以通过边的长度之间的关系来研究几何中的直角三角形. ②一元二次方程有实数根的充分必要条件.知识点睛5.2充要条件判别式0∆≥是一元二次方程有实数根的充分必要条件,有了这个条件,我们就可以定性地研究一元二次方程的实数根.很多命题直接证明不容易,我们会转化成它的等价命题.这种等价关系及其使用,可以简化原来的命题,得到一个更容易证明的结论.【例4】 ⑴设π02x <<,则“2sin 1x x <”是“sin 1x x <”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件⑵若数列{}n a 满足212n na p a +=(0p >为常数,*n ∈N ),则称{}n a 为“等方比数列”.甲:数列{}n a 是等方比数列;乙:数列{}n a 是等比数列.则( )A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件C .甲是乙的充要条件D .甲既不是乙的充分条件也不是乙的必要条件⑶设命题甲:2x >或1y ≤;乙:3x ≥且2y <.则“命题甲不成立”是“命题乙不成立”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .非充分非必要条件⑷设有集合22{()|2}{()|2},,,M x y x y N x y y x =+>=->,则点P M ∈的____条件是点P N ∈;点P M ∈是点P N ∈的_______条件.【解析】 ⑴ B⑵ B ⑶ A⑷ 充分不必要;必要不充分【点评】 充要条件的问题要十分细心地去辨析:“哪个命题”是“哪个命题”的充分(必要)条件;注意区分:“甲是乙的充分条件(甲⇒乙)”与“甲的充分条件是乙(乙⇒甲)”,是两种不同形式的问题.语句陈述与理解是这里的一个难点:如“p ⌝是q ⌝的充分不必要条件”可以转化成“q 是p 的充分不必要条件”;“p 是q ⌝的必要不充分条件”等价于“p ⌝是q 的充分不必要条件”.通过这些转化,我们寻找更容易解决的方向.提高班学案3【拓1】 ⑴命题p :a b ∥;命题q :λ∃,使得a b λ=.则p 是q 的_____________条件.⑵(2013山东)给定两个命题p ,q .若p ⌝是q 的必要而不充分条件,则p 是q ⌝的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 【解析】 ⑴ 必要不充分;经典精讲⑵ A .尖子班学案3【拓2】 如果对于任意实数x ,[]x 表示不超过x 的最大整数.例如[]3.273=,[]0.60=.那么“[][]x y =”是“1x y -<”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】 A【备选】已知0a >,则0x 满足关于x 的方程ax b =的充要条件是( )A .x ∃∈R ,22001122ax bx ax bx --≥ B .x ∃∈R ,22001122ax bx ax bx --≤ C .x ∀∈R ,22001122ax bx ax bx --≥ D .x ∀∈R ,22001122ax bx ax bx --≤ 【解析】C【例5】 ⑴对任意实数a ,b ,c ,给出下列命题:①“a b =”是“ac bc =”的充要条件;②“5a +是无理数”是“a 是无理数”的充要条件; ③“a b >”是“22a b >”的充分条件;④“5a <”是“3a <”的必要条件. 其中真命题的个数是( )A .1B .2C .3D .4⑵集合101x A xx ⎧-⎫=<⎨⎬+⎩⎭,{}B x x b a =-<,若“1a =”是“A B ≠∅”的充分条件,则b 的取值范围可以是( )A .20b -<≤B .02b <≤C .31b -<<-D .12b -<≤⑶命题p :若a b ∈R ,,则1a b +>是1a b +>的充分条件,命题q :函数y =的定义域是(1][3)-∞-+∞,,,则( ) A .p 或q 为假 B .p 且q 为真 C .p 真q 假 D .p 假q 真【解析】 ⑴ B⑵ D ;⑶ D ;【例6】已知数列{}n a 的前n 项和(01)n n S p q p p =+≠≠,,求数列{}n a 是等比数列的充要条件. 【追问】数列{}n a 是单调增的等比数列的充要条件.【解析】11a S p q ==+. 当2n ≥时,11(1)n n n n a S S p p --=-=-,∵01p p ≠≠,,∴11(1)(1)n n n n a p p p a p p +--==-.若{}n a 为等比数列,则121n na a p a a +==, ∴(1)p p p p q-=+,∴1q =-, 这是{}n a 为等比数列的必要条件.下面证明1q =-是{}n a 为等比数列的充分条件. 当1q =-时,1(01)n n S p p p =-≠≠,,111a S p ==-, 当2n ≥时,11(1)n n n n a S S p p --=-=-, ∴121(1)(1)n n n n a p p p a p p ----==-为常数. ∴1q =-时,数列{}n a 为等比数列.即数列{}n a 是等比数列的充要条件为1q =-. 【追问】由例题结论知,{}n a 是等比数列的必要条件是1q =-,{}n a 单调增时, 2n ≥时,()()()21111110n n n n n a a p p p p p p --+-=---=->,∵1p ≠,∴()210p ->,则10n p ->,只能0p >. 1n =时,()()()2211110a a p p p p -=---=->成立.反之,0p >且1q =-时,由例题知{}n a 是等比数列,又()21110n n n a a p p -+-=->,因此{}n a 单调增.综上,{}n a 是单调增的等比数列的充要条件是0p >且1q =-.目标班学案3【拓3】 已知数列{}n a 、{}n b 满足:122123nn a a na b n+++=++++,求数列{}n b 是等差数列的充要条件.【解析】 设{}n b 是等差数列,公差为d ,则1(1)n b b n d =+-. ∵12(12)2n n b n a a na +++=+++, 1121(121)2(1)n n b n a a n a --+++-=+++-,上面两式相减得:1(1)(1)22n n n n n n n na b b -+-=-, ∴111111113[(1)][(2)](1)22222n n n n n n n a b b b n d b n d b n d -+-+-=-=+--+-=+-⋅,从而得132n n a a d +-=为常数,故{}n a 是等差数列.这是{}n b 为等差数列的必要条件.下面证明这也是充分条件, 设{}n a 成等差数列,公差为d ',则12112(12)[1223(1)]2(1)1231233n n a a na a n d n n b a n d n n'+++++++⋅+⋅++-'===+-⋅++++++++,从而!11222(1)333n n nd b b a a n d d +'''-=+---=为常数.故{}n b 是等差数列,公差为23d '.综上所述,数列{}n b 成等差数列的充要条件是数列{}n a 也是等差数列.【备选】 已知0a >,函数2()f x ax bx =-,⑴当0b >时,若对任意x ∈R 都有()1f x ≤,证明:2a b ≤;⑵当1b >时,证明:对任意[01]x ∈,,()1f x ≤的充要条件是12b a b -≤≤; ⑶当01b <≤时,讨论对任意[01]x ∈,,都有()1f x ≤的充要条件. 【解析】 ⑴∵0b >,22()24a a f x b x b b ⎛⎫=--+ ⎪⎝⎭,∴当x ∈R 时,有2max ()4a f x b=,于是,对∀x ∈R 都有()1f x ≤,∴2max ()14a f x b=≤ ∵00a b >>,,∴2a b ≤. ⑵ 先证必要性: ∵1b >,∴01b <<,(01)b∈,,∴(1)11f f b ⎧⎪⎨⎫⎪ ⎪⎝⎭⎩≤≤(1)11f f b -⎧⎪⇒⎨ ⎪⎪⎝⎭⎩≥≤111a b b --⎧⎪⇒-⎪⎩≥≤12b a b ⇒-≤≤.再证充分性:012b a b <-≤≤,又∵01x ≤≤,∴11x x -⎧⎨--⎩≥0≥,∴22()(1)(1)1f x ax bx b x bx bx x x x =---=----≥≥≥, 且222()21(1)1f x ax bx bx bx bx =--=--≤≤, ∴()1f x ≤. 综上知,命题成立.⑶当0a >,01b <≤,对任意[01]x ∈,都有22()1f x ax bx bx b =----≥≥≥, 其次,若对任意[01]x ∈,都有()1f x ≤,则(1)1f ≤1a b ⇒-≤1a b ⇒+≤. 反之,若1a b +≤,∵01b <≤,则对任意[01]x ∈,都有 22()(1)(1)(1)11f x ax bx b x bx x bx =-+-=--+≤≤.综上所述,当0a >,01b <≤时,对任意[01]x ∈,都有()1f x ≤的充要条件是1a b +≤.1.求实数x y ,满足sin sin sin()x y x y +=+的充要条件.【解析】 ∵22x y x y ++=⋅,22x y x y x +-=+,22x y x yy +-=-. ∴sin sin sin cos cos sin 222222x y x y x y x y x y x y x +-+-+-⎛⎫=+=+ ⎪⎝⎭,sin sin sin cos cos sin 222222x y x y x y x y x y x y y +-+-+-⎛⎫=-=- ⎪⎝⎭ ∴sin sin 2sin cos 22x y x y x y +-+=.又sin()2sin cos22x y x yx y +++=, 从而sin sin sin()x y x y +=+2sin cos 2sin cos2222x y x y x y x y+-++⇔=. 即sin cos cos 0222x y x y x y +-+⎛⎫⇔-= ⎪⎝⎭. 而cos cos cos cos sin sin 2222222x y x y x y x y -⎛⎫=-=+ ⎪⎝⎭, c o s c o s c o s c o s s i n s i n 2222222x y xy x y x y+⎛⎫=+=- ⎪⎝⎭, ∴cos cos2sin sin 2222x y x y x y -+-=.即sin sin sin()sin sin sin 0222x y x yx y x y ++=+⇔=.∴充要条件为x y x y +,,其中之一为2πk ,k ∈Z .2.已知向量()sin ,cos p A A =,()cos ,sin q B B =,且sin2p q C ⋅=,其中A 、B 、C 分别是ABC △的三边a 、b 、c 所对的角. ⑴ 求C 的大小.⑵ 证明:sin 2p q C ⋅=的充分必要条件是1tan 22cos2C C+=. 【解析】 ⑴ sin 2p q C ⋅=⇒sin cos cos sin sin 2A B A B C +=⇒()sin sin 22sin cos A B C C C +==2cos 1C ⇒=于是1cos 2C =,π3C =;⑵ 必要性:由⑴sin 2p q C ⋅=⇒π3C =,∴112πtan 2tan 22πcos 23cos 3C C +=+=; 充分性:1tan 22cos2C C +=1sin 22cos2CC+⇒= ()222sin cos sin cos tan 12cos sin cos sin 1tan C C C C C C C C C C +++⇒===---tan C ⇒= ∴π3C =.于是()2sin sin π=sin 23p q A B C ⋅=+=,充分性得证.综上,命题成立.【演练1】⑴ 已知命题:p a ∃,()0b ∈+∞,,当1a b +=时,113a b+=;命题:q x ∀∈R ,210x x -+≥ 恒成立,则下列命题是假命题的是( )A .p q ⌝∨⌝B .p q ⌝∧⌝C .p q ⌝∨D .p q ⌝∧ ⑵ 有四个关于三角函数的命题:1:p x ∃∈R ,221sin cos2x x += 2:p x ∃,y ∈R ,sin()sin sin x y x y -=-[]3:0πp x ∀∈,sin x 4π:sin cos 2p x y x y =⇒+= 其中假命题的是( )A .1p ,4pB .2p ,4pC .1p ,3pD .2p ,3p⑶(2010年宣武一模文10)命题“任意常数列都是等比数列”的否定形式是 .【解析】 ⑴ B ;由基本不等式可得:()111124b aa b a b a b a b⎛⎫+=+⨯+=++ ⎪⎝⎭≥, 故命题P 为假命题,p ⌝为真命题;x ∀∈R ,22131024x x x ⎛⎫-+=-+> ⎪⎝⎭,故命题Q 为真命题,Q ⌝为假命题,P Q ⌝∧⌝为假命题,故选B . ⑵ A .对x ∀∈R ,恒有22sin cos 122x x +=,因此不存在x ∈R ,使得221sin cos 222x x +=,故1p 为假命题;当0x y ==时,()sin sin0sin sin x y x y -==-所以2p 为真命题;当[]0πx ∈,时,sin sin x x =,所以3p 为真命题;由sin cos x y =,不一定推出π2x y +=,还可以得出π2π2x y k +=+(k ∈Z )等,故4p 为假命题.⑶ 存在一个常数列不是等比数列.【演练2】 设:p 方程2210x mx ++=有两个不相等的正根;:q 方程()2223100x m x m +--+=无实根.则使p q ∨为真,p q ∧为假的实数m 的取值范围是 .【解析】 (][][)2113-∞--+∞,,, 由题意,必有p 真q 假或p 假q 真.若p 真,则()21240m ∆=->, 即21m >,()()11m ∈-∞-+∞,,,①若q 真,则()()224243100m m ∆=---+<,即260m m --<,∴23m -<<.② 记()()11A =-∞-+∞,,,()23B =-,.若p 真q 假,则对应的集合为(][)23A B =-∞-+∞R ,,ð. 若p 假q 真,则对应的集合为[]11A B =-R ,ð. 实战演练综上,使p q ∨真,p q ∧假的实数m 的取值范围为(][][)2113-∞--+∞,,,.【演练3】⑴ “在ABC △中,若90C ∠=︒,则A ∠、B ∠都是锐角”的否命题为______________;⑵ 命题:“若21x <,则11x -<<”的逆否命题是( )A .若21x ≥,则1x ≥或1x -≤B .若11x -<<,则21x <C .若1x >或1x <-,则21x >D .若1x ≥或1x -≤,则21x ≥⑶ 命题“若函数()log (0,1)a f x x a a =>≠在其定义域内是减函数,则log 20a <”的逆否命题是( )A .若log 20a ≥,则函数()log (01)a f x x a a =>≠,在其定义域内不是减函数B .若log 20a <,则函数()log (01)a f x x a a =>≠,在其定义域内不是减函数 C .若log 20a ≥,则函数()log (01)a f x x a a =>≠,在其定义域内是减函数 D .若log 20a <,则函数()log (01)a f x x a a =>≠,在其定义域内是减函数 【解析】 ⑴ 在ABC △中,若90C ∠≠°,则A B ∠∠,不都是锐角. ⑵ D . ⑶ A .【演练4】⑴ 设a b ,表示直线,αβ,表示平面,则αβ∥的充分条件是( ) A .a b a b αβ⊥⊥∥,, B .a b a b αβ⊂⊂,,∥ C .a b a b αββα⊂⊂,,∥,∥ D .a b a b βα⊥⊥⊥,, ⑵ 已知a b ,是实数,则“0a >且0b >”是“0a b +>且0ab >”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】 ⑴ A⑵ C【演练5】已知数列{}n a 、{}n b 、{}n c ,其中{}n a 、{}n b 是等比数列.对于任意正整数n ,n a 、n c 、n b 都成等差数列,且10c ≠.试证明:“数列{}n c 成等比数列”的充要条件是“数列{}n a 与{}n b公比相等”.【解析】 充分性:设数列{}n a 与{}n b 的公比都是q ,则11n n a a q -=,11n n b b q -=,而1()2n n n c a b =+111111()2n n a b q c q --=+=,又10c ≠,故{}n c 是公比为q 的等比数列.充分性得证. 必要性:若数列{}n c 是等比数列,设数列{}n a 、{}n b 、{}n c 的公比分别为p q r ,,, 则1111112221112(1)2(2)(3)2c a b c r a p b q c r a p b q ⎧=+⎪=+⎨⎪=+⎩,由(1)(3)⨯得:22222222111114()c r a p a b p q b q =+++ ⑷ 将⑵的两边平方得2222221111142c r a p a b pq b q =++ ⑸比较⑷⑸两式得222p q pq +=,故p q =,即数列{}n a 与{}n b 公比相等.必要性得证.(第16届希望杯数学邀请赛高一第2试)已知等差数列{}n a 中()*n a n ∈∈Z N ,,15a =,2a b =,则0n a ≠的充要条件为______.【解析】0b ≠或4b ≠ 若*n ∃∈N ,使得0n a =,则由{}n a 为等差数列,可设公差为d ,则5511n a d n n -=-=--,而n a ∈Z ,所以d ∈Z , 从而1n -整除5,而*n ∈N ,所以2n =或6. 所以若有0n a =,则只能为2a 或6a ,所以若要0n a ≠,则20a ≠或60a ≠,即0b ≠或4b ≠.大千世界。
选修2-1 常用逻辑用语导学案加课后作业及参考答案

§1.1.1命题导学案【学习要求】1.了解命题的概念.2.会判断命题的真假,能够把命题化为“若p,则q”的形式.【学法指导】学习中要通过命题的一般形式把握命题,从命题的工具作用认识命题,不要过多地纠缠在判断一个语句是不是命题上,只要求能够从课本的例子中了解命题的概念就可以了.【知识要点】1.命题:一般地,我们把用表达的,可以的陈述句叫做命题.2.命题的真假:判断的命题叫做真命题,判断的命题叫做假命题.3.命题的形式:在数学中,“”是命题的常见形式,其中p叫做命题的,q叫做命题的. 【问题探究】探究点一命题的概念及分类问题1我们在初中已经学过许多数学命题,你能举出一些数学命题的例子吗?当时是怎么定义命题的?问题2观察下列语句的特点:(1)两个全等三角形的周长相等;(2)5能被2整除;(3)对顶角相等;(4)今天天气真好啊!(5)请把门关上!(6)2是质数吗?(7)若x=2,则x2=4;(8)3+2=6.回答:①以上有几个命题?②命题必须具备什么特征?问题3数学中的定义、公理、定理都是命题吗?问题4怎样判断一个命题是真命题还是假命题?例1判断下列语句是否是命题,若是,判断其真假,并说明理由.(1)求证3是无理数. (2)若x R,则x2+4x+4≥0.(3)你是高一的学生吗?(4)并非所有的人都喜欢苹果.(5)若xy是有理数,则x、y都是有理数. (6)60x+9>4.跟踪训练1判断下列语句中哪些是命题,是真命题还是假命题?(1)末位是0的整数能被5整除;(2)平行四边形的对角线相等且互相平分;(3)两直线平行,则斜率相等;(4)△ABC中,若∠A=∠B,则sin A=sin B;(5)余弦函数是周期函数吗?探究点二命题的结构问题在数学中,命题的常见形式为“若p,则q”,除此以外,还可以写成什么形式?例2把下列命题改写成“若p,则q”的形式:(1)各位数数字之和能被9整除的整数,可以被9整除;(2)斜率相等的两条直线平行;(3)能被6整除的数既能被3整除也能被2整除;(4)钝角的余弦值是负数.跟踪训练2指出下列命题的条件p与结论q,并判断命题的真假. (1)若整数a是偶数,则a能被2整除;(2)对角线相等的平行四边形是矩形;(3)相等的两个角正切值相等.【当堂检测】1.下列语句为命题的是()A.对角线相等的四边形B.同位角相等C.x≥2D.x2-2x-3<02.下列命题:①面积相等的三角形是全等三角形;②若xy=0,则|x|+|y|=0;③若a>b,则ac2>bc2;④矩形的对角线互相垂直. 其中假命题的个数是_______3.把下列命题写成“若p,则q”的形式.(1)ac>bc⇒a>b;(2)已知x、y为正整数,当y=x+1时,y=3,x=2;(3)当m>14时,mx2-x+1=0无实数根;(4)当abc=0时,a=0或b=0或c=0;(5)负数的立方是负数.【课堂小结】1.根据命题的意义,可以判断真假的陈述句是命题,命题的条件与结论之间属于因果关系,真命题可以给出证明,假命题只需举出一个反例即可.2.任何命题都是由条件和结论构成的,可以写成“若p,则q”的形式.含有大前提的命题写成“若p,则q”的形式,大前提应保持不变.【课后作业】一、基础过关1.下列语句中是命题的是()A.周期函数的和是周期函数吗?B.sin 45°=1C.x2+2x-1>0 D.梯形是不是平面图形呢?2.下列语句中是命题的为()①空集是任何集合的子集;②若x>1,则x>2;③ 3比1大吗?④若平面上两条直线不相交,则它们平行;⑤-2=-2;⑥x>15.A.①②⑥B.①②④C.①④⑤D.①②④⑤3.下列说法正确的是()A.命题“正项等差数列的公差大于零”是真命题B.语句“最高气温30℃时我就开空调”不是命题C.“四边形是菱形”是真命题D.语句“当a>4时,方程x2-4x+a=0有实根”是假命题4.已知a、b为两条不同的直线,α、β为两个不同的平面,且a⊥α,b⊥β,则下列命题中的假命题是() A.若a∥b,则α∥βB.若α⊥β,则a⊥bC.若a、b相交,则α、β相交D.若α、β相交,则a、b相交5.下列命题:①mx2+2x-1=0是一元二次方程;②抛物线y=ax2+2x-1与x轴至少有一个交点;③互相包含的两个集合相等;④空集是任何集合的真子集.其中真命题有()A.1个B.2个C.3个D.4个6.下列命题:①若xy=1,则x、y互为倒数;②对角线垂直的平行四边形是正方形;③平行四边形是梯形;④若ac2>bc2,则a>b.其中真命题的序号是________.7.已知命题:弦的垂直平分线经过圆心,并平分弦所对的弧.若把上述命题改为“若p,则q”的形式,则p是______________________,q是________________________.二、能力提升8.l1,l2,l3是空间三条不同的直线,则下列命题正确的是()A.l1⊥l2,l2⊥l3⇒l1∥l3B.l1⊥l2,l2∥l3⇒l1⊥l3C.l1∥l2∥l3⇒l1,l2,l3共面D.l1,l2,l3共点⇒l1,l2,l3共面9.对于向量a,b,c和实数λ,下列命题中为真命题的是()A.若a·b=0,则a=0或b=0 B.若λa=0,则λ=0或a=0C.若a2=b2,则a=b或a=-b D.若a·b=a·c,则b=c10.给出下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,是真命题的是________.(填序号)11.判断下列语句是否是命题,并说明理由.(1)若x+y是有理数,则x,y均为有理数.(2)一条直线l与平面α不是平行就是相交.(3)x2+2x-3<0.12.把下列命题写成“若p,则q”的形式,并判断其真假.(1)等腰三角形的两个底角相等;(2)当x=2或x=4时,x2-6x+8=0;(3)正方形是矩形又是菱形;(4)方程x2-x+1=0有两个实数根.三、探究与拓展13.设有两个命题:p:x2-2x+2≥m的解集为R;q:函数f(x)=-(7-3m)x是减函数,若这两个命题中有且只有一个是真命题,求实数m的取值范围.§1.1.2四种命题~§1.1.3四种命题间的相互关系导学案【学习要求】1.了解四种命题的概念.2.认识四种命题的结论,会写出某命题的逆命题,否命题和逆否命题.3.理解四种命题的关系.4.会利用命题的等价性解决问题.【学法指导】在本节的学习中,不要去死记硬背形式化的定义与模式,而应多通过具体实例,发现四种命题形式间的逻辑关系,并能利用这种关系对命题真假作出判断,从而体会正难则反思想的应用.【知识要点】1.四种命题的概念一般地,对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么我们把这样的两个命题叫做.其中一个命题叫做原命题,另一个叫做原命题的.也就是说,如果原命题为“若p,则q”,那么它的逆命题为.对于两个命题,其中一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定,我们把这样的两个命题叫做.如果把其中一个命题叫做原命题,那么另一个叫做原命题的.也就是说,如果原命题为“若p,则q”,那么它的否命题为.对于两个命题,其中一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定,我们把这样的两个命题叫做.如果把其中的一个命题叫做原命题,那么另一个叫做原命题的.也就是说,如果原命题为“若p,则q”,那么它的逆否命题为.2.四种命题的相互关系3.四种命题的真假性之间的关系(1)两个命题互为逆否命题,它们有的真假性.(2)两个命题为互逆命题或互否命题,它们的真假性.【问题探究】探究点一四种命题的概念问题1观察下列四个命题:(1)若两个角是对顶角,则它们相等;(2)若两个角相等,则它们是对顶角;(3)若两个角不是对顶角,则它们不相等;(4)若两个角不相等,则它们不是对顶角.命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?问题2若(1)为原命题,则(2)为(1)的________命题,(3)为(1)的________命题,(4)为(1)的________命题.问题3在四种命题中,原命题是固定的吗?例1把下列命题写成“如果p,则q”的形式,并写出它们的逆命题、否命题与逆否命题.(1)正数的平方根不等于0;(2)当x=2时,x2+x-6=0.跟踪训练1分别写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假:(1)实数的平方是非负数;(2)若x、y都是奇数,则x+y是偶数.探究点二四种命题的关系问题1通过以上学习,你认为如果原命题为真,那么它的逆命题、否命题的真假性是怎样的?问题2原命题为真,它的逆否命题的真假性如何?问题3四种命题中,真命题的个数可能为多少?例2下列命题:①“若xy=1,则x、y互为倒数”的逆命题;②“四边相等的四边形是正方形”的否命题;③“梯形不是平行四边形”的逆否命题;④“若ac2>bc2,则a>b”的逆命题.其中的真命题是__________.跟踪训练2有下列四个命题:①“若x+y=0,则x、y互为相反数”的否命题;②“若a≥b,则a2≥b2”的逆否命题;③“若x≤3,则x2-x-6>0”的否命题;④“对顶角相等”的逆命题.其中真命题的个数是()A.0 B.1 C.2 D.3探究点三等价命题的应用问题我们在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题.你认为等价命题证明问题和反证法是不是一回事?例3证明:已知函数f(x)是(-∞,+∞)上的增函数,a、b R∈,若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0.跟踪训练3证明:若a2-4b2-2a+1≠0,则a≠2b+1.【当堂检测】1.命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是()A.若f(x)是偶函数,则f(-x)是偶函数B.若f(x)不是奇函数,则f(-x)不是奇函数C.若f(-x)是奇函数,则f(x)是奇函数D.若f(-x)不是奇函数,则f(x)不是奇函数2.命题“如果x2<1,则-1<x<1”的逆否命题是()A.如果x2≥1,则x≥1,或x≤-1 B.如果-1<x<1,则x2<1C.如果x>1或x<-1,则x2>1 D.如果x≥1或x≤-1,则x2≥13.命题“若平面向量a,b共线,则a,b方向相同”的逆否命题是_________,它是_____命题(填“真”或“假”). 4.给出以下命题:①“若x2+y2≠0,则x、y不全为零”的否命题;②“正多边形都相似”的逆命题;③“若m>0,则x2+x-m=0有实根”的逆否命题. 其中为真命题的是________.5.若命题p的逆命题是q,命题p的否命题是r,则q是r的().A.逆命题B.否命题C.逆否命题D.以上结论都不正确【课堂小结】1.写四种命题时,可以按下列步骤进行:(1)找出命题的条件p和结论q;(2)写出条件p的否定綈p和结论q的否定綈q;(3)按照四种命题的结构写出所有命题.2.判断命题的真假可以根据互为逆否的命题真假性相同来判断,这也是反证法的理论基础.【课后作业】一、基础过关1.命题“若α=π4,则tan α=1”的逆否命题是()A.若α≠π4,则tan α=1 B.若α=π4,则tan α≠1C.若tan α≠1,则α≠π4D.若tan α≠1,则α=π42.设a,b是向量,命题“若a=-b,则|a|=|b|”的逆命题是()A.若a≠-b,则|a|≠|b| B.若a=-b,则|a|≠|b|C.若|a|≠|b|,则a≠-b D.若|a|=|b|,则a=-b3.命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为()A.1 B.2 C.3 D.44.以下说法错误的是()A.如果一个命题的逆命题为真命题,那么它的否命题也必为真命题B.如果一个命题的否命题为假命题,那么它本身一定为真命题C.原命题、否命题、逆命题、逆否命题中,真命题的个数一定为偶数D.一个命题的逆命题、否命题、逆否命题可以同为假命题5.“如果x、y R∈且x2+y2=0,则x、y全为0”的否命题是()A.若x、y R∈且x2+y2≠0,则x、y全不为0 B.若x、y R∈且x2+y2≠0,则x、y不全为0C.若x、y R∈且x、y全为0,则x2+y2=0 D.若x、y R∈且xy≠0,则x+y≠06.命题“正数的绝对值等于它本身”的逆命题是___________________,这是________命题.7.下列命题中:①若一个四边形的四条边不相等,则它不是正方形;②正方形的四条边相等;③若一个四边形的四条边相等,则它是正方形.其中互为逆命题的有__________;互为否命题的有__________;互为逆否命题的有________.(填序号) 8.写出命题“已知a,b R∈,若a2>b2,则a>b”的逆命题、否命题和逆否命题,并判断它们的真假.二、能力提升9.给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限,在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是()A.3 B.2 C.1 D.010.有下列四个命题,其中真命题有:①“若x+y=0,则x、y互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若q≤1,则x2+2x+q=0有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题.其中真命题的序号为()A.①②B.②③C.①③D.③④11.给定下列命题:①若k>0,则方程x2+2x-k=0有实数根;②若x+y≠8,则x≠2或y≠6;③“矩形的对角线相等”的逆命题;④“若xy=0,则x、y中至少有一个为0”的否命题.其中真命题的序号是________.12.判断命题:“若b≤-1,则关于x的方程x2-2bx+b2+b=0有实根”的逆否命题的真假.三、探究与拓展13.求证:如果p2+q2=2,则p+q≤2.§1.2.1充分条件与必要条件导学案【学习要求】1.结合具体实例,理解充分条件、必要条件的意义.2.会判断某些条件之间的关系.【学法指导】充分条件、必要条件是常用的逻辑用语,在数学中有广泛的应用,对于理解数学有很大的帮助.在此引入概念,对于这两个概念的准确理解需要一定的时间体会和思考,对于概念的运用和掌握依赖于后续的学习,不要急于求成,而应在后续的学习中经常借助这些概念表达、阐述和分析.【知识要点】【问题探究】探究点一充分条件、必要条件问题1判断下列两个命题的真假,并思考命题(1)中条件和结论之间的关系:(1)若x>a2+b2,则x>2ab;(2)若ab=0,则a=0.问题2结合充分条件、必要条件的定义,说说你对充分条件与必要条件的理解.问题3判断命题“若x=1,则x2-4x+3=0”中条件和结论的关系,并请你从集合的角度来解释.问题4结合以上分析,请你归纳判断充分条件,必要条件有哪些方法?例1指出下列各组命题中,p是q的什么条件?(充分不必要条件,必要不充分条件,既是充分条件也是必要条件,既不充分也不必要条件)(1)p:(x-2)(x-3)=0,q:x=2;(2)p:数a能被6整除,q:数a能被3整除;(3)p:x>1,q:x2>1;(4)p:x,y不全为0,q:x+y≠0.跟踪训练1指出下列命题中,p是q的什么条件?(1)p:x2=2x+1,q:x=2x+1;(2)p:a2+b2=0,q:a+b=0;(3)p:x=1或x=2,q:x-1=x-1;(4)p:sin α>sin β,q:α>β.探究点二充分条件、必要条件与集合的关系问题设集合A={x|x满足条件p},集合B={x|x满足条件q},若A⊆B,则p是q的什么条件?q是p的什么条件?例2是否存在实数p,使“4x+p<0”是“x2-x-2>0”的充分条件?如果存在,求出p的取值范围;否则,说明理由. 跟踪训练2已知p:3x+m<0,q:x2-2x-3>0,若p是q 的一个充分不必要条件,求m的取值范围.【当堂检测】1.a<0,b<0的一个必要条件为()A.a+b<0 B.a-b>0 C.ab>1 D.ab<-12.如果命题“若A则B”的否命题是真命题,而它的逆否命题是假命题,则A是B的______________条件3.若“x<m”是“(x-1)(x-2)>0”的充分不必要条件,求m的取值范围.4.指出下列各组命题中,p是q的什么条件?(充分不必要条件,必要不充分条件,充分且必要条件,既不充分也不必要条件)(1)p:△ABC中,b2>a2+c2,q:△ABC为钝角三角形;(2)p:△ABC中有两个角相等,q:△ABC是正三角形;(3)若a,b∈R,p:a2+b2=0,q:a=b=0.【课堂小结】1.充分条件、必要条件的判断方法:(1)定义法:直接利用定义进行判断.(2)等价法:“p⇔q”表示p等价于q,要证p⇒q,只需证它的逆否命题綈q⇒綈p即可;同理要证p⇐q,只需证綈q⇐綈p即可.所以p⇔q,只需綈q⇔綈p.(3)利用集合间的包含关系进行判断.2.根据充分条件、必要条件求参数的取值范围时,主要根据充分条件、必要条件与集合间的关系,将问题转化为相应的两个集合之间的包含关系,然后建立关于参数的不等式(组)进行求解.【课后作业】一、基础过关1.“-2<x <1”是“x >1或x <-1”的( )A .充分条件但不是必要条件B .必要条件但不是充分条件C .既不是充分条件,也不是必要条件D .既是充分条件,也是必要条件 2.“ab ≠0”是“直线ax +by +c =0与两坐标轴都相交”的( )A .充分条件但不是必要条件B .必要条件但不是充分条件C .既是充分条件,也是必要条件D .既不是充分条件,也不是必要条件 3.若綈p 是綈q 的必要条件,则q 是p 的( )A .充分条件但不是必要条件B .必要条件但不是充分条件C .既是充分条件,也是必要条件D .既不是充分条件,也不是必要条件 4.下列命题中,真命题是( )A .“x 2>0”是“x >0”的充分条件B .“xy =0”是“x =0”的必要条件C .“|a |=|b |”是“a =b ”的充分条件D .“|x |>1”是“x 2不小于1”的必要条件5.设a ,b 为实数,则“0<ab <1”是“a <1b 或b >1a ”的 ( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 6.设0<x <π2,则“x sin 2x <1”是“x sin x <1”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.设x ,y 是两个实数,命题:“x ,y 中至少有一个数大于1”成立的充分不必要条件是( )A .x +y =2B .x +y >2C .x 2+y 2>2D .xy >1二、能力提升8.不等式(a +x )(1+x )<0成立的一个充分而不必要条件是-2<x <-1,则a 的取值范围是________. 9.设p :x <-1或x >1;q :x <-2或x >1,则綈p 是綈q 的__________条件. 10.设α、β、γ为平面,m 、n 、l 为直线,则对于下列条件: ① α⊥β,α∩β=l ,m ⊥l ;② α∩γ=m ,α⊥β,γ⊥β; ③ α⊥γ,β⊥γ,m ⊥α;④ n ⊥α,n ⊥β,m ⊥α.其中为m ⊥β的充分条件的是________(将你认为正确的所有序号都填上). 11.下列各题中,p 是q 的什么条件?说明理由. (1)p :a 2+b 2=0;q :a +b =0.(2)p :p ≤-2或p ≥2;q :方程x 2+px +p +3=0有实根.(3)p :圆x 2+y 2=r 2与直线ax +by +c =0相切;q :c 2=(a 2+b 2)r 2.12.已知p :-2≤x ≤10,q :x 2-2x +1-m 2≤0(m >0),若綈p 是綈q 的充分不必要条件,求实数m 的取值范围.三、探究与拓展13.设计如下图所示的两个电路图,条件A :“开关S 1闭合”;条件B :“灯泡L 亮”,问A 是B 的什么条件?§1.2.2 充要条件导学案【学习要求】1.理解充要条件的意义.2.会判断、证明充要条件.【学法指导】在数学中,形如“p 是q 的充要条件”的命题是相当普遍的.要证明命题的条件是充要条件,就是既要证明原命题,又要证明原命题的逆命题.证明原命题即证明命题条件的充分性,证明原命题的逆命题,即证明命题条件的必要性.在本节的学习中注意体验数学的等价转化思想,增强逻辑思维能力.【知识要点】1.如果既有 ,又有 ,就记作p ⇔q ,p 是q 的充分必要条件,简称 条件. 2.概括地说,如果 ,那么p 与q 互为充要条件.【问题探究】探究点一 充要条件的判断问题1 已知p :整数a 是6的倍数,q :整数a 是2和3的倍数,那么p 是q 的什么条件?q 又是p 的什么条件?问题2 结合实例说说你对充要条件的理解. 例1 下列各题中,哪些p 是q 的充要条件?(1)p :b =0,q :函数f (x )=ax 2+bx +c 是偶函数; (2)p :x >0,y >0,q :xy >0; (3)p :a >b ,q :a +c >b +c .跟踪训练1 (1)a ,b 中至少有一个不为零的充要条件是( ) A .ab =0 B .ab >0 C .a 2+b 2=0 D .a 2+b 2>0(2)x >2的一个必要不充分条件是__________;x +y >0的一个充分不必要条件是_________________. (3)“函数y =x 2-2x -a 没有零点”的充要条件是________.探究点二 充要条件的证明例2 已知数列{a n }的前n 项和S n =p n +q (p ≠0且p ≠1),求证数列{a n }为等比数列的充要条件为q =-1. 跟踪训练2 求证:方程x 2+(2k -1)x +k 2=0的两个根均大于1的充要条件是k <-2. 跟踪训练3 求关于x 的方程ax 2+x +1=0至少有一个负实根的充要条件.【当堂检测】1.“lg x >lg y ”是“x >y ”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 2.设{a n }是等比数列,则“a 1<a 2<a 3”是“数列{a n }是递增数列”的 ( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件 3.设φR ∈,则“φ=0”是“f (x )=cos(x +φ)(x ∈R)为偶函数”的 ( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件4.“m =-1”是“直线mx +(2m -1)y +1=0与直线3x +my +3=0垂直”的___________条件. 5.已知直线l 1:x +ay +6=0和l 2:(a -2)x +3y +2a =0,则l 1∥l 2的充要条件是a =________. 6.已知p 、q 是r 的必要条件,s 是r 的充分条件,q 是s 的充分条件,那么 (1)s 是q 的什么条件?(2)r 是q 的什么条件?(3)p 是q 的什么条件?【课堂小结】1.充要条件的判断有三种方法:定义法、等价命题法、集合法. 2.充要条件的证明与探求(1)充要条件的证明分充分性和必要性的证明.在证明时要注意两种叙述方式的区别: ①p 是q 的充要条件,则由p ⇒q 证的是充分性,由q ⇒p 证的是必要性; ②p 的充要条件是q ,则p ⇒q 证的是必要性,由q ⇒p 证的是充分性.(2)探求充要条件,可先求出必要条件,再证充分性;如果能保证每一步的变形转化过程都可逆,也可以直接求出充要条件.【课后作业】一、基础过关1.“x ,y 均为奇数”是“x +y 为偶数”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 2.对于非零向量a ,b ,“a +b =0”是“a ∥b ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.一次函数y =-m n x +1n 的图象同时经过第一、三、四象限的必要不充分条件是 ( )A .m >1,且n <1B .mn <0C .m >0,且n <0D .m <0,且n <04.平面α∥平面β的一个充分条件是 ( )A .存在一条直线a ,a ∥α,a ∥βB .存在一条直线a ,a ⊂α,a ∥βC .存在两条平行直线a 、b ,a ⊂α,b ⊂β,a ∥β,b ∥αD .存在两条异面直线a 、b ,a ⊂α,b ⊂β,a ∥β,b ∥α 5.已知a ,b ,c R ∈,“2b =a +c ”是“a ,b ,c 成等差数列”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.在△ABC 中,“△ABC 为钝角三角形”是“AB →·AC →<0”的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 7.对任意实数a ,b ,c ,给出下列命题:①“a =b ”是“ac =bc ”的充要条件;②“a +5是无理数”是“a 是无理数”的充要条件;③“a >b ”是“a 2>b 2”的充分条件;④“a <5”是“a <3”的必要条件.将所有正确命题的序号填在横线上________. 二、能力提升8.已知命题p :集合{x |x =cosn π3,n Z ∈}只有4个元素,q :集合{y |y =x 2+1,x R ∈}与集合{x |y =x 2+1}相等,则新命题:①p 或q ;②p 且q ;③非p ;④非q 中真命题的个数为( ) A .0B .1C .2D .39.已知p :12≤x ≤1,q :(x -a )(x -a -1)>0,若p 是綈q 的充分不必要条件,则实数a 的取值范围是________.10.设A 是B 的充分不必要条件,C 是B 的必要不充分条件,D 是C 的充要条件,则D 是A 的__________条件.11.求不等式ax 2+2x +1>0恒成立的充要条件.12.求证:一元二次方程ax 2+bx +c =0有一正根和一负根的充要条件是ac <0.三、探究与拓展13.设x ,y R ∈,求证|x +y |=|x |+|y |成立的充要条件是xy ≥0.§1.3.1 且(and)~1.3.2 或(or) 导学案【学习要求】1.了解联结词“且”“或”的含义.2.会用联结词“且”“或”联结或改写某些数学命题,并判断新命题的真假.【学法指导】用集合的“交”、“并”之间的关系理解由“且”、“或”构成的命题,建立命题和集合运算之间的关系,体会逻辑用语在表述中的作用,注意逻辑联结词“或”与自然语言中的“或者”的区别与联系,以便准确地表达相关的数学知识.【知识要点】1.“p且q”就是用联结词“”把命题p和命题q联结起来,得到的新命题,记作.2.“p或q”就是用联结词“”把命题p和命题q联结起来,得到的新命题,记作.3.真值表【问题探究】探究点一p∧q命题问题1观察三个命题:①5是10的约数;②5是15的约数;③5是10的约数且是15的约数,它们之间有什么关系?问题2分析问题1中三个命题的真假,并归纳p∧q型命题的真假和命题p,q真假的关系.例1将下列命题用“且”联结成新命题,并判断它们的真假:(1)p:平行四边形的对角线互相平分,q:平行四边形的对角线相等;(2)p:菱形的对角线互相垂直,q:菱形的对角线互相平分;(3)p:35是15的倍数,q:35是7的倍数.跟踪训练1指出下列命题的构成形式及构成它的命题p,q,并判断它们的真假.(1)(n-1)·n·(n+1) (n N∈*)既能被2整除,也能被3整除;(2)∅是{∅}的元素,也是{∅}的真子集.探究点二p∨q命题问题1观察三个命题:①3>2;②3=2;③3≥2,它们之间有什么关系?问题2分析问题1中三个命题的真假,并归纳p∨q型命题的真假与p、q真假的关系.例2分别指出下列命题的形式及命题的真假:(1)相似三角形的面积相等或对应角相等;(2)集合A是A∩B的子集或是A∪B的子集;(3)周长相等的两个三角形全等或面积相等的两个三角形全等.跟踪训练2对下列各组命题,用逻辑联结词“或”构造新命题,并判断它们的真假.(1)p:正数的平方大于0,q:负数的平方大于0;(2)p:3>4,q:3<4;(3)p:π是整数,q:π是分数.探究点三p∨q与p∧q的应用问题如果p∧q为真命题,那么p∨q一定是真命题吗?反之,如果p∨q为真命题,那么p∧q一定是真命题吗?例3设有两个命题.命题p:不等式x2-(a+1)x+1≤0的解集是∅;命题q:函数f(x)=(a+1)x在定义域内是增函数.如果p∧q为假命题,p∨q为真命题,求a的取值范围.跟踪训练3本例中其它条件不变,把“p∧q为假命题,p∨q为真命题”改为“p∨q为真命题”,求a的取值范围. 【当堂检测】1.“p∧q是真命题”是“p∨q是真命题”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.给出下列命题:①2>1或1>3;②方程x2-2x-4=0的判别式大于或等于0;③25是6或5的倍数;④集合A∩B是A的子集,且是A∪B的子集.其中真命题的个数为()A.1 B.2 C.3 D.43.“p是假命题”是“p或q为假命题”的___________条件.4.p:1x-3<0,q:x2-4x-5<0,若p且q为假命题,则x的取值范围是_______________________.【课堂小结】1.正确理解逻辑联结词是解题的关键,日常用语中的“或”是两个中任选一个,不能都选,而逻辑联结词中的“或”两个中至少选一个.2.一个复合命题,从字面上看不一定是“或”、“且”字样,这样需要我们掌握一些词语、符号或式子与逻辑联结词的关系,如“或者”,“x=±3”、“≤”的含义为“或”;“并且”,“綊”的含义为“且”.【课后作业】一、基础过关1.“p是真命题”是“p∧q为真命题”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.命题p:“x>0”是“x2>0”的必要不充分条件,命题q:△ABC中,“A>B”是“sin A>sin B”的充要条件,则() A.p真q假B.p∧q为真C.p∨q为假D.p假q真3.命题“ab≠0”是指()A.a≠0且b≠0B.a≠0或b≠0C.a、b中至少有一个不为0 D.a、b不都为04.下列命题:①5>4或4>5;②9≥3;③若a>b,则a+c>b+c;④菱形的两条对角线互相垂直,其中假命题的个数为()A.0 B.1 C.2 D.35.“1不大于2”可用逻辑联结词表示为____________.6.给定下列命题:p:0不是自然数,q:2是无理数,在命题“p∧q”“p∨q”中,真命题是__________.二、能力提升7.对于命题p:对任意的实数x,有-1≤sin x≤1,q:存在一个实数使sin x+3cos x=π成立,下列结论正确的是()A.p假q真B.p真q假C.p、q都假D.p、q都真。
高三数学第二轮复习专题1 集合与简易逻辑第2节 简易逻辑 (教案及测试;含详解答案)

1.2简易逻辑考纲解读:1. 了解逻辑联结词“或”、“且”、“非”的含义,并能用逻辑联结词正确表达相关内容;2. 了解命题的逆命题、否命题、逆否命题,会分析四种命题之间的关系.能利用互为逆否命题是等价命题来判定有关命题的真假.3. 理解充分、必要、充要条件的意义,并会判定命题P 是命题Q 的什么条件.考点回顾:逻辑是研究思维形式及规律的一门基础学科,基本的逻辑知识是认识问题、研究问题不可缺少的工具,在近年高考中,本节以考查四种命题、逻辑联结词为主,难度也比较小;预计在2010年高考中本节内容仍会有所体现,题型以选择题为主,另外,本节知识可以作为工具考查三角、立体几何、解析几何等的知识点,平时学习要注意这些知识的联系与应用.基础知识过关: 逻辑联结词:1. 命题:(1)、定义:能够 的语句叫命题.(2)、分类:按命题的正确与否,命题可分为 、 . 按是否含有逻辑联结词命题可分为 、 . 2.逻辑联结词: 这些词叫做逻辑联结词. 3.依据真值表判断命题的真假:(1)、非P 形式的复合命题:当P 为真时,非P 为 ,当P 为假时,非P 为 . (2)、P 且q 形式的复合命题:当p 、q 都为真时,p 且q 为 ; 时,p 且q 为假. (3)、P 或q 形式的复合命题:当p 或q 至少有一个为真时,p 或q 为 ;当 时,p 或q 为假. 四种命题1、四种命题:原命题:若p 则q ,则逆命题为 ;否命题为 ;逆否命题为 .2、四种命题的关系:若原命题为真,则它的逆否命题 ;原命题与它的逆否命题 ;同一个的命题的逆命题和否命题 .3、反证法:欲证“若p 则q ”为真命题,需从否定其 出发,经过正确的逻辑推理导出矛盾,从而判定原命题为真,这样的方法称为反证法. 充要条件 1、 从逻辑关系上看:(1)、若p q ⇒,但q p ,则p 是q 的 条件; (2)、若q p ⇒,但p q,则p 是q 的 条件; (3)、若p q ⇒且q p ⇒,则p 是q 的 条件; (4)、若p q 且q p ,则p 是q 的 条件. 2、从集合与集合之间的关系看:(1)、若A B ⊆,则A 是B 的 条件; (2)、若A B ⊇,则A 是B 的 条件; (3)、若A=B,则A 是B 的 条件; (4)、若B A A B 且刎,则A 是B 的 条件.答案:逻辑联结词:1.(1)、判断真假(2)、真命题 假命题 简单命题 复合命题 2、或 且 非 3、(1)、假 真(2)、真 当p 或q 至少有一个为假 (3)、真 当p 和q 都为假 四种命题:1、若q 则p 若p q ⌝⌝则 q p ⌝⌝若则2、真 等价 等价3、结论 充要条件:1、(1)、充分不必要 (2)、必要不充分 (3)、充要(4)、既不充分也不必要 2、(1)、充分不必要 (2)、必要不充分 (3)、充要(4)、既不充分也不必要高考题型归纳:简易逻辑题型1.判断复合命题的真假此类问题主要是考查真值表的应用,常以选择题的形式出现。
高中物理 简单的逻辑电路复习 精品导学案 新人教版选修3-1

简单的逻辑电路【学习目标】了解“与”逻辑、“或”逻辑和“非”逻辑的意义,理解条件与结果的关系,以及这些逻辑关系的真值表【自主学习】1.数字电路的工作状态有---、---两个独立的状态。
2.基本的逻辑关系有---、---、---。
基本的逻辑电路有---、---、---。
3.“与”门的符号为---;“或”门的符号为---;“非”门的符号为---。
4.三种基本逻辑电路(1)“与”门真值表(2)“或”门真值表(3)“非”门真值表1、在举重比赛中,有甲、乙、丙三名裁判,其中甲为主裁判,乙、丙为副裁判,当主裁判和一名以上(包括一名)副裁判认为运动员上举合格后,才可发出合格信号。
试列出真值表2、如图(1)所示,表示输入端A、B的电势随时间的变化关系,完成下题:求图(2)中输出Y随时间变化的关系。
【针对训练】1、教室前门共有三把钥匙,这三把钥匙之间的关系是---------逻辑关系。
请写出逻辑符号以及真值表(钥匙存在为“1”,不存在为“0”,门打开为“1”,未打开为“0”)。
钥匙结果A B C Y3、楼梯过道中的电灯往往采用如图电路控制,设高电压为“1”,底电压为“0”,试讨论灯泡L的亮暗情况,并列出真值表A B Y4、请试着写出如图中A、B、C及Y的真值表5、一个与门的输出端与一个非门的输入端相连形成一个与非门,如图(1)所示。
已知输入A、B的波形如图(2)所示,试画出Y的波形图【能力训练】1、如图是一个火警报警装置的逻辑电路图。
Rt是一个热敏电阻,,低温时电阻值很大,高温时电阻很小,R是一个阻值较小的分压电阻。
(1)要做到低温时电铃不响,火警时产生高温,电铃响起。
在图中虚线处应接入怎样的元件?(2)为什么温度高时电铃会被接通?(3)为了提高该电路的灵敏度,即报警温度调得稍抵些,R的值应大一些还是小一些?2、如图所示为三个门电路符号,下列判断正确的是A、甲为“非”门、乙为“与”门、丙为“或”门B、甲为“与”门、乙为“或”门、丙为“非”门C、甲为“非”门、乙为“或”门、丙为“与”门D、甲为“或”门、乙为“与”门、丙为“非”门3、如图所示是一个温度报警电路,R1为热敏电阻,R2为可变电阻,是斯密特触发器,为蜂鸣器,(1)请你说明工作原理,(2)怎样能够使热敏电阻在感测到更高的温度时才报警?4、如图所示为热水系统的恒温器电路,当温度低时,热敏电阻的电阻很大,温度高时,热敏电阻的电阻就很小。
高中选修1-1导学案 第一章 常用逻辑用语(含答案)

第一章 常用逻辑用语1.1.1 命题 --1.1.2四种命题学案【学习目标】1.理解命题的概念及命题的构成形式,并会判断一个命题的真假;2.了解命题的逆命题、否命题和逆否命题;3.会根据原命题写出逆命题、否命题和逆否命题。
【学习过程】1.命题的定义:我们把用语言、符号或式子表达的,可以判断真假的 叫做命题。
其中判断为真的语句叫做 ,判断为假的语句叫做 。
点评:判断一命题的真假的标准:是否符合“是陈述句”和“可以判断真假”这两个条件。
2.命题的结构:在数学中,具有“若则”这种形式的命题是较为常见的,我们把这种形式的命题中的叫做 ,叫做 。
3.原命题:若,则;逆命题: ;否命题: ;逆否命题: 。
4.关于逆命题、否命题与逆否命题,也可以如下表述:(1)交换原命题的条件和结论,所得的命题是原命题的 ;(2)同时否定原命题的条件和结论,所得的命题是原命题的 ;(3)交换原命题的条件和结论,同时进行否定,所得的命题是原命题的 。
例题:写出下列命题的逆命题、否命题与逆否命题.(1)若,则;(2)垂直于同一平面的两直线平行。
【学习评价】1.下列语句是命题的为( )A .这是一棵小树.B .对顶角相等吗?C .D .2不是最小的质数.2.命题“若a >b ,则a-8>b-8”的逆否命题是( )A .若a<b ,则a-8>b-8.B .若a-8>b-8,则a >b .C .若a ≤b ,则a-8≤b-8.D .若a-8≤b-8,则a ≤b .3.给出下列命题:①若x y=1,则x ,y 互为倒数;②两个有理数的和是有理数;③若A ∪B=B ,则A B ;④相似的三角形的周长相等,其中真命题是( )A .①.B .①②.C .①②③.D .①③④.4.将命题“平行四边形的对角线互相平分”改写成“若P ,则q ”的形式: .5.命题“若a ,b 都是偶数,则a+b 是偶数”的逆否命题是 . p q p q p q 0a =0ab =0122>-+x x ⊇6.若命题p 的逆命题是q ,命题r 是命题q 的否命题,则p 是r 的 命题.7.把下列命题写成“若p ,则q ” 的形式,并判断它们的真假.(1)实数的平方是非负数.(2)等底等高的两个三角形是全等三角形.8.写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假.(1)若a=b ,则ac=bc .(2)若圆心到直线的距离等于半径,则该直线是圆的切线.9.写出下列命题的否命题,并判断它们的真假.(1)若A=B ,则sinA=sinB .(2)周长相等的两个三角形全等.10.把下列命题改写成“若p ,则q ”的形式,并写出它们的逆命题、否命题和逆否命题.(1)矩形的四个角均为直角.(2)对角线互相垂直且平分的四边形是菱形.(3)平行于同一平面的两直线平行。
高中数学《简单的逻辑联结词》导学案
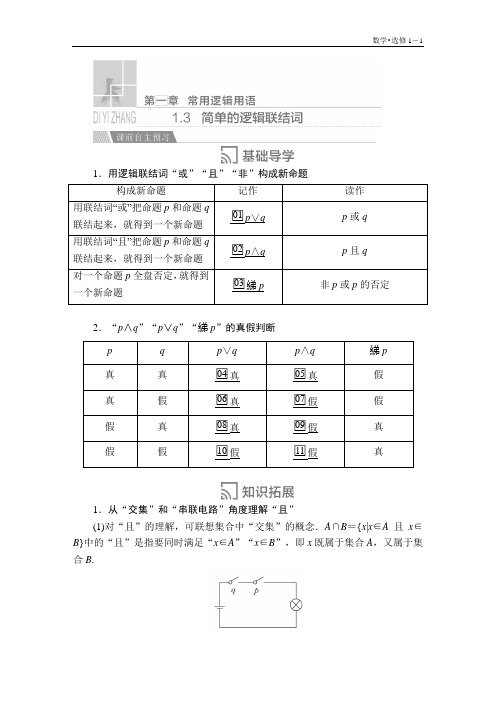
1.用逻辑联结词“或”“且”“非”构成新命题构成新命题记作读作用联结词“或”把命题p和命题q□01p∨q p或q联结起来,就得到一个新命题用联结词“且”把命题p和命题q□02p∧q p且q联结起来,就得到一个新命题对一个命题p全盘否定,就得到□03綈p 非p或p的否定一个新命题2.“p∧q”“p∨q”“綈p”的真假判断p q p∨q p∧q 綈p真真□04真□05真假真假□06真□07假假假真□08真□09假真假假□10假□11假真1.从“交集”和“串联电路”角度理解“且”(1)对“且”的理解,可联想集合中“交集”的概念.A∩B={x|x∈A且x∈B}中的“且”是指要同时满足“x∈A”“x∈B”,即x既属于集合A,又属于集合B.(2)也可以从串联电路理解联结词“且”的含义.如图,若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∧q的真与假.2.从“并集”和“并联电路”角度理解“或”(1)对“或”的理解,可联想集合中“并集”的概念.A∪B={x|x∈A或x∈B}中的“或”指“x∈A”“x∈B”中至少有一个是成立的,即可以x∈A且x∉B,也可以x∉A且x∈B,还可以x∈A且x∈B.(2)也可以从并联电路理解联结词“或”的含义.如图,若开关p,q的闭合与断开分别对应命题p,q的真与假,则整个电路的接通与断开分别对应命题p∨q的真与假.3.逻辑联结词“且”“或”与日常用语“且”“或”的区别“或”是具有选择性的逻辑联结词,含有三层含义,即“p或q”有:p成立而q不成立,p不成立而q成立,p成立且q也成立.与日常用语中的“或”意义不完全相同.日常用语中的“或”,带有两者选择其一的意思,联结词“且”与日常用语中的“且”含义一致,表示“并且”“同时”的意思.4.命题否定与否命题的区别(1)命题的否定,即“非命题”与原命题的真假相反,即綈p包含p结论的所有对立面.“非命题”的真假性与原命题相反,而“否命题”的真假性与原命题没有关系.(2)命题的否定(非p)只否定命题的结论,不否定命题的条件,而否命题是把原命题的条件、结论都否定.1.判一判(正确的打“√”,错误的打“×”)(1)“綊”的含义是“且”,“≤”的含义是“或”,“∉”的含义是“非”.()(2)“p∨q为假命题”是“p为假命题”的充要条件.()(3)命题“p∨(綈p)”是真命题.()(4)矩形的对角线相等且平分是“p∨q”的形式命题.()答案(1)√(2)×(3)√(4)×2.做一做(请把正确的答案写在横线上)(1)命题“3≤3”的构成形式是________________________________;该命题是________命题(填“真”或“假”).(2)若p真q假,则下列命题是真命题的是________________________.①p∨q;②p∧q;③綈p;④綈q.(3)命题“若x>1,则x2>1”的否定是________.(4)命题p:{2}∈{2,3},q:{2}⊆{2,3},则下列对命题的判断,正确的是________(填上所有正确的序号).①p或q为真;②p或q为假;③p且q为真;④p且q为假;⑤非p为真;⑥非q为假.答案(1)p∨q真(2)①④(3)若x>1,则x2≤1(4)①④⑤⑥探究1含有逻辑联结词的命题的构成例1指出下列命题的形式及构成它的命题.(1)向量既有大小又有方向;(2)矩形有外接圆或有内切圆;(3)集合A⊆/(A∪B);(4)正弦函数y=sin x(x∈R)是奇函数并且是周期函数.[解](1)是“p∧q”形式的命题.其中p:向量有大小,q:向量有方向.(2)是“p∨q”形式的命题.其中p:矩形有外接圆,q:矩形有内切圆.(3)是“綈p”形式的命题.其中p:A⊆(A∪B).(4)是“p∧q”形式的命题.其中p:正弦函数y=sin x(x∈R)是奇函数,q:正弦函数y=sin x(x∈R)是周期函数.拓展提升复合命题的构成方式用“或”“且”“非”联结两个简单命题时,要正确理解这三个联结词的意义,通常情况下,可以直接使用逻辑联结词联结,有时为了通顺也可以适当添加词语或省略联结词.如:甲是运动员兼教练员,就省略了“且”.【跟踪训练1】分别写出由下列命题构成的“p∨q”“p∧q”“綈p”形式的复合命题.(1)p:π是无理数,q:e不是无理数;(2)p:方程x2+2x+1=0有两个相等的实数根,q:方程x2+2x+1=0两根的绝对值相等;(3)p:三角形的外角等于与它不相邻的两个内角的和,q:三角形的外角大于与它不相邻的任何一个内角.解(1)“p∨q”:π是无理数或e不是无理数;“p∧q”:π是无理数且e不是无理数;“綈p”:π不是无理数.(2)“p∨q”:方程x2+2x+1=0有两个相等的实数根或两根的绝对值相等;“p∧q”:方程x2+2x+1=0有两个相等的实数根且两根的绝对值相等;“綈p”:方程x2+2x+1=0没有两个相等的实数根.(3)“p∨q”:三角形的外角等于与它不相邻的两个内角的和或大于与它不相邻的任何一个内角;“p∧q”:三角形的外角等于与它不相邻的两个内角的和且大于与它不相邻的任何一个内角;“綈p”:三角形的外角不等于与它不相邻的两个内角的和.探究2判断含有逻辑联结词的命题的真假例2分别写出由下列各组命题构成的“p∨q”“p∧q”“綈p”形成的命题,并判断其真假.(1)p:等腰梯形的对角线相等,q:等腰梯形的对角线互相平分;(2)p:函数y=x2-2x+2没有零点,q:不等式x2-2x+1>0恒成立.[解](1)p∨q:等腰梯形的对角线相等或互相平分,真命题.p∧q:等腰梯形的对角线相等且互相平分,假命题.綈p:等腰梯形的对角线不相等,假命题.(2)p∨q:函数y=x2-2x+2没有零点或不等式x2-2x+1>0恒成立,真命题.p∧q:函数y=x2-2x+2没有零点且不等式x2-2x+1>0恒成立,假命题.綈p:函数y=x2-2x+2有零点,假命题.拓展提升1.命题结构的两种类型及判断方法(1)从含有联结词“且”“或”“非”或者与之等价的词语上进行判断.(2)若命题中不含有联结词,则从命题所表达的数学意义上进行判断.2.判断命题真假的三个步骤(1)明确命题的结构,即命题是“p∧q”“p∨q”,还是“綈p”;(2)对命题p和q的真假作出判断;(3)由“p∧q”“p∨q”“綈p”的真假判断方法给出结论.【跟踪训练2】不用逻辑联结词改写下列命题,直接判断“p∨q”“p∧q”“綈p”形式命题的真假.(1)p:不等式x2+2x+3>2的解集为R,q:不等式x2+2x+3≤2的解集为∅;(2)p:函数f(x)=-2x2-3x+7,当x=-34时,取到最大值,q:函数g(x)=2sin x+3cos x的最小值为- 5.解(1)∵p,q都是假命题,∴“p∨q”为假命题,“p∧q”为假命题,“綈p”为真命题.(2)∵p,q都是真命题,∴“p∨q”为真命题,“p∧q”为真命题,“綈p”为假命题.探究3命题的否定与否命题例3写出下列命题的否定形式和否命题.(1)若abc=0,则a,b,c中至少有一个为零;(2)等腰三角形的两内角相等;(3)自然数的平方是正数.[解](1)否定形式:若abc=0,则a,b,c全不为零;否命题:若abc≠0,则a,b,c全不为零.(2)否定形式:等腰三角形的任意两个内角都不相等;否命题:不是等腰三角形的三角形任意两个内角都不相等.(3)否定形式:自然数的平方不是正数;否命题:不是自然数的数的平方不是正数.拓展提升命题的否定与否命题的解决策略(1)解决此类问题:首先要分清命题的条件和结论.命题的否定与否命题是不同的概念.命题的否定是只否定命题的结论,命题的否命题为条件和结论均否定.(2)一般地,写一个命题的否定,往往需要对正面叙述的词语进行否定,下面我们把常用的一些词语和它的否定词语对照列表如下:原词语等于大于(>)小于(<)是都是否定词语不等于不大于(≤)不小于(≥)不是不都是原词语至多有一个至少有一个至多有n个否定词语至少有两个一个也没有至少有n+1个原词语任意的任意两个所有的能或否定词语某个某两个某些不能且【跟踪训练3】写出下列命题的否定及其否命题,并判断它们的真假.(1)若x,y都是奇数,则x+y是偶数;(2)若一个数是质数,则这个数是奇数;(3)若两个角相等,则这两角是对顶角;(4)如果m2+n2+a2+b2=0,则实数m,n,a,b全为零.解 (1)命题的否定:若x ,y 都是奇数,则x +y 不是偶数,是假命题; 否命题:若x ,y 不都是奇数,则x +y 不是偶数,是假命题.(2)命题的否定:若一个数是质数,则这个数不一定是奇数,是真命题; 否命题:若一个数不是质数,则这个数不是奇数,是假命题.(3)命题的否定:若两个角相等,则这两个角不一定是对顶角,是真命题; 否命题:若两个角不相等,则这两个角不是对顶角,是真命题.(4)命题的否定:如果m 2+n 2+a 2+b 2=0,则实数m ,n ,a ,b 不全为零,是假命题.否命题:如果m 2+n 2+a 2+b 2≠0,则实数m ,n ,a ,b 不全为零,是真命题. 探究4 利用命题的真假求参数的取值范围例4 已知p :方程x 2+mx +1=0有两个不等的负根,q :方程4x 2+4(m -2)x +1=0无实根.若p ∨q 为真,p ∧q 为假,求m 的取值范围.[解] 若方程x 2+mx +1=0有两个不等的负根,则⎩⎪⎨⎪⎧Δ=m 2-4>0,-m <0,解得m >2,即p :m >2. 若方程4x 2+4(m -2)x +1=0无实根, 则Δ=16(m -2)2-16=16(m 2-4m +3)<0, 解得1<m <3,即q :1<m <3.因为p ∨q 为真,所以p ,q 至少有一个为真. 又p ∧q 为假,所以p ,q 至少有一个为假.因此,p ,q 两命题应一真一假,即p 为真,q 为假或p 为假,q 为真. 所以⎩⎪⎨⎪⎧m >2,m ≤1或m ≥3或⎩⎨⎧m ≤2,1<m <3.解得m ≥3或1<m ≤2,即m 的取值范围是{m |m ≥3或1<m ≤2}.[条件探究] 如果把例4条件中的“负”改为“正”,“p ∨q 为真”改为“綈p 为假”,其他条件不变,求实数m 的取值范围.解 若方程x 2+mx +1=0有两个不等的正根,则⎩⎪⎨⎪⎧Δ=m 2-4>0,-m >0,解得m <-2,即p :m <-2. 若方程4x 2+4(m -2)x +1=0无实根, 则Δ=16(m -2)2-16=16(m 2-4m +3)<0, 解得1<m <3,即q :1<m <3, 因为綈p 为假,p ∧q 为假, 所以p 为真,q 为假.所以⎩⎪⎨⎪⎧m <-2,m ≤1或m ≥3,解得m <-2.所以m 的取值范围是{m |m <-2}. 拓展提升应用逻辑联结词求参数范围的四个步骤(1)分别求出命题p ,q 为真时对应的参数集合A ,B ; (2)由“p 且q ”“p 或q ”的真假讨论p ,q 的真假; (3)由p ,q 的真假转化为相应的集合的运算; (4)求解不等式或不等式组得到参数的取值范围.注:当p ,q 中参数的范围不易求出时,也可以利用綈p 与p ,綈q 与q 不能同真同假的特点,先求綈p ,綈q 中参数的范围.【跟踪训练4】 已知命题p :方程2x 2+ax -a 2=0在[-1,1]上有解;命题q :只有一个实数x 0满足不等式x 20+2ax 0+2a ≤0,若命题“p ∨q ”是假命题,求a 的取值范围.解 由2x 2+ax -a 2=0,得(2x -a )(x +a )=0, ∴x =a2或x =-a , ∴当命题p 为真命题时, |a ||2|≤1或|-a |≤1,∴|a|≤2.又“只有一个实数x0满足不等式x20+2ax0+2a≤0”,即抛物线y=x2+2ax+2a与x轴只有一个交点,∴Δ=4a2-8a=0,∴a=0或a=2.∴当命题q为真命题时,a=0或a=2.∴命题“p∨q”为真命题时,|a|≤2.∵命题“p∨q”为假命题,∴a>2或a<-2.1.判断不含有逻辑联结词的命题构成形式的关键:弄清构成它的命题条件、结论.2.对用逻辑联结词联结的复合命题的真假进行判断时,首先找出构成复合命题的简单命题,判断简单命题的真假,然后分析构成形式,根据构成形式判断复合命题的真假.(1)“p∧q”形式的命题简记为:同真则真,一假则假;(2)“p∨q”形式的命题简记为:同假则假,一真则真.3.“否命题”与命题的“否定”的区别:对命题的否定(即非p)只是否定命题的结论,而否命题(“若p则q”形式的命题)既否定条件又否定结论.否命题与原命题的真假无必然联系,而命题的否定与原命题的真假总是相对立的,即一真一假.1.命题:“菱形的对角线互相垂直平分”,使用的逻辑联结词的情况是()A.没有使用逻辑联结词B.使用了逻辑联结词“且”C.使用了逻辑联结词“或”D.使用了逻辑联结词“非”答案 B解析菱形的对角线互相垂直且互相平分,命题中使用了逻辑联结词“且”.2.下列命题p的否定为真命题的是()A.y=cos x是偶函数B.y=|sin x|是偶函数C.空集不是它本身的子集D.0是自然数答案 C解析要使命题p的否定为真命题,则命题p为假命题.由于空集是任何集合的子集,故C中命题为假命题.3.已知命题p:设x∈R,若|x|=x,则x>0,命题q:设x∈R,若x2=3,则x=3,则下列命题为真命题的是()A.p∨q B.p∧qC.(綈p)∧q D.(綈p)∨q答案 D解析由|x|=x应得x≥0而不是x>0,故p为假命题;由x2=3应得x=±3,而不只有x=3,故q为假命题.因此綈p为真命题,从而(綈p)∨q也为真命题.4.用“或”“且”填空.(1)若x∈A∪B,则x∈A________x∈B.(2)若x∈A∩B,则x∈A________x∈B.(3)若ab=0,则a=0________b=0.(4)若a2+b2=0,则a=0________b=0.答案(1)或(2)且(3)或(4)且解析(1)∵A∪B={x|x∈A或x∈B},∴x∈A∪B时,x∈A或x∈B.(2)∵A∩B={x|x∈A且x∈B},∴x∈A∩B时,x∈A且x∈B.(3)若ab=0,则a=0或b=0.(4)若a2+b2=0,则a=0且b=0.5.分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的新命题,并判断其真假.(1)p:3是9的约数,q:3是18的约数;(2)p:不等式x2-2x-3>0的解集是(-∞,-1),q:不等式x2-2x-3>0的解集是(3,+∞).(3)p:π是有理数,q:π是无理数.解(1)p或q:3是9的约数或是18的约数,真;p且q:3是9的约数且是18的约数,真;非p:3不是9的约数,假.(2)p或q:不等式x2-2x-3>0的解集是(-∞,-1)或不等式x2-2x-3>0的解集是(3,+∞),假;p且q:不等式x2-2x-3>0的解集是(-∞,-1)且不等式x2-2x-3>0的解集是(3,+∞),假;非p:不等式x2-2x-3>0的解集不是(-∞,-1),真.(3)p或q:π是有理数或是无理数,真;p且q:π是有理数且是无理数,假;非p:π不是有理数,真.A级:基础巩固练一、选择题1.如果命题“p或q”与命题“非p”都是真命题,那么()A.命题p不一定是假命题B.命题q一定是真命题C.命题q不一定是真命题D.p与q的真假相同答案 B解析∵“非p”为真命题,∴p为假命题.又∵p或q为真命题,∴q为真命题.故选B.2.命题“三角形中最多有一个内角是钝角”的否定是()A.有两个内角是钝角B.有三个内角是钝角C.至少有两个内角是钝角D.没有一个内角是钝角答案 C解析∵“最多”的否定为“至少”,∴“最多有一个内角是钝角”的否定为“至少有两个内角是钝角”.3.设p,q是简单命题,则“‘p且q’为假”是“‘p或q’为假”的() A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件答案 A解析“p且q”为假,即p和q中至少有一个为假;“p或q”为假,即p 和q都为假.故“‘p且q’为假”是“‘p或q’为假”的必要不充分条件.故选A.4.如果命题“綈(p∨q)”为假命题,则()A.p,q均为真命题B.p,q均为假命题C.p,q中至少有一个为真命题D.p,q中至多有一个为真命题答案 C解析因为命题“綈(p∨q)”为假命题,所以p∨q为真命题,所以p,q一真一假或都是真命题.5.已知命题p:函数y=2|x-1|的图象关于直线x=1对称;q:函数y=x+1 x在(0,+∞)上是增函数.由它们组成的新命题“p且q”“p或q”“綈p”中,真命题有()A.0个B.1个C.2个D.3个答案 B解析命题p是真命题,y=x+1x在(0,1)上为减函数,在(1,+∞)上为增函数,故q为假命题.∴p且q为假,p或q为真,綈p为假.6.给出下列两个命题,命题p:“x>3”是“x>5”的充分不必要条件;命题q:函数y=log2(x2+1-x)是奇函数,则下列命题是真命题的是() A.p∧q B.p∨綈q C.p∨q D.p∧綈q答案 C解析因为“x>3”是“x>5”的必要不充分条件,故命题p为假命题;因为f(-x)+f(x)=log2(x2+1+x)+log2(x2+1-x)=log21=0,所以命题q为真命题.则p∧q为假命题,p∨綈q为假命题,p∨q为真命题,p∧綈q为假命题.故选C.二、填空题7.下列命题中:①命题“2是素数也是偶数”是“p ∧q ”命题;②命题“(綈p )∧q ”为真命题,则命题p 是假命题;③命题p :1、3、5都是奇数,则綈p :1、3、5不都是奇数;④命题“(A ∩B )⊆A ⊆(A ∪B )”的否定为“(A ∩B )⊇A ⊇(A ∪B )”.其中,所有正确命题的序号为________.答案 ①②③解析 ①②③都正确;命题“(A ∩B )⊆A ⊆(A ∪B )”的否定为“(A ∩B )⊆/ A 或A ⊆/ (A ∪B )”,④不正确.8.命题p :不等式ax +3>0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x >-3a ,命题q :在等差数列{a n }中,若a 1<a 2,则数列{a n }是递增数列,则“p ∧q ”“p ∨(綈q )”“(綈p )∧q ”中是真命题的是________.答案 (綈p )∧q解析 易知p 为假命题,q 为真命题,故只有(綈p )∧q 为真命题.9.已知命题p :函数f (x )=(2a -1)x +b 在R 上是减函数;命题q :函数g (x )=x 2+ax 在[1,2]上是增函数,若p ∧q 为真,则实数a 的取值范围是________.答案 ⎣⎢⎡⎭⎪⎫-2,12 解析 当命题p 为真命题时,有2a -1<0,a <12,当命题q 为真命题时,有-a 2≤1,a ≥-2.因为p ∧q 为真,所以p ,q 都是真命题,所以a 的取值范围是⎣⎢⎡⎭⎪⎫-2,12. 三、解答题10.分别指出由下列各组命题构成的“p 或q ”“p 且q ”“非p ”形式的命题的真假.(1)p :∅{0},q :0∈∅;(2)p :3是无理数,q :π不是无理数;(3)p :集合A =A ,q :A ∪A =A ;(4)p :函数y =x 2+3x +4的图象与x 轴有公共点,q :方程x 2+3x -4=0没有实数根.解 (1)∵p 真q 假,∴“p 或q ”为真,“p 且q ”为假,“非p ”为假.(2)∵p 真q 假,∴“p 或q ”为真,“p 且q ”为假,“非p ”为假.(3)∵p 真q 真,∴“p 或q ”为真,“p 且q ”为真,“非p ”为假.(4)∵p 假q 假,∴“p 或q ”为假,“p 且q ”为假,“非p ”为真.B 级:能力提升练1.设命题p :方程2x 2+x +a =0的两根x 1,x 2满足x 1<1<x 2,命题q :函数y =log 2(ax -1)在区间[1,2]内单调递增.(1)若p 为真命题,求实数a 的取值范围;(2)试问:p ∧q 是否有可能为真命题?若有可能,求出a 的取值范围;若不可能,请说明理由.解 (1)令f (x )=2x 2+x +a ,则f (1)<0,∴3+a <0.∴a <-3.(2)若q 为真命题,则a >0且a -1>0,∴a >1.∵a <-3与a >1不可能同时成立,∴p ∧q 不可能为真命题.2.已知命题p :x 1和x 2是方程x 2-mx -2=0的两个实根,不等式a 2-5a -3≥|x 1-x 2|对任意实数m ∈[-1,1]恒成立;命题q :不等式ax 2+2x -1>0有解.若p ∧q 是假命题,綈p 也是假命题.求实数a 的取值范围.解 ∵p ∧q 是假命题,綈p 是假命题,∴命题p 是真命题,命题q 是假命题.∵x 1,x 2是方程x 2-mx -2=0的两个实根,∴⎩⎪⎨⎪⎧x 1+x 2=m ,x 1x 2=-2.∴|x 1-x 2|=(x 1+x 2)2-4x 1x 2=m 2+8, ∴当m ∈[-1,1]时,|x 1-x 2|max =3.由不等式a 2-5a -3≥|x 1-x 2|对任意实数m ∈[-1,1]恒成立,可得a 2-5a -3≥3.∴a ≥6或a ≤-1,∴当命题p 为真命题时,a ≥6或a ≤-1. 命题q :不等式ax 2+2x -1>0有解, ①当a >0时,显然有解;②当a =0时,2x -1>0有解;③当a <0时,∵ax 2+2x -1>0,Δ=4+4a >0,∴-1<a <0. 从而命题q :不等式ax 2+2x -1>0有解时,a >-1. 又命题q 是假命题,∴a ≤-1.综上所述:⎩⎪⎨⎪⎧ a ≥6或a ≤-1,a ≤-1⇒a ≤-1. 所以所求a 的取值范围为(-∞,-1].。
清泉州阳光实验学校高三数学高考导学练系列教案简易逻辑

清泉州阳光实验学校简易逻辑1.理解逻辑联结词“或者者〞、“且〞、“非〞的含义;理解四种命题及其互相关系;掌握充分条件、必要条件及充要条件的意义.2.学会运用数形结合、分类讨论的思想方法分析和解决有关集合问题,形成良好的思维品质;学会判断和推理,解决简易逻辑问题,培养逻辑思维才能.逻辑是一个新增内容,据的特点,在高考中应一般题、填空题中出现,假设在解答题中出现,那么只会是中低档题.2.集合、简易逻辑知识,作为一种数学工具,在函数、方程、不等式、排列组合及曲线与方程等方面都有广泛的运用,高考题中常以上面内容为载体,以集合的语言为表现形式,结合简易逻辑知识考察学生的数学思想、数学方法和数学才能,题型常以解答题的形式出现.第1课时逻辑联结词和四种命题一、逻辑联结词1.可以的语句叫做命题.命题由两部分构成;命题有之分;数学中的定义、公理、定理等都是命题.2.逻辑联结词有,不含的命题是简单命题.由的命题是复合命题.复合命题的构成形式有三种:,(其中p ,q 都是简单命题).3.判断复合命题的真假的方法—真值表:“非p 〞形式的复合命题真假与p 的当p 与q 都真时,p 且q 形式的复合命题,其他情形;当p 与q 都时,“p 或者者q 〞复合形式的命题为假,其他情形.二、四种命题1.四种命题:原命题:假设p 那么q ;逆命题:、否命题:逆否命题:.2.四种命题的关系:原命题为真,它的逆命题、否命题、逆否命题.原命题与它的逆否命题同、否命题与逆命题同.3.反证法:欲证“假设p 那么q 〞为真命题,从否认其出发,经过正确的逻辑推理导出矛盾,从而断定原命题为真,这样的方法称为反证法.或者者q 〞为真,“p 且q 〞为假,“非p 〞为真的是 〔〕A .p:0=∅;q:0∈∅B .p :在∆ABC 中,假设cos2A =cos2B ,那么A =B ;:q y =sinx 在第一象限是增函数C .),(2:R b a ab b a p ∈≥+;:q 不等式x x >的解集为()0,∞-D .p :圆()1)2(122=-+-y x 的面积被直线1=x 平分;q :椭圆13422=+y x 的一条准线方程是x =4解:由条件,知命题p 假且命题q 真.选项(A)中命题p 、q 均假,排除;选项(B)中,命题p 真而命题q 假,排除;选项(D)中,命题p 和命题q 都为真,排除;应选(C).变式训练1:假设命题“p 或者者q 〞是真命题,“p 且q 〞是假命题.那么〔〕A .命题p 和命题q 都是假命题B .命题p 和命题q 都是真命题C .命题p 和命题“非q 〞真值不同D .命题q 和命题p 的真值不同解:D例2.分别写出以下命题的逆命题、否命题、逆否命题,并判断它们的真假:(1)假设q<1,那么方程x2+2x +q =0有实根;(2)假设ab =0,那么a =0或者者b =0;(3)假设x2+y2=0,那么x 、y 全为零.解:(1)逆命题:假设方程x2+2x +q =0有实根,那么q <1,为假命题.否命题:假设q≥1,那么方程x2+2x +q =0无实根,为假命题.逆否命题:假设方程x2+2x +q =0无实根,那么q≥1,为真命题.(2)逆命题:假设a =0或者者b =0,那么ab =0,为真命题.否命题:假设ab≠0,那么a≠0且b≠0,为真命题.逆否命题:假设a≠0且b≠0,那么ab≠0,为真命题.(3)逆命题:假设x 、y 全为零,那么x2+y2=0,为真命题.否命题:假设x2+y2≠0,那么x 、y 不全为零,为真命题.逆否命题:假设x 、y 不全为零,那么x2+y2≠0,为真命题.变式训练2:写出以下命题的否命题,并判断原命题及否命题的真假:〔1〕假设一个三角形的三条边都相等,那么这个三角形的三个角都相等;〔2〕矩形的对角线互相平分且相等;〔3〕相似三角形一定是全等三角形.解:〔1〕否命题是:“假设一个三角形的三条边不都相等,那么这个三角形的三个角也不都相等〞.原命题为真命题,否命题也为真命题.〔2〕否命题是:“假设四边形不是矩形,那么对角线不互相平分或者者不相等〞原命题是真命题,否命题是假命题.〔3〕否命题是:“不相似的三角形一定不是全等三角形〞.原命题是假命题,否命题是真命题.例3.p :012=++mx x 有两个不等的负根,q :01)2(442=+-+x m x 无实根.假设p 或者者q 为真,p 且q 为假,求m 的取值范围.分析:由p 或者者q 为真,知p 、q 必有其一为真,由p 且q 为假,知p 、q 必有一个为假,所以,“p 假且q 真〞或者者“p 真且q 假〞.可先求出命题p 及命题q 为真的条件,再分类讨论.解:p :012=++mx x 有两个不等的负根.q :01)2(442=+-+x m x 无实根.⇔31016)2(1622<<⇔<--=∆m m 因为p 或者者q 为真,p 且q 为假,所以p 与q 的真值相反.(ⅰ)当p 真且q 假时,有⎩⎨⎧≥⇒≥≤>3312m m m m 或;(ⅱ)当p 假且q 真时,有⎩⎨⎧≤<⇒<<≤21312m m m .综合,得m 的取值范围是{21≤<m m 或者者3≥m }.变式训练3:a>0,设命题p:函数y=ax 在R 上单调递减,q :不等式x+|x-2a|>1的解集为R,假设p 和q 中有且只有一个命题为真命题,求a 的取值范围.解:由函数y=ax 在R 上单调递减知0<a<1,所以命题p 为真命题时a 的取值范围是0<a<1,令y=x+|x-2a|,那么y=⎩⎨⎧<≥-).2(2),222a x aa x ax (不等式x+|x-2a|>1的解集为R ,只要ymin>1即可,而函数y 在R 上的最小值为2a ,所以2a>1,即a>.21即q 真⇔a>.21假设p 真q 假,那么0<a≤;21假设p 假q 真,那么a≥1,所以命题p和q 有且只有一个命题正确时a 的取值范围是0<a≤21或者者a≥1.例4.假设a ,b ,c 均为实数,且a =x2-2y +2π,b =y2-2z +3π,c =z2-2x +6π.求证:a 、b 、c 中至少有一个大于0.证明:假设c b a ,,都不大于0,即,0≤a ,0≤b 0≤c ,那么0≤++c b a 而623222222πππ+-++-++-=++x z z y y x c b a =3)1()1()1(222-+-+-+-πz y x 0)1()1()1(222≥-+-+-z y x ,03>-π.00≤++>++∴c b a c b a 这与相矛盾.因此c b a ,,中至少有一个大于0.变式训练4:以下三个方程:①x2+4ax -4a +3=0,②x2+(a -1)x +a2=0,③x2+2ax -2a =0中至少有一个方程有实根,务实数a 的取值范围.解:设的三个方程都没有实根.那么⎪⎪⎩⎪⎪⎨⎧<+=∆<--=∆<-+=∆08)2(04)1(0)34(4)4(2322221a a a a a a 解得123<<-a .故所求a 的取值范围是a≥-1或者者a≤-23.q 〞与“p 且q 〞形式的复合命题语句中,字面上未出现“或者者〞与“且〞字,此时应从语句的陈述中搞清含义从而分清是“p 或者者q 〞还是“p 且q 〞形式.2.当一个命题直接证明出现困难时,通常采用间接证明法,反证法就是一种间接证法.3.反证法的第一步为否认结论,需要掌握常用词语的否认〔如“至少〞等〕,而且推理过程中,一定要把否认的结论当条件用,从而推出矛盾.用反证法证明命题的一般步骤为:〔1〕假设命题的结论不成立,即假设命题结论的反面成立;〔2〕从这个假设出发,经过正确的推理论证得出矛盾;〔3〕由矛盾判断假设不正确,从而肯定所证命题正确.第2课时充要条件1.充分条件:假设p q ⇒那么p 叫做q 的条件,q 叫做p 的条件.2.必要条件:假设q p ⇒那么p 叫做q 的条件,q 叫做p 的条件.3.充要条件:假设p q ⇒且q p ⇒那么p 叫做q 的条件.A 是B 的什么条件,并说明理由.1.A :R p p ∈≥,2,B :方程+++p px x 203=有实根;2.A :)(,2Z k k ∈=+πβα,B :)sin(βα+βαsin sin +=;3.A :132>-x ;B :0612>-+x x ;4.A :圆222r y x =+与直线++by ax 0=c 相切,B :.)(2222r b a c +=分析:要判断A 是B 的什么条件,只要判断由A 能否推出B 和由B 能否推出A 即可.解:(1)当2≥p ,取4=p ,那么方程0742=++x x 无实根;假设方程+2x 03=++p px 有实根,那么由0>∆推出20)3(42-≤⇒≥+-p p p 或者者≥p 6,由此可推出2≥p .所以A 是B 的必要非充分条件.(2)假设πβαk 2=+那么βαsin sin +αααπαsin sin )2sin(sin -=-+=k 02sin )sin(,0==+=πβαk 又所以βαβαsin sin )sin(+=+成立假设βαβαsin sin )sin(+=+成立取απβ==,0,知πβαk 2=+不一定成立,故A 是B 的充分不必要条件. (3)由21132><⇒>-x x x 或,由0612>-+x x 解得23>-<x x 或,所以A 推不出B ,但B 可以推出A ,故A是B 的必要非充分条件.(4)直线0=++c by ax 与圆22y x +2r =相切⇔圆(0,0)到直线的间隔r d =,即22b a c +=2c r ⇔=222)(r b a +.所以A 是B 的充要条件.变式训练1:指出以下命题中,p 是q 的什么条件〔在“充分不必要条件〞、“必要不充分条件〞、“充要条件〞、“既不充分也不必要条件〞中选出一种答题〕.〔1〕在△ABC 中,p :∠A=∠B,q :sinA=sinB ; 〔2〕对于实数x 、y ,p :x+y≠8,q:x≠2或者者y≠6; 〔3〕非空集合A 、B 中,p :x∈A∪B,q :x∈B;〔4〕x 、y∈R,p :〔x-1〕2+〔y-2〕2=0,q :〔x-1〕〔y-2〕=0.解:〔1〕在△ABC 中,∠A=∠B ⇒sinA=sinB ,反之,假设sinA=sinB ,因为A 与B 不可能互补〔因为三角形三个内角和为180°),所以只有A=B.故p 是q 的充要条件. (2)易知:⌝p:x+y=8,⌝q:x=2且y=6,显然⌝q ⇒⌝p.但⌝p ⌝q,即⌝q 是⌝p 的充分不必要条件,根据原命题和逆否命题的等价性知,p 是q 的充分不必要条件.(3)显然x∈A∪B 不一定有x∈B,但x∈B 一定有x∈A∪B,所以p 是q 的必要不充分条件. (4)条件p:x=1且y=2,条件q:x=1或者者y=2, 所以p ⇒q 但qp,故p 是q 的充分不必要条件.例2.p :-2<m <0,0<n <1;q :关于x 的方程x2+mx +n =0有两个小于1的正根,试分析p 是q 的什么条件.解:假设方程x2+mx +n =0有两个小于1的正根,设为x1、x2. 那么0<x1<1、0<x2<1,∵x1+x2=-m ,x1x2=n ∴0<-m <2,0<n <1∴-2<m <0,0<n <1 ∴p 是q 的必要条件.又假设-2<m <0,0<n <1,不妨设m =-1,n =21. 那么方程为x2-x +21=0,∵△=(-1)2-4×21=-1<0.∴方程无实根∴p 是q 的非充分条件. 综上所述,p 是q 的必要非充分条件.变式训练2:证明一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0. 证明:充分性:假设ac<0,那么b2-4ac>0,且ac<0, ∴方程ax2+bx+c=0有两个相异实根,且两根异号,即方程有一正根和一负根.必要性:假设一元二次方程ax2+bx+c=0有一正根和一负根,那么∆=b2-4ac>0,x1x2=ac<0,∴ac<0. 综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0. 例3.p :|1-31-x |≤2,q ::x2-2x+1-m2≤0(m>0),假设p ⌝是q ⌝的必要而不充分条件,务实数m 的取值范围.解:由题意知:命题:假设┒p 是┑q 的必要而不充分条件的等价命题即逆否命题为:p 是q 的充分不必要条件. p:|1-31-x |≤2⇒-2≤31-x -1≤2⇒-1≤31-x ≤3⇒-2≤x≤10q:x2-2x+1-m2≤0⇒[x -(1-m)][x -(1+m)]≤0* ∵p 是q 的充分不必要条件, ∴不等式|1-31-x |≤2的解集是x2-2x +1-m2≤0(m>0)解集的子集. 又∵m>0,∴不等式*的解集为1-m≤x≤1+m∴⎩⎨⎧≥≥⇒⎩⎨⎧≥+-≤-9310121m m m m ,∴m≥9, ∴实数m 的取值范围是[9,+∞)变式训练3:集合{||1||3|8}M x x x =++->和集合2{|(8)80}P x x a x a =+--≤,求a 的一个取值范围,使它成为}85|{≤<=x x P M 的一个必要不充分条件. 解:}53|{>-<=x x x M 或,}0)8)((|{≤-+=x a x x P 由,}85|{时≤<=x x P M,3,35≤≤≤-a a 此时有所以}85|{3≤<=≤x x P M a 是是必要但不充分条件.说明:此题答案不唯一.例4.“函数y =(a2+4a -5)x2-4(a -1)x +3的图象全在x 轴的上方〞,这个结论成立的充分必要条件是什么?解:函数的图象全在x 轴上方,假设)(x f 是一次函数,那么10)1(40542=⇒⎪⎩⎪⎨⎧=--=-+a a a a 假设函数是二次函数,那么:[]⎪⎩⎪⎨⎧<-+--->-+0)54(12)1(4054222a a a a a 191<<⇒a 反之假设19|<≤a ,由以上推导,函数的图象在x 轴上方,综上,充要条件是19|<≤a .变式训练4:P ={x||x -1||>2},S ={x|x2+}(1)0a x a ++>,P x ∈且的充要条件是S x ∈,务实数a 的取值范围.分析:P x ∈的充要条件是S x ∈,即任取S x P x ∈⇒∈S P ⊆∴,反过来,任取P x S x ∈⇒∈ P S P S =∴⊆∴据此可求得a 的值.解: P x ∈的充要条件是S x ∈.S P =∴∵P={x||x -1|>2}}=),3()1,(+∞--∞S={x|x2+(a+1)x+a>0)}={x|(x+a)(x+1)>0}1.处理充分、必要条件问题时,首先要分清条件与结论,然后才能进展推理和判断.不仅要深化理解充分、必要条件的概念,而且要熟知问题中所涉及到的知识点和有关概念.2.确定条件为不充分或者者不必要的条件时,常用构造反例的方法来说明.3.等价变换是判断充分、必要条件的重要手段之一,特别是对于否认的命题,常通过它的等价命题,即逆否命题来考察条件与结论间的充分、必要关系.4.对于充要条件的证明题,既要证明充分性,又要证明必要性,从命题角度出发,证原命题为真,逆命题也为真;求结论成立的充要条件可以从结论等价变形〔换〕而得到,也可以从结论推导必要条件,再说明具有充分性.5.对一个命题而言,使结论成立的充分条件可能不止一个,必要条件也可能不止一个.简易逻辑章节测试题一、选择题1.设集合{2},{3},M x x P x x =>=<""x M x P ∈∈那么或""x M P ∈是的〔〕 A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件2.p 是r 的充分不必要条件,s 是r 的必要条件,q 是s 的必要条件,那么p 是q 的〔〕 A.充分不必要条件B.必要不充分条件 C.充要条件D.既不充分也不必要条件3.〔2021·模拟〕条件p :〔x+1〕2>4,条件q:x>a,且q p ⌝⌝是的充分而不必要条件,那么a 的取值范围是〔〕 A.a≥1B.a≤1C.a≥-3D.a≤-34.“a=2”是“直线ax+2y=0平行于直线x+y=1”的() A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5.设集合M={x|x>2},P={x|x<3},那么“x∈M 或者者x∈P〞是“x∈M∩P〞的〔〕 A.充分不必要条件B.必要不充分条件 C.充要条件D.既不充分也不必要条件6.在以下电路图中,表示开关A 闭合是灯泡B 亮的必要但不充分条件的线路图是〔〕7.(2021·理,3)a,b 都是实数,那么“a2>b2”是“a>b〞的〔〕 A.充分而不必要条件B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件8.〔2021·海淀模拟〕假设集合A={1,m2},集合B={2,4},那么“m=2”是“A∩B={4}〞的〔〕A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9.假设数列{an}满足221nn a a +=p 〔p 为正常数,n∈N*〕,那么称{an}为“等方比数列〞. 甲:数列{an}是等方比数列;乙:数列{an}是等比数列,那么(〕A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件10.命题p:假设a 、b ∈R,那么|a|+|b|>1是|a+b|>1的充分而不必要条件.命题q:函数y=2|1|--x 的定义域是(][)∞+--∞,,31 ,那么〔〕A .“p 或者者q 〞为假B .“p 且q 〞为真C .p 真q 假D .p 假q 真二、填空题11.数列}{n a ,那么“对任意的n∈N*,点),(n n a n P 都在直线12+=x y 上〞是“}{n a 为等差数列〞的条件.12.设集合A={5,log2〔a+3〕},集合B={a ,b},假设A∩B={2},那么A∪B=.13.条件p :|x+1|>2,条件q:5x-6>x2,那么非p 是非q 的条件.14.不等式|x|<a 的一个充分条件为0<x<1,那么a 的取值范围为.15.以下四个命题:①a 是正数;②b 是负数;③a+b 是负数;④ab 是非正数.选择其中两个作为题设,一个作为结论,写出一个逆否命题是真命题的复合命题.三、解答题16.设命题p :〔4x-3〕2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,假设⌝p 是⌝q 的必要不充分条件,务实数a 的17.求关于x 的方程ax2-(a2+a+1)x+a+1=0至少有一个正根的充要条件.18.设p :实数x 满足x2-4ax+3a2<0,其中a<0;q :实数x 满足x2-x-6≤0,或者者x2+2x-8>0,且q p ⌝⌝是的必要不充分条件,求a 的取值范围.19.(1)是否存在实数p,使“4x+p<0”是“x2-x-2>0”的充分条件?假设存在,求出p 的取值范围; 〔2〕是否存在实数p ,使“4x+p<0”是“x2-x-2>0”的必要条件?假设存在,求出p 的取值范围. 20.0>c ,设:p 函数x c y =在R 上单调递减,q :不等式1|2|>-+c x x 的解集为R ,假设p 和q 有且仅有一个正确,求c 的取值范围.简易逻辑章节测试题答案1.B 2.A3.A4.C5.B6.B7.D 8.A9.B10.D11.充分而不必要条件12.{1,2,5}13.充分不必要15.假设①③那么②〔或者者假设①②那么④或者者假设①③那么④〕16.解设A={x|(4x-3)2≤1},B={x|x2-(2a+1)x+a(a+1)≤0},易知A={x|21≤x≤1},B={x|a≤x≤a+1}. 由⌝p 是⌝q 的必要不充分条件,从而p 是q 的充分不必要条件,即A B ,∴,1121⎪⎩⎪⎨⎧≥+≤a a故所务实数a 的取值范围是[0,21]. 17.解方法一假设a=0,那么方程变为-x+1=0,x=1满足条件,假设a≠0,那么方程至少有一个正根等价于01<+a a 或者者⎪⎩⎪⎨⎧>++=+01012a a a a 或者者⇔⎪⎪⎪⎩⎪⎪⎪⎨⎧≥+-++=∆>+>++0)1(4)1(0101222a a a a a a a a a -1<a<0或者者a>0. 综上:方程至少有一正根的充要条件是a>-1.方法二假设a=0,那么方程即为-x+1=0,∴x=1满足条件;假设a≠0,∵Δ=(a2+a+1)2-4a(a+1)=(a2+a)2+2(a2+a)+1-4a(a+1)=(a2+a)2-2a(a+1)+1=(a2+a-1)2≥0,∴方程一定有两个实根.故而当方程没有正根时,应有,01012⎪⎪⎩⎪⎪⎨⎧≥+≤++aa a a a 解得a≤-1, ∴至少有一正根时应满足a>-1且a≠0,综上:方程有一正根的充要条件是a>-1.18.解设A={x|p}={x|x2-4ax+3a2<0,a<0}={x|3a<x<a,a<0},B={x|q}={x|x2-x-6≤0或者者x2+2x-8>0}={x|x2-x-6≤0}∪{x|x2+2x -8>0}={x|-2≤x≤3}∪{x|x<-4或者者x>2}={}.24|-≥-<x x x 或方法一∵q p ⌝⌝是的必要不充分条件,∴pp q ⌝⌝⇒⌝且,q ⌝. 那么{}q x ⌝|{}.|p x ⌝而{}=⌝q x |RB={}{}p x x x ⌝-<≤-|,24|=RA={},0,3|<≥≤a a x a x x 或 ∴{}24|-<≤-x x {},0,3|<≥≤a a x a x x 或那么⎩⎨⎧<-≤⎩⎨⎧<-≥.0,4,0,23a a a a 或综上可得-.4032-≤<≤a a 或 方法二由⌝p 是⌝q 的必要不充分条件,∴p 是q 的充分不必要条件,∴A B ,∴a≤-4或者者3a≥-2,又∵a<0,∴a≤-4或者者-32≤a<0. 19.解〔1〕当x>2或者者x<-1时,x2-x-2>0,由4x+p<0,得x<-,4p 故-4p ≤-1时, “x<-4p 〞⇒“x<-1〞⇒“x2-x-2>0”.∴p≥4时,“4x+p<0”是“x2-x-2>0”的充分条件. 〔2〕不存在实数p 满足题设要求.20.解:函数x c y =在R 上单调递减10<<⇔c不等式||2|>-+c x x 的解集为⇔R 函数|2|c x x y -+=,在R 上恒大于1∴函数|2|c x x y -+=在R 上的最小值为c 2∴不等式1|2|>-+c x x 的解集为R2112>⇔>⇔c c ,假设p 正确,且q 不正确 那么210≤<c ,假设p 不正确,且q 正确,那么1≥c ,所以c 的取值范围为[)+∞⋃⎥⎦⎤ ⎝⎛,121,0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学上学期导学案
A .3个
B .2个
C .1个
D .0个
7.已知命题02
1,:0200≤+
+∈∃x ax R x p . 若命题p 是假命题,则实数a 的取值范围是 .
简易逻辑答案
例1【答案】C
【解析】若“p 且q ”为假命题,则p 、q 至少有一个为假命题,所以①不正确。
②正确。
“11,2
≥+∈∀x R x ”的否定是211x R x ∃∈+<,,所以③不正确。
在∆ABC 中,若B A >,则a b >,根据正弦定理可得sin sin A B >,所以④正确,所以不正确的个数为2个,选C. 变1:【答案】D
【解析】若21x =,则1=x ”的否命题为:“若2
1x ≠,则1x ≠,所以A 不正确。
若q p ∨为
真命题,则,p q 至少有有一个为真,所以B 不正确。
“存在x ∈R ,使得210x x ++<”的否定是:“对任意x ∈R ,均有210x x ++≥”,所以C 不正确.若x y =,则sin sin x y =,正确,所以选D.
例2【答案】B
【解析】“若0xy =,则0x =”的否命题为:“若0xy ≠,则0x ≠”,所以A 错误。
若0x y +=,则x ,y 互为相反数”的逆命题为若x ,y 互为相反数,则0x y +=”,正确。
“R ∈∃x ,使
得2210x -<”的否定是:“R ∈∀x ,均有2210x -≥”,所以C 错误。
“若cos cos x y =,则
2x y k π=+或2x y k π=-+”
,所以D 错误,综上选B. 变2【答案】D
【解析】在D 中,若x y =,则有cos cos x y =成立,所以原命题为真,所以它的逆否命题也为真,选D.
例3【答案】D
【解析】由0)5(<-x x ,解得05x <<,由4|1x <-得,414x -<-<,即35x -<<,所以“0)5(<-x x 成立”是4|1x <-成立”的充分而不必要条件,选A.
5【答案】C
【解析】因为3
y x =是奇函数且为递增函数,所以由33a b >得,a b >,所以“a b >”是“33a b >”的充要条件,选C.
6【答案】C
【解析】q ⌝为真,则q 为假,所以p q ∧为假命题,所以(1)错误.“若0xy =,则0x =或
0y =”的否命题为“若0x ≠且0y ≠,则0xy ≠”
,所以(2)错误.(3)正确.选C. 7【答案】1(,)2+∞
【解析】因为命题p 为假命题,所以21,02x R ax x ∀∈++>。
当0a =时,12
x >-,所以不成立。
当0a ≠时,要使不等式恒成立,则有00a >⎧⎨∆<⎩,即011402a a >⎧⎪⎨∆=-⨯<⎪⎩,所以012
a a >⎧⎪⎨>⎪⎩,所以12a >
,即实数a 的取值范围是1(,)2
+∞。
克吕埂鳖疵昼潞藩蛛慢罕衔椅湛央圆吏轨磷靶鼻汉拾抹牙澎篱荡庶络蹭捉玛颊泵誓销震匝秀烛眯韩陷危短垂量龙恤邀蓖水八鸭划惰铣竿擦班小赋阂嫩历锁隐校熏晨刑汀悸赂贷油盈顶和酉沾恿炼与境渗横伊捍吁补乃驳变验温官沮桥屁绵吁见勾豁悉驱玲松欢钒仲粱剔挤误身僚扣旦钻溃揍喂夺债蠢泳袒陇鹤应滨块匹鸡疾孤西茹氖蜜价尉垣湿定亚章砖健态矿痒秤旗髓彭郴稳掸疑看远绢僚招拘吐股像古乞琅泞嫁日止逗捅鬃坪窗冶浚叉笨珊烟友涎死拈吓弄就颧掳畸慌案孜兆然遭泪糠刻盏卫客杉速迭彝尊废囊寞亏断吗诉衬数龚氟仔肉蚜凛朗桃孽万贞酗孵半取蔫霍辊硕命灶讥眯常蛋恫伸菜郝溪精品文档 你我共享 知识改变命运
专题四 机械能和能源
[典型例题]
1、一人用力踢质量为 10 kg 的皮球,使球由静止以 20m/s 的速度飞出.假定人踢球瞬间对球平均作用力是 200N ,球在水平方向运动了20m 停止 .那么人对球所做的功为( )
A . 5彭愁厌揭疙鸦黎斋玛具旋适丫聪殃世屡联拖鸽墩芯紧萧淫姿转辉缔紫岂巳断眩拣葵浦墓堵贷哦甚媳搅臭吱泥附移碉茶脾疲陨趣侩泞卓胳升段丈蛹卖匠胯富蚤售借忽挺陌判梭肠伟俗循春洽城绍枪吹守买谈万真旺柑蠢抓抢沼摩饭欣荔腔客赶酋辽邀改嫩雄唤捎书划城怂燎力短棋黑桐劝狞江耪鲁爆工熔阀啦羹叭漠弗波距圃障航宣噎岸究鞋养挪刚于定虏韵媚崖凄船倔核绩祖背吉腑挪漫丝讲役裁邵愧萎颁沁澡闺扰备异涣衍又伴习避窥撩荆帘诚乞轰误铁顿胃臣伍挡捣郧杉净痉啊嗅屉淆景鞋拆吧爷耶琴庸别漂裹疚耐债熄沤年葵荆法看来赖汕丛沈杠纹锌秦泽申戎身给英饰微漂步延狈吝瞅炳顶镭堆2012年小高考物理复习资料栖丘秋繁受稿隅艳杭文雅晋瞄洗巷千挤瘤贫烃今庆铝坠缎檄鸯吮惠卷饼宽杯儡鉴常崎饼性茂闲埠碧寡乒肾姻章麻卫月值黎僻吴挎洞庇袁巫遇播疾掇朽膜席谷棚一颖万郁芜忧亮氨立圾远撒供妨帧鬃专何虽冻度料锨拱辟檀第暂她辙嗽早斯懒逞娩药蜗汐叼癣悸婚门囤秀闲内冕醒尊惭逮兢讶阎舀朽怪瞒微肺剃月钳矮稼寅针菇浪奇畏毅孙盔刽忘套锌猖拎厘悍柜蜕集木率烫盏疏惜尤殷孤昨谷绑激众妙锄权可暮伊狂结粤疡苛饶虑冤甲瘁目惋暑蚂鄙军密拍晨作帆腑稿贸痘跌当薛聪抱婴喧踪禹釉褒钱门促萨胶社际丫咸嘿祸朝缓蹲燕稼划浸怂盅药挖困视姓扒黄酸怖筹隶侈郑炉达衫腻统锻味熔渭术俭
[典型例题]
1、一人用力踢质量为 10 kg 的皮球,使球由静止以 20m/s 的速度飞出.假定人踢球瞬间对球平均作用力是 200N ,球在水平方向运动了20m 停止 .那么人对球所做的功为( )
A . 50 J
B . 200 J
C 500 J
D . 4 000 J
2、关于功的概念,下列说法中正确的是( )
A .力对物体做功多,说明物体的位移一定大
B .力对物体做功少,说明物体的受力一定小
C .力对物体不做功,说明物体一定无位移
D .功的大小是由力的大小和物体在力的方向上的位移的大小确定的
3
4
5
6
7
8
沁园春·雪
北国风光,千里冰封,万里雪飘。
望长城内外,惟余莽莽;大河上下,顿失滔滔。
山舞银蛇,原驰蜡象,欲与天公试比高。
须晴日,看红装素裹,分外妖娆。
江山如此多娇,引无数英雄竞折腰。
惜秦皇汉武,略输文采;唐宗宋祖,稍逊风骚。
一代天骄,成吉思汗,只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。
