本时间序列分析第三章(下)
《时间序列分析》讲义 第三章 平稳时间序列分析

k
1 k1 2 k2,k
2
自相关系数
自相关系数的定义
k
k 0
平稳AR(p)模型的自相关系数递推公式
k 1k 1 2 k 2 p k p
常用AR模型自相关系数递推公式
AR(1)模型 k 1k , k 0
AR(2)模型
1,
k
1
1 2
1k1 2 k2
k 0 k 1 k2
自回归系数多项式
(B) 11B 2B2 pBp
特征方程
中心化AR(p)模型
xt 1 xt1 2 xt2 p xt p t
可以看成p阶常系数非齐次线性差分方程
xt 1 xt1 2 xt2 p xt p t
它对应的齐次方程的特征方程为
p 1 p1 p1 p 0
1 12
协方差函数
在平稳AR(p)模型两边同乘xt-k,再求期望
E(xt xtk ) 1E(xt1xtk ) p E(xt p xtk ) E(t xtk )
根据
E( t xtk ) 0 ,k 1
得协方差函数的递推公式
k 1 k1 2 k 2 p k p
例题
例3.3 求平稳AR(1)模型的协方差
12
2 2
,
0,
k 0 k 1
k 2 k 3
偏自相关系数
滞后k偏自相关系数由Yule-Walker方程 确定
zt a1 zt1 a2 zt2 a p zt p h(t)
齐次线性差分方程
zt a1 zt1 a2 zt2 a p zt p 0
齐次线性差分方程的解
特征方程
p a1p1 a2p2 ap 0
特征方程的根称为特征根,记作1,2,…,p
时间序列分析第三章平稳时间序列分析

注:图中,S号代表序列的观察值;连续曲线代表拟合序列曲线;虚线代表拟合序列的95%上下置信限。
所谓预测就是要利用序列以观察到的样本值对序列在未来某个时刻的取值进行估计。
目前对平稳序列最常用的预测方法是线性最小方差预测。
线性是指预测值为观察值序列的线性函数,最小方差是指预测方差达到最小。
在预测图上可以看到,数据围绕一个范围内波动,即说明未来的数值变化时平稳的。
二、课后习题第十七题:根据某城市过去63年中每年降雪量数据(单位:mm)得:(书本P94)程序:data example17_1;input x@@;time=_n_;cards;2579588397 110;proc gplot data=example17_1;plot x*time=1;symbol c=red i=join v=star;run;proc arima data=example17_1;identify var=x nlag=15minic p= (0:5) q=(0:5);run;estimate p=1;run;estimate p=1 noin;run;forecast lead=5id=time out=results;run;proc gplot data=results;plot x*time=1 forecast*time=2 l95*time=3 u95*time=3/overlay;symbol1c=black i=none v=start;symbol2c=red i=join v=none;symbol3c=green i=join v=none l=32;run;(1)判断该序列的平稳性与纯随机性该序列的时序图如下(图a)图a由时序图显示过去63年中每年降雪量数据围绕早70mm附近随机波动,没有明显趋势或周期,基本可以看成平稳序列,为了稳妥起见,做了如下自相关图(图b)图b时序图就是一个平面二维坐标图,通常横轴表示时间,纵轴表示序列取值。
人大版应用时间序列分析(第5版)习题答案
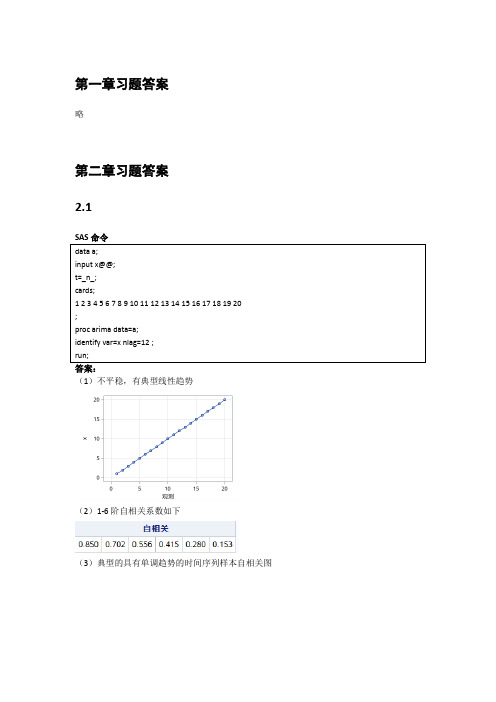
第一章习题答案略第二章习题答案2.1答案:(1)不平稳,有典型线性趋势(2)1-6阶自相关系数如下(3)典型的具有单调趋势的时间序列样本自相关图2.2答案:(1)不平稳(2)延迟1-24阶自相关系数(3)自相关图呈现典型的长期趋势与周期并存的特征2.3答案:(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列2.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列(2)差分后序列为平稳非白噪声序列2.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
(2)单位根检验显示带漂移项0阶延迟的P值小于0.05,所以基于adf检验可以认为该序列平稳(3)如果使用adf检验结果,认为该序列平稳,则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳,那么一阶差分后序列为平稳非白噪声序列2.8答案(1)时序图和自相关图都显示典型的趋势序列特征(2)单位根检验显示该序列可以认为是平稳序列(带漂移项一阶滞后P值小于0.05)(3)一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--() 221112() 1.96110.7t Var x φ===--() 22213=0.70.49ρφ==()12122221110.490.7=0110.71ρρρφρρ-==-(4) 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有:,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=()1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=() 1112223340.70.15=0φρφφφ====-()3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩() ()模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩() 3.5证明:该序列的特征方程为:320c c λλλ--+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
空间分布的测度和时间序列分析

上一页
下一页
返回目录
第三章 空间分布的测度和时间序列
退出
§1 空间分布的测度
二 点状分布的测度
2 中心位置及其测度
区域重心的测度补充
在实际问题的分析中;对于一个较大的行政区域: 可以将Xi;Yi取为各次级行政区域单元;譬如省 市 区的首府坐标; Mi可以为不同的属性值譬如;人口 产值等
退出
§1 空间分布的测度
二 点状分布的测度
2 中心位置及其测度
区域重心的测度补充
假设某一个区域由n个小区单元构成;其中;第i个
小区单元的中心坐标为Xi;Yi;Mi为该小区单元某 种属性意义下的重量;则该属性意义下的区域重
心坐标为:
n
Mi Xi
n
MiYi
P(x, y)
x i1 n
, y i1 n
第五步: S=5;I=2;T=5;7
①v2刚得到P标号;故考察v2 v2;v5∈A且v5是T标号 点;则修改为:
T ( v 5 ) m T ( v 5 ) P ( i v 2 , ) n W 2 5 m 1 , 8 5 6 i 1 n ②在所有的T标号中;Tv5最小;于是令Pv5=13
上一页
下一页
返回目录
退出
第三章 空间分布的测度和时间序列
§1 空间分布的测度
第三步: S=3;I=6;T=2;3;5;7 ①v6刚得到P标号;故考察v6 v6;v2;v6;v5; v6;v7∈A且v2 v5 v7是T标号点;则修改为:
T ( v 2 ) m T ( v 2 ) P ( i v 6 , ) n W 6 2 m 9 , 5 3 i 8 n T ( v 5 ) m T ( v 5 ) P ( i v 6 , ) n W 6 5 m , 5 1 i 1 n 1 T ( v 7 ) m T ( v 7 ) P ( i v 6 , ) n W 6 7 m , 5 9 i 1 n ②在所有的T标号中;Tv3最小;于是令Pv3=6
本时间序列分析第三章(上)新

时间序列分析
1
第三章 ARMA模型的特性
第三章 ARMA模型的特性
2
第三章 ARMA模型的特性
本章主要介绍ARMA模型的一些非常重 要的特性,这对我们了解和使用ARMA模型 是必不可少的一部分内容,也是本课程的重 点、难点内容之一。
3
3
第三章 ARMA模型的特性
本章要考察 ARMA模型
23
第三章 ARMA模型的特性
ⅰ)若 1, 2 ,, n 为不同实根 yt c11t c2t2 cntn
ⅱ)若 1, 2 ,, n 中有相同实根(有重根),不妨 设前d个特征根为d重重根,后n-d个特征根为不等实 根,则
yt
(c1
c2t cd t d 1 )1t
cd
t
1 d 1
(2) 模型的等价逆转形式:
X t I j X t j at 相当于AR(∞); 其中Ij:逆函数 j 1
7
模型的三种表示形式:
第三章 ARMA模型的特性
差分方程形式
传递形式
逆转形式 8
3. B算子(后移算子)
第三章 ARMA模型的特性
BX t X t1
B2 X t B(BX t ) BX t1 X t2
G1 1 1 G2 1G1 2G0
格林函数为:1,0.3,-0.44,-0.768 G3 1G2 2G1
X t 0.8X t1 0.5X t2 at 0.4at1 G j 1G j1 2G j2
格林函数为:1,1.2,1.46,1.768,2.144
这种求解方法的缺点是:必须逐步递推。
第三章 ARMA模型的特性
Gj 1j
j 0,1,2,
时间序列分析(张能福)第三章

第一节线性差分方程一、后移算子B定义为三、齐次方程解的计算1 、AR(n) 过程自相关函数ACF 1阶自回归模型AR(1) Xt= Xt-1+ at 的k阶滞后自协方差为:Xt= 1Xt-1+ 2Xt-2 + at 该模型的方差0以及滞后1期与2期的自协方差1, 2分别为一般地,n阶自回归模型AR(n) Xt= 1Xt-1+ 2Xt-2 +…nXt-n + at 其中:zi 是AR(n) 特征方程(z)=0 的特征根,由AR(n) 平稳的条件知,|zi|<1; 因此,当zi 均为实数根时,k呈几何型衰减(单调或振荡);当存在虚数根时,则一对共扼复根构成通解中的一个阻尼正弦波项,k呈正弦波衰减。
对MA(1) 过程其自协方差系数为二、偏自相关函数从Xt 中去掉Xt-1 的影响,则只剩下随机扰动项at ,显然它与Xt-2 无关,因此我们说Xt 与Xt-2 的偏自相关系数为零,记为MA(1) 过程可以等价地写成at 关于无穷序列Xt ,Xt-1 ,…的线性组合的形式:与MA(1) 相仿,可以验证MA(m) 过程的偏自相关函数是非截尾但趋于零的。
ARMA(n,m) 的自相关函数,可以看作MA(m) 的自相关函数和AR(n) 的自相关函数的混合物。
当n=0 时,它具有截尾性质;当m=0 时,它具有拖尾性质;当n、m都不为0时,它具有拖尾性质从识别上看,通常:ARMA(n ,m) 过程的偏自相关函数(PACF )可能在n阶滞后前有几项明显的尖柱(spikes ),但从n阶滞后项开始逐渐趋向于零;而它的自相关函数(ACF )则是在m阶滞后前有几项明显的尖柱,从m阶滞后项开始逐渐趋向于零。
对k=1 ,2,3,…依次求解方程,得上述……序列为AR 模型的偏自相关函数。
偏自相关性是条件相关,是在给定的条件下,和的条件相关。
换名话说,偏自相关函数是对和所解释的相关的度量。
之间未被由最小二乘原理易得,是作为关于线性回归的回归系数。
第3章 时间序列分析(精讲)

①逐期增长量: y1 y0 , y2 y1, , yn yn1. ②累积增长量: y1 y0 , y2 y0 , , yn y0.
yn y0 y1 y0 y2 y1 yn yn-1 .
(3)平均增长量:是逐期增长量的平均数
平均增长量
逐期增长量之和 逐期增长量的个数
2、时间序列速度指标(考试时由可能出大题计算这些指标)
(2)加法模型:Y=T+S+C+I—各个因素对 发展的影响是相互独立的;
二、时间序列的特征指标(重要,有考点)
1.时间序列水平指标 (1)平均发展水平:一个时间内各个时间
的指标值加以平均得到的平均数。
1)由时期序列计算序时平均数(一段时间的数据)
y
y1
y2
n
yn
1 n
n i 1
yi
2)由时点序列计算序时平均数(一个时间点的数据)——时间间 隔相等
y
y0 y1 y1 y2
2
2
yn1 yn 2
y0 2
y1
yn1
yn 2
n
n
3)由时点序列计算序时平均数(一个时间点的数据)——时间间
隔不相等
y
y0
2
y1
t1
y1
2
y2
t2
yn1 2
yn
tn
t1 t2 tn1 tn
(2)增长量:反映报告期比基期增长的绝对数量 增长量=报告期水平-基期水平 增长量分为逐期增长量和累积增长量
1.常用的数学模型:
^
(1)直线趋势模型:y a bt
^
(2)指数趋势模型: y abt
^
(3)二次曲线趋势模型:y a bt ct2
第三章平稳时间序列分析

t Pp t tt t t x B x x B x Bxx ===---221第3章第三章平稳时间序列分析一个序列通过预处理被识别为平稳非白噪声序列,那就说明该序列是一个蕴含着有关信息的平稳序列。
3.1 方法性工具 3.1.1 差分运算 一、p 阶差分记t x ∇为t x 的1阶差分:1--=∇t t t x x x记t x 2∇为t x 的2阶差分:21122---+-=∇-∇=∇t t t t t t x x x x x x以此类推:记t p x ∇为t x 的p 阶差分:111---∇-∇=∇t p t p t p x x x 二、k 步差分记t k x ∇为t x 的k 步差分:k t t t k x x x --=∇3.1.2 延迟算子 一、定义延迟算子相当与一个时间指针,当前序列值乘以一个延迟算子,就相当于把当前序列值的时间向过去拨了一个时刻。
记B 为延迟算子,有延迟算子的性质:1.10=B2.若c 为任一常数,有1)()(-⋅=⋅=⋅t t t x c x B c x c B3.对任意俩个序列{t x }与{t y },有11)(--±=±t t t t y x y x B4.n t t n x x B -=5.)!(!!,)1()1(0i n i n C B C B i n i i n ni i n-=-=-∑=其中二、用延迟算子表示差分运算 1、p 阶差分t p t p x B x )1(-=∇ 2、k 步差分t k k t t t k x B x x x )1(-=-=∇-3.2 ARMA 模型的性质 3.2.1 AR 模型定义 具有如下结构的模型称之p 阶自回归模型,简记为AR(p):ts Ex t s E Var E x x x x t s t s t t p tp t p t t t ∀=≠===≠+++++=---,0,0)(,)(,0)(,0222110εεεσεεφεφφφφε (3.4)AR(p)模型有三个限制条件:条件一:0≠p φ。
应用时间序列分析第三章课后答案

应用时间序列分析第三章课后答案第三章应用时间序列分析课后答案第3-5节,最近考试题目:第一节序列的定义与平稳性第二节相关系数矩阵与平稳过程第三节非平稳序列第四节非平稳序列的特征值与协方差第五节离散时间序列分析是对连续时间序列进行研究和分析的一种重要方法。
本章主要内容有:时间序列的定义、平稳性、相关性、时间序列的构成及其表示方式、离散时间序列的概念、离散时间序列的时间趋势、离散时间序列的一般模型、随机过程及其应用、连续时间序列分析等。
第四节非平稳序列的特征值与协方差特征值又称为特征向量或自协因子,它反映了该特征值与其他各特征值之间的关系。
如果已知某个时间序列的全部平稳序列,那么由这些平稳序列的特征值就可以计算出每个观测值的特征值;若只知道观测值,而不知道这些观测值与哪些特征值相关,则需利用相关系数矩阵计算各观测值的协方差阵。
本节还将介绍可变参数模型,即通过改变或增加参数的办法来得到另外一组新的平稳或非平稳序列。
第五节离散时间序列分析是对连续时间序列进行研究和分析的一种重要方法。
本章首先介绍了一些基本概念,如时间序列的平稳性、特征值、协方差、自相关函数、脉冲响应等;然后介绍了时间序列的一阶、二阶和高阶矩;接着介绍了一些常见的平稳序列;最后给出了两类时间序列分解方法。
第六节连续时间序列分析本章内容较多,在此仅举几例,望同学们能够理解并掌握。
如当时间序列在均值附近单调递减时,可假设 x 和 y 的斜率相同,记为x→/ y,再用相关系数矩阵公式计算相关系数,这样便简化了运算。
这也正是统计中时间序列处理的实际情况。
有时需要作几次回归拟合才能取得满意效果,这就是所谓的多元回归分析。
时间序列中的趋势项具有比较稳定的形态。
时间序列分析--第三章平稳时间序列分析

2019/9/23
课件
25
Green函数递推公式
原理 xt( BG )x(tB )tt (B)G(B)t t
方法
待定系数法
递推公式
2019/9/23
G G0j 1k j1kGjk, j1,2, ,其中 k 0k ,k ,kpp
非齐次线性差分方程的通解
齐次线性差分方程的通解和非齐次线性差分方程的
特解之和 z t
zt ztzt
2019/9/23
课件
10
3.2 ARMA模型的性质
AR模型(Auto Regression Model) MA模型(Moving Average Model) ARMA模型(Auto Regression Moving
2019/9/23
课件
38
例3.5:— (4 )x t x t 1 0 .5 x t 2t
自相关系数不规则衰减
2019/9/23
课件
39
偏自相关系数
定义
对于平稳AR(p)序列,所谓滞后k偏自相关系数就 是指在给定中间k-1个随机变量 的 xt1,xt2, ,xtk1 条件下,或者说,在剔除了中间k-1个随机变 量的干扰之后, x 对 tk x影t 响的相关度量。用数 学语言描述就是
2019/9/23
课件
29
例3.3:求平稳AR(1)模型的协方差
递推公式
k 1k11k0
平稳AR(1)模型的方差为
0
2
1 12
协方差函数的递推公式为
k
1k
2 112
,k1
2019/9/23
课件
时间序第三章试卷题

时间序列分析第三章试卷一、选择题(每题2分,共20分)1. 在时间序列分析中,下列哪个模型是通过样本自相关函数和偏自相关函数进行识别的?A. MA(q)模型B. AR(p)模型C. ARMA(p,q)模型D. 以上都是2. 下列关于平稳性的说法,正确的是?A. 强平稳意味着随机过程的分布随时间变化B. 弱平稳仅假设随机过程的前两阶矩随时间变化C. 平稳性可以通过样本均值和方差进行检验D. 平稳性是统计推断的基础3. 在AR(p)模型的参数估计中,常用的方法是?A. 最小二乘法(OLS)B. 迭代法C. Yule-Walker方程D. 以上都是4. 下列哪个统计量用于检验残差序列是否为白噪声?A. AICB. BICC. Q统计量D. R方5. 在ARMA模型的识别中,如果自相关系数和偏自相关系数都表现出拖尾性质,那么最可能的模型是?A. MA(q)模型B. AR(p)模型C. ARMA(p,q)模型D. 无法确定6. 下列关于时间序列图的说法,错误的是?A. 可以用来判断序列的平稳性B. 可以用来判断序列的纯随机性C. 总是能准确反映序列的真实趋势D. 可以作为模型选择的参考7. 在时间序列分析中,白噪声是指?A. 序列的均值和方差都不随时间变化B. 序列的自相关系数始终为零C. 序列的偏自相关系数始终为零D. 以上都是8. 下列哪个模型在参数估计时,需要用到非线性方程组?A. AR(p)模型B. MA(q)模型C. ARMA(p,q)模型D. 以上都不是9. 在平稳性检验中,常用的方法包括?A. 时序图法B. 自相关图法C. 混成检验法D. 以上都是10. 下列关于AIC和BIC的说法,正确的是?A. AIC和BIC都用于模型选择B. AIC值越小,模型越好C. BIC值越大,模型越好D. 以上都是二、填空题(每题2分,共20分)1. 在时间序列分析中,样本自相关函数用于衡量序列在不同时间点上的______关系。
时间序列分析方法 第03章 平稳ARMA模型

第三章 平稳ARMA 过程一元ARMA 模型是描述时间序列动态性质的基本模型。
通过介绍ARMA 模型,可以了解一些重要的时间序列的基本概念,并且为描述单变量时间序列的动态性质提供一类十分有用的模型。
§3.1 预期、平稳性和遍历性3.1.1 预期和随机过程假设可以观察到一个样本容量为T 的随机变量t Y 的样本:},,,{21T y y y这意味着这些随机变量之间的是相互独立且同分布的。
例3.1 假设T 个随机变量的集合为:},,,{21T εεε ,),0(~2σεN i 且相互独立,我们称其为高斯白噪声过程产生的样本。
对于一个随机变量t Y 而言,它是t 时刻的随机变量,因此即使在t 时刻实验,它也可以具有不同的取值,假设进行多次试验,其方式可能是进行多次整个时间序列的试验,获得I 个时间序列:+∞=-∞=t t t y }{)1(,+∞=-∞=t t t y }{)2(,…,+∞=-∞=t t I t y }{)(将其中仅仅是t 时刻的观测值抽取出来,得到序列:},,,{)()2()1(I t t t y y y ,这个序列便是对随机变量t Y 在t 时刻的I 次观测值,也是一种简单随机子样。
定义3.1 假设随机变量t Y 是定义在相同概率空间},,{P ℜΩ上的随机变量,则称随机变量集合},2,1,0,{ ±±=t Y t 为随机过程。
例3.2 假设随机变量t Y 的概率密度函数为:]21exp[21)(22t t Y y y f t σσπ= 此时称此时密度为该过程的无条件密度,此过程也称为高斯过程或者正态过程。
定义3.2 可以利用各阶矩描述随机过程的数值特征:(1) 随机变量t Y 的数学期望定义为(假设积分收敛):⎰==+∞∞-tt Y t t t dy y f y Y E t )()(μ (3.1) 此时它是随机样本的概率极限:∑==∞→I i i t I t y I P Y E 1)(1lim)( (3.2) (2) 随机变量t Y 的方差定义为(假设积分收敛): 20)(t t t Y E μγ-= (3.3) 例3.3 几种重要类型的随机过程1) 假设},,{21 εε是一个高斯白噪声过程,随机过程t Y 为常数加上高斯白噪声过程:t t Y εμ+=则它的均值和方差分别为:μεμμ=+==)()(t t t E Y E2220)()(σεμγ==-=t t t t E Y E(2) 随机过程t Y 为时间的线性趋势加上高斯白噪声过程:t t t Y εβ+=则它的均值和方差分别为:t E t Y E t t t βεβμ=+==)()(2220)()(σεμγ==-=t t t t E Y E3.1.2 随机过程的自协方差函数将j 个时间间隔的随机变量构成一个随机向量),,,(1'=--j t t t t Y Y Y X ,通过随机试验可以获得该随机向量的简单随机样本。
时间序列分析第三章王燕第1-6题习题解答

E ( xt ) 0
;
0.7 xt 1 t ,即 xt
t
1 0.7 B
0.7i t i
i 0
所以有: Var ( xt ) (3)
0.7
i 0
2i
Var ( t )
2
1 0.7
2
2
0.51
1.96 2 ;
;
k 1 k 0.7k ,
1 1
2 2 ˆT (l )] lim Var[ xT l x l 1 12 12
.
证毕。
(3) 自相关系数 k ,由 AR(2)的递推公式,得:
1
1 0.8 16 0.695652 1 2 1 0.15 23
2 11 2 0 0.8 0.695652 0.15 1 0.406522
3 12 2 1 0.8 0.406522 0.15 0.695652 0.22087 ;
得 E ( xt ) 0 ; (2)
1 0.8, 2 0.15
1 2 2 (1 2 )(1 1 2 )(1 1 2 )
Var ( xt ) 0
1 0.15 2 1.982331 2 ; (1 0.15) (1 0.8 0.15)(1 0.8 0.15)
k 0
2 ,所以 2 0.7 0.49
(4) 因为是 AR(1)模型,偏相关系数一阶截尾,所以 22
0。
2 2. 已知某 AR(2)模型为: xt 1 xt 1 2 xt 2 t , t ~ WN (0, ) ,
第三章 线性平稳时间序列分析

λ + α1λ
p 1
+ + α p = 0
特征根 λ1 , λ2 ,… , λ p 为互不相同的实根 这时齐次线性差分方程的解为 t zt = c1λ1t + + c p λ p 特征根 λ1 , λ2 ,… , λ p 中有相同实根 这时齐次线性差分方程的解为 特征根 λ1 , λ2 ,… , λ p 中有复根 这时齐次线性差分方程的解为
j
j k
根据 Cauchy 不等式,我们可以得到
G j G j k ≤ ∑ G 2 ∑ G 2k ∑ j j j =∞ j =∞ j =∞
∞ ∞ ∞
12
<∞
所以级数
j =∞
∑GG
j∞Leabharlann j k收敛,故 { X t } 为平稳序列.
上海财经大学 统计与管理学院
10
,
3.1.2 线性过程的因果性和可逆性
1 j =1
(3.8)
其中
1 G 1 ( B ) = I ( B) = 1 ∑ I j B j j =1 ∞
(3.9)
称将 X t 变换为 ε t 的线性算子:
I ( B ) = ∑ I j B j , I 0 = 1
j =0
∞
为逆函数 逆函数,称(3.8)为 X t 的逆转形式 逆转形式,也称为无穷阶自回归. 逆函数 逆转形式
j =0 ∞
便于使用的条件是: 便于使用的条件是:
∑ Gj < ∞
∞
j =0
(3.7)
上海财经大学 统计与管理学院 13
在理论研究和实际问题的处理时, 通常还需要用 t 时刻及 t 时刻以前的 X t j ( j = 0,1, ) 来表示白噪声 ε t ,即
时间序列分析 第三章prc

取前k个方程构成的方程组即Yule-Walker方程组
解Yule-Walker方程组可以得到参数 ( k1 , k 2 ,, kk ) 的解, 最后一个参数的解即为延迟K偏自相关系数
1 k1 0 k 2 1 kk k 1 2 k1 1 k2 0 kk k 2 k k1 k 1 k 2 k 2 kk 0
2
, , ,
1
1 2 =0 3
1 1 2 kk 2 0
k 1 k2 k 3
课堂练习 计算AR(3)模型的偏自相关系数
33和44
AR模型偏自相关系数的截尾性
i 1 1 2 i 2 记 i i , i 1, 2, , k , ik k 对于AR( p )模型有: 11 2 2 p p 1 Dk
例3.5续:考察如下AR模型的偏自相关图
理论偏自相关系数 样本偏自相关图
(1) xt 0.8xt 1 t
0.8 , k 1 kk ,k 2 0
例3.5续:考察如下AR模型的偏自相关图
理论偏自相关系数 样本偏自相关图
(2) xt 0.8xt 1 t
t s t t k t k
ˆ )( x Ex ˆ )] E[( x Ex ˆ )2 ] E[( xt Ex t t k t k kk t k t k ˆ )( x Ex ˆ )] E[( xt Ex t t k k t xt , xt k xt 1 , , xt k 1 kk 2 ˆ ) ] E[( x Ex
时间序列分析方法智慧树知到课后章节答案2023年下哈尔滨工业大学

时间序列分析方法智慧树知到课后章节答案2023年下哈尔滨工业大学哈尔滨工业大学第一章测试1.英国的工业革命所进行的时间是()。
A:18世纪70年代到19世纪中期 B:18世纪60年代到19世纪上半期 C:18世纪60年代到18世纪末 D:18世纪30年代到18世纪末答案:18世纪60年代到19世纪上半期2.时间序列通常会受到哪些因素的影响()。
A:长期趋势 B:循环波动 C:季节变化 D:随机波动答案:长期趋势;循环波动;季节变化;随机波动3.时间序列分析有助于比较两个或多个序列。
()A:错 B:对答案:错4.可以应用时间序列模型准确地通过对历史数据分析预测未来发生的结果。
()A:错 B:对答案:错5.时间序列往往呈现某种趋势性或出现周期性变化的现象。
()A:错 B:对答案:对6.平稳时间序列差分后还是平稳时间序列。
()A:错 B:对答案:对7.时间序列分析有助于了解企业的行为。
()A:对 B:错答案:对8.一个时间序列的年度数据包含长期和周期性变化。
()A:错 B:对答案:对9.在计算年度数据的季节性指数时,删除最高和最低的实际滑动平均,减少了季节性变化。
()A:错 B:对答案:错10.一个时间序列的变化模式每年都会重复出现,这叫做季节性变化。
()A:错 B:对答案:对11.时间序列数据中的连续观测是独立且同分布的。
()A:错 B:对答案:错第二章测试1.纯随机序列的均值是零,方差是定值。
()A:错 B:对答案:错2.对于各种时间序列的ADF平稳性检验,其拟合方程式应该都相同。
()A:错 B:对答案:错3.由于观察值序列的有限性,纯随机序列的样本自相关系数可能不为零。
()A:对 B:错答案:对4.严平稳序列一定是宽平稳序列。
()A:错 B:对答案:错5.宽平稳序列一定是严平稳序列。
()A:错 B:对答案:错6.宽平稳序列的二阶矩一定存在。
()A:对 B:错答案:错7.当序列服从正态分布时,宽平稳和严平稳等价。
时间序列分析第三章平稳时间序列分析

时间序列分析第三章平稳时间序列分析轴表示序列取值。
时序图可以直观地帮助我们掌握时间序列的一些基本分布特征。
根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界的特点。
如果观察序列的时序图,显示出该序列有明显的趋势性或周期性,那它通常不是平稳序列。
从图上可以看出,数值围绕在0附近随机波动,没有明显或周期,其本可以视为平稳序列,时序图显示该序列波动平稳。
procarimadata=e某ample3_1;identifyvar=某nlag=8;run;图一图二样本自相关图图三样本逆自相关图2图四样本偏自相关图图五纯随机检验图实验结果分析:(1)由图一我们可以知道序列样本的序列均值为-0.06595,标准差为1.561613,观察值个数为84个。
(2)根据图二序列样本的自相关图我们可以知道该图横轴表示自相关系数,综轴表示延迟时期数,用水平方向的垂线表示自相关系数的大小。
我们发现样本自相关图延迟3阶之后,自相关系数都落入2倍标准差范围以内,而且自相关系数向0.03衰减的速度非常快,延迟5阶之后自相关系数即在0.03值附近波动。
这是一个短期相关的样本自相关图。
所以根据样本自相关图的相关性质,可以认为该序列平稳。
(3)根据图五的检验结果我们知道,在各阶延迟下LB检验统计量的P值都非常小(<0.0001),所以我们可以以很大的把握(置信水平>99.999%)断定该序列样本属于非白噪声序列。
procarimadata=e某ample3_1;identifyvar=某nlag=8minicp=(0:5)q=(0:5);run;IDENTIFY命令输出的最小信息量结果3某个观察值序列通过序列预处理,可以判定为平稳非白噪声序列,就可以利用ARMA模型对该序列建模。
建模的基本步骤如下:A:求出该观察值序列的样本自相关系数(ACF)和样本偏自相关系数(PACF)的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)计算yt的样本自协方差函数
(4)计算yt的样本自相关函数 (见Excel文件)
k 协方差 相关系数
0 189.6
1 2 3 -149.7 87.6 -31.1 -0.78956 0.462025 -0.16403
i 1 j 1 i j
n
n
j i
(l1 l2 l3
1 2 0 0 1 1 ln ) 2 1 0 n 1 n 2 n 3
n 1 l1 n 2 l2 n 3 l3 0 l 0 n
第三章 ARMA模型的特性
本章共有四节内容:
※第一节 ※第二节 格林函数和平稳性 逆函数和可逆性
※第三节 自协方差函数
※第四节 自谱
第三节 自协方差函数 一、自相关函数 1.自相关函数的引入 2. 理论自相关函数与样本自相关函数 3. 格林函数与自协方差函数之间的关系 4. ARMA模型自协方差函数及其特点 二、偏自相关函数
t t k
(3)样本自相关函数
(注:样本数据也先进行零 均值化处理) N 1 ˆk Xt Xt k N t k 1
ˆk ˆk ˆ0
t k 1
)
cov(X t , X t k ) VarX t VarX t k
k k 0
N
X t X t k
一、自相关函数 1. 自相关函数的引入
AR(1)模型:
X t 1 X t 1 at
问题:
Xt与Xt-2是否有相关关系?有怎样的相关关系? 怎样去度量这种相关关系?
对MA(1)模型呢?
Xt与Xt-j虽不直接相关,但有一定的相关关系,这就是我 们这一节将要给大家介绍的自相关函数。
2. 理论自相关函数与样本自相关函数
k=0,1,2,…,N;
该式是自协方差 k 的估计,称为样本自协方差函数, 相应的自相关估计称为样本自相关函数。
例1: Xt 的样本数据如下:求其样本自协方差函数 和样本自相关函数 Xt:47 64 23 71 38 64 55 41 59 48 计算步骤(1)计算样本均值; (2)对原序列Xt进行零均值化处理,得到yt;
协差阵为正定阵,对平稳序列而言,自协方差的正定性 是最本质的,常常是相关分析和参数估计的条件。
设随机变量Xt,Xt-1,Xt-2,…Xt-n+1的任一线性函数为:
Lt l1 X t l2 X t 1 ln X t n1
由于对平稳过程而言,有
cov[X i , X j ]
2 ) Xt:零均值平稳时间序列; at ~ NID(0, a
任何一个ARMA模型都可转化为等价的零均值ARMA模型。
(1)自协方差函数 cov(Xt,Xt-k)=(若Xt零均值平稳)E(XtXt-k)=γk (2)理论自相关函数
自协方差函数 cov(Xt,Xt-k)=γk 自相关函数
( X ,X
k k ; 0 0 1
n 1 n 2 n 3 2 z Pn 1
z2 0 ;
(6) 对样本自相关函数的说明
* ˆk
1 N k
t k 1
X t X t k
N
* ˆ N * ˆk k ˆ0 N k
(5)协差阵
k cov[X t , X t k ] E[( X t )( X t k )]
1 2 0 0 1 1 n 2 1 0 n 1 n 2 n 3 n 1 1 2 1 n 2 1 1 1 2 n 3 z 2 1 1 0 n 1 n 2 n 3
由此得知任何平稳过程的自协方差阵和自相关阵 都是正定的。 相应的,自协方差函数和自相关函数也都是正 定的。
对一般的Xt,k步滞后自相关ρk最令人满意的估计是
ˆk ˆk ˆ0
其中
1 N k ˆk ( X t X )( X t k X ) N t 1
1 N ˆ0 ( X t X ) 2 N t 1
N
2 X t t 1
ቤተ መጻሕፍቲ ባይዱ
(4)自协方差函数和自相关函数的性质 一个平稳过程的自协方差函数具有以下性质:
0 0 k k k 0 k
0 1 k k k 1 k
由此可知,自相关函数和自协方差函数是关于 零点对称的。一个正态平稳过程Xt能够被其均值和协 方差函数(或等价地,均值、方差和自相关函数) 完全刻划。
i 1 j 1 n n n n
li l j
i 1 j 1
j i
所以Lt的方差为
var[Lt ] li l j
i 1 j 1
n
n
j i
若li不全为0,则上式必然大于0(方差大于等 于0)。
由于对任意不全为零的常数 l1 , l2 ,, ln 有
l l
j i
可利用协方差的运算法则得到Lt的方差
var(Lt ) cov(Lt , Lt ) cov(l1 X t l 2 X t 1 l n X t n 1 , l1 X t l 2 X t 1 ln X t n 1 ) li l j cov(X t 1i , X t 1 j )
t k 1
N
X t X t k
N 2 t
X
t 1
N ˆk N k
N 1 ˆk Xt Xt k N t k 1
ˆk ˆk ˆ0
t k 1
N
X t X t k
N
2 X t t 1
这是因为后者的方差要小于前者;后者是正定序列,
