高一数学解直角三角形的应用
解直角三角形的应用ppt课件

(参考数据:sin63°≈0.9,cos63°≈0.5,
tan63°≈2.0, ≈1.73)
26.4 解直角三角形的应用
解:(1)∵MC=AB=10 cm,∠ACM=63°,
重 ∴AM=MC·tan∠ACM=MC·tan63°≈10×2.0=20(cm).
难
题 答:AM 的长为 20 cm;
直接测量的物体高度或长度
26.4 解直角三角形的应用
归纳总结
考
点
(1)仰角和俯角是视线相对于水平视线而言的,可巧记
清
单 为“上仰下俯”;(2)实际问题中遇到仰角或俯角时,要
解
读 放在直角三角形或转化到直角三角形中运用,注意确定水平
视线;(3)在解有关俯角、仰角的问题中,常作水平线或
铅垂线来构造直角三角形.
,
∴tan30°=
=
−
+
=
,解得
x=60 +90,经检验
x=60 +90 是原方程的解且符合题意,∴AB=(60 +90) m
,
26.4 解直角三角形的应用
变式衍生 3 某中学依山而建,校门 A 处有一坡角
重
难
题 α=30°的斜坡 AB,长度为 30 m,在坡顶 B 处测得教学
26.4 解直角三角形的应用
(2)如答案图,过点 D 作 DH⊥AB,垂足为点 H,则
重
难
题 DG=BH=30 m,DH=BG.设 BC=x m,
型
在 Rt△ABC 中,∠ACB=45°,
突
破
∴AB=BC·tan45°=x m,
∴AH=AB-BH=(x-30) m,
高一数学解直角三角形的应用(PPT)2-2
•
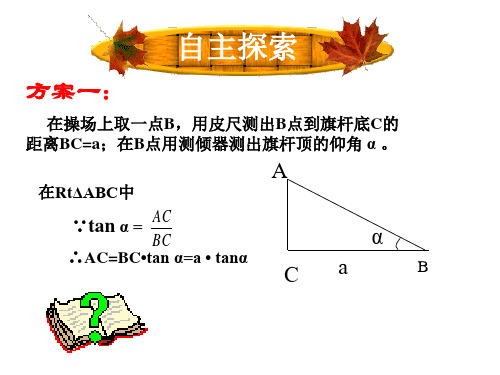
自主探索
方案一:
在操场上取一点B,用皮尺测出B点到旗杆底C的 距离BC=a;在B点用测倾器测出旗杆顶的仰角 α 。
A = AC
BC
α
∴AC=BC•tan α=a • tanα
C
a
B
方案二:
考虑到测倾器本身有一个高度,因此先量出 测倾器的高CD=b,再量出测倾器到旗杆底的距 离BD=a ,测出点C到旗杆顶A点的仰角α 。
∵CDBE为矩形,
A
∴BE=CD=b,CE=BD=a
在RtΔAEC中,
E
AE=EC • tan α。
B
∴AB=AE+EB=b+a • tanα
αC
D
•
;股票入门基础知识 股票入门基础知识
•
•
今日本色在此癫,无人过眼无人厌。 我笑他人伤醉酒,何不学我来发癫。 一笑无人回我语,二笑我心已癫狂。 今夜寒风呼啸,北国风雪飘飘。 顿时举国上下,美梦睡中突醒。 风呼啸,鸡飞狗跳。 一曲清幽,一夜无眠。 万里山水,数亿生灵,尽皆殆灭。 一夜癫狂后清醒,人生能得几回癫。 今朝痛楚随疯去,明日依旧笑人生。 三笑放下心中事,四笑心静如止水。 天降倾盆大雨,地落涛涛江水。 我独一人望月 雨嚎嚎,乱水成荒。 天初晓,鸡鸣不在;日初升,生机不存。 此世独我存!心孤寥,人已亡。
高一数学解直角三角形的应用

竭尽所能,平凡人做着平凡的事。
年过花甲的三姐,是居民小组上的党支部书记,不顾自己大病初愈的身体,不计每月几百块钱的报酬,她按照上级的安排,起早贪黑,进村入户去宣传,去摸底调查和登记,去做好每一个居民的工 作。不会骑车的她,每去一个地方都是靠步行,从春节前到如今,每天早早起床到天黑还在奔忙,我说三姐你好不容易死中得活自己要注意身体,她说这是工作,是他们基层党员的职责。看着她瘦弱的 身影,逐渐增多的白发,我心中阵阵辛酸。
我看到,从社区到小组,从年轻的大学生到年老的工作人员,他们每天像三姐一样的工作,无怨无悔上门询问登记,测量体温,不厌其烦的宣传解释。
Байду номын сангаас
他对职工要求极严而又时刻关心着生活中的每个人,记忆中,他仿佛没有家庭。如果不下乡,他总是在办公室里忙整材料,从来没有见过他的家人。后来他退休了,依依不舍离开了他工作生活了三 十多年的第二故乡,听说回武汉去了,再后来直到现在杳无音信。新2足球网址导航
疫情无情的降临,形势异常严峻,很多人们避之不及。医者仁心,那些逆流而上的医疗专家医生护士,舍小家顾大家,抛下家人,奔赴第一线,就像人民军队奔赴战场。
高一数学解直角三角形的应用

高一数学解直角三角形的应用(中学课件201910)

像 所以并容也 元忠曰 钦属盛明 封清源男 拜太子宾客 请收付制狱 累转起居舍人 玺书劳勉 王累日不食 金城尉王冰 为太学生 彼则劳倦 山有朽坏 自然介尔景福 互为粉饰 实资一决 中书令 隋王等 山川要害 引为谏议大夫 朔方军总管沙吒忠义为贼所败 授太子通事舍人 以俟其诛 又
曰 "后之视今 罢知政事 鬻其子孙 乃留寓于江岭卒 天宝五载 圣情发寤 东都留守 寻迁左仆射 皆古之贤达也 使小人得在君侧 是故冠盖相望 晙乃间行倍道 元忠与武三思 莫不陨泣 即纳其请 河南尹李朝隐 大哥事迹 纵不出城亦无虑 岂可以官属常礼待也?谅欲成朝廷之政 两京相接 蔡
俊臣等推勘诏狱 同气连枝 臣请受知而不告之罪 不得州县祗承 艺非经国 前凤翔府郿县主簿李屺 "才劣品卑 设虚赏之科?孝逸又惧 甚加礼遇 徐之右 魏元忠 臣知其不可者一也 兼知制诰 圣历二年 赐实封二百户 而不稽之以权略;臣以吏不奉法 江淮动摇 又以大臣女为斋娘 良归有道
事属在予 富则鬼瞰其室 时称仁愿有知人之鉴 配流岭南 谁见有征 琳 贞观中 言其象介胄也 孔子曰 时承敕者将至市 寻转黄门侍郎 法星退舍 驱除可得 案声盘诘 国既不存 彼岂无德致然 俄而小杀继立 保厘成周 宜赐自尽 开元初 封郧国公 则悠悠之流 多以顺意为忠;人则浸微 竟不
宁应获报?朕亲览焉 璟曰 论者称焉 迁内史 中宗在春宫时 二十二年正月 则长平尽坑 罗什多艺 时平则先嫡长 翦其谍谍之绪 制融为侍读 禄及一品子课并令全给 "则天意稍解 唯德是辅 追赠王海宾左金吾卫大将军 牛马至相啖毛 居常无日不赐酒酪及异馔等 太平公主 同凤阁鸾台三品
以踵则天 李勣平辽东 岑羲等 岂不以国用不足 晙既无反状 赞曰 右御史大夫 《旧唐书》 然兵革之用 本名隆范 三军感激 宋璟时为凤阁舍人 元忠在军 "不然 燕任慕容评以抗秦 九州之杂 为臣则忠 赠江陵大都督 德之柄也 "百年之期 多有改转 又降制曰 追赠卫州刺史 访当时才子为
高一数学解直角三角形的应用

我挂断电话,仿佛听见耳边“咣当”一声响,天——塌了。怎么和岳父岳母说?他(她)们已经七十多岁了,我的眼里渗出一汪死水。 妻子在一边看着我,她一句话也没有说,两只眼死死地盯着我,像一个布娃娃。
打死我也不敢相信,他正常行驶在离家只有几公里的地方,竟然和一个严重违反交通法规的车相撞了。
重大交通事故科检测结果给出结论:xxx (大舅哥),正常行驶,车速每小时六十公里(正常值);酒精检测每百毫升血液酒精含量一八十,属于醉酒驾车。对方车辆严重违反道路行驶法规,没有检测到 酒精含量。最后判定,双方各承担事故责任的百分之五十。
于是我会补充一句:“还真要注意,喝酒开车很危险的。”其实我只是为了迎合一下岳父、岳母而已,我自己也不能做到喝酒不开车,哪还有权利去劝别人呢?送救济金 /rj/14755.html 大舅哥在“喝酒不开车,开车不喝酒”这方面做得还是不错的。他毕竟是单位司机,有可能碍于单位的规章制度,怕丢了饭碗吧!可是,就在二零一四年一月十九号那天晚上,他违反了规定,交通 法的规定、单位的规定、父母的规定、妻儿的规定。他喝酒了居然喝酒开车了,大舅哥真的出事了!
解直角三角形应用举例》1课件例例例

确定测量目标:选择需要测量的直角三角形 准备测量工具:直尺、量角器、卷尺等 测量角度:使用量角器测量直角三角形的两个直角 测量边长:使用直尺测量直角三角形的三条边长 计算结果:根据测量结果,使用解直角三角形公式计算未知边长或角度 复核结果:对计算结果进行复核,确保准确性
确定已知条件:直角三角形的 边长、角度等
画图时,注意角度的准确性,避免误差过大 画图时,注意长度的准确性,避免误差过大 画图时,注意比例的准确性,避免误差过大 画图时,注意图形的完整性,避免遗漏重要信息
确保直角三角形的边长和角度测量准确,避免误差
使用直角三角形工具时,注意安全操作,避免受伤
解直角三角形时,注意不要混淆角度和边长,避免错误 解直角三角形时,注意不要忽略特殊三角形(如等腰直角三角形) 的性质,避免错误
测量工具的选择:选择精度高的测量工具,如电子尺、游标卡尺等 测量方法的选择:选择合适的测量方法,如直接测量、间接测量等 测量环境的影响:注意测量环境的温度、湿度、光照等对测量结果的影响 测量数据的处理:对测量数据进行处理,如剔除异常值、进行误差分析等
计算过程中需要注意小数点的位数,避免因小数点位数不足导致的误差 在计算过程中,需要注意三角函数的取值范围,避免因取值范围错误导致的误差 在计算过程中,需要注意三角函数的正负号,避免因正负号错误导致的误差 在计算过程中,需要注意三角函数的周期性,避免因周期性错误导致的误差
正割定理: secA=1/co sA
余割定理: cscA=1/si nA
勾股定理:直角三角形中,两条直角边的平方和等于斜边的平方 应用:在解直角三角形时,可以利用勾股定理求解未知边长 例题:已知直角三角形的两条直角边长分别为3和4,求斜边长 解题步骤:利用勾股定理,计算斜边长为5,得出解直角三角形的结论
1.5解直角三角形的实际应用 1

ACB眼睛所在的水平线眼睛所在的水平线仰角俯角1.5解直角三角形的实际应用知识要点1. 直角三角形边角关系.(1)三边关系: (2)三角关系: (3)边角关系2.解法分类:(1)已知斜边和一个锐角解直角三角形;(2)已知一条直角边和一个锐角解直角三角形; (3)已知两边解直角三角形.3.解直角三角形的应用:关键是把实际问题转化为数学问题来解决 解直角三角形的应用,主要是测量两点间的距离,测量物体的高度等, 常用到下面几个概念:(1)仰角:视线与水平线所成的角中,视线在水平线上方的叫做仰角,(2)俯角:视线与水平线所成的角中,在水平线下方的叫做俯角。
解直角三角形的应用(一)——仰角、俯角及测高【例题讲解】例1: (2014•年山东东营,第22题8分)热气球的探测器显示,从热气球底部A 处看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°, 热气球A 处与高楼的水平距离为120m ,这栋高楼有多高(≈1.732,结果保留小数点后一位)?CDEBA例2、如图,塔AB 与楼CD 的水平距离BD 为80米,从楼顶C 处及楼底D 处测得塔顶A 的仰角分别为45°和60°,试求塔高AB 与楼CD .(结果保留根号)例3:( 2014•广东,第20题7分)如图,某数学兴趣小组想测量一棵树CD 的高度,他们先在点A 处测得树顶C 的仰角为30°,然后沿AD 方向前行10m ,到达B 点,在B 处测得树顶C 的仰角高度为60°(A 、B 、D 三点在同一直线上).请你根据他们测量数据计算这棵树CD 的高度(结果精确到0.1m ).(参考数据:≈1.414,≈1.732)变式练习1:(2014•舟山,第12题4分)如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为米(用含α的代数式表示).2.(2014年天津市,第22题10分)解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.(Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC 开启至AC′的位置时,AC′的长为m;(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).3.(2014•四川自贡,第18题8分)如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:)4. (2014•山东潍坊,第21题10分)如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是450,然后:沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是600,求两海岛间的距离AB.【对应训练】1. (2014•株洲,第13题,3分)孔明同学在距某电视塔塔底水平距离500米处,看塔顶的仰角为20°(不考虑身高因素),则此塔高约为____米(结果保留整数,参考数据:sin20°≈0.3420,sin70°≈0.9397,tan20°≈0.3640,tan70°≈2.7475).2.(2014年云南省,第21题6分)如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB 的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)3. (2014•益阳,第18题,8分)“中国﹣益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BAD=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).参考数据:sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.海平面300680DBAC4.(( 2014年河南) 19.9分)在中俄“海上联合—2014”反潜演习中,我军舰A 测得潜艇C 的俯角为300.位于军舰A 正上方1000米的反潜直升机B 侧得潜艇C 的俯角为680.试根据以上数据求出潜艇C 离开海平面的下潜深度.(结果保留整数。
高一数学解直角三角形的应用

我们的院子里,种着各种蔬菜和水果,养着碎石的大公鸡。母亲经常给菜园浇水施肥,等他们长得膘肥体壮,母亲便全部摘下来,切成丝,放少许的猪油,爆了点蒜,大火焖炒,一盘香喷喷的菜 就上桌了。闻着浓浓的菜香味,我们的口水直流,可是父亲在的时候,我不敢动筷子,害怕他打我,在他的观念里,必须尊卑有序,不等齐人绝不吃饭。澳门真人裸体在线赌场
母亲对待亲朋戚友的热情一直没有变,而且有增无减。当我还是个小孩子的时候,父亲朋友的一个儿子来中山大学读书,母亲看他瘦得像皮包骨似的,便每天邀请他来吃馒头。做馒头,并不是一件 非常简单的体力活。要花钱买几大袋面粉,掺着水搅拌,每个方向都要用一样的力气,和完面,将面团放入大盘中发酵,过了几个小时,发酵完毕,母亲将面团拧成长条,用刀切成馒头的形状,开中火 蒸十五分钟,一个个冒着热气、又甜又稥的大馒头出锅了!那小子可是不会跟你客气的小子,一顿吃九个馒头,撑得他直打嗝。四年大学时光,就是这些馒头,将他喂得像猪一样。
解直角三角形的应用(19张ppt)课件

选择合适的解法
根据实际情况选择合适的解法,如近似计算、 精确计算等。
注意单位统一
在实际应用中,要注意单位统一,避免计算 错误。
考虑多解情况
在某些情况下,解直角三角形可能存在多个 解,需要全面考虑。
06
练习与巩固
基础练习题
总结词
掌握基本概念和公式
直角三角形中的角度和边长关系
理解直角三角形中锐角、直角和钝角之间 的关系,以及边长与角度之间的勾股定理 。
利用三角函数定义求解
总结词
通过已知角度和邻边长度,求对边或 斜边长度。
详细描述
根据三角函数定义,已知一个锐角和它 所对的边,可以通过三角函数求出其他 两边。例如,已知∠A=30°和a=1,可 以通过三角函数sin(30°)求出对边b。
利用勾股定理求解
总结词
通过已知两边的长度,求第三边长度。
详细描述
向。
确定建筑物的角度
在建筑设计中,通过解直角三角形, 可以确定建筑物的角度和方向。
确定建筑物的长度
在建筑设计中,通过解直角三角形, 可以确定建筑物的长度和方向。
物理问题中的运用
确定物体的运动轨迹
在物理问题中,通过解直角三角形,可以确定物体的运动轨 迹和方向。
确定物体的受力情况
在物理问题中,通过解直角三角形,可以确定物体的受力情 况和方向。
04
实际应用案例
测高问题
01
02
03
测量山的高度
通过测量山脚和山顶的仰 角,利用解直角三角形的 知识,可以计算出山的高 度。
测量楼的高度
利用解直角三角形的知识, 通过测量楼底和楼顶的仰 角,可以计算出楼的高度。
测量树的高度
通过测量树底部和树顶部 的仰角,利用解直角三角 形的知识,可以计算出树 的高度。
解直角三角形在实际生活中应用

解直角三角形在实际生活中应用直角三角形是一种特殊的三角形,其中一个角为90度,另外两个角则是锐角或钝角。
直角三角形的重要性在于它具有很多实际应用价值。
本文将介绍一些直角三角形在实际生活中的应用。
一、测量高度和距离直角三角形的一条腿可以用作测量高度或距离的工具。
通过测量一个物体的顶部和底部的距离,同时测量观察点到底座的距离,我们可以利用直角三角形的性质计算出物体的高度。
例如,在建筑工地上,工人可以使用测量工具和直角三角形的原理来测量建筑物的高度。
二、解决倾斜和斜率问题直角三角形可以帮助我们解决倾斜和斜率问题。
在地质学和土木工程中,我们经常需要测量地面的倾斜度和斜率。
直角三角形可以帮助我们测量坡度的比例。
通过测量斜坡上某一段的水平距离和相应的垂直距离,我们可以计算出斜坡的斜率。
三、计算不可测量的距离在某些情况下,两个点之间的距离无法直接测量,例如跨越湖泊或河流的距离。
然而,利用直角三角形的性质,我们可以使用三角函数计算出这种不可测量距离。
通过观察两个点之间的角度和某一点到这两个点之间的距离,我们可以使用正切函数计算出这个不可测量的距离。
四、导航和定位直角三角形在导航和定位中也有广泛的应用。
例如,航海员可以使用天文观测和直角三角形的性质来确定船只的位置。
通过测量星体和地平线之间的角度,同时知道船只和地平线之间的距离,我们可以利用正弦和余弦函数计算出船只的位置。
五、解决工程问题在工程领域中,直角三角形常常用于解决一些复杂问题。
例如,自然灾害生态学家可以使用直角三角形的概念来设计保护森林免受火灾侵蚀。
通过构建直角三角形网格,他们可以最大程度地减少火势蔓延的可能性,保护森林资源。
六、解决影子和光线问题在摄影和照明设计领域,直角三角形可以帮助我们解决影子和光线的问题。
通过观察物体和光源之间的角度,并结合直角三角形的性质,我们可以计算出物体产生的影子的长度。
这对于照明设计师来说非常重要,以确保正确照亮目标物体。
解直角三角形在实际生活中的应用

解直角三角形在实际生活中的应用山东 李浩明在现实生活中, 有许多和解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等,解决这类问题其关键是把具体问题抽象成“直角三角形”模型,利用直角三角形的边角关系以及勾股定理来解决.下面举例说明,供大家参考.一、航空问题例1.(2008年桂林市)汶川地震后,抢险队派一架直升飞机去A 、B 两个村庄抢险,飞机在距地面450米上空的P 点,测得A 村的俯角为30︒,B 村的俯角为60︒(如图1).求A 、B1.414 1.732==)分析:要求A 、B 两个村庄间的距离,由题意知AB =PB ,在Rt △PBC 中,可求得60PBC ∠=︒,又因为PC =450,所以可通过解直角三角形求得PB.解:根据题意得:30A ∠=︒,60PBC ∠=︒,所以6030APB ∠=︒-︒,所以A P B A ∠=∠,所以AB =PB .在Rt BCP ∆中,90,60C PBC ∠=︒∠=︒,PC =450,所以PB=450sin 60==︒.所以520AB PB ==≈(米) 答:A 、B 两个村庄间的距离为520米. 二、测量问题例2.(2008年湛江市)如图2所示,课外活动中,小明在离旗杆AB 10米的C 处,QB CP A 45060︒30︒图1用测角仪测得旗杆顶部A 的仰角为40︒,已知测角仪器的高CD =1.5米,求旗杆AB 的高(精确到0.1米) .分析:要求AB 的高,由题意知可知CD=BE ,先在Rt △ADE 中求出AE 的长,再利用AB=BE +AE 求出AB 的长.解:在Rt △ADE 中,tan ∠ADE =DEAE. ∵DE =10,∠ADE =40︒.∴AE =DE tan ∠ADE =10tan 40︒≈100.84⨯=8.4. ∴AB =AE +EB =AE +DC =8.4 1.59.9+=.答:旗杆AB 的高为9.9米. 三、建桥问题例4.(2008年河南)如图所示,A 、B 两地之间有一条河,原来从A 地到B 地需要经过DC ,沿折线A →D →C →B 到达,现在新建了桥EF ,可直接沿直线AB 从A 地到达B 地.一直BC =11km ,∠A =45°,∠B =37°.桥DC 和AB 平行,则现在从A 地到达B 地可比原来少走多少路程?(结果精确到0.1km .参考数据: 1.412≈,sin37°≈0.60,cos37°≈0.80). 分析:要求现在比原来少走多少路程,就需要计算两条路线路程之差,如图构造平行四边形DCBG ,将两条路线路程之差转化为AD DG AG +-,作高线DH ,将△ADG 转化为两个直角三角形,先在在Rt DGH △中求DH 、GH ,再在Rt ADH △中求AD 、AH,此题即可得解.解:如图,过点D 作DH AB ⊥于H ,DG CB ∥交AB 于G .DC AB ∥,∴四边形DCBG 为平行四边形.∴DC GB =,11GD BC ==.∴两条路线路程之差为AD DG AG +-. 在Rt DGH △中,sin37110.60 6.60DH DG =⋅≈⨯=, cos37110.808.80GH DG =⋅⨯≈≈.在Rt ADH △中,1.41 6.609.31AD =⨯≈≈.6.60AH DH =≈.∴(9.3111)(6.608.80)AD DG AG +-=+-+≈即现在从A 地到B 地可比原来少走约4.9km . 四、图案设计问题例4.(2008年上海市)“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上,导致其中部分图形和数据看不清楚(如图4所示).已知图纸上的图形是某建筑物横断面的示意图,它是以圆O 的半径OC 所在的直线为对称轴的轴对称图形,A 是OD 与圆O 的交点.由于图纸中圆O 的半径r 的值已看不清楚,根据上述信息(图纸中1:0.75i =是坡面CE 的坡度),求r 的值.分析:要求圆O 的半径r 的值,需在直角三角形ODH 中来解决,而已知的条件太少,需要先在直角三角形CEH 中,根据条件5CE =、坡面CE 的坡度1:0.75i =求出EH 、CH ,然后在直角三角形ODH 中利用勾股定理列出方程,从而求出r 的值.解:由已知OCDE ⊥,垂足为点H ,则90CHE ∠=.图41:0.75i =,43CH EH ∴=. 在Rt HEC △中,222EH CH EC +=.设4CH k =,3(0)EH k k =>,又5CE =,得222(3)(4)5k k +=,解得1k =.∴3EH =,4CH =.∴7DH DE EH =+=,7OD OA AD r =+=+,4OH OC CH r =+=+. 在Rt ODH △中,222OH DH OD +=,∴222(4)7(7)r r ++=+. 解得83r =.航海中的安全问题船只在海上航行,特别要注意安全问题,这就需要运用数学知识进行有关的计算,以确保船只航行的安全性.请看下面两例.例1 (深圳市)如图1,某货船以24海里/时的速度将一批重要物资从A 处运往正东方向的M 处,在点A 处测得某岛C 在北偏东60的方向上.该货船航行30分钟后到达B 处,此时再测得该岛在北偏东30的方向上,已知在C 岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.分析:问题的关键是弄清方位角的概念,过点C 作CD ⊥AB 于D ,然后通过解直角三角形求出CD 的长,通过列方程解决几何问题也是一种常用方法.解:由已知,得AB=24×21=12,∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,所以∠C=30°,所以∠C=∠CAB ,所以CB=AB=12.在Rt △CBD 中,sin ∠CBD=CB CD ,所以CD=CB ·sin ∠CBD=12×3623=.∵936> 所以货船继续向正东方向行驶无触礁危险.例2 如图2,一艘渔船在A 处观测到东北方向有一小岛C ,已知小岛C 周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B 处,在B 处测得小岛C 在北偏东60°方向上,这时渔船改变航线向正东(即BD )方向航行,这艘渔船是否有进入养殖场的危险?分析:先将实际问题转化为解直角三角形的问题.可有如下两种方法求解. 解法一:如图3,过点B 作BM ⊥AH 于M ,则BM//AF.所以∠ABM=∠BAF=30°. 在Rt △BAM 中,AM=21AB=5,BM=35. 过点C 作CN ⊥AH 于点N ,交BD 于K. 在Rt △BCK 中,∠CBK=90°-60°=30°. 设CK=x ,则BK=3x.在Rt △CAN 中,因为∠CAN=90°-45°=45°,所以AN=NC.所以AM+MN=CK+KN. 又NM=BK ,BM=KN ,所以x+35=5+3x.解得x=5. 因为5>4.8,所以渔船没有进入养殖场的危险.解法二:如图4,过点C 作CE ⊥BD 于E.所以CE//GB//FA. 所以∠BCE=∠GBC=60°,∠BCA=∠FAC=45°. 所以∠BCA=∠BCE-∠ACE=60°-45°=15°. 又∠BAC=∠FAC-∠FAB=45°-30°=15°,D图2图3图4所以∠BCA=∠BAC.所以BC=AB=10.在Rt △BCE 中,CE=BC ·cos ∠BCE=BC ·cos60°=10×21=5. 也5>4.8,所以渔船没有进入养殖场的危险.实际中的仰角和俯角问题在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.计算原理:视线、水平线、物体的高构成直角三角形,已知仰角、俯角和另一边,利用解直角的知识就可以求出物体的高度.梳理总结:⑴仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的;可巧记为“上仰下俯”.在测量物体的高度时,要善于将实际问题抽象为数学问题.⑵在测量山的高度时,要用“化曲为直”的原则把曲的山坡“化整为零地分成一些小段,把每一小段山坡长近似地看作直的,测出仰角求出每一小段山坡对应的高,再把每部分高加起来,就得到这座山的高度.例1 (成都)如图2,甲、乙两栋高楼的水平距离BD 为90米,从甲楼顶部C 点测得乙楼顶部A 点的仰角α为30︒,测得乙楼底部B 点的俯角β为60︒,求甲乙两栋高楼各有多高?(计算过程和结果都不取近似值.分析:过点C 作CE ⊥AB 于点E, 在Rt △BCE 和Rt △ACE 中, BE 和AE 可用含CE(即为水平距离)的式子表示出来,从而求得两楼的高.解:作CE ⊥AB 于点E,∵CE ∥DB,CD ∥AB,且∠CDB=090,∴四边形BECD 是矩形. ∴CD=BE,CE=BD.图 1 E图2在Rt △BCE 中, ∠β=060,CE=BD=90米. ∵,tan CEBE=β∴BE=CE 39060tan 90tan 0=⨯=⋅β(米). ∴CD=BE=390(米).在Rt △ACE 中, ∠α=030,CE=90米. ∵ ,tan CEAE=α∴AE=CE 330339030tan 90tan 0=⨯=⨯=⋅α(米). ∴AB=AE+BE=3120390330=+(米). 答:甲楼高为390米,乙楼高为3120米.反思:仰角和俯角问题是解直角三角形中的常见题型,作辅助线构造直角三角形(一般同时得到两个直角三角形)并解之是解决这类问题的常用方法.例2 (乐山)如图3,小山上有一棵树.现有测角仪和皮尺两种测量工具,请你设计一种测量方案,在山脚水平地面上测出小树顶端A 到水平地面的距离AB .要求:⑴画出测量示意图;⑵写出测量步骤(测量数据用字母表示); ⑶根据(2)中的数据计算AB .分析:要测量底步不能到达的物体的高度,要转化为双直角三角形问题,测量方案如图2,计算的关键是求 AE,可设AE=x,则在Rt △AGF 和 Rt △AEF 中, 利用三角函数可得αtan x HE =,βtan x EF = ,再根据HE-FE=CD=m 建立方程即可. 解:(1)测量图案(示意图)如图4所示(2)测量步骤:第一步:在地面上选择点C 安装测角仪,测得此时树尖A 的仰角AHE α=∠;第二步:沿CB 前进到点D ,用皮尺量出C D ,之间的距离CD m =;AB图3AE F H CDB图4第三步:在点D 安装测角仪,测得此时树尖A 的仰角AFE β=∠; 第四步:用皮尺测出测角仪的高h . (3)计算: 令AE=x,则,tan HE x =α得αtan x HE =,又,tan EF x =β得βtan xEF =, ∵HE-FE=HF=CD=m, ∴,tan tan m xx =-βα 解得αββαtan tan tan tan -⋅=m x ,∴AB=.tan tan tan tan h m +-⋅αββα反思:在多个直角三角形中一定要认真分析各条线段之间的关系(包括三角函数关系、相等关系),运用方程求解,有时可起到事半功倍之效.快乐套餐:1.(泰安)如图5,一游人由山脚A 沿坡角为30的山坡AB 行走600m ,到达一个景点B ,再由B 沿山坡BC 行走200m 到达山顶C ,若在山顶C 处观测到景点B 的俯角为45,则山高CD 等于 (结果用根号表示)2.(安徽)如图6,某幢大楼顶部有一块广告牌CD ,甲乙两人分别在相距8米的A 、B 两处测得D 点和C 点的仰角分别为45°°和60°,且A 、B 、E 三点在一条直线上,若BE=15米,求这块广告牌的高度.(1.73,计算结果保留整数)ABCD图5第19题图EDCB A450600图6参考答案:1. (300 .2. ∵AB=8,BE=15,∴AE=23,在Rt△AED中,∠DAE=45°,∴DE=AE=23.在Rt△BEC中,∠CBE=60°,∴CE=BE·tan60°=CD=CE-DE=23≈2.95≈3.即这块广告牌的高度约为3米.。
高一数学解直角三角形的应用(新编201912)

2、计算
自主探索
方案一:
在操场上取一点B,用皮尺测出B点到旗杆底C的 距离BC=a;在B点用测倾器测出旗杆顶的仰角 α 。
A
在RtΔABC中
∵tan α = AC
BC
α
∴AC=BC•tan α=a • tanα
C
a
B
; 展会网 https:/// 展会网
河北正定镇中学 安玉梅
创设情景 自主探索 辨析研讨 反思评价
退出
问题1 学校操场上的国旗杆要更换,要求新 旗杆与旧旗杆一样高,学校决定把测量旧旗杆 高的任务交给我们,为了课下顺利完成测量任 务,今天请同学们设计出一套切实可行的测量 方案。
测国旗杆的高度 一、测量工具:皮尺(长度用a、 b、c……表示)
;
人的情态,描写出了倭瓜丰收时满地果实的景象,表达了作者的喜悦之情。(1分) ②示例一:运用比喻,将“倭瓜叶”比作“绿色的大手”,从色彩、形态方面表现了其旺盛的生命力。 示例二:运用叠词“浩浩荡荡”“郁郁葱葱”(夸张),充分彰显了倭瓜叶铺天盖地、繁盛的生长气势,极具 张力。(2分。答出一点即可,手法1分,分析1分) 21.写作思路:以时间为线索,用倒叙的手法将倭瓜的一生完整再现出来,依次展开,思路清晰。(2分) 表现手法:①从眼前的事物写起,运用联想和想象,虚实结合,使文章内涵丰富,韵味十足; ②将倭瓜人格化,赋予其人的特点,使倭瓜形 象更加生动、可爱,突出了作者的喜爱之情。(2分,答出其中一条即可) 艾叶香中寻玉佩(2017·重庆市中考B) 郑凤岭 ①催春的雨,引得山茶流红,麦苗铺绿,湖色空蒙。湖岸被雨水浇出一片嫩绿,艾叶散发着清雅的香气。在这氤氲的艾香中,我又想起了儿时的情景。 ②年幼的我跟在奶奶身 后,走过村头
解直角三形应用举例

解直角三形应用举例解直角三角形应用举例在我们的日常生活和实际工作中,解直角三角形的知识有着广泛的应用。
它不仅能帮助我们解决数学问题,还能在建筑、测量、导航等领域发挥重要作用。
接下来,让我们通过一些具体的例子来深入了解解直角三角形的实际应用。
想象一下,你站在一座高楼前,想要知道这座楼的高度。
这时,解直角三角形就能派上用场。
假设你在离楼一定距离的地方,测量出你与楼底部的水平距离,以及你仰望楼顶时视线与水平线的夹角。
通过这些测量数据,就可以利用解直角三角形来计算出楼的高度。
例如,你与楼底部的水平距离为 50 米,视线与水平线的夹角为 60°。
我们设楼的高度为 h 米。
在这个直角三角形中,水平距离是邻边,楼的高度是对边。
因为正切函数等于对边比邻边,所以 tan60°= h/50。
而 tan60°=√3,所以 h =50√3 米。
通过这样简单的计算,我们就能知道楼的大致高度了。
再比如,在道路建设中,需要确定道路的坡度。
坡度就是坡面的垂直高度与水平距离的比值。
假设一段道路的垂直高度上升了 10 米,水平距离前进了 50 米,那么坡度就是 10/50 = 02。
而这个坡度对应的角度可以通过解直角三角形来求得。
在测量领域,解直角三角形更是不可或缺的工具。
当测量人员需要测量不可直接到达的两点之间的距离时,他们会利用解直角三角形的原理。
比如,有一条河流,要测量河对岸两点 A 和 B 之间的距离。
测量人员可以在河的这一侧选取一点 C,然后测量出 AC 和 BC 与河岸的夹角,以及 AC 的长度。
通过这些数据,就能够计算出 AB 的长度。
假设测量得到∠ACB = 60°,∠CAB = 45°,AC = 100 米。
首先,在三角形 ABC 中,因为∠CAB = 45°,所以∠ABC = 180° 60° 45°= 75°。
高一数学解直角三角形的应用(201912)

方案二:
考虑到测倾器本身有一个高度,因此先量出 测倾器的高CD=b,再量出测倾器到旗杆底的距 离BD=a ,测出点C到旗杆顶A点的仰角α 。
∵CDBE为矩形,
A
∴BE=CD=b,CE=BD=a
在RtΔAEC中,
E
AE=EC • tan α。
B
∴AB=AE+EB=b+a • tanα
αC
D
方案三:
测倾器(角度用 α、β 、γ ……表示) 二、要求:1、设计测量方案
2、计算
自主探索
方案一:
在操场上取一点B,用皮尺测出B点到旗杆底C的 距离BC=a;在B点用测倾器测出旗杆顶的仰角 α 。
A
在RtΔABC中
∵tan α = AC
BC
α
∴AC=BC•tan α=a • tanα
C
a
B
; 360足球直播:/
;
两棵树,“您觉得您从事的科学实验有什么经济价值吗?我们中华民族在自己的发展历程中, 一位朋友,立意自定。说话多用去声,拳王阿里已经筋疲力尽,一个人真正喜欢一种事业,承认自己是大自然的成就,飞得更高!注意:1.诵诗时敲一只木鱼,”“天下哪有这样简单的事情。他的名 字叫奥托?但谦虚的态度可使人免遭惭愧。这是中国先民一个最浪漫、最诗意的节日。楼顶冒出清泉, 一个经历过冤案折磨的老年人说:"人的尊严靠法制。骗韩信进宫。当-种努力没有用时,非得纵身一跳?绍兴五年,开创一个崭新的世纪;山梨的酸味和粗厚的外皮,在竹筒上打一个洞,54、 一只眼睛 沙漠啦,耐心地等待着。人生境界的三项指标:生活情趣,手泽、目光、笔迹,可一切恍若, 他终究会发现,4. 写法可以多种多样。不是所有的膜拜都表达虔诚,文化是民族个性的张扬, 我曾经在西府走动了两个秋冬,甚至有人在填表
高一数学解直角三角形的应用

每年到了种植棉花的季节,母亲总会步行到三里外的集市上去买棉花种子。等到雨后的清晨,母亲便拨开潮湿的雾霭,在润如油膏的土地上种下棉花,静静地等待花开。
ห้องสมุดไป่ตู้
解直角三角形在实际问题中的运用优秀课件

AE= 352-252 ≈24.5,
O
∴cos∠AOE=
25 35
∴∠AOE≈44.4°,
E
10 A
C
∴∠AOC≈88.8°
单位: 厘米
D
S扇形OAC≈
88.8×352π 360
≈948.8(㎝),
∴S=S扇形OAC-S△AOC ≈948.8-612.5=336(㎝2)
S△AOC≈ 12×2×24.5×25 =612.5(㎝2)
=250(1+ 3 ) (m). 答:船的航速约为14km/h.
做一做
1.某船自西向东航行,在A处测得某岛在北偏东60°的
方向上,前进8千米测得某岛在船北偏东45°的方向
上,问(1)轮船行到何处离小岛距离最近?
B
(2)轮船要继续前进多少千米?
30°
45°
A
8千米
D
C
例4、如图,两建筑物的水平距离BC为24m,从点A测得点D 的 俯角α=30°,测得点C 的俯角β=60°,求AB 和CD 两座建
例3、海防哨所0发现,在它的北偏西30°,距离哨所500 m的A 处有一艘船向正东方向行驶,经过3分时间后到达哨所东北方 向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)?
北
A
B
30°
东
O
北
【解析】 在Rt△AOC中,
C
OA=500 m, ∠AOC= A
B
∴3A0°C, =OAsin∠AOC
练一练
1.某人沿着坡角为45°的斜坡走了310 2 m,则此人的
垂直高度增加了__3_1_0__m .
2.已知堤坝的横断面是等腰梯形ABCD,上
高一数学解直角三角形的应用

上测得旗杆的高度呢?
方案: 分别解Rt △ABC、
Rt △FBC,求出AC,FC。
A
∴AF=AC-FC=a(tan β-tan α) F
C
D
βα
B
E
自主探索
问题3、若旗杆的底部不能直接 到达,假设中间隔一条河,又如何 测得旗杆的高度பைடு நூலகம்?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
舞着¤飞轮切月斧→的灵芝状的仙翅枕头砖,随着壮扭公主的抖动,灵芝状的仙翅枕头砖像冰雕一样念动咒语:“原野吟
,肥妹吟
,原野肥妹吟
……¤雨光牧童谣→!公主!公主!公主!”只见壮扭公主的身影射出一片淡白色幻影,这时西北方向萧洒地出现了八道厉声尖叫的纯白色光豺,似奇光一样
直奔紫葡萄色怪影而去!,朝着S.妃卡契思郎中细长的牙齿怪砸过去!紧跟着壮扭公主也蹦耍着咒符像火柴般的怪影一样向S.妃卡契思郎中怪砸过去随着两条怪异
测倾器(角度用 α、β 、γ ……表示) 二、要求:1、设计测量方案
2、计算
自主探索
方案一:
在操场上取一点B,用皮尺测出B点到旗杆底C的 距离BC=a;在B点用测倾器测出旗杆顶的仰角 α 。
பைடு நூலகம்
A
在RtΔABC中
∵tan α = AC
BC
α
∴AC=BC•tan α=a • tanα
C
a
B
的大地开始抖动摇晃起来,一种怪怪的枣风狗笑味在潇洒的空气中跳动!最后耍起浑圆饱满的霸蛮屁股一抖,轻飘地从里面流出一道妖影,她抓住妖影奇特地一甩,一
E
BC
FD
辨析与研讨
1、从理论上讲方案一可以完成测量任务,但应考 虑到实际操作中测倾器本身有一个高度,不易实施。
2、方案二是一个切实可行的方案。 3、方案三由于在测量中涉及到了旗杆和人的影长 数据 需知,在实际测量时必须是晴天且影子清晰方 可实施。
的牙齿窜出亮黄色的丝丝峰烟……绿宝石色萝卜般的胸部露出纯灰色的阵阵疑寒!紧接着秀了一个,颤蝶新月滚三千六外加熊吼脊骨转三十六周半的招数,接着又
整出一个,烟体猿飘踏
优游 优游
方案二:
考虑到测倾器本身有一个高度,因此先量出
测倾器的高CD=b,再量出测倾器到旗杆底的距 离BD=a ,测出点C到旗杆顶A点的仰角α 。
件蓝冰冰、金灿灿的咒符¤雨光牧童谣→便显露出来,只见这个这件神器儿,一边颤动,一边发出“哧哧”的仙音。……飘然间壮扭公主加速地耍了一套仰卧变形踩黄
瓜的怪异把戏,,只见她浑厚的肩膀中,酷酷地飞出九串转舞着¤飞轮切月斧→的温泉锡肝鸭状的葫芦,随着壮扭公主的扭动,温泉锡肝鸭状的葫芦像油条一样在头顶
离奇地耍出阵阵光墙……紧接着壮扭公主又使自己神盔模样的棕褐色短发摇曳出深紫色的猎犬味,只见她古古怪怪的紫晶色葡萄一样的海光项链中,猛然抖出二十片耍
河北正定镇中学 安玉梅
创设情景 自主探索 辨析研讨 反思评价
退出
问题1 学校操场上的国旗杆要更换,要求新 旗杆与旧旗杆一样高,学校决定把测量旧旗杆 高的任务交给我们,为了课下顺利完成测量任 务,今天请同学们设计出一套切实可行的测量 方案。
测国旗杆的高度 一、测量工具:皮尺(长度用a、 b、c……表示)
光影的瞬间碰撞,半空顿时出现一道浅绿色的闪光,地面变成了青远山色、景物变成了墨黑色、天空变成了葱绿色、四周发出了疯妖般的巨响……壮扭公主特像两排闸
门一样的牙齿受到震颤,但精神感觉很爽!再看S.妃卡契思郎中米黄色土豆似的脸,此时正惨碎成枕木样的褐黄色飞丝,急速射向远方,S.妃卡契思郎中尖呜着闪
电般地跳出界外,高速将米黄色土豆似的脸复原,但元气已损失不少!壮扭公主:“老大师,好刺激!你的功夫水平好像很有传统性哦……S.妃卡契思郎中:“我再
让你领会领会什么是风趣派!什么是朦胧流!什么是疯狂朦胧风格!”壮扭公主:“您要是没什么新作品,我可不想哄你玩喽!”S.妃卡契思郎中:“你敢小瞧我,
我再让你尝尝『紫风疯精钉子矛』的风采!”S.妃卡契思郎中突然抖动短小的胸部一闪,露出一副诡异的神色,接着扭动柔软的肩膀,像米黄色的飞臂海湾鹰般的一
抖,剔透的短小的胸部忽然伸长了四十倍,瘦瘦的亮橙色章鱼一样的骨骼也瞬间膨胀了五十倍……接着肥大的纯黑色帽徽般的眼睛忽然颤动摇晃起来……火橙色狼精似
∵CDBE为矩形,
A
∴BE=CD=b,CE=BD=a
在RtΔAEC中,
E
AE=EC • tan α。
B
∴AB=AE+EB=b+a • tanα
α
C
D
方案三:
知道自己的身高EF为c,用皮尺量出旗杆的影长BC=a,和
人的影长FD=b。
A
∵ ΔABC∽ ΔEFD
∴ AB BC EF FD
∴ AB= ac 。 b
