Microsoft Mathematics计算三重积分-微积分上的应用
三重积分计算题与实际生活有关的

三重积分计算题与实际生活有关的一、引言在数学中,三重积分是一种重要的数学工具,用于计算多变量函数在三维空间中的体积、质量、质心等物理量。
虽然在学术和科研领域中有着广泛的应用,但三重积分在实际生活中也有着重要的应用价值。
本文将探讨三重积分计算题与实际生活的关联,以及其在工程、地理和医学等领域中的应用。
二、三重积分的基本概念在开始讨论三重积分在实际生活中的应用之前,我们先来了解一下三重积分的基本概念。
三重积分是对三维空间内的函数进行积分运算,通常用于计算三维区域内的体积。
其数学表达式为∭f(x, y, z) dV,表示对空间内的某个区域进行积分。
根据不同的坐标系,三重积分可以表示为直角坐标系、柱坐标系或球坐标系下的积分形式。
通过对三维空间内的函数进行三重积分运算,可以得到该函数在空间内的总量或总值。
三、三重积分在工程中的应用在工程领域,三重积分广泛应用于计算物体的体积、质量及重心等物理量。
在机械设计中,通过对零件的三维模型进行三重积分计算,可以准确地得到零件的体积和质量,为零件的加工和制造提供了重要的参考数据。
另外,在建筑设计中,对建筑结构或土地的三维模型进行三重积分计算,可以帮助工程师确定建筑物的体积和重心,从而保证建筑结构的稳定性和安全性。
三重积分在工程领域的应用为工程设计和制造提供了重要支持。
四、三重积分在地理学中的应用在地理学领域,三重积分也有着重要的应用价值。
地理学家经常需要计算地球上的地形、地貌及地下资源等空间分布的特征。
通过对地理空间内的各种地形或资源分布进行三重积分计算,可以得到地球表面或地下的总体积、总资源量等物理量。
这些数据对于地理学家研究地质构造、资源分布和环境保护等方面具有重要意义。
三重积分还可以帮助地理学家对地球上各种自然灾害如地震、火山喷发等进行风险评估和预测,为地质灾害防治提供了重要的技术支持。
五、三重积分在医学中的应用在医学领域,三重积分也被广泛应用于对人体组织和器官的体积、密度、质量等生理特征的研究和计算。
重积分三重积分的应用课件.ppt

解 立体的图形为 设1为 在第一卦限内
的部分, 利用对称性得
z 1
M 4M1 4 ( x, y, z)dv
1
o
y
4( x y )dv 柱坐标变换 x
1
1
1
4 2 d rdr r(cos sin )dz
0
0
r2
4
2 (cos sin )d
1
r
2
(1
r
2
)dr
0
0
16。 15
13
设有一平面薄片占有 y
平面闭区域D, 在点(x,y)
处具有连续面密度
=(x,y),下面利用元素
y
•d
D
法求该平面薄片对两坐
标轴的转动惯量。
O
x
x
先将物体分割为许多小部分,考虑其中的一
个部分d,它的质量元素为
dm ( x, y)d
这个部分d对于x轴以及对于y轴的转动惯
量元素为
dIx y2( x, y)d dI y x2( x, y)d
F
x, y, a 一致。
F0
x r
,
y,a rr
o x
x
y
• P(x,y,0) y
cos,cos ,cos , (r x2 y2 a2 )
dF {dFx , dFy , dFz }
{| d F | cos,| d F | cos ,| d F | cos },
( x, y)xd ( x, y) yd a( x, y)d
14
y
以这些元素为被积表达 式,在闭区域D上积分, 可得
y
•d
D
Ix y2( x, y)d ,OD源自I y x2( x, y)d
三重积分讲解

三重积分是微积分学中的一个重要部分,也是解决许多实际问题的基础。
以下是对三重积分的详细讲解:1.三重积分的概念:三重积分是将一个函数的积分运算转化为三个不同的积分,即分别对三个变量进行积分。
其一般形式为:∫∫∫f(x,y,z)dxdydz其中f(x,y,z)是待求积分的函数,而∫∫∫是三重积分的符号。
2.三重积分的物理背景:三重积分有着深刻的物理背景。
在物理学中,一个物体的质量分布、能量分布或者电荷分布等可以用三重积分来表示。
例如,一个物体的质量分布可以表示为空间中的密度函数f(x,y,z),那么该物体的总质量就可以通过三重积分来计算。
3.三重积分的计算方法:三重积分的计算通常采用“分割、近似、求和、取极限”的方法。
具体步骤如下:(1)分割:将积分区域分割成许多小的立方体,每个立方体称为一个“小块”。
(2)近似:用每个小块的中心点(x',y',z')来近似该小块上的积分,即用该点的函数值f(x',y',z')来近似该小块上的积分。
(3)求和:将所有小块的积分值相加,得到粗略的积分值。
(4)取极限:将小块的尺寸逐渐缩小,使得粗略的积分值逐渐接近精确的积分值。
4.三重积分的几何意义:三重积分可以理解为空间物体的质量,即空间物体占据空间区域,在点(x,y,z)处的体密度为f(x,y,z),整个空间物体的总质量就是将f(x,y,z)累积遍整个空间区域。
5.三重积分的性质:三重积分具有与一元定积分相同的性质,例如可加性、可移性、可换序性等。
同时,三重积分也具有与二重积分不同的性质,例如三重积分可以通过“分割、近似、求和、取极限”的过程得到精确的积分值,而二重积分则不能。
6.三重积分的实际应用:三重积分在许多实际应用领域有着广泛的应用,例如物理学中的质量分布、电荷分布、能量分布等问题,工程学中的体积计算、质量平衡等问题,以及统计学中的数据分布等问题。
通过三重积分,我们可以更好地理解和解决这些问题。
Mathematic在数学中的应用

五、四种软件的比较
选用何种数学软件? 如果仅仅是要求一般的计算或者是普通用户日常使用, 首选的是MathCAD,它在高等数学方面所具有的能力,足 够一般客户的要求,而且它的输入界面也特别友好。 如果要求计算精度、符号计算和编程方面的话,最好同 时使用Maple和Mathematica,它们在符号处理方面各具特 色,有些Maple不能处理的,Mathematica却能处理,诸如 某些积分、求极限等方面,这些都是比较特殊的。 如果要求进行矩阵方面或图形方面的处理,则选择 MATLAB,它的矩阵计算和图形处理方面则是它的强项,同 时利用MATLAB的NoteBook功能,结合Word6.0/7.0的编辑 功能,可以很方便地处理科技文章。
比较如下的输入方式
若采用浮点数输入,则计算结果为近似值 (1)1./3+2/5 (2)2^100 (3)2.^100
一个是精确计算2的100次方,一个是近似计算2 的100次方
2:常数与函数
Mathematica软件中提供了数学上通用的一些常 数,下表中给出了其中一部分常数 常数 Pi E I 数学含义 圆周率 常数 Infinity 数学含义 正无穷大
Mathematica的进一步说明
它吸取了不同类型软件的一些优点: (1)具有BASIC的简单易学的交互式方法 (2)具有MathCAD\Matlab那样强的数值计算能力 (3)具有Maple的和SMP那样的符号计算能力 (4)具有APL和LISP那样的人工智能列表处理能力 (5)像C和PASCAL那样的结构化设计语言 Mathematica的开发者 Stephen Wolfram是Mathematica的创始人,并被公认为是 当今科学计算的先驱。 Wolfram1959年出生于伦敦。他曾在 牛津大学和加州理工学院接受教育,15岁发表了第一篇科技 论文,1979年20岁时在加州理工学院获得理论物理学博士学 位。 他从1973年开始使用计算机,1981年主持开发了第一个计算 机代数系统SMP。
二重积分与三重积分的应用与解析

二重积分与三重积分的应用与解析积分是微积分学中的重要概念,它被广泛应用于数学、物理学和工程学等多个领域。
其中,二重积分和三重积分是积分的不同维度的扩展,它们在实际问题的求解中具有重要作用。
本文将重点讨论二重积分和三重积分的应用以及解析方法。
一、二重积分的应用二重积分是在二维平面上对某个闭区域内的函数进行求和,它的应用广泛涉及到面积、质心、质量等问题。
1. 面积计算二重积分可以用来计算平面上某个区域的面积。
给定一个平面区域,可以通过将该区域细分成许多小面积的矩形,然后对每个小面积进行积分求和得到整个区域的面积。
2. 几何中心计算对于一些具有均匀密度的平面物体,可以使用二重积分来计算其几何中心位置。
通过将物体分割成小面积的矩形,并求得每个小面积的坐标乘以密度的积分,然后除以物体总的质量,即可得到几何中心位置。
3. 质量计算二重积分可以用来计算平面上具有变化密度的物体的总质量。
类似于几何中心的计算方法,通过划分小面积的矩形,并对每个小面积的坐标乘以密度的积分进行求和,可以得到物体的总质量。
二、二重积分的解析方法对于一般的二重积分,可以利用多种解析方法进行求解。
下面介绍两种常用的解析方法:1. 直角坐标系下的解析方法在直角坐标系下,对于给定的二重积分,可以利用定积分的性质分别对x和y 进行积分。
具体步骤如下:(1)先确定积分的范围,即确定积分的上下限。
(2)对x进行积分,如果积分中包含y的项,则要将y看作常数进行求解。
(3)对y进行积分,将之前得到的结果中不包含y的项看作常数进行求解。
(4)将两次积分的结果相乘,得到最终的解。
2. 极坐标系下的解析方法在极坐标系下,对于特定的问题,使用极坐标系可以简化积分的计算过程。
具体步骤如下:(1)将二维区域转换为极坐标系下的区域。
(2)确定极坐标下的积分范围。
(3)利用极坐标下的积分公式进行求解,替换掉定积分中的x和y。
三、三重积分的应用三重积分是在三维空间中对某个闭区域内的函数进行求和,它的应用广泛涉及到体积、质量、质心等问题。
mathematica长方体三重积分

mathematica长方体三重积分长方体是一种常见的几何体,它有六个面,六个面分别是正方形,长方形和矩形。
我们可以通过三重积分来求解长方体的体积。
对于一个长方体,假设它的长、宽、高分别为a、b、c。
我们可以将长方体分割成许多小的体积元素,每个体积元素的体积为ΔV = Δx * Δy * Δz。
其中Δx、Δy和Δz分别是在x、y和z方向上的微小长度。
现在,让我们来考虑在长方体内的一个点P,它的坐标为(x, y, z)。
我们可以通过限定x的范围为[0, a],y的范围为[0, b],z的范围为[0, c],来确定点P在长方体内。
这样,我们可以将长方体的体积表示为:V = ∫∫∫ dV = ∫∫∫ Δx * Δy * Δz其中,积分符号∫表示对变量的积分,∫∫∫表示对三个变量的积分。
接下来,我们需要确定如何计算Δx、Δy和Δz。
由于长方体的形状是规则的,我们可以将每个方向上的长度分成n个小段,即Δx = a/n,Δy = b/n,Δz = c/n。
这样,我们可以将长方体的体积积分表示为:V = ∫∫∫ (a/n) * (b/n) * (c/n)将上述方程进行展开和计算,可以得到:V = (abc) * (1/n^3) * ∫∫∫ dx * dy * dz其中,积分的范围为x从0到a,y从0到b,z从0到c。
我们可以通过数值计算的方法来求解上述积分。
首先,我们将长方体的边长a、b、c和分割数n进行给定。
然后,我们将积分的范围和积分表达式输入到Mathematica中,并进行数值计算。
最后,我们得到长方体的体积。
通过以上的步骤,我们可以利用Mathematica进行长方体的三重积分计算。
这种方法既简单又高效,可以帮助我们快速求解长方体的体积。
希望本文对您有所帮助,谢谢阅读。
三重积分的概念及其计算

= ∫ dx
a
∫
dy
∫
f (x, y, z )dz
y1(x )
z1 ( x , y )
所以有
∫∫∫ f (x, y, z )dV
D
= ∫ dx
a
b
y2 ( x )
∫
z 2 ( x ,y )
dy
∫
f (x, y, z )dz (2)
y1 (x )
z1 ( x , y )
公式 (2) 将三重积分化为先 z , 后 y , x 的三次积分 同理对于区域
I =
∫−1 dx ∫x
1
1
2
dy ∫
x 2 +y 2
0
f (x , y , z )dz
.
例 化三重积分
I = ∫∫∫ f ( x, y, z)dxdydz 为三次积分
Ω
Ω : z = xy 与 x + y = 1, z = 0 所围成的区域
x+ y=1
z
z=xy
y
1
o
1
.
x
例 化三重积分
I = ∫∫∫ f ( x, y, z)dxdydz 为三次积分
Ω2
z = x2 + y2 + 1
y
x+ y = 4
.
1
o
4
x
例 计算 I = ∫∫∫ f ( x , y , z)dxdydz
z Ω: 曲面 z = x + y 2 + 1,平面 x + y = 4 及三个坐标面所围区域
Ω2
取第一卦限部分
z = x2 + y2 + 1
y
三重积分的概念,计算,应用

z = 1−r2
Drθ
∫∫ rdrdθ ∫
Drθ
0
zdz = ∫
0
1 π 2 dθ ∫ r (1 − r )dr = 02 4
=
∫∫ dxdy ∫
D xy
z2 ( x, y )
z1 ( x , y )
三、三重积分的一般计算
1. 先一后二法
x= x2(y, z)
x
同理: 同理:
o y Dyz
x = x1 ( y, z )
z
(y,z) y,z)
若Ω = {( x, y, z ) | ( y, z ) ∈ Dyz , x1 ( y, z ) ≤ x ≤ x2 ( y, z )}, Dyz = PrjYZ Ω 则 : ∫∫∫ fdv =
Ω Ω
VΩ = Ω 的体积,则: m ⋅ VΩ ≤
∫∫∫ f ( x, y , z ) dv ≤ M ⋅ V
Ω
这些性质与 二重积分类 似!
Ω
三、三重积分的一般计算
1. 先一后二法
z = z2(x, y)
z
设f ( x, y, z )在Ω上连续,Ω如图:
o
z = z1 ( x, y )
y
Dxy = PrjXY Ω, 且∀( x, y ) ∈ Dxy时:z1 ( x, y ) ≤ z ≤ z2 ( x, y ) x Dxy
x2 y2 z 2 求I = ∫∫∫ z 2 dxdydz, 其中Ω : 2 + 2 + 2 ≤ 1 例2 a b c Ω
zc
z o Dz
解:)将Ω向Z轴投影得: c ≤ z ≤ c (1 − (2)用平面z = z截Ω得截面投影区域:
第07章5节 三重积分的应用
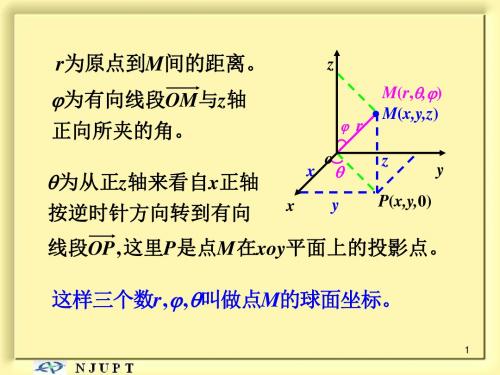
r
rd
d
y
dv r sindrdd
2
d
这就是球面坐标系中的体积元素。
5
二、 三重积分的球面坐标形式
2 f ( x , y , z ) dxdydz F ( r , , ) r sindrdd
其中F (r , , ) f (r sin cos , r sin sin , r cos )。
(1)坐标系的选取
(2)积分顺序的选定(直角)
(3)定出积分限
18
坐标系
适用范围 长方体 四面体 任意形体
体积元素
变量代换
直角坐标
dxdydz
xx y y zz
x r cos y r sin zz
x r cos sin y r sin sin z r cos
0 r , 0 , 0 2
z M(r,,) M(x,y,z) z y P(x,y,0)
r
o x x
②三组坐标面
y
r =常数,即以原点为心的球面。
=常数,即以原点为顶点、z轴为轴的圆锥面。 =常数,即以z轴为边的半平面。
2
③点M的直角坐标与 球面坐标的关系为
dy
R2 x 2 y 2
0
( x y )dz
2 2
解 (1) 是以原点为球心,以R 为半径的上半球面与xoy面所围 成的空间区域。 : 0 r R,0 ,0 2 2 x
2 R
z
o
y
I d 2 d r 2 sin2 r 2 sindr 0 0 0 R 4 4 3 4 2 R 。 2 sin d r dr 0 0 15
高数大一知识点三重积分

高数大一知识点三重积分高等数学是大学数学专业的一门重要课程,对于数学专业的学生来说,掌握高数知识点是非常重要的。
在大一的高等数学课程中,三重积分是一个非常重要的知识点。
下面将从基本概念、计算方法和应用等几个方面来介绍三重积分。
一、基本概念三重积分是对三维空间中的函数进行积分运算。
如果一个三维空间中的函数在某个区域上是连续的,那么可以对这个函数进行三重积分。
三重积分可以看作是对空间中的体积进行求和的过程。
在三重积分中,我们需要确定积分函数、积分区域、积分方向和积分顺序等要素。
二、计算方法三重积分的计算方法有直接计算法和间接计算法两种。
直接计算法是将积分区域划分成小的立体元,然后对每个立体元进行积分计算,最后将所有立体元的积分结果相加得到最终的积分结果。
间接计算法是利用高斯公式和格林公式来进行计算。
高斯公式是将三重积分转化为对闭合曲面上的二重积分,然后再将二重积分转化为对曲线上的一重积分。
格林公式则是将曲线积分转化为坐标轴上的一重积分。
利用这两个公式,可以将三重积分的计算转化为一重积分的计算,简化了计算的步骤。
三、应用三重积分在物理学、工程学和计算机图形学等领域有着广泛的应用。
在物理学中,三重积分可以用来计算物体的质量、重心、转动惯量等物理量。
例如,在力学中,我们可以通过对物体密度分布函数进行三重积分来计算物体的质量。
在工程学中,三重积分可以用来计算物体的体积、质量、质心等。
例如,在建筑工程中,我们可以通过对建筑结构进行三重积分来计算结构的体积和质量。
在计算机图形学中,三维模型的表面可以通过三重积分来进行渲染和着色。
例如,通过对三维物体的颜色分布进行三重积分,可以得到物体在不同方向上的颜色分布,从而实现逼真的渲染效果。
四、总结三重积分是大一高等数学中的一个重要知识点,掌握三重积分的基本概念、计算方法和应用是非常重要的。
通过对三重积分的学习和应用,可以提高数学建模和问题求解的能力,并在物理学、工程学和计算机图形学等领域中发挥重要作用。
三重积分计算浅析

Abstract We present the calculation methods of triple int egrals in different coordinate systems , such as cylindricalandsphericalcoordinaFes anddiscussFhenaFureofFripleinFegralcalculaionformulasinFhese coordinaFes. A number of deformaFionFreaFmenFs are also ilusFraFed. Keywords FripleinFegral symmeFry PacobideFerminanF cylindricalcoordinaFes sphericalcoordinaFes
作者简介:方汶铭(1979 —),男,浙江义乌,硕士 ,讲师,从事代数编码
理论研究,Email:fwm@ysu. edu. cn.
解法1利用直角坐标计算三重积分
" I = C%2 + 5y2 + 7))d&
Байду номын сангаас
=
J—a
%
J—
/a—2
dy .______ (3% 叮—/一一2
+ 5y2 丿
+7)')dz
= 4"a5
法”(亦称为投影法),下面利用“先二后一法,亦称 为截面法或切片法)进行计算,此计算方法运用得 当可以减小计算量•在本题中运用“先二后一”的方 法计算时 需要考虑使用三重积分的 性质将其分成
三项进行计算,主要计算过程如下:
" I = (3%2 + 5y2 + 7)2 )d^
高等数学-第九章 三重积分及应用

例. 计算积分 zdxdydz 其中由曲面
zx2y2,yx2及平面 y1,z0所围 .
法一: 积分域为
0zx2y2 : x2 y1
1x 1
x2 y2
原式 dxdy z dz
Dxy
0
11
x2 y2
d x d y zdz
1 x 2
0
z
x
y
例. 计算积分 zdxdydz 其中由曲面
z { ( x ,y ,z ) |a z b ,( x ,y ) D z }b
f(x,y,z)dv
b
z a
adzD Zf(x,y,z)dxdy
x
Dz
y
适用范围:
积分区域介于两个平行于坐标面的平面之间;
在平行于坐标面的截面上二重积分易算 典型题目: 被积函数只为某一变量的函数;且截面面积易求
f(x,y,z)dxdydz
d 1 2 ( ( ) ) d r r 1 2 ( ( , , ) )f ( r s i n c o s , r s i n s i n , r c o s) r 2 s i n d r
适 用 范 围 : 积 分 区 域 为 球 形 区 域 、 被 积 函 数 为 f ( x 2 y 2 z 2 ) 型
例(截面法): 计算积分 z2dxdydz, 其中是两个球
x2y2z2R2及 x2y2z22R z
( R > 0 )的公共部分.
D 2z
z R
R
2
提示: 被积函数缺 x , y
D1z
o x
y
原式 =
R2 z2 dz
0
dxdy
D1z
R R
z2 dz
2
三重积分的应用

求面密度为常量、 的均匀圆形薄片: 例 4 求面密度为常量、 半径为 R 的均匀圆形薄片: 2 2 2 x + y ≤ R , z = 0 对位于在 z 轴上的点 对位于在 轴上的点
M 0 (0,0, a ) 处的单位质点的引力.(a > 0) 处的单位质点的引力.
解 由区域的对称性知 Fx = Fy = 0, M ≈ ( x, y)dσ G(0 a ) ( x , y ) Fz = ∫∫ dσ z 3 r D ( 0, 0, a ) 1 = Ga ∫∫ 3 dσ r 2 2 2 2 D (x + y + a ) dF 1 2π R o = Ga ∫0 dθ ∫0 y 3 rdr dσ ( x, y) 2 2 2 (r + a )
dF = dFxi + dFy j + dFzk
dFx = dFy = G( x x0)ρ( x, y, z)dv , ,
x
z
( x0 , y0 , z0 )
r3 G( y y0)ρ( x, y, z)dv r
3
,
m =1 r dF
( x , y, z )
dFz =
G(z z0)ρ( x, y, z)dv r3
三、引力
利用定积分可以解决平面上一个细棒对细棒之外 一个质点的引力问题。 一个质点的引力问题。 问题: 外一质点的引力? 问题:如何求一空间立体 对 外一质点的引力? (1)空间两质点间的引力 )
F = Fxi + Fy j + Fzk
Gm( x x0) F = Gm( y y0) , Fx = , y 3 r3 r Gm(z z0) o Fz = , r3
,
∫∫∫ zρ ( x , y , z )dv
高等数学-第九章 三重积分及应用

例. 计算积分 zdxdydz 其中由曲面
zx2y2,yx2及平面 y1,z0所围 .
法一: 积分域为
0zx2y2 : x2 y1
1x 1
x2 y2
原式 dxdy z dz
Dxy
0
11
x2 y2
d x d y zdz
1 x 2
0
z
x
y
例. 计算积分 zdxdydz 其中由曲面
积 分 区 域 为 柱 体 区 域 或 投 影 域 适 用 极 坐 标 表 示 ; 被 积 函 数 为 f(x2y2)型
例. 计算三重积分
dxdydz 1x2 y2
,
其中由抛物面
x2y24z与平面 zh(h0)所围成 .
z
2 4
zh
h
解: 在柱面坐标系下 : 02 h
0 2
原式 =
2
d
0
2 0
h 1 2
d
h
2 4
d
z
202 h12(h42)d
[1 (4h)ln 1(4h)4h]
4
o x
y
4、球坐标代换
设 M (x,y,z) R 3,其柱坐(标 ,,为 z),令OM r,
ZOM , 则(r,,) 就称为点M 的球坐标.
xrsinco s yrsin sin
zrco s
0 r
例. x2y2z2az(a0)
: 0 2,
02,
0racos
z a
r y x
例 : 锥 面z x2y2 与球面 x2y2z2R2所围立体.
:
0 2
04
0rR
z rR
4
oy x
三重积分的应用

微积分III(H)论文三重积分的应用指导老师:苏德矿小组成员:李颖聪周晓旭李翘楚陈乃铭俞智超谢煜彬姚世豪王亮熙三重积分的应用微积分III (H )论文小组成员:李颖聪 周晓旭 李翘楚 陈乃铭 俞智超 谢煜彬 姚世豪 王亮熙在微积分III 学习的过程中,我们注意到,三重积分的概念并不是直接定义的,而是由体密度的概念引出的。
由此给出了三重积分的定义:如果当有界闭区域中各小闭区域的直径中的最大值趋于零时,这和式的极限总存在,则称此极限为函数f(x y z )在闭区域上的三重积分。
不直接给出三重积分的定义,而是用实际的例子引出其概念,可见三重积分较为抽象,不借助实际应用较难理解。
同时也体现了三重积分的应用的重要性。
在此我们浅析几个三重积分的实际应用。
一、求立体的重心首先我们要区分,质心和重心在概念上其实并不相同。
质心是与物体(质点系)质量分布有关的一个点。
若假想该质点系的总质量集中于该点,则其对于坐标轴的矩等于该系各质点质量对同一坐标轴矩之和。
重心,是在重力场中,物体处于任何方位时所有各组成质点的重力的合力都通过的那一点。
规则而密度均匀物体的重心就是它的几何中心。
不规则物体的重心,可以用悬挂法来确定。
物体的重心,不一定在物体上。
但是我们在处理计算的过程中一般是用同样的方法,并不加以区分。
设一立体在空间占据区域T ,那么立体的体积为TV dxdydz=⎰⎰⎰设(,,)x y z ρρ=(,,)x y z T ∈是立体在点(x,y,z )的密度,其中T 是它所占据的空间区域,那么该立体的质量为(,,)TM x y z dxdydzρ=⎰⎰⎰立体重心的坐标公式为:1Tx xdxdydzV=⎰⎰⎰,1Ty ydxdydzV=⎰⎰⎰,1Tz zdxdydzV=⎰⎰⎰.其中x ,y ,z 是区域T 的几何重心的坐标。
例:求平面0x =,0z =,1y =,3y =,23x z +=所围之棱柱的重心坐标。
解:先求棱柱的体积 3332013330103203(3)21(3)292z TV dxdydz dx dy dzxdx dy x dx x x -==-==-=-=⎰⎰⎰⎰⎰⎰⎰⎰⎰现在求重心的坐标338201022199xT x xdxdydz xdx dy dz -===⎰⎰⎰⎰⎰⎰, 338201022299x T y ydxdydz dx ydy dz -===⎰⎰⎰⎰⎰⎰, 3382010221992x T z zdxdydz dx dy zdz -===⎰⎰⎰⎰⎰⎰二、求刚体转动惯量转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I 或J 表示。
微积分的基本思想,三重积分在现实生活中的作用
微积分的基本思想,三重积分在现实生活中的作用为什么我们在现实生活中会需要三重积分。
我们要把它分解开来。
我们先来分析一下,为什么我们需要积分,然后是二重积分,最后是三重积分。
如何理解积分对于简单的图形,我们有现成的公式来求它们的面积。
但我们如何求下面图形的面积呢?答案是,我们可以使用积分。
描这里的积分就可以理解为曲线下面的面积。
假设我们想求一条奇怪的曲线下面的面积,它看起来像这样:用公式法求这样的面积是很困难的。
我们希望用更简单的形状去近似或者代替它,比如矩形,面积公式是长乘以宽。
那我们为什么不在曲线下画一堆矩形,求这些矩形的面积,然后把所有的小矩形面积加起来,来近似计算曲线下的面积,就像这样:这是个不错的近似值,值为所有绿色矩形的面积之和。
每个矩形都有相同的宽度,以使计算更容易。
宽度等于一个我们称之为Δx的量(概念上,Δx是x的变化)。
每个矩形的高度是不同的,但它是由函数f(x)给出的,由图中弯曲的黑线表示。
为了体现高度是不同的,从左边开始的第一个矩形的高度是f(x₁),第二个矩形的高度是f(x₂),以此类推。
一般来说,第i个矩形的高度为f(xᵢ)。
矩形的面积是高度乘以宽度,所以其中一个矩形的面积等于f(xᵢ)*Δx。
如果我们把所有的矩形面积加起来,我们就可以得到曲线下的近似面积。
但是我们的近似值并不那么精确,我们可以通过增加矩形的数量使近似值更准确,就像这样:注意,Δx现在更小了。
而且,这个和比上一个更准确。
我们可以继续把图形分成越来越小的矩形,使值更加精确。
最终,随着矩形的数量接近无穷大(每个矩形的宽度接近0),近似面积越来越接近实际面积。
这个总和被称为积分。
积分就是这样写出来的。
积分符号∫看起来像一个大的S。
当一个叫戈特弗里德-莱布尼茨的德国人发展微积分时,他认为积分是一个无限的和。
dx "代表Δx,即每个矩形的宽度,它现在是无限小的。
这个 "dx "被称为微分。
