电路分析基础第三章作业答案
《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出,P2=6W吸收,P3=16W吸收,P4=-lOW发出,PS=-7W发出,PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开:UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合:12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。
电路分析基础第三章作业答案
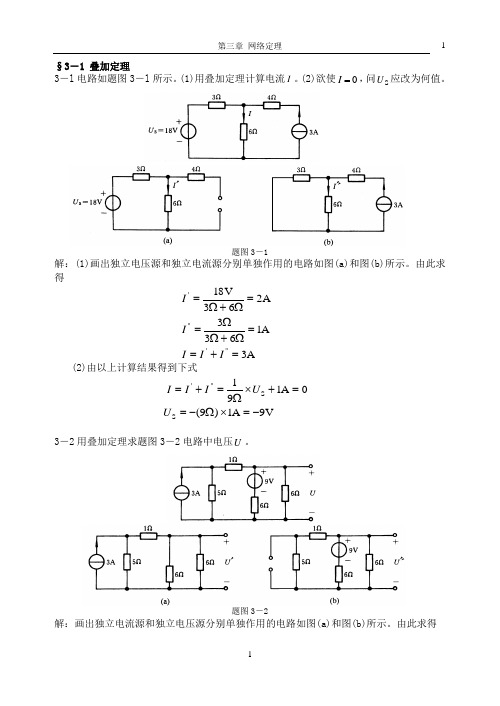
§3-1 叠加定理3-l 电路如题图3-l 所示。
(1)用叠加定理计算电流I 。
(2)欲使0=I,问S U 应改为何值。
题图3-1解:(1)画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得A3 A1633 A 263V 18"'"'=+==Ω+ΩΩ==Ω+Ω=I I I I I(2)由以上计算结果得到下式V 9A 1)9(0A 191 S S "'-=⨯Ω-==+⨯Ω=+=U U I I I3-2用叠加定理求题图3-2电路中电压U 。
题图3-2解:画出独立电流源和独立电压源分别单独作用的电路如图(a)和图(b)所示。
由此求得V8V 3V 5 V3V 9)363V 53A 3)31(55 "'"'=+=+==⨯Ω+ΩΩ==Ω⨯⨯Ω+Ω+ΩΩ=U U U U U3-3用叠加定理求题图4-3电路中电流i 和电压u 。
题图3-3解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V )3cos 104( A )3cos 52( V3cos 10)2(A 3cos 53cos 1232332321554V V 8636326363 A 263632V8 "'"'"""''t u u u t i i i t i u t t i u i +=+=-=+==Ω-=-=⨯+-⨯+⨯++==⨯Ω+⨯+ΩΩ+⨯==Ω+⨯+Ω=3-4用叠加定理求题图3-4电路中的电流i 和电压u 。
题图3-4解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V 3V 6V 3 A 3A 2A 1V 6)-A 4(3A 26V 12 1 0A)4(321 KVL )b (V33A 16V 6 1 0V 62)31( KVL )a ("'"'"""""1""1"'''''1'1'=+-=+==+=+==⨯Ω==Ω=⨯Ω==-⨯Ω++⨯Ω-=⨯Ω-==Ω=⨯Ω==-+Ω+Ωu u u i i i i ui i u i u i i u i i u u i 最后得到得到代入方程电路列出图得到代入方程电路列出图3-6用叠加定理求题图3-6电路中电流i 。
课后答案3电路分析基础【史】

课后答案3电路分析基础【史】第4章4.1选择题1.关于叠加定理的应用,下列叙述中正确的是( D )。
A.不仅适用于线性电路,而且适用于非线性电路B.仅适用于非线性电路的电压、电流计算C.仅适用于线性电路,并能利用其计算各分电路的功率进行叠加得到原电路的功率D.仅适用于线性电路的电压、电流计算2.关于齐次定理的应用,下列叙述中错误的是( B )。
A.齐次定理仅适用于线性电路的计算B.在应用齐次定理时,电路的某个激励增大K倍,则电路的总响应将同样增大K倍C.在应用齐次定理时,所讲的激励是指独立源,不包括受控源D.用齐次定理分析线性梯形电路特别有效3.关于替代定理的应用,下列叙述中错误的是( C )。
A.替代定理不仅可以应用在线性电路,而且还可以应用在非线性电路B.用替代定理替代某支路,该支路可以是无源的,也可以是有源的C.如果已知某支路两端的电压大小和极性,可以用电流源进行替代D.如果已知某支路两端的电压大小和极性,可以用与该支路大小和方向相同的电压源进行替代4.关于戴维宁定理的应用,下列叙述中错误的是( A )。
A.戴维宁定理可将复杂的有源线性二端电路等效为一个电压源与电阻并联的电路模型B.求戴维宁等效电阻是将有源线性二端电路内部所有的独立源置零后,从端口看进去的输入电阻C.为得到无源线性二端网络,可将有源线性二端网络内部的独立电压源短路、独立电流源开路D.在化简有源线性二端网络为无源线性二端网络时,受控源应保持原样,不能置于零5.在诺顿定理的应用,下列叙述中错误的是( C )。
A.诺顿定理可将复杂的有源线性二端网络等效为一个电流源与电阻并联的电路模型B.在化简有源线性二端网络为无源线性二端网络时,受控源应保持原样,不能置于零C.诺顿等效电路中的电流源电流是有源线性二端网络端口的开路电流D.诺顿等效电路中的电阻是将有源线性二端网络内部独立源置零后,从端口看进去的等效电阻6.关于最大功率传输定理的应用,下列叙述中错误的是( C )。
(完整版)电路分析基础习题第三章答案(史健芳)(DOC)

第3章3.1 选择题1.必须设立电路参考点后才能求解电路的方法是( C )。
A.支路电流法B.回路电流法C.节点电压法D.2b法2.对于一个具有n个结点、b条支路的电路,他的KVL独立方程数为( B )个。
A.n-1 B.b-n+1 C.b-n D.b-n-13.对于一个具有n个结点、b条支路的电路列写结点电压方程,需要列写( C )。
A.(n-1)个KVL方程B.(b-n+1)个KCL方程C.(n-1)个KCL方程D.(b-n-1)个KCL方程4.对于结点电压法中的无伴电压源,下列叙述中,(A )是错误的。
A.可利用电源等效变换转化为电流源后,再列写结点电压方程B.可选择该无伴电压源的负极性端为参考结点,则该无伴电压源正极性端对应的结点电压为已知,可少列一个方程C.可添加流过该无伴电压源电流这一新的未知量,只需多列一个该无伴电压源电压与结点电压之间关系的辅助方程即可D.无伴受控电压源可先当作独立电压源处理,列写结点电压方程,再添加用结点电压表示控制量的补充方程5.对于回路电流法中的电流源,下列叙述中,( D )是错误的。
A.对于有伴电流源,可利用电源等效变换转化为电压源后,再列写回路电流方程B.对于无伴电流源,可选择合适的回路,使只有一个回路电流流过该无伴电流源,则该回路电流为已知,可少列一个方程C.对于无伴电流源,可添加该无伴电流源两端电压这一新的未知量,只需多列一个无伴电流源电流与回路电流之间关系的辅助方程即可D.电流源两端的电压通常为零6.对于含有受控源的电路,下列叙述中,( D )是错误的。
A.受控源可先当作独立电源处理,列写电路方程B.在结点电压法中,当受控源的控制量不是结点电压时,需要添加用结点电压表示控制量的补充方程C.在回路电流法中,当受控源的控制量不是回路电流时,需要添加用回路电流表示控制量的补充方程D .若采用回路电流法,对列写的方程进行化简,在最终的表达式中互阻始终是相等的, 即:R ij =R ji3.2 填空题1.对于具有n 个结点b 条支路的电路,可列出 n-1 个独立的KCL 方程,可列出 b-n+1 个独立的KVL 方程。
电路分析基础(英文版)课后答案第三章

0 = ¡26i1 ¡ 90i2 + 124i3
[a] Solving, i1 = 5 A; therefore the 80 V source is delivering 400 W to the circuit.
[b] Solving, i3 = 2:5 A; therefore p8− = (6:25)(8) = 50 W
v1 + v1 ¡ v2 = 4:5
1
8
53
54 CHAPTER 3. Techniques of Circuit Analysis
v2 + v2 ¡ v1 + v2 ¡ 30 = 0
12 8
4
Solving, v1 = 6 V v2 = 18 V Thus, i = (v1 ¡ v2)=8 = ¡1:5 A v = v2 + 2i = 15 V
DE 3.8 Use the lower node as the reference node. Let v1 = node voltage across the 7.5 − resistor and v2 = node voltage across the 2.5 − resistor. Place the dependent voltage source inside a supernode between the node voltages v and v2. The node voltage equations are
3
Techniques of Circuit Analysis
Drill Exercises
DE 3.1 [a] 11,8 resistors, 2 independent sources, 1 dependent source
电路分析第3章作业参考答案

第3章电路等效及电路定理P3-2 电路如图P3-2所示,应用叠加定理计算电流x i ,并计算Ω10电阻吸收的功率。
图P3-2 图1 图2解:1)15V 单独作用,如图1示 2)4A 单独作用,如图2示A i x 6.0401040401040101215'=+⨯+⨯+= A i x 92.14401101121101''-=⨯++-= 3)共同作用 A i i i x xx 32.1)92.1(6.0'''-=-+=+= 4)10Ω电阻的功率:W R i p x4.1710)32.1(22=⨯-==,吸收17.4WP3-5 用叠加定理求如图P3-5所示电路的电压x u 。
4Ω4Ω4Ω图P3-5 图1 图2解:1)10V 单独作用,如图1示由KVL 得:04)5(21010''''=++⨯++-x x x xi i i i ,得:A i x 38.0135'==,V i u xx 8.310''== 2)2A 单独作用,如图2示由KVL 得:0)2(4)52(210''''''''=++++⨯+x x x xi i i i ,得:A i x 46.0136''-=-=,V i u xx 6.410''''-== 3)共同作用 V u u u x x 2.1)6.4(8.3'''-=-+=+=P3-9 求图P3-9所示电路的输入电阻in R 。
(分别用电源法和伏安法)图P3-9 图1 图2解:1)电源法:设端口处电压和电流如图1所示:由25Ω电阻VCR得:)5.1(25IIiu-+⨯= 1)控制量:50uI= 2)联立两个方程:iu3100=,因此输入电阻:Ω===3.333100iuRin2)伏安法:端口处电压和电流如图2所示,设控制量AI1=,则:VIu5050==,AIIui5.15.125=-+=,因此输入电阻:Ω===3.335.150iuRinP3-11电路如图P3-11所示,利用电源变换求i。
电路分析第三章习题解答
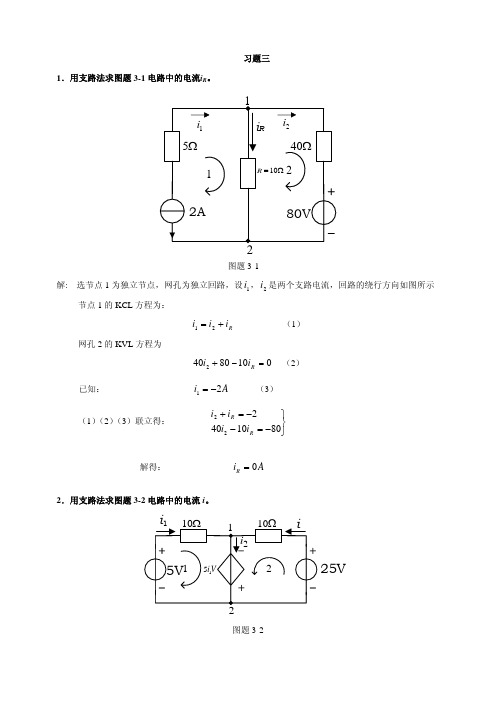
+
10Ω
u1
30Ω
+ uo
78Ω
50V
39Ω
4
图题 3-11 解:选节点 4 为参考节点,列出节点方程为
u n1 = 50V − 1 1⎞ ⎛ 1 ' u n1 + ⎜ + ⎟u n 2 = −i x 10 ⎝ 30 10 ⎠
(1)
(2)
1 ⎞ ⎛ 1 ' ⎜ + ⎟u n3 = i x 39 78 ⎝ ⎠
50Ω
30Ω
i1 5A
15Ω
30Ω
10Ω
5i 1
图题 3-12 解: (1)原电路等效为下面电路
1
50Ω
2
30Ω
i1 5A
15Ω
30Ω
10Ω
5i1 30
3
选节点 3 作为参考节点,列出节点方程
1 ⎞ 1 ⎛1 u n1 ⎜ + ⎟ − u n 2 = 5 A ⎝ 15 50 ⎠ 50 −
(1)
1 1 1 1 ⎞ 1 ⎛ 1 u n1 + ⎜ + + + ⎟u n 2 = − i1 (2) 50 6 ⎝ 50 30 10 30 ⎠
u n1 = 5i
(1)
1 1 ⎛1 1 1⎞ − u n1 + ⎜ + + ⎟u n 2 − u n3 = 0 (2) 3 6 ⎝3 4 6⎠ 1 30 ⎛1 1⎞ − u n 2 + ⎜ + ⎟u n3 = − ix 6 8 ⎝6 8⎠ u n3 − u n1 = 24
辅助方程: i = (1) (2) (3) (4) (5)联立得: (3)
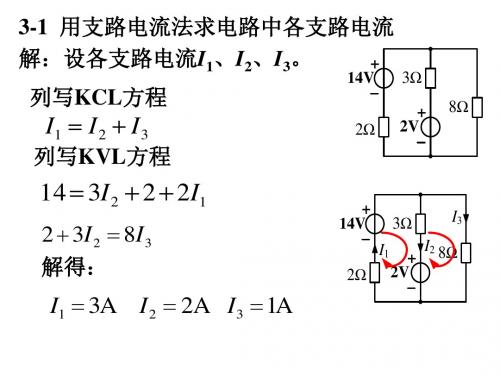
电路分析第三章答案
uS1 I1R1 I 2 R2 uS 2 uS 2 I 4 R4 I 3 R3 I 2 R2 I 3 R3 I 5 R5 ri3
附加方程:
I 3 iS
3-4 电路如图,列写支路电流方程 设电流I1、I2、I3、I4、I5、I6、U5 uS2 R + 列写节点①②③的KCL方程 I2 2 3 I1 I 2 I 5 I 5 I 6 I 4 ① I5 R5 ② iS5 + uS4
p1 4i 2W 8V电压源的功率: p2 8I1 28W
4V电压源的功率:
受控源的功率: p2 U n3 2i1 4W
3-16 用节点分析法,求图 示电路中的电压U1和电流I 解:(1)给节点编号, 以节点④为参考节点,列 写节点方程。
U n1 0.5U1 U n1 U n 2 (1 2) 0.5I 2U n1 U n3 (1 2) 0.5I 2
R3 R 3
3-13 列写图示电路的节点电压方程 解:给节点编号,以节点 4A ③为参考节点,列写节点 ① 方程。 + 1Ω
10V 2A
② + 3V 1Ω
+ 5V ③
2Ω
U n1 (1 0.5) U n 2
Un2 5
10 24 2
3-14 列写图示电路的节点电压方程 解:给节点编号,以节点 4Ω ③为参考节点,列写节点 ① 2Ω ② 方程。 + 2A +
I6
I 2 I3 I6
列写回路1、2、3的 KVL方程
I1 + + U5 − R1 U1 R42 − I4 1 + + uS1 βU1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3-1 叠加定理3-l 电路如题图3-l 所示。
(1)用叠加定理计算电流I 。
(2)欲使0=I,问S U 应改为何值。
题图3-1解:(1)画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得A3 A1633 A 263V 18"'"'=+==Ω+ΩΩ==Ω+Ω=I I I I I(2)由以上计算结果得到下式V 9A 1)9(0A 191 S S "'-=⨯Ω-==+⨯Ω=+=U U I I I3-2用叠加定理求题图3-2电路中电压U 。
题图3-2解:画出独立电流源和独立电压源分别单独作用的电路如图(a)和图(b)所示。
由此求得V8V 3V 5 V3V 9)363V 53A 3)31(55 "'"'=+=+==⨯Ω+ΩΩ==Ω⨯⨯Ω+Ω+ΩΩ=U U U U U3-3用叠加定理求题图4-3电路中电流i 和电压u 。
题图3-3解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V )3cos 104( A )3cos 52( V3cos 10)2(A 3cos 53cos 1232332321554V V 8636326363 A 263632V8 "'"'"""''t u u u t i i i t i u t t i u i +=+=-=+==Ω-=-=⨯+-⨯+⨯++==⨯Ω+⨯+ΩΩ+⨯==Ω+⨯+Ω=3-4用叠加定理求题图3-4电路中的电流i 和电压u 。
题图3-4解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V 3V 6V 3 A 3A 2A 1V 6)-A 4(3A 26V 12 1 0A)4(321 KVL )b (V33A 16V 6 1 0V 62)31( KVL )a ("'"'"""""1""1"'''''1'1'=+-=+==+=+==⨯Ω==Ω=⨯Ω==-⨯Ω++⨯Ω-=⨯Ω-==Ω=⨯Ω==-+Ω+Ωu u u i i i i ui i u i u i i u i i u u i 最后得到得到代入方程电路列出图得到代入方程电路列出图3-6用叠加定理求题图3-6电路中电流i 。
题图3-6解:画出12V 和18V 独立电压源单独作用的电路如图(b)和图(c)所示。
由此求得mA1.0mA 1.0mA2.0mA 1.030403010403040301060V 18 mA 2.010201040V 12"'33"33'=-=+=-=+⨯Ω⨯+⨯+Ω⨯-==Ω⨯+Ω⨯=i i i i i3-7用叠加定理求题图3-7单口网络的电压电流关系。
题图3-7解:外加电流源,如图(a)所示,用叠加定理求端口电压电流关系。
由外加电流源单独作用的图(b)电路和单口网络内部独立电源作用的图(c)电路,可以求得V102V 10V 6V 4A 33636V 1236323636"'"'''+⨯Ω=+==+=⨯+⨯+⨯+=⨯Ω=⨯Ω+⨯=i u u u u i i u§3-2戴维宁定理3-8求题图3-8各单口网络的戴维宁等效电路。
题图3-8解:(a) 计算单口网络的开路电压和将电压源用短路代替后单口的等效电阻为Ω=Ω⨯==⨯++=91001090 V 10V 10010504010o oc R u最后得到单口网络的等效电路如图(a')所示。
(b) 计算单口网络的开路电压和将电压源用短路代替后单口的等效电阻为 Ω=Ω⨯==⨯+=241004060 V 8.4V 12406040o oc R u最后得到单口网络的等效电路如图(b')所示。
(c) 计算单口网络的开路电压和将电压源用短路代替后单口的等效电阻为 Ω=Ω+==⨯⨯⨯+=-k 60k )5010( V 24V 103001050V 9o 63oc R u 最后得到单口网络的等效电路如图(c')所示。
(d) 计算单口网络的开路电压和将电压源用短路代替后单口的等效电阻为 Ω=Ω+⨯+Ω==⨯+=100180901809040 V 27V 811809090o oc R u最后得到单口网络的等效电路如图(d')所示。
3-9用戴维宁定理求题圈3-9电路中电压U 。
题图3-9解:计算负载电阻40Ω断开后,单口网络的开路电压和输出电阻为Ω=Ω+Ω==⨯Ω-=603030 V 20A 5.030V 35o oc R u 由图(b)所示等效电路求得V8V 20604040-=⨯+-=U3-10 用戴维宁定理求题图3-10电路中的电压u 。
题图3-10解:断开20k Ω负载电阻,求得余下单口网络的等效电路,从图(b)可以求得V5.0)V 1(202020k 20 V 1V )1815(603030o oc -=-⨯+=Ω=-=-⨯+=u R u3-12 用诺顿定理求题图3-12电路中电流i 。
题图3-12解:断开负载电阻,求出单口网络的诺顿等效电路,得到图(b)所示电路,由此求得A252Aμ50 k 20 A 50k 60V 3k 60V 18k 60V 15o sc μμ-=-=Ω=-=Ω-=Ω-+Ω=i R i3-13用戴维宁-诺顿定理求题图3-13电路中电流I 。
题图3-13解:断开负载电阻,求出单口网络的戴维宁-诺顿等效电路,得到图(b)和图(c)所示电路,由此求得A1A 3201010 V 30A 31010 A 340V 120oc o sc =⨯+==⨯Ω=Ω==Ω=I U R I3-14用戴维宁-诺顿定理求题图3-14电路中电流i 。
题图3-14解:断开负载电阻,求出单口网络的戴维宁-诺顿等效电路,得到图(b)和(c)所示电路,由此求得A5A 5.7100200200A 5100200V 1500 020A 5.7A 6A 3100100100 V 1500A 6200A 3100scoc o sc oc =⨯Ω+ΩΩ==Ω+Ω=Ω===+⨯+==⨯Ω+⨯= i i i u R i u3-15 求题图3-15所示各单口的诺顿等效电路。
题图3-15(a)解:(a) 将电阻与受控源的并联进行等效变换,得到图(b)所示电路,用结点分析法先计算单口网络的开路电压。
Vα2645A145α26 15 α32A 1)151151(ococococ-==Ω-Ω=+=Ω+ΩUU UI IU 得到代入再将单口网络短路后,计算短路电流,作后求输出电阻和画出诺顿等效电路,如图(c)所示。
Ω--==-=Ω==Ω-Ω=+=Ω+Ω+Ωα26α1590A α635.7 A 145α21215 α32A 1)5.71151151(scoc o sc I U R U I U U I IU 得到代入题图3-15(b)(b) 解:先求出单口网络的开路电压,再求其短路电流和输出电阻,画出诺顿等效电路,如图(c)所示Vα640 A 5.020V 10 )b (Vα62010A α53010 V10)(5)10(15 KVL scoc o sc oc -===Ω=-==-==-⨯Ω+Ω+ΩI U R I I U I I I I 求得从图求得方程列出α3-16 电路如题图3-16(a)和(b)所示。
已知10mAV,5.12==I U 。
求该单口网络的戴维宁等效电路。
题图3-16解:将电阻单口网络用电阻和电压源串联等效电路代替,如图所示。
由此得到5k V 10 A102105.2V 20A 1010)b ()105V 5.12105.2V 5.12V 20(V 5.12 )a (o oc 333ooc oc33o Ω==⨯=Ω⨯-⨯=+Ω⨯-Ω⨯-⨯=--R U R U U R 求解得到得到由图得到由图3-17 用戴维宁定理求题图3-17电路中电流i 。
若Ω=10R时,电流i 又为何值。
题图3-17解:断开负载支路,求出ab 两点间单口网络的的戴维宁等效电路,得到图(b)所示等效电路,从中计算出电流i 。
先计算戴维宁等效电路参数Ω=Ω+⨯+Ω+⨯==222222222 0 o oc R u 输出电阻为由于电桥处于平衡状态由图(b)电路求得电流iA 122V 4=Ω+Ω=i由于电桥处于平衡状态,当电阻Ω=10R 时,不会影响戴维宁等效电路,因此不影响电流的数值。
3-18用戴维宁定理求题图3-18电路中电流i 。
题图3-18解:将短路线看作为负载,求余下单口网络的戴维宁等效电路,得到图(c)所示等效电路,由此求得电流i 。
从图(a)电路中,断开短路线求单口网络的开路电压A 2A 163663V 24 V 12A 23V 2V 163A 16363V 2463611oc =⨯+-Ω+Ω==⨯Ω-+=⨯Ω-⨯Ω+⨯+⨯+=i i u 其中从图(b)电路中,用在端口上外加电流源求端口电压的方法求输出电阻Ω==⨯Ω=⨯Ω+⨯⨯Ω=⨯Ω+⨯+⨯Ω=44232363633Sba o SS S S 1ba i u R i i i i i u最后由图(c).电路求得电流A 34V 12 =Ω=i3-28 欲使题图3-28电路中电压V20=u,问电阻应为何值?题图3-28解:断开负载电阻,求出单口网络的戴维宁等效电路,最后得到图(c)所示电路。
10V 20V 866104 V 8A 24L LLo oc Ω==⨯+Ω-=Ω-=⨯Ω-⨯Ω==⨯Ω=R R R u i ii R u3-29 求题图3-29所示单口网络的戴维宁等效电路。
题图3-29解:由图(a)电路计算开路电压,由图(b)计算输出电阻,最后得到戴维宁等效电路,如图(c)所示。
Ω-==-=-⨯Ω+⨯==⨯Ω+ΩΩ=88)3(126126 V 12V 1861212o oc iu R ii i uu3-30 求题图3-30所示单口网络的戴维宁等效电路和诺顿等效电路。
题图3-30解:.在端口外加电源求端口电压电流关系055011o o =⨯Ω=-+⨯Ω==-=i u u i u i i i这表明单口网络的端口电压为零,电流也等于零,其特性曲线是ui 平面的坐标原点,该单口网络既不存在戴维宁等效电电路,也不存在诺顿等效电路。
换句话说,该单口在外加电流源时,电压不存在唯一解,因此不存在戴维宁等效电路。
