第7章、单位根检验内容及案例
金融计量学单位根检验法

SSR (a) e ˆt2(a)
其中:SSR (a ) 表示给定a时的残差平方 和函数。
由此,Point-Optimal 检验统计 量定义为:
SSR(a)aSSR(1)
PT
f0
其中:f 0 表示频率为0的残差谱估计。
图7-6 EViews中ERS 点最优检验对话框
7.3.3 Phillips- Perron检验
图7-4 EViews中的各种 单位根检验对话框
7.3.1 ERS-DFGLS检验
ERS-DFGLS检验是Elliott, Rothenberg, and Stock (1996)提出的 一种单位根检验法,全称为DickeyFuller Test with GLS Detrending (DFGLS),即“使用广义最小二乘法去除 趋势的DF检验”。
Phillips-Perron检验,是一种非参 数单位根检验法。该检验的特点是使用 DF检验中的AR(1)模型形式,即以下三 种形式中的一种:
yytt
c c
t yt1 yt1 t
t
yt yt1 t
所以,PP检验不使用ADF检验中的AR(p)
形式。
PP检验的统计量可以写成:
f000.5T(f02f000.5)Sse(ˆ)
最后,使用ADF检验的模型形式
对y
d t
进行检验,即:
p
ytd ytd1
y d
i t(i1)
t
i2
H0: 0
H A : a
7.3.2 ERS Point-Optimal检验
ERS Point-Optimal 检验需要首 先利用模型(6.24)获得残差序列,即:
e ˆt(a)d(yt a)d(xt a)ˆ
单位根检验PPT课件

AR(1)过程 {yt}为一随机步游过程。
14
单位根检验:定义
❖ 看图识平稳 :15源自单位根检验:定义❖ 看图识平稳 :
16
单位根检验:定义
❖ 看图识平稳 :
17
单位根检验:定义
❖ I(d)过程:有时原始序列是非平稳过程,但对 原始序列经过d次差分后可变为平稳过程,则 原序列记为I(d)过程;
12
单位根检验:定义
❖ AR(1)过程是平稳序列吗?
❖ 定理:若| |1,则AR(1)过程是平稳过程。因
为
(1)
Eyt
1
(2)cov(
yt
,
yt
h
)
2 |h| 1 2
var(
yt
)
1
2
2
(3) (t, h) |h|
❖ 证明过程略
13
单位根检验:定义
❖ 如果 | |1 ,AR(1)过程 {yt}还是平稳过程吗? 为什么?
❖ 经济时间序列多为I(1)或I(2)过程; ❖ 显然,I(0)过程是平稳序列 。
18
单位根检验:定义
❖ 当回归模型中含有非平稳的I(d)序列时,常规 的统计推断都不再成立,因此必须检验被解 释变量和解释变量是不是平稳的。标准的检 验方法是“单位根检验”。
19
单位根检验:定义
❖ 一个随机过程的平稳性取决于其特征方程的 根的值。若所有的根都位于单位圆之外,则 该过程是平稳的。若某个(些)根的值位于单位 圆上或单位圆内,则该过程是非平稳的。若 特征方程的根取值为1,则称其为单位根。对 单位根的检验(即对随机过程单整阶数的检验) 也就是对随机过程平稳性的检验。
单位根检验的EViews操作课件

如何进一步学习时间序列分析的相关知识
01
阅读时间序列分析相关的专业书籍和学术论文,深入理解时间 序列分析的基本原理和方法。
02
学习EViews软件的使用方法,掌握各种时间序列分析工具和命
令。
参加时间序列分析相关的课程和培训,与专业人士交流学习,
03
提高自己的分析能力。
THANKS FOR WATCHING
设,认为数据不存在单位根。
03
根据单位根检验结果,可以进一步进行其他相关分析和建 模。
04
单位根检验的EViews操 作实例
单个时间序列数据的单位根检验
01
打开EViews软件,选择 “File”菜单中的“New”选 项,创建一个新的工作文件。
02
在工作文件中,选择 “Quick”菜单中的“Empty Group”选项,创建一个空的 工作组。
单位根检验的原理
单位根检验基于ADF(Augmented Dickey-Fuller)检验和PP(Phillips-Perron )检验等统计方法,通过构建适当的回归模型并检验其残差是否具有单位根来确 定时间序列数据是否平稳。
如果残差存在单位根,则说明时间序列数据是非平稳的,即存在一个单位根;如 果残差不存在单位根,则说明时间序列数据是平稳的。
02
EViews软件介绍
EViews软件的特点
界面友好
01
EViews软件采用直观的图形界面,方便用户进行数据处理和统
计分析。
功能强大
02
EViews提供了丰富的数据处理、模型估计、统计分析和预测功
能,满足各种研究需求。
兼容性好
03
EViews支持多种数据格式和软件接口,方便与其他软件进行数
单位根检验内容及标准规定样式分析

第八章 单位根检验由于非平稳过程可能存在严重的伪回归问题,所以在对序列进行估计之前,需要检验序列的平稳性。
本章介绍了严格的平稳性的统计检验方法--单位根检验。
在简要介绍四种主要的非平稳随机过程以产输出单位根检验原理之后,文章主要介绍ADF 检验及PP 检验法,以及介结构突变和单位根检验。
8.1 四种典型非平稳过程简介前面我们知道,若一个时间序列含有某种变动趋势,即该序列的均值或自协方差函数随时间而改变,则称该序列为非平稳序列。
下面介绍四种典型的非平稳过程。
8.1.1随机游走过程t t t y y ξ+=-1,t=1,2,... (8.11)若}{t ξ为独立随机分布,即()0=t E ξ,()∞<=2σξt D 。
则称}{t y 为随机游走过程(Random Walk Process )。
随机游动过程是单位根过程的特例。
在现实经济社会中,如股票价格的走势便是随机游走序列。
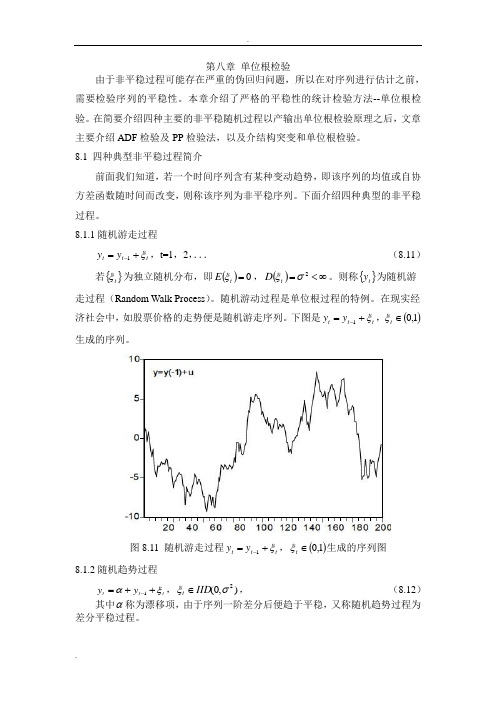
下图是t t t y y ξ+=-1,()1,0∈t ξ生成的序列。
图8.11 随机游走过程t t t y y ξ+=-1,()1,0∈t ξ生成的序列图8.1.2随机趋势过程t t t y y ξα++=-1,),0(2σξIID t ∈, (8.12)其中α称为漂移项,由于序列一阶差分后便趋于平稳,又称随机趋势过程为差分平稳过程。
图8.12 t t t y y ξ++=-11.0,()1,0∈t ξ生成的序列8.1.3趋势平稳过程t t t y ξβα++= ,其中t t t νρξξ+=-1,1<ρ,),0(2σν∈t (8.13)由于t t t y ξαβ+=-,即当减去退势后为平稳过程,故趋势平稳过程又称为退势平稳过程。
由t t t y ξβα++=,t t t νρξξ+=-1知:11)1(--+-+=t t t y ξβα (8.14)将(4)两边同时乘以ρ,与(3)两边同时相减,整理可得:t t t y t y νρβα+++=-1'' , ),0(2σν∈t (8.15)其中,ρβρααα+-=',ρβρβ-=' 这样便得出趋势平稳过程的另一种形式。
平稳性和单位根检验

单尾检验
2 ADF检验Augment DickeyFuller test
• 为什么将DF检验扩展为ADF检验
• DF检验假定时间序列是由具有白噪声随机误差 项的一阶自回归过程AR1生成的; 但在实际检验 中;时间序列可能由更高阶的自回归过程生成;或 者随机误差项并非是白噪声;用OLS法进行估计 均会表现出随机误差项出现自相关;导致DF检验 无效;
0.025 -3.95 -3.80 -3.73 -3.69 -3.68 -3.66 3.59 3.47 3.42 3.39 3.38 3.38 3.25 3.18 3.14 3.12 3.11 3.11
0.05 -3.60 -3.50 -3.45 -3.43 -3.42 -3.41 3.20 3.14 3.11 3.09 3.08 3.08 2.85 2.81 2.79 2.79 2.78 2.78
趋势平稳过程
• 差分平稳过程和趋势平稳过程
– 具有随机性趋势的时间序列通过差分的方法消除随 机性趋势; 该时间序列称为差分平稳过程difference stationary process;
– 具有确定性趋势的时间序列通过除去趋势项消除确 定性趋势; 该时间序列称为趋势平稳过程trend stationary process;
–例如上述带截距项的随机游走序列;即为I1序列;
• I0代表一平稳时间序列;
• 现实经济生活中只有少数经济指标的时间序列 表现为平稳的;如利率等;
• 大多数指标的时间序列是非平稳的;例如;以当 年价表示的消费额 收入等常是2阶单整的;以不 变价格表示的消费额 收入等常表现为1阶单整;
• 大多数非平稳的时间序列一般可通过一次或多 次差分的形式变为平稳的;
m
单位根检验

单整:如果一个时间序列经过一次差分变成平稳的,则称原序列是1阶单整的,记为I(1)。
一般地,如果时间序列经过d次差分后变成平稳序列,则称原序列是d阶单整序列,记为I(d)。
单位根检验:单位根检验是指检验序列中是否存在单位根,因为存在单位根就是非平稳时间序列了.单位根就是指单位根过程,可以证明,序列中存在单位根过程就不平稳,会使回归分析中存在伪回归。
单位根检验是随机过程的问题。
定义随机序列{ x_t},t=1,2,…是一单位根过程,若x_t=ρx_t-1 +ε,t=1,2… 其中ρ=1,{ε }为一平稳序列(白噪声),且E[ε ]=0, V(ε )=σ <∞, Cov(ε ,ε )=μ <∞这里τ=1,2…。
特别地,若{ε}是独立同分布的,且E[ε]=0,V(ε)=σ<∞,则上式就变成一个随机游走序列,因此随机游走序列是一种最简单的单位根过程。
将定义式改写为下列形式:( 1-ρL)x_t =ε,t=1,2,…其中L 为滞后算子,1-ρL为滞后算子多项式,其特征方程为1-ρz=0,有根z= 1/ρ。
当ρ=1时,时间序列存在一个单位根,此时{x_t }是一个单位根过程。
当ρ<1时,{x_t }为[1]。
而当ρ〉1时,{x_t }为一类具有所谓爆炸根的非平稳过程,它经过差分后仍然为非平稳过程,因此不为单整过程。
一般情况下,单整过程可以称作单位根过程。
单位根检验时间序列的单位跟研究是时间序列分析的一个热点问题。
时间序列矩特性的时变行为实际上反映了时间序列的非平稳性质。
对非平稳时间序列的处理方法一般是将其转变为平稳序列,这样就可以应用有关平稳时间序列的方法来进行相应得研究。
对时间序列单位根的检验就是对时间序列平稳性的检验,非平稳时间序列如果存在单位根,则一般可以通过差分的方法来消除单位根,得到平稳序列。
对于存在单位根的时间序列,一般都显示出明显的记忆性和波动的持续性,因此单位根检验是有关协整关系存在性检验和序列波动持续性讨论的基础。
单位根检验

影响
31
针对第四个问题,Perron提出
1. xt c t xt1 t H0 : 0
如果拒绝零假设,那么检验过程停止,该过 程是平稳过程 .不能拒绝,说明存在单位根,过 程非平稳,那么回归模型中的时间趋势项是不 是多余的参数呢?如果是,会导致检验的势降 低,进入步骤2.
包含一个确定性趋势和一个随机趋势
单位根过程
满足下面表达式的过程成为单位根过程
(1 B)xt t 1 t1 (B)t
其中
(1) 0,
j0
2 j
,程对时间序列的增量进行刻画,增 量平稳,但水平变量不平稳。
2. xt c t xt1 t H0 : 0
使用统计量 3 ,检验零假设. F统计量 (r为约束条件, k为无约束模型中的待估计参数)
j
[RSS(restricted) RSS(un restricted)] / RSS(restricted) / (T k)
单位根检验
非平稳过程
多数经济变量的时间序列都有随着时间增 加而增长的趋势, 不具有均值回复的特点.
两种刻画: 带趋势的平稳随机过程(前面已讲) 单位根过程
随机趋势过程
有一类随机过程, 如果再 t 时刻扰动项发生 变化, 那么它的影响会一直存在下去,不会随 着时间 t 增大会立刻衰减到0. 这样过程成为 随机趋势过程。 随机游动(走) 带常数项的随机游动 单位根过程
(B)ts (B)ts1 (B)t xt
所以
xt s
t
s
1
单位根检验内容及案例
第八章 单位根检验由于非平稳过程可能存在严重的伪回归问题,所以在对序列进行估计之前,需要检验序列的平稳性。
本章介绍了严格的平稳性的统计检验方法--单位根检验。
在简要介绍四种主要的非平稳随机过程以产输出单位根检验原理之后,文章主要介绍ADF 检验及PP 检验法,以及介结构突变和单位根检验。
8.1 四种典型非平稳过程简介前面我们知道,若一个时间序列含有某种变动趋势,即该序列的均值或自协方差函数随时间而改变,则称该序列为非平稳序列。
下面介绍四种典型的非平稳过程。
8.1.1随机游走过程t t t y y ξ+=-1,t=1,2,... (8.11) 若}{t ξ为独立随机分布,即()0=t E ξ,()∞<=2σξt D 。
则称}{t y 为随机游走过程(Random Walk Process )。
随机游动过程是单位根过程的特例。
在现实经济社会中,如股票价格的走势便是随机游走序列。
下图是t t t y y ξ+=-1,()1,0∈t ξ生成的序列。
图8.11 随机游走过程t t t y y ξ+=-1,()1,0∈t ξ生成的序列图8.1.2随机趋势过程t t t y y ξα++=-1,),0(2σξIID t ∈, (8.12)其中α称为漂移项,由于序列一阶差分后便趋于平稳,又称随机趋势过程为差分平稳过程。
图8.12 t t t y y ξ++=-11.0,()1,0∈t ξ生成的序列8.1.3趋势平稳过程t t t y ξβα++= ,其中t t t νρξξ+=-1,1<ρ,),0(2σν∈t (8.13)由于t t t y ξαβ+=-,即当减去退势后为平稳过程,故趋势平稳过程又称为退势平稳过程。
由t t t y ξβα++=,t t t νρξξ+=-1知:11)1(--+-+=t t t y ξβα (8.14)将(4)两边同时乘以ρ,与(3)两边同时相减,整理可得:t t t y t y νρβα+++=-1'' , ),0(2σν∈t (8.15)其中,ρβρααα+-=',ρβρβ-='这样便得出趋势平稳过程的另一种形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 单位根检验由于非平稳过程可能存在严重的伪回归问题,所以在对序列进行估计之前,需要检验序列的平稳性。
本章介绍了严格的平稳性的统计检验方法--单位根检验。
在简要介绍四种主要的非平稳随机过程以产输出单位根检验原理之后,文章主要介绍ADF 检验及PP 检验法,以及介结构突变和单位根检验。
8.1 四种典型非平稳过程简介前面我们知道,若一个时间序列含有某种变动趋势,即该序列的均值或自协方差函数随时间而改变,则称该序列为非平稳序列。
下面介绍四种典型的非平稳过程。
8.1.1随机游走过程t t t y y ξ+=-1,t=1,2,... (8.11)若}{t ξ为独立随机分布,即()0=t E ξ,()∞<=2σξt D 。
则称}{t y 为随机游走过程(Random Walk Process )。
随机游动过程是单位根过程的特例。
在现实经济社会中,如股票价格的走势便是随机游走序列。
下图是t t t y y ξ+=-1,()1,0∈t ξ生成的序列。
图8.11 随机游走过程t t t y y ξ+=-1,()1,0∈t ξ生成的序列图8.1.2随机趋势过程tt t y y ξα++=-1,),0(2σξIID t ∈, (8.12)其中α称为漂移项,由于序列一阶差分后便趋于平稳,又称随机趋势过程为差分平稳过程。
图8.12t t t y y ξ++=-11.0,()1,0∈t ξ生成的序列8.1.3趋势平稳过程t t t y ξβα++=,其中t t t νρξξ+=-1,1<ρ,),0(2σν∈t (8.13)由于t t t y ξαβ+=-,即当减去退势后为平稳过程,故趋势平稳过程又称为退势平稳过程。
由t t t y ξβα++=,t t t νρξξ+=-1知:11)1(--+-+=t t t y ξβα(8.14)将(4)两边同时乘以ρ,与(3)两边同时相减,整理可得:t t t y t y νρβα+++=-1'', ),0(2σν∈t (8.15)其中,ρβρααα+-=',ρβρβ-=' 这样便得出趋势平稳过程的另一种形式。
图8.13t t t y t y ν+++=-101.001.0,),0(2σν∈t 生成的序列8.1.4趋势非平稳过程t t t y t y ξβα+++=-1,),0(2σξIID t ∈(8.16)其中α称为漂移项,t β称为趋势项。
这种过程在实际经济中很少见。
8.2 单位根检验 8.2.1 DF 检验考虑AR(1)回归模型,),0(2σξIID t ∈ (8.21)(1) 如果 -1< β <1,则}{t y 平稳。
(2) 如果β=1,t y 序列是非平稳序列。
(8.21)式可写成:t t y ξ=∆显然t y 的差分序列是平稳的。
(3) 如果 ρ 的绝对值大于1,(8.21)式可写成:。
序列发散,且其差分序列是非平稳的。
因此,判断一个序列是否平稳,可以通过检验β是否严格小于1来实现。
生成随机游走过程:t t t y y ξ+=-1,00=y ,),0(2σξIID t ∈, OLS 估计式为:t t t y y ξβ+=-1零假设和备择假设分别为1:;1:10<=ββH H得到β的估计值βˆ,并对其进行显著性检验的方法,构造检验βˆ显著性的 t 统计量。
但是,Dickey-Fuller 研究了这个t 统计量在原假设下已经不再服从t 分布,t t t y y ξβ+=-1t t t y y ξβ+-=∆)1(它依赖于回归的形式(是否引进了常数项和趋势项) 和样本长度T 。
构造DF 统计量∑=--=-=Tt t y s s DF 221/)(1ˆ)ˆ(1ˆξβββ, ∑=-=TT tTs 22ˆ11)(ξξ (8.22)Mackinnon 进行了大规模的模拟,给出了不同回归模型、不同样本数以及不同显著性水平下的临界值,如表8.21。
8.21DF 分布百分位数表模型(a ):数据生成过程:t t t y y ξ+=-1,00=y ,),0(~2σξIID t OLS 估计式:t t t y y ξβ+=-1 1:0=βH ;1:1<βH模型(b ):数据生成过程:t t t y y ξ+=-1,00=y ,),0(~2σξIID t OLS 估计式:t t t y y ξβα++=-1 10:0==βα;H ;11:1<≠βα;H模型(c ):数据生成过程:t t t y y ξα++=-1,00=y ,),0(~2σξIID tOLS 估计式:t t t y y ξγβα+++=-t 101:00===γβαα,;H ;01:00≠<≠γβαα,;H这样,就可以根据需要,选择适当的显著性水平,通过t 统计量来决定能否拒绝原假设。
这一检验被称为Dickey-Fuller 检验(DF 检验)根据Mackinnon 给出的临界值,若用样本计算的DF>临界值,则接受原假设,t y 非平稳;若DF<临界值,则拒绝原假设,接受备择假设。
2.ADF 检验(Augmented Dickey-Fuller Test) 关于AR(p)过程,t=1,2,…. (8.23)上式存在p 阶序列相关,用p 阶自回归过程来修正,在上式两端减去1-t y ,通过添项和减项的方法,可得(8.24) 其中 , 。
零假设和备择假设为:1:0=βH ;1:1<βH 。
原假设为至少存在一个单位根;备选假设为:序列不存在单位根。
序列t y 可能还包含常数项和时间趋势项。
判断φ的估计值φˆ是接受原假设或者接受备选假设,进而判断一个高阶自相关序列AR(p) 过程是否存在单位根。
类似于DF 检验,Mackinnon 通过模拟也得出了不同回归模型、不同样本数以及不同显著性水平下的临界值。
这使我们能够很方便的在设定的显著性水平下判断高阶自相关序列是否存在单位根。
并且,Said-Dickey (1984)证明(8.24)式中的β 的DF 统计量的分布与(8.11)式中β的DF 统计量相似。
当(8.24)式中分别加入漂移项和趋势项后,其β的DF 统计量的分布分别与(8.12)式和(8.13)式中β的DF 统计量相似。
这样,DF 和ADF 检验法可以共用一个DF 分布百分位数表,作为临界值的参考。
在进行ADF 检验时,必须注意以下两个实际问题:第一,必须为回归定义合理的滞后阶数,通常采用AIC 准则来确定给定时间序列模型的滞后阶数。
在实际应用中,还需要兼顾其他的因素,如系统的稳定t p i i t i t t y y y ξηβα+++=∑-=--111Δ∑==pi i 1ββ∑+=-=p i j j i 1βηt p t p t t t y y y y ξβββα+++++=--- 2211性、模型的拟合优度等。
第二,选择哪种形式很重要,检验显著性水平的t 统计量在原假设下的渐近分布依赖是否存在常数项、趋势项,对应临界值也不同。
若原序列中不存在单位根,则检验回归形式选择含有常数,意味着所检验的序列的均值不为0;若原序列中存在单位根,则检验回归形式选择含有常数,意味着所检验的序列具有线性趋势,一个简单易行的办法是画出检验序列的曲线图,通过图形观察原序列是否在一个偏离0的位置随机变动或具有一个线性趋势,进而决定是否在检验时添加常数项。
若原序列中不存在单位根,则检验回归形式选择含有常数和趋势,意味着所检验的序列具有线性趋势;若原序列中存在单位根,则检验回归形式选择含有常数和趋势,意味着所检验的序列具有二次趋势。
同样,决定是否在检验中添加时间趋势项,也可以通过画出原序列的曲线图来观察。
如果图形中大致显示了被检验序列的波动趋势呈非线性变化,那么便可以添加时间趋势项。
8.3.PP 检验Phillips 和Perron 构建了PP 统计量p p t ,检验一阶自回归AR (1)的平稳性,对于(8.31)方程原假设和备择假设为接受原假设,则存在单位根;拒绝原假设则不存在单位根。
PP 统计量具体构造形式如下: σγγφφˆ2)()(210ˆ00210ˆ,f s f T f t t p p --= (8.82)式中,0f 是频率为零时的残差谱密度估计值,φˆt 是φˆ的t 统计量,σˆ是回归残差的标准差,0γ是回归残差的一致估计量。
同ADF 检验的t 统计量一样,通过模拟可以给出PP 统计量在不同显著水平下的临界值。
PP 检验中的滞后阶数可以有AIC 准则等方法确定。
8.3结构突变与单位根检验tt t y y ξβ+=-1⎩⎨⎧<=1:1:10ββH H8.31三种形式的结构突变首先从理论上分析三种突变情况。
第一,均值突变的随机游走过程和均值突变的退势平稳过程;第二,斜率突变的随机游走过程和斜率突变的退势平稳过程;第三,均值、斜率双突变的随机游走过程和均值斜率双突变的退势平稳过程。
以样本容量T 为200,突变点发生在t=100为例定义三种类型的虚拟变量如下:1)脉冲式虚拟变量101t 101t 01≠=⎩⎨⎧=,DP ,如下图:图8.31脉冲式虚拟变量2)阶跃式虚拟变量100t 100t 01≤>⎩⎨⎧=,DL ,如下图:图8.32 阶跃式虚拟变量3)累进式虚拟变量12t t 2101121t i i t t i i i i i t t t t t t DT <≥<≤⎪⎩⎪⎨⎧--=,,如下图:图8.33 累进式虚拟变量8.32三种外生结构突变模型Perron (1990)给出了结构突变点已知条件下的单位根检验方法。
结构突变点已知时,称其为外生性结构突变点。
假定发生结构突变的时点已知为b t 。
模型1:原假设:t y 为均值突变(水平)的单位根过程;备择假设:t y 为含有一个均值突变点(水平)的退势平稳过程。
H10:t y 为均值突变(水平)的单位根过程,即t y 在b t +1期发生脉冲式突变,表达式为:tt t DP y y t ξρα+++=-1 (8.31)其中t DP 代表脉冲虚拟变量。
定义为:1+ t t 1t t 01t bb ≠+=⎩⎨⎧=,DP其中b t +1表示突变发生时点。
因为模型是动态,一个时刻的脉冲式信息冲击要扩散到序列的以后各个时期。
(8.31)可以写为:⎪⎩⎪⎨⎧∑∑++=+++=tt tt y t y t ξαξρα00y y bb t t t t ≤>,, (8.32)H11:t y 为含有一个均值突变点(水平)的退势平稳过程,表达式为tt DL y t ξρβα+++=t (8.33)其中t DL 是阶跃式虚拟变量,定义为:bbtt t DL ≤>⎩⎨⎧=t t 01,模型2:原假设:t y 为结构突变的单位根过程;备择假设:t y 为斜率突变的退势平稳过程。
