2第 2 章 二维线性时、空不变系统分析
第2章 线性控制系统的运动分析(合肥工业大学 现代控制理论-王孝武)

(3)
将(3)式代入(2)式
b1 2b2t 3b3t kbk t
2
k 1
a(b0 b1t b2t bk t )
2 k
等式两边t 的同次幂的系数相等,因此有
b1 ab0 1 1 2 b2 ab1 a b0 2 2! 1 1 k bk abk 1 a b0 k k!
(13)
a0 (t ) I a1 (t ) A a2 (t ) A2 an1 (t ) An1
i 0, 1 , , (n 1)为待定系数。 ai (t ) 的计算方法为: 其中, ai (t ),
1)A 的特征值互异 应用凯-哈定理, λi 和 A 都满足 A 的特征方程。因此, λi 也可以 满足(13)式。
e λit a0 (t ) a1 (t ) λi a2 (t ) λi2 an1 (t ) λin1
(其中,i 1,2,, n ) 写成矩阵形式 e λ1t 1 λ1 λ2t e 1 λ2 λnt e 1 λn 于是
(12)
An1 A An an1 An a2 A3 a1 A2 - a0 A
将(11)式代入(12)式,不断地进行下去,可以看出: 都是 An1 、An2 、 、A 、I 的线性组合 A n 、 An 1 、 A n 2 、
(t ) e
At
1 2 2 1 k k 1 At A t A t 2! k!
0 1 x1 1 x x 2 3 x2 2
0 x(0) 1
求齐次状态方程的解。
线性系统的运动分析第二章PPT课件

t0)
x(t)(t)x(0) 则有: x(t)(tt0)x(t0)
线性定常系统的状态转移矩阵
9
说明1:状态转移矩阵必须满足以下两个条件:
1)状态转移矩阵初始条件: (t0t0)I
2)状态转移矩阵满足状态方程本身: (tt0)A (tt0)
说明2:对于线性定常系统来说,状态转移矩阵就是矩阵指 数函数本身。
即 A d I : e A ) 0 ti ( ( i I A ) p i 0 p i T e A
24
(2)当A具有n重特征根 i :约当标准型 约当矩阵A的矩阵指数函数
eit
eAtTeAtT1
T
0
0
teit
1 tn1eit (n1)!
T1
teit
0
eit
其中: T为使A化为约当标准型的非奇异变换矩阵。
故上式成立,意为 t 0 至 t 2 的状态转移过程可分解为t 0 至 t 1
及 t 1 至 t 2 的分段转移过程。
11
3、分解性:设A为n×n阶矩阵,t1和t2为两个独立 自变量,则有:
e e e A(t1t2)
A1t A2t
4、可逆性: e At 总是非奇异的,必有逆存在,且:(eAt)1 eAt
23
(1)当A的特征值 1,2,,n为两两相异时:对角线标准型
e1t eAtTeAtT1 T
0
0 T1
ent
其中: T为使A化为对角线标准型的非奇异变换矩阵。
求状态转移矩阵的步骤:
1) 先求得A阵的特征值 i 。
2) 求对应于 i 的特征向量 p i ,并得到T阵及T的逆阵。
3) 代入上式即可得到状态转移矩阵的值。
▪ 直接求解法:根据定义 ▪ 拉氏反变换法 ▪ 标准型法求解:对角线标准型和约当标准型 ▪ 待定系数法: 凯莱-哈密顿定理
第二章 线性不变系统.

§1.7 傅里叶变换 Fourier Transform
常用傅里叶变换对
5. {d (x-a)}=exp(-j2pfxa) {exp(j2pfax)}= d (fx-fa)
6.
1 {cos (2pf 0 x) [d ( f x f 0 ) d ( f x f 0 )] 2 1 {sin(2pf 0 x) [d ( f x f 0 ) d ( f x f 0 )] 2j
0
圆对称函数的F.T. 仍是圆对称函数, 称为F-B (傅-贝)变 换,记为
-1{G()}
G() =
{g(r)}, g(r) =
§1-2 二维傅里叶变换 2-D Fourier Transform
傅里叶-贝塞尔变换
例: 利用F-B变换求圆域函数的F.T.
1, r 1 , 定义: circ(r ) 0, 其它 r x2 y 2
1
是圆对称函数
{circ(r )} 2p rJ 0 (2pr )dr
0
作变量替换, 令r’ =2pr, 并利用:
J
0
2p 0
x
0 ( )d
xJ1 ( x)
J1 (2p )
{circ(r )}
1 2p
2
r ' J 0 (r ' )dr'
§1.7 傅里叶变换 Fourier Transform
用算符表示系统
g(x, y) = ℒ{f(x, y)}
线性系统定义:
输入
f(x, y)
ℒ{
}
输出
g(x, y)
令 g1(x, y) = ℒ{f1(x, y)}, g2(x, y) = ℒ{f2(x, y)} 若对任意复常数a1, a2有: ℒ{a1 f1 (x, y) + a2 f2 (x, y) } = ℒ{a1 f1 (x, y)} + ℒ{a2 f2 (x, y) } = a1 ℒ{f1 (x, y)} + a2 ℒ{f2 (x, y) } = a1 g1 (x, y) + a2 g2 (x, y)
线性系统理论(第2章)2[1].1
![线性系统理论(第2章)2[1].1](https://img.taocdn.com/s3/m/21fd85f8700abb68a882fb01.png)
2、对于线性定常系统情况
系数矩阵 A 和 B 均为常阵,只要其元的值为有限值,则条件 满足,解存在且唯一。
3
2010-10-08
三、零输入响应和零状态响应
线性系统满足叠加原理。 即线性系统在初始状态和输入向量作用下的运动,可分解为两 个单独的分运动: 初始状态作用 → 自由运动 输入向量作用 → 强迫运动
Φ ( t ) = e A(t) , t 0 Φ (t t0 ) = e A(t t0 ) , t t0
则系统零输入响应可表达式为:
φ(t;0, x0 ,0) = Φ(t) x0 , t 0 φ (t; t0 , x0 ,0) = Φ(t t0) x0 , t t0
物理意义: Φ(t t0 ) 就是将时刻 t 0 之状态 x0 映射到时刻 t 之状态 x 的一个线性变换。
12 22
1n 1 e t 2n 1 e t
1 2
n2
n 1 n t n e
④ 对给定 n n 常阵 A ,先求出预解矩阵:
(sI - A)-1
则有
e At = L-1 (sI - A)-1
二、零状态响应
给定初始状态为零的线性定常系统的强迫方程:
& = Ax + Bu, x (0) = 0, t 0 x
其中,x 为 n 维状态向量,u为p 维输入向量,A和B 分别为 n ×n 和 n × p 常阵。
8
2010-10-08
结论 2 : 零状态响应的表达式为:
(t;0,0, u) = e A(t ) Bu( )d ,
第2 章
线性系统的运动分析
2.1 引言
一、运动分析的实质
傅立叶光学

Linear Systems
1.线性系统 3)线性系统的定义 g(x, y) = {f(x, y)}
定义: 如果 g1(x, y) = 输入
f(x, y)
{
}
输出
g(x, y)
{f1(x, y)}, g2(x, y) =
{f2(x, y)}
若对任意复常数a1, a2有: {a1 f1 (x, y) + a2 f2 (x, y) } =
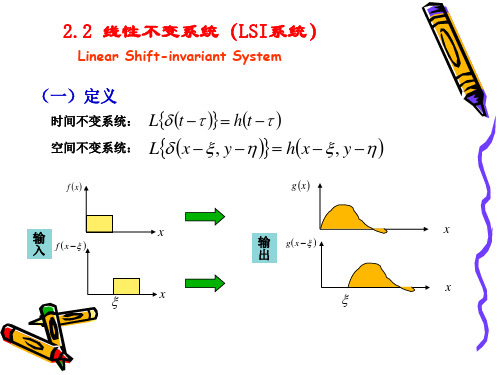
2.2 线性不变系统
输入输出关系: 空域
Linear Shift-Invariant System
2.二维线性空不变系统 2-D Linear Space Invariant Systems
+∞
∵ f ( x, y ) = f ( x, y ) ∗ δ ( x, y ) = ∫
∴ g (x, y) =
逆傅立叶变换的物理意义:物函数f(x,y)可看作是无数振幅不同 ( F ( f x , f y )df x df y) 方向不同( cosα=λfx cosβ= λ fy )的平面波线性叠加的结果。 这种方法通常称为傅立叶分解
1.线性系统
2.1 线性系统 Linear Systems
4)线性系统的分析与综合:
g(x, y) =
=
叠加积分
{f(x, y)}
+∞
∫∫ ∫∫
f (ξ ,η )
{ δ ( x − ξ , y − η ) }d ξ d η
−∞ +∞
=
f (ξ ,η ) h ( x , y ; ξ ,η ) d ξ dη
−∞
只要知道各个脉冲响应函数(点扩散函数), 系统 的输出即为脉冲响应函数的线性组合. 问题是如 何求对任意点的脉冲δ (x-ξ, y- η)的响应h(x, y;Linear Space Invariant Systems
二维线性系统

H(fx,fy)的模称振幅传递函数. H(fx,fy)的复角称相位传递函数. 的模称振幅传递函数 振幅传递函数. 的复角称相位传递函数 相位传递函数.
2.2. 3. 二维线性不变系统的本征函数: 二维线性不变系统的本征函数 本征函数
若ℜ{f(x ,y)}=a f(x ,y), 式中a为复常数,则称 ,y) 为算 , 式中a为复常数,则称f(x }表征的系统的本征函数 表征的系统的本征函数。 符ℜ{ }表征的系统的本征函数。 系统的本征函数是一特定的输入函数, 系统的本征函数是一特定的输入函数,输入输出之间仅差 别一个复常数,复指数基元就是线性空不变系统的本征函数。 别一个复常数,复指数基元就是线性空不变系统的本征函数。
叠加积分 一般写成
)
∫
∞
−∞
f (ξ 2 , η 2 )h ( x 2 − ξ 2 , y 2 − η 2 ) d ξ 2 d η 2
= f ( x2 , y2 ) ∗ h( x2 , y2 )
g(x, y) = f (x, y) ∗ h(x, y)
线性空不变系统
2.2. 2. 二维线性不变系统的传递函数: 二维线性不变系统的传递函数 传递函数
F( f x , f y ) = ∫
逆变换: 逆变换
若输入空间域函数f(x,y),其付里变换为: ,其付里变换为 若输入空间域函数
∫ f ( x, , y) = ∫ ∫
∞
∞
−∞ −∞ ∞ ∞
f ( x, y) exp − j2π ( f x x + f y y) dxdy
[
−∞ −∞
F( f x , f y )exp j2π ( f x x + f y
[
] y)]df df
线性系统理论(郑大忠)第2章

2013/11/22
线性系统理论
23
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
R1 C + uC iL R2 iC + -
由此,得 和,
X QX
X PX PQX
X QX QPX
显然, PQ QP I
即矩阵P和Q互逆。
结论:系统的任意选取的两个状态X和 X 之间 为线性非奇异变换的关系。
2013/11/22
线性系统理论
18
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
2013/11/22
线性系统理论
2
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
一、状态和状态空间
1、系统动态过程的两类数学描述 2、状态和状态空间的定义
2013/11/22
线性系统理论
3
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、系统动态过程的两类数学描述
线性系统理论
21
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
电路系统如图所示,设各组元件的参数值为已 知,取电压源e(t)为输入变量,电阻R2端电压uR2为输 出变量。 C
R1 iC + e (t ) -
L
+ uC iL R2
二维线性系统分析

二维线性系统分析二维线性系统是指由两个线性方程组成的系统。
它是线性代数中的重要概念,在许多领域的数学研究中都有重要应用,如电路分析、控制理论、信号处理等。
本文将介绍二维线性系统的基本定义和性质,以及分析该系统的方法。
首先,我们来定义二维线性系统。
一个二维线性系统可以表示为以下形式的方程组:```x'(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)```其中,`x(t)`是一个二维列向量,表示系统的状态;`u(t)`是一个输入列向量;`y(t)`是一个输出列向量;`A`、`B`、`C`、`D`是常数矩阵,分别表示系统的状态转移矩阵、输入矩阵、输出矩阵和直接通过矩阵。
接下来,我们将介绍二维线性系统的性质和特点。
1.线性性:二维线性系统是由线性方程组成的,因此它满足叠加和比例原理。
如果输入`u1(t)`对应的状态响应是`x1(t)`,输入`u2(t)`对应的状态响应是`x2(t)`,那么对于任意常数`a`和`b`,`a*u1(t)+b*u2(t)`对应的状态响应是`a*x1(t)+b*x2(t)`。
2.齐次性:当输入为零时,系统的状态满足齐次方程`x'(t)=Ax(t)`。
这意味着零输入条件下的系统响应只取决于初始状态`x(0)`。
3.稳定性:二维线性系统的稳定性可以通过判断状态转移矩阵`A`的特征值来确定。
如果所有特征值的实部都小于零,则系统是渐进稳定的。
接下来,我们将介绍如何分析二维线性系统。
1.状态方程求解:给定初始状态`x(0)`和输入`u(t)`,我们可以通过状态方程求解系统的状态响应。
通过对状态方程进行拉普拉斯变换,可以得到系统的传递函数:```X(s)=(sI-A)^(-1)*B*U(s)Y(s)=C*(sI-A)^(-1)*B*U(s)+D*U(s)```其中,`X(s)`和`U(s)`分别是`x(t)`和`u(t)`的拉普拉斯变换,`I`是单位矩阵。
2.频域分析:通过对传递函数进行频域分析,可以得到系统的频率响应和稳定性。
第1,2章 线性空间与线性变换

§1·4 线性变换(Linear Transformations)
一、 线性变换的概念
1. 线性变换的来历;
Definition: (i)T是V上的映射:T:VV。 (ii) T具有线性性:
T(+)=T()+T()
(保持加法的三角形法则)
T(k)=kT( )
(保持比例关系)
2 线性变换的性质:
2 坐标变换公式
已知 ➢空间中两组基:
{1, 2,..., n} {1, 2 ,..., n}
满足:(1, 2 ,..., n ) (1,2 ,..., n )Cnn
➢: (12...n )X ; (12...n )Y
讨论X和Y的关系
X=CY
例 已知空间R中两组基(I){Eij}
(II);{ 2 1 0 1 0 0 0 0 } 0 0 1 0 3 1 0 3
Rmn ;Cmn 。
F[t]n ={f(x)=a0 + a1x+ a2x2+...+an-1xn-1 :aiR}
运算:多项式的加法和数乘
•C[a,b]={f(x):f(x)在[a,b]上连续}
运算:函数的加法和数乘
•Example: V=R+,F=R, a b=ab, a=a
不是线性空间的集合
要点:
• 集合V 与数域F • 向量的加法和数乘向量运算 (运算之后的结果跑不出去) • 八条运算律 (能够保证向量的混合运算几乎与数的运算一样完美)
常见的线性空间
F=R或C
Fn={X=(x1,x2,…,xn)T:x F}
运算:向量加法和数乘向量
Fmn = {A=[aij]mn:a ijF}; 运算:矩阵的加法和数乘矩阵
二维线性系统分析傅里叶变换

bn
t t
2
t
g ( x) sin(2nf0 x)dx 0
采用指数傅里叶级数展开,可以使展开系数的表达式统一而简洁。
§1-2 二维傅里叶变换
指数傅里叶级数
满足狄氏条件的函数 g(x) 具有有限周期t,可以在(-,+ )展为 指数傅里叶级数:
g ( x)
n
c
cos( 2 x )
2 cos( 6 x) 3
前3项的和
1/2
an
2/ 频谱图
1 2 2 cos( 2x) cos( 6x) ...... 2 3
…
fn
0
1
3
-2/3
三角傅里叶展开的例子
练习 0-15:求函数 g(x)=rect(2x)*comb(x) 的傅里叶级数展开系数 宽度 =1/2 周期 t =1
展开系数Cn 频率为n/t的分量
§1-2 二维傅里叶变换 2-D Fourier Transform
从傅里叶级数到傅里叶变换
非周期函数可以看作周期为无限大的周期函数:
1 1 1 t 2 g ( x) lim t g ( x) exp( j 2 n x)dx exp( j 2 n x) t t t 2 n t
傅里叶-贝塞尔变换
例: 利用F-B变换求圆域函数的F.T.
1, r 1 定义: circ(r ) , 0, 其它 称函数
1
r x2 y 2
是圆对
{circ(r )} 2 rJ 0 (2r )dr
0
作变量替换, 令r’ =2r, 并利用:
J
0
中科大-傅里叶光学Ch2【2】

二:线性系统系统↔变换,线性系统,线性性质和迭加积分不变线性系统:传递函数 二维抽样定理1:线性性质和迭加积分系统 表示一个系统最合适的方法是一个数学算符: 数学算符g 2 ( x2 , y2 ) = S{g1 ( x1 , y1 )} , S{}算符 ↔ 变换 g1表示系统的输入, 2 表示系统相应的输出 g线性系统:S{as ( x1 , y1 ) + bt ( x1 + y1 )} = aS{s ( x1 , y1 )} + bS{t ( x1 , y1 )}线性的好处是: 输入函数可分解某些基元函数的线性组合,基元函数通过系统后输出 函数(基元响应函数)可方便求出,对线性系统其输出即为基元响应函 数的线性组合光学中基元函数:⎧δ 函数(点基元、球面波) ⎨ ⎩指数函数(余弦基元、平面波)分解 → 变换 → 综合 线性系统: 基元 → S {} → ∑S{ }以点基元为例:δ 函数分解 输入函数g1 ( x1 , y1 ) ⎯⎯⎯ δ 函数的线性组合(筛选性) →∞g1 ( x1 , y1 ) =−∞∫ ∫ g (ζ ,η )δ ( x − ζ , y1 1∞ −∞1− η )d ζ dη系统输出函数g2 ( x2 , y2 ) = S{ ∫ ∫ g1 (ζ ,η )δ ( x1 − ζ , y1 −η )dζ dη} 把 g 1 (ζ , η ) 看 作 加 在 基 元 δ ( x1 − ζ , y1 − η ) 上 的 权 重 因 子∞g 2 ( x2 , y2 ) =令h( x2 , y2 ; ζ ,η ) = S{δ ( x1 − ζ , y1 − η )}−∞∫ ∫ g (ζ ,η )S{δ ( x − ζ , y1 11− η )}dζ dηh( x2 , y2 ; ζ ,η )表征系统在输出平面的( x2 , y2 )点上 对输入平面坐标(ζ ,η )上的δ 函数的输入响应函数h( x2 , y2 ; ζ ,η )称为系统的脉冲响应∞∴ 输出:g 2 ( x2 , y2 ) =−∞∫ ∫ g (ζ ,η )h( x , y ; ζ ,η )dζ dη1 2 2线性系统的性质完全由它对单位脉冲的响应表征问题:h( x2 , y2 ;ζ ,η )是位置的函数,通通知N多点源的响应 → 输出2:空不变线性系统:传递函数有无点源的输出函数不随输入函数的空间位置而变 ?有→空不变线性系统.对理想成像系统空不变线性系统是必备的物函数g1 ( x1 , y1 ) → 像函数g 2 ( x2 , y2 )物平移g1 ( x1 − x0 , y1 − y0 ) → 像函数形式不变g2 ( x2 − Mx0 , y2 − My0 )→脉冲响应就简单了,例:响应函数 物平面中位于坐标原点的单位脉冲δ ( x1, y1 ) ⎯⎯⎯⎯ h( x2 , y2 ) →响应函数 位于x1 = ζ ,y1 = η点的δ ( x1 − ζ , y1 −η) ⎯⎯⎯⎯ h( x2 − Mζ , y2 − Mη) →∞输出:g 2 ( x2 , y2 ) =−∞∫ ∫ g (ζ ,η )h( x1∞ 12− M ζ , y2 − Mη ) d ζ dη物、像坐标取合适,如4F系统,M = 1输出:g 2 ( x2 , y2 ) =−∞∫ ∫ g (ζ ,η )h( x2− ζ , y2 − η ) d ζ dηg 2 = g1 ∗ h对于空不变线性系统:输出函数g2是输入函数g1和系统脉冲响应h的卷积 卷积表示一输出,是描述描述空不变系统的,系统的成像特性完全由h体现h是在空域中描述系统的全部成像特性传递函数卷积的F.T.性质:F { g2} =F { g1 ∗ h}⇒G2 ( f x , f y ) = H ( f x , f y )G1 ( f x , f y )∞H ( fx , f y ) =−∞∫ ∫ h(ζ ,η ) exp[− j 2π ( f ζ + f η )]dζ dηx y函数 H 称为成像系统的传递函数,表示系统的频域 称为成像系统的传递函数 的效应,同样可以体现系统的全部成像特性输入线性空不变系统输出空域:g1 (ζ ,η ) ∗ h( x2 − ζ , y2 − η ) ⇒ g 2 ( x2 , y2 )↓ ↓ ↓F { g1 (ζ ,η )} F {h( x2 − ζ , y2 − η )}F { g 2 ( x2 , y2 )}频域:G1 ( f x , f y ) • H ( f x , f y ) ⇒ G 2 ( f x , f y )1、H ( f x , f y )表示各个f x , f y 频率分量在振幅上透过率为多少, 位相发生多少移动。
2.2 线性不变系统
输入一个单 一频率的余 弦信号 系统 输出
只有输入频率的余弦信号,则是线性不变系统; 只有输入频率的余弦信号,则是线性不变系统; 还含有其他的频率,则不是线性不变系统! 还含有其他的频率,则不是线性不变系统!
g (t ) = K1 A2 sin ω1 (t − t0 ) + K 2 AB cos ω 2 (t − t0 ) = K1 g1 (t ) + K 2 g 2 (t )
从上式看出,此滤波器具有均匀性和叠加性, 从上式看出,此滤波器具有均匀性和叠加性,因此是一个 线性滤波器。 线性滤波器。
即
τ ' f 1 (t ) = A sin ω 1 (t − τ ) = f 1 (t − τ )
即:
{
}
g (x, y ) = f ( x, y ) * h( x, y )
输出函数 = 输入函数 * 单位脉冲响应
说明:系统的输出函数等于输入函数与系统的单位 说明:系统的输出函数等于输入函数与系统的单位 输出函数等于输入函数与系统的 脉冲响应的卷积 的卷积。 脉冲响应的卷积。
(二)线性不变系统的传递函数
如果例子中的输入有一个时间延迟
则输出响应可以表示成: 则输出响应可以表示成:
g '1 (t ) = A 2 sin ω 1 (t − τ − t 0 ) = g 1 (t − τ )
即输出响应同样有一个延迟 , 因此这个理想的滤波器是一个线性时间不变滤波器。 线性时间不变滤波器 因此这个理想的滤波器是一个线性时间不变滤波器。
08-二维线性系统分析4-线性不变系统、抽样

1/X
+∞ +∞
Gs(fx) 0
1/X
fx
Gs(fx) 0 fx
只有使这些频谱函数互不重叠, 只有使这些频谱函数互不重叠 才有可 能用滤波的方法,从中提取出原函数的 能用滤波的方法 从中提取出原函数的 频谱, 进而求出原函数. 频谱 进而求出原函数
g ( x, y ) = f ( x , y ) h ( x, y )
G(fx, fy) = F (fx, fy) H (fx, fy)
二维线性不变系统 例: P22 1.4(2)
输入: 输入
1 x x g ( x) = comb rect ∧ ( x) 3 50 3
间隔为3的 间隔为 的 脉冲阵列, 脉冲阵列 基频为1/3 基频为 g(x) 1 在有限空间 区域不为零, 区域不为零 |x|<25 三角波, 三角波 底宽为2 底宽为
§1.4 抽样定理 二,函数的抽样
由抽样值还原出原函数的条件
1 ≥ 2 Bx , X 1 ≥ 2 By Y
中各个区域(间隔为 间隔为1/X,1/Y) 则Gs中各个区域 间隔为 Gs(fx) 的频谱就不会重叠, 的频谱就不会重叠 有可能用滤 波的方法,提取出原函数的频谱 波的方法 提取出原函数的频谱 -Bx 0 Bx fx G, 进而求出原函数 进而求出原函数. 1/X 1 1 X ≤ , Y ≤ 称为奈奎斯特(Niquest)间隔 间隔 2Bx 2 B y 称为奈奎斯特
此理想低通滤波器的频率 特性为频域中的门函数
第2章二维线性系统分析-PPT课件

§2-2 二维线性不变系统
二、二维线性空不变系统
推广到二维空间函数
一个二维脉冲函数在输入面上位移时,线性系统的
响应函数形式始终与在原点处输入的二维脉冲函数的响 应函数形式相同,仅造成响应函数相应的位移,即:
{d(x-x, y-h)}=h (x-x, y-h)
脉冲分解
脉冲响应
叠加积分
§2-2 二维线性不变系统
一、二维线性时不变系统
设系统在 t = 0时刻对脉冲的响应为 h(t),即:
{d(t)}=h (t)
若输入脉冲延迟时间 t ,其响应只有相应的时 间延迟t ,而函数形式不变,即
{d (t - t )}=h (t - t )
则此线性系统称为时不变系统。系统的性质不随 所考察的时间而变,是稳定的系统。时间轴平移 了,响应也随之平移同样的时间,即具有平移不 变性。
这样的系统称为二维线性空不变系统。
线性不变系统 h (x, y; x, h) = h (x-x, y-h)
的脉冲响应:
观察点 输入脉冲 坐标 坐标
二个坐标的 相对间距
线性不变系统的输入--输出变换关系不随空间位置变化。
d (x,y)
§2-2 二维线性不变系统
二、二维线性空不变系统 例:
空不变(二维)系统:等晕成像系统
= {a1 f1 (x, y)} + {a2 f2 (x, y) } = a1 {f1 (x, y)} + a2 {f2 (x, y) } = a1 g1 (x, y) + a2 g2 (x, y)
则称该系统为线性系统。
§2-1 线性系统
线性系统具有叠加性质
第2章 线性系统动态分析

2)待定系数法计算 e
At
根据凯莱-哈密顿定理,对n阶方阵A,当 k n时, k 可用A的(n-1)次多项式表示,故 e At 可用A A 的(n-1)次多项式表示,即
e 0 (t ) I 1 (t ) A n1 (t ) A
At
n1
(2-28)
式中, 0 ,, n 1 为待定的一组关于t的标量函数, 其求解需要先计算A的特征值。
结合性质1,有
Φ(0) A
3. 证明
Φ(t )Φ( ) Φ(t )
Φ (t )Φ ( ) e At e A 1 1 1 1 ( I At A 2 t 2 A k t k )(I A A 2 2 A k k ) 2! k! 2! k! k t i k i k A i 0 i! (k i )! k 0
x (t0 ) ——n维状态向量在 t t0初始时刻的初值;
) 式(2-1)的解 x (t(其中 t 的解或零输入响应。
即
t0)称为自由运动
设式(2-1)的解为式(2-5)所示的向量幂级数,
x(t ) b0 b1 (t t 0 ) b2 (t t 0 ) bk (t t 0 )
n 0 (t ) 1 (t )1 n 1 (t )1 1 e 1t 0 (t ) 1 (t ) 2 n 1 (t ) n 1 e 2t 2 0 (t ) 1 (t ) n n 1 (t ) n 1 e nt n
0
1 2 1 k 2 k x (t ) I A(t t 0 ) A (t t 0 ) A (t t 0 ) x (t 0 ) 2! k!
线性系统与线性空不变系统.ppt

非相干成像系统的本征函数(3)
因而有:
L cos
fax fb y
A fa ,fb cos
fa x
f b
y
fa ,fb
这表明,对于脉冲响应是实函数的空间不变线性系统,余弦输入 将产生同频率的余弦输出。
同时产生与频率有关的振幅衰减和相位移动,其大小决定于传递 函数的模和幅角。
物理的空间不变线性系统,输入平面和输出平面常常是不同的两 个平面,需要建立两个坐标
从研究输入和输出之间关系的角度来看,输入和输出两种信号放 在同一坐标系中是方便的,因此对输入平面和输出平面的坐标做 归一化(不管两者是否表示同一种物理量),使得从数值上有
x x x 和 y y y
脉冲响应函数变为 hx, y;, hx , y
叠加积分变为“卷积积分”
gx , y f ,hx , y dd f x, y hx, y
光学成象系统可以把物平面划分为若干个等晕区,把每个等晕区 当作空间不变线性系统处理
二维不变线性系统的传递函数
如果不变线性系统的输入是空域函数,其傅里叶变换为
F fx , f y
课堂练习
给定一个不变线性系统,输入函数是有限延伸的三角波
gx
1 3
com
b
x 3
rect
x 75
*
x
对下列传递函数,用图解法确定系统输入函数的频谱,传递函数、
输出函数的频谱,以及系统的输出的输出。
H f rect f rect f
4 2
习题
教科书P22习题1.1,1.3,1.4
f0
常用函数及其傅里叶变换(2)
(5)阶跃函数
1,
stepx
1
《傅里叶光学》,《信息光学》第二章 二维线性系统分析

g x, y L f x, y L F f x , f y exp j 2 f x x f y y df x df y 同理,根据线性叠加性质,有
g x, y
根据傅里叶变换有
f , h x , y d d
f x, y h x, y
2、线性不变系统
3)线性不变系统的传递函数
g x, y f x, y h x, y
卷积定理
G fx , f y H fx , f y F fx , f y
g nX , mY sin c 2B x nX sin c 2B y mY
x y
若取最大允许的抽样间隔,则
g x, y n m g , 2B 2B n m y x
n m sin c 2 B x sin c 2 B y x y 2 Bx 2 By
F f , f L exp j 2 f x f y df df
x y x y x
y
?
g x, y G f x , f y exp j 2 f x x f y y df x df y
2、线性不变系统
G f x , f y = F g x, y
H f x , f y = F h x, y
F fx , f y
F f x, y
输出频谱 从空间域入手计算系统的输出
传递函数
输入频谱
第二章 二维线性系统

令
ℒ h( x, y; ,) ( x , y )
g ( x, y )
系统的脉冲响应
则
f ( , )h( x, y; , )d d
对空间的一个点(函数),经过线性系统后变
为 h( x, y; ,) ,它不再是一个点,称为“晕”。
i 1
n
即系统对线性叠加的作用等于对每个分函数作用的 线性叠加,称这种系统为线性系统。
如果输入函数f(x,y)是非常复杂的函数,可以将 f(x,y)分
解成某些“基元”函数(基本函数)的线性组合,则f(x,y) 通过线性系统后,输出函数可以是系统对“基元”函数作 用后的线性组合。常用的“基元”函数有函数、余弦函数、 复指数函数。 二、线性系统的脉冲响应 根据函数的筛选性,f(x,y)可以写为
f ( x, y; f a , f b ) 称为线性不变系统的本征函数,H(fa,fb)是本征值。
四、线性不变系统的滤波特性
空间域 频率域
g ( x, y) f ( x, y) h( x, y)
G( f x , f y ) F ( f x , f y ) H ( f x , f y )
从频率域可以看出,通过系统后,F(fx,fy) 被改变了,改变了多少由 H(fx,fy)决定。即不同 fx、fy 值的H值不同,该频率的输入函数经过系 统后变化不同,即某些频率分量被滤除、衰减或发生相移等。所以 系统就好象一个滤波器,滤波特性决定于 H(fx,fy)。
§2—2 线性不变系统
一、线性不变系统定义 当 有
ℒ f ( x, y ) g ( x, y) ℒ f ( x x0 , y y0 ) g ( x x0 , y y 0 )
5线性系统与线性空不变系统

间不变性不能在整个视场内成立,我们也可把视场分成若干
个区域,在每个区域内使空间不变性近似成立。这样划分的 区域称为等晕区。对于每个等晕区都有各自的h。因此,对
线性不变系统的讨论是具有普遍意义的。
空间频率的两种意义
4 线性不变系统的传递函数
空间频率类似于时域函数的时间频率,时间倒数称作频率, 长度倒数称作空间频率,即在单位长度内周期函数变化的 周数(单位为:周/mm,线对/mm,L/mm,等 ) 信息光学中有两种空间频率,一种是对二维图象进行频谱 分析得到的图象频谱对应的空间频率,这是一种空间强度 分布,单位为:周/mm,线对/mm,L/mm,等,其大小是没 有限制的,可以是无穷大 另一种是对电磁波场进行频谱分析得到的平面波对应的空 间频率,因为电磁波在均匀介质中波长是常数,在其传播 方向上空间频率是不变的。因而其对应在三维空间坐标上 的每个方向的空间频率(单位为:光波数/mm )表示出的 意义实际上是电磁波的传播方向,或其传播方向与坐标轴 的夹角,而且大小受到光波长的限制,最大是波长的倒数。 下章再详细讲这两者区别
就可以通过叠加积分而完全确定系统的输出 。另外,如果系 统的输入和输出之间满足叠加积所描述的关系,就可以认为这
是一个线性系统。
为了更好地理解叠加积分的物理意义,我们以线性光学成像
系统为例加以说明:
f ( x, y )
2 脉冲响应
一辐输入图像可看成是一个点物的集合,只要能确定所有
点物的像,就可以完备地描述这一成像系统的效应。但要
Le xp j 2 (x y ) H ( , ) e xp j 2 (x y) e xp j 2 (x y )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f (x, y) F( fx, fy ) exp[ j2π( fxx fy y)]dfxdfy F -1 F( fx, fy ) (2.7b)
式中, x, y, f x , f y 均为实变量。
h(x2, y2;,) L { (x1 , y1 )} (2.5)
图 2.1 线性系统的脉冲响应
将脉冲响应代入式 (2.4), 得到系统输出为:
g(x2, y2 ) f (,)h(x2, y2;,)dd (2.6)
式 (2.6) 通常称为“叠加积分”,它描述了空间线 性系统的输入和输出之间的关系。
也就是满足叠加性和均匀性的系统。可见,线性 系统对几个激励的线性组合的整体响应等于单个 激励所产生的响应的线性组合。
2.1.2 脉冲响应和叠加积分 任何输入函数都可以分解为某种“基元”函数的
线性组合,相应的输出函数便可通过这些基元函 数的线性组合来求得,基元函数通常是指不能再 进行分解的基本函数单元。在线性系统分析中, 常用的基元函数有 函数、阶跃函数、余弦函数和 复指 数函数等。对光学系统来说,主要有二维 函数和复指数函数。 首先研究 函数作为基元函数的情况。根据
2.2.2 可分离变量函数的傅立叶变换
一般函数的二维傅里叶变换是很复杂的,但如果 函数在直角坐标系中是可分离的,即:
பைடு நூலகம்
f (x, y) fx (x) f y ( y)
(2.8)
利用一维和二维傅里叶变换定义可证明,
它的二维傅里叶变换也是可分离的,可以 表示成两个一维傅里叶变换的乘积
F { f (x, y)} F { fx (x)}F { fy ( y)}
第 2 章 二维线性时、空不变系统分析
内容提要:
一个信息系统是某种装置,当施加激励时,便产 生相应的响应。激励常称为系统的输入,响应则 称为系统的输出。例如电路网络,它的输入和输 出是一维时间序列电信号,光学成像系统的输入 和输出是物与像,是二维空间分布的图像信号。
本章介绍线性时、空系统的理论,常见的时空信 号及其傅立叶变换,图像信号的采集,为二维光 电信息系统分析奠定数学基础。
函数的筛选性质,任何输入都可以表达为:
f (x1, y1) f ( ,) (x1 , y1 )dd
上式表明,函数f (x1, y1) 可以分解成为在x1 y1 平 面上不同位置处无穷多个幅度为 f ( ,) 的 ( ,)
函数的线性组合,f (,) 为坐标位于 ( ,) 处的
函数在叠加时的权重。输入 f (x1, y1) 通过系统后的 输出为:
g(x2, y2,t) L { f (x1, y1,t)}
(2.1)
系统对任何两个输入的和 的响应分别为
g1(x2, y2,t) L { f1(x1, y1,t)}
(2.2a)
g2 (x2, y2,t) L { f2 (x1, y1,t)}
(2.2b)
如果该系统对以上两个任意输入的线性组合
(1)
在任一 (x, y) 区域绝对可积;
(2) f (x, y) 在任一矩形区域,必须只有有限个间
断f (点x, 和y) 有限个极大极小点;
(3)
没有无穷大间断点。
f (x, y)
f (x, y) fx (x) f y ( y)
物理上存在的信号均存在傅里叶变换。从应用角 度来看,可以认为傅里叶变换总是存在的。
(2.9)
实际上,许多光学元器件能够用可分离变量函数 表示,如光学十字架,因此,这一性质是很有用 的。
2.2.3 具有圆对称函数的二维傅里叶变换——傅里叶 -贝塞尔变换
光学系统通常是以传播方向为光轴的轴对称系统。 在垂直于光轴的物(像)平面、透镜平面、光瞳平面 上放置的透镜、光瞳等元器件常常具有圆对称性。 此时用极坐标比直角坐标更方便。假设平面上的 极坐标为;平面上的极坐标为,则:
a1 f1(x1, y1,t) a2 f2(x1, y1,t) 的响应为,
L {a1 f1(x1, y1,t) a2 f2(x1, y1,t)} L {a1 f1(x1, y1,t)}L {a2 f2(x1, y1,t)}
a1L { f1(x1, y1,t)} a2L { f2(x1, y1,t)} a1g1(x2, y2,t) a2g2(x2, y2,t) 这里a1和a2为任意复常数,则称该系统为线性系统。
式 (2.7b) 表示函数 f (x, y)是各种频率为 fx , f y 的余(正) 弦函数的叠加,叠加时的权重因子是 F( fx , f y ) 。因 此, F( f x , f y ) 常称为函数 f (x, y) 的频谱。
傅里叶变换存在的充分条件有若干形式,绝对可 积和狄里赫利条件是其中一种,它可具体表述为:
Lxg{121(x(2xyy,12y2 ,t1),y1L{f11)(}x1, yh1(, tx)2} 2 , y2 2 ;0,0)
2.1 二维线性时、空不变系统
2.1.1 二维线性系统的定义
数学上,可以把二维系统定义为一个用算符L{ } 来表示的变换,该算符把在 x1 y1 平面上定义的二
维输入函数 f (x1, y1,t) 变换为定义在 x2 y2平面上的 二维输出函数g(x2, y2,t), 记为
g(x2 , y2 ) L { f (,) (x1 , y1 )dd}
根据线性系统的性质,可将算符L{ }先作用于各 基元函数,再把各基元函数得到的响应叠加起来, 得到:
g(x2, y2 ) f (,)L { (x1 , y1 )dξd} (2.4)
L { (x1 , y1 )}的意义是物面上位于 ( ,)处的单 位脉冲激励通过系统后的输出,把它定义为系统 的脉冲响应函数(见图2.1)
2.2 二维傅里叶变换
傅里叶变换是研究线性不变系统的重要数学工具 在光信息系统中用来研究光学系统的频谱特性。 本节先简要介绍二维傅里叶变换,然后给出典型 函数的二维傅里叶变换。
2.2.1 二维傅里叶变换的定义及存在条件 若函数 f (x, y)在整个x y平面上绝对可积且满足狄
里赫利条件,其傅里叶变换及傅里叶逆变换存在, 并可定义为:
