《小方差无偏估计》PPT课件
小方差无偏估计UMVUE

UMvue方法在某些特定情况下可能无法提供准确的方差估计。例如,当数据存在异常值或离群点时,该方法的 效果可能会受到影响。此外,对于一些复杂的数据结构和模型,UMvue方法的适用性和性能可能需要进行进一 步的研究和验证。
04
小方差无偏估计
定义与性质
定义
小方差无偏估计(UMvue)是指估计量不仅无偏,而且具有较小的方差。
重要性及应用领域
重要性
umvue方法在统计学中具有重要地位,因为它能够提供更精 确的参数估计,尤其是在样本量较小的情况下。通过最小化 方差,umvue方法有助于提高估计的准确性和可靠性。
应用领域
umvue方法广泛应用于各种统计领域,如回归分析、线性模 型、方差分析等。它对于处理小样本数据、非线性和非正态 分布的情况特别有用,能够提供更稳健和可靠的估计结果。
实例三:复杂统计模型的小方差无偏估计
复杂统计模型
实例分析
复杂统计模型是指包含多个变量和复 杂关系的统计模型,例如时间序列分 析、多元回归分析等。
我们可以使用实际数据或模拟数据来 估计复杂统计模型的参数,并评估小 方差无偏估计的准确性和效率。
小方差无偏估计
在复杂统计模型中,小方差无偏估计 需要使用更高级的算法和技术来实现, 例如贝叶斯推断、马尔科夫链蒙特卡 罗等方法。
02
无偏估计
定义与性质
定义
无偏估计是指一个估计量的期望值等于被估计参数的真实值。
性质
无偏估计具有一致性、无偏性和有效性的性质,即随着样本量的增加,无偏估 计量逐渐趋近于真实值,且其方差最小。
无偏估计的优缺点
优点
无偏估计能够提供被估计参数的较准 确的估计,特别是在样本量较大时, 其估计精度较高。
第2.3节 最小方差无偏估计和有效估计

例1(p54例2.20) 设X ( X1 , X 2 ,
, X n )T 是来自总
*2 体( , 2 )的一个样本,已知X 和Sn 是 和 2 的无偏 *2 估计,证明X 和Sn 分别是 和 2 的MVUE .
证 设L( X )满足EL( X ) 0, 则
因而
L exp{
Βιβλιοθήκη T ( x1 , x2 ,
, xn ) L( x , )dx1dx2 , xn ) L( x , )dx1dx2
dxn dxn
T ( x1 , x2 ,
n
其中L( x , ) f ( xi ; );
i 1
ln f ( X ; ) 2 (3) I ( ) E ( ) 0 ( g( ))2 则对一切 ,有 D(T ( X )) ,其中 nI ( ) ( g( ))2 为罗-克拉美下界,I ( )称为Fisher 信息量。 nI ( ) 1 特别是当g( ) 时,有 D(T ( X )) . nI ( )
定理2.9 设总体X的分布函数为F ( x , ), 是
未知参数,X ( X1 , X 2 ,
, X n )T 是来自总体X的一 , X n )是的充分完备
*
个样本,如果T T ( X1 , X 2 ,
ˆ是的任一无偏估计,记 ˆ E ( ˆ |T) 统计量,
ˆ *是的唯一的MVUE . 则
1
ˆ( X )] 2 E{[ L( X ) EL( X )][( ˆ( X ) E ˆ( X )]} D[ L( X )] D[ ˆ( X )] D[ ˆ( X )] D[ L( X )] D[
最小方差无偏估计UMVUE

ˆ (t )=E (1 | T t ), 其中t xi
t (t 1)
故
= T (T 1)
n( n 1)
n ( n 1)
为θ的无偏估计.且 Var ( ) Var ( 1 )
二、最小方差无偏估计
ˆ 定义: 设 是的一个无偏估计量, 若对于的任一方差 存在的无偏估计量 , 都有 ˆ Var ( ) Var ( ) , ˆ 则称 是 的一致最小方差无偏估计, 记为UMVUE.
的微分可在积分号下进行,即
i 1
n g ( ) T ( x1 , x2 ,, xn ) ( p( xi ; ))dx1 dxn i 1
n T ( x1 , x2 ,, xn )[ ln( p( xi ; ))] i 1
n
而 x ln p( x, ) ln ,
d 1 x d ln p( x, ) 2
2
2
2
1 X I ( ) E ln p( X , ) E 2
例7 ( x1 , x2 ,, xn )是P( )( 0)的一个样本, 证明 : x是 的有效估计
证明 : 因为x是样本均值, 故, E x EX , x是的U .E Var ( X ) Var ( x) n n
总体X的分布律为 : P{ X x}
(1)I(θ)越大,总体分布中包含未知参数的信息越多。 (2) I()的另一表达式为
2 ln p( x; ) I ( ) E ( ), 2 2 p( x; ) ( 存在,满足正则条件) 2
2-3 最小方差无偏估计和有效估计

由定理 2.9
ˆ E(X |T ) X
ˆ 2 E (Sn | T ) Sn
2 2
,
。
分别是
2 和 惟一的最小方差无偏估计。
13
例 2.21
设 ( X1 , X 2 ,, X n ) 是来自总体 X 服从区间 (0, )
上均匀分布的一个样本。求 的最小方差无偏估计。
由式(2.19)得
ˆ1 | T ) E ( ˆ2 | T )] 0 ,对一切 。 E [ E (
由于T 是完备统计量,由定义 1.5 得
ˆ1 | T ) E ( ˆ2 | T )) 1,对一切 , P ( E (
ˆ * E ˆ1 | T 是 的最小方差无偏估计。
ˆ1 ( X ) D[ L( X ) ˆ ( X )] DL( X ) D ˆ( X ) D ˆ ( X ) E ˆ ( X )] 2 E [ L( X ) EL( X )][
ˆ ( X ) D ˆ( X ) , DL( X ) D
ˆ( X ) 是 的 MVUE。 故
是 的最小方差无偏估计。
16
1.最小方差无偏估计提供了一种优良的估计, 然而一个更深入的问题是:无偏估计的方差是否可 以任意小?如果不可以,那么它的下界是多少?这 个下界等否达到?
2. 要直接验证某个估计量是最小方差无偏估计量 是困难的. 若能求出无偏估计中方差的下界, 而且又 能说明参数 的一切无偏估计中存在某个估计 的 方差能达到这个下界,那么 就是 的最小方差无 偏估计. 下面给出一个判别准则:
即 的 充 分 偏 估 计 是 惟 一 的 。 再 由 定 理 2.8 知 ,
11
4-一致最小方差无偏估计

例 设总体为泊松分布 ( ), 计算Fisher信息量. P 解 P( )的分布列为 x p( x; ) e , x 0 ,1, , x! 可以看出正则条件满足 ,且
于是
ln p( x; ) xln ln( x! ) , x ln p( x; ) 1.
关于相合性的两个常用结论
1. 样本 k 阶原点矩是总体 k 由大数定律证明 阶原点矩的相合估计.
ˆ 2. 设 n是 的无偏估计 ˆ 量, 且 lim Var( n ) , 则 0
ˆ n 是 的相合估计.
n
用切比雪夫不 等式证明
ˆ ˆ 定理 设θn θn ( x1 ,x2 , xn )是的一个估计量, ˆ ˆ lim E (θn ) θ, lim Var( θn ) 0 , 若
注:定理说明若无偏估 计不是充分统计量的函 数, 则将其对充分统计量求 条件期望可以得到一个 新 的无偏估计,从而降低 了无偏估计的方差 .
统计的一个基本原则: 在充分统计量存在时, 任何统计推断可以基于 充分 统计量进行,这可以简 化统计推断的程序,通 常将该原 则称为充分性原则 .
例1 设X 1 , X 2 , , X n 是来自b(1, p)的样本,则X是p 的充分统计量.求 p 2的无偏估计.
推广
ˆ ˆ 定理 若 n1, , nk 分别是 1, , k的相合估计, g( 1, , k )是 1, , k的连续函数,则 ˆ ˆ ˆ g( , , )是的相合估计.
n1 nk
注: 样本均值是总体均值的 相合估计
样本方差是总体方差的 相合估计 样本标准差是总体标准 差的相合估计
相合估计量仅在样本容量 n 足够大时,才显示其优越性.
第三节一致最小方差无偏估计

I( ) E[ ln p( X ; )]2
为总体分布的费希尔 (Fisher) 信息量.
Fisher 信息量是统计学中的一个基本概念, 很多的统计结果都与Fisher信息量 I ( )有关。
解释为总体分布中性质显示,“
的信息越多
例1 设X 1 , X 2 , , X n 是来自b(1, p)的样本,则X是p 的充分统计量.求 p 2的无偏估计.
解
1, X 1 1, X 2 1; ˆ 构造估计 1 0, 其他.
ˆ ) P ( x 1, x 1) p p E ( 1 1 2 ˆ E ( ˆ | T t ) P ( ˆ 1| T t)
xp( x , y )dxdy EX
[ x ( y )]{ [ ( y ) ]h( x | y )dx } pY ( y )dy 0
[ x ( y )][ ( y ) ] pY ( y )h( x | y )dxdy
证明 2ln p( X ; θ )
E θ
2
2ln p( x; θ ) θ 2 p( x; θ )dx
1 p( x; θ ) p( x; θ )dx θ θ p( x; θ )
1 p( x; θ ) p( x; θ ) 1 2 p( x; θ ) 2 p( x; θ )dx 2 θ p( x; θ ) p ( x; θ ) θ 1 p( x; θ ) p( x; θ ) 1 2 p( x; θ ) 2 p( x; θ )dx 2 θ p( x; θ ) p ( x; θ ) θ
数理统计:最小方差无偏估计

2
Eˆ
2
2E
ˆ
Eˆ
Eˆ
=E
ˆ Eˆ
2
Eˆ
2
注意: 和Eˆ都是定值.
Var ˆ [Bias(ˆ)]2
定义:Bias(ˆ)=E(ˆ)
方差
随机误差 (有效性)
偏倚平方 系统误差 (无偏性)
7
为了说明UMVUE的计算方法,需要用到条件期望, 回顾如下。
1. 条件期望定义
若随机变量Y 在 X x 条件下的分布为 f ( y | x) ,且
则称
y f (y | x) , 或者 y f ( y | x)dy - y
E Y | X x y f ( y | x) (离散型)
ci为任意常数,i 0,1, , n
E
c0
n
ci
Xi
|
T
c0
n
ciE Xi | T
i1
i1
(2) E E X T EX . (重期望公式)
内层:给定T时,关于X求条件期望.
外层:是T的函数,关于T求期望。
11
(3) E[g(T)X|T]=g(T) E[X|T], 其中g(t)是任何实值函数;
E(X |Y y)
E(X |Y )
Y取确定值y的条件下
Y取值随机的条件下
若记 g( y) E( X |Y y), 则 g(Y ) E( X |Y ) 作为随机变量Y
的函数, 我们可称之为在给定Y的条件下X的条件期望, 它是随机变量.
2-3 最小方差无偏估计和有效估计 PPT课件

估计量就一定是最小方差无偏估计量。那么,在什么情况 下,它才是惟一的呢?显然,如果它又是完备统计量,便 可保证其惟一性。
9
定理 2.9 设总体 X 的分布函数为F( x; ), ,
( X , X , , X )为其样本,若T T( X , X , X )是 的
1
2
n
1
2
n
充分完备统计量,ˆ为 的一个无偏估计,则
ˆ E(ˆ | T )
(2.18)
为 的惟一的最小方差无偏估计。
证明 设ˆ 和ˆ 是 的任意两个无偏估计,由定理 2.8
1
2
知, E(ˆ | T )和E(ˆ | T )也是 的无偏估计,
1
2
即对一切 ,有
E
[E(ˆ 1
|
T
)]
,
E
[E(ˆ 2
|
T
§2.3 最小方差无偏估计
最小方差无偏估计和有效估计是在某种意义下的最 优估计,两者既有区别又有密切的关系。如果求出
参数 的一个估计量ˆ,判别其是否为最小方差无偏
估计或有效估计,显然具有重要的意义。倘若能直
接求出参数 的最小方差无偏估计或有效估计,则
将更加令人满意,本节将研究这些问题。
1
一、最小方差无偏估计
ˆ*
E
ˆ 1
|T
是 的最小方差无偏估计。
11
注意: 定理 2.9 提供了一种寻求 的最小方差无偏估
计量的方法,即先找到 的一个充分完备统计量 T T (X1, X2,L , X n ) 和一个无偏估计ˆ ,再求条件数学期 望 E(ˆ | T ) 即可。例如,对泊松总体 P() ,由例 1.9 知 X 是参数 的充分完备统计量且又是 的一个无偏 估计,所以 E(X | X ) X 是 的最小方差无偏估计。
最小方差无偏估计UMVUEPPT幻灯片25页PPT

6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
Thank you
最小方差无偏估计UMVUEPPT幻灯片
56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
数理统计课件_2.3最小方差无偏估计和有效估计

12.3 最小方差无偏估计和有效估计最小方差无偏估计是在某种意义下的最优估计,两者既有区别又有密切的关系,如果求出参数θ的一个估计量ˆθ,则判别其是否为最小方差无偏估计或有效估计,就具有重要的意义。
倘若能直接求出参数θ的最小方差无偏估计,则将更加令人满意,本节将研究这些问题。
一.最小方差无偏估计由定义2.4知,最小方差无偏估计(MVUE)是在无偏估计类中,使均方误差达到最小的估计量,即在均方误差最小意义下的最优估计。
它是在应用中,人们希望寻求的一种估计量。
定理 2.7 设ˆ()X θ是θ的一个无偏估计,ˆD θ<∞,若对任何满足条件:()0EL X =,()DL X <∞的统计量()L X ,有ˆ[()()]0E L X X θ= 则ˆ()X θ是θ的MVUE。
其中12(,,,)n Χ=ΧΧΧ .证明 设1ˆ()X θ是θ的任一无偏估计,记1ˆ()()L θΧ=Χˆ()θ−Χ,则()L X 为0的无偏估计,由2于 1ˆ()D X θˆ[()()]D L X X θ=+ˆ()()2{[()DL X D X E L X θ=++ ˆ()][()EL X X θ−ˆ()]}E X θ− =ˆ()()DL X D X θ+ˆ()D X θ≥ 故ˆ()X θ是θ的MVUE。
例 2.19 设12(,,,)n Χ=ΧΧΧ 是来自正态总体2(,)N µσ的一个样本,已知Χ和2*n S 分别是µ和2σ的无偏估计,证明Χ和2*n S 分别是µ和2σ的MVUE。
证明(略)设()L X 满足()0EL X =,则有2211exp{()}02ni i L X dx µσ=−−=∫∫…i (2.15) 上式关于µ求导,并利用(2.15)式得22111()exp{()}02nni ii i L x Xdx µσ==−−=∑∫∫ (i)故有{()}0E L X Χ=,所以Χ是µ的MVUE. 式(2.15)关于µ求二阶导数,得222111()exp{()}02nni ii i L x Xdx µσ==−−=∑∑∫∫…i (*)式(2.15)关于2σ求导,得3222111()exp{()}02nni ii i L x xdx µµσ==…−−−=∑∑∫∫ (**)利用22211()()()nni i i i x x n x µµµ==−=−−−∑∑,式(2.15),(*),(**) 可得222111()exp{()}02nni ii i L x x xdx µσ==−−−=∑∫∫…故有*2{()}0nE L X S =, 所以*2n S 是2σ的MVUE。
最小方差无偏估计
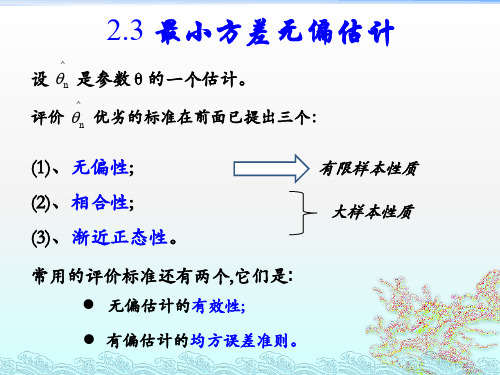
^
是 g(θ) 的 UMVUE 的充要条件为:
ˆ ,U ) E ( g ˆ U ) 0, U U 0 , Cov ( g
上述条件等价于 g(θ) 的 UMVUE g ( x) 与任意一个 0的无偏估计都不相关。
定义2.3.3:假如参数的无偏估计存在,则称此参数为
可估参数。 定义2.3.4:设 F ={p(x; θ): θ∈Θ}是一个参数分布族。 g(θ) 是 Θ 上的一个可估参数,Ug 是 g(θ) 的无偏估计类。 假如 g ( x) 是这样的一个无偏估计,对一切 g ( x) U ( g ), 有
^*
上式左端作为a的二次多项式,可求得: ˆ ( )) Cov 2 (U , g 左端最小值为 0 Var (U )
ˆ ( )) 0. 因此Cov (U , g
(充分性“” ) 设g ˆ ( )满足Cov ( g ˆ ,U ) 0, U U 0 , .
~( ) - g ˆ ( ), 对任意一个其它的无偏估计g ( ), 令U g ~( ) - g ˆ ( )为0的无偏估计。 则U g ~( )) Var (U g ˆ ( )) 则 : Var( g
但当估计类缩小时,一致最小均方差估计有可能存在。
三、一致最小方差无偏估计
由上一节知,一致最小均方误差估计不存在。我们现在把
范围缩小到无偏估计来考虑。 由 MSE 的定义可知无偏估计的均方误差就是方差。所以最
好的无偏估计就是方差最小的无偏估计。 这里我们将参数 θ 用其函数 g(θ) 代替,g(θ) 的估计用
均方误差要求系统偏差和随机误差越小越好
例2.3.3:设 x1, x2, …, xn是来自正态分布 N(μ, σ2) 的一个
小方差无偏估计和有效估计

04
比较与讨论
小方差无偏估计与有效估计的异同
定义
小方差无偏估计是指估计量不仅 无偏,而且具有最小方差的估计; 有效估计则是指具有最小均方误 差的估计。
性质
小方差无偏估计强调的是无偏性 和方差最小,而有效估计则关注 均方误差的最小化。
条件
小方差无偏估计要求估计量必须 是无偏的,而有效估计则要求在 所有无偏估计中具有最小均方误 差。
研究背景与意义
研究背景
在实际应用中,我们常常需要估计未知参数,而估计的准确性对于后续分析和决策至关重要。因此,寻找更优的 估计方法一直是统计学研究的重点。小方差无偏估计和有效估计作为两种重要的估计方法,在理论研究和实际应 用中都具有重要的地位。
研究意义
通过对小方差无偏估计和有效估计的研究,我们可以深入理解参数估计的本质,探索更优的估计方法,提高估计 的准确性和可靠性。这不仅有助于推动统计学理论的发展,还能为实际问题的解决提供更有效的工具。
小方差无偏估计和有效估 计
• 引言 • 小方差无偏估计 • 有效估计 • 比较与讨论
01
引言
定义与概念
小方差无偏估计
指估计量在所有无偏估计量中方差最 小,即除了要估计的参数真值外,其 它所有无偏估计量与该估计量的方差 之差达到最小。
有效估计
指在所有无偏估计量中,该估计量的 方差小于或等于其他任何无偏估计量 的方差,且与真实值之差的平方的期 望值最小。
未来研究方向与展望
研究方向
展望
未来研究可以进一步探讨小方差无偏估计和 有效估计的理论基础、性质和应用,以及如 何在实际问题中应用和改进这两种估计方法。
随着统计学和数据分析的不断发展,小方差 无偏估计和有效估计的应用范围将更加广泛, 理论体系将更加完善,为解决实际问题提供 更加有效的工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Problem: 无偏估计的方差是否可以任意小? 如果不能任意小, 那么它的下界是什么?
定理3: (UMVUE准则) 设 x1, , xn 是总体X的样本,
(2) I()的另一表达式为
I ( ) E(2 ln p(x; )), (2 p(x; ) 存在,满足正则条件)
2
2
例3:设总体为Poisson分布,即
p(x; ) x e , x 0,1, 2.....
x!
则 I ( ) 1 .
例4: 设总体为指数分布Exp(1/θ),即
正 则 条
(3) p(x; ) 存在且对中一切 有
件
p(x; )dx
p( x; ) dx
(4) E( ln p(x; ))2 存在
则称
I ( )
def
E(
ln
p(x; ))2
为总体分布的Fisher信息量.
注:
(1)I(θ)越大,总体分布中包含未知参数的信息越多。
达到下界, 则T必为g( ) 的最小方差无偏估计. 但
ˆ (x1, , xn ) 是θ的任一无偏估计, Var
如果对任一个满足 E(x1, , xn ) 0的(x1, , xn ),都有
Cov ( ,) 0,
则ˆ是的UMVUE. 反之亦成立.
例2: n设x1 , , xn 为来自Exp(1/θ) 的样本,则
注:定理2表明: 若无偏估计不是充分统计量的函数,则将之对充分
统计量求条件期望可得一个新的无偏估计,且它为充分统计量的函
数且方差会减小. 即, 考虑点估计只需在充分统计量的 函数中进行, 这就是 — 充分性原则.
例1.设 (x1 , , xn ) 为来自b(1,p) 的样本, 求p2的U.E
解:前已求过: x (或T nx) 为p 的充分统计量
p( x;
)
1
exp{
x },
x
0,
0.
则 I ( ) 1 . 2
注: 常见分布的信息量 I()公式
两点分布X ~ b(1,p)
I ( p) 1
P(X x) px (1 p)1x , x 0,1
p(1 p)
泊松分布 X ~ P(), 0.
I () 1
指数分布 X ~ Exp(),
I () 2
正态分布 X ~ N(,1), X ~ N(0, 2 ),
I() 1
I ( 2 ) 1 2 4
X ~ N(, 2),
1
I
(
,
2
)
2
0
0
1
2
4
2、定理4 (Cramer-Rao不等式):
p(xi ; )dx1
dxn
则有 Var(T ) [g( )]2 nI ( )
特别地对θ的无偏估计有
Var(T ) 1
nI ( )
上述不等式的右端称为C-R下界, I() 为Fisher信息量.
注:
(1) 定理对离散型总体也适用.只需改积分号为求和号。
(2) 在定理4条件下, 若g( ) 的无偏估计量T 的方差VarT
dxn
i 1
的微分可在积分号下进行,即
g( )
T ( x1, x2 ,
, xn )
n
(
i 1
p(xi ; ))dx1
dxn
T (x1, x2 ,
n
, xn )[ ln( i1
p(xi ; ))]
n i 1
第六章 第三节
最小方差无偏估计
一、Rao-Blackwell定理 二、最小方差无偏估计 三、 Cramer-Rao不等式
一、Rao-Blackwell 定理
优良的无偏估计都是充分统计量的函数.
定理1: 设X和Y是两个r.v.,EX=μ,VarX>0,令 (y) E(X | Y y)
则有
E(Y ) ,Var((Y )) Var(X )
T xi 为θ 的充分统计量,证明: i 1 x T 为θ的UMVUE. n
三、罗-克拉美(Cramer–Rao )不等式
1、 Fisher信息量的定义.
设总体X 的概率函数为p(x; ),,且满足条件:
(1)是实数轴上的一个开区间;
(2) 支撑S {x | p(x; ) 0}与无关;
设总体X 的概率函数为p(x ; ),, 满足上面定义
中是的g(条)的件一;个x1,无…偏.,x估n 是计来. 自g总 (体) X的g一(个) 存样在本,, T(x1,….,xn )
且对中一切 有 g( )
T (x1, x2 ,
n
, xn ) p(xi ; )dx1
其中等号成立的充要条件为X与 (Y)几乎处处相等.
将之应用在参数估计中可得:
定理2: 设总体的概率函数为p(x;θ), x1, , xn
是样本,T T (x1, , xn ) 是θ的充分统计量,
对θ的任一无偏估计 ˆ (x1, , xn ),令 E(ˆ | T ),则
也是的无偏估计,且Var Varˆ
i 1
为θ的无偏估计.且 Var( )
t(t 1) n(n 1)
Var ( 1 )
二、最小方差无偏估计
定义: 设ˆ是的一个无偏估计量,若对于的任一方差 存在的无偏估计量 , 都有
Var(ˆ) Var( ) , 则称ˆ是 的一致最小方差无偏估计,记为UMVUE.
令θ=p2 , 则
进一步改进:
ˆ1
1 , 0,
x1
1, x2 else
1
为θ的无偏估计.
因为 T
n
xi 是充分统计量
,由定理2,
从而可令
i1 =E(1 | T ) (T ),
(t
故
)=E(ˆ1 | T
= T (T 1)
n(n 1)
n
t), 其中t xi 可得 (t)=
