计数型GRR-KAPPA(MSA第四版-测量系统分析)全公式
测量系统分析MSA手册第四版-测量系统分析msa

对可重复测量系统推荐的实施方法 试验程序范例 计量型测量系统研究- 指南 用于确定稳定性的指南 确定偏倚的指南- 独立样本法 确定偏倚的指南- 控制图法 确定性的指南 确定重复性和再现性的指南 极差法 平均值和极差法 方差分析法(ANOVA)
计数型测量系统研究 风险分析法 信号检查(signal detection)方法 分析方法 其他测量概念和实践 不可重复的测量系统的实践 稳定性研究 变差研究 识别过大的零件内部变差的影响
3
MSA手册第四版
第 E 节 平均值和极差法—额外的处理 第 F 节 量具性能曲线 第 G 节 通过多次读值减少变差 第 H 节 聚焦标准差法计算 GRR 附录 附录 A 方差分析的概念 附录 B
GRR 对能力指数 Cp 的影响 公式 分析 图形分析 附录 C 附录 D 量具 R 研究 附录 E 用误差修正术语替代 PV 计算 附录 F P.I.S.M.O.E.A 误差模型 术语 参考文献 范例表格 索引
第 D 节 测量资源的开发 量具资源选择过程
第 E 节 测量问题 第 F 节 测量不确定度 第 G 节 测量问题分析 第二章 用于评估测量系统的基本概念 第 A 节 背景 第 B 节 选择/开发试验程序 第 C 节 测量系统研究的准备 第 D 节 结果分析
第三章 第A节 第B节
第C节
第四章 第A节 第B节 第C节 第D节
4
MSA手册第四版
第一章 测量系统总指南 第一章---第 A 节 引言、目的及术语
引言
测量数据的使用比以前更多更广泛了。例如,现在是否对制造过程进行调整的决定通常以测 量数据为基础,将测量数据或一些从它们所计算出的统计值,与这一过程的统计控制限 (statistical control limits)相比较,如果该比较过程已超出统计控制,则进行某种调整,否 则,该过程将被允许在没有调整的状态下运行。测量数据的另一个用处是确定在两个或更多 变量之间是否存在显著的相互关系。例如,如果怀疑一个模塑零件上的一个关键尺寸和注射 材料的温度有关。这种可能的关系可以通过采用所谓回归分析的统计方法来研究,即比较关 键尺寸的测量值和注射材料的温度测量值
计数型GRR-KAPPA(MSA第四版-测量系统分析)全公式

计数型GRR-KAPPA(MSA第四版-测量系统分析)全公式380.0%312.5%508.8%0.5
(+0.05/
-0.05)Ppk:0.5
0.77评价⼈A
评价⼈B
评价⼈C
######(苏州)有限公司
#### TECHNOLOGY CO .,LTD GAGE R & R CHART
量规/量仪:尺⼨编号:⼯件机种:测量⼈数:实验次数:样品数量:评定结果:
评估⽇期:统计⼈员:GR&R值:24%
最⼩有效率:最⼤漏失率:最⼤误判率:最⼩KAPPA值:⽬标尺⼨:
变差来源
总检查数
相配数
错误的拒收
错误的接受
不相配
95%UCI
计算所得结果
95%LCI
总检查数
⼀致的数量
95%UCI
计算所得结果
95%LCI
样本:
补充:
kappa⼤于0.75表⽰有很好的⼀致
对于产品控制的情况下,当测量结果与决定准则是确定“符合或不
符合某特性的规范”(如:100%检验或抽样),样品(或标准)必须被选择,但不需要包括整个过程范围。
测量系统的评估是以特性公差为基础(如对公差的%GRR)。
在过程研究情况下,当测量结果与决定准则是确定“过程稳定性、
⽅向以及是否符合⾃然的过程变差”(如:SPC、过程控制、能⼒及过程改进),在整个作业过程范围的样本可获得性变得⾮常重要。
当评估⼀测量系统对过程控制的适⽤性时(如对过程变差
的%GRR),推荐采⽤过程变差的独⽴估计法(过程能⼒研究)。
如果Ppk⼤于1,则将测量系统与过程进⾏⽐较
如果Ppk⼩于1,则将测量系统与公差进⾏⽐较。
超详细MSA测量系统分析讲解

2.线性的分析方法和接受准则
●回顾:
1.什么是线性?
●线性指南
1.在量具的操作范围内,选择g(子组数)≥5个零件 2.检验每个零件,以确定基准值 3.一个人测量每个零件m(子组容量)≥10次 4.计算每次测量的零件偏倚及零件偏倚的平均值。(偏倚i,j=Xi,j -基准值) 5.在线性图上画出单值偏倚和基准的偏倚值 6.计算并画出最佳拟合线和置信带 7.画出“偏倚=0”线,评审该图指出特殊原因和线性的可接受性 (即“偏倚=0”线必须完全在拟合线置信带以内)
MSA
课前思考
1.什么是MSA ? 2.什么时候做MSA? 3.谁做MSA? 4.哪些测量系统需要做MSA? 5.在哪里做MSA? 6.怎么做MSA?原理是什么?
MSA
第一单元
MSA的基本概念
MSA
二.MSA的基本概念
1.测量的定义
●测量:被定义为“对某具体事物赋予数字(或数值),以表示它们 对于特定特性之间的关系”。这定义由C.Eisenhart(1963)首次提出 。赋予数字的过程被定义为测量过程。而数值的指定被定义为测量值 。
3.MSA与FMEA(潜在失效模式及后果分析)
a. FMEA可以用来识别特殊特性,为SPC和MSA确定控制和分析的 对象
b.可以建立测量系统FMEA,管理测量系统的风险
MSA
一.MSA的概述介绍
(二)MSA 与汽车行业五大质量手册
4.MSA与SPC(统计过程控制)
测量系统对适当的数据分析来说是很关键的,在收集过 程数据之前就应很好地对它加以了解。这些测量系统缺少 统计控制,或它们的变差在过程总变差中占很大比例,就 可能做出不恰当的决定。
MSA测量系统分析

风险分析法测量数据表 No:评价次数
Ref:基准值 评价值
风险分析法——Kappa系数的计算方法
➢假设检验分析——交叉表分析法 评价人之间交叉评价,计算Kappa系数,确定评价人之间意见的一致程度。
A-B交叉表
0 A
1
总计
计算 期望的计算 计算 期望的计算 计算 期望的计算
B
0
1
44
6
15.7 34.4
5. 选择类型 6. 选择子组 7. Xbar-R选项 8. 定义检验项
9. 统计 10. 质量工具 11. 能力分析 12. 正态
13. 选择子组 14. 定义公差带
Cpk值判定
稳定性判定和不合格的原因
失控判定规则
✓1点超出控制限 ✓连续9点在基准值的一侧 ✓连续6点上升或下降 ✓连续14点交替上下 ✓连续3点中有2点在2σ线以外 ✓连续5点中有4点在1σ线以外 ✓连续15点在1σ线以内 ✓连续8点中无1点在1σ线以内
5.选择测量值 6.输入参考值 7.输入公差值
测量系统偏倚判定和接受准则
Cg、Cgk VDA要求的检具能 力,判定标准与 Cpk值判定一致, 即Cgk≥1.33则检 具能力满足。
偏倚判定准则
✓P<0.05:偏倚显著,不能接受 ✓P>0.05:偏倚不显著,可以接受
偏倚接受准则
➢|偏倚%|<10%时可接受 ➢10%≤ |偏倚%|≤30%时可接受需改进 ➢|偏倚%|>30%时拒绝接受
1. 统计 2. 质量工具 3. 量具研究
4. 量具R&R研究 (嵌套)
8. 定义公差值
5. 定义部件 6. 定义测量人 7. 定义测量值
GR&R计算结果判定准则
MSA量测系统分析

真值取得之方式: a 使用标准片 b 使用更高级数的量测仪器量测,
实际产品取得真值
c 重复量测产品10次,取其平均值作 为真值
量测仪器实际操作者
1
操作方式
由一位作业者, 使用相同量测 仪器,以常规方 式对每件样本 或标准件量测 ≧10次
实际使用的仪器
1
Agenda:
• MSA概述 • 计量型数据MSA • --偏性 • --线性 • --稳定性 • --GRR • 计数型数据MSA
Process Variation
• Process Variation = 6σ
▲ %Bias = | Bias | Tolerance
X 100 (%Bias due to Tolerance) • Tolerance = USL - LSL
偏性操作
准备项目 样本
操作人员 量测仪器
条件 取已知真值的样本或标准件1pcs
Small Histogram (PQE.STA 16v*345c) Bias y = 298 * 10 * normal (x, -2.115436, 4.422915)
252
234
216
各適當刻度的零件加以量 198 180 162
144
126
108
90
測分析,可決定線性
72 54 36
18
0 <= -20
稳定性操作
准备项目
条件
样本
标准件或实际产品1pcs
操作人员 量测仪器实际操作者
量测仪器 实际使用的仪器
数量
操作方式
1
1. 取一個標準件或實
際產品“定時”量
測3~5次視為一回
2. 密集量測30點(縮
MSA测量系统分析全套表格模板(全公式未加密)
1、2、3、4、5、线性GRR计数型Kappa分析MSA测量系统分析全套表格模板稳定性偏倚Excel原件可在本文档左侧回形针处取出再现性Kappa=(Po-Pe)/(1-Pe)A*参考 交叉表A01总计Po:0.95Pe:0.51B*参考 交叉表B01总计Po:0.97Pe:0.51C*参考 交叉表C01总计Po:0.96Pe:0.5130期望的数量26.4636.5463数量38487期望的数量数量60363一致性好6666Kappa 一致性好判定误发期望的数量638728 4.76%可接受2.30%可接受 4.76%可接受3.45%可接受可接受5.75%可接受01参考总计62063871501C0.90有效性判定重复性检查总数匹配数漏发A A B 评价人评价人%B 93.33%可接受判 定判定0.9383.33%2530 3.17%36.5450.4687数量638715090.00%可接受0.92A C 一致性好150期望的数量B 期望的数量36.9651.0488数量6387150期望的数量26.0435.9662数量38588期望的数量6387数量60248.7284150数量6387150期望的数量35.28数量28284总计01Kappa 判 定A*B 0.89一致性好C 3027A*C 0.93一致性好参考B*C 参考总计可接受期望的数量27.7238.280.90一致性好数量615Page 11 of 11。
MSA GRR计算公式

MSA GRR计算公式
MSAGRR是一种用于衡量测量系统可靠性的方法。
GRR代表了GaugeRepeatabilityandReproducibility,即重复性和再现性。
MSA GRR计算公式是一种用于计算GRR的公式,它可以帮助我们了解测量系统的精度和可靠性。
MSA GRR计算公式包括以下几个要素:
1.测量系统误差:包括重复性误差和再现性误差。
重复性误差是指在相同条件下,同一测量员使用同一测量工具进行多次测量时,所得结果的差异。
再现性误差是指在不同条件下,不同测量员使用同一测量工具进行测量时,所得结果的差异。
2.零件离散程度:用于衡量被测零件的离散程度,其值越大表示测量系统所测量的零件变化范围越大。
3.相对扩大误差(%R&R):用于计算测量系统的可靠性,其值越小表示测量系统越可靠。
MSA GRR计算公式为:
%R&R = (GRR/总变差)× 100%
其中,GRR = 2.5 ×(测量系统误差/零件离散程度)
总变差 = 6 ×(测量系统误差/零件离散程度)
通过这个公式,我们可以计算出测量系统的可靠性水平,以便进行必要的改进和优化。
在实际运用中,我们应该根据实际情况选择合适的数据采集方法和样本数量,以尽可能减小误差和提高测量系统的可靠性。
测量系统分析MSA手册第四版

● 均一性
√ 整个正常操作范围内重复性的变化 √ 重复性的同义词
6
MSA手册第四版
测量系统必须稳 定和一致 标准和可追溯性
国家测量协会 (NMI)
可追溯性(Traceability)
系统变差(system variation)
测量系统变差可以分类为: ● 能力(capability)
√ 短期获取读数的变异性
如果交互作用产生变差过大,那么数据的质量会很低,从而造成测量数据无法利用。例如, 一个具有大量变差的测量系统,在分析制造过程中使用是不适合的,因为测量系统变差可能 会掩盖制造过程的变差。管理一个测量系统的许多工作是监视和控制变差。其它的还需要把 重点集中在了解测量系统与其环境有什么样的相互作用,以便获得可接受质量的数据。 目的
表征数据质量最通用的统计特性是测量系统的偏倚和方差。所谓偏倚的特性,是指数据相对 参考(基准)值的位置,而被称为变差的特性是指数据的分布宽度。
低质量数据最普通的原因之一是变差太大。一组数据中的变差多是由于测量系统及其环境相
4
MSA手册第四版
互作用造成的。例如,一个用来测量一罐液体容积的测量系统,可能对该测量系统所处的环 境中的大气温度较敏感。在这种情况下,数据的变差可能是因为环境温度变化造成的。因此, 对测量的数据很难解释,因此,该测量系统不尽理想。
基本的设备(basic equipment)
● 分辨力(discrimination)、可读性(readability)、解 析度(resolution)
√ 别名:最小可读单位、测量解析度、最小刻度 极限、或探测的最小极限
√ 由设计所确定的固有特性 √ 一个测量仪器或输出的最小刻度单位 √ 通常被显示为测量单位 √ 10:1 的比例法则 ● 有效解析度(effective resolution) √ 特定应用条件下,一个测量系统对过程变差的
MSA GRR第四版计算方法
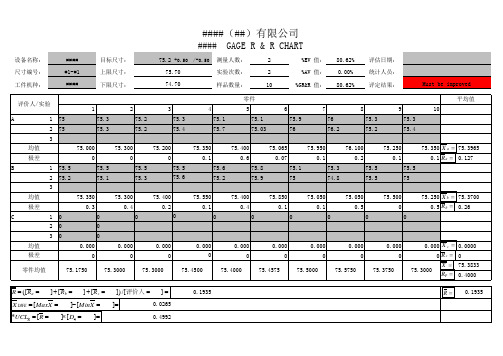
K1 0.8862 0.5908
K2 0.7071 0.5231
K3 0.7071 0.5231 0.4467 0.4030 0.3742 0.3534 0.3375 0.3249 0.3146
75.5750
75.3750
75.3000 X 75.3833 RP 0.4000
R ([Ra ___] [Rb ___] [Rc ___]) /[评价人 ___]
X DIFE [MaxX ___][MinX ___]
0.0265
*UCLR [R ___][D4 ___]
####(##)有限公司
#### GAGE R & R CHART
设备名称: 尺寸编号: 工件机种:
#### #1-#1 ####
目标尺寸: 上限尺寸: 下限尺寸:
75.2 +0.50 /-0.50 测量人数:
2
75.70
实验次数:
2
74.70
样品数量:
10
%EV 值: %AV 值: %GR&R 值:
80.62% 0.00% 80.62%
评估日期: 统计人员: 评定结果:
Must be improved
评价人/实验
A
1
2
3
均值
极差
B
1
2
3
均值
极差
C
1
2
3
均值
极差
零件均值
零件
平均值
1
2
3
4
5
6
7
8
9
10
75
75.3
75.2
75.3
75.1
计数型测量系统分析KAPPA报告(MSA第四版)

>30% 被认为是不可接受的。
补充:
kappa大于0.75表示有很好的一致 如果Ppk大于1,则将测量系统与过程进行比 较 如果Ppk小于1,则将测量系统与公差进行比 较
总检查数 相配数 错误的拒 收错误的接 受 不相配 95%UCI 计算所得 结果 95%LCI
总检查数 一致的数 量 95%UCI 计算所得 结果 95%LCI
0
1
1
0
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
0
1
1
1
1
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
A、基准
A
0
MSA GRR计算公式

MSA GRR计算公式为了确保产品质量的稳定性和一致性,制造业在生产过程中常常需要进行测量系统分析(Measurement System Analysis,简称MSA)。
而在MSA中,GRR(Gauge Repeatability and Reproducibility)是一种常用的计算方法,用来评估测量系统的可靠性和准确性。
GRR计算公式是通过分析测量数据的方差来评估测量系统的误差来源,包括重复性误差和再现性误差。
重复性误差是由同一操作者在相同条件下重复测量同一样本时引起的误差,而再现性误差是由不同操作者在相同条件下测量同一样本时引起的误差。
GRR计算公式如下:GRR = √(MSR - MSE)其中,MSR代表测量系统的方差,而MSE代表测量误差的方差。
在实际应用中,我们通常需要收集一组测量数据来进行GRR计算。
首先,选择一组合适的样本,确保样本能够代表整个生产过程中的变异性。
然后,选择一定数量的操作者和重复测量次数,以模拟实际生产环境中的操作情况。
接下来,我们需要计算重复性误差和再现性误差的方差。
通过统计分析方法,我们可以得到测量系统的方差MSR和测量误差的方差MSE。
最后,将这两个方差代入GRR计算公式中,即可得到GRR的值。
GRR的结果通常以百分比的形式表示,表示测量系统的误差占总变异性的比例。
一般来说,GRR值越小,说明测量系统的误差越小,可靠性和准确性越高。
在实际应用中,我们可以根据GRR的结果来评估测量系统的可接受性。
通常情况下,GRR值小于10%被认为是可接受的,而大于10%则需要进一步分析和改进测量系统。
除了GRR计算公式外,还有其他一些衍生的计算方法,如Gauge R&R Study和ANOVA方法。
这些方法在实际应用中可以根据具体情况选择使用,以评估和改进测量系统的性能。
总结起来,MSA GRR计算公式是一种常用的评估测量系统可靠性和准确性的方法。
通过分析测量数据的方差,我们可以得到测量系统的误差来源,并评估其可接受性。
MSA计量型测量系统分析GRR表格(全公式自动生成未加密)

331012345678910Total 1.A 10.29-0.56 1.340.47-0.80.020.59-0.31 2.26-1.36 1.942.20.41-0.681.170.5-0.92-0.110.75-0.21.99-1.251.663.30.64-0.58 1.270.64-0.84-0.210.66-0.17 2.01-1.31 2.114.均值Mean0.44667-0.60667 1.260000.53667-0.85333-0.100000.66667-0.22667 2.08667-1.306670.190333Sum A 1.34-1.82 3.78 1.61-2.56-0.32-0.68 6.26-3.92 5.71005. 极差Rang0.350.120.170.170.120.230.160.140.270.110.1840006.B 10.08-0.47 1.190.01-0.56-0.20.47-0.63 1.8-1.680.017.20.25-1.220.941.03-1.20.220.550.082.12-1.6211.3048.30.07-0.68 1.340.2-1.280.060.83-0.34 2.19-1.50.899.均值Mean0.13333-0.79000 1.156670.41333-1.013330.026670.61667-0.29667 2.03667-1.600000.068333Sum B0.4-2.37 3.47 1.24-3.040.08 1.85-0.89 6.11-4.8 2.050010. 极差Rang0.180.750.4 1.020.720.420.360.710.390.180.51300011.C 10.04-1.380.880.14-1.46-0.290.02-0.46 1.77-1.49-2.2312.2-0.11-1.131.090.2-1.07-0.670.01-0.56 1.45-1.77-2.5613.3-0.15-0.960.670.11-1.45-0.490.21-0.491.87-2.16-2.8414.均值Mean-0.07333-1.156670.880000.15000-1.32667-0.483330.08000-0.50333 1.69667-1.80667-0.254333Sum C -0.22-3.47 2.640.45-3.98-1.450.24-1.515.09-5.42-7.6315. 极差Rang0.19000.42000.42000.09000.39000.38000.20000.10000.42000.67000.3280000.168889-0.851111.0988890.366667-1.06444-0.185550.454444-0.34222 1.940000-1.571110.0014441.520000-7.660009.890000 3.300000-9.58000-1.67000 4.090000-3.0800017.460000-14.14000.13 3.5111110.34166723D4 3.27 2.5750.3509690.879792D300-0.348080.00000A2 1.88 1.02312345678910UCLx0.35100.35100.35100.35100.35100.35100.35100.35100.35100.3510LCLx-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481UCL R 0.87980.87980.87980.87980.87980.87980.87980.87980.87980.8798LCL R0.00000.00000.00000.00000.00000.00000.00000.00000.00000.0000公差:6σpp变差PV PV 1.104596PV TVTV#DIV/0!TV基于公差base%#DIV/0!基于零件变差%#DIV/0!基于过程变差%#DIV/0!基于过程能力%#DIV/0!公式A Formulandc 5.0936924公式B FormulaX^2/nkr 0.0001878 3.167450088.362122291.88836694.647300Source DF SS MS F P Source DF SS MS F PParts 988.361939.81799492.291420.00000988.361939.81799245.610.000002 3.16726 1.5836379.406050.000002 3.16726 1.5836339.6170.00000180.358980.019940.433720.9741160 2.758930.0459878 3.117920.03997Total 8994.647118994.64711Source VarComp Stdev %Contribu %TV %Toleranc Source VarComp Stdev %Contribut %TV%Tolerance 0.098110.313228.27%28.75%#DIV/0!0.091430.302377.76%27.86%#DIV/0!0.045980.21443 3.87%19.68%#DIV/0!0.039970.19993 3.39%18.42%#DIV/0!0.052120.22830 4.39%20.96%#DIV/0!0.051460.22684 4.37%20.90%#DIV/0!0.052120.22830 4.39%20.96%#DIV/0!0.051460.22684 4.37%20.90%#DIV/0!0.000000.000000.00%0.00%#DIV/0!1.08867 1.0433991.73%95.78%#DIV/0! 1.08645 1.0423392.24%96.04%#DIV/0!Reproducibility Reproducibility Operator Operator Operators*Part 极差图Range chartSUMSQ(sum(men-part))/r sumSQ(all)n=part k=men ANOVA Table With Operator*Part Interaction ANOVA Table Without Operator*Part InteractionParts Operators Gauge R&R With Operator*Part Interaction Gauge R&R Without Operator*Part InteractionTotal Gauge R&R Total Gauge R&R Repeatability Repeatability Operators Operators*Part Repeatability Repeatability Total Part - To - Part Part - To - Part 注:当分析结果超出要求后,利用均值极差图分析原因When analysis result is out of spec,need analyse the root cause by mean and range chart 。
MSA计数测量系统分析KAPPA表
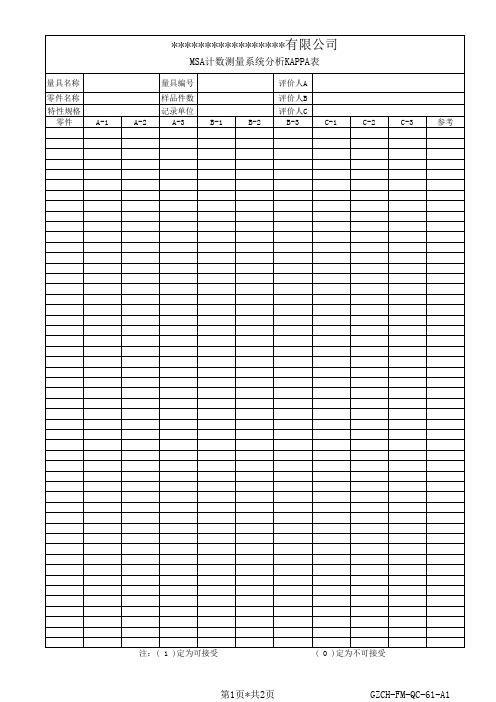
A*B交 叉表
A 0.00 数量 期望的数量
1.00 数量
总
期望的数量
计
数量
期望的数量
A*C交 叉表
A 0.00
1.00 总 计
A*参 考交
数量 期望的数量 数量 期望的数量 数量 期望的数量
A 0.00
1.00 总 计
C*参 考交
数量 期望的数量 数量 期望的数量 数量 期望的数量
C 0.00
1.00 总 计
0 0.0 150 150.0
参考 0.00
150 150.0
0 0.0 150 150.0
1.00 0
0.0 0
0.0 0
0.0
1.00 0
0.0 0
0.0 0
0.0
总计
150 150.0
0 0.0 150 150.0
kappa 结论:
B*参 考交
总计
150 150.0
0 0.0 150 150.0
判断测量系统 评价人可接受的条件 件, 评可价能人需不要可改接进受的条 件, 需要改进
有效性 ≥90% ≥80%
<80%
错误率 ≤2%
≤5%
错误警报 率
≤5%
≤10%
>5%
>10%
检测者 Op
制表者 Pe
可接受
□
日期 Date
批准 Ap
不可接受 □
日期 Date
日期 Date
第2页*共2页
GZCH-FM-QC-61-A1
*****************有限公司
MSA计数测量系统分析KAPPA表
量具名称
量具编号
评价人A
零件名称
MSA第四版讲议

时间1
稳定性 时间2
什么是MSA?
可利用平均值—极差控制图来研究稳定性
1
0.9
0.8
0.7
0.6
0.5
0.4 1
0.12 0.11
0.1 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01
0 1
Xbar chart by Operator
UCL 0.88 CL 0.807 LCL 0.735
量具(Gage) 人(People) 测量技术(Measurement Technique) 测量程序(Measurement Procedure) 软件(Software) 环境(Environment) 其它因素(Other Factors)
什么是MSA?
测量系统的分辨率的意义:
2
3
R chart by Operator UCL 0.125
CL 0.038
LCL 0
2
3
什么是MSA?
平均值失控表示:系统不再正确地测量(偏倚已经 改变) 可能的原因:需要校准等
极差图失控表示:不稳定的重复性 可能的原因:部件松动、气路堵塞、电压变化等
量具稳定性分析
量具稳定性工作指南
1.使用在偏倚和线性分析中作为样件的基准/标准件
测量系统的接受准则
偏倚:测量结果的观测平均值与基准值的差值(也 叫准确度);
基
准
值
偏倚
观测的平均值
什么是MSA?
偏倚较大,可能的原因:
标准或基准值误差;检验校准程序 仪器磨损; 维护或修理 制造的仪器尺寸不对; 仪器测量了错误的特性; 仪器校准不当; 复查校准方法 评价人员使用仪器不当; 复查检验说明书 仪器修正计算不正确
MSA计数型大样法分析 公式自动计算
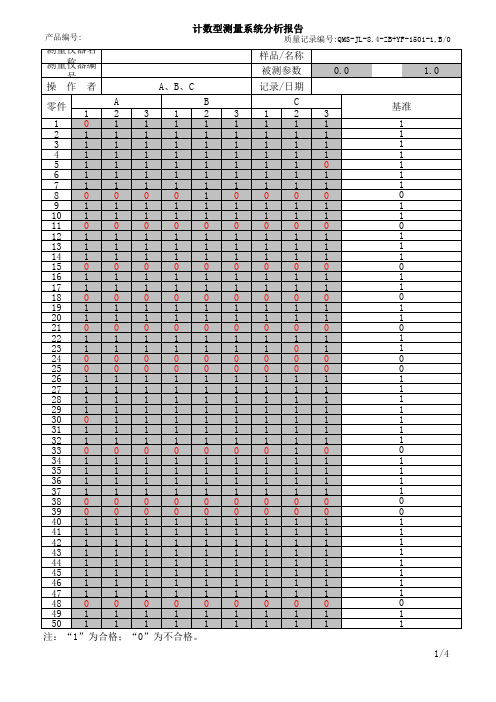
40 1 1 1 1 1 1 1 1 1
41 1 1 1 1 1 1 1 1 1
42 1 1 1 1 1 1 1 1 1
43 1 1 1 1 1 1 1 1 1
44 1 1 1 1 1 1 1 1 1
45 1 1 1 1 1 1 1 1 1
46 1 1 1 1 1 1 1 1 1
47 1 1 1 1 1 1 1 1 1
C
0.00
1.00
A
0.00
计算
32
3
期望的计算
7.9
27.1
1.00
计算
2
113
期望的计算
26.1
88.9
计算
34
116
总计
期望的计算
34.0
116.0
B 与 C 交叉表
C
0.00
1.00
B
0.00
计算
31
1
期望的计算
7.3
24.7
1.00
计算
3
115
期望的计算
26.7
91.3
计算
34
116
总计
期望的计算
计数型测量系统分析报告
质量记录编号:QMS-JL-8.4-ZB+YF-1501-1,B/0
测量系统有效性分析
来源 总受检数
符合数 有效率
%评价人
(评价人自己在所有试验上一致)
A
B
C
50
50
50
48
49
47
96.0%
98.0%
94.0%
得分与计数
(评价人所有试验上与基准一致)
A
B
C
GRR讲解及分析公式【精选】

C
XC2 XC21 XC22 XC23
XC3 XC31 XC32 XC33
XC24
XC34
XC25
XC35
XC26
XC36
XC27
XC37
XC28
XC38
XC29
XC39
XC2A
XC3A
XCbar
RC RC1 RC2 RC3
RC4
RC5 RC6 RC7 RC8 RC9 RCA RCbar
分析方法
计算公式 XAbar=(XA11+ XA12 +…+ XA3A)/30 XBbar=(XB11+ XB12 +…+ XB3A)/30 XCbar=(XC11+ XC12 +…+ XC3A)/30 Xbardiff=MAX(XAbar, XBbar, XCbar )-MIN (XAbar, XBbar, XCbar ) RAbar=(RA1 + RA2 + …+RAA )/10 RBbar=(RB1 + RB2 + …+RBB )/10 RCbar=(RC1 + RC2 + …+RCC )/10 Rbar=(RAbar + RBbar + RCbar ) /3
当评价人变异(%AV)为主要变异点时, 一般采取以下措施:
1、对检查员进行使用与判读培训 。 2、重新检讨检查作业方法。 3、测量仪器(设备)刻度盘的刻度不够清
晰,更换更容易分辩的刻度盘。 4、检讨环境等因素对测量仪器(设备)稳
定性的影响。
应用实例
某公司在加工一个新产品时,拟作测量系 统分析,随机抽取10个样本,用游标卡尺 进行测量,由3个检查员测试,每个零件测 3次,其测试结果列于表1,其Gage R&R 分析结果列于表2。
MSA

MSA(测量系统分析)和SPC(统计过程控制)的运用及注意事项
一、先后顺序(在APQP 和PPAP中)
1、在制作运用时应先进行MSA(测量系统分析)。
(第一步)
2、再进行SPC(统计过程控制)过程能力研究。
(第二步)
二、MSA和SPC所包含的内容:
1、MSA(测量系统分析):计量型(GRR)双R值
计数型(Kappa)
2、SPC(统计过程控制):过程能力研究
三、数据要求:
MSA(测量系统分析)
R&R(GRR)值:测量系统的%GRR小于10%,ndc大于等于5,符合使用要求。
Kappa分析要求:Kappa值保证在0.75以上,低于0.4表示不能接受。
SPC(统计过程控制)
过程能力要求中CPK应保证在1.33以上、PPK应保证在1.67以上。
四、何情况下应进行分析和控制
1、当过程、测量系统不稳定时。
2、有新品开发时(APQP和PPAP阶段)。
3、当有新购置的量检具时。
4、当客户要求时。
五、如果进行测量系统分析时,应依据《控制计划》所出现的(尺
寸/内在质量/材料成分等进行检查)监视测量设备进行系统分析,如是品质部内部测量系统分析也可是非汽车件,但最好是汽车件识别出的关键尺寸进行检。
测量系统分析MSA手册第四版

上受控状态 √ 别名:漂移(drift)
● 线性(linearity)
√ 在量具正常工作量程内的偏倚变化量 √ 多个独立的偏倚误差在量具工作量程内的关系
√ 是测量系统的系统误差所构成
宽度变差(width variation)
● 精密度 2(precision)
表征数据质量最通用的统计特性是测量系统的偏倚和方差。所谓偏倚的特性,是指数据相对 参考(基准)值的位置,而被称为变差的特性是指数据的分布宽度。
低质量数据最普通的原因之一是变差太大。一组数据中的变差多是由于测量系统及其环境相
4
MSA手册第四版
互作用造成的。例如,一个用来测量一罐液体容积的测量系统,可能对该测量系统所处的环 境中的大气温度较敏感。在这种情况下,数据的变差可能是因为环境温度变化造成的。因此, 对测量的数据很难解释,因此,该测量系统不尽理想。
术语 如果不建立一套术语来引述共同的统计特征和相关的测量系统要项,那么讨论测量系统的分 析可能会造成混淆和误解。本节将用于本手册的术语汇总如下。
在本手册中使用了以下术语:
● 测量被定义为“对某具体事物赋予数字(或数值),以表示它们对于特定特性之间 的关系。这个定义由C.Eisenhart(1963)首次提出。赋予数字的过程被定义为测量过程, 而数值的指定被定义为测量值。
√ 每个重复读数之间的“接近”程度 √ 是测量系统的随机误差所构成
● 重复性
√ 一个评价人多次使用一件测量仪器,对同 一零件的某一特性进行多次测量下的变差
√ 是在固定和已定义的测量条件下,连续(短期) 多次测量中的变差
√ 通常指 E.V.-设备变差(equipment variation) √ 设备(量具)能力或潜能 √ 系统内部变差
计数型GRR KAPPA MSA第四版 测量系统分析

3
80.0%312.5%508.8%0.5
(+0.05/-0.05)Ppk:
0.5
0.77评价人A
评价人B
评价人C
最小KAPPA值:目标尺寸:
评估日期:统计人员:GR&R值:24%
测量人数:实验次数:样品数量:
评定结果:
最小有效率:最大漏失率:最大误判率:量规/量仪:尺寸编号:工件机种:公司
#### TECHNOLOGY CO .,LTD GAGE R & R CHART
变差来
源
总检查
数
相配数
错误的
拒收
错误的
接受
不相配
95%UCI
计算所
得结果
95%LCI
总检查
数
一致的
数量
95%UCI
计算所
得结果
95%LCI
样本:
补充:
kappa大于0.75表示有很好的一致
对于产品控制的情况下,当测量结果与决定准则是确定“符合或不符
合某特性的规范”(如:100%检验或抽样),样品(或标准)必须被
选择,但不需要包括整个过程范围。
测量系统的评估是以特性公差为
基础(如对公差的%GRR)。
在过程研究情况下,当测量结果与决定准则是确定“过程稳定性、方
向以及是否符合自然的过程变差”(如:SPC、过程控制、能力及过
程改进),在整个作业过程范围的样本可获得性变得非常重要。
当评
估一测量系统对过程控制的适用性时(如对过程变差的%GRR),推荐
采用过程变差的独立估计法(过程能力研究)。
如果Ppk大于1,则将测量系统与过程进行比
如果Ppk小于1,则将测量系统与公差进行比。
MSA.第四版

偏倚
观测平均值
基准值
11
上海伟众汽车科技有限公司
三、对测量系统分析要分析什么
10
稳定性(位置变差) :别名:漂移。是测量系统在某个 持续时间内,测量同一基准或零件的单一特性时获得的测量 总变差。换句话说。稳定性是随时间变化的偏倚值。
偏倚3 偏倚2 偏倚1 时间
参考值
12
上海伟众汽车科技有限公司
三、对测量系统分析要分析什么
11 线性(位置变差) : 就是量具在正常工作量程内的偏倚变化量; 是多个独立的偏倚误差在量具工作量程内的关系。
偏倚2 偏倚1 无偏 倚
观测的平 均值
基准 值
值1
值N
13
上海伟众汽车科技有限公司
三、对测量系统分析要分析什么
12
重复性EV (宽度变差) :是由一个评价人,采用同一 种测量仪器,在固定的和已定义的测量条件下,连续(短期 内)多次测量同一零件的同一特性时获得的测量变差。 我们可以把重复性看作设备变差:它是设备本身固有的变差 或性能——仪器的变差,是从规定的测量条件下连续试验得 到的普通原因变差。
生产用量具的变差
观察过程的变差 σ2 观 =σ2实 +σ2测 由于变差源的作用结果 式中: σ2观: 观测到的过程标准差 σ2实:实际的过程(零件)标准差 σ2测: 测量系统标准差
因此: σ2 观 >σ2实
为此,我们要对测量系统进行分析,要识别测量系统的普通原因和特殊原 因,以便采取决策措施,使测量系统的变差减小到最小程度,使得测量系 统观测到的过程变差值尽可能接近和真实地反映过程的变差。这就要求, 测量系统的最大(最坏)的变差必须小于过程变差或规范公差。
评价人A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9
预期 16.3 34.7
计数
6 93
预期 31.7 67.3
计数 48 102
预期 48.0 102.0
合计
51 51.0
99 99.0 150 150.0
Kappa A B C
基准
A — 0.86 0.78 0.88
B 0.86
— 0.79 0.92
C 0.78 0.79
— 0.77
有效率 漏失率 误判率 A 84.0% 6.3% 4.9% B 90.0% 6.3% 2.0% C 80.0% 12.5% 8.8%
预期 16.0
计数
9
预期 35.0
计数 51
预期 51.0
合计 1
5 47 31.0 47.0
94 103 68.0 103.0
99 150 99.0 150.0
B
0
1
合计
B、基准-交叉表
基准
0
1
计数 45
2
预期 15.0 32.0
计数
3 100
预期 33.0 70.0
计数 48 102
预期 48.0 102.0
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
1
0
0
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
1
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
0
0
1
0
1
1
0
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
0
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
######(苏州)有限公司
#### TECHNOLOGY CO .,LTD GAGE R & R CHART
量规/量仪:
测量人数: 3 最小有效率: 80.0% 评估日期:
尺寸编号:
实验次数: 3 最大漏失率: 12.5% 统计人员:
工件机种:
样品数量: 50 最大误判率: 8.8%
GR&R值:
24%
0
31
1
32
1
33
1
34
0
35
1
36
1
37
0
38
1
39
0
40
141Biblioteka 142043
1
44
1
45
0
46
1
47
1
48
0
49
1
50
0
A-2 A-3 B-1 B-2 B-3 C-1 C-2 C-3 基准
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
1
0
1
0
0
1
1
目标尺寸: 0.5 (+0.05/ -0.05) Ppk: 0.5 最小KAPPA值: 0.77
评定结果:
评价人A
评价人B
评价人C
零件 A-1
1
1
2
1
3
0
4
0
5
0
6
1
7
1
8
1
9
0
10
1
11
1
12
0
13
1
14
1
15
1
16
1
17
1
18
1
19
1
20
1
21
1
22
0
23
1
24
1
25
0
26
0
27
1
28
1
29
1
30
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
基准值 0.476901 0.509015 0.576459 0.566152 0.57036 0.544951 0.465454 0.502295 0.437817 0.515573 0.488905 0.559918 0.542704 0.454518 0.517377 0.531939 0.519694 0.484167 0.520496 0.477236 0.45231 0.545604 0.529065 0.514192 0.599581 0.547204 0.502436 0.521642 0.523754 0.561457 0.503091 0.50585 0.487613 0.449696 0.498698 0.543077 0.409238 0.488184 0.427687 0.501132 0.513779 0.566575 0.46241 0.470832 0.412453 0.493441 0.486379 0.587893 0.483803 0.446697
代码 + + × × + + + × + × + + + + + + × × + + × + + + × + + + × + × + + + × + + + + -
A
0
1
合计
A、B-交叉表
B
0
计数 44
预期 15.7
