数字化信息编码与数制转换
数制与编码

第一章数制与编码1.1 数制数制是计数的方法,通常采用进位计数制。
在进位计数制的多位编码中,数制是:⏹ 每一位的构成方法,以及⏹ 从低位到高位的进位规则。
常用的数制:⏹ 二进制(Binary )、 ⏹ 八进制(Octal )、 ⏹ 十进制(Decimal )、 ⏹ 十六进制(Hex-decimal )。
例如:十进制:⏹ 每一位——十进制数由0~9个数字符号(数码)和小数点组成, ⏹进位规则——“逢十进一”(基数为10)。
1.1.1 记数法和分析方法记数法——位置记数法, 分析方法——按权展开式。
例如:十进制数(652.5)10=6×102+5×101+2×100+5×10-1左边为“位置记数法”,右边为“按权展开式”。
代数式为:∑⨯=iiikD 10说明:每一个数位上的数码有不同的权值, ⏹ 权值从左到右以基数的幂次由大到小, ⏹ 数位从左到右由高位到低位排列。
例如:二进制数(101.11)2 = 1×22+0×21+1×20+1×2-1+1×2-2任意进制(基数为R )记数法:∑--=----==110121).()(n mi iiR m n n R R kk k k k k k D八进制和十六进制的按权展开式以此类推。
位置记数法 按权展开式1.1.2 数制转换数值相等,记数方法(数值)不同的数之间的转换。
数制转换的本质是——权值的转换。
1.1.2.1 任意进制到十进制的转换利用任意进制数的按权展开式,可以将一个任意进制数转换成等值的十进制数。
例如:(1011.01)2 =1×23+0×22+1×21+1×20+0×2-1+1×2-2=(11.25)10例如:(8FA.C)16=8×162+F ×161+A ×160+C ×16-1=2048+240+10+0.75=(2298.75)101.1.2.2 “十 二”进制转换考查整数部分,数的二进制按权展开式:设:(D )10可以由n 位二进制数表示,即 (D )10=(k n -1k n -2,…,k 1k 0)2 存在:(D )10=k n -1×2n -1+k n -2×2n -2+…+k 1×21+k 0×20 (D )10/2= k n -1×2n -2+k n -2×2n -3+…+k 1×20 + k 0 / 2((D )10/2商的整数部分)/2= k n -1×2n -3+k n -2×2n -4+…+k 2×20 + k 1 / 2“孤立”余数后,整数的商再除以基数2,依次类推;余数依次为从低到高位的二进制数位。
数制的转换与编码

数制的转换十进制数和二进制,八进制,十六进制数的转换。
1将二进制,八进制,十六进制数转换为10进制数。
用对应的数位的值乘以进制的权值,然后累加。
(前面讲过)2 将十进制数转换为二进制,八进制,十六进制数。
将十进制数除以对应的进制,取其余数,然后逆序陈列即可。
(辗转相除法)例如将十进制数194进行转换成二进制。
194除以2得到97余097除以2得到48 余148除以2 得到24 余024除以2 得到12 余012除以2 得到6 余06除以2得到3 余03除以 2 得到1 余 11除以2 得到0 余1 逆序即可得到11000010同理可以得到八进制数为302Q可以得到十六进制数位D2H上面讲述的都是针对整数的情况,非整数,也可以用同样的方法,只是把除变为乘,逆序变为正序即可,可以根据精确到的位数求对应的进制数。
如将十进制234.56转换为2进制,精确到小数点后第5位小数点前面可以同上,对于小数点后用0.56*2(二进制)若是八进制则乘以8,十六进制则乘以16(这里转换为2进制为例)得到1.12取整数部分1 余下0.12用0.12乘以 2 得到0.24取整数部分0用0.24乘以 2得到 0.48取整数部分为0用0.48乘以 2得到 0.96取整数部分为 0用0.96乘以 2得到 1.92取整数部分为 1用0.92乘以 2得到 1.84取整数部分为 1…所以结果为 11101010.10001。
3 将十六进制,八进制,转换成二进制的转换。
①十六进制数是四位二进制数,将八进制数是三位二进制数。
将十六进制数转换为二进制,只需用四位二进制表示十六进制的一个数,例如0用0000表示,1用0001表示,2用0010表示,…A用1010表示,B用1011表示,C 用1100表示,D用1101表示,E用1110表示,F用1111表示。
(0—15)如12FB3H用二进制表示为0001 0010 1111 1011 0011同理八进制的数也可以表示(0—7)如将13507Q转换为二进制001 011 110 000 111②将二进制转换成为八进制,十六进制,只需将二进制数进行三位(八进制),四位(十六进制)划分即可例如1101011000111010 转换成八进制先划分从低位开始划分不够位数的补01/ 101/ 011/ 000/ 111/ 010补0为001/ 101/ 011/ 000/ 111/ 010变换成八进制的数即为153072Q同理转换成十六进制的数为1101/0110/0011/1010 转换成十六进制的数字即为D63AH4 将十六进制数转换为八进制的转换。
计算机《数制和编码进制转换》公开课教案设计

数制与编码——进制变换【学情剖析】本课内容是在学生已经学习了计算机发展与应用、计算机系统的组成等知识的基础长进行,已经初步知道了人与计算机进行信息互换往常使用程序设计语言,程序设计语言经历了三个阶段:机器语言、汇编语言和高级语言。
机器语言是机器指令序列,是一串 0 和 1 构成的二进制编码,是独一能被计算机识其余语言。
那么要认识计算机是怎样将我们发出的信息变换成数字编码以前,我们一定先认识掌握各样数制及互相间的变换。
这节课内容许多,学生理解起来比较困难,依据讲堂需要和学生特色,既要让学生有信心、热忱地学习新知识,又要让他们主动踊跃地参加到整个教课活动中来。
【课时安排】 2 课时【讲课形式】讲解、多媒体教课【教课方法】讲解法、练习法、问答法、演示法【教课器具】计算机、黑板、多媒体、课件【教课目的】知识目标 : 1、认识数制、基、基数及位权的观点;2、掌握二进制、十进制、八进制、十六进制的表示方法;3、掌握二进制与十进制间互相变换的方法。
技术目标 : 1、培育学生逻辑运算能力;2、培育学生剖析问题、解决问题的能力;3、培育学生独立思虑问题的能力。
感情目标:经过数制变换的学习培育学生的计算机科学修养 , 同时,让学生领会到仔细的学习态度,谨慎仔细的学习习惯。
【教课要点】1、进制、基数、位权的观点。
2、二进制与十进制间互相变换方法。
【教课难点】二进制与十进制间互相变换【教课过程】一、师生问好,考勤二、复习旧识,导入新课(以下教师的语言、活动简称“师” ,学生的活动简称“生” )前引入:师:我想大家做一道算:110+110= ?(学生几乎都回答等于220)。
师:那么 220 个答案是不呢?能够,也能够不。
在学本以前,回答220 是正确的,但是,在我学完今日的知后,答案就不一是220了。
什么呢?( 设疑,学生思虑,教师点名个别学生回答)师:到数字,有好多同学可能会的很可笑,不就是1234⋯⋯是的,在生活中,我用的一般都是十制。
数字电路_2数制和编码

? 区位码——GB 2312的所有字符分布在一个94行×94列的二维平面内,行号称为区号,列号称 为位号。区号和位号的组合就可以作为汉字字符的编码,称为汉字的区位码。
加法
减法
十六进制
? 由于二进制数在使用时位数太长,不容易记忆,所以又推出了十六进制数。 ? 十六进制数有两个基本特点:
? 它由十六个字符 0~9以及A,B,C,D,E,F组成(它们分别表示十进制数 10~15);
? 十六进制数运算规律是逢十六进一,即基 R=16=2 4,通常在表示时用尾部标志 H或下标 16以示区别。 例如:十六进制数 4AC8可写成( 4AC8 )16,或写成 4AC8H 。
B表示。 例如:二进制数 10110011 可以写成( 10110011 )2,或写成 10110011B ? 对于十进制数可以不加注基数;
十进制
(D) 0 1 2 3 4
56
7
8
9 10
二进制 (B) 0 1 10 11 100 101 110 111 1000 1001 1010
计算机采用二进制数
(101.11)B= 1×22 +0×21+1×20+1×2-1+1×2-2 =(5.75)D
各数位的权是2的幂
十进制数 →二进制数 将整数部分和小数部分分别进行转换。
整数部分 ---除2取余,逆序排列 ; 合并
小数部分 ---乘2取整,顺序排列。
? 十进制数 44.375 转换成二进制等于多少?
(44.375)D=(?)B
十六进制数 →二进制数
? 十六进制数转换为二进制数时正好与上面所述相反,只要将每位的十六进制数对应的 4 位二进制写出来就行了。
计算机中的数制及其编码

一、计算机中的数制及其转换
2. 数制之间的转换
(4) 二、十六进制之间的转换
二进制十六进制: 以小数点为界,分别向左、向右四位一组分段,不足四位 补0(整部在前,小数部分在后),然后将每段换成对应的十 六进制数码。 十六进制二进制: 将每位十六进制数码换成对应的四位二进制数,然后去前 后无效的0。 例7 (10110101.10101011)2 =(1011 0101. 1010 1011)2 =(B5.AB)16 (56A.C4)16 =(0101 0110 1010. 1100 0100)2
一、计算机中的数制及其转换
2. 数制之间的转换
(2) 十进制数转换为非十进制数
例4 (123.45)10 =(? 2 123……..1 2 61…….1 2 30……0 2 15…...1 2 7…..1 2 3…..1 2 1….1 0 )2 低位
0
1
高位
除 到 商 为 0 时 停 止
1
1 0 0 1
一、计算机中的数制及其转换
2. 数制之间的转换
(1) 非十进制数转换为十进制数
例2:(345.67)8 = 3*82 + 4*81 + 5*80 + 6*8-1 + 7*8-2 = 192 + 32 + 5 + 0.75 + 0.109375 = (229.859375)10
例3: (2FA.D)16 = 2*162 + 15*161 + 10*160 + 13*16-1 = 512 + 240 + 10 + 0.8125 = (762.8125)10
+101.0001 1111.0001 10.1 ×100 000 000 +101 10100 101.0001 11001.0101 101 101 101
第二讲(数制转换与码制)

将(376.4)8转换为十进制数。
1
3 64 7 8 6 1 4 0 . 125 ( 254 . 5 ) 10
将(3AB.11)16转换为十进制数。
( 3 AB . 11 ) 16 3 16 10 16 11 16 1 16
3 2 1 0
将(207)8转换为十进制数。
( 207 ) 8 2 8
2
08 78
1
0
2 64 7 1
135
将(7F)16转换为十进制数
1 0 ( 7 F ) 16 7 16 15 16 7 16 15 1 127
§3.1非十进制数转换为十进制数
§3.3二进制数、八进制数、十六进制数间的转换
八进制数、十六进制数转换为二进制数 将(764.23)8、(F09.B8)16转换为二进制数
八进制 7
6
4
.
2
3
二进制 111 110 100 . 010 011 所以(764.23)8=(111110100.010011)2 十六进制 F 0 9 . B 8
若十进制数较大时,不必逐位去除2,可算出2的幂与十 进制对比,如: (261)10 =(?)2 ∵28 =256 而 261 – 256 = 5 ,(5)10=(101)2
∴(261)10=(100000101)2 将(0.25)10转换为二进制数。
0.25 2 0.50 2 1.00
……..取出整数0作为小数部分的最高位 ……..取出整数1作为小数部分的最低位
由于最后的小数小于0.5,根据“四舍五入”的原则,应为0。
所以,(382.45) 10=(17E.73) 16。
1-2计算机的数制与编码
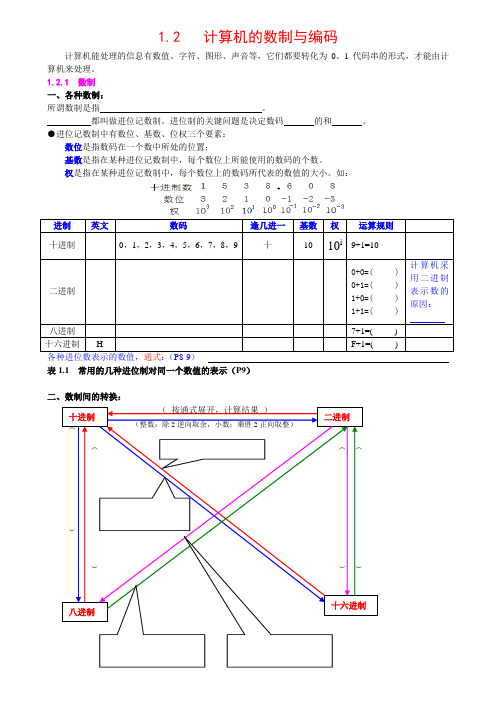
1.2 计算机的数制与编码计算机能处理的信息有数值、字符、图形、声音等,它们都要转化为0、1代码串的形式,才能由计算机来处理。
1.2.1 数制 一、各种数制:所谓数制是指 。
都叫做进位记数制。
进位制的关键问题是决定数码 的和 。
●进位记数制中有数位、基数、位权三个要素: 数位是指数码在一个数中所处的位置;基数是指在某种进位记数制中,每个数位上所能使用的数码的个数。
权是指在某种进位记数制中,每个数位上的数码所代表的数值的大小。
如:表1.1 常用的几种进位制对同一个数值的表示(P9)二、数制间的转换:例:(重点:十进制与二进制的互相转换)●各种进制转十进制●十进制转各种进制●二进制转八进制、八进制转二进制与二进制转十六进制、十六进制转二进制练习:P39:20、21、22、23、24、25、26、27、28、29(写在课本上)如何检查?(计算器!)1.2.2 ASCII码●通称为字符。
字符没有数值意义。
为了便于计算机的应用推广,这些字符必须用统一的规定编码方式来表示。
目前在国际上广泛采用“”表示、和作为使用的等。
●ASCII码的英文全称:,中文。
●ASCII码用位0、1代码串来编码一个符号,每个符号占的存储空间,字节最高位(左)为,作奇偶校验用。
(注:1字节= 位,一个字符的ASCII码占位,余下位用作)●ASCII码给出了个数码,个英文字母,个通用符号,个动作控制符的编码标准。
◆例:查表P308(1)字母“A”的ASCCII的二进制表示为:,十六进制表示为:,十进制表示为:(2)将字符“2”的ASCII码当成数值,转换为十进制数得到50,数字字符“5”的ASCII码转换为十进制数应得到●ASCII码的比较:(详见附录1:P308)空格(space)的ASCCII码是32‘0’~‘9’的ASCCII码是48~57‘A’~‘Z’的ASCCII码是65~90‘a’~‘z’的ASCCII码是97~1221.2.3 汉字编码1.国标码GB 2312-80《》1级汉字个,按顺序排列、2级汉字个,按排列,汉字有6763个,常用符号、字母、图形符号等682个,共计7445个。
中职计算机应用基础(计算机常用数制转换与信息编码)逐字稿(数制转换超级简单易懂)
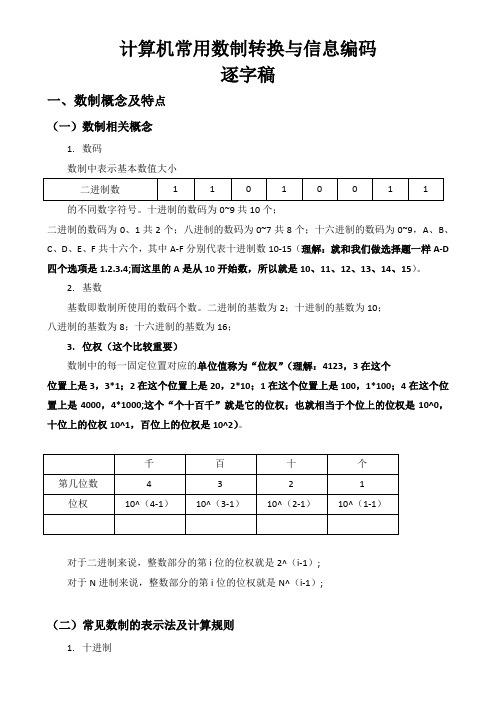
计算机常用数制转换与信息编码逐字稿一、数制概念及特点(一)数制相关概念1.数码数制中表示基本数值大小的不同数字符号。
十进制的数码为0~9共10个;二进制的数码为0、1共2个;八进制的数码为0~7共8个;十六进制的数码为0~9,A、B、C、D、E、F共十六个,其中A-F分别代表十进制数10-15(理解:就和我们做选择题一样A-D 四个选项是1.2.3.4;而这里的A是从10开始数,所以就是10、11、12、13、14、15)。
2.基数基数即数制所使用的数码个数。
二进制的基数为2;十进制的基数为10;八进制的基数为8;十六进制的基数为16;3.位权(这个比较重要)数制中的每一固定位置对应的单位值称为“位权”(理解:4123,3在这个位置上是3,3*1;2在这个位置上是20,2*10;1在这个位置上是100,1*100;4在这个位置上是4000,4*1000;这个“个十百千”就是它的位权;也就相当于个位上的位权是10^0,十位上的位权10^1,百位上的位权是10^2)。
对于二进制来说,整数部分的第i位的位权就是2^(i-1);对于N进制来说,整数部分的第i位的位权就是N^(i-1);(二)常见数制的表示法及计算规则1.十进制(1)表示法十进制数用D表示,如十进制数15,可表示成15D、(15)D或(15)10(2)计算规则进位规则是“逢十进一”,借位规则是“借一当十”。
(计算机直接表现在你面前的一般不会是二进制,它会转成八进制、十进制、十六进制给你展示,一般十进制、十六进制比较多,这样比较直观,不会是一长串的0101数字)我们来看一下“二进制”、“八进制”、“十六进制”,感觉有种倍数的关系,都是2的倍数,21、23、24、那我们分别介绍一下,这个“11”这个数字在各个数制中怎么表示呢常见数制的位权(三)二进制与十进制的相互转换1.二进制化为十进制例1:10110B转换成十进制数例2:一个字节等于8位(1B=8bit)11110011B转换成十进制数2.十进制数转二进制数方法:除2取余法,商作为下次的被除数,直到被除数为0停止,最后将余数按从下由上的顺序写出来即可。
1.2.2《数字化与编码-二进制与数制转换》教学设计20232024学年高中信息技术人教_中图版必修

1.2.2《数字化与编码二进制与数制转换》教学设计【教材分析】本节课教学内容选自人教中图版《信息技术》必修 1《数据与计算》第一章《认识数据与大数据》中《数字化与编码》的第二课时《二进制与数制转换》。
本节课与生活联系比较紧密,计算机需要将各种类型的数据编码表示为二进制数,存储在计算机中。
教材中涉及到ASCII码表和编码技术相关知识,这些知识以进制转换为基础。
学好这节课,可以帮助学生更好的理解后面数据编码的知识。
本节课通过游戏活动引导学生探究生活实例背后的科学知识,并在此过程中进行思考,培养学生的计算思维。
【教学目标】1.通过自学课件、微课和学习平台上的学习资源,自主学习并掌握十进制转二进制及十六进制转十进制的方法。
(信息意识、数字化学习与创新)2.在游戏参与中,理解二进制的基本原理及掌握二进制转十进制的方法。
(信息意识,计算思维)3.通过像素画填色,掌握十六进制转十进制的方法,并能运用所学知识解决生活中的问题。
(计算思维)4.了解二进制与中国传统文化之渊源,增强民族自豪感,形成良好的学习态度和价值观。
(信息社会责任)【教学重难点】1.教学重点:二进制的特征及各数制的相互转换方法。
2.教学难点:掌握各数制间的转换,并能运用所学知识解决生活中的问题。
【教学策略】通过“猜生日”游戏情境导入,引导学生由浅入深探究二进制的特征及各数制的转换方法,利用“颜色码的数制转换”等生活实例,巩固二进制及各数制在生活中的应用。
本节课主要采用了任务驱动法、讲授法和分层教学等教学方法。
游戏体验:介绍“猜生日”游戏(如下图)及其规则。
1.师生同玩游戏:找一位学生和老师搭档现场玩一次游戏(由学生说,教师猜)。
学生回答后,教师能马上准确无误地猜出其出生日期。
2.提出问题:教师是如何做到的?3.思考:我们现在从计算机屏幕上看到的1.创设情境,以一张错题图片导入,教师和学生共同分析出错题目,从错题原因浅入浅出的引出新授内容——权值。
数字电子技术-数制与编码-

000 0 0
000 1 1
001 2 0
8
100 8
0
9
100 9
1
10 101 A 0
(0010
1111
1011.1110
10103)2
001 1
3
11 101 B 1
=(2FB.EA)16
4 010 4 12 110 C
0
0
5 010 5 13 110 D 例 1 - 9 : ( 4B E5 .9 7D )16 = ( 0 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 . 10101 0 1 1 1 1 1 0 11) 2
7
• 84由21B于CD是代码,代码本身不是数,没有大小之分; • 必须4位一组,最高位、最低位的0不可去掉;
10n
0.0 1
0.1 1
10
10 0
10
3
104 105 106 107
108 109 1010
2n 0.2 0.5 1 2 4 8 16 32 64 128 25 512 1024
5
6
请熟练记住上表中二进制的权,在数制转换时非常有用。
最小的10位二进制数(1000000000)2=(29)10=(512)
四位二进制代码
一位十进制数字
22
(1)8421BCD码
• 选取0000⁓1001表示十进制数0⁓9。
10进制数 0 1
• 按自然顺序的二进制数表示所对应的十进制数字。
2
• 是有权码,从高位到低位的权依次为8、4、2、1, 3
故称为8421码。
4
数制和编码的概念及转换

数制和编码的概念及转换数制是一种表示数值的方式,常见的数制有十进制、二进制、八进制和十六进制等。
十进制是我们平时常用的数制,它使用基数为10的数字系统,由0到9共10个数字组成。
二进制是计算机使用的一种数制,它使用基数为2的数字系统,由0和1两个数字组成。
八进制是一种数制,它使用基数为8的数字系统,由0到7共8个数字组成。
十六进制是一种数制,它使用基数为16的数字系统,由0到9和A到F共16个数字组成,其中A表示10,B表示11,C表示12,D表示13,E表示14,F表示15。
编码是将字符、数字、符号等信息转化成特定的数字或符号的过程。
常见的编码方式有ASCII码、Unicode和UTF-8等。
ASCII码是英文字符编码的一种方式,它使用7位二进制数表示128个英文字符,包括字母、数字和常见的符号。
Unicode是一种编码系统,它为世界上各种文字字符规定了统一的编码,可以表示几乎所有的字符。
UTF-8是一种多字节编码方式,它是Unicode的一种实现方式,可以表示Unicode字符集中的任何字符。
数制转换是指将一个数值从一种数制表示转换成另一种数制表示的过程。
转换方法如下:1. 二进制转十进制:将每一位上的数乘以2的相应次幂,并求和。
2. 十进制转二进制:用除2取余法,将十进制数除以2,并将余数从低位到高位排列,直到商为0。
3. 八进制转十进制:将每一位上的数乘以8的相应次幂,并求和。
4. 十进制转八进制:用除8取余法,将十进制数除以8,并将余数从低位到高位排列,直到商为0。
5. 十六进制转十进制:将每一位上的数乘以16的相应次幂,并求和。
6. 十进制转十六进制:用除16取余法,将十进制数除以16,并将余数从低位到高位排列,直到商为0。
以上是一些常见的数制和编码的概念及转换方法,不同的数制和编码方式在不同的场景中有不同的应用。
1.3数字化信息编码与数据表示

计算机采用二进制表示和处理信息的原因:使用电子器件表示两种物理状态容易实现1.两种状态的系统稳定性高2.二进制运算规则简单,硬件容易实现3.易于转换,利于简化计算机内部结构4.适合逻辑运算5.一.进制计数制概念编码:指采用少量的基本符号,选用一定的组合规则,以表示大量复杂多样的信息基本符号1.数制:计数制是指计数的方法,即采用一组计数符号的组合来表示任意一个数的方法2.数码:每种数制都有的固定的基本符号(0~R-1)。
如二进制,有0,1两个数码3.基数:一种计数制中所使用的数码个数,基数为R 就称为R 进制4.位权:R 进制小数点第i 位的权为R^i-15.二.UCS即通用八位编码字符集(全世界现代书面语言所使用的所有字符的标准编码)CJK UCS 表意文字部分采用中、日、韩统一的汉字编码BIG5香港、台湾地区繁体中文,共有汉字13053个GBK Windows 全拼输入法使用的字符集,共20902个汉字字符GB2312-80国标码采用2字节表示一个汉字,共收集7445个图形字符682个一般符号、数字、拉丁字母、希腊字母、汉字拼音1.3755个一级汉字:1601~5589(16区~55区)2.3008个二级汉字:5601~8794(56区~87区)3.汉字内码:指为在计算机内部对汉字进行存储、处理、传输而编制的汉字代码机内码:指汉字信息处理系统内部标识汉字的编码,由国标码演化而来把表示国标码的2字节的最高位都置11.国标码(汉字信息交换码):用于汉字信息处理系统之间或者与通信系统之间进行信息交换的编码2.区位码:GB 2312-80国标字符集将汉字编码分成94区与94位,用汉字所在的区号和位号来表示汉字的编码3.三.汉字外码:汉字输入码是为输入汉字而对汉字编制的代码,供计算机外部用户使用按编码规则分流水码:区位码(无重码)重码率最低(1)音码:搜狗,QQ 拼音(2)形码:五笔字形输入法,郑码(3)音形结合码:自然码、华码(4)1.四.字形库硬字库:安装在卡上,插在微机的扩充槽里,使用时不占内存1.软字库:存放在磁盘上,因其使用时需将汉字库调入内存,所以占用一部分内存2.五.奇偶校验码水平奇偶校验码:以多个字符作为校验单位横向生成校验码位(一般要使用数据缓冲器)1.垂直及偶校验码:以一个字符作为校验单位纵向生成校验码位2.六.1.3.1 进制计数制概念分区1.3 的第1 页1.3.2 数字化信息编码与数据表示分区1.3 的第2 页汉字字形码:计算一个n x n 点阵汉字字形的存储容量:容量=n x n/8(B )(1)1.寻址空间:已知计算机有n 根地址线:寻址空间=2^n (B )(1)2.内存容量:存储容量=末地址-首地址+1H(1)3.图像数据容量:图像数据容量(B )=分辨率X 颜色深度/8(bit →Byte )分辨率=图像水平像素点数X 垂直像素点数①.颜色深度为n ,则颜色总数为2^n②.(1)4.音频文件大小容量:音频文件大小(B )=采样频率(Hz )X 采样位数(bit )X 声道数X 时间(S )/8(1)5.视频文件大小容量:视频文件大小(B ):分辨率X 颜色深度X 帧频X 时间(S )/8(1)6.电池功率=电池电压(V )X 电池容量(mAh 毫安时)/10007.正数“0”负数“1”反码反码=原码符号位不变,其余取反补码补码=原码补码=反码+1(最低位)8.计算公式分区1.3 的第3 页。
听新2024秋季高一必修1信息技术人教中图版第1章认识数据与大数据《数字化与编码:二进制与数制转换》

教学设计:听新2024秋季高一必修1 信息技术人教中图版第1章认识数据与大数据《数字化与编码:二进制与数制转换》一、教学目标(核心素养)1.信息意识:培养学生认识到二进制在信息技术中的基础地位,理解其在数据存储与处理中的重要性。
2.数字化学习与创新:通过动手操作,学生能够熟练掌握二进制与十进制之间的转换方法,并能应用于简单问题的解决中,提升数字化学习与创新能力。
3.计算思维:引导学生理解二进制的基本概念和原理,培养其逻辑推理能力和问题解决能力,形成初步的计算思维。
4.信息社会责任:在探讨二进制应用时,引导学生认识到信息安全与隐私保护的重要性,增强信息安全意识。
二、教学重点•二进制数的表示方法及特点。
•二进制与十进制之间的转换方法(包括手工转换和简单算法)。
三、教学难点•理解二进制为何成为计算机内部信息处理的基础。
•熟练掌握二进制与十进制之间转换的逆向思维过程。
四、教学资源•多媒体课件(含动画演示二进制转换过程)。
•实物教具(如计数板、卡片,用于模拟二进制表示)。
•在线互动平台(如课堂问答系统),用于即时反馈和讨论。
•教材及配套习题册。
五、教学方法•讲授法:介绍二进制的基本概念及重要性。
•演示法:利用多媒体和实物教具直观展示二进制与十进制的转换过程。
•互动讨论法:组织学生分组讨论二进制的应用实例,促进思维碰撞。
•实践操作法:安排学生动手进行二进制与十进制转换的练习,加深理解。
六、教学过程1. 导入新课•情境导入:播放一段简短的动画,展示日常生活中计算机处理信息的快速与高效,引出问题:“计算机是如何识别和存储这些信息的呢?”激发学生好奇心。
•引导思考:简要介绍计算机内部使用二进制的原因,为新课学习铺垫。
2. 新课教学•二进制基础:•定义讲解:明确二进制的定义,即只包含0和1两个数码的数制。
•重要性阐述:通过实例说明二进制在计算机科学中的基础地位。
•二进制表示法:•展示法:利用计数板或PPT,演示二进制数的表示方法。
数制转换的作用

数制转换的作用数制转换是指将一个数字表示从一种数制转换成另一种数制的过程。
数制转换在计算机科学、数学、电子工程等领域中被广泛应用,其作用十分重要。
本文将从不同的角度探讨数制转换的作用。
一、数制转换在计算机科学中的作用在计算机科学领域中,数制转换是十分常见的操作。
计算机以二进制形式来处理和存储数据,而人们通常使用十进制来表达数字。
因此,需要进行二进制到十进制的数制转换。
数制转换在计算机科学中的作用主要体现在以下几个方面:1. 数据存储和传输:计算机内部的数据存储和传输都是以二进制形式进行的。
然而,当人们需要将数据从计算机中读取或者将数据传输到计算机中时,通常需要将数据转换成十进制形式,以便人们理解和使用。
2. 程序设计:在程序设计中,经常需要进行位操作或者使用二进制运算符。
因此,掌握二进制数制转换对于理解和编写程序是至关重要的。
3. 地址转换:计算机内存中的地址通常是以二进制形式表示的。
当需要将二进制地址转换成十进制地址时,数制转换就发挥了重要作用。
二、数制转换在数学中的作用在数学领域中,数制转换也有其重要的作用。
数制转换主要涉及到不同进制的数之间的转换,如二进制、八进制、十进制和十六进制等。
数制转换在数学中的作用主要体现在以下几个方面:1. 进一制和进位制:数制转换是进一制和进位制的具体应用。
在进位制中,当某一位的数超过进制数时,需要向高位进位。
而在进一制中,当某一位的数达到最大值时,需要向高位进一。
因此,掌握数制转换可以帮助我们理解和应用进位制和进一制。
2. 数字表达的灵活性:不同的数制有不同的特点和应用场景。
例如,八进制和十六进制在计算机科学中被广泛使用,因为它们可以更紧凑地表示二进制数据。
而十进制在日常生活中更为常见,因为它更符合人们的思维习惯。
因此,数制转换可以帮助我们在不同场景下选择合适的数制来表示数字。
3. 数字逻辑和编码:数制转换在数字逻辑和编码中也有重要应用。
例如,将二进制数转换成格雷码可以简化数字电路的设计。
计数制与信息编码教案

计数制与信息编码一.数制转换1. 进制十进制:有0~9共十个数字,逢十进一二进制:有0~1共两个数字,逢二进一八进制:有0~7共八个数字,逢八进一十六进制:有0~9、A、B、C、D、E、F共十六个数字逢十六进一2. 按权展开式365=300+60+5=3×102+6×101+5×100按权展开式权值(基数):101024=(111)2=( )10(26)8=( )10(3B)16=( )103. 非十进制转换十进制(08年)下列采用4种不同数制表示的数中,数值最小..的一个是A. (101001.11)2B. (52.7)8 C.(44.9)10D.(2B.F)16(11年)下列各进制的数中最小..的是A. (213)10B. (10A)16C. (335)8D. (110111000)2(12年)下列各数中,数值最大..的是A. (3E5)16B. (745)8C. (1111110101)2D. (978)10(13年)二进制数1011对应的十进制数为A. 10B. 11C. 12D. 134. 十进制转换非十进制(13.75)10=( )2(26.5)10=( )8(28.625)10=( )165. 二进制与八进制之间的相互转换采用3位二进制对应1位八进制(000-111)2<->( )85.3Q= B101110.011111B= Q10100011.1101B= Q6. 二进制与十六进制之间的相互转换采用4位二进制对应1位十六进制(0000-1111)2<->( )169.BH= B10101011.11001101B= H1010111.100111B= H(14年)与二进制数101110等值的十六进制数是 H。
二、算术运算和逻辑运算1. 算术运算①加法:0+0=0,0+1=1,1+0=1, 1+1=0(有进位)(1101)2+(1010)2=( )2(1011)2+(1101)2=( )2②减法:0-0=0,0-1=1(有借位),1-0=1, 1-1=0(1101)2-(1010)2=( )2 (1010)2-(101)2=( )2③乘法:0×0=0,0×1=0,1×0=0,1×1=1(1011)2×(11)2=( )2④除法:(11001)2÷(101)2=( )22. 逻辑运算①与:AND或^二进制数1110^1101的结果是。
第2章 数制与信息编码

转换后的结果为:(0.534)10=(0.88B43)16
大学计算机基础
2.3 进位计数制
例子2-12:将(50.25)10转换成十六进制数。 解析:对于这种既有整数又有小数部分的十进制 数,可将其整数部分和小数部分分别转换成八进 制数,然后再把两者连接起来即可。 因为(50)10=(32)16,(0.25)10=(0.40)16 所以(50.25)10=(32.40)16
大学计算机基础
2.3 进位计数制
十六进制进位计数制具有如下特点:
有16个数符,分别为0、1、2、3、4、5、6、7、8、9、A、B、C、
D、E、F;
基数为16; 逢十六进一(加法运算),借一当十六(减法运算); 按权展开式。对于任意一n位整数和m位小数的十六进制数D,均
可按权展开为:D=Hn-1×16n-1+…+H1×161+H 0×16 0+
当R=16时,表示十六进制进位计数制,可使用0、1、
2、…、9、A、B、C、D、E、F共16个基本数符。
大学计算机基础
2.3 进位计数制
按基数进位和借位是指在执行加法或减法 时,遵守“逢R进一,借一当R”的规则,如 十进制数为“逢十进一,借一当十”,二进 制数的规则为“逢二进一,借一当二”。
大学计算机基础
2.1信息技术概述
信息技术的处理对象是信息和数据。
信息是人们在从事日常生产生活(如工业、农
业、军事、商业、管理、文化教育、医学卫生、 科学研究等)活动的过程中所涉及到的数字、 符号、文字、语言、图形、图像等的总称。
数据是存储在某种媒体上并且可以加以鉴别的
符号资料。
大学计算机基础
大学计算机基础
2.3 进位计数制
设计主题活动切入项目式教学——以《编码与数制转换》一课为例

设计主题活动切入项目式教学——以《编码与数制转换》一课为例在当今信息技术高速发展的时代,编码与数制转换是计算机科学中的重要概念。
为了更好地教授这门课程,提高学生的学习兴趣和理解能力,设计一个主题活动切入的项目式教学模式是非常有效的方法。
本文将以《编码与数制转换》一课为例,介绍如何设计主题活动切入的项目式教学。
一、项目式教学简介项目式教学是指在学习过程中,学生通过参与一个或多个真实世界的问题或项目,进行跨学科的学习与合作。
这种教学模式能够培养学生的合作能力、解决问题的能力和创新思维,使学生更好地将理论知识应用到实际中。
二、《编码与数制转换》主题活动设计1. 活动目标- 理解不同的数制及其在计算机中的应用;- 掌握二进制、十进制和十六进制之间的转换方法;- 了解编码的基本概念和常见编码方式。
2. 活动内容- 活动一:数制转换游戏学生分组进行数制转换的游戏,每组的成员需要在规定时间内将给定的数值转换成指定的数制,并与其他小组进行比赛。
用竞争的方式激发学生的学习兴趣,加强对数制转换的理解和记忆。
- 活动二:编码解码挑战学生以小组形式,设计一个简单的编码解码挑战。
每个小组可以选择不同的编码方式,如ASCII码、汉字编码等。
学生需要解码其他小组设计的信息,并提供正确的解答。
通过设计和解码挑战,学生能够深入理解编码的原理和应用。
- 活动三:身边的编码学生以个人为单位,记录身边常见的编码方式。
可以是条形码、二维码、邮政编码等。
学生需要收集相关信息,介绍编码的原理和实际应用场景。
通过实地观察和研究,学生能够加深对编码的理解,并将其与课堂学习相结合。
3. 活动实施- 在课堂上引入活动主题,并讲解与项目相关的知识内容;- 分组进行活动,指导学生设计各自的项目;- 学生进行项目实施,教师给予指导和支持;- 学生展示成果,进行相互评价和讨论。
4. 活动评价- 活动过程中的小组合作情况;- 活动成果的质量与准确性;- 学生在展示中的表现和解答能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学目标
• 理解并掌握进位计数制概念 • 掌握数制的转换 • 掌握计算机中数据的表示方法 • 了解常用信息编码的分类
重点难点
• 掌握二进制与十进制的相互转换 • 掌握二进制与八进制的相互转换 • 掌握二进制与十六进制的相互转换 • 掌握十进制与十六进制的相互转换
教学内容
D
图1-2 将二进制数转变成十六进制数
3、十六进制与十进制的相互转换
十六进制数与十进制数相互转换时,可以分 成两步完成:将待转换的十六进制数转换成二进 制,然后再将二进制数转换成十进制。
四、计算机中的存储单位
1.位 计算机中所有的数据都是以二进制来表示的,
一个二进制代码称为一位,记为bit。位是计算机 中最小的信息单位。
一、数字化信息编码的概念 二、进位计数制 三、不同进制之间的转换 四、计算机中数据的表示方法 五、常用信息编码
一、数字化信息编码的概念
计算机中的信息也称为数据。由于二进 制电路简单、可靠且具有很强的逻辑功能, 因此数据在计算机中均以二进制表示,并用 它们的组合表示不同类型的信息。
二、进位计数制
1.十进制 日常生活中最常见的是十进制数,用十个不同的符号来表示:0、1、
八进制的数较二进制的数书写方便,常应用在电子计算机的计算中。
三、不同进制之间的转换
1.二进制与十进制的相互转换 二进制数要转换成十进制数非常简单,只需
将每一位数字乘以它的权2n,再以十进制的方法 相加就可以得到它的十进制的值(注意,小数点 左侧相邻位的权为20,从右向左,每移一位,幂 次加1)。
【例1】(10110.011) B=1×24+0×23+1×22+1×21+0×20+0×2-1 +1×2-2+1×23=(22.375)余”的方法。具体过程介绍如下:
1.将十进制数除2,保存余数。
2.若商为0,则进行第三步,否则,用商代替 原十进制数,重复第1步。
3.将所有的余数找出,最后得到的余数作为 最高位,最先得出的余数作为最低位,由各余数 依次排列而成的新的数据就是转换成二进制的结 果。
2、二进制数与十六进制数的相互转换
由于16=24,所以在将二进制数转换成十 六进制数时,从最右侧开始,每四位二进制 数划为一组,用一位十六进制数代替,也称 为“以四换一”;十六进制数转换成二进制 数时正好相反,一位十六进制数用四位二进 制数来替换,也称“以一换四”。
0110 0101 1101
6
5
常用的存储存容量单位有B、KB、MB、GB, TB它们之间的关系是:
1KB=1024B, 1MB=1024KB, 1GB=1024MB ,1TB=1024GB。
五、常用信息编码
1.ASCII码 2.国标码 3.汉字字模
小结
• 理解信息在计算机中的表示方法 • 理解二进制、十六进制 • 掌握不同进制间数据的转换方法 • 理解并掌握信息在计算机中的存储方式 • 了解常用信息编码
2、3、4、5、6、7、8、9,称为代码。
2.二进制 二进制数只有两个代码“0”和“1”,所有的数据都由它们的组合
来实现。二进制数据在进行运算时,遵守“逢二进一,借一当二”的 原则。 3.十六进制
十六进制数采用0~9和A、B、C、D、E、F六个英文字母一 起构成十六个代码。 (半斤八两)
4.八进制 八进制数采用0,1,2,3,4,5,6,7八个数码,逢八进位。
2.字节 在对二进制数据进行存储时,以八位二进制
代码为一个单元存放在一起,称为一个字节,记 为Byte。字节是计算机中次小的存储单位。
3.字 一条指令或一个数据信息,称为一个字。字是
计算机进行信息交换、处理、存储的基本单元。
4.字长 CPU中每个字所包含的二进制代码的位数,
称为字长。字长是衡量计算机性能的一个重要 指标。
【例2】将(236)D转换成二进制。 转换过程如图1-1所示。
2 2 36 2 118 2 59 2 29 2 14 27 23 21 0
…………… 0 …………… 0 …………… 1 …………… 1 …………… 0 …………… 1 …………… 1 …………… 1
二进制数的低位 二进制数的高位
图1-1 将十进制数转变成二进制数
作业
1.(100101)2=( 2.(64)10=( 3.(25)10=( 4.(3C)16=( 5. (41)8=( 6.(17)10=(
)8=(
)16
)2
)8=(
)16
)2=(
)8
)2
)2=(
)16
