实验五六七算法思路及流程图
算法的求解流程图解题技巧

算法的求解流程图解题技巧求解算法问题时,流程图是一个非常有用的工具。
流程图可以帮助我们清晰地理解算法的执行过程,并且可以帮助我们更好地理解算法中的各个步骤和判断条件。
在解题过程中,我们可以通过以下技巧来有效地使用流程图。
1. 了解问题和约束条件:在开始绘制流程图之前,我们首先要充分了解问题的要求和约束条件。
对于一些复杂的问题,我们可能需要将问题分解为更小的子问题,并逐个解决。
2. 确定算法的输入和输出:在绘制流程图时,我们需要明确算法的输入和输出。
输入可以是任意类型的数据,如整数、字符串、数组等。
输出可以是单个结果,也可以是多个结果。
明确输入和输出可以帮助我们确定算法流程的起点和终点。
3. 使用适当的符号和形状:在绘制流程图时,我们可以使用不同的符号和形状来表示算法中的各个步骤和判断条件。
例如,使用矩形框表示顺序执行的步骤,使用菱形框表示判断条件,使用箭头表示程序流程的转向。
4. 使用合适的线条和注释:在绘制流程图时,我们可以使用不同的线条来表示程序流程的顺序、并行和循环。
例如,使用实线表示主要流程,使用虚线表示分支流程,使用圆角表示循环。
此外,我们还可以在图中添加合适的注释和解释,以便更好地理解算法的执行过程。
5. 分析和优化流程图:在绘制完流程图后,我们需要对其进行分析和优化。
我们可以通过逐个步骤地执行流程图,来确保它能够正确地解决问题。
如果发现流程图存在问题或不足之处,我们可以进行修改和优化,直到流程图满足问题的要求。
6. 尽量简化流程图:在绘制流程图时,我们应该尽量简化图形和步骤。
简化的流程图更易于理解和维护。
我们可以通过合并重复的步骤、去除冗余的条件和循环等方式来简化流程图。
7. 使用合适的命名和注释:当绘制流程图时,我们应该使用合适的命名和注释,以便更好地理解和解释各个步骤和条件。
我们可以使用有意义的变量名和函数名来表示算法中的各个变量和函数。
此外,我们还可以在图中添加适当的注释,以便更好地解释算法的执行逻辑。
567的分成练习题

567的分成练习题一、题目描述假设有一组数字:567。
请将这个数字分成两个部分,使得两部分相加的和最大。
要求编写程序实现这个功能,并输出结果。
二、解题思路为了使两个部分相加的和最大,我们需要将数字567尽可能均匀地分成两部分,即让两个部分的差值尽可能小。
为了达到这个目标,我们可以考虑从最高位开始逐个遍历数字的每一位。
首先,我们将数字567转换成一个字符串,以便于按位进行处理。
然后,我们可以从最高位的左边开始遍历字符串,将每一位的数字添加到两个部分中的一个。
具体的步骤如下:1. 将数字567转换成字符串,记为numStr。
2. 初始化两个部分的和为0,分别记为part1Sum和part2Sum。
3. 从最高位开始遍历numStr的每一位:- 将当前位的数字转换为整数,记为digit。
- 如果当前位是第一位(即最高位),或者part1Sum和part2Sum 的差值小于digit:- 将digit添加到第一个部分中,即part1Sum += digit。
- 否则:- 将digit添加到第二个部分中,即part2Sum += digit。
4. 输出部分一和部分二分别包含的数字。
三、示例代码```pythondef split_number(num):numStr = str(num)part1Sum = 0part2Sum = 0for i in range(len(numStr)):digit = int(numStr[i])if i == 0 or abs(part1Sum - part2Sum) < digit:part1Sum += digitelse:part2Sum += digitreturn part1Sum, part2Sumnum = 567part1, part2 = split_number(num)print("部分一:", part1)print("部分二:", part2)```四、运行结果```部分一: 59部分二: 67```根据以上的分成练习题的要求,我们通过编写程序计算得出,将数字567分成两个部分,使得两部分相加的和最大时,部分一为59,部分二为67。
VC++上机实验-实验1程序的灵魂
实验1程序的灵魂――算法1.实验目的(1)掌握算法的概念,会设计简单的算法。
(2)掌握掌握用流程图来表达算法的方法。
(3)熟悉用伪代码来表示算法的方法。
(4)掌握用Word来画流程图的方法。
(5)进一步熟悉C程序的编辑、编译、连接和运行的过程。
2.实验内容和步骤(1)用传统流程图求解以下问题的算法:有两个瓶子A和B,分别盛放醋和酱油,要求将它们互换(即A瓶原来盛醋,现在盛酱油,B瓶则相反)。
(第二章习题2.4(1))解:显然,如果只有两个瓶子,肯定不能完成此任务,必须有一个空瓶C作为过渡。
即先将A瓶中的醋倒给C瓶,再将B瓶中的酱油倒给A瓶,再将C瓶中的醋倒给B瓶,即可实现题目要求。
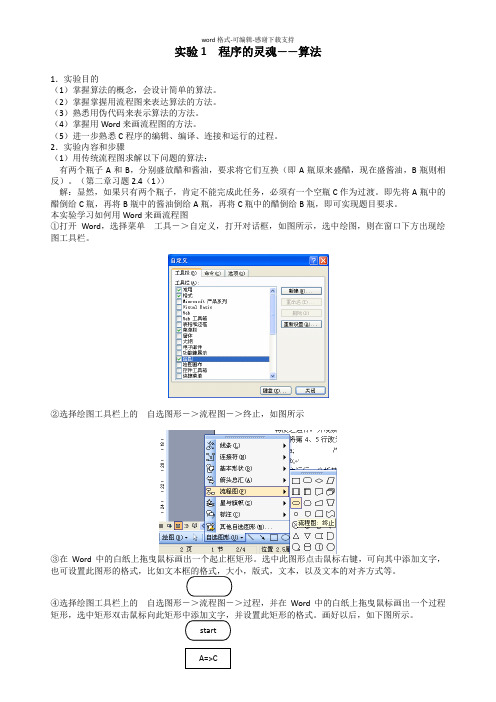
本实验学习如何用Word来画流程图①打开Word,选择菜单工具->自定义,打开对话框,如图所示,选中绘图,则在窗口下方出现绘图工具栏。
自选图形->流程图->终止,如图所示②选择绘图工具栏上的③在Word中的白纸上拖曳鼠标画出一个起止框矩形。
选中此图形点击鼠标右键,可向其中添加文字,④选择绘图工具栏上的自选图形->流程图->过程,并在Word中的白纸上拖曳鼠标画出一个过程⑤选择绘图工具栏上的箭头,然后在以上两个框之间自向而下拖动,则画出一个箭头,选择此箭头,调整其位置,并用鼠标右键点击之,设置其属性。
(在画图和调整图形位置时分别按住键盘上的shif 和ctrl 看会发生什么情况)⑦试考虑,将以上流程图中的第三个框和第四个框互换位置可以吗?为什么。
(2)用流程图求解问题以下问题:有3个数a 、b 、c ,要求按大小顺序把它们输出。
(3)用流程图求解以下问题求1+2+3+4+…….+100的和。
并编程实现。
(4)用流程图求解以下问题:判定某一年是否为闰年。
并编程实现。
(2)(3)#include<stdio.h>void main(){int sum=0,i;for(i=1;i<=100;i++)sum+=i;printf(“1+2+3+……+100=%d\n”,sum); }(4)。
沪教版(54制)数学四上:第4单元《正推

先用树状算图表示,再写出算式:
10 输入
10 10
×
×10
A
+22
输出
B ÷2
?
1A00 22
+
1B22 2
÷
(10×10 +22)÷2
6? 1
=(100 +22)÷2
= 122÷2
= 61(岁) 答:王爷爷今年61岁。
根据流程图画出树状算图,并列出综合式计算。
输入
256 +48 ÷4 -28 ?
课堂讲义
4.螺旋状液晶 (1)分子排列特点:分子分层排列,每层分子的排列方向相同,相邻各 层分子的取向相差一个小角度,形成各层分子排列方向依次旋转,构 成一个螺旋状结构. (2)特性及应用:具有显著的温度效应,可以用来探测温度,医学上检 查肿瘤,检查电路中的短路点.
预习导学
一、液体的性质
1.具有一定的体积,不易被 压缩.
2.宏观物理性质上表现为各向
同性.
3.没有一定的形状,具有 一定的体积 .
预习导学
4.液体微观结构与 非晶体非常类似,非晶体可以看作粘性极
大的 液体 ,所以严格地说,只有 才晶体能叫做真正的固体.
5.液体的扩散现象比固体进行得 .快
6.分子的热运动:主要表现为在平衡位置附近
正推
你看到什么? 计算盒及通道
两个正方体中都有一个通道。如果将数球7 放入第一个通道中,数球7再从另一个出口出来时, 它会显示几呢?
如果放入第二个通道,结果又会是怎样的呢?
7
输入
+5
A
÷6
输出
?
如果数球7,放入通道中,出口时,数球是几?
7+5=12 12÷6=2
还可以用树状算图表示,我们一起来试一试。
求给定命题公式的真值表并根据真值表求公式的主范式

求给定命题公式的真值表并根据真值表求公式的主范式(求给定命题公式的真值表并根据真值表求公式的主范式)专业网络工程班级 1202班学号 12407442姓名张敏慧2013.12.14目录一.实验目的 .......................................................3二.实验内容 (3)求任意一个命题公式的真值表 ..................................................................... ..... 3 三.实验环境 (3)四. 实验原理和实现过程(算法描述) (3)1.实验原理 ..................................................................... ...................................... 3 2.实验流程图 ..................................................................... .................................. 5 五.实验代码 (6)六. 实验结果 (14)七. 实验总结 (19)- 1 -一.实验目的本实验课程是网络工程专业学生的一门专业基础课程,通过实验,帮助学生更好地掌握计算机科学技术常用的离散数学中的概念、性质和运算;通过实验提高学生编写实验报告、总结实验结果的能力;使学生具备程序设计的思想,能够独立完成简单的算法设计和分析。
熟悉掌握命题逻辑中的真值表、主范式等,进一步能用它们来解决实际问题。
二.实验内容求任意一个命题公式的真值表,并根据真值表求主范式详细说明:求任意一个命题公式的真值表本实验要求大家利用C/C,,语言,实现任意输入公式的真值表计算。
一般我们将公式中的命题变元放在真值表的左边,将公式的结果放在真值表的右边。
实验报告魔方阵程序(3篇)

第1篇一、实验目的1. 熟悉Python编程语言的基本语法和常用数据结构。
2. 学习使用嵌套循环实现复杂数据结构的构建。
3. 掌握随机数生成和排序算法在程序中的应用。
4. 提高编程能力和问题解决能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 开发工具:PyCharm三、实验内容本实验旨在设计一个魔方阵程序,实现以下功能:1. 生成一个nn的魔方阵。
2. 魔方阵中,每一行的数字之和等于n。
3. 魔方阵中,每一列的数字之和等于n。
4. 魔方阵中,对角线的数字之和等于n。
四、实验步骤1. 导入所需的库```pythonimport random```2. 定义一个函数,用于生成nn的魔方阵```pythondef generate_magic_square(n):初始化一个nn的二维数组,用于存储魔方阵的数字 magic_square = [[0] n for _ in range(n)]num = 1 用于存储当前要填充的数字i, j = 0, n // 2 初始化起始位置while num <= n n:将数字num填充到当前位置magic_square[i][j] = numnum += 1判断下一个位置new_i, new_j = (i - 1) % n, (j + 1) % n 如果当前位置已被填充,则移动到新位置if magic_square[new_i][new_j] != 0:i, j = (i + 1) % n, jelse:i, j = new_i, new_jreturn magic_square```3. 定义一个函数,用于检查魔方阵是否正确```pythondef check_magic_square(magic_square, n):检查每一行的数字之和是否等于nfor i in range(n):if sum(magic_square[i]) != n:return False检查每一列的数字之和是否等于nfor j in range(n):if sum(magic_square[i][j] for i in range(n)) != n:return False检查对角线的数字之和是否等于nif sum(magic_square[i][i] for i in range(n)) != n or sum(magic_square[i][n - i - 1] for i in range(n)) != n:return Falsereturn True```4. 主函数```pythondef main():n = int(input("请输入魔方阵的阶数:"))magic_square = generate_magic_square(n)if check_magic_square(magic_square, n):for row in magic_square:print(' '.join(map(str, row)))else:print("生成的魔方阵不正确!")```5. 运行程序```pythonif __name__ == "__main__":main()```五、实验结果当输入阶数n为5时,程序输出如下魔方阵:```1 2 3 4 512 13 14 15 1011 16 17 18 196 7 8 9 205 4 3 2 1```六、实验总结通过本次实验,我们成功设计并实现了一个魔方阵程序。
实验7 算法流程图
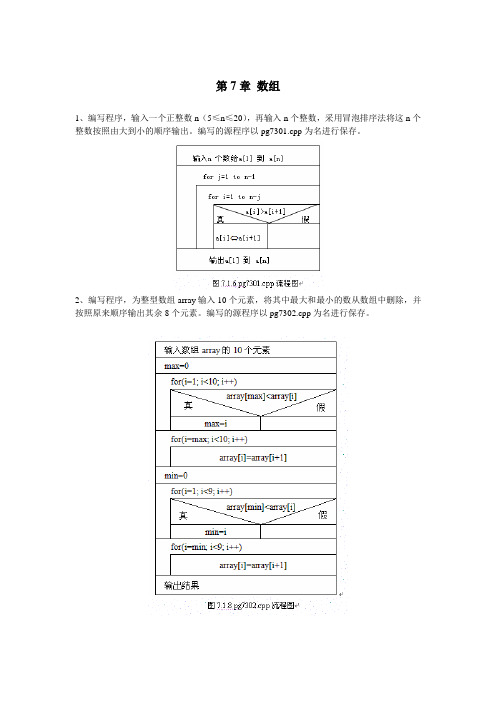
第7章数组
1、编写程序,输入一个正整数n(5≤n≤20),再输入n个整数,采用冒泡排序法将这n个整数按照由大到小的顺序输出。
编写的源程序以pg7301.cpp为名进行保存。
2、编写程序,为整型数组array输入10个元素,将其中最大和最小的数从数组中删除,并按照原来顺序输出其余8个元素。
编写的源程序以pg7302.cpp为名进行保存。
3、编写程序,输入一个正整数n(2≤n≤6),为n×n的方阵a输入各元素值,然后求出该方阵主对角线元素的和。
编写的源程序以pg7303.cpp为名进行保存。
4、编写程序,输入两个正整数m和n(2≤m≤5,2≤n≤5),为m×n的矩阵a输入各元素值,然后求出该矩阵所有元素的平均值。
编写的源程序以pg7304.cpp为名进行保存。
5、编写程序,输出九九乘法表。
编写的源程序以pg7305.cpp为名进行保存。
6、编写程序,输入一个以回车符结束的字符串(少于80个字符),分别统计其中英文字母、数字和其他字符的个数。
编写的源程序以pg7306.cpp为名进行保存。
7、编写程序,不使用字符串库函数,输入一个以回车符结束的字符串(少于80个字符),在原字符数组中,将其逆序存放,然后输出。
编写的源程序以pg7307.cpp为名进行保存。
8、编写程序,输入一个字符串(少于80个字符),在原字符数组中,删除所有的非英文字母后,组成新的字符串输出。
例如,输入“8a2Wer#QqsD”,则会输出“aWerqQSD”。
编写的源程序以pg7308.cpp为名进行保存。
用流程图表示计算5!的算法

用流程图表示计算5!的算法下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!1. 开始2. 定义变量 i 为 1,变量 factorial 为 13. 当 i 小于等于 5 时,执行以下操作:将 factorial 乘以 i将 i 加 14. 输出 factorial 的值5. 结束下面是对每个流程的详细解释:1. 开始:这是算法的起始点。
普里姆实验报告

一、实验目的1. 理解普里姆算法的基本原理和步骤。
2. 掌握使用C语言实现普里姆算法的方法。
3. 熟悉最小生成树的概念及其在实际应用中的重要性。
4. 通过实验验证普里姆算法的正确性和效率。
二、实验环境1. 操作系统:Windows 102. 编程语言:C语言3. 开发环境:Visual Studio三、实验原理普里姆算法是一种贪心算法,用于在加权无向图中寻找最小生成树。
最小生成树是指一个无向图的所有顶点构成的树,其边权值之和最小。
普里姆算法的基本思想是从某个顶点开始,逐步增加边,直到包含所有顶点为止。
四、实验步骤1. 定义邻接矩阵:首先定义一个二维数组表示图的邻接矩阵,其中元素表示两个顶点之间的边权值。
2. 初始化数据结构:定义一个结构体表示顶点,包含顶点的编号和距离。
初始化一个数组存储所有顶点的结构体。
3. 选择起始顶点:选择一个顶点作为起始顶点,将其距离设置为0,其余顶点的距离设置为无穷大。
4. 遍历邻接矩阵:对于每个顶点,遍历其邻接矩阵,找到距离最小的边,将其加入最小生成树中,并更新相邻顶点的距离。
5. 重复步骤4:重复步骤4,直到所有顶点都被加入最小生成树中。
6. 输出结果:输出最小生成树的边和权值。
五、实验代码```c#include <stdio.h>#include <stdlib.h>#define MAXVEX 6#define INF 10000typedef struct {int adjvex; // 邻接顶点的位置int lowcost; // 与adjvex顶点相连的边的权值} MinNode;typedef struct {char vexs[MAXVEX]; // 顶点表MinNode adjmatrix[MAXVEX][MAXVEX]; // 邻接矩阵int numVertexes, numEdges; // 图中当前顶点的数量和边的数量} MGraph;void CreateMGraph(MGraph G) {int i, j, k, w;printf("请输入顶点数量和边数量:\n");scanf("%d %d", &G->numVertexes, &G->numEdges);printf("请输入顶点信息:\n");for (i = 0; i < G->numVertexes; i++) {scanf("%s", G->vexs[i]);}for (i = 0; i < G->numVertexes; i++) {G->adjmatrix[i][j].adjvex = 0;G->adjmatrix[i][j].lowcost = INF;}}for (k = 0; k < G->numEdges; k++) {printf("请输入边(%d)的两个顶点和权值:\n", k + 1); scanf("%d %d %d", &i, &j, &w);G->adjmatrix[i][j].adjvex = j;G->adjmatrix[i][j].lowcost = w;G->adjmatrix[j][i].adjvex = i;G->adjmatrix[j][i].lowcost = w;}}void Prim(MGraph G, int u) {int min, i, j, k;MinNode adjvex;int visited[MAXVEX] = {0}; // 标记顶点是否被访问过visited[u] = 1;printf("%c ", G.vexs[u]); // 输出起始顶点for (i = 1; i < G.numVertexes; i++) {min = INF;k = u;if (visited[j] == 0 && G.adjmatrix[k][j].lowcost < min) { min = G.adjmatrix[k][j].lowcost;adjvex = G.adjmatrix[k][j];k = j;}}printf("%c ", G.vexs[k]); // 输出当前顶点visited[k] = 1;G.adjmatrix[u][k].lowcost = INF;G.adjmatrix[k][u].lowcost = INF;}}int main() {MGraph G;int u;printf("请输入起始顶点编号:\n");scanf("%d", &u);CreateMGraph(&G);Prim(G, u);return 0;}```六、实验结果1. 输入顶点数量和边数量:6 82. 输入顶点信息:A B C D E F3. 输入边(1)的两个顶点和权值:0 1 14. 输入边(2)的两个顶点和权值:0 2 25. 输入边(3)的两个顶点和权值:1 2 36. 输入边(4)的两个顶点和权值:1 3 67. 输入边(5)的两个顶点和权值:2 3 48. 输入边(6)的两个顶点和权值:2 4 59. 输入边(7)的两个顶点和权值:3 4 710. 输入边(8)的两个顶点和权值:4 5 811. 输入起始顶点编号:0实验结果:A B C D E F七、实验总结通过本次实验,我们成功实现了普里姆算法,并验证了其在实际应用中的有效性。
算法和流程图(及N-S流程图)

算法和流程图(及N-S流程图)算法和流程图2.1.1算法计算机语⾔只是⼀种⼯具。
光学习语⾔的规则还不够,最重要的是学会针对各种类型的问题,拟定出有效的解决⽅法和步骤即算法。
有了正确⽽有效的算法,可以利⽤任何⼀种计算机⾼级语⾔编写程序,使计算机进⾏⼯作。
因此,设计算法是程序设计的核⼼。
并⾮只有“计算”的问题才有算法。
⼴义地说,为解决⼀个问题⽽采取的⽅法和步骤,称为“算法”。
不要把“计算⽅法”(computational method)和“算法”(algorithm)这两个词混淆。
前者指的是求数值解的近似⽅法,后者是指解决问题的⼀步⼀步的过程。
在解⼀个数值计算问题时,除了要选择合适的计算⽅法外,还要根据这个计算⽅法写出如何让计算机⼀步⼀步执⾏以求解的算法。
对于计算机外⾏来说,他们可以只使⽤别⼈已设计好的现成算法,只需根据算法的要求给以必要的输⼊,就能得到输出的结果。
对他们来说,算法如同⼀个“⿊箱⼦”⼀样,他们可以不了解“⿊箱⼦”中的结构,只是从外部特性上了解算法的作⽤,即可⽅便地使⽤算法。
但对于程序设计⼈员来说,必须会设计算法,并且根据算法编写程序。
对同⼀个问题,可以有不同的解题⽅法和步骤。
例如,求1+2+3+…+100,可以先进⾏1+2,再加3,再加4,⼀直加到100,也可采取100+ (1+99)+(2+98)+…+(49+51)+50=100+50+49×100=5050。
还可以有其它的⽅法。
当然,⽅法有优劣之分。
有的⽅法只需进⾏很少的步骤,⽽有些⽅法则需要较多的步骤。
⼀般说,希望采⽤⽅法简单,运算步骤少的⽅法。
因此,为了有效地进⾏解题,不仅需要保证算法正确,还要考虑算法的质量,选择合适的算法。
⼀个计算问题的解决过程通常包含下⾯⼏步:确⽴所需解决的问题以及最后应达到的要求。
必须保证在任务⼀开始就对它有详细⽽确切的了解,避免模棱两可和含混不清之处。
分析问题构造模型。
在得到⼀个基本的物理模型后,⽤数学语⾔描述它,例如列出解题的数学公式或联⽴⽅程式,即建⽴数学模型。
实验八-队列(循环队列)的表示和实现-舞伴问题

浙江大学城市学院实验报告课程名称数据结构基础实验项目名称实验八队列(循环队列)的表示和实现学生姓名*** 专业班级信管1104 学号3110****实验成绩指导老师(签名)日期一.实验目的和要求1、掌握队列的存储结构及基本操作。
2、掌握循环队列的设置及循环队列的各种基本操作的实现。
3、通过具体的应用实例,进一步熟悉和掌握队列的实际应用。
二.实验内容1、建立头文件SeqQueue.h,定义顺序存储的循环队列存储结构,并编写循环队列的各种基本操作实现函数。
同时建立一个验证操作实现的主函数文件test3_2.cpp,编译并调试程序,直到正确运行。
2、选做:编写程序,实现舞伴问题。
假设在周末舞会上,男士们和女士们进入舞厅时,各自排成一队,跳舞开始时,依次从男队和女队的队头上各出一人配成舞伴,若两队初始人数不相同,则较长的那一队中未配对者等待下一轮舞曲。
要求设计一个函数void partner(),模拟上述舞伴配对问题。
基本要求:1) 由键盘输入数据,每对数据包括姓名和性别;2) 输出结果包括配成舞伴的女士和男士的姓名,以及未配对者的队伍名称和队头者的姓名;3) 要求利用SeqQueue.h中已实现的顺序循环队列的基本操作函数来实现。
函数void partner() 添加到文件test3_2.cpp中,在主函数中进行调用测试。
3、填写实验报告,实验报告文件取名为report8.doc。
4、上传实验报告文件report8.doc、源程序文件test3_2.cpp及SeqQueue.h 到Ftp服务器上自己的文件夹下。
三. 函数的功能说明及算法思路(包括每个函数的功能说明,及一些重要函数的算法实现思路)1)InitQueue(Queue &q)实现初始化队列的功能2)EnQueue(Queue &q,ElemType item)向队列插入元素item3)OutQueue(Queue &q)队列头位元素出列,并返回该值4)PeekQueue(Queue &q)返回队头元素值5)EmptyQueue(Queue &q)判断队列Q是否为空,若空返回1,否则返回06)ClearQueue(Queue &q)清空队列7)partner()实现舞伴的配对操作。
最短路径问题设计

目录第1章绪论 (1)1.1 问题描述 (1)1.2 问题分析 (1)1.3 相关标识(名词定义) (1)1.4 本文主要研究内容 (2)第2章算法设计与实现 (3)2.1 穷举法 (3)2.1.1穷举法描述 (3)2.1.2穷举法设计 (3)2.1.3 穷举法分析 (6)2.2 回溯法 (6)2.2.1 回溯法描述 (6)2.2.2 回溯法设计 (6)2.2.3 回溯法分析 (9)2.3 贪心法 (10)2.3.1 贪心法描述 (10)2.3.2 贪心法设计 (10)2.3.3 贪心法分析 (12)2.4 动态规划法 (12)2.4.1 动态规划法描述 (12)2.4.2 动态规划法设计 (12)2.4.3 动态规划法分析 (14)第3章实验结果分析与算法对比 (15)3.1 输入数据 (15)3.2 实验结果与分析 (15)3.3 算法分析与对比 (17)第4章总结与展望 (18)参考文献 (19)第1章 绪论1.1 问题描述最短路径问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。
经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。
本文主要解决的问题是:给定带权有向图G =(V , E),对任意顶点i v ,j v ∈V (i ≠j ),求顶点i v 到顶点j v 的最短路径。
即给定一个有向图,再给出任意2个不相邻的顶点,求2个顶点之间的最短距离。
1.2 问题分析给定一个带权有向图G =(V , E )中的各个顶点之间的权值,对任意输入2个顶点i v ,j v ∈V (i ≠j ),求出从i v 到j v 的最短路径。
第一讲 算法与程序设计PPT课件

参考算法一:
①将3毫升的量杯装满 ②将3毫升量杯中的水注入5毫升量杯 ③将3毫升的量杯装满 ④将3毫升量杯中的水注入5毫升量杯,注满后3毫升量杯中剩余1毫升水。
返回
.
26
参考算法二:
①将5毫升的量杯装满 ②将5毫升量杯中的水注入3毫升量杯,注满后5毫升量杯中剩余2毫升水 ③将3毫升量杯倒空 ④将5毫升量杯中剩余的2毫升注入3毫升量杯 ⑤将5毫升量杯装满 ⑥将5毫升量杯中的水注入3毫升量杯,注满后5毫升量杯中剩余4毫升水 ⑦将3毫升量杯倒空 ⑧将5毫升量杯中的水注入3毫升量杯,注满后5毫升量杯中剩余1毫升水
算法与程序设计
一、算法及其描述方法
.
1
第一节 算法与程序
.
2
.
3
.
4
.
5
.
6
计 硬件系统
算
机 系
软件系统
系统软件
统
应用软件
★软件的重要组成部分是:程序 想一想:什么是程序?
.
7
什么是程序
计算机的任何动作都是在执行人给它的指令。 人们针对某一需要而为计算机编制的指令序列称 为程序 。
程序指示计算机如何去解决问题或完成任务 的一组可执行的指令。
.
11
一个完整的算法有三个部分:输入、处理、输出。
.
12
算法与程序的关系是什么呢?
算法是程序的灵魂,是解决问题的步骤。程序代 码只是实现的手段。
.
13
例题:
某学校要进行学生电脑编程竞赛,竞赛将评出10名获奖 者,分为一、二、三等奖。奖项设置一等奖获得人数要 少于二等奖人数,二等奖人数要少于三等奖人数。问一 二三等奖人数各为多少?
返回
算法的基本步骤

算法的基本步骤嘿,咱今儿个就来聊聊算法的基本步骤。
你说算法这玩意儿,就像一个神秘的魔法盒子,打开它,就能看到好多奇妙的东西。
算法第一步,那得是明确问题呀!就好比你要去一个地方,你得先知道目的地在哪儿吧。
这可不是随便说说就行的,得认真琢磨,把问题的关键给揪出来。
你想想看,要是连要干啥都不清楚,那不就像无头苍蝇一样乱撞啦?接下来,设计方案可就重要啦!这就好像盖房子得先有个设计图一样。
你得好好想想,用什么方法能又快又好地解决问题。
这里面的门道可多了去了,得开动脑筋,发挥想象力。
就像厨师做菜,得想好要用哪些食材,怎么搭配才能做出美味佳肴。
然后呢,就是实现算法啦!这就好比把设计图变成实实在在的房子。
你得按照设计好的步骤,一步一步地去做。
这可不能马虎,一个小细节没处理好,可能就会前功尽弃哦。
就像走路一样,一步一个脚印,踏踏实实地往前走。
再之后,测试可不能少啊!你得看看自己做的对不对,有没有漏洞。
这就像给自己做的东西做个“体检”一样。
要是有问题,赶紧改正,可不能让它带着“病”运行呀。
最后一步,优化可别小瞧啦!就像你买了新衣服,还得修剪修剪线头,让它更合身一样。
把算法再打磨打磨,让它更高效,更完美。
你说这算法的基本步骤,像不像一场奇妙的冒险?每一步都充满了挑战和惊喜。
有时候可能会遇到困难,但是别怕呀,办法总比困难多嘛!你看那些厉害的程序员,不就是靠着这一步步走过来的嘛。
咱平时生活中也到处都有算法的影子呢。
比如说你每天上学走哪条路最快,这其实也是一种算法呀。
或者你怎么安排时间,能在一天里做最多的事情,这也是算法在起作用呢。
所以说呀,算法可不仅仅是那些高深莫测的代码,它就在我们身边,无处不在。
我们要好好理解它,运用它,让我们的生活变得更美好,更高效。
你说是不是这个理儿?反正我是这么觉得的!哈哈!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N
N
输出i的值 i++;
7-3.用循环结构语句编程并输出下图,其行数和每行的数据
个数有键盘给出。例如:键盘输入:5和8,则运行结果如下
提示:整个图案分成上下两部分。上下两部分图案输出的行 数受第一个输入参数(5)的控制,每行输出的数据个数受第 二个参数(8)的控制。可设置变量i,j,每行(i)输出j个i;此 外,每行还需要输出i个空格。 故在每行输出时,可利用一个循环控制输出的空格数,一个 循环控制输出的数据。
int n,i=0,r; double result=0;
输入n r=n%2;
result=result+r*pow(10.0,i); i++; n=n/2;
n==0
设置输出格式(只输出result整数部分) cout<<fixed; cout.precision(0);
输出result;
7-1.
图案下部
图案上部
switch(first) { case 1: switch(second) { case 1: cout<<“剪刀平剪刀."<<endl; break; case 2: cout<<"石头胜剪刀."<<endl; break; case 3: cout<<"剪刀胜布."<<endl; break; default : cout<<" 第二次输入有误!"<<endl ; break; } break; case 2: switch(second) { …………. } break; case 3: switch(second) { ………….. } break; default : cout<<“第一次输入有误!"<<endl; }
2 2 2 2 2 2 2
100 50 25 12 6 3 1 0
0 0 1 0 0 1 1
把余数“当成” 十进制数处理
位权100 位权101
位权10i-1
故,可设变量 result=0×100+0×101+1×102+0×103+0×104+1×105+1×106 =1100100
算法NS流程图
5-1
模拟二人猜拳游戏:1.剪刀
2.石头
3.布。
提示:由于有两个游戏者,每个游戏者都有三种可能的输入,因此要使用 switch嵌套语句,对第一个游戏者的某种输入(如输入1),再针对第二 个游戏者的不同输入就可以得到相应的输赢信息。
定义变量 int first, second;
从键盘输入 first和 second的值(1:剪刀;2:石头;3: 布);
定义变量i,n(需要分解的数); 从键盘输入a的值
i=2;
i<=n n%i==0 n=n/i; Y n!=1; N
cout<<i<<"*";
i++;
cout<<i;
6-3. 编程实现十进制整数和八进制整数之间的转换
(即将10进制数转换为8进制数,或将8进制数转换为 10进制数)。
示例
(100)10= (1100100)2
定义变量i,j,a,b; a,b分别表示行数和每行数据个数
i=a;
i=1; i<=a j=1; j<=i 输出一个空格符号 j++; j<=i+b 输出i j++; i++;
输出间隔符******(利用循环实行)
i>=1 j=1; j<=i 输出一个空格符号 j++; j<=i+b 输出i j++; i--;
开始
5-2
输入n
n%3==0
成立 不成立 不成立 不成立
键盘输入一个数,判定:能不能 被3、5和7整除,并如果失败输出失败 的具体原因。
n%5==0
成立
输出该数 不能被3整除
输出该数 不能被5整除 输出该数 不能被7整除
n%7==0
成立
输出该数 能被3、5、7整除
结束
5-3
输入某年某月某日,判断这一天是这一年的第几天。
peach=(peach+1)*2; day=day-1; 输出peach
6-2.将一个正整数分解质因数。例如:输入90,打 印出90=2*3*3*5。
算法分析: 分解质因数的算式叫短除法。求一个数分解质因数, 要从最小的质数除起,一直除到结果为质数为止。因 此,对n进行分解质因数,应先找到一个最小的质数 i(2),然后按下述步骤完成: (1)如果i<=n,则执行如下步骤, (2) 如果n能被i整除,用n除以i的商,作为新的正整数n, 判断n是否为1,如果n不为1,打印输出i和*号(说明 因数分解还没有完),如果n为1,打印输出i,说明分 解质因数的过程已经结束。重复执行步骤(2)。 (3)如果n不能被i整除,则i=i+1,重复执行步骤(1)
方法二:
用倒推法计算,其基本思想是:从最后一天起逐次推出前一天 的桃子数,直到推出第1天吃桃子前的全部桃子数为止。根据 题意,猴子某天吃桃子前的桃子数是前一天吃桃子之前的桃子 数的一半再减1,即: Peachn=(Peachn-1)/2-1 或 Peachn-1=(Peachn+1)*2 这样就可以从第n天的桃子数倒推出第n-1天的桃子数(都是 指该天未吃桃子前的数),从第n-1天的桃子数倒推出第n-2天 的桃子数….. 一直可递推求出第1天的桃子数(最初值)。 反复的递推过程可以用循环结构实现。 定义变量day,peach=1; 从键盘输入天数day day>1
提示:先根据输入的年份y,确定是否为闰年(闰年算法可参 考流程图),然后再判断m是几月(可用swith语句),根据 常识(一月大,二月平,三月大…..)即可获知天数。
定义变量year,month,day,sum_day=0; 输入需要判断的年份year、month、day
year%4==0&&year%100!=0 || year%100==0&&year%400==0
T
swith(month) { case 12: sum_day=30+sum_day; case 11: sum_day=31+sum_day; ………….. case 3: sum_day=29+sum_day; case 2: sum_day=31+sum_day; case 1: sum_day=sum_day+day; }
6-1.一只猴子摘了N个桃子,第一天吃了一半又多吃了一
个,第二天又吃了余下的一半又多吃了一个,到第十天的时候 发现还有一个。
思路分析与算法:
首先分析一下用代数方法如何求解此题。 设小猴子共摘了x了桃子,根据题意可有: • 第1天吃掉x/2+1个,剩下x/2-1=(x-2)/2个 • 第2天吃掉((x-2)/2)/2+1个,剩下 (x-2)/2-(((x-2)/2)/2+1)=(x-2)/2-(x-2+22)/22=(x-2-22)/22个 • …… • 以此类推 • 第i天剩下:(x-2-22-…-2i)/2i个; 由题意可得第9天剩下:(x-2-22-…-29)/29=1个桃子,即第10 天剩下的1个桃子。借此方程可得: x=29+29+28+27+26+25+24+23+22+2=1534个
个位:n%10 十位:n/10%10 百位:n/100
定义变量i=1; i<=1000
Y Y
i%3==0&&i%7!=0 i>=1&&i<10 i%10==5 输出i的值
N N
N
Y
Y Y
i>=10&&i<99 i%10==5||i/10==5 输出i的值
N
N
Y Y
i>=100&&i<999
i%10==5||(i/10)%10==5||i/100==5
计算多项式 前n项的和。截止到最后项的值与1的差小于0.02。
定义变量n,x,y,item x=0,y=1,item,n=1; y>0.02 item=(n*(n+2))/((n+1)*(n+3)) x=x+item; n++; y=1-x; 输出x
7-2.求1-1000中能被3整除,且不能被7整除,且 至少有一位数是5的整数。 算法描述: (1)定义一个变量i,并赋初值为1; (2)当i小于等于1000时,判断变量i是否能被3整除 ,并不能被7整除; (3)如果满足(2)中的整除条件,则分别判断变量i的 个位、十位、百位是否有一位数为5; (4)如果满足(3)中“是否有一位数为5”的条件,则 输出变量i。并将变量i加1,重复执行步骤(2)。直到 关于i的条件不满足为止。
F
swith(month) { case 12: sum_day=30+sum_day; case 11: sum_day=31+sum_day; ………… case 3: sum_day=28+sum_day; case 2: sum_day=31+say+day; } 输出sum_day
x=29+29+28+27+26+25+24+23+22+2
定义变量day,peach; 从键盘输入天数day peach=(int)pow((double)2,day-1);
