无网格法
自适应无网格及网格和无网格混合算法

在地质工程领域,自适应无网格及网格和无网格 混合算法可以用于模拟地质体的变形和破坏过程 ,为地质灾害防控提供技术支持。
感谢您的观看
THANKS
由于无网格算法是基于点的计算方法,可 以更好地处理复杂形状和边界条件。
适用于动态问题
无网格算法适用于处理动态问题,例如流 体动力学、结构动力学等。
无网格算法的发展历程
无网格算法的研究始于20世纪90年代,最初是为了解着计算机技术的发展,无网格算法逐渐成为研究的热点,并被广泛应用于工程 和科学领域。
自适应无网格及网格和无网格混合算法在其他领域中的应
用前景
自适应无网格及网格和无网格混合算法也可以应 用于其他领域,如固体物理、生物医学工程、地 质工程等。
在固体物理领域,自适应无网格及网格和无网格 混合算法可以用于研究材料的力学性能和物理性 质,如弹性模量、热导率等。
在生物医学工程领域,自适应无网格及网格和无 网格混合算法可以用于模拟生物组织的力学性能 和药物传递过程,为药物开发和组织工程提供有 效的工具。
广泛的应用前景。
网格与无网格混合算法在流体动力学中的应用
在流体动力学领域,网格与无网格混合算法结合了传统有限元素法和无 网格法的优点,能够更好地处理流场的运动和变化。
网格与无网格混合算法可以有效地解决边界层流动、分离流动和湍流等 复杂流动问题,提高计算精度和效率。
网格与无网格混合算法在航空航天、汽车和船舶等领域具有广泛的应用 前景,可以用于气动性能评估、流体控制和流体传动等方面的研究。
与传统的网格算法不同,无网格算法不需要对计算域进行网 格划分,因此可以避免网格生成、更新和修复等繁琐过程, 提高了计算效率。
无网格算法的优点
无需网格生成
无网格算法的最大优点是无需进行繁琐的 网格生成,节省了大量时间和人力。
[硕士]题解无网格法及其与有限元法的比较研究初步_pdf
![[硕士]题解无网格法及其与有限元法的比较研究初步_pdf](https://img.taocdn.com/s3/m/8b58c6db51e79b8968022675.png)
ห้องสมุดไป่ตู้摘要
近几十年来,有限元法(FEM)由于其通用性和灵活性已经成为工程数值领域的主要方法, 但是有限元法在分析大变形、不连续性等问题时存在缺陷。无网格法(MLM)正是基于这些缺 陷提出的。本文在分析了无网格法的研究历史和现状、分类和优缺点的基础上,基于算例分 别采用无网格伽辽金法(EFGM)和有限元法进行数值模拟,对两者在结构体离散、刚度矩阵 建立、等效节点荷载施加、边界条件的引入等方面进行了比较分析,并指出了各自的优缺点。
文章简述了无网格法中另外的比较成熟的方法——配点法,并基于一维算例在相同条件 下分别与无网格伽辽金法计算结果进行了对比。相比于无网格伽辽金法,配点法计算效率高、 位移边界条件容易实现、但系数矩阵是非对称的、稳定性较差。
本文简单介绍了克立格法,并将其应用到求解无网格法形函数的过程中,建立了克立格 无网格伽辽金(KEFG)法(简称克立格无网格法)。用克立格无网格伽辽金法分析了一维杆件 算例,并与相同材料参数条件下运用无网格伽辽金法得到的结果进行对比,结果表明该方法 具有很好的稳定性和点插值性,方便施加位移边界条件,在固定端的误差相对于无网格伽辽 金法要小,且计算量远小于无网格伽辽金法。
最后运用无网格伽辽金法求解了土体的二维固结问题,并与相同条件下运用有限元法得 到的结果进行比较。结果表明两种方法计算结果比较吻合,说明该方法可以有效地模拟工程 问题。
关键字: 无网格伽辽金法;有限元法;配点法;克立格法。
I
筑龙网
Abstract
In recent decades, the finite element has become a major field of engineering numerical methods, as it is universal and flexible. But defects of the finite element method exist in analyzing large deformation, non-continuityand so on. The meshless method is proposed basing on these defects. The element-free Galerkin method (EFGM) and finite element method (FEM) are adopted to numerically simulate a numerical example basing on the development history and present situation, classification, advantages and disadvantages analysis of the meshless in this text. And comparisons are also made between the results by this two methods basing on the numerical examples in structure discrete, stiffness matrix establishment, application of equivalent node loads and boundary conditions application, etc. And theirs advantages and disadvantages are pointed out.
无网格法的理论及应用

为了验证该方法的有效性和可行性,我们进行了一系列实验。实验过程中采 用了某稠油油田的实际数据集,包括地层压力、温度、渗透率等参数。同时,采 用了可视化评估指标,以便直观地评估计算结果的准确性。实验结果表明,该方 法在稠油热采数值模拟过程中具有较高的计算精度和计算效率,可为稠油热采技 术的优化提供有力支持。
1、算法开发:针对稠油热采的物理化学过程,开发相应的数值模拟算法, 如有限元法、有限差分法等。
2、软件架构:设计并实现数值模拟软件的架构,包括前后处理、求解器等 模块,以便用户进行快速高效的计算。
3、数据处理:针对稠油热采数值模拟过程中产生的大量数据,开发相应的 数据处理技术,如数据压缩、可视化等。
无网格法的数值积分采用移动最小二乘法(Moving Least Squares,MLS) 来实现。该方法通过对节点进行加权,构造一个局部近似函数来逼近真实的解。 数值积分通过在节点上建立局部近似函数,然后对该函数进行求导和积分来计算。 无网格法的数值积分具有高精度和高效性,同时避免了传统网格法中的网格生成 和数据处理问题。
1、结构分析
无网格法在结构分析中具有广泛的应用,可以处理各种复杂形状和材料属性 的结构。例如,桥梁、建筑物和飞机等结构分析中,无网格法能够适应复杂的几 何形状和非均匀的材料属性,同时提高计算效率和精度。此外,无网格法在疲劳 分析和振动分析中也得到了广泛应用。
2、流体分析
无网格法在流体分析中也有着广泛的应用,可以处理各种复杂的流体流动问 题。例如,无网格法可以应用于计算流体动力学(CFD)中的复杂流场模拟、燃 烧模拟以及噪声辐射模拟等。无网格法能够适应复杂的几何形状和流场特性,提 高计算精度和效率。
参考内容
稠油热采是一种重要的石油开采方法,具有提高采收率、降低开采成本等优 势。随着计算机技术的不断发展,数值模拟已成为稠油热采领域的重要工具。本 次演示旨在探讨稠油热采数值模拟自适应网格法计算软件的开发研究及实例应用。
无网格法 流体

无网格法(无网格流体模拟)简介无网格法(无网格流体模拟)是一种用于模拟流体行为的数值计算方法。
与传统的网格法相比,无网格法不需要预先划分网格,因此可以灵活地模拟各种复杂的流体现象。
无网格法的主要优势在于能够处理大变形、大位移和自适应网格等问题,在计算效率和精度方面都有较好的表现。
背景在过去的流体模拟中,通常使用网格来离散模拟空间。
然而,传统的网格法存在一些缺点。
首先,网格法需要预先划分网格,这在处理复杂几何体或大变形情况下往往具有挑战性。
其次,网格法在处理液体表面的运动时可能会出现不准确或不稳定的情况。
最后,网格法需要对整个领域进行求解,计算成本相对较高。
无网格法的基本原理无网格法通过将流体领域内的粒子进行离散化,并采用不同的数值计算技术来模拟流体的行为。
在传统的无网格法中,粒子通常是拉格朗日粒子(Lagrangian Particle),它们可以自由移动和变形,并且可以在计算中重新连接和分离。
无网格法的核心是描述流体的运动方程。
在拉格朗日粒子的模拟中,通常使用基于质点的方法来计算粒子运动的方程。
在每个时间步长中,根据质点的受力和刚体动力学原理,可以确定质点的加速度、速度和位置。
通过不断迭代计算所有质点的运动方程,可以得到流体领域内的流体运动状态。
除了描述粒子运动方程之外,无网格法还需要考虑粒子之间的相互作用和液体的流动特性。
为了模拟粒子之间的相互作用,可以使用诸如领域分解、体积渗透、弹簧网格等技术。
而为了模拟流体的流动特性,可以使用诸如斯托克斯流体方程、连续介质力学等数值方法。
无网格法的应用无网格法在计算流体力学和计算物理等领域都具有广泛的应用。
在流体力学方面,无网格法可以模拟复杂的流体现象,如自由表面流动、液滴碰撞、流体-结构相互作用等。
在计算物理方面,无网格法可以用于模拟固体材料的变形和破裂行为,如弹性体的形变、破坏和碎裂等。
此外,无网格法还具有适应性网格的特点,可以根据流体的运动状态自动调整粒子的分布和连接,从而实现更高的计算效率和精度。
导体面目标电磁散射特性分析的无网格方法研究.

电子工程设计技术要依赖于适当的物理结构模型和数值分析方法,电磁散射领域现有的比较成熟的数值算法:有限元、矩量法、等都是以网格为基础的。
他们的技术核心、编程难点以及计算的瓶颈FDTD 都在于网格的生成和优化,尤其对结构优化、动态仿真问题,网格必须反复生成,需要耗费大量的人力和时间。
因此,一种新的脱离网格的数值方法──无网格法,简称,得到学者(Meshless Methord MLM的广泛关注。
目前,相关文献中提出的无网格算法主要有:扩散单元法(Diffuse Element Method[1]、无网格迦辽金法(Element Free Galerkin Method[2]和核点再生法(Reproducine Kernel Particle Method[3]。
迄今为止,无网格方法在电磁场计算领域才初步应用[4-6],在波动方程求解方面还很少有报道。
本文将无网格迦辽金法推广应用于电磁散射与辐射问题的数值计算。
首先详细论述了移动最小二乘近似的基本原理,其次通过变分对方程进行数值离散,结合电磁场积分方程导出了无网格迦辽金方法分析电磁场散射问题的Galerkin 计算方程。
并且,给出导体方板的电磁波散射特性的计算实例,验证了所述算法。
移动最小二乘法原理1 (u x 无网格法中最常用的构造近似函数的方法之一是移动最小二乘近似。
待求函数在计算点 x 邻域内的近似函数为:((1mh T j i i p a a −−=⎛⎞⎛⎞⎛⎞==⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠∑-u x,x x x p x x , (1i p−⎛⎞⎜⎟⎝⎠x 其中,是 m 维完全多项式基函数,在二维情况下通常可取线性基函数[]1,,T x y −⎛⎞=⎜⎟⎝⎠p x , m ,=3 (2(i a x 是待定系数,它的选取要使近似函数和待求函数的加权离散误差的模 J 最小:(((2n T i i I I w x x P x a x u =⎡⎤=−−⎣⎦∑J , (3导体面目标电磁散射特性分析的无网格方法研究李灵侠1,张民 2,梁春恬1(天津城市建设学院基础部,天津;西安电子科技大学理学院,陕西西安1. 3003842. 710071摘要: 将无网格迦辽金法推广应用于导体面目标电磁散射与辐射问题的研究。
无网格法介绍

无网格法是在建立问题域的系统代数方程时,不需要利用预定义的 无网格法是在建立问题域的系统代数方程时, 网格信息,或者只利用更容易生成的更灵活、 网格信息,或者只利用更容易生成的更灵活、更自由的网格进行域 离散的方法。(刘桂荣,2009) 离散的方法。(刘桂荣,2009) 。(刘桂荣
无网格法概述
无网格法求解过程 FEM对比 对比) (与FEM对比)
导出无网格法公式
基于弱强式的无网格法
• MFree弱-强式法 弱 强式法 强式法(NWS)的核心思想是针对某一问题同时采用强式和 的核心思想是针对某一问题同时采用强式和 局部弱式建立起离散系统方程式,即对不同组别的节点根据其不同 局部弱式建立起离散系统方程式, 条件分别形成不同类型的方程,其中局部弱式被用于位于或接近导 条件分别形成不同类型的方程, 数边界条件的所有节点,强式被用于除此之外的其他节点。 数边界条件的所有节点,强式被用于除此之外的其他节点。 • 代表方法:MWS 代表方法: • MWS特点。MWS法使用最少数量的背景网格用于积分,对各类力学 特点。 法使用最少数量的背景网格用于积分, 特点 法使用最少数量的背景网格用于积分 问题均可得到稳定而精确的解,是目前近乎理想的无网格法。 问题均可得到稳定而精确的解,是目前近乎理想的无网格法。
构造无网格形函数
PIM形函数性质
• 一致性 如果单项式的完备阶数是p,则该形函数具有 C p 一致性 如果单项式的完备阶数是 , • 再生性 PIM基函数可再生包含在其基函数当中的任意函数。 基函数可再生包含在其基函数当中的任意函数。 基函数可再生包含在其基函数当中的任意函数 • 线形独立性 PIM基函数在支持域上是线性独立的 基函数在支持域上是线性独立的 • δ 函数性
目
无网格方法的研究应用与进展

第24卷第4期(总第109期)机械管理开发2009年8月Vol.24No.4(SUM No.109)MECHANICAL MANAGEMENT AND DEVELOPMENT Aug.20090引言有限元法(FEA)是随着电子计算机的发展而迅速发展起来的一种现代计算方法,但FEA是基于网格的数值方法,在分析涉及特大变形(如加工成型、高速碰撞、流固耦合)、奇异性或裂纹动态扩展等问题时遇到了许多困难。
同时,复杂的三维结构的网格生成和重分也是相当困难和费时的。
近年来,无网格得到了迅速的发展,受到了国际力学界的高度重视。
与有限元的显著特点是无网格法不需要划分网格,只需要具体的节点信息,采用一种权函数(或核函数)有关的近似,用权函数表征节点信息。
克服了有限元对网格的依赖性,在涉及网格畸变、网格移动等问题中显示出明显的优势。
1无网格方法的概述无网格方法(Meshless Method)是为有效解决有限元法在数值模拟分析时网格带来的重大问题而产生的,其基本思想是将有限元法中的网格结构去除,完全用一系列的节点排列来代之,摆脱了网格的初始化和网格重构对问题的束缚,保证了求解的精度[1]。
是一种很有发展的数值模拟分析方法。
目前发展的无网格方法有:光滑质点流体动力学法(SPH)、无网格枷辽金法(EFGM)、无网格局部枷辽金法(MLPGM)、扩散单元法(DEM)、Hp-clouds无网格方法;有限点法(FPM)、无网格局部Petrov-Galerkin 方法(MLPG)、多尺度重构核粒子方法(MRKP)、小波粒子方法(WPM)、径向基函数法(RBF)、无网格有限元法(MPFEM)、边界积分方程的无网格方法等。
这些方法的基本思想都是在问题域内布置一系列的离散节点,然后采用一种与权函数或核函数有关的近似,使得某个域上的节点可以影响研究对象上的任何一点的力学特性,进而求得问题的解。
2无网格方法国内外研究的进展无网格法起源于20世纪70年代。
有限元、边界元、无网格法的比较

首先,从五个方面进行有限元和无网格方法比较,分别是网格划分、形函数的产生、边界条件、系统离散方案、系统方程的求解:1、网格划分有限元方法:连续体被划分成由有限个称作单元的小网格组合而成的离散结构。
单元划分是前处理过程中非常重要的部分, 通常占整个分析过程中大部分时间。
由于单元能按不同的联结方式进行组合,且单元本身又可以有不同的形状,因此可以模拟几何形状复杂的求解域。
无网格方法:问题域由一系列任意分布的节点来代替, 不需要用单元或网格来进行场变量插值, 也无须描述节点之间的关系。
节点的生成可完全由计算机自动完成, 这大大节省了分析人员的时间, 也相对较容易在分析过程中对节点进行重新划分。
几何体边界是由节点替代(而非离散) , 如图1所示,两个节点之间的任意一点可由近似函数插值。
(a)有限元法中光滑曲线边界由三角形直线边代替(b)无网格法中光滑边界由节点替代图1 网格-节点示意图2、形函数的产生:有限元法和无网格法都可从哈密尔顿原理推出, 它们之间最关键的区别是形函数的构造。
有限元法:形函数是定义于单元的局部近似函数,因此函数的连续性、光滑性在网格的分界处必然受到限制,计算后还需要进一步的后处理。
形函数可以直接插值得到,故相对较容易构造且相同类型的单元具有相同的形函数。
无网格方法:形函数是围绕每一个节点建立插值函数构成的,不同的点具有不同的形函数,形函数定义于全域,具有较好的连续性和光滑性,不需要后处理过程。
3、边界条件有限元法:施加边界条件并不很困难, 通常在网格划分时使网格形式满足边界条件特点, 本质边界条件可直接加在节点上。
无网格方法:本质边界条件不仅依赖边界点,而且也与内部点有关,无网格法不能直接施加本质边界条件都是用离散的点来代替连续的边界值,这样会给本质边界条件的精确实现造成困难。
,拉格朗日乘子法和罚函数法是两种基本的方法。
4、系统离散方案有限元法是建立在虚功原理上的。
若给出控制微分方程,对于固体结构或流体, 都可以从加权残值法推出更普遍意义上的有限元公式,其可以得到一个对称的刚度矩阵。
典型无网格法

无网格法典型无网格法V伽辽金型无网格法V配点型无网格法V基于局部弱形式和边界积分方程的无网格法V最小二乘无网格法V物质点法V EFG¾MLS¾Galerkin V RKPM¾RK¾Galerkin V PIM¾PIG l ki¾Galerkin等效积分弱形式(虚位移原理)MLS 近似:()()u =x N x dV 计算量大精度高稳定性V 精度高,稳定性好V 需要背景网格进行积分V 系数矩阵对称V 不易施加本质边界条件处理V背景网格积分,,d I i J j N N ΩΩ∫()()()()=ΔΩ+ΔΓP N x f x N x t x 11I I I I I II I ==∑∑零能模态V 单位分解积分11.函数ψk (x )只定义在子域Ωk 上;2.子域Ωk 相互重叠,且它们完全覆盖了域Ω;3l=3.函数ψk (x )满足单位分解条件1()d ()()d k k k f f ψΩΩ∩Ω=ΩΩ∑∫∫x x x配点型无网格法V FPM¾MLS¾CollocationV SPH¾KA¾Collocationp es ess c ouds V Hp meshless clouds ¾PUC ll ti¾Collocation基于局部弱形式和边界积分方程的无网格法V MLPG¾MLS¾LPGV LBIE¾MLS¾LBIENV BNM¾MLS¾BIEgn pn 1iI IJ iJJ p m v ==∑1IJ p Ip Jpp m m N N ==∑质量阵求逆iIp iJv?质量阵求逆!gpn n 11I IJ p IpJ p m m m N ====∑∑对角质量阵iI I iIp m v =V已知t k 时刻的物理量,求t k +1时刻的物理量11.更新网格结点数据kk Ip Ipm m N=∑ppn k k kiIip Ip p m v N=1p ppp =∑int,ext,kk k iI iIiIf ff=−2.在背景网格结点上积分动量方程并施加固定边界条件1k k k pp f t+=+ΔiIiI iI10,0k k iIiIp f +==在固定边界上6.更新密度,应力k k k 1/(1)p p iipρρε+=+Δ1k k kkij ij ij ij+=ijpijp ijp ijp r σσσ+Δ+Δkk k kk r σσΔ=ΔΩ−ΔΩ其中ijpijpijpijpijpk ijpσΔ根据弹塑性本构关系更新7.进行下一个时间步循环。
无网格——精选推荐

第一章绪论计算流体力学的发展现状计算流体力学(Computational Fluid Dynamics)是现代流体力学中的一个重要学科分支。
作为一门多学科交叉融合而形成的新兴学科,它是流体力学、计算数学和计算机科学相结合的产物。
随着计算机性能的飞速提高以及数值计算方法的不断发展,计算流体力学技术正在逐渐走向成熟。
计算流体力学经历了数值求解拉普拉斯方程、小扰动速势方程、全速势方程、Euler方程和Navier-Stokes方程等发展阶段。
20世纪80年代以前,由于受到计算机技术的限制,计算流体力学的数值模拟主要以求解拉普拉斯方程、小扰动速势方程、全速势方程为主,其中有代表性的是基于拉普拉斯方程的面源法以及有限差分法求解小扰动速势方程和全速势方程。
在随后的二十多年中,在计算机技术发展的推动和广大计算流体力学工作者的努力下,计算流体力学在求解Euler方程和Navier-Stokes方程以及数值模拟复杂流场方面都取得了重大突破。
在此期间,计算流体力学数值模拟的方法以有限差分法、有限体积法、有限元法为主。
随着诸如TVD格式、ENO格式、NND格式等高阶精度、高分辨率差分格式的提出,计算流体力学对激波、漩涡等复杂问题的模拟能力也有了很大的提高。
目前,计算流体力学工作者正致力于研究和发展更高精度(二阶以上)的计算格式和方法,以适应更精细、更复杂的流动研究和设计的需要。
计算流体力学研究的一个重要分支是计算网格的生成技术,它是计算流体力学走向工程实用阶段所必须面临的关键技术之一。
一般来讲,适合工程使用的网格生成技术应该具备以下特点:(1) 网格生成过程直观明了、简单易行、效率高、自动化程度好。
(2) 通用性、普适性好,对复杂外形、复杂流动的适应能力强。
(3) 网格几何灵活性好,尺度变化易于控制,网格自适应加密简便易行。
目前,已经成熟并走向工程实用中的计算网格有结构网格、非结构网格以及结构非结构的混合网格。
在结构网格方面,出现了代数生成网格法、解微分方程生成网格法、保角变换法等多种网格生成方法,网格类型也由单一的C型网格、0型网格、H型网格发展到嵌套网格和多块对接网格等。
无网格法和有限元法的比较

收稿日期:2006-08-15作者简介:胡玮军,女,邵阳学院机械与能源工程系,讲师,硕士研究生。
文章编号:1001-4179(2007)02-0128-03无网格法和有限元法的比较胡玮军(邵阳学院机械与能源工程系,湖南邵阳422004)摘要:无网格法是在有限元的基础上发展起来的新的数值方法,在处理大变形或网格 畸变 等问题时具有明显的优势。
有限元法的形函数和离散系统方程是建立在网格上的,而无网格法在问题域中采用一系列分散节点来建立场变量插值,形函数定义于全域,随插值节点的移动而变化,故无网格法具有更高的计算精度,前处理工作量大大减少,无需后处理过程。
由于无网格法中系统刚度矩阵较大,因此需要更多的CPU 计算时间。
关 键 词:有限元法;无网格法;比较;数值方法中图分类号:O241 文献标识码:A1 概述有限元法(Finite Elemen t Method)是基于网格的数值方法,它通用、灵活并被作为一种工业标准广泛遵循,但其在分析涉及特大变形(如:加工成型、高速碰撞、流固耦合)、奇异性或裂纹动态扩展等问题时遇到了许多困难。
在有限元法中,单元和网格既是分析解决问题的载体,同时也是对其应用的制约,主要表现在: 单元网格剖分等前处理数据准备工作量大,尤其是对三维问题; 在分析大变形问题时必须防止网格畸变或缠结; 在求解裂纹扩展、液体晃动、材料相变和成形等不定边界或可动边界问题时,需要随时找出新的边界位置,并在新的解域内重新划分网格; 对时间相关问题更要按时段反复重分网格,工作量惊人,甚至使分析失败。
近年来,无网格法(Meshfree Mothed)得到了迅速发展,它不需要划分网格,克服了有限元法对网格的依赖,在涉及网格畸变、网格移动等问题时显示出明显的优势,同时无网格法的前处理过程也比有限元更为简单。
2 有限元法和无网格法的比较2.1 网格划分在有限元法中,连续体被划分成由有限个称作单元的小网格组合而成的离散结构。
光滑粒子流体动力学方法SPH课件

粒子近似法
与SPH核近似法相关的连续积分表示式,可转化为支 持域内所有粒子叠加求和的离散化形式。
f x f xW x x, hdx
N
f
x
j
W
x
x
j
,
hV
j
j 1
N
f
j 1
xj W xxj,h
1
j
jV j
N
f
j 1
xj W xxj,h
边界处理
当类型I的虚粒子成为邻近边界处的实粒子的相邻粒子时,则会 在沿着两粒子的中心线处对实粒子产生一个作用力。
PBij
D
r0 rij
n1
r0 rij
n2
xij rij2
,
0,
r0 rij
1
r0 rij
1
式中:参数n1和n2一般取值分别为12和4。D是由具体问题而定的参数, 一般取与速度最大值的平方相等的量级。截止半径r0在此问题的模拟 分析中非常重要,在一般情况下, r0的取值与粒子的初始间距的大小 相近。
目录
➢SPH计算公式 ➢光滑函数 ➢最近相邻粒子搜索法(NNPS) ➢人工粘度 ➢边界处理 ➢交界面处理 ➢光滑长度的更新
➢SPH方程的求解 ➢SPH程序结构 ➢激波管问题
SPH计算公式
1、密度的粒子近似法
由于粒子的分配与光滑长度的变化主要依赖于密度,故在SPH法 中密度近似法非常重要。
在SPH法中有两种方法对密度进行展开,第一种方法是对密度直 接用SPH近似法,称为密度求和法。第二种方法是连续性密度法,通 过应用SPH近似法的概念对连续性方程进行转换而得到。
全配对粒子搜索法
10_无网格方法

a( x) A1 ( x) B( x)u (8)
把式(8)代入式(1)得近似函数为
u ( x, x) pT ( x) A1 ( x) B( x)u N T ( x, x)u (9)
U T RA T a d V T RB T a d 0
式中 RA a A a 和 RB a B a 为余量。 虽然 U 和V
T T T Tຫໍສະໝຸດ
为任意权函数,但在实际应用时,不可能也不需要取无穷多个权函数。 与试函数表达式类似,可以把权函数也写成已知基函数的组合,即
pT ( x) [1, x, y, x 2 , xy, y 2 ]
m6
m 10
基函数的个数 m 、 基函数中包含的完备多项式的最高阶数 n 和问题的维数 nDim 之间的关系为
m
(n 1)(n 2) (n nDim ) nDim !
(3)
在移动最小二乘近似的(MLS)中,坐标 ai ( x ) 的选取应该使近似位移
p ( x) [1, x, y, r cos , r sin , r sin sin , r cos sin ] 2 2 2 2
T
式中:r 为某点距裂纹尖端的距离, 为该点与裂纹尖端连线与裂纹线的夹角。
若把式(1)作为有限单元容许位移函数,则 p1 ( x) 1 可以保证单元容许位
求解方法。只要试函数是利用离散点来建立的,则由紧支试函
数加权余量法导出的各种近似方法都称为无网格方法。
紧支近似函数 紧支近似函数是定义在局部区域(支撑区域)中的函数,它只 在支撑域中有定义,而在支撑域外为零。在二维问题中,支撑 域一般为圆形或矩形,与求解域相比,支撑域是一个很小的区 域,并且是可以互相重叠。有限元网格表示的区域是不能彼此 重叠的。
固体力学中的无网格方法

• • • • • 无网格方法的概述 无网格方法的近似方案 不连续性近似 离散化实现 基本边界条件的实现
无网格方法的概述
无网格法是在建立问题域的系统代 数方程时,不需要利用预定义的网 格信息,或者只利用更容易生成的 更灵活、更自由的网格进行域离散 的方法。(刘桂荣,2009)
无网格方法的概述
最近几年,Duarte和Oden等人提出了单位分解法, 并且认识到基于移动最小二乘法的近似方法实际上是 单位分解法的一种特例,从而将这类近似方法加以扩 展;Liu等人也对此类方法做了大量的研究工作,并对 其收敛性给以证明。
无网格方法的概述
无网格法求解过 程(与FEM对比)
无网格方法的概述
无网格方法模拟裂纹扩展
无网格方法的近似方案
• 核函数近似方法 • 移动最小二乘近似(MLS) • 单位分解法
无网格方法的近似方案
核函数近似方法
核函数近似方法最初主要用于SPH方 法。它对函数u(x)利用核函数进行近 似 u ( x ) x y , h u ( y ) d x y , h 被称为核函数或权函数,h是紧 支集尺寸的一个度量。
无网格方法的概述
一条构造无网格方法的途径是采用 移动最小二乘法(moving least square approximation method,简记为MLS)进 行近似。Nayroles等人最早将移动最小二 乘近似用于Galerkin方法,并将之称为扩 散单元法(difflnse elernent methods,简 称DEM)。Belytschko等人提出了无单元 的Galerkin法(element free galerkin method,简称EFG)。这类方法具有较 好的协调性及稳定性。
计算固体力学(有限元以及无网格方法)

σz ≠ 0
E 1− µ2
平面应变问题的弹性矩阵只需将上页中的 E 换成
µ 换成 1 − µ 即可。 即可。
µ
1 E (1 − µ ) µ [D] = (1 + µ )(1 − 2µ ) 1 − µ 0
µ
1− µ 1 0
0 1 − 2µ 2(1 − µ ) 0
第二章 平面弹性力学的有限元法
2.2 三角形常应变单元 3 单元中的应变和应力
{ε } = [ B ]{δ }e
i ( xi , yi )
y
vm
Hale Waihona Puke m ( xm , y m )
vi
um
vj
uj
ui
j(x j , y j )
由于[ 是常量, 由于[B]是常量,单元内各点应变分 量也都是常量, 量也都是常量,这是由于采用了线性位 移函数的缘故, 移函数的缘故,这种单元称为三角形常 应变单元。 应变单元。
2.2 三角形常应变单元 2 位移试函数
由于位移函数适用于单元中的任意 一点,所以代入3个节点的坐标后, 一点,所以代入3个节点的坐标后,得 出节点处位移函数为
ui = α1 + α 2 xi + α 3 yi
u j = α1 + α 2 x j + α 3 y j u m = α 1 + α 2 xm + α 3 y m
y
vm
m ( xm , y m )
vi
um
vj
uj
i ( xi , yi )
ui
j(x j , y j )
O
x
三角形单元
1 xi 1 ∆ = 1 xj 2 1 xm yi
无网格法 流体

无网格法流体介绍无网格法流体的定义和背景引述无网格法流体在科学计算和工程应用中的重要性解释无网格法的基本思想和原理着重介绍无网格法在流体模拟中的应用描述无网格法流体模拟的一般步骤包括数据准备、网格生成和流体模拟等关键步骤强调无网格法在流体模拟中的优势和独特之处比较网格法和无网格法的差异和优缺点概述无网格法在不同领域中的应用情况包括工程流体力学、生物流体学和天气模拟等方面讨论无网格法流体模拟的发展趋势和前景提出可能的改进和创新方向总结无网格法流体的重要性和应用前景强调进一步开展相关研究的意义和必要性以上是《无网格法流体》的大纲,该文将以简洁的语言呈现无网格法流体模拟的基本原理、步骤、优势、应用领域和发展趋势,以及结论的总结。
本文将介绍无网格法流体的概念和定义。
无网格法流体(Mesh-free Fluid)是一种基于流体力学原理的数值模拟方法,用于模拟液体或气体在复杂几何形状中的流动行为。
与传统的网格方法(Grid-based Method)不同,无网格法在建立数值模型时不需要网格结构,而是以粒子为基本计算单元。
无网格法流体的核心思想是将流体连续介质看作一系列粒子,通过离散化的方式模拟流体运动。
在模拟过程中,粒子之间的相互作用和影响被计算和更新,从而实现对流体的模拟和预测。
与传统网格方法相比,无网格法具有更高的自由度和适应性,能够处理复杂的流体现象和几何形状。
无网格法流体广泛应用于各个领域,包括工程、物理学和计算机图形学等。
它在模拟自然界中的流体行为、计算流体力学、研究海洋环境、仿真特殊效果等方面具有重要的作用。
通过使用无网格法流体,研究人员和工程师能够更准确地预测和分析复杂流体系统的行为,为各个领域的科学研究和工程设计提供有力的支持。
本文将探讨无网格法流体在不同领域的应用,例如仿真、计算流体力学等。
无网格法流体在仿真领域具有广泛的应用。
通过使用无网格法,可以更精确地模拟涉及流体的各种物理过程,如水流、燃烧等。
Ls-dyna中无网格法的一点心得
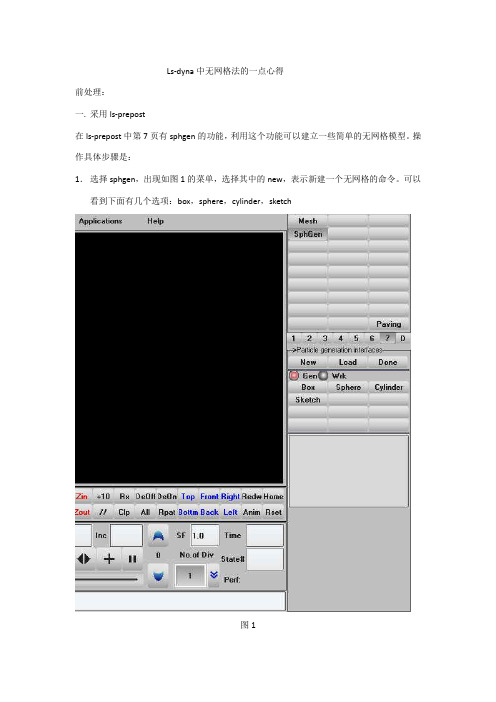
Ls-dyna中无网格法的一点心得前处理:一.采用ls-prepost在ls-prepost中第7页有sphgen的功能,利用这个功能可以建立一些简单的无网格模型。
操作具体步骤是:1.选择sphgen,出现如图1的菜单,选择其中的new,表示新建一个无网格的命令。
可以看到下面有几个选项:box,sphere,cylinder,sketch图12.选择box,出现如图2所示的菜单,即为创建一个具有长方体形的无网格模型。
图2可以看到有坐标x,y,z,而且标号为x1,x2,y1,y2,z1,z2,表示以p1点(x1,y1,z1)起点,以向量(由(x1,y1,z1)指向(x2,y2,z2))为对角线创建一个长方形的box。
NX,NY,NZ表示X,Y,Z方向的sph粒子的数量。
Box name和part id都需要用户制定,当给定part的id,比如“1”后,即表明创建的sph单元属于part1,然后点“enter”,可以看到material id也被激活,可以看到如图3的标识,点击这个按钮,就可以为这个part选择相应的材料了。
图3点这个按钮出现如图4的对话框,选择一种材料,如elastic,点击edit,出现如图5的窗口图4图5可以选择add,或者newid,新建一种材料,比如点击add,可以看到mid的选项下面出现了1的标号,代表材料id为“1”,然后填写相应的属性,填写完成选择“accept”,表示接受这种材料类型。
如果还要创建,那么选择“add”,如果想保持当前的数据,只是想把材料id改为别的数值,那么点击“newid”。
创建了材料之后,选择done推出当前窗口,再选择done结束材料的创建。
在sph的主窗口下,选择apply,可以看到我们创建的box形的sph模型,出现在窗口中,如图6所示。
如果不选择“done”,可以继续创建sph模型。
图63.我们现在创建的box使用的缺省尺寸1,1,1。
用户可以根据需要采用不同的尺寸和sph 的数量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
无网格法(Mesh-less method)
无网格方法(Mesh-less method)是在数值计算中不需要生成网格,而是按照一些任意分布的坐标点构造插值函数离散控制方程,就可方便地模拟各种复杂形状的流场。
该法大致可分成两类:一类是以Lagrange方法为基础的粒子法(Particle method),如光滑粒子流体动力学(Smoothed particle hydrodynamics,简称SPH)法,和在其基础上发展的运动粒子半隐式(Moving-particle semi-implicit,简称MPS)法等;另一类是以Euler方法为基础的无格子法(Gridless methods),如无格子Euler/N—S算法(Gridless Euler/Navier-Stokes solution algorithm)和无单元Galerkin法(Element free Galerkin,简称EFG)等。
无网格方法可以方便地利用坐标点计算模拟复杂形状流场计算,但不足之处是在高雷诺数流动时提高数值计算精度较困难。
无网格方法中比较常见的还有径向基函数方法(Radious Basis Function),主要使用某径向基函数(如(MQ)f(r)=r^5)的组合,来逼近原函数。
吴忠敏院士在这方面有比较突出的工作。
最近在了解有限元法和无网格法,介绍中知道它们都是数值计算方法,主要区别一个是基于网格的,一个是无需借助于网格的。
但从有关数值计算方法的书和其他资料中,基本上没有见提到有限元法和无网格法,数值计算方法的书中基本上主要内容都包括:插值和拟合、数值微分和数值积分、求解线性方程组的直接法和迭代法、计算矩阵特征值和特征向量和常微分方程数值解等等。
而在有限元法和无网格法的具体算法计算过程中也都会用到上述数值计算方法中的某些。
