(完整word版)八年级几何辅助线专题训练.doc

合集下载

(word版)全等三角辅助线-半角模型-动点问题(含答案)

全等三角形典型题目合集【专题一】倍长中线与截长补短1．如图1，ABC=+，那么ACB∠有∠与ABC∠的平分线，若AB AC CD∆中，AD是BAC怎样的数量关系呢？（1）通过观察、实验提出猜想：ACB∠的数量关系，用等式表示为：．∠与ABC（2）小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：如图2，延长AC到F，使CF CD=，连接DF．通过三角形全等、三角形的性质等知识进行推理，就可以得到ACB∠与ABC∠的数量关系．想法2：在AB上取一点E，使AE AC=，连接ED，通过三角形全等、三角形的性质等知识进行推理，就可以得到ACB∠的数量关系．∠与ABC请你参考上面的想法，帮助小明证明猜想中ACB∠的数量关系（一种方法即可）．∠与ABC2．【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，ABC ∆中，若8AB =，6AC =，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE AD =，请根据小明的方法思考：（1）由已知和作图能得到ADC EDB ∆≅∆的理由是．A ．SSSB ．SASC ．AASD ．HL（2）求得AD 的取值范围是．A ．68AD <<B ．68ADC ．17AD << D ．17AD【感悟】解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】（3）如图2，AD 是ABC ∆的中线，BE 交AC 于E ，交AD 于F ，且AE EF =．求证：AC BF =．3．阅读下面的题目及分析过程，并按要求进行证明．已知：如图，E 是BC 的中点，点A 在DE 上，且BAE CDE ∠=∠．求证：AB CD =．分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等，因此，要证明AB CD =，必须添加适当的辅助线，构造全等三角形或等腰三角形．现给出如下三种添加辅助线的方法，请任意选择其中两种对原题进行证明．（1）延长DE 到F ，使得EF DE =；（2）作CG DE ⊥于G ，BF DE ⊥于F 交DE 的延长线于F ；（3）过点C 作//CF AB 交DE 的延长线于F ．4．（1）如图，在四边形ABCD中，AB AD=，90B D∠=∠=︒，E、F分别是边BC、CD上的点，且12EAF BAD ∠=∠．求证：EF BE FD=+；（2）如图，在四边形ABCD中，AB AD=，180B D∠+∠=︒，E、F分别是边BC、CD上的点，且12EAF BAD∠=∠，（1）中的结论是否仍然成立？（3）如图，在四边形ABCD中，AB AD=，180B ADC∠+∠=︒，E、F分别是边BC、CD延长线上的点，且12EAF BAD∠=∠，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．5．问题背景：（1）如图①：在四边形ABCD中，AB AD=，120BAD∠=︒，90B ADC∠=∠=︒，E，F 分别是BC，CD上的点，且60EAF∠=︒．探究图中线段BE，FE，FD之间的数量关系，请在右面横线上直接写出结论．（2）如图②，若在四边形ABCD中，AB AD=，180B ADC∠+∠=︒．E、F分别是BC、CD上的点，且12EAF BAD∠=∠，上述结论是否仍然成立？说明理由．6．如图，四边形ABDC中，90D ABD∠=∠=︒，点O为BD的中点，且OA平分BAC∠．（1）求证：CO平分ACD∠；（2）求证：AB CD AC+=．7．如图，90B C ∠=∠=︒，M 是BC 的中点，AM 平分DAB ∠，求证：DM 平分ADC ∠．【专题二】半角模型1．如图正方形ABCD ，E 、F 分别为BC 、CD 边上一点．（1）若45EAF ∠=︒，求证：EF BE DF =+；（2）若该正方形ABCD 的边长为1，如果CEF ∆的周长为2．求EAF ∠的度数．2．如图，正方形ABCD ，E ，F 分别为BC 、CD 边上一点．①若45EAF ∠=︒，求证：EF BE DF =+；②若AEF ∆绕A 点旋转，保持45EAF ∠=︒，问CEF ∆的周长是否随AEF ∆位置的变化而变化？3．已知，在四边形ABCD 中，点E 、F 分别在边BC 、DC 上，连接AF 、EF ．（1）如图1，若四边形ABCD 为正方形，且45EAF ∠=︒，求证：EF BE DF =+；（2）如图2，若四边形ABCD 中，AB AD =，180B D ∠+∠=︒，12EAF BAD ∠=∠，试问（1）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由．4．正方形ABCD ，E 、F 分别为BC 、CD 边上一点，AH EF ⊥交EF 于点H ． ①若45EAF ∠=︒．求证：EF BE DF =+；②若5AB =，求ECF ∆的周长；③求证：AH CD =．5．通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．原题：如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，连接EF ，求证：EF BE DF =+．（1）思路梳理AB AD =，∴把ABE ∆绕点A 逆时针旋转90︒至ADG ∆，可使AB 与AD 重合． 90ADG B ∠=∠=︒，180FDG ADG ADC ∴∠=∠+∠=︒，则点F 、D 、G 共线．根据，易证AFG ∆≅ ，从而得EF BE DF =+；（2）类比引申如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒点E 、F 分别在边BC 、CD 上，45EAF ∠=︒．若B ∠、D ∠都不是直角，但当B ∠与D ∠满足等量关系时，仍有EF BE DF =+，请给出证明；（3）联想拓展如图3，在ABC ∆中，90BAC ∠=︒，AB AC =，点D 、E 均在边BC 上，且45DAE ∠=︒，猜想BD 、DE 、EC 应满足的等量关系，并写出推理过程．【专题三】动点问题1．如图，已知ABC ∆中，10AB AC cm ==，8BC cm =，点D 为AB 的中点．如果点P 在线段BC 上以3/cm s 的速度由点B 向C 点运动，同时，点Q 在线段CA 上由点C 向A 点运动．（1）若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD ∆与CQP ∆是否全等，请说明理由．（2）若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD ∆与CQP ∆全等？2．如图，在ABC ∆中，28AB AC cm ==，20BC cm =，点D 是AB 边的中点，若有一动点P 在BC 边上由点B 向点C 运动，点Q 在CA 边上由点C 向A 运动．（1）P 、Q 两点的运动速度均为3/cm s ，经过2秒后，BPD ∆与CPQ ∆是否全等，说明理由（2）若点P 的运动速度为2.5/cm s ，点Q 的运动速度为3.5/cm s ，是否存在某一时刻，使BPD CQP ∆≅∆．3．如图，已知四边形ABCD 中，10AB =厘米，8BC =厘米，12CD =厘米，B C ∠=∠，点E 为AB 的中点．如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CD 上由C 点向D 点运动．（1）若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPE ∆与CQP ∆是否全等？请说明理由．（2）当点Q 的运动速度为多少时，能够使BPE ∆与CQP ∆全等．4．如图，16AB AC cm ==，10BC cm =，点D 为AB 的中点，点P 在边BC 上以每秒2cm 的速度由点B 向点C 运动，同时，点M 在边CA 上由点C 向点A 匀速运动．（1）当点M 的运动速度与点P 的运动速度相同，经过1秒后，BPD ∆与CMP ∆是否全等？请说明理由；（2）若点M 的运动速度与点P 的运动速度不相等，当点M 的运动速度为多少时，能够使BPD ∆与CMP ∆全等？5．如图，ABC ∆中，D 为AB 的中点，5AD =厘米，B C ∠=∠，8BC =厘米．（1）若点P 在线段BC 上以3厘米/秒的速度从点B 向终点C 运动，同时点Q 在线段CA 上从点C 向终点A 运动，①若点Q 的速度与点P 的速度相等，经1秒钟后，请说明BPD CQP ∆≅∆； ②点Q 的速度与点P 的速度不相等，当点Q 的速度为多少时，能够使BPD CPQ ∆≅∆；（2）若点P 以3厘米/秒的速度从点B 向点C 运动，同时点Q 以5厘米/秒的速度从点C 向点A 运动，它们都依次沿ABC ∆三边运动，则经过多长时间，点Q 第一次在ABC ∆的哪条边上追上点P ？全等三角形典型题目合集解析【专题一】倍长中线与截长补短1．解：（1）2∠=∠，ACB ABC故答案为：2∠=∠，ACB ABC（2）想法1AD是BAC∠的平分线，∴∠=∠，BAC CAB=，AF AC CF=+，且CD CF∴=+，AF AC CD又AB AC CD=+，AB AF∴=，又AD AD=，∴∆≅∆，ABD AFD∴∠=∠，B F=，CD CF∴∠=∠，F CDF又ACB F CDF∠=∠+∠，ACB F∴∠=∠，2∴∠=∠，ACB B2想法2AD 是BAC ∠的平分线，BAC CAB ∴∠=∠，又AC AE =，AD AD =，AED ACD ∴∆≅∆，ED CD ∴=，C AED ∠=∠，又AB AC CD =+，AB AE BE =+，AE AC =，CD BE ∴=，DE BE ∴=，B EDB ∴∠=∠，又AED B EDB ∠=∠+∠，2AED B ∴∠=∠，又C AED ∠=∠，2C B ∴∠=∠．2．（1）解：在ADC ∆和EDB ∆中AD DEADC BDE BD CD=⎧⎪∠=∠⎨⎪=⎩，()ADC EDB SAS ∴∆≅∆，故选B ；（2）解：由（1）知：ADC EDB ∆≅∆，6BE AC ∴==，2AE AD =，在ABE ∆中，8AB =，由三角形三边关系定理得：86286AD -<<+，17AD ∴<<，故选C ．（3）证明：延长AD 到M ，使AD DM =，连接BM ， AD 是ABC ∆中线，CD BD ∴=，在ADC ∆和MDB ∆中DC DB ADC MDB DA DM =⎧⎪∠=∠⎨⎪=⎩ADC MDB ∴∆≅∆，BM AC ∴=，CAD M ∠=∠，AE EF =，CAD AFE ∴∠=∠，AFE BFD ∠=∠，BFD CAD M ∴∠=∠=∠，BF BM AC ∴==，即AC BF =．3．解：方法一：延长DE 到F ，使得EF DE =，连接BF ．在DEC ∆和FEB ∆中，12DE FE BE CE =⎧⎪∠=∠⎨⎪=⎩，DEC FEB ∴∆≅∆，D F ∴∠=∠，DC FB =，BAE D ∠=∠，BAE F ∴∠=∠，BA BF ∴=，AB CD ∴=．方法二：作CG DE ⊥于G ，BF DE ⊥于F 交DE 的延长线于F CG DE ⊥，BF DE ⊥，90CGE BFE ∴∠=∠=︒，在CGE ∆和BFE ∆中，12CGE BFE BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩， CGE BFE ∴∆≅∆，BF CG ∴=，在ABF ∆和DCG ∆中，90BAF CDG BFA CGD BF CG ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，ABF DCG ∴∆≅∆，AB CD ∴=．方法三：过点C 作//CF AB 交DE 的延长线于F ． //CF AB ，BAE F ∴∠=∠，B FCE ∠=∠，在ABE ∆和FCE ∆中，BAE F B FCE BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，ABE FCE ∴∆≅∆，AB FC ∴=，BAE D ∠=∠，BAE F ∠=∠，D F ∴∠=∠，CF CD ∴=，AB CD ∴=．4．证明：（1）延长EB 到G ，使BG DF =，连接AG ．90ABG ABC D ∠=∠=∠=︒，AB AD =，ABG ADF ∴∆≅∆．AG AF ∴=，12∠=∠．113232EAF BAD ∴∠+∠=∠+∠=∠=∠． GAE EAF ∴∠=∠．又AE AE =，AEG AEF ∴∆≅∆．EG EF ∴=．EG BE BG =+．EF BE FD ∴=+（2）（1）中的结论EF BE FD =+仍然成立．（3）结论EF BE FD =+不成立，应当是EF BE FD =-．证明：在BE 上截取BG ，使BG DF =，连接AG ．180B ADC ∠+∠=︒，180ADF ADC ∠+∠=︒，B ADF ∴∠=∠．AB AD =，ABG ADF ∴∆≅∆．BAG DAF ∴∠=∠，AG AF =．BAG EAD DAF EAD ∴∠+∠=∠+∠12EAF BAD =∠=∠． GAE EAF ∴∠=∠．AE AE =，AEG AEF ∴∆≅∆．EG EF ∴=EG BE BG =-EF BE FD ∴=-．5．解：（1）EF BE DF =+，理由如下：如图①中，延长FD 到点G ．使DG BE =．连结AG ．在ABE ∆和ADG ∆中，DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩，()ABE ADG SAS ∴∆≅∆，AE AG ∴=，BAE DAG ∠=∠，12EAF BAD ∠=∠， GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠， EAF GAF ∴∠=∠，在AEF ∆和GAF ∆中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，()AEF AGF SAS ∴∆≅∆，EF FG ∴=，FG DG DF BE DF =+=+，EF BE DF ∴=+；故答案为EF BE DF =+．（2）结论EF BE DF =+仍然成立；理由：延长FD 到点G ．使DG BE =．连结AG ，如图②，在ABE ∆和ADG ∆中，DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩，()ABE ADG SAS ∴∆≅∆，AE AG ∴=，BAE DAG ∠=∠，12EAF BAD ∠=∠， GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠， EAF GAF ∴∠=∠，在AEF ∆和GAF ∆中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，()AEF AGF SAS ∴∆≅∆，EF FG ∴=，FG DG DF BE DF =+=+，EF BE DF ∴=+；6．证明：（1）过O 点作OE AC ⊥于点E ． 90ABD ∠=︒且OA 平分BAC ∠OB OE ∴=，又O 是BD 中点OB OD ∴=，OE OD ∴=，OE AC ⊥，90D ∠=︒∴点O 在ACD ∠ 的角平分线上 OC ∴平分ACD ∠．（2）在Rt ABO ∆和Rt AEO ∆中OA OA OB OE =⎧⎨=⎩Rt ABO Rt AEO(HL)∴∆≅∆，AB AE ∴=，在Rt CDO ∆和Rt CEO ∆中OC OC OE OD =⎧⎨=⎩Rt CDO Rt CEO(HL)∴∆≅∆，CD CE ∴=，AB CD AE CE AC ∴+=+=．7．证明：如图：过点M 作ME AD ⊥，垂足为E ， AM 平分DAB ∠，34∴∠=∠，MB AB ⊥，ME AD ⊥，ME MB ∴=（角平分线上的点到角两边的距离相等），又MC MB =，ME MC ∴=，MC CD ⊥，ME AD ⊥，DM ∴平分ADC ∠（到角的两边距离相等的点在这个角的平分线上）；【专题二】半角模型答案1．（1）证明：如图，延长CD 至E '，使DE BE '=，连接AE '，四边形ABCD 为正方形，AB AD CB CD ∴===，90BAD B ∠=∠=︒，90ADE ABE '∴∠=︒=∠，在ADE '∆和ABE ∆中，AD AB ADE ABE DE BE =⎧⎪∠'=∠⎨⎪'=⎩，()ADE ABE SAS '∴∆≅∆，AE AE '∴=，DAE BAE '∠=∠，45EAF ∠=︒，45DAF BAE ∴∠+∠=︒，45DAF DAE E AF EAF ''∴∠+∠=∠=︒=∠，在△E AF '和EAF ∆中，AE AE E AF EAF AF AF '=⎧⎪∠'=∠⎨⎪=⎩，∴△()E AF EAF SAS '≅∆，E F EF ∴'=，E F DE DF BE DF '='+=+，EF BE DF ∴=+；（2）延长CD 至E '使DE BE '=，连接AE '，由（1）知，()ADE ABE SAS '∆≅∆，AE AE '∴=，DAE BAE '∠=，设BE x =，DF y =，正方形ABCD 的边长为1，1CE x ∴=-，1CF y =-，CEF ∆的周长为2，2CE CF EF ∴++=，112x y EF ∴-+-+=，EF x y BE DF DE DF E F ''∴=+=+=+=，在△EAF '和EAF ∆中，AE AEE F EF AF AF '=⎧⎪'=⎨⎪=⎩，∴△()E AF EAF SSS '≅∆，EAFEAF '∴∠=∠， DAE DAF BAE DAF EAF '∴∠+∠=∠+∠=∠，90DAF EAF BAE ∠+∠+∠=︒，45EAF ∴∠=︒．2．①证明：四边形ABCD 为正方形，AB AD CB CD ∴===，90BAD B ∠=∠=︒，把ABE ∆绕点A 逆时针旋转90︒可得到ADE ∆'，AE AE ∴'=，DE BE '=，90E AE ∠'=︒，90ADE ADC ∠'=∠=︒， 45EAF ∠=︒，45E AF E AE EAF ∴∠'=∠'-∠=︒，E AF EAF ∴∠'=∠，在△E AF '和EAF ∆中，AE AE E AF EAFAF AF '=⎧⎪∠'=∠⎨⎪=⎩， ∴△()E AF EAF SAS '≅∆，E F EF ∴'=，E F DE DF BE DF '='+=+，EF BE DF ∴=+；②解：不变化；理由如下：CEF ∆的周长CE CF EF CE CF BE DF CB CD =++=+++=+． CEF ∴∆的周长不随AEF ∆位置的变化而变化．3．解：（1）如图①，延长CB 到G ，使BG FD =，90ABG D ∠=∠=︒，AB AD =，ABG ADF ∴∆≅∆，BAG DAF ∴∠=∠，AG AF =，12EAF BAD ∠=∠， DAF BAE EAF ∴∠+∠=∠，EAF GAE ∴∠=∠，在AEG ∆和AEF ∆中，AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩，AEF AEG ∴∆≅∆，EF EG EB BG EB DF ∴==+=+；（2）（1）中的结论还成立，理由如下：把ADF ∆绕点A 顺时针旋转DAB ∠的度数得到ABG ∆，如图②，② ADF ABG ∴∠=∠，GAF BAD ∠=∠，AG AF =，BG DF =，180ABC ADC ∠+∠=︒，180ABC ABG ∴∠+∠=︒，∴点G 在CB 的延长线上，GE BG BE ∴=+，12EAF BAD ∠=∠， 12EAF GAE ∴∠=∠， EAF GAE ∴∠=∠，在AEG ∆和AEF ∆中，AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩，()AEG AEF SAS ∴∆≅∆，EF GE ∴=，EF BE BG BE DF ∴=+=+．4．①证明：将ADF ∆绕点A 顺时针旋转90︒得到ABG ∆，由旋转的性质得，DF BG =，AF AG =，DAF BAG ∠=∠．90FAG BAG BAF DAF BAF BAD ∠=∠+∠=∠+∠=∠=︒，45EAF ∠=︒，45EAF EAG ∴∠=∠=︒．在AEF ∆和AEG ∆中，AF AG EAF EAG AE AE =⎧⎪∠=∠⎨⎪=⎩，()AEF AEG SAS ∴∆≅∆，EF EG BG BE DF BE ∴==+=+，EF BE DF ∴=+． ②四边形ABCD 是正方形，5AB BC CD AD ∴====，EF BE DF =+，EFC ∴∆的周长()()210EF EC CF BE EC CF DF BC =++=+++==． ③AEF AEG ∆≅∆ 又AH 、AB 分别是AEF ∆和AEG ∆对应边上的高，AH AB ∴=．5．解：（1）如图1，AB AD =， ∴把ABE ∆绕点A 逆时针旋转90︒至ADG ∆，可使AB 与AD 重合． BAE DAG ∴∠=∠，90BAD ∠=︒，45EAF ∠=︒，45BAE DAF ∴∠+∠=︒，EAF FAG ∴∠=∠，90ADC B ∠=∠=︒，180FDG ∴∠=︒，点F 、D 、G 共线，在AFE ∆和AFG ∆中AE AG EAF FAG AF AF =⎧⎪∠=∠⎨⎪=⎩，()AFE AFG SAS ∴∆≅∆，EF FG ∴=，即：EF BE DF =+．故答案为：SAS ，AFE ∆；（2）180B D ∠+∠=︒时，EF BE DF =+；如图2，AB AD =， ∴把ABE ∆绕点A 逆时针旋转90︒至ADG ∆，可使AB 与AD 重合， BAE DAG ∴∠=∠，90BAD ∠=︒，45EAF ∠=︒，45BAE DAF ∴∠+∠=︒，EAF FAG ∴∠=∠，180ADC B ∠+∠=︒，180FDG ∴∠=︒，点F 、D 、G 共线，在AFE ∆和AFG ∆中AE AG EAF FAG AF AF =⎧⎪∠=∠⎨⎪=⎩，()AFE AFG SAS ∴∆≅∆，EF FG ∴=，即：EF BE DF =+．故答案为：180B D ∠+∠=︒；（3）猜想：222DE BD EC =+，证明：如图3，连接DE '，根据AEC ∆绕点A 顺时针旋转90︒得到ABE ∆'， AEC ABE ∴∆≅∆'，BE EC ∴'=，AE AE '=，C ABE ∠=∠'，EAC E AB ∠=∠'，在Rt ABC ∆中，AB AC =，45ABC ACB ∴∠=∠=︒，90ABC ABE ∴∠+∠'=︒，即90E BD ∠'=︒，222E B BD E D ∴'+='，又45DAE ∠=︒，45BAD EAC ∴∠+∠=︒，45E AB BAD ∴∠'+∠=︒，即45E AD ∠'=︒，在△AE D '和AED ∆中，AE AE E AD DAE AD AD '=⎧⎪∠'=∠⎨⎪=⎩，∴△()AE D AED SAS '≅∆，DE DE ∴='，222DE BD EC ∴=+．【专题三】动点专项答案1．解：（1）经过1秒后，3PB cm =，5PC cm =，3CQ cm =， ABC ∆中，AB AC =，∴在BPD ∆和CQP ∆中，BD PC ABC ACB BP CQ =⎧⎪∠=∠⎨⎪=⎩，()BPD CQP SAS ∴∆≅∆．（2）设点Q 的运动速度为(3)/x x cm s ≠，经过ts BPD ∆与CQP ∆全等；则可知3PB tcm =，83PC tcm =-，CQ xtcm =，AB AC =，B C ∴∠=∠，根据全等三角形的判定定理SAS 可知，有两种情况：①当BD PC =，BP CQ =时，②当BD CQ =，BP PC =时，两三角形全等；①当BD PC =且BP CQ =时，835t -=且3t xt =，解得3x =，3x ≠，∴舍去此情况； ②BD CQ =，BP PC =时，5xt =且383t t =-，解得：154x =；故若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为15/4cm s 时，能够使BPD ∆与CQP ∆全等．2．解：（1）BPD CPQ ∆≅∆， D 是AB 的中点，14BD ∴=．又326BP =⨯=，20614CP ∴=-=，326CQ =⨯=， AB AC =，B C ∴∠=∠，在BPD ∆和CPQ ∆中，BD CP B C BP CQ =⎧⎪∠=∠⎨⎪=⎩，BPD CPQ ∴∆≅∆．（2）存在，设经过t 秒时BPD CPQ ∆≅∆．依题意 2.5BP t =， 3.5CQ t =，20 2.5PC t =-．若BPD CPQ ∆≅∆必须有BP CP =，即2.520 2.5t t =-，解得4t =．故当4t =秒时BPD CPQ ∆≅∆．3．解：（1）全等，理由如下：当运动1秒后，则3BP CQ cm ==， 835PC BC BP cm cm cm ∴=-=-=， E 为AB 中点，且10AB cm = 5BE cm ∴=，BE PC ∴=，在BPE ∆和CQP ∆中BE PC B C BP CQ =⎧⎪∠=∠⎨⎪=⎩()BPE CQP SAS ∴∆≅∆；（2）BPE ∆与CQP ∆全等， ∴有BEP CQP ∆≅∆或BEP CPQ ∆≅∆，当BEP CQP ∆≅∆时，则BP CP =，5CQ BE cm ==，设P 点运动的时间为t 秒，则383t t =-，解得43t =秒， Q ∴点的速度4155()34cm =÷=，当BEP CPQ ∆≅∆时，由（1）可知1t =（秒)， 3BP CQ ∴==，Q ∴点的速度313()cm =÷=，即当Q 点每秒运动154cm 或3cm 时BEP CQP ∆≅∆． 4．解：（1）结论：，BPD ∆与CMP ∆全等理由：1t s =时，2PB =，2CM =，182BD AB ==，1028PC =-=， AB AC =，B C ∴∠=∠，在BDP ∆和CPM ∆中， BD CP B C BP CM =⎧⎪∠=∠⎨⎪=⎩，BDP CPM ∴∆≅．（2）由题意BPD ∆与CMP ∆全等， CM PB ≠，8CM BD ∴==，5PC PB ==， 52t ∴=， ∴点M 的运动速度5168/25cm s =÷=． 5．解：（1）①313BP =⨯=，313CQ =⨯=，BP CQ ∴=， D 为AB 的中点，5BD AD ∴==，5CP BC BP =-=， BD CP ∴=，在BPD ∆与CQP ∆中， BD CP B C BP CQ =⎧⎪∠=∠⎨⎪=⎩， BPD CQP ∴∆≅∆； ②设点Q 运动时间为t 秒，运动速度为/vcm s ， BPD CPQ ∆≅， 4BP CP ∴==，5CQ =， 433BP t ∴==， 515443CQ v t∴===；（2）设经过x 秒后，点Q 第一次追上点P ，由题意得53210x x -=⨯，解得：10x =， ∴点P 运动的路程为31030⨯=， 30282=+， ∴此时点P 在BC 边上， ∴经过10秒，点Q 第一次在BC 边上追上点P ．。

【强烈推荐】八年级数学三角形辅助线大全(精简、全面)(word版可编辑修改)

【强烈推荐】八年级数学三角形辅助线大全(精简、全面)(word版可编辑修改)编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（【强烈推荐】八年级数学三角形辅助线大全(精简、全面)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为【强烈推荐】八年级数学三角形辅助线大全(精简、全面)(word版可编辑修改)的全部内容。

(完整word版)八年级数学上几何证明中的辅助线添加方法

八年级数学（上）几何证明中的辅助线添加方法数学组田茂松八年级数学的几何题, 有部分题需要做出辅助线才能完成。

有的时候, 做不出恰当的辅助线,或者做不出辅助线, 就没有办法完成该题的解答。

为了能够更好的让学生在做几何题时得心应手, 现在将八年级数学中几何题的辅助线添加方法总结如下。

常见辅助线的作法有以下几种:1.遇到等腰三角形, 可作底边上的高, 利用“三线合一”的性质解题, 思维模式是全等变换中的“对折”。

2.遇到三角形的中线, 倍长中线, 使延长线段与原中线长相等, 构造全等三角形, 利用的思维模式是全等变换中的“旋转”。

3.遇到角平分线, 可以自角平分线上的某一点向角的两边作垂线, 利用的思维模式是三角形全等变换中的“对折”, 所考知识点常常是角平分线的性质定理或逆定理.4.过图形上某一点作特定的平分线, 构造全等三角形, 利用的思维模式是全等变换中的“平移”或“翻转折叠”。

5.截长法与补短法, 具体做法是在某条线段上截取一条线段与特定线段相等, 或是将某条线段延长, 是之与特定线段相等, 再利用三角形全等的有关性质加以说明．这种作法, 适合于证明线段的和、差、倍、分等类的题目。

6.特殊方法：在求有关三角形的定值一类的问题时, 常把某点到原三角形各顶点的线段连接起来, 利用三角形面积的知识解答。

常见辅助线的作法举例:例. 如图1, ， . 求证: .分析：图为四边形, 我们只学了三角形的有关知识, 必须把它转化为三角形来解决。

证明: 连接（或）∵//AB CD , //AD BC （已知） ∴∠1＝∠2, ∠3＝∠4 （两直线平行, 内错角相等）在ABC ∆与CDA ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已证公共边已证CA AC ∴ABC ∆≌CDA ∆（ASA ） ∴AD BC =（全等三角形对应边相等）例. 如图2,在中, , , , 的延长于 .求证: .分析: 要证 , 想到要构造线段 , 同时与的平分线垂直, 想到要将其延长。

八年级全等三角形----辅助线篇(含答案)

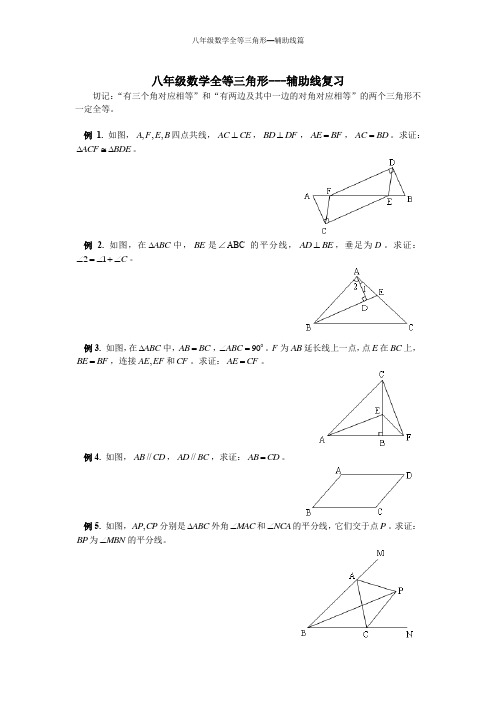
八年级数学全等三角形---辅助线复习切记：“有三个角对应相等”和“有两边及其中一边的对角对应相等”的两个三角形不一定全等。

例 1. 如图，,,,A F E B 四点共线，AC CE ⊥，BD DF ⊥，AE BF =，AC BD =。

求证：ACF BDE ∆≅∆。

例 2. 如图，在ABC ∆中，BE 是∠ABC 的平分线，AD BE ⊥，垂足为D 。

求证：21C ∠=∠+∠。

例3. 如图，在ABC ∆中，AB BC =，90ABC ∠=o。

F 为AB 延长线上一点，点E 在BC 上，BE BF =，连接,AE EF 和CF 。

求证：AE CF =。

例4. 如图，AB //CD ，AD //BC ，求证：AB CD =。

例5. 如图，,AP CP 分别是ABC ∆外角MAC ∠和NCA ∠的平分线，它们交于点P 。

求证：BP 为MBN ∠的平分线。

例6. 如图，D 是ABC ∆的边BC 上的点，且CD AB =，ADB BAD ∠=∠，AE 是ABD ∆的中线。

求证：2AC AE =。

例7. 如图，在ABC ∆中，AB AC >，12∠=∠，P 为AD 上任意一点。

求证：AB AC PB PC ->-。

同步练习一、选择题：1. 能使两个直角三角形全等的条件是( ) A. 两直角边对应相等 B. 一锐角对应相等 C. 两锐角对应相等D. 斜边相等2. 根据下列条件，能画出唯一ABC ∆的是( ) A. 3AB =，4BC =，8CA =B. 4AB =，3BC =，30A ∠=oC. 60C ∠=o ，45B ∠=o ，4AB =D. 90C ∠=o ，6AB =3. 如图，已知12∠=∠，AC AD =，增加下列条件：①AB AE =；②BC ED =；③C D ∠=∠；④B E ∠=∠。

其中能使ABC AED ∆≅∆的条件有( )A. 4个B. 3个C. 2个D. 1个（第3题）（第4题）（第5题）（第6题） 4. 如图，已知AB CD =，BC AD =，23B ∠=o ，则D ∠等于( )A. 67oB. 46oC. 23oD. 无法确定二、填空题：5. 如图，在ABC ∆中，90C ∠=o ，ABC ∠的平分线BD 交AC 于点D ，且:2:3CD AD =，10AC cm =，则点D 到AB 的距离等于__________cm ；6. 将一张正方形纸片按如图的方式折叠，,BC BD 为折痕，则CBD ∠的大小为_________；三、解答题：7. 如图，ABC ∆为等边三角形，点,M N 分别在,BC AC 上，且BM CN =，AM 与BN 交于Q 点。

八年级三角形辅助线作法及答案解析

三角形辅助线作法一.“分角两边作垂线，垂直平分连两端” 例1. 如图，在ABC Rt 中，ACB 90A 30∠=∠=，,BD 平分ABC ∠；若CD 3cm =，求AD 的长度？分析：本题不添辅助线也可以求得AD 的长度，但环节要多，书写的步骤也就较多，浪费时间；若过ABC ∠的平分线AD 的点D 向AB 垂线，根据角平分线的性质可以得出DE CD 3cm ==;在AED Rt 有A 30∠=,所以()AD 2DE 236cm ==⨯=.点评：本题的关键是通过过ABC ∠的平分线AD 的点D 向AB 垂线后，使得DE CD 3cm ==的转换后，使得线段AD 的长度在AED Rt便可轻松求得；真可谓是“分角两边作垂线，线段相等好转换”. 例2.如图所示，△ABC 中，AB=AC ，∠BAC=120°，AC 的垂直平分线EF 交AC 于点E ，交BC 于点F ．求证：BF=2CF ．分析：根据题中条件容易求出B C 30∠=∠=；本题从结论出发自然会想到“在直角三角形中，30°锐角所对的直角边等于斜边的一半”这条性质，而这一个“结”，在当我们连结AF 解开了. 略证：连结AF∵AB AC = ,∴B C ∠=∠ ; 又BAC 120∠=,∴B C 120∠+∠= ∴B C 30∠=∠=.∵EF 垂直平分AC ∴FA FC = ∴FAC C 30∠=∠= 又BAC 120∠= ∴BAF 1203090∠=-=∵B 30∠= ∴BF 2AF = ∵FA FC = ∴BF 2CF =点评：本题的关键是通过连结AF ，使得FA FC =的转换后，使得在BAF Rt 中有BF 2AF =，然后进一步证得BF 2CF =；真可谓是“垂直平分两端连，线段相等好转换”.二.“等腰作三线，解答更方便”例. 如图，,AB AE AC AD ==,点B C D E 、、、在同一直线上.求证：BC ED =分析：本题通过证明ABC ≌AED 能证明BC ED =.但本题若作AF BE ⊥更为简捷.略证：过A 作AF BE ⊥，垂足为F .又∵,AB AE AC AD == ∴,BF EF CF DF ==（三线合一）∴BF CF EF DF -=-即BC ED =点评：本题的关键是抓住,AB AE AC AD ==即ABE 和ACD 都是等腰三角形的特点，在等腰三角形的性质中的“三线合一”中的等腰三角形的“底边上的高线与底边上的中线互相重合”，两次推理即可完成推理，这比通过证明三角形全等少了一大半的环节；真是“等腰作三线，解题更方便”. 所谓“作三线” 也就是作等腰三角形底边上的高线或作等腰三角形底边上的中线或作等腰三角形顶角的平分线.三、“图中出现‘T ’字形，连成等腰三角形”例.已知：ABC ∆中，高AD 与BE 相交于点F ,且AD BD =,G I 、分别是 AC BF 、上的点，且AG BI =，H 为IG 的中点. 求证：DH IG ⊥分析：我们学了等腰三角形的“三线合一”后，证明垂直关系又多了一条途径，本题中的“T ”形（见图中的粗线部分）中，有H 为IG 的中点，若连结DI DG 、，并证明到,根据等腰三角形的“三线合一”的等腰三角形的底边上的中线与底边上的高线互相重合即可证明DH IG ⊥.根据题中的条件能证明DI DG =.略证：连结DI DG 、.∵AD 与BE 是ABC 的BC AC 、的高 ∴AD BC BE AC ⊥⊥、 ∴ADC BEC 90∠=∠=∴EBC C 90DAC C 90∠+∠=∠+∠=， ∴EBC DAC ∠=∠ 于是在BDI 和DAG 中有: AD BD =,EBC DAC ∠=∠,AG BI = ∴BDI ≌DAG ∴DI DG = ∵H 为IG 的中点∴DH IG ⊥(三线合一).点评：本题的关键是在图中出现的“T ”形（见图中的粗线部分）中，有H 为IG 的中点，连结DI DG 、后，非常容易联想到证明DI DG =构成等腰三角形，根据等腰三角形的“三线合一“获得证明.请记住“图中出现‘T ’字形，连成等腰三角形”.四.“线段和差要证好，‘截长补短’不可少”例1.已知：如图，ABC ∆中，,AB AC A 108=∠=,CD 平分BCA ∠交AB 于D .求证：BC CE BD =+分析: 证明线段的和差关系比较抽象，有许多要通过“截长补短”的办法来添辅助线来破题.本题采用截长法，若在BC 上截取CE CA =,连结DE 后易证CDE ≌CDA （SAS ）,所以DEC A 108∠=∠= ∴DEB 180DEC 18010872∠=-∠=-= ∵,AB AC A 108=∠= ∴()1B 180108362∠=-= 在BDE 中，BDE 180B BED 180367272∠=-∠-∠=--= ∴BED BDE ∠=∠ ∴BD BE =.由BC CE BE =+可得BC CE BD =+.例2.如图，已知：ABC ∆中，12A ∠=∠，AD 评分ACB ∠求证：AC BC DE =+分析: 证明线段的和差关系比较抽象，有许多要通过“截长补短”的办法来添辅助线来破题.本题采用截长法或补短法均可，下面我们采用“补短法”. 延长CB 至E ,使CE CA =,此时由于有CE CB BE =+,所以AC CB BE =+;由题中的条件容易证明ACD ≌ECD （SAS ）,得出E A ∠=∠;∵,12A 1E 2∠=∠∠=∠+∠∴E 2∠=∠ ∴BD BE =E∴AC CB BE =+.点评：在证明一条线段等于另外两条线段的和差，可以在较长的一条线段上截取一条线段等于和差中其中一较短的一线段，称为“截长法”；在较段的一条线段的延长线上截取一条线段和原线段的和等于和差中较长的一条线段，称为“补短法”. “截长补短”法的核心还是通过辅助线构造全等三角形来转换，上面两例就是这样.真是“线段和差要证好，‘截长补短’不可少”.五.“两边之间夹中线，倍长中线全等见”例.已知：ABC ∆中，AD 是BC 边上的中线，AB 3AC 5==，;求AD 的取值范围？分析:在几何图形中，求一条线段的取值范围，我们自然会联想到三角形的三边之间的关系，而本题的已知的AB 3AC 5==，和要求取值范围的线段AD 并非为同一三角形的三边，所以我们要想办法把这三条线段“搬”到同一三角形中；本题若采取倍长中线的办法可以获得解决.如图，若延长AD 至E ,使DE AD =连结BE ;容易证明ACD ≌EBD （SAS ）, ∴BE AC 5==；在ABE 中，有BE AB AE BE AB -<<+,即：2AE 8<<,又AE AD DE 2AD =+=, ∴,22AD 8<<故1AD 4<<.点评：在几何解答题中，要把分散的条件在图中集中起来（也就是“化归”），常常要通过构造全等三角形来变更有些角或线段的位置，倍长中线是比较重要的途径.请记住: “两边之间夹中线，倍长中线全等见”.。

【强烈推荐】八年级数学三角形辅助线大全(精简、全面)精编版

三角形作辅助性方法大全1.在利用三角形的外角大于任何和它不相邻的内角证明角的不等关系时，如果直接证不出来，可连结两点或延长某边，构造三角形，使求证的大角在某个三角形外角的位置上，小角处在内角的位置上，再利用外角定理证题例：已知 D ABC 内任一点，求证：/ BDC >/BAC证法（一）：延长BD 交AC 于E ,•••/ BDC >△ EDC 的外角， •••/ BDC >/ DEC同理：/ DEC >Z BAC •••/ BDC >Z BAC证法（二）：连结AD ，并延长交BC 于F•••/ BDF 是厶ABD 的外角,•••/ BDF >Z BAD 同理/ CDF >Z CAD•••/ BDF +Z CDF >Z BAD +Z CAD 即：/ BDC >Z BAC2.有角平分线时常在角两边截取相等的线段，构造全等三角形例：已知，如图， AD ABC 的中线且/ 1 = / 2,/ 3 = / 4, 求证：BE + CF > EF证明：在 DA 上截取DN = DB ，连结NE 、NF ，贝U DN 在厶BDE和厶NDE 中，DN = DB/ 1 = / 2ED = ED•••△ BDE ◎△ NDE• BE = NE 同理可证：CF = NF在厶 EFN 中, EN + FN > EF • BE + CF > EF3. 有以线段中点为端点的线段时，常加倍延长此线段构造全等三角形例：已知，如图， AD ABC 的中线，且/ 1 = / 2, / 3 = / 4,求证：BE + CF >EF 证明：延长 ED 至U M ，使DM = DE ，连结 CM 、FM△ BDE 和厶CDM 中，BD = CD/ 1 = / 5ED = MD•••△ BDE ◎△ CDM• CM = BE又•••/ 1 = / 2, / 3 = / 4/ 1 + / 2 +/ 3 + / 4 = 180°=DCCFC•••/ 3 +Z 2 = 90°即/ EDF = 90/ EDF = 90△ EDF 和厶MDF 中ED = MD/ FDM = / EDFDF = DF• △ EDF ◎△ MDF• EF = MF•••在△ CMF 中，CF + CM > MFBE + CF > EF（此题也可加倍 FD ，证法同上）4.在三角形中有中线时，常加倍延长中线构造全等三角形 .例：已知，如图， ADABC 的中线，求证： AB + AC >2AD证明：延长AD 至E ，使DE = AD ，连结BE•/ AD ABC 的中线• BD = CD在厶ACD 和厶EBD 中BD = CD/ 1 = / 2AD = ED• △ ACD EBD •/△ ABE 中有 AB + BE >AE • AB + AC > 2AD5. 截长补短作辅助线的方法截长法：在较长的线段上截取一条线段等于较短线段；补短法：延长较短线段和较长线段相等.这两种方法统称截长补短法 .当已知或求证中涉及到线段 a 、b 、c 、d 有下列情况之一时用此种方法: ① a > b ② a ±3 = c ③ a ±3 = c ±i例：已知，如图，在△ ABC 中，AB > AC ，/ 1 = / 2, P 为AD 上任一点，求证：AB — AC > PB - PC证明：⑴截长法：在AB 上截取AN = AC ，连结PN在厶APN 和厶APC 中，AN = AC/ 1 = / 2AP = AP• △ APN ◎△ APCME•PC = PN•/△ BPN 中有PB —PC v BN••• PB —PC v AB —AC⑵补短法：延长AC至M，使AM = AB，连结PM在厶ABP和厶AMP中AB = AM/ 1 = / 2AP = AP•△ ABP ◎△ AMP•PB = PM又•••在△ PCM 中有CM > PM —PC• AB —AC > PB —PC练习：1.已知，在△ ABC中，/ B = 60o,AD、CE是厶ABC的角平分线,并且它们交于点0求证：AC = AE + CD2•已知，如图，AB // CD / 1 = / 2，/3 = / 4.求证：BC = AB + CD6. 证明两条线段相等的步骤：①观察要证线段在哪两个可能全等的三角形中，然后证这两个三角形全等。

(word版)全等三角形精选证明及辅助线作法(培优)

（初中几何）全等三角形精选题目1.已知：如图，AE =AC ， AD =AB ，∠EAC =∠DAB ，求证：△EAD ≌△CAB ．2.如图，△ABC 与△DCB 中，AC 与BD 交于点E ，且∠A =∠D ，AB =DC ．（1）求证：△ABE ≌DCE ；（2）当∠AEB =50°，求∠EBC 的度数？3.如图，已知BE 、CF 是的高，且BP =AC ，CQ =AB ，求证：AP ⊥AQ ，AP =AQ4.如图，在等边△ABC 中， BD =CE ， AD 与BE 相交于点P ，求∠APE 的度数．EDCBAE OP F QCBA DP ECBAACBE D5.如图，已知等腰Rt △OAB 中，∠AOB =90°，等腰Rt △EOF 中，∠EOF =90°，连结AE 、BF ．请猜想线段AE 和线段BF 的关系，并证明你给出的结论.6.如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线，交AB 于点E ，交AD 于点F ，求证：∠ADC ＝∠BDE ．7.如图，四边形ABCD 是正方形，G 是BC 上任意一点（点G 与B 、C 不重合），AE ⊥DG 于E ，CF ∥AE 交DG 于F .求证：AE =DE +EF .OFEBAFD C BAGFE DCBA8. 正方形四条边都相等，四个角都是90°，如图，已知正方形ABCD 在直线MN 的正上方，BC 在直线MN 上，点E 是直线MN 上一点，以AE 为边在直线MN 的上方作正方形AEFG.（1）如图1，当点E 在线段BC 上（不与点B 、C 重合）时： ① 判断△ADG 和△ABE 是否全等，并说明理由：② 过点F 作FH ⊥MN ，垂足为点H ，观察并猜想线段BE 和线段CH 的数量关系，并说明理由：（2）如图2，当点E 在射线CN 上（不与点C 重合）时： ①判断△ADG 和△ABE 是否全等，并说明理由：②过点F 作FH ⊥MN ，垂足为点H ，已知GD =4，求△CFH 的面积.图1 图29.如图，在四边形ABCD 中，BC > BA ，AD=CD ，BD 平分∠ABC ，求证：∠A +∠C =180°.E H FGDCBAN MEN MHFGD CBA DCBA10.如图，已知AD ∥BC ，点E 是CD 上一点，连接AE 、BE ，且AE 、BE 恰好是∠DAB 和∠ABC 的角平分线.求证：AB =AD ＋BC .11.如图，在△ABC 中，D 是BC 边的中点，E 是AD 上一点，BE =AC ，BE 的延长线交AC 于点F ，求证：∠AEF =∠EAF ．12.如图，在△ABC 中，D 是BC 的中点，过点D 作射线交AB 于点E ，交CA 的延长线与点F ，若∠AEF =∠F ，求证：BE=CF .EDCBAF ED CB A F E DCBA13.在四边形ABCD 中，AB ∥DC ，点E 为BC 边上的中点，∠BAE =∠EAF ，AF 与DC 的延长线相交于于点F ，试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.14.如图，△ABC 中，BD =DC =AC ，E 是DC 的中点，求证，AD 平分∠BAE.15.如图：在四边形ABCD 中，AD ∥BC ，AB=AD+BC ，E 是CD 的中点，求证：AE ⊥BE .AFEDCBEDCB AEDCB A16.如图，在线段AE 同侧作两个等边三角形△ABC 和△CDE （∠ACE ＜120°），点P 与点M 分别是线段BE 和AD 的中点，请探索△CPM 是什么三角形，并进行证明.17.已知：如图，△ABC 中，∠ABC =45°，CD ⊥AB 于点D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，H 是BC 边的中点，连结DH 与BE 相交于点G .（1）求证：BF =AC ；（2）CE 和BF 有怎样的数量关系，写出判断并给出证明；（3）CE 与BG 的大小关系如何？试证明你的结论.MP DC BEACEFHGD BA。

(完整版)圆中的辅助线专题训练

(完整版)圆中的辅助线专题训练完整版圆中的辅助线专题训练一、题目：在如图所示的两个圆中，圆A的半径为r，圆B的半径为2r。

已知圆A上有一点P，连接AP，并延长与圆B相交于点M。

连接AM，并延长与圆B相交于点N。

连接BN。

1. 若AP与圆B的切线交BN于点O，证明：∠MOB=90°。

证明步骤：首先，连接OP。

由于AP为圆A上的切线，根据切线定理，可知∠AMP=90°。

又由于AM与圆B相交于点M，根据圆的性质可知∠AMO=∠MPO。

由于M、N、P、O四点共圆，因此∠MOT=∠MPN。

综上所述，有∠MOT=∠MPN，而由于直线与切线的性质，∠MPN=∠MNT，所以∠MOT=∠MNT。

由于∠MOT和∠MNT是同位角，所以∠MOB=∠MNB=∠MNT=90°。

因此，证明了∠MOB=90°。

2. 若∠MOB=90°，判断：点P是否在圆A上的切线上？判断方法：首先，通过连接OM和OB，构成直角三角形MOB。

根据直角三角形的性质可知，若∠MOB=90°，则MB的平方等于MO的平方加上OB的平方。

若∠MOB=90°，则MO的平方加上OB的平方等于光点M到圆B的弦BN的平方。

若∠MOB=90°，则光点M到圆B的弦BN的平方等于点A到圆B的切线AP与切点T的距离的平方。

因此，通过计算MO的平方加上OB的平方、光点M到圆B的弦BN的平方和点A到圆B的切线AP与切点T的距离的平方，即可判断点P是否在圆A上的切线上。

二、总结：在给定的题目中，我们通过证明及判断确定了圆中辅助线的性质。

通过建立合适的几何关系和利用直角三角形的性质，我们可以有效地解决与圆中辅助线相关的问题。

在实际应用中，我们可以运用这些方法来解决类似的几何问题，提高我们的解题能力。

这就是完整版圆中的辅助线专题训练的内容。

以上是我为您准备的文档，希望能对您有所帮助！如有其他问题，欢迎继续咨询。

初二辅助线练习题推荐

初二辅助线练习题推荐作为初二学生，在数学学习中，掌握线段的辅助线绘制方法是非常重要的。

辅助线不仅能够帮助我们解题，还能够提高我们的思维能力和解题的灵活性。

下面我将向大家推荐一些初二辅助线练习题，希望对大家的学习有所帮助。

一、平行四边形的辅助线题目1：已知平行四边形ABCD中，AB=10cm, BC=8cm，以点A 为起点，用适当的辅助线绘制的正方形BEFG，连接DG，求DG的长度。

解题思路：首先，我们可以将平行四边形ABCD绘制出来，并连接对角线AC，形成等腰直角三角形ADC。

然后，我们通过画辅助线，将正方形BEFG绘制出来。

最后，连接DG，并求出其长度。

通过这道题目的练习，我们可以锻炼辅助线的运用能力和平行四边形的性质。

题目2：在平行四边形ABCD中，AB=6cm，BC=8cm，以点A为起点，用适当的辅助线绘制的矩形AEFG，连接CG，求CG的长度。

解题思路：我们可以利用平行四边形的性质，绘制出矩形AEFG，进而连接CG，并求出其长度。

通过这道题目的练习，可以加深对平行四边形及其性质的理解，提高画辅助线的技巧。

二、三角形的辅助线题目3：在三角形ABC中，已知AC=12cm，BC=9cm，以BC为底边，作一个正方形BCDE，连接AE，求AE的长度。

解题思路：我们可以从直角三角形ABC出发，先绘制正方形BCDE，然后连接AE，并求出AE的长度。

这道题目可以帮助我们熟练运用辅助线的方法，加深对三角形性质和直角三角形的理解。

题目4：在三角形ABC中，已知AB=8cm，AC=10cm，以AC为底边，作一个矩形ACDE，连接BE，求BE的长度。

解题思路：我们可以通过绘制矩形ACDE，连接BE，并求出BE的长度。

这道题目可以帮助我们巩固辅助线的方法，加深对三角形的认识，提高解题的灵活性。

三、数形结合的辅助线题目5：在平行四边形ABCD中，已知AD=12cm，同时AB是一条边长为6cm的正方形ABEF的对角线，求平行四边形ABCD的面积。

人教版八年级数学全等三角形中的常见辅助线(举一反三)(含解析)

人教版八年级数学全等三角形中的常见辅助线(举一反三)(含解析)本文介绍了全等三角形中的常见辅助线，包括角分线上点向角两边作垂线和截取法构全等两种方法。

第一种方法是过角平分线上一点向角两边作垂线，利用角平分线上的点到两边距离相等的性质来证明问题。

举例来说，已知BP平分∠ABC，PD⊥BC于D，BF+BE＝2BD，要求证∠BFP+∠BEP＝180°。

另外，还有一些变式题，例如已知∠AOB＝90°，OM是∠AOB的平分线，将三角板的直角顶点P在射线OM上滑动，两直角边分别与OA、OB交于C、D，要求解出PC和PD之间的数量关系。

第二种方法是利用对称性，在角的两边截取相等的线段，构造全等三角形。

例如，在四边形ABCD中，BC＞BA，∠A+∠C＝180°，且∠C＝60°，BD平分∠ABC，要求证BC＝AB+DC。

还有一些变式题，例如已知△ABC中，∠A＝60°，BD，CE分别平分∠ABC和∠ACB，BD、CE交于点O，要求判断BE，CD，BC的数量关系。

本文还提到了一些其他问题，例如在△ABC中，∠XXX是直角，∠B＝60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F，要求判断FE与FD之间的数量关系。

此外，还有一些类似的变式题，需要读者自行思考和解答。

需要注意的是，本文中有一些格式错误和明显有问题的段落需要删除，同时每段话也需要进行小幅度的改写，以使其更加准确、清晰和易于理解。

在△ABC中，通过截取AE＝AC的方式，连接DE，得到△ADE≌△ADC。

因此，我们可以证明XXX。

对于图②，我们知道AD是△ABC的外角∠CAE的平分线，交BC的延长线于点D，且∠D＝25°。

我们需要求解∠B的度数。

对于△XXX，我们可以通过以下方式求解∠B的度数：∠B＋∠C＋∠A＝180°。

因为∠C＝2∠B，所以∠A＝180°－3∠B。

沪教版初中数学八年级上册学案：19.2证明举例-常见辅助线的作法常考题型讲解及练习word版含答案

证明举例——常见辅助线的作法由于证明的需要，可以在原来的图形上添画一些线，即添加辅助线来完成一些几何证明。

辅助线通常画虚线。

以下来介绍一些常用的添辅助线的方法： 1．添线构造基本图形有了基本图形就会有一系列的熟悉的结论因此可以更好的帮助解题例1、已知线段AC 与BD 相交于点O ，联结AB DC 、，E 为OB 的中点，F 为OC 的中点，联结EF （如图所示）．（1）添加条件A D ∠=∠，OEF OFE ∠=∠，求证：AB DC =．（2）分别将“A D ∠=∠”记为①，“OEF OFE ∠=∠”记为②，“AB DC =”记为③，添加条件①、③，以②为结论构成命题1，添加条件②、③，以①为结论构成命题2．命题1是命题，命题2是命题（选择“真”或“假”填入空格），并证明你的结论。

2．根据定理使用的要求添线一些几何定理的使用需要特定图形的支持，所以添加这样的图形就可以使用定理了。

(1) 平行线的相关结论是在三线八角的图形中得出的，因此要使用这些结论就必须有三线八角的图形。

例2、已知直线a // b ，先填空，再证明图①和图②，并归纳出图④中各角的和。

图①中，∠A +∠B +∠C =____________；图②中，∠A +∠B +∠C +∠D =____________；图③中，∠A +∠B +∠C +∠D +∠E =____________；图④中，∠A +∠B +∠C + …… + ∠P =____________；（2）全等三角形可以很好提供边角相等的证明，因此证明边角相等时可以构造全等三角形。

OD C AB EF例3、如图，已知△ABC 为等边三角形，延长BC 到D ，延长BA 到E ，使AE = BD ，联结CE 、DE求证：CE = DE ．1、按照题目的要求添线一些特定的条件或结论是需要特定的图形才能得以解决的，所以遇到这样的式子就需要添加特定的图形从而得以使用该式子 “倍长中线”法例4、如图，已知在△ABC 中，AD 是中线，BE 交AD 于点F ，AE = EF 求证：AC = BF ．练习1、已知：如图，在△ABC 和△DEF 中，AM 、DN 是边BC EF 、的中线且AB ＝DE ，AC ＝DF ，AM ＝DN.求证：△ABC ≌△DEF.（有两边及第三边上中线对应相等的两个三角形全等）EADCBEFBDA MC BAN EFD“截长补短”法例5、如图，已知△ABC 中，AD 是∠BAC 的角平分线，∠B = 2∠C求证：AB +BD =AC ．练习1、如图，已知在ΔABC 中，，AB AC =，AD 平分，求证：BC AB CD =+．旋转添线：例6、如图，已知在正方形ABCD 中，E 在BC 上，F 在DC 上，BE+DF=EF ．求证：45EAF ∠=︒．DCB A108A ∠=ABC ∠CBADECAFDB练习1、如图，在△ABC 中，∠ABC=90°，AB=BC ，D 为AC 中点，AB 的延长线上任意一点E ，FD ⊥DE 交BC 延长线于F ，求证：DE=DF.基础知识巩固练习1．把命题“直角三角形的两个锐角互为余角”改写成“如果…那么…”的形式是这个命题是（填“真”或“假”）命题。

(完整版)相似三角形中的辅助线专题训练【可修改文字】

可编辑修改精选全文完整版相似三角形中的辅助线专题训练一、基本图形：二、基本方法：证相似，实不难，A字字仔细看；如没有，辅助线，各种情况常相见。

三、实例演习：（一）遇燕尾，作平行，构造字一般行。

1、BE＝AD，求证：EF·BC＝AC·DF（二）遇梯形，延长腰，构成A字瞧一瞧。

2、梯形ABCD中，AD∥BC，CH平分∠BCD，BH＝3AH，四边形AHCD的面积为21，求△HBC的面积。

（三）遇平分，作等腰，三线合一要记牢。

3、AC⊥BC，AE⊥DE，2∠ADE＝∠B，AC：BC＝3：1，求AE：DG（四）直角多，垂线作，再难题目你能做。

4、平行四边形ABCD中，CE⊥AE，CF⊥AF，求证：AB·AE＋AD·AF＝AC2HDCBAEDCBAGEDCBAA BCDEF四、巩固练习：（做题目，看情况，灵活运用最恰当。

） 1、BD ：DC ＝2：1，E 为AD 中点，求①BE ：EF ②AF ：FC2、平行四边形ABCD 中，E 为AB 中点，AF ：FD ＝1：2，求AG ：GC3、D 为BC 中点，求证：AF ：BF ＝AE ：EC4、AC ⊥BC ，CD ⊥AB ，FG ⊥AB ，E 为CD 中点，求证：FG 2＝CF ·BF 5、AB ＝AC ，AD 为中线，CF ∥AB ，求证：BP 2＝PE ·PF6、AD 平分∠BAC ，EF 垂直平分AD ，求证：ED 2＝EB ·EC7、矩形ABCD 中，E 为AD 中点，EF ⊥EC ，求证：△AEF ∽△ECF8、AB ＝AC ，AB ⊥BC ，AD 为中线，BE ⊥AD ，求证：①AE ＝2EC ②∠AEB ＝∠CED 9、∠BAC ＝90°，AE ⊥BC ，BD ＝DC ＝EC ＝1，求AC 的长10、AB ＝AC ，BD 为高，求证：BC 2＝2AC ·CDFE DC BA G F E DC B A A BC DE FA B C D E F G PA BC D E F AB CD EF AB CD E F P AB C D E PAB CDEA BCDPA B CD E。

数学初二做辅助线的练习题

数学初二做辅助线的练习题在数学学科中，辅助线是解决问题的常用方法之一。

通过在图形中引入辅助线，能够帮助我们更好地理解和解决问题。

下面，我们将通过一些初二数学的练习题来学习如何运用辅助线。

1. 题目：已知一个等边三角形ABC，点D是边BC的中点。

连接AD并延长至E，使得AE=AD，连接BE，证明AE与BC垂直。

解析：在该题中，我们需要证明AE与BC垂直。

为了更好地理解问题，我们可以在图形中引入辅助线。

做法：1）在三角形ABC中，连接AC，构成一个等腰三角形。

2）连接BD，并延长至F，使得BF=BD。

3）连接EF。

4）观察三角形ABF和三角形AED，我们发现它们是等边三角形。

5）由于等边三角形的性质，BF=AE ，且BF与AE平行。

6）根据平行线的性质，AE与BC垂直。

通过引入辅助线，我们更容易观察到等边三角形的性质，从而解决了该问题。

2. 题目：在平行四边形ABCD中，点E是边BC的中点，连接AE 和CD交于点F，证明EF=DF。

解析：在该题中，我们需要证明EF=DF。

为了更好地理解问题，我们可以在图形中引入辅助线。

做法：1）连接AD和BE，并延长至交点G。

2）观察三角形EFG和三角形DFG，我们发现它们是全等三角形。

3）由于全等三角形的性质，EF=DG，又由于DG=DF，所以EF=DF。

通过引入辅助线，我们能够得到全等三角形，从而证明了EF=DF。

3. 题目：在平行四边形ABCD中，点E是边AB的中点，点F是边BC的中点，连接AC并延长至交点G，连接BD并延长至交点H，证明GH平分AC。

解析：在该题中，我们需要证明GH平分AC。

为了更好地理解问题，我们可以在图形中引入辅助线。

做法：1）连接EG和FH。

2）观察四边形EGFH，我们发现它是一个平行四边形。

3）由于平行四边形的性质，中线GH平分对角线AC。

通过引入辅助线，我们能够得到平行四边形的性质，从而证明了GH平分AC。

通过以上的练习题，我们可以看到在解决数学问题时，引入辅助线是一种非常有效的方法。

八年级数学与角有关的辅助线(过程训练二)(人教版)(含答案)

学生做题前请先回答以下问题问题1：看到平行想什么？问题2：a，b，c是同一平面内的三条直线，如果a∥b，b∥c，那么a∥c，理由是什么？问题3：已知：如图，AB∥EF，∥B=25°，∥D=30°，∥E=10°，则∥BCD=_____．拿到题以后，首先要读题标注，然后观察图形，分析思路．请概述你的思路．与角有关的辅助线（过程训练二）（人教版）一、单选题(共5道，每道20分)1.已知，如图，AB∥CD，∥B=40°，∥D=20°，求∥BED的度数．解：如图，过点E作FH∥AB，∥AB∥CD（已知）∥CD∥FH∥AB（平行于同一条直线的两条直线互相平行）___________________________横线处应填写的过程最恰当的是( )A.∥∥1=∥B，∥2=∥D（两直线平行，内错角相等）∥∥1=40°，∥2=20°（等量代换）∥∥BED=∥1+∥2=40°+20°=60°（等量代换）B.∥∥1=∥B=40°，∥2=∥D=20°（两直线平行，内错角相等）∥∥BED=∥1+∥2=40°+20°=60°（等量代换）C.∥∥1=∥B，∥2=∥D（两直线平行，内错角相等）∥∥B=40°，∥D=20°（已知）∥∥1=40°，∥2=20°（等量代换）∥∥BED=∥1+∥2=40°+20°=60°（等量代换）D.∥∥1=∥B（两直线平行，内错角相等）∥∥B=40°（已知）∥∥1=40°（等量代换）∥∥2=∥D（已知）∥D=20°（已知）∥∥2=20°（等量代换）∥∥BED=∥1+∥2=40°+20°=60°（等量代换）答案：C解题思路：试题难度：三颗星知识点：与角有关的辅助线2.如图，AB∥CD，∥1=70°，∥2=60°，求∥B的度数．解：如图，过点G作HK∥AB，______________________________∥∥3=180°-∥2-∥4=180°-60°-70°=50°（平角的定义）∥∥B=180°-∥3=180°-50°=130°（等式的性质）横线处应填写的过程最恰当的是( )A.∥AB∥CD（已知）∥CD∥HK∥AB（平行于同一条直线的两条直线互相平行）∥∥B+∥3=180°（两直线平行，同旁内角互补）∥∥1=∥4，∥1=70°（已知）∥∥4=70°（等量代换）∥∥2=60°（已知）B.∥AB∥CD（已知）∥∥1=∥4（两直线平行，内错角相等）∥B+∥3=180°（两直线平行，同旁内角互补）∥∥1=70°（已知）∥∥4=70°（等量代换）C.∥AB∥CD（已知）∥CD∥HK∥AB（平行于同一条直线的两条直线互相平行）∥∥1=∥4=70°（两直线平行，内错角相等）∥B+∥3=180°（两直线平行，同旁内角互补）∥∥2=60°（已知）D.∥AB∥CD（已知）∥CD∥HK∥AB（平行于同一条直线的两条直线互相平行）∥∥1=∥4（两直线平行，内错角相等）∥B+∥3=180°（两直线平行，同旁内角互补）∥∥1=70°（已知）∥∥4=70°（等量代换）∥∥2=60°（已知）答案：D解题思路：试题难度：三颗星知识点：与角有关的辅助线3.已知，如图，AB∥CD，E是AC上一点，∥B=30°，∥D=60°．求证：BE∥ED.证明：如图，______________________________∥∥BED=∥1+∥2=30°+60°=90°（等量代换）∥BE∥ED（垂直的定义）以上空缺处所填最恰当的是( )A.过点E作EF∥AB∥AB∥CD（已知）∥CD∥EF∥AB（平行于同一条直线的两条直线互相平行）∥∥B=∥1，∥D=∥2（两直线平行，内错角相等）∥∥1=30°，∥2=60°（等量代换）B.过点E作EF∥AB∥AB∥CD（已知）∥CD∥EF∥AB（平行于同一条直线的两条直线互相平行）∥∥B=∥1，∥D=∥2（两直线平行，内错角相等）∥∥B=30°，∥D=60°（已知）∥∥1=30°，∥2=60°（等量代换）C.过点E作EF∥AB∥CD∥∥B=∥1，∥D=∥2（两直线平行，内错角相等）∥∥B=30°，∥D=60°（已知）∥∥1=30°，∥2=60°（等量代换）D.过点E作EF∥AB∥CD∥EF∥AB（平行于同一条直线的两条直线互相平行）∥∥B=∥1，∥D=∥2（两直线平行，内错角相等）∥∥B=30°，∥D=60°（已知）∥∥1=30°，∥2=60°（等量代换）答案：B解题思路：试题难度：三颗星知识点：与角有关的辅助线4.已知：如图，CE平分∥ACD，点G是AB上一点，GF∥CE．若∥1=60°，∥2=20°，求∥BAC的度数．解：如图，过点A作HK∥GF.∥GF∥CE（已知）∥CE∥HK∥GF（平行于同一条直线的两条直线互相平行）______________________________∥∥1=60°（已知）∥∥4=60°（等量代换）∥∥BAC=∥3+∥4=20°+60°=80°（等量代换）横线处应填写的过程最恰当的是( )A.∥∥2=∥3=20°，∥4=∥5（两直线平行，内错角相等）∥CE平分∥ACD（已知）∥∥1=∥5=60°（角平分线的定义）B.∥∥2=∥3=20°（两直线平行，内错角相等）∥CE平分∥ACD（已知）∥∥1=∥5（角平分线的定义）∥∥4=∥5（已知）∥∥4=∥1（等量代换）C.∥∥2=∥3，∥4=∥5（两直线平行，内错角相等）∥∥2=20°（已知）∥∥3=20°（等量代换）∥CE平分∥ACD（已知）∥∥1=∥5=60°（角平分线的定义）D.∥∥2=∥3，∥4=∥5（两直线平行，内错角相等）∥∥2=20°（已知）∥∥3=20°（等量代换）∥CE平分∥ACD（已知）∥∥1=∥5（角平分线的定义）∥∥1=∥4（等量代换）答案：D解题思路：试题难度：三颗星知识点：与角有关的辅助线5.已知：如图，AB∥CD，∥B=30°，∥BEF=120°，∥EFD=130°，求∥D的度数．解：如图，过点E作MN∥AB，过点F作PQ∥AB，∥MN∥PQ（平行于同一条直线的两条直线互相平行）∥AB∥CD（已知）∥MN∥CD，PQ∥CD（平行于同一条直线的两条直线互相平行）即AB∥MN∥PQ∥CD______________________________∥∥3=∥BEF-∥1=120°-30°=90°（等式的性质）∥∥4=180°-∥3=180°-90°=90°（等式的性质）∥∥EFD=130°（已知）∥∥2=∥EFD-∥4=130°-90°=40°（等式的性质）∥∥D=40°（等量代换）横线处应填写的过程最恰当的是( )A.∥∥B=∥1，∥D=∥2（两直线平行，内错角相等）∥3+∥4=180°（两直线平行，同旁内角互补）∥∥B=30°（已知）∥∥1=30°（等量代换）∥∥BEF=120°（已知）B.∥∥B=∥1（两直线平行，内错角相等）∥D=∥2（两直线平行，同位角相等）∥3+∥4=180°（两直线平行，同旁内角互补）∥∥1=30°（等量代换）∥∥BEF=120°（已知）C.∥∥B=∥1，∥D=∥2（两直线平行，内错角相等）∥3+∥4=180°（两直线平行，同旁内角互补）∥∥1=30°（等量代换）∥3=90°（等式的性质）∥4=90°（等式的性质）∥2=40°（等式的性质）D.∥∥B=∥1（两直线平行，内错角相等）∥∥B=30°（已知）∥∥1=30°（等量代换）∥∥D=∥2（两直线平行，内错角相等）∥3+∥4=180°（两直线平行，同旁内角互补）答案：A解题思路：试题难度：三颗星知识点：平行线的性质第 11 页共 11 页。

初二下册数学辅助线练习题

初二下册数学辅助线练习题在初二下册的数学课程中，辅助线是一个非常重要的概念和工具。

通过使用辅助线，我们可以更好地理解和解决各种数学问题。

在这篇文章中，我将为您提供一些初二下册数学辅助线练习题，帮助您加深对这一概念的理解和掌握。

一、平行四边形面积计算1.已知平行四边形的底边长为8cm，高度为6cm，试计算其面积。

解析：我们可以使用辅助线将平行四边形分成两个三角形，然后计算三角形的面积并相加得到最终的平行四边形面积。

以下是详细步骤：步骤1：根据已知条件画出平行四边形，并标记出底边和高度。

步骤2：添加辅助线，将平行四边形分成两个三角形。

步骤3：计算两个三角形的面积。

由于两个三角形具有相同的底边和高度，所以它们的面积相等。

步骤4：将两个三角形的面积相加，得到平行四边形的面积。

根据以上步骤，我们可以得出平行四边形的面积为48平方厘米。

二、直角三角形边长计算2.已知一个直角三角形的斜边长为10cm，一个直角边长为6cm，试计算另一个直角边的长度。

解析：我们可以使用辅助线将直角三角形划分成两个直角相似三角形，然后通过比例关系计算未知直角边的长度。

以下是详细步骤：步骤1：根据已知条件画出直角三角形，并确定斜边和已知直角边。

步骤2：添加辅助线，将直角三角形划分成两个直角相似三角形。

步骤3：根据相似三角形的性质，我们可以得出一个比例关系：斜边与该直角边的比值等于另一个直角边与该直角边的比值。

步骤4：根据比例关系，我们可以得出未知直角边的长度。

根据以上步骤，我们可以计算出另一个直角边的长度为8cm。

三、菱形对角线长度计算3.已知菱形的一条对角线长度为12cm，另一条对角线长度为16cm，试计算菱形的面积。

解析：我们可以使用辅助线将菱形划分为四个直角三角形，然后计算这些三角形的面积并相加，得到菱形的面积。

以下是详细步骤：步骤1：根据已知条件画出菱形，并标记出两条对角线的长度。

步骤2：添加辅助线，将菱形划分为四个直角三角形。

(完整word版)初二辅助线专题1

辅助线专题一、找全等三角形的方法：（1）可以从结论出发，寻找要证明的相等的两条线段（或两个角）分别在哪两个可能全等的三角形中；（2）可以从已知条件出发，看已知条件可以确定哪两个三角形全等；（3）可从条件和结论综合考虑，看它们能确定哪两个三角形全等；（4）若上述方法均不可行，可考虑添加辅助线，构造全等三角形。

二、三角形中常见辅助线的作法：①延长中线构造全等三角形；②利用翻折，构造全等三角形；③引平行线构造全等三角形；④作连线构造等腰三角形。

精解名题一、截长补短法截长补短法，具体作法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明。

这种作法，适合于证明线段的和、差、倍、分等类的题目。

1、如图1，在△ABC中，∠ABC=60°，AD、CE分别平分∠BAC、∠ACB．求证：AC=AE+CD．方法提炼：遇到求证一条线段等于另两条线段之和时，一般方法是截长补短法：截长：在长线段中截取一段等于另两条中的一条，然后证明剩下部分等于另一条；补短：将一条短线段延长，延长部分等于另一条短线段，然后证明新线段等于长线段。

1）对于证明有关线段和差的不等式，通常会联系到三角形中两线段之和大于第三边、之差小于第三边，故可想办法将其放在一个三角形中证明。

2）在利用三角形三边关系证明线段不等关系时，如直接证明不出来，可连接两点或延长某边构成三角形，使结论中出现的线段在一个或几个三角形中，再运用三角形三边的不等关系证明。

二、中线倍长法若遇到三角形的中线，可倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”。

2、已知三角形的两边长分别为7和5，那么第三边上中线长x的取值范围是（）．3、如图，已知ΔABC中，AD是∠BAC的平分线，AD又是BC边上的中线。

求证：ΔABC是等腰三角形。

方法提炼：题目中如果出现了三角形的中线，常加倍延长此线段，再将端点连结，便可得到全等三角形。

(word完整版)二倍角问题辅助线的添加规律

二倍角问题辅助线的添加规律一些几何题中常含有一个角是另一个角的二倍的条件,处理这类问题常用如下的方法添加辅助线：（1）作二倍角的平分线,构成等腰三角形.如下图，在△ABC中,∠ABC=2∠C，作∠ABC的角平分线交AC于点D，则∠DBC=∠C，△DBC是等腰三角形。

（2)延长二倍角的一边,使其等于二倍角的另一边，构成两个等腰三角形,利用等腰三角形的性质证题。

如下图,在△ABC中，∠B=2∠C,可延长CB到D，使BD=AB，连接AD，则△ABD、△ADC都是等腰三角形.【典例】已知,如下图所示，在△ABC中,∠C=2∠A，AC=2BC,求证：∠B=90°.思路一：要证∠B=90°，可设法证∠B等于某个直角。

由∠C=2∠A，可联想作∠C的角平分线CE，则△ACE是等腰三角形，如果作这个等腰三角形底边上的高ED，则出现直角，再证∠B=∠CDE即可.【证法一】如下图,作∠C的平分线CE交AB于点E，过E作ED⊥AC于D.则∠ACE=∠A，∴AE=CE.∵ED⊥AC，∴CD=1/2AC。

∵AC=2BC，∴CD=CB。

则可证得△CDE≌△CBE.即∠B=∠CDE=90°.思路二：作∠C的平分线CD，将△CDA沿CD翻折过来,得△CDE。

要证∠ABC=90°，需证CD=ED,BC=BE。

【证法二】如下图，作∠C的平分线CD，延长CB到E，使CE=AC，∴AC=BC+BE. ∵AC=2BC,∴BC=BE.在△ACD和△ECD中，AC=EC，∠ACD=∠ECD,CD=CD，∴△ACD≌△ECD。

∴∠A=∠E,又∠DCB=∠DCA=∠A，∴∠E=∠DCB. ∴DC=DE. ∴∠ABC=90°.思路三：延长AC到D,使CD=BC，连接BD，则△CBD和△ABD都是等腰三角形，由条件AC=2BC，可联想到取AC的中点E，连接BE，则∠DBE=90°。

要证∠ABC=90°，只需证∠ABE=∠DBC。

(word完整版)初中数学中考几何如何巧妙做辅助线大全,推荐文档

人教版北师大初中数学中考几何如何巧妙做辅助线大全人们从来就是用自己的聪明才智创造条件解决问题的，当问题的条件不够时，添加辅助线构成新图形，形成新关系，使分散的条件集中，建立已知与未知的桥梁，把问题转化为自己能解决的问题，这是解决问题常用的策略。

一．添辅助线有二种情况：1按定义添辅助线：如证明二直线垂直可延长使它们,相交后证交角为90°；证线段倍半关系可倍线段取中点或半线段加倍；证角的倍半关系也可类似添辅助线。

2按基本图形添辅助线：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形，因此“添线”应该叫做“补图”！这样可防止乱添线，添辅助线也有规律可循。

举例如下：（1）平行线是个基本图形：当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线（2）等腰三角形是个简单的基本图形：当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。

出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。

（3）等腰三角形中的重要线段是个重要的基本图形：出现等腰三角形底边上的中点添底边上的中线；出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。

（4）直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。

出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。

（5）三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线，当有中位线三角形不完整时则需补完整三角形；当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形；当出现线段倍半关系且与半线段的端点是某线段的中点，则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。