流体静力学基本方程
化工原理公式及各个章节总结汇总

第一章 流体流动与输送机械1. 流体静力学基本方程:gh p p ρ+=022. 双液位U 型压差计的指示: )21(21ρρ-=-Rg p p )3. 伯努力方程:ρρ222212112121p u g z p u g z ++=++4. 实际流体机械能衡算方程:f W p u g z p u g z ∑+++=++ρρ222212112121+ 5. 雷诺数:μρdu =Re6. 范宁公式:ρρμλfp d lu u d l Wf ∆==⋅⋅=22322 7. 哈根-泊谡叶方程:232d lup f μ=∆ 8. 局部阻力计算:流道突然扩大:2211⎪⎭⎫ ⎝⎛-=A A ξ流产突然缩小:⎪⎭⎫ ⎝⎛-=2115.0A A ξ第二章 非均相物系分离1. 恒压过滤方程:t KA V V V e 222=+令A V q /=,A Ve q e /=则此方程为:kt q q q e =+22第三章 传热1. 傅立叶定律:n t dAdQ ϑϑλ-=,dxdt A Q λ-= 2. 热导率与温度的线性关系:)1(0t αλλ+= 3. 单层壁的定态热导率:bt t AQ 21-=λ,或mA b tQ λ∆=4. 单层圆筒壁的定态热传导方程: )ln1(21221r r t t l Q λπ-=或m A b tt Q λ21-=5. 单层圆筒壁内的温度分布方程:C r l Qt +-=ln 2λπ(由公式4推导)6. 三层圆筒壁定态热传导方程:34123212141ln 1ln 1ln 1(2r r r r r r t t l Q λλλπ++-=7. 牛顿冷却定律:)(t t A Q w -=α,)(T T A Q w -=α8. 努塞尔数λαl Nu =普朗克数λμCp =Pr 格拉晓夫数223μρβtl g Gr ∆= 9. 流体在圆形管内做强制对流:10000Re >,1600Pr 6.0<<,50/>d lk Nu Pr Re 023.08.0=,或kCp du d ⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=λμμρλα8.0023.0,其中当加热时,k=,冷却时k= 10. 热平衡方程:)()]([1222211t t c q T T c r q Q p m s p m -=-+=无相变时:)()(12222111t t c q T T c q Q p m p m -=-=,若为饱和蒸气冷凝:)(12221t t c q r q Q p m m -== 11. 总传热系数:21211111d d d d b K m ⋅+⋅+=αλα 12. 考虑热阻的总传热系数方程:212121211111d d R R d d d d b K s s m ⋅++⋅+⋅+=αλα 13. 总传热速率方程:t KA Q ∆=14. 两流体在换热器中逆流不发生相变的计算方程:⎪⎪⎭⎫⎝⎛-=--22111112211lnp m p m p m c q c q c q KA t T t T 15. 两流体在换热器中并流不发生相变的计算方程:⎪⎪⎭⎫ ⎝⎛+=--22111122111lnp m p m p m c q c q c q KA t T t T 16. 两流体在换热器中以饱和蒸气加热冷流体的计算方程:2221ln p m c q KAt T t T =--第四章 蒸发1. 蒸发水量的计算:110)(Lx x W F Fx =-=2. 水的蒸发量:)1(1x x F W -= 3. 完成时的溶液浓度:WF F x -=4. 单位蒸气消耗量:rr D W '=,此时原料液由预热器加热至沸点后进料,且不计热损失,r 为加热时的蒸气汽化潜热r ’为二次蒸气的汽化潜热5. 传热面积:mt K QA ∆=,对加热室作热量衡算,求得Dr h H D Q c =-=)(,1t T t -=∆,T 为加热蒸气的温度,t 1为操作条件下的溶液沸点。
流体静力学基本方程

流体静力学基本方程一、静止液体中的压强分布规律重力作用下静止流体质量力:X=Y=0,Z=-g代入 Zdz)Ydy (Xdx dp ++=ρ (压强p 的全微分方程)得:dp =ρ(-g )dz =-γdz积分得: p=-γz +c即: 常数=+γpz 流体静力学基本方程对1、2两点: γγ2211p z p z +=+结论: 1)仅在重力作用下,静止流体中某一点的静水压强随深度按线性规律增加。
2)自由表面下深度h 相等的各点压强均相等——只有重力作用下的同一连续连通的静止流体的等压面是水平面。
3)推广:已知某点的压强和两点间的深度差,即可求另外一点的压强值。
p 2=p 1+γΔh4)仅在重力作用下,静止流体中某一点的静水压强等于表面压强加上流体的容重与该点淹没深度的乘积。
观看录像: 水静力学 观看动画: 静水力学基本方程演示 >>二、静止液体中的压强计算自由液面处某点坐标为z 0,压强为p 0;液体中任意点的坐标为z ,压强为p ,则:γγ00p z pz +=+∴坐标为z 的任意点的压强 :p =p 0+γ(z 0-z ) 或 p =p 0+γh三、静止液体中的等压面静止液体中质量力――重力,等压面垂直于质量力,∴静止液体中的等压面必为水平面算一算:1. 如图所示的密闭容器中,液面压强p 0=9.8kPa ,A 点压强为49kPa ,则B 点压强为39.2kPa ,在液面下的深度为3m 。
四、绝对压强、相对压强和真空度的概念1.绝对压强(absolute pressure ):是以绝对真空状态下的压强(绝对零压强)为起点基准计量的压强。
一般 p =p a +γh2. 相对压强(relative pressure ):又称“表压强”,是以当时当地大气压强为起点而计算的压强。
可“+”可“– ”,也可为“0”。
p '=p-p a3.真空度(Vacuum ):指某点绝对压强小于一个大气压p a 时,其小于大气压强p a 的数值。
流体静力学方程式

流体静力学方程式流体静力学是研究流体在静止状态下的力学性质的学科。
它是流体力学的一个分支,研究流体静止时的压力、密度、重力等因素对流体的影响。
本文将介绍流体静力学的方程式及其应用。
正文流体静力学方程式是描述流体静止时的力学行为的数学表达式。
主要包括两个方程式:流体静力平衡方程和流体连续性方程。
一、流体静力平衡方程流体静力平衡方程是基于力的平衡原理得出的。
它可以用来描述流体内外压力的均衡状态。
在一个封闭的容器中,流体的压力在各个方向上必须保持平衡。
这个平衡关系可以用以下方程式表示:P = ρg其中,P是压力场的梯度,ρ是流体的密度,g是重力加速度。
这个方程式表明流体中各个点的压力梯度与密度和重力加速度之间存在着一定的关系。
二、流体连续性方程流体连续性方程是基于流体质量守恒原理得出的。
它描述了流体在任意两个点之间质量的守恒关系。
对于一个不可压缩的流体(密度恒定),流体连续性方程可以用以下方程式表示:·v = 0其中,·v表示流体速度场的散度。
这个方程式表明流体在任意两个点之间的流量守恒,流出的质量等于流入的质量。
这两个方程式是流体静力学中的基本方程,通过它们可以计算流体静止时的压力分布和速度分布。
在实际的工程应用中,它们被广泛用于分析和设计涉及流体静力学的系统,如水坝、水管等。
总结起来,流体静力学方程式是描述流体静止时力学行为的基本数学表达式。
通过流体静力平衡方程和流体连续性方程,我们可以了解流体静态时的压力分布和速度分布,进而应用于实际工程中的设计和分析。
这些方程式为我们提供了深入理解流体静力学的基础,有助于我们更好地应对与流体静力学相关的问题。
流体静力学基本方程式的应用

ρρAC、:ρ9B
:指示液的密度 流体的密度
9
第一节 流体静力学基本方程式
(3)斜管压差计 ❖ 当被测量的流体的压差更小时,可采用斜管压差计。
R'=R/sinα
10
10
第一节 流体静力学基本方程式
2.液位的测量
h =(ρ0-ρ)R/ρ
11
11
5
5
第一节 流体静力学基本方程式
三、流体静力学基本方程式
p = p0 + g h
(1)液体内静压强随液体的深度的增大而增大, 等深处形成等压面。
(2)当液面上方的压力p0有改变时,液体内部各
点的压力p也发生同样大小的改变,称为帕斯卡原
理。
6
第一节 流体静力学基本方程式
四、流体静力学基本方程式的应用 ❖ 1.压力与压力差的测量
第一章 流体流动
目录
第一节 流体静力学基本方程式 第二节 流体流动的基本方程式 第三节 流体在管内的流动 第四节 流速和流量的测量
第一节 流体静力学基本方程式
一、流体的密度
❖ 1.混合液体的密度
1 xwA xwB xwn
m A B
n
❖ 2.混合气体的密度
3
m AxVA A xVB AxVn
(1)U形管压差计 (2)微差压差计 ❖ 2.液位的测量
7
7
图1-3 U型管压差计
第一节 流体静力学基本方程式
(1)U形管压差计
p1- p2=(ρA-ρ)gR
ρA:指示液的密度 ρ: 流体的密度
8
8
第一节 流体静力学基本方程式
(2)微差压差计 ❖ 若所测的压力差很小,可采用微差压差计。
化工原理-流体静力学方程

pa p2 Bg Z m AgR 于是 p1 Bg(m R) p2 Bg Z m AgR
18
一、压强与压强差的测量
上式化简,得
p1 p2 (A B )gR BgZ
若
Z 0
则 p1 p2 (A B )gR
若U管的一端与被测流体连接,另一端与大 气相通,此时读数反映的是被测流体的表压强。
不同基准压力之间的换算 表压力 = 绝对压力-大气压力 真空度 = 大气压力-绝对压力 真空度 = -表压力
5
第1章 流体流动
1.2 流体静力学基本方程式 1.2.1 静止流体的压力 1.2.2 流体静力学基本方程式
6
流体静力学方程
微元立方流体
边长:dx、dy、dz 密度:ρ
图1-6 微元流体的静力平衡
例1-7 附 图
25
动画16
三、液封高度的计算
设备内操作条件不同,采用液封的目的也就 不同。流体静力学原理可用于确定设备的液封 高度。具体见[例1-8]、[例1-9]。
26
三、液封高度的计算
1-与真空泵相通的不凝性气体出口 2-冷水进口 3-水蒸气进口 4-气压管 5-液封槽
例1-9 附图
27
练习题目
ΔP,在此情况下,单位面积上所受的压力,称
为压力强度,简称压强,俗称压力,其表达式
为
p P A
ห้องสมุดไป่ตู้
p lim P A0 A
4
静止流体的压力
压力的单位 在SI单位制中,压力单位是N/m2或Pa。 其 他 单 位 还 有 : 1atm = 101300 N/m2 =
101.3kPa = 1.033kgf/cm2 = 10.33mH2O = 760mmHg
流体静力学基本方程.

§2-3 流体静力学基本方程
三、静止液体中的等压面 1. 一族水平面 2. 联通器
同种、连续、静止的流体中,水平面为等压面; 两种互不相混流体的分界面既是水平面,又是等压面。
§2-3 流体静力学基本方程
例2 -1 压强计算
已知: pa 9.8 N / cm2 h1 100 cm h2 20 cm oil 0.00745 N / cm3 hg 0.133 N / cm3
求: 解:
hc hD pc ? 列o - o等压面方程
pc pD pa oil h1 hg h2
9.8 0.00745100 0.133 20
13.205 N / cm2
另: 若想计算左端容器中液面的压力,则有 p pc H 2Oh
§2-3 流体静力学基本方程
p1
z2
p2
C'
§2-3 流体静力学基本方程
五、流体静力学基本方程的物理意义和几何意义
1. 几何意义 各项具有长度的量纲 z : 位置水头 p : 压强水头
z p' c : 测压管水头
z p' pa ' c : 静力水头
测压管水头相等,为一水平面
§2-2 流体平衡微分方程及其积分
例2-2 (压力计算题) 某选矿厂自高位水池引出一条管路 AB 向球磨车间供
水。现因检修停水,关门了阀门B 。问此时 B 处的绝对压 强和相对压强各为多少?
解 设大气压 pa 98000 N m,2 水的重度 9800 N m3 , 由式(2-16),可求得 点的压强为
图解关系:
p pa p' pv pa p pvmax pa
流体静力学方程式

一、流体静力学基本方程
P P0 hg
(公式推导)Βιβλιοθήκη P0 h它是用来描述静止流体内部的压力沿高度变化的表达式。
关于此方程式的说明如下:
⑴在静止连续的同一液体内,处于同一水平面上的各 点压力相等,此压力相等的水平面称为等压面;
⑵当液体的上方压力为P0有变化时,必将引起液体 内部各点压力发生同样大小的变化,这就是帕斯卡 原理;
⑶流体静力学方程可改成:
P P0 h
g
需要注意的是:只有静止的流体才适用于静力学方程。
等压面 同一水平面上为等压面应满足的条件: 1、静止; 2、连通; 3、连通的介质为同一均质流体; 4、质量力只有重力。
例题
如图,开口容器内装有油和水,油层高h1,密度 为700 kg/m3,水层高度h2,密度为1000 kg/m3。问: PA=Pa,PB=Pb
油
PA
Pa
水
PB
Pb
谢谢观看!
第二讲流体静力学基本方程及其应用

第二讲流体静力学基本方程及其应用【学习要求】1.理解流体静力学方程的意义;2.掌握流体静力学方程的应用。
【预习内容】1.在均质流体中,流体所具有的与其所占有的之比称为。
任何流体的密度都随它的和而变化,但对液体的密度影响很小,可忽略,故常称液体为的流体。
2.流体静压力的两个重要特性分别是:(1);(2)。
3.1atm = mmHg = Pa = mH2O【学习内容】一、流体静力学基本方程式1.流体静力学基本方程式的形式p2 = p1+ ρ ( z1—z2 )g 或p2 = p1+ hρg流体静力学方程表明:在重力作用下静止液体内部的变化规律。
即在液体内部任一点的流体静压力等于。
2.流体静力学基本方程式的意义流体静力学方程表明:(1)当作用于流体面上方的压强有变化时;(2)当流体面上方的压强一定时,静止流体内部任一点压强的大小与流体本身的和有关,因此在的的同一液体处,处在都相等。
二、流体静力学基本方程式的应用1.流体进压强的测量(1)U形管压差计①U形管压差计由、及管内指示液组成。
②指示液要与被测流体不,不起,其密度要,通常采用的指示液有、、及等。
③U形管压差计可用来测量压强差,也可以用来测量或。
【典型例题】例1用U形管测量管道中1、2两点的压强差。
已知管内流体是水,指示液是密度为1595 kg/m3的CCl4,压差计读数为40cm,求压强差(p1– p2)。
若管道中的流体是密度为2.5kg/m3的气体,指示液仍为CCl4,U形管读数仍为40cm,则管道中1、2两点的压强差是多少Pa?【例2】某蒸汽锅炉用本题附图中串联的汞-水U形管压差计以测量液面上方的蒸气压。
已知汞液面与基准面的垂直距离分别为h1 = 2.3 m,h2 = 1.2 m,h3 = 2.5 m,h4 = 1.4m,两U形管间的连接管内充满了水。
锅炉中水面与基准面的垂直距离h5 = 3.0m,大气压强p a = 99kPa。
试求锅炉上方水蒸汽的压强p0为若干(Pa)?【随堂练习】1.大气压强为750mmHg时,水面下20m深处水的绝对压强为多少Pa?2.水平导管上的两点接一盛有水银的U形管压差计(如图所示),压差计读数为26mmHg。
流体静力学基本方程
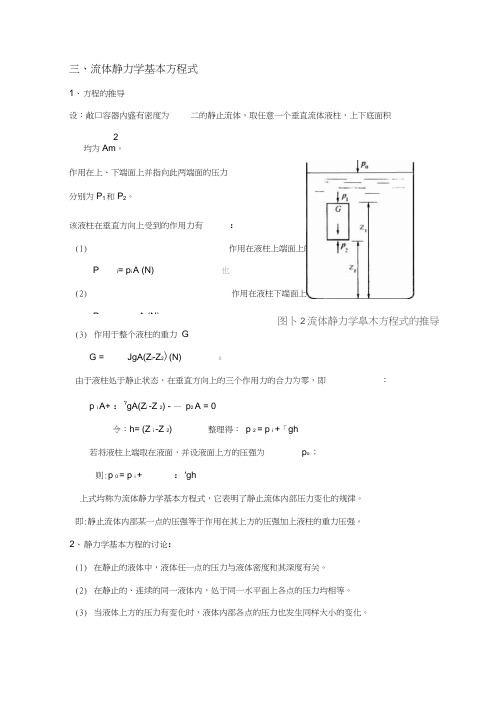
图卜2流体静力学皐木方程式的推导(3) 作用于整个液柱的重力 GG = JgA(Z i -Z 2)(N) 0由于液柱处于静止状态,在垂直方向上的三个作用力的合力为零,即 :p i A+ :?gA(Z i -Z 2) - — p 2 A = 0令:h= (Z i -Z 2) 整理得: p 2 = p i +「gh若将液柱上端取在液面,并设液面上方的压强为p o ; 则:p 0 = p i + :'gh上式均称为流体静力学基本方程式,它表明了静止流体内部压力变化的规律。
即:静止流体内部某一点的压强等于作用在其上方的压强加上液柱的重力压强。
2、 静力学基本方程的讨论:(1) 在静止的液体中,液体任一点的压力与液体密度和其深度有关。
(2) 在静止的、连续的同一液体内,处于同一水平面上各点的压力均相等。
(3) 当液体上方的压力有变化时,液体内部各点的压力也发生同样大小的变化。
三、流体静力学基本方程式1、 方程的推导设:敞口容器内盛有密度为 二的静止流体,取任意一个垂直流体液柱,上下底面积2均为Am 。
作用在上、下端面上并指向此两端面的压力分别为P 1和P 2。
该液柱在垂直方向上受到的作用力有: (1) 作用在液柱上端面上的总压力 P iPi = p i A (N) 也 (2) 作用在液柱下端面上的总压力 P 2P = p A (N)压强差的也大小可利用一定高度的液体柱来表示。
p P (5) 整理得:z 1g1二z 2g 也为静力学基本方程P g (6) 方程是以不可压缩流体推导出来的,对于可压缩性的气体,只适用于压强变 化不大的情况。
3、静力学基本方程的应用(1)测量流体的压差或压力①U 管压差计U 管压差计的结构如图。
对指示液的要求:指示液要与被测流体不互溶,不起 A化学作用,且其密度:7指应大于被测流体的密度:、。
通常采用的指示液有:水、油、四氯化碳或汞等。
I测压差:设流体作用在两支管口的压力为 p 1和P 2,且P i > P 2 , A-B 截面为等压面 即:P A 二P B 根据流体静力学基本方程式分别对 U 管左侧和U 管右侧进行计算整理得: P i - P 2 =:〔'指一'Rg讨论: (a )压差(p i -P 2)只与指示液的读数 R 及指示液冋被测流体的密度差有关。
流体静力学基本方程

流体静力学基本方程流体静力学是研究流体在静止状态下的力学性质和平衡条件的学科。
它是流体力学的基础,对于理解和解决与静止流体有关的问题至关重要。
在流体静力学中,存在着一些基本方程,它们描述了流体静力学的基本原理和规律。
第一个基本方程是压力的定义。
在流体静力学中,压力是指单位面积上的力的大小。
它可以通过一个简单的公式来计算,即压力等于作用在单位面积上的力的大小。
这个基本方程是流体静力学研究中最基础的概念之一。
第二个基本方程是流体静压力的方程。
它描述了流体静止时由于重力而产生的压力分布。
根据这个方程,流体静压力与液体的密度、重力加速度以及液体的深度有关。
具体而言,它可以表示为P=ρgh,其中P是压力,ρ是液体的密度,g是重力加速度,h是液体的深度。
这个方程揭示了在静止的流体中,压力随着深度的增加而增加。
第三个基本方程是流体静力学的平衡条件。
它描述了流体在静止状态下达到平衡所满足的条件。
根据这个方程,流体中的每一点都处于力的平衡状态,即外力和压力力的合力为零。
这个方程是解决静止流体平衡问题的基础,通过它可以推导出各种与静止流体有关的性质和现象。
流体静力学基本方程的研究对于很多工程和科学领域都具有重要意义。
在建筑工程中,我们需要了解流体静力学基本方程来设计和分析水坝、水库等工程结构。
在航空航天工程中,流体静力学的研究可以帮助我们理解和解决航空器中的静压力、静气压力等问题。
在环境科学中,流体静力学的基本方程可以应用于水体的污染扩散和水质调控等方面。
总之,流体静力学基本方程是研究静止流体力学的基础。
它们描述了流体静力学的基本原理和规律,是解决与静止流体相关问题的重要工具。
通过对这些基本方程的理解和应用,我们能够更好地理解和分析静止流体的性质和行为,为相关领域的工程和科学问题提供有效的解决方法。
工程流体力学公式

工程流体力学公式1.流体静力学公式:(1) 压强公式:P = ρgh,其中P为压强,ρ为流体密度,g为重力加速度,h为液面高度。
(2)压力公式:P=F/A,其中P为压力,F为作用力,A为受力面积。
2.流体力学基本方程:(1)质量守恒方程:∂(ρ)/∂t+∇·(ρv)=0,其中ρ为密度,t为时间,v为速度矢量。
(2) 动量守恒方程:∂(ρv)/∂t + ∇·(ρvv) = -∇P + ∇·τ +ρg,其中P为压力,τ为应力张量,g为重力加速度。
(3) 能量守恒方程:∂(ρe)/∂t + ∇·(ρev) = -P∇·v +∇·(k∇T) + ρg·v,其中e为单位质量的总能量,T为温度,k为热传导系数。
3.流体动力学方程:(1)欧拉方程:∂v/∂t+(v·∇)v=-∇(P/ρ)+g,其中v为速度矢量,P为压力,ρ为密度,g为重力加速度。
(2)再循环方程:∂v/∂t+(v·∇)v=-∇(P/ρ)+g+F/M,其中F为体积力,M为质量。
4.流体阻力公式:(1) 粘性流体的阻力公式:F = 6πμrv,其中F为阻力,μ为粘度,r为流体直径,v为速度。
(2)粘性流体在管道中的流量公式:Q=(π/8)ΔP(R^4)/(Lμ),其中Q为流量,ΔP为压差,R为半径,L为管道长度,μ为粘度。
5.流体力学定律:(1) Pascal定律:在封闭的液体容器中,施加在液体上的外力将均匀传递到液体的每一个点。
(2) Bernoulli定律:沿着流体流动方向,速度增大则压力减小,速度减小则压力增大。
除了上述公式之外,还有许多与特定问题相关的公式,如雷诺数、流体阻力系数、泵和液力传动公式等。
这些公式是工程流体力学研究和设计的基础,可以帮助工程师分析和解决与流体运动和相互作用有关的问题。
流体主要计算公式

流体主要计算公式流体是液体和气体的统称,具有流动性和变形性。
流体力学是研究流体静力学和动力学的学科,其中主要涉及到流体的力学性质、运动规律和力学方程等内容。
在流体力学的研究中,有一些重要的计算公式被广泛应用。
下面将介绍一些常见的流体力学计算公式。
1.流体静力学公式:(1)压力计算公式:P=F/A-P表示压力-F表示作用力-A表示受力面积(2)液体静力学公式:P=hρg-P表示液体压力-h表示液体高度-ρ表示液体密度-g表示重力加速度2.流体动力学公式:(1)流体流速公式:v=Q/A-v表示流速-Q表示流体流量-A表示流体截面积(2)流体流量公式:Q=Av-Q表示流体流量-A表示流体截面积-v表示流速(3)连续方程:A1v1=A2v2-A1和A2表示流体截面积-v1和v2表示流速(4) 流体动能公式:E = (1/2)mv^2-E表示流体动能-m表示流体质量-v表示流速(5)流体的浮力公式:Fb=ρVg-Fb表示浮力-ρ表示液体密度-V表示浸泡液体的体积-g表示重力加速度3.流体阻力公式:(1)层流阻力公式:F=μAv/L-F表示阻力-μ表示粘度系数-A表示流体截面积-v表示流速-L表示流动长度(2)湍流阻力公式:F=0.5ρACdV^2-F表示阻力-ρ表示流体密度-A表示物体的受力面积-Cd表示阻力系数-V表示物体相对于流体的速度4.比力计算公式:(1)应力计算公式:τ=F/A-τ表示应力-F表示力-A表示受力面积(2)压力梯度计算公式:ΔP/Δx=ρg-ΔP/Δx表示压力梯度-ρ表示流体密度-g表示重力加速度(3) 万斯压力计算公式:P = P0 + ρgh-P表示压力-P0表示参考压力-ρ表示流体密度-g表示重力加速度-h表示液体的高度以上是一些流体力学中常见的计算公式,涉及到压力、流速、阻力、浮力以及比力等方面的运算。
这些公式在解决流体力学问题时非常有用,可以帮助我们理解和分析流体的运动和力学性质。
1.2_流体静力学基本方程解析

3 液封高度的计算
例:如图示。(P24 例题1-8)
已知:炉内p≤10.7kpa(表压)
求:h=? 解:如图等压面0-0´。 p1=炉内压力=pa+10.7×103Pa p2= pa+gh
b
pa h
0´
a
0
1
2
由 p2= p1
a-乙炔发生炉
b-液封管
解得: h=1.09 m 为了安全起见,实际应略小于1.09 m 。
F=ma=Va
2
表面力
表面力是由与流体表面相接触的物质(包括相邻流体)
施加给该流体的作用力,其大小与作用面积成正比。 垂直于表面的力
作用于流体上的表面力 平行于表面的力
(1)压力是垂直作用于表面的力,作用在流体单位面积上的 压力称为压强。 (2)剪切力是平行作用于表面的力,作用在流体单位面积上 的剪切力称为剪应力。 压强和剪应力的单位均为N/m2或Pa。
p
或
+ gz = 常数
p1 p + gz1= 2+ gz2
p0 …(2) 1-15a …(3) 1-15b p h
p2=p1+g(z1-z2)
p=p0+gh
(1)(2)(3)三式为流体静力学基本方程式
静力学方程的讨论:
1 适用范围:仅适用于静止的、不可压缩性流体在重力场
中的情况,且为连续的同一流体。如气体, p 变化不大,
因为p0=p0´, 所以
pa pb = R( A B ) g
注意: (1) 静压强也有基准, 在同一计算中,应注意用统一的压强基准;
(2) 压力基准可以任意选取,但选定后计算中通常不能随意改变;
1.2 流体静力学基本方程式

C p = 1 . 01 kJ ⋅ kg − 1 ⋅ K − 1 ,管内流速取 8 ~ 15 m ⋅ s −1
水
ρ = 1000 kg ⋅ m−3 ,µ = 1cp = 1×10−3 SI 单位(Pa.s), 单位(Pa.s) (Pa.s),
图2-3 U管压差计
② 倾斜式压差计
p
A1 h1 = A2 L ⇒ h1 = h2 = L sin α
A2 L A1
A2
L
h2 h
A1
α
图2-4 倾斜式压差计
p = ρ g h = ρ g (h1 + h2 )
h1
A = ρ gL 2 + sin α A 1 = KL K = f ( ρ ,α ) = 0 . 2 , . 4 , . 6 , . 8 L 0 0 0
p a = ρ 液 gh = p b = ρ 指 gR h =
图2-7 远距离测量液位
ρ指 R ρ液
3.确定液封高度
h=
p1
pa − p ρ液 g
ቤተ መጻሕፍቲ ባይዱ
p
pa
图2-6 测量液位的连通器 图2-8 冷凝器
4.倾析器 4.倾析器 互不相溶且密度不同的液体混合物, 互不相溶且密度不同的液体混合物, 可在倾析器中进行分层, 可在倾析器中进行分层,使两种液体互 相分离。如图2 按静力学方程, 相分离 。 如图 2 - 9 , 按静力学方程 , 考 点和B点有: 虑A点和B点有:
P1 P2 + z1 = + z2 ρg ρg
流体静力学基本方程式的适用条件是

流体静力学基本方程式的适用条件流体静力学是研究静止的流体力学现象的学科,主要研究流体静力学基本方程式的解法和应用。
流体静力学基本方程式包括质量守恒方程、动量守恒方程和能量守恒方程。
这些方程式适用于静止的流体,即不受外力而处于平衡状态的流体。
下面我们将详细介绍流体静力学基本方程式的适用条件。
一、质量守恒方程质量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内质量的守恒。
质量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
二、动量守恒方程动量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内动量的守恒。
动量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
5. 流体是粘性的,即流体内存在摩擦力。
三、能量守恒方程能量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内能量的守恒。
能量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
5. 流体是绝热的,即流体内不存在热传导。
以上是流体静力学基本方程式的适用条件,下面我们将通过实例来进一步说明。
实例:一艘船停泊在湖面上,船底面积为10平方米,船重为50吨,水的密度为1000千克/立方米。
求船底受到的水的压力。
解析:根据质量守恒方程可知,流体在静止状态下,密度不随位置和时间的变化而变化,因此可以将水的密度视为恒定值1000千克/立方米。
流体力学公式大全

流体力学公式大全流体力学是研究流体静力学和流体动力学的学科,涉及到流体的运动规律、压力分布、速度场等内容。
在工程和物理学领域,流体力学有着广泛的应用,包括飞机设计、水利工程、汽车空气动力学等方面。
本文将为大家详细介绍流体力学中常见的公式,希望能够帮助大家更好地理解和应用流体力学知识。
1. 流体静力学公式。
在静止的流体中,压力的分布可以用以下公式表示:\[ P = \rho \cdot g \cdot h \]其中,P为压力,ρ为流体密度,g为重力加速度,h为流体的高度。
2. 流体动力学公式。
在流体运动时,流体的速度场可以用以下公式表示:\[ \frac{Dv}{Dt} = -\frac{1}{\rho} \cdot \nabla P + g \]其中,Dv/Dt表示速度的变化率,ρ为流体密度,∇P为压力的梯度,g为重力加速度。
3. 纳维-斯托克斯方程。
描述了流体运动的基本规律,可以用以下形式表示:\[ \rho \cdot \frac{Dv}{Dt} = -\nabla P + \mu \cdot \nabla^2 v + \rho \cdot g \]其中,μ为流体的动力粘度,∇^2v为速度的散度。
4. 伯努利方程。
描述了流体在不同位置之间的能量转换关系,可以用以下公式表示:\[ P + \frac{1}{2} \cdot \rho \cdot v^2 + \rho \cdot g \cdot h = \text{常数} \]其中,P为压力,ρ为流体密度,v为流体速度,h为流体的高度。
5. 应力张量。
描述了流体内部的应力分布情况,可以用以下矩阵表示:\[ \tau = \begin{bmatrix} \tau_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} &\tau_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \tau_{zz} \end{bmatrix} \] 其中,τ为应力张量,下标表示不同方向上的应力分量。
流体静力学基本方程式

第一节流体静力学基本方程式流体静力学是研究流体在外力作用下达到平衡的规律。
在工程实际中,流体的平衡规律应用很广,如流体在设备或管道内压强的变化与测量、液体在贮罐内液位的测量、设备的液封等均以这一规律为依据。
1-1-1 流体的密度一、密度单位体积流体所具有的质量,称为流体的密度,其表达式为:1-1)式中ρ——流体的密度,kg/m3;m——流体的质量,kg ;3V——流体的体积,m 3。
不同的流体密度不同。
对于一定的流体,密度是压力P 和温度T 的函数。
液体的密度随压力和温度变化很小,在研究流体的流动时,若压力和温度变化不大,可以认为液体的密度为常数。
密度为常数的流体称为不可压缩流体。
流体的密度一般可在物理化学手册或有关资料中查得,本教材附录中也列出某些常见气体和液体的密度值,可供查用。
二、气体的密度气体是可压缩的流体,其密度随压强和温度而变化。
因此气体的密度必须标明其状态,从手册中查得的气体密度往往是某一指定条件下的数值,这就涉及到如何将查得的密度换算为操作条件下的密度。
但是在压强和温度变化很小的情况下,也可以将气体当作不可压缩流体来处理。
对于一定质量的理想气体,其体积、压强和温度之间的变化关系为pVp'V 'T T '将密度的定义式代入并整理得'T'pTp'1-2)式中p——气体的密度压强,Pa;V——气体的体积,m 3;T——气体的绝对温度,K ;上标“ '”表示手册中指定的条件。
一般当压强不太高,温度不太低时,可近似按下式来计算密度。
pMRT或M T0 p T0 p22.4 Tp0 0Tp0 1-3a) (1-3b)式中 p ——气体的绝对压强, kPa 或 kN/m 2;M ——气体的摩尔质量, kg/kmol ; T ——气体的绝对温度, K ;R ——气体常数, 8.314kJ/(kmol ·K ) 下标“ 0”表示标准状态( T 0=273K ,p 0=101.3kPa )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体静力学基本方程
一、静止液体中的压强分布规律
重力作用下静止流体质量力:X=Y=0,Z=-g
代入 Zdz)Ydy (Xdx dp ++=ρ (压强p 的全微分方程)
得:dp =ρ(-g )dz =-γdz
积分得: p=-γz +c
即: 常数=+γp
z 流体静力学基本方程
对1、2两点: γγ2211p z p z +=+
结论: 1)仅在重力作用下,静止流体中某一点的静水压强随深度按线性规律增加。
2)自由表面下深度h 相等的各点压强均相等——只有重力作用下的同一连续连通的静止流体的等压面是水平面。
3)推广:已知某点的压强和两点间的深度差,即可求另外一点的压强值。
p 2=p 1+γΔh
4)仅在重力作用下,静止流体中某一点的静水压强等于表面压强加上流体的容重与该点淹没深度的乘积。
观看录像: 水静力学 观看动画: 静水力学基本方程演示 >>
二、静止液体中的压强计算
自由液面处某点坐标为z 0,压强为p 0;液体中任意点的坐标为z ,
压强为p ,则:
γγ0
0p z p
z +=+
∴坐标为z 的任意点的压强 :p =p 0+γ(z 0-z ) 或 p =p 0+γh
三、静止液体中的等压面
静止液体中质量力――重力,等压面垂直于质量力,
∴静止液体中的等压面必为水平面
算一算:
1. 如图所示的密闭容器中,液面压强p 0=9.8kPa ,A 点压强为49kPa ,
则B 点压强为39.2kPa ,在液面下的深度为3m 。
四、绝对压强、相对压强和真空度的概念
1.绝对压强(absolute pressure ):是以绝对真空状态下的压强(绝
对零压强)为起点基准计量的压强。
一般 p =p a +γh
2. 相对压强(relative pressure ):又称“表压强”,是以当时当地大气压强为起点而计算的压强。
可“+”可“– ”,也可为“0”。
p '=p-p a
3.真空度(Vacuum ):指某点绝对压强小于一个大气压p a 时,其小于大气压强p a 的数值。
真空度p v =p a -p
注意:计算时若无特殊说明,均采用相对压强计算。
问题:流体能否达到绝对真空状态?若不能,则最大真空度为多少?
不能,最大真空度等于大气压强与汽化压强的差值。
绝对压强基准
绝对真空p
=0
相对压强基准
大气压强p a
压强
p 1
p ' p 2 p v
p a
p<p a
p>p a
问题:露天水池水深5m 处的相对压强为:49kPa
A. 5kPa ;
B. 49kPa ;
C. 147kPa ;
D. 205kPa 。
例1 求淡水自由表面下2m 深处的绝对压强和相对压强。
解: 绝对压强: p =p 0+ρgh =p a +ρgh =101325 N/m 2+9800×2 N/m 2
=120925 N/m 2=1.193标准大气压
相对压强:p '=p -p a =ρgh =9800×2N/m 2 =19600 N/m 2
=0.193标准大气压
例2 如图,h v =2m 时,求封闭容器A 中的真空度。
解:设封闭容器内的绝对压强为p ,真空度为p v 。
则:p =p a -ρgh v
根据真空度定义:p v =p a - p
=p a -( p a -ρgh v )=ρgh v =9800×2N/m 2=19600 N/m 2
问题:某点的真空度为65000 Pa ,当地大气压为0.1MPa ,该点的绝对压强为: C
A. 65000P a ;
B. 55000P a ;
C. 35000P a ;
D. 165000P a 。
问题: 绝对压强p 与相对压强p ’ 、真空度p v 、当地大气压p a 之间的关系是: C
A. p =p'+p v ;
B. p'=p +p a
C. p v = p a -p
D. p'= p a - p
五、流体静力学基本方程的几何意义与能量意义
常数=+γp
z
位置水头z :任一点在基准面0-0以上的位置高度。
表示单位重量液体对基准面O -O 的位
能——比位能。
测压管高度 p '/γ:表示某点液体在相对压强p ’作用下能够上升的高度。
——相对压强高度
静压高度p/γ:表示某点液体在绝对压强p 作用下能够上升的高度。
——绝对压强高度
压强水头——比压能(单位重量液体所具有的压力能)
测压管水头( z +p '/γ):位置水头与测压管高度之和。
单位重量流体的总势能。
静压水头面 A B
Z A p'A /γ Z B
p B /γ 测压管水头面
p a /γ
O
O
静压水头(z+p/γ):位置水头与静压高度之和。
比势能:比位能与比压能之和。
观看录像水静力学
几何意义与能量意义:同一静止液体内各点,比位能与比压能可以互相转化,比势能保
持不变。
问题1:仅在重力作用下,静止液体中任意一点对同一基准面的单位势能为 B ?
A. 随深度增加而增加; C. 随深度增加而减少;
B. 常数; D. 不确定。
问题2:试问图示中A、 B、 C、 D点的测压管高度,测压管水头。
(D点闸门关闭,
以D点所在的水平面为基准面)
A:测压管高度0m,测压管水头6m
B:测压管高度2m,测压管水头6m
C:测压管高度3m,测压管水头6m
D:测压管高度6m,测压管水头6m
例:试标出图示盛液容器内A. B和C三点的位置水头、压强水
头和测压管水头。
以图示O—O为基准面。
解:压强水头为相对压强的液柱高度,即测压管高度;位置
水头为液体质点至基准面的位置高度。
显然,A点压强水头p A/ρg,位置水头z A和测压管水头(z A+p A/ρg),
如图所示。
在静止液体内部任意质点的测压管水头均相等,即z A+p A/ρg=c。
因此,以A点的测压管水头为依据,B点的位置水头z B和压强水头p B/ρg即可以确定(如图所示)。
至于C点,因为位于测压管水头之上,其相对压强为负值,即p C< p a。
故该点的压强水头为-p Cv/ρg,位置水头为z C,如图所示。
复习题(判断题)
1、静水压强是既有大小又有方向的矢量。
对
2、一个工程大气压等于98kPa,相当于10m水柱的压强。
对
3、如果某点的相对压强为负值,则说明该处发生了真空。
对
4、容器中两种不同液体的分界面是水平面,但不一定是等压面。
错
5、静水内任意一点的静水压强均相等。
错
6、静止液体的自由表面是一个水平面,也是等压面。
对
思考题
1.什么是等压面?等压面的条件是什么?
等压面是指流体中压强相等的各点所组成的面。
只有重力作用下的等压面应满足的条件是:静止、连通、连续均质流体、同一水平面。
2.盛有液体的敞口容器作自由落体时,容器壁面AB上的压强分布如何?
∵dp=ρ(X dx+Y dy+Z dz)=ρ(g-g)dz=0
∴p =const,自由液面上p = 0 ∴p = 0
3.若人所能承受的最大压力为 1.274MPa(相对压强),则潜水员的极限潜水深度为多少?潜水员的极限潜水深度为:1.274×106÷9800=130(米)
4.为什么虹吸管能将水输送到一定的高度?
因为虹吸管内出现了真空。
