第十届(2018)全国大学生数学竞赛(非数学类)预赛试题

全国大学生数学竞赛(非数学类)大纲及历年预赛试卷

—1—
余弦函数，以及它们的和与积 7. 欧拉(Euler)方程. 8. 微分方程的简单应用五、向量代数和空间解析几何 1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积. 2. 两向量垂直、平行的条件、两向量的夹角. 3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦. 4. 曲面方程和空间曲线方程的概念、平面方程、直线方程. 5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和
f ( y) x2[1 f ( y)]3
1 x2 (1 f ( y))
f ( y) [1 f ( y)]2 x2[1 f ( y)]3
解法 2 方程 xe f (y) ey ln 29 取对数，得 f ( y) ln x y ln ln 29
（1）
方程（1）的两边对 x 求导，得 f ( y) y 1 y x
4．设函数 y y(x) 由方程 xe f ( y) ey ln 29 确定，其中 f 具有二阶导数，且 f 1 ，
则
d2 y dx 2
________________.
解法 1 方程 xe f ( y) ey ln 29 的两边对 x 求导，得
e f ( y) xf ( y) ye f ( y) e y y ln 29
即
[ 1 f ( y) y]xe f ( y) ye y ln 29 x
因 e y ln 29 xe f ( y) 0 ，故 1 f ( y) y y，即 y
1
，因此
x
x(1 f ( y))
d2 y dx 2
y
1 x2 (1 f
( y))
f ( y) y x[1 f ( y)]2
点到直线的距离. 6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次

历届大学生高等数学竞赛真题及答案非数学类14页

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分，共20分）1．计算=--++⎰⎰y x y x x yy x Dd d 1)1ln()(____________，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，令u t -=1，则21t u -=2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ，则23)(2--=A x x f ，解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________.解: 因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面 2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。

历届全国大学生数学竞赛预赛试题

全国高校生数学竞赛预赛试卷〔非数学类〕2021年第一届全国高校生数学竞赛预赛试卷〔非数学类〕一、填空题〔每题5分，共20分〕1．计算()ln(1)d yx y x y ++=⎰⎰，其中区域D 由直线1=+y x 及两坐标轴所围成三角形区域.2．设)(x f 是连续函数，且满意22()3()d 2f x x f x x =--⎰，那么()f x =.3．曲面2222x z y =+-平行平面022=-+z y x 的切平面方程是.4．设函数)(x y y =由方程29ln )(y y f e xe =确定，其中f 具有二阶导数，且1≠'f ，那么=22d d xy.二、〔5分〕求极限x enx x x x ne e e )(lim 20+++→ ，其中n 是给定的正整数. 三、〔15分〕设函数)(xf 连续，10()()g x f xt dt =⎰，且A x x f x =→)(lim 0，A 为常数，求()g x '并探讨)(x g '在0=x 处的连续性.四、〔15分〕平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ，L 为D 的正向边界，试证：〔1〕⎰⎰-=---Lx y Lx y x ye y xe x ye y xe d d d d sin sin sin sin ；〔2〕2sin sin 25d d π⎰≥--Ly y x ye y xe .五、〔10分〕x x e xe y 21+=，x x e xe y -+=2，x x x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解，试求此微分方程. 六、〔10分〕设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时，0≥y ，又该抛物线及x 轴及直线1=x 所围图形的面积为31.试确定c b a ,,，使此图形绕x 轴旋转一周而成的旋转体的体积V 最小. 七、〔15分〕)(x u n 满意1()()1,2,n xnnu x u x xe n -'=+=，且ne u n =)1(，求函数项级数∑∞=1)(n n x u 之和.八、〔10分〕求-→1x 时，及∑∞=02n n x 等价的无穷大量.2021年第二届全国高校生数学竞赛预赛试卷〔非数学类〕一、〔25分，每题5分〕〔1〕设22(1)(1)(1)nn x a a a =+++，其中||1,a <求lim .n n x →∞〔2〕求21lim 1x x x e x -→∞⎛⎫+ ⎪⎝⎭. 〔3〕设0s >，求0(1,2,)sx n n I e x dx n ∞-==⎰.〔4〕设函数()f t 有二阶连续导数，1(,)r g x y f r ⎛⎫== ⎪⎝⎭，求2222g gx y∂∂+∂∂. 〔5〕求直线10:0x y l z -=⎧⎨=⎩及直线2213:421x y z l ---==--的间隔 .二、〔15分〕设函数()f x 在(,)-∞+∞上具有二阶导数，并且()0f x ''>，lim ()0x f x α→+∞'=>，lim ()0x f x β→-∞'=<，且存在一点0x ，使得0()0f x <. 证明：方程()0f x =在(,)-∞+∞恰有两个实根.三、〔15分〕设函数()y f x =由参数方程22(1)()x t t t y t ψ⎧=+>-⎨=⎩所确定，且22d 3d 4(1)y x t =+，其中()t ψ具有二阶导数，曲线()y t ψ=及22132t u y e du e-=+⎰在1t =出相切，求函数()t ψ.四、〔15分〕设10,nn n k k a S a =>=∑，证明：〔1〕当1α>时，级数1n n na S α+∞=∑收敛；〔2〕当1α≤且()n s n →∞→∞时，级数1n n na S α+∞=∑发散.五、〔15分〕设l 是过原点、方向为(,,)αβγ，〔其中2221)αβγ++=的直线，匀称椭球2222221x y z a b c++≤〔其中0c b a <<<，密度为1〕绕l 旋转.〔1〕求其转动惯量；〔2〕求其转动惯量关于方向(,,)αβγ的最大值和最小值. 六、(15分)设函数()x ϕ具有连续的导数，在围绕原点的随意光滑的简洁闭曲线C 上，曲线积分422d ()d 0Lxy x x yx yϕ+=+⎰的值为常数. 〔1〕设L 为正向闭曲线22(2)1x y -+=，证明422d ()d 0L xy x x yx y ϕ+=+⎰；〔2〕求函数()x ϕ；〔3〕设C 是围绕原点的光滑简洁正向闭曲线，求422d ()d Cxy x x yx y ϕ++⎰.2021年第三届全国高校生数学竞赛预赛试卷〔非数学类〕一、计算以下各题〔此题共3小题，每题各5分，共15分〕〔1〕求11cos 0sin lim xx x x -→⎛⎫⎪⎝⎭；〔2〕.求111lim (12)n n n n n →∞⎛⎫+++ ⎪+++⎝⎭；〔3〕()2ln 1arctan ttx e y t e⎧=+⎪⎨=-⎪⎩，求22d d yx.二、〔此题10分〕求方程()()24d 1d 0x y x x y y +-++-=的通解. 三、〔此题15分〕设函数()f x 在0x =的某邻域内具有二阶连续导数，且()()()0,0,0f f f '''均不为0，证明：存在唯一一组实数123,,k k k ，使得四、〔此题17分〕设2221222:1x y z a b c∑++=，其中0a b c >>>，2222:z x y ∑=+，Γ为1∑及2∑的交线，求椭球面1∑在Γ上各点的切平面到原点间隔的最大值和最小值. 五、〔此题16分〕S 是空间曲线2231x y z ⎧+=⎨=⎩绕y 轴旋转形成的椭球面的上半部分〔0z ≥〕〔取上侧〕，∏是S 在(,,)P x y z 点处的切平面，(,,)x y z ρ是原点到切平面∏的间隔，,,λμν表示S 的正法向的方向余弦. 计算：〔1〕()d ,,SzS x y z ρ⎰⎰；〔2〕()3d Sz x y z S λμν++⎰⎰ 六、〔此题12分〕设()f x 是在(,)-∞+∞内的可微函数，且()()f x mf x '<，其中01m <<，任取实数0a ，定义1ln (),1,2,...n n a f a n -==，证明：11()n n n a a ∞-=-∑肯定收敛.七、〔此题15分〕是否存在区间[]0,2上的连续可微函数()f x ，满意(0)(2)1f f ==，()1f x '≤，2()d 1f x x ≤⎰请说明理由.2021年第四届全国高校生数学竞赛预赛试卷〔非数学类〕一、〔本大题共5小题，每题6分，共30分〕解答以下各题〔要求写出重要步骤〕. 〔1〕求极限21lim(!)n n n →∞. 〔2〕求通过直线2320:55430x y z l x y z +-+=⎧⎨+-+=⎩的两个相互垂直的平面1π和2π，使其中一个平面过点(4,3,1)-. 〔3〕函数(,)ax byz u x y e+=，且20ux y∂=∂∂. 确定常数a 和b ，使函数(,)z z x y =满意方程20z z zz x y x y∂∂∂--+=∂∂∂∂. 〔4〕设函数()u u x =连续可微，(2)1u =，且3(2)d ()d L x y u x x u u y +++⎰在右半平面及途径无关，求(,)u x y .〔5〕求极限1limx x x t +. 二、〔此题10分〕计算20sin d x e x x +∞-⎰.三、〔此题10分〕求方程21sin 2501x x x=-的近似解，精确到0.001.四、〔此题12分〕设函数()y f x =二阶可导，且()0f x ''>，(0)0f =，(0)0f '=，求330()lim ()sin x x f u f x u→，其中u 是曲线()y f x =上点(,())P x f x 处的切线在x 轴上的截距.五、〔此题12分〕求最小实数C ，使得满意10()d 1f x x =⎰的连续函数()f x 都有10f dx C ≤⎰.六、〔此题12分〕设()f x 为连续函数，0t >. 区域Ω是由抛物面22z x y =+和球面 2222x y z t ++=(0)z >所围起来的部分. 定义三重积分222()()d F t f x y z v Ω=++⎰⎰⎰，求()F t 的导数()F t ''.七、〔此题14分〕设1n n a ∞=∑及1n n b ∞=∑为正项级数，证明：〔1〕假设()111lim 0n n n n n a a b b →∞++->，那么级数1n n a ∞=∑收敛；〔2〕假设()111lim 0n n n n n a a b b →∞++-<，且级数1n n b ∞=∑发散，那么级数1n n a ∞=∑发散. 2021年第五届全国高校生数学竞赛预赛试卷〔非数学类〕一、解答以下各题〔每题6分，共24分，要求写出重要步骤〕sin d xx x+∞⎰不是肯定收敛的. ()y y x =由323322x x y y +-=确定，求()y x 的极值.0)y x =≥上的点A 作切线，使该切线及曲线及x 轴所围成的平面图形的面积为34，求点A 的坐标.二、〔总分值12分〕计算定积分2sin arctan d 1cos xx x e I x xππ-⋅=+⎰. 三、〔总分值12分〕设()f x 在0x =处存在二阶导数(0)f ''，且()lim 0x f x x→=.证明：级数11n f n ∞=⎛⎫⎪⎝⎭∑收敛.四、〔总分值12分〕设(),()0()f x f x m a x b π'≤≥>≤≤，证明2sin ()d baf x x m≤⎰. 五、〔总分值14分〕设∑()()()333d d 2d d 3d d I xx y z y y z x z z x y ∑=-+-+-⎰⎰.试确定曲面∑，使积分I 的值最小，并求该最小值.六、〔总分值14分〕设22d d ()()a aC y x x y I r x y -=+⎰，其中a 为常数，曲线C 为椭圆222x xy y r ++=lim ()a r I r →+∞. 七、〔总分值14分〕推断级数()()1111212n n n n ∞=+++++∑的敛散性，假设收敛，求其和.一、填空题〔共有5小题，每题6分，共30分〕1x y e =和1x y xe =是齐次二阶常系数线性微分方程的解，那么该方程是 .22:2S z x y =+和平面022:=++z y x L . 那么及L 平行的S 的切平面方程是 .()y y x =由方程21sin d 4y x t x tπ-⎛⎫= ⎪⎝⎭⎰0d d x y x== .1(1)!nn k kx k ==+∑，那么=∞→n n x lim . 130()lim 1x x f x x e x →⎛⎫++= ⎪⎝⎭，那么=→20)(lim x x f x . 二、〔此题12分〕设n 为正整数，计算21d 1cos ln d d n eI x x x π-⎛⎫= ⎪⎝⎭⎰. 三、〔此题14分〕设函数()f x 在]1,0[上有二阶导数，且有正常数,A B 使得()f x A ≤，|"()|f x B ≤. 证明：对随意]1,0[∈x ，有22|)('|BA x f +≤. 四、〔此题14分〕〔1〕设一球缺高为h ，所在球半径为R . 证明该球缺体积为2)3(3h h R -π，球冠面积为Rh π2；〔2〕设球体12)1()1()1(222≤-+-+-z y x 被平面6:=++z y x P 所截的小球缺为Ω，记球缺上的球冠为∑，方向指向球外，求第二型曲面积分五、〔此题15分〕设f 在],[b a 上非负连续，严格单增，且存在],[b a x n ∈，使得⎰-=b a nn n dx x f ab x f )]([1)]([.求n n x ∞→lim . 六、〔此题15分〕设2222212n n n n A n n n n =++++++，求⎪⎭⎫ ⎝⎛-∞→n n A n 4lim π.一、填空题〔每题6分，共5小题，总分值30分〕〔1〕极限2222sin sin sin lim 12n n n n n n n n πππ→∞⎛⎫⎪+++= ⎪+++ ⎪⎝⎭. 〔2〕设函数(),z z x y =由方程,0z z F x y yx ⎛⎫++= ⎪⎝⎭所确定，其中(),F u v 具有连续偏导数，且0u v xF yF +≠那么z z x y xy∂∂+=∂∂ .〔3〕曲面221z x y =++在点()1,1,3M -的切平面及曲面所围区域的体积是 . 〔4〕函数()[)[)3,5,00,0,5x f x x ⎧∈-⎪=⎨∈⎪⎩在(]5,5-的傅立叶级数在0x =收敛的是 .〔5〕设区间()0,+∞上的函数()u x 定义域为()20xt u x e dt +∞-=⎰，那么()u x 的初等函数表达式是 .二、〔12分〕设M 是以三个正半轴为母线的半圆锥面，求其方程. 三、〔12分〕设()f x 在(),a b 内二次可导，且存在常数,αβ，使得对于(),x a b ∀∈，有()()()f x f x f x αβ'=+，那么()f x 在(),a b 内无穷次可导. 四、〔14分〕求幂级数()()30211!nn n x n ∞=+-+∑的收敛域及其和函数.五、〔16分〕设函数()f x 在[]0,1上连续，且()()11000,1f x dx xf x dx ==⎰⎰.试证：〔1〕[]00,1x ∃∈使()04f x >；〔2〕[]10,1x ∃∈使()14f x =.五、〔16分〕设(),f x y 在221x y +≤上有连续的二阶偏导数，且2222xx xy yy f f f M ++≤. 假设()()()0,00,0,00,00x y f f f ===，证明：()221,x y f x y dxdy +≤≤⎰⎰.2021年第八届全国高校生数学竞赛预赛试卷〔非数学类〕一、填空题〔每题5分，总分值30分〕 1、假设()f x 在点x a =可导，且()0f a ≠，那么()1lim nn f a n f a →∞⎛⎫⎛⎫+ ⎪ ⎪⎝⎭ ⎪= ⎪⎪⎝⎭. 2、假设()10f =，()1f '存在，求极限()()220sin cos tan3lim1sin x x f x x xI ex→+=-.3、设()f x 有连续导数，且()12f =，记()2x z f e y =，假设z z x∂=∂，求()f x 在0x >的表达式. 4、设()sin 2xf x ex =，求02n a π<<，()()40f .5、求曲面22 2x z y =+平行于平面220x y z +-=的切平面方程.二、〔14分〕设()f x 在[]0,1上可导，()00f =，且当()0,1x ∈，()01f x '<<，试证当()0,1a ∈，()()()2300d d aaf x xf x x >⎰⎰.三、〔14分〕某物体所在的空间区域为222:22x y z x y z Ω++≤++，密度函数为222x y z ++，求质量()222d d d M xy z x y z Ω=++⎰⎰⎰.四、〔14分〕设函数()f x 在闭区间[]0,1上具有连续导数，()00f =，()11f =，证明：()10111lim 2n n k k n f x dx f n n →∞=⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭∑⎰.五、〔14分〕设函数()f x 在闭区间[]0,1上连续，且()10d 0I f x x =≠⎰，证明：在()0,1内存在不同的两点12,x x ，使得()()12112f x f x I+=. 六、〔14分〕设()f x 在(),-∞+∞可导，且()()(2f x f x f x =+=.用级数理论证明()f x 为常数.2021年第九届全国高校生数学竞赛预赛试卷〔非数学类〕一、1. 可导函数f (x )满意⎰+=+xx tdt t f x xf 01sin )(2)(cos ，那么()f x .2．求⎪⎭⎫ ⎝⎛+∞→n n n 22sin lim π.3. 设(,)w f u v =具有二阶连续偏导数，且==+u x cy v x cy -，，其中c为非零常数. 那么21xx yy w w c -. 4. 设()f x 有二阶导数连续，且(0)'(0)0,"(0)6f f f ===，那么240(sin )lim x f x x→. 5. 不定积分sin 2sin 2(1sin )x e xI dx x -=-⎰. 6. 记曲面222z x y =+和z =围成空间区域为V ，那么三重积分Vzdxdydz ⎰⎰⎰.二、〔此题总分值14分) 设二元函数(,)f x y 在平面上有连续的二阶偏导数. 对任何角度α，定义一元函数假设对任何α都有(0)0dg dtα=且22(0)0d g dt α>. 证明)0,0(f 是(,)f x y 的微小值.三、(此题总分值14分) 设曲线Γ为在上从(1,0,0)A 到(0,0,1)B 的一段. 求曲线积分⎰Γ++=xdz zdy ydx I .四、(此题总分值15分) 设函数()0f x >且在实轴上连续，假设对随意实数t ，有||()1t x e f x dx +∞---∞≤⎰，那么,()a b a b ∀<，2()2b a b a f x dx -+≤⎰. 五、(此题总分值15分) 设{}n a 为一个数列，p 为固定的正整数。

前三届全国大学生高等数学竞赛真题及答案(大纲)非数学类

中国大学生数学竞赛竞赛大纲为了进一步推动高等学校数学课程的改革和建设，提高大学数学课程的教学水平，激励大学生学习数学的兴趣，发现和选拔数学创新人才，更好地实现“中国大学生数学竞赛”的目标，特制订本大纲。

一、竞赛的性质和参赛对象“中国大学生数学竞赛”的目的是：激励大学生学习数学的兴趣，进一步推动高等学校数学课程的改革和建设，提高大学数学课程的教学水平，发现和选拔数学创新人才。

“中国大学生数学竞赛”的参赛对象为大学本科二年级及二年级以上的在校大学生。

二、竞赛的内容“中国大学生数学竞赛”分为数学专业类竞赛题和非数学专业类竞赛题。

中国大学生数学竞赛（非数学专业类）竞赛内容为大学本科理工科专业高等数学课程的教学内容，具体内容如下：一、函数、极限、连续1．函数的概念及表示法、简单应用问题的函数关系的建立.2．函数的性质：有界性、单调性、周期性和奇偶性.3．复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4．数列极限与函数极限的定义及其性质、函数的左极限与右极限.5．无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6．极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.7．函数的连续性（含左连续与右连续）、函数间断点的类型.8．连续函数的性质和初等函数的连续性.9．闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理).二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5. 微分中值定理，包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L’Hospital)法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三、一元函数积分学1.原函数和不定积分的概念.2.不定积分的基本性质、基本积分公式.3.定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz )公式. 4. 不定积分和定积分的换元积分法与分部积分法. 5. 有理函数、三角函数的有理式和简单无理函数的积分. 6. 广义积分.7. 定积分的应用：平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值．四.常微分方程1. 常微分方程的基本概念：微分方程及其解、阶、通解、初始条件和特解等.2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli )方程、全微分方程.3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程：),()n (x f y =),,(y x f y '='' ),(y y f y '=''.4. 线性微分方程解的性质及解的结构定理.5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6. 简单的二阶常系数非齐次线性微分方程：自由项为多项式、指数函数、正弦函数、余弦函数，以及它们的和与积 7. 欧拉(Euler )方程. 8. 微分方程的简单应用五、向量代数和空间解析几何1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.2. 两向量垂直、平行的条件、两向量的夹角.3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦.4. 曲面方程和空间曲线方程的概念、平面方程、直线方程.5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7. 空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程. 六、多元函数微分学1. 多元函数的概念、二元函数的几何意义.2. 二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.3. 多元函数偏导数和全微分、全微分存在的必要条件和充分条件.4. 多元复合函数、隐函数的求导法.5. 二阶偏导数、方向导数和梯度.6. 空间曲线的切线和法平面、曲面的切平面和法线.7. 二元函数的二阶泰勒公式.8. 多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.七、多元函数积分学1. 二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标).2.两类曲线积分的概念、性质及计算、两类曲线积分的关系.3.格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.4.两类曲面积分的概念、性质及计算、两类曲面积分的关系.5.高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算.6.重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等)八、无穷级数1.常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2.几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.3.任意项级数的绝对收敛与条件收敛.4.函数项级数的收敛域与和函数的概念.5.幂级数及其收敛半径、收敛区间（指开区间）、收敛域与和函数.6.幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.7.初等函数的幂级数展开式.8.函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l，l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

第十届全国大学生数学竞赛决赛试题参考答案及评分标准(非数学类)

第十届全国大学生数学竞赛决赛试题参考答案及评分标准（非数学类，2019年3月30日）一、填空题（本题满分30分，每小题6分）1、设函数在点在处连续，则的值为答案：2、设则答案：3、设曲线L是空间区域的表面与平面的交线，则答案：4、设函数由方程确定，其中具有连续二阶偏导数，则答案：5、已知二次型，则的规范形为答案：二、设内三阶连续可导，满足，又设数列满足严格单调减少且计算【解】由于在区间（-1,1）内三阶可导，在处有Taylor公式又，所以分①由于数列严格单调且，则，且为严格单调增加趋于正无穷的数列，注意到，故由Stolz定理及①式，有分分三、设上具有连续导数，且证明：对于成立【证明】令则故函数在上严格单调增加，记的反函数为，则定义在上，且4分于是根据积分中值定理，存在使得分因此注意到则即分四、计算三重积分：，其中【解】采用“先二后一”法，并利用对称性，得其中分用极坐标计算二重积分，得交换积分次序，得分作变量代换:并利用对称性，得所以.分五、之和.【解】级数通项令分其中.因为所以满足解这个一阶线性方程，得由得,故且分六、设A是n阶幂零矩阵,即满足证明:若A的秩为r，且则存在n阶可逆矩阵P其中为r阶单位矩阵. 【证】存在n阶可逆矩阵H,Q，使得因为所以有分对QH作相应分块为则有因此分而所以显然，所以为行满秩矩阵.8分因为使得分令则有分七、设为单调递减的正实数列,收敛，证明：收敛，所以对任意给定，存在自然数，使得当时,有因为单调递减的正数列，所以分注意到当时，有令得到分下面证明：对于任意自然数n，如果满足则有事实上,即得到分利用（2），令可以得到即分又由知，存在自然数，使得分取则当时，有因此分。

第十届全国大学生数学竞赛决赛(非数学类)获奖名单

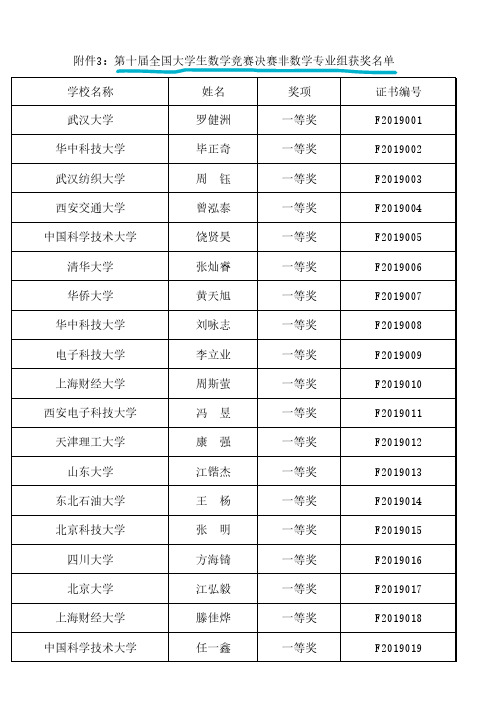
太原理工大学北京大学清华大学
华南理工大学哈尔滨工业大学
丽水学院燕山大学电子科技大学北京航空航天大学厦门大学合肥工业大学宣城校区同济大学华东理工大学合肥工业大学西安交通大学湖北工业大学华中科技大学中国民航大学陆军工程大学国防工程学院陆军勤务学院山东大学
王金宇高铭齐倪赞林吴珍谦李雨杭苏文张再哲李诚佳乐洋何鸿光陈家鑫刘聪颖詹研朱基宏潘翔宇刘子文阚腾吴昊曹晨廖雪文王一宁
二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖二等奖
F2019083 F2019084 F2019085 F2019086 F2019087 F2019088 F2019089 F2019090 F2019091 F2019092 F2019093 F2019094 F2019095 F2019096 F2019097 F2019098 F2019099 F2019100 F2019101 F2019102 F2019103
张庆达
河海大学
石蕴
内蒙古科技大学
覃康朔
浙江大学
任梓洋
三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖
济南大学
胡广富
贵州大学
张繁盛
江苏大学
曾宇
长安大学
周星星
空军工程大学
涂捷
北京邮电大学
韩帅杰
上海财经大学
洪世哲
中国石油大学（北京）克拉玛依校区郭涛

历届全国大学生高等数学竞赛真题及答案非数学类

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分，共20分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=， v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解: 因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。

历年全国大学生高等数学竞赛真题及答案(2009-2011非数学类).

1
1 2 4 2 3 1 5 16
2 (12t t )dt 2 t t t
令t 1u ，则u 1t2 ，du 2tdt ，u2 12t2 t4 ，u(1u) t2 (1t)(1t) ，
0
(*) 2 (12t2 t4 )dt
1
2
d y
则 2 ________________.
dx
f (y ) y
x
解方程xe e ln 29 的两边对求导，得
y
(x y ) ln(1 ) u ln u u ln v
1x y
坐标轴所围成三角形区域.
0 1
解令，则，，
x y u,x v x v,y u v dxdy det dudv dudv
1 1
2 ．设f (x) 是连续函数，且满足f (x) 3x 2 f (x)dx 2 , 则f (x) ____________.
0
处的切平面方程是2(x 2) 2(y 1) (z 5) 0 ，即曲面z y 2 平行平面
2
2x 2y z 0 的切平面方程是2x 2y z 1 0 。
4 ．设函数y y (x) 由方程 f (y ) y 确定，其中具有二阶导数，且，
xe e ln 29 f f 1
处的法向量为(z (x , y ), z (x , y ),1) ，故(z (x , y ), z (x , y ),1) 与(2,2,1) 平行，
x 0 0 y 0 0 x 0 0 y 0 0
D x dxdy D dudv
1x y 1u
1 u ln u u u u
4 2 10
解得A 。因此f (x) 3x 。

历届全国大学生数学竞赛真题及答案非数学类

高数竞赛预赛试题〔非数学类〕〔参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

〕2021年第一届全国大学生数学竞赛预赛试卷一、填空题〔每题5分，共20分〕1．计算=--++⎰⎰y x yx x yy x D d d 1)1ln()(，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令vx u y x ==+,，那么vu y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v u uv u u u u u〔*〕令u t -=1，那么21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，⎰+--=0142d )21(2(*)t t t⎰+-=1042d )21(2t t t 151651322153=⎥⎦⎤⎢⎣⎡+-=t t t 2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 那么=)(x f .解:令⎰=20d )(x x f A ，那么23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得。

因此。

3．曲面平行平面022=-+z y x 的切平面方程是.解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面22=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面平行平面022=-+z y x 的切平面方程是0122=--+z y x 。

第十届全国大学生数学竞赛决赛参考答案

准考证号
Þ
省市
学校
第 5 页, 共 7 页
得
分
阅卷人
六、 (本题满分 11 分) 设 A 是 n 阶幂零矩阵, 即满足 A2 = O . n 证明: 若 A 的秩为 r , 且 1 6 r < , 则存在 n 阶可逆矩阵 P , 使得 2 ! O I O r P 1 AP = , 其中 Ir 为 r 阶单位矩阵. O O O
座位号
注意到当 m < n 时, 有
n X k =m k X i =1 n X k =1 n 1 X k =1
(Ak
Ak
1 )bk = An bn
= lim = lim = lim
机
n!1
密
2 a2 an n+1 n!1 2 an 2 an +1
2 lim nan = lim
n Stolz 1 H H H H lim 2 2 2 n!1 1/a n!1 1/a 1/an n n+1 = lim
2 f 2 (a ) an n 2 (a ) n!1 a2 f n n
第十届全国大学生数学竞赛决赛参考答案
（非数学类, 2019 年 3 月 30 日）
座位号
绝密 F 启用前
(14 金融工程–零蛋大)
考试形式：闭卷考试时间： 150 分钟满分： 100 分
题号满分一 30 二 12 三 12 四 12 五 12 六 11 七 11 总分 100
考场号
得分注意：本试卷共七大题, 满分 100 分, 考试时间为 150 分钟. 1: 所有答题都须写在试卷密封线右边, 写在其他纸上一律无效: 2: 密封线左边请勿答题, 密封线外不得有姓名及相关标记:

第十届全国大学生数学竞赛非数学类预赛试题

第十届全国大学生数学竞赛（非数学类）预赛试题及一、填空题（本题满分24分, 共4小题, 每小题6分)（1）设(0,1),α∈则()lim (1)n n n αα→+∞+-=＿＿＿＿＿＿＿.（2）若曲线()y y x =由+cos +sin 1yx t te ty t =⎧⎨+=⎩确定，则此曲线在0t =对应点处的切线方程为（3）23/2ln((1)x dx x ++⎰=（4）201-cos lim x x →=＿＿＿＿＿＿＿.f t ()0t ≠(1)0f =二 (本题满分8分) 设函数在时一阶连续可导，且，求函数f x -y 22()，使得曲线积分2222L ⎰y (2-f (x -y ))⎡⎤⎣⎦dx +xf (x -y )dy 与路径无关，其中L 为任一不与直=±y x 线相交的分段光滑闭曲线.f x ()0,11)3(f x ≤≤三 (本题满分14分) 设在区间[ ]上连续，且 .证明：11141)3f (x )dx dx (f x ⎰≤≤⎰.四 (本题满分12分)计算三重积分22⎰⎰⎰x +y ()dV （V ）（V ），其中是由222x +y +(z -2)≥4，222x +y +(z -1)≤9，0z ≥所围成的空心立体.五 (本题满分14分) 设(,)f x y 在区域D M ≤，11(,)A x y ，22(,)B x y 是D 内两点，线段AB 包含在D 内。

证明：1122|(,)(,)|||f x y f x y M AB -≤，其AB ||AB 中表示线段的长度.)0(f x >六(本题满分14分) 证明：对于连续函数，有11lnf (x )dx ≥⎰⎰ln f (x )dx .七 (本题满分14分) 已知{}k a ，{}k b 是正项数列，且10,k k b b δ+-≥>，δ为一常数.证明：若级数1k k a +∞=∑收敛，则级数11k k k+∞=+.1,2,k。

大学生高等数学竞赛试题汇总及答案

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009-2010年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(16/15，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f ,则=)(x f ____________.解:令⎰=2d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面 022=-+z y x 的切平面方程是0122=--+z y x 。

大学数学竞赛试题及答案

大学数学竞赛试题及答案一、选择题（每题5分，共20分）1. 下列哪个选项不是实数？A. √2B. πC. -1D. i答案：D2. 函数f(x)=x^2在区间[-2, 2]上的最大值是：A. 0B. 4C. -4D. 2答案：B3. 以下哪个数列是等差数列？A. 1, 4, 9, 16B. 1, 1/2, 1/3, 1/4C. 2, 4, 6, 8D. 1, 2, 3, 4答案：C4. 矩阵A和B满足AB=BA，那么A和B：A. 一定是方阵B. 一定是可逆矩阵C. 一定是对角矩阵D. 一定是正交矩阵答案：A二、填空题（每题5分，共20分）1. 计算极限：lim (x→0) (sin x)/x = ______。

答案：12. 求不定积分：∫x^2 dx = ______。

答案：(1/3)x^3 + C3. 设函数f(x)=x^3-3x+2，求f'(x) = ______。

答案：3x^2-34. 已知矩阵A=\[\begin{array}{cc}1 & 2\\3 & 4\end{array}\]，求A的行列式det(A) = ______。

答案：-2三、解答题（每题15分，共30分）1. 证明：如果一个数列是单调递增且有界的，则该数列必定收敛。

证明：假设数列{a_n}是单调递增的，即对任意的n，有a_n ≤ a_{n+1}。

又因为该数列有界，所以存在实数M和m，使得对所有的n，有m ≤ a_n ≤ M。

由于数列是单调递增的，我们可以构造一个新的数列{b_n}，其中b_n = a_{n+1} - a_n。

由于{a_n}是单调递增的，所以数列{b_n}非负。

又因为{a_n}有界，所以存在一个实数N，使得对所有的n > N，有b_n < 1。

这意味着从某一项开始，数列{a_n}的增长速度将小于1，因此数列{a_n}必定收敛。

2. 计算定积分：∫[0, π] sin x dx。

1_2018全国大学生数学竞赛(非数学类)获奖名单(1)

（全国赛）非数学专业 340304
51
44
华南理工大学
17金融
（全国赛）非数学专业 340503
23
44
华南理工大学
自动化4班
（全国赛）非数学专业 340504
83
44
广东工业大学光电信息科学与工程（全国赛）非数学专业 340604
10
44
华南理工大学
16高分子甲班
（全国赛）非数学专业 340301
71
37
赵崇斌
广东工业大学计算机科学与技术（全国赛）非数学专业 340604
56
37
邓百川佛山科学技术学院
网络工程
（全国赛）非数学专业 340303
29
36
何铭震
华南理工大学
16自动化
（全国赛）非数学专业 340304
77
36
李创芝
广东工业大学电气工程及其自动化（全国赛）非数学专业 340403
光电信息科学与工程（全国赛）非数学专业 340402
48
38
苏榕进佛山科学技术学院计算机科学与技术（全国赛）非数学专业 340504
17
38
王雪毅
华南理工大学
16电气卓越班
（全国赛）非数学专业 340601
12
38
吴镇锋
华南理工大学
机械电子工程
（全国赛）非数学专业 340602
8
38
萧智聪
广东理工学院
姓名吴佩津刘恩波吴珍谦徐书恒潘建辉梁炜焜罗洪博李国燊魏焕陈文庆刘鸿生皮宇帆陈灿豪李岩罗子豪李东安熊志进颜祖耀吕不悔黄晓楠金雪晴康世贸李锦辉邵威谢杰恩陈卓然邓凯欣梁昌曜谌绍泉刘谦潘锦诚陈浩标经菠奚圣羽肖云红张欣庄培溪李呈辉孙凌瑜陈力郭俊锋潘怀远王维镛张华健曹逸鹏

历届全国大学生数学竞赛真题及答案非数学类

高数竞赛预赛试题〔非数学类〕〔参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

〕2021年第一届全国大学生数学竞赛预赛试卷一、填空题〔每题5分，共20分〕1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，那么v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，令u t -=1，那么21t u -=2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 那么=)(x f .解:令⎰=20d )(x x f A ，那么23)(2--=A x x f ，解得。

因此。

3．曲面平行平面022=-+z y x 的切平面方程是.解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面平行平面 022=-+z y x 的切平面方程是0122=--+z y x 。

4．设函数)(x y y =由方程29ln )(y y f e xe =确定，其中f 具有二阶导数，且1≠'f ，那么.解:方程29ln )(y y f e xe =的两边对x 求导，得因)(29ln y f y xe e =，故，即，因此二、〔5分〕求极限x enx x x x ne e e )(lim 20+++→ ，其中n 是给定的正整数. 解:因故因此三、〔15分〕设函数)(x f 连续，⎰=10d )()(t xt f x g ，且，A 为常数，求)(x g '并讨论)(x g '在0=x 处的连续性.解:由与函数)(x f 连续知，0)(limlim )(lim )0(000===→→→xx f x x f f x x x 因⎰=10d )()(t xt f x g ，故0)0(d )0()0(10===⎰f t f g ，因此，当0≠x 时，，故当0≠x 时，这说明)(x g '在0=x 处连续.四、〔15分〕平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ，L 为D 的正向边界，试证：〔1〕⎰⎰-=---Lx y Lx y x ye y xe x ye y xe d d d d sin sin sin sin ；〔2〕2sin sin 25d d π⎰≥--Ly y x ye y xe .证:因被积函数的偏导数连续在D 上连续，故由格林公式知〔1〕y x ye y xe x x ye y xe Dx y Lx y d d )()(d d sin sin sin sin ⎰⎰⎰⎥⎦⎤⎢⎣⎡-∂∂-∂∂=---而D 关于x 与y 是对称的，即知因此〔2〕因故由知即 2sin sin 25d d π⎰≥--Ly y x ye y xe五、〔10分〕x x e xe y 21+=，x x e xe y -+=2，x x x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解，试求此微分方程.解设x x e xe y 21+=，x x e xe y -+=2，x x x e e xe y --+=23是二阶常系数线性非齐次微分方程的三个解，那么x x e e y y 212-=--与x e y y -=-13都是二阶常系数线性齐次微分方程的解，因此0=+'+''cy y b y 的特征多项式是0)1)(2(=+-λλ，而0=+'+''cy y b y 的特征多项式是因此二阶常系数线性齐次微分方程为02=-'-''y y y ，由)(2111x f y y y =-'-''与知，1112)(y y y x f -'-''=)(2)2(42222x x x x x x x x e xe e e xe e e xe +-++-++= 二阶常系数线性非齐次微分方程为六、〔10分〕设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,又该抛物线与x 轴及直线1=x 所围图形的面积为31.试确定c b a ,,,使此图形绕x 轴旋转一周而成的旋转体的体积最小.解因抛物线c bx ax y ln 22++=过原点，故1=c ，于是即而此图形绕x 轴旋转一周而成的旋转体的体积即令得即因此七、〔15分〕)(x u n 满足),2,1()()(1 =+='-n e x x u x u x n n n, 且, 求函数项级数之与.解即由一阶线性非齐次微分方程公式知即因此由知，0=C ，于是下面求级数的与：令那么即由一阶线性非齐次微分方程公式知令0=x ，得C S ==)0(0，因此级数的与八、〔10分〕求-→1x 时, 与等价的无穷大量.解令2)(t x t f =，那么因当10<<x ，(0,)t ∈+∞时，2()2ln 0t f t tx x '=<，故xt t ex t f 1ln22)(-==在(0,)+∞上严格单调减。

第十届全国大学生数学竞赛(非数学类)答案

第十届全国大学生数学竞赛（非数学类）预赛试题及答案一、填空题（本题满分24分, 共4小题, 每小题6分)（1）设(0,1),α∈则()lim (1)n n n αα→+∞+-=＿0＿＿＿＿＿＿.解由于 1111,n n α⎛⎫⎛⎫+<+ ⎪ ⎪⎝⎭⎝⎭则 αααααα-=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+<⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=-+11111111)1(n n n n n n n ，于是 ααα-<-+<11)1(0nn n ，应用两边夹法则，()lim (1)0n n n αα→+∞+-=. （2）若曲线()y y x =由+cos +sin 1yx t t e ty t =⎧⎨+=⎩确定，则此曲线在0t =对应点处的切线方程为0(1)y x -=--解：当0t =时，1,0x y ==，对cos x t t =+两边关于t 求导：1sin dx t dt =-，01t dxdt ==，对+sin 1y e ty t +=两边关于t 求导：cos 0y dy dy e y t t dt dt +++=，01t dy dt ==-，则01t dydx ==-.所以，切线方程为0(1)y x -=--.（3）21ln(1)C 2x x +-++ 解1：tan ln(tan sec )ln(tan sec )sin sec x t t t dt t t d t t=+==+⎰⎰ln(tan sec )sin sin ln(tan sec )sint ln(tan sec )t t d t t t t d t t =+=+-+⎰⎰21sin ln(tan sec )sint(sec tan sec )tan sec t t t t t t dt t t =+-++⎰sin sin ln(tan sec )cos tt t t dt t=+-⎰21sin ln(tan sec )ln |cos |C ln(1)C 2t t t t x x =+++-++.解2：ln(x d =+⎰1x dx ⎛⎫=-21xx dxx=-+⎰21ln(1)C2x x-++（4）21coslimx x→-=＿＿＿3＿＿＿＿.解答：2001coslimx xxx→→⎡-=⎢⎣⎦211lim2x x→=+2211lim2x x x→⎡⎤=++⎢⎥⎣⎦1lim2x→=++⎢⎥⎣⎦220011cos21cos313lim lim1322322x xx xx x→→--=++=++=.二 (本题满分8分) 设函数()f t在0t≠时一阶连续可导，且(1)0f=，求函数22()f x y-，使得曲线积分2222(2())()Ly f x y dx xf x y dy⎡⎤--+-⎣⎦⎰与路径无关，其中L为任一不与直线y x=±相交的分段光滑闭曲线.解：设22(,)(2())P x y y f x y=--，22(,)()Q x y xf x y=-，由题设可知，积分与路径无关，于是有(,)Q x y Px y∂∂=∂∂，由此可知222222()()()1x y f x y f x y'--+-=-----------5分记22t x y=-，则得微分方程()()1tf t f t'+=，即(())1tf t'=，())tf t t C=+又(1))0f=，可得1,C=-1())1f tt=-，从而22221()1f x yx y-=--.------------8分三 (本题满分14分) 设()f x在区间[0,1]上连续，且1()3f x≤≤.证明：1100141()()3f x dx dxf x≤≤⎰⎰.证明. 由柯西不等式111()()f x dx dx f x ⎰⎰≥201⎛⎫= ⎪ ⎪⎝⎭⎰. --------4分又由于 ()()()1()30f x f x --≤，则()()()1()3/()0f x f x f x --≤，即 3()4()f x f x +≤， 103()4()f x dx f x ⎛⎫+≤ ⎪⎝⎭⎰. ----------10分由于21111000313()()()4()f x dx dx f x dx f x f x ⎛⎫≤+ ⎪⎝⎭⎰⎰⎰⎰故 11141()()3f x dx dx f x ≤≤⎰⎰. -----------14分四 (本题满分12分)计算三重积分22()V xy dV +⎰⎰⎰（），其中V （）是由222(2)4x y z ++-≥，222(1)9x y z ++-≤，0z ≥所围成的空心立体.解：（1）1sin cos ,sin sin ,1cos ():03,0,02x r y r z r V r ϕθϕθϕϕπθπ==-=⎧⎨≤≤≤≤≤≤⎩123222225()8()sin sin 315V x y dV d d r r dr ππθϕϕϕπ+==⋅⋅⎰⎰⎰⎰⎰⎰ ----------4分（2）2sin cos ,sin sin ,2cos ():02,0,02x r y r z r V r ϕθϕθϕϕπθπ==-=⎧⎨≤≤≤≤≤≤⎩222222225()8()sin sin 215V x y dV d d r r dr ππθϕϕϕπ+==⋅⋅⎰⎰⎰⎰⎰⎰ ----------8分（3）3cos ,sin ,10():02x r y r z V r θθθπ⎧==≤≤⎪⎨≤≤≤≤⎪⎩3022223510()22()1)(1243)55V r x y dV rdrd dz d dr πθθπ≤+===-⋅+⎰⎰⎰⎰⎰⎰12322222222()()()()256()()()()3V V V V x y dV x y dV x y dV x y dV π+=+-+-+=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰------12分五 (本题满分14分) 设(,)f x y 在区域DM ≤，11(,)A x y ，22(,)B x y 是D 内两点，线段AB 包含在D 内。

第十届全国大学生数学竞赛非数学专业复赛试题参考答案

y y
.
从上式中去掉对数符号，有
b x2 1 ex2dx ea2 eb2 , b a 0. ..........................10 分 a
三、解：显然，曲线 C 所围的平面图形位于第一象限. 当 x 1, y 1时， C 的方程为： ln x ln y 1，即 xy e ；
五、证明：令 h x, y f x, y g x, y . 显然 h x, y 在有界闭区域 D 上连续，因
此它在 D 上存在最大值 M 和最小值 m ，即存在两点 P1, P2 D ，使得
h P1 m, h P2 M .
.......................................4 分
2
当 x 1, 0 y 1时， C 的方程为： ln x ln y 1 ，即 x e ； y
当 0 x 1, y 1时， C 的方程为： ln x ln y 1 ，即 y e ； x
当 0 x 1, 0 y 1时， C 的方程为： ln x ln y 1，即 xy 1 . e
0
x
0
.............................................2 分
对上式左边交换积分次序，有

2 dx 2 f t x f t dt

2 f t dt
t f t xdx .
0
x
0
0
而
t
0
f
t

x dx

t
0
a
a
b ex2d x2 a

第十届（2018）全国大学生数学竞赛（非数学类）预赛试题

第十届全国大学生数学竞赛（非数学类）预赛试题及一、填空题（本题满分24分, 共4小题, 每小题6分)（1）设(0,1),则lim (1)n n n=＿＿＿＿＿＿＿．（2）若曲线()yy x 由+cos +sin 1yx t t ety t确定，则此曲线在0t 对应点处的切线方程为（3）223/2ln(1)(1)xx dx x =（4）321cos cos2cos3limxx x xx=＿＿＿＿＿＿＿.f t ()0t(1)0f 二 (本题满分8分) 设函数在时一阶连续可导，且，求函数f xy 22()，使得曲线积分2222Ly(2f (x y ))dx xf (xy )dy 与路径无关，其中L 为任一不与直y x 线相交的分段光滑闭曲线．f x ()0,11)3(f x 三 (本题满分14分) 设　在区间[]上连续，且　.证明：11141)3f (x)dxdx(f x .四 (本题满分12分）计算三重积分22xy ()dV （V ）（V ），其中是由222x y(z 2)4，222xy(z 1)9，0z 所围成的空心立体.五 (本题满分14分) 设(,)f x y 在区域D 内可微，且22f f M xy，11(,)A x y ，22(,)B x y 是D 内两点，线段AB 包含在D 内。

证明：1122|(,)(,)|||f x y f x y M AB ，其AB ||AB 中表示线段的长度.)0(f x 六(本题满分14分) 证明：对于连续函数，有11lnf (x)dxln f (x)dx .七 (本题满分14分) 已知{}k a ，{}k b 是正项数列，且10,kkb b ，为一常数.证明：若级数1k k a 收敛，则级数121211()()k k k k k kk a a a b b b b b 收敛.1,2,k。

第十届(2018)全国大学生数学竞赛(非数学类)预赛试题

全国大学生数学竞赛(非数学类)大纲及历年预赛试卷

历届大学生高等数学竞赛真题及答案非数学类14页

历届全国大学生数学竞赛预赛试题

前三届全国大学生高等数学竞赛真题及答案(大纲)非数学类

第十届全国大学生数学竞赛决赛试题参考答案及评分标准(非数学类)

第十届全国大学生数学竞赛决赛(非数学类)获奖名单

历届全国大学生高等数学竞赛真题及答案非数学类

历年全国大学生高等数学竞赛真题及答案(2009-2011非数学类).

历届全国大学生数学竞赛真题及答案非数学类

第十届全国大学生数学竞赛决赛参考答案

第十届 全国大学生数学竞赛 非数学类 预赛试题

大学生高等数学竞赛试题汇总及答案

大学数学竞赛试题及答案

1_2018全国大学生数学竞赛(非数学类)获奖名单(1)

历届全国大学生数学竞赛真题及答案非数学类

第十届全国大学生数学竞赛(非数学类)答案

第十届全国大学生数学竞赛非数学专业复赛试题参考答案

第十届（2018）全国大学生数学竞赛（非数学类）预赛试题

第十届全国大学生数学竞赛非数学类预赛试题