(人教版)高中数学平面直角坐标系优秀课件1
合集下载
平面直角坐标系ppt优秀课件

益。──高尔基 • ● 生活就像海洋,只有意志坚强的人,才能到达彼岸。──马克思 • ● 浪费别人的时间是谋财害命,浪费自己的时间是慢性自杀。──列
宁
• ● 哪里有天才,我是把别人喝咖啡的工夫都用在工作上的。──鲁迅 • ● 完成工作的方法,是爱惜每一分钟。──达尔文 • ● 没有伟大的愿望,就没有伟大的天才。──巴尔扎克 • ● 读一切好的书,就是和许多高尚的人说话。──笛卡尔 • ● 成功=艰苦的劳动+正确的方法+少谈空话。 ──爱因斯坦
y
4
(4)单位长度一般
3 2
取相同的
1
-3 -2 -1-1 O1 2 3
x
-2
-3 -4
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
1
-3 -2 -1 O1 2 3
X
X
3 2 1 O -1 -2 -3 -1
-2
(A)
(B)
3Y 2 1
-3 -2 -1-1 O1 2 3 X
-2 -3
3Y 2 1
则a=_4__,b=_5___。
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在__第__二__或__四__象__限。
7.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
· 纵轴 y 5
B(0,5)
4
3 2
·A(5,2)
1
-4 -3 (-2,-3)D
-3
-4
·C(2,-3)
例3.在下面直角坐标系中描出下列各组点,
并将各组的点用线段依次连接起来.
宁
• ● 哪里有天才,我是把别人喝咖啡的工夫都用在工作上的。──鲁迅 • ● 完成工作的方法,是爱惜每一分钟。──达尔文 • ● 没有伟大的愿望,就没有伟大的天才。──巴尔扎克 • ● 读一切好的书,就是和许多高尚的人说话。──笛卡尔 • ● 成功=艰苦的劳动+正确的方法+少谈空话。 ──爱因斯坦
y
4
(4)单位长度一般
3 2
取相同的
1
-3 -2 -1-1 O1 2 3
x
-2
-3 -4
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
1
-3 -2 -1 O1 2 3
X
X
3 2 1 O -1 -2 -3 -1
-2
(A)
(B)
3Y 2 1
-3 -2 -1-1 O1 2 3 X
-2 -3
3Y 2 1
则a=_4__,b=_5___。
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在__第__二__或__四__象__限。
7.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
· 纵轴 y 5
B(0,5)
4
3 2
·A(5,2)
1
-4 -3 (-2,-3)D
-3
-4
·C(2,-3)
例3.在下面直角坐标系中描出下列各组点,
并将各组的点用线段依次连接起来.
人教版平面直角坐标系 PPT

7.1.2 平面直角坐标系(一)
笛卡尔 ,法国著名哲学家,数学家。 1596年出生于法国拉镇,法国巴黎普 瓦捷大学毕业,获法律学位。 数学方面的主要成就 哲学专著《方法论》一书中的《几何 学》,第一次将x看作点的横坐标,把 y看作是点的纵坐标,将平面内的点与 一种坐标对应起来。
如何确定直线上点的位置?
C·
y
4
3 ·A
2
·B
1
x -6 -5 -4 -3 -2 -1 o 1 2 3 4 5 6 -1
-2
D·
· -3 E
-4
· F -5 -6
新课 讲授
如何根据坐标(4,2)确定点
y
4 3 2
.P
1
O -3 -2 -1 -1 1 2 3 4
x
-2
-3
-4
P就是所求作的点
如何确定平面上点的位置?
(-2,3)小强
(9)如果∣3x+2∣+∣2y-1∣=0,那么点P(x,y)和Q(x+1,y-2) 分别在哪个象限?
告诉大家 本节课你的收获!
-2
F· -3
·G
做 一
做
在平面直角坐标系中描出下列
y
各点:
E(0,4)
A(3,4)
B(-2,34)
3
B(-2,3)
2
A(3,4)
C(-4,-1)
1
D(2.5,-2) E(0,4)
-4 -3 -2 -1 O 1 2 3 4 x
C(-4,-1)
-1 -2
D(2.5,-2)
-3
17
-4
我在第二象限
我在第一象限
·E (2,0)
1234
笛卡尔 ,法国著名哲学家,数学家。 1596年出生于法国拉镇,法国巴黎普 瓦捷大学毕业,获法律学位。 数学方面的主要成就 哲学专著《方法论》一书中的《几何 学》,第一次将x看作点的横坐标,把 y看作是点的纵坐标,将平面内的点与 一种坐标对应起来。
如何确定直线上点的位置?
C·
y
4
3 ·A
2
·B
1
x -6 -5 -4 -3 -2 -1 o 1 2 3 4 5 6 -1
-2
D·
· -3 E
-4
· F -5 -6
新课 讲授
如何根据坐标(4,2)确定点
y
4 3 2
.P
1
O -3 -2 -1 -1 1 2 3 4
x
-2
-3
-4
P就是所求作的点
如何确定平面上点的位置?
(-2,3)小强
(9)如果∣3x+2∣+∣2y-1∣=0,那么点P(x,y)和Q(x+1,y-2) 分别在哪个象限?
告诉大家 本节课你的收获!
-2
F· -3
·G
做 一
做
在平面直角坐标系中描出下列
y
各点:
E(0,4)
A(3,4)
B(-2,34)
3
B(-2,3)
2
A(3,4)
C(-4,-1)
1
D(2.5,-2) E(0,4)
-4 -3 -2 -1 O 1 2 3 4 x
C(-4,-1)
-1 -2
D(2.5,-2)
-3
17
-4
我在第二象限
我在第一象限
·E (2,0)
1234
《平面直角坐标系》课件(共21张PPT)

C
A.
F 点(0,3)在____轴上;
点(3,-2)在第_____象限;
B
(0,3),(-2,0),(6,0) ,
两条互相垂直且有公共原点的数轴
(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于0;
G 原点 轴正半轴 C.
这四组点关于直线x=2对称.
A
连接起来的图形像“房子” (0,3),(-2,0),(6,0) ,
观察所描出的图形,它像什么?
y
连接起来的图形像“房子” D
E
C
F
B
G
oA
x
① D(- 3,5),E(- 7,3), C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0), A(0,0),B(0,3); -1
y
D
与y轴平行的直线上点的坐标的特征
E ③(1,0),(1,-6),
若点 P(2m - 1,3)在第二象限,则( )
o
若点P(m+5,m-2)在y轴上,则m=
.
x
解答下列问题: ① D(- 3,5),E(- 7,3),
若点P在第三象限且到x轴的距离为 2 ,
(1)若CA平行于x轴,BC平行于y轴,则点C的
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点? 已知线段AB=3,AB∥x轴,若A点坐标为
(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于0;
纵轴上的点横坐标为0.
若点 P(2m - 1,3)在第二象限,则( )
A.
(-1,-3),(2,-1),(-3,4)这些点所在的象限,说说你是怎么判断的.
① D(- 3,5),E(- 7,3),
③(1,0),(1,-6),
《平面直角坐标系》PPT精品课件

第三种类型
y
4
A3
2
1
A(0,2 2 ), B(2 2,0), C(0, 2 2 ), D( 2 2,0)
-4 B-3 -2 -1 0 1 2 3D 4 5 x
-1
-2 -3 C
以正方形的中心为原点, 两条对角线分别为x轴和y 轴建系
建立坐标系常用的方法有哪些? (1)以图形上的某已知点或线段的中点为原点; (2)以图形上某线段所在直线为x轴(或y 轴); (3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
y
5
4
A
3
2C
横坐标
1
x0
-4 -3 -2 -1O 1 2 3 4 5 x
-1
-2
-3 D
B y-04
P(x0,y0)
纵坐标
分别写出右图中各点的坐标. A(3,4) B(-3,-4) C(0,2) D(0,-3) E(-4,0) F(5,0)
y
5
4
A(3,4)
3
E(-4,0)
2 C(0,2) 1
F(5,0)
-2
-3 D(0,-3) B(-3,-4-)4
点的位置
横坐标的符号(或值) 纵坐标的符号(或值)
在x轴的正半轴上
+
0
在x轴的负半轴上
-
0
在y轴的正半轴上
0
+
在y轴的负半轴上
0
-
y
5
B4 3
2
C
1
A
-4
-3
-2
-1
O -1
1
2 3 4x
-2
-3 -4 E
在平面直角坐标系中,两条坐标轴(即横轴和纵 轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区 域,我们把这四个区域分别称为第一,二,三,四 象限,坐标轴上的点不属于任何一个象限.
《平面直角坐标系》PPT优质课件

3Y 2 1
-3 -2 -1-1O1 2 3 X
-2 -3
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
概念2
平面直角坐标系的象限
y 4
第二象限
3
2
1
第一象限
–4 –3 –2 –1 O 1 2 3 4 x –1
–2
第三象限
–3
第四象限
–4
坐标平面被两条坐标轴分成四个部分,每个部分称为 象限 ,
(2)能在给定的平面直角坐标系中根据点的坐标描出点的位 置,由点的位置写出点的坐标。
(3)运用平面内的点的坐标特征解决问题时要注意数形结合, 不宜死记硬背.
知识回顾 问题探究 课堂小结 随堂检测 作业布置
课本第68页练习题1、2题。
向右为正方向;竖直的数轴称为纵轴或
1
y轴,一般取向上为正方向;两坐标轴 –4 –3 –2 –1 O 1 2 3 4 x
–1
的交点为平面直角坐标系的原点。
–2
–3
–4
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
如何正确画出平面直角坐标系?
y
1.选原点
4
2.作两轴
思考:已知点的坐标确定点的位置
y
5
A(3,4)
4
已知平面直角坐标系内一点的坐标,分别 3 以点的横坐标、纵坐标在数轴上表示点的垂足 2
,作x轴、y轴的垂线,两垂线的交点即为要找
1
的点。
-2 -1 0 -1
-2
· A(3,4)
1 2 3 4x
知识回顾 问题探究 课堂小结 随堂检测
-3 -2 -1-1O1 2 3 X
-2 -3
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
概念2
平面直角坐标系的象限
y 4
第二象限
3
2
1
第一象限
–4 –3 –2 –1 O 1 2 3 4 x –1
–2
第三象限
–3
第四象限
–4
坐标平面被两条坐标轴分成四个部分,每个部分称为 象限 ,
(2)能在给定的平面直角坐标系中根据点的坐标描出点的位 置,由点的位置写出点的坐标。
(3)运用平面内的点的坐标特征解决问题时要注意数形结合, 不宜死记硬背.
知识回顾 问题探究 课堂小结 随堂检测 作业布置
课本第68页练习题1、2题。
向右为正方向;竖直的数轴称为纵轴或
1
y轴,一般取向上为正方向;两坐标轴 –4 –3 –2 –1 O 1 2 3 4 x
–1
的交点为平面直角坐标系的原点。
–2
–3
–4
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
如何正确画出平面直角坐标系?
y
1.选原点
4
2.作两轴
思考:已知点的坐标确定点的位置
y
5
A(3,4)
4
已知平面直角坐标系内一点的坐标,分别 3 以点的横坐标、纵坐标在数轴上表示点的垂足 2
,作x轴、y轴的垂线,两垂线的交点即为要找
1
的点。
-2 -1 0 -1
-2
· A(3,4)
1 2 3 4x
知识回顾 问题探究 课堂小结 随堂检测
《平面直角坐标系》PPT课件

由CD长为6; CB长为4; 可得D ; B ; A的坐标分 别为D 6 ; 0 ; B 0 ; 4 ; A6;4
B 0;4
C 0;0
0
A 6;4
D 6;0
x
做一做
例2 如图;正三角形ABC的边长为 6 ; 建立适当的直角坐 标系 ;并写出各个顶点的坐标
y
解: 如图;以边AB所在 的直线为x 轴;以边AB 的中垂线y 轴建立直角 坐标系
布置作业
作业:
A类:课本习题5 5
B类:完成A类同时;补充:
1已知点A到x轴 y轴的距离均为4;求A点坐标;
2已知x轴上一点A3;0;B 3;b ;且AB=5;
求b的值
C类:建立坐标系表示右面图形各顶点的坐标
直角梯形上底3;下底5;底角60˚
y
o
x
练习提高
随堂练习:
课本 随堂练习
练习
1如图;某地为了发展城市群;在现有的四个中小城市A;B;C;D附近 新建机场E;试建立适当的直角坐标系;并写出各点的坐标
2点A1a;5;B3 ;b关于y轴对称;则 a + b =______
3在平面直角坐标系内;已知点P a ; b ; 且a b < 0 ; 则点P的位置 在________
在一次寻宝游戏中;寻宝人已
11 2
2
3
经找到了2和3;2的两个标志点;并
3
且知道藏宝地点的坐标为4;4;除4ຫໍສະໝຸດ 此外不知道其他信息 如何确定直
角坐标系找到宝藏 与同伴进行交
流
做一做
例1 如图; 矩形ABCD的长宽分别是6 ; 4 ; 建立适当的 坐标系;并写出各个顶点的坐标
y
解: 如图;以点C为坐标 原点; 分别以CD ; CB所 在的直线轴建 立直角坐标系 此时C点 坐标为 0 ; 0
B 0;4
C 0;0
0
A 6;4
D 6;0
x
做一做
例2 如图;正三角形ABC的边长为 6 ; 建立适当的直角坐 标系 ;并写出各个顶点的坐标
y
解: 如图;以边AB所在 的直线为x 轴;以边AB 的中垂线y 轴建立直角 坐标系
布置作业
作业:
A类:课本习题5 5
B类:完成A类同时;补充:
1已知点A到x轴 y轴的距离均为4;求A点坐标;
2已知x轴上一点A3;0;B 3;b ;且AB=5;
求b的值
C类:建立坐标系表示右面图形各顶点的坐标
直角梯形上底3;下底5;底角60˚
y
o
x
练习提高
随堂练习:
课本 随堂练习
练习
1如图;某地为了发展城市群;在现有的四个中小城市A;B;C;D附近 新建机场E;试建立适当的直角坐标系;并写出各点的坐标
2点A1a;5;B3 ;b关于y轴对称;则 a + b =______
3在平面直角坐标系内;已知点P a ; b ; 且a b < 0 ; 则点P的位置 在________
在一次寻宝游戏中;寻宝人已
11 2
2
3
经找到了2和3;2的两个标志点;并
3
且知道藏宝地点的坐标为4;4;除4ຫໍສະໝຸດ 此外不知道其他信息 如何确定直
角坐标系找到宝藏 与同伴进行交
流
做一做
例1 如图; 矩形ABCD的长宽分别是6 ; 4 ; 建立适当的 坐标系;并写出各个顶点的坐标
y
解: 如图;以点C为坐标 原点; 分别以CD ; CB所 在的直线轴建 立直角坐标系 此时C点 坐标为 0 ; 0
《平面直角坐标系》ppt课件

坐标系的建立
确定原点
选择平面内的任意一点作为原点,作为两条数轴 的公共起点。
确定正方向
在水平数轴上选取正方向,通常以向右为正;在 垂直数轴上选取正方向,通常以向上为正。
单位长度
根据实际需要确定数轴上的单位长度,通常以厘 米或毫米为单位。
坐标系的分类
绝对坐标标 系。
平面直角坐标系
目录
• 平面直角坐标系的基本概念 • 平面直角坐标系中的点 • 平面直角坐标系中的直线 • 平面直角坐标系中的距离公式 • 平面直角坐标系的应用
01
平面直角坐标系的基本 概念
定义与性质
定义
平面直角坐标系是由两条互相垂直、 原点重合的数轴构成的平面几何图形。
性质
具有方向性、单位性、正交性等性质, 是描述平面内点位置的重要工具。
05
平面直角坐标系的应用
在几何中的应用
确定点位置
01
通过平面直角坐标系,可以确定平面内任意点的位置,并描述
其坐标。
计算距离和角度
02
利用坐标系,可以方便地计算两点之间的距离和两点之间的夹
角。
绘制图形
03
通过坐标系,可以绘制各种几何图形,如直线、圆、椭圆等。
在代数中的应用
代数方程表示
平面直角坐标系可以将代数方程表示为图形,便于理解和解决代 数问题。
点到直线的距离公式
总结词
点到直线最短距离的平方
详细描述
给定点$P(x_0, y_0)$和直线$Ax + By + C = 0$,则点到直线的距离公式为:$d^2 = frac{|Ax_0 + By_0 + C|^2}{A^2 + B^2}$。
高中数学2.1.2平面直角坐标系中的基本公式课件一 新人教B必修2

平面直角坐标系中的基本公式
学习目标
1. 理解两点间的距离的概念,掌握两点间的距 离公式,并会求两点间的距离. 2.理解坐标法的意义,并会用坐标法研究问 题.
课前自主学案 课堂互动讲练 知能优化训练
课前自主学案
温故夯基
平面直角坐标系中点的坐标(初中所学):在平面直 角坐标系中,有序实数对构成的集合与坐标平面 内点的集合具有一一对应关系.有序实数对(x,y) 与点P对应时,(x,y)叫做点P的坐标.其中x叫做 点P的横坐标.y叫做点P的纵坐标.
7.使用“坐标法”来处理几何问题,体会“数形结 合”的数学思想方法. 8.列方程或方程组求解问题的方法,也是解析 几何中常用的基本方法.
9.两点间距离公式与中点公式是两个重要的基 本公式.公式的推导过程中所使用的“分解”、“ 综合”方法,充分体现了转化思想. 这里所说的“分解”与“综合”方法,是指把坐标平 面上的问题投影到两个坐标轴上,从而分解为两
【点评】 涉及到无理式,其中含二次三项 式的,我们联想到两点间的距离公式,即构 造两点间的距离公式,再结合平面几何知识 求解.
跟踪训练 3 函数 y= x2+1+ x2-4x+8的 最小值.
解:∵函数的解析式可化为
y= x2+1+ x2-4x+8 = x-02+0-12+ x-22+0-22. 令 A(0,1),B(2,2),P(x,0),则问题转化为在 x 轴上 求一点 P(x,0),使得|PA|+|PB|取最小值. ∵A 关于 x 轴的对称点为 A′(0,-1), ∴(|PA|+|PB|)min=|A′B| = 2-02+2+12= 4+9= 13. 即函数 y= x2+1+ x2-4x+8的最小值为 13.
知新益能
1.两点间的距离公式 (1)两点 P1(x1,y1),P2(x2,y2)的距离表示为 d(P1, P2)=___x_2-__x_1__2+___y_2_-__y_1_2 . ①当 P1P2 平行于 x 轴时,d(P1,P2)=_|_x_2-__x_1_|_; ②当 P1P2 平行于 y 轴时,d(P1,P2)=_|_y_2-__y_1_|_; ③当 P2 点是原点时,d(P1,P2)=__x_21_+__y_21__. (2)算术平方根 x-a2+y-b2的几何意义是 表示两点 P1(x,y),P2(a,b)的距离.
学习目标
1. 理解两点间的距离的概念,掌握两点间的距 离公式,并会求两点间的距离. 2.理解坐标法的意义,并会用坐标法研究问 题.
课前自主学案 课堂互动讲练 知能优化训练
课前自主学案
温故夯基
平面直角坐标系中点的坐标(初中所学):在平面直 角坐标系中,有序实数对构成的集合与坐标平面 内点的集合具有一一对应关系.有序实数对(x,y) 与点P对应时,(x,y)叫做点P的坐标.其中x叫做 点P的横坐标.y叫做点P的纵坐标.
7.使用“坐标法”来处理几何问题,体会“数形结 合”的数学思想方法. 8.列方程或方程组求解问题的方法,也是解析 几何中常用的基本方法.
9.两点间距离公式与中点公式是两个重要的基 本公式.公式的推导过程中所使用的“分解”、“ 综合”方法,充分体现了转化思想. 这里所说的“分解”与“综合”方法,是指把坐标平 面上的问题投影到两个坐标轴上,从而分解为两
【点评】 涉及到无理式,其中含二次三项 式的,我们联想到两点间的距离公式,即构 造两点间的距离公式,再结合平面几何知识 求解.
跟踪训练 3 函数 y= x2+1+ x2-4x+8的 最小值.
解:∵函数的解析式可化为
y= x2+1+ x2-4x+8 = x-02+0-12+ x-22+0-22. 令 A(0,1),B(2,2),P(x,0),则问题转化为在 x 轴上 求一点 P(x,0),使得|PA|+|PB|取最小值. ∵A 关于 x 轴的对称点为 A′(0,-1), ∴(|PA|+|PB|)min=|A′B| = 2-02+2+12= 4+9= 13. 即函数 y= x2+1+ x2-4x+8的最小值为 13.
知新益能
1.两点间的距离公式 (1)两点 P1(x1,y1),P2(x2,y2)的距离表示为 d(P1, P2)=___x_2-__x_1__2+___y_2_-__y_1_2 . ①当 P1P2 平行于 x 轴时,d(P1,P2)=_|_x_2-__x_1_|_; ②当 P1P2 平行于 y 轴时,d(P1,P2)=_|_y_2-__y_1_|_; ③当 P2 点是原点时,d(P1,P2)=__x_21_+__y_21__. (2)算术平方根 x-a2+y-b2的几何意义是 表示两点 P1(x,y),P2(a,b)的距离.
人教版平面直角坐标系ppt课件内容完整

与坐标有关的新定义问题若定义:f=(a,b)=(-a,b),g=(m,n)=(m,-n),例如f(1,2)=(-1,2),g=(-4,-5)=(-4,5),则g(f(2,-3))=(B)A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
总结这节课我们学会了什么?1. 平面直角坐标系的相关概念:平面内两条互相垂直、原点重合和数轴,组成平面直角坐标系水平的数轴叫做 x 轴 或 横 轴竖直的数轴叫做 y 轴 或 纵 轴 .由点A 分别向x轴和y轴作垂线,垂足M 在x轴上的坐标就是点A 的 横坐标垂足N 在y轴上的坐标就是点A 的 纵坐标
由A 点分别作x轴
有序数对(3,4),
和y轴的垂线。
就叫做点A 的坐标.
垂足M 在x轴上
记作A(3,4)
的坐标是3
类似地,
垂足N 在y轴上的
B(-3 ,-4)C(0,2
坐标是4
D(0,-3)
点坐标有了平面直角坐标系,平面内的点就可用一个有序数对来表示了
笛卡尔(1596~1650):法国伟大的数学家,最早引入坐标系,用代数方法研究 几何图形,是解析几何的创始人.同时他 还是伟大的哲学家、物理学家.
点到y轴的距离
归纳总结点到x轴的距离等于点的点到y轴的距离等于点的
纵坐标横坐标
练习点 M(-5,3 ) 到 x 轴的距离是 3,到y轴的距离是 5 .
练习已知点P(3,a), 并且P点到x轴的距离是2个单位长度,求P点的坐标.解:因为P 到x 轴的距离是2,所以a 的值可以等于±2,因此P(3,2) 或P(3,-2).
个单位长度,则第
与坐标系有关的规律探究问题在平面直角坐标系中,孔明做走棋的游戏其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第三步向上走 1个单位,第四步向右走1个单位……依此类推,第n步的走法是:当 n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除余数为2时,则向右走2个单位当走完第100步时,棋子所处位置的坐标是( )A.(66,34) B.(67,33) C.(100,33) D.(99,34)
总结这节课我们学会了什么?1. 平面直角坐标系的相关概念:平面内两条互相垂直、原点重合和数轴,组成平面直角坐标系水平的数轴叫做 x 轴 或 横 轴竖直的数轴叫做 y 轴 或 纵 轴 .由点A 分别向x轴和y轴作垂线,垂足M 在x轴上的坐标就是点A 的 横坐标垂足N 在y轴上的坐标就是点A 的 纵坐标
由A 点分别作x轴
有序数对(3,4),
和y轴的垂线。
就叫做点A 的坐标.
垂足M 在x轴上
记作A(3,4)
的坐标是3
类似地,
垂足N 在y轴上的
B(-3 ,-4)C(0,2
坐标是4
D(0,-3)
点坐标有了平面直角坐标系,平面内的点就可用一个有序数对来表示了
笛卡尔(1596~1650):法国伟大的数学家,最早引入坐标系,用代数方法研究 几何图形,是解析几何的创始人.同时他 还是伟大的哲学家、物理学家.
点到y轴的距离
归纳总结点到x轴的距离等于点的点到y轴的距离等于点的
纵坐标横坐标
练习点 M(-5,3 ) 到 x 轴的距离是 3,到y轴的距离是 5 .
练习已知点P(3,a), 并且P点到x轴的距离是2个单位长度,求P点的坐标.解:因为P 到x 轴的距离是2,所以a 的值可以等于±2,因此P(3,2) 或P(3,-2).
个单位长度,则第
与坐标系有关的规律探究问题在平面直角坐标系中,孔明做走棋的游戏其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第三步向上走 1个单位,第四步向右走1个单位……依此类推,第n步的走法是:当 n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除余数为2时,则向右走2个单位当走完第100步时,棋子所处位置的坐标是( )A.(66,34) B.(67,33) C.(100,33) D.(99,34)
平面直角坐标系PPT优秀课件1

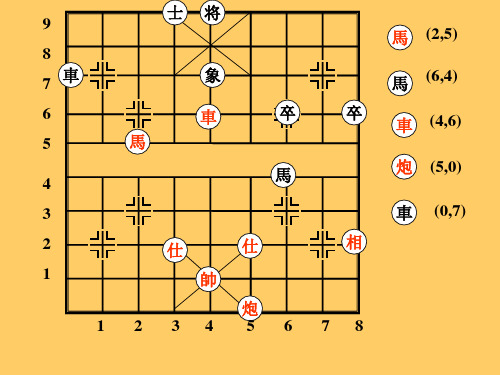
如: (2,5)→(3,5)→(3,4) →(4,4)→(5,4)→(5,3) →(5,2)
四、练习与小结
如图,写出表示下列各点的有序数对:
A ( 3 , 3 );B(5,2);C( 7 , 3 );D (10 , 3 ); I ( 4 , 8 ).
E (10 , 5 ); F ( 7 , 7 ); G ( 5 , 7 ); H ( 3 , 6 );
讨论:①图表 表示什么意思? ②路径中每一 对有序数对表达的 含义是什么?
6大道 5大道 4大道 3大道 2大道 1大道 A
B
6街
Байду номын сангаас
1街
2街
3街
4街
5街
三、例题应用
例 如图,点A表示3街与5大道的十字路口,点B表 示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么 你能用同样的方法写出由A到B的其他几条路径吗?
6大道 5大道 4大道 3大道 2大道 1大道 A
B
6街
1街
2街
3街
4街
5街
三、例题应用
例 如图,点A表示3街与5大道的十字路口,点B表 示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么 你能用同样的方法写出由A到B的其他几条路径吗?
四、练习与小结
小结:谈谈你本节课的收获.
五、布置作业
预习下一节内容.
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
四、练习与小结
如图,写出表示下列各点的有序数对:
A ( 3 , 3 );B(5,2);C( 7 , 3 );D (10 , 3 ); I ( 4 , 8 ).
E (10 , 5 ); F ( 7 , 7 ); G ( 5 , 7 ); H ( 3 , 6 );
讨论:①图表 表示什么意思? ②路径中每一 对有序数对表达的 含义是什么?
6大道 5大道 4大道 3大道 2大道 1大道 A
B
6街
Байду номын сангаас
1街
2街
3街
4街
5街
三、例题应用
例 如图,点A表示3街与5大道的十字路口,点B表 示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么 你能用同样的方法写出由A到B的其他几条路径吗?
6大道 5大道 4大道 3大道 2大道 1大道 A
B
6街
1街
2街
3街
4街
5街
三、例题应用
例 如图,点A表示3街与5大道的十字路口,点B表 示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么 你能用同样的方法写出由A到B的其他几条路径吗?
四、练习与小结
小结:谈谈你本节课的收获.
五、布置作业
预习下一节内容.
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
课件平面直角坐标系.ppt
例题:已知平面直角坐标系
如图所示,某船从O港航行,
北
先在A(-10,10)处停泊,再沿直 60
线航行到达B(30,60)港,试画 50
出该船的航线.
40
画法:
1.如图,画点A(-10,10), 30
点B(30,60)。
2、连结OA,AB。 折线OAB就是该船 的航线
20
A
10
-10 O 10
-10
横坐标是正数,纵坐标是负数的点在第_四___ 象限,横坐标是负数,纵坐标是正数的点在 第_二___象限
若xy>0,则点M(x,y)在第__一__,三__象限;若xy <0,则点M (x,y)在第__二__,四___象限.
若a/b>0,则点A(-2a,3b)在第_二__,四___象限; 若a/b<0,则点B (a/2,b)在第__二__,四___象限, 点C (b/3,-a)在第__一__,三___象限.
· y
①(0 , 6), (-4, 3), (4 , 3) (0 , 6)
6
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
5
A(-4,3)
4
· · C(-2,3)
3
2
· ·B(4,3) D(2,3)
观察所得的 图形,你觉 得它象什么?
1
-4 -3 -2 -1 o
1234
6
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
5
A(-4,3)
4
· · C(-2,3)
3
2
· ·B(4,3) D(2,3)
1
-4 -3 -2 -1 o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P8第2题
y
A
B (x-2,0)
P (x,y)
Cx (x+2,0)
2.已知点 A为定点,线段BC在定直线l上滑动,已知|BC|=4, 点A到直线l的距离为3,求△ABC的外心的轨迹方程
1.解:以直线 l为 x轴,过点 A 与 l垂直的直线为 y轴建立直角坐标系,则 点 A(0,3)。 设 ABC 的外心为 P ( x, y ), 因为 P 是线段 BC 的垂直 平分线上的点,所以 B 、 C 的坐标分别为 ( x 2,0) ( x 2,0) 因为 P 也在线段 AB 的垂直平分线上,所以 PA PB
1.在同一直角坐标系下,求满足下列图形的伸缩变换:
曲线4x2+9y2=36变为曲线 x2 y2 1
1解 : 设 伸 缩 变 换 x y xy, 0
代入x2+y2=1得2x22y2 1
又4x29y236 则
1 3 1
2
得
x
1 3
x
y
1 2
y
2.求双曲线 C:x2-6y42 =1 经过 φ:x2′y′==3yx,变换后所得曲
•
5.一切表现形式都应该是创造的成果 。今天 的浪漫 或许是 明天的 现实, 当下的 现实也 可能是 昨天的 浪漫。 重要的 是我们 的作品 是否揭 示生命 本质, 精神是 否向真 向善向 上,以 及手上 的“主 义”是 否与我 们的诉 求达成 一致。
•
6.而批评要做的,就是把真正的创造 性成果 点亮, 让不同 形式、 不同风 格、不 同创造 性诉求 的佳作 ,在反 复的研 读与辨 析中沉 淀价值 。
C
边AB所在的直线x轴,建立直角
坐标系,由已知,点A、B、F的
E
坐标分别为
c
设 由 A点 b (2 0C ,的 c 02 坐 ) ,5 标 Ba 2 为 , ( c( 可 x ,0, 得 y )) 到 ,, F则 |A (点 C 2 E |2 ,的 0 坐 | ).A 标 B O |为 2 (A ) ( 5 |x 2 B , FC y 2 |) 2 , .B x
y
Y=f(x)
O
曲线的方程 方程的曲线
1.平面直角坐标系 (1)平面直角坐标系的作用:使平面 上的点与 坐标 、曲线与 建立联系, 从而实现 数与形 的结合. (2)坐标法解决几何问题的“三部曲”: x 第一步:建立适当坐标系,用坐标和方 程表示问题中涉及的 几何元素,将几何 问题转化为 代数 问题;第二步:通过 代数运算解决代数问题;第三步:把代 数运算结果翻译成 几何 结论.
(3)建立平面直角坐标系的原则:
(4)建立平面直角坐标系步骤:
根据图形的几何特点选择适当
①设点(点与坐标的对应)
的直角坐标系的一些规则:
②列式(方程与坐标的对应)
①如果图形有对称中心,选对称中心为原点.
③化简
②如果图形有对称轴,可以选对称轴为坐标轴,
③使图形上的特殊点尽可能多地在坐标轴上.④说明(即得所要求的方程)
线 C′的焦点坐标.
[解] 设曲线 C′上任意一点 P′(x′,y′),由上述可知,将
x=13x′,代入 y=2y′,
x2-6y42 =1,得x′9 2-4y6′4 2=1,化简得x′9 2-
y1′62=1,即x92-1y62 =1 为曲线 C′的方程,可见仍是双曲线,
则焦点 F1(-5,0),F2(5,0)为所求.
•
3.批评文章却写得天花乱坠,一再上 演“皇 帝的新 衣”闹 剧。这 些批评 牵强附 会、肆 意升华 ,外延 无限扩 张,乃 至另起 炉灶, 使批评 成为原 创式的 畅想, 早已失 去了与 原作品 的联系 。
•
4.评庸俗化表现为概念代替文本,行 为代替 写作。 较之个 体性的 埋头创 作,不 少诗人 似乎更 喜欢混 个脸熟 ,在这 样的背 景和语 境下, 诗歌批 评基本 沦为诗 人间的 交际和 应酬。 哪怕是 纷纷攘 攘的流 派或主 义之争 ,也往 往是你 方唱罢 我登场 ,名目 噱头不 少,却 未见得 与文学 和读者 有何关 系。
即 x 2 ( y 3)2 22 y 2 整理得 x 2 6 y 5 0 这就是所求的轨迹方程 。
问题2: 2(1).怎样由正弦曲线y=sinx得到曲线y=sin2x?
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx? 写出其坐标变换。
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写出其坐标变换。
(2)曲线 x2y22x0变成曲线 x21y624x0
3(1).在同一平面直角坐标系中,将直线 x-2y=2 变成直线
2x′-y′=4,求满足图象变换的伸缩变换.
解:设变换为x′=λx(λ>0), 代入第二个方程,得 y′=μy(μ>0),
2λx-μy
=4,与 x-2y=2 比较系数得 λ=1,μ=4,即xy′′==4xy,. 因此,
•
7.诗歌批评庸俗化趋势亟须扭转。文 学批评 的职业 公信力 需要树 立,批 评家需 要贡献 学术良 知。果 真如此 ,对诗 歌和读 者,都 将是福 音。
•
8.中国音乐在发展过程中,不断承传 自我, 吸收各 地音乐 ,器乐 发达, 演奏形 式丰富 。金、 石、土 、革、 丝、木 、匏、 竹,皆 可作乐 器。乐 曲类型 已有祭 神乐、 宴乐、 军乐、 节庆乐 等区别 。玄宗 时已有 超百人 的大型 交响乐 团,其 演员按 艺术水 平分为 “坐部 伎”与 “立部 伎”。
2.已知点 A为定点,线段BC在定直线l上滑动,已 知|BC|=4,点A到直线l的距离为3,求△ABC的外 心的轨迹方程.
1(例1).已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF
分别为边AC,AB上的中线,建立适当的平面直角坐标
系探究BE与CF的位置关系。 y
解:以△ABC的顶点A为原点O,
问题: 1.两个定点的距离为6,点M 到这两个定点 的距离的平方和为26,求点M的轨迹方程。
求轨迹的常用方法:如果题目中的条件有明显的等量关系或者可 以推出某个等量关系,即可用求曲线方程的五个步骤直接求解.
问题: 1.两个定点的距离为6,点M 到这两个定点的距离的平 方和为26,求点M的轨迹方程。
注 (1) 0,0
(2)把图形看成点的运动轨迹,平面图 形的伸缩变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不 变,在同一直角坐标系下进行伸缩变换。
例2:在直角坐标系中,求下列方程所对应的图形经过
伸缩变换 x 2 x
y
3y
后的图形。(1)2x+3y=0; (2)x2+y2=1
O
2 x
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?写出 其坐标变换。
在正弦曲线上任取一点P(x,y),保持横坐标x不变, 将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。
设点P(x,y)经变换得到点为 p x, y
x x
y
3
y
2
通常把 2 叫做平面直角坐标系中的一个坐标伸 长变换。
解: 1由伸缩变换xy23xy 得
代入2x+3y=0 得x+y=0
x
y
1 2 1 3
x y
2由伸缩变换xy 23xy得xy
1 2 1 3
x y
x2
代入x2+y2=1得4
+
y 2 9
=1
练习:
1. (P8 4. )在同一直角坐标系中,求下列方程所对应的图形
经过伸缩变换
x
y
1x 3 1y 2
即 x 2 y 2 c 2 5 [(x c )2 y 2 ].
整 理 得 2 x 2 2 y 2 2 c 2 5 c x 0 .
因 为 B E (x c ,y ),C F (c x , y ), 所 以 B EC F(x2 c)(c2 x)y22 0.因此,BE与CF互相垂直.
22 2
根据几何特点选择适当的直角坐标系的一些规则: (1)如果图形有对称中心,可以选择对称中心为坐标原点; (2)如果图形有对称轴,可以选择对称轴为坐标轴; (3)使图形上的特殊点尽可能地在坐标轴上。
后的图形。
(1)
x2 y2 1 94
(2)
x2 18
y2 12
1
(3) y2 2x
x 3x
2. (P8
5).在同一直角坐标系中经过伸缩变换
y
y 后,
曲线C变为 x29y2 9 ,求曲线C的方程并画出图形。
3. (P8 6).在同一直角坐标系中,求满足下列图形的伸缩变换:
(1)直线 x-2y=2变成直线 2xy4
(3)怎样由正弦曲线y=sinx得到曲 线y=3sin2x? 写出其坐标变换。
y
y=3sin2x
y=sinx
2
O
x
(3)怎样由正弦曲线y=sinx得到曲线 y=3sin2x? 写出其坐标变换。 在正弦曲线y=sinx上任取一点P(x,y),保持纵坐 标将不纵变坐,标将变横为坐原标来x的缩3为倍原,来就的得到12 正,弦在曲此线基础上,
经过变换x′=x,后,直线 y′=4y
x-2y=2
变成直线
2x′-y′=4.
课堂小结:
(1)体会坐标法的思想,应用坐标 法解决几何问题;
(2)掌握平面直角坐标系中的伸缩 变换。
作业:
1.在同一直角坐标系下,求满足下列图形的伸缩变换:
曲线4x2+9y2=36变为曲线 x2 y2 1
2.求双曲线 C:变换后所得曲 线 C′的焦点坐标.
设P(x,y)是平面直角坐标系中任意一点,保持纵坐标
不变,将横坐标x缩为原来 1 ,得到点 px, y 2 坐标对应关系为:
