地震作用下桥梁结构横向碰撞模型及参数分析
第三节 水平地震作用下横向框架内力分析、竖向荷载作用下横向框架内力分析
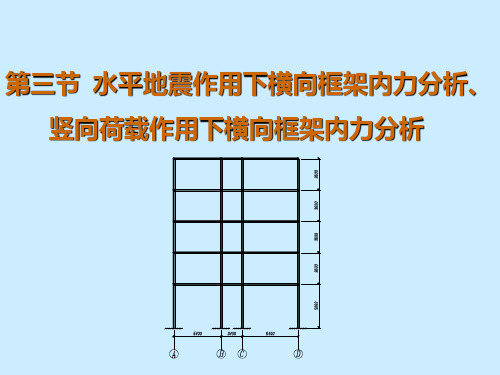
走道板传给横梁的自重
1、楼(屋)盖荷载传递形式
八、竖向荷载作用下横向框架内力分析
中纵梁自重
边纵梁自重
中纵梁上墙、门窗自重(顶层无)
P2
边纵梁上墙、窗自重(顶层无)
P1
板传给中纵梁自重
次梁自重
板传给边纵梁自重
次梁自重
次梁传来的荷载
次梁上墙重
(顶层无)
次梁传来的荷载
次梁上墙重
(顶层无)
板传给次梁自重
板传给次梁自重
边柱集中力矩
C
D
q
' 2
走道板传给横梁的活载
板传给中纵梁活载
P2 板传给次梁活载
M 2 P2e2
中柱集中力矩
1、楼(屋)盖荷载传递形式
八、竖向荷载作用下横向框架内力分析
竖向荷载计算
恒载
楼面活荷载 (屋面取活荷载)
楼面活荷载 (屋面取雪荷载)
2、竖向荷载计算
八、竖向荷载作用下横向框架内力分析 举例说明:
恒荷载作用下弯矩二次分配
3、竖向荷载作用下的内力计算
八、竖向荷载作用下横向框架内力分析
上柱
0.340
3.80 2.87 -1.27 5.41 0.340
3.80 1.90 -0.94 4.76 0.340
3.80 1.90 -0.79 4.91 0.299
2.94 1.90 -0.37 4.47
下柱 0.514 3.41 5.75 1.90 -0.24 7.41 0.340 3.41 3.80 1.90 -1.27 4.43 0.340 3.41 3.80 1.90 -0.94 4.76 0.340 3.41 3.80 1.47 -0.79 4.48 0.419 4.77 4.11 0.00 -0.51 3.60
非规则梁桥横桥向地震碰撞反应分析

梁 桥地 震反 应 的影 响具 有极 为 重 要 的现 实 意义 。本 文
结合 西 部 山 区某 一 实 际典 型 多 跨 连 续 梁 桥 , 析 了 梁 分
体 与抗 震 挡 块 间 的 碰 撞 对 结 构 横 桥 向地 震 反 应 的影
响, 探讨 了减 轻 碰撞 和限 制相对 位移 的措 施 和方法 。
下 横 向碰撞 对连 续梁 桥 地震 反 应 的影 响 。我 国的公 路 桥 梁抗震 设计 细则 (T T B 2— 1— 0 8 也 仅 把挡 块 JG 0 0 20 ) 作 为一种 构 造措施 。实 际上 , 有 些 结 构 中 , 在 挡块 的作
型 , 部 结 构 采 用 跨 度 为 3 预 应 力 T梁 , 宽 为 上 0m 桥
梁体 与抗震挡 之间的碰 撞力 , 同时减小矮墩 区桥墩的墩顶横 向位移和墩底 塑性转 角 , 不显 著增加 高墩 区桥墩 的墩顶位移
和墩 底 塑性 转 角 。 关 键 词 :地 震 ; 梁 ; 撞 ; 震 挡 ; 震 反 应 桥 碰 抗 地 中 图分 类 号 :U 4 . 42 5 文 献 标 识 码 :A
所示 。
应 用美 国 ̄ J 大 学 编制 的 D a .D l 程 序 进行 m, I 、 I ri 3 Xl] n o 结构 地震 反应 分 析 。在计 算模 型 [ 1 a ] , 体 与 图 () 中 梁 墩柱 分别 用 弹性梁 单元 、 弹塑 性 梁柱 单 元 模 拟 , 单元 的 质量 采用 堆 积 集 中质 量 代 表 , 胶 支 座 采 用 弹 簧 连 接 橡
单元 模 拟 ; 凝 土结 构 的阻 尼 比取 为 5 , 行 线性 和 混 % 进
用 对 主体结 构 的地震 反应 有 较 大 的影 响 。 目前 对非 规 则 梁桥横 桥 向地震 碰撞 效应 的研究 基本 上是 空 白 。 我 国西 部 由于 地 形 条 件 的 限 制 , 梁 结 构 一 般 由 桥
桥梁地震碰撞的三维撞击模型及非线性响应分析_禚一

Fy ( t) = - μf·Fx ( t) ,当 xi ( t) - xj( t) - gp > 0 且
·yi ( t) - ·yj( t) > 0
Fy ( t) = μf ·Fx ( t) ,当 xi ( t) - xj( t) - gp > 0 且
·yi ( t) - ·yj( t) < 0
Fy ( t) = 0,当 xi ( t) - xj( t) - gp > 0 且 ·yi ( t) -
3D impact model and non-linear response analysis for
seismic pounding of bridges
Zhuo Yi1,2 Li Zhongxian1 Wang Fei2
( 1. Key Laboratory of Coast Civil Structure Safety of the Ministry of Education,Tianjin University,Tianjin 300072,China; 2. The Third Railway Survey and Design Institute Group Corporation,Tianjin 300142,China)
向撞击力 Fy( t) 相同,这里不再赘述。
图 1 三维 Kelvin 碰撞单元力学模型 Fig. 1 Mechanical model of 3D Kelvin pounding element
2 基于 FENAP 平台的三维 Kelvin 碰撞单元 模块开发
FENAP 平台是课题组基于纤维梁柱单元模型的 基本原理开发的一套实用精细化模拟分析平台[18-19], 包含了多种混凝土和钢材的本构模型。可进行结构 或构件的复杂非线性静力及动力响应分析,能够有效 地考虑构件 的 刚 度 退 化、强 度 退 化 等 损 伤 效 应,模 拟 轴力和双向弯矩的多维耦合效应等复杂非线性行为。 在桥梁构件的非线性静、动力模拟方面已取得了较好 的模拟效果。本文在 FENAP 平台基础上,基于三维撞 击模型的力学原理,利用 ABAQUS 所提供的 UEL 用户 单元子程序接口[20],开发了三维 Kelvin 碰撞单元模块 FENAP /3D-Kelvin-Pounding,并 采 用 ABAQUS / Standard 隐式非 线 性 求 解 器 进 行 动 力 求 解。图 2 给 出 了 FENAP 平台引入三维 Kelvin 碰撞单元模块结构框图。
地震下城市高架桥横向偏心碰撞响应与防撞效果分析

橡胶 支座 , 寸为 35mm× 8mm, 尺 2 8 单个 支座 的水 平 刚度为 13×1 k / . 0 N m。盖梁两 端均 设置 了钢 筋混 凝
收稿 日期 :0 1 0 1 2 1 —6— 4 作者简介 : 岩 石 男 18 95年 出 生 助 教
石 家庄 铁道 大 学学报 (自然科 学版 )
第2 4卷
土 抗震 挡块 , 块长 ×宽 ×高为 2 0e 3 m × 0e 挡 0 m× 0 e 5 m。地震 响 应分 析时 将结 构 体 系简 化 为 图 1 示 的 所
单 墩横 向偏 心 碰撞模 型 , 中 , 其 m为 上部 结构 质量 , e=12m 为梁体 与抗 震挡 块 间偏心 距 , 为 结 构碰 撞 . C 阻 尼 , 为碰撞 刚度 ( 5X1。 N m) A 为初始 间隙 , 身高 度 为 5m; 了考 虑板 式橡 胶支 座 与墩顶 和 k 取 0 k / , 。 墩 为 梁 底接 触 面之 间产 生 的滑动 , 采用 双线 性模 式来 模 拟支 座 的力学 特性 ]其水 平 方 向的恢 复力 模 型如 图 2 , 所 示 。假设 桥梁 位 于地震 烈度 9度 区 , 取 表 1中 的 1 地震 波 , 用 结构 分 析 软件 S P 00将 每条 地 选 0条 应 A 20 震 波 的加速 度 峰值调 整 为 04g, 结构 横 向输入 ; 墩 采 用 弹 塑性 梁 柱 单元 模 拟 , 座 采用 非 线 性 We . 沿 桥 支 n
表 现 为非线 性 , 略该 间 隙可能会 导 致 非 常不 保 守 甚 至错 误 的结 果 。汶川 大 地 震 中 , 梁 结 构 横 向抗 震 忽 桥
挡 块遭 到 严 重破 坏 引 , 中部分 是 由于梁 体与 其发 生 碰撞 而 引起 。 目前 , 国规 范 仅对 挡块 进行 构 造设 其 我 计 , 其强 度 、 对 刚度及 其 与梁 体 间距等 均未 得 到足够 的 重视 。 国 内外 学 者 引分 别 建立 考 虑初 始 间 隙 的 横 向碰 撞模 型进 行 了地 震 响应 研 究 , 结果 表 明横 向间 隙处 的碰撞 对 结 构 的抗 震 性 能 有 很 大影 响 , 以上 但 研 究 皆基 于对 心碰撞 , 有考 虑桥 梁 上部 结 构 的质心 与挡 块 质心 的竖 向间距 , 没 即横 向 间隙 处 的碰 撞 实 际
地震下城市高架桥横向偏心碰撞响应与防撞效果分析

地震下城市高架桥横向偏心碰撞响应与防撞效果分析石岩;秦洪果【期刊名称】《石家庄铁道大学学报(自然科学版)》【年(卷),期】2011(024)004【摘要】为适应材料因温度等因素的变化而产生的横向伸缩变形及其对结构的影响,通常梁体与挡块之间会留有一定间隙.针对城市高架桥中梁体与挡块在强震作用下的横向碰撞现象,建立了考虑上部结构与挡块间偏心距和支座非线性的横桥向单墩碰撞模型.采用非线性地震反应时程分析方法,研究了初始间隙及其大小对桥梁结构横向地震反应的影响,并评估了设置橡胶缓冲垫后的防撞效果.研究结果表明:城市高架简支梁桥横向间隙处的偏心碰撞放大了桥墩的地震需求,通过在挡块内侧安装橡胶缓冲垫,可以大幅减小间隙处的碰撞力,将有效改善桥梁结构的横向抗震性能.%To allow for transverse temperature movement, the shear keys are placed with a slight gap from the girders. In this paper, based on pounding phenomenon between girder and shear keys at transverse gaps, a pounding model of single column that considers the eccentric distance between shear keys and girders, and nonlinear behaviors of bearing has been developed. With the time history analysis method of the nonlinear seismic responses, the effects of transverse gap and its size on seismic response of simply-supported girder bridges are analyzed, and the effect of installation of the rubber shock absorbing devices inside shear keys is evaluated. The results indicate that the eccentric pounding at the transverse gaps amplifies the responses of piers, and installation of therubber shock absorbing devices inside shear keys can significantly reduce the impact force between the girder and shear keys and effectively improve the lateral seismic performance.【总页数】5页(P23-27)【作者】石岩;秦洪果【作者单位】石家庄铁道大学土木工程学院,河北石家庄050043;中交远洲交通科技集团有限公司,河北石家庄050051【正文语种】中文【中图分类】U442.5【相关文献】1.地震作用下横向碰撞对连续梁桥地震反应的影响 [J], 邓育林;彭凯;李建中2.地震作用下高速铁路简支箱梁桥横向偏心碰撞反应分析 [J], 石岩;王军文;王东升;李建中3.地震下城市高架桥横向偏心碰撞响应与防撞效果分析 [J], 石岩;秦洪果4.双柱式简支-桥面连续梁桥横向地震碰撞和防撞措施分析 [J], 龙佩恒;李雅婷;李士锣;焦驰宇5.考虑地震动空间效应的城市高架桥梁地震碰撞响应分析 [J], 李忠献;岳福青;周莉;刘旭锴因版权原因,仅展示原文概要,查看原文内容请购买。
地震作用下横向碰撞对连续梁桥地震反应的影响

p c fe t. a tefc s
Ke wor e rh u k fe t o ln a ,c n i u u ide rd e,p un i g ef c y ds a t q a e e c ,n n i e r o tn o sg r rb g i o d n fe t
Ab t a t T e p u d n ewe n c mp n n s o t cu e h s s n f a t n l e c s n t e t cu a s r c h o n i g b t e o o e t f a s t r a i i c n if n e o h s u r g i u u r tr l
维普资讯
第2 3卷第 2期 20 0 7年 4月
结
构
工
程
师
V0 . 3.N . 12 o2
Ap . 2 7ห้องสมุดไป่ตู้r 00
S r c u a En i e r tu t r l gn e s
地震时梁桥支座的横向受力分析研究

地震时梁桥支座的横向受力分析研究在公路和铁路工程抗震设计规范(试行)中,对支座部件及支座联接梁、墩台锚螺栓的横向抗震强度,是按水平地震荷载P=1.5KHW0计算,同时规定P由活动与固定支座共同承受,且不计摩擦力的减少作用。
根据这一规定,支座在横桥向只承受水平剪力,然而大量支座螺栓在地震中却表现出扭弯破坏,同时一些按这一方法计算很安全的支座在地震中破坏了,是不是我们对支座在地震中的受力情况和受力过程还远远的认识不够呢?是这样。
标签桥梁梁高受力横向结构一、支座只受纯剪力吗?国内外对支座的横向计算的基本假定:1.将沿梁高分布的质量全部集中到墩顶位置,即完全忽略梁高的影响。
2.将每墩两侧上部结构的质量的一半,集中到该墩墩顶作为集中质量。
3.活动支座与固定支座共同承受水平地震荷载P,即完全忽略了活动与固定支座在构造和受力上的显著差异。
根据这些基本假定,支座在横向的动力图式就被不真实的简化,得到W0,然后取C2rβ的上限值1.5。
人们的认识随着客观事物的发展在深化,我国辽南、唐山一丰南地震极大的丰富了支座横向的受力情况和受力过称,它不仅要受到剪切,同时还将受到横向弯矩和扭矩,现有支座的横向计算,既不能控制其强度,也没有真实的反映它的受力过程和受力情况。
现采用的支座横向计算图式,由这个图式,上部结构的全部质量M仅仅在支座水平面产生剪力P。
但是当考虑梁高的影响时,其实际的动力計算图,由这个图式,上部结构质量M不仅在支座水平面产生剪力,同时还将产生横向倾覆弯矩。
设自振频率为ω,墩顶水平振幅及角振幅为及,H1、为上部结构与支座高度,H0为墩高,为上部结构在处的质量,M为上部结构的总质量。
,由图1a)得:(1)由于梁的刚度较大,因此对沿梁高的振型可采用直线,则处的振幅为,由图1b)得上部结构质量在支座截面产生的剪力及弯矩为:(2)(3)令,并设:代入式(3)得:(4)下面我们来分析在横向只设置了两个支座的受力情况,当上部结构将剪力弯矩传到支座时,由图2得到每一支座受到的水平剪力及竖向拉压力N为:(5)式(5)中,为上部结构质量中心至支座底的高度,由于≥ 故:(6)式(6)中b为两支座间的横向水平距离,由于/b值在0.25~3之间,故值在0.5~6之间,这就是说支座在横向不仅仅只是受到纯剪切,而且受到弯矩的作用。
地震作用下桥梁梁体与横向挡块动态碰撞研究

地震作用下桥梁梁体与横向挡块动态碰撞研究地震作为破坏力巨大的一种自然灾害,多次给人民的生命财产安全造成了严重的危害。
桥梁作为灾后救援和重建的重要通道,其抗震性能对救灾人员和物资能否以最快的速度到达起到了决定性的作用。
简支梁(板)桥、连续梁(板)桥是修建最普遍的桥型,它们抗震性能应该给予重点关注。
在这种类型的桥梁中,上部结构的落梁是桥梁倒塌的首要原因,应当尽量避免。
因此,许多研究人员对此展开了大量的研究,但是大多数人关注的是占落梁事故大多数的纵向落梁,并提出了很多的防落梁措施和开发了多种多样的防落梁设备;与之相对,横向落梁研究就少了很多。
最常见横向落梁措施是设置横向抗震挡块,它肩负着避免落梁破坏发生的重任。
就是这样一个重要的构件,其设计却无章可循,基本靠设计人员的经验或者借鉴其他工程,这样一来在地震中它能发挥多大的作用就不得而知了;而且,梁体和挡块之间的碰撞会增加桥墩的受力,但具体增加程度也很难一概而论。
为了弄清楚该问题,本文开展了一些有益研究。
本文从解析的角度来研究梁体与横向挡块的碰撞。
从碰撞问题的模拟和求解入手,对常用接触单元法的几种具有代表性的模型进行讨论,提出了用弹簧-振子模型代表接触单元模型碰撞过程的基本思路,通过求解弹簧-振子运动方程,得到碰撞问题中碰撞力-相对压入量、碰撞力-碰撞持续时间、相对压入量-碰撞持续时间关系等所关心的物理量。
该改进求解方法对存在大量能量耗散的碰撞问题尤为有效,可以得到精确解或者无限接近精确解的近似解,适合将其用于考虑梁体与挡块碰撞效应的桥梁地震响应问题求解。
同时,得到的挡块受力可以为挡块的细节设计提供参考。
综合考虑了恢复系数(它的大小直接代表了碰撞中能量耗散的多少)和其他各种影响碰撞过程的因素,发现Hertz模型求解的最大碰撞力和最大相对压入量与Hertzdamp模型的精确解之间存在着一定的关系。
在其他参数相同的情况下,该关系只与恢复系数有关,利用一元四次多项式进行了拟合,效果非常好。
浅源强震下RC梁式桥横向碰撞参数研究

撞效应 的影 响。研究 表明抗震挡块对于 防止横 向落梁有显著的抑制作用 , 了铁路 R 建议 C梁式 桥抗震挡块 的合理刚度及
初始 问隙取 值 , 提炼 了墩 高及跨径 对各项响应指标 的影 响规律 。研究成果 可供梁式桥抗震设计及规范修编参考 。
关键词 :R C梁式桥 ; 抗震挡块 ; 横向碰撞模型 ; 源地 震 ; 浅 参数分析
10 4 2 长安大学 公 路学院 , 0 04;. 西安
摘 要 :针对地震作用下桥梁结构梁体与横向挡块间的碰撞现象, 采用非线性动力分析方法对影响碰撞效应的主
要 因素进行 了系统研究 。基于刚体碰撞理论 , 建立能考虑碰撞过 程 中能量 损失 的桥梁横 向碰撞 接触单元 分析模 型 , 研究 了典 型的浅 源强震作用下挡块碰撞 刚度 、 梁体与挡块 问初始 间隙 、 桥梁 墩高 以及 跨径 等 因素 对铁路 R C简支梁 桥地震碰
式 中 ,为 碰 撞过 程 的恢 复 系数 , 于完 全 弹性 碰 撞 , e 对 恢 复 系数 e ; 于完 全 塑性 碰 撞 , 复 系数 e= 对 于 =1对 恢 0; 混凝 土 材料 , 可取 为 0 6 ] 为工 程 常用 阻尼 系数 ; . 56。 E c 为考 虑 碰撞 过程 中 考 虑 能 量 耗 散 的 等 效 阻 尼 ; 挡 K为
振 第3 1卷第 4期
动
与
冲
击
J OURNAL OF VI BRAT ON I AND HOCK S
浅 源 强震 下 R C梁 式 桥 横 向碰 撞 参 数研 究
江 辉 ,李 宇 ,杨庆山 ,朱 唏
70 6 ) 104 ቤተ መጻሕፍቲ ባይዱ
(. 1 北京交通大学 土木建筑工程学 院 , 北京
地震作用下城市高架连续梁桥碰撞单元刚度参数分析

的取法也不尽相 同。为 了探讨 碰撞单 元刚 度对城 市高架连 续 梁桥地震碰撞反应 的影响 , 本文 建立 典型多跨 连续梁桥的分析
图 1 K li ev n模 型
模型 , 采用参数分 析方 法探讨城 市高架连续梁桥碰撞单元刚度
的合理取值
Ke i模 型_ ] ln v 4 的接触 单元 由一个 连接 弹 簧和 一个 阻 尼 器并联而成 , 如图 1 所示 。Ke i模 型用弹簧刚度模拟桥梁碰撞 ln v 时实际的法向接触刚度 , 通过阻尼器模拟碰撞过程 中能量的损失 ;
的长度 , 中上部箱梁与桥墩 的截面特性如表 1 其 所示 。 分 析时采用 表 2中的 8条地 震波 , 速度 峰值 均调 整 为 加
0 4 。分析 时考虑行 波效 应对碰 撞反应 的影 响 , B、 .g 对 C类场
地视波 速分别取 1 0 s 3 0 s并沿 纵桥 向输入 , 5 m/ 和 5m/ , 计算结
2 连 续梁 桥碰撞 分 析模型及 输入 地震 波
为 了探讨碰撞单元刚 度对多跨 连续梁桥 地震碰撞 反应 的 影 响, 采用如图 3 示的三联 连续梁桥地 震碰撞 分析模 型 , 所 选 用 的跨径组合 为 4 0 ×4 m+4 0 ×4 m+4 0 墩高为 1 . 5 ×4 m, 57 m,
图 4 碰撞 力随弹簧刚度的变化
变化 不超 过 2 1 。 .
! Q
左联
.
中联
一 .
±
右联
32 碰撞单元弹簧刚度对桥 梁结构位移 的影 响 .
图 5 图 6的计算结果 表 明: 、 相邻 联梁 体最大 相对 位移 的
计算结果受碰撞弹簧刚度的影 响不如碰撞力 明显 , 最大相对 位
桥梁结构的地震响应分析与减振控制

桥梁结构的地震响应分析与减振控制地震是一种破坏性极大的自然灾害,对于桥梁结构来说,地震会造成巨大的冲击与振动,进而危及桥梁的安全性。
因此,对于地震响应的分析及减振控制显得尤为重要。
本文将探讨桥梁结构的地震响应分析与减振控制的相关内容。
一、地震响应分析地震响应分析是指通过数学模型及计算方法,对桥梁结构在地震作用下的响应情况进行预测与分析。
通过对桥梁结构的地震响应分析,有助于我们了解结构的抗震性能,并为后续的减振控制提供依据。
1. 结构模型在进行地震响应分析时,需要建立相应的地震桥梁模型。
通常,我们可以采用有限元方法将桥梁结构离散化为节点和单元,通过计算每个节点的运动参数来研究地震作用下的响应情况。
2. 加速度输入地震响应分析需要考虑地震加速度对桥梁结构的影响。
我们可以通过研究历史地震数据或使用合成地震波来模拟实际地震的加速度输入,并将其作用于结构模型,进行地震响应分析。
3. 结构响应通过进行地震响应分析,可以得到桥梁结构在地震作用下的位移、加速度、内力等响应参数。
这些参数可以帮助我们评估结构的抗震性能,并为减振控制提供基础数据。
二、减振控制减振控制是指通过一系列的措施与方法,减少或消除桥梁结构在地震作用下的振动响应。
在进行桥梁结构的减振控制时,我们可以从结构设计、材料选择、减震装置等多个方面入手。
1. 结构设计在桥梁结构的设计阶段,可以采用抗震设计的原则,通过增强结构的抗震能力来降低地震响应。
例如,合理设置剪力墙、增加桥墩的承载能力等,可以提高结构的整体稳定性,减小地震引起的破坏。
2. 材料选择合理的材料选择也是减振控制的重要方面。
在桥梁结构的设计中,可以选用具有较好抗震性能的材料,如高强度混凝土、增强型钢材等。
这些材料在地震作用下具有较好的韧性和延性,能够减少结构受到的破坏程度。
3. 减震装置减震装置是减振控制中常用的一种手段。
通过设置减振器或减震支座等装置,可以将一部分地震能量转化为其他形式的能量,从而减小结构的振动幅度。
地震作用下桥梁结构横向碰撞模型及参数分析

摘 要 :针对桥梁结构在地震作用下梁体与横向挡块间的碰撞现象, 采用非线性时程积分法, 研究了横向地震作
用下梁体与挡块 问的碰撞效应 。通过 对刚体碰撞模型分析 , 推导 出阻尼 常数 与恢 复系数 间的关系表达 式 , 此基础上 建 在 立了能考虑碰撞过程 中能量损失 的桥梁横 向碰撞模型 , 并对碰撞刚度 、 初始 间隙 、 复系数 以及桥梁跨径等参数进行 了影 恢
D 大, 可将其视 为刚 体 , 与挡块 在 发 生 碰 撞 时 , 于 碰 撞 持 时 很 由 短 , 向碰 撞过 程 可 以等效 为 图 横 1 刚体碰撞模型, 其中 m为刚体 质 量 , 碰撞 刚度 , k为 C代表 碰 撞 图 1 刚体碰撞模型 过程 中的能量 损 失 , 假定 在 t 0 = 时刻 发生 碰撞 。 建立 系统 的运 动方 程
维普资讯
振
动
与
冲
击
第2 6卷第 9期
J OURNAL OF VI BRATI ON AND S HOCK
地 震作 用 下桥 梁 结构 横 向碰 撞模 型 及 参数 分 析
邓育林 , 彭天波 , 李建 中
( 同济大学桥梁系 , 上
【 o =o ( ) =t ( ) , 0 , 0
( 1 )
() 2
对 于 小阻 尼情 况 , 式解 为 : 上
() =A x ( ( tsn d t e p 一 E )iw t J
式中 = / 2 t )< , U/ d = ̄ 一 E, c (mo 1A= 0 , d / ( 1 J
在桥梁 工程 中 , 了 防止 落 梁 的震 害 或 保 证 支 座 为 的抗震 安全 性 , 常采 用 设 置挡 块 的抗震 措 施 。 目前 , 通 各 国学 者对 挡块 的抗 震性 能研 究 不 多 , 国外 ,hri 在 Sevn Maei ’ l l 对简支 梁 桥上 部结 构与 横 向约束 挡块 间 碰撞 k6 效应 进 行 了研 究 , 析表 明碰撞 刚度 、 始 间隙 和 结 构 分 初 周期 影 响很 大 , 同时 指 出忽 略 碰撞 效 应 , 会低 估 挡块 将 及 下部 结构 的地 震 需 求 , 抗 震 设 计 中造 成 不 安 全 的 在 结果 。其 不 足是 采 用 的是 线 性 碰 撞 模 型 , 有 考 虑 碰 没 撞过 程 中 的能 量 损 失 。而 在 国 内 , 目前 的桥 梁 工 程 抗 震规 范仅 把挡 块 作 为 一 种 构 造措 施 , 际上 挡块 的作 实 用对 主体 结构 的 地震 反 应 有 较 大 的影 响 , 而 在 地 震 因 反 应 分析 中, 析 挡 块 的作 用 以及 横 向碰 撞 效 应 就 很 分 有 意义 。本 文 通 过 刚 体 碰 撞 模 型分 析 , 导 出 阻尼 常 推 数 与恢 复系 数 间 的关 系 , 此基 础上 建 立 了简 支 梁 桥 在 横 向碰撞 简 化模 型 , 进 行 了参 数 分 析 , 到 了一些 结 并 得 论 和规律 , 减轻地 震 作用 下碰 撞效 应提 供依 据 。 为
横向地震作用对匝道曲线桥梁地震响应的影响分析

____________________________________________________________桥隧工程觀横向地震作用对匝道曲线桥梁地震响应的影响分析罗彦,刘鑫(广西交通工程检测有限公司,广西南宁530012)摘要:文章以某匝道连续梁桥为例,基于OpenSees软件建立了该桥梁空间三维非线性有限元分析模型,充分考作用下桥墩、支座的非线主梁的,对比研究了只考虑纵向作用、横向地震作用和纵-横向双向地震作用下桥的,分析了横向地震作用对该匝道曲线桥的影响&分析表明:横向作用对匝道曲线桥的影常显著,与只考虑纵向作用,纵-横向双向作用下桥梁的著,主梁径向的改变到49.9%;在匝道曲线桥抗能分析时应该考虑纵横向双向作用,只考虑单向地震作用将严重桥梁的抗震需求&关键词:曲线梁桥;横向地震;非线性地震响应;弯扭耦合中图分类号:U442.5文献标识码:A DOI:10.13282/k..wccst.2020.10.041文章编号:673-4874(2020)10-0147-040引言道曲线梁桥良好的地形适,公路和城市立交中都得到了广泛的应用,程道路线路之间的常见桥型,由于桥的高程差的使得这种匝道曲线梁桥不仅在平面线形状,而且面的纵,造成了桥空间重的不规作用下,这种空间不规使得匝道曲线梁桥的的直桥和平面曲线梁桥都要更,中更生严重的。
通过研究作用道曲线梁桥的机理能够为其抗震设计和抗能分析提供指导,对桥梁系统的能重要意义。
近年来,国内外众多学者都对匝道曲线梁桥的抗能进行了研究。
陈彦江等3以道曲线梁桥,通过台实验研究了纵向、横向纵向+横向作用下桥的&张⑷通过数值分析研究了作用市区工人路匝道桥的倒塌机理。
等中的道曲线梁桥,探讨了小半线桥的损伤模拟方法,通过数值模拟研究了FPS对小半道曲线梁桥的.效&龚强闪中回交匝道桥,通过OpenSees软件了考虑的桥梁,分析了作用征,结果表明作用基本都会生滑移破坏,与桥梁实际震害基本一致&作者简介:罗彦(971—),高级工程师,主要从事公路设计及检测工作;刘蠡(985—),硕士,工程师,主要从事桥梁检测及加固设计工作。
双柱式简支-桥面连续梁桥横向地震碰撞和防撞措施分析

[ 文章编号 】 1 0 0 2 — 8 4 1 2 ( 2 0 1 3 ) 0 4 — 0 0 6 1 — 0 6
DO I : 1 0 . 3 9 6 9 / j . i s s n . 1 0 0 2—8 41 2 . 2 0 1 3 . 0 4 . 0 1 0
双柱 式 简 支 一桥 面 连 续 梁 桥 横 向地震 碰 撞 和 防撞 措 施 分 析
在 横桥 向 地 震 作 用 下 主 梁 与 抗 震 挡 块 间 的 碰撞 行 为 , 建 立了考虑支座非线性 、 墩 柱 弹 塑性 以 及 桩 土 相 互 作 用 的 碰 撞 模 型 。 在
此 基 础 上 分 析 了 主 梁 与 抗 震 挡 块 间 的碰 撞 效应 , 探 讨 了减 轻 碰 撞 的 措 施 和 方 法 , 并 比 较 了 两 种 措 施 的 防 撞 效 果 。结 果 表 明 : 主梁 与抗 震 挡 块 间 的 碰 撞 不 仅 产 生 巨 大 的 碰撞 力 , 还会 增大桥 墩的地 震需求 , 对 结构抗 震不利 ; 在 抗 震 挡 块 内 侧 安 装 橡 胶 缓 冲 垫 和 采 用 铅 芯橡 胶 支 座 均 能 减 小 碰 撞 力 、 墩 顶 底 的剪 力 和 塑 性 转 角 , 但后者的防撞效果更好 。 [ 关键 词] 地震 ; 简 支 一桥 面 连 续 梁 桥 ; 横 向碰 撞 ; 防撞 措 施
A bs t r a c t: Th e po u n di ng b e t we e n c o mpo n e n t s o f a s t r u c t u r e ha s s i g n i f i c a nt i n lue f n c e s o n t he s t r u c t ur a l pe r f o r ma nc e u n de r e a r t h qu a k e. Ai mi n g a t t he t r a ns v e r s e p o u nd i n g o f Si mpl y s u pp o r t e d— c o n t i n uo u s b id r g e un d e r t r a n s v e r s e e a th r qu a k e, a p o u nd i ng m o de l o f
横桥向地震作用下简支梁桥偏心碰撞反应参数研究

横桥向地震作用下简支梁桥偏心碰撞反应参数研究石岩;王军文;李建中;艾庆华【摘要】汶川大地震中桥梁结构横向抗震挡块遭到严重破坏,其中部分是由于梁体与其发生碰撞所致。
针对桥梁结构横向抗震挡块与梁体在强震作用下的碰撞现象,建立了考虑上部结构与挡块间偏心距、支座非线性和墩柱弹塑性的横桥向单墩碰撞模型。
采用非线性地震反应时程分析方法,详细研究了偏心距、碰撞刚度、初始间隙、桥墩线刚度、上部结构与盖梁质量比、上下部结构周期比以及墩柱弹塑性等参数对桥梁结构横向地震反应的影响。
结果表明:考虑偏心的碰撞进一步增强了系统的非线性,低高度梁(e<70cm)不考虑偏心碰撞分析可能导致不保守的结果,需引起重视。
【期刊名称】《振动与冲击》【年(卷),期】2012(000)018【总页数】6页(P132-136,142)【关键词】简支梁桥;横向地震;碰撞模型;偏心碰撞效应;抗震挡块【作者】石岩;王军文;李建中;艾庆华【作者单位】石家庄铁道大学土木工程学院,石家庄 050043; 石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室,石家庄 050043;石家庄铁道大学土木工程学院,石家庄 050043; 石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室,石家庄 050043;同济大学桥梁工程系,上海 200092;石家庄铁道大学土木工程学院,石家庄 050043【正文语种】中文【中图分类】U442.5在历次地震中,桥梁落梁破坏的情况时有发生。
为了避免横桥向落梁等灾难性损坏或为保证支座的抗震安全性,通常在横桥向设置挡块等抗震措施。
在强震作用下,桥梁上下部结构的不同相振动极易导致梁体与抗震挡块间发生碰撞。
汶川大地震中,较多桥梁抗震挡块遭到严重破坏[1-2],其中部分是由于梁体与其发生碰撞所致。
目前,国内外学者对地震引起的横桥向碰撞效应进行了一些研究[3-6],结果表明横向碰撞对结构的抗震性能有较大影响,但以上研究大都建立在对心碰撞的基础上,且假定墩柱在弹性范围内工作,而桥梁上部结构的质心与挡块质心实际上不在同一水平面上,即梁体与挡块间的碰撞属偏心碰撞,在强震作用下墩柱也往往会进入塑性区域。
横桥向地震作用下简支梁桥偏心碰撞反应参数研究

3 e at n o B d eE g e r g T n l n es y S a g a 2 0 9 C ia .D p r me t f r g n i ei , o a i r t , h n h i 0 0 2, hn ) i n n U v i
Absr c : ta t Du i g rn W e c u n a h ua e,s me ae a s a e s f b d e s f r d e e e n h a e r q k t o ltr l he r k y o r g s uf e s v r da g patal i e ma e ri l y
撞进一步增强 了系统的非线性 , 低高度梁 ( < 0c 不考虑偏心碰撞分析可能导致不保守的结果 , e 7 m) 需引起重视 。
关键词 :简支梁桥 ; 向地震 ; 横 碰撞模 型 ; 偏心碰撞效应 ; 抗震挡块 中图分类号 :U 4 . 425 文献标识码 :A
Efe t f p r m e e s o e s i c e t i o d n e po s s o f c s o a a t r n s im c e c n rc p un i g r s n e fa sm p y-u o t d g r r br d e un r t a s e s a t qu ke i l s pp r e ide i g de r n v r e e r h a
振 第3 l卷第 1 8期
动
与
冲
击
Vo _ N . 8 2 2 l3l o 1 Ol
J OURNAL BRAT1 OF VI 0N AND H0C S K
横桥 向地震 作 用 下简 支梁 桥偏 心 碰撞 反应 参 数 研 究
土木工程中的横向地震力分析

土木工程中的横向地震力分析地震是一种常见的自然灾害,给土木工程的稳定性和安全性提出了极大的挑战。
在土木工程设计中,横向地震力分析是其中一个关键环节。
本文将从基本概念、分析方法和实例等方面论述土木工程中的横向地震力分析。
【概念】横向地震力是指地震作用下建筑物或结构物所受到的地震力。
而横向地震力分析即是对建筑物或结构物在地震作用下产生的横向力进行计算和分析,以确定其稳定性和安全性。
在土木工程中,横向地震力分析是非常重要的。
由于地震的瞬时冲击力和无规律性,容易导致建筑结构的振动和破坏,因此横向地震力分析必须考虑到地震的特点并进行准确的计算。
【分析方法】横向地震力分析涉及到很多复杂的计算方法,如现行的等效静力法、弹性动力法、非线性静力法和弹塑性静力法等。
一种常用的方法是等效静力法,它将地震作用视为静水压力的分布。
在等效静力法中,可以通过计算地震加速度和建筑物质量的乘积来确定地震作用下的横向地震力。
但是等效静力法对于非线性效应的考虑较少,因此在实际工程中往往与其他方法结合使用。
弹性动力法是一种基于固体力学和结构动力学原理的方法。
它将建筑物视为一个弹性系统,并考虑到地震波的频率和振幅等因素,通过求解方程组来计算横向地震力。
弹性动力法可以提供更准确的地震力分析结果,但需要具备较高的工程计算和结构动力学理论知识。
对于复杂的工程结构,非线性静力法和弹塑性静力法往往是更实用的方法。
这两种方法可以考虑结构的非线性行为,如材料的弹塑性变形、连接件的滑动和变形等。
通过引入非线性参数,可以更准确地分析横向地震力对结构的影响。
【实例分析】为了更好地理解横向地震力分析的应用,我们以某高层建筑的设计为例进行分析。
在这个实例中,首先通过地震波的地面运动记录数据,计算出地震作用下的加速度。
然后使用等效静力法,将加速度乘以建筑物的质量,得到横向地震力。
接着,使用弹性动力法对结构进行分析,考虑到建筑物的固有频率和振动特性,得到更准确的地震力分布。
地震作用下桥梁结构碰撞单元参数确定研究

1)地震作 用 的 存 在 不 仅 会 导 致 桥 面 板 之 间 发生碰撞,同时 还 会 导 致 桥 面 板 与 桥 台 之 间 产 生 一 定 的 碰 撞 ;进 而 直 接 损 坏 支 座 ,并 增 大 桥 墩 的 延 性需求。
相邻桥跨之 间 均 存 在 伸 缩 缝,当 发 生 地 震 作 用 时 ,伸 缩 缝 处 会 产 生 一 定 的 碰 撞 ,且 碰 撞 力 的 大 小会因桥跨间动力特性的不同而不同。一旦碰撞 力达到上限值时,会 导 致 伸 缩 缝 处 的 混 凝 土 发 生 剥落[12],进而使 得 桥 跨 间 产 生 更 大 的 相 对 位 移, 严重时会导 致 桥 梁 的 塌 落。 基 于 此,在 对 桥 梁 结 构 进 行 设 计 时 ,需 要 考 虑 其 抗 震 性 能 ,即 进 行 抗 震 设计以使其在地震作用下具有一定的变形能力。 本文将分析地震作用下桥梁结构碰撞效应中的碰 撞单元参数确定原则 。 [3]
烄αmax +10犜(βmη-1)αmax
犜 <0.1s
犛=烅 烆
βmηαmax
( ) βmαmax
犜g 犜
γ
0.1s≤ 犜 ≤ 犜g 犜 > 犜g
(1)
2018 年 第 4 期
马 坤 :地 震 作 用 下 桥 梁 结 构 碰 撞 单 元 参 数 确 定 研 究
91
式中:αmax为峰值加 速 度,g ;犜g 为 特 征 周 期,s;犜 为结构自身对应周期,s;γ 为衰减 指 数;βm 为 动 力 放大系数最大值;η 为 阻 尼 调 整 系 数,γ ,βm,η 为 量纲为一的量。
马 坤
(贵 州 省 交 通 规 划 勘 察 设 计 研 究 院 股 份 有 限 公 司 贵 阳 550081)
地震作用下高墩桥梁横向碰撞效应研究

地震作用下高墩桥梁横向碰撞效应研究
邓育林;雷凡;何雄君
【期刊名称】《桥梁建设》
【年(卷),期】2014(044)003
【摘要】为提升高墩大跨连续刚构桥的防震减灾能力,对其合理的减震措施进行研究.以我国西部山区强地震带一座高墩大跨桥梁为例,利用SAP2000 Nonlinear有限元程序建立桥梁结构空间非线性计算模型,分析其横向地震响应规律及其碰撞效应.分析结果表明:对于高墩大跨连续刚构桥,在过渡墩墩顶设置弹性挡块时,很难实现对过渡墩与刚构墩地震响应的有效控制,且碰撞产生的撞击力极易使弹性挡块破坏,从而失去限位功能;在过渡墩墩顶设置弹塑性挡块,并选取适当的挡块屈服强度,可有效地控制过渡墩、刚构墩地震响应以及上部结构位移.
【总页数】7页(P25-31)
【作者】邓育林;雷凡;何雄君
【作者单位】武汉理工大学交通学院,湖北武汉430063;武汉理工大学交通学院,湖北武汉430063;武汉理工大学交通学院,湖北武汉430063
【正文语种】中文
【中图分类】U442.55
【相关文献】
1.高墩桥梁在地震作用下梁体与挡块之间的非线性碰撞效应研究 [J], 彭刚辉;郑史雄
2.地震作用下两联连续梁桥纵向碰撞效应研究 [J], 黄志霜;姚昌荣;李亚东
3.强震作用下大跨高墩桥梁伸缩缝处碰撞效应的参数研究 [J], 师新龙
4.近断层地震作用下曲线桥碰撞效应及影响试验研究 [J], 李娜娜;许维炳;陈彦江;闫维明
5.地震作用下考虑桥台-土相互作用的多跨简支板梁桥碰撞效应研究 [J], 邓育林;魏征;葛雄
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 3 碰撞刚度对撞击力的影响 ( 12条波平均 )
( a) 碰撞刚度为 k3 ( b) 碰撞刚度为 k4
图 4 碰撞刚度对挡块变形的影响 ( 12条波平均 )
比较图 3和图 4, 可以看出 , 当碰撞刚度为 k5左右 时 ,即碰撞刚度为 5. 0 ×104 kN /m ,无论对哪条地震波 输入 ,最大撞击力均在 103 kN 左右 ,并且挡块的变形需 求在 5 cm 以内 ,均在可接受范围内 。因此 ,柔性防撞装 置的刚度取 104 kN /m 量级时 ,可达到最大撞击力和最 大变形需求的平衡 ,取得较好的防撞效果 。 212 恢复系数的影响 碰撞过程中必定伴有能量损失 ,其能量损失常采 用阻尼器代表 ,阻尼 c的大小与碰撞过程的恢复系数 e 有关 ,对于完全弹性碰撞 , 恢复系数 e = 1; 完全塑性碰 撞 ,恢复系数 e = 0。为了解恢复系数对碰撞的影响 , 比 较了恢复系数 e的不同取值对碰撞反应的影响 。
106
振 动 与 冲 击 2007年第 26卷
从图 3可以看出 , 碰撞刚度变化对撞击力有很大 的影响 ,碰撞刚度大 ,则撞击力大 , 碰撞刚度小 , 则撞击 力小 ,且随着碰撞刚度的减小 , 撞击力迅速单调减小 , 此为在刚性撞击物前设置柔性防撞装置提供了根据 。
7. 6
Calexico Fire Station
6. 5
San Ramon
5. 8
PGA / g
0. 349 0. 156 0. 345 0. 368 0. 477 0. 11 0. 426 0. 367 0. 263 0. 364 0. 275 0. 154
卓越周期 / s
0. 68 0. 36 0. 16 0. 34 0. 42 0. 42 0. 29 0. 78 0. 52 0. 62 0. 36 0. 62
碰撞接触时间 。对式 ( 2)求二阶导数并代入 t = t0 得 :
-
A exp
(
-
ξω n
t0)Βιβλιοθήκη [(1-2ξ2 )ωn sinωd t0
+
2ξωd co sωd t0 ] = 0
(3)
碰撞接触时间为上式的最小正解 ,即
t0
π
=
-
ω
n
a rc tanλ,λ 1 - ξ2
=
2ξ 1
1 - ξ2 - 2ξ2
在桥梁工程中 ,为了防止落梁的震害或保证支座 的抗震安全性 ,通常采用设置挡块的抗震措施 。目前 , 各国学者对挡块的抗震性能研究不多 ,在国外 , Shervin M aleki[ 6, 7 ]对简支梁桥上部结构与横向约束挡块间碰撞 效应进行了研究 ,分析表明碰撞刚度 、初始间隙和结构 周期影响很大 ,同时指出忽略碰撞效应 ,将会低估挡块 及下部结构的地震需求 ,在抗震设计中造成不安全的 结果 。其不足是采用的是线性碰撞模型 ,没有考虑碰 撞过程中的能量损失 。而在国内 ,目前的桥梁工程抗 震规范仅把挡块作为一种构造措施 ,实际上挡块的作 用对主体结构的地震反应有较大的影响 ,因而在地震 反应分析中 ,分析挡块的作用以及横向碰撞效应就很 有意义 。本文通过刚体碰撞模型分析 ,推导出阻尼常 数与恢复系数间的关系 ,在此基础上建立了简支梁桥 横向碰撞简化模型 ,并进行了参数分析 ,得到了一些结 论和规律 ,为减轻地震作用下碰撞效应提供依据 。
选取了 12条典型地震波沿桥梁横向输入 ,假设桥 梁位于地震烈度 8度区 ,考虑罕遇地震作用 ,故将每条 地震波的加速度峰值调整到 0. 4 g, 12条典型地震波分 别见表 1。
No.
地震记录
1
1940 E I Centro
2
1952 Kern County
3
1995 Kobe
4
1994 Northridge
关键词 : 横向地震 ; 非线性 ;碰撞效应 ;碰撞模型 ;参数分析 中图分类号 : U442. 5 + 5 文献标识码 : A
最近二十余年 ,地球上发生的多次地震灾害对桥 梁抗震设计理论产生了巨大影响 ,并且开展了一系列 深入研究 。其中地震作用下 ,结构的碰撞被认为是影 响结构地震反应和结构抗震性能的一个重要因素 。许 多桥梁结构地震震害表明 :桥梁连接构造处的碰撞是 引起结构破坏的主要原因之一 [ 1, 2 ] 。从历次大地震中 可知碰撞不但造成构造设施的损坏 ,而且还会引起相 应构件内力急剧增大 ,对下部结构的延性能力要求增 加 ,甚至造成桥梁墩台脆性剪切破坏 [ 3 - 5 ] 。
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
第 9期 邓育林等 : 地震作用下桥梁结构横向碰撞模型及参数分析
105
·
e
=-
x ( t0 )
υ
=
0
1
-
1 2ξ2
exp
[
-
ξ (π - a rc tanλ) ] · 1 - ξ2
co s ( a rc tanλ)
(6)
工程中常见的阻尼比 ξ都小于 0. 2, 由式 ( 4)可知
arctanλ较 小 , 从 而 利 用 数 学 级 数 展 开 , 式 ( 6 ) 可 近
似为 :
·
e
=-
x ( t0
υ
)
≈
exp ( -
0
πξ
)
1 - ξ2
(7)
即:
ξ=
- lne
π2 + ( lne) 2
c = 2mωnξ = 2ξ km
(8)
2 碰撞计算模型
分析的桥梁为某高速公路 1跨 25m 的简支 T梁 , 横断面由六片 T梁组成 , T梁中心距为 2. 2 m ,上部结 构宽 12. 5 m ,总重 471 t。全桥共设 12块圆板式橡胶支 座 ,尺寸为 325 ×88 mm ,单个支座的水平刚度为 1. 3 × 103 kN /m。桥台两侧均设置了钢筋混凝土抗震挡块 , 挡块长 ×宽 ×高为 100cm ×30cm ×50cm。分析时假定 桥台不发生变形且不考虑挡块的屈服和破坏 ,此时桥 梁碰撞模型可以简化为如图 2所示 。
5
1994 Northridge
6
1971 San Fernando
7
1987 W hittier
8
1989 Loma Prieta
9
1999 Chi2Chi, Taiwan
10
1999 Chi2Chi, Taiwan
11
1979 ImperialValley
12
1980 L ivermore
表 1 选取的地震波
用下梁体与挡块间的碰撞效应 。通过对刚体碰撞模型分析 ,推导出阻尼常数与恢复系数间的关系表达式 ,在此基础上建 立了能考虑碰撞过程中能量损失的桥梁横向碰撞模型 ,并对碰撞刚度 、初始间隙 、恢复系数以及桥梁跨径等参数进行了影 响分析 。分析结果表明 :最大撞击力随碰撞刚度和桥梁跨径的增大而增大 ,但随初始间隙的变化规律不明显 ;恢复系数对 碰撞效应影响很大 ,忽略碰撞过程中的能量损失会高估碰撞反应 。为减轻梁体与横向挡块间的碰撞效应 ,提出了挡块刚 度的合理取值 。
第 26卷第 9期
振 动 与 冲 击 JOURNAL OF V IBRATION AND SHOCK
Vol. 26 No. 9 2007
地震作用下桥梁结构横向碰撞模型及参数分析
邓育林 , 彭天波 , 李建中
(同济大学桥梁系 ,上海 200092)
摘 要 : 针对桥梁结构在地震作用下梁体与横向挡块间的碰撞现象 ,采用非线性时程积分法 ,研究了横向地震作
图 2 碰撞模型
其中 m 为上部结构总质量 , k0为板式橡胶支座总 水平刚度 , 其值为 1. 56 ×104 kN /m , c0为结构阻尼 , 其 值为 271。碰撞刚度 k的取值由于缺乏试验依据 , 本次 分析采用挡块的弯曲刚度并考虑剪切变形的影响 , 为 5
×106 kN /m。碰撞过程中的能量损失采用阻尼器代 表 ,阻尼 c的大小与碰撞过程的恢复系数 e有关 , 对于 完全弹性碰撞 ,恢复系数 e = 1; 完全塑性碰撞 , 恢复系 数 e = 0。对于混凝土材料建议 [8 ] e取 0. 65,阻尼 c采用 式 ( 8)来计算 。本文中所建立的有限元模型的模拟均 采用美国加州大学伯克利分校开发的有限元分析软件 OpenSees来实现 。
从图 4可以看出 , 随着碰撞刚度的减小 , 挡块的最 大变形逐渐增大 , 因此最大撞击力和最大变形需求是 一对矛盾的参数 ,为保证结构安全 , 期望最大撞击力比 较小 ,但要求挡块必须要有足够的变形能力 。
不同地震波 ,增大的幅度不尽相同 , 这与碰撞过程中最 大撞击力发生时间的先后有关 。2)比较图 5 ( a)和图 5 ( c) ,当碰撞刚度较大时 , 恢复系数 e对碰撞反应的影 响更为显著 。
位置
震级
Imp e ria lV a lley
6. 9
Taft L incoln School
7. 4
Kakogawa
6. 9
Saticoy, 090
6. 7
Saticoy, 180
6. 7
A thenaeum
6. 6
Jo slin
6
Gilroy A rray #2
6. 9
Chy014
7. 6
Chy006
图 5 ( a)为碰撞刚度为 k3时 , 恢复系数 e的不同取 值对碰撞反应的影响 , 图 5 ( b)为碰撞刚度为 k4时 , 恢 复系数 e的不同取值对碰撞反应的影响 , 图 5 ( c)为碰 撞刚度为 k5时 , 恢复系数 e的不同取值对碰撞反应的 影响 ,分析时初始间隙均取 5 cm。从图 5可以看出 : 1) 随着恢复系数 e的增大 , 最大撞击力不断增大 , 但对于
