张量分析(Tensor Analysis)

合集下载

(完整版)《张量分析》报告

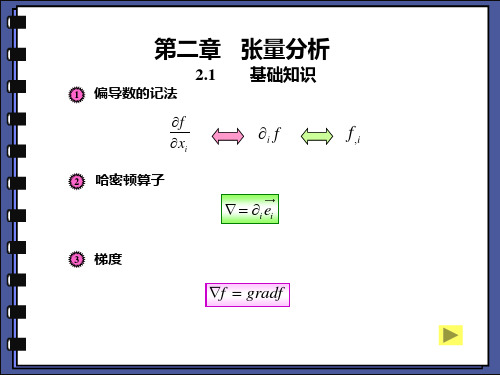
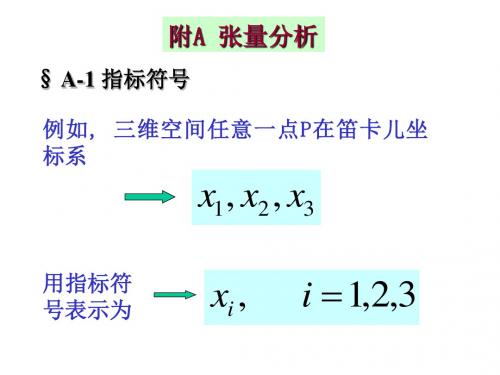
一爱因斯坦求和约定1.1指标变量的集合：n n y y y x x x ,...,,,...,,2121表示为：n j y n i x j i ...,3,2,1,,...,3,2,1,==写在字符右下角的指标，例如xi 中的i 称为下标。

写在字符右上角的指标，例如yj 中的j 称为上标；使用上标或下标的涵义是不同的。

用作下标或上标的拉丁字母或希腊字母，除非作了说明，一般取从1到n 的所有整数，其中n 称为指标的范围。

1.2求和约定若在一项中，同一个指标字母在上标和下标中重复出现，则表示要对这个指标遍历其范围1，2，3，…n 求和。

这是一个约定，称为求和约定。

例如：333323213123232221211313212111bx A x A x A b x A x A x A bx A x A x A =++=++=++筒写为：ijijbx A =ｊ——哑指标ｉ——自由指标，在每一项中只出现一次，一个公式中必须相同遍历指标的范围求和的重复指标称为“哑标”或“伪标”。

不求和的指标称为自由指标。

1.3 Kronecker-δ符号（克罗内克符号）和置换符号Kronecker-δ符号定义j i ji ij ji ≠=⎩⎨⎧==当当01δδ置换符号ijkijk e e =定义为:⎪⎩⎪⎨⎧-==的任意二个指标任意k j,i,当021)(213,132,3的奇置换3，2，1是k j,i,当112)(123,231,3的偶置换3，2，1是k j,i,当1ijk ijke ei,j,k 的这些排列分别叫做循环排列、逆循环排列和非循环排列。

置换符号主要可用来展开三阶行列式：231231331221233211231231133221332211333231232221131211a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++==因此有：ijmjimii i i jijAA aa a a a ==++=δδδδδ332211kijjkiijkkjiikjjikijkee e e e e e ==-=-=-=同时有：ijjijij iiiijijijkj ikilkljkijjjiiijijijkjikiie e aa aa a a a aa δδδδδδδδδδδδδδδδδδδ=⋅=++=========++=332211332211331001010100131211232221333231321333222111321321321-=====δδδδδδδδδδδδδδδδδδδδδδδδδδδe e k j i k j i k j i k k k j j j i i i ijk333222111321321321r q p r q p r q p k k k j j j i i i pqr ijke e δδδδδδδδδδδδδδδδδδ⋅=ipp i p i p i p i δδδδδδδδδ==++11332211krkqkpjrjqjpiriqippqrijke e δδδδδδδδδ=jqirjriqjrjqiriqkqrijke e kp δδδδδδδδ-===321321322311332112312213322113312312332211333231232221131211k j i ijkkjiijkaa a e a a a e aa a a a a a a a a a a a a a a a a aaaa a aaa a A ==---++==Kronecker-δ和置换符号符号的关系为：itjsjtiskstkije e δδδδ-=二张量代数2.1张量的加法(减法)两个同阶、同变异(结构) 的张量可以相加(或相减)。

张量分析基础

张量的性质
张量的定义
— 张量是与坐标系有联系的一组量，并满足一定的坐标变换规律。
张量的性质
— 任何两个张量相乘所得到的新张量的阶数等于原张量阶数之和； — 两个张量间的比例系数一般是一个张量，其阶数等于原张量阶数之和； — 张量的变换规律与坐标乘积的变换规律相同； — 变换矩阵与二阶张量的区别
二阶对称张量
δ ij =
1 i = j 0 i ≠ j
[ ]
1 0 0 δ ij = 0 1 0 0 0 1
δ ij Pj = Pi δ ij Pi = Pj
δ ijT jl = Til δ ilT jl = T ji
i, j , k顺序轮换 i, j , k反序轮换两个以上角标同
反对称三重积
ei × e j = ε ijk e j
傀标
Pi = Tij Q j
自由下标
[A] + [B][C][D] = [E][F]
Aij + BikCkl Dlj = Eik Fkj
坐标变换
坐标轴变换
e1* a11 * e 2 = a 21 * e3 a 31 a12 a 22 a 32
*∧
X3’
X3
θ23
a13 e1 a 23 e 2 a 33 e3
x1* a11 * x 2 = a 21 * x 3 a 31
a12 a 22 a 32
a13 x1 a 23 x 2 a 33 x 3
Neuman原理
物质张量、场张量
— 物质张量是建立晶体在外场作用下的响应与外场之间关系的物理性能，物质张量受到晶体对称性的制约，如弹性系数 — 场张量：外场张量及晶体对外场响应后所产生的新的物理量，不受晶体对称性的制约，如应力、电场 — 晶体响应，受外场、物理性能和晶体对称性的共同影响，如应变

张量分析(Tensor Analysis)

ds 2 (dx1 ) 2 (dx 2 ) 2 (dx3 ) 2
利用克罗内克符号，上式可写成：
ds ij dx dx
2 i
j
克罗内克符号的一些常用性质：
i j xi x j
x j ij x i
i
j i k
j k
D) 置换符号
置换符号eijk=eijk定义为:
r i dr i dx x
空间一点P的位置矢量可用直角坐标表示为：
r z ji j
式中 ij 为沿坐标轴 zj 方向的单位矢量。
r r z j z j j i i ij i x z x x
r 上式表明， i 是单位矢量 ij 的线性组合，因此也是矢量。 x
基矢量（续）
r r i 变化时位置矢量r的变化，因此 i i 表征当 x i 的方向是沿坐标曲线 x x x r 的切线方向。矢量 i 可以取作曲线坐标系的基矢量（协变基矢量）： x
r z j gi i i i j x x
注意：对于在曲线坐标系中的每一点，都有三个基矢量。基矢量一般不是单位矢量，彼此也不正交；基矢量可以有量纲，但一点的三个基矢量的量纲可以不同；
1 张量的概念
在三维空间，一个矢量（例如力矢量、速度矢量等）在某参考坐标系中，有三个分量；这三个分量的集合，规定了这个矢量；当坐标变换时，这些分量按一定的变换法则变换。
在力学中还有一些更复杂的量。例如受力物体内一点的应力状态，有9个应力分量，如以直角坐标表示，用矩阵形式列出，则有：
xx xy xz ij yx yy yz zx zy zz
克罗内克符号 i j 的定义是:

第二章张量(清华大学弹塑性力学)

利用爱因斯坦求和约定，写成：
xi aij x j
其中 j 是哑指标，i 是自由指标。
19
Appendix A.1
张量基本概念
★ 在表达式或方程中自由指标可以出现多次，但不得
在同项内出现两次，若在同项内出现两次则是哑指标。例：
若i为自由指标
ji , j fi 0
ji , j fii 0
个独立的自由指标，其取值范围是1～n，则这个方
程代表了nk 个分量方程。在方程的某项中若同时出现m对取值范围为1～n的哑指标，则此项含相互迭
加的nm个项。
27
Appendix A.1
张量分析初步
矢量和张量的记法，求和约定符号ij与erst 坐标与坐标转换张量的分量转换规律，张量方程张量代数，商判则
3. 换标符号，具有换标作用。例如：
d s2 ij d xi d x j d xi d xi d x j d x j
即：如果符号的两个指标中，有一个和同项中其它因子的指标相重，则可以把该因子的那个重指标换成的另一个指标，而自动消失。
30
Appendix A.2
符号ij与erst
Appendix A.1
张量基本概念
★ 指标符号也适用于微分和导数表达式。例如，三维
空间中线元长度 ds 和其分量 dxi 之间的关系
d s d x1 d x2 d x3
2 2 2
2
2 可简写成： d s d xi d xi
场函数 f(x1, x2, x3) 的全微分：
21n1 22n2 23n3 T2
31n1 32n2 33n3 T3
18

张量分析翻译英文原文

TensorTensors are geometric objects that describe linearrelations between vectors, scalars, and other tensors.Elementary examples of such relations include thedot product, the cross product, and linearmaps.Vectors and scalars themselves are also tensors.A tensor can be represented as a multi-dimensionalarray of numerical values. The order (also degree orrank )of a tensor is the dimensionality of the arrayneeded to represent it, or equivalently, the number ofindices needed to label a component of that array. For example, a linear map can be represented by a matrix, a 2-dimensional array, and therefore is a 2nd-order tensor. A vector can be represented as a 1-dimensional array and is a1st-order tensor. Scalars are single numbers andare thus 0th-order tensors.Tensors are used to represent correspondences between sets of geometric vectors. For example, the Cauchy stress tensor T takes a direction v as input and produces the stress T (v ) on the surfacenormal to this vector for output thus expressinga relationship between these two vectors, shown in the figure (right).Because they express a relationship between vectors, tensors themselves must beindependent of a particular choice of coordinate system. Taking a coordinate basis or frame of reference and applying the tensor to it results in an organized multidimensional array representing the tensor in that basis, or frame of reference. The coordinate independence of a tensor then takes the form of a "covariant" transformation law that relates the array computed in one coordinate system to that computed in another one. This transformation law is considered to be built into the notion of a tensor in a geometric or physical setting, and the precise form of the transformation law determines the type (or valence ) of the tensor.Tensors are important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as elasticity, fluid mechanics, and general relativity. Tensors were first conceived by Tullio Levi-Civita and Gregorio Ricci-Curbastro, who continued the earlier work of Bernhard Riemann and Elwin Bruno Christoffel and others, as part of the absolute differential calculus . The concept enabled an alternative formulation of the intrinsic differential geometry of a manifold in the form of the Riemann curvature tensor.[1] Cauchy stress tenso r , a second-order tensor. The tensor's components, in a three-dimensional Cartesian coordinate system, form the matrix whose columns are the stresses (forces per unit area) acting on the e 1, e 2, and e 3 faces of the cube.HistoryThe concepts of later tensor analysis arose from the work of Carl Friedrich Gauss in differential geometry, and the formulation was much influenced by the theory of algebraic forms and invariants developed during the middle of the nineteenth century.[2]The word "tensor" itself was introduced in 1846 by William Rowan Hamilton[3] to describe something different from what is now meant by a tensor.[Note 1] The contemporary usage was brought in by Woldemar V oigt in 1898.[4]Tensor calculus was developed around 1890 by Gregorio Ricci-Curbastro under the title absolute differential calculus, and originally presented by Ricci in 1892.[5] It was made accessible to many mathematicians by the publication of Ricci and Tullio Levi-Civita's 1900 classic text Méthodes de calcul différentiel absolu et leurs applications (Methods of absolute differential calculus and their applications).[6]In the 20th century, the subject came to be known as tensor analysis, and achieved broader acceptance with the introduction of Einstein's theory of general relativity, around 1915. General relativity is formulated completely in the language of tensors. Einstein had learned about them, with great difficulty, from the geometer Marcel Grossmann.[7]Levi-Civita then initiated a correspondence with Einstein to correct mistakes Einstein had made in his use of tensor analysis. The correspondence lasted 1915–17, and was characterized by mutual respect:I admire the elegance of your method of computation; it must be nice to ride through these fields upon the horse of true mathematics while the like of us have to make our way laboriously on foot.—Albert Einstein, The Italian Mathematicians of Relativity[8]Tensors were also found to be useful in other fields such as continuum mechanics. Some well-known examples of tensors in differential geometry are quadratic forms such as metric tensors, and the Riemann curvature tensor. The exterior algebra of Hermann Grassmann, from the middle of the nineteenth century, is itself a tensor theory, and highly geometric, but it was some time before it was seen, with the theory of differential forms, as naturally unified with tensor calculus. The work of Élie Cartan made differential forms one of the basic kinds of tensors used in mathematics. From about the 1920s onwards, it was realised that tensors play a basic role in algebraic topology (for example in the Künneth theorem).[citation needed] Correspondingly there are types of tensors at work in many branches of abstract algebra, particularly in homological algebra and representation theory. Multilinear algebra can be developed in greater generality than for scalars coming from a field, but the theory is then certainly less geometric, and computations more technical and less algorithmic.[clarification needed]Tensors are generalized within category theory bymeans of the concept of monoidal category, from the 1960s.DefinitionThere are several approaches to defining tensors. Although seemingly different, the approaches just describe the same geometric concept using different languages and at different levels of abstraction.As multidimensional arraysJust as a scalar is described by a single number, and a vector with respect to a given basis is described by an array of one dimension, any tensor with respect to a basis is described by a multidimensional array. The numbers in the array are known as the scalar components of the tensor or simply its components.They are denoted by indices giving their position in the array, in subscript and superscript, after the symbolic name of the tensor. The total number of indices required to uniquely select each component is equal to the dimension of the array, and is called the order or the rank of the tensor.[Note 2]For example, the entries of an order 2 tensor T would be denoted T ij, where i and j are indices running from 1 to the dimension of the related vector space.[Note 3]Just as the components of a vector change when we change the basis of the vector space, the entries of a tensor also change under such a transformation. Each tensor comes equipped with a transformation law that details how the components of the tensor respond to a change of basis. The components of a vector can respond in two distinct ways to a change of basis (see covariance and contravariance of vectors),where the new basis vectors are expressed in terms of the old basis vectors as,where R i j is a matrix and in the second expression the summation sign was suppressed (a notational convenience introduced by Einstein that will be used throughout this article). The components, v i, of a regular (or column) vector, v, transform with the inverse of the matrix R,where the hat denotes the components in the new basis. While the components, w i, of a covector (or row vector), w transform with the matrix R itself,The components of a tensor transform in a similar manner with a transformation matrix for each index. If an index transforms like a vector with the inverse of the basis transformation, it is called contravariant and is traditionally denoted with an upper index, while an index that transforms with the basis transformation itself is called covariant and is denoted with a lower index. The transformation law for an order-m tensor with n contravariant indices and m−n covariant indices is thus given as,Such a tensor is said to be of order or type (n,m−n).[Note 4] This discussion motivates the following formal definition:[9]Definition. A tensor of type (n, m−n) is an assignment of a multidimensional arrayto each basis f = (e1,...,e N) such that, if we apply the change of basisthen the multidimensional array obeys the transformation lawThe definition of a tensor as a multidimensional array satisfying a transformation law traces back to the work of Ricci.[1]Nowadays, this definition is still used in some physics and engineering text books.[10][11]Tensor fieldsMain article: Tensor fieldIn many applications, especially in differential geometry and physics, it is natural to consider a tensor with components which are functions. This was, in fact, the setting of Ricci's original work. In modern mathematical terminology such an object is called a tensor field, but they are often simply referred to as tensors themselves.[1]In this context the defining transformation law takes a different form. The "basis" for the tensor field is determined by the coordinates of the underlying space, and thedefining transformation law is expressed in terms of partial derivatives of thecoordinate functions, , defining a coordinate transformation,[1]As multilinear mapsA downside to the definition of a tensor using the multidimensional array approach is that it is not apparent from the definition that the defined object is indeed basis independent, as is expected from an intrinsically geometric object. Although it is possible to show that transformation laws indeed ensure independence from the basis, sometimes a more intrinsic definition is preferred. One approach is to define a tensor as a multilinear map. In that approach a type (n,m) tensor T is defined as a map,where V is a vector space and V* is the corresponding dual space of covectors, which is linear in each of its arguments.By applying a multilinear map T of type (n,m) to a basis {e j} for V and a canonical cobasis {εi} for V*,an n+m dimensional array of components can be obtained. A different choice of basis will yield different components. But, because T is linear in all of its arguments, the components satisfy the tensor transformation law used in the multilinear array definition. The multidimensional array of components of T thus form a tensor according to that definition. Moreover, such an array can be realised as the components of some multilinear map T. This motivates viewing multilinear maps as the intrinsic objects underlying tensors.Using tensor productsMain article: Tensor (intrinsic definition)For some mathematical applications, a more abstract approach is sometimes useful. This can be achieved by defining tensors in terms of elements of tensor products of vector spaces, which in turn are defined through a universal property. A type (n,m) tensor is defined in this context as an element of the tensor product of vectorspaces,[12]If v i is a basis of V and w j is a basis of W, then the tensor product has anatural basis . The components of a tensor T are the coefficients of the tensor with respect to the basis obtained from a basis {e i} for V and its dual {εj}, i.e.Using the properties of the tensor product, it can be shown that these components satisfy the transformation law for a type (m,n) tensor. Moreover, the universal property of the tensor product gives a 1-to-1 correspondence between tensors defined in this way and tensors defined as multilinear maps.OperationsThere are a number of basic operations that may be conducted on tensors that again produce a tensor. The linear nature of tensor implies that two tensors of the same type may be added together, and that tensors may be multiplied by a scalar with results analogous to the scaling of a vector. On components, these operations are simply performed component for component. These operations do not change the type of the tensor, however there also exist operations that change the type of the tensors.Raising or lowering an indexMain article: Raising and lowering indicesWhen a vector space is equipped with an inner product (or metric as it is often called in this context), operations can be defined that convert a contravariant (upper) index into a covariant (lower) index and vice versa. A metric itself is a (symmetric) (0,2)-tensor, it is thus possible to contract an upper index of a tensor with one of lower indices of the metric. This produces a new tensor with the same index structure as the previous, but with lower index in the position of the contracted upper index. This operation is quite graphically known as lowering an index.Conversely the matrix inverse of the metric can be defined, which behaves as a (2,0)-tensor. This inverse metric can be contracted with a lower index to produce an upper index. This operation is called raising an index.ApplicationsContinuum mechanicsImportant examples are provided by continuum mechanics. The stresses inside a solid body or fluid are described by a tensor. The stress tensor and strain tensor are both second order tensors, and are related in a general linear elastic material by a fourth-order elasticity tensor. In detail, the tensor quantifying stress in a 3-dimensional solid object has components that can be conveniently represented as a 3×3 array. The three faces of a cube-shaped infinitesimal volume segment of the solid are each subject to some given force. The force's vector components are also three in number. Thus, 3×3, or 9 components are required to describe the stress at this cube-shaped infinitesimal segment. Within the bounds of this solid is a whole mass of varying stress quantities, each requiring 9 quantities to describe. Thus, a second order tensor is needed.If a particular surface element inside the material is singled out, the material on one side of the surface will apply a force on the other side. In general, this force will not be orthogonal to the surface, but it will depend on the orientation of the surface in a linear manner. This is described by a tensor of type (2,0), in linear elasticity, or more precisely by a tensor field of type (2,0), since the stresses may vary from point to point.Other examples from physicsCommon applications include∙Electromagnetic tensor(or Faraday's tensor) in electromagnetism∙Finite deformation tensors for describing deformations and strain tensor for strain in continuum mechanics∙Permittivity and electric susceptibility are tensors in anisotropic media∙Four-tensorsin general relativity (e.g. stress-energy tensor), used to represent momentum fluxes∙Spherical tensor operators are the eigen functions of the quantum angular momentum operator in spherical coordinates∙Diffusion tensors, the basis of Diffusion Tensor Imaging, represent rates of diffusion in biologic environments∙Quantum Mechanicsand Quantum Computing utilise tensor products for combination of quantum statesApplications of tensors of order > 2The concept of a tensor of order two is often conflated with that of a matrix. Tensors of higher order do however capture ideas important in science and engineering, as has been shown successively in numerous areas as they develop. This happens, for instance, in the field of computer vision, with the trifocal tensor generalizing the fundamental matrix.The field of nonlinear optics studies the changes to material polarization density underextreme electric fields. The polarization waves generated are related to the generating electric fields through the nonlinear susceptibility tensor. If the polarization P is not linearly proportional to the electric field E, the medium is termed nonlinear. To a good approximation (for sufficiently weak fields, assuming no permanent dipole moments are present), P is given by a Taylor series in E whose coefficients are the nonlinear susceptibilities:Here is the linear susceptibility, gives the Pockels effect and secondharmonic generation, and gives the Kerr effect. This expansion shows the way higher-order tensors arise naturally in the subject matter.Generalizations[edit]Tensors in infinite dimensionsThe notion of a tensor can be generalized in a variety of ways to infinite dimensions. One, for instance, is via the tensor product of Hilbert spaces.[15]Another way of generalizing the idea of tensor, common in nonlinear analysis, is via the multilinear maps definition where instead of using finite-dimensional vector spaces and their algebraic duals, one uses infinite-dimensional Banach spaces and their continuous dual.[16] Tensors thus live naturally on Banach manifolds.[17]Tensor densitiesMain article: Tensor densityIt is also possible for a tensor field to have a "density". A tensor with density r transforms as an ordinary tensor under coordinate transformations, except that it is also multiplied by the determinant of the Jacobian to the r th power.[18] Invariantly, in the language of multilinear algebra, one can think of tensor densities as multilinear maps taking their values in a density bundle such as the (1-dimensional) space of n-forms (where n is the dimension of the space), as opposed to taking their values in just R. Higher "weights" then just correspond to taking additional tensor products with this space in the range.In the language of vector bundles, the determinant bundle of the tangent bundle is a line bundle that can be used to 'twist' other bundles r times. While locally the more general transformation law can indeed be used to recognise these tensors, there is aglobal question that arises, reflecting that in the transformation law one may write either the Jacobian determinant, or its absolute value. Non-integral powers of the (positive) transition functions of the bundle of densities make sense, so that the weight of a density, in that sense, is not restricted to integer values.Restricting to changes of coordinates with positive Jacobian determinant is possible on orientable manifolds, because there is a consistent global way to eliminate the minus signs; but otherwise the line bundle of densities and the line bundle of n-forms are distinct. For more on the intrinsic meaning, see density on a manifold.SpinorsMain article: SpinorStarting with an orthonormal coordinate system, a tensor transforms in a certain way when a rotation is applied. However, there is additional structure to the group of rotations that is not exhibited by the transformation law for tensors: see orientation entanglementand plate trick. Mathematically, the rotation group is not simply connected. Spinors are mathematical objects that generalize the transformation law for tensors in a way that is sensitive to this fact.Einstein summation conventionThe Einstein summation convention dispenses with writing summation signs, leaving the summation implicit. Any repeated index symbol is summed over: if the index i is used twice in a given term of a tensor expression, it means that the term is to be summed for all i. Several distinct pairs of indices may be summed this way.。

张量分析简答题

22
张量分析
Tensor Analysis
x2
x1'
x2' x2
x
' 2
e2'
e2 e1'
x1' x1
e1
令：αi' j cos(ei' ,e j )
x1
( i' , j 1,2 )
则：αi' j

ccooss((ee21''
,e1 ) ,e1 )
cos(e1' cos(e2'
标为哑指标。如：
ai xi (i 1,2, n)
a1x1 a2 x2 an xn
n i 1
ai
xi
又如： ii jj 11 22 33 x y z
11
张量分析
Tensor Analysis
1
求和约定仅对字母指标有效，如 33 z
Aij jk Aik
ij jk ik
ij jk kl il
xi x j
xi, j
ij
aii a jk
jk
18
张量分析
Tensor Analysis
§A－2 张量的定义和代数运算
1. 矢量的基本运算
矢量a 分量ai
a a1e1 a2e2 a3e3 aiei

23

31 32 33
x xy xz
yx
y

yz

zx zy z
10
张量分析
Tensor Analysis

张量分析书籍附详尽易懂

n个
称为n维仿射空间。E n 中旳每一种元素称为点。
记：
o (0, ,0),
x (x1,, xn ) ,
(x1, , xn )
且分别称为放射空间旳原点、位置矢量和负矢量。
对于n维仿射空间，全部旳位置矢量构成一种集合：
V0 x (x1,, xn ) xi , xi F,1 i n
(1 t)(1,1) t(1,1) a t b
(1 2t,1 2t) a t b
当 t b 时：
(2t 1,2t 1) (1,1)
当 t a 时：
(2t 1,2t 1) (1,1)
由此可得 a 0 ，b 1 。显然 r1 等 r2 价。
r1 与 r5 ： (取 s b5 b1 )
域上旳矢量空间。且仍记为V0 。
数域上旳矢量空间V0 具有如下性质：x, y, z V0 ,、 F
（1）
x yyx
（2）
(x y) z x ( y z)
（3）V0中存在称为有关加法旳单位元素o，使得：
xo x
x V0
（4）V0中每一种元素x都存在唯一旳(-x )，使得：
x (x) o
当t=b时：位置矢量标
定b点。即：
S
(4b 2,3 2b) (2,1)
由此拟定b=1 。
x2
当t=a时：位置矢量标
3
2
定a点。即：
1
(4a 2,3 2a) (1,1.5 )
由此拟定a=0.75 。
图中画出了计算成果。
x2 3
2 u ab
1
2 (a)
u xy
x1
4
6
u xy u ab
1
2
。 Vx空间中旳矢量称为约束矢量。

(完整版)张量分析中文翻译

张量张量是用来描述矢量、标量和其他张量之间线性关系的几何对象。

这种关系最基本的例子就是点积、叉积和线性映射。

矢量和标量本身也是张量。

张量可以用多维数值阵列来表示。

张量的阶（也称度或秩）表示阵列的维度，也表示标记阵列元素的指标值。

例如，线性映射可以用二位阵列--矩阵来表示，因此该阵列是一个二阶张量。

矢量可以通过一维阵列表示，所以其是一阶张量。

标量是单一数值，它是0阶张量。

张量可以描述几何向量集合之间的对应关系。

例如，柯西应力张量T 以v 方向为起点，在垂直于v 终点方向产生应力张量T(v)，因此，张量表示了这两个向量之间的关系，如右图所示。

因为张量表示了矢量之间的关系，所以张量必须避免坐标系出现特殊情况这一问题。

取一组坐标系的基向量或者是参考系，这种情况下的张量就可以用一系列有序的多维阵列来表示。

张量的坐标以 “协变”（变化规律）的形式独立，“协变”把一种坐标下的阵列和另一种坐标下的阵列联系起来。

这种变化规律演化成为几何或物理中的张量概念，其精确形式决定了张量的类型或者是值。

张量在物理学中十分重要，因为在弹性力学、流体力学、广义相对论等领域中，张量提供了一种简洁的数学模型来建立或是解决物理问题。

张量的概念首先由列维-奇维塔和格莱格里奥-库尔巴斯特罗提出，他们延续了黎曼、布鲁诺、克里斯托费尔等人关于绝对微分学的部分工作。

张量的概念使得黎曼曲率张量形式的流形微分几何出现了替换形式。

历史现今张量分析的概念源于卡尔•弗里德里希•高斯在微分几何的工作，概念的制定更受到19世纪中叶代数形式和不变量理论的发展[2]。

“tensor ”这个单词在1846年被威廉·罗恩·哈密顿[3]提及，这并不等同于今天我们所说的张量的意思。

[注1]当代的用法是在1898年沃尔德马尔·福格特提出的[4]。

“张量计算”这一概念由格雷戈里奥·里奇·库尔巴斯特罗在1890年《绝对微分几何》中发展而来，最初由里奇在1892年提出[5]。

张量分析课件

P = ∑αij Ej （i=1,2,3） i
j =1
3
Pi′ = ∑ α i′j′ E j′ （i'=1,2,3）
j ′ =1
3
代入
将一阶张量Ej和Pi的变换规律
Pi′ = ∑ Ai′i Pi
3
代入
E j′ = ∑ Aj ′j E j
j =1
i =1 3
∑A
i =1
3
i ′i i
P = ∑∑ α i′j′ Aj′j E j
证：刚体定轴转动:
ω
(Z轴)转轴
刚体
(
)
v τi A ni O′ ri
v
刚体定轴转动
r2 r r I 质点：ij = m(rij δ ij − ( r )i ( r ) j ) O
v Ri
= m(δ ij xk xk − xi x j ) (i, j, k=1, 2, 3)
例3. 设质量为m的质点位于点（x1, x2, x3）, 证明在正交变换下，由九个分量构成的一个物理量Iij是一个二阶张量, 其中： I ij = m(δ ij xk xk − xi x j ) (i, j=1, 2, 3) —称Iij为质点的惯性积，有Iij定义的物理量叫惯性矩. 证：质点：I ij = m(δ ij xk xk − xi x j ) (i, j, k=1, 2, 3) 九个分量:
δij在坐标变换后，其各个分量的值不变. 即在任意坐标系中按上式定义的二价对称δ符号是一个二阶张量.
例3. 设质量为m的质点位于点（x1, x2, x3）, 证明在正交变换下，由九个分量构成的一个物理量Iij是一个二阶张量, 其中： I ij = m(δ ij xk xk − xi x j ) (i, j=1, 2, 3) —称Iij为质点的惯性积，有Iij定义的物理量叫惯性矩.

张量分析-第1讲LJ

a2 F3 a3 F2 a c b1 a b c1 a3 F1 a1 F3 a c b2 a b c2 a1 F2 a2 F1 a c b3 a b c3
所以有： a b c a c b a b c
g1和g 2
g1和g 2 不是单位矢量，即它们有量纲的，一般地说，
其长度也不为单位长度。此外它们也并不正交。矢量F可以在 g1和g 2 上分解:
F F g1 F g 2
1 2
(平行四边形法则)
则有: F g 1 F 1g 1 g 1 F 2 g 2 g 1
F g 1 F 1g 1 g 1 F 2 g 2 g 1
e2 b2 c2
e3
e3 b3 b2 c3 b3 c2 e 1 b3 c1 b1c3 e 2 b1c2 b2 c1 e 3 c3
b3 a 2 F3 a3 F2 e 1 a3 F1 a1 F3 e 2 a1 F2 a 2 F1 e 3 F3
j 1
F2 ' e 2 ' e1 F1 e 2 ' e 2 F2 e 2 ' e 3 F3 2 ' j F j
j 1 3
3
F3' e 3' e1 F1 e 3' e 2 F2 e 3' e 3 F3 3' j F j
j 1
矢量场函数的散度: 矢量场函数的旋度:
i F x Fx j y Fy
Fx Fy Fz F z y x
k Fz Fy Fx Fz Fy Fx i k j y z y z z x x Fz

《张量分析本科》课件

2
流体力学
流体力学中的张量可描述液体和气体的流动性质，从而帮助工程师设计和优化流体系统。
3
材料科学
张量在材料的力学行为、热膨胀和磁性等方面的研究中起着重要作用，有助于材料性能的改进。
经济学中的张量应用
金融风险评估市场分析关联性，对风险评估和投资决策具有重要意义。
《张量分析本科》PPT课件
这个课程将介绍张量的定义、基本概念、运算和性质，以及它在物理学、工程学和经济学等领域的应用。
张量的定义和基本概念
张量是一个多维数组，具有特定的变换规律。它在数学和物理学中扮演着重要角色，能够描述物体在各个方向上的变化。
张量的运算和性质
张量可以进行加法、乘法等运算，还具有一些特殊的性质，如对称性、反对称性和行列式等。这些运算和性质是研究和应用张量的基础。
学科交叉
张量分析作为一门综合性学科，促进了不同学科之间的交流与合作，推动了学科发展的跨越性进展。
学习资源推荐
1 书籍和教材推荐
2 网上教程和视频
《张量分析导论》、《张量分析教程》等是学习和研究张量分析的重要参考资源。
有许多免费的网上教程和视频，可以帮助初学者快速入门和掌握张量分析的基本概念和应用。
张量在市场需求、价格和产量之间的关系分析中，能够提供深入洞察和科学决策支持。
张量分析可以用于挖掘大规模数据集中的模式和趋势，为经济预测和决策提供准确和可靠的依据。
张量分析的重要性
科学研究
张量分析在各个学科的科学研究中发挥着重要作用，帮助解决复杂问题和揭示自然规律。
技术发展
随着科技的发展和应用领域的拓展，张量分析为新技术的发展提供了关键理论基础。
张量的坐标表示和变换规律

张量分析

张量分析研一熊焕君 2017.9.281.引论：我们对标量和矢量都非常熟悉。

标量是在空间中没有方向的量，其基本特征是只需要一个数就可以表示，且当坐标系发生转动时这个数保持不变，因此也称其为不变量。

而矢量是个有方向的量，三维空间中矢量需要一组三个数（分量）来表示，其基本特征是当坐标系发生转动时，这三个数按一定规律而变化。

然而在数学物理问题中，还常出现一些更为复杂的量，如描述连续体中一点的应力状态或一个微元体的变形特征等，仅用标量和矢量不足以刻画出他们的性质。

要描述这些量则有必要将标量和矢量的概念加以引申和扩充，即引入新的量——张量。

在概念上，张量和矢量有许多类同之处。

一方面张量也表示某一客观存在的几何量或物理量，显然张量作为一个整体是与描述它所选取的坐标系无关，可像矢量代数那样，用抽象法进行描述；另一方面也可像矢量一样采用坐标法进行描述，此时张量包含有若干个分量元素，各个分量的取值与具体的坐标系相关联。

张量的主要特征是，在坐标系发生变化时，其分量取值遵守着一定的转化定律。

张量方法的核心内容是研究一个复杂的量集坐标转换规律。

我们知道，一个物理定律如果是正确的，就必须不依赖于用来描述它的任何坐标系，张量方法就是既采用坐标系，而又摆脱具体坐标系的影响的不变方法。

于是我们可以在简单的直角坐标系中建立描述某一运动法则的支配方程，如果需要可以用张量方法将其转换到任意一个曲线坐标系中去。

例如对于很大一类边值问题，若选用恰当的曲线坐标系，其边界条件可以简化的表达，那么我们就可以将支配方程用张量方法转化到所采用的坐标系中来，从而使问题的求解容易处理。

2.记号与约定张量是包含有大量分量元素的复杂量集，必须使用适当的记号和约定，才能使其表达形式简化紧凑，从而使分析和讨论有序地进行。

从某种意义上讲，可以说张量是对记号的研究。

所以我们必须熟悉各种约定记号，才能对张量这个工具运用自如。

在张量方法中对一个量的标记采用字母标号法。

数学中的张量分析方法

数学中的张量分析方法在数学中，张量分析是一种用于描述多维空间中变量关系的数学工具。

它在许多领域中被广泛应用，包括物理学、工程学、计算机科学和经济学等。

本文将介绍张量的基本概念和常见的应用方法。

一、张量的定义和性质1. 张量的定义张量是一个多维数组，可以表示为多个分量的组合。

在欧几里德空间中，一阶张量是向量，二阶张量是矩阵。

高阶张量可以看做是多个矩阵的组合。

2. 张量的性质张量具有坐标系无关性，即其分量在不同坐标系下具有相同的转换法则。

这使得张量在描述物理量时具有普适性和通用性。

二、张量的运算法则1. 张量的加法和减法张量的加法和减法都是对应分量相加或相减。

要求参与运算的张量具有相同的维度。

2. 张量的数乘张量的数乘是将每个分量都乘以一个标量。

数乘并不改变张量的维度。

3. 张量的张量积张量的张量积是两个张量的分量进行乘积并按照一定规则相加得到的新张量。

它在向量叉乘、矩阵乘法等问题中有广泛应用。

4. 张量的缩并运算张量的缩并是对张量的某些分量进行求和，并将结果保留在一个新的张量中。

它常用于求解线性方程组、协方差矩阵等问题。

三、张量的应用举例1. 物理学中的应用张量在物理学中有广泛的应用，如流体力学中的应力张量、电动力学中的麦克斯韦张量等。

它们描述了物质在空间中的运动和相互作用。

2. 工程学中的应用张量在工程学中用于描述物体的形变、应力分布等。

它在结构力学、弹性力学、热传导等领域中有着重要的作用。

3. 计算机科学中的应用张量在图像处理、模式识别、机器学习等领域中被广泛应用。

例如，卷积神经网络中的卷积操作就可以用张量运算进行描述。

4. 经济学中的应用张量在经济学中用于描述多个经济变量之间的关系。

它可以用来分析供求关系、生产函数等经济现象。

结语：张量分析作为一种重要的数学工具，为我们研究和解决各种问题提供了强有力的帮助。

通过对张量的定义、性质和运算法则的了解，我们可以更好地理解和应用张量，进而推动科学的发展和进步。

张量分析-第2讲

张量分析第2讲张量分析张量分析及其应用张量分析pdf张量分析黄克智pdf张量分析视频物理学中的张量分析张量分析简明教程张量分析及其应用pdf弹性力学与张量分析
张量分析 ( Tensor analysis)
华中科技大学力学系罗俊
版权所有 2011 华中科技大学力学系
1
1.5 坐标变换
已知某物理量或数学物理方程在一个坐标系的表达式, 求它在其它坐标系的相应形式。旧坐标系新坐标系
10
3. n阶张量设物理量T共有3 个分量，且满足坐标变换关系:
n
T
' ' i1 i n
T
' ' i1 in
' i1 j1
' i2 j2
' in j2
j1 j n
则称T为n阶张量。 T
称为n阶张量T的逆变分量。
总共多少种分量? 每种多少个分量? 坐标变换关系如何写? 指标升降关系如何写?
T ab 是二阶张量，将a, b在基矢上分解 :
T ab a i g i b j g j ai g i b j g j a i b j g i g j ai b j g i g j
相应地:
T T g i g Ti g g j T g i g j Tij g g
5
坐标变换系数求法
协变变换旧---新
j x i 'j i ' x
j' x i j ' i x
逆变变换
i' x ij ' j x
i x ij ' j ' x
互逆
新---旧
4. 矢量分量的坐标变换关系根据基矢的坐标变换关系可以得到矢量分量的坐标变换关系:

第二章张量分析

P也可用另外三个变量 x，1' x，2' 来x 表3' 示，即
P P x1' , x 2' , x 3' P x i'
这种坐标系记为 xi。' 这两组变量
x1 , 和x 2 , x 3 表示x同1' 一, x空2' , x 3'
间点的位置。两者由下列坐标变换联系起来：
xi xi xi'
aigi a jg j aia j gi g j
aiaj 0
令
gij gi g j
g ij g i g j
gi j gi g j g j gi
它们分别称为协变度量张量、逆变度量张量和混合度量张量
考虑到矢量a的任意性 g ji gi g j i j
可知：基矢量 g与i 是g i 正交的，它们称为互逆基矢量互逆基矢量间具有下列关系：
gig j g k gi g j g k gig j g k eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为和ijk 。ijk
由此定义可知
123 g1g 2g3
123 g1g 2g3
对于矢量 a 0 ，则有
a 2 a a a i g i a j g j a i a j g i g j ai gi a j g j ai a j gi g j
(ii) x 2' (常数 C)为2 通过z轴的平面； (iii) x3' (常z 数 C)3为垂直于z轴的平面；
和坐标曲线：
(i) x1' 和r C1 x的2' 交线 (zC线2 )是直线； (ii) x 2' 和 C2 的x3'交线z (r线C3)是直线；

(完整版)《张量分析》报告

写在字符右上角的指标，例如yj 中的j 称为上标；使用上标或下标的涵义是不同的。

用作下标或上标的拉丁字母或希腊字母，除非作了说明，一般取从1到n 的所有整数，其中n 称为指标的范围。

1.2求和约定若在一项中，同一个指标字母在上标和下标中重复出现，则表示要对这个指标遍历其范围1，2，3，…n 求和。

这是一个约定，称为求和约定。

不求和的指标称为自由指标。

tensor(张量)

张量（Tensor）是一种多维数组或矩阵的数学对象，广泛应用于数学、物理学和计算机科学等领域。

在机器学习和深度学习中，张量是存储和处理数据的主要数据结构。

在计算机科学中，张量可以被看作是一种多维数组，具有固定形状（即各个维度的大小）和数据类型。

例如，0维张量是一个标量（scalar），1维张量是一个向量（vector），2维张量是一个矩阵（matrix），3维及以上的张量则可看作是更高维度的数组。

在深度学习中，张量是神经网络的输入、输出和参数的表示形式。

通过张量，神经网络可以对数据进行传递和处理。

张量的形状描述了数据的维度，而张量的数据类型决定了数据的表示方式（如整数、浮点数等）。

张量可以进行各种数学运算，如加法、减法、乘法、除法等。

在深度学习中，通常使用张量来表示输入数据、模型参数、损失函数和梯度等。

常见的机器学习框架（如TensorFlow和PyTorch）提供了张量操作的库函数，使得处理张量变得更加高效和方便。

通过这些库函数，我们可以对张量进行各种数学运算、逐元素操作、矩阵乘法等，从而构建和训练复杂的神经网络模型。

总之，张量是一种多维数组或矩阵的数学对象，广泛应用于数学、物理学和计算机科学等领域。

在机器学习和深度学习中，张量是存储和处理数据的主要数据结构，用于表示输入、输出、参数和梯度等。

张量分析初学者必看

A 张量分析
x1 x1 cos x2 sin x2 x1 sin x2 cos
x1 x1 cos x2 sin x2 x1 sin x2 cos
坐标变换式
xi ii xi xi ii xi
ii cos(xi , xi ) ii cos(xi , xi )
Aijk xi y j zk
代表27项的和式
二、自由指标
§ A-1 指标符号
A11 x1 A12 x2 A13 x3 b1 A21 x1 A22 x2 A23 x3 b2 A31 x1 A32 x2 A33 x3 b3
筒写为
Aij x j bi
j ——哑指标 i——自由指标，在每一项中只出现一次，一个公式中必须相同
A 张量分析
张量的定义——在坐标系变换时,满足如下变
换关系的量称为张量
ijkl ii jjkk llijkl
张量的阶——自由指标的数目
不变性记法
ijkl ei e j ek el
§A-3 坐标变换与张量的定义
一、加(减)法
§A-4 张量的代数运算
四、两个张量的点积
A 张量分析
两个张量点积的结果仍为张量。新张量的阶数是原两个张量的阶数之和减 2
A B ( Aijk ei e j ek ) ( Brs t er es et ) Aijk Brs t ei e j kr es et Aijk Bkst ei e j es et S
§ A-1 指标符号三、 Kronecker- 符号和置换符号 (Ricci符号) Kronecker-符号定义

张量

本条目或章节存有多项争议或问题。

请协助改善本条目或在讨论页针对议题发表看法。

∙类似爱好者站点。

自2010年12月起标示本模板。

∙品质低劣，需要完全重写。

自2010年12月起标示本模板。

∙可能需要进行清理，以符合维基百科的质量标准。

自2010年12月起标示本模板。

目录[隐藏]∙ 1 背景知识∙ 2 方法的选择∙ 3 例子∙ 4 方法细节∙ 5 张量密度∙ 6 张量阶∙7 参阅o7.1 记法常规o7.2 基础o7.3 应用∙8 外部链接∙9 参考书籍∙10 张量软件[字的列表来表述。

最后，象二次型这样的量需要用多维数组来表示。

后面这些量只能视为张量。

实际上，张量的概念相当广泛，可以用于上面所有的例子；标量和向量是张量的特殊情况。

区别标量和向量以及区别这两者和更一般的张量的特征是表示它们的数组的指标的个数。

这个个数称为张量的阶。

这样，标量是0阶张量(不需要任何指标)，而向量是一阶张量。

张量的另外一个例子是广义相对论中的黎曼曲率张量，它是维度为<4,4,4,4>(3个空间维度 + 时间维度 = 4个维度)的4阶张量。

它可以当作256个分量(256 = 4 × 4 × 4 × 4)的矩阵(或者向量，其实是个4维数组)。

只有20个分量是互相独立的，这个事实可以大大简化它的实际表达。

[编辑]方法细节有几种想象和操作张量的等价方法；只有熟悉了这个课题，其内容是等价的这个事实才会变得明显。

现代(无分量)方法把张量首先视为抽象对象，表达了多线性概念的某种确定类型。

其著名的性质可以从其定义导出，作为线性映射或者更一般的情况；而操作张量的规则作为从线性代数到多重线性代数的推广出现。

这个处理方法在高等的研究中大量的取代了基于分量的方法，其方式是更现代的无分量向量方法在基于分量的方法用于给出向量概念的基本引例之后就取代了传统的基于分量的方法。

可以说，口号就是“张量是某个张量空间的元素”。

张量分析(Tensor Analysis)

(完整版)《张量分析》报告

张量分析基础

张量分析(Tensor Analysis)

第二章 张量(清华大学弹塑性力学)

张量分析翻译 英文原文

张量分析简答题

张量分析书籍附详尽易懂

(完整版)张量分析中文翻译

张量分析课件

张量分析-第1讲LJ

《张量分析本科》课件

张量分析

数学中的张量分析方法

张量分析-第2讲

第二章 张量分析

(完整版)《张量分析》报告

tensor(张量)

张量分析初学者必看

张量

第二章张量(清华大学弹塑性力学)

张量分析翻译英文原文

第二章张量分析