映射和集合类型
集合与映射关系

集合与映射关系集合与映射关系是数学中的重要概念,它们在各个领域都有广泛应用。
本文将介绍集合与映射关系的定义、性质以及一些实际应用。
一、集合的定义与性质集合是由一些确定的元素所构成的整体。
集合的定义不依赖于元素的进一步性质,而只关注元素的归属关系。
通常用大写字母表示集合,例如A、B、C等。
集合有以下几个性质:1. 唯一性:集合中的元素是唯一的,不存在重复元素。
2. 无序性:集合中的元素没有顺序之分,即元素之间的排列顺序不影响集合的本质。
3. 全称性:集合包含了全部元素,即集合没有漏掉任何一个元素。
二、映射关系的定义与性质映射关系是将一个集合中的元素对应到另一个集合中的元素的规则。
映射关系通常用小写字母表示,例如f、g、h等。
映射关系有以下几个性质:1. 单射性:对于映射关系中的每个元素,它在定义域中只有唯一的对应元素。
2. 满射性:对于映射关系中的每个元素,它都有一个对应的元素在值域中。
3. 双射性:既满足单射性又满足满射性的映射关系。
三、集合与映射关系的应用集合与映射关系的应用广泛存在于数学、计算机科学以及自然科学等领域。
1. 在数学中,集合和映射关系是研究各个数学分支的基础。
例如在集合论中,我们可以通过集合与映射关系来定义其他数学对象,如数、矩阵等。
在代数学中,通过映射关系可以将一个集合映射到另一个集合,进而进行数学运算。
2. 在计算机科学中,集合与映射关系是数据结构和算法设计的基础。
例如集合可以用来表示一组数据,映射关系可以用来描述不同数据之间的对应关系。
这些概念在数据库、图论以及人工智能等领域都有广泛应用。
3. 在自然科学中,集合与映射关系可以用来描述物理系统中的元素和它们之间的相互作用。
例如在统计力学中,我们可以用集合和映射关系来描述分子之间的相互作用及其对宏观物理性质的影响。
总结:集合与映射关系是数学中重要的概念,能够描述元素间的归属关系和对应关系。
它们不仅在数学中有广泛的应用,还在计算机科学和自然科学等领域发挥着重要作用。
简述序列类型、集合类型和映射类型的区别。

简述序列类型、集合类型和映射类型的区别。
序列类型、集合类型和映射类型的区别在于他们在所存储的元素上的不同。
序列类型:序列类型是按照索引(index)存储元素的,也就是说,每个元素都有一个唯一的索引,而且元素以插入顺序存储,因此有序。
序列类型有列表(list)、元组(tuple)等。
集合类型:集合类型保存的元素是不重复的,没有索引,而且无序。
集合类型有集合(set)等。
映射类型:映射类型是由键值对组成的,每个键值对都有一个唯一的键,也称为字典(dict)。
键值对无序且不重复。
集合与映射

1.3 考研真题1.3.1 考点分析
关于集合与映射的考查,集中在集合的表示和运算,以及函数的表示和函数的某些简单特性(周期性、奇偶性、单调性等)的证明.
不妨令m=min{f(a),f(b),m′},则对任意x∈[a,b],有m≤f(x)≤M.因此,在区间I的任何闭子区间上f(x)有界. 思考题1. 设f(x)对任意的x∈R有f(x)=f(x2),且f(x)在x=0和x=1 处连续,试证明f(x)在R上为常数.(上海交通大学,2003)
(1) 交换律A∪B=B∪A, A∩B=B∩A. (2) 结合律A∪(B∪D)=(A∪B)∪D, A∩(B∩D)=(A∩B)∩D. (3) 分配律A∪(B∩D)=(A∪B)∩(A∪D), A∩(B∪D)=(A∩B)∪(A∩D). (4) 对偶律(De Morgan公式)(A∪B)c=Ac∩Bc, (A∩B)c=Ac∪Bc.1.1.2 映射
(2) 单调函数. 对函数y=f(x),x∈D,若对任意x1,x2∈D,当x1<x2时成立f(x1)≤f(x2)(或f(x1)<f(x2)),则称函数f在D上单调增加(或严格单调增加),通常记作f↑(或f严格↑);若对任意x1, x2∈D,当x1<x2时成立f(x1)≥f(x2)(或f(x1)>f(x2)),则称函数f在D上单调减少(或严格单调减少),通常记作f↓(或f严格↓).
(3) 奇、偶函数.设函数f的定义域D关于原点对称,即x∈D-x∈D.如果对一切x∈D,成立f(-x)=f(x),则称f是偶函数;如果对一切x∈D,成立f(-x)=-f(x),则称f是奇函数.
第1章 集合、映射与关系

≜
{������ ∶ ������, ������ ∈ ������}称为������形成的关于������的等价类或以������为代
例 : 设 ������ = {������, ������, ������, ������, ������} , ������ 上 的 一 个 等 价 关 系 ������ =
• 补集运算(余集运算)
基本集合:限制在一定范围内的研究对象的全体形成 的集合称为基本集合(全集). 补集(余集):给定基本集合������及其子集������ (⊂ ������), 称 差集������\������为集������的补集(余集), 记������������ = ������\������.
第1章 集合、映射与关系
1.1 集合
1、集合的概念
• 若干个 (有限或无限) 确定的事物的全体叫做一个集合, 通常用大写字母������, ������, ������, ⋯ 表示集合. • 组成一个集合的事物叫做这个集合的元素, 用小写字 母 ������, ������, ������, ⋯表示集合的元素.
① 元������与元������有关系������即(������, ������) ∈ ������时, 简记为������������������.
② 若������, ������ 之间的二元关系������ 具有性质∀������ ∈ ������, ∃! ������ ∈ ������ , 使得������������������, 则关系������决定了������到������的一个映射. 因此, 二元关系是映射概念的推广.
• 多个集合的直积(笛卡尔积) ������1 × ������2 × · · ·× ������������ = { ������1 , ������2 , ⋯ , ������������ ∶ ������������ ∈ ������������ , ������ = 1, 2, ⋯ , ������}
高中数学奥赛辅导 第六讲 集合与映射

数学奥赛辅导 第六讲 集合与映射知识、方法、技能这一讲主要介绍有限集的阶,有限集上的映射及其性质,这些在与计数有关的数学竞赛问题中应用极广,是参赛者必不可少的知识Ⅰ.有限集元素的数目 1.有限集的阶有限集A 的元素数目叫做这个集合的阶,记作|A|[或n(A)]. 2.集族的阶若M 为由一些给定的集合构成的集合,则称集合M 为集族.设A 为有限集,由A 的若干个子集构成的集合称为集合A 的一个子集族,求满足一定条件的集族的阶是一类常见的问题.显然,若|A|=n ,则由A 的所有子集构成的子集族的阶为2n . Ⅱ.映射,映射法定义1 设X 和Y 是两个集合(二者可以相同).如果对于每个X x ∈,都有惟一确定的Y y ∈与之对应,则称这个对应关系为X 到Y 的映射.记为.Y y X x Y X ∈→∈→或这时,Y x f y ∈=)(称为X x ∈的象,而x 称为y 的原象,特别当X 和Y 都是数集时,映射f 称为函数.定义2 设f 为从X 到Y 的一个映射.(1)如果对于任何x 1、.),()(,,21212为单射则称都有f x f x f x x X x ≠≠∈ (2)如果对于任何Y y ∈,都有X x ∈,使得f (x )=y ,则称f 为满射; (3)如果映射f 既为单射又为满射,则称f 为双射;(4)如果f 为满射且对任何Y y ∈,恰有X 中的m 个元素x 1、x 2、…x m ,使得.)(,,,2,1,)(倍数映射的倍数为为则称m f m i y x f i ==定理1 设X 和Y 都是有限集,f 为从X 到Y 的一个映射, (1)如果f 为单射,则|X|≤|Y| (2)如果f 为满射,则|X|≥|Y| (3)如果f 为双射,则|X|=|Y|(4)如果f 为倍数为m 的倍数映射,则|X|=m|Y|. 这个定理的结果是显然的.定理2 设有限集f a a a A n },,,,{21 =是A 到A 上的映射,),()(1x f x f =),,)](([)(1*+∈∈=N r A x x f f x f r r 则f 是一一映射(即双射)的充要条件是:对任意).11,()(,)(1,,-≤≤∈≠=≤≤∈∈**i i i s i i m i i i m s N s a a f a a f n m N m A a i 而使得存在证明:必要性.若f 是双射,则i i a a f ==)(1(此时m i =1),或者.)(11i i i a a a f ≠=在后一种情形下,不可能有.)()(1112i i i a a f a f ==否则,a i 1在A 中有两个原象a i 和a i 1,与f 是双射不合,而只可能有2222)(,,)(),2()(12i i i i i i i i i a a f a a a a f m a a f =≠===如果或者此时,则依同样的道理,不可能有或者此时而只可能有),3()(,,)()(33212====i i i i i i i m a a f a a a f a f213,,)(3i i i i i a a a a a f ≠=.如此等等.因为A 是有限集,所以经过有限次(设经过m 次)后,有i s i i m a ai f a a f i ≠=)(,)(而).11,(-≤≤∈*i m s N s这表明当f 是双射时,对任一A a i ∈都存在着映射圈:i im i i i a a a a a i →→→→-121在这个映射圈中,诸元素互异,且),1(1i i i a m n m 只有一个元素=≤≤充分性.如果对任意i i s i i m i i i i a a f a a f n m N m A a ≠=≤≤∈∈*)(,)(,1,,而使存在)1,(1-*≤≤∈i m s N s ,这说明从A 中任一元素a i 出发,都可以得到一个包含m i 个互异元素的映射圈,显然f 是双射.定理3 在命题1的条件下,若对i i m i i i a a f N m A a =∈∈*)(,,使存在,则对任意.)(,i i tm a a f N t i =∈*有这是明显的事实,证明从略.赛题精讲例1:设集合,30001|{},,14,20001|{≤≤=∈+=≤≤=y y B Z k k x x x A 集合||},,13B A Z k k y ⋂∈-=求.【解】形如4k +1的数的数可分三类:)(912,512,112Z l l l l ∈+++,其中只有形如12l +5的数是形如3k -1的数..167||},1997,,17,5{,1660),(20005121=⋂=⋂≤≤∈≤+≤B A B A l Z l l 所以所以得令例2:有1987个集合,每个集合有45个元素,任意两个集合的并集有89个元素,问此1987个集合的并集有多少个元素.【解】显然,可以由题设找到这样的1987个集合,它们都含有一个公共元素a ,而且每两个集合不含a 以外的公共元素.但是,是否仅这一种可能性呢?由任意两个集合的并集有89个元素可知,1987个集合中的任意两个集合有且仅有一个公共元素,则容易证明这1987个集合中必有一个集合中的元素a 出现在A 以外的45个集合中,设为A 1,A 2,…,A 45,其余的设为A 46,A 47,…,A 1996.设B 为A 46,…,A 1996中的任一个集合,且B a ∉,由题设B 和A ,A 1,A 2,…,A 45都有一个公共元素,且此46个元素各不相同,故B 中有46个元素,与题设矛盾,所以这1987个集合中均含有a .故所求结果为1987×44+1=87429.即这1987个集合的并集有87429个元素. 例3:集合n B B B A ,,,},9,2,1,0{21 =为A 的非空子集族,并且当,2||≤⋂≠j i B B j i 时 求n 的最大值.【解】首先考虑至多含三个元素的A 的非空子集族,它们共有175310210110=++C C C 个,这说明.175max ≥n下证,.175max ≤n 事实上,设D 为满足题设的子集族,若,,4||,B b B D B ∈≥∈设且 则B 与B-{b}不能同时含于D ,以B-{b}代B ,则D 中元素数目不变.仿此对D 中所有元素数目多于4的集合B 作相应替代后,集族D 中的每个集合都是元素数目不多于3的非空集合,故.175max ≤n .所以,.175max =n在许多问题中,计数对象的特征不明显或混乱复杂难以直接计数,这时可以通过适当的映射将问题划归为容易计数的对象,然后再解决,从而取得化难为易的效果.例4:设},,,2,1{n S =A 为至少含有两项的公差为正的等差数列,其项都在S 中且当将S 的其他元素置于A 中之后,均不能构成与A 有相同公差的等差数列.求这种A 的个数(只有两项的数列也视为等差数列) 【解】当k n 2=为偶数时,满足题中要求的每个数列A 中必有连续两项,使其前一项在集{1,2,…,k}和{k +1,k +2,…,2k }中各任取一数,并以二数之差作为公差可以作出一个满足要求的数列A.容易看出,这个对应是双射.故知A 的个数为.422n k = 当n =2k +1为奇数时,情况完全类似.惟一的不同在于这时第二个集合},2,1{n k k ++ 有k +1个元素.故A 的个数为.4/)1()1(2-=+n k k例5:设a n 为下述自然数N 的个数:N 的各位数字之和为n 且每位数字都只能取1、3或4.求证对每个自然数n ,a 2n 都是完全平方数.【证明】记各位数字之和为n 且每位数字都是1或2的所有自然数的集合为S n ,并记,3,2,1,||2121--+=≥===n n n n n f f f n f f f S 时有且当则这意味着{f n }恰为菲波那契数列.作对应'1M M S n →∍如下:先将M 的数字中自左至右的第一个2与它后邻的数字相加,其和作为一位数字;然后再把余下数字中第一个2与它后邻的数字相加,所得的和作为下一位数字;依此类推,直到无数再相加为止.所得的新自然数M′除最后一位数可能为2之外,其余各位数字均为1、3或4.若记所有M ′的集合为T n ,则容易看出,上述对应是由S n 到T n 的双射,从而有n n n f S T ==||||,且显然有,4,3,2=+=-n a a f n n n ①对于任一数字和为2n ,各位数字均为1或2的自然数M ,必存在正整数k ,使得下列两条之一成立:(1)M 的前k 位数字之和为n ;(2)M 的前k 位数字之和为n -1,第k +1位数字为2.则立即可得 ,3,2,2122=+=-n f f f n n n ② 由①和②得到,2122222--+==+n n n n n f f f a a),(122222----=-n n n n f a f a ③因为.0,2,4,2,12242432=-====f a f a a a 所以于是由③递推即得,,3,2,1,22 ==n f a n n即n a 2为完全平方数.应用映射还可以证明某些与计数相关的不等式和等式.这时可以通过分别计数来证明等或不等,也可以不计数而直接通过适当的映射来解决问题.例6:将正整数n 写成若干个1和若干个2之和,和项顺序不同认为是不同的写法,所有写法种数记为a (n ).将n 写成若干个大于1的正整数之和,和项顺序不同认为是不同的写法,所有写法的种数记为)(n β.求证对每个n ,都有).2()(+=n n βα【证法1】将每项都是1或2,各项之和为n 的所有数列的集合记为A n ,每项都是大于1的正整数,各项之和为n 的所有数列的集合记为B n ,则问题就是证明|,|||2+=n n B A 显然,只需在两集之间建立一个双射就行了.i k ik i i n m a m i i i a a a A a a a a 其余的其中设,1,2,),,,(212121≤<<≤≤====∈= 均为1且令.21n a a a m =+++1211i a a a b +++= ,,22112122121121+++++++++++=+++=+++=--m i i k ik i i k i i i a a a b a a a b a a a b k k k k),,,,,(121+=k k b b b b b①则定义.2+∈n B b2+∈→∍n n B b a A②则f 为双射.事实上,若a a A a a n '≠∈'且,,,则或者数列a 和a ′中的2的个数不同,或者2的个数相同但位置不全相同.无论哪种情形,由①和②知f a f b a f b 即不同与,)()('='=为单射,另一方面,对任何2+∈n B b 利用①式又可确定,n A a ∈使得,,)(为满射即f b a f =从而f 为由A n 到B n +2的双射.【证法2】使用证一中的记号.n n B A 和对于任意的令,),,,,(2121+-∈=n m m A a a a a a,,2;,1,).,,,(11121A a a A a a a a a a m n m m ∈'=∈'=='+-时当时当显然 容易看出,映射 n n n A A a af A ⋃∈'→∍++12是双射,故有).()1()2(n n n ααα++=+注意到2)2(,1)1(==αα,便知,)(n f n =α这里|f n |为菲波那契数列.对于任意的令2121),,,,(+-∈=n k k B b b b b b⎩⎨⎧>-=='--2)1,,,,(2),,,(121121k k k k k b b b b b b b b b b 当当则当,,,2;,2,21容易验证时当时时+∈'>∈'='=n k n k B b b B b b b 映射n n n B B b b B ⋃∈'→∍++12为双射,故有),()1()2(n n n βββ++=+==+n f n )2(β所以a (n )【证法3】显然有),4(2)2(),3(1)1(βαβα===即命题于n =1,2时成立.设命题于,.2,)1(1k n k n k k n =+=≥+≤既然命题于时命题成立须证当时成立令与之间的双射与与故存在时都成立.,,11312+++++f k k k k n f f B A B A k⎩⎨⎧>∈=+2),()()(1k k k k b a f A a a f a f 当当则f 为由.321的双射到+++⋃⋃n n k k B B A A对于任意的令和任意,),,,(),,,,(32212121+++-⋃∈'=∈=k k l k m m B B b b b b A a a a a a⎩⎨⎧==∈='+-,1,,2,),,,(1121m k m k m a A a A a a a a 当当 ⎩⎨⎧∈'∈+∈'∈=++++.,)1,,,)2,,,(34212421k k l k k l B b B b b b B b B b b b b 当当 43212:.:+++++∈→'∍⋃⋃∈'→∍k k k k k k B b b B B h A A a a A g 则映射都是双射,从而复合映射42:++∈→∍k k B b a A g f h为双射,故有)4()2(+=+k k βα,于是由数学归纳法知命题对所有自然数n 都成立.映射法还可以与其他方法结合起来使用,而且大多数竞赛题是这种类型.例如映射法可与抽屉原理、构造法、反证法等各种方法结合起来.例7:设oxyz 是空间直角坐标系,S 是空间中的一个有限点集,S x ,S y ,S z 分别是S 中所有点的坐标平面oyz ,ozx ,oxy 上的正投影所成的集合.求证.||||||||2z y x S S S S ⋅⋅≤(1992年IMO 试题5)【证明】对每点令,),(x S j i ∈∑∈=∈=ixS j i ijij TS S j i x j i x T ),(}},,(|),,{(显然有由柯西不等式有2),(2),(),(2||||||1||ij S j i x ijS j i S j i T S TS xxx∑∑∑∈∈∈⋅=⋅⋅≤①考虑集合},,|),{(),(2121),(ij ij ij ij ij S j i T t t t t T T T T V x∈=⨯⨯=∑∈其中显然,|V|=2),(||ij S j i T x∑∈定义映射f 如下z y S S i x j x j i x j i x V ⨯∈'→'∍)),(),,((),,(),,,(,不难看出f 为单射,因此有||||||z y S S V ⋅≤由①、②即得||||||||2z y x S S S S ⋅⋅≤.例8:设集合},10,,2,1{ =A A 到A 的映射f 满足下列两个条件: ①对任意;)(,30x x f A x =∈②对每个.)(,,291,a a f A a k Z k k ≠∈≤≤∈+使得至少存在一个求这样的映射的总数. (1992年日本奥林匹克预选赛题) 【解】注意到10=5+3+2,30=5×3×2.这提示我们将A 划分成三个不相交的子集},{},,{},,,,{2132154321c c b b b a a a a a A ⋃⋃=.因为f 满足条件①和②,所以f 是A 到A 上的双射,并且由定理2的证明过程得知A 中存在映射圈,因此,定义映射,)(,)(;)(,)(,)(,)(,)(:32211554433221b b f b b f a a f a a f a a f a a f a a f f ======= .)(,)(;)(122113c c f c c f b b f ===因为30是5、3、2的最小公倍数,故由定理2和定理3知f 是满足题目条件①和②惟一的一类映射.因此,f 的总数目相当于从10个元素中选取5个,再从剩下的5个中选取3个,最后剩下的两个也选上,它们分别作圆排列的数目,它等于.120960)!1)(!2)(!4(2235510=⋅⋅⋅C C C例9:设集合A={1,2,3,4,5,6},映射A A f →:,其三次复合映射f ·f ·f 是恒等映射,这样的f 有多少个? (1996年日本数学奥林匹克预选赛题)【解】因为集合A 上的三次复合映射是恒等映射,所以定理2和定理3推知符合条件的映射f 有三类:(1)f 是恒等映射;(2)A 中存在一个三元映射圈),,(互异c b a a c b a →→→,而其他三个元素是不动点; (3)A 中存在两个三元映射圈).,,,,,(互异和c b a c b a a c b a a c b a ''''→'→'→'→→→类型(1)的f 只有1个.对于类型(2),先从6个元素中选出3个元素20,,36=C c b a 的方法有种,又a 、b 、c 作圆排列有(3—1)!=2种,故这样的f 有20×2=40个.对于类型(3),首先6个元素平分成两组有10236=÷C 种分法,每组分别作圆排列又有(3—1)!(3—1)!=4种方式,所以这样的f 有10×4=40个. 综上所述,所求的f 有 1+40+40=81个.例10:把正三角形ABC 的各边n 等分,过各分点在△ABC 内作各边的平行线,得到的图形叫做正三角形ABC 的n 格点阵. (1)求其中所有边长为||1BC n的菱形个数; (2)求其中所有平行四边形的个数. (1988年国家集训队选拔考试题) 【解】延长AB 至.||1||||,,BC nC C B B C AC B ='='''使得至作出正三角形C B A ''的n+1格点阵(图I —3—1—1).边2+''n C B 上有个点,依次编码为0,1,2,…,n+1. 在△ABC 中边长为n1|BC|的菱形可以按边不平 行于BC 、AC 与AB 分为三类.容易看出,这三类 中菱形个数相同.边不平行BC 且边长为n1|BC|的 所有菱形集合记作S.由正整数1,2,…,n 组成 的所有有序的数对(i ,j ),i <j 所构成的集合记作T.很明显,,||2n C T =设菱形EFGH ∈S ,延长它的两条邻边HG 与GF ,分别交.),(,1,T j i n j i j i C B ∈≤<≤''则与于点令(i ,j )是菱形EFGH 在S 到T 的映射ϕ下的像,这样便建立了S 到T 的映射ϕ.容易验证,映射ϕ是双射.因此,,||||2n C T S ==所以所求的边长为n1|BC|的菱长个数为32n C . 其次,将平行四边形按边不平行于BC 、AC 与AB 分为三类,这三类的平行四边形个数应相同,边不平行BC 的所有平行四边形集合记作V.非负整数0,1,2,…,n+1构成的所有有序四元数组(i ,j ,k ,l ),10+≤<<<≤n l k j i 构成的集合记作W.很明显,42||+=n C W .设α是V 中平行的四边形,延长它的四条边分别交l k j i C B ,,,于点'',其中10+≤<<<≤n l k j i ,则ϕαββ的映射到在是令W V W l k j i .),,,(∈=下的像.这样便定义了V 到W 的一个映射ϕ.容易验证,ϕ是双射.因此,.||||42+==n C W V 从而所求平行四边形的个数为423+n C .。
集合类型

理解集合类集合类存放于java.util包中集合类存放都对象引用而非对象本身出于表达上便利我们称集合中对象就指集合中对象引用(reference)集合类型主要3种:set(集)、list(列表)和map(映射)其中List和Set接口都继承自Collection接口而Map接口和俩不同不继承于Collection 接口(1)集Set集(set)最简单一种集合它对象不按特定方式排序只简单把对象加入集合中就像往口袋里放东西对集中成员访问和操作通过集中对象引用进行所以集中不能重复对象集也多种变体可以处理方案排序等功能如TreeSet它把对象添加到集中操作将变为按照某种比较规则将其插入到序对象序列中它处理方案SortedSet接口也就加入了对象比较办法通过对集中对象迭代我们可以得到一个升序对象集合1:HashSet 能够快速定位一个元素但它要求存入HasgSet对象必须处理方案HashCode 办法2:TreeSet 将放入其中元素按序存放(2)列表ListList接口与其处理方案类容量可变列表可以按照索引访问集合中元素序集合列表数据结构中分别表现为:数组和向量、链表、堆栈、队列1:ArrayList:处理方案一个数组它规模可变并且能像链表一样被访问它提供功能类似Vector类但不同步它以Array方式处理方案List允许快速随机存取2:LinkedList:处理方案一个链表提供最佳顺序存取适合插入和移除元素由这个类定义链表也可以像栈或队列一样被解决(3)映射Map映射与集或列表明显区别映射中每个项都成对Map把键对象和值对象进行关联容器映射中存储每个对象都一个相关关键字(Key)对象关键字决定了对象映射中存储位置检索对象时必须提供相应关键字就像字典中查单词一样关键字应该唯一也就说Map中键对象不允许重复这为了保证查询结果一致性关键字本身并不能决定对象存储位置它需要对过一种散列(hashing)技术来解决产生一个被称作散列码(hash code)整数值散列码通常用作一个偏置量该偏置量相对于分配给映射内存区域起始位置由此确定关键字/对象对存储位置理想情况下散列解决应该产生给定范围内均匀分布值而且每个关键字应得到不同散列码1:HashMap:处理方案一个键到值映射哈希表通过键取得值对象允许存储空对象而且允许键空(由于键必须唯一当然只能一个)2:HashTable:处理方案一个映象所键必须非空为了能高效工作定义键类必须处理方案hashcode()办法和equal()办法这个类前面java处理方案一个继承并且通常能处理方案映象其类中更好解决Dictionary子类确省线程同步不允许关键字或值为null当元素顺序很重要时选用TreeMap当元素不必以特定顺序进行存储时解决HashMap.Hashtable解决不被导购因为HashMap提供了所类似功能并且速度更快当你需要多线程环境下解决时HashMap也可以转换为同步编写源代码过程中解决到集合类要根据不同需求来决定解决哪种集合类比如要经常遍历集合内元素就要解决List如果要保证集合中不存重复数据就要用Set;如果要通过某一键来查找某一值就要解决Map。
高等工程数学课件--第1章 集合与映射

定义1.2.3 设X、Y、Z是三个非空集合,并设 有两个映射 f1 : X Y , f2 : Y Z , 由 f1 , f 2 确定 X 到 Z 的映射 f3 : x f2 ( f1 ( x))( x X ) 称为映射 f1 和 f 2 的乘积(product),记为 f 3 f 2 f1 定理1.2.1 设有映射 f1 : X Y , f2 : Y Z , f3 : Z W , 则
lim An Ak .
n k 1
如果 An n 1是单调递减集合序列,则
lim An Ak .
n k 1
1.2 映 射(mapping)
定义1.2.1 设X、Y是两个非空集合,如果存在一
个X 到Y 的对应法则 f ,使得对 X中的每一个元素 x 都有Y中唯一的一个元素 y 与之对应,则称 f 是X 到Y的一个映射,记为 y f (x).
若 B A ,则称 A\B 为B 在A中的余集或B c 的补集,记为 B 。
定理 1.1.1 设A、B、C是三个集合, Ai (i I )为集合X的 子集,则
(1) A ( B C ) ( A B) ( A C ); A ( B C ) ( A B) ( A C );
(2) f 是X 到 Y的满映射当且仅当 Y R( f ).
非空集合,X 到自身的双映射称为X的一 一变换(one-to-one transformation);如果X 是有限集,X 的一一变换称为X 的置换 (permutation)。
非空集合X 上的恒等映射是一个双映射。 例. 微分算子,积分算子,矩阵。
定理1.2.3 映射f :X→Y是可逆映射的充分必 要条件是 f 是X到Y的双映射。 定理1.2.4 设映射f : X→Y , g :Y→Z,则 (1) 如果 f 和 g 都是单映射,则g f 是单映射;
集合与映射

集合与映射【高考要求】【知识精讲】板块一:集合的含义与表示(一)知识内容1•集合的有关概念⑴ 集合的含义:一般地把一些能够确定的不同的对象看成一个整体,就说这个整体是由这些对象的全体构成的集合(或集)•构成集合的每个对象叫做这个集合的元素(或成员)•⑵元素用小写字母a,b,c,…表示;集合用大写字母A,B,C,… 表示•⑶ 不含任何元素的集合叫做空集,记作.一.⑷集合的分类:有限集、无限集⑸集合元素的性质:确定性、互异性、无序性2•元素与集合间关系:属于•;不属于■'•3•集合表示法⑴列举法:把集合的所有元素都列举出来或列出几个元素作为代表,其它元素用省略号表示,并写在大括号“ {}内'的表示集合的方法•例如:{1, 2,3 , 4 , 5},{1, 2,3, 4, 5;"}⑵描述法:用集合所含元素的共同特征表示集合的方法称为描述法,形如{x|描述特点}例如:大于3的所有整数表示为:{x. Z|x 3}方程x 2 _2x _5 =0的所有实数根表示为:{x 三R | x 2「2x 「5 = 0 } ⑶常用集合及符号: 自然数集N非零自然数集N*或N + 整数集Z 有理数集Q 实数集R(二)典例分析:1•集合的有关概念【例1】以下元素的全体不能够构成集合的是()•A.中国古代四大发明B.地球上的小河流C.方程x 2 -1 0的实数解D.周长为10cm 的三角形垂A 1 :判断下列元素的全体能否构成集合,并说岀理由。
1、 所有的老人2、 所有的正方形3、 5~8岁的所有人4、 很小的实数可以构成集合【例2】已知x • R ,则集合{ _1,x 2 _2x }中元素x 所应满足的条件为 _________________ .绘三2:已知x • R ,则集合{3, x,x 2 -2x }中元素x 所应满足的条件为 ___________________ .2. 集合与元素间的关系【例3】用“ ”或填空:⑴ 若 A ={ x | x 2 _3x _4 =0},贝U -1 A ; -4 ___________ A ;⑵ 0—0 ;⑶ 0 _{0}.的」 3:用符号“ ”或“”填空⑴ 0 ________ N , 丘 ____________ N , 716 ______ N⑵—— Q , n Q3•集合的表示方法【例4】下列命题正确的有( )⑴集合 込| y =x 2 -门与集合1 x,y | y =x 2 -心是同一个集合; ⑵-丄,0.5这些数组成的集合有5个元素;2 42⑶集合〈x , y | xy < 0 , x, y • R [是指第二和第四象限内的点集.A . 0个B . 1个C. 2个D . 3个2练債4:用列举法表示下列集合⑴方程2x2 x -6 =0的根;⑵ 不大于8且大于3的所有整数;⑶ 函数y =3x • 2与y =丄的交点组成的集合.x板块二:集合间的基本关系(一)知识内容1•子集:对于两个集合A,B,如果集合A中的任意一个元素都是集合B的元素,我们就说集合A为集合B的子集,记作A §B (或B二A),读作“A包含于B ”(或’B包含A ”. 规定:;:二是任意集合的子集.2•真子集:如果集合A B,但存在元素x• B,但x - A,我们称集合A是集合B的真子集,记作A二B (或B耳A).-是任意非空集合的真子集.3.相等:如果集合A是集合B的子集(A B),且集合B是集合A的子集(B二A),此时,集合A与集合中的元素是一样的,我们说集合A与集合B相等,记作A =B .(二)典例分析【例5】用适当的符号填空:⑴■ _____ {0}⑵ 2_{(1, 2)}⑶ 0{x | x2 -2x +5 =0}⑷{3, 5} ______ {x | x2 -8x +15 =0}⑸{3, 5} ______ N⑹{x | x =2n +1, n W Z} ___{ x | x =4k ±1, k € Z}⑺{(2 , 3)} —{(3 , 2)}【例6】已知 A ={ x _2 _x _5} , B ={ x m • 1 _ x _2m _1}, B 二A,求m 的取值范围.録壬 5:设A ={ x| _仁:x :::3}, B ={ x I x .a},若A二B,则a的取值范围是 ____________ 【例7】{a , b, c} 4 A 4{ a , b , c , d , e , f},求满足条件的A的个数.【例8】求集合{a,b}的子集的个数,真子集的个数,非空真子集的个数,并推导出{1, 2, 3, 4, 5/ ' , 100}的子集和真子集的个数.(推导结论)板块三:集合的基本运算(一)知识内容1.相关概念:⑴ 并集:一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集,记作A U B (读作’A 并 B ”,即A U B ={x |x€ A,或x€ B}.⑵ 交集:一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作 A ^B (读作“A 交 B ”,即A^B ={x |x€ A,且x€ B}.⑶全集:一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,通常记作U .补集:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作ej A,即q A ={ x | x • U ,且x '' A}.(二)典例分析【例9】已知全集U ={ 1 , 2,3, , A 二{1, 2, 3, 4,5} , B ={4 , 5, 6, 7, 8},C ={3 , 5 , 7,9}求:A B , AB , A(e U B), q A B , A (B C)粽习6:已知全集U =R , A ={ x 3x +2 a—1} , B ={ x x £/} , C ={ x _x —4 >0} 求:A B , AB , A (e U B) , Qj A B , A (B C)圾「:’7 :设全集U =R , M =fm |方程mx2 _x 一1 =0有实数根],N -「n |方程x2-x - n =0有实数根[,求ej M N .【例10】若U为全集,下面三个命题中真命题的个数是()⑴若A B =_,则熔A心U B二U⑵若 A B =U,贝V 熔 A [U B⑶若 A B =._,贝V A =B =,A . 0个B . 1个C. 2个D . 3个【例11】已知集合A =fa2,a • 1,七〉B =「a _3,2a _1,a2• 1?,若A B 亠3?,求实数a的值.離习8 :设全集I ={ x | x < 20 且x 为质数}.若 A 口^B ={3 , 5} , ]B = {7 ,19}且痧A ^={2,17求集合A,B .【例12】若集合A ={ -1,1} , B ={x| mx =1},且A B二A,则m的值为(A. 1B. -1C. 1 或-1D. 1 或-1 或0统习9:设集合 A - ;x | x2-3x * 2 =0 ' B - ;x | x22( a ' 1)x ' (a^5^^。
映射的概念分析

映射的概念分析映射是数学中的一个重要概念,它描述了一个集合中的每个元素与另一个集合中的元素之间的对应关系。
在数学中,我们可以将映射理解为函数,其中一个集合是定义域,另一个集合是值域。
映射可以用于描述数学模型、图论、集合论等各种数学领域中的概念与关系。
映射有很多种形式,可以分为单射、满射和双射三种类型。
首先,单射是指一个集合中的不同元素在映射的结果中有不同的映射元素。
换句话说,映射的结果中不存在重复的映射元素。
对于集合A到集合B的映射f:A →B,如果对于集合A中的任意两个不同的元素a1和a2,有f(a1)≠f(a2),那么这个映射就是单射。
可以通过绘制函数图像来判断一个映射是否为单射,如果函数的图像没有任何两点在同一水平线上,那么这个函数是单射。
其次,满射是指映射的结果包含了值域中的每一个元素。
也就是说,对于集合A 到集合B的映射f:A→B,如果对于集合B中的任意一个元素b,存在集合A 中的元素a,使得f(a)=b,那么这个映射就是满射。
可以通过在值域上滑动水平线来判断一个映射是否为满射,如果水平线与函数的图像相交于每个y值上至少一个点,那么这个函数就是满射。
最后,双射是指一个集合中的每个元素与另一个集合中的元素存在唯一的对应关系。
也就是说,对于集合A到集合B的映射f:A→B,既是单射又是满射,那么这个映射就是双射。
可以通过绘制函数的图像并判断是否为一一映射来判断一个映射是否为双射。
映射还有一些衍生的概念。
首先是像、原像和逆映射。
对于映射f:A→B,如果b是集合B中的一个元素,a是集合A中满足f(a)=b的元素,那么b是元素a的像,元素a是元素b的原像。
逆映射是指如果映射f:A→B是双射,那么可以构造一个逆映射f^(-1):B →A,满足f^(-1)(f(x))=x和f(f^(-1)(y))=y。
其次是复合映射。
如果映射f:A→B和映射g:B→C都存在,那么可以定义一个复合映射h:A→C,使得h(x)=g(f(x))。
Python中的组合数据类型

Python中的组合数据类型计算机不仅能对单个变量表⽰的数据进⾏处理,通常情况下,计算机更需要对⼀组数据进⾏批量处理。
这种能够表⽰多个数据的类型称为组合数据类型。
Python语⾔最常⽤的组合数据类型有3⼤类,分别是集合类型、序列类型和映射类型。
集合类型是⼀个元素集合,元素之间⽆序,相同元素在集合中唯⼀存在。
序列类型是⼀个元素向量,元素之间存在先后关系,通过序列号访问,元素之间不排他。
序列类型的典型代表是字符串类型和列表类型。
映射类型是“键-值”数据项的组合,每⼀个元素是⼀个键值对,表⽰为(key,value)。
映射类型的典型代表是字典类型。
集合类型是⼀个具体的数据类型,⽽序列类型和映射类型都是⼀类数据类型的总称。
1、集合类型概述Python语⾔中的集合类型与数学中的集合概念⼀致,即包含0个或多个数据项的⽆序组合。
集合是⽆序组合,⽤⼤括号({ })表⽰,他没有索引和位置的概念,集合中的元素可以动态的增加和删减。
集合中的元素不可重复,元素类型只能是不可变数据类型,例如整数、浮点数、字符串、元组。
相⽐⽽⾔,列表、字典和集合类型本⾝都是可变数据类型,不能作为集合的元素出现。
创建集合直接⽤⼤括号表⽰,集合间没有顺序,不能⽐较,不能排序。
如果向集合输⼊重复的元素,会⾃动去重。
代码演⽰如下:string = "Python真简单啊"num = 8A = {1,"2",'34',5.0,6+7j,string,num}#内容可以是变量代表的数据print(A)#输出结果为{1, '2', 5.0, 8, '34', 'Python真简单啊', (6+7j)}B = {string,num,A}#不可以含有集合A,会报错print(B)#报错情况为:Traceback (most recent call last):File "C:\Users\Durova\Desktop\demo.py", line 5, in <module>B = {string,num,A}TypeError: unhashable type: 'set'集合类型有四种基本的操作,分别为交集(&)、并集(|)、补集(^)、差集(-),如下表:演⽰如下:>>> S = {1,2,3,4,5}>>> T = {4,5,6,7,8}>>> S-T{1, 2, 3}>>> S|T{1, 2, 3, 4, 5, 6, 7, 8}>>> S&T{4, 5}>>> S^T{1, 2, 3, 6, 7, 8}集合类型有⼀些常⽤的操作函数或⽅法,如下表:这些函数或⽅法的使⽤与普通函数或⽅法⼀致,前⾯的教程中已经有演⽰,这⾥仅演⽰较为特殊的set()函数。
01 集合与映射

一般的,任取一个正整数 m ,都能将 Z 分解成 m 个两两不相交的非空子集的并, ,使得每个子集恰好是由除以 m 余数相同 的整数组成的。特别地,取 m 2, Z 则被 分解成偶数子集和奇数子集的并。
设 M 2 ( R)
(a ) a
ij
ij
R; i , j 1, 2
是 R 上一切二阶矩阵组成的集合,令 A0 (aij ) 秩(aij ) 0 A1 (aij ) 秩(aij ) 1
例 A集合表示三个学生,B集合表示两门课,三个学 生 的某种选课法的集合表示可以: A {a, b, c}, B {1 2} ,
用A B的子集表示R {(a,1), (b,1), (b, 2)}
属于子集R表明:第一个分量与第二个分量有关系 不属于R表明:第一个分量与第二个分量无关系
二元关系
有序对集合中元素的个数
二元关系
定义 设A,B是两个集合, A B的子集R称为A,B 间的一个二元关系.当(a,b)∈R时,称a与b具有关 系R,记作aRb;当(a,b) R时,称a与b不具有关 系R,记作aR’b.
二元关系
例 A集合表示三个学生,B集合表示两门课。三个 A 学生选课的所有选法的数学表示可以: B
通过以上2个例子,可概括集合分类的定义.
设 A 为任一个集合,而 是 A 的一些 子集组成的集合, {Ai A i I }
定义
其中 I 是指标集,如果 iI (1) Ai (2) Ai A j i, j I且i j
历史上(困扰人们很久)的著名问题:
⑴二倍立方体问题:作一个立方体使其体积 为一已知立方体体积的两倍。 ⑵三等分任意角问题:给定一个任意角,将 其三等分。 ⑶圆化方问题:给定一个圆(已知半径为 r ),作一个正方形使其面积等于已知圆的面 积。 ⑷n等分一个圆周。 这些问题直到近世代数理论出现后才得到完 全的解决。
集合与映射的概念与应用

特征值和特征向量是矩阵理论中的重要概念,它们描述了 矩阵对应的线性变换在某些特定方向上的行为。这也可以 看作是一种集合到集合的映射。
矩阵的秩与映射的像
矩阵的秩可以看作是矩阵对应的线性变换像空间的维度, 它反映了映射的像集合的大小。
图论中顶点集和边集对应关系
图的定义
图由顶点集和边集组成,其中边集中的元素是顶点集中元素的无序对或有序对。这可以看作是一种从顶点集 到边集的映射关系。
05
04
集合的补集
对于一个全集U,由所有不属于集合A 的元素所组成的集合称为集合A的补集 ,记作CuA。
常见数集及其符号表示
整数集
用Z表示,包括所有 正整数、负整数和 零。
实数集
用R表示,包括所有 有理数和无理数。
自然数集
用N表示,包括所 有正整数。
有理数集
用Q表示,包括所 有可以表示为两个 整数之比的数。
运算规则
复合映射满足结合律,即(h○f)○g=h○(f○g)。
03
集合与映射关系探讨
集合间关系对映射影响分析
子集与超集
若集合A是集合B的子集, 则A中的每个元素都映射 到B中的某个元素上,但B 中不一定每个元素都有A
中的对应元素。
相等集合
两个集合相等当且仅当它 们包含相同的元素,此时 它们之间的映射是双射,
拓扑排序
03
在计算机科学中,拓扑排序是一种基于偏序关系的排序算法,
它用于解决具有先后依赖关系的任务调度问题。
函数作为特殊映射讨论
单射、满射与双射
函数作为映射的一种特殊情况,可以是单射 、满射或双射,分别对应不同的映射性质和 特征。
复合函数与逆函数
通过复合和逆操作,可以构造出更复杂的函数和映 射关系,进而解决更广泛的问题。
集合的函数和映射的定义及性质

集合的函数和映射的定义及性质一、集合的函数定义及性质函数是一种对应关系,它将一个集合中的每个元素都与另一个集合中的元素对应起来。
在数学中,函数可以用来描述一种映射关系。
下面是函数的定义及其性质。
1. 定义:给定两个集合A和B,一个从A到B的函数f是这样一个映射关系,对于A中的每个元素a,都有唯一的对应元素b在B中,称为f(a) = b。
用数学符号表示为f: A → B。
2. 性质:a. 单射:如果对于任意两个不同的元素a1和a2,其映射后的结果f(a1)和f(a2)也不相同,则称函数f为单射。
b. 满射:如果对于B中的每个元素b,都能找到A中的至少一个元素a,使得f(a)=b,则称函数f为满射。
c. 双射:如果函数f既是单射又是满射,则称函数f为双射。
d. 逆映射:如果函数f是双射,那么可以定义它的逆映射g,满足g(f(a)) = a和f(g(b)) = b,其中a属于集合A,b属于集合B。
二、映射的定义及性质映射是一种函数的特殊情况,它有更严格的性质要求。
下面是映射的定义及其性质。
1. 定义:给定两个集合A和B,一个从A到B的映射是这样一个函数f,对于A中的每个元素a,都有唯一的对应元素b在B 中,称为f(a) = b。
用数学符号表示为f: A → B。
2. 性质:a. 总映射:如果对于A中的每个元素a,都能找到B中的唯一元素b使得f(a) = b,则称映射f为总映射。
b. 单值映射:如果对于A中的每个元素a,其映射后的结果f(a)都是唯一的,即不存在不同的元素a1和a2使得f(a1) = f(a2),则称映射f为单值映射。
c. 线性映射:如果对于A中的每个元素a,其映射后的结果f(a)都满足f(ka) = kf(a),其中k为常数,则称映射f为线性映射。
以上是关于集合的函数和映射的定义及性质的简要介绍。
希望对你有所帮助。
高等代数 集合与映射

§1 集合·映射
§5 线性子空间
§2 线性空间的定义 §6 子空间的交与和
与简单性质
§7 子空间的直和
§3 维数·基与坐标
§8 线性空间的同构
§4 基变换与坐标变换
§6.1 集合·映射
一、集合 二、映射
§6.1 集合 映射
一、集合(set)
1、定义
把一些事物汇集到一起组成的一个整体就叫做集合; 组成集合的这些事物称为集合的元素(element). ☆ 常用大写字母A、B、C 等表示集合;
(8)M=Z,M´=2Z,
σ:σ(n)=2n, n Z
(双射) (双射)
§6.1 集合 映射
4、可逆映射
定义 设映射 : M M ', 若有映射 : M ' M , 使得 IM , IM
则称σ为可逆映射(invertible mapping),τ为σ的 逆映射,记作σ-1.
§6.1 集合 映射
☆集合的表示方法一般有两种:描述法、列举法
描述法(description): 给出这个集合的元素所具有的特征性质. M={x | x具有性质P}
列举法(enumeration): 把构成集合的全部元素一一列举出来. M={a1,a2,…,an}
§6.1 集合 映射
例1 M {( x, y) x2 y2 4, x, y R}
用小写字母a、b、c 等表示集合的元素.
当a是集合A的元素时,就说a 属于A,记作 a A ; 当a不是集合A的元素时,就说a不属于A,记作 a A .
§6.1 集合 映射
注意
关于集合没有一个严谨的数学定义,只是有一 个描述性的说明.集合论的创始人是19世纪中期德 国数学家康托尔(G.Cantor),他把集合描述为: 所谓集合是指我们直觉中或思维中确定的,彼此有 明确区别的那些事物作为一个整体来考虑的结果; 集合中的那些事物就称为集合的元素.即,集合中 的元素具有:确定性、互异性、无序性.
第一次课预备知识—集合数域和映射

1Bσ = σ1A. 映射的乘法适合结合律.设σ, τ, ψ分别是集合A到B,B到C,C到D的映射,映射乘法的结合律就是
(ψτ )σ = ψ(τ σ).
设σ是集合A到B的一个映射,用
σ(A) 3
代表A在映射σ下像的全体,称为A在映射σ下的像集合. 显然
σ(A) ⊂ B.
3.满射——如果σ(A) = B,映射σ 称为映上的或满射. 满射判定——若对任意的b ∈ B, ∃a ∈ A 使得σ(a) = b,则σ为满射. 4. 单射——如果在映射σ下,A中不同元素的像也一定不同,即由x, y ∈ A, x = y, 一定有σ(a) = σ(y), 那么映射σ就称为1-1的或单射. 单射的判定——若σ(x) = σ(y),可推出x = y,则σ为单射. 5. 双射——一个映射如果既是单射又是满射就称对应或双射.
因为为满射所以b中每个元素都有原像又因为是单射所以每个元素只有一个原像定义不难证明如果分别是a到bb到c的双射那么乘积就是a到c的一个双射
第一次课 预备知识—集合、数域和映射
一、集合 集合是数学中最基本的概念之一,所谓集合就是指作为整体看的一堆东西.组成集合的东西称为
这个集合的元素. 用 a∈A
表示a是集合A的元素,读为:a属于A. 用
我们使用如下记号: 当然也可以写成
n
a1 + a2 + · · · + +an = ai,
i=1
n
a1a2 · · · an = ai.
i=1
a1 + a2 + · · · + +an =
ai,
1≤i≤n
a1a2 · · · an =
ai.
1≤i≤n
Python数据类型之“集合(Sets)与映射(Mapping)”

Python数据类型之“集合(Sets)与映射(Mapping)”⼀、集合类型(Sets)集合对象是不同的(不可重复)hashable对象的⽆序集合。
常见⽤法包括:成员关系测试、移除序列中的重复、以及科学计算,例如交集、并集、差分和对称差分。
通俗点来说,集合是⼀个⽆序不重复元素的数据集,其基本功能是进⾏成员关系测试和消除重复元素。
⽬前有两种内置的集合类型:set 和 frozenset。
set类型是可变的--可以使⽤add() 和 remove()等⽅法更改其内容。
由于它是可变的,它没有hash值,因此它不能被当做字典的键值或另⼀集合的元素。
frozenset类型是不可变的和 hashable的,它的内容不能再创建后改变,因此它可以⽤作字典的键值或作为另⼀个集合的元素。
set类构建函数class set([iterable])class frozenset([iterable])set的构建⽅式将⼀个⽤逗号分割的元素列表放在⼀堆花括号内可以创建⼀个⾮空set集合,如{'Tom', 'Jerry', 'Peter'}给set的构建函数传递⼀个空值将会创建⼀个空set集合(注意:{}表⽰的是⼀个空字典⽽不是空set集合)给set的构架你函数传⼀个⾮空iterable参数将会创建⼀个⾮空set集合注意:再次强调,⼀个set集合内的元素必须是hashable的(不可变的)。
要想表⽰⼀个set的set,那么内部的set必须是frozenset对象,因为frozenset是不可变的,是hashable的。
set构建⽰例>>> {'Tom', 'Jerry', 'Peter'} # 使⽤花括号创建⾮空set集合{'Jerry', 'Tom', 'Peter'}>>> set() # 使⽤set构建函数创建空set集合set()>>> set((1, 2, 3 ,4)) # 使⽤set构建函数创建⾮空set集合{1, 2, 3, 4}>>> set((1, 2, 3 ,['a', 'b', 'c'])) # set集合中的元素必须是不可变的、可哈希的Traceback (most recent call last):File "<stdin>", line 1, in <module>TypeError: unhashable type: 'list'set 和 frozenset都⽀持的操作作为⽆序集合,set不记录元素位置或插⼊顺序。
人教版高中数学必修一课件:集合-映射
已知 ⑴
的映A射有多{1少,个2?,3},取,适B当的{对5应,法6}则
A到B ⑵以 为定义域, 为值域的函数有多少个?
⑶在所有的以 为定义域, 为值域的函数中,
满足 A
B 的函数有多少个?
A
B
f (1) f (2) f (3)
9
A B {a,b,c, d,e,, x, y, z}
A {a, b, c, d ,, x , y , z } B {a, b, c, d , , x , y , z }
考察下面的问题,集合A,B与集合C之间有什么关系?
(1)A={2,4,6,8,10}, B={3,5,8,12} ,C={8}; (2)A={x|x是我班的女同学},
B={x|x是我班戴眼镜的同学}, C={x|x是我班戴眼镜的女同学}.
发现:集合C是由集合A中和集合B中的公共元素所 组成的.
交集
一一映射:设A,B是两个集合,f : A B 是集合A到集合B
的映射,如果在这个映射下,对于A中的不同元素,在集合B中 有不同的象,而且B中每一个元素都有原象,那么这个映射叫做 A到B上的一一映射
7
• 答:主要有两点区别: • (1) 映射要求A中的元素在B中有唯一的象,
而一一映射不仅要求A中的元素在B中有唯 一的象,还要求A中不同的元素在B中有不 同的象; • (2) 映射不需要B中的元素都有原象,而一 一映射则要求B中的每一个元素都必须有原 象。
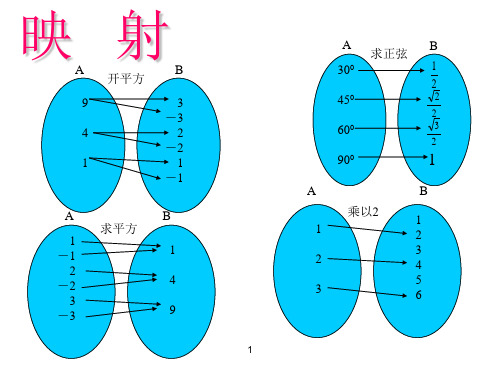
映射
A 开平方
B93来自-342-2
1
1
-1
A
B
求平方
1
-1
1
2
-2
4
3
-3
9
A 求正弦 B
解析映射的定义

解析映射的定义
映射,也称为函数,是从一个集合到另一个集合的规则。
它将集合中的每个元素映射到另一个集合中的唯一元素。
映射可以用数学符号表示为:f:A→B,其中A是起始集合,B是目标集合,f是映射规则。
映射的定义包括以下要素:
1. 起始集合:映射的起始集合是指映射中所有元素的集合,也称为定义域。
2. 目标集合:映射的目标集合是指映射中每个元素对应的唯一元素的集合,也称为值域。
3. 映射规则:映射规则是指将起始集合中的每个元素映射到目标集合中的唯一元素的规则。
映射的定义可以用实际例子来说明。
例如,假设有一个集合
A={1,2,3}和另一个集合B={a,b,c}。
我们可以定义一个映射f:A→B,其中f(1)=a,f(2)=b,f(3)=c。
这个映射规则将集合A中的每个元素映射到集合B中唯一的元素。
映射在数学、计算机科学和物理学等领域中广泛应用。
在数学中,映射是构建函数和证明定理的重要工具。
在计算机科学中,映射被用于算法、数据结构和编程语言中。
在物理学中,映射被用于描述物理系统和预测其行为。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Python dictionaries are implemented as resizeable hash tables. If you are familiar with Perl, then we can say that dictionaries are similar to Perl’s associative arrays or hashes.
Built-in Functions
Built-in Methods
Related Modules
7
*本章主题
* 映射类型: 字典
* 操作符
* 内建函数
* 内建方法
* 字典的键
* 集合类型
* 操作符
* 内建函数
* 内建方法
* 相关模块
第七章
Python的字典是作为可变的哈希表实现的。如果你熟悉Perl的话, 就可以发现字典与Perl中的"关系数组"或散列相似。
Mapping and Set Types
映射和集合类型
Chapter Topics
Mapping Type: Dictionaries
Operators
Built-in Functions
Built-in Methods
Dictionary Keys
Set Types
Operators
字典是Python语言中唯一的映射类型。映射类型对象里哈希值(键) 和指向的对象(值)是一对多的关系。 它们与Perl中的哈希类型(译者注:又称关联数组)相似,通常被认为是可变的哈希表。一个字典对象是可变的,它是一个容器类型,能存储任意个数的Python对象,其中也包括其他容器类型。字典类型和序列类型容器类(列表、元组)的区别是存储和访问数据的方式不同。序列类型只用数字类型的键(从序列的开始起按数值顺序索引)。映射类型可以用其他对象类型做键;一般最常见的是用字符串做键(keys)。和序列类型的键不同,映射类型的键(keys)直接,或间接地和存储的数据值相关联。但因为在映射类型中,我们不再用"序列化排序"的键(keys),所以映射类型中的数据是无序排列的。
CORE NOTE: What are hash tables and how do they relate to dictionaries?
核心笔记:什么是哈希表?它们与字典的关系是什么?
Sequence types use sequentially ordered numeric keys as index offsets to store your data in an array format. The index number usually has nothing to do with the data value that is being stored. There should also be a way to store data based on another associated value such as a string. We do this all the time in everyday living. You file people’s phone numbers in your address book based on last name, you add events to your calendar or appointment book based on date and time, etc. For each of these examples, an associated value to a data item was your key.
in this chapter, we take a look at Python’s mapping and set types. As in earlier chapters, an introduction is followed by a discussion of the applicable operators and factory and built-in functions (BIFs) and methods. We then go into more specific usage of each data type.
As it turns out, this does not hinder our use because mapping types do not require a numeric value to index into a container to obtain the desired item. With a key, you are “mapped” directly to your value, hence the term “mapping type.” The reason why they are commonly referred to as hash tables is because that is the exact type of object that dictionaries are. Dictionaries are one of Python’s most powerful data types.
Hash tables are a data structure that does exactly what we described. They store each piece of data, called a value, based on an associated data item, called a key. Together, these are known as key-value pairs. The hash table algorithm takes your key, performs an operation on it, called a hash function, and based on the result of the calculation, chooses where in the data structure to store your value. Where any one particular value is stored depends on what its key is. Because of this randomness, there is no ordering of the values in the hash table. You have an unordered collection of data.
哈希表是一种数据结构:它按照我们所要求的去工作。哈希表中存储的每一条数据,叫做一个值(value),是根据与它相关的一个被称作为键(key)的数据项进行存储的。键和值合在一起被称为“键-值 对”(key-value pairs)。 哈希表的算法是获取键,对键执行一个叫做哈希函数的操作,并根据计算的结果,选择在数据结构的某个地址中来存储你的值。任何一个值存储的地址皆取决于它的键。正因为这种随意性,哈希表中的值是没有顺序的。你拥有的是一个无序的数据集。
本章中,我们来讨论Python语言中的映射类型和集合类型。和前面的章节一样,我们首先做一个介绍,然后在来讨论可用操作符,工厂函数、内建函数(BIF)和方法。然后我们再来看看每种数据类型的详细用法。
Байду номын сангаас
7.1 Mapping Type: Dictionaries
映射类型:字典
Dictionaries are the sole mapping type in Python. Mapping objects have a one-to-many correspondence between hashable values (keys) and the objects they represent (values). They are similar to Perl hashes and can be generally considered as mutable hash tables. A dictionary object itself is mutable and is yet another container type that can store any number of Python objects, including other container types. What makes dictionaries different from sequence type containers like lists and tuples is the way the data are stored and accessed. Sequence types use numeric keys only (numbered sequentially as indexed offsets from the beginning of the sequence). Mapping types may use most other object types as keys; strings are the most common. Unlike sequence type keys, mapping keys are often, if not directly, associated with the data value that is stored. But because we are no longer using “sequentially ordered” keys with mapping types, we are left with an unordered collection of data.
序列类型用有序的数字键做索引将数据以数组的形式存储。一般,索引值与所存储的数据毫无关系。还可以用另一种方式来存储数据:基于某种相关值,比如说一个字符串。我们在日常生活中一直这么做。你把人们的电话号码按照他们的姓记录在电话簿上,你按照时间在日历或约会簿上添加事件,等等。在这些例子中,你的键(key)就是和数据项相关的值。
