抛物线的焦点弦问题 (1)
专题21 抛物线的焦点弦 微点1 抛物线的焦点弦常用结论试题及答案

专题21 抛物线的焦点弦 微点1 抛物线的焦点弦常用结论及其应用专题21 抛物线的焦点弦微点1 抛物线的焦点弦常用结论及其应用 【微点综述】在抛物线与直线的关系中,过抛物线焦点的直线与抛物线的关系尤为重要,这是因为在这一关系中具有一些很有用的性质,这些性质常常是高考命题的切入点.本文对此作一些介绍. 一、常用结论不妨设抛物线方程为()220y px p =>,如图1,准线2px =-与x 轴相交于点P ,过焦点,02p F ⎛⎫⎪⎝⎭的直线l 与抛物线相交于()()1122,,,A x y B x y 两点,O 为原点,α为AB 与对称轴正向所成的角,AB 的中点为C ,又作111,,AA l BB l CC l ⊥⊥⊥,垂足分别为111,,A B C ,则有如下结论(1)~(9):(1)221212,4p x x y y p ==-. (2)焦半径长公式:12,22p pAF x BF x =+=+(坐标式);夹角式:,1cos 1cos p pAF BF αα==-+(A 在x 轴上方,B 在x 轴下方).(3)焦点弦长公式:1222,sin pAB x x p AB α=++=.(4)通径长公式:2AB p =(通径最短).(5)AF ,BF 的数量关系:22112,sin 2p AB p AF BF AF BF p α⋅+=⋅==. (6)三角形AOB 的面积:2,2sin AOF AOBBOF AF S p S S BFα==△△△. (7)中点弦斜率:若AB 斜率为k ,()00,C x y ,则0pk y =. (8)直线,PA PB 的斜率之和为零0PA PB k k +=,即APF BPF ∠=∠. (9)焦点弦与圆有关的结论,如图2, ①以AB 为直径的圆M 与准线相切; ①以AF 为直径的圆C 与y 轴相切; ①以BF 为直径的圆D 与y 轴相切;①分别以,,AB AF BF 为直径的圆之间的关系:圆C 与圆D 外切;圆C 与圆D 既与y 轴相切,又与圆M 相内切.(10)由焦点弦得出有关直线垂直关系的结论,如图3,①以AB 为直径的圆的圆心在准线上的射影1M 与,A B 两点的连线互相垂直,即11M A M B ⊥;①以AF 为直径的圆的圆心在y 轴上的射影1C 与,A F 两点的连线互相垂直,即11C A C F ⊥;①以BF 为直径的圆的圆心在y 轴上的射影1D 与,B F 两点的连线互相垂直,即11D B D F ⊥;①以11A B 为直径的圆必过原点,即11A F B F ⊥; ①1M F AB ⊥.(11)点1,,A O B 三点共线;点1,,A O B 三点共线.(12)如图4,点A ,B 是抛物线()20y px p =>,O 为原点,若90AOB ∠=︒,则直线AB 过定点()2,0p .图4证明:(1)因为焦点坐标为,02p F ⎛⎫⎪⎝⎭,当AB 不垂直于x 轴时,可设直线AB 的方程为:2p y k x ⎛⎫=- ⎪⎝⎭,由222p y k x y px⎧⎛⎫=-⎪ ⎪⎝⎭⎨⎪=⎩得:2220ky py kp --=,212122,p y y y y p k ∴+==-,2242121222244y y p p x x p p p =⋅==.当AB x ⊥轴时,直线AB 方程为2p x =,则1y p =,2y p =-,①212y y p =-,同上也有:2124p x x =.(2)由抛物线的定义易得1112,22p p AF AA x BF BB x ==+==+. 又()1cos ,1cos A F p AF AA p x x p AF AF αα==+-=+∴=-,同理可证1cos pBF α=+.(3)由(2)可得弦长:121222,221cos 1cos sin p p p p pAB AF BF x x x x p AB AF BF ααα=+=+++=++=+=+=-+.(4)当AB x ⊥轴时,直线AB 方程为2px =,则1y p =,2y p =-,①通径长公式:2AB p =. (5)由212122,py y y y p k+==-,得()()2222221212121222222222p p k p y y y y y y k x x p p p k ⎛⎫+ ⎪++-+⎝⎭+====,又()()22221212121212,42224424p p p p p p p p x x AF BF x x x x x x x x ⎛⎫⎛⎫=∴⋅=++=+++=+++ ⎪⎪⎝⎭⎝⎭()21222222sin sin p p p p x x p αα=++=⋅=, 222112sin 2sin AF BF AB p AF BF AF BF AF BF p pαα++===⋅=⋅⋅. (6)点O 到直线AB 的距离d 就是的AOB ∆高,sin 2p h d α===, 221112sin 2,122sin 22sin 2AOF AOB BOFAF d AF S p p pS AB h S BF BF d ααα⋅⋅∴=⋅=⋅⋅===⋅⋅△△△. (7)2211222,2y px y px ==,由点差法得()()()()221212121212121212022,2,y y p py y p x x y y y y p x x k x x y y y --=-∴+-=-∴===-+.(8)()()1122,,,,,02p A x y B x y P ⎛⎫- ⎪⎝⎭,2p y k x ⎛⎫=- ⎪⎝⎭,122112121222222222PA PBp p p p k x x k x x y y k k p p p p x x x x ⎛⎫⎛⎫⎛⎫⎛⎫-++-+ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭∴+=+=⎛⎫⎛⎫++++ ⎪⎪⎝⎭⎝⎭, 分子2221221122202222242p p p p p p p k x x k x x k x x k ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-++-+=-=⨯-= ⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭, ∴直线,PA PB 的斜率之和为零:0PA PB k k +=,即APF BPF ∠=∠.(9)①如图2,过M 点作1MM l ⊥于1M ,则1MM 是梯形11AA B B 的中位线,由抛物线的定义知()()11111111,,222AA AF BB BF MM AA BB AF BF AB ==∴=+=+=, 即以AB 为直径的圆M 与准线相切,同理可证①,①. ①,AF BF AB +=∴分别以,,AB AF BF 为直径的圆有以下关系:圆C 与圆D 外切;圆C 与圆D 既与y 轴相切,又与圆M 相内切.(10)①准线与圆M 相切,∴圆M 的圆心在准线上的射影1M 就是切点,直径所对的圆周角是直角,11M A M B ∴⊥.同理可证①,①:1111,C A C F D B D F ⊥⊥. ①由抛物线的定义知11,AA AF BB BF ==,1BB //NF //1111,AA AA F AFA A FN ∴∠=∠=∠, 111BB F BFB B FN ∠=∠=∠,而111111,2AFA A FN BFB B FN A FN NFB π∠+∠+∠+∠=π∴∠+∠=,即11A F B F ⊥. ①易知10,2p M y ⎛⎫- ⎪⎝⎭,又11010,0,,,1,2M F AB M F AB y p p F k k k k M F AB p y ⎛⎫∴=-=∴⋅=-∴⊥ ⎪⎝⎭.(11)由(1)知2222221221212122224422,,44OAy y x y p p p p x x y y p k x y x y y p----==-∴==÷===.1221122,,,,22OB OA y y p BB l B y k k p p -⎛⎫⊥∴-∴===∴⎪⎝⎭-点1,,A O B 三点共线.同理可证:点1,,A O B 三点共线.(12)11,1,1,1OA OB OA OB k k st t s⊥∴⋅=-∴⋅=-∴=-.设()()222,2,2,2A pt pt B ps ps ,则()()22212AB p s t k s t p s t -==+-,直线AB 方程为()2122y pt x pt s t-=-+, 即()222212,,,2x pt x pst x p y pt y y y x p s t s t s t s t s t s t s t-=+-∴=+∴=+∴=-+++++++,∴直线AB 过定点()2,0p . 二、应用举例例1.(2022太原一模)1.已知抛物线24y x =的焦点为F ,过焦点F 的直线交抛物线于A B 、两点,O 为坐标原点,若AB =6,则AOB ∆的面积为A B .C .D .4例2.(2022晋中二模)2.已知抛物线24y x =的焦点为F ,过焦点F 的直线交抛物线于,A B 两点,O 坐标原点,若AOB 的面积为AB = A .24B .8C .12D .163.过抛物线2y ax =(>0)的焦点F 作一直线交抛物线于P 、Q 两点,若线段PF 与FQ 的长分别为p 、q ,则11p q+等于 A .2B .12aC .4aD .4a4.直线过抛物线24y x =的焦点F 且交抛物线于A ,B 两点,A 在x 轴上方,若=5AF ,求BF .5.直线过抛物线24y x =的焦点F 且交抛物线于A ,B 两点,A 在x 轴上方,直线倾斜角为60︒,求OAFS.6.若抛物线23y x =,过焦点F 作倾斜角为30的直线与抛物线交于A ,B ,求AB . 7.直线过抛物线22y x =的焦点F 且交抛物线于A ,B 两点,若25=12AB AF BF <,,求AF .8.若抛物线24y x =,过焦点F 作两条互相垂直的直线分别于抛物线交于A ,B 和C ,D ,求()min AB CD +.9.若抛物线24y x =,过焦点F 作直线与抛物线交于A ,B ,若=3AF BF ,求直线l 方程.10.若抛物线23y x =,过焦点F 且倾斜角为30的直线交抛物线于A ,B 两点,求OABS.11.斜率为k 的直线过抛物线24y x =的焦点且与抛物线交于A ,B 两点,O 为原点,M 为AB 中点,且2OFMS =,求k .【强化训练】(2022·云南玉溪·高二期末)12.直线10x -=与抛物线24y x =交于A ,B 两点,则AB =( )A .B .8C .D .1613.过抛物线24y x =的焦点F 的直线与其交于A ,B 两点,AF BF >,如果5AF =,那么BF =( )A B .54C .52D .3214.过抛物线24y x =的焦点作两条互相垂直的弦AB 、CD ,则11AB CD+=( ) A .2 B .4 C .12D .1415.设抛物线2:2(0)C y px p =>的焦点为 F ,点M 在 C 上,5MF =,若以 MF 为直径的圆过点(0,2),则C 的方程为 A .24y x =或 28y x = B .22y x =或 28y x = C .24y x =或 216y x = D .22y x =或 216y x =(2022·黑龙江·哈尔滨三中模拟预测)16.已知直线l 过抛物线2:4C y x =的焦点,并且与抛物线C 交于不同的两点A 、B ,若()02,M y 为线段AB 的中点,则||AB 的值为( )A .4B .5C .6D .8(2022·广东佛山·模拟预测)17.已知抛物线C :()220y px p =>的焦点为F ,过焦点且斜率为l 与抛物线C 交于A ,B (A 在B 的上方)两点,若AF BF λ=,则λ的值为( )AB C .2D 18.已知抛物线2:8W x y =-,点()11,A x y ,()22,B x y 是曲线W 上两点,若128y y +=-,则AB 的最大值为( ) A .10B .14C .12D .16(2022·江苏·南京市第一中学高三开学考试)19.已知以F 为焦点的抛物线2:4C y x =上的两点A ,B ,满足133AF FB λλ⎛⎫=≤≤ ⎪⎝⎭,则弦AB 的中点到C 的准线的距离的最大值是( ) A .2B .83C .103D .4(2022全国·高二月考) 20.已知抛物线C ①214y x =,过抛物线焦点的直线交抛物线于A ,B 两点,若直线AO ,BO 分别交直线y =x -2于E ,F 两点,则|EF |的最小值( )A .253B .3C .12825D (2022·辽宁实验中学模拟预测)21.已知抛物线24y x =的焦点为F ,过F 的直线交抛物线于A ,B 两点,准线为l ,过点A 作1AA l ⊥,垂足为1A ,1A AF ∠的角平分线交l 于点M ,过B 作抛物线的切线交l 于点N ,则MN =_________.(2022·青海·海东市第一中学模拟预测)22.已知抛物线C :22y px =(p >0)的焦点为F ,过点F 且斜率为1的直线与抛物线C 相交于A ,B 两点,与抛物线C 的准线交于点E ,若2AB EF =,则p =________. (2022·江苏南通·高二期末)23.直线l 过抛物线()220x py p =>的焦点为()0,1F ,且与抛物线交于A 、B 两点,则2AF BF-的最小值为_______. (2022·四川省内江市第六中学高二月考)24.如图,已知抛物线1C 的顶点在坐标原点,焦点在x 轴上,且过点()3,6,圆222:680C x y x +-+=,过圆心2C 的直线l 与抛物线和圆依次交于P ,M ,N ,Q ,则3PN QM +的最小值为___________.(2022·广东广州·高二期末)25.已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为2,过点F 的直线l 与抛物线C 交于()11,P x y ,()22,Q x y 两点,若124y y +=,则线段PQ 的长度为__________. (2022·全国·高二月考)26.已知抛物线C :22(0)y px p =>的焦点为F ,点M N ,在抛物线上,且M N F ,,三点共线;点P 在准线上,PN NM = ,则pMF= __. 27.已知抛物线()2:20C x py p =>,直线l 经过抛物线C 的焦点,且垂直于抛物线C的对称轴,直线l 与抛物线C 交于M ,N 两点,且4MN =. (1)求抛物线C 的方程;(2)已知点()2,1P ,直线():2m y k x =+与抛物线C 相交于不同的两点A ,B ,设直线P A 与直线PB 的斜率分别为1k 和2k ,求证:12k k ⋅为定值. (2022·湖南衡阳·三模)28.已知抛物线C :()20y ax a =>的焦点是F ,若过焦点F 的直线与C 相交于A ,B 两点,所得弦长AB 的最小值为2. (1)求实数a 的值;(2)设P ,Q 是抛物线C 上不同于坐标原点O 的两个不同的动点,且以线段PQ 为直径的圆经过点O ,作OM PQ ⊥,M 为垂足,试探究是否存在定点N ,使得MN 为定值,若存在,则求出该定点N 的坐标及定值MN ,若不存在,请说明理由. (2022·河北秦皇岛·三模)29.已知抛物线2:2(0)C y px p =>上的点M 与焦点F 的距离为9,点M 到x 轴的距离为.(1)求抛物线C 的方程.(2)经过点F 的直线与抛物线C 交于,A B 两点,E 为直线=1x -上任意一点,证明:直线,,EA EF EB 的斜率成等差数列.(2022·浙江省杭州学军中学模拟预测)30.如图,在平面直角坐标系xOy 中,已知抛物线2:2(0)C y px p =>的焦点为F ,准线为l ,过点F 且斜率大于0的直线交抛物线C 于A ,B 两点,过线段AB 的中点M 且与x 轴平行的直线依次交直线OA ,OB ,l 于点P ,Q ,N .(1)求证:||||PM NQ =;(2)若线段NP 上的任意一点均在以点Q 为圆心、线段QO 长为半径的圆内或圆上,若≤NABSp 的取值范围;(2022·江苏·扬州中学模拟预测)31.已知抛物线H :()220y px p =>的焦点为F ,抛物线H 上的一点M 的横坐标为5,O 为坐标原点.2cos 3OFM ∠=-.(1)求抛物线H 的方程;(2)若一直线经过抛物线H 的焦点F ,与抛物线H 交于A ,B 两点,点C 为直线=1x -上的动点,求证:π2ACB ∠≤. (2022·江西·上饶市第一中学模拟预测)32.已知抛物线()220y px p =>的焦点为F ,过焦点FA 、B 两点(点A 在第一象限),交抛物线准线于G ,且满足83BG =. (1)求抛物线的标准方程;(2)已知C ,D 为抛物线上的动点,且OC OD ⊥,求证直线CD 过定点P ,并求出P 点坐标;(3)在(2)的条件下,求PC PD ⋅的最大值. (2022·江苏南京·模拟预测)33.已知圆F :()2221x y -+=,动圆P 与圆F 内切,且与定直线3x =-相切,设动点P 的轨迹为E . (1)求E 的方程;(2)若直线l 过点F ,且与E 交于A ,B 两点,与y 轴交于M 点,满足MA AF λ=,MF FB μ=(0λ>,0μ>),试探究λ与μ的关系.参考答案:1.A【详解】解:设直线AB 的方程为:()1y k x =- ,与抛物线方程联立可得:2440y y k--= ,则:12y y -==,21221416,2y y k k ⎛⎫-=+=∴= ⎪⎝⎭,三角形的面积为:1211122S OF y y =⨯⨯-=⨯=.本题选择A 选项. 2.A【详解】抛物线24y x = 的焦点F 坐标为(10)F ,,过焦点(10)F ,的直线设为1x my =+ ,设1122(,),(,)A x y B x y ,联立214x my y x=+⎧⎨=⎩ 有2440y my --= ,所以有121244{y y my y +==- ,由1211122AOB S OF y y ∆=⋅⋅-=⋅,所以有m =,1224AB y =-== ,故选A. 3.C【分析】设PQ 直线方程是14y kx a -=则x 1,x 2是方程2104ax kx a--=的两根,借助韦达定理即可得到11p q+的值. 【详解】抛物线2(0)y ax a =>转化成标准方程:21x y a=, ∴焦点F 坐标1(0,)4a,准线方程为14x a =-,设过1(0,)4F a 的AB 直线方程为14y kx a=+, ∴214y kx a y ax⎧=+⎪⎨⎪=⎩,整理得2104ax kx a --=. 设1(A x ,1)y ,2(B x ,2)y由韦达定理可知:1214x x =,12k x x a+=, 212121()2k y y k x x a a∴+=++=,12122111()()4416y y kx kx a a a =++=, 根据抛物线性质可知,14ap y =+,22p q y =+, 2122122111241()()444k ay y p q a a p p k p q pq y y a+++++====+++,∴11p q+的值为4a ,故选:C .【点睛】涉及直线与圆锥曲线相交时,未给出直线时需要自己根据题目条件设直线方程,要特别注意直线斜率是否存在的问题,避免不分类讨论造成遗漏,然后要联立方程组,得一元二次方程,利用根与系数关系写出1212,x x x x +⋅,再根据具体问题应用上式,其中要注意判别式条件的约束作用. 4.54【分析】根据抛物线的焦点弦性质计算.【详解】由对称性,不妨设AB 的倾斜角α为锐角,52p >=, 由结论2可得:23255,5,cos ,31cos 5415AF BF αα=∴=∴=∴==-+.5【分析】由焦点弦的性质求得AF ,【详解】由题意211==4,=sin1201412212AOFAF SOF AF ∴⋅︒=⨯⨯- 6.12【分析】由抛物线的焦点弦长公式22sin pl α=(α是焦点弦所在直线倾斜角)计算. 【详解】222312sin 12p AB α===⎛⎫ ⎪⎝⎭.7.56【分析】根据抛物线的焦点弦长公式22sin pl α=(α为焦点弦所在直线的倾斜角,由对称性,设α为锐角)求出弦所在直线的倾斜角的正弦,再由焦半径公式较短的1cos pAF α=+,较长的1cos pBF α=-计算.【详解】设AB 倾斜角为α,且α为锐角,则2225115==,sin cos ,1sin 125615AB AF ααα∴=∴=∴==+. 8.16【分析】设出直线AB 的倾斜角为θ,根据抛物线焦点弦的结论得到AB 与CD ,利用三角函数的恒等变换及有界性求出最小值.【详解】设直线AB 的倾斜角为θ,则2224sin sin p AB θθ==,2224πcos sin 2p CD θθ==⎛⎫+ ⎪⎝⎭, 所以2222224444161sin cos sin cos sin 2sin 24AB CD θθθθθθ+=+===,当π4θ=或3π4时,2sin 21θ=,()min 16AB CD += 90y -=0y +=.【分析】由焦点弦性质求得直线AB 的倾斜角的余弦值,从而得直线斜率,得直线方程. 【详解】先设直线AB 倾斜角α为锐角,1cos 13,cos ,tan :1)1cos 2AF k l y x BF αααα+==∴=∴===--. 由对称性直线l 方程还可以为3(1)yx ,综上,直线l0y -0y +. 10.94【分析】求出直线AB 的方程,与抛物线联立后得到两根之和,两根之积,利用弦长公式求出AB ,利用点到直线距离公式求出原点到直线AB 的距离,从而求出三角形OAB 的面积. 【详解】由题意得:3,04F ⎛⎫ ⎪⎝⎭,直线AB的斜率为tan 30︒故直线AB的方程为34y x ⎫=-⎪⎝⎭, 将23y x =联立得:217303216x x -+=,设()()1122,,,A x y B x y , 则1212219,216x x x x +==,则12AB ==, 点()0,0O 到直线AB的距离为38d ==, 所以1139122284OABSAB d =⋅=⨯⨯= 11.12±.【分析】由焦点弦的性质求解.【详解】设(,)M x y ,设0y >,24p =,2p =, 2OFMS=,又112OFM S y ∆=⨯⨯,12,42y y ∴=∴=,所以2142p k y ===,由对称性,12k =-也适合. 综上,12k =±. 12.D【分析】焦点弦长度等于12x x p ++.【详解】抛物线24y x =的焦点为()1,0在直线10x -=上,故AB 是抛物线的焦点弦,则由2104x y x⎧-=⎪⎨=⎪⎩得:21410x x -+=, 所以,1214x x +=,所以,1214216AB x x p =++=+= 故选:D. 13.B【分析】设(),A x y ,根据5AF =,利用抛物线定义求得点A 的坐标,进而得到直线AF 的方程,求得点B 的坐标,再利用抛物线定义求解. 【详解】解:抛物线的焦点()1,0F ,准线方程为=1x -, 设(),A x y ,则15AF x =+=,故4x =,此时4y =, 即()4,4A ,则直线AF 的方程为014041y x --=--,即()413y x =-, 代入24y x =得241740x x -+=,解得4x =(舍)或14x =, 则15144BF =+=, 故选:B . 14.D【分析】根据抛物线的焦点弦长公式计算. 【详解】抛物线24y x =,可知24p =, 设直线1l 的倾斜角为θ,则2l 的倾斜角为π2θ-,显然2πθ≠, 过焦点的弦,22sin pAB θ=,2222πcos sin 2p pCD θθ==- ①2211sin cos 112224AB CD p p p θθ+=+==, 故选:D . 15.C【详解】①抛物线C 方程为22(0)y px p =>,①焦点(,0)2pF ,设(,)M x y ,由抛物线性质52p MF x =+=,可得52p x =-,因为圆心是MF 的中点,所以根据中点坐标公式可得,圆心横坐标为52,由已知圆半径也为52,据此可知该圆与y 轴相切于点(0,2),故圆心纵坐标为2,则M 点纵坐标为4, 即(5,4)2pM -,代入抛物线方程得210160p p -+=,所以p=2或p=8. 所以抛物线C 的方程为24y x =或216y x =. 故答案C.【点睛】本题主要考查了抛物线的定义与简单几何性质,圆的性质和解直角三角形等知识,属于中档题,本题给出抛物线一条长度为5的焦半径MF ,以MF 为直径的圆交抛物线于点(0,2),故将圆心的坐标表示出来,半径求出来之后再代入到抛物线中即可求出p 的值,从而求出抛物线的方程,因此正确运用圆的性质和抛物线的简单几何性质是解题的关键. 16.C【分析】先求出抛物线的准线方程,分别过,,A B M 作准线的垂线,垂足分别为111,,A B M ,由抛物线的定义可得出答案.【详解】抛物线2:4C y x =的准线方程为:=1x - 分别过,,A B M 作准线的垂线,垂足分别为111,,A B M 则点()02,M y 到准线的距离为213+=根据抛物线的定义可得11,AF AA BF BB ==,且111222AA BB AF BF ABMM ++===所以1||26AB MM == 故选:C17.C【分析】设直线l 的倾斜角为θ,求得1cos 3θ=.过A 作1AA ⊥准线于1A ,过B 作1BB ⊥准线于1B ,过B 作1BC AA ⊥于C .由抛物线定义求出()1AC BF λ=-和()1AB BF λ=+. 在直角三角形ABC 中,利用余弦的定义表示出1cos 3ACAB θ==,即可解得.【详解】设直线l 的倾斜角为θ,根据条件可得tan θ=1cos 3θ=.过A 作1AA ⊥准线于1A ,过B 作1BB ⊥准线于1B ,过B 作1BC AA ⊥于C . 由抛物线定义可得:11,AF AA BF BB ==.因为AF BF λ=,所以()11111AC AA AC AA BB AF BF BF λ=-=-=-=-. 而()1AB AF BF BF λ=+=+.在直角三角形ABC 中,()()11cos 13AC BF AB BF λθλ-===+,解得:2λ=. 故选:C 18.C【分析】确定抛物线的准线方程,由抛物线定义可得()124AF BF y y +=-+,结合条件可得12AF BF +=,结合抛物线的几何性质可得当且仅当A ,F ,B 三点共线时12AB ≤,即可得答案.【详解】设抛物线2:8W x y =-的焦点为F ,则(0,2)F -,焦准距4p =,准线方程为2y =, 根据抛物线的定义得,()124AF BF y y +=-+. 又128y y +=-,所以12AF BF +=.因为AF BF AB +≥,当且仅当A ,F ,B 三点共线时等号成立,即12AB ≤, 所以AB 的最大值为12, 故选:C 19.B【分析】根据抛物线焦点弦的性质以及AF FB λ=,联立可得121,x x λλ==,进而可用对勾函数的性质求12AB λλ=++的最值,进而可求.【详解】解法1:抛物线24y x =的焦点坐标为()1,0,准线方程为=1x -,设()11,A x y ,()22,B x y ,则①AF BF λ=,由抛物线定义可知()1211x x λ+=+①,①121x x λλ=+-,又因为AF FB λ=,所以()()11221,1,x y x y λ--=-,即()1211x x λ-=-②,由①①可得:121,x x λλ==所以()()121112AB AF BF x x λλ=+=+++=++.①133λ≤≤,当=3λ时,1162=3AB λλ=++,当1=3λ时,1162=3AB λλ=++,①max 11623λλ⎛⎫++= ⎪⎝⎭,则弦AB 的中点到C 的准线的距离2AB d =,d 最大值是83.①弦AB 的中点到C 的准线的距离的最大值是83,故选:B.解法2:弦AB 的中点到C 的准线的距离22222sin 22sin sin pAB p d θθθ====,根据结论121cos 10,112λθλλ-⎡⎤==-∈⎢⎥++⎣⎦,223sin 1cos ,14θθ⎡⎤=-∈⎢⎥⎣⎦,2282,sin 3d θ⎡⎤=∈⎢⎥⎣⎦, 故选:B. 20.D【分析】设AB 的方程为y =kx +1代入214y x =,得x 2-4kx -4=0,设()()1122,,A B x y x y ,,得出根与系数的关系,再得出直线OA 的方程为11y y x x =,与2y x =-联立求得点E 、F 的坐标,表示出线段EF ,运用函数的性质可求得最小值得选项. 【详解】由抛物线C ①214y x =,得焦点为()01,,设AB 的方程为y =kx +1代入214y x =,得x 2-4kx -4=0,设()()1122,,A B x y x y ,,所以124x x k +=,124x x =-,12||x x -=216+16>0k ∆=,直线OA 的方程为11y y x x =,联立11121111112,228144Ey x x x x y y x x y x x x x =-⎧⎪⇒===⎨=--⎪-⎩; 同理可得284F x x =-,,所以||EF === 令()430k t t -=≠,则3+4t k=,所以||EF = 当>0t时,||EF = 当0t<时,||EF =≥当253t =-,即43k =-时,取等号,所以|EF| 故选:D.【点睛】方法点睛:(1)解答直线与抛物线的题目时,时常把两个曲线的方程联立,消去x (或y )建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系;(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.有时若直线过x 轴上的一点,可将直线设成横截式. 21.0【分析】设()()1122,,,A x y B x y ,求出1A AF ∠的角平分线方程1122y y x y -=,得到1121,2y M y ⎛⎫-- ⎪⎝⎭;求出在()22,B x y 处的切线方程为: 222224y y x y y ⎛-=⎫- ⎪⎝⎭,得到2221,2y N y ⎛⎫-- ⎪⎝⎭.由124y y =-,整理得M 、N 重合.即可求得.【详解】抛物线24y x =的焦点为()1,0F ,准线为l :=1x -.因为过F 的直线交抛物线于A ,B 两点,所以可设直线AB :1x my =+.设()()1122,,,A x y B x y ,则241x xy y m =+=⎧⎨⎩,消去x 得:2440y my --=.所以2121216160,4,4m y y m y y ∆=+>+==-.不妨设10y >,则2140y y =-<. 因为过点A 作1AA l ⊥,垂足为1A ,所以()111,A y -,1110112A F y yk -==--- 设1A F 的中点为E ,则10,2y E ⎛⎫ ⎪⎝⎭,所以1112AE A F k k y =-=,所以直线AE : 1122y y x y -=. 令=1x -,解得:1122y y y =-,所以1121,2y M y ⎛⎫-- ⎪⎝⎭. 对于点()22,B x y ,因为20y <,由24y x =可得:y =-y '=. 所以在()22,B x y处的切线的斜率为22k y ==,切线方程为:()2222x x y y y =--,即222224y y x y y ⎛-=⎫- ⎪⎝⎭.令=1x -,解得:2222y y y =-,所以2221,2y N y ⎛⎫-- ⎪⎝⎭. 因为124y y =-,所以214y y =-所以1111422422y y y y y -=-=-+-,即1121,2y N y ⎛⎫--+ ⎪⎝⎭所以M 、N 重合. 所以MN =0. 故答案为:0. 22.2【分析】过点F 且斜率为1的直线方程为2p y x =-,联立抛物线C 的方程,求出AB ,EF ,由2AB EF =,即可求出p 的值.【详解】过点F 且斜率为1的直线方程为2p y x =-, 联立抛物线C 的方程,得22304p x px -+=,所以3422p pAB p p =++=, 又因为令2p y x =-中2p x =-,则,2p E p ⎛⎫-- ⎪⎝⎭,又因为,02p F ⎛⎫ ⎪⎝⎭,所以EF ,又因为2AB EF =,所以242p p =,解得p =2. 故答案为:2.23.2##2-+【分析】推导出抛物线的焦半径的性质111AF BF +=,再利用基本不等式可求得2AF BF-的最小值. 【详解】易知12p=,可得2p =,所以,抛物线的方程为24x y =. 若直线l 与y 轴重合时,则该直线与抛物线只有一个交点,不合乎题意. 所以,直线l 的斜率存在,设直线l 的方程为1y kx =+,联立214y kx x y =+⎧⎨=⎩可得244x kx =+,即2440x kx --=,216160k ∆=+>,由韦达定理可得124x x k +=,124x x =-.所以,()()122121212124111111112224k x x AF BF y y kx kx k x x k x x +++=+=+=+++++++ 222441484k k k +==-++,所以,111BF AF =-,则212212AF AF AF BF AF AF ⎛⎫-=--=+- ⎪ ⎪⎝⎭22≥=,当且仅当AF 2AF BF-的最小值为2.故答案为:2. 24.16+【分析】设抛物线的标准方程,将点代入抛物线方程,求得抛物线方程,由抛物线的焦点弦性质,求得111||||3PF QF +=,根据抛物线的性质及基本不等式,即可求得答案.【详解】解:设抛物线的方程:()220y px p =>,焦点为F ,则3623p =⨯,则212p =,①抛物线的标准方程:212y x =,焦点坐标()3,0F ,准线方程为3x =-, 圆222:680C x y x +-+=的圆心为()3,0,半径为1,由直线PQ 过圆的圆心即抛物线的焦点,可设直线l 的方程为:3my x =-, 设P 、Q 坐标分别为()11,x y 和()22,x y ,由2123y x my x =⎧⎨=-⎩联立,得212360y my --=,21441440m ∆=+>恒成立, 由韦达定理得:1212y y m +=,1236y y ⋅=-,①()1212612x x m y y m +=++=,22121291212y y x x ⋅==⨯,①()22112111112661333931269m PF QF x x m +++=+==+++++, 则()()11313134334PN QM PF QF PF QF PF QF PF QF ⎛⎫+=+++=++=+++ ⎪ ⎪⎝⎭(334434416QF PF PF QF ⎛⎫=+++≥++=+ ⎪ ⎪⎝⎭当且仅当)1233PF x x =⇒++时等号成立,故答案为:16+25.8【分析】确定2P =,设直线方程并和抛物线方程联立,求得114y y =-,进而求出12x x +,根据抛物线的弦长公式求得答案.【详解】由题意知2p =,故24y x =,其焦点为(1,0),设直线l 的方程为1,(0)x ky k =+≠ ,联立24y x =,得:2440y ky --= ,216(1)0k ∆=+> ,由于()11,P x y ,()22,Q x y ,则11114,4y y k y y +==-,而124y y +=,故22212121212()2162(4)64444y y y y y y x x +---+=+=== , 故PQ 的长为12628x x p ++=+=, 故答案为:8 26.23【分析】作辅助线,由PN NM =可知PN NM =,由三角形相似结合抛物线定义可求得2MF NF =,从而推得23PF PM =,从而由p FK PF MF ME PM ==求得答案. 【详解】如图,设抛物线准线交x 轴与点K ,分别过M N ,作ME NG ,垂直于抛物线的准线于E G ,, 由PN NM =,得PN NM = ,由抛物线定义可知NF NG FM ME ==,,由PNG PME ∽ ,得12,,PM PM PNPM PN PM ME NG MF NF MF NF =∴=∴= ,2MF NF ∴=,则1111236263NF NM PM PF PN NF PM PM PM ===+=+=,,23p FK PF MF ME PM ∴=== , 故答案为:23. 27.(1)24x y = (2)证明见解析【分析】(1)将MN 用p 表示,得出p 的值,进而得抛物线方程;(2)联立直线与抛物线的方程,根据斜率计算公式结合韦达定理即可得结果. (1)由题意可得24p =,得2p =, ①抛物线2:4C x y =. (2)证明:():2m y k x =+,联立()224y k x x y ⎧=+⎨=⎩,得2480x kx k --=.由216320k k ∆=+>,得0k >或2k <-,设()11,A x y ,()22,B x y ,则124x x k +=,128x x k =-,①2212121212121111442222x x y y k k x x x x ----=⋅=⋅---- ()()()121212222488411616164x x x x x x k k +++++-++====.28.(1)12(2)存在,定点N 为()0,1,MN 为定值1【分析】(1)根据抛物线和过焦点的直线联立方程,根据焦点弦的计算,即可求解.(2)联立方程,得到根与系数的关系,根据以线段PQ 为直径的圆经过点O ,转化成0OP OQ ⋅=,可得直线过定点,再由OM PQ ⊥,根据直角三角形的特征即可找到N 的位置,即可求解. (1)抛物线C :()20y ax a =>化为标准方程为:21x y a =,其焦点10,4F a ⎛⎫⎪⎝⎭,因为斜率一定存在,设其方程为114y k x a=+, 联立方程得:12141y k x a x ya ⎧=+⎪⎪⎨⎪=⎪⎩,整理得:212104k x x a a --=,0∆>恒成立.其中()11,A x y ,()22,B x y ,112k x x a +=,()21121121122k y y k x x a a a+=++=+, 因为焦点弦长2112112k y AB y a a a=++=+,所以当210k =时,弦长min 12AB a ==. 所以,实数a 的值为12. (2)由题意可知直线PQ 的斜率存在,设其方程为()0y kx t t =+≠.联立方程得:22y kx tx y =+⎧⎨=⎩,整理得:2220x kx t --=,2480k t ∆=+>.其中()33,P x y ,()44,Q x y ,342x x k +=,342x x t =-, 因为以PQ 为直径的圆经过点O ,所以0OP OQ ⋅=.又因为2222343434344220224x x t OP OQ x x y y x x t t t ⋅=+=+⋅=-+=-+=, ①0t ≠,①2t =.所以直线PQ 过定点()0,2T ,又因为OM PQ ⊥,所以OMT △为直角三角形, 所以当N 为斜边OT 中点时,MN 为定值, 此时112MN OT ==. 所以定点N 为0,1,MN 为定值1.29.(1)24y x =; (2)证明见解析.【分析】(1)由条件结合抛物线的定义列方程求p 即可;(2)联立方程组,利用设而不求的方法证明2EA EB EF k k k +=即可.【详解】(1)设点00(,)M x y,由题意可知0y =所以202px =,解得08x =. 因为08922p pMF x =+=+=,所以2p =. 所以抛物线C 的方程为24y x =.(2)设直线AB 的方程为2212121,,,,44y y x my A y B y ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,联立方程组24,1,y x x my ⎧=⎨=+⎩消去x 得2440,y my --=,所以12124,4y y m y y +==-.设()1,E n -,则()()22121212121222221212244411114444EA EBy y y y y y y y n n y n y n k k y y y y ⎛⎫+++-+- ⎪--⎝⎭+=+=⎛⎫⎛⎫++++ ⎪⎪⎝⎭⎝⎭22122212244244y y n n y y ⎛⎫-++ ⎪⎝⎭==-++, 又因为2EF nk =-,所以2EA EB EF k k k +=,即直线,,EA EF EB 的斜率成等差数列.【点睛】解决直线与抛物线的综合问题的一般方法为设而不求法,要证明直线,,EA EF EB 的斜率成等差数列只需证明2EA EB EF k k k +=即可. 30.(1)证明见解析(2)0<≤p【分析】(1)设22121212,,,,022⎛⎫⎛⎫>> ⎪ ⎪⎝⎭⎝⎭y y A y B y y y p p ,即可表示M 、N 的坐标,再由直线OA 的方程,得到P 点坐标,同理可得Q 点坐标,从而得证;(2)依题意可得OQ PQOQ QN ⎧≥⎪⎨≥⎪⎩,即可求出1y 、2y ,再根据三角形面积求出p 的取值范围;(1)解:设22121212,,,,022⎛⎫⎛⎫>> ⎪ ⎪⎝⎭⎝⎭y y A y B y y y p p , 则22121212,,,,,042222⎛⎫+++⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭y y y y p y y p M N F p , 由于A ,F ,B 三点共线,则1222122222=--y y y py p p p ,整理得212y y p =-, 又12:OA pl y x y =, 则22112,42⎛⎫-+ ⎪⎝⎭y p y y P p ,同理可得22212,42⎛⎫-+ ⎪⎝⎭y p y y Q p 则2222221212||444+-+=-=y y y p y p PM p p p, 222222||424-+=+=y p p y p QN p p,所以||||=PM QN ,即证;(2)解:若线段NP 上的任意一点均在以点Q 为圆心、线段QO 长为半径的圆内或圆上,即OQ PQ OQ QN ⎧≥⎪⎨≥⎪⎩,则22222222121222222222122424424y p y y y y p p y p y y y p p p ⎧⎛⎫⎛⎫-+-⎛⎫⎪+≥ ⎪⎪ ⎪⎝⎭⎪⎝⎭⎝⎭⎨⎛⎫⎛⎫⎪-++⎛⎫+≥ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎩, 化简得4422112215168164-+≥-p y y p y p ,2212≥y p , 即24422211221541681644-≥-+≥-≥-p p y y p p y p可得1y =,又因为212y y p =-,2212=-=-p y p y,12221212222-===+-AB y y p k y y y y p p可得2⎛⎫- ⎪⎝⎭p N p,58⎛⎫ ⎪⎝⎭p M p,12=-=h y y ,119228=⨯⨯=⨯≤NABp SNM h 2329≤p,即0<≤p 31.(1)24y x =; (2)证明见解析.【分析】(1)根据点在抛物线上的性质,结合锐角三角函数定义进行求解即可;(2)将直线方程与抛物线方程联立,根据一元二次方程根与系数关系,结合平面向量夹角公式进行计算证明即可. (1)因为抛物线H 的方程为22y px =,M 抛物线H 上且的横坐标为5, 所以M的纵坐标为当点M的坐标为(时,过点M 作MN OF ⊥,垂足为N ,因为2cos 3OFM ∠=-,所以2cos 3MFN ∠=,所以tan MFN ∠=又tan 52MN MFN FN ∠==-52=-所以100p +=,所以0=,又0p >所以2p =,同理当点M 的坐标为(5,时,2p =所以抛物线H 的方程为24y x =; (2)设直线AB :1x my =+,()11,A x y ,()22,B x y ,()1,C n -,由214x my y x=+⎧⎨=⎩,得2440y my --=, 则124y y m +=,124y y =-,21242x x m +=+,121=x x .()111,CA x y n =+-,()221,CB x y n =+-()()2212121212120CA CB x x x x y y n y y n m n ⋅=++++-++=-≥,所以cos ,0CA CB 〈≥〉,所以π2ACB ∠≤. 【点睛】关键点睛:利用平面向量夹角公式是解题的关键. 32.(1)24y x =(2)证明见解析;P 点坐标为(4,0) (3)16-【分析】(1)过点B 作准线的垂线,垂足为H ,设准线与x 轴相交于点M ,由直线的斜率得出倾斜角,利用三角函数及抛物线的定义求出||MF 即可得解;(2)设直线CD 的方程为:x my t =+,211,4y C y ⎛⎫ ⎪⎝⎭,222,4y D y ⎛⎫⎪⎝⎭,联立方程组,由根与系数的关系求出12y y ,再由OC OD ⊥建立斜率的方程即可得解; (3)由向量的数量积坐标运算化简,利用二次函数求最值. (1)过点B 作准线的垂线,垂足为H ,设准线与x 轴相交于点M ,如图,由题知,直线l 的倾斜角为π3.①在R t BGH 中,π3GBH ∠=, 又①83BG =,①43BH =,①43BF =.①4GF BG BF =+=,①在R t GFM 中,又3MFG π∠=,①2MF =,①2p =,①抛物线的标准方程为24y x =. (2)由(1)可知,抛物线方程为24y x =,设直线CD 的方程为:x my t =+,211,4y C y ⎛⎫ ⎪⎝⎭,222,4y D y ⎛⎫⎪⎝⎭, 直线与抛物线联立:24x my ty x=+⎧⎨=⎩,得:2440y my t --=,则124y y m +=,124y y t ,①14OC k y =,24OD k y =且OC OD ⊥,①12161614OC OD k k y y t⋅===--则4t =, ①直线CD 过定点(4,0),即P 点坐标为(4,0), (3)由(2)可知P 点坐标为(4,0),①()2222212121216161616y y PC PD y y y y m ⋅=-+++=--, ①PC PD ⋅的最大值为16-. 33.(1)28y x = (2)λμ=【分析】(1)根据直线与圆的位置关系可得3R x =+,根据圆与圆的位置关系可得1R =,列出方程,解之即可;(2)设直线l 的方程为()2y k x =-、()11,A x y 、()22,B x y ,法一:由平面共线向量的坐标表示和定点分比公式可得()241k λλ=+、()241k μμ=+,列出方程,解之即可;法二:联立抛物线方程,利用韦达定理和平面共线向量的坐标表示,化简计算可得112x x λ=-、222x μ=-,证明0λμ-=即可.【详解】(1)设(),P x y ,圆P 的半径为R ,由题可知,点P 在直线3x =-右侧, 因为圆P 与定直线3x =-相切,所以3R x =+. 又圆P 与圆F内切,所以11R PF =+=,所以31x +=,化简得28y x =,即E 的方程为28y x =.(2)解法一:由(1)得()2,0F ,设直线l 的方程为()2y k x =-,()11,A x y ,()22,B x y , 则()0,2M k -,因为MA AF λ=,由定点分比公式可知121x λλ=+,121ky λ-=+ 因为点A 在E 上,所以2118y x =,即()2241611k λλλ=++,所以()241k λλ=+. 同理,由MF FB μ=,可得222,11x k y F μμμμ⎛⎫-+ ⎪++⎝⎭, 所以221x μμ=+,2201k y μμ-+=+,即()221x μμ+=,22ky μ=, 因为点B 在E 上,所以2228y x =,即()221614k μμμ+=,所以()241k μμ=+.由()()4141λλμμ+=+,得()()10λμλμ-++=, 因为0λ>,0μ>,所以10λμ++≠,即0λμ-=.解法二:设直线l 的方程为()2y k x =-,()11,A x y ,()22,B x y ,则()0,2M k -.由()282y x y k x ⎧=⎪⎨=-⎪⎩,整理得()22224840,k x k x k -++=, 由韦达定理可知212248k x x k ++=,124x x =.因为MA AF λ=,即()()1122,22,x y k x y λ+=--,所以112x x λ=-. 由MF FB μ=,可得()()222,22,k x y μ=-,所以222x μ=-. 所以()()()()()()211112121212222420222222x x x x x x x x x x x x λμ-+---=-===------, 即λμ=.。
抛物线焦点弦问题

抛物线焦点弦问题河北省武安市第一中学郅武强抛物线焦点弦问题较多,由焦点引出弦的几何性较集中,现总结如下:一.弦长问题:例斜率为1的直线经过抛物线24y x =的焦点,与抛物线相交A .B两点,求线段AB 的长。
分析:利用弦长公式12d x =-能解此题,但运算量较大也较复杂,如果能够运根据抛物线的定义,11AF x =+同理 21BF x =+于是得122AB AF BF x x =+=++由题已知{214y x y x=-=消去y 得2610x x -+=故126x x += ∴628AB =+= 注:焦点弦在标准抛物线方程下的计算公式:12AB x x p =++或12AB y y p=++。
二. 通径最短问题:例:已知抛物线的标准方程为22y px =,直线l 过焦点,和抛物线交与A.B 两点,求AB 的最小值并求直线方程。
解:①如果直线l 的斜率不存在,则直线l 的方程为2px =2A B p =②如果斜率存在,不妨设斜率为k ,则直线的方程为(2p y k x =-,与抛物线方程联立方程组得22( 2y pxp y k x ==-⎧⎨⎩消去y 得22222(2 04k p k x k p p x -++=若0k ≠ 则222440k p p ∆=+>1222px x p k +=+则1222222p p AB x x p p p p k k =++=++=+当k →∞时 AB最小即min 2AB p = 此时 2px =三.两个定值问题:例:过抛物线22y px =的焦点的一条直线和抛物线相交,两个焦点的横、纵坐标为1x 、2x 、1y 、2y ,求证:2114p x y =,212y y p =-。
证明:①联立22( 2y px p y k x ==-⎧⎨⎩消去y 得22222(2 0(04k p k x k p p x k -++=≠2124p x x =同理消去y 可得 212y y p =-;②斜率为0时,直线与抛物线不能有两个交点;③斜率不存在时,2114p x y = ,212y y p =-同样是定值;从上所述:2114p x y =,212y y p =-四.一个特殊直角问题:过抛物线22(0 y px P =>的焦点F 的直线与抛物线交与A 、B 两点,若点A 、B 在抛物线的准线上的射影分别是1A ,1B 求证:1190A FB ︒∠=。
(完整版)抛物线的焦点弦_经典性质及其证明过程
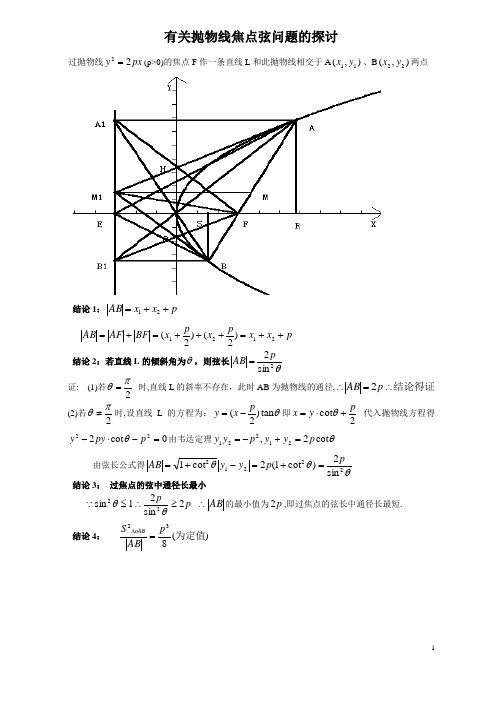
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
抛物线的焦点弦性质

法二:由题知AB不与x轴平行 p 设AB方程为x my ,(m R) 2 y 2 2 px p 2 p y 2 p (my ) 2 x my 2 y
即:y 2 pmy p 0
2 2
A
y1 y2 p (定值)
2
O
F B
1 当AB x轴时,
O B
F
x
20 AB斜率存在时设为k,(k 0)
2
y p 2 py 2 消元得y 2 ( p )即y p2 0 k 2 k 2 2 2 y1 y1 p 2 y1 y2 - p ;x1 x2 2 p 2 p 4
p 则直线AB方程为y=k(x- ) 代入抛物线方程y2 2 px 2
1 同理, k
以代k得B(2pk2, -2pk) .
1 2 x p ( k ) 0 k2 y p( 1 k ) 0 k
1 1 2 k 2 (k ) 2 k k
2
x0 y0 2 ( ) 2 p p
即 y02 = px0-2p2,
2 px y1 2 px1 y1 y2 2 px 2 px1 y y y1 y1 y2 y1 y2 y1 y2 y1 y2
2 2 px 4 p 2 y1 2 px1 , y1 y2 4 p2 y y1 y2 y1 y2
2 p | y1 y2 | 4 p2
当且仅当|y1|=|y2|=2p时,等号成立.
例3. A、B是抛物线 y2 = 2px(p>0)上的两点,且OA⊥OB, (5)求O在AB上的射影M轨迹方程. y (5)法一:设M(x3, y3), 则 kOM 3 x3 x
[很全]抛物线焦点弦的有关结论
![[很全]抛物线焦点弦的有关结论](https://img.taocdn.com/s3/m/ef2d77a3c1c708a1284a44ba.png)
p2 .
4
综上: x1x2
p2 .
4
(2)Q x1
y12 2p
,
x2
y22 2p
, y12 y2 2
p4
y1 y2
p2,
但 y1 y2 0, y1 y2 p 2
(2)另证:设
AB :
x
my
p 2
与
y2
2 px 联立,得
y2
2 pmy
p2
0,
y1 y2
y 2 2 px
t
y2
2 pay
2 pt
0
y1 y2 2 pt ②
由①②得 t p 2
AB 恒过焦点 p ,0 2
5
抛物线 y 2 2 pxp 0
成立。
,过(2p,0)的直线与之交于 A、B 两点,则 OA⊥OB。反之也
小结: (1)抛物线中的焦点弦问题很多都可以转化为这个直角梯形中的问题,在解决这类问题 时注意对这个梯形的运用; (2)万变不离其宗,解决问题的关键仍然是抛物线定义.
m
n
mn
sin y1 y2 mn
S AOB
1 m nt
2
y1 y2 1 m nt
mn 2 mn
y1 y2
而 S AOB
p2 4
n m
m n
1 2
m n
mn
p2 2
t
y1 y2
p2 2
①
l : x ay 又可设
抛物线焦点弦问题(附答案解析)

(难度3星)1.(2019·安徽高二期末(文))在平面直角坐标系xxx 中,抛物线x 关于x 轴对称,顶点为坐标原点,且经过点(2,2).(1)求抛物线x 的标准方程;(2)过点x (1,0)的直线交抛物线于M 、N 两点,P 点是直线x :x =−1上任意一点.证明:直线xx、xx、xx 的斜率依次成等差数列.【答案】(1)x 2=2x ;(2)证明见解析【解析】(1)因为抛物线x 关于x 轴对称,可设抛物线为x 2=2xx ,而点(2,2)在抛物线上, 从而有22=2x ×2,得x =1,故抛物线方程为x 2=2x ;(2)设点x (−1,x )是直线x 上任意一点,—直线交抛物线于M 、N 两点,所以直线xx 的斜率不等于0,可设直线xx :x =xx +1交抛物线于x (x 1,x 1)、x (x 2,x 2),由{x =xx +1x 2=2x可得:x 2−2xx −2=0 从而有x 1+x 2=2x ,x 1x 2=−2,x xx =x 1−x x 1+1,x xx =x 2−x x 2+1,x xx =−x 2且在直线上,所以有:x 1=xx 1+1,x 2=xx 2+1x xx +x xx =x 1−x x 1+1+x 2−x x 2+1=2xx 1x 2+(2−xx )(x 1+x 2)−4x x 2x 1x 2+2x (x 1+x 2)+4 =−2xx 2−4x 2x +4=−x ,而2x xx =−x ,即证x xx +x xx =2x xx .得证直线xx ,xx ,xx 的斜率成等差数列.【(难度2星)2.(2020·河南高二期末(理))已知x 是抛物线x :x 2=2xx(x >0)的焦点,x (1,x )是抛物线上一点,且|xx |=2.(1)求抛物线x 的方程;(2)直线x 与抛物线x 交于x ,x 两点,若xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =−4(x为坐标原点),则直线x是否会过某个定点若是,求出该定点坐标,若不是,说明理由.【答案】(1)x 2=4x ;(2)是,x (2,0).【解析】(1)由抛物线的定义知|xx |=1+x 2=2,∴x =2,∴抛物线x 的方程为:x 2=4x*(2)由题意知:可设xx 的方程为:x =xx +x ,代入x 2=4x 有x 2−4xx −4x =0,设x (x 1,x 1),x (x 2,x 2),则x 1⋅x 2=−4x ,∴x 1⋅x 2=(x 1⋅x 2)216=x 2,∴xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =x 1⋅x 2+x 1⋅x 2=x 2−4x =−4∴x =2∴xx 的方程为x =xx +2,恒过点x (2,0).所以直线x 过定点(2,0).?(难度2星)3.(2020·江西高二期末(文))已知抛物线x :x 2=2xx (x >0)的焦点F 为圆x 2+x 2−2x =0的圆心.(1)求抛物线C 的标准方程;(2)过抛物线的焦点F 的直线l 与抛物线相交于xx 两点,且|xx |=5,求直线l 的方程.【答案】(1)x 2=4x (2)x =2x −2或x =−2x +2【解析】(1)圆的标准方程为(x −1)2+x 2=1,圆心坐标为(1,0),即焦点坐标为x (1,0),则x 2=1,x =2得到抛物线x 的方程x 2=4x(2)设直线x 的方程为:x =xx +1联立抛物线x 的方程x 2=4x 消x 整理得: 》x 2−(4x 2+2)x +1=0 ∴x 1+x 2=4x 2+2根据焦点弦的性质可知:|xx |=x 1+x 2+x =4x 2+4 又因为|xx |=5∴4x 2+4=5解得x =±12所以所求直线x 的方程为:x =2x −2或x =−2x +2(难度2星)4.(2019·四川高二期末(文))已知点x (−2,0),x (3,0),动点x (x ,x )满足: xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =x 2−6.(1)求动点P 的轨迹x ;-(2)已知点x (14,0),若曲线E 上一点M 到x 轴的距离为12,求|xx |的值.【答案】(1)焦点在x 轴,开口向右的抛物线x 2=x ;(2)12【解析】(1)x 点坐标为(x ,x ),则有:xx⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(−2−x ,−x ),xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(3−x ,−x ) ∴xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =x 2−x −6+x 2=x 2−6,即:x 2=x ,∴点P 的轨迹为焦点在x 轴,开口向右的抛物线.(2)由题意可得:x x =±12代入方程求得x x =14,所以x (14,±12),而x (14,0)∴|xx |=√(14−14)2+(±12−0)2=12 ,即|xx |=12.。
(完整版)抛物线的焦点弦_经典性质及其证明过程
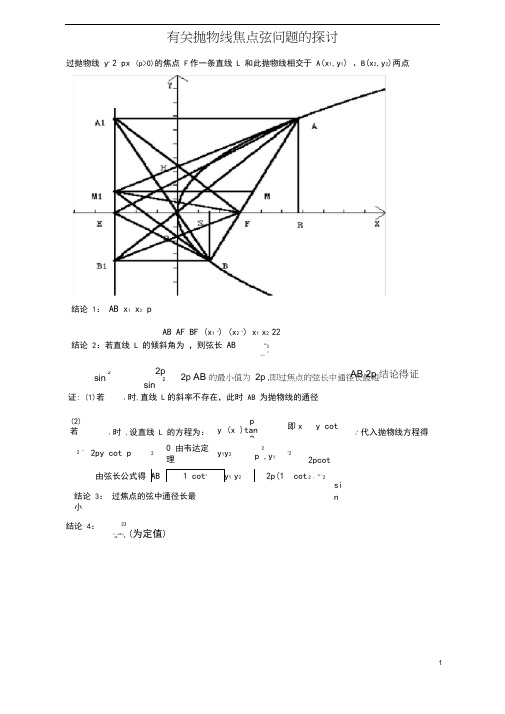
有关抛物线焦点弦问题的探讨过抛物线 y 22 px (p>0)的焦点 F 作一条直线 L 和此抛物线相交于 A (x 1,y 1) 、B (x 2,y 2)两点结论 1: AB x 1 x 2 pAB AF BF (x 1 p) (x 2 p) x 1 x 2 22结论 2:若直线 L 的倾斜角为 ,则弦长 AB 2p 2sin2结论 4:23S ABoAB p8(为定值)(2)若2时 ,设直线 L 的方程为: py (x )tan2 即xy cot2p代入抛物线方程得2 y2py cot p 2 0 由韦达定理y 1y 2 2 p ,y 1y22pcot2 )2p )2由弦长公式得 AB 1 cot 2y 1 y 2 2p(1 cot证: (1)若2时,直线 L 的斜率不存在,此时 AB 为抛物线的通径si n结论 3: 过焦点的弦中通径长最小 AB 2p 结论得证 2sin2p 2sin2p AB 的最小值为 2p ,即过焦点的弦长中通径长最短同理 B 1FOB 1FBA 1FB 1 90A 1FB 1 F2结论 8:(1)AM 1 BM 1 (2)M 1F AB (3) M 1F AF BF(4)设 AM 1 与 A 1F 相交于 H ,M 1B 与 FB 1相交于 Q 则M 1,Q ,F ,H 四点共圆 (5) AM 12M 1B 24M 1M 2证:由结论( 6)知 M 1 在以 AB 为直径的圆上 AM 1 BM 1A 1FB 1为直角三角形, M 1 是斜边 A 1 B 1 的中点A 1M 1 M 1F M1FA 1M1A 1FAA 1F AFA 1AA 1FFA 1MAA 1M190AFA 1A1FM190M 1FABM 1F2AFBFAM 1BM 1 AM1B 90又 A 1FB 1FA 1FB 1 90 所以 M 1,Q , F,H 四点共圆, AM 1 2M 1B 2AB 22 2 2 2AF BF 2AA 1 BB 1 22MM 1 24MM 1 2结论 9: (1) A 、O 、B 1 三点共线 ( 2)B ,O ,A 1 三点共线(3)设直线 AO 与抛物线的准线的交点为 B 1,则 BB 1平行于 X 轴( 4)设直线 BO 与抛物线的准线的交点为 A 1,则 AA 1平行于 X 轴S OAB SOBF1S 0AFOFBF 1sin 2OF AF sin OF 2S OABAB结论 5: (1) 证x 1AFP 3y 1y 22y1 2p ,x 2BF 2p 2sinOF AB sinp22psin2 sin 22 p2sin(2) x 1x 2=2 y22px 1x 2(y 1y 2)24P 2P 2结论 6:以 AB 证:设 M 为 AB 的中点,过 A 点作准线的垂线 过 M 点作准线的垂线 MM 1,由梯形的中位线性质和抛物线的定义知 为直径的圆与抛物线的准线相切AA 1, 过 B 点作准线的垂线 BB 1,MM 1结论 7:连接 A 1F 、 AA 1 AF,AA 1 BB 1 AF BF22B 1 F 则 A 1FAA 1F B 1FAB 2故结论得证AFA 1 AA 1 //OF AA 1FA 1FO A 1FO A 1FA41E,因为直线 L 的倾斜角为证:因为 k oAy1 x1y12 y12p,k oBoB 1y 11y2 p2y2,而 y 1y 2 p2 p2p2所以 k oA2p2 p y22y 2 pk oB 1所以三点共线。
探究抛物线中的焦点弦问题

'
'
A´
A F Q 90
Q
x
B´
探究二:角度(圆与直线位置关系)问题
已 知 过 抛 物 线 y 2 p x ( p 0 )的 焦 点 F 的 直 线
2
交 抛 物 线 于 A, B两 点 , A , B 为 A, B在 准 线 上 的射影, y
'
'
A´ Q
x
以 Q为 圆 心 , 以 A B
P
x
A Q B 90
B´
探究二:角度问题
已 知 过 抛 物 线 y 2 p x ( p 0 )的 焦 点 F 的 直 线
2
交 抛 物 线 于 A, B两 点 , A , B 为 A, B在 准 线 上 的射影,
y
'
'
A ´
N
C
以 F B为 直 径 的 圆 切 y轴 于 N 点
2
交 抛 物 线 于 A, B两 点 , 这 两 点 的 横 坐 标 分 别 为 x 1, x 2,
y
问 :A B ?
A´
(x1,y1)
A B x1 x 2 p
x
B´
(x2,y2)
探究二:角度(圆与直线位置关系)问题
已 知 过 抛 物 线 y 2 p x ( p 0 )的 焦 点 F 的 直 线
'
'
为 直 径 的 圆 切 A B于 F 点
B´
探究二:角度问题
已 知 过 抛 物 线 y 2 p x ( p 0 )的 焦 点 F 的 直 线
2
交 抛 物 线 于 A, B两 点 , A , B 为 A, B在 准 线 上 的射影,
抛物线的焦点弦问题

(3)x2 2 py,
| AB | y1 y2 p
(4)x2 2 py, | AB | p y1 y2
例:过抛物线y2 2 px( p 0)的焦点的一条直线和
这条抛物线相交,两个交点的纵坐标为y1,y2 ,
求证 : y1 y2 p2.
y
证法 :因直线AB过定点F且与x轴
变题3 : 设M (a,0)是抛物线y2 2 px B
( p 0)的轴上的一个定点, 过M的
直线交抛物线于A(x1, y1)、B (x2, y2 )
两点,求证 : y1 y2与x1x2均为定值.
2.过抛物线 y2 2 px( p 0)的焦点的一条直线和
这条抛物线相交 , 两个交点的纵坐标为 y1、y 2,
|
PF
|
- y0
p 2
例1 :
(1)抛物线y2 x上一点P到焦点的
距离为2,则P点的坐标为__答_案__: P___74_,.
7
2
(2)抛物线y2 2x上两点A, B到焦点的距离
之和是5,则线段AB中点横坐标是 _答_案_:_2..
例2.斜率为1的直线过抛物线y2 4x的焦点,
交抛物线于A, B两点, 通过点A
A
和 抛 物线顶点的直线交抛物 o
线的准线于点D ,求 证 :直线
F DB
x
DB平行于抛物线的对称轴.
分析 我们用坐标法证明,即通 过建立抛物线及直线的方程, 借
图2.3 5
助方程研究直线DB与抛物线对
称轴之间的位置关系.
建立如图2.3 5所示的直角坐标系,只要证明 点D的纵坐标与点B的纵坐标相等即可.
抛物线焦点弦8个结论

抛物线焦点弦8个结论抛物线是一种常见的二次曲线,在数学和物理学中有广泛的应用。
抛物线的焦点是其特殊的性质之一,下面将介绍抛物线焦点的八个结论。
一、焦点到顶点的距离等于焦半径的长度。
抛物线的焦半径是从焦点到抛物线的准线的垂直距离,而抛物线的顶点是其最高点。
这个结论表明,焦点到顶点的距离等于焦半径的长度。
二、焦半径与准线垂直。
焦半径是从焦点到抛物线上的任意一点的线段,而准线是抛物线的对称轴。
这个结论说明,焦半径与准线垂直。
三、焦点到直线的距离等于焦半径的长度。
抛物线上的任意一点与其焦点之间的距离等于该点到抛物线的准线的垂直距离。
这个结论说明,焦点到直线的距离等于焦半径的长度。
四、焦点到抛物线的切线的距离等于焦半径的长度。
抛物线上的任意一点与其焦点之间的距离等于该点到抛物线的切线的垂直距离。
这个结论表明,焦点到抛物线的切线的距离等于焦半径的长度。
五、焦点是抛物线上的所有切线的焦点。
抛物线上的任意一点都可以作为抛物线的切点,而焦点是抛物线上的所有切线的焦点。
这个结论说明,抛物线上的所有切线都会经过焦点。
六、抛物线上的所有切线与准线的交点都在焦点上。
抛物线上的任意一点都可以作为抛物线的切点,而抛物线上的所有切线与准线的交点都在焦点上。
这个结论表明,抛物线上的所有切线都会与准线在焦点上相交。
七、焦点是抛物线上的所有法线的焦点。
抛物线上的任意一点都可以作为抛物线的切点,而焦点是抛物线上的所有法线的焦点。
这个结论说明,抛物线上的所有法线都会经过焦点。
八、抛物线上的所有法线与准线的交点都在焦点上。
抛物线上的任意一点都可以作为抛物线的切点,而抛物线上的所有法线与准线的交点都在焦点上。
这个结论表明,抛物线上的所有法线都会与准线在焦点上相交。
通过以上八个结论,我们可以更好地理解抛物线的性质和特点。
抛物线焦点的研究不仅对于数学学科有重要意义,也在物理学、工程学等领域中有广泛的应用。
对于工程设计、物理实验等方面的问题,我们可以利用抛物线焦点的性质来解决。
抛物线焦点弦性质经典30条 (1)

112t1 2 1 2t t P P+ 2= P P p y 2 抛物线性质 30 条已知抛物线 y 2= 2 px ( p > 0) ,AB 是抛物线的焦点弦,点 C 是 AB 的中点.9. C 'F ⊥ AB ;证明: C 'F ⋅ AB = ( p , -y 1 + y22 ) ⋅ (x 2 - x 1, y 2 - y 1)14. 过抛物线准线上任一点 P 作抛物线的切线,则过两切点 Q 1、Q 2的弦必过焦点;并且 PQ 1 ⊥ PQ 2 .pAA’垂直准线于 A’, BB’垂直准线于 B’, CC’垂直准线于 C’,CC’交抛物 y 2 - y 2 y 2 y 2 y 2 - y 2 证明:设点 P (- 2 , t )(t ∈ R ) 为准线上任一点,过点 P 作抛物线的切线,切线于点 M ,准线交 x 轴于点 K. 求证:= p (x 2 - x 1 ) + 1 2 = 2 - 1 + 1 2 = 0y 2 2p p2 2 2 2 点 为 Q ( , y ) , y = 2 px 两 边 对 x 求 导 得1. | AF |= x 1 + 2 ,| BF |= x 2 + 2 ,2 p1 12 yy ' = 2 p , y ' = p , ∴ p = K=y - t ,∴ y 2 - 2ty - p 2 = 0,2. CC ' = AB = ( AA ' + BB ' ) ;y yPQy 2 + p2 22 p 210. AF =1- c os α; BF = 1+ cos α;显 然 ∆ = 4t 2 + 4 p 2> 0,切 点 有 两 个 , 设 为 证 明 : 作AH垂 直 x轴 于 点 H , 则y 2y 2 2Q 1 ( 1 , y 1 ),Q 2 ( 2, y 2 ), 则 y 1 + y 2 = 2t , y 1 y 2 = -p , | AF |=| AA ' |=| KF | + | FH |= p + | AF | cos α,∴| AF |=p. 同理可1- cos α证另一个.2 p ∴ k FQ - kFQ 2 = 2 p y 1 - y 2 p y 2 = y 2 p 2py 1 - y 2 - p 22py 2 y 2 - p 23.以 AB 为直径的圆与准线 L 相切;证明:CC’是梯形 AA’BB’的中位线,1 -2 p 2 - 1 22 p 2 | AB |=| AF | + | BF |=| AA '| + | BB '|= 2 | CC '|= 2r= 2 py 1 - 2 py 2= 2 p - 2 p = 0, 所以 Q Q 过焦点. y 2+ y y y 2 + y y y + y y + y 1 21111. ; 1 1 22 1 212 1 2Py 2p y 2p y 2 y 2 y 2 + y 2p 2 2PQ 1 ⋅ PQ 2 = ( 1 + , y 1 -t )⋅( 2 + , y 2 -t ) = 1 2 + 1 2+ + y 1y 2 -t (y 1 + y 2 ) +t 4. ∠AC 'B = 90;(由 3 可证)5. ∠A 'FB ' = 90;证明:由 AF = 1- c os α ; BF = 1+ cos α;得证.2p 2 2p 2= -p 2+ y 2 + y 2- 2= - p 2 + ( y 4p 24 4 + y )2 - 2 y y - 2 = - p 2 + 4t 2 + 2 p 2 - 2 = 证明: AA ' FK ,∴∠A 'FK = ∠FA 'A ,| AF |=| AA ' |,∴∠AA 'F = ∠AFA ',∴∠A 'FK =1 ∠AFK ,212. 点 A 处的切线为 y 1 y = p (x + x 1 ) ;2 4 2 4 2 4∴ PQ 1 ⊥ PQ 2 .'1 证明:(方法一)设点 A 处切线方程为 y - y = k (x - x ) ,与 y2 = 2 px 联立, 同理: ∠B FK = 2 ∠BFK ,得证.11得ky 2- 2 py + 2 p ( y - kx ) = 0, 由 ∆ = 0 ⇒ 2x k 2- 2 y k + p = 0,15.A 、O 、 B '三点共线;B 、O 、 A '三点共线;1111证 明 : A 、 O 、 B '三 点 共 线6. C 'F = 1A 'B ' .解关于 k 的一元二次方程(它的差别式也恰为 0)得: k = y 1 2x = p,得证. y⇐ k OA = k OB ' ⇐ x 1 y 2 = - 2y 1 ⇐ 1 y 2 = -y 1 ⇐ y 1 y 2 = - p . 2证明:由∠A 'FB ' = 90得证.证 法 二 : ( 求 导 )y 2 = 2 px 11两 边 对 x 求 导 得2 2 p 2同理可证:B 、O 、 A '三点共线.2 yy ' = 2 p , y ' = p , y ∴ y ' | x = x 1 = p , 得证.y 116. y ⋅ y = - p 2; x ⋅ x = p7. AC ' 垂直平分 A 'F ; BC '垂直平分 B 'F ;12124p 2' 1 ' ' ' = 1 ' ' ' ' 证 明 : 设 AB 的 方 程 为 y = k (x - 2) , 与 y = 2 p x 联 立 , 得证明:由 C F = A B 2可知, | C F | 2 | A B |=| C A |,ky 2 - 2 py - kp 2 = 0,又 | AF |=| AA ' |,∴得证. 同理可证另一个.2 py 2 y 2 p 4 p 2 13. AC ' 是切线,切点为 A ; BC '是切线,切点为 B ;∴ y + y = , y y = - p 2 , ∴ x x = 1 ⋅ 2= = . 证 明 : 易 求 得 点 A 处 的 切 线 为 y 1 y = p (x + x 1 ) , 点 B 处 的 切 线 为1 2 k1 22 p1 22 p 2 p 4 p 24 8. AC ' 平分 ∠A 'AF , BC ' 平分 ∠B 'BF ,A ’F 平分 ∠AFK , B ’F 平分 y 2 y = p (x + x 2 ) ,解得两切线的交点为C '(- p ,y 1 + y 2) ,得证. 2 217. AB = x 1 + x 2 + p = sin 2 αp p∠BFK .证明:由 AC ' 垂直平分 A 'F 可证.证明: AB = | AB |= AF + FB = x 1 + 2 + x 2 + = x 1 + x 2 + p ,2 p = 2 p 1+ cot 2α = 2 p . 得证. sin 2αAF BF 1 + 1 k 2 ( y + y ) 2 - 4 y y 1 2 1 21 + 1 (2 p ) 2 + 4 p 2 k 2 k 1 + 1 k 22 0,p 2( y + y )2- 4y y 1 2 1 2p 2 2 ( k ) + 1 1 2 1+ 1 k 2 1+ 1 k 2 11 21 2 2 AF APAP AA p 2 25. 设 CC’交抛物线于点 M ,则点 M 是 CC’的中点;28.设点 A 、B 在准线上的射影分别是 A 1,B 1,则 PA 垂直平分 A 1F , PB 垂18. S ∆AOB =2 sin α;C ( x + x , y + y ), C '(- p ,y + y),∴CC '中点横坐标为 x + x - p , 直平分 B 1F ,从而 PA 平分∠A AF ,PB 平分∠B BF1 p p 证:1 2 1 2 1 2 1 22 2 2 2 4 证明: k ⋅ k=p ⋅ 10 - y 1 = p⋅ (- 1y 1) = - 1,∴ PA ⊥ A F ,证明:S ∆AOB = S ∆OFA + S ∆OFB = ⋅ = y 1 + y 2 2PAA 1Fy p p y p 12 2 4把 y =2代入 y = 2 px ,得1- (- )1= p 2 2p 2 2 2222= 21+ cot α= 2 sin α.y 1 + y 2 + 2y 1 y 2 = 2 px , ∴ 2 px 1 + 2 px 2 - 2 p = 2 p x , x = x 1 + x 2 - p .又| AF |=| AA 1 | ,所以 PA 垂直平分 A 1F. 同理可证另一个. 4 4 4y 2 p ypx + x - p证法二: k AF = 1= 1 ,k AP = ,k AA = 0, 所以点 M 的横坐标为 x = 1 2 .点 M 是 CC’的中点.y - p y - p 2 2 y 1 11 1 32 ∆AOB⎛ p ⎫2 pp 2当弦 AB 不过焦点时,设 AB 交x 轴于点 D (m , 0) (m > 0) ,设分别以 A 、B 2 p 219.= 2⎪ (定值);证:由 AB=sin 2α、S ∆AOB =2 sin α得证.k - kk - k ⎝ ⎭为切点的切线相交于点 P ,求证:26.点 P 在直线 x = -m 上证明:设 AB : x = ty + m , 与 y 2= 2 px 联立,得∴ t an ∠FAP - tan ∠PAA = AF AP - APAA 111+ k ⋅ k 1+ k ⋅ k 12py p p p21 - -0 2py - (y2 - p 2 )py 2 - 2 pty - 2 pm = 0,∴ y + y = 2 pt , y y = -2 pm ,y 2 - p 2y 1 y 1 y1 p py2 + p3 p p p 20. S ∆ABC ' =21 2 1 2= 1 - 1 = 1 - = 1 - = - = 0sin α⎧ P A : y y = p ( x + x )y 2y 2y + y2py p py 2 - p 2 + 2p 2y y (y 2 + p 2 ) y yy又由⎨1 1, 相减得( y- y ) y =1-2 ,∴ y =12,1+ 1 ⋅ 1+ ⋅0 1 1 1 1 111证明: S ∆ ABC ' = 1 | AB | ⋅ | PF |= 1 ⋅ 2 p ⋅ 2 2 12⎩ P B : y 2 y = p ( x + x 2 )y 2+ y y y222 2y 2 - p 2 y 1y 1p 2代入 y 1 y = p (x + x 1 ) 得, 1 1 2= px + 1 ,∴ y 1 y 2 = 2 p x ,∴ x = -m , ∴ t an ∠FAP = tan ∠PAA , ∴∠FAP = ∠PAA . 同理可证另一个= p ⋅ p 2 (1+ 1 )= k 2 sin 2 α22得证.1129. ∠PFA = ∠PFB 证明:21. AB ≥ 2 p ;证明:由 AB2 psin 2 α得证.∆PAA 1 ≅ ∆PAF ⇒∠PFA = ∠PA 1A ,同理:∠PFB = ∠PB 1B ,∴只需证∠PA 1A = ∠PB 1B , 易证: | PA 1 |=| PF |=| PB 1 |,∴∠PA 1B 1 = ∠PB 1 A 1, ∴∠PA 1 A = ∠PB 1B ,30. | FA | ⋅ | FB |=| PF |2p p p p 2 y 2 y 2 y 2 + y 2 p 2 2 p证:| AF | ⋅| BF |= (x 1 + )(x 2 + ) = x 1x 2 + (x 1 + x 2) + = 1 2 + 1 2 + ,22. k AB =y 1 + y 2; 证明:由点差法得证.2 2 2 4 P ( y 1 y 2 , y 1 + y 2 ),4p 2 4 423. tan α=y 1=y 2 ;2 p 2 ⎛ y y p ⎫2⎛ y + y ⎫2y 2 y 2 y 2 + y 2 p 2 PP ∴| PF |2 = 1 2 - ⎪+ 1 2 ⎪ = 1 2 + 1 2 + , 得证. x 1 - 2x 2 - 2⎝ 2 p 2 ⎭ ⎝ 2 ⎭4 p 2 4 4 证明:作 AA 垂直 x 轴于点 A ,在∆AA F 中,tan α= AA 2 =y 1 , 同理2 2 2FA p27. 设 PC 交抛物线于点 M ,则点 M 是 PC 的中点;2x 1 - 2x + x y + y y + y x + x - 2m 可证另一个.证明: C ( 1 2 , 1 2 ), P (-m , 1 2 ),∴PC 中点横坐标为 1 2,2 2 2 4 把 y = y 1 + y 2 2代入 y 2= 2 px ,得24. A 'B ' 2= 4 AF ⋅ BF ;y 2 + y 2 +2y y 2px +2px -4pm x + x -2m 1 2 1 2 = 2px , y 1y 2 = -2pm ,∴ 1 2 = 2px , x = 1 2 .证明: A 'B ' 2= 4 AF ⋅ BF ⇔| y - y |2= 4(x + p )(x + p)4 4 4121 2 22⇔ y 2 + y 2 - 2y y = 4x x + 2 px + 2 px + p 2⇔ -2y y = 4x x + p 2 ,所以点 M 的横坐标为 x =x 1 + x 2 - 2m.点 M 是 PC 的中点.1 21 2 1 21 2 1 2 1 24p2由 y ⋅ y = - p 2, x ⋅ x = 得证. 4( 2 p )2 + 4 p 2kAB p 2 - ( y 1 + y 2 ) 2 2 p 2 + ( p )2k S4 =。
抛物线焦点弦典型例题

抛物线焦点弦典型例题设AB 是过抛物线y 2=2px (p >0)焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则(1)x 1·x 2=p 24. (2)y 1·y 2=-p 2.(3)|AB |=x 1+x 2+p =2p sin 2α(α是直线AB 的倾斜角). (4)1|AF |+1|BF |=2p为定值(F 是抛物线的焦点). [典例1] 过抛物线y 2=4x 的焦点F 的直线l 与抛物线交于A ,B 两点,若|AF |=2|BF |,则|AB |等于( )A .4B.92 C .5 D .6[一般解法] 易知直线l 的斜率存在,设为k ,则其方程为y =k (x -1).由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x 得k 2x 2-(2k 2+4)x +k 2=0, 得x A ·x B =1,①关注公众号《品数学》,获取更多干货!因为|AF |=2|BF |,由抛物线的定义得x A +1=2(x B +1),即x A =2x B +1,②由①②解得x A =2,x B =12, 所以|AB |=|AF |+|BF |=x A +x B +p =92. [应用结论] 法一:由对称性不妨设点A 在x 轴的上方,如图,设A ,B 在准线上的射影分别为D ,C ,作BE ⊥AD 于E ,设|BF |=m ,直线l 的倾斜角为θ,则|AB |=3m ,由抛物线的定义知|AD |=|AF |=2m ,|BC |=|BF |=m ,所以cos θ=|AE ||AB |=13,所以tan θ=22,则sin 2θ=8cos 2θ,所以sin 2θ=89.又y 2=4x ,知2p =4,故利用弦长公式|AB |=2p sin 2θ=92. 法二:因为|AF |=2|BF |,1|AF |+1|BF |=12|BF |+1|BF |=32|BF |=2p =1,解得|BF |=32,|AF |=3,故|AB |=|AF |+|BF |=92. [答案] B[典例2] 设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为( ) A.334B.938C.6332D.94[一般解法] 由已知得焦点坐标为F ⎝⎛⎭⎫34,0,因此直线AB 的方程为y =33⎝⎛⎭⎫x -34,即4x -43y -3=0.与抛物线方程联立,化简得4y 2-123y -9=0,故|y A -y B |=(y A +y B )2-4y A y B =6.因此S △OAB =12|OF ||y A -y B |=12×34×6=94. [应用结论] 由2p =3,及|AB |=2p sin 2 α,关注公众号《品数学》,获取更多干货! 得|AB |=2p sin 2α=3sin 230°=12. 原点到直线AB 的距离d =|OF |·sin 30°=38, 故S △AOB =12|AB |·d =12×12×38=94. [答案] D[典例3] 如图,过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于点A ,B ,交其准线l 于点C ,若F 是AC 的中点,且|AF |=4,则线段AB 的长为( )A .5B .6 C.163 D.203[一般解法] 如图,设l 与x 轴交于点M ,过点A 作AD ⊥l 交l 于点D ,由抛物线的定义知,|AD |=|AF |=4,由F 是AC 的中点,知|AD |=2|MF |=2p ,所以2p =4,解得p =2,所以抛物线的方程为y 2=4x .设A (x 1,y 1),B (x 2,y 2),则|AF |=x 1+p 2=x 1+1=4,所以x 1=3,可得y 1=23,所以A (3,23),又F (1,0),所以直线AF 的斜率k =233-1=3,所以直线AF 的方程为y =3(x -1),代入抛物线方程y 2=4x 得3x 2-10x +3=0,所以x 1+x 2=103,|AB |=x 1+x 2+p =163.故选C. [应用结论] 法一:设A (x 1,y 1),B (x 2,y 2),则|AF |=x 1+p 2=x 1+1=4,所以x 1=3,又x 1x 2=p 24=1,所以x 2=13,所以|AB |=x 1+x 2+p =3+13+2=163. 法二:因为1|AF |+1|BF |=2p ,|AF |=4,所以|BF |=43,所以|AB |=|AF |+|BF |=4+43=163. [答案] C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
百度文库- 让每个人平等地提升自我!
抛物线的焦点弦问题
一、学习任务:
1、会利用弦长计算公式解决有关二次曲线的弦长计算问题
2、会利用抛物线定义解决有关抛物线的焦点弦问题
2.学会解决直线与抛物线相交问题的综合问题.
二、探究新知:
例1、过点M(2,0)作斜率为1的直线l,交拋物线y2=4x于A、B两点,求|AB|.
例2、斜率为1的直线l,经过拋物线y2=4x的焦点F,且与抛物线相交于A、B两点,求|AB|.
思考:若把上面问题中的拋物线方程y2=4x改为一般抛物线方程y2=2p x,则|AB|为?有没有什么规律性?
变式:已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.
(1)若直线l的倾斜角为60°,求|AB|的值;
(2)若|AB|=9,求线段AB的中点M到准线的距离.
变式:在上题中,若求的是| AF|和| BF|呢,又该怎样计算?
变式:已知过抛物线y2=4x的焦点F的弦长为36,求弦所在的直线方程?
规律总结:已知直线l经过抛物线y2=2p x的焦点F,且与抛物线相交于A(x1,y1)、B(x2,y2)两点.则下列四个式子x1+x2,x1 x2,y1+y2,y1 y2是否为定值?
1。
