立体几何之空间轨迹1

合集下载

专题22立体几何中的轨迹问题-1

专题22 立体几何中的轨迹问题【题型归纳目录】题型一：由动点保持平行求轨迹题型二：由动点保持垂直求轨迹题型三：由动点保持等距（或定长）求轨迹题型四：由动点保持等角（或定角）求轨迹题型五：投影求轨迹题型六：翻折与动点求轨迹【典例例题】题型一：由动点保持平行求轨迹例1．（多选题）（2022·广东梅州·高一期末）1．如图，已知正方体1111ABCD A B C D -的棱长为2，点M 为1CC 的中点，点P 为正方形1111D C B A 上的动点，则（）A ．满足MP //平面1BDA 的点PB ．满足MP AM ^的点PC ．存在点P ，使得平面AMP 经过点BD ．存在点P 满足5PA PM +=例2．（多选题）（2022·重庆南开中学模拟预测）2．已知正四棱锥P ABCD -的侧面是边长为6的正三角形，点M 在棱PD 上，且2PM MD =，点Q 在底面ABCD 及其边界上运动，且//MQ 面PAB ，则下列说法正确的是（）A ．点Q 的轨迹为线段B ．MQ 与CD 所成角的范围为,32ππ⎡⎤⎢⎣⎦C ．MQD ．二面角M AB Q --例3．（多选题）（2022·全国·高一单元测试）3．已知正方体1111ABCD A B C D -的边长为2，M 为1CC 的中点，P 为侧面11BCC B 上的动点，且满足//AM 平面1A BP ，则下列结论正确的是（）A ．1AM B M^B ．1//CD 平面1A BPC ．AM 与11A B 所成角的余弦值为23D ．动点P 例4．（多选题）（2022·江苏扬州·高一期末）4．如图，正方体1111ABCD A B C D -的棱长为2，E 是棱1DD 的中点，F 是侧面11CDD C 上的动点，且满足1//B F 平面1A BE ，则下列结论中正确的是（）A ．平面1A BE 截正方体1111ABCD ABCD -所得截面面积为92B ．点F 的轨迹长度为4πC ．存在点F ，使得11B F CD ^D ．平面1A BE 与平面11CDDC 所成二面角的正弦值为13例5．（2022·湖南师大附中三模）5．已知棱长为3的正四面体ABCD ，E 为AD 的中点，动点P 满足2PA PD =，平面a 经过点D ，且平面//a 平面BCE ，则平面a 截点P 的轨迹所形成的图形的周长为 .例6．（2022·山西·太原五中高一阶段练习）6．如图，在正四棱锥S ABCD -中，E 是BC 的中点，P 点在侧面SCD V 内及其边界上运动，并且总是保持PE ∥平面SBD ．则动点P 的轨迹与SCD V 组成的相关图形最有可能是图中的（）A ．B ．C ．D ．例7．（2022·安徽省宣城中学高二期末）7．已知正方体1111ABCD A B C D -的棱长为2,E F ､分别是棱1AA ､11A D 的中点，点P 为底面四边形ABCD 内（包括边界）的一动点，若直线1D P 与平面BEF 无公共点，则点P 的轨迹长度为（）A ．2BCD ．例8．（2022·河南安阳·高二期末（理））8．如图，在正方体1111ABCD A B C D -中，E 是棱1CC 的中点，F 是侧面11BCC B 内的动点，且1//A F 平面1AD E ，下面说法中正确的是（将所有正确的序号都填上）①存在一点F ，使得11//A F D E ；②存在一点F ，使得1A F BE ^；③点F 的轨迹是一条直线；④三棱锥1F AD E -的体积是定值．【方法技巧与总结】（1）线面平行转化为面面平行得轨迹（2）平行时可利用法向量垂直关系求轨迹题型二：由动点保持垂直求轨迹例9．（2022·湖北·高一期末）9．直四棱柱1111ABCD A B C D -的底面是边长为13AA =，点M 为1CC 的中点，点O 为1A M 的中点，则点O 到底面ABCD 的距离为 ;若P 为底面ABCD 内的动点，且1A P PM ^，则动点P 的轨迹长度为．例10．（2022·湖南·雅礼中学二模）10．已知菱形ABCD 的各边长为2,60D Ð=o .如图所示，将ACB △沿AC 折起，使得点D 到达点S 的位置，连接SB ，得到三棱锥S ABC -，此时3SB =.则三棱锥S ABC -的体积为，E 是线段SA 的中点，点F 在三棱锥S ABC -的外接球上运动，且始终保持EF AC ^，则点F 的轨迹的周长为.例11．（2022·四川雅安·高一期末）11．点M 是棱长为2的正方体1111ABCD A B C D -的内切球O 球面上的动点，点N 为BC 边上中点，若1AM B N ^，则动点M 的轨迹的长度为．例12．（多选题）（2022·湖北孝感·高二期末）12．如图，已知正方体ABCD —1111D C B A 的棱长为1，P 为正方形底面ABCD 内一动点，则下列结论正确的有（）A ．三棱锥1B -11A D P 的体积为定值B ．存在点P ，使得11D P AD ^C ．若11D P B D ^，则P 点在正方形底面ABCD 内的运动轨迹是线段ACD ．若点P 是AD 的中点，点Q 是1BB 的中点，过P ，Q 作平面α垂直于平面11ACC A ，则平面α截正方体111ABCD A B C D -的截面周长为例13．（多选题）（2022·全国·高二专题练习）13．已知棱长为4的正方体1111ABCD A B C D -中，14AM AB =uuuu r uuu r ，点P 在正方体的表面上运动，且总满足0MP MC ⋅=uuu r uuu u r，则下列结论正确的是（）A ．点P 的轨迹所围成图形的面积为5B ．点P 的轨迹过棱11A D 上靠近1A 的四等分点C ．点P 的轨迹上有且仅有两个点到点C 的距离为6D ．直线11B C 与直线MP 所成角的余弦值的最大值为35例14．（2022·全国·高一专题练习）14．在正方体1111ABCD A B C D -中，点P 在侧面11BCC B 及其边界上运动，并且总保持1AP BD ^，则动点P 的轨迹是　（）A ．线段1BC B ．线段1BC C ．1BB 中点与1CC 中点连成的线段D ．CB 中点与11B C 中点连成的线段例15．（2022·河南许昌·三模（文））15．如图，在体积为3的三棱锥P-ABC 中，PA ，PB ，PC 两两垂直，1AP =，若点M 是侧面CBP 内一动点，且满足AM BC ^，则点M 的轨迹长度的最大值为（）A ．3B ．6C ．D ．例16．（2022·浙江·杭州市富阳区场口中学高二期末）16．如图，在直三棱柱111ABC A B C -中，ABC V 是边长为2的正三角形，13AA =，N 为棱11A B 上的中点，M 为棱1CC 上的动点，过N 作平面ABM 的垂线段，垂足为点O ，当点M 从点C 运动到点1C 时，点O 的轨迹长度为（）A ．π2B ．πC ．3π2D 例17．（2022·浙江·高二阶段练习）17．已知正四棱锥S ABCD -AC ，DB 交于点O ，SO ^平面ABCD ，1SO =，E 为BC 的中点，动点P 在该棱锥的侧面上运动，并且PE AC ^，则点P 轨迹长度为（）A ．1B C D ．2例18．（2022·云南·昆明一中高三阶段练习（理））18．已知四面体ABCD ，2AB BC CD DA BD =====，二面角A BD C --为60°，E 为棱AD 中点，F 为四面体ABCD 表面上一动点，且总满足BD EF ^，则点F 轨迹的长度为．【方法技巧与总结】（1）可利用线线线面垂直，转化为面面垂直，得交线求轨迹（2）利用空间坐标运算求轨迹（3）利用垂直关系转化为平行关系求轨迹题型三：由动点保持等距（或定长）求轨迹例19．（2022·四川成都·高二期中（理））19．如图，已知棱长为2的正方体A ′B ′C ′D ′－ABCD ，M 是正方形BB ′C ′C 的中心，P 是△A ′C ′D 内（包括边界）的动点，满足PM =PD ，则点P 的轨迹长度为．例20．（多选题）（2022·山东·模拟预测）20．如图，正方体1111ABCD A B C D -的棱长为2，点M 是其侧面11ADD A 上的一个动点（含边界），点P 是线段1CC 上的动点，则下列结论正确的是（）A ．存在点P ，M ，使得平面11B D M 与平面PBD 平行B ．存在点P ，M ，使得二面角--M DC P 大小为23πC ．当P 为棱1CC 的中点且PM =时，则点M 的轨迹长度为23πD ．当M 为1A D 中点时，四棱锥M ABCD -例21．（多选题）（2022·福建·莆田二中模拟预测）21．在棱长为1的正方体1111ABCD A B C D -中，点M 是11A D 的中点，点P ，Q ，R 在底面四边形ABCD 内（包括边界），1PB ∥平面1MC D R 到平面11ABB A 的距离等于它到点D 的距离，则（）A ．点PB ．点QC ．PQ 12-D ．PR 例22．（2022·江西·模拟预测（理））22．已知正方体1111ABCD A B C D -的棱长为3，点P 在11A C B △的内部及其边界上运动，且DP P 的轨迹长度为( )AB ．2πC ．D ．3π例23．（多选题）（2022·辽宁·高一期末）23．如图，正方体1111ABCD A B C D -棱长为2，点M 是其侧面11ADD A 上的动点（含边界），点P 是线段1CC 上的动点，下列结论正确的是（）A ．存在点P ，M ，使得平面11B D M 与平面PBD 平行B ．当点P 为1CC 中点时，过1A PD ，，点的平面截该正方体所得的截面是梯形C ．过点A ，P ，M 的平面截该正方体所得的截面图形不可能为五边形D ．当P 为棱1CC 的中点且PM =时，则点M 的轨迹长度为2π3例24．（2022·河南安阳·模拟预测（文））24．在四边形ABCD 中，//BC AD ，12AB BC CD AD ===，P 为空间中的动点，2PA PB AB ===，E 为PD 的中点，则动点E 的轨迹长度为（）A B C D 例25．（2022·四川达州·高二期末（理））25．正方体1111ABCD A B C D -的棱长为1，点P 在正方体内部及表面上运动，下列结论错误的是（）A ．若点P 在线段1D C 上运动，则AP 与1AB 所成角的范围为ππ,32⎡⎤⎢⎥⎣⎦B ．若点P 在矩形11BDD B 内部及边界上运动，则AP 与平面11BDD B 所成角的取值范围是ππ,42⎡⎤⎢⎥⎣⎦C ．若点P 在11D B C △内部及边界上运动，则AP D ．若点P 满足1AP =，则点P 轨迹的面积为π2例26．（2022·江西省乐平中学高一期末）26．已知正方体1111ABCD A B C D -1,,B D C 的平面为a ，点P 是平面a内的动点，1A P =P 的轨迹长度等于（）A ．πB C D ．2π【方法技巧与总结】（1）距离，可转化为在一个平面内的距离关系，借助于圆锥曲线定义或者球和圆的定义等知识求解轨迹（2）利用空间坐标计算求轨迹参考答案：1．AD【分析】利用线面平行的判定定理可以证得点P 的轨迹，进而判断A ；建立空间直角坐标系，得到(2,0,0)A ，(0,2,1)M ，P 为正方形1111D C B A 上的点，可设(,,2)P x y ，且02x ££，02y ££，进而对BCD 各个选项进行计算验证即可判断并得到答案.【详解】对于A ，取11B C 的中点Q ，11D C 的中点N ，又点M 为1CC 的中点，由正方体的性质知1//MQ A D ，//NQ BD ，MQ NQ Q =I ，1A D BD D Ç=，所以平面//MQN 平面1BDA ，又MP Ì平面MQN ，MP \∥平面1BDA ，故点P 的轨迹为线段NQ ==A 正确；对B ，方法一：在平面11BCC B 中过M 作ME AM ^，交11B C 于E ，设1C E x =，则3AM =，ME =，AE ==由222AM ME AE +=，可解得12x =，同理，在平面11DCC D 中过M 作MF AM ^，交11D C 于F ，可得112C F =，因为ME MF M =I ，所以AM ^平面MEF ，因为MP AM ^，所以MP Ì平面MEF ，所以点P 的轨迹为线段EF ，故B 不正确；方法二：以D 为原点，分别以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系，则(2,0,0)A ，(0,2,1)M ，设(,,2)P x y ，且02x ££，02y ££，(2,,2)AP x y =-uuu r ，(,2,1)MP x y =-uuu r ，(2,2,1)AM =-uuuu r ()22212230AM MP x y x y ⋅=-+-+=-+-=uuuu r uuu r ，即32y x =+，又02x ££，02y ££，则点P 的轨迹为线段EF ，30,,22E æöç÷èø,1,2,22F æöç÷èø且EF ==B 错误；对于C ，方法一：取1DD 中点G ，连接,AG MG ，正方体中，易得//AB MG ，所以平面ABM 截正方体的截面为平面ABMG ，显然P Ï平面ABMG ，故不存在点P ，使得平面AMP 经过点B ，故C 错误；方法二：设(,,2)P x y ，且02x ££，02y ££，若平面AMP 经过点B ，则DP aDA bDB cDM =++uuu r uuu r uuu r uuuu r ，且1a b c ++=，又(,,2),(2,0,0),(2,2,0),(0,2,1)DP x y DA DB DM ====uuu r uuu r uuu r uuuu r ,所以()()()(),,22,0,02,2,00,2,1x y a b c =++，即()(),,222,22,x y a b b c c =++，因此222221x a b y b c c a b c =+ìï=+ïí=ïï++=î，从而2x =-，不合题意，所以不存在点P ，使得平面AMP 经过点B ,故C 错误；对于D ，方法一：延长1CC 至M ¢，令11C M C M ¢=，则MP M P ¢=，所以PA PM PA PM AM ¢¢+=+³，因为4AM ¢==>，所以存在点P 满足5PA PM +=，故D 正确.方法二：点M 关于平面1111D C B A 的对称点的为(0,2,3)M ¢，三点共线时线段和最短，故4PA PM AM ==¢³>+，故存在点P 满足5PA PM +=，故D 正确.故选：AD.2．ACD【分析】作出与面PAB 平行且过MQ 的平面，即可得出点Q 的轨迹判断A ，当点Q 在E 处时，异面直线所成角小于3π可判断B ，当MQ NE ^时求出MQ 可判断C ，作出二面角的平面角求正切值判断D 即可.【详解】对于A ，取点N ,E ，使得2AN ND =，2BE EC =，连接,ME NE ,MN ，如图，由线段成比例可得//,//MN PA NE AB ，PA Ì平面PAB ，MN Ë平面PAB ，所以//MN 平面PAB ，同理可得//NE 平面PAB ，又,NE MN Ì平面MNE ，MN NE N Ç=，所以平面//MNE 平面PAB ，故当点Q ME Î时，总有//MQ 面PAB ，所以点Q 的轨迹为线段，故A 正确；对于B ，由//CD NE 知MQ 与CD 所成角即为MQ 与NE 所成角，在MEN V 中，1π2,6,33MN PA NE AB MNE PAB ====Ð=Ð=，由余弦定理可得ME =1cos 2MEN Ð==>，可知π3MEN Ð<，即Q 运动到E 点时，异面直线所成的角小于π3，故B 错误；对于C ，当MQ NE ^时，MQ 最小，此时πsin 23MQ MN =⋅==C 正确；对于D ，二面角M AB Q --即平面MAB 与底面ABCD 所成的锐角，连接,AC BD 相交于O ，连接PO ，取点H ，使得2OH HD =，连接MH ，过H 作HG AB ^于G ，连接MG ，如图，由正四棱锥可知，^PO 面ABCD ，由2OH HD =，2PM MD =知//MH PO，1133MH PO \==´HG AB ^可得//HG AD ，556GH AD \==，MH ^Q 面ABCD ，AB MH \^，又HG AB ^，HG MH H =I ，AB \^平面MHG ，AB MG \^，MGH \Ð即为二面角的平面角，tan MH MGH GH \Ð==故D 正确.故选：ACD3．BCD 【分析】建立空间直角坐标系，利用空间夹角公式、空间向量数量积的运算性质逐一判断即可.【详解】如图建立空间直角坐标系，设正方体棱长为2，则1(0,0,2),(0,2,2),(0,0,0),(2,1,0),(,,0)A A B M P x y ，所以1(0,2,2),(,,0),(2,1,2)A B BP x y AM =--==-uuur uuu r uuuu r ，由//AM 平面1A BP ，得1AM a A B bBP =+uuuu r uuur uuu r ，即022122bx a by a +=ìï-+=íï-=-î，化简可得：320x y -=，所以动点P 在直线320x y -=上，对于选项A ：11(2,1,2),(2,1,0),221(1)(2)030AM B M AM B M =-=-⋅=´+´-+-´=¹uuuu r uuuu r uuuu r uuuu r ，所以AM uuuu r 与1B M uuuur 不垂直，所以A 选项错误；对于选项B ：111//,CD A B A B Ì平面11,A BP CD Ë平面1A BP ，所以1//CD 平面1A BP ，B 选项正确；对于选项C：11112(0,0,2),cos ,3A B AM A B >=-<==uuuu r uuuu r uuuu r ，C 选项正确；对于选项D ：动点P 在直线320x y -=上，且P 为侧面11BCC B 上的动点，则P 在线段1PB 上，14,2,03P æöç÷èø，所以1PB ==D 选项正确；故选：BCD.4．AC【分析】取CD 中点G ，连接BG 、EG ，计算截面1A EGB 的面积后判断A 的正误，取11C D 中点M ，1CC 中点N ，则点F 的运动轨迹为线段MN ，故可判断B 的正误，取MN 的中点F ，则可判断11B F CD ^，故可判断C 的正误，而11B FC Ð即为平面1B MN 与平面1,CDD C 所成二面角，计算其正弦值后可判断D 的正误.【详解】取CD 中点G ，连接BG 、EG ，则等腰梯形1A EGB 为截面，而1A E GB ==，1A B EG ==故梯形1A EGB92=，A 正确；取11C D 中点M ，1CC 中点N ，连接11,,,,B M B N MN NE MG ，则1111//,=NE A B NE A B ，故四边形11A B NE 为平行四边形，则得11//B N A E ，而1B N Ë平面1A BE ，1A E Ì平面1A BE ，故1B N //平面1A BE ，同理1//B M 平面1A BE ，而111=B N B M B I ，11,B N B M Ì平面1B MN ，故平面1//B MN 平面1A BE ，∴点F 的运动轨迹为线段MNB 错误；取MN 的中点F，则11B N B M ==，∴1B F MN ^，∵1//MN CD ，∴11B F CD ^，C 正确；因为平面1//B MN 平面1A BE 且1MN C F ^，1MN B F ^，∴11B FC Ð即为平面1B MN 与平面1CDDC所成二面角，11111sin B C B FC B F Ð===，D 错误．故选：AC.5．【分析】设BCD △的外心为O ，以O 为坐标原点可建立空间直角坐标系，设(),,P x y z ，根据2PA PD =可求得P点轨迹是以G æççè为球心，2为半径的球；延长,,AB AF AC 到点,,M Q N ，使得AB BM =，AF FQ =，AC CN =，由面面平行的判定可证得平面//BCE 平面MND ，则平面MND 为平面a ，可知点G 到平面DMN 的距离d 即为点G 到直线DQ 的距离，由向量坐标运算可知DG DQ ^，得到1d =，由此可求得截面圆半径，利用圆周长的求法可求得结果.【详解】设BCD △的外心为O ，BC 的中点为F ，过O 作BC 的平行线，则以O 为坐标原点，可建立如图所示空间直角坐标系，BCD QV 为等边三角形，3BC =，23OD DF \==OA \=，(A \，()D，0,F æöç÷ç÷èø，设(),,P x y z ，由2PA PD =得：((2222224x y z x y z ⎡⎤++=++⎢⎥⎣⎦，整理可得：2224x y z ææ++=ççççèè，\动点P的轨迹是以G æççè为球心，2为半径的球；延长,,AB AF AC 到点,,M Q N ，使得AB BM =，AF FQ =，AC CN =，则//CE DN ，//BE MD ，又,DN MD Ì平面MND ，,CE BE Ë平面MND ，//CE \平面MND ，//BE 平面MND ，由CE BE E =∩，,CE BE Ì平面BCE ，\平面//BCE 平面MND ，即平面MND 为平面a ，则点G 到平面DMN 的距离d 即为点G 到直线DQ的距离，DG æ=ççèuuur Q，(0,DQ =-uuur ，220DG DQ \⋅=-+=uuur uuur ，即DG DQ ^，\点G 到直线DQ 的距离1d DG ==uuur ，\截面圆的半径r ==\球被平面a截得的截面圆周长为2r π=，即平面a 截点P的轨迹所形成的图形的周长为.故答案为：.【点睛】关键点点睛：本题考查立体几何中的动点轨迹相关问题的求解，解题关键是能够利用空间向量法求得动点所满足的轨迹方程，从而确定动点轨迹为球，利用平面截球所得截面圆周长的求法可求得结果.6．A【分析】先分别取CD 、S C 的中点M 、N ，再证明面EMN ∥面SBD ，可知当P 在MN 上移动时，PE Ì面EMN ，能够保持PE ∥平面SBD ，进而得到选项A 符合题意．【详解】分别取CD 、S C 的中点M 、N ，连接MN ，ME ，NE ，又∵E 是BC 的中点，∴EM BD ∥，EN SB ∥，又∵,EM EN Ë面SBD ，,BD SB Ì面SBD ， ∴EM ∥面SBD ，EN ∥面SBD ，又∵EM EN E =I ， ,EM EN Ì平面EMN ，∴面EMN ∥面SBD ，∴当P 在MN 上移动时，PE Ì面EMN ，此时能够保持PE ∥平面SBD ，则动点P 的轨迹与SCD V 组成的相关图形是选项A故选：A ．7．B【分析】取BC 的中点G ，连接11,,G D G AD A ，易证1//AD 平面BEF ，1//GD 平面BEF ，从而得到平面1//AD G 平面BEF ，即可得到P 的轨迹为线段AG ，再求其长度即可.【详解】取BC 的中点G ，连接11,,G D G AD A ，如图所示：E F ､分别是棱1AA ､11A D 的中点，所以1//EF AD ，又因为EF Ì平面BEF ，1AD Ë平面BEF ，所以1//AD 平面BEF .因为1//FD BG ，1=FD BG ，所以四边形1FBGD 为平行四边形，所以1//FB GD .又因为FB Ì平面BEF ，1GD Ë平面BEF ，所以1//GD 平面BEF .因为111GD AD D =I ，所以平面1//AD G 平面BEF .因为点P 为底面四边形ABCD 内（包括边界）的一动点，直线1D P 与平面BEF 无公共点，所以P 的轨迹为线段AG =故选：B8．①②④【分析】取11B C 的中点G ，1BB 的中点H ，连接1A G ，1A H ，GH ，由面面平行的性质可判断①③④，由线面垂直的性质可判断②，【详解】如图，取11B C 的中点G ，1BB 的中点H ，连接1A G ，1A H ，GH ，则平面1//AGH 平面1AD E ，所以点F 在线段GH 上运动，即点F 的轨迹是线段GH ，故③错误.当点F 位于点H 时，11//A F D E ，故①正确．取AD 的中点N ，BC 的中点M ，连接1A N ，MN ，1B M ，则BE ^平面11A B MN ，设11GH B M F Ç=，则11A F BE ^，所以存在一点F 使得1A F BE ^，故②正确.平面1//AGH 平面1AD E ，所以点F 到平面1AD E 的距离是定值，所以三棱锥1F AD E -的体积是定值，故④正确．故答案为：①②④9．942π【分析】结合图像,根据正方形的性质即可求出点到平面的距离，再利用直径所对圆周角为直角的性质，将其迁移到空间中，得到P 点轨迹，即为以OP 的长为半径的球与平面ABCD 相交所截得的圆，再根据勾股定理，即可求解．【详解】解：由点O 为1A M 的中点可得，点O 到平面1111D C B A 的距离是点M 到平面1111D C B A 距离的一半，则点O 到平面1111D C B A 的距离为34，故点O 到平面ABCD 的距离为39344-=；1A P PM ^Q ，点O 为1A M 的中点，111524OP A M \===，设以O 为球心，OP 的长为半径的球与平面ABCD 所截得的圆的半径为r ，则3r ==，则动点P 的轨迹即为以正方形ABCD 的中心为圆心，3ABCD 内的圆弧，如图，R 为QP 中点，所以HR QP ^,所以cos RH QHR QH Ð===,所以23QHP QHR πÐ=Ð=，P 点轨迹所形成的圆弧长为32423πππæö´-´=ç÷èø．故答案为：94；2π.10．【分析】取AC 中点M ，由题可得AC ^平面SMB ，进而可得三棱锥S ABC -的高3sin 2h SBM SB Ð=⋅=，利用锥体体积公式可得三棱锥的体积，设点F 轨迹所在平面为a ，则F 轨迹为平面a 截三棱锥的外接球的截面圆，利用球的截面性质求截面圆半径即得.【详解】取AC 中点M ，则,,AC BM AC SM BM SM M ^^=I ，∴AC ^平面SMB ，SM MB ==，又3SB =，∴30SBM MSB ÐÐ==o ，则三棱锥S ABC -的高3sin 2h SBM SB Ð=⋅=，三棱锥S ABC -体积为213232V =´=作EH AC H ^于，设点F 轨迹所在平面为a ，则平面a 经过点H 且AC a ^，设三棱锥S ABC -外接球的球心为,,O SAC BAC V V 的中心分别为12,O O ，易知1OO ^平面2,SAC OO ^平面BAC ，且12,,,O O O M 四点共面，由题可得1121602OMO O MO ÐÐ==o，113O M SM =解Rt 1OO M △，得11OO M =，则三棱锥S ABC -外接球半径r =，易知O 到平面a 的距离12d MH ==，故平面a 截外接球所得截面圆的半径为1r ==∴截面圆的周长为12l r π=，即点F ..11【分析】分别取1DD 、1CC 的中点G 、H ，连接BH 、AG 、GH ，证明A 、B 、G 、H 四点共面，并计算出球心到平面ABGH 的距离，可计算得出截面圆的半径，利用圆的周长公式可求得结果.【详解】如图，正方体1111ABCD A B C D -的内切球O 的半径1R =，由题意，分别取1DD 、1CC 的中点G 、H ，连接BH 、AG 、GH ，在正方体1111ABCD A B C D -中，四边形ABHG 为平行四边形，所以A 、B 、G 、H 四点共面，则CH BN =，1BC BB =，1190C CB B BN Ð=Ð=o，所以，1BCH B BN @△△，所以，1BNB BHC Ð=Ð，1B N BH \^，AB ^Q 平面11BB C C ，1B N Ì平面11BB C C ，1AB B N \^，AB BH B =Q I ，1B N \^平面BAGH ，所以，动点M 的轨迹就是平面BAGH 截内切球O 的交线，取1BB 的中点E ，连接,EG BD ，则四边形BEGD 为平行四边形，易知点O 为EG 的中点，过点E 在平面11BB C C 内作EF BH ^，AB ^Q 平面11BB C C ，EF Ì平面11BB C C ，则EF AB ^，AB BH B =Q I ，EF \^平面BAGH ，sin sin EBF BHC Ð=Ð=，所以，sin EF BE EBF =Ð=因为点O 为EG 的中点，则O 到平面BAGH 的距离为d =，截面圆的半径r ==所以动点M 的轨迹的长度为截面圆的周长2r π=【点睛】关键点点睛：本题解题关键是确定出M 的轨迹是平面BAGH 截内切球O 的交线，在利用球中的勾股定理即可解决.12．ACD【分析】结合选项逐个求解，体积问题利用锥体体积公式可得，垂直问题利用向量求解，截面周长根据截面形状可求.【详解】对于A ，P 为正方形底面ABCD 时，三棱锥111P A B D -的高不变，底面积也不变，所以体积为定值，所以A 正确；对于B ，以D 为坐标原点，建立如图所示的空间直角坐标系，设(),,0P x y ，则()()10,0,1,1,0,0D A ，()1,,1D P x y =-uuuu r ，()11,0,1AD =-uuuu r；若11D P AD ^，则110D P AD ⋅=uuuu r uuuu r，即1x =-，与题意矛盾，所以B 不正确；对于C ，()11,1,1DB =uuuu r，由11D P B D ^得1x y +=，所以P 的轨迹就是线段AC ，所以C 正确；对于D ，因为1,BD AC BD AA ^^，所以BD ^平面11ACC A ；因为平面a ^平面11ACC A ，所以//BD 平面a ；以BD 为参照线作出平面a 与正方体各个侧面的交线，如图，易知每个侧面的交线均相等，，所以截面周长为D 正确.故选：ACD.【点睛】正方体中的动点问题，可以借助空间向量来处理，把位置关系，角度关系转化为向量运算.13．ACD【分析】首先根据动点P 满足的条件及正方体的结构特征得到动点P 的轨迹，然后利用轨迹的特征判断选项A ，B ，C ，对于选项D ，将线线角转化为线面角，运用线面角的定义找出线面角进行求解.【详解】如图，过点M 作1//MF AA ，在AD 上取一点N ，使MN MC ^，连接,NC EC FC ,，过点N 作1//NE AA ，连接EF ，易知//MF NE ，\ ,,,E F M N 四点共面；又MF MC ^Q ，MN MF M =I ，MC \^面MNEF ，即点P 的轨迹为矩形MNEF （不含点M ），设AN x =，则MN =又5MC ==QNC ==222MN MC NC \+= 解得 34x =，即34AN =54MN \=， NC =对于A ，矩形MNEF 的面积为：5454S MN MF =⋅=´=，A 正确；对于B ，134A E AN ==，B 错误；对于C ，CF ==在Rt CMN V 中，C 到MN 的距离范围是：5æççèMN \上存在一点到点C 的距离为6；在Rt CMF V 中，C 到MF 的距离范围是：(MF \上存在一点到点C 的距离为6；但在Rt CNE V 、Rt CEF V 中不存在到点C 的距离为6的点，C 正确；对于D ，直线11B C 与直线MP 所成的最小角就是直线11B C 与平面MNEF 所成的角，11//B C BC Q \直线11B C 与平面MNEF 所成的即是直线BC 与平面MNEF 所成的角，延长,NM CB 交于点G ，则MGB Ð即是直线BC 与平面MNEF 所成的角，//AN GB Q AN AMGB MB \= 94GB \= 在Rt MGC V 中，4sin 5MC MGC GC Ð== 3cos 5MGC \Ð=，D 正确；故选：ACD.【点睛】本题考查动点轨迹，点、线、面位置关系，线线角、线面角以及几何体中一些线段的最值，考查了空间想象能力、逻辑思维能力、运算求解能力，属于难题.14．A【分析】1BD ^平面1ACB ，又点P 在侧面11BCC B 及其边界上运动，故点P 的轨迹为面1ACB 与面11BCC B 的交线1CB .【详解】连接111,,,,AC BD B C BA AB ，因为1,^^DD AC AC BD ，且1DD BD D =I ，所以AC ^平面1BDD ，1BD Ì平面1BDD ，所以1AC BD ^，因为11111,A D AB A B B A ^^，且1111A D A B A =I ，所以1AB ^平面11BA D ，1BD Ì平面11BA D ，所以11^AB BD ，且1AB AC A =I ，所以1BD ^平面1ACB ，AP Ì平面1ACB ，所以1BD AP ^，点P 的轨迹为面1ACB 与面11BCC B 的交线1CB ，故选：A.15．A【分析】根据题意可知，点M 的轨迹为Rt ABC △斜边上的高线，即可根据等面积法以及基本不等式求出点M 的轨迹长度的最大值．【详解】如图所示：，因为PA ，PB ，PC 两两垂直，所以AP ^平面PCB ，即有^AP BC ，而AM BC ^，所以^BC 平面APM ，即BC PM ^，故点M 的轨迹为Rt ABC △斜边上的高线PD ．因为三棱锥P-ABC 的体积为3，所以111332PB PC ´´´´=，即18PB PC ´=，由等积法可得，3PD ==£=，当且仅当PB PC ==故选：A ．16．B【分析】根据条件先判断出点O 的轨迹为圆的一部分，再由弧长公式求解即可.【详解】取AB 中点P ，连接PC ，C 1N ，如图，因为PC ⊥AB ，PN ⊥AB ，且PN ∩PC =P ，所以AB ⊥平面1PCC N ，AB Ì平面ABM ,所以平面ABM ⊥平面1PCC N ，平面ABM ∩平面1PCC N = PM ，过N 作NO ⊥PM ，NO Ì平面1PCC N ，所以NO ⊥平面ABM ，当点M 从点C 运动到点C 1时，O 点是以PN 为直径的圆Q (部分)，如图，当M 运动到点1C 时，O 点到最高点，此时11π3,3PC CC CPC ==Ð=，所以π6OPQ Ð=，从而2π3OQP Ð=，所以弧长2π3π32l =⋅=，即点O 的轨迹长度为π.故选: B 17．B【分析】取,,SC CD OC 的中点分别为,,G F H ，利用线面垂直的判定定理可得AC ^平面EFG ，进而可得点P 轨迹为折线,EG GF ，结合条件即得.【详解】取,,SC CD OC 的中点分别为,,G F H ，连接,,,EF EG FG GH ，则GH SO ，EF BD ∥，又SO ^平面ABCD ，BD AC ^，∴GH ^平面ABCD ，EF AC ^，∴GH AC ^，又EF GH H Ç=，∴AC ^平面EFG ，因为动点P 在该棱锥的侧面上运动，并且PE AC ^，故点P 轨迹为折线,EG GF ，由题可知1SO =，1,OB SB SA ===∴EG GF ==，故点P 故选：B.18【分析】取BD 中点O ，易知AOC Ð是二面角A BD C --的平面角，由线面垂直的判定可得BD ^平面AOC ，即有AOC Ð是二面角A BD C --的平面角，取CD ，OD 中点M ，N ，利用线面平行、面面平行的判定有面//AOC 面EMN ，进而有BD ^平面EMN ，即可知F 轨迹.【详解】取BD 中点O ，易得BD AO ^，BD CO ^，AO CO O =I ，所以BD ^平面AOC ，则AOC Ð是二面角A BD C --的平面角，即60AOC Ð=°，又AO CO ==AC =CD ，OD 中点M ，N ，所以//EM AO ，AO Ì面AOC ，EM Ë面AOC ，故//EM 面AOC ，又//MN CO ，同理：//MN 面AOC ，而EM MN M Ç=，,EM MN Ì面EMN ，所以面//AOC 面EMN ，则BD ^平面EMN ，因为F 为四面体ABCD 表面上一动点，且总满足BD EF ^，所以点F 轨迹是△EMN19【分析】利用空间直角坐标系可知，平面A ′C ′D 内的P 满足0x y z +-=， PM =PD 的P 满足23x y z ++=，则可得32333x y x z -ì=ïïí+ï=ïî，P 是△A ′C ′D 内（包括边界），则302x ££，点P 的轨迹线段12PP ．【详解】如图建立空间直角坐标系，则()()()()0,0,0,2,0,2,0,2,2,1,2,1D A C M ¢¢()()2,0,2,0,2,2DA DC ¢¢==uuur uuuu r设平面DA C ¢¢的法向量(),,n x y z =r则有220220x z y z +=ìí+=î，令1x =，则1,1y z ==-则()1,1,1n r=-设(),,P x y z ，则(),,DP x y z =uuu r∵n DP ^r uuu r，则0x y z +-=又∵PM =PD=整理得：23x y z ++=联立方程230x y z x y z ++=ìí+-=î，则32333x y x z -ì=ïïí+ï=ïî可得023********x x x ìï££ï-ï££íï+ï££ïî，可得302x ££当0x =时，()10,1,1P ，当32x =时，233,0,22P æöç÷èø在空间中，满足PM =PD 的P 为过MD 的中点且与MD 垂直的平面a两个平面的公共部分为直线，即点P 的轨迹为a I 平面A ′C ′D 12PP =．20．ACD【分析】当M 为1AA 中点，P 为1CC 中点时，即可判断A 选项；由二面角--M DC P 的平面角为1ÐMDD 即可判断B 选项；取1DD 中点E ，先求出点M 在侧面11AA D D 内运动轨迹为以E 为圆心半径为2的劣弧，即可判断C 选项；先求出四棱锥M ABCD -外接球的半径，再将外接球的内接正四面体补成正方体即可判断D 选项.【详解】对于A 选项，当M 为1AA 中点，P 为1CC 中点时，易得11//BD B D ，又BD Ì平面PBD ，11B D Ë平面PBD ，则11//B D 平面PBD ，同理可得1//MB 平面PBD ，又1111MB B D B Ç=，则平面11B D M 与平面PBD 平行，故A 正确；对于B 选项，因为CD ^平面11ADD A ，DM Ì平面11ADD A ，则CD DM ^，又1CD DD ^，可知二面角--M DC P 的平面角为1ÐMDD ，显然其范围为0,2π⎡⎤⎢⎥⎣⎦，故B 错误；对于C 选项，取1DD 中点E ，连接,,PE ME PM ，则PE ^平面11,^AA D D PE ME ，则2===ME ，则点M 在侧面11AA D D 内运动轨迹为以E 为圆心半径为2的劣弧，分别交AD ､11A D 于2M ､1M ，则1123Ð=Ð=M ED M ED π，则123Ð=M EM π，劣弧21M M 的长为2233ππ´=.故C 正确；对于D 选项，当M 为1A D 中点时，易知AMD V 为等腰直角三角形，AM DM ^，又AB ^平面11ADD A ，则AB DM ^，又,AB AM Ì平面ABM ，AB AM A =I ，则DM ^平面ABM ，则DM BM ^，又DC BC ^，可知四棱锥M ABCD-外接球的球心即为BD 的中点，所以四棱锥M ABCD -，设四棱锥M ABCD -外接球的内接正四面体的棱长为x ，将四面体拓展成正方体，其中正四面体棱为正方体的面对角线，故正，正方体的体对角线为外接球的直径，所以223ö⋅=÷÷ø，得2163x =，所以正四面体的表面积为2142x ´⋅=D 正确.故选：ACD.21．BCD【分析】对于A ，取BC 的中点N ，连接AN ，1B N ，根据面面平行的判定可证得平面1//ANB 平面1DMC ，从而得点P 的轨迹为线段AN ，解三角形计算可判断；对于B ，连接DQ ，由勾股定理得12DQ =，从而有点Q 的轨迹是以点D 为圆心，以12为半径的14圆，由圆的周长计算可判断；对于C ，过点D 作'DP AN ^于'P ，交点Q 的轨迹于'Q ，此时''P Q 的长度就是PQ 长度的最小值，由三角形相似计算得'DP ，由此可判断；对于D ，由已知得点R 到直线AB 的距离等于它到点D 的距离，根据抛物线的定义知点R 的轨迹是以点D 为焦点，以AB 为准线的抛物线，以AD 的中点为坐标原点O ，过点O 且垂直于AD 的直线为x 轴建立平面直角坐标系，则抛物线的方程为22x y =，设与直线AN 平行且与抛物线相切的直线l 的方程为：2+0x y n -=，联立22+02x y n x y -=ìí=î，整理得()2244+2+0y n y n -=，由0D =，解得14n =-，再根据平行线间的距离可求得PR 长度的最小值．【详解】解：对于A ，取BC 的中点N ，连接AN ，1B N ，则1//AN MC ，11//AB DC ，所以//AN平面1DMC ，1//AB 平面1DMC ，又//AN 平面1DMC ，1//AB 平面1DMC ，1AN AB A =I ，所以平面1//ANB 平面1DMC ，又点P 在底面四边形ABCD 内（包括边界），1PB ∥平面1MC D ，所以点P 的轨迹为线段AN ，因为AN ===，所以点PA 不正确；对于B ，连接DQ ，因为Q 在底面ABCD上，1D Q =2==，解得12DQ =，所以点Q 的轨迹是以点D 为圆心，以12为半径的14圆，如下图所示，所以点Q 的轨迹的长度为112424ππ´´´=，故B 正确；对于C ，过点D 作'DP AN ^于'P ，交点Q 的轨迹于'Q ，此时''P Q 的长度就是PQ 长度的最小值，而'',B AP D BAN ADP Ð=ÐÐ=Ð，所以'ABN DP A V :V ，所以'AD DPAN AB='1DP =，解得'DP =，所以''''12P Q DP DQ =-=，所以PQ12，故C 正确；对于D ，因为点R 到平面11ABB A 的距离等于它到点D 的距离，由正方体的特点得点R 到直线AB 的距离等于点R 到平面11ABB A 的距离，所以点R 到直线AB 的距离等于它到点D 的距离，根据抛物线的定义知点R 的轨迹是以点D 为焦点，以AB 为准线的抛物线，以AD 的中点为坐标原点O ，过点O 且垂直于AD 的直线为x 轴建立平面直角坐标系，如下图所示，则102D æöç÷èø，，102A æö-ç÷èø，，()10N ，，直线AB 的方程为12y =-，直线AN 的方程为210x y --=，则抛物线的方程为22x y =，设与直线AN 平行且与抛物线相切的直线l 的方程为：2+0x y n -=，联立22+02x y n x y -=ìí=î，整理得()2244+2+0y n y n -=，()22Δ4+2160n n =-=，解得14n =-，所以直线l 的方程为：1204x y --=，则直线AN 与直线l 的距离为：d ==，所以PR，故D 正确，故选：BCD.。

立体几何中动点轨迹问题

立体几何中动点轨迹问题
利用三维几何的动点轨迹问题在各行各业有着重要的应用价值。

它在工程、科学技术、数学计算等许多领域有着重要的意义。

三维几何中的动点轨迹是指，当受力作用的粒子穿过物体时，根据物体的几何结构及力场的排列，形成其穿过物体的轨迹。

因此，可以根据这条轨迹来衡量力和物体之间的作用情况，从而可以对物体的几何结构进行各种复杂的计算。

更为重要的是，动点轨迹的计算并不仅仅体现在二维的计算上，而是可以达到真实的三维空间中，进行相对复杂的计算。

可以针对不同的物体及力场结构，研究其动点轨迹的特征，用于研究各种解释力学和其他相关问题。

此外，动点轨迹的计算可以在力学计算、结构分析、宽度计算、流体力学等计算领域大有裨益，可以帮助解决各类技术问题，提高决策效率。

总之，通过三维几何中的动点轨迹问题，可以研究几何结构、探究力学解释、分析流体力学等规律，为各行各业带来重要的实践价值。

立体几何动点轨迹问题

立体几何动点轨迹问题立体几何里的动点轨迹问题啊，就像一场在三维空间里的神秘舞蹈，那些动点就像舞者，它们的轨迹让人捉摸不透，可一旦搞清楚了，又觉得特别有趣。

我记得在高中上立体几何课的时候，老师在黑板上画了一个复杂的立体图形，然后说有个动点在这个图形里按照一定规则运动，让我们找出它的轨迹。

当时我就懵了，感觉像是在看一场没有头绪的魔术表演。

老师在讲台上滔滔不绝地讲着各种定理和方法，我却在下面听得云里雾里。

有一次考试就碰到了一道动点轨迹的难题。

那是一个正方体，在它的棱上有一个动点，规定这个动点到正方体某个面的距离始终保持不变。

我看着题目，脑海里就像一团乱麻。

我先试着在草稿纸上把正方体画出来，可是怎么画都觉得不太对劲，那线条歪歪扭扭的，就像喝醉了酒的蚯蚓。

我想象着那个动点在正方体的棱上慢慢移动，可就是想不出它到底会画出什么样的轨迹。

我旁边的同桌倒是很淡定，他拿着铅笔在纸上比划着。

我凑过去看，他一边画一边说：“你看，这个动点到那个面的距离不变，就相当于它在和这个面平行的一个平面上运动。

”我似懂非懂地点点头，可还是不太明白。

他无奈地看了我一眼，然后拿了一个橡皮擦，放在正方体的模型上，说：“你把这个橡皮擦当成动点，现在你看，它沿着棱移动的时候，是不是始终在一个平面内？”我仔细一看，好像有点明白了。

就像一个小蚂蚁在正方体的框架上爬行，但是只能在一个特定高度的平面上爬，这样它的轨迹就不是随意的了。

还有一道题是关于圆锥里的动点。

一个动点在圆锥的母线和底面圆周之间运动，并且它到圆锥顶点的距离和到底面圆心的距离有一定的比例关系。

这可把我难住了，我看着圆锥的图形，想象着那个动点像个调皮的小精灵在圆锥里穿梭。

我尝试着建立空间直角坐标系，想用坐标来表示动点的位置，可是那些坐标值就像调皮的数字，在我脑袋里跳来跳去，怎么都理不顺。

我叹了口气，觉得自己像是迷失在立体几何的迷宫里，找不到出口。

不过，经过不断地练习和老师的耐心讲解，我慢慢地开始掌握了一些门道。

立体几何中的轨迹问题(总结+讲义+练习)

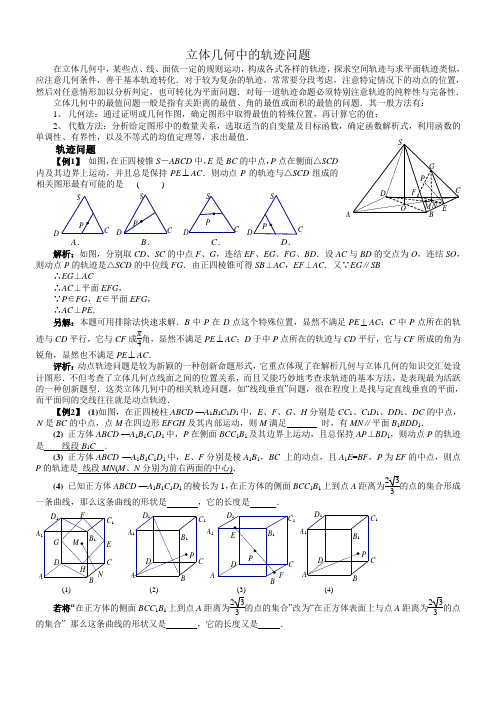
立体几何中的轨迹问题在立体几何中，某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与求平面轨迹类似，应注意几何条件，善于基本轨迹转化．对于较为复杂的轨迹，常常要分段考虑，注意特定情况下的动点的位置，然后对任意情形加以分析判定，也可转化为平面问题．对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性．立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题．其一般方法有： 1、几何法：通过证明或几何作图，确定图形中取得最值的特殊位置，再计算它的值；2、代数方法：分析给定图形中的数量关系，选取适当的自变量及目标函数，确定函数解析式，利用函数的单调性、有界性，以及不等式的均值定理等，求出最值．轨迹问题【例1】如图，在正四棱锥S －ABCD 中，E 是BC 的中点，P 点在侧面△SCD 内及其边界上运动，并且总是保持PE ⊥AC ．则动点P 的轨迹与△SCD 组成的相关图形最有可能的是 ( )解析：如图，分别取CD 、SC 的中点F 、G ，连结EF 、EG 、FG 、BD ．设AC 与BD 的交点为O ，连结SO ，则动点P 的轨迹是△SCD 的中位线FG ．由正四棱锥可得SB ⊥AC ，EF ⊥AC ．又∵EG ∥SB∴EG ⊥AC∴AC ⊥平面EFG ，∵P ∈FG ，E ∈平面EFG ， ∴AC ⊥PE ．另解：本题可用排除法快速求解．B 中P 在D 点这个特殊位置，显然不满足PE ⊥AC ；C 中P 点所在的轨迹与CD 平行，它与CF 成π4角，显然不满足PE ⊥AC ；D 于中P 点所在的轨迹与CD 平行，它与CF 所成的角为锐角，显然也不满足PE ⊥AC ．评析：动点轨迹问题是较为新颖的一种创新命题形式，它重点体现了在解析几何与立体几何的知识交汇处设计图形．不但考查了立体几何点线面之间的位置关系，而且又能巧妙地考查求轨迹的基本方法，是表现最为活跃的一种创新题型．这类立体几何中的相关轨迹问题，如“线线垂直”问题，很在程度上是找与定直线垂直的平面，而平面间的交线往往就是动点轨迹．【例2】 (1)如图，在正四棱柱ABCD —A 1B 1C 1D 1中，E 、F 、G 、H 分别是CC 1、C 1D 1、DD 1、DC 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 满足时，有MN ∥平面B 1BDD 1．(2) 正方体ABCD —A 1B 1C 1D 1中，P 在侧面BCC 1B 1及其边界上运动，且总保持AP ⊥BD 1，则动点P 的轨迹是线段B 1C ．(3) 正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是棱A 1B 1，BC 上的动点，且A 1E =BF ，P 为EF 的中点，则点P 的轨迹是线段MN (M 、N 分别为前右两面的中心)．(4) 已知正方体ABCD —A 1B 1C 1D 1的棱长为1，在正方体的侧面BCC 1B 1上到点A 距离为233的点的集合形成一条曲线，那么这条曲线的形状是，它的长度是．若将“在正方体的侧面BCC 1B 1上到点A 距离为23 3 的点的集合”改为“在正方体表面上与点A 距离为233的点的集合” 那么这条曲线的形状又是，它的长度又是．1AC C 1AEC C 1A AB1A 1(1)(2)(3)(4)DDA ．B ．C ．D ． A【例3】 (1)(04北京)在正方体ABCD -A 1B 1C 1D 1中，P 是侧面BB 1C 1C 内一动点，若P 到直线BC 与直线C 1D 1的距离相等，则动点P 的轨迹所在的曲线是 ( D )A ． A 直线B ．圆C ．双曲线D ．抛物线变式：若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1：2(或2：1)”，则动点P 的轨迹所在的曲线是椭圆 (双曲线)． (2)(06北京)平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹是 (A )A ．一条直线B ．一个圆C ．一个椭圆D ．双曲线的一支解：设l 与l 是其中的两条任意的直线，则这两条直线确定一个平面，且斜线AB 垂直这个平面，由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内，故动点C 都在这个平面与平面α的交线上，故选A ． (3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1，M 在棱AB 上，且AM =13，点P 到直线A 1D 1的距离与点P 到点M 的距离的平方差为1，则点P 的轨迹为抛物线．(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3，长为2的线段MN 点一个端点M 在DD 1上运动，另一个端点N 在底面ABCD 上运动，则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为 π6．【例4】 (04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与△ABC 组成图形可能是：( D )【例5】四棱锥P -ABCD ，AD ⊥面P AB ，BC ⊥面P AB ，底面ABCD 为梯形，AD =4，BC =8，AB =6，∠APD =∠CPB ，满足上述条件的四棱锥的顶点P 的轨迹是( )A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分分析：∵AD ⊥面P AB ，BC ⊥平面P AB ∴AD ∥BC 且AD ⊥P A ，CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴AD P A =CB PB ∴PB =2P A在平面APB 内，以AB 的中点为原点，AB 所在直线为x 轴建立平面直角坐标系，则A (-3，0)、B (3，0)，设P (x ，y )(y ≠0)，则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0) ∴P 的轨迹是(B )BABCDA3P A BC D立体几何中的轨迹问题（教师版）1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为（D ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分简析本题主要考查点到直线距离的概念，线面垂直及抛物线的定义．因为B 1C 1⊥面AB 1，所以PB 1就是P 到直线B 1C 1的距离，故由抛物线的定义知：动点的轨迹为抛物线的一段，从而选D ．2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（B ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（C ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（A ）．A ．圆或圆的一部分B ．抛物线或其一部分C ．双曲线或其一部分D ．椭圆或其一部分简析由条件易知：AC 是平面BB 1D 1D 的法向量，所以EP 与直线AC 成等角，得到EP 与平面BB 1D 1D 所成的角都相等，故点P 的轨迹有可能是圆或圆的一部分．5．已知正方体ABCD A B C D -1111的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD 内的动点，且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为（A ）． A ．抛物线B ．双曲线C ．直线D ．圆简析在正方体ABCD A B C D -1111中，过P 作PF ⊥AD ，过F 作FE ⊥A 1D 1，垂足分别为F 、E ，连结PE ．则PE 2=a 2+PF 2，又PE 2-PM 2=a 2，所以PM 2=PF 2，从而PM ＝PF ，故点P 到直线AD 与到点M 的距离相等，故点P 的轨迹是以M 为焦点，AD 为准线的抛物线．6．在正方体ABCD A B C D -1111中，点P 在侧面BCC 1B 1及其边界上运动，总有AP ⊥BD 1，则动点P 的轨迹为__________．简析在解题中，我们要找到运动变化中的不变因素，通常将动点聚焦到某一个平面．易证BD 1⊥面ACB 1，所以满足BD 1⊥AP 的所有点P 都在一个平面ACB 1上．而已知条件中的点P 是在侧面BCC 1B 1及其边界上运动，因此，符合条件的点P 在平面ACB 1与平面BCC 1B 1交线上，故所求的轨迹为线段B 1C ．本题的解题基本思路是：利用升维，化“动”为“静”，即先找出所有点的轨迹，然后缩小到符合条件的点的轨迹．7．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面∆SCD 内及其边界上运动，总有PE ⊥AC ，则动点P 的轨迹为_______________．答案线段MN （M 、N 分别为SC 、CD 的中点）8．若A 、B 为平面α的两个定点，点P 在α外，PB ⊥α，动点C （不同于A 、B ）在α内，且PC ⊥AC ，则动点C 在平面内的轨迹是________．（除去两点的圆） 9．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与∆ABC 组成的图形可能是：（D ）A A AP PP PB C B C B C B C A B C D简析动点P 在侧面ABC 内，若点P 到AB 的距离等于到棱BC 的距离，则点P 在∠ABC 的内角平分线上．现在P 到平面BCD 的距离等于到棱AB 的距离，而P 到棱BC 的距离大于P 到底面BCD 的距离，于是，P 到棱AB 的距离小于P 到棱BC 的距离，故动点P 只能在∠ABC 的内角平分线与AB 之间的区域内．只能选D ． 10．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（B ）． A ．圆 B ．椭圆 C ．双曲线 D ．抛物线解题的要领就是化空间问题为平面问题，把一些重要元素集中在某一个平面内，利用相关的知识去解答，象平面几何知识、解析几何知识等．11．已知正方体ABCD A B C D -1111的棱长为1，在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线，那么这条曲线的形状是_________，它的长度为__________．简析以B 为圆心，半径为33且圆心角为π2的圆弧，长度为36π． 12．已知长方体ABCD A B C D -1111中，AB BC ==63,，在线段BD 、A C 11上各有一点P 、Q ，PQ 上有一点M ，且PM MQ =2，则M 点轨迹图形的面积是．提示轨迹的图形是一个平行四边形．13．已知棱长为3的正方体ABCD A B C D -1111中，长为2的线段MN 的一个端点在DD 1上运动，另一个端点N 在底面ABCD 上运动，求MN 中点P 的轨迹与正方体的面所围成的几何体的体积．简析由于M 、N 都是运动的，所以求的轨迹必须化“动”为“静”，结合动点P 的几何性质，连结DP ，因为MN=2，所以PD=1，因此点P 的轨迹是一个以D 为球心，1为半径的球面在正方体内的部分，所以点P 的轨迹与正方体的表面所围成的几何体的体积为球的体积的18，即1843163⨯⨯=ππ． 14．已知平面//α平面β，直线l α⊂，点l P ∈，平面α、β间的距离为4，则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是（）简析：如图，设点P 在平面β内的射影是O ，则OP 是α、β的公垂线，OP=4．在β内到点P 的距离等于5的点到O 的距离等于3，可知所求点的轨迹是β内在以O 为圆心，3为半径的圆上．又在β内到直线l 的距离等于29的点的集合是两条平行直线m 、n ，它们到点O 的距离都等于32174)29(22<=-，所以直线m 、n 与这个圆均相交，共有四个交点．因此所求点的轨迹是四个点，故选C ．16．在四棱锥ABCD P -中，⊥AD 面PAB ，⊥BC 面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，CPB APD ∠=∠，满足上述条件的四棱锥的顶点P 的轨迹是（）A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分简析：因为⊥AD 面PAB ，⊥BC 面PAB ，所以AD//BC ，且︒=∠=∠90CBP DAP ．又8BC ,4AD ,CPB APD ==∠=∠，可得CPB tan PB CB PA AD APD tan ∠===∠，即得2ADCBPA PB == 在平面PAB 内，以AB 所在直线为x 轴，AB 中点O 为坐标原点，建立平面直角坐标系，则A （-3，0）、B（3，0）．设点P （x ，y ），则有2y )3x (y )3x (|PA ||PB |2222=+++-=，整理得09x 10y x 22=+++由于点P 不在直线AB 上，故此轨迹为一个不完整的圆，选B ．17．如图，定点A 和B 都在平面α内，定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点．且AC PC ⊥，那么动点C 在平面α内的轨迹是（）A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点简析：因为PC AC ⊥，且PC 在α内的射影为BC ，所以BC AC ⊥，即︒=∠90ACB ．所以点C 的轨迹是以AB 为直径的圆且去掉A 、B 两点，故选B ．18．如图，在正方体1111D C B A ABCD -中，P 是侧面1BC 内一动点，若P 到直线BC 与直线11D C 的距离相等，则动点P 的轨迹所在的曲线是（）A ．直线B ．圆C ．双曲线D ．抛物线简析：因为P 到11D C 的距离即为P 到1C 的距离，所以在面1BC 内，P 到定点1C 的距离与P 到定直线BC 的距离相等．由圆锥曲线的定义知动点P 的轨迹为抛物线，故选D ．19．已知正方体1111D C B A ABCD -的棱长为1，点P 是平面AC 内的动点，若点P 到直线11D A 的距离等于点P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（）A ．抛物线B ．双曲线C ．椭圆D ．直线简析：如图4，以A 为原点，AB 为x 轴、AD 为y 轴，建立平面直角坐标系．设P （x ，y ），作AD PE ⊥于E 、11D A PF ⊥于F ，连结EF ，易知1x |EF ||PE ||PF |2222+=+=又作CD PN ⊥于N ，则|1y ||PN |-=．依题意|PN ||PF |=，即|1y |1x 2-=+，化简得0y 2y x 22=+- 故动点P 的轨迹为双曲线，选B ．20．如图，AB是平面a的斜线段，A为斜足，若点P在平面a内运动，使得△ABP的面积为定值，则动点P的轨迹是（）（A）圆（B）椭圆（C）一条直线（D）两条平行直线分析：由于线段AB是定长线段，而△ABP的面积为定值，所以动点P到线段AB 的距离也是定值．由此可知空间点P在以AB为轴的圆柱侧面上．又P在平面内运动，所以这个问题相当于一个平面去斜切一个圆柱(AB是平面的斜线段)，得到的切痕是椭圆．P的轨迹就是圆柱侧面与平面a的交线．21．如图，动点P在正方体1111ABCD A B C D-的对角线1BD上．过点P作垂直于平面11BB D D的直线，与正方体表面相交于M N，．设BP x=，MN y=，则函数()y f x=的图象大致是（）分析：将线段MN投影到平面ABCD内，易得y为x一次函数．22．已知异面直线a，b成︒60角，公垂线段MN的长等于2，线段AB两个端点A、B分别在a，b上移动，且线段AB长等于4，求线段AB中点的轨迹方程．图5简析：如图5，易知线段AB的中点P在公垂线段MN的中垂面α上，直线'a、'b为平面α内过MN的中点O分别平行于a、b的直线，'a'AA⊥于'A，'b'BB⊥于'B，则P'B'AAB=⋂，且P也为'B'A的中点．由已知MN=2，AB=4，易知,2AP,1'AA==得32'B'A=．则问题转化为求长等于32的线段'B'A的两个端点'A、'B分别在'a、'b上移动时其中点P的轨迹．现以'OB'A∠的角平分线为x轴，O为原点建立如图6所示的平面直角坐标系．A BCDMNPA1 B1C1D1yxOyxOyxOyxO图6设)y ,x (P ，n |'OB |,m |'OA |==，则)n 21,n 23('B ),m 21,m 23('A - )n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++- 消去m 、n ，得线段AB 的中点P 的轨迹为椭圆，其方程为1y 9x 22=+．点评：例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起，相互交汇和渗透，有利于培养运用多学科知识解决问题的能力．立体几何中的轨迹问题1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为（） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（） A ．圆或圆的一部分 B ．抛物线或其一部分 C ．双曲线或其一部分 D ．椭圆或其一部分 5．已知正方体ABCD A B C D -1111的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD 内的动点，且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为（） A ．抛物线B ．双曲线C ．直线D ．圆6．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与∆ABC 组成的图形可能是（） A A AP PP PB C B C B C B CA B C DA B C D 7．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（）A ．圆B ．椭圆C ．双曲线D ．抛物线8．已知平面//α平面β，直线l α⊂，点l P ∈，平面α、β间的距离为4，则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是（）A ．一个圆B ．两条平行直线C ．四个点D ．两个点9．在四棱锥ABCD P -中，⊥AD 面PAB ，⊥BC 面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，CPB APD ∠=∠，满足上述条件的四棱锥的顶点P 的轨迹是（） A ．圆 B ．不完整的圆 C ．抛物线 D ．抛物线的一部分 10．如图，定点A 和B 都在平面α内，定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点．且AC PC ⊥，那么动点C 在平面α内的轨迹是（）A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点11．已知正方体1111D C B A ABCD -的棱长为1，点P 是平面AC 内的动点，若点P 到直线11D A 的距离等于点P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（）A ．抛物线B ．双曲线C ．椭圆D ．直线12．如图，AB 是平面a 的斜线段，A 为斜足，若点P 在平面a 内运动，使得△ABP 的面积为定值，则动点P 的轨迹是（）A ．圆B ．椭圆C ．一条直线D ．两条平行直线 13．如图，动点P 在正方体1111ABCD A B C D -的对角线1BD 上．过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设BP x =，MN y =，则函数()y f x =的图象大致是（）14．在正方体ABCD A B C D -1111中，点P 在侧面BCC 1B 1及其边界上运动，总有AP ⊥BD 1，则动点P 的轨迹为________．15．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面∆SCD 内及其边界上运动，总有PE ⊥AC ，则动点P 的轨迹为_______________．16．若A 、B 为平面α的两个定点，点P 在α外，PB ⊥α，动点C （不同于A 、B ）在α内，且PC ⊥AC ，则动点C 在平面内的轨迹是________．17．已知正方体ABCD A B C D -1111的棱长为1，在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线，那么这条曲线的形状是_________，它的长度为__________．18．已知长方体ABCD A B C D -1111中，AB BC ==63,，在线段BD 、A C 11上各有一点P 、Q ，PQ 上有一点M ，且PM MQ =2，则M 点轨迹图形的面积是．19．已知棱长为3的正方体ABCD A B C D -1111中，长为2的线段MN 的一个端点在DD 1上运动，另一个端点N 在底面ABCD 上运动，则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是．20．已知异面直线a ，b 成︒60角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且线段AB 长等于4，求线段AB 中点的轨迹方程．ABC D MNP A 1B 1C 1D 1 yxOyxOyxOyx O。

2022高考数学立体几何—空间中的动点问题全文

可编辑修改精选全文完整版立体几何—空间中的动点问题专题综述空间中的动点问题是指在一定的约束条件下，点的位置发生变化，在变化过程中找出规律，将动点问题转化为“定点”问题、将空间问题转化为平面问题、将立体几何的问题转化为解析几何的问题等,目的是把问题回归到最本质的定义、定理或现有的结论中去.立体几何中考查动点问题，往往题目难度较大，渗透化归与转化思想，对学生的逻辑推理能力要求较高.一般考查动点轨迹、动点的存在性、定值、范围、最值等问题，除了利用化动为定、空间问题平面化等方法，在几何体中由动点的变化过程推理出结果以外，也可以通过建系，坐标法构建函数，求得结果.专题探究探究1：坐标法解决动点问题建立空间直角坐标系，使几何元素的关系数量化，借助空间向量求解，省去中间繁琐的推理过程.解题步骤与空间向量解决立体几何问题一致，建立适当的空间直角坐标系由动点的位置关系，如在棱上或面内，转化为向量的关系，用参数表示动点的坐标通过空间向量的坐标运算表示出待求的量若求最值或取值范围，转化为函数问题，但要注意自变量的取值范围.一般坐标法用于解决动点的存在性问题、求最值、求范围问题.说明：对于求最值、范围问题，也可以直接通过几何体中的某个变量，构建函数，求最值或范围.(2022湖北省宜昌市模拟) （多选）在正方体1111ABCD A B C D -中，点为线段1AD 上一动点，则（） A. 对任意的点，都有1B D CQ ⊥ B. 三棱锥1B B CQ -的体积为定值 C. 当为1AD 中点时，异面直线1B Q 与所成的角最小D. 当为1AD 中点时，直线1B Q 与平面11BCC B 所成的角最大【审题视点】以正方体为载体考查定点的定值、最值问题，正方体便于建立空间直角坐标系，可选择用坐标法解决.【思维引导】选项，可以用几何知识证明；选项，设出点坐标，用坐标表示出异面直线成角的余弦值或线面角的正弦值，求最值，得出点位置.【规范解析】解：对于：连接，1.CD因为在正方体1111ABCD A B C D -中， 1B D ⊥平面1ACD ，CQ ⊂平面1ACD ， 1B D CQ ⊥，故正确；对于：平面11//ADD A 平面11BCC B ，平面11ADD A 与平面11BCC B 的距离为正方体棱长，1123111326B B CQ Q BCB V V a a a --==⨯⋅=，为定值，故正确；对于：以为坐标原点，直线分别轴，建立空间直角坐标系如下图：设正方体1111ABCD A B C D -的棱长为2， ()[](),0,20,2Q x x x -∈，则1(2,2,2)B ， ()2,2,0B ， (0,2,0)C ，因此()12,2,B Q x x =---， ()2,0,0BC =-，设异面直线1B Q 与所成的角为θ，则当时，，当时，当时，故当与1D 重合时，异面直线1B Q 与所成的角最小，故不正确；对于： ()12,2,B Q x x =---，又是平面11BCC B 的一个法向量，设直线1B Q 与平面11BCC B 所成的角为α，则，所以当1x =时，sin α取得最大值63，而0,2πα⎡⎤∈⎢⎥⎣⎦，因此α取得最大值，即当为1AD 中点时，直线1B Q 与平面11BCC B 所成的角最大，故正确. 故选.ABD用一个参数表示动点的坐标，并求出参数范围，即为函数定义域转化为函数求最值，求出当函数取最值时的x 的值【探究总结】典例1是一道典型的研究动点问题的多选题，难度中等，但能够反映出坐标法研究最值范围问题的思路.建系设坐标，写出参数范围根据向量运算构造函数求最值.(2021安徽省蚌埠市联考) 已知圆柱1OO 底面半径为1，高为π，是圆柱的一个轴截面，动点从点出发沿着圆柱的侧面到达点，其距离最短时在侧面留下的曲线Γ如图所示．将轴截面绕着轴1OO 逆时针旋转(0)θθπ<<后，边11B C 与曲线Γ相交于点.P（1）求曲线Γ长度；（2）当2πθ=时，求点1C 到平面的距离；（3）证明：不存在(0)θθπ<<，使得二面角D AB P --的大小为.4π探究2：化动为定点的位置在变化的过程中，有些量或位置关系是不变的，比如点到平面的距离不变，从而使几何体的体积不变；动点与另外一定点的连线与某条直线始终垂直，与某个平面始终平行.在证明体积为定值、证明位置关系时，要动中寻定，将动态的问题静态化：将动点转化为定点，寻找动直线所在的确定平面，从而解决问题.答题思路：1.动点到平面的距离为定值：证明平面，动点到平面的距离即为定点到平面的距离；2.为动点，为定点，证明：证明所在平面与垂直；3.为动点，为定点，证明平面：证明所在平面与平面平行.(2021湖南省四校联考) 在正三棱柱中，,，分别为的中点，P 是线段DF 上的一点．有下列三个结论：①平面；②;③三棱锥的体积时定值，其中所有正确结论的编号是 A. ①②B. ①③C. ②③D. ①②③【审题视点】求证关于动直线的线面平行或线线垂直，三棱锥的体积为定值问题，要化动为定.【思维引导】证明动直线所在平面与已知平面平行；证明定直线与动直线所在平面垂直；寻找过点与平面平行的直线，即得出点到平面的距离.【规范解析】解：如图，对于①，在正三棱柱中，，分别为的中点，平面平面，由平面，得平面，故①正确；对于②，在正三棱柱中，平面平面，平面平面平面，，平面平面,故②正确；对于③，平面平面，平面到平面的距离为定值，而有为定值，故是定值,线面平行，转化为面面平行异面直线垂直，转化为线面垂直体积的定值问题，转化点到平面的距离是定值，即通过线面平行或面面平行，得出动点到平面距离为定值故③正确．故选D ．【探究总结】立体几何证明中经常出现，求证关于动直线的线面平行与线线垂直问题，其思路是转化为证明动直线所在的定平面与其他平面或直线的位置关系.关键是分析动点,动线或动面间的联系,在移动变化的同时寻求规律.(2021云南省曲靖市联考) 如图所示的几何体中，111ABC A B C -为直三棱柱，四边形为平行四边形，2CD AD =，60ADC ∠=︒，1.AA AC =（1）证明：，1C ，1B 四点共面，且11A C DC ⊥；（2）若1AD =，点是上一点，求四棱锥的体积，并判断点到平面11ADC B 的距离是否为定值？请说明理由．探究3：巧用极端位置由于点位置连续变化，使研究的图形发生连续的变化，利用点的位置变化“极端”位置，避开抽象及复杂的运算，得到结论.常见题型：1.定值问题：几何体中存在动点，但所求结果是确定的，即随着动点位置的改变不会影响所求的量，故可以考虑动点在极端位置的情况，优化解题过程.2.范围问题：几何体中存在动点，结果会随着动点位置改变而改变，当动点从一侧极端位置移动到令一个极端位置的过程中，所求量在增大、或减小、或先增后减、或先减后增，通过求出极端位置处的值，及最值，从而得出范围；3.探究问题：探究满足条件的点是否存在，也可以转化为求出范围，从而得出结论.(2021湖南省株洲市模拟) 在正四面体中, 为棱的中点, 为直线上的动点,则平面与平面夹角的正弦值的取值范围是 .【审题视点】本例可用极端位置法分析，也可以建系，用坐标法解决.【思维引导】借助极端位置分析，不难看出经过和底边中线的平面与平面垂直，点在移动的过程中，存在一个位置使平面与经过和底边中线的平面平行，即平面平面，此时两平面所成角为，角最大；当点移动到无穷远时，平面平面,此时两平面所成角最小.【规范解析】解：由下左图设为的中心，为的中点，则在正四面体中平面，为中点，为的中点，，故平面连接，并延长交于点，连接，并延长交于点，则过点的平面交直线于点. 则平面平面即平面与平面的夹角的正弦值为1，点从取最值的位置处移动至直线的无穷远处的过程中，平面与平面的夹角逐渐减小，即当点在无穷远处时，看作，如下右图故平面与平面的夹角即为平面与平面的夹角，求出其正弦值为. 综上可知:面与面的夹角的正弦值的取值范围为.【探究总结】借助极端位置解决典例3中的问题，首先利用几何知识，明确点在移动的过程中，所求量的变化情况，若在极端位置处取“最值”，问题就简化为求出极端位置处的值.(2021浙江省杭州市高三模拟)高为1的正三棱锥的底面边长为，二面角与二面角A PB C --之和记为，则在从小到大的变化过程中，的变化情况是（）A ．一直增大B ．一直减小C ．先增大后减小D ．先减小后增大专题升华结合几何知识，两平面成角的变化过程，即动点从一个极端位置变化到另一极端位置时，夹角大小的增减情况在极端位置处取“最值”，直接求出点该处时的夹角的正弦值，即为范围区间的一个端点几何体中研究动点问题往往难度较大，开放性强，技巧性高.总体思路是：用几何知识，经过逻辑推理，证明位置关系或求出表示出所求量；或者建立空间直角坐标系，将几何问题代数化，用空间向量研究动点问题，省去了繁杂的推理环节，但计算量较大.解决动点问题的策略不局限与上述方法，常用的的方法还有：运用条件直接推算，借助条件将几何体还原到长方体中去；构造函数，数形结合；还将空间问题转化为平面几何解决，如化折为直、利用解析几何的知识解决. 但只要我们熟练掌握这些基本方法,并灵活加以应用,不仅能化繁为简,化难为易,而且还可以得到简捷巧妙的解法.【答案详解】变式训练1【解答】解：（1）在侧面展开图中为的长，其中AB AD π==，∴曲线Γ的长为2;π（2）当2πθ=时，建立如图所示的空间直角坐标系，则有()0,1,0A -、()0,1,0B 、1,0,2P π⎛⎫- ⎪⎝⎭、()11,0,C π-，、(1,1,)2AP π=-、1(1,0,)OC π=-设平面的法向量为(,,)n x y z =，则2002n AB y n AP x y z π⎧⋅==⎪⎨⋅=-++=⎪⎩，取2z =得(,0,2)n π=，所以点1C 到平面的距离为12||||4OC n d n ππ⋅==+；（3）假设存在满足要求的(0)θθπ<<，在（2）的坐标系中，()sin ,cos ,P θθθ-，，设平面的法向量为111(,,)m x y z =，则111120sin (cos 1)0y x y z θθθ=⎧⎨-+++=⎩，取11x =得sin (1,0,)m θθ=，又平面的法向量为(1,0,0)k =，由二面角D AB P --的大小为4π，则|cos ⟨,m k ⟩2212|sin .21sin θθθθ==⇒=+ sin (0)2πθθθ<<<，0θπ∴<<时，均有sin θθ<，与上式矛盾．所以不存在(0)θθπ<<使得二面角D AB P --的大小为.4π 变式训练2【解答】（1）证明：因为111ABC A B C -为直三棱柱，所以，且，又四边形为平行四边形，//BC AD ，且BC AD =，，且，四边形为平行四边形，，1B 四点共面；，又1AA ⊥平面，AC ⊂平面，，四边形11A ACC 为正方形，连接1AC 交1A C 于，，在ADC ∆中，2CD AD =，，由余弦定理得，，所以，AD AC ⊥，又1AA ⊥平面ABCD ，AD ⊂平面ABCD ，1AA AD ⊥，，1AA ⊂平面11A ACC ，，AD ⊥平面11A ACC ，1AC ⊂平面11A ACC ，所以，又，平面，1A C ⊥平面， 1DC ⊂平面，（2）解：由（1）知：1A C ⊥平面，在Rt DAC 中，由已知得3AC =，，四棱锥的体积，//BC AD ，点到平面的距离为定值，即为点到平面的距离变式训练3【解析】解：设二面角为，二面角A PB C --为，当时，正三棱锥趋向于变为正三棱柱，；当时，正三棱锥趋向变为平面，.当正三棱锥为正四面体时，且，，故.当从小变大时，要经过从变为小于的角，然后变为的过程，故只有选项符合.故选：.静夜思[ 唐] 李白原文译文对照床前明月光，疑是地上霜。

立体几何中的动点轨迹问题

同理，在平面 AA1D1D 内满足条件的点的轨迹长度为52π．在平面 A1B1C1D1 内满足条件的点的轨迹为以 A1 为圆心，A1F 为半径的14圆弧，长度为 2π×4×14＝2π．同理，在平面 ABCD 内满足条件的点的轨迹为以 A 为圆心，AE 为半径的圆弧，长度为 2π×3×14 ＝32π．故轨迹的总长度为52π＋52π＋2π＋32π＝172π．
的长度最小．因为 B1N1＝D1N1＝ 5，B1D1＝2 2，所以△B1N1D1 的边 B1D1 上的高为
52－ 22＝ 3，则 S△B1N1D1＝12×2 2× 3＝ 6，则当 B1N⊥D1N1 时，B1N 最
小，即 B1Nmin＝2S△DB1N1N1 1D1＝2
6＝2 5
530．
总结提炼
与平行有关的轨迹问题的解题策略 (1)线面平行转化为面面平行得轨迹； (2)平行时可利用法向量垂直关系求轨迹．
模型 3 动点保持等距关系
3 (2023·湖北联考节选)已知正方体 ABCD－A1B1C1D1 的棱长为 3，P 为正方体表 53
面上的一个动点，A1P＝2 3，则点 P 的轨迹长度为___2__π__．
【解析】如图，点 P 的轨迹一部分是在平面 ABB1A1，A1B1C1D1， ADD1A1 三个面内以 2 3为半径，圆心角为π6的三段圆弧，另一部分是在平面 BCC1B1，CDD1C1，ABCD 三个面内以 3为半径，圆心角为π2 的三段圆弧．故点 P 的轨迹的长度为112×2π×2 3×3＋14×2π× 3×3＝523π．
点击对应数字即可跳转到对应题目
1
2
3
4
5
6
7
8
9
配套精练
2 ．如图，正方体 ABCD － A1B1C1D1 的棱长为 2 ， E ， F 分别为

新高考数学重难点培优专题讲义——立体几何小题专练(含详细答案解析)

立体几何小题培优讲义高考规律立体几何是高考的热点内容，属于高考的必考内容之一.从近几年的高考情况来看，高考对该部分的考查，小题主要体现在三个方面：一是有关空间线面位置关系的判断；二是空间几何体的体积和表面积的计算，难度较易；三是常见的一些经典常考压轴小题，涉及到空间角、空间距离与轨迹问题等，难度中等或偏上．知识梳理【知识点1 空间几何体表面积与体积的常见求法】1.求几何体体积的常用方法(1)公式法：直接代入公式求解.(2)等体积法：四面体的任何一个面都可以作为底面，只需选用底面面积和高都易求出的形式即可.(3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，三棱柱补成四棱柱等.(4)分割法：将几何体分割成易求解的几部分，分别求体积.2.求组合体的表面积与体积的一般方法求组合体的表面积的问题，首先应弄清它的组成部分，其表面有哪些底面和侧面，各个面的面积应该怎样求，然后根据公式求出各个面的面积，最后相加或相减.求体积时也要先弄清各组成部分，求出各简单几何体的体积，再相加或相减.【知识点2 几何体与球的切、接问题的解题策略】1.常见的几何体与球的切、接问题的解决方案：常见的与球有关的组合体问题有两种：一种是内切球，另一种是外接球.常见的几何体与球的切、接问题的解决方案：2.空间几何体外接球问题的求解方法：空间几何体外接球问题的处理关键是确定球心的位置，常见的求解方法有如下几种：(1)涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题求解.(2)若球面上四点P,A,B,C构成的三条线段P A,PB,PC两两垂直，且P A=a，PB=b，PC=c，一般把有关元素“补形”成为一个球内接长方体，根据4R2=a2+b2+c2求解.(3)利用平面几何体知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.【知识点3 几何法与向量法求空间角】1.几何法求异面直线所成的角(1)求异面直线所成角一般步骤：①平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线；②证明：证明所作的角是异面直线所成的角；③寻找：在立体图形中，寻找或作出含有此角的三角形，并解之；④取舍：因为异面直线所成角的取值范围是，所以所作的角为钝角时，应取它的补角作为异面直线所成的角.2.用向量法求异面直线所成角的一般步骤：(1)建立空间直角坐标系；(2)用坐标表示两异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；(4)注意两异面直线所成角的范围是，即两异面直线所成角的余弦值等于两向量夹角的余弦值的绝对值.3.几何法求线面角(1)垂线法求线面角(也称直接法)；(2)公式法求线面角(也称等体积法)：用等体积法，求出斜线P A在面外的一点P到面的距离，利用三角形的正弦公式进行求解.，其中是斜线与平面所成的角，h是垂线段的长，l是斜线段的长.4.向量法求直线与平面所成角的主要方法:(1)分别求出斜线和它在平面内的射影直线的方向向量，将题目转化为求两个方向向量的夹角(或其补角)；(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角.5.几何法求二面角作二面角的平面角的方法：作二面角的平面角可以用定义法，也可以用垂面法，即在一个半平面内找一点作另一个半平面的垂线，再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角.6.向量法求二面角的解题思路:用法向量求两平面的夹角：分别求出两个法向量，然后通过两个平面的法向量的夹角得到两平面夹角的大小.【知识点4 立体几何中的最值问题及其解题策略】1.立体几何中的几类最值问题立体几何中的最值问题有三类：一是空间几何体中相关的点、线和面在运动，求线段长度、截面的面积和体积的最值；二是空间几何体中相关点和线段在运动，求有关角度和距离的最值；三是在空间几何体中，已知某些量的最值，确定点、线和面之间的位置关系．2.立体几何中的最值问题的求解方法解决立体几何中的最值问题主要有两种解题方法：一是几何法，利用几何体的性质，探求图形中点、线、面的位置关系；二是代数法，通过建立空间直角坐标系，利用点的坐标表示所求量的目标函数，借助函数思想方法求最值；通过降维的思想，将空间某些量的最值问题转化为平面三角形、四边形或圆中的最值问题．【知识点5 立体几何中的轨迹问题及其解题策略】1.立体几何中的轨迹问题立体几何中的轨迹问题，这是一类立体几何与解析几何的交汇题型，既考查学生的空间想象能力，即点、线、面的位置关系，又考查用代数方法研究轨迹的基本思想，培养学生的数学运算、直观想象等素养．2.立体几何中的轨迹问题的求解方法解决立体几何中的轨迹问题有两种方法：一是几何法：对于轨迹为几何体的问题，要抓住几何体中的不变量，借助空间几何体（柱、锥、台、球）的定义；对于轨迹为平面上的问题，要利用降维的思想，熟悉平面图形（直线、圆、圆锥曲线）的定义．二是代数法：在图形中，建立恰当的空间直角坐标系，利用空间向量进行求解．【知识点6 以立体几何为载体的情境题的求解策略】1.以立体几何为载体的几类情境题以立体几何为载体的情境题大致有三类：(1)以数学名著为背景设置问题，涉及中外名著中的数学名题名人等；(2)以数学文化为背景设置问题，包括中国传统文化，中外古建筑等；(3)以生活实际为背景设置问题，涵盖生产生活、劳动实践、文化精神等．2.以立体几何为载体的情境题的求解思路以立体几何为载体的情境题都跟图形有关，涉及在具体情境下的图形阅读，需要通过数形结合来解决问题.此类问题的求解过程主要分四步：一是要读特征，即从图形中读出图形的基本特征；二是要读本质，即要善于将所读出的信息进行提升，实现“图形→文字→符号”的转化；三是要有问题意识，带着问题阅读图形，将研究图形的本身特征和关注题目要解决的问题有机地融合在一起；四是要有运动观点，要“动手”去操作，动态地去阅读图形．【题型1 求几何体的体积与表面积】【例1】（2023·江苏徐州·沛县湖西中学模拟预测）在三棱锥P−ABC中，三条侧棱P A，PB，PC两两垂直，且PA=PB=PC=2，若三棱锥P−ABC的所有顶点都在同一个球的表面上，则该球的体积是（）A．4√3πB．4√2πC．6πD．12π【变式1-1】（2023·陕西铜川·统考一模）我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸，若盆中积水深九寸，则平地降雨量是（）（注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸；③V台=13(S上+S下+√S上⋅S下)ℎ）A．6寸B．4寸C．3寸D．2寸【变式1-2】（2023·全国·模拟预测）如图，已知正四棱台ABCD−A1B1C1D1的高为2,AB=2A1B1,P,Q分别为B1C1,C1D1的中点，若四边形PQDB的面积为152，则该四棱台的体积为（）A．563B．56C．283D．28【变式1-3】（2023·山东·统考一模）陀螺起源于我国，在山西夏县新石器时代的遗址中，就出土了目前发现的最早的石制陀螺因此，陀螺的历史至少也有四千年，如图所示为一个陀螺的立体结构图，若该陀螺底面圆的直径AB=12cm，圆柱体部分的高BC=6cm，圆锥体部分的高CD=4cm，则这个陀螺的表面积是（）A．(144+12√13)πcm2B．(144+24√13)πcm2C．(108+12√13)πcm2D．(108+24√13)πcm2【题型2 与球有关的截面问题】【例2】（2023·陕西咸阳·武功县普集高级中学校考模拟预测）已知球O的一个截面的面积为2π，球心O到该截面的距离比球的半径小1，则球O的表面积为（）A．8πB．9πC．12πD．16π【变式2-1】（2023·全国·校联考模拟预测）上、下底面均为等边三角形的三棱台的所有顶点都在同一球面上，若三棱台的高为3，上、下底面边长分别为√15，2√6，则该球的表面积为（）A．32πB．36πC．40πD．42π【变式2-2】（2023·河南·信阳高中校联考模拟预测）如图，在三棱锥A−BCD中，AB,AC,AD两两垂直，且AB=AC=AD=3，以A为球心，√6为半径作球，则球面与底面BCD的交线长度的和为（）A．2√3πB．√3πC．√3π2D．√3π4【变式2-3】（2023·江西南昌·江西师大附中校考三模）已知正方体ABCD−A1B1C1D1的棱长为2，E为棱CC1上的一点，且满足平面BDE⊥平面A1BD，则平面A1BD截四面体ABCE的外接球所得截面的面积为（）A．136πB．2512πC．83πD．23π【题型3 体积、面积、周长、距离的最值与范围问题】【例3】（2023·福建莆田·莆田一中校考一模）如图，在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等，如图①.若用剩下的部分折成一个无盖的正三棱柱形容器，如图②.则这个容器的容积的最大值为（）A．a327B．a336C．a354D．a372【变式3-1】（2023·全国·模拟预测）在直三棱柱ABC−A1B1C1中，∠BAC=60°，侧面BCC1B1的面积为2√3，则直三棱柱ABC−A1B1C1外接球的表面积的最小值为（）A．4πB．8πC．4√3πD．8√3π【变式3-2】（2023·山东·山东省实验中学校考二模）正四棱柱ABCD−A1B1C1D1中，AB=2，P为底面A1B1C1D1的中心，M是棱AB的中点，正四棱柱的高ℎ∈[√2,2√2]，点M到平面PCD的距离的最大值为（）A．2√63B．83C．4√23D．329【变式3-3】（2023·湖南长沙·长沙一中校考模拟预测）已知A，B，C，D是体积为20√53π的球体表面上四点，若AB=4，AC=2，BC=2√3，且三棱锥A－BCD的体积为2√3，则线段CD长度的最大值为（）A．2√3B．3√2C．√13D．2√5【题型4 几何体与球的切、接问题】【例4】（2023·河北邯郸·统考三模）三棱锥S−ABC中，SA⊥平面ABC，AB⊥BC，SA=AB=BC．过点A分别作AE⊥SB，AF⊥SC交SB、SC于点E、F，记三棱锥S−FAE的外接球表面积为S1，三棱锥S−ABC的外接球表面积为S2，则S1S2=（）A．√33B．13C．√22D．12【变式4-1】（2023·福建龙岩·统考模拟预测）如图，已知正方体的棱长为2，以其所有面的中心为顶点的多面体为正八面体，则该正八面体的内切球表面积为（）A．π6B．πC．4π3D．4π【变式4-2】（2023·全国·模拟预测）为了便于制作工艺品，某工厂将一根底面半径为6cm，高为4cm的圆柱形木料裁截成一个正四棱台木料，已知该正四棱台上底面的边长不大于4√2cm，则当该正四棱台的体积最大时，该正四棱台外接球的表面积为（）A．128πcm2B．145πcm2C．153πcm2D．160πcm2【变式4-3】（2023·浙江温州·乐清市知临中学校考二模）如今中国被誉为基建狂魔，可谓是逢山开路，遇水架桥.公路里程､高铁里程双双都是世界第一.建设过程中研制出用于基建的大型龙门吊､平衡盾构机等国之重器更是世界领先.如图是某重器上一零件结构模型，中间最大球为正四面体ABCD的内切球，中等球与最大球和正四面体三个面均相切，最小球与中等球和正四面体三个面均相切，已知正四面体ABCD棱长为2√6，则模型中九个球的表面积和为（）A．6πB．9πC．31π4D．21π【题型5 空间线段以及线段之和最值问题】【例5】（2023·湖南长沙·长郡中学校联考模拟预测）已知底面边长为a的正四棱柱ABCD−A1B1C1D1内接于半径为√3的球内，E，F分别为B1C1，C1D1的中点，G，H分别为线段AC1，EF上的动点，M为线段AB1的中点，当正四棱柱ABCD−A1B1C1D1的体积最大时，|GH|+|GM|的最小值为（）A．√2B．3√22C．2D．1+√2【变式5-1】（2023·安徽合肥·合肥市第六中学校考模拟预测）已知在长方体ABCD−A1B1C1D1中，AB=BC= 1，AA1=√3，在线段A1D上取点M，在CD1上取点N，使得直线MN//平面ACC1A1，则线段MN长度的最小值为（）A．√33B．√213C．√37D．√217【变式5-2】（2023·四川绵阳·模拟预测）如图，棱长为2的正方体ABCD−A1B1C1D1中，点P在线段AD1上运动，以下四个命题：；④|C1P|+①三棱锥D−BPC1的体积为定值；②C1P⊥CB1；③直线DC1与平面ABC1D1所成角的正弦值为12|DP|的最小值为√10．其中真命题有（）A．1个B．2个C．3个D．4个【变式5-3】（2023·天津和平·耀华中学校考二模）粽子，古称“角黍”，早在春秋时期就已出现，到晋代成为了端午节的节庆食物．现将两个正四面体进行拼接，得到如图所示的粽子形状的六面体，其中点G在线，则下列说法正确的是（）段CD（含端点）上运动，若此六面体的体积为163A．EF=2B．EF=4C．EG+FG的最小值为3√2D．EG+FG的最小值为2√6【题型6 空间角问题】【例6】（2023·全国·模拟预测）已知正三棱柱ABC−A1B1C1的侧面积是底面积的6√3倍，点E为四边形ABB1A1的中心，点F为棱CC1的中点，则异面直线BF与CE所成角的余弦值为（）A．2√3913B．√3913C．√3926D．3√3926【变式6-1】（2023·河北保定·统考二模）如图，在长方体ABCD−A1B1C1D1中，AB=BC=1，AA1=2，对角线B1D与平面A1BC1交于E点．则A1E与面AA1D1D所成角的余弦值为（）A．13B．√33C．23D．√53【变式6-2】（2023·全国·模拟预测）在正方体ABCD−A1B1C1D1中，若点N是棱BB1上的动点，点M是线段A1C1（不含线段的端点）上的动点，则下列说法正确的是（）A．存在直线MN，使MN//B1C B．异面直线CM与AB所成的角可能为π3C．直线CM与平面BND所成的角为π3D．平面BMC//平面C1NA【变式6-3】（2023·四川遂宁·统考三模）如图，正方体ABCD−A1B1C1D1的棱长为2，线段B1D1上有两个动点E,F（E在F的左边），且EF=√2．下列说法不正确的是（）A．当E运动时，二面角E−AB−C的最小值为45∘B．当E,F运动时，三棱锥体积B−AEF不变C．当E,F运动时，存在点E,F使得AE//BFD．当E,F运动时，二面角C−EF−B为定值【题型7 翻折问题】【例7】（2023·四川泸州·统考一模）已知菱形ABCD的边长为6，∠BAD=60°，将△BCD沿对角线BD翻折，使点C到点P处，且二面角A−BD−P为120°，则此时三棱锥P−ABD的外接球的表面积为（）A．21πB．28√21πC．52πD．84π【变式7-1】（2023·福建福州·福建省福州第一中学校考模拟预测）在矩形ABCD中，AB=3,AD=4，将△ABD 沿对角线BD翻折至△A′BD的位置，使得平面A′BD⊥平面BCD，则在三棱锥A′−BCD的外接球中，以A′C为直径的截面到球心的距离为（）A．√43510B．6√25C．√23910D．√11310【变式7-2】（2023·湖北恩施·校考模拟预测）如图，矩形ABCD中，E、F分别为BC、AD的中点，且BC=2AB=2，现将△ABE沿AE向上翻折，使B点移到P点，则在翻折过程中，下列结论不正确的是（）A．存在点P，使得PE∥CFB．存在点P，使得PE⊥EDC．三棱锥P−AED的体积最大值为√26D．当三棱锥P−AED的体积达到最大值时，三棱锥P−AED外接球表面积为4π【变式7-3】（2023·四川·校联考模拟预测）如图，已知△ABC是边长为4的等边三角形，D,E分别是AB,AC 的中点，将△ADE沿着DE翻折，使点A到点P处，得到四棱锥P−BCED，则下列命题错误的是（）A．翻折过程中，该四棱锥的体积有最大值为3B．存在某个点P位置，满足平面PDE⊥平面PBCC．当PB⊥PC时，直线PB与平面BCED所成角的正弦值为√33πD．当PB=√10时，该四棱锥的五个顶点所在球的表面积为523【题型8 立体几何中的轨迹问题】【例8】（2023·全国·模拟预测）如图，正方体ABCD−A1B1C1D1的棱长为3，点P是平面ACB1内的动点，M，N分别为C1D1，B1C的中点，若直线BP与MN所成的角为θ，且sinθ=√55，则动点P的轨迹所围成的图形的面积为（）A．3π4B．π2C．π3D．π4【变式8-1】（2023·海南省直辖县级单位·文昌中学校考模拟预测）已知四棱柱ABCD−A1B1C1D1的底面ABCD 为正方形，侧棱与底面垂直，点P是侧棱DD1上的点，且DP=2PD1,AA1=3,AB=1.若点Q在侧面BCC1B1（包括其边界）上运动，且总保持AQ⊥BP，则动点Q的轨迹长度为（）A．√3B．√2C．2√33D．√52【变式8-2】（2023·河北·统考模拟预测）已知正四棱锥（底面为正方形，且顶点在底面的射影为正方形的中心的棱锥为正四棱锥）P－ABCD的底面正方形边长为2，其内切球O的表面积为π3，动点Q在正方形ABCD 内运动，且满足OQ=OP，则动点Q形成轨迹的周长为（）A．2π11B．3π11C．4π11D．5π11【变式8-3】（2023·全国·校联考模拟预测）如图，已知正方体ABCD−A1B1C1D1的棱长为2，P为空间中一点且满足∠APB1=∠ADB1，则以下说法正确的有（）A．若P在面AB1C1D上，则其轨迹周长为8√6π9B．若A1P⊥AB1，则D1P的最小值为√3+1−√6C．P的轨迹围成的封闭曲面体积为32√6π227+4√3πD．四棱锥P-ABCD体积最大值为4(2√6+√2+3)9【题型9 以立体几何为载体的情境题】【例9】（2023·云南大理·统考一模）我国古代数学名著《数书九章》中有“天池盆测雨”题，在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为36寸，盆底直径为12寸，盆深18寸.若某次下雨盆中积水的深度恰好是盆深的一半，则该天池盆中水的体积为（）A．1404π立方寸B．1080π立方寸C．756π立方寸D．702π立方寸【变式9-1】（2023·广东广州·广东实验中学校考一模）阿基米德多面体是由边数不全相同的正多边形为面的多面体．如图所示的阿基米德多面体有四个全等的正三角形面和四个全等的正六边形面，该多面体是由过正四面体各棱的三等分点的平面截去四个小正四面体得到．若该多面体的所有顶点都在球O的表面上，且点O到正六边形面的距离为√62，则球O的体积为（）A．7√1424πB．7√143πC．11√2224πD．11√223π【变式9-2】（2023·河南·校联考模拟预测）如图1所示，宫灯又称宫廷花灯，是中国彩灯中富有特色的汉民族传统手工艺品之一．图2是小明为自家设计的一个花灯的直观图，该花灯由上面的正六棱台与下面的正六棱柱组成，若正六棱台的上、下两个底面的边长分别为4dm和2dm，正六棱台与正六棱柱的高分别为1dm 和6dm，则该花灯的表面积为（）A．(108+30√3)dm2B．(72+30√3)dm2C．(64+24√3)dm2D．(48+24√3)dm2【变式9-3】（2023·河南郑州·统考模拟预测）《九章算术·商功》：“斜解立方，得两堑堵，斜解堑堵，其一为阳马，其一为鳖臑”.意思是一个长方体沿对角面斜解（图1），得到一模一样的两个堑堵（图2），再沿一个堑堵的一个顶点和相对的棱斜解（图2），得一个四棱锥称为阳马（图3），一个三棱锥称为鳖臑（图4）.若长方体的体积为V，由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为V1，V2，V3，则下列等式错误的是（）A．V1+V2+V3=V B．V1=2V2C．V2=2V3D．V2−V3=V61．（2023·北京·统考高考真题）坡屋顶是我国传统建筑造型之一，蕴含着丰富的数学元素．安装灯带可以勾勒出建筑轮廓，展现造型之美．如图，某坡屋顶可视为一个五面体，其中两个面是全等的等腰梯形，两个面是全等的等腰三角形．若AB=25m,BC=AD=10m，且等腰梯形所在的平面、等腰三角形所在的平，则该五面体的所有棱长之和为（）面与平面ABCD的夹角的正切值均为√145A．102m B．112mC．117m D．125m2．（2023·全国·统考高考真题）已知△ABC为等腰直角三角形，AB为斜边，△ABD为等边三角形，若二面角C−AB−D为150°，则直线CD与平面ABC所成角的正切值为（）A．15B．√25C．√35D．253．（2023·全国·统考高考真题）已知圆锥PO的底面半径为√3，O为底面圆心，P A，PB为圆锥的母线，∠AOB=120°，若△PAB的面积等于9√34，则该圆锥的体积为（）A．πB．√6πC．3πD．3√6π4．（2023·天津·统考高考真题）在三棱锥P−ABC中，点M,N分别在棱PC,PB上，且PM=13PC，PN=23PB，则三棱锥P−AMN和三棱锥P−ABC的体积之比为（）A．19B．29C．13D．495．（2021·浙江·统考高考真题）如图已知正方体ABCD−A1B1C1D1，M，N分别是A1D，D1B的中点，则（）A．直线A1D与直线D1B垂直，直线MN//平面ABCDB．直线A1D与直线D1B平行，直线MN⊥平面BDD1B1C．直线A1D与直线D1B相交，直线MN//平面ABCDD．直线A1D与直线D1B异面，直线MN⊥平面BDD1B16．（2023·全国·统考高考真题）下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（）A．直径为0.99m的球体B．所有棱长均为1.4m的四面体C．底面直径为0.01m，高为1.8m的圆柱体D．底面直径为1.2m，高为0.01m的圆柱体7．（2023·全国·统考高考真题）已知圆锥的顶点为P，底面圆心为O，AB为底面直径，∠APB=120°，PA=2，点C在底面圆周上，且二面角P−AC−O为45°，则（）．A．该圆锥的体积为πB．该圆锥的侧面积为4√3πC．AC=2√2D．△PAC的面积为√38．（2023·全国·统考高考真题）已知点S,A,B,C均在半径为2的球面上，△ABC是边长为3的等边三角形，SA⊥平面ABC，则SA=．9．（2023·全国·统考高考真题）在正方体ABCD−A1B1C1D1中，AB=4,O为AC1的中点，若该正方体的棱与球O的球面有公共点，则球O的半径的取值范围是．10．（2023·全国·统考高考真题）在正方体ABCD−A1B1C1D1中，E，F分别为AB，C1D1的中点，以EF为直径的球的球面与该正方体的棱共有个公共点．11．（2023·全国·统考高考真题）在正四棱台ABCD−A1B1C1D1中，AB=2,A1B1=1,AA1=√2，则该棱台的体积为．12．（2023·全国·统考高考真题）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为．立体几何小题【题型1 求几何体的体积与表面积】 (4)【题型2 与球有关的截面问题】 (7)【题型3 体积、面积、周长、距离的最值与范围问题】 (10)【题型4 几何体与球的切、接问题】 (13)【题型5 空间线段以及线段之和最值问题】 (18)【题型6 空间角问题】 (23)【题型7 翻折问题】 (30)【题型8 立体几何中的轨迹问题】 (35)【题型9 以立体几何为载体的情境题】 (40)立体几何是高考的热点内容，属于高考的必考内容之一.从近几年的高考情况来看，高考对该部分的考查，小题主要体现在三个方面：一是有关空间线面位置关系的判断；二是空间几何体的体积和表面积的计算，难度较易；三是常见的一些经典常考压轴小题，涉及到空间角、空间距离与轨迹问题等，难度中等或偏上．【知识点1 空间几何体表面积与体积的常见求法】1.求几何体体积的常用方法(1)公式法：直接代入公式求解.(2)等体积法：四面体的任何一个面都可以作为底面，只需选用底面面积和高都易求出的形式即可.(3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，三棱柱补成四棱柱等.(4)分割法：将几何体分割成易求解的几部分，分别求体积.2.求组合体的表面积与体积的一般方法求组合体的表面积的问题，首先应弄清它的组成部分，其表面有哪些底面和侧面，各个面的面积应该怎样求，然后根据公式求出各个面的面积，最后相加或相减.求体积时也要先弄清各组成部分，求出各简单几何体的体积，再相加或相减.【知识点2 几何体与球的切、接问题的解题策略】1.常见的几何体与球的切、接问题的解决方案：常见的与球有关的组合体问题有两种：一种是内切球，另一种是外接球.常见的几何体与球的切、接问题的解决方案：2.空间几何体外接球问题的求解方法：空间几何体外接球问题的处理关键是确定球心的位置，常见的求解方法有如下几种：(1)涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题求解.(2)若球面上四点P,A,B,C构成的三条线段P A,PB,PC两两垂直，且P A=a，PB=b，PC=c，一般把有关元素“补形”成为一个球内接长方体，根据4R2=a2+b2+c2求解.(3)利用平面几何体知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.【知识点3 几何法与向量法求空间角】1.几何法求异面直线所成的角(1)求异面直线所成角一般步骤：①平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线；②证明：证明所作的角是异面直线所成的角；③寻找：在立体图形中，寻找或作出含有此角的三角形，并解之；④取舍：因为异面直线所成角的取值范围是，所以所作的角为钝角时，应取它的补角作为异面直线所成的角.2.用向量法求异面直线所成角的一般步骤：(1)建立空间直角坐标系；(2)用坐标表示两异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；(4)注意两异面直线所成角的范围是，即两异面直线所成角的余弦值等于两向量夹角的余弦值的绝对值.3.几何法求线面角(1)垂线法求线面角(也称直接法)；(2)公式法求线面角(也称等体积法)：用等体积法，求出斜线P A在面外的一点P到面的距离，利用三角形的正弦公式进行求解.是斜线与平面所成的角，h是垂线段的长，l是斜线段的长.4.向量法求直线与平面所成角的主要方法:(1)分别求出斜线和它在平面内的射影直线的方向向量，将题目转化为求两个方向向量的夹角(或其补角)；(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角.5.几何法求二面角作二面角的平面角的方法：作二面角的平面角可以用定义法，也可以用垂面法，即在一个半平面内找一点作另一个半平面的垂线，再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角.6.向量法求二面角的解题思路:用法向量求两平面的夹角：分别求出两个法向量，然后通过两个平面的法向量的夹角得到两平面夹角的大小.【知识点4 立体几何中的最值问题及其解题策略】1.立体几何中的几类最值问题立体几何中的最值问题有三类：一是空间几何体中相关的点、线和面在运动，求线段长度、截面的面积和体积的最值；二是空间几何体中相关点和线段在运动，求有关角度和距离的最值；三是在空间几何体中，已知某些量的最值，确定点、线和面之间的位置关系．2.立体几何中的最值问题的求解方法解决立体几何中的最值问题主要有两种解题方法：一是几何法，利用几何体的性质，探求图形中点、线、面的位置关系；二是代数法，通过建立空间直角坐标系，利用点的坐标表示所求量的目标函数，借助函数思想方法求最值；通过降维的思想，将空间某些量的最值问题转化为平面三角形、四边形或圆中的最值问题．【知识点5 立体几何中的轨迹问题及其解题策略】1.立体几何中的轨迹问题立体几何中的轨迹问题，这是一类立体几何与解析几何的交汇题型，既考查学生的空间想象能力，即点、线、面的位置关系，又考查用代数方法研究轨迹的基本思想，培养学生的数学运算、直观想象等素养．2.立体几何中的轨迹问题的求解方法解决立体几何中的轨迹问题有两种方法：一是几何法：对于轨迹为几何体的问题，要抓住几何体中的不变量，借助空间几何体（柱、锥、台、球）的定义；对于轨迹为平面上的问题，要利用降维的思想，熟悉平面图形（直线、圆、圆锥曲线）的定义．二是代数法：在图形中，建立恰当的空间直角坐标系，利用空间向量进行求解．【知识点6 以立体几何为载体的情境题的求解策略】1.以立体几何为载体的几类情境题以立体几何为载体的情境题大致有三类：(1)以数学名著为背景设置问题，涉及中外名著中的数学名题名人等；(2)以数学文化为背景设置问题，包括中国传统文化，中外古建筑等；(3)以生活实际为背景设置问题，涵盖生产生活、劳动实践、文化精神等．。

立体几何中轨迹问题的处理技巧与方法

ʏ陈婷立体几何中的轨迹问题,是立体几何与解析几何的知识交汇点㊂这类问题,立意新颖,重视不同知识的交叉与渗透,重视对数学知识与数学能力的考查与应用,是培养同学们数学核心素养的好素材㊂一㊁直接法直接法就是直接利用立体几何的相关知识,合理分析和研究问题中各个元素之间的关系,或者直接利用轨迹定义进行求解的方法㊂例1 如图1,在正方体A B C D -A 1B 1C 1D 1中,P 是侧面B C C 1B 1上的一个动点,若点P 到直线B C 与直线C 1D 1的距离相等,则动点P 的轨迹是下列哪种线的一部分( )㊂图1A.直线 B .圆C .双曲线 D .抛物线分析:根据题设条件,利用空间点线面的位置关系,直接得到动点P 到直线B C 与到点C 1的距离相等,再结合解析几何中抛物线的定义,可得对应的答案㊂解:根据正方体的性质,可知C 1D 1ʅ平面B C C 1B 1,所以动点P 到直线C 1D 1的距离与到点C 1的距离相等㊂又动点P 到直线B C 与到直线C 1D 1的距离相等,所以动点P 到直线B C 与到点C 1的距离相等㊂根据抛物线的定义,可得动点P 的轨迹是一条抛物线的一部分㊂应选D ㊂二㊁转化法转化法就是将立体几何问题转化为平面几何问题,进行合理降维处理,进而应用平面几何㊁解析几何等相关知识来分析与求解的方法㊂例2 (2022年高考北京卷)已知正三棱锥P -A B C 的六条棱长均为6,S 是әA B C 及其内部的点构成的集合㊂设集合T ={Q ɪS |P Q ɤ5},则T 表示的区域的面积为( )㊂A .3π4B .πC .2πD .3π分析:根据题设条件,结合正三棱锥的性质,合理构建点P 在底面әA B C 内的射影点O ,结合集合的创新设置进行合理转化,将空间中的距离问题转化为平面上的距离问题加以分析与求解㊂解:设点P 在底面әA B C 内的射影为点O ㊂依题意知әA B C 是边长为6的正三角形,所以A O =B O =C O =23㊂因为P A =P B =P C =6,所以P O =62-(23)2=26㊂若P Q =5,则O Q =P Q 2-P O 2=1,可知动点Q 的轨迹是在底面әA B C 内,以O 为圆心,半径为r =1的圆及其内部,其对应的面积为πr 2=π㊂应选B ㊂三㊁解析法解析法就是利用解析几何在研究轨迹方面的一整套比较完整的理论体系,通过坐标法进行代数运算与逻辑推理的一种求轨迹的方法㊂解析法是解决立体几何图形的二维轨迹问题的常用方法之一㊂例3 (多选题)如图2所示,在正方体A B C D -A 1B 1C 1D 1中,E 是C C 1的中点,点P 在底面A B C D 内运动,若P D 1,P E 与底面A B C D 所成的角相等,则动点P 的轨迹是( )㊂71知识结构与拓展高一数学 2023年4月Copyright ©博看网. All Rights Reserved.图2A.圆的一部分B.椭圆的一部分C.经过线段B C靠近B的三等分点D.经过线段C D靠近C的三等分点分析:根据题意得D P=2P C,以点D为坐标原点,建立平面直角坐标系,通过坐标法进行讨论求解㊂解:由正方体的性质得D D1ʅ平面A B C D,E Cʅ平面A B C D,所以øD P D1,øC P E分别为P D1,P E与底面A B C D所成的角,所以øD P D1=øC P E㊂因为t a nøD P D1=D D1D P,t a nøC P E= C EP C,又D D1=2C E,所以D P=2P C㊂在平面A B C D中,以D为坐标原点,建立平面直角坐标系,如图3所示㊂图3设正方体的边长为a,点P(x,y),xȡ0,yȡ0,则点D(0,0),C(a,0),所以D P2= x2+y2,P C2=(x-a)2+y2,所以x2+y2= 4(x-a)2+4y2,整理得3x2+3y2-8a x+ 4a2=0,显然3x2+3y2-8a x+4a2=0表示圆的方程,所以动点P的轨迹是圆的一部分,A正确,B错误㊂线段B C靠近B的三等分点的坐标为a,23a,线段C D靠近C的三等分点的坐标为23a,0,分别代入方程3x2+3y2-8a x+4a2=0,可得3a2+3ˑ23a2-8a2+4a2=13a2ʂ0,3ˑ23a2+ 3ˑ02-8aˑ23a+4a2=0,所以23a,0在圆3x2+3y2-8a x+4a2=0上,a,23a不在圆3x2+3y2-8a x+4a2=0上,C错误,D 正确㊂应选A D㊂四㊁性质法性质法就是利用轨迹的相关知识来解决立体几何中轨迹问题的一种基本方法㊂有些空间图形的轨迹不一定是二维的,转化为平面问题比较困难,这时可借助性质法来处理㊂例4已知棱长为3的正方体A B C D-A1B1C1D1中,长为2的线段M N的一个端点M在D D1上运动,另一个端点N在底面A B-C D上运动,则线段M N的中点P的轨迹与正方体的面所围成的几何体的体积为㊂分析:不论әMD N如何变化,点P到点D的距离始终等于1㊂从而点P的轨迹是一个以点D为球心,半径为1的球的18,由此可求出体积㊂解:如图4所示,端点N在正方形A B C D内运动㊂图4因为әMD N为直角三角形,P为斜边MN的中点,所以不论әMD N如何变化,点P到点D的距离始终等于1㊂利用立体几何的性质,可知动点P的轨迹是一个以点D为球心,半径为1的球的18,所以所求体积V= 18ˑ43ˑπˑ13=π6㊂作者单位:江苏省海安高级中学(责任编辑郭正华)8 1知识结构与拓展高一数学2023年4月Copyright©博看网. All Rights Reserved.。

与立体几何有关的轨迹问题

Ｃ
如图５，已知正方体
：二：
ＡＢＣＤ
ＡＢＤ－ＡＢＣＤ的棱长为１点ＭＣ－，
Ｂ
在Ａ上且Ｍ－Ｑ平棱ｌ，ａ＝￣是面Ｂ，
ＡＣ内的动点，点Ｑ到直线ＢＤ若
Ａ。的距离与点Ｑ到点Ｍ的距离Ｄ的平方差为ｌ，则点Ｑ的轨迹为（）．Ａ．物线抛Ｂ双曲线．Ｃ椭圆．
・
名师专题讲座
２１年期０第１２
与立体几何有关的轨迹问题
■ 唐建明
近几年的高考题中现了一些与立体几何有关的轨迹问题．些问题大致可分为两大类：体几何中的轨迹问题与以这立
空间图形为载体的圆锥曲线问题．
何中点、、的基本知识，要掌握有关的轨迹问题：１空线面还（）间中到两定点的距离相等点的轨迹是以这两个点为端点的线
二、以空间图形为载体的圆锥曲线问题
解决这类问题，了要熟练掌握立体几何中点、、的除线丽
一
中学鸯数理亿．学饼版
解：连接Ｅ易知△ＥＡ，ＡＦ为直角ｉ角形，Ｐ则Ａ一÷ ＥＦ
一
．ห้องสมุดไป่ตู้
故点Ｐ到定点Ａ的距离为定值，由球面的定义 Ⅻ ，选
、
立体几何中的轨迹问题

立体几何中动点轨迹问题的几种解题方法_柳双生

六、试用猜想证明法求解
猜想证明法也是解决空间轨迹问题的一种可以尝试着使用的方法，这往往是以立体几何的定理及空间图形的定义为依据，大胆猜想 , 然后通过验证，以
z ∩
面
P O y α
α ，过点 P 且与直线 l 成 30o 角的
三、应用坐标法求解
用代数方法研究几何问题是解析几何的本质 , 通过建立直角坐标系,设出动点坐标,将几何问题转化成代数问题来解决 , 这是探求空间图形中的轨迹问题常用的一种方法 . 例３. 正方体 ABCD-A1B1C1D1 的棱长为 1 ，点 P 是平面 ABCD 上的动点，且动点 P 到直线 A1D1 的距离与动点 P 到直线 AB 的距离的平方和为 2 ，则动点的轨迹是（）
）
A. 一条线段
M
D1 A1
B. 椭圆的一部分 C. 双曲线的一部分 D. 抛物线的一部分
分析：在平面 A1B1C1D1 中，过点 P 作 PM ⊥A1D1，垂足为点 M, 在平面 ADD1A1 中过点 M 作 MN ∥AA1，交 AD 于点 N ，又因为 PN=PB ，MN=BB1，所以 △ PMN
直线交面 α 于点 M ，若点 M 的轨迹为一圆锥曲线，求其离心率 .
M x
达到解决的目的 . 例６. 在正四棱锥 S-ABCD 中，E 是 BC 的中点，点 P 在侧面 △SCD 内及其边界上运动，并且总是保持 PE⊥AC ，则动点 P 的轨迹是（）

高中数学立体几何微专题1动态问题之轨迹

立体几何微专题1 :动态问题之轨迹立体几何动态问题的分为以下基本类型：点动问题、线动问题、面动问题、体动问题、多动问题等，很多的动态问题只要知道轨迹，把空间转化为平面问题要解决，立体几何中某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与求平面轨迹类似，应注意几何条件，善于转化为平面问题.轨迹的几何判断方法：动点P满足如下轨迹定义条件时（1）平面内到定点距离等于定长（圆）；（2）空间中到定点距离等于定长（球面）；（3）两不同平面公共点的集合（直线）；（4）平面内到两定点距离之和为定值（大于定点间的距离）（椭圆）；（5）平面内到两定点距离之差的绝对值为定值（小于定点间的距离）（双曲线）；（6）平面内到定直线距离等于到定点（不在定直线上）距离（抛物线）©考点突破[例1] （2004北京，理4）如图，在正方体力NCD-4/C；〃中，尸是侧面内••封点，若「到直线"C与直线的距离相等，则动点「的轨迹所在的曲线是（）A,直线H,圆 C.双曲线 D.抛物线解析：选D.由于G〃，平面Mga连接尸G，则产C；_LGR，即点尸到直线qq的距离即尸q,因此，动点尸到定点G与定直线BC的距离相等，由抛物线的定义可知，动点尸的轨迹为抛物线.[例2] （2006北京，理4）平面口的斜线力疗交1于点过定点/的动直线/与X/垂直，且交a于点C ,则动点。

的轨迹是（）A. 一条直线B. 一个圆C. 一个桶圆D.双曲线的一支解析：选A.设/与「是其中的两条任意的直线，则这两条直线确定一个平面，且斜线回垂直于这个平面,由过平面外一点有且只有一个平面与己知直线垂直可知过定点刃与山?垂直所有直线都在这个平面内，故动点C都在这个平面与平面b的交线上，故选A.[例3] （2008浙江，理10）如图，川匕是平面戊的斜线段，凡为斜足，若点户在平面内运动，使得A4用尸的面枳为定值，则动点P的轨迹是（A.圆B.椭圆C. 一条直线D.两条平行直线解析：选人由题意知，点尸到线段乂月的距离为定值，则点尸在以为旋转轴的圆柱表面上一点।故平面a斜截圆柱，所得图形为椭圆.［例4］（2015浙江,文7）如图,斜线段45与邛面仪所成的角为60、B为斜足，平面a上的动点户满足乙匕13 = 30"则点尸的轨迹是（）A.直线B.抛物线C.椭圆D.双曲线的一支解析：选C由题可知，当尸点运动时，在空间中，满足条件的/尸绕旋转形成一个圆锥，用一个与圆锥高成60口角的平面截圆锥，所得图形为椭圆.［例5］（2012浙江模拟）如果一个平面与一个圆柱的轴成］（0<tz<-）2角，则该平面与圆柱侧面的交线是一个椭圆，当以=2时;椭圆的离心率是6百八1 8B, — C. 一 D.—2 2 2解析：选既由题意得，椭圆的短半轴长等于底面半径小即5=人若平面与圆柱的轴所成角为30,则平面与圆柱底面成60 ,从而可得椭圆的长半轴长为4二—-—= r L1|I a = 2b t故总= J］- （2）-=---cos 60 V a 2[例6](2013西城模)如图，正方体4武力-/用£口中，F 为底面/用⑦ 上的动点, PE 工邓：于E ，且/Y =/%，则点P 的轨迹是()A.线段 B,圆弧 C ，椭圆的一部分 D.抛物级的一部分解析：选/t 由题意知，\A {AP^\A X EP,则点P 在线段/五的中垂面上运动，从而与底面力人力的交线为线段.[例7](2011广州・•模，理SO 如图所示，已知正方体/狄力-的棱长为3长为2的线段上W 的一个端点M 在棱Z)口上运动，另一端点N 在正方形⑷?CD 内运动，则河、的中点的轨迹的面积为()A. 4 笈B. 2 乃C. 7T 解析：选D.易知I)J)] 1平面/BCD ,乙MDN = 90 ,取线段的中点尸，则QF 二4= 所以点尸的轨迹是以。

高考专题立体几何中轨迹、翻折、探索性问题

返回导航
12
解析：如图所示，连接 AC1 交平面 A1BD 于 O，连接 EO, 由题意可知 AC1⊥平面 A1BD，所以∠AEO 是 AE 与平面 A1BD 所成的角，所以∠AEO＝α.
返回导航
13
由 sin α＝255可得 tan α＝2，即AEOO＝2. 在四面体 A-A1BD 中，BD＝A1D＝A1B＝2 6， AB＝AD＝AA1＝2 3，所以四面体 A-A1BD 为正三棱锥，O 为△BDA1 的重心，
返回导航
17
∴平面 BCE∥平面 MND，即平面 MND 为平面 α，则点 G 到平面 DMN 的距离 d 即为点 G 到直线 DQ 的距离， ∵D→G＝0， 33，－ 36，D→Q＝(0，－2 3，－ 6)， ∴D→G·D→Q＝－2＋2＝0，即 DG⊥DQ， ∴点 G 到直线 DQ 的距离 d＝|D→G|＝1， ∴截面圆的半径 r＝ 22－12＝ 3，∴球被平面 α 截得的截面圆周长为 2πr＝2 3π，即平面 α 截点 P 的轨迹所形成的图形的周长为 2 3π.
返回导航
19
解： (1)证明：在△ABD 中，由余弦定理得，BD＝ AB2＋AD2－2AB·ADcos A＝ 4＋1－2×2×1×12＝ 3，
∴AD2＋BD2＝AB2，得 AD⊥DB，翻折后有 A′D⊥DB，又平面 A′BD⊥平面 BCD，且平面 A′BD∩平面 BCD＝DB，根据平面与平面垂直的性质定理可得 A′D⊥平面 BCD，又∵BC⊂平面 BCD，∴A′D⊥BC. 在平行四边形 ABCD 中，AD⊥DB，BC∥AD，∴BC⊥DB， ∵A′D∩DB＝D，∴BC⊥平面 A′DB， ∵BC⊂平面 A′BC，∴平面 A′BC⊥平面 A′BD．
返回导航
15

第七章 §7.10 立体几何中的动态、轨迹问题-2025高中数学大一轮复习讲义人教A版

§7.10立体几何中的动态、轨迹问题重点解读“动态”问题是高考立体几何问题最具创新意识的题型，它渗透了一些“动态”的点、线、面等元素，给静态的立体几何题赋予了活力，题型更新颖．同时，由于“动态”的存在，也使立体几何题更趋多元化，将立体几何问题与平面几何中的解三角形问题、多边形面积问题以及解析几何问题之间建立桥梁，使得它们之间灵活转化．题型一平行、垂直中的动态轨迹问题例1如图，在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，E ，F ，G ，H ，N 分别是CC 1，C 1D 1，DD 1，CD ，BC 的中点，M 在四边形EFGH 边上及其内部运动，若MN ∥平面A 1BD ，则点M 轨迹的长度是()A.3aB.2aC.3a 2D.2a 2答案D 解析连接HN ，GN (图略)，∵在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，E ，F ，G ，H ，N 分别是CC 1，C 1D 1，DD 1，CD ，BC 的中点，则GH ∥BA 1，HN ∥BD ，又GH ⊄平面A 1BD ，BA 1⊂平面A 1BD ，∴GH ∥平面A 1BD ，同理可证得NH ∥平面A 1BD ，又GH ∩HN ＝H ，GH ，HN ⊂平面GHN ，∴平面A 1BD ∥平面GHN ，又∵点M 在四边形EFGH 上及其内部运动，MN ∥平面A 1BD ，则点M 在线段GH 上运动，即满足条件，又GH ＝22a ，则点M 轨迹的长度是2a 2.思维升华动点轨迹的判断一般根据线面平行、线面垂直的判定定理和性质定理，结合圆或圆锥曲线的定义推断出动点的轨迹，有时也可以利用空间向量的坐标运算求出动点的轨迹方程．跟踪训练1正四棱锥S －ABCD 的底面边长为2，高为2，E 是边BC 的中点，动点P 在正四棱锥表面上运动，并且总保持PE ⊥AC ，则动点P 的轨迹的周长为()A.6＋2B.6－2C ．4D.5＋1答案A 解析如图，设AC ，BD 交于O ，连接SO ，由正四棱锥的性质可得SO ⊥平面ABCD ，因为AC ⊂平面ABCD ，故SO ⊥AC .又BD ⊥AC ，SO ∩BD ＝O ，SO ，BD ⊂平面SBD ，故AC ⊥平面SBD .由题意，PE ⊥AC 则动点P 的轨迹为过E 且垂直AC 的平面与正四棱锥S －ABCD 的交线，即平面EFG ，则AC ⊥平面EFG .由线面垂直的性质可得平面SBD ∥平面EFG ，又由面面平行的性质可得EG ∥SB ，GF ∥SD ，EF ∥BD ，又E 是边BC 的中点，故EG ，GF ，EF 分别为△SBC ，△SDC ，△BCD 的中位线．由题意BD ＝22，SB ＝SD ＝22＋2＝6，故EG ＋EF ＋GF ＝12×(6＋6＋22)＝6＋ 2.即动点P 的轨迹的周长为6＋ 2.题型二距离、角度有关的动态轨迹问题例2已知长方体ABCD －A 1B 1C 1D 1的外接球的表面积为5π，AA 1＝2，点P 在四边形A 1ACC 1内，且直线BP 与平面A 1ACC 1所成的角为π4，则长方体的体积最大时，动点P 的轨迹长为()A ．πB.2π2C.π2D.2π4答案C解析因为长方体ABCD －A 1B 1C 1D 1的外接球的表面积为5π，设外接球的半径为R ，所以4πR 2＝5π，解得R ＝52R ＝－52(舍去)，即外接球的直径为5，设AB ＝a ，BC ＝b ，则a 2＋b 2＋22＝5，可得a 2＋b 2＝1，所以V ＝2ab ≤a 2＋b 2＝1，当且仅当a ＝b ＝22时，等号成立．如图，设AC ，BD 相交于点O ，因为BO ⊥AC ，BO ⊥AA 1，AC ∩AA 1＝A ，AC ，AA 1⊂平面A 1ACC 1，所以BO ⊥平面A 1ACC 1，因为直线BP 与平面A 1ACC 1所成的角为π4，所以∠BPO ＝π4，故OP ＝12，则点P 的轨迹是以O 为圆心，半径r ＝12的半圆弧，所以动点P 的轨迹长为πr ＝π2.思维升华距离、角度有关的轨迹问题(1)距离：可转化为在一个平面内的距离关系，借助于圆锥曲线定义或者球和圆的定义等知识求解轨迹．(2)角度：直线与面成定角，可能是圆锥侧面；直线与定直线成等角，可能是圆锥侧面．跟踪训练2已知三棱锥P －ABC 的外接球O 的半径为13，△ABC 为等腰直角三角形，若顶点P 到底面ABC 的距离为4，且三棱锥P －ABC 的体积为163，则满足上述条件的顶点P 的轨迹长度是________．答案43π解析设底面等腰直角三角形ABC 的直角边的边长为x (x >0)，∵顶点P 到底面ABC 的距离为4且三棱锥P －ABC 的体积为163，∴13×12x 2×4＝163，解得x ＝22，∴△ABC 的外接圆半径为r 1＝12×2×22＝2，∴球心O 到底面ABC 的距离d 1＝R 2－r 21＝13－22＝3，又∵顶点P 到底面ABC 的距离为4，∴顶点P 的轨迹是一个截面圆的圆周(球心在底面ABC 和截面圆之间)且球心O 到该截面圆的距离d 2＝1，∵截面圆的半径r 2＝R 2－d 22＝13－1＝23，∴顶点P 的轨迹长度是2πr 2＝2π×23＝43π.题型三翻折有关的动态轨迹问题例3在矩形ABCD 中，E 是AB 的中点，AD ＝1，AB ＝2，将△ADE 沿DE 折起得到△A ′DE ，设A ′C 的中点为M ，若将△ADE 沿DE 翻折90°，则在此过程中动点M 形成的轨迹长度为________．答案2π8解析如图，设AC 的中点为M 0，△ADE 沿DE 翻折90°，此时平面A ′DE ⊥平面ABCD ，取CD 中点P ，CE 中点Q ，PQ 中点N ，连接PQ ，MP ，MQ ，MN ，M 0P ，M 0Q ，M 0N .MP ＝M 0P ＝12AD ＝12，MQ ＝M 0Q ＝12AE ＝12，PQ ＝12DE ＝22，△MPQ 和△M 0PQ 是等腰直角三角形，且在旋转过程中保持形状大小不变，故动点M 的轨迹是以N 为圆心，12PQ 为半径的一段圆弧，又MP ∥A ′D ，MP ⊄平面A ′DE ，A ′D ⊂平面A ′DE ，∴MP ∥平面A ′DE ，同理MQ ∥平面A ′DE ，又∵MP ∩MQ ＝M ，∴平面MPQ ∥平面A ′DE ，又平面A ′DE ⊥平面ABCD ，故平面MPQ ⊥平面ABCD ，又平面MPQ ∩平面ABCD ＝PQ ，MN ⊥PQ ，故MN ⊥平面ABCD ，又M 0N ⊂平面ABCD ，∴MN ⊥M 0N ，故动点M 形成的轨迹长度为14π·PQ ＝2π8.思维升华翻折有关的轨迹问题(1)翻折过程中寻找不变的垂直的关系求轨迹．(2)翻折过程中寻找不变的长度关系求轨迹．(3)可以利用空间坐标运算求轨迹．跟踪训练3(2024·连云港模拟)在矩形ABCD 中，AB ＝3，AD ＝1，点E 在CD 上，现将△AED 沿AE 折起，使平面AED ⊥平面ABC ，当E 从D 运动到C 时，求点D 在平面ABC 上的射影K 的轨迹长度为()A.22 B.223 C.π2 D.π3答案D解析由题意，将△AED 沿AE 折起，使平面AED ⊥平面ABC ，在平面AED 内过点D 作DK ⊥AE ，垂足K 为D 在平面ABC 上的射影，连接D ′K ，由翻折的特征知，则∠D ′KA ＝90°，故K 点的轨迹是以AD ′为直径的圆上一段弧，根据长方形知圆半径是12，如图当E 与C 重合时，∠D ′AC ＝60°，所以AK ＝12，取O 为AD ′的中点，得到△OAK 是正三角形．故∠KOA ＝π3，所以∠KOD ′＝2π3，射影K 的轨迹长度为12×2π3＝π3.课时精练一、单项选择题1．在正方体ABCD －A 1B 1C 1D 1中，Q 是正方形B 1BCC 1内的动点，A 1Q ⊥BC 1，则Q 点的轨迹是()A ．点B 1B ．线段B 1C C ．线段B 1C 1D ．平面B 1BCC 1答案B 解析如图，连接A 1C ，因为BC 1⊥A 1Q ，BC 1⊥A 1B 1，A 1Q ∩A 1B 1＝A 1，A 1Q ，A 1B 1⊂平面A 1B 1Q ，所以BC 1⊥平面A 1B 1Q ，又B 1Q ⊂平面A 1B 1Q ，所以BC 1⊥B 1Q ，又BC 1⊥B 1C ，所以点Q 在线段B 1C 上．2.(2023·佛山模拟)如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，点P 为正方形A 1B 1C 1D 1内的动点，满足直线BP 与下底面ABCD 所成角为60°的点P 的轨迹长度为()A.33B.3π6 C.3 D.3π2答案B 解析直线BP 与下底面ABCD 所成的角等于直线BP 与上底面A 1B 1C 1D 1所成的角，连接B 1P ，如图，因为BB 1⊥平面A 1B 1C 1D 1，PB 1⊂平面A 1B 1C 1D 1，所以BB 1⊥PB 1，故∠BPB 1为直线BP 与上底面A 1B 1C 1D 1所成的角，则∠BPB 1＝60°，因为BB 1＝1，所以PB 1＝BB 1tan 60°＝33，故点P 的轨迹为以B 1为圆心，33为半径，位于平面A 1B 1C 1D 1内的14圆，故轨迹长度为14×2π×33＝3π6.3.如图，在三棱柱ABC －A 1B 1C 1中，M 为A 1C 1的中点，N 为侧面BCC 1B 1上的一点，且MN ∥平面ABC 1，若点N 的轨迹长度为2，则()A ．AC 1＝4B ．BC 1＝4C ．AB 1＝6D ．B 1C ＝6答案B 解析如图，取B 1C 1的中点D ，BB 1的中点E ，连接MD ，DE ，ME ，由MD ∥A 1B 1∥AB ，DE ∥BC 1，又MD ⊄平面ABC 1，AB ⊂平面ABC 1，所以MD ∥平面ABC 1，同理可得DE ∥平面ABC 1，又MD ∩DE ＝D ，MD ，DE ⊂平面MDE ，所以平面MDE ∥平面ABC 1，又MN ∥平面ABC 1，故点N 的轨迹为线段DE ，又由DE ＝12BC 1＝2，可得BC 1＝4.4.已知四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 为正方形，侧棱与底面垂直，点P 是侧棱DD 1上的点，且DP ＝2PD 1，AA 1＝3，AB ＝1.若点Q 在侧面BCC 1B 1(包括其边界)上运动，且总保持AQ ⊥BP ，则动点Q 的轨迹长度为()A.3B.2C.233D.52答案D 解析如图，在侧棱AA 1上取一点R ，使得AR ＝2RA 1，连接PR ，BR ，过点A 作AN ⊥BR 交BR 于点M ，交BB 1于点N ，连接AC ，CN ，BD ，由PR ∥AD ，可知PR ⊥AN ，BR ，PR ⊂平面BPR ，BR ∩PR ＝R ，从而AN ⊥平面BPR ，BP ⊂平面BPR ，所以BP ⊥AN ，又由BP 在平面ABCD 内的射影BD ⊥AC ，所以BP ⊥AC ，AN ，AC ⊂平面ACN ，AN ∩AC ＝A ，知BP ⊥平面ACN ，CN ⊂平面ACN ，所以BP ⊥CN ，所以动点Q 的轨迹为线段CN ，在Rt △ABN ，Rt △RAB 中，∠BAN ＝∠ARB ，所以Rt △ABN ∽Rt △RAB ，则BN AB ＝AB RA ，得BN ＝12，易得CN ＝BN 2＋BC 2＝122＋12＝52.5.如图，已知正方体ABCD －A 1B 1C 1D 1的棱长为1，E ，F 分别是棱AD ，B 1C 1的中点．若点P 为侧面正方形ADD 1A 1内(含边界)动点，且B 1P ∥平面BEF ，则点P 的轨迹长度为()A.12B ．1C.52D.π2答案C 解析取A 1D 1的中点M ，连接AM ，B 1M ，AB 1，EM ，FM ，如图所示，在正方体ABCD －A 1B 1C 1D 1中，AD ∥B 1C 1且AD ＝B 1C 1，因为E ，F 分别是棱AD ，B 1C 1的中点，则AE ∥B 1F 且AE ＝B 1F ，所以四边形AB 1FE 为平行四边形，则AB 1∥EF ，因为AB 1⊄平面BEF ，EF ⊂平面BEF ，所以AB 1∥平面BEF ，同理可证AM ∥平面BEF ，因为AB 1∩AM ＝A ，AB 1，AM ⊂平面AB 1M ，所以平面AB 1M ∥平面BEF ，因为AM ⊂平面AA 1D 1D ，若P ∈AM ，则B 1P ⊂平面AB 1M ，所以B 1P ∥平面BEF ，所以点P 在侧面AA 1D 1D 内的轨迹为线段AM ，由勾股定理可得AM ＝AA 21＋A 1M 2＝52.6．已知菱形ABCD 边长为2，∠ABC ＝60°，沿对角线AC 折叠成三棱锥B ′－ACD ，使得二面角B ′－AC －D 为60°，设E 为B ′C 的中点，F 为三棱锥B ′－ACD 表面上动点，且总满足AC ⊥EF ，则点F 轨迹的长度为()A ．23B ．33 C.3 D.332答案D 解析连接AC ，BD 交于点O ，连接OB ′，四边形ABCD 为菱形，∠ABC ＝60°，所以AC ⊥BD ，OB ′⊥AC ，△ABC ，△ACD ，△AB ′C 均为正三角形，所以∠B ′OD 为二面角B ′－AC －D 的平面角，于是∠B ′OD ＝60°，又因为OB ′＝OD ，所以△B ′OD 为正三角形，所以B ′D ＝OB ′＝OD ＝2×32＝3，取OC 的中点P ，取CD 的中点Q ，连接EP ，EQ ，PQ ，所以PQ ∥OD ，EP ∥OB ′，所以AC ⊥EP ，AC ⊥PQ ，EP ∩PQ ＝P ，所以AC ⊥平面EPQ ，所以在三棱锥B ′－ACD 表面上，满足AC ⊥EF 的点F 轨迹为△EPQ ，因为EP ＝12OB ′，PQ ＝12OD ，EQ ＝12B ′D ，所以△EPQ 的周长为3×32＝332，所以点F 轨迹的长度为332.二、多项选择题7．(2024·济南模拟)已知正方体ABCD －A 1B 1C 1D 1的各顶点均在表面积为12π的球面上，P 为该球面上一动点，则()A ．存在无数个点P ，使得PA ∥平面A 1B 1C 1D 1B ．当平面PAA 1⊥平面CB 1D 1时，点P 的轨迹长度为2πC ．当PA ∥平面A 1B 1CD 时，点P 的轨迹长度为2πD ．存在无数个点P ，使得平面PAD ⊥平面PBC答案ACD 解析因为该球的表面积为4πr 2＝12π，故半径r ＝3，且正方体的棱长满足(2r )2＝3a 2＝12，故棱长a ＝2，选项A ，由题意可知平面ABCD ∥平面A 1B 1C 1D 1，且PA ∥平面A 1B 1C 1D 1，故PA ⊂平面ABCD ，则P 的轨迹为正方形ABCD 的外接圆，故有无数个点P 满足，故A 正确；选项B ，易知AC 1⊥平面CB 1D 1，且平面PAA 1⊥平面CB 1D 1，PA ⊂平面PAA 1，故P 的轨迹为矩形AA 1C 1C 的外接圆，其周长为2πr ＝23π，故B 错误；选项C ，因为PA ∥平面A 1B 1CD ，设过PA 且与平面A 1B 1CD 平行的平面为α，则P 的轨迹为α与外接球的交线，其半径为a 2＝1，周长为2π，故C 正确；选项D ，若平面PAD ⊥平面PBC ，则点P 在以四边形ABCD 为轴截面的某个圆柱面上，该圆柱面与球面交线为曲线，故有无数个点P 满足，故D 正确．8．(2023·长沙模拟)在棱长为1的正方体ABCD －A 1B 1C 1D 1中，M 为正方体表面上的动点，N 为线段AC 1上的动点，若直线AM 与AB 的夹角为π4，则下列说法正确的是()A ．点M 的轨迹确定的图形是平面图形B ．点M 的轨迹长度为π2＋22C ．C 1M 的最小值为2－1D ．当点M 在侧面BB 1C 1C 上时，33AN ＋MN 的最小值为1答案BCD 解析如图，建立空间直角坐标系，则D (0,1,0)，C 1(1,1,1)，∵直线AM 与AB 的夹角为π4，当点M 在侧面AA 1D 1D 上时，AB ⊥AM ，不合题意；当点M 在底面A 1B 1C 1D 1和侧面CC 1D 1D (不包含边界)上时，点M 到直线AB 的距离大于AB 的长度，此时，AM 与AB 的夹角大于π4；当点M 在侧面AA 1B 1B 和底面ABCD 上时，可知线段AB 1，AC 满足题意；当点M 在侧面BCC 1B 1上时，由AB ⊥BM ，可知BM ＝AB ，此时弧B 1C 为所求．∴M 点的轨迹为线段AC ，AB 1，弧B 1C ，显然线段AC ，AB 1，弧B 1C 不共面，∴A 错误；对于B ，点M 的轨迹长度为π2＋22，∴B 正确；对于C ，若M 在线段AC 上，则C 1M 的最小值为1，同理，若M 在线段AB 1上，则C 1M 的最小值也为1，若M 在弧B 1C 上，则C 1M 的最小值为C 1B －1＝2－1，∴C 正确；对于D ，M (1，y ，z )(0≤y ≤1,0≤z ≤1)，且y 2＋z 2＝1，由题意设N (λ，λ，λ)，λ∈[0,1]，则33AN ＋MN ＝λ＋(1－λ)2＋(y －λ)2＋(z －λ)2≥λ＋(1－λ)2＝λ＋(1－λ)＝1，当且仅当y ＝z ＝λ，且y 2＋z 2＝1，即y ＝z ＝λ＝22时，等号成立，∴D 正确．三、填空题9．已知正方体ABCD －A 1B 1C 1D 1的棱长为2，M 为棱B 1C 1的中点，N 为底面正方形ABCD上一动点，且直线MN 与底面ABCD 所成的角为π3，则动点N 的轨迹长度为________．答案43π9解析如图所示，取BC 中点G ，连接MG ，NG ，由正方体的特征可知，MG ⊥底面ABCD ，故MN 与底面ABCD 的夹角即为∠MNG ，所以∠MNG ＝π3，则MG NG ＝tan π3⇒NG ＝233，故点N 在以G 为圆心，233为半径的圆上，又N 在底面正方形ABCD 上，即点N 的轨迹为图示中的圆弧 EF ，易知BG EG ＝1233＝32⇒∠EGB ＝π6⇒∠EGF ＝π－π6－π6＝2π3，所以动点N 的轨迹长度为233×2π3＝43π9.10.如图所示，在平行四边形ABCD 中，E 为AB 中点，DE ⊥AB ，DC ＝8，DE ＝6.沿着DE 将△ADE 折起，使A 到达点A ′的位置，且平面A ′DE ⊥平面ADE .设P 为△A ′DE 内的动点，若∠EPB ＝∠DPC ，则点P 的轨迹长度为______．答案4π3解析建立如图所示的空间直角坐标系，则D (0,0,0)，C (0,8,0)，E (6,0,0)，B (6,4,0)，设P (x ,0，z )，则PD →＝(－x ,0，－z )，PC →＝(－x ,8，－z )，PE →＝(6－x ,0，－z )，PB →＝(6－x ,4，－z )，∴cos ∠EPB ＝cos 〈PE →，PB →〉＝PE →·PB →|PE →||PB |→＝(6－x )2＋z 2(6－x )2＋z 2(6－x )2＋16＋z 2，cos ∠DPC ＝cos 〈PD →，PC →〉＝PD →·PC →|PD →||PC |→＝x 2＋z 2x 2＋z 2x 2＋64＋z 2，∵∠EPB ＝∠DPC ，∴cos ∠EPB ＝cos ∠DPC ，∴(6－x )2＋z 2(6－x )2＋z 2(6－x )2＋16＋z 2＝x 2＋z 2x 2＋z 2x 2＋64＋z 2，整理化简得x 2＋z 2－16x ＋48＝0，即(x －8)2＋z 2＝16，∴点P 的轨迹为圆弧，所在圆交A ′E 于P 1(6,0,23)，交DE 于P 2(4,0,0)，则|P 1P 2—→|＝(6－4)2＋(0－0)2＋(23－0)2＝4，∴ 12PP 所对应的圆心角α＝π3，∴弧长l ＝αr ＝π3×4＝4π3，即点P 的轨迹长度为4π3.。

立体几何中的轨迹问题(微专题)

立体几何中的轨迹问题(微专题)
目录
• 轨迹问题的定义与类型 • 轨迹问题的解题思路 • 常见轨迹问题及解法 • 轨迹问题的应用与拓展
01
轨迹问题的定义与类型
定义
• 轨迹问题是指根据已知条件，求一个或多个几何元素在空间中按照一定规律运动的轨迹。这些轨迹可以是点的轨迹、线的轨迹或面的轨迹。
类型
01
02
03
点的轨迹
研究一个点在空间中按照一定规律运动的路径。
线的轨迹
研究一条线段或射线在空间中按照一定规律运动的路径。
面的轨迹
研究一个平面或曲面在空间中按照一定规律运动的路径。
02
轨迹问题的解题思路
确定动点轨迹的条件
确定动点的运动条件
01
动点在运动过程中受到的约束条件，如速度、加速度、力等。
保其准确性和稳定性。例如，汽车发动机的活塞运动轨迹、数控机床的
刀具运动轨迹等。
02
航天科技
在航天科技领域，轨迹问题对于卫星、火箭和空间站的发射、运行和对
接至关重要。例如，通过计算卫星的轨道参数，可以预测其运行轨迹和
位置。
03
物理实验
在物理实验中，轨迹问题常用于描述物体运动的状态和规律。例如，通
过研究抛物线轨迹、圆周运动轨迹等，可以验证物理定理和定律。
拓展与提高
复杂轨迹问题
对于更复杂的轨迹问题，可能需要运用更高级的数学工具和方法进行求解。例如，运用微分几何、变分法等理论来研究更一般的曲线和曲面运动。
实际应用案例
通过研究实际应用案例，可以深入了解轨迹问题的具体应用和解决技巧。例如，研究卫星轨道、行星运动等天文学领域的经典案例。
数学建模
通过数学建模，可以将现实生活中的问题抽象为数学模型，运用轨迹理论进行求解。这有助于提高解决实际问题的能力，培养数学建模思维。

立体几何中的轨迹问题汇总

立体几何中的轨迹问题汇总例析空间中点的轨迹问题的转化求空间图形中点的轨迹既是中学数学学习中的一个难点，又是近几年高考的一个热点，这是一类立体几何与解析几何的交汇题，既考查空间想象能力，同时又考查如何将空间几何的轨迹问题转化为平面的轨迹问题来处理的基本思想。

一．轨迹为点例1已知平面βα||，直线α⊂l ，点P l ∈，平面βα,之间的距离为8，则在β内到P 点的距离为10且到直线l 的距离为9的点的轨迹是 ( )A ．一个圆 B.两条直线 C.两个点 D.四个点解析:设Q 为β内一动点，点P 在β内射影为O ，过O, l 的平面与β的交线为l '，ΘPQ=10，∴OQ==-228106点Q 在以O 为圆心6为半径圆上，过Q 作QM l '⊥于M ，又Θ点Q 到直线l 的距离为9∴QM=178922=-则点Q 在以l '平行距离为17的两条平行线上Θ两条平行线与圆有四个交点∴这样的点Q 有四个，故答案选D 。

点评:本题以空间图形为背景，把立体几何问题转化到平面上，再用平面几何知识解决，要熟记一些平面几何点的轨迹。

二．轨迹为线段例2．如图，正方体1111ABCD A B C D -中，点P 在侧面11BCC B 及其边界上运动，并且总保持1AP BD ⊥，则动点P 的轨迹是（）。

βαlMOQPA. 线段1B CB.线段1BCC. 1BB 中点与1CC 中点连成的线段D. BC 中点与11B C 中点连成的线段解：连结11,,AB AC B C ，易知111BD A AB ⊥所以11111,,AB BD AC BD B C BD ⊥⊥⊥，所以1BD ⊥面1AB C ，若P ∈1B C ，则AP ⊂平面1AB C ，于是1BD AP ⊥，因此动点P 的轨迹是线段1B C 。

评注：本题是由线面垂直的性质从而求出点P 的轨迹。

例3 已知圆锥的轴截面SAB 是边长为2的等边三角形，O 为底面中心，M 为SO 的中点，动点P 在圆锥底面内(包括圆周)，若MP AM ⊥，则点P 的轨迹是________。

立体几何中的轨迹问题（详细版）

⽴体⼏何中的轨迹问题（详细版）⽴体⼏何中的轨迹问题⾼考数学有⼀类学科内的综合题，它们的新颖性、综合性，值得我们重视，在知识⽹络交汇点处设计试题是⾼考命题改⾰的⼀个⽅向，以空间问题为为背景的轨迹问题作为解析⼏何与⽴体⼏何的交汇点，由于知识点多，数学思想和⽅法考查充分，求解⽐较困难。

通常要求学⽣有较强的空间想象能⼒，以及能够把空间问题转化到平⾯上，再结合解析⼏何⽅法求解，以下精选⼏个问题来对这⼀问题进⾏探讨，旨在探索题型规律，揭⽰解题⽅法。

⼀、⽤空间运动的观点来得到点的轨迹。

例1：直线PA 是平⾯M 的⼀条斜线，斜⾜为A ，动直线PB 过点P 且与直线PB 垂直，且交平⾯M 于点B ，求动点B 的轨迹。

解：先探讨直线PB 的运动轨迹，由于直线PB 始终与PA 垂直，可知PB 的运动轨迹应是直线PA 的垂直平⾯N 。

再结合点B⼀定在平⾯M 内，所以点B 的轨迹应该是两个平⾯的交线，所以点B 的轨迹是⼀条直线。

针对以上解法，我们对这⼀问题作⼀深层次的探讨：若直线PA 与平⾯M 成α⾓，直线PB 始终与直线PA 成β⾓，再来求点B 的轨迹。

由上述解法可知，我们只要得到直线PB 的空间轨迹，再来考察该轨迹与平⾯M 的交线即可。

由简单的模型模拟即可知，直线PB 的轨迹是⼀个圆锥⾯，再⽤⼀个平⾯截圆锥⾯，这⼀知识在平⾯解析⼏何中圆锥曲线的来历中有提到，即所得曲线可能是圆、椭圆、抛物线、双曲线。

因此，我们在以下命题：直线PA 是平⾯M 的⼀条斜线，且与平⾯M 成α⾓，斜⾜为A ，动直线PB 过点P 且与直线PB 成β⾓，交平⾯M 于点B ，求动点B 的轨迹。

结论：（1）若α=90°，β≠90°，则动点B 的轨迹是⼀个圆；（2）若α≠90°，β=90°，动点B 的轨迹是⼀条直线；（3）若α≠90°，β≠90°，则①若90°>α>β，则轨迹是椭圆；②若α=β，则轨迹是抛物线；③若α<β，则轨迹是双曲线。

立体几何中轨迹问题的求解方法

中学数学研究
2007 年第6 期
立体几何中轨迹问题的求解方法
浙江师范大学数理学院数学系 (3 100 ) 夏锦 2 4
立体几何中的轨迹问题， 0 4 年高考北在20 京卷、天津卷和重庆卷中闪亮登场”成为高考 “ ，命题的一个创新点. 这类题型立意新颖、构思巧妙，注重多元联系和多元应用，集知识的交汇性、综合性，方法的灵活性，能力的迁移性于一体，极富思考性和挑战性，因此学生求解起来颇感困考试时经常弃而不答，难，令人惋惜! 本文通过实例来说明立体几何中轨迹问题求解的常
招(tl + tZ ) 刃则x 二
弓
， y
奥尹，尸轨故点迹
目望 - J n 匕 __2
方是招，誓)， 1 ， g 程 (2 )2+(V J 一2 肺 r
__ _ 2
，
’ 一工 y ’
0
忿
1 0
x
I 0
x
} O
x
(A )
(B)
(C)
(D)
所以点P 轨迹是在五，下的中垂面上以0 为中心，长轴长为6，短轴长为2 的椭圆. 点评: ( 1 若把条件中“ ) 异面直线 a ，成 b 0 角” 6 。改成“ 异面直线 a ，成 9 。，尸点 b 0 角”则
1 ‘ ，。，一 ‘ ~ 。~ AM 二青，‘尸是平面月 — 点 13(刃 ‘ r‘ 3 ’ 、‘ ~ ’阴 ‘ “ ‘ ，一
分析:过尸作尸土A刀及尸土面 B。〕 Q H
40
内的动点，且满足尸到直线AIDI 平方差为1，则尸点的轨迹
为( ).
解.
丫夕，尸 Z+P “ 知1+xZ 二 1干由 M G =2， +y“2，所以求轨是位圆xZ+少=1 所的迹单 .

立体几何中的共面轨迹问题

方形 A B CD 的面积 , 又 C1 G = B E , O G 在面
A B CD 上的射影与 EF 的交点为 M , 问在面 A B CD 内是否存在两个定点 , 使 M 到这两个
A 2 B 2 C2 D 2 中 , B 1 D 1 与 A 2 C2 成 60° 角 , 侧棱 A1A2 = 2 , M 、 N 分别在 B 1 D 1 与 A 2 C2 所在直
线上运动 , 若 M N = 4 , 求 M N 的中点 P 的轨迹.
定点的距离的和为定值 ?若存在 , 求出这两个定点 ; 若不存在 , 请说明理由 .
分析过 G 作 GP ⊥ CD , 垂足为 P , 则
GP ⊥面 A B CD , ∴O G 在面 A B CD 内的射影
分析设正方体中心为 O , 上下两底面中心为 O 1 、 O 2 . 过 O 作平面α ⊥ O 1 O 2 , 无论
高中数学教与学 2004 年
立体几何中的共面轨迹问题
吴明德
( 江苏省泰兴市第一高级中学 ,225400) 高中阶段虽然没有学习系统的空间解析几何知识 , 但并不妨碍我们用平面解析几何的方法处理一些简单的立体几何轨迹问题. 两种几何知识的交汇融合与综合应用 , 对培养学生的空间想象能力和数学实践能力大有益处 . 现略举几例供参考 . 例 1 如图 1 , 在单位正方体 A B CD A 1 B 1 C1 D 1 中 , E 、 F 分别为 A 1 D1 、 B 1 C1 的中
B D 为 ⊙O 2 的直径 , B C ⊥ CD , 由三垂线定 t1 = x + y,
即
t2 =
3
x
①
- y,