多元统计分析实例
完整版本多元统计分析实例汇总

多元统计剖析实例院系 : 商学院学号 :姓名 :多元统计剖析实例本文采集了 2012 年 31 个省市自治区的农林牧渔和有关农业数据 , 经过对对采集的数据进行比较剖析对 31 个省市自治区进行分类 . 选用了 6个指标农业产值 , 林业产值 . 牧业总产值 , 渔业总产值 , 乡村居民家庭拥有生产性固定财产原值 , 乡村居民家庭经营耕地面积 .数据以下表 :一. 聚类法设定 4 个群聚 , 采纳了系统聚类法 . 下表为 spss 剖析以后的结果 .聚类表群集组合初次出现阶群集阶群集 1 群集 2 系数群集 1 群集 2 下一阶1 5 7 226.381 0 0 132 2 9 1715.218 0 0 53 22 24 1974.098 0 0 74 1 29 5392.690 0 0 65 2 30 6079.755 2 0 66 1 2 11120.902 4 5 87 4 22 21528.719 0 3 118 1 26 23185.444 6 0 149 12 20 26914.251 0 0 1910 27 31 35203.443 0 0 2011 4 28 50321.121 7 0 2212 11 13 65624.068 0 0 2413 5 25 114687.756 1 0 1714 1 21 169600.075 8 0 2215 8 18 188500.814 0 0 2116 17 19 204825.463 0 0 2117 5 14 268125.103 13 0 2018 3 23 387465.457 0 0 2619 6 12 425667.984 0 9 2320 5 27 459235.019 17 10 2321 8 17 499195.430 15 16 2522 1 4 559258.810 14 11 2823 5 6 708176.881 20 19 2424 5 11 854998.386 23 12 2825 8 10 1042394.608 21 0 2626 3 8 1222229.597 18 25 2927 15 16 1396048.280 0 0 2928 1 5 1915098.014 22 24 3029 3 15 3086204.552 26 27 3030 1 3 6791755.637 28 29 0Rescaled Distance Cluster CombineCASE 0 5 1015 20 25 Label Num +--------- +--------- +--------- +--------- +---------+内蒙 5 -+吉林7 -+云南25 -+-+江西14 -+ +-+陕西27 -+-+ |新疆31 -+ +-+安徽12 -+-+ | |广西20 -+ +-+ +------- +辽宁 6 ---+ | |浙江11 -+----- + |福建13 -+ |重庆22 -+ +--------------------------------- +贵州24 -+ | |山西 4 -+--- + | |甘肃28 -+ | | |北京 1 -+ | | |青海29 -+ +--------- + |天津 2 -+ | |上海9 -+ | |宁夏30 -+--- + |西藏26 -+ |海南21 -+ |河北 3 ---+----- + |四川23 ---+ | |黑龙江8 -+-+ +------------- + |湖南18 -+ +--- + | | |湖北17 -+-+ +-+ +------------------------- + 广东19 -+ | |江苏10 ------- + |山东15 ----------- +----------- +河南16 ----------- +群集成员事例 4 群集1: 北京 12: 天津 13: 河北 14: 山西 15: 内蒙 26: 辽宁 17: 吉林 28: 黑龙江 29: 上海 110: 江苏 111: 浙江 112: 安徽 113: 福建 114: 江西 115: 山东 316: 河南 117: 湖北 118: 湖南 119: 广东 120: 广西 121: 海南 122: 重庆 123: 四川 124: 贵州 125: 云南 126: 西藏 427: 陕西 128: 甘肃 129: 青海 130: 宁夏 131: 新疆 2从 SPSS剖析结果能够获得 , 内蒙 , 吉林 , 黑龙江 , 新疆为第 2族群 , 这一族群的特色是农业收入可能不高 , 可是农民的固定财产 , 和耕地面积特别高 , 农民的充裕程度或许机械化程度较高; 山东是第 3族群 , 这一族群中六个指标都处于较高水平,农林牧渔四项收入都处于较高水平并且农民充裕; 西藏处于第 4族群 , 这是因为 , 西藏人员较少 , 自然条件恶劣 , 可使用耕地少 , 可是 , 因为国家的扶助 , 农民的固定 财产许多 , 农民相对而言比较富裕 ; 大部分省份属于第 1族群 , 这一族群的特色在 于六项指标都没有较为突出的一项, 或许农林牧渔收入的原来就少, 或许是农民 的固然比较辛苦 , 整体的农业收入较高 , 可是农民的收入水平比较低, 固定财产较 少 .三. 鉴别法X 1,X 2,X 3,X 4,X 5,X 6分别代表农业产值 , 林业产值 . 牧业总产值 , 渔业总产值 , 乡村居民家庭拥有生产性固定财产原值, 乡村居民家庭经营耕地面积 .剖析事例办理纲要未加权事例N百分比有效31 100.0清除的缺失或越界组代码 0 .0 起码一个缺失鉴别变量 0 .0 缺失或越界组代码还有起码一 0.0个缺失鉴别变量共计 0 .0 共计31 100.0实验结果剖析 :组统计量有效的 N (列表状态)Average Linkage (Between Groups) 均值 标准差 未加权的已加权的1农业总产值 1463.8900 1062.0348625 25.000 林业总产值 118.5768 87.02052 25 25.000 牧业总产值 830.3664 671.10440 25 25.000渔业总产值291.4128346.719022525.000乡村居民家庭拥有生产性固定14432.3400 5287.92950 25 25.000 财产原值乡村居民家庭经营耕地面积 1.5496 .88484 25 25.000 2 农业总产值1582.2975 543.92851 4 4.000林业总产值93.3500 37.71131 4 4.000 牧业总产值1021.3175 372.88255 4 4.000 渔业总产值38.3500 27.49067 4 4.000 乡村居民家庭拥有生产性固定30226.4175 4233.77839 4 4.000 财产原值乡村居民家庭经营耕地面积9.4975 3.30626 4 4.000 3 农业总产值3960.6200 . a 1 1.000林业总产值107.0100a1 1.000 .牧业总产值2285.9200 . a 1 1.000 渔业总产值1267.0700 . a 1 1.000 乡村居民家庭拥有生产性固定19168.1400 . a 1 1.000 财产原值乡村居民家庭经营耕地面积 1.6400 . a 1 1.000 4 农业总产值53.3900 . a 1 1.000林业总产值 2.5600 . a 1 1.000牧业总产值59.0200a1 1.000 .渔业总产值.2200 . a 1 1.000乡村居民家庭拥有生产性固定52935.0700 . a 1 1.000财产原值乡村居民家庭经营耕地面积 1.8900 . a 1 1.000 从表上能够看出 , 组均值之间差值很大 . 各个分组 , 在 6 项指标上均值有较明显的差别 .组均值的均等性的查验Wilks 的 Lambda F df1 df2 Sig.农业总产值.773 2.640 3 27 .070林业总产值.928 .699 3 27 .561牧业总产值.801 2.238 3 27 .107渔业总产值.691 4.019 3 27 .017乡村居民家庭拥有生产性固定.253 26.538 3 27 .000财产原值组均值的均等性的查验Wilks 的 Lambda F df1 df2 Sig.农业总产值.773 2.640 3 27 .070林业总产值.928 .699 3 27 .561牧业总产值.801 2.238 3 27 .107渔业总产值.691 4.019 3 27 .017乡村居民家庭拥有生产性固定.253 26.538 3 27 .000财产原值乡村居民家庭经营耕地面积.190 38.263 3 27 .000 由表中能够知道 ,13456 指标之间的 sig 值较小 ,2 指标 sig 值有 0.561 较大 ,可是仍说明接受原假定 , 各指标族群间差别较大 .汇聚的组内矩阵农业总产值林业总产值牧业总产值渔业总产值有关性农业总产值 1.000 .449 .895 .400 林业总产值.449 1.000 .489 .481牧业总产值.895 .489 1.000 .294渔业总产值.400 .481 .294 1.000乡村居民家庭拥有生产性固定-.093 -.262 -.052 -.040财产原值乡村居民家庭经营耕地面积.056 -.033 .181 -.104汇聚的组内矩阵乡村居民家庭拥有生产性固定资乡村居民家庭经产原值营耕地面积有关性农业总产值-.093 .056林业总产值-.262 -.033牧业总产值-.052 .181渔业总产值-.040 -.104乡村居民家庭拥有生产性固定 1.000 .326财产原值乡村居民家庭经营耕地面积.326 1.000从表中能够知道 , 查验结果 p 值>0.05, 此时 , 说明协方差矩阵相等,能够进行 bayes 查验 .Fisher剖析法协方差矩阵的均等性的箱式查验对数队列式AverageLinkage(BetweenGroups) 秩对数队列式1 6 61.1252 . a . b3 . c . b4 . c . b汇聚的组内 6 62.351打印的队列式的秩和自然对数是组协方差矩阵的秩和自然对数。
多元统计分析课件第六章-判别分析例题与操作过程可修改文字

.
(一) 操作步骤 1. 在SPSS窗口中选择Analyze→Classify→Discriminate,调 出判别分析主界面,将左边的变量列表中的“group”变量选 入分组变量中,将—变量选入自变量中,并选择Enter independents together单选按钮,即使用所有自变量进行判 别分析。
1
5
50.06 23.03 2.83 23.74 112.52 63.3
1
6
33.24 6.24 1.18 22.9 160.01 65.4
2
7
32.22 4.22 1.06 20.7 124.7 68.7
2
8
41.15 10.08 2.32 32.84 172.06 65.85
2
9
53.04 25.74 4.06 34.87 152.03 63.5
由此表可知,两个Fisher判别函数分别为:
y1 74.99 1.861X1 1.656X 2 0.877 X3 0.798X 4 0.098X 5 1.579X 6 y2 29.482 0.867X1 1.155X 2 0.356X 3 0.089X 4 0.054X 5 0.69 X 6
判别分析例题
例1:设有两个正态总体 G1 和 G2 ,已知:
(1)
ห้องสมุดไป่ตู้
10 15
(2)
20 25
18 12 1=12 32
20 7
2
=
7
5
试用距离判别法判断:样品:
X
20 20
,应归属于哪一类
判别分析例题 解:比较X到两个总体的马氏距离的大小
所以X属于正态总体 G1
例2:
多元统计分析案例具体操作只是分享

一、多元回归分析高磷钢的效率(Y)与高磷钢的出钢量(X1)及高磷钢中的FeO含量(X2)有关, 所测数据如下表,利用SPSS拟建立回归方程:Y=b0+b1*X1+b2*X2,步骤如下:(1)操作过程在数据输入之后,依次单击“分析”——“回归”——“线性”,在弹出的“线性回归”对话框中,将出钢量X1和FeO含量X2设为自变量,效率设为因变量,回归方法设为“进入”。
如下图:图1.1(2)(3回归方程的回归系数:b0=75.144,b1=0.215,b2=-0.843 拟合回归方程:Y=0.215*X1-0.843*X2+75.144 1)回归方程的显著性检验(F 检验):检验假设:012:0m H βββ==⋅⋅⋅==,1:j H β⋅⋅⋅各(j=1,2,,m)不全为0,0.05α= SS 总=SS 回+SS 残,其中F ~F(m ,n-m-1)根据方差分析表(Anova ),MS 回=66.799,MS 残=14.759,从而F=4.515,F>F 0.05(2,10)(Sig<0.05),可知在显著性水平α=0.05,拒绝原假设H 0,自变量和因变量之间存在显著性的线性关系。
2)回归方程拟合优度检验:R 2=0.475,说明高磷钢的效率变异的47.5%可由其岀钢量和FeO 的含量的变化来解释。
3)对各自变量指明方程中的每一个自变量对Y 的影响(即方差分析和决定系数检验整体)。
A 、回归系数的显著性检验(t 检验):j b 为偏回归系数的估计值,jb S 是j b 的标准误。
检验假设:H 0:0=j β,j t 服从自由度为1--=m n ν的t 分布。
如果12--≥m n ,/j t |t |α,则在α=0.05水平上拒绝H 0,接受H 1,说明j X 与Y 有线性回归关系。
非标准化系数b1=0.215,b2=-0.843,对于b1,t1=2.889,|t1|>t 0.05/2(10),拒绝原假设,说明在给定的显著水平α=0.05下,X1对Y 有显著的影响;对于b2,t2=-1.538,t 0.05/2(10)>|t2|> t 0.1/2(10),说明在给定的显著水平α=0.05下,接受原假设,X2对Y 没有显著的影响。
多元统计分析案例分析

多元统计分析案例分析多元统计分析是指采用多个统计方法和技术对数据进行综合分析的一种分析方法。
它可以帮助研究者揭示出多个变量之间的复杂关系,并进一步分析它们的影响和作用。
下面以一份市场调研报告为例,介绍如何运用多元统计分析进行案例分析。
案例背景:饮料公司在上海市开展了一项市场调研,调查了300名消费者对其产品的购买行为和偏好。
调研对象包括消费者的年龄、性别、收入水平、产品购买频率、产品品牌偏好等变量。
1.数据准备:将调研数据录入电脑,确保数据的准确性和完整性。
对于缺失值进行处理,可以采用删除、插补等方法。
2.描述性统计分析:首先对数据进行描述性统计分析,包括计算平均值、标准差、频数等。
了解数据的分布情况和基本统计信息,例如了解不同性别的样本比例,不同年龄段的购买频率等。
3.相关性分析:通过相关系数分析来研究各个变量之间的关系,包括变量间的线性相关性和非线性相关性。
可以计算皮尔逊相关系数或斯皮尔曼相关系数来评估变量之间的关联程度。
4.回归分析:通过回归分析可以研究一个或多个自变量对因变量的影响程度。
可以先进行单变量回归分析,确定哪些自变量对因变量有显著影响。
然后进行多元回归分析,建立一个多元回归模型,研究多个自变量对因变量的综合影响。
5.研究假设检验:通过假设检验来验证研究假设的可靠性。
例如,可以进行t检验或方差分析来判断一些自变量对因变量的影响是否显著。
6.因素分析:可以利用因素分析来研究多个自变量之间的共同特征。
通过提取主成分或因子,将原始变量转化为更少的几个综合变量,以便对数据进行更简洁的分析和解释。
7.聚类分析:通过聚类分析可以将样本划分为不同的类别或群体,以研究不同自变量组合的消费者群体特征和购买行为。
8.判别分析:通过判别分析可以建立分类模型,将样本分为多个已知类别,以研究哪些自变量最能有效地区分不同群体。
9.结果解释和报告撰写:将多元统计分析的结果进行解释和总结,并撰写报告。
报告中应包括对分析方法的描述、数据的描述和分析结果的解释。
多元统计分析数据

多元统计分析数据一、聚类分析例1、为深入了解我国人口的文化程度状况,现利用1990年全国人口普查数据对全国30个省市自治区进行聚类分析。
分析选用了三个指标:(1)大学以上文化程度的人口占全部人口的比例(DXBZ);(2)初中文化程度的人口占全部人口的比例(CZBZ);(3)文盲半文盲人口占全部人口的比例(WMBZ),分别用来反映例2、根据信息基础设施的发展状况,对世界20个国家和地区进行分类。
这里选取了发达国家、新兴工业化国家、拉美国家、亚洲发展中国家、转型国家等不同类型的20个国家作聚类分析。
描述信息基础设施的变量主要的有六个:call——千人拥有电话号码,movecall——每千户居民蜂窝移动电话,fee——高峰时期每三分钟国际电话成本,computer——每千人拥有的计算机数,mips——每千例3、为了研究1982年全国各地区农民家庭收支的分布规律,根据抽样调查资料进行分类处理,共抽取28个省、市、自治区的样本,每个样本有六个指标,这六个指标反映了平均每人生活消费的支出情况,其原始数据见表3。
例4为了研究世界各国森林、草原资源的分布规律,共抽取了21个国家的数据,每个国家4项指标,原始例5 若要从沪市的蒲发银行、齐鲁石化、东北高速、武钢股份、东风汽车等53家上市公司中优选适合开放式基金组合投资的10只股票,我们以总股本和流通股本为分类标志,根据这53家公司的总股本和A股流通股本数据(见表5.3),用聚类分析法将它们分成若干类,再从各类公司中选出比较活跃的股票建立股票池。
例6沪市上市公司2001年末总股本在10000—12000万股、流通股本在3600—5050万股之间共有23家(对于股本结构在其它范围内的上市公司,用雷同的方法,可以建立相应的每股收益预测模型),各公司2000年及2001年有关的财务数据见表。
二、判别分析例1、人文发展指数是联合国开发计划署于1990年5月发表的第一份《人类发展报告》中公布的。
多元统计分析案例分析
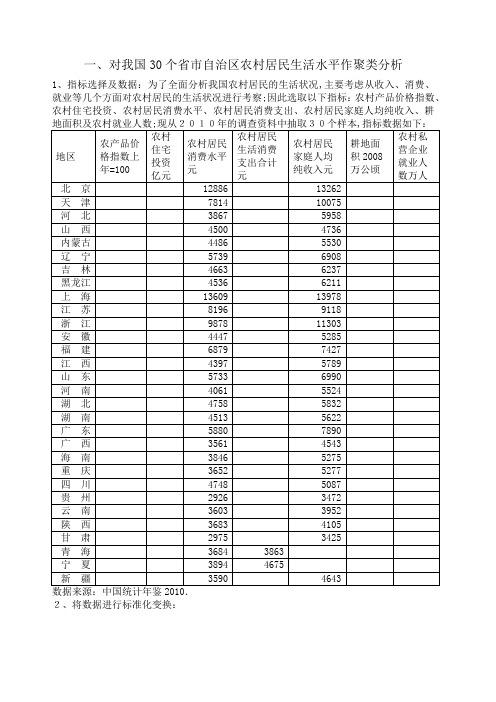
一、对我国30个省市自治区农村居民生活水平作聚类分析1、指标选择及数据:为了全面分析我国农村居民的生活状况,主要考虑从收入、消费、就业等几个方面对农村居民的生活状况进行考察;因此选取以下指标:农村产品价格指数、农村住宅投资、农村居民消费水平、农村居民消费支出、农村居民家庭人均纯收入、耕2、将数据进行标准化变换:第一类:北京、上海、浙江;第二类:天津、、辽宁、、福建、甘肃、江苏、广东;第三类:浙江、河北、内蒙古、吉林、黑龙江、安徽、山东、河南、湖北、四川、云南;第四类:山西、青海、宁夏、新疆、重庆、贵州、陕西、湖南、广西、江西、;从分类结果上看,根据2010年的调查数据,第一类地区的农民生活水平较高,第二类属于中等水平,第三类、第四类属于较低水平;二、判别分析从上可知,只有一个地区判别组和原组不同,回代率为96%; 下面对新疆进行判别:判别函数分别为:Y1= + + + +Y2=+ + + +Y3= + + +将西藏的指标数据代入函数得:Y1=Y2=Y3=计算Y值与不同类别均值之间的距离分别为:D1=D2=D3=D4=经过判别,D4最小,所以新疆应归于第四类,这与实际情况也比较相符;三,因子分析:分析数据在上表的基础上去掉两个耕地面积和农村固定资产投资两个指标;经spss软件分析结果如下:1各指标的相关系数阵:从中可以看出,大部分指标的相关系数都比较高,各变量之间的线性关系较明确,能够从中提取公共因子,适合因子分子;2检验:由上表可知:巴特利特球度检验统计量的观测值为.相应的概率p接近为0.如果显着性水平a为,由于显着性水平小于,拒绝零假设,认为相关系数矩阵与单位阵有显着差异,同时,KOM值为,根据Kaiser给出的度量标准可知原有变量适合进行因子分析3各指标的贡献率如下表:从中可以看出,各个指标的贡献率都在百分之五十之上比较高;从上表中可以看出,第一个因子的特征根为.解释原有五个变量总方差的68%,累积方差贡献率为%;第二个因子的特征根为,解释原有变量总方差%,累计方差贡献率为%;4碎石图:5因子载荷阵如下:由上表可知,各指标在第一个因子上的载荷比较高,说明第一个因子很重要;第二个因子与原有变量的相关性较小,它对原有变量的解释作用不显着;为便于对各因子进行命名,对因子载荷阵实施正交旋转;旋转之后的因子载荷阵:6从上表可见,每个因子只有几个指标的因子载荷较大,因此可根据上表进行分类;将五个指标按高载荷分成两类:四,主成分分析:1各指标间的相关系数矩阵如下表所示:可以看到有些指标之间的相关性较强,如果直接进行综合分析会造成信息重叠,所以用主成分分析将多个指标化成几个不相关的综合指标;2求相关矩阵的特征值和特征向量:从上表可知,前两个特征值累计贡献率已达%;说明前两个主成分基本包含了全部指标具有的信息;因此,取前两个特征值,并计算相应的特征向量:3由上述因子分子的因子载荷阵计算主成分的特征向量阵为:所以,前两个主成分为:第一个主成分:F1= X1++ ++第二个主成分:F2=在第一主成分中第二、三、四个指标的系数较大,这三个指标起主要作用,刻划了农居民的收入支出状况的综合指标;在第二主成分中,第一个指标系数较大,是农产品价格水平指标;4因子得分:根据上表写出以下因子得分函数:F1=农产品价格指数+农村居民消费+消费支出+家庭人均纯收入+就业人数F2=农产品价格指数+农村居民消费消费支出+家庭人均纯收入就业人数5综合评价:以两个因子的方差贡献率为权数,综合评价模型为:Z=+旋转之后的方差贡献率F1= X1++ ++F2=将各地区指标值代入上式得到各地区农村生活水平的综合值及排名:6对结果进行分析:从中可以看出,各地区的农村居民生活水平存在差异;其中,北京、上海、浙江、江苏地区的综合评价值排名前列,说明这几个城市农村居民的生活水平比较高;主要表现在农民收入水平和消费水平两个方面;这几个城市属于沿海地区,经济比较发达,工农业发展遥遥领先于其他地区;其次,天津、山东、福建、辽宁、广东综合评价值相对较低;不过也处于全国前十的地位;青海、贵州、广西、重庆、新疆、甘肃、陕西、云南等几个地区农村居民生活水平发展比较落后;原因是这些地区大多位于中国中西部,地理位置不佳,交通不便,经济发展水平不高,进而影响到农村经济的发展;农村居民收入水平和消费水平均比较低;因此,要提高这些地区农民的生活水平,政府应该加大这些地区的基础设施建设,提高这些地区农村居民的收入水平;。
多元统计分析案例

一.搜集的必要性消费是实现国民经济良性循环的关键,而消费结构是否合理,又是消费的关键问题。
考察消费结构是研究和衡量居民消费水平,生活质量的一条重要的途径,可以从侧面反映一国宏观经济发展的基本状况,是联合国划分一国经济发展阶段的重要手段之一。
改革开放以来,我国的经济政治体制改革直接影响了农村居民生活水平及消费结构。
二提出使用的多元消费结构是一种客观存在,消费结构的分类则是人们主观的产物,可以根据实际需要对消费结构进行不同的分类,消费结构首先可以分为宏观消费结构与微观消费结构两个类型。
宏观消费结构是指我国考察的消费资料最终实现的分布,如个人消费与公共消费各自所占的比重,个人消费与社会集团以及社会集团各自的比重,各地区和城乡居民消费各自的比重。
微观消费结构是从单个家庭和个人着眼考察的消费结构,是指居民生活消费内容的组成方式,是宏观消费的基础。
三.进行选定多元统计方法的研究设计和实现的步骤因子分析的基本思想是通过对变量的相关系数矩阵的内部结构进行分析,从中找出少数几个能够控制员是变量的因子,建立因子分析模型,利用公共因子再现原始变量之间的相关关系,达到简化变量,降低变两位数和对原始变量在解释及命名的目的。
设有m个原始变量,表示为x1,x2,…,xm,根据因子分析的要求,假设这些变量已经标准化(均值为0,标准差为1),假设m个变量可以由n个因子f1,f2,…,fn表示为线性组合,即:x1=a11f1+a12f2+…+a1nfn+ε1x2=a21f1+a22f2+…+a2nfn+ε2…xm=am1f1+am2f2+…+amnfn+εm上式为因子分析的数学模型,如果利用矩阵形量向量,它的每一个分量表示一个指标或变量;F称为因子向量,每一个分量表示一个因子,由于它们出现在每个原始变量的线性表达式中,所以又称为公共因子;矩阵A为因子载荷矩阵,其元素aij称为因子载荷;ε称为特殊因子,表示原始变量中不能由因子解释的部分,均值为0。
(完整版)多元统计分析实例汇总

多元统计分析实例院系: 商学院学号:姓名:多元统计分析实例本文收集了 2012年31个省市自治区的农林牧渔和相关农业数据,通过对对 收集的数据进行比较分析对31个省市自治区进行分类.选取了 6个指标农业产值, 林业产值.牧业总产值,渔业总产值,农村居民家庭拥有生产性固定资产原值,农 村居民家庭经营耕地面积. 数据如下表: 地区 农业总产值林业总产■{牧业总产■{渔业总产侬村居民家庭拥有生产性匡江 京津北西蒙宁林龙海苏江徽建西东南北南东西南庆川州南藏西肃海夏疆北天河山内辽吉黒上江浙安福江山河湖湖广广海重四贵云西陕甘青宁新166.29 54,33 154.16 12. 98 12?67. 090. 5 195.99 2.7S105.01 61. 66 1Y508. 571. 583095.29 77, 3S 1747. 66 177.74 1V904. 83 L3934?. 41 79.0? 293. E3 & 42 ^SOS. 38 Z 51171.^7 57. 7G IIIS .ES 戈& OS 加宪9.旳10.4 1539- 65128.68162L23 618.74 24997. 92 3. TS1166. E390. 1 1130. 3G 34. 14 24937. 06 S. 272315. 64 134. 5 1350. 63 92 31507. 91IM 56171. 439.55 72. 59 57. 45 4L46. 13 0. 262966.72 99.75 1226.13 1235.4 14541. 03 L35 1229. 3& 142.L4 549・ 01 637. 05 22747. 83 0. 54 1867. G4 209.5 1119.73 334.43 1E134. 35 1. 39 1263. 71 256.45 ^81.23 903. 36 11S21.38 (X ?3 1003.21 22S.91 7S2. es 333. 06 gggg. 3i 1. 57 3960. 62 107*01 2285. 22 12G7. 07 mea. iq L 643958. 95 140.85 2255. ei 86.4 12980. 72 1. 622438. 06 100.05 1334. 04 626.23 10313.13 L T12S51.^9 259.97 1483. E8 即9 94 8904. 32 1. 222229. 2T 222,74 1134,14 914, 05 S516. 720.53 1724 245.56 1072.77 331. 74 11851.56 1. 37 460. 72 137.35 214. 14 236.27 113S7. 05 0. 33 341.S1 43胡S 453 9 躬.99 12295. T4 L 292764.9 151.5 2269. E5 153. 77 13759.171.14364. S& 54 1勺 ^21. 55 2& 21 11957. 31LIS1398. IT 225. S3 912. 9? 63.1 IWO. 92 1. 653.39 2.5B 59. 02 0. 22 52935. OT L 391526.23 58.44 593. 72 14” 61 12273. 06 1. 529S4. 24 20.07 231. 72 1.8 1948E ・ 44 2. 72 117. 09 4.5? 137.03 a 56 21919.铀 L 33 240. 4& 9.77 105. 72 13. 36 24265.19 3・69 1675 43.04 ^85. 37 15. 26 35070. 31 5* 76.聚类法设定4个群聚,采用了系统聚类法.下表为SPSS分析之后的结果.Rescaled Dista nee Cluster Comb ine群集成员案例4群集1:北京12:天津1 10 15 20 25Label Num ^^"————————— + ————————— + —————————+————————— +————————— ^^"内蒙 5 -+吉林7 -+云南25 - + -+江西14 -+ +-+陕西27 -+-+ |新疆31 -+ +-+安徽12 -+-+ 11广西20 —+ + — + +—————+辽宁 6 ---+ | |浙江11 -+——+ |福建13 -+ 1重庆22 -+ + ---贵州24 -+ 1山西 4 -+—+ |甘肃28 -+ | |北京 1 -+ | |青海29 -+ + ....... +天津 2 -+ 1上海9 -+ 1宁夏30 -+—+西藏26 -+海南21 -+河北 3 ———+—————^^"四川23 - + |黑龙江8 - + -+ +--------------- 湖南18 -+ +---+ |湖北17 -+-+ +-+广东19 -+ | |江苏10 .... +山东15 ....... + ..... 河南16 ....... ++ |+ ,||+从SPSS分析结果可以得到,内蒙,吉林,黑龙江,新疆为第2族群,这一族群的特点是农业收入可能不高,但是农民的固定资产,和耕地面积非常高,农民的富余程度或者机械化程度较高;山东是第3族群,这一族群中六个指标都处于较高水平,农林牧渔四项收入都处于较高水平而且农民富余;西藏处于第4族群,这是因为,西藏人员较少,自然条件恶劣,可使用耕地少,但是,由于国家的扶持,农民的固定资产较多,农民相对而言比较富足;大多数省份属于第1族群,这一族群的特点在于六项指标都没有较为突出的一项,或者农林牧渔收入的本来就少,或者是农民的虽然比较辛苦,总体的农业收入较高,但是农民的收入水平比较低,固定资产较三.判别法Xi,X2,X3,X4,X5,X6分别代表农业产值,林业产值.牧业总产值,渔业总产值,农村居民家庭拥有生产性固定资产原值,农村居民家庭经营耕地面积.实验结果分析:从表上可以看出,组均值之间差值很大.各个分组,在6项指标上均值有较明显的差异.由表中可以知道,13456指标之间的sig 值较小,2指标sig 值有0.561较大, 不过仍说明接受原假设,各指标族群间差异较大.从表中可以知道,检验结果P值>0.05,此时,说明协方差矩阵相等,可以进行bayes检验.Fisher 分析法协方差矩阵的均等性的箱式检验典型判别式函数摘要由表中看出,函数1,2的特征值达到0.911,0.822比较大,对判别的贡献大..农村居民家庭拥有生产性固定资产原值 对判别数据所属群体无用.由表中可知, 3个Fishe 判别函数分别为:y i2.928 2.269 0.003X 2 0.002X 20.626X 6 0.489X 6y 30.975 0.009X 20.01X 3 0.03X 4 0.037X 6该表是原始变量与典型变量(标准化的典型判别函数)的相关系数,相关系数的绝对值越大,说明原始变量与这个判别函数的相关性越强.从表中可以看出相关性较强.符合较好.由上表可知各类别重心的位置,通过计算观测值与各重心的距离,距离最小的即为该观测值的分类.贝叶斯分析法该表为贝叶斯函数判别函数的取值,从图中可以知道三类贝叶斯函数.0.003x 1 0.051x 2 0.004x 30.006x 40.002x 5 1.675x 6 61.646将各样品的自变量值代入上述4个BayeS 判别函数,得到函数值。
多元统计分析经典案例

29
Copyright CAE
当你看一张map时 .. 问你自己
• 它意味着什么? • 它对理解数据有什么附加的作用? • 它对我们所知道的市场/顾客的思考方式是否适 合?
– 如果不是 - 错在什么地方?
• 它是否帮助我更好地了解市场?
30
Copyright CAE
当你看一张map时 .. 问你自己
Bird
Dog
40% 40% 20% 20% 50%
Cat
10%
16
Copyright CAE
现在我们用颜色和动物名称两个变量 来做2-维的图表
努力来显示..
- 那些动物在颜色方面最相似,那些区别最大? - 那些颜色更倾向那类动物 - 那些动物和那些颜色有更强的相关性,那些相关性很弱
17
Copyright CAE
Copyright CAE
相关性分析 Correspondence Analysis
9
Copyright CAE
结构
• • • • • • 什么是相关性分析? 尝试通过练习了解它 输入的类型 设计录入的格式 执行分析 解释和表述分析的结果
10
Copyright CAE
什么是相关性分析?
• 经常也称作 Brand Mapping 或 CORAN Mapping
6
Copyright CAE
我们通常使用的多元分析技术…...
• • • • • • • • 相关性分析(Brand Mapping ) 主成分分析 因子分析 多元回归 聚类分析/市场细分 联合性分析/ 平衡(Trade off) 分析 判别分析 etc. etc. etc.
7
Copyright CAE
多元统计分析实例

4.从Model Summary(b)可知:复相关系数 R Square为0.860
5. 将x1=600,x2=2.5带入y关于x1、x2的二元线性回归方程: y=0.32x1-84.361x2+184.613
中即可求得E(y)的点估计为165,也可以用SPSS求出。置信水平为0.95的置信区 为(105,225)
第三次 多元统计作业
1. 设已有六个样品,每个样品对某项指标进行了测试,分别等于1,2,5,7,9,10.它们 先各自成一类,供六类,使用类与类之间的最大距离进行聚类分析。 利用SPSS,进行最大距离法聚类,输出结果如下:
B
Std. Error
184.613
72.304
Beta
t
Sig.
2.553 .027
95% Confidence Interval for B
Lower Bound
Upper Bound
25.473 343.754
x1
.320
.097
.389 3.301
.007 .106
.533
x2
-8、设河流的一个断面的年径流量为y,该断面上的上游流域的年平均降水量为x1,年平均
饱和差为x2,现共有14年的观测记录:
时间(a) x1
x2
y
时间(a) x1
x2
y
1
720
1.80
290
8
579
2.22
151
2
553
2.67
多元统计分析实例

多元统计分析实例以下是一个关于消费者行为的多元统计分析的实例。
假设我们是一家零售公司,想要了解什么因素会影响消费者的购买决策,并基于这些因素进行市场定位。
为了达到这个目标,我们收集了一些数据,包括消费者的年龄、性别、收入水平、购买意愿以及他们对不同产品特征的偏好等。
我们将使用多元统计分析来探索这些变量之间的关系,以便更好地了解消费者购买决策的驱动因素。
首先,我们可以使用主成分分析(PCA)来寻找这些变量的主要维度。
主成分分析可以将原始的多个相关变量转化为少数几个无关的主成分,以便更好地解释方差。
通过观察主成分的贡献率和载荷矩阵,我们可以确定哪些变量对于解释数据的方差最为重要。
例如,我们可能发现年龄和收入是最主要的驱动因素。
接下来,我们可以使用聚类分析来将消费者分成不同的群体。
聚类分析可以帮助我们确定具有相似特征和购买偏好的消费者群体。
基于这些群体的特征,我们可以对市场细分进行差异化定位和营销策略的制定。
例如,我们可能发现年轻人更偏好购买价格较低的产品,而高收入人群更倾向于购买奢侈品。
然后,我们可以使用相关分析来探索消费者的购买意愿和产品特征之间的关系。
相关分析可以帮助我们了解不同变量之间的相关性及其强度。
例如,我们可能发现购买意愿和产品质量之间存在正相关关系,这意味着消费者更愿意购买质量较高的产品。
最后,我们可以使用回归分析来建立预测模型,以预测消费者的购买意愿。
回归分析可以帮助我们确定哪些变量对于解释购买意愿最为重要,并建立一个可以预测消费者行为的数学模型。
例如,我们可能发现消费者的收入和购买意愿之间存在正相关关系,这意味着收入较高的消费者更倾向于购买高价位的产品。
通过这些多元统计分析的方法,我们可以更全面地了解消费者行为的驱动因素,并基于这些因素来优化市场定位和营销策略。
这将帮助我们实现更准确的预测和决策,提高业务的竞争力。
多元统计典型相关分析实例

多元统计典型相关分析实例第一篇:多元统计典型相关分析实例1、对体力测试(共7项指标)及运动能力测试(共5项指标)两组指标进行典型相关分析Run MATRIX procedure:Correlations for Set-1 X1 X2 X3 X4 X5 X6 X7 X1 1.0000.2701.1643-.0286.2463.0722-.1664 X2.2701 1.0000.2694.0406-.0670.3463.2709 X3.1643.2694 1.0000.3190-.2427.1931-.0176 X4-.0286.0406.3190 1.0000-.0370.0524.2035 X5.2463-.0670-.2427-.0370 1.0000.0517.3231 X6.0722.3463.1931.0524.0517 1.0000.2813 X7-.1664.2709-.0176.2035.3231.2813 1.0000Correlations for Set-2 X8 X9 X10 X11 X12 X8 1.0000-.4429-.2647-.4629.0777 X9-.4429 1.0000.4989.6067-.4744 X10-.2647.4989 1.0000.3562-.5285 X11-.4629.6067.3562 1.0000-.4369 X12.0777-.4744-.5285-.4369 1.0000两组变量的相关矩阵说明,体力测试指标与运动能力测试指标是有相关性的。
Correlations Between Set-1 and Set-2 X8 X9 X10 X11 X12 X1-.4005.3609.4116.2797-.4709 X2-.3900.5584.3977.4511-.0488 X3-.3026.5590.5538.3215-.4802 X4-.2834.2711-.0414.2470-.1007 X5-.4295-.1843-.0116.1415-.0132X6-.0800.2596.3310.2359-.2939 X7-.2568.1501.0388.0841.1923 上面给出的是两组变量间各变量的两两相关矩阵,可见体力测试指标与运动能力测试指标间确实存在相关性,这里需要做的就是提取出综合指标代表这种相关性。
多元统计分析及实例讨论

添加标题
百米跑成绩
添加标题
跳远成绩
添加标题
百米跨栏
添加标题
1500米跑成绩
添加标题
铅球成绩
添加标题
例3 奥运会十项全能 运动项目
添加标题
跳高成绩
添加标题
得分数据的因子分 析
添加标题
400米跑成绩
添加标题
铁饼成绩
添加标题
撑杆跳远成绩
添加标题
标枪成绩
1
0.59
1
0.35 0.42 1
0.34
0.51
0.38
1
0.63 0.49 0.19 0.29 1
0.40
0.52
0.36
0.46 0.34
1
0.28 0.31 0.73 0.27 0.17 0.32 1
0.20
0.36
0.24
0.39 0.23 0.33
0.24
1
0.11 0.21 0.44 0.17 0.13 0.18 0.34 0.24 1
1. 因子分析基本思想简介
单击此处 添加大标 题内容
多元统计分析是以p个变量的n次观测数所组成的数据为依据。 简化数据结构(降维) 将某些较复杂的数据结构通过变量变换等方法使相互依赖的变量变成互不相关的;将
高维空间数据投影成到低维空间数据; 分类与判别(归类) 对所考察观测点(或变量)按相似程度进行分类或归类; 变量间的相互联系 相互依赖关系:分析一个或几个变量的变化是否依赖于另一 些变量的变化;变量间相关关系:分析两组变量相互关系; 多元数据的统计推断 多元正态分布的均值向量与协方差阵的估计及其假设检验; 多元统计分析的理论基础 多维随机变量及其分布,抽样分布
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多元统计分析实例院系: 商学院学号: 姓名:多兀统计分析实例本文收集了 2012年31个省市自治区的农林牧渔和相关农业数据,通过对对 收集的数据进行比较分析对31个省市自治区进行分类•选取了 6个指标农业产值 林业产值.牧业总产值,渔业总产值,农村居民家庭拥有生产性固定资产原值,农 村居民家庭经营耕地面积. 数据如下表: 江 区 京津北H 蒙宁林龙海苏江徽建西东南北南东西南庆川州南藏西肃海夏牘地北天河山内辽吉黒上江浙安福江山河湖湖广广海重四贵77西陕甘青宁新农业总产值 林业驰产{牧业总产懾业总产侬村居民家庭拥有生产性[5166.2954.83 154.16 12 98 12767. 09 0・5195.^9 £ 79 105. 01 61, 66 17508. 57 1. 58 3095.29 77.88 1747. 66 1?7. 74 17904. S3 1789847-41 79, 07 298. 83 8. 42 ^808. 38 2.51171.-57 97. 7G U1S. 86 26. 08 293曲.旳 10. 4 1539.65128. 68 16ZL 23 618. 74 249^7. 92 3. 781166.ES90. 1 1130. 36 34. 14 24937. SB S. 272315. 64 134. 51350. 63 77. 92 31507. 91 13. 56171.48 9.5572. 59 57. 45 4146. 13 0. 262966.72 99. 75 1226,18 1235.4 14541. 03 L251229.36 142.14 549. 01 687. 05 22747. 33 6 541867.64 209. 5 1119.73 334. 43 15134. 35 1. 391263.71 256. 45 48L 28 p03. 36 11821. 38 731003.21 228. 91 752. 63 333. 06 gggg. 31 L 57 39&0.储 107.01 22S5. 92 1267. 07 19168.14 L &4 3958.^5 140. 85 2255. 61 SS.4 12980. 72 1. &2 2488. 06 100.05 1334, X 626, 23 10813. 13 1. 71 2651.69 259. 97 1488. 58 279. 94 3904. 32 1. 22 2229. 27222.74 1134.14 914. 05 8516. 72 0.53 1724 245. 56 1072. 77 331. 74 11851. 56 L 37 4S0. 72 137.85 214. 14 236.27 11387. 06 0. 83 341.51 43.48 453. 9 44. 99 122S5. 74 L 29 2764- 9 151. 52269. 86 163. 77 13759.17 1.14364. 54.19421. 55 28. 21 11957. 31 L 181398.17225. S3 912. 97 63.1 19020. 92 1.. 6 53.39 2” 56 59. 02 0. 22 52935. 07 L 891526.23 58. 44 598. 72 14. 61 12273. 06 L 52984,24 20. 07 231. 72 1,8 1$486. 44 2. 72 117-09 4.57 137. 08 0. 56 21919.甜 L 33 240, 4&9・77 105, 72 13. 36 24266.19 3・69 1675収04485. 37 15* 26 35Q70. 315 76.聚类法设定4个群聚,采用了系统聚类法.下表为spss分析之后的结果.C A S E 0 5 10 15 20 25 内蒙 5 -+吉林7 -+云南25 - + -+江西14 -+ +-+陕西27 - + -+ |新疆31 -+ +- +安徽12 -+-+ 11广西20 —+ + — + +——————— +辽宁 6 ---+ | |浙江11 -+—+ 1福建13 -+ 1重庆22 -+ + ............... ....... + 贵州24 -+ 1|山西 4 -+ -+ | |甘肃28 -+ | | |北京 1 -+ | | |青海29 + + + | 1天津 2 -+ 1|上海9 -+ 1|宁夏30 -+ - +|西藏26 -+ |海南21 -+ |河北 3 | 1四川23 - + | |黑龙江8 -+-+ + .......... + |湖南18 -+ + + | | |湖北17 - + -+ +-+ + -------------- ■...... + 广东19 -+ | |江苏10 --——+ |山东15 ...... + ....... +河南16 ...... +从SPSS分析结果可以得到,内蒙,吉林,黑龙江,新疆为第2族群,这一族群的特点是农业收入可能不高,但是农民的固定资产,和耕地面积非常高,农民的富余程度或者机械化程度较高;山东是第3族群,这一族群中六个指标都处于较高水平农林牧渔四项收入都处于较高水平而且农民富余;西藏处于第4族群,这是因为,西藏人员较少,自然条件恶劣,可使用耕地少,但是,由于国家的扶持,农民的固定资产较多,农民相对而言比较富足;大多数省份属于第1族群,这一族群的特点在于六项指标都没有较为突出的一项,或者农林牧渔收入的本来就少,或者是农民的虽然比较辛苦,总体的农业收入较高,但是农民的收入水平比较低,固定资产较少•三.判别法X1,X2,X3,X4,X5,X6分别代表农业产值,林业产值.牧业总产值,渔业总产值,农村居民家庭拥有生产性固定资产原值,农村居民家庭经营耕地面积实验结果分析:从表上可以看出,组均值之间差值很大.各个分组,在6项指标上均值有较明显的差异.由表中可以知道,13456指标之间的sig 值较小,2指标sig 值有0.561较大, 不过仍说明接受原假设,各指标族群间差异较大.从表中可以知道,检验结果p值>0.05,此时,说明协方差矩阵相等,可以进行bayes检验.Fisher 分析法协方差矩阵的均等性的箱式检验典型判别式函数摘要由表中看出,函数1,2的特征值达到0.911,0.822比较大,对判别的贡献大由表中可知,3个Fishe判别函数分别为y i 2.928 0.003X20.626X6y2 2.269 0.002X2 0.489X6y3 0.975 0.009X2 0.01X3 0.03X4 0.037X6农村居民家庭拥有生产性固定资产原值对判别数据所属群体无用该表是原始变量与典型变量(标准化的典型判别函数)的相关系数,相关系数的绝对值越大,说明原始变量与这个判别函数的相关性越强.从表中可以看出相关性较强.符合较好.由上表可知各类别重心的位置,通过计算观测值与各重心的距离,距离最小的即为该观测值的分类.贝叶斯分析法该表为贝叶斯函数判别函数的取值,从图中可以知道三类贝叶斯函数y1 0.03X1 0.029X2 0.03X3 0.002X4 0.001X5 0.153X1 8.418第一类:第二y2 0.06X10.42X2 0.009X3 0.004X40.004X5 4.286X6 38.18类;第三y3 0.02X-I0.010X20.002X30.010X40.001X5 1.X620.732类;第四类:『4 0.OO3X-I 0.051X20.004x30.006x40.002x5 1.675x661.646将各样品的自变量值代入上述4个BayeS判别函数,得到函数值。
比较函数值,哪个函数值比较大就可以判断该样品判入哪一类.判别结果检验**.错误分类的案例从上图可以看出本次判别分析的结果比较贴近,只有第10统计量在分布上出现不同.从总体而言,判别效果较好.3.主成分分析通过SPSS主成分统计分析,得到如下数据.F i F2从以上表可以知道,成分,的特征值都>1,并且解释了71.886%的方差,达到了主成分分析的要求.所以只要提取两个因子即可满足要求.其他因子不予以提得到以下数据.F, 0.875X, 0.72X2 0.836X3 0.724X4 0.428X5 0.194X6得到主成分F20.33X, 0.0987X2 0.428X3 0.138X4 0.723X5 0.862X6解释:第一类因子F1中Xi X2 X3 X4载荷系数较大.主要解释了各省区自然条件的状况和农林牧渔收入.可抽象为农业的环境因子.第二类因子F2中X5 X6载荷比较大.主要解释了各个省区农民的经济和耕地状况.可抽象于农业的农民因子.4.因子分析:通过主城分析得到旋转之前的因子与载荷.与因子公式.F 1 0.875X 1 0.72X 2 0.836X 3 0.724X 4 0.428X 5 0.194X 6 F 2 0.33X 1 0.0987X 2 0.428X 3 0.138X 4 0.723X 5 0.862X 6下图为旋转矩阵以及旋转之后的因子F i F 2得到的旋转之后的因子 ,解释:第一类因子F1中X1 X2 X3 X4载荷系数较大.主要解释了各省区自然条件的状况和农林牧渔收入.可抽象为农业的环境因子第二类因子F2中X5 X6载荷比较大.主要解释了各个省区农民的经济和耕地 状况.可抽象于农业的农民因子 .F 1 0.934% 0.657X 2 0.926X 30.649% 0.191X 5 F 2 0.052X 1 0.309X 1 0.156X 1 0.349% 0.818%0.074X 60.880%旋转之后的矩阵有了明显的变化 ,因子的特征载荷增大。
