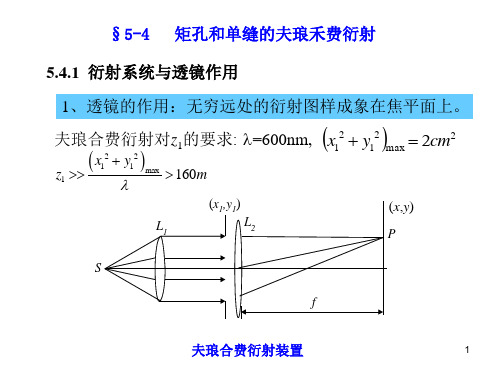
高斯光束的矩孔和圆孔衍射_蔡祥宝
调制空心高斯光束通过圆孔与园环光阑的衍射特性

Absr c :F o t e COL NS fr ta t r m h U o mul a.t e d frc in o di e olw u sa e ms h i a to fmo f d h lo Ga s i n b a i
( G s ho g n ua p r r n i ua pr r w r s de .T es uai e H B )truh an l a e uea dcr l a e ue ee t id h i lt n r— r t c r t u m o
摘要: 为了研究 空心 高斯光束及其通过 圆孔与 园环光 阑的衍射特性 , C L I S 式出发 , 从 O LN 公 利用 Ma -
pe l软件进行 了具体的数值计算. 结果表 明: 取空心高斯光束阶数值 为 1 , O 当圆孔孔径在 1~1 1 . 倍束 腰 时, 横截 面上 光强调制 明显 . 轴上光强随 F的变化趋势为 : 当菲涅耳数小于 4 出现调 制现 象 ; , 当菲 涅耳数大于 4时 , 衍射调制被抑制. 圆环 内孔 径为 0 9倍束 腰 , . 当外孔小 于 13倍 束腰时 , . 衍射后 轴 上光强随 F出现周期振荡 的调制特性 ; 当外孔大于 15倍束腰时 , 射后轴上光强调制被有效压抑. . 衍 上述结果为选择光阑提供 了合理参数 .
sz ie,i h eo trcr u a pe ur sls h n 1 3 tme ft e b a was ie,t e h — ft u e ic l a r e i e st a . i so h e m itsz r t h n te a x ili t n i iti t n p a d lto h r ce it so e idi s ilto swi i— a n e st d srbu o sa pe rmo u ain c a a t rsi fp ro c o c l in t F n y i c a h c e sn .W h 1 h mo ult n c a a trs c ia e s t o t r cr u a p ru e i raig ie t e d a o h r c e t s d s pp a a he u e ic l a e r s i ii r r t big rt a . i so e be m itsz . g e h n 1 5 tme ft a was ie h tr o i r c in. e f rd f a t s o
圆环孔径衍射高斯光束远场发散角研究

Fa r -f i e l d d i v e r g e n c e f o r Ga u s s i a n b e a m u n de r
a n n u l a r a pe r t u r e d i fr a c t i o n
Wa n g Ch a o ,D o n g Ke y a n ,J i a n g Lu n ,A n Ya n '
该 条件 一般 能 够被 满 足 。
关键 词 :衍射 光 学 ; 高斯 光束 ; 圆环孔 径 ; 远 场发散 角
中 图分类 号 : 0 4 3 6 . 1 ; T N 9 2 9 . 1 1 文 献标 志码 : A 文 章 编 号 :1 0 0 7 — 2 2 7 6 ( 2 0 1 5 ) 1 2 — 3 6 3 4 — 0 5
王 超 . 一 , 董 科研 , 江 伦1 , 2 , 安 岩1 , 2
( 1 . 长春 理 工 大学 空 间光 电技 术 国 家地 方联 合 工程研 究 中心 ,吉林 长春 1 3 0 0 2 2 ;
2 . 长春 理 工大 学 空地激 光通信 技 术重 点 学科 实验 室,吉林 长春 1 3 0 0 2 2 )
e x p r e s s i o n ,a nd he t f r -f a ie l d d i v e r g e n c e s s o l v e d b y he t s e t wo e x p r e s s i o ns we r e n e rl a y i d e n i t c a 1 .Th e e r r o r wa s n o mo r e t h a n 2. 7 % .Co mp re a d wi h t t h e t r a it d i o n a l me ho t d o f g e t in t g t h e b e m a d i v e r g e n c e b y n ume ic r a l
圆孔衍射图样

二者常常同时存在。 例如,不是极细缝情况下的双缝干涉,就应该 既考虑双缝的干涉,又考虑每个缝的衍射。
2024/10/13
26
光学仪器的分辨本领
二、圆孔夫琅禾费衍射
S
D
圆孔衍射图样:由一个中央亮斑和一组明暗相间的同心圆环组成;
2024/10/13
k 1 k 3.3
d
最高3级; 共7条谱线
43
P398 例题10-2 用波长=546.1nm的绿光垂直照射每厘米有3000条刻 线的光栅,该光栅的刻痕宽和透光缝宽相等,问:
能看到几条光谱线?各谱线衍射角多大?
2024/10/13
44
作业: P401,选择题:1,2,8,9 P404, 一. 1
R 1 D
1.22
人眼瞳孔:D =2~6mm
=68~23
望远镜: DM = 6m
= 0.023
例题:汽车二前灯相距1m,设 解:人眼的最小可分辨角
=500nm 人眼瞳孔直径为 5mm。
问:1)人眼的最小分辨角?
2)对迎面而来的汽车,离多远能 分辨出两盏亮灯?
0
1.22
D
L0 1m
L 8200m
1m
L?
2024/10/13
32
望远镜: 不可选择,但 D R
▲ 世界上最大的光学望远镜: D=8m
建在了夏威夷山顶。 ▲世界上最大的射电望远镜:
D = 305 m 建在了波多黎各岛的
Arecibo,能探测射到整个
地球表面仅1012W的功率,
也可探测引力波。
2024/10/13
33
光学谐振腔理论-第8节-高斯光束的传输

05 高斯光束的未来发展与应 用
高斯光束在光学通信中的应用
高速光通信
高斯光束在光学通信中具有较高的传输速度和较低的信号衰减,有助于实现高 速、大容量的光通信系统。
远程通信
高斯光束具有较好的光束质量和传输稳定性,适用于长距离的光纤通信,有助 于实现远程、稳定的通信连接。
高斯光束在光学传感中的应用
03 高斯光束的调制与控制
高斯光束的相位调制
01
相位调制是指通过改变高斯光束的相位分布来改变其波前的状 态。
02
常见的相位调制方法包括利用液晶空间光调制器、光栅或其他
光学元件对高斯光束进行相位调制。
相位调制在光学通信、光学传感和光学计算等领域有广泛应用,
03
可以实现光束的聚焦、散焦、波形转换等功能。
高斯光束的波前测量
波前测量概述
波前是描述光束相位变化的物理量,高斯光束的波前测量有助于 了解光束的传播特性和干涉、衍射等光学现象。
波前测量方法
常用的波前测量方法有干涉法、散斑法、剪切干涉法等,可以根据 高斯光束的特点和测量精度要求选择合适的方法。
测量误差来源
波前测量误差主要来源于光束的聚焦、光束截面分布、光学元件的 误差等因素。
高斯光束的聚焦特性
聚焦原理
高斯光束经过透镜聚焦后,其横截面 上的强度分布会发生变化,形成明暗 相间的干涉条纹。
干涉条纹
干涉条纹的形状取决于透镜的焦距和 光束的束腰半径。当透镜焦距一定时 ,束腰半径越小,干涉条纹越密集; 反之,则越稀疏。
02 高斯光束在光学谐振腔中 的应用
光学谐振腔对高斯光束的影响
偏振态调制是指通过改变高斯光 束的偏振状态来改变其电磁场分
布。
常见的偏振态调制方法包括利用 偏振片、电光晶体或液晶等对高
标准和优美厄米-高斯光束通过圆环孔衍射的比较

标准和优美厄米-高斯光束通过圆环孔衍射的比较苏婷燕;顾菊观;曹佳妍;杜琴画;胡凯【摘要】标准厄米-高斯光束(Standard Hermite-Gaussian beam,SHGB)和优美厄米-高斯光束(Elegant Hermite-Gaussian beam,EHGB)是厄米-高斯光束的两个特殊解.应用柯林斯(Collins)公式研究两种光束通过圆环孔的衍射特性,用Matlab软件进行一些数值模拟.模拟结果表明:这两种光束通过圆环孔的衍射存在明显差异,在x、y轴方向上SHGB衍射光强始终比EHGB大,差异来源于标准厄米-高斯光束与优美厄米-高斯光束的场分布的差异.【期刊名称】《物理与工程》【年(卷),期】2015(025)001【总页数】5页(P71-75)【关键词】标准厄米-高斯光束;优美厄米-高斯光束;圆环孔;衍射【作者】苏婷燕;顾菊观;曹佳妍;杜琴画;胡凯【作者单位】湖州师范学院理学院,浙江湖州 313000;湖州师范学院理学院,浙江湖州 313000;湖州师范学院理学院,浙江湖州 313000;湖州师范学院理学院,浙江湖州 313000;湖州师范学院理学院,浙江湖州 313000【正文语种】中文激光通过复杂光学系统的传输特性,一直是科学工作者感兴趣的研究课题[1-8,10-14].目前,对标准厄米-高斯光束的研究相对比较多,而对优美厄米-高斯光束[13,14]的研究则相对较少;另外,对于圆环孔的衍射研究虽然有涉及但是能查阅到的文献相对比较少,而且研究方向比较单一.基于这些情况,本文对比两种光束,并运用柯林斯公式研究了标准厄米-高斯光束和优美厄米-高斯光束通过圆环孔的衍射特性,利用Matlab进行一些数值模拟并分析衍射特性.二维标准厄米-高斯光束的场分布可用下式表示[6,10,11,13,14]二维优美厄米-高斯光束的场分布可用下式表示[6,13,14]其中,E0是振幅;k是波数;px,py分别为在x和 y方向的复曲率半径;Np,Nq分别为p阶和q阶厄米多项式;ωx,ωy分别为厄米-高斯光束在x和y方向的束腰大小.两种光束表达式区别主要在于:二者厄米多项式中相差系数p=4,q=6阶数的两种光束的光强分布如图1所示(图中纵坐标I为相对光强).由图可知,虽然两者只在厄米多项式中相差系数,但是其光强分布相差甚远.SHGB光束的光强远远比EHGB光束的大;且SHGB光束边缘的光强比中心的大,而EHGB光束光强集中在中心.显然,可猜测这两种光束通过圆环孔的衍射肯定也存在很大差异.二维的标准厄米-高斯光束通过半径为r的圆孔的近轴ABCD光学系统,它的输出场可用柯林斯衍射积分表示为将硬边圆孔的窗口函数拓展为一组有限复高斯函数之和[9]式中,al和bl分别为展开系数和复高斯函数系数.标准厄米-高斯光束通过半径为r的圆孔后,出射场用柯林斯衍射积分公式运算可得出射场分布二维标准厄米-高斯光束通过圆孔的出射场分布的传输近似分析解与文献[10]、文献[11]一致.类似地,可求得二维优美厄米-高斯光束经积分运算通过圆孔的出射场分布对于光束通过圆环孔的解析结果,利用公式E=E2(r2)-E2(r1)即可求得相应光束通过圆环孔的光强,而r2,r1分别是圆环孔的外半径和内半径.对式(5)、式(7)进行积分计算,应用Matlab分别得到SHGB与EHGB光束通过圆环孔(内半径r1=0.5mm,外半径为r2=1.0mm)的衍射特性.假设束腰在孔面上,取E0=1,λ=632.8nm,ωx=ωy=ω0=1mm.厄米-高斯光束的厄米多项式的微分表达式为则p=4,q=6[6]时:对于SHGB:由图2(a)、(b)(I为相对光强)可知,z轴上相对光强的振动变化随着观察屏远离衍射屏(即圆环孔)其振动逐渐消失;从一开始的几何投影区,到距离孔较远的菲涅耳衍射区(即近场衍射区域),到相距甚远的夫琅禾费衍射区(即远场衍射区),3个区之间是逐步发生改变的[10].比较图2可以发现SHGB光束与EHGB光束通过圆环孔的衍射,在菲涅耳衍射区SHGB的整体光强比EHGB的小;SHGB光束菲涅耳衍射区过渡到夫琅禾费衍射区对应的z比EHGB光束要大,其原因是SHGB光束光强分布不集中;在夫琅禾费衍射区,SHGB的整体光强比EHGB的大,并且SHGB衰减相对比较缓慢,而EGHB相对衰减较快,其原因是由两束光的光强分布差异引起的.根据图2,比较图3(a)、(b)、(c)、(d)(I为相对光强)可知,在菲涅耳衍射区两种光束的衍射存在明显差异,EGHB的衍射峰比SGHB的衍射峰多,且整体衍射光强较小,其原因是EGHB光强整体分布比SGHB相应减小.比较图3(e)、(f)、(g)、(h)可知,在夫琅禾费衍射区,两种光束通过圆环孔的衍射图样有相近,但仍然存在一定的分布形状差异,其原因是两束光的光强分布有较大的差异;其衍射强度都是SHGB衍射光强较大.y轴方向的衍射光强图样和分布情况与x轴方向相似,不再以图表示,其原因是光强分布是一致的.本文用柯林斯公式分析和由Matlab软件进行数值模拟得到了厄米多项式p=4,q =6的标准厄米-高斯光束和优美厄米-高斯光束通过圆环孔的衍射光强分布图.模拟结果表明:SHGB光束、EHGB光束通过圆环孔的衍射,光强I跟z的关系变化趋势基本一致,SHGB光束菲涅耳衍射区过渡到夫琅禾费衍射区对应的z比EHGB光束要大,SHGB衰减比EGHB相对比较缓慢,SHGB整体衍射光强比EHGB要大.在x、y轴方向上SHGB衍射光强始终比EHGB大;两种光束通过圆环孔的衍射图样有相近,但仍然存在一定的分布形状差异.[1] Gu Juguan,Zhao Daomu,Mei Zhangrong,et al.Propagation characteristic of the two-dimensionaal off-axial Hermie-cosh-Gaussian beams through rectangular apertured and misaligned optical systems [J].Optik &Laser Technology,2005(37):173-179.[2] Gu Juguan,Zhao Daomu.Relative phase shift of two-dimensional cosine-Gaussian beams passing through apertured paraxial ABCD optical systems[J].Optik,2004,115(2):67-70.[3]顾菊观,甘亮勤,徐海斌,等.厄米-高斯光束通过双矩孔的传输特性[J].激光与红外,2006,36(7):584-586.[4]徐海斌,甘亮勤,顾菊观.厄米-高斯光束通过硬边光阑的自由传输特性[J].激光与红外,2005,35(10):779-781.[5]戴兵,贺安之,朱兆青.一类与椭圆和矩形相关的孔径的夫琅禾费衍射研究[J].大学物理,2003,22(3):5-8.[6]吕百达.激光光学[M].3版.北京:高等教育出版社,2003:10-12.[7]季小玲,吕百达.厄米-高斯光束通过多个硬边光阑复杂光学系统变换的计算机模拟[J].强激光与粒子束,2003,15(9):845-849.[8] Gu Juguan,Zhao Daomu.Propagation characteristics of Gaussian beams through a paraxial ABCDoptical system with an annular aperture [J].Journal of Modern Optics,2005,52(8):1065-1072.[9] Wen J J,Breazeale M A.A diffraction beam field expressed as thesuperposition of Gaussian beams[J].J Acoust.Soc.Am.1988(83):1752-1756.[10]杨平,顾菊观,张亚萍,等.厄米-高斯光束通过圆孔衍射的两种计算方法比较[J].物理与工程,2011,21(5):20-23.[11]杨平,顾菊观,张亚萍,等.厄米-高斯光束通过三角形与圆形围成孔的衍射[J].广西物理,2011,32(2):28-30.[12]张亚萍,顾菊观,杨平,等.平顶-高斯光束通过圆形与三角形围成孔的衍射[J].物理通报,2012(8):23-25.[13] Saghafi S,Sheppard C J R,Piper J A.Characterising elegant and standard Hermite-Gaussian beam modes[J].Optics Communications,2001(191):173-179.[14] Lu Baida,Ma Hong.A comparative study of elegant and standard Hermite-Gaussian Beams[J].Optics Communications,2000(174):99-104.。
第六章高斯光束详解

波阵面是垂直于z轴的平面,平面上各点的振幅 相等,相位相同。
振幅A0与x,y无关,即垂直于光束传播方向的 横截面上的光强是均匀的。
1.2 均匀同心光束
波峰
E( x, y, z) A1 eikr r
K 2
r x2 y2 z2
特点:
k
k
波谷
波阵面是与点光源为球心的球面,球面上各点 的相位相同。
高斯光束的透镜变换要点示意
A
A’
(a)
C ω
ω ˊ Cˊ
-R
Rˊ
高斯光束透镜变换
(b)
4.2 求解实际问题的三个步骤:
入射高斯光束:
腰到透镜的距离z
束腰半径ω 0, 透镜的焦距f′
出射高斯光束:
束腰位置z′ 束腰半径ω0′
① 根据束腰位置z和束腰半径ω 0,求出入射高
斯激光束在透镜上的光束截面半径ω 和波面半 径R;
2
z ' 100.00mm
入射光束的束腰位于 透镜前焦点
出射光束的束腰位 于透镜的后焦点
4.3 透镜变换和几何光学成像规则的对照
0
1
z 02
2
1
2
R
z
1
02 z
2
1 1 R' R
'
1 f'
0
=
2
1+
2 R
2
z
R
1
R' 2
2
消去中间变量
1
z F
2
0
z 2
1
02
高斯激光束的传播过程中
光束半径ω 与z之间不符
合线性关系.
ω
高斯光束经圆形光阑衍射的远场发散特性

高斯 光束 是一个 经典 的光 束模 型 , 在实 际 的光 学系 统 中或多 或少用 到光 阑特别 是 圆形 光 阑 。因此 , 而 高斯 光 束经 圆形光 阑 的衍 射特 别受 到光学 工作 者们 的关 注 。傍 轴高斯 光 束经 圆形光 阑弱 衍射后 的远 场可 视为另 一 个 参数 略为不 同 的傍 轴高 斯光 束口 。沈锋 等人研 究 了各种 不 同中心遮 拦和 不 同光 束截 断 比对高斯 光束 远场 环 ] 围能量分 布 的影响口 。吕百 达 和赵道 木等人 采 用不 同的方 法 分别 给 出 了傍 轴 高 斯光 束 经带 光 阑 AB D 光 学 ] C
第 2 4卷第 9期
21 0 2年 9月
强 激 光 与 粒 子 ‘ 束
HI GH POW ER LASER A ND PARTI CLE BEAM S
V o . 4,NO 12 .9
Se .,2 2 p 01
文 章 编 号 : 10 —3 2 2 1 )924 —6 0 14 2 ( 0 2 0 — 0 70
传 输公式 , 利用 标量 角谱法 分析 了高斯 衍射 光束 的远 场特性 ] 并 。通过采 用两 种不 同 的处 理方 法 , 国泉 等 周 人 给 出了高斯 光束经 圆形 光 阑衍射后 的远 场矢 量结 构[ ] 8 。由于 圆形光 阑半 径对 高 斯衍 射 光 束远 场 发 散角 的 影 响对实 际应 用至关 重要 , 因此 有必要 研究 高斯 衍射 光束 的远场 发散 特性 。E M. r g 等 人导 出 了傍 轴高 斯 . Dve 光束 经 圆形光 阑衍射 后远 场发 散角 的近似 解析 表达式 [ 但 所得 结果 不适用 于 发散 度较 大 或横 向光 斑 尺寸 可 1 , 与 波长相 比拟 的高斯 衍射 光束 。 目前 , 生 大角 度 光 束 的激 光 光 源不 断 诞 生 ; 产 同时 微 型衍 射 光 学 元件 普 遍 使
矩孔,单缝圆孔的弗朗禾费衍射
积分式表示孔径上各点子波的相干叠加。叠 加结果取决于各点发出的子波与中心点发出 子波的位相差。
5
夫琅合费衍射与傅立叶变换(1) 傅里叶变换的分类
傅里叶 变换
时间域 变换
空间域 变换
f(t)
(时间)频谱f(ω)
时间空间频率 可互相转化
f (z) (空间)频谱f (k)
f (x,y)
角谱f (kx,ky)
a
C
2 a
b
2 b
exp iklx1 my1 dx1dy1
22
16
E~ x, y
a
C
2 a
b
2 b
exp iklx1 my1 dx1dy1
22
a
b
C
2 a
exp
ik
lx1
dx1
2 b
exp
ik
my1
dy1
2
2
sin kla sin kmb Cab 2 2
kla kmb 2 2
2 2 r l r l f
v ky k y 1 y 1 y . y方向上的空间频率
2 2 r l r l f
f(x,y) 可 表 示 为 空 间 频 率 (u,v) 连 续 的 基 元 函 数
F(u,v)exp[i2(ux+vy)]的线性叠加; F(u,v)是这些基元函数
的权重,叫做函数f(x,y)的傅立叶变换或空间频谱.
E
x1
,
y1
exp
ik
x1
x f
y1
y f
dx1dy1
E x, y C
E
x1,
y1
exp
i
kx x1 k y y1
圆孔衍射

实验10 圆孔衍射当光在传播过程中经过障碍物,如不透明物体的边缘、小孔、细线、狭缝等时,一部分光会传播到几何阴影中去,产生衍射现象。
光的衍射现象是光的波动性的一种表现。
研究光的衍射现象不仅有助于加深对光本质的理解,而且能为进一步学好近代光学技术打下基础。
衍射使光强在空间重新分布,利用光电元件测量光强的相对变化,是测量光强的方法之一,也是光学精密测量的常用方法。
一、实验目的1.观察圆孔衍射现象,加深对衍射理论的理解。
2.会用光电元件测量圆孔衍射的相对光强分布,掌握其分布规律。
二、实验仪器H e -N e 激光器、单缝及二维调节架、光电探测器及移动装置、数字式万用表、钢卷尺等。
三、实验原理圆孔衍射的基础是惠更斯-菲涅尔原理,,经过计算可以得到:在沿光传播方向圆孔的中轴线上,总是光强极大(设平面光波沿圆孔轴线传播),偏开中轴线一定角度,诸子波相干叠加正好相消,则出现第一级暗线,由于圆孔激起子波的轴对称性,暗线将是暗环,再增大偏开轴线角度,可得到一系列暗环,暗环之间为亮环,即衍射次极大。
直径为D 的圆孔的夫琅和费衍射光强的径向分布可通过贝塞耳函数表示。
夫琅和费圆孔衍射图样的中央圆形(零级衍射)亮斑通常称为艾里斑,艾里斑的大小可用半角宽度即第一级暗环对应的衍射角为:D λθθ22.1sin ==圆孔衍射各极小值的位置(衍射角)在0.610π,1.116π,1.619π,… 处,各极大值的位置(衍射角)在0,0.0819π,0.133π,0.187π,… 处,其相对光强I/I0依次为1,0.0175,0.042,0.0016,…。
零级衍射的圆亮斑集中了衍射光能量的83.8% 。
夫琅和费衍射不仅表现在单缝衍射中,也表现在小孔的衍射中,如图10-1所示。
平行的激光束垂直地入射于圆孔光阑1上,衍射光束被透镜2会聚在它的角平面3上,若在此焦平面上放置一接收屏,将呈现出衍射条纹。
衍射条纹为同心圆,它集中了84%以上的光能量,P 点的光强分布为:()2102⎥⎦⎤⎢⎣⎡=x x J I I (10-1)()x J 1为一阶贝塞尔函数,它可以展开成x 的级数()()()1212!1!1+∞=⎪⎭⎫ ⎝⎛+-=∑k o k k x k k x J (10-2)x 可以用衍射角θ及圆孔半径a 表示θλπsin 2ax = (10-3) 式中λ是激光波长(e e N H —激光器8.623=λ纳米)。
高斯光束夫琅和费衍射测径技术

高斯光束夫琅和费衍射测径技术
郭强;白贵儒
【期刊名称】《光学仪器》
【年(卷),期】1997(000)0Z1
【摘要】在文[1]基础上,对比平面波衍射测细丝直径方法,讨论了高斯光束Fraunhofer 衍射测径的几个技术性问题。
在衍射原理基础上,对用 Gaussian 光束测细丝直径这种方法给予了理论上的解决和实验上的校准,表明用 Gaussian 光束测细丝直径优于用平面波衍射测细丝直径,理论和实验结果有较好的吻合。
【总页数】5页(P93-97)
【作者】郭强;白贵儒
【作者单位】宁波大学物理系;宁波大学物理系 315211 宁波;315211 宁波
【正文语种】中文
【中图分类】TG806
【相关文献】
1.高斯光束夫琅和费衍射径技术 [J], 郭强;白贵儒
2.RDMS测径仪与ORBIS测径仪的比较与应用 [J], 张子强;邳海东;王海滨
3.一种可变物距的测径光学系统:变距测径仪的设计 [J], 冯炳华; 李复新
4.高斯光束夫琅和费衍射测径技术 [J], 郭强;白贵儒
5.管道柔性测径清管器的设计及测径盘性能分析 [J], 张行;刘彤;刘思敏;许学峰;高孟琦;闫增瑞;张仕民
因版权原因,仅展示原文概要,查看原文内容请购买。
高斯光束的圆孔夫琅禾费衍射

、o . 7 NO 1 ,1 2 .
新 乡学院学报 : 自然科 学版
J u n l f n i gUn v r i Nau a ce c i o o r a Xix a ie s y: t r l in eEd t n o n t S i
21 0 0年 2月
让高 斯光束 通过 一孔径 ,当高斯光 束 的传 播距 离足 够远 ,该光ቤተ መጻሕፍቲ ባይዱ束 的衍 射光 场可 等效 为衍射远 场 ,即夫 琅禾 费衍 射场 ,按照菲 涅耳. 基尔霍 夫衍 射原理 则高 斯光束 衍射 场 中任一 点 P处 的光场分 布为 :
() j )( 一 ( + y/) d , 尸 =f , e (i 4 r) d 7 ( ) k x / 7 p
Fe . 0 0 b 2 1
高斯 光束 的圆孔夫琅禾费衍射
侯 茹
( 商洛 学 院 物 理与 电子工 程系 ,陕西 商州 7 6 0 2 0 0)
摘
要 :利 用菲涅耳. 耳霍 夫衍射 原理 对 高斯 光束 通过有 限 圆孔 的夫琅 禾 费衍 射进 行 了详 细 的理 论分析 , 基
给 出 了高斯 光束在 的 夫琅 禾 费衍射 区的光 场分 布 ,并 与平 面波的 的 圆孔 夫琅禾 费衍射 进行 了粗略 的比较 。 关键 词 : 高斯 光束 ;夫琅 禾费衍射 ;圆孔 衍射
0 引 言
在研究 激光衍 射 时 ,通 常将激 光光束 简化 为平 面波或 球面波 【 卜 ,使 许 多问题 得 以简 化 ,但 是 ,激光束 最常见 、最 具代 表性 的是高斯 光束 ,即从 激光 器谐 振腔 中发 出的激光 既不是 平 面波 ,也不是球 面波 ,而是
场分 布服从 高斯 规 律的高 斯光束 【。笔 者对 高斯 光束 通过 一有 限 圆孔 的夫 琅 禾费衍 射 问题 进行 了分析 ,给 3 】
厄米-高斯光束通过圆孔衍射的两种计算方法比较

把硬 边 圆孔 函数拓展 为一 组有 限项 复 高斯 函数 之
和 的方 法 , 用 C ln 积 分公 式 , 到 了厄 米一 运 ol s i 得 高
E 2 一『 ( 击= Ⅺ
e i x k p × 历
基金项 目
21 0 0年 浙 江 省 自然科 学基 金 项 目 ( 1 0 0 ) 20 Y6 0 6 5 、0 8年 省 新 世 纪 高 等 教 育 教学 改革 研 究 项 目( 00 4 、 州 师 范 学 院 大 学 生 YB 8 6 ) 湖
to a e e pa de nt i ie s m fc mpl x Gau s a u to s,t p o ma ea a yt— i n c n b x n d i o afn t u o o e s in f nc i n hea pr xi t n l i
物理 与工 程
Vo. 1 No 5 2 1 12 . 0 1
厄 米一 斯光 束 通过 圆 孑 衍 射 的两 种计 算 方法 比较 高 L
杨 平 顾 菊观 张 亚萍 陈小 燕 沈 曼辰 ( 湖州 师 范学院理 学 院, 浙江 湖 州 3 3 0 ) 1 0 0
( 收稿 日期 :2 1—31 ) 0 10 —4
近几 年来 , 关 各 种 光 束 通 过 各 种 孔 径 的衍 有 射 现象 的讨论 见诸 许 多 文献 .计算 衍 射 场 的 光强
分 布一般 均 以基 尔 霍夫 衍 射 理 论 作 为 依 据 , 由 但
于积 分形 式 的复 杂 性 , 常 难 以得 到 解 析 解 .因 通 此 出现 了各种 类型 的近 似计 算 方法 _ ] 】 .本 文用
摘 要 应用 C ln 公 式和 硬边 圆孔 函数 拓 展为 有 限复高 斯 函数和 的方 法 , ol s i 推导 出厄米一 高斯 ( r t— u s n 光束 通过 圆孔 的衍 射场分布 的近 似解 析公 式.模 拟 结果表 明使 用 Hemi Ga si ) e a 该解 析公 式所得 结果 和直 接对 C ln ol s公 式进 行 数值 计 算 的结 果 符合 较 好 , 讨论 两 i 并 种方 法的差 异性 以及各 自的优缺 点.
第三章 高斯光束及其特性

§3.1 基模高斯光束
出射光束的束腰位置和尺寸
随入射光束的变化:
l (l F ) f 2 l F 2 2 (l F ) f
0
F ( l F )2 f 2
0
§3.1 基模高斯光束
0 F (l F ) f
2 2
0
l固定的情况下:
1 2
1 1 i q2 R2 22
高斯光束是非均匀的、 曲率中心不断变化的球面波
注意区别f与F
q C q z2 lC
1 1 1 1 i 2 R1 F 1 q1 F
§3.1 基模高斯光束
束腰距离透镜分 别为l和l’
§3.1 基模高斯光束
傍轴波面通过焦距为f的薄透镜: (应用牛顿公式)其波前曲率半径 满足:
1 1 1 R2 ( z ) R1 ( z ) f
A B 1 AR1 ( z ) B R2 ( z ) , CR1 ( z ) D C D 1/ f 0 1
§3.1 基模高斯光束
2)高斯光束在自由空间的传输规律:
( z ) 0
z 2 ( z ) 1 , lim 2 z z f f
2
( z ) 的渐近线夹角θ定义为光束的发散角
§3.1 基模高斯光束
,z 0 f R ( z ) z 等相位面的曲率半径 2 f ,z f 近似球面波! z 曲率中心随z变化 z , z f
§3.1 基模高斯光束
3)基模高斯光束的特征参数: 用q参数表征高斯光束
0 x2 y2 x2 y2 z u00 ( x, y, z ) c00 exp[ 2 ]exp{ i[k ( z ) arctg ]} ( z) (z) 2 R( z ) f
第三章 高斯光束及其特性精选全文

R2 ( z )
AR1(z) CR1(z)
DB,
A C
B
D
1 1 /
f
0
1
反映了近轴球面波曲率半径的传输与光学系统矩阵元之间的关系
§3.1 基模高斯光束
球面波的传播规律可以统一写成
R2
AR1 CR1
B D
结论:具有固定曲率中心的普通傍轴球面波可以由其曲率半径R 来描述,传播规律由变换矩阵确定。
f
2 2
2 F
q
(1
l F
)q (l q (1
l l
)
ll F
)
F
F
0
(l
F F )2
f
2 0
§3.1 基模高斯光束
出射光束的束腰位置和尺寸 随入射光束的变化:
l
l(l F ) (l F )2
f f
2 2
F
0
(l
F F )2
f
2 0
§3.1 基模高斯光束
0
(l
§3.1 基模高斯光束
球面反射镜对高斯光束的自再现变换:
F 1 R(l) 2
F
1 2
R球面
R球面 R(l)
当入射在球面镜上的高斯光束波前曲率半径正好等于球面镜的曲率半径 时,在反射时高斯光束的参数将不发生变化,即像高斯光束与物高斯光 束完全重合。通常将这种情况称为反射镜与高斯光束的波前相匹配。
第三章 高斯光束及其特性
本章大纲
§3.1 基模高斯光束 掌握高斯光束q参数的表达 高斯光束在线性光学系统中的变换 高斯光束的自再现变换与稳定球面腔模式的关系
§3.2 高阶高斯光束 了解高阶高斯光束的特性。
高斯光束微圆孔衍射变换的数值仿真实验

高斯光束微圆孔衍射变换的数值仿真实验
常山;毛杰健;桑志文;吴志伟
【期刊名称】《实验技术与管理》
【年(卷),期】2011(028)001
【摘要】高斯光束的微圆孔衍射变换在微光学、激光技术以及微光机电技术中发挥着基础性作用,通过数值计算模拟实验可以对它进行研究与探索.由菲涅尔一基尔霍夫衍射公式得到单色点源平面屏衍射的积分式,类推得到高斯光束圆孔衍射的积分式,并给出这一积分式的一种数值计算方法.利用Matlab软件进行了高斯光束微圆孔衍射变换的数值仿真实验研究,这有助于激光束的实际衍射实验及其测控理论与技术的研究以及光学教学的改革.
【总页数】5页(P80-83,87)
【作者】常山;毛杰健;桑志文;吴志伟
【作者单位】上饶师范学院物理与电子信息学院,江西,上饶,334001;上饶师范学院物理与电子信息学院,江西,上饶,334001;上饶师范学院物理与电子信息学院,江西,上饶,334001;上饶师范学院物理与电子信息学院,江西,上饶,334001
【正文语种】中文
【中图分类】O436.1;TN241
【相关文献】
1.高斯光束微圆孔衍射的“再现”与“自再现”研究 [J], 常山;何洁;肖清武;吴志伟;王华
2.高斯光束微圆孔衍射的整形变换 [J], 常山;肖清武;何洁;王华;吴志伟
3.高斯光束微圆孔菲涅耳衍射的束型转变 [J], 常山;毛杰健;杨建荣
4.高斯光束的微圆孔衍射变换的计算及其仿真 [J], 常山;桑志文;吴波;毛杰健
5.3类高斯光束的圆孔衍射特性 [J], 韩振海
因版权原因,仅展示原文概要,查看原文内容请购买。
3类高斯光束的圆孔衍射特性

3类高斯光束的圆孔衍射特性
韩振海
【期刊名称】《物理实验》
【年(卷),期】2016(036)006
【摘要】利用标量衍射理论,将空心高斯光束、贝塞尔高斯光束、平顶高斯光束3类高斯光束的圆孔衍射场进行傅里叶变换,并运用D-FFT算法对其圆孔衍射特性进行了数值计算,得到了衍射场中轴向和径向的光强分布特点,分析了光学参量对衍射结果的影响.分析结果表明:衍射特性与衍射距离、光束的阶数、圆孔束腰半径比等因素有关.
【总页数】7页(P12-18)
【作者】韩振海
【作者单位】河西学院物理与机电工程学院,甘肃张掖734000
【正文语种】中文
【中图分类】O436.1
【相关文献】
1.贝塞尔–高斯光束圆孔衍射场的传播特性 [J], 徐寿泉
2.高斯光束微圆孔菲涅耳衍射的束型转变 [J], 常山;毛杰健;杨建荣
3.高斯光束圆孔衍射特性 [J], 李汝烯;白凤翔;李汝恒;张学清;环敏
4.调制空心高斯光束通过圆孔与园环光阑的衍射特性 [J], 王家驷
5.准直圆孔衍射高斯光束远场发散度 [J], 王超;江伦;董科研;安岩;姜会林
因版权原因,仅展示原文概要,查看原文内容请购买。
平面波入射时二元光学型光栅的衍射场分布

平面波入射时二元光学型光栅的衍射场分布
蔡祥宝
【期刊名称】《南京邮电学院学报》
【年(卷),期】1999(019)002
【摘要】应用标量衍射理论分析了平面波入射时二元光学型光栅的衍射场分布规律,并进行了数值分析和实验验证。
【总页数】4页(P54-56,63)
【作者】蔡祥宝
【作者单位】南京邮电学院;基础课部
【正文语种】中文
【中图分类】O436.1
【相关文献】
1.平面波倾斜入射时的夫琅和费衍射花样 [J], 曹国荣
2.细光束斜入射时一维及正交光栅的衍射图样 [J], 蔡履中;马宝民
3.平行光斜入射光栅时的衍射特性研究 [J], 申志荣
4.对光线斜入射时衍射光栅的条纹分析 [J], 于广誉
5.衍射光栅斜入射时的明纹条数 [J], 和伟
因版权原因,仅展示原文概要,查看原文内容请购买。
贝塞尔-高斯光束通过圆孔与圆环光阑的衍射

贝塞尔-高斯光束通过圆孔与圆环光阑的衍射
屈军;孟凯;汪六三;丁培宏;崔执凤
【期刊名称】《激光技术》
【年(卷),期】2008(032)004
【摘要】为了研究贝塞尔-高斯光束通过圆孔硬边光阑和圆环光阑的衍射特性,从Collins公式出发,采用数值模拟的方法模拟出光强分布.模拟结果表明,贝塞尔-高斯光束经圆孔光阑衍射后轴上光强随菲涅耳数F呈周期振荡;贝塞尔-高斯光束经圆环光阑后轴上光强随F呈振动衰减.在F相同时,贝塞尔-高斯光束经圆孔光阑衍射后横向光强分布比经圆环光阑衍射后横向光强分布平滑,孔径越小,光强调制越明显;当孔径与束腰相等时候,横向光强分布与菲涅耳数没有关系.
【总页数】3页(P393-395)
【作者】屈军;孟凯;汪六三;丁培宏;崔执凤
【作者单位】安徽师范大学,物理与电子信息学院,芜湖,241008;安徽师范大学,物理与电子信息学院,芜湖,241008;中国科学院,安徽光学精密机械研究所,合肥,230031;安徽师范大学,物理与电子信息学院,芜湖,241008;安徽师范大学,物理与电子信息学院,芜湖,241008
【正文语种】中文
【中图分类】O435
【相关文献】
1.贝塞尔高斯光束通过硬边光阑的衍射损耗 [J], 王莉
2.贝塞尔–高斯光束圆孔衍射场的传播特性 [J], 徐寿泉
3.受光阑限制贝塞耳-高斯光束的衍射特性 [J], 刘永欣;葛卫国;吕百达
4.高阶贝塞尔-高斯光束通过圆孔硬边光阑的传输特性 [J], 李汝烯;赵承良;陆璇辉;李汝恒
5.高阶贝塞尔-高斯光束通过圆环形硬边光阑的传输特性 [J], 李汝烯;李汝恒;赵承良;陆璇辉
因版权原因,仅展示原文概要,查看原文内容请购买。
高斯光束对颗粒衍射测量的影响

高斯光束对颗粒衍射测量的影响
杨初平;何振江;杨冠玲
【期刊名称】《激光技术》
【年(卷),期】2002(026)004
【摘要】理论推导了高斯光束的圆孔夫琅和费衍射结果并与平行平面波的圆孔夫琅和费衍射结果进行比较,数值计算和理论分析表明,当激光光束的束宽半径远大于圆孔半径时,两者的衍射结果是非常接近的;当激光光束的束宽半径接近于圆孔半径时,高斯光束的衍射偏离平行光衍射.考虑光强的高斯分布,给出了某一粒度颗粒群的衍射结果.
【总页数】3页(P311-313)
【作者】杨初平;何振江;杨冠玲
【作者单位】华南师范大学物理系,广州,510631;华南师范大学物理系,广
州,510631;华南师范大学物理系,广州,510631
【正文语种】中文
【中图分类】O435
【相关文献】
1.用激光衍射法实现颗粒细度的测量技术 [J], 谭国锋
2.改进的光衍射式颗粒粒径测量系统的设计及研究 [J], 王荣;李振华;卞保民;刘成林;纪运景
3.光衍射法测量水中颗粒计数及大小分布 [J], 叶桂军
4.夫琅和费衍射颗粒粒度测量中的改进Chin-Shifrin反演算法 [J], 陈泉;刘伟;窦智;
杨林;申晋
5.高斯光束衍射测量中暗点漂移的研究 [J], 李景镇;马选民;周泗忠
因版权原因,仅展示原文概要,查看原文内容请购买。
