数值计算方法第二章参考答案
计算方法一二章答案

4
x3=0.3466 x7=0.3572 ∴ x ≈ 0.3574
1) 2) 4) 3)
x=1+1/x2 x3=1+x2 x2=x3-1 x2=1/(x-1)
方程求根
解:1) x 1 1 x2
|1’(x)|= | -2 1 x3 |= 2
(x)
1 1.53 | x0=1.5 =0.59 <1(收敛)
2) x 3 1 x 2
| 2’(x)|= | 1 3
(1)单调区间:
令f’(x)=ex-4=0, x=ln4≈1.4,所以有两个单调区间: [- ∞,1.4](递减)和[1.4, ∞](递增)
(2)有根区间:∴ 存在两个有根区间为:[0,1] 和[2,3]
[- ∞,1.4]区间:f(0)=1>0,f(1)=e-4<0,所以有根区间为:[0,1] [1.4,+ ∞]区间:f(2)=e2-8<0,f(3)=e3-12>0,所以有根区间为:[2,3]
方程求根
3:用简单迭代法求方程ex-4x=0的根,并验 证收敛性,精确到4位有效数字。
解:2.在区间[0,1]上构造收敛的公式并计算
x=ln(4x)= φ2(x) (1)两种等价形式: x=ex/4=φ1(x); xk (2) x=ex/4=φ1(x): e |φ1’(x)|=ex/4<1 (收敛), 迭代公式为: xk 1
数值计算第一二章答案

数值计算第⼀⼆章答案第⼀章数值计算中的误差习题⼀1.1 下列各近似数的绝对误差限是最末位的半个单位,试指出它们各有⼏位有效数字。
1x =-3.105 , 2x =0.001, 3x =0.100, 4x =253.40, 5x =5000, 6x =5?310.答案:4,1,3,6,4,1.1.2 设100>*x >10,x 是*x 的有五位有效数字的的近似数,求x 的绝对误差限。
答案:当104x x 答案:()10.0005e x ≤()20.0005e x ≤()30.0005e x ≤ ()40.005e x ≤ ()50.5e x ≤ ()60.5e x ≤1)()()()()123123e x x x e x e x e x ++=++≤()()()123e x e x e x ++3221.5100.15100.510---≤?=?≤?2123()0.1510x x x ε-++=?123123123()()0.0004993...0.0004994r x x x e x x x x x x ε++++==≤++123x x x ++=-3.004 精确到⼩数点后两位,所以有三位有效数字。
2)()()()()()()12424112424114224()e x x x x x e x x e x x x x e x x x e x x e x =+=++ =()()()241142124)x x e x x x e x x x e x ++() ()()241142124x x e x x x e x x x e x ≤++ =660.5100.31050.0005 3.1050.510--?+?+?? 所以43124() 1.71275100.510x x x ε--=?≤?124x x x =43.105100.0003105--?=-41241244124() 1.7127510()0.5515...3.10510r x x x e x x x x x x ε--?===?()()2222424244444()()1x x e x x e x e e x e x x x x x x ??≈-≤+325105420.5100.5100.197316100.77868100.1997100.510253.40253.40------??=+=?+?≈?24x x 50.3946310-≈?知有0位有效数字∴522440.1997100.5r x e x x x -≤≈1.4 x+yz,xyz 和xyz中哪⼀个的相对误差可能超过所有单项(x,y,z )的相对误差的五倍答案:()()()()(()())r r r r r r x yz x yz e x yz e x e yz e x e y e z x yz x yz x yz x yz+≈+=++++++ 如果5yz x yz >+ 5x x y z>+且两式同号,则()r e x yz +可能⼤于()r e x ,()r e y ,()r e z 的5倍。
(完整word版)《数值计算方法》复习资料全

《数值计算方法》复习资料课程的性质与任务数值计算方法是一门应用性很强的基础课,在学习高等数学,线性代数和算法语言的基础上,通过本课程的学习及上机实习、使学生正确理解有关的基本概念和理论,掌握常用的基本数值方法,培养应用计算机从事科学与工程计算的能力,为以后的学习及应用打下良好基础。
第一章数值计算方法与误差分析一考核知识点误差的来源类型;绝对误差和绝对误差限,相对误差和相对误差限,有效数字;绝对误差的传播。
二复习要求1. 知道产生误差的主要来源。
2. 了解绝对误差和绝对误差限、相对误差和相对误差限和有效数字等概念以及它们之间的关系。
3. 知道四则运算中的误差传播公式。
三例题例1设x*= =3.1415926…近似值x=3.14=0.314×101,即m=1,它的绝对误差是-0.001 592 6…,有即n=3,故x=3.14有3位有效数字.x=3.14准确到小数点后第2位.又近似值x=3.1416,它的绝对误差是0.0000074…,有即m=1,n=5,x=3.1416有5位有效数字.而近似值x=3.1415,它的绝对误差是0.0000926…,有即m=1,n=4,x=3.1415有4位有效数字.这就是说某数有s位数,若末位数字是四舍五入得到的,那么该数有s位有效数字;例2 指出下列各数具有几位有效数字,及其绝对误差限和相对误差限:2.000 4 -0.002 00 9 000 9 000.00=2.000 4=0.200 04×101, 它的绝对误差限0.000 05=0.5×10 1―5,即解因为x1m=1,n=5,故x=2.000 4有5位有效数字. a=2,相对误差限1x 2=-0.002 00,绝对误差限0.000 005,因为m =-2,n=3,x 2=-0.002 00有3位有效数字. a 1=2,相对误差限εr ==0.002 5x 3=9 000,绝对误差限为0.5×100,因为m =4, n=4, x 3=9 000有4位有效数字,a =9,相对误差限εr ==0.000 056x 4=9 000.00,绝对误差限0.005,因为m =4,n=6,x 4=9 000.00有6位有效数字,相对误差限为εr ==0.000 000 56由x 3与x 4可以看到小数点之后的0,不是可有可无的,它是有实际意义的. 例3 ln2=0.69314718…,精确到10-3的近似值是多少?解 精确到10-3=0.001,意旨两个近似值x 1,x 2满足,由于近似值都是四舍五入得到的,要求满足,近似值的绝对误差限应是ε=0.0005,故至少要保留小数点后三位才可以。
黄云清版数值计算方法习题解答

第一章 引论〔习题〕2.证明 : 记 x x f =)( ,则)()(***x x x x x xx x f E r +-=-=)(21**x E x x x x x xr ≈-⋅+=.3.证明: 令: )()()(b a fl b a fl b a **-*=δ可估计: 1|)(|-≥*c b a fl β 〔c 为b a *阶码〕,故: 121||--≤c t c ββδt-=121β 于是:)1)()(δ+*=*b a b a fl .4.解 (1) )21()122x x x++.(2) )11(2x x x x x-++.(3) xx x x x x x cos 1sin )cos 1(sin cos 12+≈+=-.6.解 a 的相对误差:由于31021|)(|-⋅≤-=a x x E .x ax x E r -=)(, 221018110921)(--⋅=⨯≤x E r . 〔1Th 〕)(a f 对于)(x f 的误差和相对误差.|11||)(|a x f E ---==()25.021011321⨯⋅≤-+---ax x a =310-33104110|)(|--⨯=-≤a f E r .9.解 递推关系: 1101.100-+-=n n n y y y (1) 取初值 10=y , 01.01=y 计算 可得: 11001.10022-⨯=-y 10001.1-=410-=6310-=y , 8410-=y , 10510-=y , …(2)取初值 50101-+=y , 2110-=y ,记: n n n y y -=ε,序列 {}n ε ,满足递推关系,且 5010--=ε , 01=ε1101.100-+-=n n n εεε, 于是: 5210-=ε, 531001.100-⨯=ε,55241010)01.100(---⨯=ε,55351002.20010)01.100(--⨯-⨯=ε,可见随着 n ε 的主项5210)01.100(--⨯n 的增长,说明该递推关系式是不稳定的.第二章 多项式插值 (习 题)1.方法一. 由 Lagrange 插值公式)()()()()(332211003x l f x l f x l f x l f x L ⋅+⋅+⋅+⋅=)1)((31)2)()(1()1)(()(2123210---=-----=x x x x x x x l ,))(1(2)1)()(1()(21221211--=--+=x x x x x x l ,x x x x x x l )1()()1()1!()(2382121232--=-⋅⋅-+=,)()1(12)()1()(2121213-+=⋅⋅-+=x x x x x x x l . 可得: )21()(23-=x x x L方法二. 令:)()21()(3B Ax x x x L +-=由 23)1(3-=-L , 21)1(3=L , 定A ,B 〔称之为待定系数法〕2.证明(1) 由于 j i j i x l ,)(δ= 故: =)(x L n ∑=ni i k i x l x)( ,当 j x x = 时有: k j j n x x L =)( , n j ,,1,0 =)(x L n 也即为 k x 的插值多项式,由唯一性,有:∑==ni k i ki x x l x)( , n k ,,1,0 =证明(2):利用Newton 插值多项式)(],[)()(0100x x x x f x f x N n -+=)()(],,[100---++n n x x x x x x f)()()()()()(00101x l x x x x x x x x x f n n =----=差商表:f(x) 一阶 二阶 … n 阶差商0x 11x 0101x x -0 )()(11020x x x x --n x 00)()(1010n x x x x --代入)(*式有:)()()()()(1)(020*******n n n x x x x x x x x x x x x x x x N -----++--+=- .)(0x l 为n 次代数多项式,由插值多项式的唯一性:有 )()(0x N x l n ≡.4.解作)(x f 以b a a ,,ε+为节点的Lagrange 插值多项式,有:)()()(22x R x L x f +=, 其中:)()()()()()()()()()(2εεεεε+-+--+-----=a fb a b x a x a f b a b x a x x L)()()()()(b f a b a b a x a x εε------+, )()()(!3)()(2b x a x a x f x R ----'''=εζ , b a <<ζ令: 0→ε 有)()(6)()()(22b x a x f x R x R --'''=→ζ, 又:)()()()([)()(2a f a b ax a f a b a x x b x L εεεεε----+----= )]()()()()(a f a b a x a f a b a x -------+εεεε )()()()()(b f a b a b a x a x εε------+)()()2()(2a f ab a b x x b --+-→)()()()(a f a b a x x b '---+ )()()()(22x P b f a b a x =--+ 故当0→ε 时,成立公式: )()()(x R x P x f +=.5.解:因为34)(3'-=x x f ,2''12)(x x f =)(x f 为凹函数.又从数值表可见:当]5.0,1.0[∈x 时,)(x f 单调下降.有反函数)(1y fx -=)(y f的Newton 插值多项式:)17440.0)(10810.0)(40160.0)(70010.0(01225.0)10810.0)(40160.0)(70010.0(01531.0)40160.0)(70010.0(0096436.0)70010.0(33500.01.0)(4+---+------+--=y y y y y y y y y y y N.337.0)0(4*≈=N x7.解 1)(37++=x x x f .有:=]2,,2,2[71f !7)()7(ξf =1,!8)(]2,,2,2[)8(810ηf f = 0=.9.证明:(1) =⋅-⋅=⋅∆++i i i i i i g f g f g f 11)(i i i i i i i i g f g f g f g f ⋅-⋅+⋅-⋅++++1111i i i i f g g f ∆+∆=+1.(3) n xnn)1()1(-=∆!)()(nh x h x x hn++此题可利用数学归纳法:设 k n = 成立,证明 1+=k n 成立.又 1=n 时是成立的.10.证明: 记: 2]2/)1([)(+=n n n f ,33321)(n n g +++=有: 3)1()()1()(+=-+=∆n n f n f n f 故: ∑-=∆=10)()(n k k f n g ∑-=-+=1)]()1([n k k f k f2]2/)1([)0()(+=-=n n f n f .13.解 作重节点差商的Newton 插值公式)1(]1,1[)1()(+--+-=x f f x P 22)1(]1,0,1,1[)1(]0,1,1[+--++--+x x f x f )1()1(]1,1,0,1,1[2-+--+x x x f重节点差商表:i x i f 一阶 二阶 三阶 四阶10-=x 110-=x 1 201=x 1 0 -212=x 1 0 0 112=x 1 2 2 1 0得 22)1()1(2)1(21)(+++-++=x x x x x P 13+-=x x .17.证: 取 ,00=x 211=x , 12=x , 21=h00=f , 11=f , 12=f记: )(i i x s M ''= , 2,1,0=i有 h x x M h x x M x S 01101)(-+-=''x M x M 102)21(2+-= )21(2)1(2)(212-+-=''x M x M x S 又三弯矩方程为:(2],,[210-=x x x f )244210-=++M M M , )24(41201M M M ++-=.分段积分:⎰⎰+''=''∆121221)]([)]([dx x s dx x s ⎰''12221)]([dx x s ⎰+-+=210201)]21([4dx x M x M ⎰-+-121221)]21()1([4dx x M x M⎰⎰-+-+-+-=121121221201)]21()1([4)]1()21([4dx x M x M dx x M x M由于⎰=-1212241)21(dx x ,⎰=-1212241)1(dx x ,⎰=--121481)1()21(dx x x ,于是:⎰++++=''∆1022212110202]2[61))((M M M M M M M dx x S 又: )24(41201M M M ++-=记 =),(20M M I ⎰∆''12))((dx x S=)()24(41[6120202220M M M M M M +++-+ ])24(81220M M +++ 由00=∂∂M I , 02=∂∂M I. 得: ⎩⎨⎧=+-=-07072020M M M M 即当: 020==M M 时,),(20M M I 达最小故:⎰=⋅⋅≥''∆12212)24(8161))((dx x S ,由最小模原理: ⎰≥''1212)]([dx x f .20.解 利用三弯矩方法 )(i i x s M ''= , 2,1,0=i10=x , 22=x , 32=x⎪⎩⎪⎨⎧-=+=++=+542364622121010M M M M M M M解得: 70-=M , 201=M , 372-=M]2,1[∈x 72431729)(231-+-=x x x x s ]3,2[∈x 105229367219)(232+-+-=x x x x s .第三章 最佳逼近与其实现 (习 题)2.解(1) ⎰'⋅'=badx x g x f g f )()(),( 不是 ),(b a c '中的内积,事实上容易验证:),(),(f g g f = , ),(),(g f g f λλ=),(),(),(w g w f w g f +=+但是0),(=f f 当且仅当 0)(≡x f . 条件不满足,因为:⎰='⋅'=badx x f x f f f 0)()(),(推出0)(≡'x f ,0)(≠=const x f . 因而 ),(g f 不是 ),(b a C '中的内积.(2) ),(g f 是 =],[10b a C {}],[)(,0)(:)(b a C x f a f x f '∈'=空间的内积,这是因为:0),(=f f 推出 0)(='x f ,C x f =)(,又],[10b a C f ∈ ,故 0)(=x f .4.解:由于 0)(],,[2≠''∈x f b a c f ,则)(x f ''于],[b a 上保号,由定理5的推论2可知:)()(1x P x f -的交错点组恰有三个交错点,且 a x =1,b x =3,即: ⎪⎪⎩⎪⎪⎨⎧=-'='-=+-==+-==+-=0)()(,)()()(,)()()(,)()()(122210223103311011αρααρααρααx f x e x x f x e x x f x e x x f x e 故:ab a f b f x f --='=)()()(21α,2)()(2)()(220x a a b a f b f x f a f +⋅---+=α记 c x =2 ,即证得(1).(2) 若 x x f cos )(= ,]2,0[],[π=b a此时由 ab a f b fc f --=')()()( 得:π2sin =c , )2sin(πarc c =,πα21-=πππα2)4(2120-+=2)/2sin(2ππarc ⋅+)4(212-+=πππππ)2sin(arc +. 误差估计:)()(10b f b f E -+=-=ααρ)4(212-+=πππ1)2sin(-+ππarc5.解:选取 α ,使得:=)(αI ||max 211x x x α-≤≤ ,达到极小,即要求 x x *)(*αϕ= ,于]1,0[上一致逼近于2x ,如图 应选*α ,使得: x x x *)(2αϕ-=,于 ]1,0[ 上有两个轮流为正负偏差点,其中之一为1,另一个假设为 ζ 于是: )()1(ζϕα-=,0)(='ζϕ , 〔 ζ为)(x ϕ的极值点〕 得: αζζα+-=-2102=-αζ解得:ζα2= ,0122=-+ζζ,212,1±-=ζ取 12-=ζ , 222-=α. 又: α 是唯一的.6.证明:由最佳一致逼近的特征定理,)(*x P n 为)(x f 的最佳一致逼近多项式,则存在2+n 个点b x x x a n ≤<<<≤+110使得: )()()(*k n k k x P x f x e -==*)1(n k P f --σ.又由于 ],[)(b a C x f ∈ ,于 ),(1+i i x x 中有一个点 i η ,1+<<i i i x x η ,使得: 0)()()(*=-=i n i i P f e ηηη,n i ,,1,0 =即: )(*x P n 为)(x f 满足插值条件: )()(*i i n f P ηη= , n i ,,1,0 =的插值多项式.7.解:求C*,使得:C x f C I bx a R C -=≤≤∈)(max min *)(记 C x f x e -=)()(, 依最佳一致逼近的特征定理:应取)](min )(max [21*],[],[x f x f C b a b a +=*)()(C x f x e -=于 ],[b a 才有两个轮流正负的偏差点,〔即 )(x f 于],[b a 上的最大值点和最小值点〕1x ,2x)(max )(],[1x f x f b a = , )(min )(],[2x f x f b a =此时: *)(max )1()(],[C x f x e b a ii --=σ即 *C 为)(x f 的零次最佳逼近多项式.8.解: 436)(23+++=x x x x f2)(34)3(62031T T T T +++=014T T ++01232112112323T T T T +++= 因为 )(413x T 与零偏差最小,故:012221121123)(T T T x P ++=421132++=x x .为)(x f 的最佳一致逼近多项式.9. 证明:我们仅证明)(x f 是偶函数时,)(x P n 亦是偶函数.由于)(x P n 为)(x f的最佳一致逼近多项式,有:)()()(max ],[f E x P x f n n a a =--和: [,max ()()()]n n a af x P x E f ----=即: )()()(max ],[f E x P x f n n a a =---)(x P n -亦是)(x f 的最佳一致逼近多项式,由最佳一致逼近多项式的惟一性,有: )()(x P x P n n =-即: )(x P n 为偶函数.11.解: 设 x a a x P 10*1)(+= , 2210*2)(x b x b b x P ++=分别为)(x f 的一次、二次最佳平方逼近多项式。
计算方法习题第二章答案

第一章 误差1 问3.142,3.141,722分别作为π的近似值各具有几位有效数字?分析 利用有效数字的概念可直接得出。
解 π=3.141 592 65…记x 1=3.142,x 2=3.141,x 3=722.由π- x 1=3.141 59…-3.142=-0.000 40…知3411110||1022x π--⨯<-≤⨯ 因而x 1具有4位有效数字。
由π- x 2=3.141 59…-3.141=-0.000 59…知2231021||1021--⨯≤-<⨯x π因而x 2具有3位有效数字。
由π-722=3.141 59 …-3.142 85…=-0.001 26…知231021|722|1021--⨯≤-<⨯π因而x 3具有3位有效数字。
2 已知近似数x*有两位有效数字,试求其相对误差限。
分析 本题显然应利用有效数字与相对误差的关系。
解 利用有效数字与相对误差的关系。
这里n=2,a 1是1到9之间的数字。
%5101211021|*||*||)(|1211*=⨯⨯≤⨯≤-=+-+-n ra x x x x ε3 已知近似数的相对误差限为0.3%,问x*至少有几位有效数字?分析 本题利用有效数字与相对误差的关系。
解 a 1是1到9间的数字。
1112*10)1(2110)19(21102110003%3.0)(--⨯+≤⨯+⨯=⨯<=a x r ε 设x*具有n 位有效数字,令-n+1=-1,则n=2,从而x*至少具有2位有效数字。
4 计算sin1.2,问要取几位有效数字才能保证相对误差限不大于0.01%。
分析 本题应利用有效数字与相对误差的关系。
解 设取n 位有效数字,由sin1.2=0.93…,故a 1=9。
411*10%01.01021|*||*||)(-+-=≤⨯≤-=n r a x x x x ε解不等式411101021-+-≤⨯n a 知取n=4即可满足要求。
计算方法各章习题及答案

第二章数值分析4^92.1 已知多项式通过下列点:1 3答案:q(x) = p(x) -r(x) X5X4X3-3X 1 .2 22.2观测得到二次多项式2的值:表中p2(x)的某一个函数值有错误,试找出并校正它.答案:函数值表中p2(-1)错误,应有p2(-1) = 0 .2.3利用差分的性质证明12■ 22■川,n2=n(n ■ 1)(2n ■ 1)/6.2.4当用等距节点的分段二次插值多项式在区间[-1,1]近似函数e x时,使用多少个节点能够保证误差不超过丄10-6.2答案:需要143个插值节点.2.5 设被插值函数f (x) • C4[a,b] , H3h)(x)是f (x)关于等距节点b — aa ^Xo :::捲:::川:::x n=b的分段三次艾尔米特插值多项式,步长h .试估计n ||f(x)-H3h)(x)||::.答案:||住)-出5)仪川:乞令人4.384第三章函数逼近3.1求f(x)二sinx,x,[0,0.1]在空间门=span{1,x, x2}上最佳平方逼近多项式,并给出平方误差.答案:f (x) =sin X的二次最佳平方逼近多项式为sin x p2(x) = -0.832 440 7 105 1.000 999 1x - 0.024 985 1x2,二次最佳平方逼近的平方误差为20.12 12■ = 0 (sinx) - P 2(x))2dx =0.989 310 7 10•3.2确定参数a,b 和c ,使得积分1 ---------------------------2 1 I (a,b,c)[ax 2 bx c -1 -x 2]dx 取最小值.J 1 — x 2810答案:a, b = 0, c =3 二3 二3.3 求多项式f (x) =2x 4 x 3 5x 2 1在[-1,1]上的3次最佳一致逼近多项式p(x)-答案:f (x)的最佳一致逼近多项式为p(x) = X ’ 7x2 3.43.4用幕级数缩合方法,求 f(x)=e x (―1兰XW1)上的3次近似多项式 p 6,3(x),并估计 || f(X )-P 6,3(X )II ::.答案:p5,3(x) =0.994 574 65 + 0.997 395 83x+0.542 968 75x 2 十 0.177 083 33x 3, || f (x) - p 6,3 (x) |^<0.006 572 327 71 一3.5 求f (x) -e x ( -1乞x 乞1)上的关于权函数「(X )-的三次最佳平方逼近小-x 2多项式 Q(x),并估计误差 || f(x)-$(x)||2 和 || f(x)-S 3(x) ||::.答案:§3(x) =0.994 571 0.997 308x 0.542 991x 20.177 347x 3,|| f (x) -S 3(x) ||2 = 0.006 894 83, || f (x) - §3(x)||严 0.006 442 575.第四章数值积分与数值微分14.1用梯形公式、辛浦生公式和柯特斯公式分别计算积分 X n dx (n -1,2,3,4),并与精确值比较.答案:计算结果如下表所示I 2 0. 5 0. 333 333 0. 250 000 0. 208 333 I 30. 5 0. 333 333 0. 250 000 0. 200 000 精确值0. 50. 333 3330. 250 0000. 200 0004.2 确定下列求积公式中的待定参数,使得求积公式的代数精度尽量高,并指明所确定的求积公式具有的代数精度.h(])仁 f (x)dx 止 A_i f (-h) + A f (0) + A f (h)11 (2)J(x)dx: 3【f(-1) 2f(X i ) 3f(X 2)]hh2⑴ of(x)dxVf(O) f(h)「h[f g f(h)]答案:(1)具有三次代数精确度 (2)具有二次代数精确度 (3)具有三次代数精确度. 4.3 设h = % - X 0,确定求积公式r (x - x o ) f (x)dx = h 1 2[ Af (x o ) + Bf (x i )] + h 3[C 「(x o ) + Df^)] + R[ f ]xo中的待定参数 A, B,C, D ,使得该求积公式的代数精确度尽量高,并给出余项表达式.37 1 if 4)(叮)6答案:A = —, B— ,C —, D — , R[f]=— _) h ,其中 (x o ,xi).202030 20 14404.4设P 2(x)是以0,h,2h 为插值点的f(x)的二次插值多项式,用F 2(x)导出计算积分3h3 4 5If (x)dx 的数值积分公式I h ,并用台劳展开法证明:I - l h h f (0) O(h ).力83h3答案:I h P 2(x)dx h[ f(0) 3f (2h)].0 4(3)取7个节点处的函数值.1sin x4.6用变步长的复化梯形公式和变步长的复化辛浦生公式计算积分Idx .要x1o 1«求用事后误差估计法时,截断误不超过10和 10 .1(1) 运用复化梯形公式计算上述积分值,使其截断误差不超过丄10」. 2(2) 取同样的求积节点,改用复化辛浦生公式计算时,截断误差是多少?(3) 要求的截断误差不超过10“ ,若用复化辛浦生公式,应取多少个节点处的函数值? 答案:(1)只需n — 7.5,取9个节点,I : 0.9464.5 给定积分I 二1sin xdx|R n [f]耳一孟宀皿盂日中0.271估2 2答案:使用复化梯形公式时,I T^ 0.946满足精度要求;使用复化辛浦生公式时,I s4 =0.946 083满足精度要求.4.7 ( 1 )利用埃尔米特插值公式推导带有导数值的求积公式1 323 1 3>5.2用矩阵的直接三角分解法解方程组 广1 0 2 0、「5、0 10 1 X 2312 4 3X 3仃10 1 0 3丿 g<7;答案: &=2 , x 3 = 2 , x 2 = 1, X| = 1 .ba f(x)dx 二 其中余项为b —a(b 「a)2[f(a)f(b)] — ' 丿[f (b)-f (a)] R[f], 2 12R[f]=U 54!30 f ( 4()),(a,b).其中(2)利用上述公式推导带修正项的复化梯形求积公式h 2 f(x)dx :T^—[ f (X N ) - f (x 。
黄云清版数值计算方法习题解答.docx

第一章引论(习题)2. 明 :f ( x)x ,xx * x x * xx x * 1E r ( f )xx( x x * )xx *x2E r( x) .3. 明:令:(a b)fl (a b)fl (a b)可估 : | fl (a b) |c 1( c a b ),故:| |1c t c 11 1 t22于是:fl ( a b) (a b) (1) .4.解 (1)2x 2 (1 x) (1 2x) .(2)2 x.( x 1 xx 1 x )1 cos xsin 2 xsin x .(3) xx(1 cos x)1 cos x6.解a 的相 差:由于| E( x) | x a1 10 3 . E r ( x)x a ,2xE r (x)1 102 1 10 2 . ( Th1)2 918f (a) 于 f (x) 的 差和相 差 .| E( f ) | | 1 x1 a |=a x 2110 3 =10 3x1 a2 0.251| E r ( f ) | 10 3 1 a 4 10 3 .9.解 推关系: y n 1 100.01 y ny n 1(1)取初y 01, y 10.01 算可得:y 2100.01 10 2 1 1.0001 1 10 4y 310 6 , y 4 10 8 , y 5 10 10, ⋯(2) 取初值 y 0 1 10 5 , y 1 10 2 ,记: ny ny n ,序列n,满足递推关系,且10 5 , 1 0 n 1100.01 nn 1 ,于是:210 5 ,3100.01 10 5 , 4 (100.01) 210 5 10 5 ,5(100.01)3 10 5 200.02 10 5 ,可见随着n 的主项(100.01)n 2 10 5 的增长,说明该递推关系式是不稳定的 .第二章 多项式插值 ( 习 题)1.方法一 . 由 Lagrange 插值公式L 3 ( x) f 0 l 0 ( x) f 1 l 1 (x) f 2 l 2 ( x) f 3 l 3 ( x)l 0 (x)x(x 21 )( x 1) 1 1 1) ,( 1)(23)( 2)x( x2 )( x3(x 1)( x21)( x 1)2(x 21)( x21) ,l 1 (x)12l 2 (x)(x !1) x( x 1)8 21) x , l 3 ( x 1)x( x21)13 1 13 ( x( x)1( x 1)x( x 2 ) .2 2( 2 )2 1 2可得:L 3 ( x)x 2 ( x 1 2)方法二 . 令: L 3 (x) x( x 1 2) (AxB)由 L 3 (1)31, L 3 (1), 定 A , B (称之为待定系数法)222.证明 (1) 由于l i ( x j )i , j 故: L n ( x)nx i k l i (x)x k j , j 0,1,i 0 ,当 x x j 时 有: L n ( x j ), nL n ( x) 也即为 x k 的插值多项式,由唯一性,有:nx i k l i (x)x k ,k0,1, , ni 0明 (2) :利用 Newton 插 多 式N n ( x) f (x 0 ) f [ x 0 , x 1 ] ( x x 0 )f [ x 0 , , x n ] ( x x 0 )(x x n 1 )f ( x)( x x 1 ) (x x n ) (x)(x 0 x 1 ) (x 0l 0x n )差商表:f(x)一二⋯n差商x 01x 11x 0 x 11( x 0x 2 ) ( x 0x 1 )x n1(x 0x 1 ) ( x 0 x n )代入 ( ) 式有: N n ( x)x x 0 (x x 0 ) ( x x n 1 )1( x 0 x 1 ) (x 0 x 2 ) ( x 0.x 0 x 1x n )l 0 ( x)n 次代数多 式,由插 多 式的唯一性:有l 0 ( x) N n (x) .4.解作 f ( x) 以 a, a , b 点的Lagrange 插 多 式,有:f ( x) L 2 ( x) R 2 (x) ,其中:L 2 ( x) ( x a) ( x b) f ( a) ( x a) (x b) f (a )( ) ( a b)( a b) ( x a) (x a )f (b) ,(b a) (b a)R 2 ( x)f ( )( x a) ( x a) ( x b) , ab3!f ( ) (x令:0 有 R 2 ( x)R( x)a) 2 ( x b) ,x a6a又: L 2 ( x)(b x) [f (a)x (a)(b (b fa)a )xa( x a)(b a f ( a)(bf (a)])a)( x a) ( x a )f (b)(b a) (b a)(b x) ( x b 2a) f (a)(b x) ( x a) f ( a)(b a) 2(b a)( x a)2f (b)P( x)(b a) 2故当0 时,成立公式: f (x)P(x)R( x) .5.解:因为 f ' ( x)4x33, f '' (x)12x 2f ( x) 为凹函数.又从数值表可见:当 x [0.1,0.5] 时, f (x) 单调下降.有反函数 x f 1 ( y)x 于0.3及0.4之间有一个根y i0.700100.401600.10810-0.17440-0.43750f 1 ( y i )0.10.20.30.40.5作差商表:y i f1 ( y i )一阶差商二阶差商三阶差商四阶差商0.700100.10.401600.2- 0.335000.108100.3- 0.340710.0096436-0.174400.4- 0.353980.02304- 0.01531- 0.437500.5- 0.380080.04784- 0.029230.01225 f1( y)的 Newton 插值多项式:N 4 ( y) 0.10.33500( y 0.70010)0.0096436 ( y0.70010)( y 0.40160)0.01531( y0.70010)( y0.40160 )( y 0.10810)0.01225( y0.70010)( y0.40160)( y0.10810)( y0.17440)x*N 4 (0)0.337.7.解 f (x) x7x 31.有:f [ 20 , 21 ,, 27 ]f ( 7) ()=1, f [ 20 , 21 , , 28 ] f (8) ( )0 .7!8!9.证明: (1)( f i g i ) f i1gi 1fi g ifi 1gi 1figi 1figi 1figif ig i gi 1f i.(3)n( 1x )( 1)n n! h nh)( x nh)x( x此题可利用数学归纳法:设 n k成立,证明n k 1 成立.又 n1时是成立的 . 10.证明:记: f (n)[n(n1) / 2]2, g(n)1323n3有: f (n)f ( n 1)f ( n) ( n 1)3n 1n 1故:g( n)f (k) [ f ( k 1)f (k)]k 0k 0f (n)f (0) [ n(n 1) / 2] 2 .13.解 作重节点差商的 Newton 插值公式P(x)f ( 1) f [ 1, 1] ( x 1) f [ 1, 1, 0] ( x1) 2f [ 1, 1, 0, 1] x(x 1) 2f [ 1, 1, 0, 1, 1] x( x 1) 2 ( x 1)重节点差商表:x if i一阶二阶三阶四阶x 0 1 1x 0 11 2x 1 0 1 0 -2x 2 1 1 0 0 1x 21 1221得 P( x) 12( x1) 2(x 1) 2 x(x 1) 2 x 3x 1 .17.证: 取 x 00,x 11 , x2 1 , h 122f 0 0 , f 1 1 ,f 21记:M is ( x i ), i0, 1, 2有x 1 x x x 01S 1 ( x) M 0hM 1h2M 0 (2x) 2M 1 xS 2 ( x) 2M 1 (1 x) 2M 2 ( x1 )2又三弯矩方程为: (f [ x 0 , x 1 , x 2 ]2 )M 0 4M 1M 224, M 11(24 M 0 M 2 ) .41 [ s ( x)] 2dx121[ s 2 ( x)] 2dx2分段积分:[ s 1 (x)] dx121 21 x)] 2dx1[ M 1 (1 x) M 2 (x1)] 2dx4M 0 (0 [ M 1 x 4 1 22211x)] 2 dx 11 )]2 dx 4 1 [ M 1 ( x2) M 0 (1 4 1 [ M 1 (1 x)M 2 (x2221 ( x 1 ) 2dx1 1(1 x) 2dx 1由于2 ,, 224 1 22411( x 1 ) (1 x)dx12,于是: 2 48112dx1[ M 02M 0 M 12M 12M 1 M 2 M 22 ](S (x))6又: M 11(24 M 0M 2 )4记I (M 0 , M 2 )1 (S (x)) 2dx= 1[ M 02M 221(24 M 0M 2 ) ( M 0 M 2 )641( 24M 0M 2 ) 2 ]8由I0 ,I0 .7M 0 M 2 0M 0 M 2 得:M 0 7M 2即当:M 0M 2 0 时,I ( M 0 , M 2 ) 达最小1( x)) 2dx 1 1 (24) 212 ,由最小模原理:故:( S6 81(x)] 2dx 12[ f .20.解利用三弯矩方法M i s ( x i ) , i 0, 1, 2x 0 1 , x 22 , x 232M 0 MM 0 4MM 1 2M161 M2 362 54解得:M 0 7 , M 1 20 , M 2 37x [1, 2]s 1 (x) 9 x 3 17x 2 43 x 72 2 x [ 2, 3]s 2 ( x)19 x 3 67x 2293 x105.22第三章 最佳逼近及其实现 ( 习 题)2.解 (1)( f , g )b (x) g ( x) dxc (a, b) 中的内积,f不是a事实上容易验证:( f , g ) (g,f ) , (f ,g )( f , g )( fg, w)( f , w)( g, w)但是( f , f ) 0 当且仅当f (x)0.条件不满足,因为:b( f , f )f ( x) f ( x)dx 0a推出 f ( x) 0 , f ( x) const 0. 因而 ( f , g ) 不是 C (a, b) 中的内积 . (2)( f , g) 是 C 01 [ a, b]f (x) : f (a)0, f (x) C [a, b]空间的内积,这是因为:( f , f ) 0 推出 f (x) 0 , f ( x) C ,又fC 01 [a, b] ,故 f (x) 0 .4.解:由于f c 2 [a, b], f ( x)0 ,则 f ( x) 于 [a, b] 上保号,由定理 5 的推论 2 可知: f (x) P 1 (x) 的交错点组恰有三个交错点,且 x 1a ,x 3b ,即:e( x 1 ) f (x 1 ) ( e( x 3 ) f (x 3 ) ( e( x 2 ) f (x 2 ) ( e ( x 2 ) f (x 2 )0 1x 1 ),1 x 3 ),1 f (x2 )f (b) f (a)1x 2 )故 :b ,0 ,a1f (a) f (x 2 )f (b) f (a) ax 2 记x 2 c ,即证得 (1).b a22(2) 若 f (x) cos x , [ a, b] [ 0,2]此时由f (b) f (a)f (c)得:b asin c2 , c arc sin( 2) , 12( 212 arc sin( 2 / )1 4) 22(22误差估计: E ( f )b f (b) 1(125.解:选取,使得:2 2arc sin( 2)4 ).arc sin(2)4)1I ( )max | x 2x | ,达到极小,1 x 1即要求 * (x)* x ,于 [ 0, 1] 上一致逼近于 x 2 ,如图应选* ,使得:( x)x 2* x ,于 [ 0, 1] 上有两个轮流为正负偏差点,其中之一为1,另一个假设为 于是: (1) () ,( )0 , (为 (x) 的极值点)得:122解得: 2,22 10 ,1, 212取2 1 ,2 2 2 . 又:是唯一的 .6.证明:由最佳一致逼近的特征定理, P n * ( x) 为 f ( x) 的最佳一致逼近多项式,则存在 n2 个点ax 0x 1x n 1 b使得: e( x k ) f (x k ) P n * ( x k ) = ( 1) kfP n * .又由于 f ( x)C[ a, b] ,于 ( x i , x i 1 ) 中有一个点i, x iix i 1 ,使得:e( i ) f ( i) P n * ( i )0 , i0, 1, , n即: P n *( x) 为 f (x) 满足插值条件:P n * ( i )f ( i ) , i 0, 1, , n的插值多项式 .7.解:求 C* ,使得:I (C*) min max f ( x) CC R a x b记e( x) f ( x) C , 依最佳一致逼近的特征定理:应取C*1[ max f (x) min f (x)]2[ a ,b][ a ,b]e(x) f (x) C *于 [a, b] 才有两个轮流正负的偏差点,(即f ( x) 于 [a, b] 上的最大值点和最小值点)x 1 , x 2f ( x 1 ) max f ( x) , f (x 2 )min f (x)[ a, b][ a, b]此时:e( x i ) ( 1) i max f (x)C *[ a, b]即 C * 为 f ( x) 的零次最佳逼近多项式 .8.解:f (x) 6 x 3 3x 2 x 46(3T 1T 3)43(T 0 T 2 ) 2T 1 4T 03311 112T32T22 T 12 T 0因为1T 3 (x) 与零偏差最小,故:4311 1111P 2 (x)3x2 x 42 T 22 T12 T2.为 f (x) 的最佳一致逼近多项式.9.证明:我们仅证明f (x) 是偶函数时, P n ( x) 亦是偶函数 .由于 P n ( x) 为 f ( x)的最佳一致逼近多项式,有:max f ( x) P n ( x)E n ( f )[ a,a ]和:max f ( x ) P n ( x ) E n ( f )[ a ,a ]即:max f ( x)P n ( x)E n ( f )[ a ,a ]P n ( x) 亦是 f ( x) 的最佳一致逼近多项式,由最佳一致逼近多项式的惟一性,有: P n ( x)P n ( x)即: P n ( x) 为偶函数 .11.解: 设P * ( x) a0 a x , P * ( x) bb x b x 21121 2分别为 f ( x) 的一次、二次最佳平方逼近多项式。
数值计算引论第2章答案

-1⎤ ⎡1 ⎢ 1 ⎥ ⎥ ,求 cond ∞ ( A) 3. 考虑 n 阶矩阵 A = ⎢ % ⎢ ⎥ ⎢ ⎥ 1⎦ ⎣
解:
1⎤ ⎡1 ⎢ 1 ⎥ ⎢ ⎥ A= % ⎥ ⎢ ⎢ ⎥ 1⎦ ⎣ A ∞ = max ∑ aij = 2
1≤i ≤ n j =1 n
故− (2)
1 < a <1 2
⎡ 0 −a −a ⎤ B = I − D A = ⎢ −a 0 −a ⎥ ⎢ ⎥ − − a a 0 ⎢ ⎥ ⎣ ⎦
−1
λ a a λI − B = a λ a = 0 a a λ λ
即
a
a
2
λ I − B = a λ a = ( λ − a ) ( λ + 2a ) = 0 a λ
λI − B = 1 λ
故 ρ ( B) = 0 < 1
λ
Jacobi 方法收敛
对于 Gauss-Seidel 方法
B = ( D − L)
−1
⎡0 −2 2 ⎤ U = ⎢0 2 −3⎥ ⎢ ⎥ ⎢ ⎣0 0 2 ⎥ ⎦
B 1 = 7 ,所以无法通过范数进行判断。
故计算其谱半径。
λ λI − B =
A−1
∞
= max ∑ aij = 2
1≤i ≤ n j =1
n
故: cond ∞ ( A) = 4
⎡ 2 −1 ⎤ ⎢ −1 2 −1 ⎥ ⎢ ⎥ ,试求 A 的 Cholesky 分解 4. 考虑矩阵 A = −1 2 −1⎥ ⎢ ⎢ ⎥ −1 2 ⎦ ⎣
解 A 分解成 A = LL
i −1
T
2 1/ 2 (1) lii = ( aii − ∑ lik ) k =1
数值方法(第2版)答案

C语言编程习题第二章习题2-25.用二分法编程求6x4 -40x2+9=0 的所有实根。
#include <stdio.h>#include <math.h>#define N 10000double A,B,C;double f(double x){return (A*x*x*x*x+B*x*x+C);}void BM(double a,double b,double eps1,double eps2){int k;double x,xe;double valuea = f(a);double valueb = f(b);if (valuea > 0 && valueb > 0 || valuea <0 && valueb < 0) return;printf("Finding root in the range: [%.3lf, %.3lf]\n", a, b);for(k=1;k<=N;k++) {x=(a+b)/2;xe=(b-a)/2;if(fabs(xe)<eps2 || fabs(f(x))<eps1) {printf("The x value is:%g\n",x);printf("f(x)=%g\n\n",f(x));return;}if(f(a)*f(x)<0) b=x;else a=x;}printf("No convergence!\n");}int main(){double a,b,eps1,eps2,step,start;printf("Please input A,B,C:\n");scanf("%lf %lf %lf",&A,&B,&C);printf("Please input a,b, step, eps1,eps2:\n");scanf("%lf %lf %lf %lf %lf",&a,&b,&step,&eps1,&eps2);for (start=a; (start+step) <= b; start += step) { double left = start;double right = start + step;BM(left, right, eps1, eps2);}return 0;}运行:Please input A,B,C:6 -40 9Please input a,b, step, eps1,eps2:-10 10 1 1e-5 1e-5Finding root in the range: [-3.000, -2.000]The x value is:-2.53643f(x)=-0.00124902Finding root in the range: [-1.000, 0.000]The x value is:-0.482857f(x)=0.00012967Finding root in the range: [0.000, 1.000]The x value is:0.482857f(x)=0.00012967Finding root in the range: [2.000, 3.000]The x value is:2.53643f(x)=-0.00124902有时若把判别语句if(fabs(xe)<eps2 || fabs(f(x))<eps1)改为if(fabs(xe)<eps2 && fabs(f(x))<eps1)会提高精度,对同一题运行结果:Finding root in the range: [-3.000, -2.000]The x value is:-2.53644f(x)=-4.26496e-007Finding root in the range: [-1.000, 0.000]The x value is:-0.482861f(x)=-7.3797e-006Finding root in the range: [0.000, 1.000]The x value is:0.482861f(x)=-7.3797e-006Finding root in the range: [2.000, 3.000]The x value is:2.53644f(x)=-4.26496e-007习题2-35. 请用埃特金方法编程求出x=tgx在4.5(弧度)附近的根。
“数值计算方法”习题解答

“数值计算方法”习题解答配套教材:数值分析简明教程,王能超 编著,高等教育出版社,第二版第二章 数值积分2.1 机械求积和插值求积1、(p.94,习题3)确定下列求积公式中的待定参数,使其代数精度尽量高,并指明求积公式所具有的代数精度: ⎰-++-≈hhh f A f A h f A dx x f )()0()()()1(210;⎰++≈10210)43()21()41()()2(f A f A f A dx x f ;⎰+≈1000)()0(41)()3(x f A f dx x f 。
【解】 (1)令2,,1)(x x x f =时等式精确成立,可列出如下方程组:⎪⎪⎩⎪⎪⎨⎧=+=+-=++)3(32)2(0)1(22020210h A A A A h A A A解得:h A h A A 34,3120===,即:⎰-++-≈h h h f f h f hdx x f )]()0(4)([3)(,可以验证,对3)(x x f =公式亦成立,而对4)(x x f =不成立,故公式(1)具有3次代数精度。
(2)令2,,1)(x x x f =时等式精确成立,可列出如下方程组:⎪⎩⎪⎨⎧=++=++=++)3(1627123)2(232)1(1210210210A A A A A A A A A解得:31,32120-===A A A ,即:])43(2)21()41(2[31)(10⎰+-≈f f f dx x f ,可以验证,对3)(x x f =公式亦成立,而对4)(x x f =不成立,故公式(2)具有3次代数精度。
(3)令x x f ,1)(=时等式精确成立,可解得:⎪⎩⎪⎨⎧==324300x A即:⎰+≈1)32(43)0(41)(f f dx x f ,可以验证,对2)(x x f =公式亦成立,而对3)(x x f =不成立,故公式(3)具有2次代数精度。
2、(p.95,习题6)给定求积节点,43,4110==x x 试构造计算积分⎰=10)(dx x f I 的插值型求积公式,并指明该求积公式的代数精度。
数值计算方法(山东联盟)知到章节答案智慧树2023年中国石油大学(华东)

数值计算方法(山东联盟)知到章节测试答案智慧树2023年最新中国石油大学(华东)第一章测试1.数值计算方法研究的误差有()参考答案:截断误差;;舍入误差.2.参考答案:只有模型误差、观测误差与舍入误差;3.参考答案:4位4.对于下列表达式,用浮点数运算,精度较高是参考答案:5.参考答案:第二章测试1.参考答案:0.56252.参考答案:;3.关于Steffensen(斯蒂芬森)迭代方法,下列命题中正确的是:参考答案:Steffensen迭代法使得某些发散的迭代格式变为收敛。
;Steffensen迭代法使得某些收敛的迭代格式加速收敛。
4.关于Newton迭代法,下列命题中正确的是:参考答案:;Newton迭代格式可能收敛也可能发散。
5.参考答案:6第三章测试1.算法的计算量与近似成正比。
2.列主元Gauss消去法与Gauss顺序消元法相比,优点是:参考答案:提高了稳定性,减少了误差的影响。
3.参考答案:平方根法与Gauss列主元消去法相比,提高了稳定性,但增加了计算量。
;只要是对称正定矩阵,就可用平方根法求解。
4.参考答案:;5.;第四章测试1.给定n+1个互异的插值节点,求插值多项式。
下列命题中正确的是:参考答案:若要求插值多项式的次数等于n,则用不同方法求出的插值多项式是相等的。
;若要求插值多项式的次数小于n,则插值多项式可能不唯一。
2.关于插值多项式对被插值函数的逼近效果,正确的命题是:参考答案:插值点靠近所有插值节点时,插值余项的绝对值较小。
3.关于差商,下列命题中正确的命题是:参考答案:;4.关于多项式插值的Runge现象,下列命题中正确的命题是:参考答案:采用分段低次多项式插值可以避免Runge现象。
;用三次样条函数插值可以避免Runge现象。
5.关于三次样条函数,下列命题中正确的命题是:参考答案:三次样条函数是连续函数。
;三次样条函数具有连续导数。
;三次样条函数具有连续的2阶导数。
第五章测试1.用正交多项式求一个函数的最佳平方逼近多项式的主要优点是节省计算量。
计算机数值方法习题解答
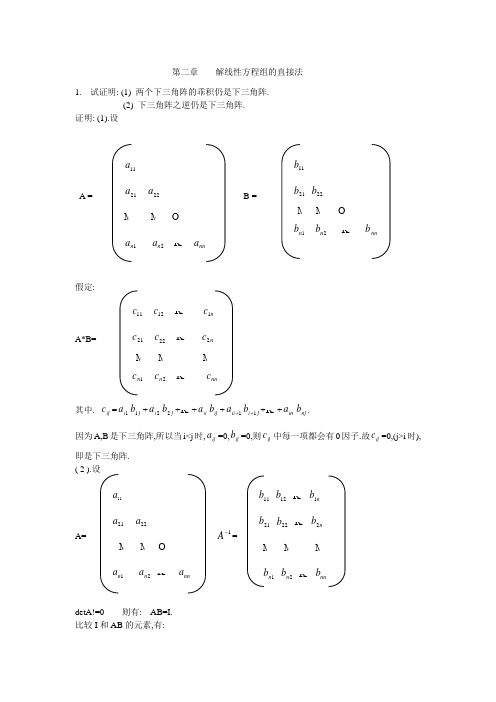
第二章 解线性方程组的直接法1. 试证明: (1) 两个下三角阵的乖积仍是下三角阵. (2) 下三角阵之逆仍是下三角阵. 证明: (1).设A =B =假定:A*B=其中.ij c =1i a j b 1+2i a j b 2+K +ii a ij b +1+ii a j i b 1++K +in a nj b .因为A,B 是下三角阵,所以当i<j 时,ij a =0,ij b =0,则ij c 中每一项都会有0因子.故ij c =0,(j>i 时),即是下三角阵.( 2 ).设A=1-A =detA!=0 则有: AB=I. 比较I 和AB 的元素,有:11a21a 22aMM O 1n a 2n a K nn a11b21b 22bM M O1n b 2n b K nn b11c 12c K n c 1 21c 22c K n c 2 M M M1n c 2n c K nn c 11a 21a 22aM M O 1n a 2n a K nn a 11b 12b K n b 1 21b 22b K n b 2MMM 1n b 2n b K nn b1=n b a b a b a b a 1111311121111110,,0,0,===K K 因为detA!=0, 可得0!,,0!,0!2211===nn a a a K 所以.0,,0,011312===n b b b K 依此类推下去,对其它行,当i<j 时,都是0=ij b . 故B 是下三角阵.2. 用Gauss 消去法求解方程组. 1x + 2x -44x =1 -1x + 2x + 3x +34x =-2 1x +32x +53x -44x =-4 2x -4x =-2 解: 消元过程:回代过程可得:4x =0,3x =-1,2x =0,1x =1.1 1 0 -4 1 -1 1 1 3 -2 13 5 -4 -4 0 1 2 -1 -2 1 1 0 -4 1 0 2 1 -1 -1 0 25 0 -5 0 1 2 -1 -21 1 0 -4 1 02 1 -1 -1 0 0 4 1 -4 0 0 1.5 0.5 -1.5 1 1 0 -4 1 0 2 1 -1 -1 0 0 4 1 -4 0 0 0 0.125 03.试写Gauss 消去法的算法:解: Gauss 消去法算法分为消元过程和回代过程,其中: 对k=1,2,K ,n-1 i=k+1,k+2,K ,n n x =n b /nn a消 ik m =ik a /kk a 回对i=n-1,n-2,K ,1 元 j=k+1,k+2,K ,n代i x =(i b -∑ijaxj)/ii a过 ij a =ija -ik m kj a 程 i b=i b -ik m k b4,用Gauss 列主元素消去法解方程组.=解:1 2 1 -2 -1 2 5 3 -2 3 2 5 3 -2 3 0 3 6 3 18 -2 -2 3 5 15 0 -0.5 -0.5 -1 -2.5 1 3 2 5 9 0 0.5 0.5 6 7.5 2 5 3 -2 3 交换1,2行 2 5 3 -2 3 1 2 1 -2 -1 Gauss 消去 0 3 6 3 18 -2 -2 3 5 15 一步 0 0 0.5 -0.5 0.5 1 3 2 5 9 0 0 -0.5 5.5 4.5 2 5 3 -2 3 2 5 3 -2 3 0 -0.5 -0.5 -1 -2.5 交换2,3行. 0 3 6 3 18 0 3 6 3 18 Gauss 消去一步 0 0 0.5 -0.5 0.5 0 0.5 0.5 6 7.5 0 0 0 5 5 回代求解得:.3,1,2,11234-====x x x x1 2 1 -2 2 5 3 -2 -2 -2 3 5 1 3 2 5 4321x x x x-13 15 95.某一装置运动轨迹为一圆锥曲线2x +bxy+c 2y +dx+ey+f=0在运动轨上测得5个不同点:1c :(14.38,3.94),2c :(11.38,2.79),)59.2,81.8(:),11.5,38.6(:),07.3,42.7(:543c c c 试写出b,c,d,e,f 所满足的方程,并用列主元素消去法求出b,c,d,e,f 的近似值. 解:依题义得方程组: 祥见教材第270页.6.设A=n n ij a *)(是实对称阵,且ii a !=0.经过Gauss 消去法一步后,A 约化为 .其中,是阶方阵.证明是对称阵. 证明:A== ;而=11aα0 2A11a 12a 13a K n a 121a 22a 23a K n a 231a 32a 33a K n a 3 M M M1n a 2n a 3n a K a 11a 12a 13a K n a 10 )2(22a )2(23a K )2(2n aMM M M 0 )2(2n a )2(3n a K )2(nn a11a α0 2A1-1121a a1 M O -11a a nnK 1 11a 12a K n a 121a 22a K n a 2M M M1n a 2n a K nn a=其中:1111)2(a a a a a j i ij ij -=,i,j=2,3,K ,n.A=T A ,ji ij a a =,i,j=1,2,K ,n..,,3,2,,)2(11111111)2(n j i a a a a a a a a a aji j i ji j i ij ijK ==-=-=亦得证2A 是对称的. 7.证明: (1) k L =的逆阵:(2)11a 12a K n a 10 11122122a a a a -K 111212a a a a n n - M M M 0 111212a a a a n n -K 1111a aa a n n nn - 1 O1k k l ,1+- 1 M O k n l ,- k1 O1k k l ,1+ 1MO nk l 1121l 131l 32l 1 M O1n l 2n l 3n l K 1=----111211n L L L K证明:(1)直接验证I L L k k =-1.=-1k k L L= I.(2).用有限归纳法证明:I n L L L L L L n n )2(111211111211--+++=--------K K .1),当k=2时.=--1211L L==I L L )12(1211-++--2),假若k=m 时成立,要让k=m+1时成立mIL L L L L m mI mL L L L L m L L L L L L L I m L L L L L L L I m L L L L L L m m m m m m m m m m m m m m m m +++++=---++++=--+++=--+++=--+++=------+-+----+-+--+--+--+----+---------1111211111112111111111121111111121111112111121111211)1()1(])1([)1(ΛK K K K K K .所以结论成立.8设nn a A ij )(=实方阵,若对i=1,2,K n.∑==>nij j ijii aa !1成立,则称A(行)严格对角占优.试证明:若严格对角占优,则A 非奇异.1 O1k k l ,1+- 1M O k n l ,- 11 O 1k k l ,1+ 1M Ok n l , 11 21l 1 31l 0 1M M O1n l 0 K 111 32l 1MO 2n l 1121l 1 31l 32l 1M M O1n l2n l证明:A 严格对角占优,所以0211>=>∑=nj ijaaGauss 消去一步得:, 且有严格对角化.n i a a a a a a a a nij j i ij j i ii ,,3,2.,2!11111111K =->-∑= 1111,2!111,2!,2!1111,2!,2!1111?a a a a a a a a a a a a a aj i nij j nij ijnij j i nij ij ni j j i ij-+=+≤-∑∑∑∑∑=====111111111111,1!1111,2!?a a a a a a a a a a a a a a a a j i ii j i ii j i nij ij j i nij ij -≤-<-=-+<∑∑==由2A 严格对角占优0!)2(22=a ,Gauss 消去法一步类似的证3A 严格对角优化.0!)3(33=a 仿此做下去可推得:0!)(=n nn a 又由0!det )()3(33)2(2211==n nn a a a a A K 亦得证A 严格对角占优.则非奇异9.设Ax= b,其中.A=b=用Dollitle 方法解此方程组.解:先求A=LU 分解,由Dolittle 分解算法.L= U== 得y=11a α 0 2A5 7 9 106 8 10 97 1089 5 7 6 5 2618 22 911.2 11.4 -0.5 11 0 0.6 15 7 9 10-0.4 -0.8 -3 -5 -6.5 -1.111.2 1 1.4-0.5 11 0 0.6 1 4321y y y y 26 18 22 926 -13.2 -21 -4.4=得x=10.用追赶法解三对角方程组AX=F,其中:A= ,F=解:先求三角分解:=由公式(6.6),(6.8)解得i i i y ,,βα)3,2,1()4,3,2(,)4,3,2(111===-====-i c i a b b i a ii i i i i i i i αββααγ (6.6)(6.8)i i α i β i γ 1 2 1/2 -3/2 2 7/2 2/7 15/7 3 26/7 7/26 83/26 4 45/25 -35 7 9 10-0.4 -0.8 -3-5 -6.5 -1.1 4321x x x x 26 -13.2 -21 -4.4 -8 5 -1 42 1 0 0 1 4 1 0 0 1 4 1 0 0 1 2 -3 6 14 -2 1b 1c 2a 2b 2c 3a 3b 3c 4a 4b1α 2γ 2α3γ 3α4λ 4α1 1β1 2β 1 3β 1)4,3,2(1111=-==-i y a f y f y ii i i i αα再公式(6.10)44y x =1+-=i i i i x y x β i=3,2,1 (6.10)得到: 2,1,4,31234-===-=x x x x。
数值计算方法课后习题答案(李庆扬等)

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
数值计算方法课后习题答案吕同富

数值计算方法课后习题答案吕同富【篇一:《数值计算方法》(二)课程教学大纲】txt>课程编号: l124008课程类别:专业必修学分数: 3 学时数:48 适用专业:信息与计算科学应修(先修)课程:数学分析、高等代数一、本课程的地位和作用数值分析(二)为数值分析课程的第二部分,它是信息与计算科学专业的一门专业必修课。
主要内容包括函数最佳逼近、数值积分、数值微分、常微分方程数值解法。
通过本课程的学习,学生将初步具备用计算机去有效地解决实际问题的能力。
二、本课程的教学目标通过本课程的学习,使学生了解和掌握求解函数最佳逼近、数值积分、数值微分、常微分方程等问题所涉及的各种常用的数值计算方法、数值方法的构造原理及适用范围。
本课程坚持理论与实践教学并重的原则,理论上主要讲述求解函数最佳逼近、数值积分、数值微分、常微分方程等问题的基本理论和基本方法。
与此同时,通过上机实验加深学生对各种计算方法的理解,为今后用计算机去有效地解决实际问题打下基础。
三、课程内容和基本要求(“*”记号标记难点内容,“▽”记号标记重点内容,“▽*”记号标记既是重点又是难点的内容)第六章函数最佳逼近 1.教学基本要求(1)理解:几类常用的正交多项式。
(2)掌握:最佳一致逼近和最佳平方逼近。
(3)掌握:曲线拟合的最小二乘法。
2.教学内容(1)*正交多项式。
(2)▽*最佳一致逼近。
(3)▽最佳平方逼近。
(4)正交多项式的逼近性质。
(5)▽曲线拟合的最小二乘法。
第七章数值积分 1.教学基本要求(1)理解:机械求积公式的基本思想、插值型求积公式的特点。
(2)掌握:newton-cotes求积公式、复合求积公式。
(3)掌握:romberg求积公式、gauss求积公式。
2.教学内容(1)*机械求积公式。
(2)▽newton-cotes求积公式。
(3)▽复合求积公式。
(4)变步长求积公式。
(5)▽romberg求积公式。
(6)▽*gauss求积公式第八章数值微分 1.教学基本要求(1)了解:数值微分的中点法。
数值计算方法课后习题答案

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
第二章 自测题答案

陈以平编写
第二章 自测题答案
1. 设 f ( x ) 可微,则求解方程 x f ( x ) 的牛顿迭代格式是_________________. 答案: x n 1 x n
xn f ( xn ) 1 f ( x n )
2. 用二分法求非线性方程 f (x)=0 在区间(a,b)内的根, 则二分 n 次后的误差限为_______. 答案:
3) 因 ( x ) 1 e x , ( x ) e x 当 x [1,2] 时, ( x ) [ ( 2), (1)] [1,2] ,且 | ( x ) | e 1 1 所以迭代格式 xk 1 ( x k ) ( k 0,1,2,) 对任意 x0 [1,2] 均收敛. 12. 试构造迭代收敛的公式求解下列方程: cos x sin x ; (2) x 4 2 x . (1) x 4 cos xk sin xk 解: (1)迭代公式 xk 1 4 cos x sin x sin x cos x 2 1 因 ( x) , ( x ) 1 ,故公式收敛. 4 4 4 2 x (2)设 f ( x) x 4 2 , 则 f (1) 0, f (2) 0, 故有根区间为[1,2]. x x 因 ( x) 4 2 , ( x) 2 ln 2 2 ln 2 1.36829 1 故不能用 xk1 4 2 k 来迭代求解. 若将原方程改写为 x ln(4 x) / ln 2, 此时 ( x) ln(4 x) / ln 2, 1 1 1 1 1 ( x) 1 4 x ln 2 4 2 ln 2 2 ln 2 ln(4 xk ) 故可用迭代公式 xk 1 来求解 ln 2
(仅供参考)数值分析课后第二章习题解答

6第二章 习题解答一、习题解答1 用二分法求解下列方程,要求误差不超过10-5 (1)x – ln x=2 在区间[2,4]内的根;(2)x e x– 1 = 0 在区间[0,1]内的根;(3)x 3 + 4x 2– 10 = 0 在区间[1,2]内的根。
解:(1)x 18 = 3.14618。
二分法程序2-1a=2;b=4;k=0;f=inline('x-log(x)-2'); ya=f(a);while (b-a)>0.00001x0=.5*(a+b);y0=f(x0); if ya*y0<0 b=x0; elsea=x0;ya=y0; end k=k+1; endformat long disp([x0,k])(2) x 17 = 0.567146。
(利用上面程序修改前两行) (3) x 17 = 1.365226。
2 证明方程 1 – x – sin x = 0 在区间[0,1]上有一根。
使用二分法求误差不大于41021−×的根需二分多少次?证明 令f (x ) = 1 – x – sin x ,则f (0) = 1,f (1)= – sin 1。
于是 f (0) f (1)< 0,故所给方程在区间[0,1]上必有根。
又因为x x f cos 1)(−−=′ 所以,函数 f (x ) 在区间[0,1]内单减。
故,方程在区间[0,1]内只有一个根。
利用二分法收敛定理,由411021201−+×≤−n 得 2n ≥ 104,所以二分法求根至少需14次二分计算能满足误差要求。
3 比较以下两种方法求 e x+ 10 x – 2 =0 的根到三位小数所需要的计算量。
(1) 在区间[0,1]内用二分法;(2) 用迭代法)2(1011n x n e x −=+,取初值 x 0 = 0。
解:(1)二分法迭代11次,x 11 = 0.090。
(利用第1题程序修改前两行) (2)不动点迭代5次,x 5 = 0.0905。
