圆周运动和能量
圆周运动与能量的综合问题 专题卷(全国通用)
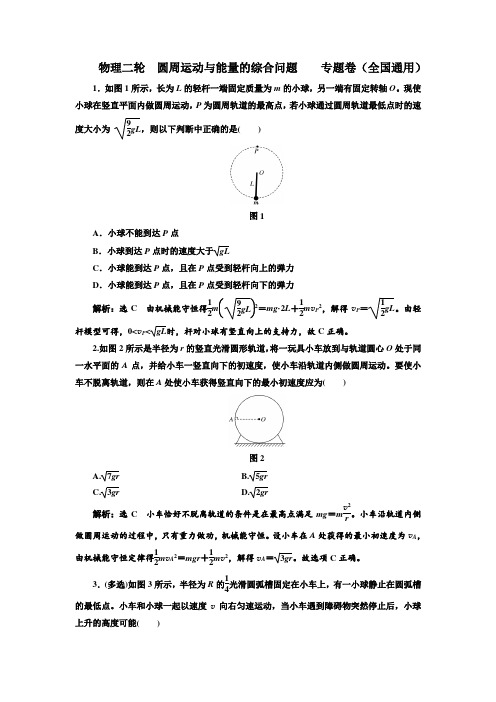
物理二轮 圆周运动与能量的综合问题 专题卷(全国通用)1.如图1所示,长为L 的轻杆一端固定质量为m 的小球,另一端有固定转轴O 。
现使小球在竖直平面内做圆周运动,P 为圆周轨道的最高点,若小球通过圆周轨道最低点时的速度大小为92gL ,则以下判断中正确的是( )图1A .小球不能到达P 点B .小球到达P 点时的速度大于gLC .小球能到达P 点,且在P 点受到轻杆向上的弹力D .小球能到达P 点,且在P 点受到轻杆向下的弹力 解析:选C 由机械能守恒得12m ⎝⎛⎭⎫92gL 2=mg ·2L +12m v P 2,解得v P =12gL 。
由轻杆模型可得,0<v P <gL 时,杆对小球有竖直向上的支持力,故C 正确。
2.如图2所示是半径为r 的竖直光滑圆形轨道,将一玩具小车放到与轨道圆心O 处于同一水平面的A 点,并给小车一竖直向下的初速度,使小车沿轨道内侧做圆周运动。
要使小车不脱离轨道,则在A 处使小车获得竖直向下的最小初速度应为( )图2A.7grB.5grC.3grD.2gr解析:选C 小车恰好不脱离轨道的条件是在最高点满足mg =m v 2r 。
小车沿轨道内侧做圆周运动的过程中,只有重力做功,机械能守恒。
设小车在A 处获得的最小初速度为v A ,由机械能守恒定律得12m v A 2=mgr +12m v 2,解得v A =3gr 。
故选项C 正确。
3.(多选)如图3所示,半径为R 的14光滑圆弧槽固定在小车上,有一小球静止在圆弧槽的最低点。
小车和小球一起以速度v 向右匀速运动,当小车遇到障碍物突然停止后,小球上升的高度可能( )图3A .等于v 22gB .大于v 22gC .小于v 22gD .与小车的速度v 无关解析:选AC 设小球的质量为m ,上升的高度为h 。
如果v 较小,小车停止运动后, 小球还没有脱离圆弧槽,则根据机械能守恒定律有12m v 2=mgh ,可得h =v 22g ,选项A 正确;如果v 较大,小车停止运动后,小球能够跑出圆弧槽,那么小球出了圆弧槽后将做斜抛运动,当小球到达最高点时,其还有水平方向上的速度,所以12m v 2>mgh ,可得h <v 22g ,选项C 正确。
圆周运动的概念

圆周运动的概念
圆周运动是表示物体以一定速度沿同心圆方向运动的物理运动
形式,圆周运动发生的场景很多,比如,星球的公转椭圆轨道运动、风速表的旋转、齿轮传动、摩擦轮、车轮滚动等等,都属于圆周运动。
圆周运动受力分析
圆周运动的受力分析,依赖两个受力,分别为:内力与外力。
内力是受体与其质心之间的力,其大小取决于受体的质量,存在于受体运动的每一点上,从而保证受体能够沿圆周维持稳定运动;外力是受体与他的外界环境之间的力,其大小取决于外界的摩擦力、重力等因素,存在于受体运动的每一点上,从而保证受体受到外界因素的制约而运动。
圆周运动的能量分析
圆周运动的能量分析,属于机械系统的能量分析,分析主要涉及动能、摩擦能、流体动能和重力轨道能,其中,动能是指圆周运动受体的动量乘以相对速度;摩擦能是指圆周运动受体与其外界环境之间的摩擦力所产生的能量;流体动能是指圆周运动受体与流体之间所产生的流体动能;而重力轨道能是指圆周运动受体所受到的重力在圆周运动方向上的分量所产生的能量。
圆周运动的特点
圆周运动的特点是,圆周运动受力体站在同心圆上时,受力体的动量沿圆周方向不变,也就是说受力体的动量永远垂直于受力体与其质心之间的虚线,因此,受力体沿着圆周维持稳定运动;另外,受力
体的运动速度与其质量以及外界的摩擦力之间存在一定的关系,受体的运动速度越大,外界的摩擦力也越大,从而保证受力体沿着圆周维持稳定运动。
匀速圆周运动物理教案:揭示圆周运动中动能和角动量的变化。

引言:在经典力学中,圆周运动是一种常见的运动形式,它不仅在自然界中广泛存在,而且在工业、交通等领域中也有着重要的应用。
匀速圆周运动是圆周运动中最简单的一种,其动能和角动量的变化规律十分有趣,本文将重点分析并揭示这一规律。
一、匀速圆周运动的基本概念和公式匀速圆周运动是指保持恒定角速度的圆周运动,它的基本概念和公式如下:1.概念(1)圆周运动:一个物体沿着一个确定轨迹做圆周运动,称为圆周运动。
(2)角度:以圆心为顶点的两条射线所夹的角度称为圆心角,记为θ(单位为弧度)。
(3)圆周位移:一个物体在圆周上运动一周所经过的路程称为圆周位移,记为L(单位为米)。
(4)角速度:单位时间内圆心角的转动速度称为角速度,记为ω(单位为弧度/秒)。
2.公式(1)角速度的定义式:ω = Δθ / Δt(2)圆周位移的定义式:L = rθ(3)速度的公式:v = ωr(4)周期T的公式:T = 2π / ω(5)向心加速度a的公式:a = v² / r = ω²r二、匀速圆周运动的动能和角动量匀速圆周运动的动能和角动量是随时间而变化的,下面我们分别来分析它们的变化规律。
1.动能的变化规律圆周运动时,一个物体所具有的动能包括轨迹上的动能和转动动能两个部分,其中,轨迹上的动能与物体在圆周上匀速运动的速度有关,而转动动能则与物体沿圆周运动时顺时针方向自转的角速度相联系。
因此,动能的总量为:K = Kt + Kr = 1/2mv² + 1/2Iω²其中,Kt为轨迹上的动能,Kr为转动动能,m为物体的质量,v为其速度,I为物体的转动惯量,ω为其角速度。
由于匀速圆周运动中,物体的角速度和速度保持不变,在考虑一定的时间间隔内动能的变化时,可以得到以下结论:(1)轨迹上的动能Kt不变;(2)转动动能Kr随时间t而增加。
这一结论可以通过下面的分析予以证明。
(1)轨迹上的动能不变圆周运动时,一个物体的速度v为常量,因此,轨迹上的动能很容易计算,为Kt =1/2mv²。
动能定理与圆周运动

动能定理与圆周运动一、动能的表达式1.定义:物体由于运动而具有的能量。
2.表达式:E=mv*v/23.单位:与功的单位相同,国际单位为焦耳。
1J=lkgm/s*s4.物理量特点(1)具有瞬时性,是状态量。
(2)具有相对性,选取不同的参考系,同一物体的动能一般不同,通常是指物体相对于地面的动能。
(3)是标量,没有方向,≥0。
5.对动能的理解(1)动能是标量,没有负值,与物体的速度方向无关。
(2)动能是状态量,具有瞬时性,与物体的运动状态(或某一时刻的速度)相对应。
(3)动能具有相对性,选取不同的参考系,物体的速度不同,动能也不同,一般以地面为参考系。
6.动能变化量物体动能的变化量是末动能与初动能之差。
二、动能定理1.动能定理的内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化。
2.动能定理的表达式(1)W=Ek1-Ek2说明:式中W为合外力做的功,它等于各力做功的代数和。
(物理意义:动能定理指出了合外力对物体所做的总功与物体动能变化之间的关系即若合外力做正功,物体的动能增加,若合外力做负功,物体的动能减小,做了多少功,动能就变化多少。
)(2)实质:动能定理从能量变化的角度反映了力改变运动的状态时,在空间上的累积效果。
3.动能定理的适用范围:不仅适用于恒力做功和直线运动,也适用于变力做功和曲线运动情况。
三、圆周运动1.圆周运动圆周运动是曲线运动的一种,也是我们高中阶段的一种重要的运动,圆周运动就是轨迹为圆的一种运动,那么这就意味着对于一个圆周运动来说,它的速度是不断地变化的,不管它的大小有没有发生改变,只要是方向发生改变,它的速度就发生了改变,因为速度是一个矢量。
这个点以后再说,圆周运动分为两种匀速圆周运动,和变速圆周运动,其中匀速圆周运动的意思是圆周运动的速率没有发生改变,并不是速度没有发生改变,所以匀速圆周运动的全称是匀速率圆周运动。
2.向心力在匀速圆周运动的实践和探索中,人们发现了一点,就是做匀速圆周运动的物体会受到一个始终和速度方向垂直的力。
匀速圆周运动势能变化

匀速圆周运动势能变化
匀速圆周运动是指物体在圆周运动中,角速度保持恒定,速度大小也保持恒定的运动。
在匀速圆周运动中,物体的势能是不发生变化的。
势能是指物体由于位置而具有的能量。
在圆周运动中,物体的位置一直保持在同一位置,因此没有势能的变化。
这是因为势能的计算公式为mgh,其中m为物体的质量,g为重力加速度,h为物体的高度。
在圆周运动中,物体的高度保持不变,因此势能也不会发生变化。
在匀速圆周运动中,物体的动能是不断发生变化的。
动能是指物体由于运动而具有的能量。
在圆周运动中,物体的速度大小保持恒定,但是方向不断变化,因此物体的动能会不断发生变化。
当物体在圆周运动中沿着圆周的方向运动时,动能最大。
这是因为物体的速度与圆周方向的夹角为0度,即物体的速度与圆周的切线方向重合,此时动能达到最大值。
当物体在圆周运动中沿着圆周的半径方向运动时,动能最小。
这是因为物体的速度与圆周方向的夹角为90度,即物体的速度与圆周的切线方向垂直,此时动能达到最小值。
在匀速圆周运动中,物体的总机械能保持不变。
机械能是指物体的动能和势能的总和。
由于势能不发生变化,因此物体的动能发生变化时,机械能的变化量与动能的变化量相等且反向。
这意味着当动能增加时,势能减少;当动能减少时,势能增加,从而保持总机械能的恒定。
在匀速圆周运动中,物体的势能保持不变,而动能会不断发生变化。
总机械能保持恒定,动能的变化与势能的变化相互抵消,从而保持总机械能的平衡。
物理圆周运动公式

物理圆周运动公式圆周运动的描述常用到以下几个关键的物理量和公式:1.角度和弧度圆周运动的第一个重要概念是角度和弧度。
角度用度(°)来表示,而弧度用弧长和半径的比值来表示。
1弧度等于圆的一部分的弧长等于半径。
即1弧度=57.3°。
2.角速度和角频率角速度(ω)是物体单位时间内所旋转的角度。
它可以通过角位移(θ)除以时间(t)得到。
即ω=θ/t。
角速度的单位是弧度/秒。
角频率(ν)是角速度的单位是弧度/秒的倒数。
即ν=1/ω。
3.周期和频率周期(T)是圆周运动完成一次的时间。
频率(f)是单位时间内完成的圆周运动的次数。
周期和频率是互相倒数的关系。
即f=1/T。
4.线速度和线速度公式线速度(v)是物体沿着轨迹运动的速度。
在圆周运动中,物体的线速度等于物体在围绕轴旋转的角速度乘以物体离轴的距离(r)。
线速度公式可以表示为:v=rω其中,v为线速度,r为物体离轴的距离(半径),ω为物体围绕轴旋转的角速度。
5.向心力和向心加速度向心力是使物体在圆周运动过程中朝向轴心的力。
它的大小为物体的质量(m)乘以线速度的平方(v^2)除以物体的离轴的距离(r)。
即Fc = mv^2/r。
向心加速度(ac)是物体在圆周运动过程中沿着轨迹心向轴心方向的加速度。
向心加速度可以表示为ac = v^2/r,也可以表示为ac = rω^2,其中v为线速度,r为物体离轴的距离,ω为角速度。
6.圆周运动的力学能量在圆周运动中,物体具有动能和势能。
动能(KE)是物体因为运动而具有的能量,可以表示为KE=1/2 mv^2、势能(PE)是物体因为位置而具有的能量,可以表示为PE = mgh。
综合考虑,圆周运动的总能量(E)等于动能和势能之和。
即E = KE + PE = 1/2 mv^2 + mgh。
以上就是一些物理圆周运动的基本概念和公式。
通过这些公式,我们可以更好地理解和描述物体在围绕轴旋转时的运动规律。
圆周运动动能定理公式

圆周运动动能定理公式1. 认识圆周运动说到圆周运动,大家可能会想起过山车、摩天轮,甚至是那些在广场上转圈的小朋友。
想象一下,坐在过山车上,心跳加速,四周风驰电掣,真是刺激得让人尖叫啊!圆周运动其实就是物体沿着一个圆形轨道移动的状态。
这种运动可不仅仅是“转一圈”那么简单哦,里面的物理学问可多得很。
1.1 圆周运动的基本概念首先,圆周运动有两个主要的特点:一是运动的轨迹是个圆,二是物体在这个过程中会一直改变方向,虽然它的速度大小可能保持不变。
就像小朋友在转圈圈,速度看似不变,但方向却在不停变化,结果就让人晕头转向。
我们通常用“角速度”和“线速度”来描述圆周运动的情况。
角速度告诉我们转得多快,而线速度则是说物体在圆周上跑得多快。
简单来说,角速度跟圆心的关系密切,线速度则和圆周的长度有关系。
1.2 动能的概念接着来说说动能。
动能就是物体由于运动而拥有的能量,听上去很高大上,其实它的道理简单得很。
想象一下,像一辆开得飞快的车,车速越快,动能就越大,真是飞得像风一样,甚至让你在座位上坐得不稳。
不过,动能的公式就简单得多,大家应该都知道,动能等于( frac{1{2mv^2 ),其中的m 是物体的质量,v 是物体的速度。
质量越大,速度越快,动能就越高,仿佛开车上了高速,风景一晃而过。
2. 圆周运动中的动能好了,咱们接下来要把这两者结合起来,看看在圆周运动中,动能又是怎么一回事儿。
其实,圆周运动中的动能并不是一成不变的。
假设你在过山车上,虽然车子的速度很快,但当它向下冲时,动能会大大增加;而在向上爬时,速度减慢,动能也会随之下降。
就像人生,有高有低,有涨有落,这才是生活的真谛。
2.1 动能的变化在圆周运动中,动能的变化还受到向心力的影响。
想象一下,你在转圈圈的时候,身体被“向心力”牢牢拉住,真是让人感到心惊胆战。
向心力就像个无形的手,时刻提醒你别跑偏了。
只要速度不变,动能就不会变化。
但是,如果速度加快,动能就会随着你的加速而增加。
圆周运动

圆周运动质点在以某点为圆心半径为r的圆周上运动,即质点运动时其轨迹是圆周的运动叫“圆周运动”。
它是一种最常见的曲线运动。
例如电动机转子、车轮、皮带轮等都作圆周运动。
圆周运动分为,匀速圆周运动和变速圆周运动(如:竖直平面内绳/杆转动小球、竖直平面内的圆锥摆运动)。
在圆周运动中,最常见和最简单的是匀速圆周运动(因为速度是矢量,所以匀速圆周运动实际上是指匀速率圆周运动)。
匀速相关公式1、v(线速度)=L/t=2πr/T=ωr=2πrf=2πnr(L代表弧长,t代表时间,r代表半径,n为频率,ω为角速度)2、ω(角速度)=θ/t=2π/T=2πf(θ表示角度或者弧度)3、T(周期)=2πr/v=2π/ω4、f(频率)=1/T6、Fn(向心力)=mrω^2=mv^2/r=mr4π^2/T^2=mr4π^2f^27、an(向心加速度)=rω^2=v^2/r=r4π^2/T^2=r4π^2n^2一、水平面内的圆周运动的两种模型模型Ⅰ圆台转动类小物块放在旋转圆台上,与圆台保持相对静止,如图1所示.物块与圆台间的动摩擦因数为μ,离轴距离为R,圆台对小物块的静摩擦力(设最大静摩擦力等于摩擦力)提供小物块做圆周运动所需的向心力.水平面内,绳拉小球在圆形轨道上运动等问题均可归纳为“圆台转动类”.图1摩擦力提供向心力临界条件圆台转动的最大角速度ωmax=,当ω<ωmax时,小物块与圆台保持相对静止;当ω>ωmax时,小物块脱离圆台轨道.模型Ⅱ火车拐弯类如图2 所示,火车拐弯时,在水平面内做圆周运动,重力mg和轨道支持力N的合力F提供火车拐弯时所需的向心力.圆锥摆、汽车转弯等问题均可归纳为“火车拐弯类”.合力提供向心力图2临界条件若v=,火车拐弯时,既不挤压内轨也不挤压外轨;若v>,火车拐弯时,车轮挤压外轨,外轨反作用于车轮的力的水平分量与F之和提供火车拐弯时所需的向心力;若v>,火车拐弯时,车轮挤压内轨,内轨反作用于车轮的力的水平分量与F之差提供火车拐弯时所需的向心力.二、两种模型的应用例1 如图3所示,半径为R的洗衣筒,绕竖直中心轴00'转动,小橡皮块P靠在圆筒内壁上,它与圆筒间的动摩擦因数为μ.现要使小橡皮块P恰好不下落,则圆筒转动的角速度ω至少为多大?(设最大静摩擦力等于滑动摩擦力)图3 图4【解析】此题属于“圆台转动类”,当小橡皮块P绕轴00'做匀速圆周运动时,小橡皮块P受到重力G、静摩擦力f和支持力N的作用,如图4所示.其中“恰好”是隐含条件,即重力与最大静摩擦力平衡f max=G,μN=mg列出圆周运动方程N=mω2min R联立解得ωmin=例2 在半径为R的半球形碗的光滑内面,恰好有一质量为m的小球在距碗底高为H处与碗保持相对静止,如图5所示.则碗必以多大的角速度绕竖直轴在水平面内匀速转动?图5【解析】此题属于“火车拐弯类”,当小球做匀速圆周运动时,其受到重力G和支持力F的作用,如图5所示.隐含条件一是小球与碗具有相同的角速度ω,隐合条件二是小球做匀速圆周运动的半径r=Rcosθ.列出圆周运动方程Fcosθ=mω2Rcosθ竖直方向上由平衡条件有Fsinθ-mg=0其中 sinθ=联立解得ω=例3 长度为2l的细绳,两端分别固定在一根竖直棒上相距为l的A、B两点,一质量为m的光滑小圆环套在细绳上,如图6所示.则竖直棒以多大角速度匀速转动时,小圆环恰好与A点在同一水平面内?图6【解析】此题属于“火车拐弯类”,当小圆环做匀速圆周运动时,小圆环受到重力G、绳OB的拉力F和绳OA的拉力F的作用,如图7所示图7隐含条件一是小圆环与棒具有相同角速度ω,隐含条件二是小圆环光滑,两侧细绳拉力大小相等,隐含条件三是小圆环做匀速圆周运动的圆心为A点、半径为r(OA).列出圆周运动方程 F+Fcosθ=mω2r由平衡条件有 Fsinθ-mg=0其中 cosθ=,sinθ=联立解得ω=练习1,如图所示,半径为R半球形碗表面光滑,一质量为m小球以角速度ω在碗一做匀速,求小球所做轨道平面离碗底距离h.如图所示,用长为L细线拴一个质量为m小球,使小球在做匀速,细线与竖直方向间夹角为θ,求:(1)细线拉力F;(2)小球周期T3、如图8所示,质量均为m的A、B两物体用细绳悬着,跨过固定在圆盘中央光滑的定滑轮.物体A与圆盘问的动摩擦因数为μ,离圆盘中心距离R.为使物体A与圆盘保持相对静止,则圆盘角速度ω的取值范围为多少?(设最大静摩擦力等于滑动摩擦力)图84、如图9所示,长度分别为l1和l2两细绳OA、OB,一端系在竖直杆,另一端系上一质量为m的小球,两细绳OA和OB同时拉直时,与竖直杆的夹角分别为30°、45°.则杆以多大角速度转动时,两细绳同时且始终拉直?绳模型底部速度杆模型底部速度例题解析轻绳模型例题1、用细绳拴着质量为m的小球,使小球在竖直平面内作圆周运动,则下列说法中,正确的是 [ ]A.小球过最高点时,绳子中张力可以为零B.小球过最高点时的最小速度为零C.小球刚好过最高点时的速度是D.小球过最高点时,绳子对小球的作用力可以与球所受的重力方向相反2、质量为m 的小球用一条绳子系着在竖直平面内做圆周运动,小球到达最低点和最高点时,绳子所受拉力之差是: [ ]A、6mgB、5mgC、2mgD、条件不充分,不能确定3、小球在竖直放置的光滑圆轨道内做圆周运动,圆环半径为r,且刚能通过最高点,则球在最低点时的速度和对圆轨道的压力分别为: [ ]A、4rg,16mgB、,5mgC、2gr,5mgD、,6mg4、图所示,在倾角α=30°的光滑斜面上,有一根长L=0.8m的细绳:一端固定在O点,另一端系一质量为m=0.2kg的小球,沿斜面作圆周运动,试计算:(1)小球通过最高点A的最小速度。
高中物理圆周运动与能量、动量问题(含答案)

圆周运动与能量、动量问题1 如图所示,竖直平面内的光滑水平轨道的左边与墙壁对接,右边与一个足够高的14光滑圆弧轨道平滑相连,木块A、B静置于光滑水平轨道上,A、B的质量分别为1.5 kg和0.5 kg.现让A以6 m/s 的速度水平向左运动,之后与墙壁碰撞,碰撞的时间为0.3 s,碰后的速度大小变为4 m/s.当A与B碰撞后会立即粘在一起运动,g 取10 m/s2,求:(1)在A与墙壁碰撞的过程中,墙壁对A的平均作用力的大小;(2)A、B滑上圆弧轨道的最大高度.答案(1)50 N(2)0.45 m解析(1)设水平向右为正方向,当A与墙壁碰撞时根据动量定理有Ft=m A v1′-m A(-v1)解得F=50 N(2)设碰撞后A、B的共同速度为v,根据动量守恒定律有m A v1′=(m A+m B)vA、B在光滑圆形轨道上滑动时,机械能守恒,由机械能守恒定律得12(m A+m B)v2=(m A+m B)gh解得h=0.45 m.2 如图所示,光滑水平面上有一具有光滑曲面的静止滑块B,可视为质点的小球A从B的曲面上离地面高为h处由静止释放,且A可以平稳地由B的曲面滑至水平地面.已知A的质量为m,B 的质量为3m,重力加速度为g,试求:(1)A刚从B上滑至地面时的速度大小;(2)若A到地面后与地面上的固定挡板P碰撞,之后以原速率反弹,则A返回B的曲面上能到达的最大高度为多少?答案(1)126gh(2)14h解析(1)设A刚滑至地面时速度大小为v1,B速度大小为v2,规12定向右为正方向,由水平方向动量守恒得3m v 2-m v 1=0,由系统机械能守恒得mgh =12m v 12+12×3m v 22联立以上两式解得:v 1=126gh v 2=166gh .(2)从A 与挡板碰后开始,到A 追上B 到达最大高度h ′并具有共同速度v ,此过程根据系统水平方向动量守恒得 m v 1+3m v 2=4m v根据系统机械能守恒得 mgh =12×4m v 2+mgh ′联立解得: h ′=14h .3 如图所示,质量为m 的b 球用长h 的细绳悬挂于水平轨道BC 的出口C 处.质量也为m 的小球a ,从距BC 高h 的A 处由静止释放,沿光滑轨道ABC 下滑,在C 处与b 球正碰并与b 黏在一起.已知BC 轨道距地面的高度为0.5h ,悬挂b 球的细绳能承受的最大拉力为2.8mg 。
力学圆周运动公式整理

力学圆周运动公式整理圆周运动是力学中的一个重要概念,描述了物体在圆周轨道上的运动特征。
本文将对圆周运动的公式进行整理和探讨,以便更好地理解和应用圆周运动的原理。
一、圆周运动的基本概念圆周运动是指物体在半径为R的圆周轨道上做匀速运动的现象。
在圆周运动中,物体的速度大小保持不变,但方向却随着时间不断改变。
这种改变的方向对应着物体在力的作用下所受到的向心力。
二、圆周运动的基本量1. 角速度(ω):角速度是描述物体在圆周轨道上旋转的快慢的物理量。
角速度的单位是弧度/秒(rad/s),可用公式表示为:ω = Δθ/Δt其中,Δθ表示角度的变化量,Δt表示时间的变化量。
2. 周期(T)和频率(f):周期是指物体完成一次圆周运动所需的时间。
频率则是指每单位时间内圆周运动的次数。
二者之间存在以下关系:T = 1/f3. 线速度(v):线速度是指物体沿圆周轨道的线段上运动的速度。
线速度的大小等于物体在单位时间内沿圆周轨道所走过的弧长。
线速度的公式为:v = ω · R其中,R为圆的半径。
三、圆周运动的运动学公式1. 位移(s):描述物体在圆周运动中位置变化的物理量。
位移的大小等于物体所走过的弧长,可以用公式表示为:s = θ · R其中,θ为物体所转过的角度。
2. 加速度(a):加速度是描述物体在圆周运动中加速或减速的物理量。
加速度的大小等于物体的线速度与角速度的乘积,即:a = ω · v = ω^2 · R其中,v为线速度。
四、圆周运动的动力学公式1. 向心加速度(ac):向心加速度是指物体在圆周运动中受到的向心力引起的加速度。
它的大小是由向心力与物体质量之比决定的,即:ac = Fc/m = ω^2 · R其中,Fc为向心力,m为物体质量。
2. 向心力(Fc):向心力是使物体保持圆周运动的中心向内的力。
根据牛顿第二定律可得到向心力的公式:Fc = m · ac = m · ω^2 · R其中,m为物体质量。
2020年高考物理《圆周运动与动能定理的综合考查》专题训练及答案解析

高考物理《圆周运动与动能定理的综合考查》专题训练1.(2015·全国卷Ⅰ,17)如图,一半径为R 、粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ 水平。
一质量为m 的质点自P 点上方高度R 处由静止开始下落,恰好从P 点进入轨道。
质点滑到轨道最低点N 时,对轨道的压力为4mg ,g 为重力加速度的大小。
用W 表示质点从P 点运动到N 点的过程中克服摩擦力所做的功。
则( )A .W =12mgR ,质点恰好可以到达Q 点B .W >12mgR ,质点不能到达Q 点C .W =12mgR ,质点到达Q 点后,继续上升一段距离D .W <12mgR ,质点到达Q 点后,继续上升一段距离【答案】:C【解析】:根据动能定理得P 点动能E k P =mgR ,经过N 点时,由牛顿第二定律和向心力公式可得4mg -mg =m v 2R ,所以N 点动能为E k N =3mgR 2,从P 点到N 点根据动能定理可得mgR -W =3mgR 2-mgR ,即克服摩擦力做功W =mgR2。
质点运动过程,半径方向的合力提供向心力即F N -mg cos θ=ma =m v 2R ,根据左右对称,在同一高度处,由于摩擦力做功导致在右边圆形轨道中的速度变小,轨道弹力变小,滑动摩擦力F f =μF N 变小,所以摩擦力做功变小,那么从N 到Q ,根据动能定理,Q 点动能E k Q =3mgR 2-mgR -W ′=12mgR -W ′,由于W ′<mgR 2,所以Q 点速度仍然没有减小到0,会继续向上运动一段距离,对照选项,C 正确。
2.如图,一半径为R 的半圆形轨道竖直固定放置,轨道两端等高,质量为m 的质点自轨道端点P 由静止开始滑下,滑到最低点Q 时,对轨道的正压力为2mg ,重力加速度大小为g 。
质点自P 滑到Q 的过程中,克服摩擦力所做的功为( )A.14mgR B.13mgR C.12mgR D.π4mgR 【答案】 C【解析】 在Q 点质点受到竖直向下的重力和竖直向上的支持力,两力的合力充当向心力,所以有FN -mg =m v2R ,FN =2mg ,联立解得v =gR ,下滑过程中,根据动能定理可得mgR -Wf =12mv2,解得Wf =12mgR ,所以克服摩擦力做功12mgR ,C 正确。
圆周运动角动量与能量的关系

圆周运动角动量与能量的关系The relationship between angular momentum and energy in circular motionIn physics, angular momentum and energy are two important physical quantities, and there is a certain relationship between them, especially in circular motion. To understand this relationship, we first need to understand the basic concepts of angular momentum and energy.Angular momentum is a vector representing the momentum of an object rotating around a point. In circular motion, the angular momentum of an object can be calculated by the formula L=mvr, where m is the mass of the object, v is the velocity of the object, and r is the distance from the object to the center of rotation. The law of conservation of angular momentum states that, in the absence of external torque, the angular momentum of the system remains constant.Energy is a measure of the motion or interaction of an object. In circular motion, the energy of an object mainly includes kinetic energy and potential energy. Kinetic energy is the energy possessed by an object due to its motion, which can be calculated by the formula 1/2mv2, where m is the mass of the object and v is the velocity of the object. Potential energy is the energy possessed by an object due to its position or state. For example, in a gravitational field, the potential energy of an object is related to its height.There is a relationship between angular momentum and energy in circular motion. According to the law of conservation of angular momentum, when an object moves on a circle without external torque, the angular momentum of the object will remain constant. This means that the product of the object's velocity v and the distance r, mvr, will remain constant. Since the velocity v is directly related to the kinetic energy 1/2mv2, the conservation of angular momentum also indirectly affects the kinetic energy of the object.On the other hand, changes in potential energy also affect the angular momentum of an object. For example, in a gravitational field, when an object moves from a lower position to a higher position, its potential energy increases, while itskinetic energy decreases. This leads to a decrease in the object's velocity v, which affects its angular momentum L=mvr. Therefore, there is a mutual influence relationship between angular momentum and energy in circular motion.Overall, angular momentum and energy are interrelated in circular motion. The conservation of angular momentum affects the kinetic energy of an object, while changes in potential energy also affect the angular momentum of an object. This relationship has important applications in physics, such as in spacecraft attitude control, wind power generation, and other fields, where the relationship between angular momentum and energy needs to be considered.在物理学中,角动量和能量是两个重要的物理量,它们之间存在一定的关系,特别是在圆周运动中。
高中物理竖直平面的圆周运动与能量相结合

1、长为L 的轻绳的一端固定在O 点,另一端拴一个质量为m 的小球,先令小球以O 为圆心,在竖直平面内做圆周运动,小球能通过最高点,如图则:心,在竖直平面内做圆周运动,小球能通过最高点,如图则:A .小球通过最高点时速度可能为零.小球通过最高点时速度可能为零B .小球通过最高点时所受轻绳的拉力可能为零.小球通过最高点时所受轻绳的拉力可能为零C .小球通过最低点时速度大小可能等于gL 2D .小球通过最低点时所受轻绳的拉力可能等于6mg 2、(14分)如图8所示,半径R =0.40m 的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A 。
一质量m=0.10kg 的小球,以初速度v 0=7.0m/s 在水平地面上向左作加速度a =3.0m/s 2的匀减速直线运动,运动4.0m 后冲上竖直半圆环,最后小球落在C 点。
(重力加速度g=10m/s 2)(1)判断小球能否过半圆环轨道的最高点B ;(2)求A 、C 间的距离。
间的距离。
3、(14分)如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC 在B点吻接(即水平即水平面是弯曲轨道的切线),圆轨道的半径R =40cm,=40cm,质量为质量为m =100g 的小球从A 点以v A =7m/s 的初速度由直轨道向右运动,物块与水平面间的动摩擦因数=m 0.2,AB 长为6m ,求:(1)小物块滑到B 点时的速度多大及小物块对B 点的压力大小点的压力大小 (2) 小物块能否过C 点,若能,求出小物块对C 点的压力,若不能,请说明原因。
(3)要使小物体从C 点脱离轨道,小球在A 点的初速度必须满足什么条件?什么条件?4、某校物理兴趣小组决定举行遥控塞车比赛。
比赛路径如图所示,赛车从起点A 出发,沿水平直线轨道运动L 后,出B 点进入半径为R 的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C 点,并能越过壕沟。
已知赛车质量m =0.1kg ,通电后以额定功率ρ=1.5W 工作,进入竖直圆轨道前受到的阻值为0.3N ,随后在运动中受到的阻力均可不计。
圆周运动的基本概念与公式推导

圆周运动的基本概念与公式推导一、圆周运动的基本概念1.圆周运动:物体沿着圆周轨道运动的现象称为圆周运动。
2.圆心:圆周运动的中心点,通常用O表示。
3.半径:从圆心到圆周上任意一点的线段,用r表示。
4.角速度:描述圆周运动快慢的物理量,表示单位时间内物体绕圆心转过的角度,用ω表示。
5.周期:圆周运动一次完整往返所需要的时间,用T表示。
6.频率:单位时间内圆周运动的次数,与周期互为倒数,用f表示。
二、圆周运动的公式推导1.线速度公式:线速度(v)= 半径(r)× 角速度(ω)2.角速度与周期的关系:角速度(ω)= 2π / 周期(T)即ω = 2π / T3.向心加速度公式:向心加速度(a)= 半径(r)× 角速度的平方(ω²)即a = rω²4.向心力公式:向心力(F)= 质量(m)× 向心加速度(a)即F = ma = mrω²三、圆周运动的分类1.匀速圆周运动:角速度恒定的圆周运动。
2.非匀速圆周运动:角速度变化的圆周运动。
四、圆周运动的应用1.匀速圆周运动的应用:2.非匀速圆周运动的应用:–匀速圆周运动的加速器五、注意事项1.在研究圆周运动时,要区分角速度、线速度、向心加速度和向心力等概念,并理解它们之间的关系。
2.注意圆周运动的分类,掌握匀速圆周运动和非匀速圆周运动的特点及应用。
3.在实际问题中,要根据题目条件选择合适的公式进行分析。
习题及方法:1.习题:一个物体在半径为2m的圆形轨道上做匀速圆周运动,角速度为2rad/s,求物体的线速度和向心加速度。
根据线速度公式v = rω,将给定的半径 r = 2m 和角速度ω = 2rad/s 代入公式,得到物体的线速度:v = 2m × 2rad/s = 4m/s根据向心加速度公式a = rω²,将给定的半径 r = 2m 和角速度ω = 2rad/s 代入公式,得到物体的向心加速度:a = 2m × (2rad/s)² = 8m/s²答案:物体的线速度为4m/s,向心加速度为8m/s²。
圆周运动知识点总结总结

圆周运动知识点总结总结1. 圆周运动的基本概念在圆周运动中,物体沿着一个圆形轨道围绕一个点或轴线做运动。
这个点或轴线被称为圆周运动的中心。
在圆周运动中,物体离中心的距离被称为半径,用符号r表示。
围绕圆心的角度称为角度,通常用符号θ表示。
当物体在圆周运动中通过一个完整的圆周,它所围绕的角度是360度,或者用弧度表示为2π弧度。
2. 圆周运动的运动学描述在圆周运动中,物体在单位时间内通过的角度称为角速度,通常用符号ω表示。
角速度是一个矢量量,它的大小等于单位时间内旋转的角度。
角速度的单位通常是弧度每秒(rad/s)。
物体在圆周运动中所围绕的圆周的长度称为弧长,通常用符号s表示。
弧长和半径之间的关系可以用下面的公式描述:s = rθ在圆周运动中,物体在单位时间内通过的弧长称为线速度,通常用符号v表示。
线速度的大小等于弧长与时间的比值,即v = s/t。
线速度和角速度之间的关系可以用下面的公式描述:v = rω这个公式表明线速度和角速度是成正比的关系。
当半径增大时,线速度也会增大;当角速度增大时,线速度也会增大。
这也说明了在圆周运动中,线速度的方向是垂直于半径的方向。
线速度的方向与角速度的方向有一定的关系,具体关系可根据右手螺旋法则来确定。
3. 圆周运动的动力学描述在圆周运动中,物体所受的向心力(或者称为离心力)是造成它做圆周运动的根本原因。
向心力的大小等于物体的质量和其线速度的平方与半径的乘积之比,即F_c = mv^2/r其中F_c表示向心力,m表示物体的质量,v表示物体的线速度,r表示物体所围绕的圆周的半径。
向心力的方向始终指向圆周运动的中心。
向心力是一种虚拟力,它并不是真实存在的力,但是它却能够改变物体的运动状态,使得物体在圆周运动中始终保持向中心的方向运动。
圆周运动中的向心力和角速度之间有一定的关系。
向心力的大小和角速度的平方成正比,即F_c = mrω^2这个关系表明当角速度增大时,向心力也会增大,从而使得物体在圆周运动中的向中心的加速度也会增大。
物理圆周运动公式3篇

物理圆周运动公式第一篇:物理圆周运动的基本概念及公式物理圆周运动是指一个质点沿着一个圆形轨道做匀速或变速的运动,它是物理学中的基本运动之一。
圆周运动是指一个质点无论沿着一个圆形轨道作何种运动,其运动过程都可以分解为两个相互垂直的分量,即径向分量和切向分量。
在圆周运动中,质点的径向分量为零,它所受的合外力沿着径向,这个合力叫做向心力。
而质点的切向分量在各个时刻的大小和方向均不同,它的方向是沿着切线方向,大小则取决于所受合外力的大小和方向。
圆周运动的公式如下:1.向心力公式向心力的大小与质点的质量、圆周半径以及圆周运动的速度有关,可以表示为:Fc = mv² / r其中,Fc 表示向心力大小,m 为质点的质量,v 表示质点在圆周运动中的速度,r 表示圆周运动的半径。
2.圆周运动的周期公式圆周运动的周期是指质点沿着圆周轨道运动一周所需的时间,可以表示为:T = 2πr / v其中,T 表示圆周运动的周期,r 表示圆周运动的半径,v 表示质点在圆周运动中的速度。
3.圆周运动的角速度公式圆周运动的角速度是指质点在圆周轨道上转动的角度每秒钟增加的大小,可以表示为:ω = Δθ / Δt其中,ω 表示角速度,Δθ 表示质点在圆周运动中的角位移,Δt 表示所需的时间。
4.圆周运动的线速度公式圆周运动的线速度是指质点在圆周轨道上的速度,可以表示为:v = ωr其中,v 表示线速度,ω 表示角速度,r 表示圆周运动的半径。
总之,圆周运动是一种非常常见的物理运动形式,应用领域广泛,规律简单易懂。
掌握圆周运动的公式和概念对于加深对物理学的理解和提高应用能力具有重要意义。
第二篇:物理圆周运动中的离心力和重力物理圆周运动是指质点沿着一个圆形轨道做匀速或变速的运动,其中的向心力是一个非常重要的概念。
除了向心力之外,在圆周运动中,还有两个重要的力:离心力和重力。
1.离心力离心力是指,当一个质点在圆周运动中,由于惯性而远离圆心的力,其大小和方向与向心力大小相等,方向相反。
专题08 带电粒子在匀强电场中的圆周运动和在电场中的能量动量问题(解析版)

高二物理期末综合复习(特训专题+提升模拟)专题08 带电粒子在匀强电场中的圆周运动和在电场中的能量动量问题一、带电粒子在匀强电场中的圆周运动1.如图所示,在竖直放置的半径为R的光滑半圆弧绝缘细管的圆心O处固定一点电荷,将质量为m,带电量为q的小球从圆弧管的水平直径端点A由静止释放,小球沿细管滑到最低点B时,对管壁恰好无压力。
已知重力加速度为g,下列说法正确的是()A.小球滑到最低点BB.小球滑到最低点BC.固定于圆心处的点电荷在AB弧中点处的电场强度大小为2mg qD.小球不能到达光滑半圆弧绝缘细管水平直径的另一端点【答案】B【详解】AB.小球从A点由静止释放,运动到B点的过程中,电场力不做功。
则由机械能守恒定律可得212mgR mv =即达到B 点的速度为v =B 正确,A 错误;C .小球沿细管滑到最低点B 时,对管壁恰好无压力,则可知小球受重力和电场力作用,根据牛顿第二定律可知22Qq mv k mg R R-=因为点电荷电场的电场线是一圈一圈的同心圆,所以可知,在半圆轨道任何一点,电场强度大小相等。
即为23Q mgE kR q==选项C 错误; D .根据点电荷的电场分布特点,可知电场线沿着半圆轨道的半径方向,所以小球从A 点运动到C 点的过程中,电场力不做功。
即小球从A 点运动到C 点的过程中,机械能守恒。
即小球可以到达光滑半圆弧绝缘细管水平直径的另一端点,选项D 错误。
故选B 。
2.用轻绳拴着一质量为m 、带正电的小球在竖直面内绕O 点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E ,如图甲所示,不计一切阻力,小球运动到最高点时的动能E k 与绳中张力F 间的关系如图乙所示,当地的重力加速度为g ,则( )A .小球所带电荷量为b mgE+ B .轻绳的长度为abCD 【答案】C【详解】A .当0F =时,由2v mg Eq m L +=;212mv a =联立解得b mg q E -=故A 错误;B .在最高点,绳对小球的拉力、重力和电场力的合力提供向心力,则有2v F mg Eq m L++=即2122mv F mg Eq L ⋅=++由2k 12E mv =可得k ()22L L E F mg Eq =++由图像可组织,图像斜率2a Lk b == 即2aL b=故B 错误; CD .当0F =时,重力和电场力的合力提供向心力,此时为最小速度,由212mv a =解得v =C 正确,D 错误。
生活中圆周运动

03
通过微积分可以计算圆周运动的轨矢量运算在处理复杂问题时的作用
描述圆周运动的物体的位置和速度
矢量运算可以用来描述圆周运动的物体的位置和速度,通过矢量的加法和减法可以得到物体在不 同时刻的位置和速度。
分析圆周运动的合成和分解
通过矢量运算可以分析圆周运动的合成和分解,如将复杂的圆周运动分解为简单的匀速直线运动 和匀变速直线运动的合成。
03
钟表、指南针等日常用品
钟表指针的旋转、指南针的指向都涉及圆周运动,这些日常用品的设计
和使用都离不开圆周运动原理。
促进科技发展,推动社会进步
航天器轨道设计
航天器的轨道设计需要精确计算和控制圆周运动的参数, 以确保航天器能够按照预定轨道稳定运行,这对于人类的 太空探索和科学研究具有重要意义。
精密机械制造
三角函数在圆周运动中应用
1 2
描述匀速圆周运动的物体的位置
三角函数可以用来描述匀速圆周运动的物体在某 个时刻的位置,通过角度和半径的关系,可以准 确地确定物体的坐标。
分析圆周运动的周期性
三角函数具有周期性,因此可以用来分析圆周运 动的周期性,如转速、周期、频率等。
3
计算向心加速度和向心力
在向心加速度和向心力的计算中,需要用到三角 函数的导数和积分,以及三角函数之间的关系, 如正弦定理、余弦定理等。
波动可以通过不同的介质进行传播,如固体、液体和气体。在传播过程中,波动会遵循一定的传播规 律,如反射、折射和衍射等。此外,波动的传播速度会受到介质性质的影响。
曲线运动在自然界和人类活动中的普遍性
自然界中的曲线运动
地球围绕太阳公转、月亮围绕地球旋转 、行星的自转等都是自然界中的曲线运 动现象。这些运动遵循着天体物理学的 规律,呈现出周期性和稳定性。
圆周运动。动能定理[技巧]
![圆周运动。动能定理[技巧]](https://img.taocdn.com/s3/m/6f63739f6429647d27284b73f242336c1eb9302c.png)
圆周运动1.物体做匀速圆周运动的条件:匀速圆周运动的运动条件:做匀速圆周运动的物体所受合外力大小不变,方向总是和速度方向垂直并指向圆心。
2.描述圆周运动的运动学物理量(1)圆周运动的运动学物理量有线速度v 、角速度ω、周期T 、转速n 、向心加速度a 等。
它们之间的关系大多是用半径r 联系在一起的。
如:T r r v πω2=⋅=,22224Tr r r v a πω===。
要注意转速n 的单位为r/min ,它与周期的关系为nT 60=。
(2)向心加速度的表达式中,对匀速圆周运动和非匀速圆周运动均适用的公式有:ωωv r r v a ===22,公式中的线速度v 和角速度ω均为瞬时值。
只适用于匀速圆周运动的公式有:224Tra π= ,因为周期T 和转速n 没有瞬时值。
3.描述圆周运动的动力学物理量———向心力(1)向心力来源:向心力是做匀速圆周运动的物体所受外力的合力。
向心力是根据力的作用效果命名的,不是一种特殊的性质力。
向心力可以是某一个性质力,也可以是某一个性质力的分力或某几个性质力的合力。
例如水平转盘上跟着匀速转动的物体由静摩擦力提供向心力;带电粒子垂直射入匀强磁场中做匀速圆周运动,由洛伦兹力提供向心力;电子绕原子核旋转由库仑力提供向心力;圆锥摆由重力和弹力的合力提供向心力。
做非匀速圆周运动的物体,其向心力为沿半径方向的外力的合力,而不是物体所受合外力。
(2)向心力大小:根据牛顿第二定律和向心加速度公式可知,向心力大小为:22224Tr m r m r v m F πω=== 其中r 为圆运动半径。
(3)向心力的方向:总是沿半径指向圆心,与速度方向永远垂直。
(4)向心力的作用效果:只改变线速度的方向,不改变线速度的大小。
几种常见的匀速圆周运动的实例图表图形受力分析利用向心力公式2tan sin mg m l θωθ=2tan (sin )mg m l d θωθ=+2tan mg m r θω=2tan mg m r θω=2Mg m r ω=4.竖直平面内圆周运动的临界问题:由于物体在竖直平面内做圆周运动的依托物(绳、轻杆、轨道、管道等)不同,所以物体在通过最高点时临界条件不同。
圆周运动概念

圆周运动概念
围绕圆周运动的精彩,总能给人以无穷的欢乐与愉悦之情,人们经常可以在公
园里看到有小朋友玩耍时,几乎总会有围绕圆周运动发生,这种活动可真是有趣又正能量啊!
圆周运动这种活动,源于古希腊和古罗马时期,当时人们经常会在庆典活动、
节庆仪式中非常活跃的做围绕圆周运动,这是非常古老的一种活动。
到了更近代的时代,人们同样可以看到围绕圆周运动的踪影,比如大家可能会记得复活节的情景,看到的就是蔓延在迷宫里的距离零的活动吧,这就是围绕圆周运动啦!
如今,圆周运动还是助推大众健身的一个非常有效的方式,已经成为很多人健
身房里常见的锻炼方式。
而且,也有很多精英运动员在大赛等活动中,非常有效地采取围绕圆周运动来学会自我有效控制,也就是训练自己,让自我运动中更上一层楼。
围绕圆周运动,也在世界各地的舞蹈比赛中,展现出它的魅力,而且人们也利
用这种运动,让大众更加贴近自然,实现轻松的是放心情。
有了古今中外的一片活跃的场景,我们也可以看到,围绕圆周运动,无时无刻
不给我们带来着无限的欢乐,喜悦之情,让我们看到健康生活所带来的极致体验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
gL
gL
2
(2)
7gL 2
1 (3) mgL 2
第 3 专题
圆周运动、航天与星体问题 知识网络
要点归纳 一、圆周运动 1.描述匀速圆周运动的相关物理量及其关系 (1)物理量:线速度 v、角速度ω、周期 T、频率 f、转速 n、向心加速度 a 等等.
v2 4π2 2 (2)关系:v= =ωr=2πrf,a= =ω r= 2 r=4π2f2r. T r T
arctan
v2 . rg
二、航天与星体问题 1.天体运动的两个基本规律 (1)万有引力提供向心力
Mm v2 4π2 2 行星卫星模型:F=G 2 =m =mrω =m 2 r r r T m1m2 双星模型:G 2 =m1ω2r1=m2ω2(L-r1) L 其中,G=6.67×10-11 N·m2/kg2
质量的轻绳通过定滑轮分别与木板和小木块连接,小木块与木板间的动摩擦因数为μ.开始时,木 块静止在木板左端, 现用水平向右的力 F 将小木块拉至木板右端, 则拉力至少做的功大小为( ) A.2μmgL B.μmgL C.
μmgL
2
D.μ(M+m)gL
【解析】方法一 当拉小木块向右缓慢移动时,拉力 F=μmg+FT=2μmg 当小木块向右运动 时到达木板的右端,有: 2
[答案] B 6.(10 分)在半径 R=5000 km 的某星球表面,宇航员做了如下实验.实验装置如图甲所示, 竖直平面内的光滑轨道由轨道 AB 和圆弧轨道 BC 组成,将质量 m=0.2 kg 的小球从轨道 AB 上高 H 处的某点静止滑下,用力传感器测出小球经过 C 点时对轨道的压力 F,改变 H 的大小,可测出相应 的 F 大小,F 随 H 的变化关系如图乙所示.求: (1)圆轨道的半径. (2)该星球的第一宇宙速度. 【解析】 (1)设该星球表面的重力加速 度为 g0,圆轨道的半径为 r.当 H=0.5 m 时,有: 1 mg0(H-2r)= mv02 (2 分) 2
所以, 小球要能通过最高点, 它在最高点时的速度 v 需要满足的条件是 v≥ gr. 当 v> gr 时, 绳对球产生拉力,轨道对球产生压力. (2)如图 3-2 所示, 轻质杆一端的小球绕杆的另一端做圆周运动及小球在竖直放置的圆环内做 圆周运动过最高点的临界问题.
图 3-2 分析小球在最高点的受力情况:小球受重力 mg、杆或轨道对小球的力 F. 小球在最高点的动力学方程为:
r
T
=4mπ f r (牛顿第二定律) 3.圆周运动的临界问题 分析圆周运动的临界问题时,一般应从与研究对象相联系的物体(如:绳、杆、轨道等)的力学 特征着手. (1)如图 3-1 所示, 绳系小球在竖直平面内做圆周运动及小球沿竖直圆轨道的内侧面做圆周运 动过最高点的临界问题(小球只受重力、绳或轨道的弹力).
第 2 专题
功和能量
知识网络
1 .美国的 NBA 篮球赛非常精彩, 因此吸引了众多观众. 在 NBA 篮球赛中经常能看到这样的场面: 在终场前 0.1 s 的时候,运动员把球投出且准确命中,获得比赛的最后胜利.已知球的质量为 m,运动员将篮球 投出时球离地的高度为 h1,动能为 Ek,篮筐距地面的高度为 h2,不计空气阻力,则篮球进筐时的动 能为( ) A.Ek+mgh1-mgh2 B.Ek-mgh1+mgh2 C.-Ek+mgh1+mgh2 D.-Ek-mgh1+mgh2 【解析】由动能定理得:Ek′-Ek=WG=mg(h1-h2) 解得:Ek′=Ek+mgh1-mgh2. [答案] A 2.如图所示,竖直放置的劲度系数为 k 的轻质弹簧上端与质量为 m 的小 球连接,下端与放在水平桌面上的质量为 M 的绝缘物块相连.小球带正电,电 荷量为 q,且与弹簧绝缘,物块、弹簧和小球组成的系统处于静止状态.现突 然加上一个竖直向上的大小为 E 的匀强电场,小球向上运动,某时刻物块对水 平面的压力为零.从加上匀强电场到物块对水平面的压力为零的过程中,小球 电势能的改变量为( ) A.
2
2
图 3-1 由于小球运动到圆轨迹的最高点时,绳或轨道对小球的作用力只能向下,作用力最小为零,所 以小球做完整的圆周运动在最高点应有一最小速度 vmin.当小球刚好能通过最高点时,有:
vmin2 mg=m r
解得:vmin=
gr .
5gR
1 1 2 2 又由机械能守恒定律有: mv 下 = mv 上 +mg·2R,可得 v 下≥ 2 2
qE(M+m)g k
B.-
qE(M+m)g k
C.
qEMg k,当物块对水平面的压力为零时,弹簧的伸长量 x2 k Mg (m+M)g = ,故这一过程中小球沿电场方向运动的距离为 x1+x2= k k qE(m+M)g 电势能的变化ΔE=-W 电=- . k
【解析】加电场前,弹簧的压缩量 x1= [答案] B 3.如图所示,已知木板的质量为 M,长度为 L;小木块的质量为 m;水平地面光滑;一根不计
L
L WF=F· =μmgL.
2 方法二 由功能关系知,拉力至少做的功等于小木块与木板摩擦产生的热量.即 WF=Q=μmgL. [答案] B 4.一个质量为 m 的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面.已知该物体做 3 匀减速运动的加速度为 g,在斜面上上升的最大高度为 h,则此过程中( ) 4 3 A.物体的动能增加 mgh B.物体的重力做功 mgh 2 1 1 C.物体的机械能损失了 mgh D.物体克服摩擦力做功 mgh 2 2 【解析】由题意可知: 3 物体受到的合外力 F= mg 4 1 其中摩擦力 f=F-mgsin θ= mg 4 h 3 由动能定理得:ΔEk=-F· =- mgh sin 30° 2 重力做功 WG=-mgh 1 h 1 物体的机械能的变化ΔE=-f·s=- mg· =- mgh 4 sin 30° 2 1 物体克服摩擦力做的功 Wf′=f·s= mgh. 2 [答案] CD 5.如图所示,质量为 M、长度为 l 的小车静止在光滑的水平面上;质量为 m 的小物块(可视为 质点)放在小车的最左端.现用一水平向右的恒力 F 作用在小物块上,使物块从静止开始做匀加速 直线运动.物块和小车之间的摩擦力为 f.物块滑到小车的最右端时,小车运动的距离为 s.在这 个过程中,以下结论正确的是( ) A.物块到达小车最右端时,具有的动能为 F(l+s) B.物块到达小车最右端时,小车具有的动能为 fs C.物块克服摩擦力所做的功为 f(l+s) D.物块和小车增加的机械能为 fs 【解析】物块到达小车最右端时,知: 物块具有的动能 Ek′=(F-f)·(l+s) 此时小车具有动能 Ek′=f·s 这一过程物块克服摩擦力所做的功为: Wf′=f·(l+s) 由功能关系知ΔE=F·(l+s)-f·l.
4.弯道问题 (1)火车的弯道、公路的弯道都向内侧倾斜,若弯道半径为 r,车辆通过速度为 v0,则弯道的 倾角应为:
v02 θ= arctan . rg
(2)飞机、 鸟在空中盘旋时受力与火车以 “v0” 过弯道相同, 故机翼、 翅膀的倾角θ=arctan
v2 . rg
(3) 骑自行车在水平路面上转弯时,向心力由静摩擦力提供,但车身的倾斜角仍为 θ =
解得:Q=mg(d1+d2)sin θ. (2 分) [答案] (1)mgd1sin θ (2)mg(d1+d2)sin θ 8.(12 分)如图所示,质量分别为 3m、2m、m 的三个小球 A、B、C,用两根长为 L 的轻绳相连, 置于倾角为 30°、高为 L 的固定光滑斜面上,A 球恰能从斜面顶端处竖直落下,弧形挡板使小球只 能竖直向下运动,碰撞过程中没有动能损失,小球落地后均不再反弹.现由静止开始释放它们,不 计所有摩擦.求: (1)A 球刚要落地时的速度大小. (2)C 球刚要落地时的速度大小. (3)在 B 球运动的过程中,两绳对 B 球做的总功. 【解析】(1)在 A 球未落地前,A、B、C 组成的系统机械能守恒,设 A 球 刚要落地时系统的速度大小为 v1,则: 1 (mA+mB+mC)v12=mAghA-mBghB1-mCghC1 (2 分) 2 1 又 hA=L,hB1=hC1=Lsin 30°= L 2 . (2 分) 2 (2)在 A 球落地后,B 球未落地前,B、C 组成的系统机械能守恒.设 B 球刚要落地时系统的速 度大小为 v2,则: 1 1 (mB+mC)v22- (mB+mC)v12=mBghB2-mCghC2 (2 分) 2 2 1 又 hB2=L,hC2=Lsin 30°= L 2 3gL (1 分) 2 在 B 球落地后,C 球在下落过程中机械能守恒,设 C 球刚要落地时系统的速度大小为 v3,则: 1 1 mCv32- mCv22=mCghC3,又 hC3=L (1 分) 2 2 代入数据解得:v2= 7gL . (1 分) 2 (3)在 B 球运动的过程中,重力和绳的拉力做功,设两绳做的总功为 W,根据动能定理可得: 1 mBgLsin 30° +W= mBv22 (2 分) 2 1 代入数据解得:W= mgL. (1 分) 2 代入数据得:v3= [答案] (1) 代入数据解得:v1=
