平面简谐波波函数
合集下载
10-2平面简谐波函数

y
0.1m
t t0
u x
o
y0 0.1cos(t )
解:
ห้องสมุดไป่ตู้
y0 0.1cos(t )
2
t 0
2
y
t 0
y0 0.1 cos[ (t t0 )
0.1m
t t0
2
]
u
t t0
A o
2
o x
x
x y ( x, t ) 0.1cos[ (t t0 ) ] u 2
推广至三维空间
2 2 2
2
——波函数
2
1 2 2 2 2 2 x y z u t
任何物理量 ,不管是力学量、电学量、热 普遍 意义 学量或其它的量,只要它与时间和坐标的关 系满足上述方程,这一物理量就以波的形式 传播,而偏导数 2 t 2的系数的倒数的平 方根就是这种波的传播速度。
u
M
o
x t 0 2
x
x
点P在 t 时刻的位移为
y P A cos[ t 0 2
x
]
沿OX轴正向传播的平面简谐波的波函数
x y ( x, t ) A cos[ (t ) 0 ] u
沿OX轴负向传播的平面简谐波的波函数
y
x y ( x, t ) A cos[ (t ) 0 ] u
*§10.2 平面简谐波的波函数
平面简谐波:在均匀、无吸收的介质中,当波 源作简谐振动时,在介质中所形成的平面波。 一、波的表达式(波函数)
数学上如何描述简谐波??
§12-2平面简谐波的波函数

x2 − x1 −1 u= = 250 cm ⋅ s t 2 − t1
轴正方向传播, 例2 一平面简谐波沿 O x 轴正方向传播,已知振 幅 A = 1.0m T = 2 . 0 s λ = 2.0m .在 t = 0 时坐 标原点处的质点位于平衡位置沿 O y 轴正方向运 动 .求 1)波函数 解:写出波函数的标准式
振动向右传播 滞后的时间
x ∆t = u
t 时刻点 P 的运动
=
t-x/u时刻点 的运动 时刻点O 时刻点
P点振动方程
yP
t
= yO
t−x u
x = A cos[ω (t − ) + ϕ0 ] u
点选取的任意性,得波函数即上式。 由P点选取的任意性,得波函数即上式。 太原理工大学物理系
方法之二
相位落后法
8m 5m 9m
−2
λ = 10 m
C B o A D 点 C 的相位比点 A 超前 AC −2 yC = 3 × 10 cos[4 π t + 2 π ]
x
点的坐标x= 带入波函数 将D点的坐标 =9m带入波函数 点的坐标
−2
λ 13 −2 = 3 × 10 cos[4 π t + π] 5
t 9 y D = 3 ×10 cos[2 π( − )](m) 0.5 10
12§12-2 平面简谐波的波函数 介质中任一质点( 介质中任一质点(坐标为 x)相对其平衡位置的 ) 位移( 位移(坐标为 y)随时间的变化关系,即 y ( x, t ) )随时间的变化关系, 称为波函数. 称为波函数.
y = y ( x, t )
各质点相对平 衡位置的位移 衡位置的位移 波线上各质点 平衡位置 平衡位置
平面简谐波的波函数解读
第十章 波动
5
物理学
第五版
10-2 平面简谐波的波函数二源自波函数的物理含义2π
2πx y A cos t
1 x一定, t 变化 令
x
y
则 y A cost
O
t
表示 x点处质点的振动方程( y — t 的关系)
y( x, t ) y( x, t T ) (波具有时间的周期性)
8m C B
第十章
0
2.0
t 1.0 s
第十章
x/m
-1.0
时刻波形图
波动
14
物理学
第五版
10-2 平面简谐波的波函数
(3) x 0.5m 处质点的振动规律并作图 t x π y 1.0 cos[ 2 π( ) ] 2.0 2.0 2 x 0.5m 处质点的振动方程
y cos[π t π] (m)
物理学
第五版
10-2 平面简谐波的波函数
一
平面简谐波的波函数
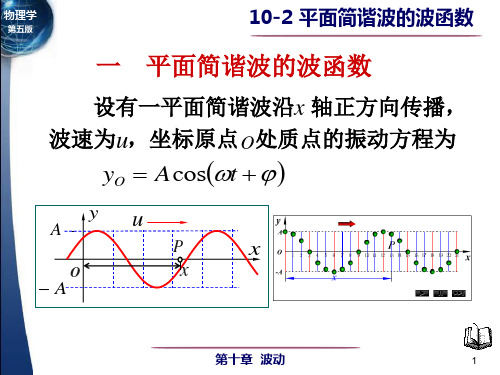
设有一平面简谐波沿x 轴正方向传播, 波速为u,坐标原点 O 处质点的振动方程为
yO A cost
u
P
A
y
x
A
O
x
第十章
波动
1
物理学
第五版
10-2 平面简谐波的波函数
yO A cost
yO 表示质点O 在 t 时刻离开平衡位置的距离. 考察波线上 P 点(坐标 x ), P 点比 O 点的 x 振动落后 t , P 点在 t 时刻的位移是 O 点
y
o
第十章 波动
x
8
物理学
第五版
5
物理学
第五版
10-2 平面简谐波的波函数二源自波函数的物理含义2π
2πx y A cos t
1 x一定, t 变化 令
x
y
则 y A cost
O
t
表示 x点处质点的振动方程( y — t 的关系)
y( x, t ) y( x, t T ) (波具有时间的周期性)
8m C B
第十章
0
2.0
t 1.0 s
第十章
x/m
-1.0
时刻波形图
波动
14
物理学
第五版
10-2 平面简谐波的波函数
(3) x 0.5m 处质点的振动规律并作图 t x π y 1.0 cos[ 2 π( ) ] 2.0 2.0 2 x 0.5m 处质点的振动方程
y cos[π t π] (m)
物理学
第五版
10-2 平面简谐波的波函数
一
平面简谐波的波函数
设有一平面简谐波沿x 轴正方向传播, 波速为u,坐标原点 O 处质点的振动方程为
yO A cost
u
P
A
y
x
A
O
x
第十章
波动
1
物理学
第五版
10-2 平面简谐波的波函数
yO A cost
yO 表示质点O 在 t 时刻离开平衡位置的距离. 考察波线上 P 点(坐标 x ), P 点比 O 点的 x 振动落后 t , P 点在 t 时刻的位移是 O 点
y
o
第十章 波动
x
8
物理学
第五版
§15-2 平面简谐波的波函数.
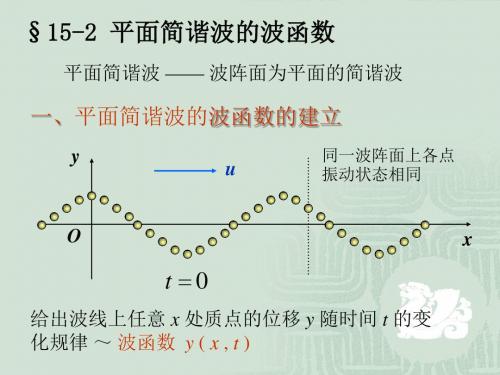
解法二
y(cm)
Ⅰ
P
O
1
u Ⅱ
234
56
x(cm)
设 P 振动表达式 yP ( t ) Acos( t )
根据 P 点的
A Acos 0
初始条件,
yP ( t ) Acos t 0.01cos t
波函数 y(x,t) 0.01cos (t x 0.01)
y(x,t) Acos 2 ( t x ) Acos( t kx) T
y(x,t) Acos( t kx)
k 2
角波数
沿x 轴负方向传播的平面简谐波的表达式
y
u
o
P
x
x O 点简谐运动方程: y0 Acost
P 点的运动方程为:
y(x,t) Acos (t x)
y(x,t) Acos 2 ( t x ) T
x 一定。令x=x1,则质点位移y 仅是时间t 的函数。
即
y
Acos
t
2
x1
上式代表x1 处质点在其平衡位置附近以角频率w 作 简谐运动。 y
A
O
t
t 一定。令t=t1,则质点位移y 仅是x 的函数。
2 x
即 y Acos t1
O
Ax
y0( t ) 3cos(4 t )
波函数
y(x,t) 3cos[4 ( t x ) ]
20
作业:P84 15-4 15-8
2
2
y0
(
t
)
0.01cos(
t
平面简谐波的波函数标准形式

平面简谐波的波函数表达式
平面简谐波的波函数表达式是y=Asin(ωx+φ),其中A为振幅,2π/ω为周期,φ为初相
平面简谐波是最基本的波动形式。
平面传播时,若介质中体元均按余弦(或正弦)规律运动,就叫平面简谐波。
如果所传播的是谐振动,且波所到之处,媒质中各质点均做同频率、同振幅的谐振动,这样的波称为简谐波,也叫余弦波或正弦波。
如果简谐波的波面是平面,这样的简谐波称为平面简谐波。
平面简谐波传播时,介质中各质点都作同一频率的简谐振动,但在任一时刻,各点的振动相位一般不同,它们的位移也不相同,但根据波阵面的定义知道,
在任一时刻处在同一波阵面上的各点有相同的相位,它们离开各自的平衡位置有相同的位移。
简谐平面波都往往被简称为简谐波或者平面波,后者频繁在量子力学中使用。
本书的量子力学部分也会大量使用平面波这个简称,无论波动是几维的。
广义来说,平面波未必是简谐的,只需要等相位面都是平面即可:例如波长随空间变化,频率随时间变化也仍然是平面波。
而简谐波也未必是平面的,球面波也可以在径向也是简谐函数。
11-2 平面简谐波的波函数

-
x u
)=
Acos ω
t
-
x u
+
0
上页 下页 返回 退出
P处质点在时刻t 的位移为:
yP (t) =
Acos ω
t
-
x u
+
0
波 函 数
因此,波线上任一点在任一时刻的位移都能 由上式给出。此即所求的沿x 轴正方向前进 的平面简谐波的波函数。
沿x轴负方向传播的平面简谐波的波函数:
上页 下页 返回 退出
2
1
2
x2 x1
2
x
x、t 都变化:
实线:t1 时刻波形;虚线:t2 时刻波形
y
u
o
x
x x
上页 下页 返回 退出
当t=t1时,y
A
cos
t1
x u
0
当t=
t1+Δt时,y
A
cos
t1
t
x u
0
在t1和t1+Δt时刻,对应的位移用x1和x2表示,则
y(t1)
A cos
t1
x1 u
0
y
A cos
2
(
t
mx
)
0
y Acos(t mkx 0 )
k 2 角波数
y
y
A cos(t
Aei
(t
mx u
)0
m2 x
i (t
Ae
0
mk ) u
)
上页 下页 返回 退出
波动表式的意义:
x 一定:令x=x1,则质点位移y 仅是时间t 的函数。
即
y
A
cos
平面简谐波波函数

大学物理
波动学基础
第2讲 平面简谐波波函数
平面简谐波波函数
平面简谐波波函数
在均匀的、无吸收的介质中, 波源作简谐运动而形成 平面简谐波.
如何描述一维平面简谐波即建立波动表达式?其所表 示的物理意义是什么?
平面简谐波波函数
(一)波函数的建立 y = y(x,t )
任选参考点 O 为 x 轴的坐标原点, O 点处 质点的简谐运动方程 为
y
∆x
O x1
x2 x
y
=
A cos ω⎜⎛ t1 ⎝
−
x u
⎞ ⎟ ⎠
相位差为
∆ϕ
= ϕ1
−ϕ2
=
2π⎜⎛ t ⎝T
−
x1 λ
⎞ ⎟
−
2π⎜⎛
t
⎠ ⎝T
−
x2 λ
⎞ ⎟ ⎠
=
2π
x2
− λ
x1
波程差 ∆x = x2 − x1 相位差和波程差的关系: ∆ϕ = 2π ∆x
λ
平面简谐波波函数
(3)当 t , x 都变时, y = y(x, t), 表示所有质元在任意时刻 的位移情况.
解: 由图得
A = 2.5cm = 0.025m,λ = 40m,
T = 4s,ω = 2π = π s−1,u = λ = 10m ⋅s−1
y (cm )
T2
Tuv
20
5
x(m )
OP
波动表达式为
y
=
A
cos
⎡ ⎢ω ⎣
⎜⎛ t ⎝
−
x u
⎞ ⎟ ⎠
+
⎤ ϕ⎥
⎦
代入 t = 0, x = 0 , y = 0 ⇒ cosϕ = 0
波动学基础
第2讲 平面简谐波波函数
平面简谐波波函数
平面简谐波波函数
在均匀的、无吸收的介质中, 波源作简谐运动而形成 平面简谐波.
如何描述一维平面简谐波即建立波动表达式?其所表 示的物理意义是什么?
平面简谐波波函数
(一)波函数的建立 y = y(x,t )
任选参考点 O 为 x 轴的坐标原点, O 点处 质点的简谐运动方程 为
y
∆x
O x1
x2 x
y
=
A cos ω⎜⎛ t1 ⎝
−
x u
⎞ ⎟ ⎠
相位差为
∆ϕ
= ϕ1
−ϕ2
=
2π⎜⎛ t ⎝T
−
x1 λ
⎞ ⎟
−
2π⎜⎛
t
⎠ ⎝T
−
x2 λ
⎞ ⎟ ⎠
=
2π
x2
− λ
x1
波程差 ∆x = x2 − x1 相位差和波程差的关系: ∆ϕ = 2π ∆x
λ
平面简谐波波函数
(3)当 t , x 都变时, y = y(x, t), 表示所有质元在任意时刻 的位移情况.
解: 由图得
A = 2.5cm = 0.025m,λ = 40m,
T = 4s,ω = 2π = π s−1,u = λ = 10m ⋅s−1
y (cm )
T2
Tuv
20
5
x(m )
OP
波动表达式为
y
=
A
cos
⎡ ⎢ω ⎣
⎜⎛ t ⎝
−
x u
⎞ ⎟ ⎠
+
⎤ ϕ⎥
⎦
代入 t = 0, x = 0 , y = 0 ⇒ cosϕ = 0
大学物理平面简谐波的波函数精选精品文档
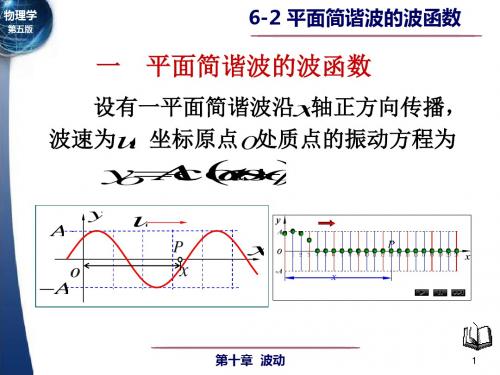
u
1m 0
λ10m 8 m 5 m 9 m
C
B oA
Dx
第十章 波动
21
物理学
第五版
选择进入下一节:
本章目录
6-1 机械波的几个概念
6-2 平面简谐波的波函数
6-3 波的能量 能流密度 6-4 惠更斯原理 波的衍射和干涉
6-5 驻波
6-6 多普勒效应
第十章 波动
22
x
A cos
t
2πx
第十章 波动
4
物理学
第五版
6-2 平面简谐波的波函数
波函数
yAcos(t[x)]
u
质点的振动速度,加速度
v y A si n (t [x)]
t
u
a 2 t2 y 2A co (ts[u x)]
第五版
6-2 平面简谐波的波函数
(3) x0.5m处质点的振动规律并作图
y1.0co2π s([t x)π] 2.0 2.0 2
x0.5m处质点的振动方程
ycoπst[π](m)
y
y/m
3
3
1.0
*
4O
2
0 2* 1.0 *4 2.0 * t / s
1 -1.0*1
*
x0.5m处质点的振动曲线
第十章 波动
15
物理学
第五版
6-2 平面简谐波的波函数
例2 一平面简谐波以速度u20ms-1
沿直线传播,波线上点 A 的简谐运动方 程
yA31 0 2co4π st)(; ( y, t单位分别为m,s).
平面简谐波的波函数

课堂练习 图示为 t = 1s 时的波形曲线,求波动方程。
提示 关键:求解原点o处质元初位相 o !
(t 0)
o
2
A
y
y(m)
0.08 m/s
0.04
(t 1)
t
25
(1
0)
2
5
o
2
2
5
9
10
o
P
0.20
x (m)
t 1s
答案: y
0.04 cos [2
5
(t
x ) 0.08
9 ]
10
(
t
x u
)
o
]
(t
x u
)
o
(t
t
x
x u
)
o
x ut
y
u
☻波速即为相位传播速度 o
( 相速 ) 。
☻行波或前进波。
x
ut
·7 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
三、微分形式的平面波波动方程
对一般的平面波:
xoy系:y f (x, t) xoy系: y f (x)
y
A
cos
[
(t
x u
)
o
]
波函数亦称 波动方程 。
ut
Ao y(0 ,t )
Δt Ax
(x,t)
o
y(x,t) y
t o
·3 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
波动方程 的几种标准形式: y
y
A
cos
[
(t
x u
提示 关键:求解原点o处质元初位相 o !
(t 0)
o
2
A
y
y(m)
0.08 m/s
0.04
(t 1)
t
25
(1
0)
2
5
o
2
2
5
9
10
o
P
0.20
x (m)
t 1s
答案: y
0.04 cos [2
5
(t
x ) 0.08
9 ]
10
(
t
x u
)
o
]
(t
x u
)
o
(t
t
x
x u
)
o
x ut
y
u
☻波速即为相位传播速度 o
( 相速 ) 。
☻行波或前进波。
x
ut
·7 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
三、微分形式的平面波波动方程
对一般的平面波:
xoy系:y f (x, t) xoy系: y f (x)
y
A
cos
[
(t
x u
)
o
]
波函数亦称 波动方程 。
ut
Ao y(0 ,t )
Δt Ax
(x,t)
o
y(x,t) y
t o
·3 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
波动方程 的几种标准形式: y
y
A
cos
[
(t
x u
平面简谐波的波函数

x t u 若点P的振动落后于点O,则波动方程为 y yo t t
y yo t t
2.已知任意一点Q的振动方程,求解波动方程 方法一 利用点Q的振动方程和距点O的距离求解O 点振动方程后,利用1中的方法求波动方程。 方法二 考察点P的振动相对于Q点是超前还是落后 的,直接利用 y yo t t 来求波动方程。
5
物理学
第五版
10-2 平面简谐波的波函数
二
波函数的物理含义
2π
2πx y A cos t
1 x一定, t 变化 令
x
y
则 y A cost
O
t
表示 x点处质点的振动方程( y — t 的关系)
y ( x, t ) y ( x, t T ) (波具有时间的周期性)
第十章 波动
6
物理学
第五版
10-2 平面简谐波的波函数
2πx 2 t 一定 x 变化 y A cos t 令 t C(定值) 2πx 则 y A cos 该方程表示 t 时刻波传播方向上各质点 的位移, 即 t 时刻的波形(y — x的关系)
波在某点的相位反映该点媒质的“运动状态”。
所以简谐波的传播也是媒质振动相位的传播。
设 t 时刻 x 处的相位经 dt 传到(x +dx)处,
x x d x 则应有 (t ) ( t d t) u u
dx —— 相速度(相速) u 于是得到 dt 即简谐波的波速就是相速。
第十章 波动
t x x0 u
11
物理学
第五版
平面简谐波的波函数

解 确定坐标原点的 Y
振动初相0
A
由图知:t=0时, A/2
u=100m /s
x=0处的质点位于
0
1
X(
A/2处 且向位移正方向运动
-A
m)
由图知:t=0时, x=1m处的质点位于平 衡位置处且向位移负方
向运动
第十章 波动
21
物理学
第五版
0
π 3
,
2.4m,
u 100(m/s)
T /u 0.024s
在 理学
第五版
左行波的波函数:
p点的相位超前于O点相位:
所以 p点的振动方程,也就是左行波的波函数为:
第十章 波动
6
物理学
第五版
波函数的几种常用形式
第十章 波动
7
物理学
第五版
演示实验安排
周三 第3节 7班 第4节 8班
第十章 波动
8
物理学
第五版
二 波函数的物理含义
1 x一定,t变化
解
确定坐标原点的振动初相0
由:t=0时,x=0处的质点位于-A/2处 且向位移的负方向运动,知
第十章 波动
18
物第理五例版学 4.一平面简谐波,波长为12m,沿 ox轴负向传播. 图(a)所示为x=1.0m处质点的振动曲线,求波动方 程。
解:t=0时此质点的相位
0.40 0.20
5.0
t/s
t=5s时质点第一次回到平
第十章 波动
28
物理学
第五版
(1/4) 2A2
o
EP Ek
Y
WpWk x = x0
Tt
y
第十章 波动
t
平面简谐波的波函数
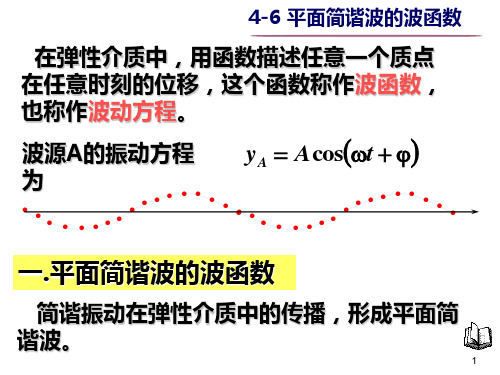
−2
−1
ϕ C − ϕ D = −2π
λ = 10 m
xC − xD
λ
− 22 = −2π = 4.4π 10
9m
u
8m C B 5m
λ = 10 m
D
oA
x
25
物理学
第五版
4-6 平面简谐波的波函数
例:已知 P 点的振动曲线如图,平面简谐 点的振动曲线如图, 轴正向传播,波长λ 波沿x轴正向传播,波长λ=4.0m。求平面波 波函数。 波函数。 y1.0cm/ div 解:首先根据振 动曲线, 动曲线,求出 P 点的振动方程, 点的振动方程, 然后任意取一点 Q ,参照两点间 的相位差, 的相位差,求波 函数。 函数。
解法 二
π
2
] m
写出波动方程的标准式
t x y = A cos[ 2π ( − ) + ϕ ] T λ
16
物理学
第五版
4-6 平面简谐波的波函数
t x y = A cos[ 2π ( − ) + ϕ ] T λ t=0 x=0
π ∂y y = 0, v = > 0 ϕ=− 2 ∂t t x π y = cos[ 2 π ( − ) − ] (m) 2 .0 2 .0 2
O
v A
y ω
17
物理学
第五版
4-6 平面简谐波的波函数
(2)求 (2)求 t = 1 . 0 s 波形图 t x π y = 1.0 cos[ 2 π ( − )− ] 2 .0 2 .0 2 π y = 1 .0 cos[ − π x ] 2 t = 1 .0 s = sin πx (m) 波形方程
y 0 = A cos[ ω t + ϕ ]
大学物理 平面简谐波的波函数

17
3)写出传播方向上点C、点D 的简谐运动方程
u
C
8m
y A 310 cos( 4 π t )m 10m 5m 9m
B
2
oA
D
x
AC
点 C 的相位比点 A 超前
cos( 4 π t 2 π )m 13 2 3 10 cos( 4 π t π)m 5 点 D 的相位落后于点 A AD 2 y D 3 10 cos( 4 π t 2 π )m 9 2 3 10 cos( 4 π t π)m 5
4
波动方程的其它形式
t x y ( x,t ) A cos[ 2 π( ) ] T λ y( x, t ) A cos(t kx )
质点的振动速度,加速度 角波数 k 2 π
(wave number)
y x v A sin[ (t ) ] t u
分析:
2 3 ( D) 2
( B)
,
由波形图可判定O点在该时刻的振动方向竖直向 上(如图示)
A x
3 由旋转矢量图可知此时的相位为 2
23
3.在下面几种说法中,正确的说法是: (C)
(A)波源不动时,波源的振动周期与波动的周期在数 值上是不同的。 (B)在波传播方向上的任一质点振动位相总是比波源 的位相超前。 (C)在波传播方向上的任一质点振动位相总是比波源 的位相滞后。 (D) 波源的振动速度与波速相同。
在t=1/v时刻:
1 v | x x2 2A sin 2 (1 ) 2A 4
即速度比为-1。
3 v | x x1 2A sin 2 (1 ) 2A 4
9-2平面简谐波的波函数

x ut
第九章 机械9波
9-2 平面简谐波的波函数
思考 1)给出下列波函数所表示的波的传播方向
和 x 0 点的初相位.
y Acos2π ( t x )
T
(向x 轴正向传播,
π)
y Acos (t x) (向x 轴负向传播 , π )
u
2)平面简谐波的波函数为 y Acos(Bt Cx)
u 1.50103 ms1
第九章 机械12波
9-2 平面简谐波的波函数
例9-2 一平面简谐波沿 Ox 轴正方向传播,波速
u 200m s-1。位于 xB 145m 处的 B 点的简谐运
动方程为
yB
0.1cos(20πt
π) 2
式中,yB的单位
为 m , t 的单位为s。求波函数。
解 x 处质点的振动 在时间上比xB 处质点
的振动落后 x xB u
y
A cos
(t
x
xB u
)
B
0.1cos
20π(t
x
145) 200
π 2
0.1cos
20π(t
x) 200
π
第九章 机械13波
第九章 机械6波
9-2 平面简谐波的波函数
2 当 t 一定时,波函数表示该时刻波线上各点
相对其平衡位置的位移,即此刻的波形.
y
A cos[ (t0
x) u
]
A y u
x
O
A
y(x,t) y(x ,t)(波具有空间的周期性)
第九章 机械9波
9-2 平面简谐波的波函数
思考 1)给出下列波函数所表示的波的传播方向
和 x 0 点的初相位.
y Acos2π ( t x )
T
(向x 轴正向传播,
π)
y Acos (t x) (向x 轴负向传播 , π )
u
2)平面简谐波的波函数为 y Acos(Bt Cx)
u 1.50103 ms1
第九章 机械12波
9-2 平面简谐波的波函数
例9-2 一平面简谐波沿 Ox 轴正方向传播,波速
u 200m s-1。位于 xB 145m 处的 B 点的简谐运
动方程为
yB
0.1cos(20πt
π) 2
式中,yB的单位
为 m , t 的单位为s。求波函数。
解 x 处质点的振动 在时间上比xB 处质点
的振动落后 x xB u
y
A cos
(t
x
xB u
)
B
0.1cos
20π(t
x
145) 200
π 2
0.1cos
20π(t
x) 200
π
第九章 机械13波
第九章 机械6波
9-2 平面简谐波的波函数
2 当 t 一定时,波函数表示该时刻波线上各点
相对其平衡位置的位移,即此刻的波形.
y
A cos[ (t0
x) u
]
A y u
x
O
A
y(x,t) y(x ,t)(波具有空间的周期性)
6_2 平面简谐波的波函数

2
4)
8 2π 1.6π B C 2π 10 x x 22 C D 2π C D 2π 4.4π 10
y A cos 2π ( t x ) (向x 轴正向传播 T x y A cos ( t ) (向x 轴负向传播 u
y ( x, t ) y ( x , t ) (波具有空间的周期性)
距离原点O为x1和x2的两质点的相位分别为
x1 t x ) 2π ( 1) u T x t x 2 (t 2 ) 2 π ( 2 ) u T
1 (t
π t 1.0s波形方程 y 1.0 cos( 2 π x) 1.0 sin(π x)
y/m
1.0
o
-1.0
2.0
x/m
t 1.0 s 时刻波形图
3) x 0.5m
处质点的振动方程
y 1.0 cos(π t π)
y
3 1.0 2 0
y/m
3 * 2 * 4 *
4
O
1
y A x轴负向 u
t x y(x,t) A cos[ 2 π( ) ] T λ
2π 2 π , T
y ( x, t ) A cos(t kx )
角波数
u
T
k
2π
沿 x 轴正向传播的平面简谐波,已知距O点x0的Q点的振动规律为
1.0
x 0.5 m
-1.0 *1
* t /s 2.0 *
处质点的振动曲线
例3 一平面简谐波以速度 谐运动方程
u 20m / s 沿直线传播,波线上点 A 的简 y A (3102 ) cos(4 π t ) .
4)
8 2π 1.6π B C 2π 10 x x 22 C D 2π C D 2π 4.4π 10
y A cos 2π ( t x ) (向x 轴正向传播 T x y A cos ( t ) (向x 轴负向传播 u
y ( x, t ) y ( x , t ) (波具有空间的周期性)
距离原点O为x1和x2的两质点的相位分别为
x1 t x ) 2π ( 1) u T x t x 2 (t 2 ) 2 π ( 2 ) u T
1 (t
π t 1.0s波形方程 y 1.0 cos( 2 π x) 1.0 sin(π x)
y/m
1.0
o
-1.0
2.0
x/m
t 1.0 s 时刻波形图
3) x 0.5m
处质点的振动方程
y 1.0 cos(π t π)
y
3 1.0 2 0
y/m
3 * 2 * 4 *
4
O
1
y A x轴负向 u
t x y(x,t) A cos[ 2 π( ) ] T λ
2π 2 π , T
y ( x, t ) A cos(t kx )
角波数
u
T
k
2π
沿 x 轴正向传播的平面简谐波,已知距O点x0的Q点的振动规律为
1.0
x 0.5 m
-1.0 *1
* t /s 2.0 *
处质点的振动曲线
例3 一平面简谐波以速度 谐运动方程
u 20m / s 沿直线传播,波线上点 A 的简 y A (3102 ) cos(4 π t ) .
平面简谐波的波函数

x 波函数 y = A cosω t − + ϕ u t − x − π / 2 −2 y = 6 × 10 cos 800π 200
§2.平面简谐波的波函数 / 四.举例 平面简谐波的波函数 举例
x 波长、 ②.波长、频率 y = A cosω t − + ϕ 波长 u t − x − π / 2 y = 6 × 10 cos 800π 200 ω = 800π 2π 2π 1 T= = = s ω 800π 400
o
o
§2.平面简谐波的波函数 / 三.波函数的物理意义 平面简谐波的波函数 波函数的物理意义
x
4. 当 u 与 x 轴反向时取 −u 。
x y = A cos ω t + + ϕ u
四、举例 1.已知波函数求各物理量 1.已知波函数求各物理量 2.已知各物理量求波函数 已知各物理量求波函数
T=
2π
(2)同一时刻波线上坐标为
ω
= 0.8s,λ =uT=20m
δ ϕ=− ( x 2 − x1 ) = −2π λ λ
2π
x1
和
x 2 两点处质点振动的位相差
δ = x 2 − x1是波动传播到 x1 和 x 2 处的波程之差,上式就是同一时刻波 线上任意两点间位相差与波程差的关系.
δ π δ =x 2 − x1 = 10 − 8 = 2m时,ϕ =-2π = − λ 5
负号表示x2处的振动位相落后于x1处的振动位相.
(3)对于波线上任意一个给定点(x一定),在时间间隔Δt内的位相差
ϕ = ω ( t 2 − t1 ) = ω t
6-02 平面简谐波的波函数

写出波动式
t x π y 1.0 cos[ 2 π( ) ] (m) 2.0 2.0 2
t x y ( x,t ) A cos[ 2 π( ) ] T λ
2)求 t 1.0s 波形图.
t x π y 1.0 cos[ 2 π( ) ] 2.0 2.0 2
t 1.0s
2
3)写出传播方向上点C、点D 的简谐运动方 x 程 2 2 y 3 10 cos 4 π( t ) y A 3 10 cos4 π t 20
u
C
8m
5m
9m
10m
D
B
oA
2
x
把点 C 的坐标代入
13 yc 3 10 cos[ 4 π t π] 5
把点 D 的坐标代入
例1 已知波函数如下,求波长、周期和波速. y 5 cos π[2.50t 0.01x](cm).
解:(比较系数法). 把波动方程改写成
t x y A cos 2π ( ) T
比较得
2.50 0.01 y 5 cos 2 π[ t x] 2 2
2 T s 0.8 s 2.5 2cm 200 cm 0.01
y
u
x
x0
已知 x0点振动方程
O
x
y x0 A cos( t )
x x0 时间落后 u
x x0
任一点
x 比 x0
相位落后 2
任一点 x 振动方程——波函数
x x0 y A cos[ ( t ) ] u x x0 y A cos[ t 2 ]
y x v A sin[ (t ) ] t u 2 y x 2 a 2 A cos[ (t ) ] t u
平面简谐波波函数
平面简谐波的特点是,它的波形是一个不断振荡的正弦波,在时间t和空间x两个方向上都呈现出波动的特征。平面简谐波在许多物理学领域中都有广泛应用,例如电磁波、声波、光波等。
平面简谐波的波函数可以用数学工具,如幂级数或傅里叶级数来表示。这些工具可以帮助我们分析平面简谐波的特性,例如波长、周期、波速等。
平面简谐波(plane harmonic wave)是物理学中常用的一种波动形式。它是由两个正弦波叠加而成的,其中一个正弦波的波长和波速是定值,另一个正弦波的波长和波速是变化的。
平面简谐波的波函数可以用下面的公式表示:
f(x,,k是波数,ω是角速度,φ是相位。
平面简谐波的波函数可以用数学工具,如幂级数或傅里叶级数来表示。这些工具可以帮助我们分析平面简谐波的特性,例如波长、周期、波速等。
平面简谐波(plane harmonic wave)是物理学中常用的一种波动形式。它是由两个正弦波叠加而成的,其中一个正弦波的波长和波速是定值,另一个正弦波的波长和波速是变化的。
平面简谐波的波函数可以用下面的公式表示:
f(x,,k是波数,ω是角速度,φ是相位。
平面简谐波的波函数

方向传播。
若O点的振动方程为
y0 A cos( t 0 )
时间推迟方法
y A
u
P
x
O
A x
点O 的振动状态
y0 A cos( t 0 )
t x u
t ux 时刻点O 的运动
点P t 时刻点 P 的运动
P点在t时刻的位移为
y
A cos[ (t
x) u
0]
平面简谐波的波动方程
*若波以速度u 沿x轴负方向传 播, 则波函数为
能否写出波动表达式?形 式如何?
y
u
.P. x
x
y
A cos[ (t
x) u
0 ]
y A
u
P
x
O
A x
波函数的其它形式
y
A cos[ (t
x) u
0 ]
y
Acos[2 ( t
T
x
)
0 ]
y
A
cos[2
(
t
x
)
0 ]
y Acos(t kx 0 )
2 2 / T
u / T
k
2
角波数,为2π长度内所 包含的完整波形的个数
二、波函数的物理含义:
y
y
A
cos[(t0
x u
)
]
o
x
t t0
(3) 若x和t 都是变量,波函数表示波线上不同质点、不同时刻
的位移 (行波)
y Acos[(t x) ]
u
A:
(t
x u
)
ห้องสมุดไป่ตู้
0
B:
(t
t
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: 由图得
A 2.5cm 0.025m, 40m,
T 4s, 2π π s1,u 10ms1
ycm
T2
Tuv
20
5
xm
O
P
波动表达式为
y
Acos
t
x
u
代入 t 0, x 0 , y 0 cos 0
波形前移Δx,,由参考圆法得
由由参参考考圆圆法法得得由 参3π2考圆π法2得
所以波动表达式为
vP
0.025
π 2
sin π2
2
2100
3π 2
0.0)时刻uuu/
的振动状态,
所以有
y
Acost
x
u
——平面简谐波波动表达式
因为
2π 2π u
T
T
所以 yx,t Acos2π t x
T
(二)波函数的物理意义
平面简谐波波函数
y
Acos
t
x
u
(1)当 x= x11((常数常数常数常数))时,,
yy====yyyy((t)),表示表示
表振y示动 表方Ac示程os振xxxx1动处t方质程元xu1振的动处方质程元.的. 处质元的处质元的振动方程
表示各质元的位移分 布函
x
O x1
x2 x
y
Acost 1x
u
相位差为
12 2π
Tt
x1 2πTt
x2
2π
x2 x1
波程差 x x2 x1 相位差和波程差的关系: 2π x
平面简谐波波函数
(3)当 t, x都变时, y= y((xxxx,tt)))),表示所有质元在任意时刻表 示所有质元在任意时刻表示所有质元在任意时刻表示所
平面简谐波波函数
y 0.025cos 2πt10x 32πm
质点振速为
v y t
0.025
π 2
π
sin2
t
x
10
3π 1
2
ms
平面简谐波波函数
v 0.025 π2sinπ2t
1x0
3π 2
ms1
所以 P点(xxxx====22220000mmmm)在 t====2222ss时的速度为 时的 速度为时的速度为时的速度为
yx,t Acostx
u
(5)一般情况下
yx,t Acos tm
ux
平面简谐波波函数
例题 如图所示为一平面简谐横波在开始时刻(t= 0 )的 波形. 有关物理量的数据一并图示,已知周期 T= 4(s), 建立 该波的波动表达式,并求图中 P点经 2(s)后的振速.
ycm
20
OP
uv
5
xm
平面简谐波波函数
大学物理
波动学基础
第2讲 平面简谐波波函数
平面简谐波波函数
平面简谐波波函数
在均匀的、无吸收的介质中, 波源作简谐运动而形成 平面简谐波.
如何描述一维平面简谐波即建立波动表达式?其所表 示的物理意义是什么?
平面简谐波波函数
(一)波函数的建立 y yx,t
任选参考点 O为 x 轴的坐标原点, O点处 质点的简谐运动方程 为
相位:
t
xu1
y
初相位: x1
O
t
u
思考题: 波线上两个距离相差一个波长 的两个质点,
它们的振动方程有何不同?振动曲线相同吗?
平面简谐波波函数
(2)当 t= t11((常数常数常数常数))时,,yy====yyyy(xxxx),表示各质元的位移
数分即布波函形表图示. 各质元的位移分布函表y 示各质元的位移分布函
有质元在 任意时刻y 的位t时移刻情波况形. t+Δt时刻波形
O Y Y
x
x xut 波的传播方向 波的传播方向 称为由故图称波为形故沿称为x正故方称向为传行播波,.波速为u====ΔΔΔ波 方方Δxx的 向向/ΔΔ传波ΔΔ的t,故播传播
平面简谐波波函数
(4)当波动向 - x轴方向传播时, 波动表达式为
y Acost x0
y
uv
P
O
x
x
任取一点 P,,距离距离距离距离 OOOO点为点为点为点为 xxxx, 当振动传到当振动传到当振动传到当振动传到 PPPP点,,PPPP点 的振点的振点的振点的振动比 O点落后一段时间
t ux
平面简谐波波函数
P点在 t 时刻的振动状态就是 O点在(t-x/u)时刻)时刻
