第五章-概率和统计的数学实验
数学实验

数学实验: 概率统计F实验一,实验目的: 运用数学软件解决概率统计问题二,实验工具: WPS软件, SPSSS软件三,实验要求:1、写出相应软件命令及具体操作截图。
2、给出结果的截图并给出相应统计结论。
3、以实验报告的形式上交,实验报告的格式自己设计。
1、已知某地某品种10头成年母水牛的体高(cm)为:137,133,130,128,127,119,136,132,128,130。
求出均值、标准差、极差、中位数、变异系数及95%置信区间。
(30分)2、某食品企业厂生产瓶装矿泉水,其自动装罐机在正常工作状态时每罐净容量(单位为ml)具正态分布,且均值为500。
某日随机抽查了10瓶水,得结果如下:505,512,497,493,508,515,502,495,490,510,问罐装机该日工作是否正常?(30分)3、分别测定了10只大耳白家兔、11只青紫蓝家兔在停食18小时后正常血糖值如下表,已知其服从正态分布,问该两个品种家兔的正常血糖值是否有显著差异?(单位:kg)(40分)大耳白57 120 101 137 119 117 104 73 53 68青紫蓝89 36 82 50 39 32 57 82 96 31 88 四,实验内容:1、已知某地某品种10头成年母水牛的体高(cm)为:137,133,130,128,127,119,136,132,128,130。
求出均值、标准差、极差、中位数、变异系数及95%置信区间。
使用软件: WPS软件(1)数据输入:(2)计算均值: =AVERAGE(A2,A3,A4,A5,A6,A7,A8,A9,A10,A11)放入C2(3)计算标准差:=STDEV(A2,A3,A4,A5,A6,A7,A8,A9,A10,A11)放入D2(4)计算极差:=MAX(A2:A11)-MIN(A2:A11)放入E2(5)计算中位数:=MEDIAN(A2,A3,A4,A5,A6,A7,A8,A9,A10,A11) F2(6)计算变异系数:=D2/C2 G2(7)自由度: 9 H2(8)自信度:0.95 J2(9)计算t分布双侧分位数:=TINV(0.05,9) I2(10)抽样平均误差:=D2/SQRT(10) K2(11)允许误差:=I2*K2 L2(12)自信下限:=C2-L2 H5(13)自信上限:=C2+L2 I5实验结果:2、某食品企业厂生产瓶装矿泉水,其自动装罐机在正常工作状态时每罐净容量(单位为ml)具正态分布,且均值为500。
高中数学第五章统计与概率5.3概率5.3.2事件之间的关系与运算教学1b高一必修第二册数学

第二十一页,共二十二页。
内容(nèiróng)总结
第五章 统计(tǒngjì)与概率。说出每一事件的实际意义,并尝试理解上述各事件之间的关系.。2理解,互斥事件和对立事件的概念 及关系。会用互斥事件与对立事件的概念公式求概率。3.会用自然语言、符号语言表示事件之间的关系与运算,加强数学抽象素养的培
2021/12/9
第十四页,共二十二页。
即时训练3 已知数学考试中,李明名成绩高于90分的概率为0.3,不低于60分且不高于90 分的概率为0.5,求: (1)李明成绩不低于60分的概率; (2)李明成绩低于60分的概率。5事件(shìjiàn)的混合运算。
2021/12/9
第十五页,共二十二页。
第五章 统计 与概率 (tǒngjì)
2021/12/9
第一页,共二十二页。
5.3 概率(gàilǜ)
5.3.2 事件(shìjiàn)之间的关系与运算
2021/12/9
第二页,共二十二页。
5.3.2 事件(shìjiàn)之间的关系与运 算
2021/12/9
第三页,共二十二页。
【导入新课】 回顾1.集合间的运算(yùn suàn)及关系
2021/12/9
第七页,共二十二页。
问题探究二:事件的和(并) (1)给定事件A,B。由所有A中的样本点与所有B中的样本点组成的事件, 称为A与B的和(或并),记作A+B(或A∪B)。 (2)事件A+B发生(fāshēng),则当且仅当事件A与事件B中至少有一个发生。
2021/12/9
第八页,共二十二页。
2021/12/9
第九页,共二十二页。
P(A)≤P(A+B) , P(B)≤P(A+B) , P(A+B)≤P(A)+P(B)
西安交大西工大 考研备考期末复习 概率论与数理统计 第五章一维随机变量2

一、问题的思考
例1(一个著名的古典概率问题——赌金分配问题)
假如在一个比赛中赢6次才算赢,赌徒甲已经赢5 次,而赌徒乙赢2次,这时中断赌博,问总的赌金应 该如何分配?
一、问题的思考
1.试验背景
贝努里试验:只有两个可能结果的随机试验。 n重贝努里试验:重复独立进行n次贝努里试验 (n次重复独立试验)。 需要考察的问题:
实例6 某公共汽车站每隔 5 分钟有一辆汽车通 过, 如果某人到达该车站的时刻是随机的, 则
(e) 此人的等车时间,
是一个随机变量.
且 ξ(e) 的所有可
能取值为: [0,5].
实例7 随机变量 ξ 为“测量某零件尺寸时的测量
误差”.
则 ξ 的取值范围为 (a, b) .
实例8 随机变量 η 为“射击时偏离靶心的距离”.
若 Y1 ~ B(1, p) ,,Yn ~ B(1, p),且相互独立, X Y1 Yn ,则 X ~ B(n, p)
结论:服从二项分布的随机变量可以表示成独立的 两点分布的随机变量之和。
二项分布描述的是n重贝努里试验中出现“成功” 次数X的概率分布。
二、二项分布的计算
(续)对例1的解答:
设赌徒甲和赌徒乙,他们赢一局的概率分别为p和 q=1-p;X表示赌徒甲在4次试验中赢的次数,Y表示赌 徒乙在4次试验中赢的次数,则
2. 随机变量的引入
实例1 在一装有红球、白球的袋中任摸一个球, 观察摸出球的颜色.
S={红色、白色} ?
非数量 可采用下列方法
将 S 数量化
(e)
红色 白色
S
1 0R
即有 ξ (红色)=1 ,
ξ (白色)=0.
数学趣味实验探索概率与统计

数学趣味实验探索概率与统计概率与统计是数学中非常重要的分支,通过实验探索概率与统计可以增加学生对这一概念的理解和兴趣。
本文将介绍几个有趣的数学实验,通过这些实验,学生可以深入了解概率与统计的概念,并在实践中感受其中的乐趣。
实验一:硬币实验材料:一枚硬币步骤:1. 同学们以一个简单问题开始这个实验:“抛掷一枚硬币,正面朝上的概率是多少?”2. 让学生分别独自进行10次试验,记录每次试验中正面朝上的次数。
3. 让学生汇总数据并计算正面朝上的概率。
实验二:骰子实验材料:一颗六面骰子步骤:1. 随机选择一个学生进行抛掷骰子实验。
2. 让学生记录每次试验的结果,并统计每个数字出现的次数。
3. 让学生将试验结果汇总,并计算每个数字出现的概率。
实验三:袋子实验材料:一袋彩色球步骤:1. 准备一袋彩色球,每个颜色的球数可以根据实际情况进行设置(例如5个红球,3个蓝球,2个绿球)。
2. 让学生闭眼从袋子中摸出一个球,并记录颜色。
3. 将摸出的球放回袋子中,重复多次实验,让学生记录每个颜色球的出现次数。
4. 让学生计算每个颜色球被摸出的概率。
实验四:生日实验材料:学生名单步骤:1. 让每个学生记录自己的生日(不需要具体年份)。
2. 让学生将自己的生日加入到一个大的生日表中。
3. 分析生日表,统计每个月中生日的分布情况,并计算生日在每个月出现的概率。
通过以上四个实验,学生可以亲身参与概率与统计的实际探索,并通过实验结果直观地了解概率和统计的概念。
同时,这些实验可以帮助学生培养观察、记录和分析数据的能力,提高他们的数学素养和逻辑思维能力。
在实施这些实验的过程中,教师应引导学生思考实验结果的意义,并与他们展开讨论。
通过对实验结果的分析和讨论,学生能够更深入地理解概率和统计的原理,并将这些原理应用到日常生活中。
总结:通过数学趣味实验,学生可以在实践中探索概率与统计的知识,培养他们对数学的兴趣和理解。
实验不仅可以增加学生对概率与统计概念的认识,还能锻炼他们的观察、记录和分析能力。
概率论与数理统计 第5章

n
n
性质2.(分布可加性):若X~2(n1),Y~2(n2),X与 Y独立,则
X + Y~2(n1+n2 )
3、2分布表及有关计算
(1)构成 P{2(n)>λ}=α,已知n, α可查表求得λ; (2)有关计算P 2 (n) 2 (n) 称为上侧α分位数
例5.1 设 X ~ N ( , 2 ) (X1,X2,…,Xn)为X的一个样本,
求(X1,X2,…,Xn)的密度。 解 (X1,X2,…,Xn)为X的一个样本,故
X i ~ N ( , 2 )
n
i 1,2,, n
f ( x1 , x2 ,, xn ) f ( xi )
16 2
解
i 1,2,,16
2 1 16 2 2 P ( X i ) P 8 2 (16) 16 2 16 i 1
2—分布的密度函数f(y)曲线
n/2 1 f ( y) 2 ( n / 2) y 0,
n y 1 2 2
e , y0 y0
2 例5.4 X ~ N ( , ) (X1,X2,X3)为X的一个样本
X 1 X 2 X 3 的分布。 求
(n)为整体记号
2
2 (n) 2 2 查表得 0 ( 25 ) 34 . 382 10) 18.307 .1 0.05 (
1 当n充分大时,近似有 (n ) (u 2n - 1) 2 2
2
练习1. P(2(n)<s)=1-p ∵P(2(n) < s)=1- P(2(n) s )=1-p ∴ P(2(n) s )=p 2 s p (n) 练习2. P(2(11)>s)=0.05,求s
_新教材高中数学第五章统计与概率

D.10张票中有1 张奖票,10人去摸,无论谁先摸,摸到奖票的概率
都是0.1
【答案】
D
(2)我们知道,每次抛掷硬币的结果出现正、反的概率都为0.5,则连
续抛掷质地均匀的硬币两次,是否一定出现“一次正面向上,一次反
面向上”呢?
【解析】 不一定.这是因为统计规律不同于确定的数学规律,对于具体的一
次试验而言,它带有很大的随机性(即偶然性),通过具体试验可以知道除上述结
状元随笔 (1)正确理解频率与概率之间的关系
随机事件的频率,是指事件发生的次数与试验总次数的比值,它具有一
定的稳定性,总在某个常数附近摆动,且随着试验次数的不断增多,这种
摆动的幅度越来越小.我们给这个常数取一个名字,叫做这个随机事件的
概率.概率可以看成频率在理论上的期望值,它从数量上反映了随机事件
发生的可能性的大小.频率在大量重复试验的前提下可以近似地作为这个
事件的概率.
(2)概率与频率的区别与联系:
频率
概率
频率反映了一个随机事件发 概率是一个确定的值,它反映
区别
生的频繁程度,是随机的 随机事件发生的可能性的大小
频率是概率的估计值,随着试验次数的增加,频率会越来越
联系
接近概率
基 础 自 测
(2)将“60分~69分”记为事件B,则P(B)≈0.140;
(3)将“60分以上”记为事件C,则P(C)≈0.067+0.282+0.403+0.140=0.892.
题型3 频率分布直方图的应用[经典例题]
例3 (1)在某次赛车中,50名参赛选手的成
绩(单位:min)全部介于13到18之间(包括13和
1
,是指试验次数相当
1 000
高中概率数学实验报告

高中概率数学实验报告实验目的通过进行概率实验,加深对概率理论的理解,探究概率实验和理论概率的关系。
实验器材- 骰子- 纸牌- 两个硬币实验步骤1. 首先,我们进行了一个简单的抛硬币实验。
通过抛两个硬币,我们观察到硬币的正反面朝上的情况,并记录下来。
共进行了100次抛硬币实验。
2. 接着,我们进行了掷骰子实验。
我们使用一个六面骰子,进行了300次掷骰子实验。
记录下了每次出现的骰子点数。
3. 最后,我们进行了一次纸牌实验。
我们使用了一副标准的扑克牌,包括52张牌,不计大小王。
我们从中抽取了30张牌,记录下了每张牌的花色和点数。
结果分析抛硬币实验我们进行了100次抛硬币实验,记录下了每次抛硬币的结果。
通过统计,我们发现正面朝上的次数为56次,反面朝上的次数为44次。
根据统计学原理,我们得出正面和反面朝上的概率分别为0.56和0.44。
实验结果与理论概率相差较小,这说明我们的实验结果与理论概率一致,加深了我们对硬币抛掷的概率理解。
掷骰子实验我们进行了300次掷骰子实验,记录下了每次点数的结果。
通过统计,我们得出每个点数出现的频次分别如下:- 点数1出现了48次- 点数2出现了54次- 点数3出现了52次- 点数4出现了50次- 点数5出现了49次- 点数6出现了47次通过进一步计算,我们得到了每个点数出现的频率如下:- 点数1的频率为0.16- 点数2的频率为0.18- 点数3的频率为0.17- 点数4的频率为0.16- 点数5的频率为0.16- 点数6的频率为0.15与理论概率进行对比发现,实验结果与理论概率也符合得较好,加深了我们对骰子点数的概率理解。
纸牌实验我们从一副标准扑克牌中抽取了30张牌,记录下了每张牌的花色和点数。
通过统计,我们得出了每个花色和点数出现的频次。
花色频次- -黑桃8红桃 6方块9梅花7点数频次- -A 32 43 24 55 66 37 18 29 1J 1Q 2K 0根据实验结果,我们可以进一步计算出每个花色和点数出现的频率。
概率论与数理统计----第五章大数定律及中心极限定理

= 1 − Φ(3.54)
=0.0002
一箱味精净重大于20500的概率为 的概率为0.0002. 一箱味精净重大于 的概率为
推论:
特别,若X~B(n,p),则当n充分大时, 特别, ~B(n 则当n充分大时,
X~N(np,npq) X~N(np,npq) np
若随机变量X~B( X~B(n, ),则对任意实数x有 ),则对任意实数 即 若随机变量X~B( ,p),则对任意实数 有
不等式证明 P{-1<X<2n+1}≥(2n+1)/(n+1)(n+1)
3. 设P{|X-E(X)|<ε}不小于 不小于0.9,D(X)=0.009.则用 不小于 则用
切比绍夫不等式估计ε的 最小值是( 切比绍夫不等式估计 的 最小值是
0.3 ).
4.(894) 设随机变量 的数学期望为 设随机变量X的数学期望为 的数学期望为µ, 标准差为σ,则由切比绍夫不等式 标准差为 则由切比绍夫不等式 P{|X-µ|≥3σ}≤( ). 1/9 5. 设随机变量X的分布律为 设随机变量 的分布律为 P{X=0.3}=0.2, P{X=0.6}=0.8, 用切比绍夫不等式估计 |X-E(X)|<0.2的概率 的概率. 的概率
1 n lim P ∑ Xi − µ < ε = 1 n→∞ n i =1
定理(贝努里利大数定律) 设每次实验中事件A发生的概率 定理(贝努里利大数定律) 设每次实验中事件A 为p,n次重复独立实验中事件A发生的次数为nA,则对任 次重复独立实验中事件A发生的次数为n 意的ε>0 意的ε>0 ,事件的频率 nA ,有 ε>
∫
+∞
−∞
概率论与数理统计实验_传染病传播问题
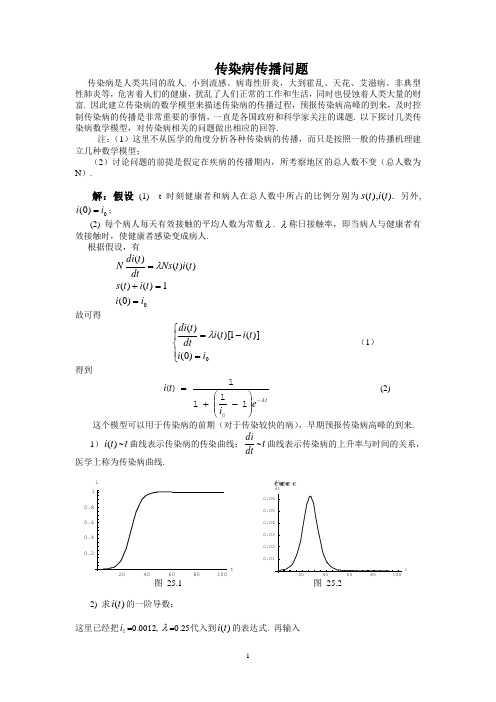
传染病传播问题传染病是人类共同的敌人. 小到流感、病毒性肝炎,大到霍乱、天花、艾滋病、非典型性肺炎等,危害着人们的健康,扰乱了人们正常的工作和生活,同时也侵蚀着人类大量的财富. 因此建立传染病的数学模型来描述传染病的传播过程,预报传染病高峰的到来,及时控制传染病的传播是非常重要的事情,一直是各国政府和科学家关注的课题. 以下探讨几类传染病数学模型,对传染病相关的问题做出相应的回答.注:(1)这里不从医学的角度分析各种传染病的传播,而只是按照一般的传播机理建立几种数学模型;(2)讨论问题的前提是假定在疾病的传播期内,所考察地区的总人数不变(总人数为N ).解:假设 (1) t 时刻健康者和病人在总人数中所占的比例分别为).(),(t i t s 另外,0)0(i i =;(2) 每个病人每天有效接触的平均人数为常数λ. λ称日接触率,即当病人与健康者有效接触时,使健康者感染变成病人. 根据假设,有)0(1)()()()()(i i t i t s t i t Ns dtt di N ==+=λ 故可得⎪⎩⎪⎨⎧=-=0)0()](1)[()(i i t i t i dt t di λ (1)得到te i t i λ-⎪⎪⎭⎫ ⎝⎛-+=1111)(0 (2)这个模型可以用于传染病的前期(对于传染较快的病),早期预报传染病高峰的到来. 1))(t i ~t 曲线表示传染病的传染曲线;dtdi~t 曲线表示传染病的上升率与时间的关系,医学上称为传染病曲线.2) 求)(t i 的一阶导数:这里已经把0i =0.0012, λ=0.25代入到)(t i 的表达式. 再输入回到)(t i 的表达式(2), 再求)(t i 的二阶导数, 令022=dt i d ,求出dt di函数的极大值点,}}]001Log[{},{{λλai ai t t +--→∞-→ ⎪⎪⎭⎫⎝⎛-=-11ln 011i t λ (3)再代入)(t i 的表达式,得21即已求出 21*=i 时,dt di 达到最大值. 即传染病的上升率达到最大,这个时刻是⎪⎪⎭⎫ ⎝⎛-=-11ln 011i t λ. 说明:病人在这个时刻增加得最快,预示着传染病高潮的到来,是医疗卫生部门特别关注的时刻.3)从(3)式可知1t 与λ成反比. 日接触率标志着该地区的卫生水平,λ越小,卫生水平越高. 而λ越小,1t 越大,传染病爆发的时刻就会越迟. 所以改善保健设施,采取有效的隔离措施,降低日接触率,可以推迟传染病高峰的到来.4)由(2)式可知,当∞→t 时,1)(→t i . 这就意味着所有的人都将被传染,处于生病状态. 这是不符合实际情况的. 事实上,传染病人经治疗后,或者痊愈,因而具有免疫力;或者死亡;所以最终病人的比例数)(t i 应该趋于零,即当∞→t 时,0)(→t i . 由此可见,需要重新修改模型假设,再建立数学模型.感染--治愈 假设:(1) 与感染模型相同; (2) 与感染模型相同;(3) 病人可以治愈. 病人每天被治愈的人数占病人总数的比例μ,称为日治愈率. 病人治愈后仍可成为被感染的健康者,所以μ1是这种传染病的平均传染期. 由假设(3)可知1)()()()()()(=+-=t i t s t i t i t s dtt di μλ0)0(i i = 故可得 ⎪⎩⎪⎨⎧=--=0)0()()](1)[()(i i t i t i t i dt t di μλ (4)变换得 ⎪⎩⎪⎨⎧=-+-=02)0()()()()(i i t i t i dt t di μλλ (5)此方程为贝努利方程,{{i [t]-> 0)()(0)(ai e e e ai e t t t t λμλμλμλμλ-+--}} 得到()te i t i μλμλλμλλ--⎪⎪⎭⎫ ⎝⎛--+-=01)(1 当μλ≠ 当μλ=时,上式不是方程的解,应从原方程出发求解.()⎪⎩⎪⎨⎧=-=020)()(i i t i dtt diλ (6) 可以利用分离变量法求解.{{i[t]->10ai t ai λ+}}即1)(1i t t i +=λ为当μλ=时的解. 所以方程组的解为: ()()⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛+≠⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--+-=----时当时;当μλλμλμλλμλλμλ101011i t e i t i t (7)分析:定义: μλσ= (8) 从λ和μ1的定义可知,σ是一个传染期内每个病人有效接触的平均人数,称为接触数. 1)作出()t t i ~曲线图,分析病人数的变化规律. 首先求出()t i 的极限,讨论极端情况. 因为()⎪⎩⎪⎨⎧≤>⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=-+∞→10111lim 1σσσμλλ,当;,当t i t (9) 这里有两条()t t i ~曲线, 都是1>σ的情形. 上面一条是0i =0.68, λ=0.25, μ=0.10时的图形; 下面一条是0i =0.0012, λ=0.25, μ=0.10时的图形. 从图25.3可见, 虽然0i 不同, 但()t i 在t 趋于无穷时有相同的极限σ11-.这是0i =0.68, λ=0.10, μ=0.10时的()t t i ~曲线.2)接触数1=σ是一个阈值. 当1≤σ时,病人比例()t i 越来越小,最终趋于零. 说明传染期内,每个病人有效接触的平均人数不超过一个人,最终导致使健康者变为病人的数量不超过病人数. 当1>σ时,病人比例()t i 的增减性取决于初始病人数0i 的大小. 当+∞→t 时,σ11)(-→t i .从上式分析可知σ越大,σ11-越大,即:病人比例()t i 随σ的增加而增加. 相反,增大治愈率μ,减少接触率λ,(即:降低σ的取值)其实际意义就是要提高医疗水平和保健水平,可以降低传染病的传播,避免传染病的爆发.3)特殊情况:当0,1==μλ时,相当于)(,时当+∞→+∞→=t μλσ的情况. 即:随着天数t 的无限增大,接触数无限增大,将导致所有的人都成为病人. 这也就是模型(一)的情况.感染--治愈--免疫考虑大多数传染病治愈后有很强的免疫力. 所以病愈的人既非健康者又非病人,被免疫的人数不再传染别人,别人也不会传染他们,他们已经退出传染系统. 另外死亡者也看作是退出传染系统.假设:(1)人群分为健康者、病人和移出者三类. 三类人在总人数N 中占的比例分别记作()()()t r t i t s ,,,三者之间满足条件:()()()1=++t r t i t s ;(2)病人的日接触率为λ,病人的日治愈率为μ,传染期接触数为μλσ=. 由假设(2)可知()()()t Ni t i t Ns dtdiNμλ-= 对移出者应有 ()t Ni dtdrN μ=,记初始时刻的健康者和病人的比例分别是()0),0(00>>i s ,移出者的初始值00=r .则得到: ()()()()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-=000,0s s i i t i t s dt dst i t i t s dt diλμλ (10) 这是非齐次非线性的微分方程组,难以求出精确的解析解.结果为 图25.5, 图25.6, 图25.7三个图形. 这是λ=0.25, μ=0.10, )0(i =0.0012时的i(t )~t,s (t)~t, r (t)~t 曲线.图25.13在理论上可以根据方程组的特点,先确定()t i 与()t s 之间的关系,然后再利用s i ,的关系,确定()t i . 将(10)式前两个方程左右两边分别相除得:()⎪⎩⎪⎨⎧=-=0111i s i sds di σ (11) 利用分离变量容易得到方程(11)的精确解()()000ln1s i s s ss i ++-=σ (12)分析:由(11)式可知,当σ1=s 时,0)(=ds t di .容易验证:当σ1<s 时,0>ds di ;当σ1>s 时,0<ds di.图形25.13中箭头表示随时间t 的增加()t s 和()t i 的变化趋势. 根据图形25.13分析可知,当+∞→t 时,()()∞∞→→→r t r t i s t s ;0;)(. 由此可得到如下结论:(1) 无论初始条件00,i s 如何,病人终将消失. 即:当+∞→t 时,()0→t i .(2) 最终未被感染的健康者的比例是()∞+∞→=s t s t lim . 在(12)式中,令0=i 可得∞s 满足的方程:0ln100=+-+∞∞s s s i s σ(13) 故∞s 是方程(13)式在⎪⎭⎫⎝⎛σ1,0内的单根. (3) 若σ10>s ,则()t i 先增加. 当σ1=s 时,()t i 达到最大值为()000ln 11s i s i m σσ+-+=. 然后()t i 减少且趋于零. ()t s 则单调减少趋于∞s .(4)若σ10≤s ,则()t i 单调减少趋于零,()t s 则单调减少趋于∞s .结果:由上述分析可以得知:(1)如果仅当病人比例()t i 有一段增长的时期才认为传染病在蔓延,这时σ1是一个阈值. 当σ10>s 时,传染病就会蔓延,而当提高阈值(即:减少传染期内接触数σ),使σ10≤s ,传染病就不会蔓延.(2) μλσ1ss =是传染期内一个病人传染健康者的平均数,故s σ称为交换数. 所以当σ10≤s 时,即有10≤s σ时,必有1≤s σ. 说明:传染期内交换数不超过1人,病人比例()t i 不会增加,传染病不会蔓延.(3) 从μλσ=表达式可知,日接触率λ越小,日治愈率μ越大,则接触数σ越小,此时有助于控制传染病的蔓延. 提高卫生水平和医疗水平是控制和降低传染病蔓延的最有效途径.(4) 在上述模型中,σ可以由实际数据估计得到:利用(13)式(一般0i 很小,可忽略不计),可得∞∞--=s s s s 00ln ln σ,其中0s 和∞s 可在传染病结束时,由统计数据获得. 或者,在医学上对血样作免疫检验也可以根据对检验有无反应,估计出0s 和∞s .。
《概率论与数理统计》5-1 中心极限定理

例5. 为了测定一台机床的质量, 将其分解成若干个部件 来称量. 假定每个部件的称量误差(单位: kg )服从区 间 1,1 上的均匀分布, 且每个部件的称量是独立的, 试 问至多分成多少个部件才能以不低于99%的概率保证 机床的称量总误差的绝对值不超过10.
1.55 1.55
2 1.55 1 0.8788.
例3. 有一批钢材, 其中80%的长度不小于3m, 现从钢材 中随机取出100根, 试利用中心极限定理求小于3m的钢 不超过30根的概率. 解 以Yn 为100根钢材中小于3m的钢材根数, 由题意知:
1 E X p, D X p 1 p n
定理5.3 独立同分布情形下大数定律
设
X1 , X 2 ,
是一个独立同分布的随机变量序列. 且
P E X , D X 2 . 则 X
证明关键步骤:
1 2 E X , D X n
Yn
B 200,0.15 .
Y np N 30 0.95, P Yn N P n np 1 p 25.5 N 30 查表得: 1.645, 即: N 38.3068, 所以可取
25.5
N 39方能以95%的把握保证在该时刻分机可以使用外
在§1.3中, 我们曾经提到频率的稳定性. 设随机事件A的概率P(A)=p, 在n重贝努利试验中事件A 发生的频率为 f n A .当n很大时, 将与p非常接近. 由 于 f n A 本质上是一个随机变量,它随着不同的n次试 验可能取不同的值, 因而需要对随机变量序列引进新 的收敛性定义.
概率论与数理统计 五大数定理

三倍标准差的概率.
解
P
X EX
3
DX
3 2
1 9
0.1111
2
例2 为了确定事件 A 的概率, 进行了10000次重复独立试验.
利用切比雪夫不等式估计:用事件A 在10000次试验中发生
的频率作为事件 A 的概率近似值时, 误差小于0.01的概率.
用来阐明大量随机现象平均结果稳定性的定理.
一、切比雪夫不等式
切比雪夫不等式:
设随机变量 X 有数学期望 EX 及方差 DX,
则对于任何正数 ,下列不等式成立:
P X EX DX 或 P X EX 1 DX
2
2
证
就 X是连续型随机变量的情况证明:
设X 的概率密度为
f x, 则 P X EX f ( x)dx
lim
n
P
i 1
n
z
1
e dt , z t 2 2
(z 为任意实数.)
2
n
考虑随机变量:
Yn X i ,
i 1
n
n
则 E(Yn ) E( X i ) n D(Yn ) D( X i ) n 2
i 1
i 1
13
例1 计算机进行加法计算时, 把每个加数取为最接近于它的整数
来计算. 设所有的取整误差是相互独立的随机变量, 并且都在
林德伯格条件
设独立随机变量 总和不起主要作用,
若每一个别随机变量对于
X1 , X 2 , , X n , ,
则当 n时,
有
lim P
n
Zn z
1
t2 z
e 2 dt.
概率论与数理统计 第四版 第五章

≈1 - Φ
60 - 300 × 0畅 2 300 × 0畅 2 × 0畅 8
= 1 - Φ(0) = 0畅 5 .
8 . 一复杂的系统由 100 个相互独立起作用的部件所组成 ,在整个运行期间
121
(1) 求收入至少 400 元的概率 ; (2) 求售出价格为1畅 2 元的蛋糕多于 60 只的概率 . 解 设第 i 只蛋糕的价格为 X i ,i = 1 ,2 ,… ,300 ,则 Xi 有分布律为
Xi 1 1畅 2 1畅 5 pk 0畅 3 0畅 2 0畅 5
由此得
E( Xi ) = 1 × 0畅 3 + 1畅 2 × 0畅 2 + 1畅 5 × 0畅 5 = 1畅 29 ,
率是多少 ?
解 以 Xi ( i = 1 ,2 ,… ,5 000) 记第 i 个零件的重量 ,以 W 记 5 000 个零件
5 000
钞 的总重量 :W = Xi .按题设 E( Xi ) = 0 .5 ,D( Xi ) = 0畅 12 ,由中心极限定理 ,可 i= 1
知 W - 5 000 × 0畅 5 近似地服从 N(0 ,1) 分布 ,故所求概率为 5 000 × 0畅 1
钞10 000
—
X
=
1 10 000 i = 1
Xi
~
N
280
,18
002 002
,
故
p1
=
—
P( X > 270)
≈ 1-
Φ
270 - 280 8
=
1-
Φ
-
5 4
=
Φ
5 4
= Φ(1畅 25) = 0畅 894 4 .
118
概率论与数理统计习题全解指南
《概率论与数理统计》课件第五章大数定律及中心极限定理

4.大样本统计推断的理论基础
是什么?
大数定律中心极限定理
随机现象中平均结果的稳定性
大数定律的客观背景
大量抛掷硬币正面出现频率
字母使用频率
生产过程中的废品率
§5.1 大数定律
背景:1. 频率稳定性2. 大量测量结果算术平均值的稳定性
回顾
随机现象的主要研究方法
概率分布
01
证:_x001A__x001B__x001B_,_x001A__x001B__x001B_,⋯, _x001A__x001B__x001B_, ⋯相互独立同分布,则_x001A__x001B__x001B__x001B_,_x001A__x001B__x001B__x001B_, ⋯,_x001A__x001B__x001B__x001B_, ⋯也相互独立同分布,由辛钦大数定律得证.
第五章 大数定律及中心极限定理
§5.1 大数定律§5.2 中心极限定理
要点:用切比雪夫不等式估算概率独立同分布,用中心极限定理计算对于二项分布,当n很大时,计算
本章要解决的问题
1.为何能以某事件发生的频率
作为该事件的概率的估计?
2.为何能以样本均值作为总体
期望的估计?
3.为何正态分布在概率论中占
解:(1)设X表示一年内死亡的人数,则~(, ),其中=,=.%. 设Y表示保险公司一年的利润,=×−.需要求的是_x001A_<_x001B_.
由中心极限定理
_x001A_<_x001B_=_x001A_×−<_x001B_ =_x001A_>_x001B_=−_x001A_≤_x001B_
且,
由中心极限定理
解:设为第i个螺丝钉的重量, 相互独立同分布. 于是,一盒螺丝钉的重量为
概率论和数理统计练习和测试-第五章-南工大应用数学系-编---苏大版-----大数定律和中心极限定理

概率论与数理统计练习与测试第五章(南工大应用数学系 编)(苏大版)大数定律与中心极限定理1. 设随机变量ξ的方差为2。
5。
利用契贝雪夫不等式估计:{}5.7||≥-ξξE P 的值。
解:由契贝雪夫不等式:2}|{|εξεξξD E P ≤≥-,又已知5.7,5.2==εξD ,故 044.05.75.2}5.7|{|2=≤≥-ξξE P 。
2. 已知某随机变量ξ的方差D ξ=1,但数学期望E ξ=m 未知,为估计m ,对ξ进行n 次独立观测,得样本观察值ξ1,ξ2,…,ξn 。
现用 {}∑=≥<-=n i i p m P m n n 15.0||1ξξξ多大时才可能使问当估计, 。
解:因∑===n i i m E n E 1,1ξξ又ξ1,ξ2,…,ξn 相互独立,故∑∑=====n i n i i i n D n n D D 1121)(1)1(ξξξ,根据契贝雪夫不等式,有 25.01}5.0|{|ξξξD E P -≤<-,即n m P 41}5.0|{|-≤<-ξ,再由p n p n -≥≥-14,41得。
3. 设在由n 个任意开关组成的电路的实验中,每次试验时一个开关开或关的概率各为12。
设m 表示在这n 次试验中遇到的开电次数,欲使开电频率mn 与开电概率p =0.5的绝对误差小于ε=0。
01,并且要有99%以上的可靠性来保证它实现。
试用德莫佛—拉普拉斯定理来估计,试验的次数n 应该是多少? 解:欲使99.0}01.0|{|≥<-p n m P ,即99.0}//01.0//|{|≥<-n pq n pq p n m P ,亦即,则t ~N (0,1)且有 ,99.001.0≥⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<pq n t P 由58.201.0995.0)58.2(≥⇒=Φpq n,以p =q =1/2代入可得 n =16641。
P43T3 4。
用某种步枪进行射击飞机的试验,每次射击的命中率为0。
概率论与数理统计第四版

第五章 大数定律及中心极限定理1.据以往经验,某种电器元件的寿命服从均值为100h的指数分布,现随机地取16只,设它们的寿命是相互独立的.求这16只元件的寿命的总和大于1920h的概率.解以X i(i=1,2,…,16)记第i只元件的寿命,以T记16只元件寿命的总和:T=钞16i=1X i,按题设E(X i)=100,D(X i)=1002,由中心极限定理知T-16×100161002近似地服从N(0,1)分布,故所求概率为P{T>1920}=1-P{T≤1920}=1-P T-16×100161002≤1920-16×100161002≈1-Ф1920-1600400=1-Ф(0.8)=1-0畅7881=0畅2119.2.(1)一保险公司有10000个汽车投保人,每个投保人索赔金额的数学期望为280美元,标准差为800美元,求索赔总金额超过2700000美元的概率.(2)一公司有50张签约保险单,各张保险单的索赔金额为X i,i=1,2,…,50(以千美元计)服从韦布尔(Weibull)分布,均值E(X i)=5,方差D(X i)=6,求50张保险单索赔的合计金额大于300的概率(设各保险单索赔金额是相互独立的).解(1)记第i人的索赔金额为X i,则由已知条件E(X i)=280, D(X i)=8002.要计算p1=P钞10000i=1X i>2700000,因各投保人索赔金额是独立的,n=10000很大.故由中心极限定理,近似地有X —=110000钞10000i=1X i~N280,80021002,故 p1=P(X —>270)≈1-Φ270-2808=1-Φ-54=Φ54=Φ(1畅25)=0畅8944.(2)E(X i)=5,D(X i)=6,n=50.故 p=P钞50i=1X i>300≈1-Φ300-50×550×6=1-Φ50300=1-Φ(2畅89)=0畅0019.这与情况(1)相反.(1)的概率为0畅8944表明可能性很大.而(2)表明可能性太小了,大约500次索赔中出现>300的只有一次.3.计算器在进行加法时,将每个加数舍入最靠近它的整数,设所有舍入误差相互独立且在(-0畅5,0畅5)上服从均匀分布.(1)将1500个数相加,问误差总和的绝对值超过15的概率是多少?(2)最多可有几个数相加使得误差总和的绝对值小于10的概率不小于0畅90?解设第k个加数的舍入误差为X k(k=1,2,…,1500),已知X k在(-0畅5,0畅5)上服从均匀分布,故知E(X k)=0,D(X k)=112.(1)记X=钞1500k=1X k,由中心极限定理,当n充分大时有近似公式P 钞1500k=1X k-1500×01500112≤x≈Φ(x).于是P{X>15}=1-P{X≤15}=1-P{-15≤X≤15}=1-P-15-01500112≤X-01500112≤15-01500112≈1-Φ151500112-Φ-151500112=1-2Φ15150012-1=1-[2Φ(1畅342)-1]=2[1-0畅9099]=0畅1802.即误差总和的绝对值超过15的概率近似地为0畅1802.(2)设最多有n个数相加,使误差总和Y=钞n k=1X k符合要求,即要确定n,使P{Y<10}≥0畅90.由中心极限定理,当n充分大时有近似公式P Y-0n112≤x≈Φ(x).811概率论与数理统计习题全解指南于是 P {Y <10}=P {-10<Y <10}=P -10n 112<Yn 112<10n 112≈Φ10n 12-Φ-10n 12=2Φ10n 12-1.因而n 需满足 2Φ10n /12-1≥0.90,亦即n 需满足 Φ10n /12≥0畅95=Φ(1畅645),即n 应满足 10n /12≥1畅645,由此得 n ≤443畅45.因n 为正整数,因而所求的n 为443.故最多只能有443个数加在一起,才能使得误差总和的绝对值小于10的概率不小于0畅90.4.设各零件的重量都是随机变量,它们相互独立,且服从相同的分布,其数学期望为0畅5kg ,均方差为0畅1kg ,问5000个零件的总重量超过2510kg 的概率是多少?解以X i (i =1,2,…,5000)记第i 个零件的重量,以W 记5000个零件的总重量:W =钞5000i =1X i .按题设E (X i )=0.5,D (X i )=0畅12,由中心极限定理,可知W -5000×0畅55000×0畅1近似地服从N (0,1)分布,故所求概率为P {W >2510}=1-P {W ≤2510}=1-P W -5000×0畅55000×0畅1≤2510-5000×0畅55000×0畅1≈1-Ф2510-5000×0畅55000×0畅1=1-Ф(2)=1-0畅9213=0畅0787畅5.有一批建筑房屋用的木柱,其中80%的长度不小于3m ,现从这批木柱中随机地取100根,求其中至少有30根短于3m 的概率.解按题意,可认为100根木柱是从为数甚多的木柱中抽取得到的,因而可当作放回抽样来看待.将检查一根木柱看它是否短于3m 看成是一次试验,检查100根木柱相当于做100重伯努利试验.以X 记被抽取的100根木柱中长度短于3m 的根数,则X ~b (100,0畅2).于是由教材第五章§2定理三得P {X ≥30}=P {30≤X <∞}911第五章 大数定律及中心极限定理=P30-100×0畅2100×0畅2×0畅8≤X -100×0畅2100×0畅2×0畅8<∞-100×0畅2100×0畅2×0畅8≈Φ(∞)-Φ30-2016=1-Φ(2畅5)=1-0畅9938=0畅0062畅本题也可以这样做,引入随机变量:X k =1, 若第k 根木柱短于3m ,0, 若第k 根木柱不短于3m , k =1,2,…,100畅于是E (X k )=0.2,D (X k )=0畅2×0畅8.以X 表示100根木柱中短于3m 的根数,则X =钞100k =1X k .由中心极限定理有P {X ≥30}=P {30≤X <∞}=P 30-100×0畅21000畅2×0畅8≤钞100k =1X k -100×0畅21000畅2×0畅8 <∞-100×0畅21000畅2×0畅8≈Φ(∞)-Ф30-2016=1-Φ(2畅5)=0畅0062畅6.一工人修理一台机器需两个阶段,第一阶段所需时间(小时)服从均值为0.2的指数分布,第二阶段服从均值为0畅3的指数分布,且与第一阶段独立.现有20台机器需要修理,求他在8小时内完成的概率.解设修理第i (i =1,2,…,20)台机器,第一阶段耗时X i ,第二阶段为Y i ,则共耗时Z i =X i +Y i ,今已知E (X i )=0畅2,E (Y i )=0畅3,故E (Z i )=0畅5.D (Z i )=D (X i )+D (Y i )=0畅22+0畅32=0畅13畅20台机器需要修理的时间可认为近似服从正态分布,即有钞20i =1Z i ~N (20×0畅5,20×0畅13)=N (10,2畅6).所求概率 p =P钞20i =1Z i ≤8≈Φ8-20×0畅520×0畅13=Φ-21畅6125=Φ(-1畅24)=0畅1075,即不大可能在8小时内完成全部工作.7.一食品店有三种蛋糕出售,由于售出哪一种蛋糕是随机的,因而售出一只蛋糕的价格是一个随机变量,它取1元、1畅2元、1畅5元各个值的概率分别为0畅3、0畅2、0畅5畅若售出300只蛋糕.21概率论与数理统计习题全解指南(1)求收入至少400元的概率;(2)求售出价格为1畅2元的蛋糕多于60只的概率.解设第i 只蛋糕的价格为X i ,i =1,2,…,300,则X i 有分布律为X i 11畅21畅5p k0畅30畅20畅5由此得E (X i )=1×0畅3+1畅2×0畅2+1畅5×0畅5=1畅29,E (X 2i )=12×0畅3+1畅22×0畅2+1畅52×0畅5=1畅713,故D (X i )=E (X 2i )-[E (X i )]2=0畅0489畅(1)以X 表示这天的总收入,则X =钞300i =1X i ,由中心极限定理得P {X ≥400}=P {400≤X <∞}=P 400-300×1畅293000畅0489≤钞300i =1X i -300×1畅293000畅0489 <∞-300×1畅293000畅0489≈1-Φ(3畅39)=1-0畅9997=0畅0003.(2)以Y 记300只蛋糕中售价为1畅2元的蛋糕的只数,于是Y ~b (300,0畅2).E (Y )=300×0畅2,D (Y )=300×0畅2×0畅8,由棣莫弗拉普拉斯定理得P {Y >60}=1-P {Y ≤60}=1-P Y -300×0畅2300×0畅2×0畅8≤60-300×0畅2300×0畅2×0畅8≈1-Φ60-300×0畅2300×0畅2×0畅8=1-Φ(0)=0畅5.8.一复杂的系统由100个相互独立起作用的部件所组成,在整个运行期间每个部件损坏的概率为0畅10.为了使整个系统起作用,至少必须有85个部件正常工作,求整个系统起作用的概率.解将观察一个部件是否正常工作看成是一次试验,由于各部件是否正常工作是相互独立的,因而观察100个部件是否正常工作是做100重伯努利试验,以X 表示100个部件中正常工作的部件数,则X ~b (100,0畅9),按题意需求概率P {X ≥85},由棣莫弗拉普拉斯定理知X -100×0畅9100×0畅9×0畅1近似地服从标准正态分布N (0,1),故所求概率为121第五章 大数定律及中心极限定理P {X ≥85}=P {85≤X <∞}=P 85-100×0畅9100×0畅9×0畅1≤X -100×0畅9100×0畅9×0畅1≤∞-100×0畅9100×0畅9×0畅1≈1-Ф-53=0畅9525.9.已知在某十字路口,一周事故发生数的数学期望为2畅2,标准差为1畅4.(1)以X —表示一年(以52周计)此十字路口事故发生数的算术平均,试用中心极限定理求X —的近似分布,并求P {X —<2}.(2)求一年事故发生数小于100的概率.解 (1)E (X —)=E (X )=2畅2,D (X —)=D (X )52=1畅4252,由中心极限定理,可认为X —~N (2畅2,1畅42/52).P {X —<2}=Φ2-2畅21畅4/52=Φ-0畅2×521畅4=Φ(-1畅030)=1-Φ(1畅030)=1-0畅8485=0畅1515.(2)一年52周,设各周事故发生数为X 1,X 2,…,X 52.则需计算p =P钞52i =1X i <100,即P {52X —<100}.用中心极限定理可知所求概率为 p =P {52X —<100}=P {X —<10052}≈Φ10052-2畅2521畅4=Φ(-1畅426)=1-0畅9230=0畅0770.10.某种小汽车氧化氮的排放量的数学期望为0.9g /km ,标准差为1畅9g /km ,某汽车公司有这种小汽车100辆,以X —表示这些车辆氧化氮排放量的算术平均,问当L 为何值时X —>L 的概率不超过0畅01.解 设以X i (i =1,2,…,100)表示第i 辆小汽车氧化氮的排放量,则X —=1100钞100i =1X i .由已知条件E (X i )=0畅9,D (X i )=1畅92得E (X —)=0畅9, D (X —)=1畅92100.各辆汽车氧化氮的排放量相互独立,故可认为近似地有221概率论与数理统计习题全解指南X —~N 0畅9,1畅92100.需要计算的是满足P {X —>L }≤0畅01的最小值L .由中心极限定理P {X —>L }=PX —-0畅90畅19>L -0畅90畅19≤0畅01畅L 应为满足1-ΦL -0畅90畅19≤0畅01的最小值,即ΦL -0畅90畅19≥0畅99=Φ(2畅33),即L -0畅90畅19≥2畅33,故L ≥0畅9+0畅19×2畅33=1畅3427,应取L =1畅3427g /km 畅11.随机地选取两组学生,每组80人,分别在两个实验室里测量某种化合物的p H .各人测量的结果是随机变量,它们相互独立,服从同一分布,数学期望为5,方差为0畅3,以X —,Y —分别表示第一组和第二组所得结果的算术平均.(1)求P {4畅9<X —<5畅1}.(2)求P {-0畅1<X —-Y —<0畅1}.解由题设E (X —)=5,D (X —)=D (Y —)=0畅380.(1)由中心极限定理知X —近似服从N (5,0畅380),故P {4畅9<X —<5畅1}=P 4畅9-50畅380<X —-50畅380<5畅1-50畅380≈Φ5畅1-50畅380-Φ4畅9-50畅380=2Φ(1畅63)-1=2×0畅9484-1=0畅8968.(2)因E (X —-Y —)=E (X —)-E (Y —)=0,D (X —-Y —)=D (X —)+D (Y —)=0畅340,由中心极限定理P {-0畅1<X —-Y —<0畅1} 321第五章 大数定律及中心极限定理=P-0畅1-00畅340<(X —-Y —)-00畅340<0畅1-00畅340≈Φ0畅1-00畅340-Φ-0畅1-00畅340=2Φ(1畅15)-1=2×0畅8749-1=0畅7498.12.一公寓有200户住户,一户住户拥有汽车辆数X 的分布律为X 012p k0畅10畅60畅3问需要多少车位,才能使每辆汽车都具有一个车位的概率至少为0畅95畅解 设需要车位数为n ,且设第i (i =1,2,…,200)户有车辆数为X i ,则由X i 的分布律知E (X i )=0×0畅1+1×0畅6+2×0畅3=1畅2,E (X 2i )=02×0畅1+12×0畅6+22×0畅3=1畅8,故D (X i )=E (X 2i )-[E (X i )]2=1畅8-1畅22=0畅36.因共有200户,各户占有车位数相互独立.从而近似地有钞200i =1X i ~N (200×1畅2, 200×0畅36).今要求车位数n 满足0畅95≤P钞200i =1X i ≤n ,由正态近似知,上式中n 应满足0畅95≤Φn -200×1畅2200×0畅36=Φn -24072,因0畅95=Φ(1畅645),从而由Φ(x )的单调性知n -24072≥1畅645,故n ≥240+1畅645×72=253畅96.由此知至少需254个车位畅13.某种电子器件的寿命(小时)具有数学期望μ(未知),方差σ2=400.为了估计μ,随机地取n 只这种器件,在时刻t =0投入测试(测试是相互独立的)直到失效,测得其寿命为X 1,X 2,…,X n ,以X —=1n钞ni =1X i 作为μ的估计,为使P {X —-μ<1}≥0畅95,问n 至少为多少?解由教材第五章§2定理一可知,当n 充分大时,421概率论与数理统计习题全解指南钞ni =1X i -n μn σ=1n钞ni =1X i -μσ/n近似地N (0,1),即X —-μσn近似地N (0,1).由题设D (X i )=400(i =1,2,…,n ),即有σ=400,于是X —-μ400n =X —-μ20n近似地服从N (0,1)分布,即有P {X —-μ<1}=P {-1<X —-μ<1}=P -120n <X —-μ20n <120n ≈Φ120n-Φ-120n =2Φ120n -1.现在要求P {X —-μ<1}≥0畅95,即要求2Ф120n -1≥0畅95,亦即要求Ф120n≥0畅975=Ф(1畅96),故需要120n≥1畅96,即 n ≥(20×1畅96)2=1536畅64畅因n 为正整数,故n 至少为1537.14.某药厂断言,该厂生产的某种药品对于医治一种疑难血液病的治愈率为0畅8,医院任意抽查100个服用此药品的病人,若其中多于75人治愈,就接受此断言,否则就拒绝此断言.(1)若实际上此药品对这种疾病的治愈率是0畅8畅问接受这一断言的概率是多少?(2)若实际上此药品对这种疾病的治愈率为0畅7,问接受这一断言的概率是多少?解由药厂断言来看100人中治愈人数X ~b (100,0畅8).(1)在治愈率与实际情况相符合条件下,接受药厂断言的概率即为P (X >521第五章 大数定律及中心极限定理75).由中心极限定理知近似地有X~N(100×0畅8, 100×0畅8×0畅2)=N(80,42),于是 p1=P(X>75)≈1-Φ75-804=1-Φ(-54)=Φ(1畅25)=0畅8944.(2)若实际上治疗率为0畅7,即X~b(100,0畅7),则治愈人数X近似地服从正态分布,即有X~N(100×0畅7, 100×0畅7×0畅3).所求概率p2=P(X>75)≈1-Φ75-100×0畅7100×0畅7×0畅3=1-Φ521=1-Φ(1畅09)=1-0畅8621=0畅1379.621概率论与数理统计习题全解指南。
概率论与数理统计-第五章

【数理统计简史】
1. 近代统计学时期
18 世纪末到 19 世纪,是近代统计学时期.这一 时期的重大成就是大数定律和概率论被引入统计 学.之后最小二乘法、误差理论和正态分布理论 等相继成为统计学的重要内容.这一时期有两大 学派:数理统计学派和社会统计学派.
【数理统计简史】 数理统计学派始于19世纪中叶,代表人物是比 利时的凯特莱( A.Quetelet , 1796-1874 ),著有 《概率论书简》《社会物理学》等,他主张用研 究自然科学的方法研究社会现象,正式把概率论 引入统计学,并最先用大数定律证明了社会生活 中随机现象的规律性,提出了误差理论.凯特莱 的贡献,使统计学的发展进入个了一个新的阶 段.
i =1 36
1 2 2 3 2 2 2 2 D( X ) = E ( X ) − E ( X ) = ( 0 + 1 + 2 + 3 ) − 4 2 5 = 4
2
二、样本与抽样 由于X1,X2,...,X36均与总体X同分布,且相互独 立,所以,Y的均值和方差分别为
E (Y ) = E ( ∑ X i ) = 36 E ( X ) = 54,
【数理统计简史】 18世纪到 19世纪初期,高斯从描述天文观测的 误差而引进正态分布,并使用最小二乘法作为估 计方法,是近代数理统计学发展初期的重大事件, 对社会发展有很大的影响.
【数理统计简史】 用正态分布描述观测数据的应用是如此普遍,以 至 在 19 世 纪 相 当 长 的 时 期 内 , 包 括 高 尔 顿 ( Galton )在内的一些学者,认为这个分布可用 于描述几乎是一切常见的数据.直到现在,有关 正态分布的统计方法,仍占据着常用统计方法中 很重要的一部分.最小二乘法方面的工作,在 20 世纪初以来,经过一些学者的发展,如今成了数 理统计学中的主要方法.
概率论与数理统计实验_传染病传播问题

传染病传播问题传染病是人类共同的敌人. 小到流感、病毒性肝炎,大到霍乱、天花、艾滋病、非典型性肺炎等,危害着人们的健康,扰乱了人们正常的工作和生活,同时也侵蚀着人类大量的财富. 因此建立传染病的数学模型来描述传染病的传播过程,预报传染病高峰的到来,及时控制传染病的传播是非常重要的事情,一直是各国政府和科学家关注的课题. 以下探讨几类传染病数学模型,对传染病相关的问题做出相应的回答.注:(1)这里不从医学的角度分析各种传染病的传播,而只是按照一般的传播机理建立几种数学模型;(2)讨论问题的前提是假定在疾病的传播期内,所考察地区的总人数不变(总人数为N ).解:假设 (1) t 时刻健康者和病人在总人数中所占的比例分别为).(),(t i t s 另外,0)0(i i =;(2) 每个病人每天有效接触的平均人数为常数λ. λ称日接触率,即当病人与健康者有效接触时,使健康者感染变成病人. 根据假设,有)0(1)()()()()(i i t i t s t i t Ns dtt di N ==+=λ 故可得⎪⎩⎪⎨⎧=-=0)0()](1)[()(i i t i t i dt t di λ (1)得到te i t i λ-⎪⎪⎭⎫ ⎝⎛-+=1111)(0 (2)这个模型可以用于传染病的前期(对于传染较快的病),早期预报传染病高峰的到来. 1))(t i ~t 曲线表示传染病的传染曲线;dtdi~t 曲线表示传染病的上升率与时间的关系,医学上称为传染病曲线.2) 求)(t i 的一阶导数:这里已经把0i =0.0012, λ=0.25代入到)(t i 的表达式. 再输入回到)(t i 的表达式(2), 再求)(t i 的二阶导数, 令022=dt i d ,求出dt di函数的极大值点,}}]001Log[{},{{λλai ai t t +--→∞-→ ⎪⎪⎭⎫⎝⎛-=-11ln 011i t λ (3)再代入)(t i 的表达式,得21即已求出 21*=i 时,dt di 达到最大值. 即传染病的上升率达到最大,这个时刻是⎪⎪⎭⎫ ⎝⎛-=-11ln 011i t λ. 说明:病人在这个时刻增加得最快,预示着传染病高潮的到来,是医疗卫生部门特别关注的时刻.3)从(3)式可知1t 与λ成反比. 日接触率标志着该地区的卫生水平,λ越小,卫生水平越高. 而λ越小,1t 越大,传染病爆发的时刻就会越迟. 所以改善保健设施,采取有效的隔离措施,降低日接触率,可以推迟传染病高峰的到来.4)由(2)式可知,当∞→t 时,1)(→t i . 这就意味着所有的人都将被传染,处于生病状态. 这是不符合实际情况的. 事实上,传染病人经治疗后,或者痊愈,因而具有免疫力;或者死亡;所以最终病人的比例数)(t i 应该趋于零,即当∞→t 时,0)(→t i . 由此可见,需要重新修改模型假设,再建立数学模型.感染--治愈 假设:(1) 与感染模型相同; (2) 与感染模型相同;(3) 病人可以治愈. 病人每天被治愈的人数占病人总数的比例μ,称为日治愈率. 病人治愈后仍可成为被感染的健康者,所以μ1是这种传染病的平均传染期. 由假设(3)可知1)()()()()()(=+-=t i t s t i t i t s dtt di μλ0)0(i i = 故可得 ⎪⎩⎪⎨⎧=--=0)0()()](1)[()(i i t i t i t i dt t di μλ (4)变换得 ⎪⎩⎪⎨⎧=-+-=02)0()()()()(i i t i t i dt t di μλλ (5)此方程为贝努利方程,{{i [t]-> 0)()(0)(ai e e e ai e t t t t λμλμλμλμλ-+--}} 得到()te i t i μλμλλμλλ--⎪⎪⎭⎫ ⎝⎛--+-=01)(1 当μλ≠ 当μλ=时,上式不是方程的解,应从原方程出发求解.()⎪⎩⎪⎨⎧=-=020)()(i i t i dtt diλ (6) 可以利用分离变量法求解.{{i[t]->10ai t ai λ+}}即1)(1i t t i +=λ为当μλ=时的解. 所以方程组的解为: ()()⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛+≠⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--+-=----时当时;当μλλμλμλλμλλμλ101011i t e i t i t (7)分析:定义: μλσ= (8) 从λ和μ1的定义可知,σ是一个传染期内每个病人有效接触的平均人数,称为接触数. 1)作出()t t i ~曲线图,分析病人数的变化规律. 首先求出()t i 的极限,讨论极端情况. 因为()⎪⎩⎪⎨⎧≤>⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=-+∞→10111lim 1σσσμλλ,当;,当t i t (9) 这里有两条()t t i ~曲线, 都是1>σ的情形. 上面一条是0i =0.68, λ=0.25, μ=0.10时的图形; 下面一条是0i =0.0012, λ=0.25, μ=0.10时的图形. 从图25.3可见, 虽然0i 不同, 但()t i 在t 趋于无穷时有相同的极限σ11-.这是0i =0.68, λ=0.10, μ=0.10时的()t t i ~曲线.2)接触数1=σ是一个阈值. 当1≤σ时,病人比例()t i 越来越小,最终趋于零. 说明传染期内,每个病人有效接触的平均人数不超过一个人,最终导致使健康者变为病人的数量不超过病人数. 当1>σ时,病人比例()t i 的增减性取决于初始病人数0i 的大小. 当+∞→t 时,σ11)(-→t i .从上式分析可知σ越大,σ11-越大,即:病人比例()t i 随σ的增加而增加. 相反,增大治愈率μ,减少接触率λ,(即:降低σ的取值)其实际意义就是要提高医疗水平和保健水平,可以降低传染病的传播,避免传染病的爆发.3)特殊情况:当0,1==μλ时,相当于)(,时当+∞→+∞→=t μλσ的情况. 即:随着天数t 的无限增大,接触数无限增大,将导致所有的人都成为病人. 这也就是模型(一)的情况.感染--治愈--免疫考虑大多数传染病治愈后有很强的免疫力. 所以病愈的人既非健康者又非病人,被免疫的人数不再传染别人,别人也不会传染他们,他们已经退出传染系统. 另外死亡者也看作是退出传染系统.假设:(1)人群分为健康者、病人和移出者三类. 三类人在总人数N 中占的比例分别记作()()()t r t i t s ,,,三者之间满足条件:()()()1=++t r t i t s ;(2)病人的日接触率为λ,病人的日治愈率为μ,传染期接触数为μλσ=. 由假设(2)可知()()()t Ni t i t Ns dtdiNμλ-= 对移出者应有 ()t Ni dtdrN μ=,记初始时刻的健康者和病人的比例分别是()0),0(00>>i s ,移出者的初始值00=r .则得到: ()()()()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-=000,0s s i i t i t s dt dst i t i t s dt diλμλ (10) 这是非齐次非线性的微分方程组,难以求出精确的解析解.结果为 图25.5, 图25.6, 图25.7三个图形. 这是λ=0.25, μ=0.10, )0(i =0.0012时的i(t )~t,s (t)~t, r (t)~t 曲线.图25.13在理论上可以根据方程组的特点,先确定()t i 与()t s 之间的关系,然后再利用s i ,的关系,确定()t i . 将(10)式前两个方程左右两边分别相除得:()⎪⎩⎪⎨⎧=-=0111i s i sds di σ (11) 利用分离变量容易得到方程(11)的精确解()()000ln1s i s s ss i ++-=σ (12)分析:由(11)式可知,当σ1=s 时,0)(=ds t di .容易验证:当σ1<s 时,0>ds di ;当σ1>s 时,0<ds di.图形25.13中箭头表示随时间t 的增加()t s 和()t i 的变化趋势. 根据图形25.13分析可知,当+∞→t 时,()()∞∞→→→r t r t i s t s ;0;)(. 由此可得到如下结论:(1) 无论初始条件00,i s 如何,病人终将消失. 即:当+∞→t 时,()0→t i .(2) 最终未被感染的健康者的比例是()∞+∞→=s t s t lim . 在(12)式中,令0=i 可得∞s 满足的方程:0ln100=+-+∞∞s s s i s σ(13) 故∞s 是方程(13)式在⎪⎭⎫⎝⎛σ1,0内的单根. (3) 若σ10>s ,则()t i 先增加. 当σ1=s 时,()t i 达到最大值为()000ln 11s i s i m σσ+-+=. 然后()t i 减少且趋于零. ()t s 则单调减少趋于∞s .(4)若σ10≤s ,则()t i 单调减少趋于零,()t s 则单调减少趋于∞s .结果:由上述分析可以得知:(1)如果仅当病人比例()t i 有一段增长的时期才认为传染病在蔓延,这时σ1是一个阈值. 当σ10>s 时,传染病就会蔓延,而当提高阈值(即:减少传染期内接触数σ),使σ10≤s ,传染病就不会蔓延.(2) μλσ1ss =是传染期内一个病人传染健康者的平均数,故s σ称为交换数. 所以当σ10≤s 时,即有10≤s σ时,必有1≤s σ. 说明:传染期内交换数不超过1人,病人比例()t i 不会增加,传染病不会蔓延.(3) 从μλσ=表达式可知,日接触率λ越小,日治愈率μ越大,则接触数σ越小,此时有助于控制传染病的蔓延. 提高卫生水平和医疗水平是控制和降低传染病蔓延的最有效途径.(4) 在上述模型中,σ可以由实际数据估计得到:利用(13)式(一般0i 很小,可忽略不计),可得∞∞--=s s s s 00ln ln σ,其中0s 和∞s 可在传染病结束时,由统计数据获得. 或者,在医学上对血样作免疫检验也可以根据对检验有无反应,估计出0s 和∞s .。
《概率》统计与概率PPT(频率与概率)

课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
概率的应用——数学建模
典例为了估计水库中鱼的尾数,可以使用以下的方法:先从水库
中捕出2 000尾鱼,给每尾鱼做上记号,不影响其存活,然后放回水库.
经过适当的时间,让其和水库中的其他鱼充分混合,再从水库中捕
出500尾,查看其中有记号的鱼,有40尾,试根据上述数据,估计水库
定义
表示法
一般地,对于事件 A 与事件
包含
关系
B,如果事件 A 发生,则事件
一定发生
B⊇A
________
B__________,称事件 B 包含
(或
事件 A(或事件 A 包含于事件
A⊆B
_______)
B)
图示
定义
表示法
给定事件 A,B,由所
有 A 中的样本点与 B
并事件
中的样本点组成的事
和
件称为 A 与 B 的_____
合格产品
D.该厂生产的产品合格的可能性是99.99%
答案:D
解析:合格率是99.99%,是指该工厂生产的每件产品合格的可能
性大小,即合格的概率.
课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
概率与频率的关系及求法
例2下面是某批乒乓球质量检查结果表:
抽取球数
优等品数
优等品出
现的频率
50
45
100
92
200
概率为78%”,这是指(
)
A.明天该地区有78%的地区降水,其他22%的地区不降水
B.明天该地区降水的可能性大小为78%
概率数学实验实验报告

一、实验目的1. 了解概率数学的基本概念和原理。
2. 掌握概率数学在现实生活中的应用。
3. 培养学生的实验操作能力和数据分析能力。
二、实验内容1. 抛掷硬币实验2. 抛掷骰子实验3. 箱子抽球实验4. 概率计算与应用三、实验器材1. 硬币一枚2. 骰子一个3. 箱子一个4. 球若干5. 记录表四、实验步骤1. 抛掷硬币实验(1)将硬币抛掷10次,记录正面朝上和反面朝上的次数。
(2)计算正面朝上和反面朝上的概率。
(3)分析实验结果,验证概率理论。
2. 抛掷骰子实验(1)将骰子抛掷10次,记录每个面出现的次数。
(2)计算每个面出现的概率。
(3)分析实验结果,验证概率理论。
3. 箱子抽球实验(1)将不同颜色的球放入箱子中,共5个球,其中红球2个,蓝球2个,黄球1个。
(2)从箱子中随机抽取球,记录抽取结果。
(3)计算每种颜色球被抽中的概率。
(4)分析实验结果,验证概率理论。
4. 概率计算与应用(1)根据实验结果,计算每种情况的概率。
(2)分析概率在现实生活中的应用,如彩票、保险等。
五、实验结果与分析1. 抛掷硬币实验实验结果显示,正面朝上的次数为5次,反面朝上的次数为5次。
计算概率为:P(正面朝上) = 5/10 = 0.5P(反面朝上) = 5/10 = 0.5实验结果与概率理论相符。
2. 抛掷骰子实验实验结果显示,每个面出现的次数如下:1面1次,2面1次,3面1次,4面1次,5面1次,6面1次。
计算概率为:P(1面) = 1/10 = 0.1P(2面) = 1/10 = 0.1P(3面) = 1/10 = 0.1P(4面) = 1/10 = 0.1P(5面) = 1/10 = 0.1P(6面) = 1/10 = 0.1实验结果与概率理论相符。
3. 箱子抽球实验实验结果显示,红球被抽中的次数为2次,蓝球被抽中的次数为2次,黄球被抽中的次数为1次。
计算概率为:P(红球) = 2/5 = 0.4P(蓝球) = 2/5 = 0.4P(黄球) = 1/5 = 0.2实验结果与概率理论相符。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 概率与统计的数学实验概率论与数理统计是数学的一个重要分支,其问题的求解也很重要。
MATLAB 语言提供了专用的统计学工具箱,其中包括大量的函数,可以直接求解概率论与数理统计领域中的问题。
5.1 概率计算基本命令5.1.1 常见分别的概率密度函数与分布函数Poisson 分布:Poisson 分布的概率密度是参数为λ的函数,且λ是正整数,即 (),0,1,2,3,...!xx p x e x x λλ-==。
可以用(),()p o i s s p d f p o i s s c d f 函数分别求出Poisson 分布的概率密度函数和分布函数,它们的调用格式为:(,)y poisspdf x λ=和(,)F poisscdf x λ=。
其中,x 为选定的一组横坐标向量,y 为x 各点处的概率密度函数的值,F 为x 各点处的概率密度函数的值。
正态分布:可以分别调用下面的命令生成正态分布的概率密度函数和分布函数(,,)y normpdf x μσ= 和(,,)F normcdf x μσ=。
其中,x 为选定的一组横坐标向量,μ为均值,σ为标准差,y 为x 各点处的概率密度函数的值,F 为x 各点处的概率密度函数的值。
2χ分布:可以分别调用下面的命令生成2χ分布的概率密度函数和分布函数2(,)y chi pdf x k =和2(,)F chi cdf x k =。
其中,x 为选定的一组横坐标向量,k 为正整数,y 为x 各点处的概率密度函数的值,F 为x 各点处的概率密度函数的值。
以下的概率密度函数和分布函数中的x ,k ,y ,F 。
T 分布:概率密度函数和分布函数:(,)y tpdf x k =和(,)F tcdf x k =。
F 分布:概率密度函数和分布函数:(,,)y fpdf x a b =和(,,)F fcdf x a b =。
,a b 为参数。
二项分布:概率密度函数和分布函数:(,,)y binopdf x n p =和(,,)F binocdf x n p =。
指数分布:概率密度函数和分布函数: exp (,)y pdf x λ=和exp (,)F cdf x λ=。
其中μ 为均值,σ为标准差。
均匀分布: 概率密度函数和分布函数:(,,)y unifpdf x a b =和(,,)F unifcdf x a b =。
其中μ为均值,σ为标准差。
例1 分别画出2(,)μσ为(1,1),(0,1),(0,9)-时的正态分布的概率密度函数和分布函数。
解 M-文件为x=[-3:0.01:3]';y1=[];y2=[];mu=[-1,0,0];sig1=[1,1,9];sig2=sqrt(sig1);for i=1:length(mu)y1=[y1,normpdf(x,mu(i),sig2(i))];y2=[y2,normcdf(x,mu(i),sig2(i))];endplot(x,y1),figure;plot(x,y2)执行后结果为概率密度函数分布函数5.1.2 常见分布的概率密度函数与分布函数由随机变量的分布函数可以计算相应的概率问题。
分布函数按{}()P x F x ξ≤=定义,由此可以得到一些常用且重要的公式,如:{}()()P a b F b F a ξ≤≤=-, {}1()P x F x ξ≥=-。
例2 假设随机变量(2,16)X N ,求该随机变量落入区间{14},{2}P X P X ≤≤≥。
解 MATLAB 命令为>> mu=2;sig=16;>> p1=normcdf(4,mu,sig)-normcdf(1,mu,sig)>> p2=1-normcdf(2,mu,sig)例3 设二维随机变量(,)ξη的联合密度函数为2,01,02(,)30,xy x x y p x y otherwise ⎧+≤≤≤≤⎪=⎨⎪⎩, 求11{,}22P ξη<<。
解 MATLAB 命令为>> syms x y;>> f=x^2+x*y/3;>> p=int(int(f,x,0,1/2),y,0,1/2) %通过对概率密度函数积分计算相应概率5.2 基本统计命令及其使用5.2.1 随机变量的均值和方差若已知离散型随机变量的分布律,可用求和命令或级数知识计算出期望和方差;若已知连续型随机变量的密度函数,可用积分命令求出均值和方差。
若已知一组随机变量样本数据构成的向量,则可以分别使用以下MATLAB 命令求出随机变量的均值和方差:()m mean x = %求样本均值1var()s x = %求样本方差2()s std x = %求样本标准差例4 试生成一组3000个正态分布随机数,使其均值为0.5,标准差为1.5,试分析这些数据实际的均值,方差和标准差。
解 先用命令(,,,)p normrnd m n μσ=生成一组均值为μ,标准差为σ的正态分布m n ⨯矩阵。
MATLAB 命令为>> p=normrnd(0.5,1.5,3000,1); %生成正态分布随机数>> [mean(p),var(p),std(p)]ans =0.5037 2.3230 1.5242即这组数据的实际均值为0.5037,方差为2.323,标准差为1.5242,与理论值比较接近。
多个随机变量的协方差矩阵,可用以下命令求出cov()C X =,其中X 的各列均表示不同的随机变量的样本值。
例5 试生成4个满足标准正态分布的随机变量,并求出它们的协方差矩阵。
解 MATLAB 命令为>> p=randn(3000,4); %矩阵p 的4列即为4个标准正态分布随机变量>> cov(p) 5.2.2 参数估计和区间估计MATLAB 工具箱中提供了由极大似然法给出相应参数估计的命令:2[,]()normfit x μσ= %该命令给出正态分布随机变量的参数估计,其中x 为样本值,2,μσ 分别为参数期望和方差的估计值。
22[,,,](,)normfit x μσμσα∆∆= %该命令给出置信度为100(1)α-的正态分布随机变量的参数估计,其中x 为样本值,22,,,μσμσ∆∆ 分别为参数期望和方差的估计值以及它们的置信区间。
()poissfit x λ= %该命令给出Poisson 分布随机变量的参数估计,其中x 为样本值,λ 参数的估计值。
[,](,)poissfit x λλα∆= %该命令给出置信度为100(1)α-的Poisson 分布随机变量的参数估计,其中x 为样本值,,λλ∆ 分别为参数的估计值以及它的置信区间。
其它分布的参数估计科可类似做出。
例6 假设均值为0.5,标准差为1.5,试生成一组3000个正态分布随机数,再将这些数据作为样本数据对参数进行估计。
(假设置信度为95%)解 MATLAB 命令为>> p=normrnd(0.5,1.5,3000,1); %生成正态分布随机数>> [mu,sig,a,b]=normfit(p,0.05) %参数估计命令mu =0.5054sig =1.5101a =0.45130.5594b =1.47281.5493即期望的估计值为0.5054,方差的估计值为1.5101,期望的置信区间为(0.4513,0.5594),方差的置信区间为(1.4728,1.5493)。
5.2.3 假设检验下面介绍正态分布均值的假设检验:[,,](,,,,)H p ci ztest x mu tail σα= %正态分布均值的Z 检验,其中x 为样本值,mu 是0H 假设中的0μ,σ为总体标准差,α为显著性水平,tail 为备择假设1H 的选择(1H 为0μμ>时1tail =;1H 为0μμ<时1tail =-;1H 为0μμ≠时0tail =(可省略))。
当检验结果0H =时表示不能拒绝0H 假设;否则拒绝0H 假设。
p 表示在假设0H 下样本均值出现的概率,ci 是0μ的置信区间。
[,,](,,,)H p ci ttest x mu tail α= %正态分布均值的T 检验,其中x 为样本值,mu 是0H 假设中的0μ,α为显著性水平,tail 为备择假设1H 的选择(1H 为0μμ>时1tail =;1H 为0μμ<时1tail =-;1H 为0μμ≠时0tail =(可省略))。
当检验结果0H =时表示不能拒绝0H 假设;否则拒绝0H 假设。
p 表示在假设0H 下样本均值出现的概率,ci 是0μ的置信区间。
注: 当标准差已知时用Z 检验法,当标准差未知时用T 检验法。
例7 试用正态分布随机数函数生成一组随机数,并对该随机数进行均值的假设检验。
解 假设已知(1,4)X N ,假设0:1H μ=,由于标准差已知,故可用Z 检验法。
MATLAB 命令为>> x=normrnd(1,2,500,1); %生成500个随机数>> [H,p,ci]=ztest(x,1,2,0.05) %用Z 检验法检验,假设显著性水平为0.05 H =p =0.9952ci =0.8242 1.1748由于结果0H =,所以接受0H 假设,即认为均值为1 。
如果认为标准差未知,则用T 检验法进行检验:MATLAB 命令为>> x=normrnd(1,2,500,1); %生成500个随机数>> [H,p,ci]=ttest(x,1,0.05) %用T 检验法检验,假设显著性水平为0.05H =p =0.9954ci =0.8183 1.1806由于结果0H =,所以接受0H 假设,即认为均值为1 。
另外,统计中还有一些常用的命令,如max()x %求最大值min()x %求最小值()median x %求中值()geomean x %求几何平均数()corrcoef x %求相关系数。
5.2.4 回归分析本节主要讲多项式拟合。
多项式拟合的命令格式为: [,](,,)p s polyfit x y n =功能:对已知的数据组,x y 进行多项式拟合,拟合的多项式的阶数为n ,其中p 为多项式的系数矩阵,s 为预测误差估计值的矩阵。
例8 设[00.10.20.30.40.50.60.70.80.91]x =, [2.32.52.12.53.23.63.03.14.15.13.8]y =。
试分别用二次,三次和七次拟合曲线来拟合这些数据,观察哪个拟合曲线的效果最好。
解 MATLAB M-文件为x=0:.1:1; %数据点y=[2.3 2.5 2.1 2.5 3.2 3.6 3.0 3.1 4.1 5.1 3.8]; %数据点p2=polyfit(x,y,2); %二次多项式拟合p3=polyfit(x,y,3); %三次多项式拟合p7=polyfit(x,y,7); %七次多项式拟合disp('二次拟合曲线'),poly2str(p2,'x') %转换成字符串形式的多项式disp('三次拟合曲线'),poly2str(p3,'x')disp('七次拟合曲线'),poly2str(p7,'x')x1=0:.01:1; %重新 取点,以便后面求拟合多项式的值y2=polyval(p2,x1); %求拟合多项式在相应点的值y3=polyval(p3,x1);y7=polyval(p7,x1);plot(x,y,'rp',x1,y2,'--',x1,y3,'k-.',x1,y7) %作图比较legend('拟合点','二次拟合','三次拟合','七次拟合')运行结果如下所示:二次拟合曲线ans =0.64103 x^2 + 1.6226 x + 2.1734三次拟合曲线ans =-4.9728 x^3 + 8.1002 x^2 - 1.2218 x + 2.3524七次拟合曲线ans =1056.2558 x^7 - 4598.0392 x^6 + 7609.4771 x^5 - 6077.9223 x^4+ 2424.1142 x^3 - 439.9012 x^2 + 27.5161 x + 2.2942拟合曲线的对比习题51 某次外语考试抽样调查结果表明,学生外语考试成绩近似服从正态分布,且其均值为72分,并已知超过96分的人数占总数的2.3%,试求出考试外语成绩介于60到80分之间概率。
