椭圆的光学性质在生活中的应用
椭圆的光学原理应用

椭圆的光学原理应用椭圆的定义椭圆是一种二维曲线,具有特定的数学定义。
它由一个平面上的点集组成,这些点到两个给定点的距离之和等于常数。
椭圆具有许多有趣的属性和特征,这些特征使得它在光学领域中具有重要的应用。
本文将介绍椭圆的光学原理及其在实际应用中的一些案例。
椭圆的光学原理在光学中,椭圆可以用来描述光的传播和聚焦。
椭圆镜是一种常见的光学器件,它利用椭圆曲线的特性来聚焦光线。
椭圆镜由一个平面镜面和一个椭圆曲线镜面组成。
当光线通过椭圆曲线镜面时,它们会被反射到焦点处,从而实现光线的聚焦。
椭圆镜的聚焦特性使得它在望远镜、显微镜、激光器等光学设备中得到广泛应用。
它可以改变光线的传播方向和聚焦距离,从而实现图像的放大和清晰。
椭圆的光学应用案例1. 望远镜椭圆曲线镜面在望远镜中发挥了重要作用。
望远镜利用椭圆镜实现光线的聚焦,从而观察远处的物体。
椭圆镜能够聚焦光线,使得物体显得更加清晰和放大。
望远镜的光学系统通常由椭圆镜和其他光学元件组成,它们共同工作来实现高倍率的放大效果。
2. 激光器激光器是一种利用激光技术产生的高强度光束的装置。
椭圆镜在激光器中用于聚焦激光光束。
激光器的椭圆镜组件可以将激光光束聚焦到一个小点上,从而实现高能量密度和高功率输出。
椭圆镜还可以改变激光光束的传播方向,使其更容易控制和引导。
3. 显微镜显微镜是一种光学仪器,用于放大微观物体的图像。
椭圆镜在显微镜中发挥着重要作用。
显微镜的椭圆镜组件能够将光线聚焦在样品上,使得样品中的微小结构能够更清晰地观察和分析。
4. 光学透镜椭圆镜还可用于光学透镜系统中。
透镜是一种光学元件,能够将光线聚焦或散射。
椭圆曲线镜面的聚焦特性使其成为制造高质量透镜的理想选择。
透镜系统利用椭圆镜的光学原理来改变光线的传播方向和强度,实现图像的放大和矫正。
总结椭圆的光学原理应用广泛,涉及到望远镜、激光器、显微镜等多个领域。
椭圆镜通过其优秀的聚焦性能,可以实现光线的聚焦和放大,从而提高光学设备的性能和解析度。
椭圆的知识点总结

椭圆的知识点总结一、椭圆的定义椭圆是平面上的一种特殊曲线,它的定义可以有多种方式。
在解析几何中,我们通常采用焦点-直线之和等于常数的定义来描述椭圆。
具体而言,椭圆定义为到两个固定点(焦点)的距离之和等于常数的点的集合。
这个常数被称为椭圆的长轴长度。
另外,椭圆还有一个短轴,它垂直于长轴且通过长轴的中点。
椭圆的长轴和短轴的长度决定了椭圆的形状。
二、椭圆的性质1. 焦点性质:椭圆有两个焦点,它们位于长轴上,且椭圆上任意一点到两个焦点的距离之和等于椭圆的长轴长度。
2. 直径性质:椭圆的直径是经过焦点的直线段,并且它恰好与椭圆相交于椭圆上的两点。
3. 周长性质:椭圆的周长可以用椭圆的半长轴和半短轴的长度来表示,即2πb+4aE(e),其中a和b分别为椭圆的长轴和短轴的长度,E(e)为第二类椭圆积分。
4. 质心性质:椭圆的质心位于椭圆的中心,且与椭圆的几何中心重合。
椭圆的质心满足椭圆上所有点到该质心的距离之和等于椭圆的长轴长度。
5. 对称性质:椭圆具有关于长轴和短轴的对称性,且同时具有关于两个焦点的对称性。
6. 离心率性质:椭圆的离心率e是一个重要的参数,它刻画了椭圆的形状。
椭圆的离心率满足0<e<1,且e=√(1-b²/a²)。
7. 焦点和直角坐标系的关系:椭圆在直角坐标系中的方程形式可以用来描述椭圆的形状,其一般方程为(x²/a²)+(y²/b²)=1。
三、椭圆的方程椭圆的方程通常以长轴和短轴的长度来表示,其一般方程为(x²/a²)+(y²/b²)=1。
在给定长轴和短轴的情况下,可以通过椭圆的方程来确定椭圆的形状和位置。
四、椭圆的焦点椭圆有两个焦点,它们分别位于长轴的两端。
椭圆上任意一点到两个焦点的距离之和等于椭圆的长轴长度。
焦点是椭圆的重要特性,它们的位置决定了椭圆的形状和方向。
五、椭圆的参数方程椭圆还可以用参数方程来描述。
高中数学——圆锥曲线的光学模型

关于圆锥曲线的光学模型及应用一、圆锥曲线的光学性质1.1椭圆的光学性质:从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上;椭圆的这种光学特性,常被用来设计一些照明设备或聚热装置.例如在F 1处放置一个热源,那么红外线也能聚焦于F 2处,对F 2处的物体加热.1.2双曲线的光学性质:从双曲线一个焦点发出的光,经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点上;(见图1.2).双曲线这种反向虚聚焦性质,在天文望远镜的设计等方面,也能找到实际应用.1.3抛物线的光学性质:从抛物线的焦点发出的光,经过抛物线反射后,反射光线都平行于抛物线的轴(如图1.3)抛物线这种聚焦特性,成为聚能装置或定向发射装置的最佳选择.例如探照灯、汽车大灯等反射镜面的纵剖线是抛物线,把光源置于它的焦点处,经镜面反射后能成为平行光束,使照射距离加大,并可通过转动抛物线的对称轴方向,控制照射方向.卫星通讯像碗一样接收或发射天线,一般也是以抛物线绕对称轴旋转得到的,把接收器置于其焦点,抛物线的对称轴跟踪对准卫星,这样可以把卫星发射的微弱电磁波讯号射线,最大限度地集中到接收器上,保证接收效果;反之,把发射装置安装在焦点,把对称轴跟踪对准卫星,则可以使发射的电磁波讯号射线能平行地到达卫星的接收装置,同样保证接收效果.最常见的太阳能热水器,它也是以抛物线镜面聚集太阳光,以加热焦点处的贮水器的.∙图1.3F 2∙∙F 1图1.2∙∙AF 1F 2D O图1.1B要探究圆锥曲线的光学性质,首先必须将这样一个光学实际问题,转化为数学问题,进行解释论证。
二、问题转化及证明2.1圆锥曲线的切线与法线的定义设直线l 与曲线c 交于P ,Q 两点,当直线l 连续变动时,P ,Q 两点沿着曲线渐渐靠近,一直到P ,Q 重合为一点M ,此时直线l 称为曲线c 在点M 处的切线,过M 与直线l 垂直的直线称为曲线c 在点M 处的法线。
2024全新椭圆的课件

通过化简这个等式,可以得到 椭圆的标准方程。
这种方法适用于已知椭圆的焦 点、长轴和短轴等信息,可以 通过这些信息来求解椭圆的标 准方程。
利用极坐标转换求解
01
将椭圆的极坐标方程转换为直角坐标方程,得到一个关于 $x$和$y$的二次方程。
02
通过解这个二次方程,可以得到椭圆的标准方程中的参数 $a$和$b$。
$frac{x^2}{a^2}
+
frac{y^2}{b^2}
=
1$
($a>b>0$),其中$a$和$b$分
别为椭圆的长半轴和短半轴。
焦点、焦距和离心率
焦点
椭圆上任意一点到两焦点的距离之和 等于长轴长。
焦距
离心率
椭圆的离心率$e$定义为 $e=frac{c}{a}$,离心率越小,椭圆 越接近于圆。
两焦点之间的距离,用$2c$表示,其 中$c=sqrt{a^2-b^2}$。
解析:(1) 利用离心率和过点条件列出 方程组,求解得到椭圆C的方程;(2) 联立直线与椭圆方程,利用判别式和垂 直平分线性质列出不等式组,求解得到 $k$的取值范围。
04
椭圆在几何图形中应用
利用椭圆性质解决几何问题
椭圆的定义和性质
椭圆是由在平面内满足“从两个 定点F1和F2出发的线段长度之和 等于常数(且大于两定点之间的 距离)的点的集合”形成的图形。
03
椭圆与直线关系分析
直线与椭圆相交条件判断
判别式法
通过联立直线与椭圆方程,消元后得到一个关于$x$(或$y$)的二次方程,利用判 别式$Delta$判断方程的根的情况,从而确定直线与椭圆的交点个数。
图形法
通过绘制直线与椭圆的图形,观察交点的个数和位置,从而判断直线与椭圆的关系。
椭圆的相关知识点

椭圆的相关知识点椭圆,这个几何学中的重要概念,一直以来伴随着我们的生活。
它作为一种特殊的曲线,在数学和物理学中有着广泛的应用。
在本文中,我将向大家介绍一些椭圆的相关知识点。
首先,让我们从椭圆的定义开始。
椭圆可以被定义为一个平面上所有到两个固定点之间距离之和等于常数的点的轨迹。
这两个固定点被称为焦点,而这个常数被称为离心率。
离心率越小,椭圆越接近于圆形;离心率越大,椭圆则越拉长。
椭圆的形状可以通过其长轴和短轴来描述。
长轴是连接两个焦点,并通过椭圆中心的直线段,而短轴则是与长轴垂直且通过椭圆中心的直径。
这两个轴对于研究椭圆的性质非常重要。
一个椭圆的周长和面积也是我们需要了解的知识点。
椭圆的周长可以通过半长轴和半短轴来计算。
周长的近似计算公式是:周长≈2π√((a²+b²)/2),其中a和b分别是半长轴和半短轴的长度。
椭圆的面积则是通过半长轴和半短轴计算的,公式为:面积≈πab。
这些公式可以帮助我们更好地理解椭圆的形状和大小。
椭圆还有一系列重要的性质和定理。
其中,焦点定理和离心率定理是最为知名的。
焦点定理指出:对于椭圆上的任意一点P,到两个焦点的距离之和等于椭圆上到该点的半直径的长度。
离心率定理则告诉我们:椭圆上任意一点P的离心率e等于点P到两个焦点的距离之和与椭圆的长轴长度之比。
这些定理不仅仅是椭圆的几何性质,还与其它学科如天文学和物理学相结合,产生了许多应用。
在实际应用中,椭圆也扮演着重要的角色。
例如,在椭圆的光学中,椭圆镜和椭圆轨道是椭圆的应用之一。
椭圆镜的特性使其被广泛用于天文望远镜、摄影镜头和雷达系统,能够将平行光线聚焦到一个点上。
而椭圆轨道则是行星和卫星运动的基础模型之一。
除了几何学和光学之外,椭圆还在数学分析和微积分学中有重要的应用。
椭圆积分和雅可比椭圆函数是这一领域的经典概念,它们在物理计算和工程问题的求解中发挥着重要的作用。
总结起来,椭圆是一个充满魅力和应用的几何概念。
圆锥曲线的光学性质(供参考)

圆锥曲线光学性质的证明及应用初探一、 圆锥曲线的光学性质 1.1椭圆的光学性质: 从椭圆一个核心发出的光,通过椭圆反射后,反射光线都汇聚到椭圆的另一个核心上; (见图1.1)椭圆的这种光学特性,常被用来设计一些照明设备或聚热装置.例如在1F 处放置一个热源,那么红外线也能聚焦于2F 处,对2F 处的物体加热。
电影放映机的反光镜也是那个原理。
证明:由导数可得切线l 的斜率02020x x b x k y a y =-'==,而1PF 的斜率010y k x c =+,2PF 的斜率020y k x c =-∴l 到1PF 所成的角α'知足()()2002222220000012222001000200tan 11y b x x c a y a y b x b cx k kb x y kk a b x y a cy xc a y α++++-'===+-+-+,()00,P x y 在椭圆上,∴20tan b cy α'=,同理,2PF 到l 所成的角β'知足2220tan 1k k b kk cy β-'==+, ∴tan tan αβ''=,而,0,2παβ⎛⎫''∈ ⎪⎝⎭,∴αβ''=1.2双曲线的光学性质 :从双曲线一个核心发出的光,通过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个核心上;(见图1.2).双曲线这种反向虚聚焦性质,在天文望远镜的设计等方面,也能找到实际应用.1.3 抛物线的光学性质 : 从抛物线的核心发出的光,通过抛物线反射后,反射光线都平行于抛物线的轴(如图1.3)抛物线这种聚焦特性,成为聚能装置或定向发射装置的最正确选择.例如探照灯、汽车大灯等反射镜面的纵剖线是抛物线,把光源置于它的核心处,经镜面反射后能成为平行光束,使照射距离加大,并可通过转动抛物线的对称轴方向,操纵照射方向.卫星通信像碗一样接收或发射天线,一样也是以抛物线绕对称轴旋转取得的,把接收器置于其核心,抛物线的对称轴跟踪对准卫星,如此能够把卫星发射的微弱电磁波讯号射线,最大限度地集中到接收器上,保证接生成效;反之,把发射装置安装在核心,把对称轴跟踪对准卫星,那么能够使发射的电磁波讯号射线能平行地抵达卫星的接收装置,一样保证接生成效.最多见的太阳能热水器,它也是以抛物线镜面聚集太阳光,以加热核心处的贮水器的.图1.3图1.2图1.1要探讨圆锥曲线的光学性质,第一必需将如此一个光学实际问题,转化为数学问题,进行说明论证。
椭圆的原理

椭圆的原理
椭圆是几何中常见的一种曲线,它具有许多独特的性质和特点,对于理解椭圆的原理,我们需要从数学和物理两个方面来进行解释。
首先,从数学角度来看,椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。
这个常数2a被称为椭圆的长轴,而两个定点F1和F2被称为焦点。
椭圆的长轴上的两个端点被称为顶点,而长轴的中点被称为中心。
椭圆的短轴则是长轴的垂直平分线,其长度为2b,其中b称为半短轴。
椭圆的离心率e是一个描述椭圆形状的重要参数,它等于焦距和长轴长度的比值,即e=c/a,其中c 是焦距的长度。
其次,从物理角度来看,椭圆也有着广泛的应用。
在天体力学中,行星围绕太阳运动的轨道就是椭圆。
根据开普勒定律,行星在椭圆轨道上的运动速度是不均匀的,它在近日点时速度最快,在远日点时速度最慢。
此外,椭圆还可以用来描述光学中的偏振现象。
当光线沿着椭圆振动时,我们称之为椭圆偏振光。
椭圆偏振光在许多光学器件中都有重要的应用,例如偏振片、椭圆偏振滤光片等。
总之,椭圆作为一种重要的几何曲线,在数学和物理中都有着广泛的应用。
通过深入理解椭圆的定义和性质,我们可以更好地理解其在现实生活中的应用,同时也可以更好地掌握相关的数学和物理知识。
希望本文对读者有所帮助,谢谢阅读!。
《椭圆的光学性质及其应用》教学设计

209第18卷 第06期2021年06月June 2021读与写杂志Read and Write PeriodicalVol.18 N o.06《椭圆的光学性质及其应用》教学设计张红梅(湖南省常德市第三中学 湖南 常德 415000)摘要:新课程的教育理念是“不但要教给学生知识,更重要的是教给学生获取知识的能力”,“要教会学生会学习”,使学生获得终身学习的本领。
而重视自学能力的培养,符合现代“终身教育,终身学习”的教育思想。
为适应未来越来越数学化的社会发展的需要,学生应该养成良好的数学自学习惯。
而数学阅读是数学自学的主要形式,数学自学能力的核心是数学阅读能力,因此教会学生学习的关键之一就是培养学生的数学阅读能力。
学生通过阅读人教版高中教材选修2-1的第75页阅读与思考可以知道圆锥曲线的光学性质以及在生活中的一些应用,通过数学阅读学生会不断地获得一些知识和技能,这又会进一步激发他们的自主学习的兴趣,并从阅读中发现疑问:“圆锥曲线的光学性质”如何证明。
本文用两种方法对椭圆的光学性质进行了证明,并且提供了其在解题与生活方面的应用举例。
把科学的数学阅读方法,纳入到课堂教学环节中去,使之与讲授、练习等有机结合,使学生养成阅读数学的好习惯,优化课堂教学结构,促进学生数学素质的提高。
关键词:椭圆;光学性质;应用;数学阅读能力中图分类号:G623.5 文献标识码:A 文章编号:1672-1578(2021)06-0209-011.教学目标(1)能推导并掌握椭圆的光学性质;(2)能利用椭圆的光学性质有关知识解决实际应用问题;(3)掌握数学建模方法,注重数学知识的应用。
教学重点:椭圆的光学性质的证明及应用。
教学难点:椭圆的光学性质的证明。
2.教学引入2.1 通过《窃听风云之椭圆》教学视频引h t t p s ://v .y o u k u .c o m /v _s h o w /i d _XMTMxNTE5OTA1Ng%3D%3D.html椭圆真的有那么神奇吗?那什么是椭圆?究竟是椭圆的什么特殊性质能使犯人屡次上当?2.2 阅读教材75页阅读与思考(1)通过阅读,你从材料中得到哪些信息、结论?能复述吗?(2)通过阅读,你对圆锥曲线光学性质及其应用产生了哪些疑问?还有哪些疑问没解决?疑问: 怎样去证明圆锥曲线的光学性质呢?以椭圆的光学性质的证明为例,其它两个曲线的光学性质的证明可以类比得到。
椭圆中的两个最大张角及其应用

椭圆是数学中非常重要的一种曲线,它具有许多独特的性质和特点。
在椭圆中,有两个最大张角,它们分别位于椭圆的长轴和短轴上。
这两个张角对椭圆的形状和性质有着重要的影响,并且在许多实际问题中也有着广泛的应用。
让我们来了解一下椭圆的基本特点。
椭圆是平面上到两个定点F1和F2的距离之和恒定的点P到两个定点的距离之和等于一个定值2a的点的轨迹。
我们可以用数学表达式(x^2/a^2)+(y^2/b^2)=1来表示一个椭圆,其中a和b分别表示椭圆长轴和短轴的长度。
在椭圆中,有两个最大的张角,它们分别位于椭圆的长轴和短轴上。
这两个最大张角对椭圆的形状和性质有着重要的影响。
第一个最大张角位于椭圆的长轴上,我们可以用角度θ1来表示它。
当我们对椭圆进行剖切时,这个张角可以帮助我们更好地理解椭圆的形状和结构。
在工程、建筑等领域,利用这个张角可以更精确地设计和制造椭圆形的结构和器件。
第二个最大张角位于椭圆的短轴上,我们可以用角度θ2来表示它。
这个张角也对椭圆的形状和性质有着重要的影响。
在实际问题中,利用这个张角可以更好地分析和解决与椭圆相关的各种数学和物理问题。
椭圆中的两个最大张角对于椭圆的形状和性质有着重要的影响,并且在实际问题中也有着广泛的应用。
我们可以通过对这两个最大张角的深入理解,更好地掌握椭圆的性质和运用,从而更好地应用到实际问题中去。
在我个人看来,椭圆是一种非常有趣和重要的曲线,它具有许多独特的性质和特点。
通过深入研究和理解椭圆中的两个最大张角,我们可以更好地掌握椭圆的形状和性质,并且更好地应用到实际问题中去。
我认为深入理解椭圆中的两个最大张角是非常有益和有意义的。
椭圆的两个最大张角在许多实际问题中都有着广泛的应用。
比如在天文学中,椭圆的形状和性质被用来描述行星、卫星和彗星的轨道。
在工程学中,椭圆的特性被用来设计和制造椭圆形的结构和器件,比如椭圆形的建筑结构、航天器的外形等。
在物理学中,椭圆的性质被用来解决与光学、声学和电磁学相关的各种问题。
椭圆光学性质

椭圆光学性质
椭圆光学性质是椭圆面特有的性质,是它们弯曲或折射
光线的能力。
它是由椭圆反射或折射面产生的光学效应,使光线有不同的轴向偏转角度,这是由于椭圆面能使每一个光线的轴向原点有不同的偏转光线的速度而产生的。
椭圆光学性质的应用领域非常广泛,主要包括折射和反
射光学,传输和分析实验,透镜成像,化学实验,生物学研究,显微镜实验,加工精密件,光学定位,精密尺度刻度和其他精密测量。
在这些应用领域中,椭圆光学性质被广泛用于改善精度,准确性和精密性方面的性能。
此外,椭圆光学性质也可以用于分析光谱,物理机械,
新材料开发,飞行测控,可视化,建筑,军事,医学和放射学的实验,以及环境监测等方面的研究。
在现代光学领域,椭圆光学性质发挥着重要作用,特别
是在生物医学研究,测量,数据分析,仪器制造,反射和传输光学等方面。
它不仅可以调节,识别和测量光线,而且还可以用于制作精确的光学元件,如镜片、滤光片、折射板、偏振片等,并用于提高光学系统的精度。
总之,椭圆光学性质具有广泛的应用前景,可以在众多
领域实现多种性能的改进,使得它成为光学领域的重要技术和工具的重要技术之一。
椭圆双曲线抛物线知识点

椭圆双曲线抛物线知识点椭圆、双曲线和抛物线是常见的曲线形状,它们在数学和物理中有广泛的应用。
本文将介绍椭圆、双曲线和抛物线的基本定义、性质、方程和常见应用。
一、椭圆(ellipse)椭圆是一个平面上的闭合曲线,该曲线的各点到两个定点(称为焦点)的距离之和是一个常数。
椭圆有两个焦点和两个短轴,两个短轴的中点称为椭圆的中心。
椭圆的长轴是通过焦点的直线,长轴的一半称为椭圆的半长轴,短轴的一半称为椭圆的半短轴。
椭圆的数学表达式为:x^2/a^2 + y^2/b^2 = 1其中a和b分别是椭圆半长轴和半短轴的长度。
椭圆的性质:1.椭圆是轴对称的,关于x轴和y轴都有对称性。
2.椭圆的离心率0<e<1,离心率越接近0,椭圆越圆。
3.椭圆的周长可以用椭圆的长轴和半短轴的长度计算。
椭圆的应用:1.椭圆的几何性质使它在图形设计和艺术中有广泛的应用。
2.椭圆的光学性质使它在透镜和镜面的设计中有应用。
3.椭圆在天体力学中用来描述行星的轨道。
4.椭圆在密码学中用来生成加密算法的公钥和私钥。
二、双曲线(hyperbola)双曲线是一个平面上的开放曲线,该曲线的各点到两个焦点的距离之差是一个常数。
双曲线有两个焦点和两个短轴,两个短轴的中点称为双曲线的中心。
双曲线的长轴是通过焦点的直线,长轴的一半称为双曲线的半长轴,短轴的一半称为双曲线的半短轴。
双曲线的数学表达式为:x^2/a^2 - y^2/b^2 = 1其中a和b分别是双曲线半长轴和半短轴的长度。
双曲线的性质:1.双曲线有两条渐进线,它们与双曲线的轴相切。
2.双曲线是非对称的,关于x轴和y轴没有对称性。
3.双曲线的离心率e>1,离心率越大,双曲线越扁。
4.双曲线的焦点和顶点与轴的关系可以用双曲线的方程来确定。
双曲线的应用:1.在物理学中,双曲线用来描述光学中的反射和折射现象。
2.在工程学中,双曲线用于设计天线的形状,以提高信号接收和发送的效果。
3.在经济学中,双曲线用来描述供求曲线和价格变动趋势。
椭圆的一个性质及应用(1)切线

椭圆的性质及应用1.椭圆上任意一点处的切线方程过椭圆C :12222=+by a x (0a b >>)上的任意一点00(,)P x y 作切线,则切线的方程为00221x x y ya b+=. 解析:①不妨设点00(,)P x y 为椭圆的上半部分上的任意一点,则()f x =22()xf x -'=0202()x f x -'=2020x a b y =-⋅,即切线的斜率2020x a k b y =-⋅,于是切线的方程为200020()x a y y x x b y -=-⋅-,2200002222x x y y x y a b a b +=+,又00(,)P x y 在椭圆上,2200221x y a b +=,因此,切线方程为00221x x y ya b+=;②同理得点00(,)P x y 为椭圆的下半部分上的任意一点时,切线方程为00221x x y ya b+=; ③当点00(,)P x y 为长轴的端点时,即(,0)P a ±满足方程00221x x y ya b+=. 所以,椭圆C :12222=+by a x (0a b >>)上的任意一点00(,)P x y 处的切线方程为00221x x y ya b+=. 1.(2011·福建卷)在直角坐标系xoy 中,直线l 的方程为40x y -+=,曲线C 的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数).(Ⅱ)设点Q 是曲线C 上的一个动点,求它到直线l 的距离的最小值.2.椭圆上任意一点处的法线方程过切点垂直与切线的直线,称为过该点的曲线的法线.利用上述结果,得出下面结论:椭圆C :12222=+by a x (0a b >>)上的任意一点00(,)P x y 的法线方程为:222200a b x y a b x y -=-. 3.椭圆的光学性质过椭圆C :12222=+by a x (0a b >>)上的任意一点00(,)P x y 作切线,则切线与焦半径1PF ,2PF 成等角.证明:如图,椭圆C :12222=+b y a x (0a b >>)上的任意一点00(,)P x y 的法线方程为:222200a b x y a b x y -=-,令0y =,得222002a b x x e x a -==,即20(,0)N e x ,那么,221000()F N c e x ae e x e a ex =+=+=+,2100()F N c e x e a ex =-=-,再根据椭圆的第二定义,10F P a ex ==+,20F P a ex =-,所以,1122PF F N PF F N=,直线PN 为12F PF ∠的平分线,所以12APF BPF ∠=∠.(也可用到角公式证明)1.(2010·安徽卷·文科)椭圆E 经过点(2,3)A ,对称轴为坐标轴,焦点1F ,2F 在x 轴上,离心率12e =. (Ⅰ)求椭圆E 的方程;(Ⅱ)求12F AF ∠的角平分线所在直线的方程. 4.椭圆已知斜率的切线方程已知椭圆C :12222=+by a x (0a b >>)的切线的斜率为k ,那么切线的方程为:y kx =或y kx =证明:设直线y kx m =+为椭圆C 的切线,这条切线与椭圆C 过00(,)P x y 的:的切线方程为00221x x y y a b +=重合的条件是002211x y a b k m-==-,20a k x m =-,20b y m =. 又2200221x y a b+=,2222m a k b =+,切线的方程为:y kx =y kx =.1.(2011·福建卷)在直角坐标系xoy 中,直线l 的方程为40x y -+=,曲线C 的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数).(Ⅱ)设点Q 是曲线C 上的一个动点,求它到直线l 的距离的最小值. 5.求椭圆的两条互相垂直切线的交点轨迹方程解:具有斜率k的椭圆的切线方程为y kx =与它垂直的的切线方程为1y x k =-,两式联立消去参数k 得2222x y a b +=+.对于斜率不存在的情形上述方程也满足,所以,所求方程为2222x y a b +=+.1.(2014·广东卷·理科)已知椭圆C :22221x y a b +=(0a b >>)的一个焦点为(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若动点00(,)P x y 为椭圆外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程. 5.椭圆的直径及共轭直径连结椭圆上任意两点的线段叫弦,过椭圆中心的弦叫直径.平行于直径DE 的弦的中点的轨迹AB 和直径DE 互为共轭直径.ABDE设直线l 不过原点,且不平行于坐标轴,l 与椭圆C :12222=+by a x (0a b >>)交于A ,B 两点,线段AB 的中点为M ,则22AB OMb k k a⋅=-.若椭圆的两直径的斜率之积为22b a-,则称这两直径为椭圆的共轭直径.特别地,若一直径所在的斜率为0,另一条直径的斜率不存在时,也称这两直径为共轭直径.1.(2015·全国卷Ⅱ·理科)已知椭圆C :2229x y m +=(0m >),直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M . (Ⅰ)证明:直线OM 的斜率与l 的斜率的乘积为定值; 6.椭圆的直径三角形把经过椭圆C :12222=+by a x (0a b >>)的中心的弦DE 称为椭圆的直径,若P为椭圆C 上异于D 、E 的点,则22PE PD b k k a⋅=-.。
椭圆的光学性质

椭圆的光学性质
椭圆是一种几何图形,具有许多有趣的光学性质。
在光学领域中,椭圆通常被
用来描述某些光学器件的特征,如反射镜和折射器。
本文将探讨椭圆在光学中的作用以及其影响。
椭圆的反射性质
当光线射入椭圆形状的反射镜时,光线在反射过程中会按照椭圆的几何形状进
行反射。
具体来说,对于椭圆反射镜,焦点处的光线将被反射到另一个焦点处,这种性质被广泛应用于望远镜和卫星接收器等光学设备中。
椭圆的折射性质
另外,当光线射入椭圆形状的介质中时,由于介质的折射性质,光线会根据椭
圆的几何形状发生折射。
这种光学性质在制造透镜和棱镜等设备时非常重要,因为它可以帮助设计师确定光线在介质中传播的路径。
椭圆的聚焦性质
除了反射和折射外,椭圆还具有一种独特的聚焦性质。
当光线从无限远处垂直
入射到椭圆形状的透镜上时,光线将被聚焦到另一个焦点处。
这种性质被广泛应用于成像系统和激光聚焦器等光学设备中。
总结
综上所述,椭圆在光学中具有多种有趣的性质,包括反射、折射和聚焦等方面。
这些性质使得椭圆成为光学设计中不可或缺的元素,为各种光学器件的设计和制造提供了重要参考。
希望本文能够帮助读者更好地了解椭圆的光学性质及其在实际应用中的重要性。
椭圆与双曲线的性质与应用

双曲线旋转对称性:绕中心点旋转 180度后与原图重合,因此也具有 旋转对称性
添加标题
添加标题
添加标题
添加标题
椭圆旋转对称性:绕中心点旋转任 意角度后与原图重合,因此具有旋 转对称性
应用:在几何学、天文学等领域有 广泛应用
椭圆与双曲线的镜面对称性
定义:椭圆与双曲线在平面直角坐标系中的对称性质 对称轴:椭圆有两条对称轴,双曲线也有两条对称轴 对称中心:椭圆有一个对称中心,双曲线也有一个对称中心 对称性质的应用:在几何、代数和物理学等领域中都有广泛的应用
椭圆与双曲线的 参数方程
椭圆与双曲线的参数方程的定义
参数方程:表示椭圆或双曲线上的 点与参数值之间的关系
参数方程的应用:用于解决几何、 物理等领域的实际问题
添加标题
添加标题
添加标题
添加标题
参数方程的建立:通过坐标变换和 参数化方法得到
参数方程的优缺点:方便计算和推 导,但不易直观理解
椭圆与双曲线的参数方程的几何意义
添加标题
添加标题
添加标题
添加标题
透镜:双曲线透镜能够将平行光线 聚焦到一点,常用于制造相机、眼 镜等光学仪器中的镜头
光束整形:双曲线光学元件可以用来 改变光束的形状和大小,例如在激光 加工和照明系统中,可以利用双曲线 光学元件对光束进行整形和校准
椭圆在行星轨道计算中的应用
椭圆轨道的稳定 性
行星轨道计算中 的椭圆参数
未来发展:随着信号处理技术的不 断进步,双曲线在信号处理中的应 用将更加广泛和深入。
椭圆与双曲线的 对称性
椭圆与双曲线的中心对称性
定义:椭圆和双曲线都是关于中心对称的几何图形 性质:椭圆关于两个焦点对称,双曲线关于两个顶点对称 应用:在几何学、天文学等领域有广泛应用 举例:以地球和月球的运动为例,解释椭圆和双曲线的中心对称性
高中数学高二下册第十二章12.4 椭圆的性质-椭圆 光学几何性质课件

• 学习椭圆应该关注椭圆常见的几何性质,比如圆与椭圆之 间的仿射变换,采用椭圆离心角表达的椭圆的参数方程及 意义等
6. 课后作业
感谢大家的支持
带着知识走向学生,不如带着学生走向知识。——牛传明 你可以像猪一样的生活,但你永远都不能像猪那样快乐! 利人乎即为,不利人乎即止。——《 墨子》 也许一个人,要走过很多的路,经历过生命中无数突如其来的繁华和苍凉后,才会变的成熟。 好好的管教你自己,不要管别人。 当你能飞的时候就不要放弃飞。 爱生而败仁者,其下愚之得欤? 当我活着,我要做生命的主宰,而不做它的奴隶。 生命如流水,只有在他的急流与奔向前去的时候,才美丽,才有意义。 三军可夺帅也,匹夫不可夺志也。——《论语·子罕》 种子牢记着雨滴献身的叮嘱,增强了冒尖的气。 合理安排时间,就等于节约时间。——培根 不要太在乎自己的长相,因为能力不会写在脸上。 只有承担起旅途风雨,才能最终守得住彩虹满天。
身体健康, 只有坚持才能获得最后的成功。
人生没有十全十美,如果你发现错了。重新再来,别人不原谅你,你可以自己原谅自己。千万不要用一个错误去掩盖另一个错误。 生命就像是一种回音,你送出了什么它就送回什么,你播种了什么就是会收获什么,你给予什么就会得到什么。 美丽的心情永远比美丽的外表重要一千倍。 曾经痛苦,才知道真正的痛苦;曾经执著,才能放下执著。 感谢上天我所拥有的,感谢上天我所没有的。
y P
F1
O Q F2
x
2. 新课 证明过程
定理:从椭圆的一个焦点发出的光线或声波,经过椭圆反射后都集中到椭圆的另一焦点上
y P
F1
O Q F2
x
3. 例题解析
3. 例题解析
4. 巩固练习
5. 课堂小结
自然哲学中的数学原理椭圆

自然哲学中的数学原理椭圆自然哲学中的数学原理椭圆在几何学和物理学等领域具有重要的地位和应用。
在本文中,我们将详细介绍椭圆的定义、性质和应用,并探讨它在自然哲学中的重要性。
首先,椭圆的定义是指平面上到两个定点F1和F2的距离之和等于常数2a的所有点P的轨迹。
这两个定点分别称为焦点,轨迹称为椭圆。
椭圆是一种特殊的植物。
在数学中,我们经常使用椭圆来研究曲线的性质,如在椅子设计中处理成形,椅子通常称为飞弧,其具体测量决定背椅内部的骨骼。
椭圆具有许多独特的性质和定理。
首先,椭圆的长轴和短轴分别是通过中心的长和短方向的直径。
长轴的长度是2a,短轴的长度是2b。
通过长轴的两个焦点分别是(a,0)和(-a,0)。
根据椭圆的定义,我们可以得到焦距的公式,即莱布尼茨椭圆焦距定理,该定理表明焦距等于椭圆的长轴长度的一半。
其次,椭圆还有其他一些重要的性质,如椭圆的离心率。
离心率是一个重要的参数,用于刻画椭圆的扁平程度。
离心率的值介于0和1之间,离心率为0时表示椭圆是一个圆。
离心率越接近1,椭圆就越扁平。
当离心率等于1时,椭圆退化为一条直线。
椭圆在自然哲学中有广泛的应用。
首先,椭圆广泛应用于天体力学和行星轨迹的研究。
根据开普勒的行星运动定律,行星绕太阳运动的轨迹是一个椭圆。
通过研究椭圆轨道的参数,我们可以推断出行星的轨道周期、平均距离和离心率等信息。
其次,椭圆还用于光学中的折射和反射现象的研究。
根据菲涅尔的反射定律和斯涅尔的折射定律,入射光线与法线的夹角和反射光线与法线的夹角之间的关系满足椭圆方程。
通过这些关系,我们可以预测光线的传播路径和反射/折射的角度。
此外,椭圆还有许多其他应用,如遥感技术中的图像处理、天线设计中的指向性和聚焦、电子测量中的误差分析等。
椭圆具有丰富的数学性质和广泛的应用,它不仅在几何学中发挥着重要的作用,而且在物理学、工程学和其他科学领域也有广泛的应用。
总之,椭圆作为自然哲学中的数学原理,具有丰富的性质和广泛的应用。
椭圆的概念是什么

椭圆的概念是什么椭圆是一种特殊的曲线,它在数学中具有重要的地位和广泛的应用。
椭圆的概念是指平面上到两个定点的距离之和等于常数的点的轨迹。
椭圆的定义可以通过几何学和代数学两种不同的方法来描述。
在几何学中,可以通过将一个平面上的点P到椭圆的焦点F1和F2的距离之和等于常量2a来定义椭圆,这里的2a是椭圆的长轴的长度。
换句话说,对于椭圆上的任意一点P,有FP1 + FP2 = 2a,其中FP1和FP2分别表示点P到焦点F1和F2的距离。
此外,椭圆还具有一个与长轴垂直的短轴,短轴的长度为2b。
在椭圆上,短轴的两个端点称为顶点,长轴的两个端点称为焦点。
在代数学中,我们可以通过一个方程来描述椭圆。
椭圆的方程为(x-h)²/a²+ (y-k)²/b²= 1,其中(h, k)是椭圆的中心点坐标,a和b分别是长短轴半径的大小。
这个方程表示平面上所有满足给定条件的点的集合。
通过该方程,我们可以得到椭圆的形状、大小和位置。
椭圆具有很多重要的性质和特点。
首先,椭圆是对称的,即它在横轴和纵轴上都具有对称性。
其次,椭圆具有两个焦点,并且任意两个焦点到椭圆上的任意一点的距离之和恒定。
这个性质被称为焦点定理,它在光学、物理学和工程学等领域有广泛的应用。
此外,椭圆还具有切线和法线的性质,它可以通过平行于椭圆的直线与椭圆相交得到切线和法线。
切线是与椭圆相切的直线,它只与椭圆相交于一个点,而法线是与切线垂直的直线。
椭圆在日常生活和科学研究中有很多应用。
首先,在天文学中,椭圆被用来描述行星的运动轨迹。
根据开普勒定律,行星绕太阳运动的轨迹是一个椭圆,其中太阳位于椭圆的一个焦点上。
其次,在力学和静力学中,椭圆也经常用来描述物体的运动轨迹和力的作用点。
此外,椭圆还在电子学、光学和地理学等学科中有广泛的应用。
例如,在光学中,椭圆被用来描述光的偏振状态。
在地理学中,椭圆被用来描述地球的形状和维度。
总结起来,椭圆是一种特殊的曲线,它具有两个焦点和长短轴的性质。
椭圆的光学性质及其应用
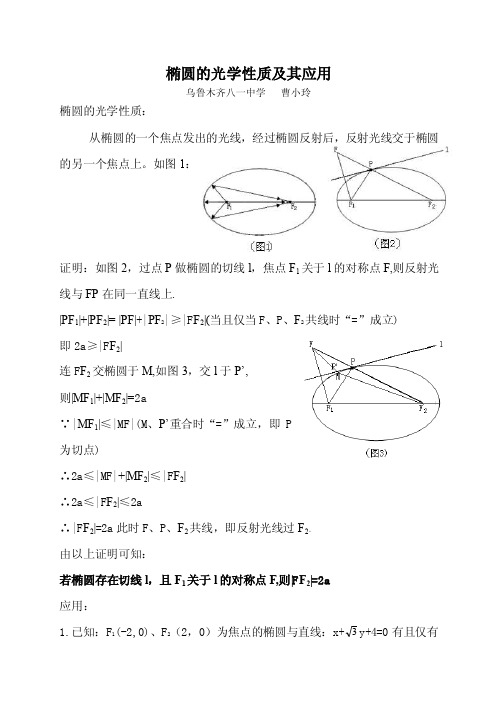
椭圆的光学性质及其应用乌鲁木齐八一中学曹小玲椭圆的光学性质:从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上。
如图1:证明:如图2,过点P做椭圆的切线l,焦点F1关于l的对称点F,则反射光线与FP在同一直线上.|PF1|+|PF2|= |PF|+|PF2|≥|F F2|(当且仅当F、P、F2共线时“=”成立)即2a≥|F F2|连F F2交椭圆于M,如图3,交l于P’,则|MF1|+|MF2|=2a∵|MF1|≤|MF|(M、P’重合时“=”成立,即P为切点)∴2a≤|MF|+|MF2|≤|F F2|∴2a≤|F F2|≤2a∴|F F2|=2a此时F、P、F2共线,即反射光线过F2。
由以上证明可知:若椭圆存在切线l,且F1关于l的对称点F,则|F F2|=2a应用:1.已知:F1(-2,0)、F2(2,0)为焦点的椭圆与直线:x+3y+4=0有且仅有一个交点,求椭圆的长轴长。
解:由条件,椭圆与直线:x+3y+4=0相切设F 1(-2,0)关于l 的对称点F (m,n ),切点为P,则F 、P 、F 2共线由对称条件,F 1F 中点在l 上,且F 1F ⊥l, ∴⎪⎪⎩⎪⎪⎨⎧=+=+⋅+-32042322m n n m ).3,3(33--⎩⎨⎧-=-=⇒F n m 即 从而,|FF 2|=|PF|+|PF 2|=|PF 1|+|PF 2|=2a 2a=72)3()23(22=-+--即长轴长27.2.电影放映机上的聚光灯泡的反射镜的轴截面是椭圆的一部分(如图所示),灯丝在焦点F 2处,而且灯丝与反射镜的顶点A 的距离|F 2A|=1.5cm,过焦点且垂直于轴的弦|BC|=5.4cm,为了使电影机片门获得最强的光线,灯泡应安在距片门多远的地方?解析:据椭圆镜面的光学性质,从椭圆的一个焦点射出的光线经过椭圆反射后应聚焦在另一个焦点上,故片门应放在另一个焦点F 1上,因此需要求出焦距。
