简明博弈论教程(10)
微观经济学-第十章-博弈论初步PPT课件

[资料] 约翰·纳什
[资料] 约翰·纳什
❖ 1994年与泽尔腾、海萨尼 分享了诺贝尔经济学奖。
❖ 他说自己只做了两件事: 一是研究过讨价还价的问 题;二是关注了经济问题 并从数学角度加以分析。
❖ 理性决策决不会无缘无故 地损害自身的利益,也就 是一个人肯定不会故意做 出对自己不利的事。
13
[案例]“华容道”里的纳什均衡(1)
1/2
1/2
▲
▲
▲
▲
1×1/2
▲▲
27
第四节 动态博弈 一、竞争者-垄断者博弈
第四节 动态博弈
一 竞争者-垄断者博弈
竞争者
进 入 不进入
竞争者
进 入 不进入
抵
垄制
断
者
不 抵
制
600
900
800
1300
1200
900
900
1300
抵
垄制
断
者
不 抵
制
600
900
800
1300
1200
900
700
1300
23
第三节 混合策略均衡 一、混合策略与策略组合
第三节 混合策略均衡
一 混合策略与策略组合
❖ 在混合策略博弈中,对于每一个混合策略组合也
存在一个支付组合。 ❖ 参与人都以一定的概率
乙厂商
q1
q2
来选择其纯策略,相应
形成“期望支付”。 甲 p1
1
p1 0,1
q1 0.7 q1 0.7
0
q1 0,1
p1厂 0.5 p1商 0p.52
0 q1 0.7
1 p1 0.5
6– 4
博弈论讲义完整PPT课件
如果两个企业联合起来形成卡特尔,选择垄断利润最大化的产量,每 个企业都可以得到更多的利润。给定对方遵守协议的情况下,每个企业都 想增加产量,结果是,每个企业都只得到纳什均衡产量的利润,它严格小 于卡特而产量下的利润。
• 请举几个囚徒困境的例子
第18页/共293页
第一章 导论-囚徒困境
知识:完全信息博弈和不完全信息博弈。 ❖完全信息:每一个参与人对所有其他参与人的(对手)的特征、
战略空间及支付函数有准确的 知识,否则为不完全信息。
第33页/共293页
第一章 导论-基本概念
• 博弈的划分:
行动顺序 信息
完全信息
静态
完全信息静态博弈 纳什均衡
纳什(1950,1951)
不完全信息
不完全信息静态博弈 贝叶斯纳什均衡
0,300 0,300
纳什均衡:进入,默许;不进入,斗争
第29页/共293页
第一章 导论
• 人生是永不停歇的博弈过程,博弈意略达到合意的结果。 • 作为博弈者,最佳策略是最大限度地利用游戏规则,最
大化自己的利益; • 作为社会最佳策略,是通过规则使社会整体福利增加。
第30页/共293页
第一章 导论-基本概念
一只河蚌正张开壳晒太阳,不料,飞 来了一只鸟,张嘴去啄他的肉,河蚌连忙合 起两张壳,紧紧钳住鸟的嘴巴,鸟说:“今 天不下雨,明天不下雨,就会有死蚌肉。” 河蚌说:“今天不放你,明天不放你,就会 有死鸟。”谁也不肯松口,有一个渔夫看见 了,便过来把他们一起捉走了。
第17页/共293页
第一章 导论-囚徒困境
✓“要害”是否在于“利己主义”即“个人理
性”?
第20页/共293页
S315大学高数第10章 博弈论初步

20
第十章 博弈论初步 第二节 同时博弈:纯策略均衡
条件策略下划线法: 用下划线分别来表示甲厂商和乙厂商的条件策略。 在甲厂商的支付矩阵中,找出每一列的最大者;在乙
厂商的支付矩阵中,找出每一行的最大者。 都有划线的支付组合为条件均衡策略。
甲厂商的策略
的个体,至少有两个,有时可以引入一个虚拟的参与 人如“自然” 。 策略(Strategies/actions) :是一项规则,一组可选择 的行动集合。 参与人应该在什么条件下选择什么样的 行动,以保证自身利益最大化。 支付(Payoffs) :参与人得到的报酬,所得到的支付 都是所有策略共同作用的结果——支付组合。
8
第十章 博弈论初步 第一节 博弈论和策略行为
博弈论重要性 20世纪70 年代以后,博弈论形成了一个完整的体系;从80 年代
开始,博弈论逐渐成为主流经济学的一部分,甚至成为微观经济学的 基础。
1994年:纳什(Nash)、泽尔腾(Selten)和海萨尼(Harsanyi) 3位数学家因在非合作博弈的均衡分析理论方面作出了开创性的贡献, 对博弈论和经济学产生了重要影响而获得了诺贝尔经济学奖。
1950年,22岁的纳什获得博士学位。博士论文为“非 合作的赛局”(后被称为“纳什均衡”) ,该论文仅28 页。
18
第十章 博弈论初步 第二节 同时博弈:纯策略均衡
1958年,纳什得了严重的精神分裂症。他的妻子艾莉 西亚,一直守护在纳什身边,并走过了唯一的儿子同 样罹患精神分裂症的震惊与哀伤……漫长的岁月证明, 与艾莉西亚结婚,也许是纳什一生中比获得诺贝尔奖 更重要的事情。
12
第十章 博弈论初步
第二节 同时博弈:纯策略均衡
第十章博弈论初步-PPT精品

▪ 1、纳什均衡的定义:
▪ 设 s(s1, .., .sn)是n人博弈G={ ; S1, .., . Sn u1,.., . un } 的一个策略组合。如果对于每个局中人 i , ui(s1 , ., .s .i 1 , si , si 1 , ., .s .n )≥ ui(s1 , ., .s .i 1 , si, si 1 , ., .s .n )
第十章 博弈论初步 Game Theory
博弈论概述 纳什均衡 序贯博弈与重复博弈 进入威慑
第一节 博弈论概述
▪ 什么是博弈? ▪ 拍卖金钱 ▪ 海盗博弈 ▪ 田忌赛马 ▪ 围棋和象棋
齐王
田忌
上
中
下
上 赢,输 赢,输 赢,输
中 输,赢 赢,输 赢,输
下 输,赢 输,赢 赢,输
一、博弈的基本要素
ui(si,si) ≥ ui(si,si) 对于所有si Si 都成立,则我们称策略组合
s(s1, .., .sn)
是该博弈的一个纳什均衡。
▪ 纳什简介: ▪ 约翰·纳什生于1928年6月13日。父亲是电子工程师
与教师,第一次世界大战的老兵。纳什小时孤独内 向。纳什的数学天分大约在14岁开始展现。他在普 林斯顿大学读博士时刚刚二十出头,但他的一篇关 于非合作博弈的博士论文和其他相关文章,确立了 他博弈论大师的地位。在20世纪50年代末,他已是 闻名世界的科学家了。 ▪ 然而,30岁的时候,纳什和他惟一儿子都罹患精神 分裂症。半个世纪之后,在他妻子(艾利西亚—— —麻省理工学院物理系毕业生)的精心照料下,和 她的儿子一样,纳什教授渐渐康复,并在1994年获 得诺贝尔经济学奖。 ▪ 影片《美丽心灵》是一部以纳什的生平经历为基础 而创作的人物传记片。该片荣获2019年奥斯卡金像 奖。
博弈论入门PPT课件

基于对其他参与 者信息的了 解程度
完全信息博 弈
不完全信息 博弈
负和博弈
根据结果
零和博弈
正和博弈
特征 合作中如何分配利益,使大家都满意。 只考虑自己的利益,不考虑对方的利益。 做出策略虽然有先后,但每一方都不知
道对方的策略。 做出策略虽然有先后,但参与者对对方
做出的策略是知道。(例如下象棋) 博弈中对其他参与者的各方面信息、可
最理想的结局:双赢
一、正和博弈各方本着相互合作,公平公 正,互利互惠的原则分配利益,让每一 个人参与者都满意的博弈。
案例:鳄鱼鸟与鳄鱼和谐相处,生存搭档 的典型。凶恶的鳄鱼可以容忍鳄鱼鸟清 理它牙缝里的残肉,因为这样可以避免 滋生细菌,它的牙就不会生虫了。
二、博弈中发生冲突的时候,充公了解对 方、取长补短,各取所需,往往会使双 方走出负和博弈和零和博弈的误区,实 现合作共赢。
一年轻人在酒吧喝酒,中途去厕所。一美女尾随 他打劫,对他说:将钱和手机都交出来,否则 我说你非礼我。年轻人转念一想,计上心来, 用手指自己的嘴和耳朵。美女误以为他是聋哑 人,想放弃。年轻人掏出一支笔和一张纸在上 面写上:你说什么呀?
美女见状拿过笔来也在纸上写了:将钱和手机都 交出来,否则我说你非礼我。这时年轻人一把 抓住美女的手,大声喊道:我要送你去派出所 。
最坏的结果:两败俱伤
战争是典型的负和博弈:二战共有61个国 家卷入,涉及人口20亿以上。二战中军 民伤亡1.9亿,其中死亡6000万,受伤 1.3亿。其中死亡的平民有2730万。盟 军中苏联军队伤亡最为惨重,死亡890 万,中国军队死亡148万,英国与美国 各死亡38万。法西斯德国军队伤亡人数 1170万,军队死亡600万,日本军队伤 亡216万。
博弈论简明教材

博弈论第一节博弈问题概述一、博弈的基本概念博弈论是近年经济学中发展得很快的一个分支。
博弈论(game theory)是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题的。
换句话说,博弈论研究当某一经济主体的决策既受到其它经济主体决策的影响,而且该经济主体的相应决策又反过来影响到其它经济主体时的决策问题和均衡问题。
在前面几讲中,除了寡头市场外,消费者的效用或厂商的利润都只依赖于他自己的选择,而与其他人的选择无关。
在这里,经济作为一个整体,各个经济主体的选择是相互影响的。
但对于单个的消费者或厂商来说,所有其它经济主体的行为都被包括在一个参数里。
这个参数就是价格。
除此以外,经济主体在决策时,面临的似乎是一个非人格化的东西。
经济主体既不需要考虑他人的选择对自己选择的影响,也何必需要考虑自己的选择对他人的影响。
而在本讲所介绍的博弈论中,消费者的效用或厂商的利润不仅依赖于自己的选择,而且依赖于具体的某一个或某一些其它经济主体的选择。
在经济学中,博弈论通常是放在寡头市场的分析中,因为在寡头市场上,某一寡头企业在决策时,不得不考虑其他寡头企业的反应。
但事实上,博弈行为是广泛存在的。
博弈分析的目的是使用博弈规则决定均衡。
博弈论的基本概念包括:参与人、行动、战略、博弈规则、信息、报偿、均衡。
参与人是指博弈中选择行动以最大化自身利益(效用、利润等)的决策主体(如个人、厂商、国家)。
行动是指参与人作的决策。
战略是指参与人选择行动的规则,它告诉参与人在什么情况下选择什么行动。
例如,“人不犯我、我不犯人;人若犯我、我必犯人”是一种战略。
这里,“犯”与“不犯”是两种不同的行动。
战略规定了什么时候选择“犯”,什么时候选择“不犯”。
博弈规则是指参与人共同接受的不同情况下的最优战略。
信息是指参与人在博弈中的知识,特别是有关其他参与人(对手)的特征和行动的知识。
报偿是参与人从博弈中获得的结果,它取决于所有参与人的行动或战略。
博弈论教程(第四版)课件第十章 不完全信息序贯博弈

合(s大海,s丽娟)由逆推法得到。
• 要求2:p大海和p丽娟都是可行的信念,而且对于处
在博弈路径上的信息集,相关推断由策略组合(s
大海,s丽娟)和贝叶斯法则给出。
验证:
策略及信念组合(s大海,s丽娟;p大海,p丽娟)=({芭蕾,
足球},{足球,芭蕾,芭蕾,芭蕾};{0.4,0.6;0.6;
到。
• 要求2:局中人的信念都是可行的,而且对于处在
博弈路径上的信息集,相关信念由策略组合和贝
叶斯推断给出。
情侣博弈的贝叶斯子博弈精炼纳什均衡的要求:
我们称策略及信念组合(s大海,s丽娟;p大海,p丽
娟)是不完全信息序贯情侣博弈的一个贝叶斯子博
弈精炼纳什均衡,如果它满足以下两个要求:
• 要求1:在给定信念组合(p大海,p丽娟)的情况下,
(六)局中人的支付函数:u大海(a大海,a丽娟;t大海),u丽娟
(a大海,a丽娟;t丽娟),行动组合(a大海,a丽娟) 由博弈路径
给出,t大海∈T大海,t丽娟∈T丽娟。
通过加入虚拟局中人的方式,进一步展开
表达不完全信息序贯情侣博弈。
• 大海的类型和丽娟的类型都是外生给定的,服从
一个预先确定的联合概率分布。
例子:均衡可以表达为(s大海,s丽娟;p大海,p丽娟)
贝叶斯子博弈精炼纳什均衡的要求
在一个不完全信息序贯博弈里,如果局中人的
策略组合和信念组合满足下述两个要求,我们就称
它们构成了博弈的贝叶斯子博弈精炼纳什均衡:
• 要求1:在给定局中人的信念的情况下,局中人的
策略组合满足序贯理性,即策略组合由逆推法得
(receiver),以后简记为 “R”。
第十章博弈论初步(可编辑修改word版)
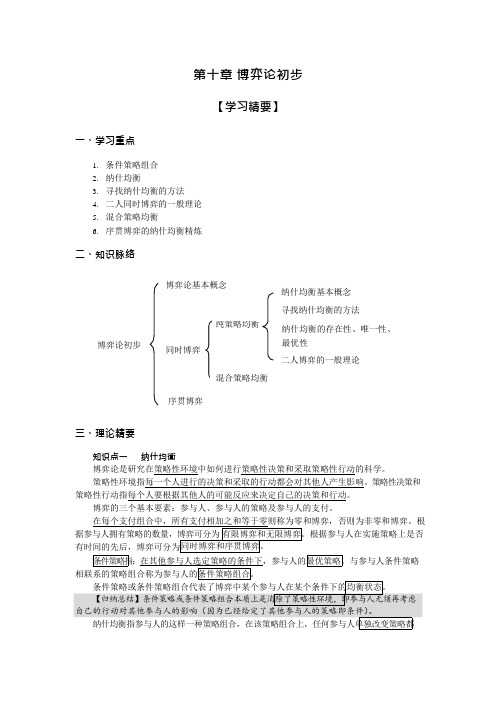
第十章 博弈论初步【学习精要】一、学习重点1. 条件策略组合2. 纳什均衡3. 寻找纳什均衡的方法4. 二人同时博弈的一般理论5. 混合策略均衡6. 序贯博弈的纳什均衡精炼二、知识脉络博弈论基本概念 纳什均衡基本概念博弈论初步 同时博弈 序贯博弈 寻找纳什均衡的方法纳什均衡的存在性、唯一性、最优性 二人博弈的一般理论三、理论精要知识点一 纳什均衡博弈论是研究在策略性环境中如何进行策略性决策和采取策略性行动的科学。
策略性环境指每一个人进行的决策和采取的行动都会对其他人产生影响。
策略性决策和策略性行动指每个人要根据其他人的可能反应来决定自己的决策和行动。
博弈的三个基本要素:参与人、参与人的策略及参与人的支付。
不会得到好处。
知识点二寻找纳什均衡的方法寻找纳什均衡的方法:条件策略下划线法。
根据纳什均衡定义和条件策略组合的定义可得:纳什均衡是所有参与人的条件策略组合的公约数,即纳什均衡是每一个参与人的条件策略组合。
条件策略下划线法:在支付矩阵中每一个参与人的条件策略所对应的支付下面划线,如果支付组合中都有划线,则该支付组合代表的策略组合即为纳什均衡。
知识点三纳什均衡的存在性、唯一性和最优性在同时博弈中,(纯策略的)纳什均衡既可能存在,也可能不存在。
在纳什均衡存在的条件下,它既可能是唯一的,也可能不唯一。
知识点四二人同时博弈的一般理论二人同时博弈(二个策略)每个参与人有9 种可能的支付矩阵,整个博弈有81 种可能的支付矩阵。
全部纳什均衡可分为五种类型:第一种:四个均衡;第二种:三个均衡;第三种:二个均衡;第四种:一个均衡;第五种:零个均衡。
知识点五混合策略均衡混合策略指赋予纯策略的概率向量。
纯策略可以是有限的,由于概率取值的无限性,以有限的纯策略为基础的混合策略一定是无限的。
混合策略组合:((p1, p2),(q1, q2)。
期望支付是指对于每一个混合策略组合,参与人都有一个期望支付即支付的期望值。
条件混合策略: 在其他参与人选择既定的混合策略条件下,参与人所选择的可以使其期望支付最大的混合策略。
高鸿业西方经济学-第10章博弈论初步dmqn.pptx

30
第十章 博弈论初步 第三节 同时博弈:混合策略均衡
二、存在纯策略均衡时的混合策略均衡
求解混合策略纳什均衡的方法不仅适用于纯策略 纳什均衡不存在的情况,而且也适用于纯策略纳什均 衡存在的情况。在后面这种情况下,纯策略纳什均衡 将作为特例被包含在相应的混合策略纳什均衡之中。
2024年9月29日星期日
12
第十章 博弈论初步 第二节 同时博弈:纯策略均衡
五、寻找纳什均衡的方法——条件策略下划线法
2.条件策略下划线方法的五步法 第二,在甲厂商的支付矩阵中,找出每一列的最大者 (每列的最大者可能不只一个),并在其下划线
2024年9月29日星期日
制作者:张昌廷(河北经贸大学)
13
第十章 博弈论初步 第二节 同时博弈:纯策略均衡
个厂商都不再有单独改变策略的倾向时,整个博弈就 达到了均衡,即博弈均衡。
博弈均衡是博弈各方最终选取的策略组合,是博 弈的最终结果,是博弈的解。
2024年9月29日星期日
制作者:张昌廷(河北经贸大学)
8
第十章 博弈论初步 第二节 同时博弈:纯策略均衡
四、纳什均衡
2.纳什均衡的概念 第一,纳什均衡的概念
2024年9月29日星期日
制作者:张昌廷(河北经贸大学)
24
第十章 博弈论初步 第三节 同时博弈:混合策略均衡
一、不存在纯策略均衡时的混合策略均衡
1.混合策略 第三,“混合”策略的概念
把甲厂商和乙厂商原来的策略叫做“纯”策略, 把赋予这些纯策略的概率向量叫做“混合”策略。
2024年9月29日星期日
2024年9月29日星期日
制作者:张昌廷(河北经贸大学)
23
第十章 博弈论初步 第三节 同时博弈:混合策略均衡
尹伯成《西方经济学简明教程》(第8版)课后习题详解(博弈论和信息经济学)

第8章博弈论和信息经济学1.简释下列概念:(1)上策均衡答:上策均衡又称占优策略均衡,是由博弈中的所有参与者的占优策略组合所构成的均衡。
因为在一个博弈里,如果所有参与人都有占优策略存在,那么,占优策略均衡是可以预测到的唯一均衡,因为没有一个理性的参与人会选择劣策略。
应该指出的是,占优策略均衡只要求每个参与人是理性的,而并不要求每个参与人知道其他参与人是理性的(也就是说,不要求“理性”是共同知识),这是因为,不论其他参与人是否是理性的,占优策略总是理性参与人的最优选择。
(2)纳什均衡答:纳什均衡是指这样一种策略集,在这一策略集中,每一个博弈者都确信,在给定竞争对手策略决定的情况下,他选择了最好的策略。
纳什均衡是由所有参与人的最优策略所组成的一个策略组合。
也就是说,给定其他人的策略,任何个人都没有积极性去选择其他策略,从而没有人有积极性去打破这个均衡。
(3)静态博弈答:静态博弈指局中人同时决策或虽非同时决策,但后决策者不知道先决策者采取什么策略的博弈。
在静态博弈中,局中人同时选择行动,或者虽然不是同时,但后行动者并不知道先行动者采取了何种具体行动,从而不能根据先行动者的行动来选择自己的行动。
(4)动态博弈答:动态博弈指局中人决策有先有后,后决策者能观察到先决策者决策情况下的博弈。
在动态博弈中,局中人的行动有先后顺序,并且后行动者能够观察到先行动者所选择的行动,从而可以根据先行动者的行动来决定自己的行动。
相应地,先行动者知道其行动会影响后行动者的行动选择,从而在决定自己的行动时会把这种影响考虑进去。
(5)极大极小化策略答:极大极小化策略指参与者所采取的使自己能够获得的极小收入极大化的策略。
极小收入是指采取某一种策略所能获得的最小收入。
以表8-1的支付矩阵为例,A采取守的策略所能获得的最小收入是2,而采取攻的策略所能获得的最小收入是-500。
表8-1 极大极小策略就表8-1所显示的策略而言,若A、B两人都采取极大极小化策略,均衡的结果是守与退的策略,两人都分别获得2的支付。
博弈论最全完整-讲解课件

• 王则柯、李杰编著,《博弈论教程》,中国人民大学 出版社,2004年版。
• 艾里克.拉斯缪森(Eric Rasmusen)著,《博弈与信 息:博弈论概论》,北京大学出版社,2003年版。
• 因内思·马可-斯达德勒,J.大卫·佩雷斯-卡斯特里罗著, 《信息经济学引论:激励与合约》,上海财经大学出版 社,2004年版。
学习交流PPT
17
约翰· 海萨尼 1920年 生于美 国
约翰·纳什 1928年生于美国
莱因哈 德·泽尔 腾, 1930 年生于 德国
学习交流PPT
18
1996年诺贝尔经济学奖获得者
英国人詹姆斯·莫里斯 (James A. Mirrlees)和 美国人威廉-维克瑞(William Vickrey)
托马斯·谢林
学习交流PPT
24
导论
三、博弈论的基本类型
学习交流PPT
25
合作博弈与非合作博弈
• 合作博弈(cooperative game) 达成有约束力的协议(binding
agreement),强调团体理性,强调效率、公 正、公平 • 非合作博弈(non-cooperative game)
强调个人理性,其结果可能有效率,也可能 无效率。
三位美国学者乔治-阿克尔洛夫(George A. Akerlof)、迈克尔-斯彭斯(A. Michael Spence)和约瑟夫-斯蒂格利茨(Joseph E. Stiglitz)
获奖理由:在“对充满不对称信息市场进行分 析”领域做出了重要贡献。
学习交流PPT
21
迈克尔·斯彭斯 1948年生于美国的 新泽西,1972年获 美国哈佛大学博士 头衔,现兼任美国 哈佛和斯坦福两所
• 也就是说,需要的是对这样的情况下该选什么 的预期的收敛。这一使得参与者能够成功合作 的共同预期的策略被称为焦点。心有灵犀一点 通。
第十章 博弈论资料重点

都有一定的规则 都有一个结果 策略至关重要,游戏者不同的策略选择常会带来不同的游戏
结果 策略和利益有相互依存性
博弈论:博弈论就是系统研究具有上述特征的博弈问 题,寻求各博弈方合理选择战略情况下博弈的解,并 对这些解进行讨论分析的理论。
博弈的分类
首先,分为非合作博弈和合作博弈两大类。本书主要 介绍非合作博弈;
其次,在非合作博弈的范围内,可分为完全理性博弈 和有限理性博弈。本书介绍大多数基本博弈概念、原 理和分析方法时都以完全理性假设为基础;
第三个层次分为静态博弈和动态博弈,外加重复博弈 这种特殊的动态博弈;
第四个层次是根据信息是否完全和完美分类,共分为 完全信息静态博弈和不完全信息静态博弈、完全且完 美信息动态博弈、完全但不完美信息动态博弈、不完 全信息动态博弈。
占优策略(上策)均衡
占优策略(上策)通俗来说是:
• “我所做的是不管你做什么我所能做的最好的” • “你所做的是不管我做什么你所能做的最好的”
占优策略均衡指博弈中的所有参与者的占优策 略组合所构成的均衡。
囚徒困境( Prisoners’Dilemma )
只达到效率很差的个体理性解,没有实现团体 理性解。 前者是稳定的,是自动实施的;尽管团体理性 解对大家都好,但它是不能自动实施的,需要改变 条件。
非合作博弈
合作博弈
《博弈论教程》课件

博弈论的应用领域
经济学
博弈论在经济学中广泛应用于 市场行为、产业组织、贸易政
策等领域。
政治学
博弈论在政治学中用于研究国 际关系、政治制度、选举行为 等领域。
社会学
博弈论在社会学中用于研究社 会结构、社会互动、社会行为 等领域。
计算机科学
博弈论在计算机科学中用于人 工智能、机器学习、网络安全
等领域。
应用场景
保险市场、拍卖、投资决策等。
04
纳什均衡
纳什均衡的定义
纳什均衡是指在博弈中,所有参与者 的最优策略组合,即在这种策略组合 下,每个参与者都认为没有更好的选 择。
纳什均衡是一种非合作博弈的解概念 ,适用于各种博弈类型,如囚徒困境 、智猪博弈等。
纳什均衡的求解方法
迭代法
通过不断迭代每个参与者的最优策略,逐步逼近纳什均衡。
03
博弈论应用
04
市场进入博弈中,企业通常会选 择不同的策略,如快速进入、缓 慢进入或等待观察等。这些策略 的选择会影响到企业的收益和市 场格局。
结论
市场进入博弈可以帮助企业制定 出最优的市场进入策略,以最大 化自身的收益。
价格战博弈
总结词
价格战博弈是博弈论中研究企业之间价格竞争的 模型。
博弈论应用
03
市场竞争、个人决策、政治选举等。
完全信息博弈
定义
参与者拥有完全的信息,即每个 参与者都了解其他参与者的策略 和收益。
特点
信息对称、策略空间明确。
应用场景
金融市场、体育比赛等。
不完全信息博弈
定义
参与者之间存在信息不对称,即某个参与者 对其他参与者的策略和收益不完全了解。
特点
不确定性、信息不完全、策略空间的模糊性。
Lect10 博弈论汇总

2.顺序(序贯)决策(Sequential Decisions)
• 一个企业先做出决策,然后对手在知道 前者行为情况下,做出决策
– 管理者今天作出的最优决策要依赖于对手如 何在明天做出反应。
决策树Game Tree
• 用决策点表明企业的决策,
– 每个决策点延伸出的分支是企业可能采取的 行动
– 序贯决策是从左到右,直到最后的支付收益
承认 1 year, 12
6 years, 6
years
years
劣策略
• 从来不会作为最优策略,也不会被选择, 会被剔除
• 劣策略应该被连续地剔除,ห้องสมุดไป่ตู้到一个不 剩
• 先找到占优策略,然后是劣策略
– 当不存在占优策略时,采用不同的概念来做 同步决策
连续地剔除劣策略
Castle 的价格
高 ($10)
• 博弈的要素:参与人;行动;信 息集;收益;行动顺序;策略;
战略和均衡战略。
博弈的种类
1. 合作博弈与非合作 博弈
厂商之间的经济博弈可以是合 作的,也可以是非合作的。 区别在于是否存在一个有约 束力的协议。如果有,就是 合作博弈;如果没有,就是 非合作博弈。前者强调团体 理性,即效率、公平和公正; 后者强调个人理性和个人最 优决策。
第10讲
博弈理论
• 博弈论(game theory)是由美国数学家冯·诺依 曼(Von. Neumann)和经济学家摩根斯坦
(Morgenstern)于1944年创立,现被广泛应用于 经济学、军事、政治科学、人工智能、生物 学、火箭工程技术等。
• 在1994年,三位博弈论专家即数学家纳什 (Nash,他的故事被好莱坞拍成了电影《美丽 心灵》,该影片获得了2002年奥斯卡金像奖
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 并且,应用进化博弈理论来研究经济系统能 够获得比传统理论更准确的结果,能够更加 现实地解释经济现象,因而在短期内为多数 经济学家所接受。从某种意义上说引入进化 博弈理论局部动态法来分析经济中参与人的 行为是经济学研究方法的一次创新。
8
9
宣判刑期 A 坦白 抵赖
B 坦白 8 ,8 10,0
22
B 鹰 A 鹰 鸽 0,V
鸽 V,0
23
24
25
26
R P S
R 0 1 -1
P -1 0 1
S 1 -1 0
Q组合
27
28
29
• 两个基本点: • 个体是与同一物种中的其它个体或其它物 种中的成员中进行博弈; • 带来高支付的策略遗传型会不断繁殖,而
其他遗传型在种群中的比例会不断下降。
21世纪经济学系列教材
中国人民大学出版社
• 第一节 进化博弈的基本思想 • 第二节 囚徒困境 • 第三节 胆小鬼博弈 • 第四节 物种间的相互作用
• 第五节 鹰鸽博弈
3
• 第六节 某些一般性理论 • 第七节 含有三种类型个体的种群动力学 • 第八章 合作及利他主义的进化解此产生了进化稳定策略 (evolutionarily stable strategy), 也就是说一旦均衡形成,偏离的运动会受 到自然选择的打击。也就是鹰群饱满后, 再试图加入的鹰将会被鹰群排挤。 • 进化上的稳定均衡最大的好处莫过于 保持稳定。但问题在于形成强势的路径依 赖,也就是胜出的不一定是最好的。因为 最好的会被当作出头鸟干掉,这是个体的 失败,集团的胜利以及集体的止步不前。
20
• 这个博弈很多人认为等同于斗鸡博弈。不 过,斗鸡是两个兼具侵略性的个体,鹰鸽
却是两个不同群体的博弈,一个和平, 一个侵略。在只有鸽子一个苞谷场里,
突然加入的鹰将大大获益,并吸引同伴加 入。但结果不是鹰将鸽逐出苞谷场,而是 一定比例共存,因为鹰群增加一只鹰的边 际收益趋零时(鹰群发生内斗),均衡将 到来。
4
5
• 进化博弈理论是经济学研究方法的一次创新, 该理论从否定传统理论赖以成立的基础—— 理性人假定出发而建立起来一个新的分析框 架,它结合了生态学、社会学、心理学及经 济学的最新发展成果,从有限理性的社会人 出发来分析参与人的资源配置行为。
6
• 进化博弈理论是经济学领域的前沿理论, 它来源于对生态现象的研究,虽然该理论 应用于经济分析的时间不长,但它为经济 学研究提供了一个全新的分析方法,较好 地克服了新古典经济学及经典博弈理论中 理性假定及多重均衡的困难。
抵赖 0,10 1,1
10
A T N
A 20,20 35,11 50,2
T 11,35 6,6 6,6
N 2,50 6,6 6,6
11
12
13
A
B 懦弱 懦弱 0,0 勇往直前 1,-1
勇往直前 -1,1 -2,-2
14
15
16
理工院系 强硬者 妥协者
人文院系 强硬者 妥协者 0,0 2,1 1 ,2 0,0
17
18
19
• 每只动物在搏斗中都选择两种策略之一,即“鹰 策略”或是“鸽策略”。 对于为生存竞争的每 只动物而言,如果“赢”相当于“+5”,“输” 相当于“-5”,“重伤”相当于“-10”,“不 受伤”即“0”,最好的结局就是对方选择鸽而 自己选择鹰策略(自己+5,对手-5),最坏的就 是双方都选择鹰策略(双方各-10)。 • 鹰鸽演进博弈的的稳定演进策略共有三种: 一种是鹰的世界,即霍布斯的原始丛林; 一种 是鸽的天堂,既各种乌托邦; 还有一种是鹰鸽 共生演进的策略,这要求混合采取强硬或者合作 的策略。
30
31
• 生物学的进化论类似于社会科学家所使用 的博弈论。 • 进化博弈是由基因事先决定的不同行为表 现型之间而不是理性选择的策略之间进行 的。 • 繁殖过程代表了更一般的传播方式,包括 社会化、教育以及模仿,而变异代表了新 策略的尝试。
32
• 第一节 进化博弈的基本思想 • 第二节 囚徒困境 • 第三节 胆小鬼博弈 • 第四节 物种间的相互作用
• 第五节 鹰鸽博弈
33
• 第六节 某些一般性理论 • 第七节 含有三种类型个体的种群动力学 • 第八章 合作及利他主义的进化解释 • 第九节 进化博弈总结
34
