1-5测量结果的不确定度估算.
测量不确定度的计算公式

测量不确定度的计算公式测量不确定度这东西,在很多科学和工程领域那可是相当重要!咱先来说说啥是测量不确定度。
简单来讲,它就是对测量结果可能存在的误差范围的一种描述。
比如说,你测量一个物体的长度,得到的结果是 10 厘米,但实际上,由于各种因素的影响,它真正的长度可能在 9.8 厘米到 10.2 厘米之间波动,这个波动范围就是测量不确定度。
那测量不确定度的计算公式是啥呢?常见的有 A 类评定和 B 类评定两种方法。
先来说说 A 类评定。
这就好比你多次测量同一个量,然后通过对这些测量数据的统计分析来估算不确定度。
比如说,你测量一个房间的温度,测了 10 次,分别是 25.1℃、25.3℃、24.9℃、25.0℃、25.2℃、24.8℃、25.1℃、25.3℃、24.9℃、25.0℃。
那首先要算这 10 个数的平均值,(25.1 + 25.3 + 24.9 + 25.0 + 25.2 + 24.8 + 25.1 + 25.3 + 24.9 + 25.0)÷ 10 = 25.0℃。
然后算每个测量值与平均值的差值,再平方。
比如第一个 25.1℃与平均值 25.0℃的差值是 0.1℃,平方就是 0.01。
把这 10 个平方差加起来,除以测量次数减 1(也就是 9),得到的就是实验标准偏差。
最后再乘以一个包含因子(通常根据测量次数和置信水平来确定),就得到了 A 类评定的不确定度。
再讲讲 B 类评定。
这通常是基于经验、信息或者其他非统计的方法来估算不确定度。
比如说,你用的测量仪器的说明书上说,它的精度是 ±0.5℃,那这 ±0.5℃就是一个 B 类不确定度的来源。
然后把 A 类和 B 类评定得到的不确定度合成,这就用到了合成不确定度的公式。
合成不确定度等于根号下(A 类评定的不确定度的平方 + B 类评定的不确定度的平方)。
举个我自己经历过的事儿吧。
有一次学校组织科学实验比赛,我们小组要测量一个小金属块的密度。
测量不确定度的两种计算方法
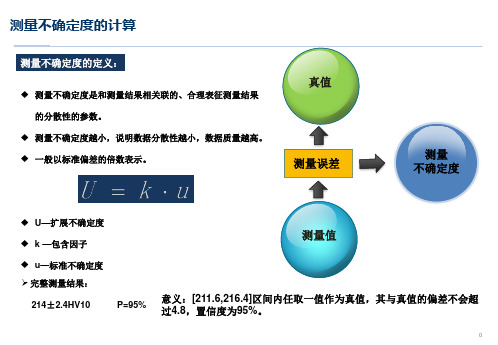
P=95%
意义:[211.6,216.4]区间内任取一值作为真值,其与真值的偏差不会超 过4.8,置信度为95%。
0
测量不确定度的计算
测量不确定度的来源:
1
测量不确定度的计算
测量不确定度的分类:
➢ 不确定度的A类评定(A类不确定度) ➢ 不确定度的B类评定 (B类不确定度) ➢ 合成不确定度
➢确认影响测量结果的因素 ➢各影响因素和测量结果之间的关系
Y=a1x1+a2x2+a3x3
➢计算个影响因素的标准确定度 依据:以往测量数据、检定证书、校准证书、设备厂家出厂说明书 ➢合成出测量值的不确定度
6
测量不确定度的计算
灵敏系数p
Y=a1x1+a2x2+a3x3
Y=a1X1X2+a2X2X3+a3X3X1
2
测量不确定度的计算
A类不确定度的计算:
定义:用对观测列进行统计分析的方法,进行不确定度的估算。
计算方法:
序号
1
测量结果 5.3
2 5.5
3 5.2
4 5.3
5 5.1
6 5.4
7 5.3
8 5.4
9 5.2
1、平均值
2、标准偏差
3
测量不确定度的计算
3、平均值标准偏差 4、平均值标准不确定度 5、平均值扩展不确定度
12
测量不确定度的计算
维氏硬度不确定度的计算 GB/T 4340.1
UE:最大允许误差下的不确定度 UCRM:标准硬度块的标准不确定度 UH:用标准硬度块检定的标准不确定度 UX:重复性的标准不确定度 Ums:压痕测量分辨率的标准不确定度
测量不确定度的简易估算

型 量 塑
t( 一1 n )
兰
! ! ! ! :
8 9 . 8 1 5 1 2 . 5 0 9 . 4 0 7 . 2 . 8 24 .9 .4 10 .3 0 8 .7 07
标准不确定度
测 量 不
即:
=△ 仪
表3
() 3
物理实验 中几种常用仪器的仪器误差 见表 3 。
A类标准不确定度 :( )
B类 标 准不 确 定 度 : ( ) u
u( ): y
确 合成标准不确定度
度 定
扩 展 不 确 定 度
√ c] [ ] [ 2 c 2
这一 方法节 约 了实 验时 间 , 高了工作 效率 。 提
3 4单次测 量的不 确定 度 .
P 09 时, ( 一 )√ 的部分数据可以从表 2中查得 。 = .5 t n 1 /n 。
表2
在很多产 品 的 检测 和 检 验 中( 如破 坏 性 试 验 ) 进 行 , 重复测 量有 时会受 到时间 和资源 的限 制 , 不确 定度 分 A类
测量 的不确定 度 的评估 方 法 。这 时 的不 确定 度 估算 只 能 根据仪 器误差 、 量方 法 、 验 条 件 以及 操作 者 技术 水 平 测 实 等实 际情 况 , 合 理估 计 , 进行 不能 一 概 而论 。在 一 般情 况 下, 简化 的做 法是 采用仪 器误差 或其数倍 的大 小作 为单 次 直 接测量 的不 确定 度 的估 计值 。 当实 验 中只 要求 测 量一 次 时 , U= 并 不意 味着 只测 一次 比多次测 量 时 的 取 △
大学物理实验_基础(二)

2 2 2
UN 1 ∂f 2 ∂f 2 ∂f 2 EN = = U x + U y + Uz + L ∂y N N ∂x ∂z
有效数字的运算规则 几个运算原则: 几个运算原则:
有效数字与有效数字运算 = 有效数字 可疑数字与可疑数字运算 = 可疑数字 (进位数可视为可靠数) 进位数可视为可靠数) 可疑数字与可靠数字运算= 可疑数字与可靠数字运算 可疑数字 可靠数字与可靠数字运算 = 可靠数字
四.间接测量结果的有效数字——有效数字的运算 间接测量结果的有效数字 有效数字的运算 规则 减运算——计算结果的小数点后应保 1 . 加 、 减运算 计算结果的小数点后应保 留的位数与所有参加运算中小数点后位数最少的那 个相同。 15. 372 个相同。例:41.8+15.41-8.372= 41.
2
g = 9.76m/s2 如 g = 9.74500m/s , 取3位有效数字
2
g = 9.74m/s
2
六.测量结果最终由不确定度定位 方法: 方法:
分度值1 分度值1mm
0 1 2 3 4
L=3.25cm 3.25
三位
分度值1 分度值1cm
0 1 2 3 4
L=3.2cm 3.2
二位
5
10
15
20
15.2mm
5
15.0mm
10
15
20
二、关于有效数字的几点说明: 关于有效数字的几点说明:
(1)非测量值(如公式中的常数,实验次 非测量值(如公式中的常数, 数等)不是有效数字, 数等)不是有效数字,如π,e等不是有效 数字。 数字。 在测量数据中, (2)在测量数据中,左边第一位非零数字 之前的零不是有效数字, 之前的零不是有效数字,但数据中间和末 尾的零应算为有效数字。 尾的零应算为有效数字。 ),0.00201(三位), 例:0.0021(二位), (二位), (三位), 0.002010(四位) (四位)
(完整版)不确定度与测量结果不确定的表达

1.2 不确定度与测量结果不确定的表达由于误差的存在,使得测量结果具有一定程度的不确定性。
为了加强国际间的交流与合作,1996年,中国计量科学研究院在国际权威文件《测量不确定度表达指南》的基础上,制定了我国的《测量不确定度规范》。
从此,物理实验的不确定度评定有了国际公认的准则。
下面将结合对测量结果的评定对不确定度的概念、分类、合成等问题进行讨论。
1.2.1 不确定度的概念不确定度是评价测量质量的一个新概念,是表达测量结果具有分散性的一个参数,它是被测量的真值在某个量值范围内的一个评定。
不确定度反映了可能存在的误差分布范围,是误差的数字指标。
不确定度愈小,测量结果可信赖程度愈高;不确定度愈大,测量结果可信赖程度愈低。
在实验和测量工作中,不确定度是作为估计而言的,因为误差是未知的,不可能用指出误差的方法去说明可信赖程度,而只能用误差的某种可能的数值去说明可信赖程度,所以不确定度更能表示测量结果的性质和测量的质量。
用不确定度评定实验结果的误差,其中包含了各种来源不同的误差对结果的影响,而它们的计算又反映了这些误差所服从的分布规律,这是更准确地表述了测量结果的可靠程度,因而有必要采用不确定度的概念。
1.2.2 测量结果的表示和合成不确定度在做物理实验时,要求表示出测量的最终结果。
在这个结果中既要包含待测量的近似真实值x,又要包含测量结果的不确定度σ,还要反映出物理量的单位。
因此,要写成物理含意深刻的标准表达形式,即σ±=xx(单位)(1—4)式中x为待测量;x是测量的近似真实值,σ是合成不确定度,一般保留一位有效数字,若首数是1或2时可取2位。
这种表达形式反应了三个基本要素:测量值、合成不确定度和单位。
在物理实验中,直接测量时若不需要对被测量进行系统误差的修正,一般就取多次测量的算术平均值x作为近似真实值;若在实验中有时只需测一次或只能测一次,该次测量值就为被测量的近似真实值。
如果要求对被测量进行一定系统误差的修正,通常是将一定系统误差(即绝对值和符号都确定的可估计出的误差分量)从算术平均值x或一次测量值中减去,从而求得被修正后的直接测量结果的近似真实值。
1-5测量结果的不确定度估算.

1.5 测量结果的不确定度估算1.5.1 不确定度的概念一般来说,真值是无法测得的,因此误差也就无法得到。
我们只能通过一定的方法对测量误差进行估计,这就需要引入不确定度的概念。
不确定度是指由于测量误差的存在而对被测量值不能肯定的程度,是对被测量的真值所处的量值范围的评定。
我们在表示完整的测量结果时,除给出被测量x 0的量值(一般用被测量的算术平均值来表示),还要同时标出测量的总不确定度∆,写成 0x x ±∆= (P ρ=)(1-11) 式中P 为置信概率,式(1-11)的含义是:区间(0x -∆,0x +∆)内包含被测量x 的真值的可能性是P 。
为了直观地评定测量结果,也常采用相对不确定度的概念。
用U r 表示相对不确定度,则有r 0100%U x ∆=⨯(1-12) 根据估计方法的不同,总不确定度可分为两类分量,一类是可以通过多次重复测量用统计学方法估算出的A 类分量∆A ,另一类是用非统计方法估算出的B 类分量∆B 。
将两类分量按方和根的方法合成,就得到测量结果的总不确定度:Δ(1-13)1.5.2 A 类不确定度分量的估算A 类不确定度分量是指可以用统计学方法估算的分量,一般指随机误差。
具体估算的方法如下:根据误差理论,当重复测量次数足够多时,可求得置信概率为0.95的A 类不确定度分量A 1.96x s ∆= (1-14)式中x s 是算术平均值的标准偏差。
但当重复测量次数较少时,随机误差不再符合正态分布。
这样,需对式(1-14)做一个修正。
即A x tS ∆=(1-15)式中t 是由测量次数决定的修正系数,它的取值与测量次数和置信概率有关。
置信概率为0.95时,t 与不同测量次数n 之间的关系如表1-1所示。
表1-1 t 与不同测量次数n 的对应关系根据重复测量的次数,从表1-1中查出相应的t 值,就可得到修正后的置信概率为0.95的A 类不确定度分量∆A 。
1.5.3 B类不确定度分量的估算1.仪器误差测量仪器和量具本身总是存在一定误差,我们习惯上称之为仪器误差,用符号∆仪表示。
测量不确定度的简易估算

果偏离真值 的差值 , 它客观存 在但人们 无法准确 得 到 。 因此 , 根据 现代 计 量 学 观 点 , 量 结 果 可信 的 程 测
度是 需要 通 过 分 析 和 评 定 测 量 不 确 定 度 来 确 定 的 。
测量不确定度是用来表征被测量的真值所处量值范 围的评定 , 是用于表征合理赋予 的被测量值的分散性
度 , 由合 成不确定 度 的倍 数来 表 示的 , U= u 是 即 k, 通 常 k 2和 3, 决 于 被 测 量 的 重 要 性 、 益 和风 取 取 效 险。
测 量不 确定 度 ຫໍສະໝຸດ 分类 可 以简 明表示 在下表 中 :
准 不确定 度 。
不确定 度也 叫测 量不 确定 度 , 它是 指 由于测 量 误
差的存在而对测量结果 ( 测量值 ) 不能肯定 的程度 , 是 表征测量结果分散性 的一个参数 , 是被测量的真值所 处 的最 值 范 围 的 评 定 。对 一 个 物 理 实 验 的 具 体数 据 来说 , 不确定度是 指测 量值 ( 近真值 ) 附近 的一个 范 围, 以及真值落于其 中的概率。不确定度小 , 量结 测 果可信赖程度 高; 不确定度大 , 测量结果可信赖程 度 低。 测 量结果 的不 确定度 一 般 包 含 若干 分 量 , 按其 数 值评定方法将其归为 A类和 B , 类 然后合成得出合成 不 确定度 , 最后 乘上 包含 因子 k 2~3 得 到扩 展 不确 ( ) 定度 。
刘 云虎
( 贵州省产品质检验检测 院, 贵州 贵 阳 50 0 ) 5 0 1
摘 要: 本文首先简要介绍 了不确定度的基本概念及不确定度的评定流程 , 并给 出了测量 不确定度在 多种情况下 的简易估算 方法 , 最后举例
测量结果的不确定度分析

测量结果的不确定度分析发表时间:2020-12-25T11:38:11.783Z 来源:《城镇建设》2020年29期作者:郭媛媛,刘晓丽[导读] 机械零件加工的质量检查技术是一门高度技术性的学科。
质量检查人员必须逐一检查制造过程中的设计要求是否得到满足。
郭媛媛,刘晓丽商丘工学院机械工程学院,河南商丘 476000摘要:机械零件加工的质量检查技术是一门高度技术性的学科。
质量检查人员必须逐一检查制造过程中的设计要求是否得到满足。
精密机器最重要的是精度,精度除了静态和准静态精度还有动态精度,而动态精度由刚性保证,所以要关注的就变成精度和刚性,其中动态精度和刚性都表现为振动,而振动可以通过检测位移量来反映。
如何开始检查机械零件,如何选择测量工具和检查工具,以及使用哪些测试方法和手段来提高检查效率,以避免错误检测和漏检。
建立适当的检查过程是机械零件质量检查的首要前提。
本文主要研究机械零件的检测和质量控制系统。
关键词:机械零件;测量结果;不确定度0 引言研究机械零件测量的不确定度是新一代GPS(几何技术规范)发展的要求,是产品控制的要求。
随着新世纪测量不确定度技术水平的发展,新一代GPS系列标准逐渐被国内外科研人员和科研机构认同,其水平可以衡量国家层面的科技和制造业水平。
不确定度理论是新一代GPS标准体系的重要理论基础,研究和完善不确定度的工程应用技术,是当前新一代GPS标准应用研究的重点之一[1]。
1 测量结果的不确定度评估测量系统的不确定性一般源于自测量人员,测量装置,测量方法和外部环境四个部分,被分为A类不确定性和B类不确定性两种。
A类型不确定性可以通过分析一系列观测数据的统计规律来评估,一般集中在重复实验的测量结果中。
B类不确定性通常根据经验或相关标准确定的概率分布进行评估[2],一般源于测量系统本身和外部环境。
所以,研究人员在分析一个测量结果的不确定性时,第一要清楚影响测量结果不确定性的组成因素并分类;第二,根据合适的评估方法来进行评估,从而获取不确定性成分;最后也是最重要的,按照一定的步骤合成不确定度的分量,最终得到系统测量结果的不确定度和扩展不确定度的组合。
5等量块测量结果不确定度评定

5等量块测量结果不确定度评定1.概述1.1 测量方法:依据JJG146-2003《量块》检定规程1.2 环境条件:温度:20.0℃相对湿度:≤60%1.3 测量标准:游标卡尺专用量块、准确度等级4等2级、测量范围(10~291.8)mm1.4 测量对象:游标卡尺专用量块、准确度等级5等、测量范围(10~291.8)mm1.5 测量过程:量块的中心长度,通过标准量块与被检量块的中心长度比较测量,两个端面量块比较的直接输出就是它们的中心长度差d。
1.6 评定结果的使用:符合上述条件下的测量结果,一般可直接使用本不确定度的评定结果。
2.数学模型d=l(1+αΔt)-l s(1+αsΔt s) (1)式中:l—被检端面量块在20℃时的中心长度;l s—标准端面量块在20℃时的中心长度;α和αs—被检端面量块和标准端面量块的热膨胀系数;Δt和Δt s—被检量块和标准量块对参考温度20℃的偏差。
3.输入量的标准不确定度评定3.1输入量l标准不确定度u(l)的评定3.1.1测量重复性引起的不确定度u(l1)实验标准差: s(y)=0.068μm在实际测量中,测量2次。
故:u(l1)= s(y)/1.414=0.068/1.414=0.048μm自由度ν(l1):ν(l1)=15-1=143.1.2仪器示值稳定性引起的不确定度u(l2)实验标准差: s(y)=0.046μm。
即有 u(l2)= s(y)=0.046μm自由度ν(l2):ν(l2)=15-1=143.1.3由于量块变动量,检定时瞄准中心偏移而引起的不确定度u(l3)125 mm时:h=0.65μmu(d3)=e2/k2=0.108/1.732=0.062μm500 mm时:h=1.0μmu(d3)=e2/k2=0.167/1.732=0.096μm自由度u(l3)的相对不确定度为1/5,ν(l3)=(1/2)×(1/5)-2=12.53.1.4仪器示值误差估算引起的不确定度u(l4)u(l4)=e3/k3=0.07/1.732=0.040μm自由度u(l4)的相对不确定度为1/4,ν(l4)=(1/2)×(1/4)-2=8比较差值给出的标准不确定度u(l)为:125 mm时:u2(l)=u2(l1)+u2(l2)+u2(l3)+u2(l4)=0.009864μm 2u (l )=0.099μm自由度125 mm 时:ν(l ) =0.0994/(0.0484/14+0.0464/14+0.0624/12.5+0.0404/8)=44 500 mm 时:ν(l )= 0.1234/(0.0484/14+0.0464/14+0.0964/12.5+0.0404/8)=29 3.2输入量l s 标准不确定度u (l s )的评定 125 mm 时:e 1=±(0.20+2×0.125)=±0.450μm u (l s )=e 1/k 1=0.450/2.58=0.174μm500 mm 时:e 1=±(0.20+2×0.5)=±1.2μm u (l s )=e 1/k 1=1.2/2.58=0.465μm自由度由正态分布知ν(l s )→∞。
测量的不确定度

在X 2S X 范围内有95%的可能包含了真值;
在X 3SX 范围内有99.7%的可能包含了真值;
在X 3S X 范围外,仅有0.3% 的可能包含了真值。
3SX 称为误差的极限,也叫坏值剔除的标准。
标准差公式推导: 有一组测量值, x1 , x2 ,, xi , xn ,各次测量 值的误差为 i xi A, i 1,2,, n, 两边求和取平均得:
X
SX
X
Xi
(3)偶然误差的估算:
在有限次测量条件下,我们可用SX对偶然误差进行 估算。由公式知, S X从统计的角度反映了平均值 X 和 某一次测量值X i 之间的偏离程度,称为测量列的标准 偏差,简称测量列的标准差。统计解释:数据列中任一 值Xi 出现在( X S X)区间的概率为68.3%。 可证明:当n
2 i
因而 即
n 1 2 Δ x δ i n
2 i
2 x i
n 1
2 δ i
n
等式右边若取n→∞ 时的极限,即是标准误差σ的定义式。 等式左边是任意一次测量值的标准偏差,记作σx 即
σx
2 x i 2 ( x x ) i
n 1
n 1
它表示测量次数有限多时,标准误差σ的一个估算值。 物理意义:如果多次测量的偶然误差遵从正态分布,则任 意一次测量的误差落在-σx到+σx区域之间的可能性(概率) 为68.3%。或者说,它表示这组数据的误差有68.3%的概率出现 在-σx到+σx的区间内。又称测量列的标准偏差。
许多仪器对其工作环境都有一定的要求,环境的变化对测量结果有着直接的影响。 比如收音机接受短波信号时,其周围电磁辐射会产生噪音的影响;
测量不确定度的评估方法

测量不确定度的评估方法发布日期:2009-12-29 来源:原创北京医院卫生部临床检验中心周琦李小鹏徐建平谢伟李少男杨振华测量不确定度(uncertainty of measurement) 定义为表征合理地赋予被测量之值的分散性,与测量结果相联系的参数。
被测量之值的最佳估计值是测量结果,常用平均值表示。
参数可以是标准偏差、标准偏差的倍数或说明了置信水准区间的半宽度。
标准不确定度(standard uncertainty)是以标准偏差表示的测量不确定度,合成标准不确定度(combined standard uncertainty)是各标准不确定度分量的合成。
扩展不确定度(expanded uncertainty)是确定测量结果区间的量,合理赋予被测量之值分布的大部分可望含于此区间。
测量不确定度评价的步骤和算法如下:一、确定被测量注明被测量和被测量所依赖的输入量,如被测数量、常数和校准标准值等。
二、建立数学模型被测量Y和所有各影响量X i(i=1,2,•••,n)之间的具体函数关系,一般表达形式为Y=f(X1,X2,•••,X n)。
若被测量Y的估计值是y,输入量Xi的估计值是x i,则表达形式是y=f(x1,x2,•••,x n)。
三、求测量数据的最佳估计值最佳估计值的确定大体上可分为两类,一类是通过实验测量得到,另一类是通过信息来源等获得。
四、列出不确定度的来源在实践中,测量不确定度的典型来源有1. 取样;2. 存储条件;3. 仪器的影响;4. 试剂纯度;5. 假设的化学反应定量关系;6. 测量条件;7. 样品的影响;8. 计算影响;9. 空白修正;10. 操作人员的影响;11. 随机影响。
五、标准不确定度分量的确定被测量y的不确定度取决于各输入量最佳估计值xi的不确定度。
有A类评定(type A evaluation of uncertainty)和B类评定(type B evaluation of uncertainty)。
测量结果的不确定度及其计算

讲座??测量结果的不确定度及其计算周舜元卫生部工业卫生实验所北京1000881概述随着生产和科学技术的进步对检测数据的准确可靠性提出了更高的要求。
过去通常用测量误差即测量结果与真值的差异来表示测量结果的准确可靠程度但由于真值通常是未知的所以误差常常也无法知道只能用约定真值代替真值来求误差。
在实际工作中更多遇到的应该是测量的不准确度这已逐渐成为人们的共识。
特别是由于国际贸易的发展检测数据的质量高低需要在国际间得到评价和承认由此开展的国际间的验证比对试验、实验室认可等活动越来越重视对测量结果不确定度的分析和表达。
国家标准《校准和检验实验室能力的通用要求》GB/T15481-1995等同采用ISO 导则25中就要求实验室的每个证书或报告均应对估算的校准和测试结果的不确定度作出说明:ISO9001也规定应保证所用设备的测量不确定度已知。
在1993年由BIPM国际计量局、IEC国际电工委员会、IFCC国际临床化学联合会、ISO国际标准化组织、IUPAC国际理论与应用化学联合会、IUPAP国际理论与应用物理联合会和OIML国际法制计量组织等7个国际机构共同发起ISO公布了“测量不确定度表示指南”从而形成了共同的基础。
2基本概念2.1测量不确定度它是一个与测量结果相关的参数用以表征可以合理赋予被测量值的分散性。
该参数可以用标准偏差或其给定倍数来表示也可以用置信水平的区间半宽度来表示。
测量不确定度通常由其所有的不确定度分量构成其中有些分量可以用测量结果的统计分析来加以评定有些分量则基于统计分析以外的方法或信息来评定。
测量不确定度一般来源于随机性和模糊性前者来自一些主客观条件不充分后者归因于事物本身概念不明确。
在具体实践中可能包括的来源如下:1对被测量的定义不完善2实现被测量的定义的方法不理想3被测量的样本抽样不能代表所定义的被测量4环境条件的测量不完善或对测量受环境条件影响的认识不周全5人员对模拟仪器的读数有偏差6测量仪器的分辨力和鉴别阈不够7赋予计量标准的值和标准物质的值不准8从外部来源取得并用于数据计算的常数和其他参数不准9与测量方法和测量程序相关联的近似性和假定性10在表面上完全相同的条件下被测量重复观测值的变化。
测量不确定度及其估算

测量不确定度及其估算作者:侯亚萍来源:《科学与财富》2018年第20期摘要:自2000年测量新国标出台以来,测量不确定度已经得到了各大实验室的认可,并被广泛应用在计量认证的准备工作中。
另外,《检测和校准实验室能力的通用要求》中规定:实验室检测和校准的工作必须加入测量不确定度的评定流程,以体现出该实验室的管理水平和测试水平。
本文就不确定度的理论概念做出解析,并做出A、B两类不确定度的估算说明,以期为相关领域的研究应用提供理论参考。
关键词:测量不确定度;专业术语;A类;B类;引言1970年以后,测量不确定度的概念开始在测量领域普及开来,大大提高了测试结果的逻辑性和可操作性。
经过不断地补充说明,测量不确定度在国际范畴已经有了较为统一的理论基础和评估方法。
我国也于2000年颁布了《检测和校准实验室能力的通用要求》明确规定了测量不确定度评估在实验室进行测量工作时不可或缺的重要环节。
一、测量不确定度理论解析测量不确定度的国际领域概念自1963年诞生以来虽屡经补充说明,但仍旧是一个难以被理解的复杂概念,尤其是进入21世纪以来,我国关于各种实验测量的学术研究也丰富起来,不少学者对于测量不确定性的国际定义也提出了不同的看法。
本文中对测量不确定度的定义也有着自己的理解:由于存在测量误差,用来表征真实测量值所处范围的量就是测量不确定度。
通常情况下,任何实验都要给出本次的测量结果,我们用X来表示。
但是,为了表示真实测量值的存在范围,我们额外引入描绘参数不确定度,用U来表示。
所以,结合不确定度的基本定义,我们可以将试验结果真实测量值的存在区间为(X-U,X+U)或(X±U)。
二、测量不确定度专业术语介绍测量不确定度的概念虽然虽然用简短几个字就能表述,但要真正的参悟其中的含义并学以致用还要涉及到很多专业术语的理解,包括不确定度A类评定、不确定度B类评定、测量误差、置信概率、修正值等,其具体列举与描述详见表2-1。
测量结果的不确定度评定

次数
1 2 3 4 5 6 7 8 9 10 平均值
测量值(mA) 46.4 46.5 46.4 46.3 46.5 46.3 46.3 46.4 46.4 46.4 46.39
➢ ①如不计其他不确定度来源,估计最佳值及其标准不确定 度
➢ ②在同一系统中在以后做单次(n′=1)测量,测量值x= 48.3mA,求该次测量的标准不确定度u(x)。
则标准差
u wn 0.0292mm
dn
查表7-3其自由度 7.5
用两种方法估计得到的标准差很接近,但自由度
有明显不同,可见用贝塞尔公式更好一些。
【例3】
某激光管发出的激光之波长,经检定为 0.63299130μm 后又用更精确的方法,测得该激光管的波长为 0.63299144μm ,试估计原检定波长的标准不确定 度及其自由度。
测量不确定度的结构
测量 不确 定度
标准不 确定度
A类标准 不确定度
B类标准不 确定度
合成标准 不确定度
U(当无需给出Up时, k=2~3)
扩展不 确定度
Up(p为包含概率)
评定不确定度的一般流程
分析不确定度来源和建立测量模型 评定输入量的标准不确定度 计算合成标准不确定度 确定扩展不确定度 报告测量结果
当用算术平均值 x 作为被测量估计值时, A
类评定的被测量估计值 x 的标准不确定度为
u(x) s(x) s(xi )
n
A类评定的标准不确定度 u(x) 的自由度为实 验标准偏差s(xi)的自由度,即ν=n-1。
测量不确定度的A类评定方法
对被测量进行独立重复测量,通过所得到的 一系列测得值,用统计分析方法获得实验标 准偏差s(xi)
测量结果的不确定度评定

– 同样是测量电阻器的损耗功率P(被测量),我们 也可以采用测量电阻器两端的电压V与流经电阻器 的电流I来获得,则被测量P的数学模型成为 P f (V , I ) VI
测量模型的输入量
• 测量模型中的输入量可以是:
– – – – (1)当前直接测量的量; (2)由以前测量获得的量; (3)由手册或其它资料得来的量; (4)对被测量有明显影响的量。
– 例如:如被测量为某种介质材料在给定频率时的相 对介电常数。由于测量方法和测量设备的限制,只 能取这种材料的一部分做成样块进行测量,如果该 样块在材料的成分或均匀性方面不能完全代表定义 的被测量,则样块就引入测量不确定度。
测量不确定度的来源4
• 4.对测量过程受环境条件的影响认识不足或对 环境条件的测量与控制不完善
ls (1 ss ) l l f ls , l , , s , ,s 1
ls ls ss l 1
ls l ls s s ls
• 设 s 和 s
测量不确定度的来源11 • 11.修正不完善
– 在有系统误差影响的情形下,应当 尽量设法找出其影响的大小,并对 测量结果予以修正,对于修正后剩 余的影响应当把它当作随机影响, 在评定测量结果的不确定度中予以 考虑。然而,当无法考虑对该系统 误差的影响进行修正时,这部分对 结果的影响原则上也应贡献于测量 结果的不确定度。
Y f ( X 1 , X 2 ,, X N )
被测量或输出量 影响量或输入量
测量模型
• 设输入量Xi的估计值为xi,被测量Y的估计值为 y,则测量模型可写成
y f ( x1 , x2 ,, x N )
测量模型与测量方法有关
不确定度和相对不确定度计算公式

不确定度和相对不确定度计算公式篇一:嘿,朋友!今天咱就来好好唠唠不确定度和相对不确定度计算公式这档子事儿!你知道吗?不确定度就像是一个神秘的影子,总是跟在测量结果后面,让我们对测量的准确性心里有点“打鼓”。
先来说说不确定度的计算公式吧。
它呀,就像是一个复杂的拼图,由好多小块儿组成。
简单点说,不确定度可以分为A 类不确定度和B 类不确定度。
A 类不确定度,就好比是你多次测量同一个量,然后通过统计学的方法算出来的那些“波动”。
比如说,你反复测量一个物体的长度,每次得到的结果都有点小差别,那这些差别综合起来算出来的就是A 类不确定度啦。
这难道不像是天气的变化,有时晴有时雨,让人捉摸不透?B 类不确定度呢,则像是那些藏在暗处的“小怪兽”,不是通过直接测量得到的,而是根据一些已知的信息估计出来的。
比如说仪器的精度、校准数据等等。
这是不是有点像你从别人的口中听说了一个神秘的地方,虽然没亲自去过,但能大概猜到那里的情况?那把A 类和B 类不确定度加起来,再开个平方,这就是总的不确定度啦!你说这过程复杂不复杂?再来说说相对不确定度的计算公式。
相对不确定度,就像是不确定度的“缩小版”。
它是不确定度除以测量值得到的。
这就好比是把一个大蛋糕切成小块,每一小块相对于整个蛋糕的大小就是相对不确定度。
想象一下,你在做实验的时候,辛辛苦苦测量出来的数据,却因为不确定度的存在,心里总是有点不踏实。
这时候,搞清楚不确定度和相对不确定度的计算公式,不就像是给自己找到了一把解开谜团的钥匙吗?咱们再举个例子,比如说你测量一个电阻的阻值,测了好几次,得到了一堆数据。
然后通过计算得出了不确定度,发现这个不确定度还不小。
这时候你是不是会想,哎呀,这测量结果到底靠不靠谱啊?要是能把相对不确定度也算出来,看看它占测量值的比例,心里不就更有数了吗?所以啊,搞清楚不确定度和相对不确定度的计算公式,对于咱们做科学实验、进行各种测量,那可真是太重要啦!它们就像是我们的测量结果的“保镖”,能让我们对测量结果更有信心,也能让我们知道什么时候该更加谨慎。
测量结果的不确定度及其计算

测量结果的不确定度及其计算
不确定度的计算可以通过多种方法进行,下面介绍几种常见的计算方法:
1.绝对误差法:通过与已知真值进行比较,计算出差值的绝对值作为
不确定度。
这种方法适用于已知真值的情况,但对于没有已知真值的实验,无法使用。
2.标准差法:通过测量一组样本值,计算出测量结果的标准差作为不
确定度。
标准差表示测量结果的离散程度,值越大表示不确定度越高。
3.极限误差法:通过测量仪器的极限误差,将其作为不确定度。
极限
误差是指仪器测量的最大误差范围。
4.相对误差法:通过计算相对误差,将其作为不确定度。
相对误差是
指测量结果与真值之间的差值与真值的比值。
不确定度的计算需要根据具体情况选择适合的方法,并在实际应用中
考虑到各种因素的影响。
此外,还需要注意不确定度的传递规律,即当多
个测量结果进行计算时,其不确定度如何传递和组合。
在实际应用中,不确定度的计算对于保证测量结果的可靠性和准确性
非常重要。
因此,科学家和工程师在进行实验或研究时,需要对测量结果
的不确定度进行充分的估计和分析,以便准确地评估和解释实验结果。
总结起来,测量结果的不确定度是描述测量结果精确程度的统计度量,可通过不同的计算方法进行估计。
准确地计算不确定度对于保证测量结果
的可靠性和准确性至关重要。
在实际应用中,科学家和工程师需要根据具
体情况选择适合的方法进行计算,并考虑不确定度的传递和组合。
测量不确定度及其估算-试验室法

§3 测量不确定度及其估算3. 1 不确定度的基本概念由于测量不可避免存在误差,所以用测量结果作为被测量真值的估计值自然要有偏差。
测量不确定度就是对测量结果的偏差做全面的评估。
不确定度是指由于测量误差的存在而对被测量值不能肯定的程度,是表征被测量的真值所处的量值范围的评定。
测量结果应给出被测量的量值X ,同时还要标出测量的总不确定度U ,写成U X x ±=的形式,这表示被测量的真值在),(U X U X +-的范围之外的可能性(或概率)很小。
显然,测量不确定度的范围越窄,测量结果就越可靠。
引入不确定度概念后,测量结果的完整表达式中应包含: ① 测量值和不确定度; ② 单位;③置信度。
我国的《国家计量规范JJG1027-91测量误差及数据处理》中把95.0=P 作为广泛采用的约定概率,当取95.0=P 时,可不必注明。
与误差表示方法一样,引入相对不确定度x E ,即不确定度的相对值%100⨯=XU E xx (1-3-1) 3. 2 不确定度的简化估算方法不确定度是由误差引起的,由于误差的复杂性,准确计算不确定度不是一件简单的事情,已经超出了本课程的范围。
因此物理实验中采用具有一定近似性的不确定度估算方法。
不确定度按其数值的评定方法可归并为两类分量: 一是多次测量用统计方法评定的A 类分量A U ; 二是用其它非统计方法评定的B 类分量B U 。
总不确定度由A 类分量和B 类分量按“方、和、根”的方法合成,即22BA U U U += (1-3-2)1.A 类分量的估算在实际测量中,一般只能进行有限次测量,这时测量误差不完全服从正态分布规律,而是服从称之为t 分布(又称学生分布)的规律。
在这种情况下,对测量误差的估计,就要在贝塞尔公式(1-2-10)的基础上再乘上一个因子。
在相同条件下对同一被测量作n 次测量,若只计算总不确定度U 的A 类分量A U ,那么它等于测量值的标准偏差x S 乘以一因子n n t P /)1(-,即x P A S nn t U )1(-=(1-3-3)式中)1(-n t P 是与测量次数n 、置信概率P 有关的量,置信概率P 及测量次数n 确定后,)1(-n t P 也就确定了,可从专门的数据表中查得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.5 测量结果的不确定度估算1.5.1 不确定度的概念一般来说,真值是无法测得的,因此误差也就无法得到。
我们只能通过一定的方法对测量误差进行估计,这就需要引入不确定度的概念。
不确定度是指由于测量误差的存在而对被测量值不能肯定的程度,是对被测量的真值所处的量值范围的评定。
我们在表示完整的测量结果时,除给出被测量x 0的量值(一般用被测量的算术平均值来表示),还要同时标出测量的总不确定度∆,写成 0x x ±∆= (P ρ=)(1-11) 式中P 为置信概率,式(1-11)的含义是:区间(0x -∆,0x +∆)内包含被测量x 的真值的可能性是P 。
为了直观地评定测量结果,也常采用相对不确定度的概念。
用U r 表示相对不确定度,则有r 0100%U x ∆=⨯(1-12) 根据估计方法的不同,总不确定度可分为两类分量,一类是可以通过多次重复测量用统计学方法估算出的A 类分量∆A ,另一类是用非统计方法估算出的B 类分量∆B 。
将两类分量按方和根的方法合成,就得到测量结果的总不确定度:Δ(1-13)1.5.2 A 类不确定度分量的估算A 类不确定度分量是指可以用统计学方法估算的分量,一般指随机误差。
具体估算的方法如下:根据误差理论,当重复测量次数足够多时,可求得置信概率为0.95的A 类不确定度分量A 1.96x s ∆= (1-14)式中x s 是算术平均值的标准偏差。
但当重复测量次数较少时,随机误差不再符合正态分布。
这样,需对式(1-14)做一个修正。
即A x tS ∆=(1-15)式中t 是由测量次数决定的修正系数,它的取值与测量次数和置信概率有关。
置信概率为0.95时,t 与不同测量次数n 之间的关系如表1-1所示。
表1-1 t 与不同测量次数n 的对应关系根据重复测量的次数,从表1-1中查出相应的t 值,就可得到修正后的置信概率为0.95的A 类不确定度分量∆A 。
1.5.3 B类不确定度分量的估算1.仪器误差测量仪器和量具本身总是存在一定误差,我们习惯上称之为仪器误差,用符号∆仪表示。
它是指仪器在规定条件下使用时,所允许的误差限值。
仪器误差是一个统称,对于具体的各类仪器和量具具有不同的表示方式。
例如,游标卡尺和螺旋测微计的仪器误差用示值误差表示。
国家标准规定,量程为0~300mm以下的游标卡尺,其示值误差在数值上等于该尺的最小分度值。
螺旋测微计分零级、一级和二级3种精度级别,通常实验室使用的为一级螺旋测微计,其示值误差随量程而异。
量程为0~25mm 的一级螺旋测微计,示值误差为±0.004mm。
对物理天平而言,仪器误差用指示值变动性误差来表示天平称衡结果的可靠程度,这是由于天平调节、操作、温差、气流以及振动等原因,致使重复称衡时各次平衡位置产生差异。
按规定,合格天平的示值变动性误差不应大于该天平的最小分度值。
对于实验室常用的WL-1型物理天平,其误差限值一般取为0.05g。
电表及电阻箱的仪器误差用准确度等级K表示。
在规定条件下使用电表测量,其示值的误差限为电表量程与准确度等级百分数(即K%)的乘积。
可见,电表的仪器误差大小由电表准确度等级和电表量程二者决定。
Δ仪可在仪器出厂说明书或仪器标牌上查到,对于精度较低的仪器,Δ仪可取为其最小分度值的一半,如米尺的示值误差为0.5mm。
在工业和商业用途上,仪器误差的置信概率一般为0.95。
2.B类不确定度分量不能用统计学方法估算的分量为B类不确定度分量,一般指系统误差。
若不特别说明,则ΔΔB C=仪(1-16)C称为置信因子,置信概率取0.95时,C=1.05。
1.5.4 直接测量量的不确定度估算及测量结果表示1.单次直接测量在实际测量过程中,有的被测量是随时间变化着的,我们无法对其进行重复测量,只能进行单次测量。
还有些被测量,对它们的测量精度要求不高,只要进行单次测量就可以了。
在单次测量中,用单次测量值x测作为被测量的最佳估计值。
测量值的不确定度与所用测量仪器的精度、测量者的估读能力及测量条件等很多因素有关,因此它的合理估计是比较复杂的。
在一般情况下,对随机误差很小的测量,可以只估计不确定度的B类分量,用仪器误差△仪作为x测的总不确定度,测量结果表示为Δx x=±测仪(1-17)有的测量随机误差可能比较大,此时可以估计一个误差限来作为单次测量的不确定度∆。
例如,用0.1s分度的秒表计时,由于人的感官灵敏度的限制与技术上的不熟练,常常造成“启动”和“停止”秒表所用的时间超过0.1s ,这必然使测量误差限超过秒表的仪器误差限。
这时可依据实际情况来估计误差限,如可取∆ = 0.2s 。
又如,用钢卷尺测量较长的距离,不可能保证尺子拉直拉平,则可依实际情况取∆ = 5mm 或更大。
总之要根据测量的不同情况以及观测者实验技巧的高低来对单次测量的总不确定度做出估计。
2.多次直接测量对多次直接测量的数据12,,n x x x ⋅⋅⋅进行处理的一般步骤是:① 计算被测量的算术平均值1/ni i x x n ==∑,把x 作为被测量的最佳估计值。
② 求出各测量值的残差i i v x x =-③用贝塞尔公式求出测量列的标准偏差S =④ 审查测量数据,如发现有异常数据,应予以舍弃。
舍弃异常数据后,再重复步骤①②③④,直至完全剔除异常数据。
⑤求出算术平均值的标准偏差x S =1-1求出总不确定度的A 类分量A Δx tS =。
⑥求出总不确定度Δ⑦ 表示出最后测量结果ΔΔ,100%r x x U x=±=⨯ 注:利用计算器的统计计算功能,将多次测量结果输入后,可直接求得x 及S 。
【例1-1】 有一组以cm 为单位的长度测量数据为2.20,2.25,2.30,2.15,2.10,2.15,2.25,2.10,2.20,2.20,2.10,2.15,2.25,2.20,2.20,2.15,2.25,2.20,2.20,3.50,据“3σ”准则判断其中是否有异常数据需剔除。
解:因为测量次数10n >,所以可以用“3σ”准则剔除异常数据。
201 2.26cm 20i i xx ===∑ 根据贝塞尔公式,用标准偏差S 代替标准误差σ:0.3cm30.9cmS S ==根据“3σ”准则,因为20 1.24cm 3S υ=>,所以3.50应舍去。
舍去3.50后,再重新计算测量数据,得 1912.19cm 19ii x x ===∑0.06cm30.18cmS S ==在这19个数据中,没有一个数据的残差大于此3S ,所以,根据准则“3σ”,这19个数据中没有异常数据。
【例1-2】 用量程为0~25mm 的一级螺旋测微计(∆仪=0.004mm )对一铁板的厚度进行了8次重复测量,以mm为单位,测量数据为:3.784,3.779,3.786,3.781,3.778,3.782,3.780,3.778,同时读得螺旋测微计的零位为 + 0.004mm,请给出完整的测量结果。
解:可求得3.781mmL=0.0029mmS=没有一个数据的残差大于3S,所以,根据准则“3σ”,这8个数据中没有异常数据,不用剔除。
但考虑到零位修正 3.7810.004 3.777(mm)L=-=0.0011mmLS=查表1-1可知,8n=时, 2.36t=,计算得:A类不确定度分量Δ0.0025mmA LtS==B类不确定度分量Δ0.004Δmm0.0038mm1.05B C===仪总不确定度Δ0.005mmL==测量结果为()3.7770.005mm100%0.13%LLrL LUL=±∆=±∆=⨯=1.5.5 间接测量量的不确定度估算及测量结果表示在很多实验中,我们进行的测量都是间接测量。
因为间接测量量是各直接测量量的函数,所以直接测量量的误差必定会给间接测量量带来误差,这被称为误差的传递。
这样一来,直接测量结果的不确定度就必然会影响到间接测量结果,这种影响的大小可以由相应的数学公式估算出来。
1.间接测量的不确定度合成公式设间接测量量y是各自相互独立的直接测量量12,,mx x x⋅⋅⋅的函数,其函数形式为()12,,my f x x x=⋅⋅⋅(1-18)设各直接测量量12,,mx x x⋅⋅⋅的测量结果分别为1122,,m mx x x x x x±∆±∆⋅⋅⋅±∆,则间接测量量y的最佳估计值为()12,,my f x x x=⋅⋅⋅(1-19)由于不确定度都是微小的量,相当于数学中的“增量”,因此间接测量量的不确定度的计算公式与数学中的全微分公式基本相同。
不同之处是:①要用不确定度ix∆等替代微分d x i等;②要考虑到不确定度合成的统计性质。
具体做法如下。
首先对函数式(1-18)求全微分:1212d d d d m mf f f y x x x x x x ∂∂∂=++⋅⋅⋅+∂∂∂(1-20)然后用不确定度1212,,,d d d d m m y x x x y x x x ∆∆∆⋅⋅⋅∆⋅⋅⋅替代,,,,并将等式右端进行方和根合成,得到间接测量量的不确定度方和根合成公式:y ∆=(1-21)对于积商形式的函数,为计算方便,可先对函数式(1-18)取对数,得()12m ln ln ,,y f x x x =⋅⋅⋅(1-22)再对上式求全微分:1212d d d d mm x x x y f f f y x f x f x f∂∂∂=+⋅⋅⋅+∂∂∂ (1-23)用不确定度1212,,,d d d d m m y x x x y x x x ∆∆∆⋅⋅⋅∆⋅⋅⋅替代,,,,后,再进行方和根合成,得到的是间接测量量的相对不确定度的方和根合成公式:yy ∆(1-24)注意:用式(1-21)~式(1-24)估算间接测量量的不确定度时,应使式中各直接测量量的不确定度具有相同的置信概率。
作粗略的不确定度估算时,也可采用间接测量量的不确定度算术合成公式: 1212m mf f f y x x x x x x ∂∂∂∆=∆+∆+⋅⋅⋅+∆∂∂∂ (1-25)1212m m x x x y f f f y x f x f x f∆∆∆∆∂∂∂=+⋅⋅⋅+∂∂∂ (1-26)用算术合成公式估算出的间接测量量的不确定度偏大。
【例1-3】 求函数式(1)N A B C =+-和(2)ABN C=的不确定度传递公式,式中A 、B 、C 为变量。
解: (1)对函数式N A B C =+-求全微分得 d d d d N A B C =+-用不确定度代替微分,再方和根合成便得到不确定度传递公式:N ∆(2)因为函数式ABN C=是积商的形式,所以先对其取对数,可得ln ln ln ln N A B C =+-再求全微分:d d d d N A B CN A B C=+-用不确定度代替微分,再方和根合成便得到相对不确定度传递公式:N N ∆= 2.间接测量的数据处理步骤① 按照直接测量量的数据处理程序求出各直接测量量的结果:121122,,m m m x x x x x x x x x =±∆=±∆⋅⋅⋅=±∆② 将各直接测量量的最佳估计值代人函数关系式中,求得间接测量量的最佳估计值:()12,,m y f x x x =⋅⋅⋅ ③ 求出间接测量不确定度的方和根合成公式:y ∆=m yf y x ⎛∆∆∂++ ∂⎝ ④ 求出间接测量值的不确定度∆⑤ 表示出最后测量结果100%r yy y y U y∆=±∆=⨯, 【例1-4】 已测得金属环的外径1 2.8800.004cm D =±,内径2 3.6000.004cmD =±,高度2.5750.004cm h =±,求体积的测量结果。
