1、第一章 行列式(简化版)
第一章 行列式

第一章行列式行列式是一个重要的数学工具.它广泛应用于理、工、农、医、经济等很多领域。
在线性代数中,行列式更是一种不可或缺的重要工具.本章主要介绍行列式的定义、性质、计算及其在求解线性方程组中的应用——Cramer(克莱姆)法则.§1.1 行列式定义一、数域定义1.1 设P是含有0和1的一个数集,若P中任意两个数的和、差、积、商(除数不为0)仍在P中,则称P为一个数域.如果数集P中任意两个数作某一运算后的结果任在P中,则称P对这个运算封闭。
因此数域的定义也可简单叙述为:含有0和1且对加法、减法、乘法、除法(除数不为0)封闭的数集称为数域. 全体有理数组成的集合、全体实数组成的集合、全体复数组成的集合都是数域,分别称为有理数域、实数域、复数域依次用Q、R、C来记。
全体整数组成的集合不是数域,因为任意两个整数的商不一定是整数.要指出的是所有的数域都包含有理数域。
这是因为如果P是一个数域,则1在P中且由于P对加法封闭,所以1+1=2,2+1=3, ,n+1全在P中,即P包含全体自然数;又因0在P中且P对减法封闭,于是 0 - n = - n在P中,所以P包含全体整数;因为任意一个有理数都可表为两个整数的商,再由P对除法的封闭性知P包含全体有理数。
即任何一个数域都包含有理数域.今后本教材中所论及的数都是指某一固定数域中的数,文中一般不再特别加以说明.二、排列为了给出n阶行列式的定义,先介绍n级排列的概念.定义1.2 由自然数1 ,2 ,…,n组成的全排列称为n级排列.记作i1 i2…i nn级排列共有n!个.n级排列中任意两个数,如果大数排在小数之前,则称这两个数构成一个逆序,否则称为顺序.一个n级排列i1 i2…i n的逆序总数称为此排列的逆序数,记作 (i1i2…i n).逆序数为奇数的排列称为奇排列;逆序数为偶数的排列称为偶排列.因 τ(1 2 … n )= 0,所以排列1 2 … n 是偶排列。
线性代数课件第一章 行列式

an1 an2
ann
0
0
(1) a a ( j1 j2 jn ) 1 j1 2 j2
j1 j2 jn
ann
(1) (1 j2
a a jn ) 11 2 j2
1 j2 jn
(1) (123 n) a11a22 ann
a11a22 ann
anjn anjn
a11 0
0
计算主对角线行列式 0 a22
a13 a23 a33
a11a22a33 a12a23a31 a13a21a32 a13a22a31 a11a23a32 a12a21a33
说明 (1)三阶行列式共有 6 项,即 3! 项.
(2)每项都是位于不同行不同列的三个元素的 乘积.
23
(3)每项的正负号都取决于位于不同行不同列 的三个元素的下标排列.
= 1 + 4 + 0 + 0 + 1+ 0 = 6 14
τ(314625)=5,314625是奇排列。 τ(314652)=6,314652是偶排列。
逆序数的性质
(12n) 0,
(n(n 1)321) n(n 1)
2
0 (i1i2
in )
n(n 1) 2
15
定义2.3 把一个排列中两个数i , j的位置互换而保持 其余数字的位置不动,则称对这个排列施 行了一个对换,记作(i , j). 两个相邻位置 数字的对换称为相邻对换,否则称为一般 对换。
数的排列称为奇排列。逆序数为偶数的排列称为偶排列。
如:314652中, 31是逆序,65是逆序,32是逆序,42是逆序 62是逆序,52是逆序数。逆序数τ(314652)=6
记τk = 排列j1j2…jn中数字k前面比k大的数的个数。则 τ(314652)= τ1 + τ2 + τ3 + τ4 + τ5 + τ6
线性代数课件第1章行列式

解 120 1 120 1 120 1
r2r1 0 1 5 1 r4r1 0 1 5 1 r3r2 0 1 5 1
D
015 6 015 6 000 7
.
123 4 003 3 003 3
120 1
r3 r4 0 1 5 1
21
003 3
课件
27
000 7
例2 计算 a b b b
式的值不变.即第 i 行乘 k 加到第 j 行上,有
a11
a12
a1n
a11 a12
a1n
ai1
ai2
ain
ai1 ai2
ain
aj1 kai1 aj2 .kai2
ajn kain aj1 aj2
ajn
an1
an2
ann
an1 an2
ann
课件
25
为叙述方便,引进以下记号:
(1)交换行列式的 i , j 两行(列),记
为行列式 d e t ( a ij ) 的元素.
定理2 n 阶行列式也可定义为
a11 a12 Da21 a22
a1n
a2n (1)ta a p11 p22
apnn
an1 an2
ann
其中 t 为行标排列 p1p2 pn 的逆序数.
课件
17
定义4 对角线以下(上)的元素均为零的行 列式称为上(下)三角行列式.
列组成的记号
a11 a12
a1n
D a21 a22
a2n
an1
a. n2
ann
为 n 阶行列式,简记为 D det(aij ) .
课件
16
n 阶行列式可表示为
第一章行列式简版2010.7
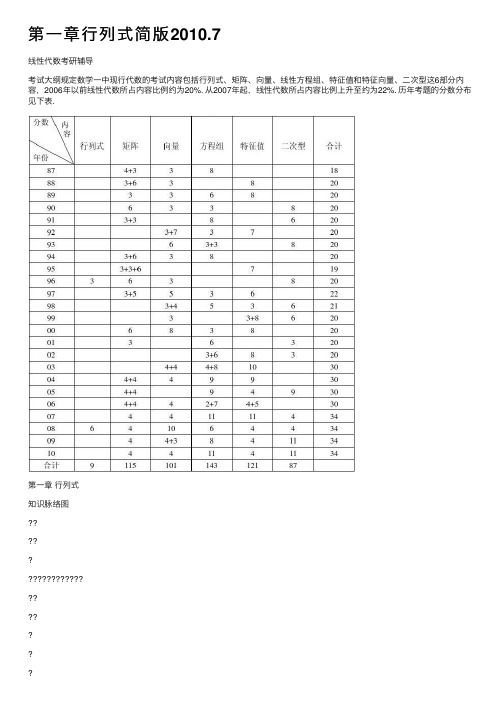
第⼀章⾏列式简版2010.7线性代数考研辅导考试⼤纲规定数学⼀中现⾏代数的考试内容包括⾏列式、矩阵、向量、线性⽅程组、特征值和特征向量、⼆次型这6部分内容,2006年以前线性代数所占内容⽐例约为20%. 从2007年起,线性代数所占内容⽐例上升⾄约为22%. 历年考题的分数分布见下表.第⼀章⾏列式知识脉络图≠==-=≠=?=???-==∑∑∑=+=数)⽅程的根⾏列式表⽰的函数(代⼏何应⽤克莱姆法则及应⽤应⽤)利⽤范德蒙⾏列式()归纳()递推()加边()拆项()消零展开()三⾓化法(⽅法展开元素的规律性,性质,计算,代数余⼦式余⼦式展开式变倍加到另⼀⾏,其值不某⾏两⾏互换,⾏列式变号(数乘)提出公因⼦拆项(加法)⼀⾏为零或两⾏成⽐例性质逆序的定义归纳定义定义⾏列式7654321 ,0 ,)1()6()5()0()4()3(0A )2()1()1(A 1,21)(111212121n j kj ij ijj i ij ij T j j j nj j j j j j ni i i k i ki A A a M A M k k k A A a a a A A a n nn τ第⼀章⾏列式考试⼤纲(⾏列式部分)考试内容⾏列式的概念和基本性质⾏列式按⾏(列)展开定理考试要求1.了解⾏列式的概念,掌握⾏列式的性质。
2.会应⽤⾏列式的性质和⾏列式按⾏(列)展开定理计算⾏列式。
基本内容⼀、⾏列式定义 1.定义111212122212n n n n nna a a a a a a a an n nj j j j j j a a a 221211)()1(τ∑-=其中逆序数()121n j j j j τ= 后⾯的1j ⼩的数的个数 2j +后⾯⽐2j ⼩的数的个数+ 1n j -+后⾯⽐1n j -⼩的数的个数.2.三⾓形⾏列式11121222000n n nn a a a a a a11212212000n n nna aa a a a =1122nn a a a =1211000n n n nn nn a a a a a - 111212122100n n a a a aa a =()()12112111n n n n n a a a τ--=-()()1212111n n n n n a a a --=-⼆、⾏列式性质和展开定理1.会熟练运⽤⾏列式性质,进⾏⾏列式计算.2.展开定理1122i k i k in kn ik a A a A a A A δ+++= A A a A a A a jk nk nj k j k j δ=+++2211三、重要公式设A 是n 阶⽅阵,则1.TA A =2.11AA --=3.1*n A A-=4.nkA k A =5.AB A B =,其中B 也是n 阶⽅阵 6.设B 为m 阶⽅阵,则0A C A A B B C B == ()010mnA CA AB BC B==- 7.范德蒙⾏列式()1222212111112111n ijn j i nn n n nx x x x x x x x x x x ≤<≤---=-∏四.有关结论 1.对于,n n n n A B ?? (1)00A A ?==?(2) A B A B ?==?2. A 为n 阶可逆矩阵()0A r A n A ≠?=?可逆A E A E→?→⾏变列变(A 与E 等价) 0AX ?=只有惟⼀零解AX b ?=有惟⼀解(克莱姆法则) A ?的⾏(列)向量组线性⽆关 A ?的n 个特征值0,1,2,,i i n λ≠= A 可写成若⼲个初等矩阵的乘积 ?)()(B r AB r = ?A A T 是正定矩阵A 是n R 中某两组基之间的过渡矩阵3. A 为n 阶不可逆矩阵0=A0AX ?=有⾮零解n A r <)(0是A 的特征值A A -=4.若A 为n 阶矩阵,)2,1(n i i =λ为A 的n 个特征值,则∏==ni i A 1λ5.若B A ~,则B A =⾏列式的基本计算⽅法:1. 应⽤⾏列式的性质化简⾏列式(例如化为三⾓形⾏列式就是⼀个常⽤⽅法)。
线性代数第一章行列式课件

a11
a12
a1n
a11 a12
a1n a11 a12
a1n
ai1 bi1 ai2 bi2
ain bin ai1 ai2
ain bi1 bi2
bin
an1
an2
ann
an1 an2
ann an1 an2
ann
性质5 将行列式的某一行(列)的所有元素同乘以 一个数 k 加到另外一行(列)上,行列式不变,即
a1,n1 a2,n1
a1n a2n
a11 a21
a12 a22
a1,n1 a2,n1
an1,1 0
an1,2 0
an1,n1 0
an1,n 1
a a n1,1
n1,2
an1,n1
其中等号左端的行列式是一个 n 阶行列式;等号右端
的行列式是左端 n 阶行列式的前 n-1 行前 n-1 列的元
素所组成的 n-1 阶行列式,即左端行列式第 n 行第 n
j 1, 2, , n
ann
a1n
(1)i j aij
ai 1,1 ai1,1
ai1, j1 ai1, j1
ai1, j1 ai1, j1
ai1,n ai1,n
an1
an, j1
an, j1
ann
定理4 设
a11 a12
a1n
D a21 a22
a2n
an1 an2
ann
是一个 n 阶行列式, Aij 为 D 的第 i 行第 j 列元素 aij 的代数余子式,则有
1
2
n ( n 1)
(1) 2 12 n
n
二、行列式的基本性质
定义6 设
1、第一章 行列式(简化版)

,
ri ↔ rj ( ci ↔ c j )
则有: D ================== − D1 .
( 换法变换 )
符号说明: 换法变换——交换行列式中某两行(列)的元素. 记为: (列) 和第 j 行 (列) ri ↔ rj , ci ↔ c j 或 ri , rj , ci , c j 或 r ( i, j ) , c ( i, j ) ——交换行列式中第 i 行 的元素.
(一)二阶和三阶行列式 1.二阶行列式的概念 定义:由四个元素 a11 , a12 , a21 , a22 排成两行两列的一个算式,称为二阶行列式. 记为:
a11 a21
a12 a22
,并规定其值等于 a11a22 − a12 a21 ,即:
a11 a21
a12 = a11a22 − a12 a21 . a22
( i 1, = = 2; j 1, 2 )的第一个下标 i 称为行下标,表明该元素所在的行数; 其中元素 aij 第二个下标 j 称为列下标,表明该元素所在的列数.
注:①行列式中的元素可以是实数、复数、字母、函数等等. ②行列式通常用大写的英文字母 D 表示. ③行列式的符号可以简记为: aij . ④二阶行列式的运算法则称为对角线法则,即:
T T
符号说明: 在线性代数中,对行元素所做的变换用小写的英文字母“ r ”表示,而对列元素所做的变换用小写的
英文字母“ c ”表示.
Ⅰ.行列式与它的转置行列式的值相等.
a11
即:设 D =
a21 an1
a12 a1n a22 a2 n an 2 ann
ri ↔ ci ( i = 1, 2, , n ) T ,则有: D ==================== D .
线性代数第一章行列式

04
式可以表示为三个向量的向量积的 二倍,即 |a b c| = 2abc。
向量积的符号由行列式的值决定,当行列式 值为正时,向量积为正;当行列式值为负时, 向量积为负。
行列式可以用来判断平行四边形的 形状,当行列式值为正时,平行四 边形为锐角;当行列式值为负时, 平行四边形为钝角。
行列式与平行四边形面积的关系
行列式可以表示平行四边形的面积,即 |a b| = ab/2。
当行列式值为正时,平行四边形的面积为正; 当行列式值为负时,平行四边形的面积为负。
行列式可以用来判断平行四边形的方向,当行 列式值为正时,平行四边形为顺时针方向;当 行列式值为负时,平行四边形为逆时针方向。
行列式与空间向量的关系
01
02
03
行列式可以表示空间向量的模长,即 |a b c| = abc。
当行列式值为正时,空间向量的模长 为正;当行列式值为负时,空间向量 的模长为负。
行列式可以用来判断空间向量的方向 ,当行列式值为正时,空间向量为右 手系;当行列式值为负时,空间向量 为左手系。
05
行列式的应用实例
在线性方程组中的应用
定义
代数余子式是去掉一个元素所在的行和列后,剩 下的元素构成的二阶行列式。
性质
代数余子式与去掉的元素所在的行和列的符号有 关。
计算方法
可以通过二阶行列式的计算法则来计算代数余子 式。
行列式的展开定理
01
定理内容
一个n阶行列式等于它的任一行 (或列)的所有元素与其对应的 代数余子式的乘积之和。
02
03
定性。
求解线性方程组
03
在求解线性方程组时,可以利用展开定理计算系数矩阵的行列
式值,从而判断方程组是否有解。
第一章 行列式讲义.

1. 每项都是处于不同行不同列的n个元素的乘积。 2. n 阶行列式是 n!项的代数和。 3. 每项的符号都是由该项元素下标排列的奇偶性 所确定。
11 2019/1/1
定义1: n! 项 ( 1) t a1 p
1
a2 p2 anpn 的和
称为 n 阶行列式 (n≥1),记作
a11 a 21 a n1
8
2019/1/1
例. 求排列 32514 的逆序数。
逆序数为奇数的排列称为奇排列。 逆序数为偶数的排列称为偶排列。 例如,123为偶排列, 321为奇排列,312为偶排列。
9 2019/1/1
二、 对换
在排列中,将任意两个元素对调,其余的元 素不动,这种作出新排列的手续叫做对换。 将相邻两个元素对换,叫做相邻对换。 定理1 一个排列中任意两个元素对换,排列将 改变奇偶性。 (证明略) 推论 奇排列对换成标准排列的对换次数为奇次, 偶排列兑换成标准排列的对换次数为偶数。
a12 at 2 as 2 an 2 a1n atn . a sn
23
2019/1/1
ann
例
1 2 0 1
3 1
1 0 1
r1 r3
0 1 1 2
1 3
1 0 1
24 2019/1/1
推论:若行列式有两行(列)相同, 则行列式为 0 。
a11 a j1 a j1
则 bij a ji ( i , j 1,2,, n) 由行列式定义
D T ( 1) t b1 j1 b2 j2 bnj n
( 1) t a j1 1a j2 2 a jn n D
22 2019/1/1
性质2:互换行列式的两行 ( 列 ),行列式变号。
第一章 行列式

第一章 行列式本章主要内容是行列式的定义、性质及其计算方法.此外还介绍了用行列式解线性方程组的克莱姆法则.§1. 全排列的逆序数本节考虑由1,2,3,…, n 这n 个数排成的不重复数字的全排列,不同的全排列共有n !个.以后对这种全排列简称排列.例如,由1,2,3这三个数有以下3!=6个排列:123, 132, 213, 231, 312, 321定义 设1p 2p …n p 是1,2,…, n 的一个排列,考察其中任意两个数,如果大的数排在小的数之前,就说有一个逆序.所有逆序的总数称为排列1p 2p …n p 的逆序数,记作τ(1p 2p …n p ).逆序数为奇数的排列称为奇排列,逆序数为偶数的排列称为偶排列. 例1. 计算由1,2,3排成的六个排列的逆序数 [解] 排列123没有逆序,逆序数τ(123)=0. 排列132中,仅有3在2之前一个逆序,τ(132)=1. 排列213中,仅有2在1之前一个逆序,τ(213)=1. 排列231中,2在1之前,3在1前,τ(231)=1+1=2. 排列312中,3在1,2之前,τ(312)=2.排列321中,3在2,1之前,又2在1前,τ(321)=2+1=3. 其中132,213,321为奇排列,123,231,312为偶排列. 例2. 求τ(42315)及τ(54321).[解] τ(42315)=3+1+1=5,τ(54321)=4+3+2+1=10. 性质1. 交换排列中的两个数,排列的奇偶性改变. [证] 先讨论交换相邻两数的情形.设排列为 1p ……S p a b 1+S p …m p (1)交换a 与b ,得排列1p ……S p b a 1+S p …m p(2) 任意一个i p 与a 或b 的大小关系在(1)与(2)两个排列中是一样的.所以当a >b 时,排列(2)的逆序数比排列(1)的逆序数减少1,当a <b 时,排列(2)的逆序数比排列(1)的逆序数增加1.因此,当(1)为奇排列时,(2)为偶排列;当(1)为偶排列时,(2)为奇排列.即排列(1)与(2)有不同的奇偶性.再讨论交换不相邻两个数的情形.设排列为1p ……S p a 1c …k c b 1+S p …m p (3)交换a 与b ,得排列1p ……S p b 1c …k c a 1+S p …m p (4)我们也可以对排列(3)中的a 依次与1c ,…,k c 进行k 次相邻的交换,得到排列 1p ……S p 1c …k c a b 1+S p …m p再对这个排列中的b 依次与a ,k c ,…,1c 进行k +1次相邻的交换,就得到排列(4).因此,经过2k +1(奇数)次相邻的交换可以由(3)得到(4).由前面已证明的结论可知,进行奇数次相邻的交换,排列的奇偶性要改变,所以排列(3)与排列(4)有不同的奇偶性. (证毕)性质2 由1,2,…,n (n >1)所作的n !个排列中,奇排列与偶排列各占一半. [证] 设奇排列有s 个,偶排列有t 个.对每一个奇排列都交换1与2,就得到s 个不同的偶排列.因此,s ≤t .同理可证t ≤s ,故s =t .(证毕)§2. 行列式的定义将2n 个数ij a (i ,j =1,2,…,n )排成n 个横行及n 个竖列的方形表格,两边再用竖线围起, 就得到n 阶行列式的记号:nnn n nn a a a a a a a a a ............ (21)2222111211其中每个数ij a 称为行列式的元素,它有两个下标,第一个下标表示该元素所在的行数,第二个下标表示所在的列数,ij a 就是i 行j 列的元素.行列式的行数是从上到下依次为第一行,第二行,…,第n 行.列数是从左到右依次为第一列,第二列,…,第n 列.行列式有两条对角线,由左上到右下那条对角钱称为主对角线,在主对角线上的元素为11a ,22a ,…,nn a .由右上到左下的对角线有时称为副对角线.n 阶行列式是由代数和组成的一个数,其定义如下.定义n 阶行列式为nnn n nna a a a a a a a a ............ (21)2222111211=21212121)1(p p P P P )P P (P a a nn ∑⋯⋯-τ…n np a其中τ(21p p …n p )是列标排列21p p …n p 的逆序数,∑nP P P 21表示对所有n !个排列求和.上述定义说明n 阶行列式是含有n !项的代数和,其中每一项是不同行不同列的n 个元素的乘积,当把这n 个元素按行标从小到大的顺序排列时,其列标排列21p p …n p 的逆序数τ(21p p …n p )若为偶数,这项冠以“+”号,若为奇数,这项冠以“-”号.根据行列式的定义,一二三阶行列式可以计算如下: 一阶行列式:11a =110)1(a -=11a 二阶行列式:22211211a a a a =22110)1(a a -+21121)1(a a -=2211a a -2112a a三阶行列式:333231232221131211a a a a a a a a a =3322110)1(a a a -+3123122)1(a a a -+3221132)1(a a a -+3122133)1(a a a -=332211a a a +312312a a a +322113a a a -312213a a a -332112a a a -322311a a a 如果在三阶行列式中,将冠以“+”号的项的三个数用实线加以连接,将冠以“-”号的项的三个数用虚线加以连接,就可以得到如下图形:利用这个图形,很容易写出三阶行列式的六项代数和.例1. 计算以下两个行列式:(1)1D =4321 (2)2D =432501123--[解] (1)1D =3241⨯-⨯=64-=2-(2)2D =)3(1)1(252403-⨯⨯-+⨯⨯+⨯⨯412)3(5320)1(⨯⨯--⨯⨯-⨯⨯--=84503200-+-++=60四阶行列式有4!=24项,要写出并计算这24个乘积的代数和是很麻烦的.对于三阶以上的高阶行列式,一般要利用下节要介绍的行列式的性质进行计算.不过,像下面例2的几个特殊的高阶行列式,却可以用定义直接得到它的值.+3321121)1(a a a -+3223111)1(a a a -例2. 利用行列式的定义计算下列的行列式1D =nn n n a a a a a a21222111000 2D =nn nn a a a a a a 000222112113D =nna a a000002211 4D =nnnn n n n n a a a a a a 112121000--[解] 行列式1D 在主对角线之上的元素全为0,这种行列式称为下三角行列式.根据定义,行列式是由不同行不同列元素的乘积的代数和,因为含0元素的项必为0,只要考察不含0元素的项.设这种项为:n n np p p )P P (P a a a 212121)1(τ-因为1D 的第一行除了11a 之外为0,所以必有11p a =11a ,1D 的第二行除了21a ,22a 之外都为0,但21a 与11a 位于同一列,与11a 不同列的只有22a ,所以22p a =22a ,依次类推,可知1D 中不含0元素的项只有如下一项:nn n )a a a 221112()1(⋅⋅⋅-τ=nn a a a 2211因此,1D =nn a a a 22112D 的主对角线之下的元素都是0,这种行列式称为上三角行列式.依次讨论第n 行,第1-n 行,…,第1行,可知2D 中不含0元素的项与1D 相同,所以2D =nn a a a 2211上三角与下三角行列式统称为三角行列式.行列式3D 中除对角线上的元素之外,其它元素都是0,这种行列式称为对角行列式,它是三角行列式的特例,因此3D =nn a a a 2211以上说明三角行列式及对角行列式的值都等于主对角线上元素的乘积.4D 在副对角线上方的元素为0,它不是三角行列式.类似于前面的讨论可知4D 中不含0元素的项只有121121121()1(n n n n )n n a a a a ---- τ,因为)121( -n n τ=12)1(+++- n =)1(21-n n ,所以 4D =1211212)1()1(n n n n n n a a a a ----即4D 等于副对角线上元素的乘积再乘以2)1()1(--n n .例3. 设)(x f =)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n n n n ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯,其中各元素)(x a ij 都是可导函数.试证)(x f '=)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n n n n ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯'''+)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n n n n ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯'''+…+)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n nn n '''⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(即对行列式求导,等于对各行求一次导的n 个行列式的和) [证] 根据行列式定义,有)(x f '='⎥⎦⎤⎢⎣⎡-∑⋯n n n P P nP P P P P P x a x a x a 12121)()()()1(21)( τ=[]∑⋯'-nn n P P nP P P P P x a x a x a1211)()()()1(21)( τ=∑⋯'-nn n P P nP P P P P x a x a x a 1211)()()()1(21)( τ+ +'-∑⋯nn n P P nP P P P P x a x a x a 1211)()()()1(21)(τ +∑⋯'-nn n P P nPP P P P x a x a x a 1211)()()()1(21)( τ=)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n n n n ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯'''+)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n n n n ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯'''+…+)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n nn n '''⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (证毕)下面的定理是对行列式定义的另一种说法. 定理. 对于上述行列式定义中的任意一项n n nP P P )P P P a a a 212121()1(τ-若对乘积21P a 22P a …n nP a 的因子顺序进行若干次交换,变为乘积11j i a 22j i a …n n j i a ,则有n n nP P P )P P P a a a 212121()1(τ-=n n n n j i j i j i j j j )i i i a a a 22112121)(()1(ττ+-换句话说,如果行列式各项的乘积21P a 22P a …n nP a 的因子不是按行标从小到大的自然顺序排列,而是任意排列成11j i a 22j i a …n n j i a ,则这项应冠以符号)((2121)1(n n j j j )i i i ⋯+⋯-ττ[证] 因为21P a 22P a …n nP a =11j i a 22j i a …n n j i a ,所以只要证明)P P P n 21()1(τ-= )((2121)1(n n j j j )i i i ττ+⋯-设21P a 22P a …n nP a 的因子经过k 次交换,成为11j i a 22j i a …n n j i a ,则行标排列1 2…n 经过k 次交换,成为排列n i i i 21.列标排列n p p p 21经过k 次交换,成为排列n j j j ⋯21,根据§1性质1,若k 为奇数,则行标排列与列标排列都同时改变奇偶性,因而)12()1(n τ-=)()(2121)1()1(n n P P P i i i , ττ---=)(21)1(n j j j τ--若k 为偶数,则行标排列与列标排列的奇偶性都不变,因而有)12()1(n τ-=)()(2121)1()1(n n P P P i i i , ττ--=)(21)1(n j j j τ-不论k 是哪一种情况,都有)()12(21)1(n p p p n ττ+-=)()(2121)1(n n j j j i i i ττ+-因为0)12(=n τ,所以要证的等式成立.(证毕)§3. 行列式的性质设n 阶行列式D =nn n n nn a a a a a a a a a ............ (212222111211)将行列式D 的第一行,第二行,…,第n 行,依次改写成第一列,第二列,…,第n 列,得到行列式 TD =nnn nn n a a a a a a a a a ............ (212)221212111T D 称为D 的转置行列式.D 中i 行j 列的元素ij a ,在T D 中位于j 行i 列的位置上.性质1. 行列式与其转置行列式相等. [证] D 中任意一项为n n nP P P )P P P a a a 212121()1(⋯-τ其中21P a 22P a …n nP a 也是T D 中不同行不同列元素的乘积,但在TD 中,其行标排列为n p p p ⋯21,列标排列则为12…n ,根据上节定理,在T D 中,这个乘积应冠以符号)()12((2121)1()1(n n P P P n )P P P τττ-=-⋯+这就证明了D 中每一项也是TD 中的一项,D 中不同的项在TD 中也是不同的,并且D 与TD 的项数一样,都是n !,因此有D=TD .(证毕)由性质1可知,行列式中的行与列具有同等地位,行列式的性质凡是对行成立的,对列也必定成立,反之也一样.因此,以下的行列式性质,我们只对行的情形加以证明,将行列式转置就可得到列的相应性质,以后不再说明.性质2. 交换行列式的两行(列),行列式变号. [证] 设D =⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯jn j j in i i a a a a a a 2121行第行第j i ←← 交换第i 行与第j 行,得1D =⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯in i i jn j j a a a a a a 2121行第行第j i ←← 其中D 与D 1中未写出的行的元素都对应相同. 根据行列式定义,D 中任一项为n j i n j i nP jP iP P P P P P a a a a 111)()1(τ-其中n j i nP jP iP P a a a a 11也是D 1中不同行不同列元素的乘积,其列标排列没有变化,但行标排列为n i j 1它是由自然顺序n j i 1交换i ,j 得到的,由§1性质1,有)1()1(n i j τ-= )1()1(n j i τ--=0)1(--=1-.根据上节定理,乘积n j i nP jP iP P a a a a 11在D 1中应冠以符号)()1(1)1(n j i P P P P n i j ττ+-=)(1)1(n j i P P P P τ--与在D 中的符号相反,这说明将D 中每一项变号,就得到D 1的所有项,故有D=-D 1.(证毕)推论 若行列式有两行(列)相同,则此行列式等于零.[证] 将这两行交换,行列式未改变,由性质2得到D=-D ,所以D=0.性质3. 行列式某一行(列)中所有元素都乘以同一个数k ,等于用数k 乘此行列式,即有 ⋯⋯⋯⋯⋯⋯⋯⋯in i i ka ka ka 21=k ⋯⋯⋯⋯⋯⋯⋯⋯in i i a a a 21 两个行列式中除第i 行之外,未写出的元素都对应相同.(这性质也可以叙述成行列式某行(列)的公因子可以提到行列式外面相乘)[证] 根据行列式定义,有 等式左边=npn ip P P P P P P a ka a i n i n)()1(1111)(τ∑⋯-=npn ip P P P P P P a a a ki n i n1111)()1(τ∑-=等式右边. (证毕)性质4. 行列式中如有两行(列)成比例,则此行列式等于零.即D =⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯jn j j in i i a a a ka ka ka 2121=0[证] 根据性质3,将D 的第i 行提出公因子k 以后,行列式的第i 行与第j 行相等,由性质2的推论得D=0. (证毕)性质5. 若行列式的某行(列)的元素都是两数之和,例如第i 行的元素都是两数之和:D =nn n n in in i i i i na a ab a b a b a a a a21221111211)()()(⋯⋯⋯⋯+++⋯⋯⋯⋯则D 等于下列两个行列式之和:D =nn n n in i i na a a a a a a a a 212111211⋯⋯⋯⋯⋯⋯⋯⋯+nnn n in i i n a a a b b b a a a 212111211⋯⋯⋯⋯⋯⋯⋯⋯ [证] 记等式右边两个行列式为D 1,D 2,则根据行列式的定义,有D=n i i n nnp ip ip P P P P P a b a a )()1(1111)(+-⋯∑τ=n i n nnp ip P P P P P a a a 1111)()1(τ∑⋯-+n i n nnp ip P P P P P a b a 1111)()1(τ∑-=D 1+D 2 (证毕)性质6. 将行列式的某行(列)乘以数k ,再加到另一行(列)上,行列式的值不变,即D =⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯jn j j in i i a a a a a a 2121=⋯⋯⋯⋯⋯⋯⋯⋯+++⋯⋯⋯⋯jn j j jnin j i j i a a a ka a ka a ka a 212211=1D D 与D 1中未写出的元素对应相同.[证] 由性质5及性质4,有1D =⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯jn j j in i i a a a a a a 2121+⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯jn j j jnj i a a a ka ka ka 2121=D+0=D 在举例之前,先引进行列式运算的几个记号: (1)“交换i ,j 两行(列)”记作j i r r ↔)(j i c c ↔. (2)“0≠k 乘i 行(列)”记作i kr )(i kc(3)“k 乘j 行(列)加到i 行(列)上”记作j i kr r +)(j i kc c +要注意:行列式经运算j i kr r +后,第i 行改变,但第j 行不变.同样,运算j i kc c +使行列式的第i 列改变,但第j 列不变.例1. 计算四阶行列式 D=123412121124021231-----[解] 计算数字的高阶行列式,有一种方法是利用行列式性质,尤其是用行列式的性质6,将行列式化为上三角行列式,于是上三角行列式主对角线上元素的乘积就是行列式的值.本题先以2乘第1行,再以2除行列式,使行列式的元素都为整数,方便计算.再用行列式性质(主要是性质6),将其化为上三角行列式.整个计算过程如下:1490134013800132211234121211240132212141312221--------++-r r r r rr r D15001100011001322194149013400110013221242342----+r r r r r r 400110011013--=)4()1(1221-⨯-⨯⨯⨯=4例2.计算行列式D =2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a[解] 这是文字元素的行列式,计算这种行列式,要先分析行列式的特点,采用适当的行列式性质进行化简计算.本行列式的特点是各行的构造相类似,对列作变换可达到化简的目的.具体运算如下.341223c c c c c c D ---2212221222122212523212523212523212523212222223342222++++-++++++++++++d d c c b b a a c c d d d d c c c c b b b b a a a a =0注意:在对行列式连续做两次以上的运算时,第一次运算以后,行列式已变化,第二次再作运算时,是对变化后的行列式作运算,而不是对原来行列式作运算.例如连续作两次运算12c c -,23c c -,当作了运算12c c -后,行列式的第2列已变化,再作23c c -时,应是第三列减去变化后的行列式的第二列,如果还是减去原行列式的第二列,就会产生错误.避免错误的方法之一,就是做了一次运算就将行列式写出来,再做第二次运算.但这样做又太麻烦了.要不麻烦,就像我们在本题中所做的那样,连续对行列式作运算34c c -,23c c -,在作运算34c c -时,第二三列并未改变,因此再做23c c -的运算时,对原行列式作23c c -,与对变化后的行列式作23c c -是一样的结果.例3. 计算n 阶行列式D =ab b b a b b b a ⋯⋯⋯⋯ (主对角线元素都为a ,其它元素都为b ).[解] 本行列式的特点是各行元素之和相等,若将第2列之后各列都加到第1列,将公因子提出,再对行作运算,就可化为上三角行列式了.具体运算过程如下.D a b b n a b a b n a b b b n a cc c n )1()1()1(21-+⋯⋯⋯⋯-+-++++=])1([b n a -+ab b a b b 111⋯⋯⋯⋯ 11213r r r r r r n --- ])1([b n a -+ba b a b a b b b -⋯⋯⋯⋯⋯-- 0000001=1)]()1([---+n b a b n a例4. 计算行列式D =111222+++z yzxzyz y xyxz xy x [解] 第一二三行依次提公因子x ,y ,z ,得D =zz y xz yy x z y xx xyz111+++再对第一二三列依次乘x ,y ,z ,得D =111222222222+++z y x z y x z y x行列式各行之和相等,可按例3的方法计算,得D11111222222222222222+++++++++++z y z y z y z y z y z y =)1(222+++z y x 11111222222++z y z y z y10101)1(222221312z y z y x r r r r +++--=1222+++z y x§4. 行列式按行(列)展开定义. 在n 阶行列式中,划去元素ij a 所在的第i 行和第j 列剩下的1-n 阶行列式记作ij M ,称为元素ij a 的余子式,而ij A =ij j i M +-)1(称为元素ij a 的代数余子式.例如三阶行列式D =321321321c c c b b b a a a则1行1列元素1a 的余子式11M 及代数余子式11A 为11M =3232c c b b ,11A =1111)1(M +-=11M =3232c c b b 2行3列元素3b 的余子式23M 及代数余子式23A 为23M =2121c c a a ,23A =2332)1(M +-=23M -=2121c c a a -由定义可知,当元素所在的(行数+列数)为偶数时,代数余子式和余子式相等,为奇数时,代数余子式和余子式相差一个符号.引理. 在n 阶行列式D 的第i 行所有元素中,除元素ij a 外,其余元素都为零,则D=ij a ij A .[证] 先证i =j =1的情形.设D =nnn n na a a a a a a 21222211100⋯⋯⋯⋯根据行列式定义,有 D=n n nnp p P P P P P P P a a a 21212121)()1(τ∑- (11>P 时,11P a =0) =n n nnp p P P P P a a a 222211)1(1)1(τ∑- (1,2≠n ,P P ) =n n nnp P P P P P a a a 2222)(11)1( τ∑-=1111M a =1111A a再证一般情形.设D =nnnj njnj n ij n j j j a a a a a a a a a a a111111111110000+-+-⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯将D 中第i 行依次与第1-i 行,2-i 行,…,1行相交换,再将得到的行列式的第j 列依次与第1-j 列,2-j 列,…,1列相交换,设得到的行列式为D 1.则D 1中1行1列的元素为ij a ,D 1中1行1列元素的余子式11M '=D 中i 行j 列的余子式ij M .由前面证过的结论,有 1D =ij a 11M '=ij a ij M 因为D 1是由D 经过)1()1(-+-j i 次行、列的交换得到的,所以有D =ij ij ij j i ij ij ij j i j i A a M a M a D =-=-=-++-+-)1()1()1(1)1()1(. (证毕)定理. 设n 阶行列式D =nnn n n n a a a a a a a a a 212222111211⋯⋯⋯⋯则有按第 i 行展开式:D =in in i i i i A a A a A a +++ 2211.(i =1,2,…,n ) 按第j 列展开式:D =nj nj j j j j A a A a A a +++ 2211.(j =1,2,…,n ) [证]D =nnn n in i i na a a a a a a a a212111211000000+⋯+++⋯+++⋯++根据§3行列式性质5,D 等于n 个行列式之和,即D =nn n n i n a a a a a a a2111121100+nn n n i n a a a a a a a2121121100+…+nnn n in n a a a a a a a211121100 根据引理,就得到按第i 行的展开式D =in in i i i i A a A a A a +++ 2211按列的展开式同理可证.(证毕)推论 行列式某一行(列)的元素与另一行(列)对应元素的代数余子式乘积之和等于零.即jn in j i j i A a A a A a +++ 2211=0,)(j i ≠,和 nj ni j i j i A a A a A a +++ 2211=0,)(j i ≠[证] 根据定理,将D 按j 行展开,有jn jn j j j j A a A a A a +⋯++2211=nnn jn j in i n a a a a a a a a111111行第行第j i ←← 在等式两边,将1j a ,2j a ,…, jn a 依次换作1i a ,2i a ,…in a ,(jnj j ,A A A ,,21不含第j 行元素)得jn in j i j i A a A a A a +⋯++2211=nnn in i in i n a a a a a a a a111111行第行第j i ←← 右边行列式有两行相同,等于零.故得jn in j i j i A a A a A a +++ 2211=0 (j i ≠)同理可证列的情况. (证毕)利用行列式的展开式,可以将计算n 阶行列式化为计算n -1阶行列式.对于数字元素的行列式,经常将某行(列)的元素除一个元素外都化为零,再按该行(列)展开,达到降阶的目的.例1 计算行列式D=1234121211240132-----[解] 第4列比较简单,并且还有一个0,所以我们对行作运算,使第4列除一个元素外,其余元素都是0,具体计算如下.022121201120132-按第4列展开02211213243)1(1--+-⨯2204013212----r r 按第3列展开224031)1(--+--=)]2)(4(20[---⨯-=8 例2 设D =2235007022220403-- 求(1)D 中第三行各元素的代数余子式之和34333231A A A A +++ (2)D 中第四行各元素余子式之和44434241M M M M +++[解](1)将34333231A A A A +++看作D 中第3行元素改为1,1,1,1后,再按第3行展开的展开式,故有34333231A A A A +++=2235111122220403-=0 (2)44434241M M M M +++=44434241A A A A +-+-=1111007022220403---按第3行展开1112224323)1(7--+-∙- =28)4(7-=-⨯例3 证明n 阶)1(>n 范德蒙(Vandermonde )行列式n V =112112222121111---⋯⋯⋯⋯n nn n n n x x x x x x x x x =∏≥>≥-1)(j i n j i x x=⋅----)())()((1141312x x x x x x x x n )()())((122423-----⋅n n n x x x x x x x x(其中记号∏表示同类因子的连乘积.)[证] 对阶数n 用数学归纳法.2=n 时,有2V =2111x x =12x x -=∏≥>≥-12)(j i jix x ,结论成立.设结论对1-n 阶范德蒙行列式成立,即设223222232232111---⋯⋯⋯⋯n nn n n n x x x x x x x x x =∏≥>≥-2)(j i n j i x x 下面要证明对n 阶范德蒙行列式,结论也成立.对n V ,从第n 行开始,直到第2行,将后行减去前行的1x 倍,即对n V 依次作运算11--n n r x r ,211---n n r x r ,…,112r x r -,得n V =)()()(0)()()(011111213231222113312211312x n x x x x x x x x x x x x x x x x x x x x x x n n n n n n n n ------------按第1列展开后,再提出各列的公因子,就得n V =)())((11312x x x x x x n -⋯--2232232111---⋯⋯⋯⋯n nn n nx x x x x x 右端的行列式是1-n 阶的范德蒙行列式,由上面的归纳假设得n V =)())((11312x x x x x x n --- ∏≥>≥-2)(j i n jix x =∏≥>≥-1)(j i n jix x即结论对n 阶范德蒙行列式也成立.由归纳法,该等式对一切2≥n 的自然数都成立.(证毕)n 阶范德蒙行列式等于2nC =2)1(-n n 个形如j i x x -的因子的乘积,例如4V 是24C =6个形如j i x x -的因子的乘积,即4V =343332312423222143211111x x x x x x x x x x x x =∏≥>≥-24)(j i j i x x =))()()()()((342423141312x x x x x x x x x x x x ------当n x x x ,,21 中有两个数相等时,就有n V =0,只有这n 个数都互不相等时,才有n V ≠0.例4 计算n 阶行列式D=na bbbb b a b bb b a ⋯⋯⋯⋯⋯21,),,2,1,(n i a b i =≠[解] 利用加边法计算.即添加一行一列,将D 表示成n +1阶行列式,再利用行列式性质进行运算得出结果.具体作法如下.将下面右边n +1阶行列式按第1列展开,可知下面的等式成立D=n a bb b b b a b bb b a bb b b00121,(右边为n +1阶)以1-乘第1行加到其它各行,得D=ba b a b a b b bbn --⋯⋯⋯⋯⋯⋯----100010001121因为0≠-b a i ),,2,1(n i ⋯=,依次以b a -11,b a -21,…,ba n -1乘第2,3,…,n +1列再加到第1列,得到D=ba b a b a b b b b b a bn ni i ----+∑= 000000000001211这是上三角行列式,故得D=)())()(1(211b a b a b a ba bn ni i ----+∑=§5. 解线性方程组的克莱姆(Cramer )法则本章最后,介绍用行列式解线方程组的克莱姆法则,即下面的定理. 定理(克莱姆法则)设有n 个方程n 个未知量的线性方程组⎪⎪⎩⎪⎪⎨⎧=+++⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯=+++=+++nn nn n n n n n n b x a x a x a b x a x a x a b x a x a x a 22112222212********* (1) 若系数行列式D=nnn n n n a a a a a a a a a 212222111211⋯⋯⋯⋯≠0则线性方程组(1)有唯一解D D x 11=,D D x 22=,…,DDx n n = 其中),,2,1(n j D j ⋯=是用常数项n b b b ,,,21⋯替换D 中第j 列所得的行列式,即j D =nnj n n j n n nj j n j j a a b a a a a b a a a a b a a .......................................1,1,121,221,22111,111,111+-+-+-[证] 这里只对2=n 的情形证明,一般情况的证明留到第二章给出.设方程组为⎩⎨⎧=+=+22221211212111b x a x a b x a x a 系数行列式D =22211211a a a a =012212211≠-a a a a以22a 乘第1方程,12a 乘第2方程,再相减得121122211)(x a a a a -=122221a b a b -以21a 乘第1方程,11a 乘第2方程,再将第2方程减第1方程得221122211)(x a a a a -=211112a b a b -因11a 0211222≠-a a a ,故得1x =12212211122221a a a a a b a b --=22211211222121a a a a a b a b =DD 1, 2x =12212211211112a a a a a b a b --=22211211221111a a a a b a b a =D D 2. 以上证明了如果方程组有解,则它的解只能是 1x =D D 1,2x =D D2 (*) 其中D=22211211a a a a ,D 1=222121a b a b ,D 2=221111b a b a若将得到的1x ,2x 的表达式(*)代入方程组中,容易验证(*)式确是方程组的解.(证毕)例 解线性方程组 ⎪⎪⎩⎪⎪⎨⎧=+-+-=+-=--=+-+067452296385243214324214321x x x x x x x x x x x x x x[解] 系数行列式为D=674121200311512-----674121201277011970------按1列展开21212771197------21c c +21112701192----21112715110231-----r r 列展开按1127152---=1271511=0271051321571211≠=-=⨯-⨯方程组有唯一解.再计算出1D =816740212560391518=------,2D =1086701215060911582-=-----3D =276041252069311812-=---,4D =270741512090318512=-----根据克莱姆法则得3278111===D D x ,42710822-=-==D D x 1272733-=-==D D x ,1272744===D D x方程组的唯一解为1x =3,2x =-4,3x =-1,4x =1.。
线性代数-行列式(完整版)
思考练习(排列的逆序数详解)
方法1 在排列x1x2…xn中,任取两数xs和xt(s<t), 则它们必在排列x1x2…xn或xnxn-1…x1中构成逆序, 且只能在其中的一个排列中构成逆序.又在排列
x1x2…xn中取两数的方法共有
C 2 n! n(n 1)
n 2!(n 2)!
2
故排列 x1x2…xn 与 xnxn-1…x1 中逆序之和为
(iii)项数为 3!=6
24
“-” 321 213 132 (奇排列)
a11 a12 a13
0
123
2
231
2
312
a21 a22 a 23 a11a22a33 a12a23a31 a13a21a32
a31 a32 a33 a13a22a31 a12a21a33 a11a23a32
n(n 1) 2
依题意,有
此即
22
N (xn xn1
x1)
n(n 1) 2
I.
方法2
n个数中比i大的数有n- i个(i=1,2,…,n),若在排列
x1x2…xn中对i构成的逆序为li个,则在xnxn-1…x1中对i构
成的逆序为(n- i)-li,于是两排列中对i构成的逆序之和
为
li+[(n-i)-li]= n-i (i=1,2,…,n)
a11a22 a12a21
数a(ij i, j 1,2)称为它的元素。
今后对任何行列式,横排称为行,竖 排 称 为 列,
aij中i称 为 行 标, j称 为 列 标, aij 表示第i行第j列元素,
左上角到右下角表示主对角线,
4
右上角到左下角表示次对角线,
第一章(第一节) 行列式

对分子的观察结果与对分母的观察结果一样。 为了更加方便写出三元线性方程组的解,更好 记忆解的解构,就提出了三阶行列式的定义。 三阶行列式的定义 给出32=9个数,排成三行三列的数表
a11 a21 a31
a12 a22 a32
a13 a23 a33
[6]
a11 a12
a13
D a21 a22 a23 a31 a32 a33
(1)每项都是三个元素的乘积,且三个元素来 自不同行、不同列,且每行一个元素,每列也是 一个元素,共3!=6项; (2)6项中三项为正,与主对角线平行的方向 的三个元素的乘积为正,与副对角线平行的方 向的三个元素的乘积为负。
b1 b2 b3
a12 a22 a32
a13 a23 a33
b1a22 a33 a12 a23b3 a13b2a32 a13a22b3 b1a23a32 a12b2a32
D
a11
a12
a21 a22
, D1
b1 b2
a12 a22
, D2
a11
b1
a21 b2
当D≠0时,有
b1 b2 D1 x1 a11 D a21 a12 a11 a22 a21 D2 , x2 a12 a11 D a22 a21 b1 b2 a12 a22
可以看出,求x1的解时,x1所在系数列被右端 常系数列替换,其余不变,求x2时,x2所在系 数列被右端常系数列替换,其余不变。这样更 加方便写出二元线性方程组的解,更好记忆。
首先定义:a11,a22,a33三个元素的连线称为主对 角线,用实线表示,a13,a22,a31三个元素的连线 称为副对角线,用虚线表示。
对分母的观察结果:
第一节行列式

an1 an2 ann
an1 an2 ann
推论 行列式的某一行(列)中所有元素的公因 子可以提到行列式符号的外面.
例如,行列式
21 24
14
D
2 5 8 3 14 2
35
35
这个性质也可以叫做行列式提取公因式性质。
要注意,公因式只能按行(列)分别提取.
性质4 若行列式的某一列(行)的元素都是两数
1 1 2 3 1 0 2 1 5 3
L5 4L4 0 0 1 1 2 2 1 6 12.
...
ann
a11 a12 ... a1n a11 a12 ... a1n ... ... ... ... ... ... ... ...
则 D ai1 ai2 ... ain bi1 bi 2 ... bin
... ... ... ... ... ... ... ...
an1 an2 ... ann an1 an2 ... ann
a2n
an1 ani ann an1 ani ann
可以推广之!
例如,第i行的元素都是两数之和:
a11
a12
...
a1n
...
... ... ...
D (ai1 bi1 ) (ai2 bi2 ) ... (ain bin )
...
...
...
...
第i行元素都
是两数之和
an1
an2
a11 a12 a1n
ai1 ai2 ain
a j1 a j2 a jn
a j1 a j2 a jn
ai1 ai2 ain
an1 an2 ann
an1 an2 ann
例如
第1章行列式

j1 j2 jn
和式中仅当 j1 n, j2 n 1,, jn1 2, jn 1时,
a1 j1 a2 j2 anjn 0
D
(1) (n(n1)321) n( n1)
a1na2,n1
an1
(1) 2 12 n
例9 证明上三角行列式
a11 a12 a1n
0 D
a22
a2n
a11a22 ann
D1
b1 b2
a12 a22
,
D2
a11 a21
b1 b2
当D a11 a12 0时, 方程组的解可表为
a21 a22
x1
D1 D
,x2
D2 D
例1
解二元线性方程组
4xx11
3x2 3x2
5 5
解: 方程组未知量的系数所构成的二阶行列式
1 3
D
3 (3) 4 15 0
43
方程组有唯一解.又
a11 a12 a1n
a11 a21 an1
D
a21
a22
a2n
,则
DT
a12
a22
an2
.
an1 an2 ann
a1n a2n ann
性质1 行列式与它的转置行列式值相等.(D=DT) 证:事实上,若记 DT=det(bij),则 bij a ji (i, j 1,2,, n)
(iii)项数为 3!=6 “-” 321 213 132 (奇排列)
推广之,有如下n 阶行列式定义
定义: n阶行列式
a11 a12 a1n
D
a21
a22
a2n
记
(1) ( j1 j2jn ) a1 j1 a2 j2 anjn det (aij )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中 D j 是把系数行列式 D 中第 j 列的元素用常数项代替后所得到的行列式. 推论 1:如果含有三个未知量三个方程的齐次线性方程组(常数项全为零的线性方程组)
0, a11 x1 + a12 x2 + a13 x3 = 0, a21 x1 + a22 x2 + a23 x3 = a x + a x + a x = 31 1 32 2 33 3 0.
,
ri ↔ rj ( ci ↔ c j )
则有: D ================== − D1 .
( 换法变换 )
符号说明: 换法变换——交换行列式中某两行(列)的元素. 记为: (列) 和第 j 行 (列) ri ↔ rj , ci ↔ c j 或 ri , rj , ci , c j 或 r ( i, j ) , c ( i, j ) ——交换行列式中第 i 行 的元素.
第 2 页
共 21 页
《线性代数讲稿》 二阶行列式的应用——求解二元一次线性方程组 设有二元一次线性方程组:
第一章
行列式
b1 , a11 x1 + a12 x2 = ( a a − a a ≠ 0 ) ,其中 a11 , a12 , a21 , a22 称为未知量 b2 . 11 22 12 21 a21 x1 + a22 x2 =
四阶
24 ( 4!)
4
………
………
………
的元素
n阶
n!
n
a11 a21 an1 =
i1i2 in j1 j2 jn
a12 a22 an 2
a1n a2 n ann ai1 j1 ai2 j2 ain jn
τ( ∑ ( −1)
i1i2 in ) +τ ( j1 j2 jn )
T
1 2 3 1 D = 2 5 8 . 7 8 9 3 6 9 a11 即:若 D = a21 a31 a12 a22 a32 a13 a11 T a23 ,则 D = a12 a33 a13 a21 a22 a23 a31 a32 . a33
注:①转置行列式可以看成是这样得到的——就是将原行列式中,关于主对角线对称的元素交换位置. ②原行列式 D 中位于第 i 行、第 j 列的元素 aij ,其在转置行列式 D 中的位置是第 j 行、第 i 列. 即:原行列式 D 中第 i 行、第 j 列的元素是 aij ,而转置行列式 D 中第 i 行、第 j 列的元素是 a ji . ③转置行列式与原行列式中主对角线上的元素相同.
注:该性质表明,在行列式中,行元素与列元素具有同等的地位, 因此,凡是对行成立的性质,对列也同样成立.
第 8 页
共 21 页
《线性代数讲稿》 Ⅱ.交换行列式中的两行(列)元素,则该行列式的值变号.
第一章
行列式
a11
即:设 D =
a21 an1
a12 a1n a22 a2 n an 2 ann
的系数行列式等于零,则该方程组有非零解(实际上有无穷多解) .
第 3 页
共 21 页
《线性代数讲稿》 2.三阶行列式的概念 定义:由九个元素排成三行三列的一个算式,称为三阶行列式.
第一章
行列式
a11 记为: a21 a31 a11
即: a21
a12 a22 a32 a12 a22 a32
a13 a23 ,并规定其值等于 a11a22 a33 + a12 a23 a31 + a13 a21a32 − a13 a22 a31 − a12 a21a33 − a11a23 a32 . a33 a13 a23 = a11a22 a33 + a12 a23 a31 + a13 a21a32 − a13 a22 a31 − a12 a21a33 − a11a23 a32 . a33
b1 b2
a12 a22
, D2 =
a11
b1
a21 b2
D1 D , x1 = 2 . D D
注:行列式 D =
a12 a22
称为二元一次线性方程组
b1 , a11 x1 + a12 x2 = 的系数行列式. b2 . a21 x1 + a22 x2 =
定理:如果二元一次线性方程组
b1 , a11 x1 + a12 x2 = b2 . a21 x1 + a22 x2 =
∑t
i =1
n
i
.
τ (123) = 0 , τ (132 ) = 1 , τ ( 213) = 1 , τ ( 231) = 2 , τ ( 312 ) = 2 , τ ( 321) = 3 .
即有三个奇排列和三个偶排列,也就是奇排列和偶排列的个数相等. 定理:在一个 n 级排列中,奇排列与偶排列各占一半,即都有
的系数行列式不等于零,即 : D =
a11 a21
a12 a22
= xj ≠ 0 ,则该方程组有唯一解:
Dj = ( j 1, 2 ) . D
其中 D j 是把系数行列式 D 中第 j 列的元素用常数项代替后所得到的行列式. 推论 1:如果含有两个未知量两个方程的齐次线性方程组(常数项全为零的线性方程组)
《线性代数讲稿》 三阶行列式的应用——求解三元一次线性方程组
第一章
行列式
定理:如果三元一次线性方程组
b1 , a11 x1 + a12 x2 + a13 x3 = b2 , a21 x1 + a22 x2 + a23 x3 = a x + a x + a x = 31 1 32 2 33 3 b3 . a11 的系数行列式不等于零,即 : D a21 = a31 a12 a22 a32 a13 Dj = xj = a23 ≠ 0 ,则该方程组有唯一解: ( j 1, 2,3) . D a33
的系数, b1 , b2 称为常数项,利用消元法求解得: x1 =
b1a22 − b2 a12 b a −b a , x1 = 2 11 1 21 . a11a22 − a12 a21 a11a22 − a12 a21
,则有: x1 =
若记: D =
a11 a21
a12 a22 a11 a21
, D1 =
=
j1 j2 jn
τ( ∑ ( −1)
j1 j2 jn )
a1 j1 a2 j2 anjn
=
i1i2 in
∑ ( −1)
τ ( i1i2 in )
ai11ai2 2 ain n
第 7 页
共 21 页
《线性代数讲稿》
第一章
行列式
二、行列式的性质
定义:将 n 阶行列式 D 中第 i 行和第 i 列的元素交换位置( i = 1, 2, n ) ,由此所得到的行列式, 称为原行列式 D 的转置行列式,记为: D 或 D′ .
主对角线:从左上角到右下角的连线;副对角线:从右上角到左下角的连线. ⑤二阶行列式的值等于主对角线上的元素乘积与副对角线上的元素乘积之差. ⑥在二阶行列式的展开式中,一共有两项,且每一项都是两个元素乘积(实际上,每一项中的这两个 元素都是来自原行列式中不同行和不同列的两个元素) ,并且有一项是“+”的,有一项是“-”的.
a31
注:①三阶行列式的运算法则可以按照如下两种法则进行: Ⅰ.对角线法则
Ⅱ. 沙路法则
②在三阶行列式的展开式中,一共有六项,且每一项都是三个元素乘积(实际上,每一项中的这三个 元素都是来自原行列式中不同行和不同列的三个元素) ,并且有三项是“+”的,有三项是“-”的.
注意:对角线法则只适用于二阶和三阶行列式. 第 4 页 共 21 页
( i 1, = = 2; j 1, 2 )的第一个下标 i 称为行下标,表明该元素所在的行数; 其中元素 aij 第二个下标 j 称为列下标,表明该元素所在的列数.
注:①行列式中的元素可以是实数、复数、字母、函数等等. ②行列式通常用大写的英文字母 D 表示. ③行列式的符号可以简记为: aij . ④二阶行列式的运算法则称为对角线法则,即:
的系数行列式等于零,则该方程组有非零解(实际上有无穷多解) .
第 5 页
共 21 页
《线性代数讲稿》 (二) n 阶行列式 1. n 级排列的概念
第一章
行列式
定义:由 n 个自然数 1, 2, , n 所组成的一个 n 元有序数组,称为一个 n 级排列(或 n 阶排列) , 记为: i1i2 in . 例如: “ 12345 ”和“ 54321 ”都是 5 级排列. “ 12321 ”不是 5 级排列. 注:①这里所说的 n 级排列不包括有重复数字出现的排列,例如: “ 56789 ” 不是 5 级排列. ②任意 n 个自然数所构成的排列不属于这里所说的 n 级排列,例如: ③所有 n 级排列的个数为 n ! 个. 2.排列的逆序和逆序数 定义: n 级排列“ 123 ( n − 1) n ”称为自然排列. 注:自然排列就是按照从小到大的顺序排列而成的排列. 定义:在一个 n 级排列 i1i2 in 中,如果有较大的数排在较小的数的前面(或如果有较小的数排在较大的数 的后面) ,则称这两个数构成该排列的一个逆序.在一个 n 级排列 i1i2 in 中,所有逆序的总数,称为该排 列的逆序数,记为:
0, a11 x1 + a12 x2 = 0. a21 x1 + a22 x2 =
的系数行列式不等于零,则该方程组只有唯一零解.即: = x j 0= ( j 1, 2 ) . 推论 2:如果含有两个未知量两个方程的齐次线性方程组
0, a11 x1 + a12 x2 = 0. a21 x1 + a22 x2 =
