图形的位似变换
2图形的位似变换PPT课件(沪科版)(共18张)

3.如图P,E,F分别是AC,AB,AD的中 点,四边形AEPF与四边形ABCD是位似图 形吗?如果是位似图形,说出位似中心 和位似比.
二:位似图形性质探究
A
C/
B/
B
O A/ C
在下列每个图形中,位似图形的对应点连线是否交于 一点?对应线段是否平行?
D A
D A
C D/ C/
A/
B/
B C
O
沪科版九(上)数学 课题: 位 似 变 换
22.4 位似变换
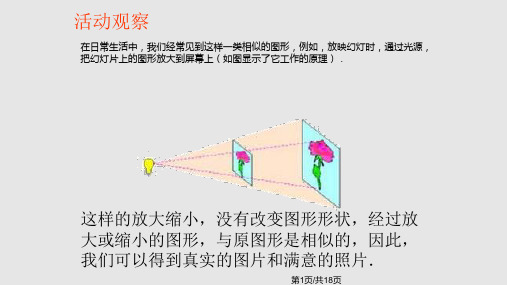
在幻灯机放映图 片的过程中,这 些图片有什么关 系呢?
幻灯机在 哪儿呢?
看看下面图形有什么特征?
对应点连线是否交于一点? 对应边的关系(位置和数量)?
一:位似图形定义
D A
C D/ A/
C/ O
B/
B
如果两个类似图形的每组对应点所在的直线都 交于一点,对应边互相平行,那么这样的两个图 形叫做位似图形, 这个交点叫做位似中心, 这 时两个类似图形的类似比又叫做它们的位似比.
同时满足下面三个条件的两个图形 才叫做位似图形.三条件缺一不可.
1.两图形类似.2.每来自对应点所在直线都经过 同一点. 3. 对应边互相平行.
显然,位似图形是类似图形的特殊情形,
其类似比又叫做它们的位似比.
1.等边三角形ABC与等边三角形A′B′C′
2.判断下列各图形哪些是位似图形: (1)五边形ABCDE与五边形A′B′C′D′E′;
似比)
五:布置作业,升华新知
• 1、必做题:自己任意画一三角形,将它放大2倍。 • 2、合作题:(部分学生) • 如图:有一边长为30m的正五边形草地ABCDE,想在
草地中间搞一个边长为5m的正五边形花圃,请你 利用位似把图形画出来。
沪科版九年级数学课件-图形的位似变换

歸納總結
从图中我们可以看到, △OAB∽△OA'B', 则 OA OB OC . OA' OB' OC '
性質:位似圖形上任意一對對應點到位似中心的距離之 比等於相似比.
二、位似圖形的畫法
1.把四邊形ABCD 縮小到原來的1/2.
6
4
A
B" 2 A'
B
-8 -6 -4 -2 O B'2 4 6 8 x
A"-2
-4
-6
你有什麼發現?
-8
位似變換後A,B的對應點為A ' ( 2 ,1 ),B' ( 2 , 0 );A"(- 2,- 1 ),B"( - 2 , 0 ).
如圖,△ABC三個頂點
y
座標分別為A(2,3),
8 6 A'
課堂小結
1. 位似圖形:如果兩個多邊形不僅相似,而且對應頂點的 連線相交於一點,對應邊互相平行或者在一條直線上,像這 樣的兩個圖形叫做位似圖形,這個點叫做位似中心.
2.位似圖的性質: (1)位似圖形一定相似,位似比等於相似比; (2)位似圖形對應點和位似中心在同一條直線上; (3)任意一對對應點到位似中心的距離之比等於位似比或
為什麼? C
解:AB∥CD.理由如下:
∵△OAB與△ODC是位似圖形, A
D ∴△OAB ∽△OCD,
O
B
∴∠OAB=∠C,
∴AB∥CD.
2. 如圖,以O為位似中心,將△ABC放大為原來的兩倍.
解:①作射線OA 、OB 、 OC ,
②分別在OA、OB 、OC 上
图形的位似变换课件

位似中心
进行位似变换的点,通常 选取原图形上的一个点作 为位似中心。
位似比
表示图形放大或缩小的比 例,通常用大于1的实数 表示放大,小于1的实数 表示缩小。
位似变换的性质
保持图形间的相对位置不变
位似变换只改变图形的大小,不改变图形上各点间的相对位置关系。
保持图形的形状不变
位似变换不会改变图形的形状,只是大小发生变化。
位似变换的应用习题
01 02
题目
在平面直角坐标系中,已知点A($- 2$,$3$),以点A为位似中心, 相似比为$1:2$,把$bigtriangleup ABC$缩小,则缩小后B点对应点坐 标为____.
题目
在平面直角坐标系中,以原点为位似中心,把矩形ABCD放大为原来的 两倍,则放大后点B对应点坐标为____.
03
题目
在平面直角坐标系中,以原点为位似中心,把线段AB缩小为原来的
$frac{1}{2}$倍,则缩小后B点对应点坐标为____.
位似变换的难题解析
题目
在平面直角坐标系中,以原点为位似中心,把线段AB缩小为原来的$frac{1}{2}$倍,若缩 小后A点对应点坐标为$(2sqrt{2},2)$,则缩小后B点对应点坐标为____.
详细描述
选取一个固定点,将图形进行位 似变换,观察变换后的图形与原 图形的相似性和对应边、对应角 的变化规律。
绕任意点的位似变换实例
总结词
通过具体实例展示绕任意点的位似变 换过程,帮助学生理解位似变换的灵 活性和应用。
详细描述
选取一个任意点,将图形进行位似变 换,观察变换后的图形与原图形的相 似性和对应边、对应角的变化规律。
VS
详细描述
绕固定点的位似变换可以用矩阵表示,其 中矩阵元素描述了缩放和旋转的几何特性。 通过矩阵变换,可以将一个图形上的点映 射到另一个位置,实现图形的缩放和旋转。
专项练习图形的位似变换与坐标

目 录
• 位似变换基本概念与性质 • 平面直角坐标系中位似变换 • 三角形和四边形位似变换探讨 • 函数图像在位似变换下性质研究 • 实际应用问题中位似变换思想运用 • 总结回顾与拓展延伸
01 位似变换基本概念与性质
位似变换定义及特点
位似变换定义
如果两个图形不仅是相似图形,而且每组对应点的连线交于 一点,对应边互相平行(或在一条直线上),那么这两个图 形叫做位似图形。这个点叫做位似中心,这时的相似比又称 为位似比。
02 平面直角坐标系中位似变 换
平面直角坐标系简介
平面直角坐标系定义
点的坐标
在平面内画两条互相垂直、原点重合 的数轴,组成平面直角坐标系。
平面内一点P的坐标由一对有序实数 (x,y)确定,其中x是点P到y轴的距离, y是点P到x轴的距离。
坐标轴及象限
水平数轴称为x轴或横轴,垂直数轴称 为y轴或纵轴。坐标轴将平面分为四个 象限。
然保持。
渐近线变换规律
反比例函数的渐近线在位似变换 下也会进行相应的平移和缩放,
但渐近线的斜率不会改变。
05 实际应用问题中位似变换 思想运用
几何证明题中位似变换思想运用
利用位似变换证明线段比例关系
01
通过构造位似图形,证明两条线段之间的比例关系,进而解决
几何证明问题。
利用位似变换证明角度相等关系
位似图形特点
两个位似图形中每组对应顶点所在的直线都交于一点,这个 交点叫做位似中心,图形上任意一对对应点到位似中心的距 离之比等于相似比。
相似比与位似中心关系
相似比
在位似变换中,如果两个相似图形的对应边长之比相等,那么这个比值就叫做 相似比。
位似中心与相似比关系
图形的位似变换与坐标

A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
(2)一般情况下,画已知图形的位似图形的结果不唯一; (3)将一个图形放大或缩小而保持形状不变.
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线都交于_位__似___中__心____ 对应线段___平___行__或__在___一__条__直___线__上_________
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
y
A
C
B
x
o
B”
A”
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐
标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以 原点O为位似中心,相似比为1/2的位似图形.
y
A(5,4)
A’(10,4)
C(5,1)
C’
0
B(3,0) B’
D(5,-1)
x
D'
E(4,-2)
E’(8,-2)
图形的位似变换
y
C( ´ 4,8)
A (2,4)
1 -1
O
-1
1
B (4,0)
D ( ´ 8,0) x
y
A (2,4)
D ( ´ -2,0) -1 O
1
1
B (4,0)
x
-1
C ( ´ -1,-2)
例题精讲
在平面直角坐标系中,已知点E(﹣4,2),F(﹣2, ﹣2),以原点O为位似中心,相似比为1/2, 把△EFO缩小,则点E的对应点E′的坐标是( ) A.(﹣2,1) B.(﹣8,4) C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1) y E O F x
课堂练习
如图,在平面直角坐标系中,将△ABC绕点P旋转180° ,得到△A1B1C1,则点A1,B1,C1的坐标分别为( A ) A.A1(-4,-6),B1(-3,-3),C1(-5,-1) B.A1(-6,-4),B1(-3,-3),C1(-5,-1) C.A1(-4,-6),B1(-3,-3),C1(-1,-5) D.A1(-6,-4),B1(-3,-3),C1(-1,-5)
复习巩固
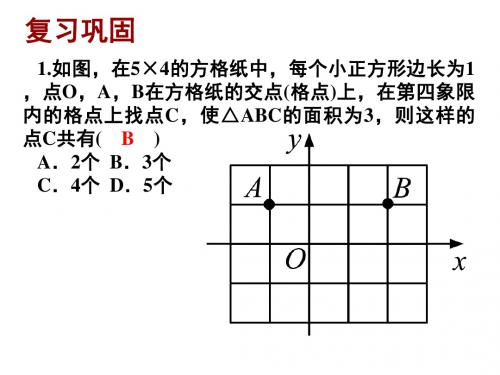
1.如图,在5×4的方格纸中,每个小正方形边长为1 ,点O,A,B在方格纸的交点 (格点)上,在第四象限 内的格点上找点 C ,使△ ABC 的面积为 3 ,则这样的 点C共有( B ) A.2个 B.3个 C.4个 D.5个
复习巩固
2.如何把三角形ABC放大为原来的2倍?
E B O D F E
C
A
F D O
C A B
探究新知
一、平移变换
y
5
A(2,4)
A′
O(0,0) → O′(3,0) A(2,4) → A′(5,4) B(4,0) → B′(7,0)
3.5图形的放大与缩小,位似变换(2)
(一)自主学习
3、画位似图形的具体步骤是: (1)在原图上选取若干个关键点,并在图上或图外任取一点P (2)以点P为端点向各关键点作射线; (3)分别在射线上截取各关键点的对应点,并使其满足缩小或 扩大的比例; (4)按照原图的形状依次连接各截取点,即可得到原图缩小或 扩大的图形。
4、一个图形经过位似变换和平移,旋转,最后得到的图形与原
图形 相似 。
(二)经典例题
例1、画一个三角形,使它与已知△ABC相似,且原三角形与所 画三角形的位似比为1:2。
A
1、在△ABC外任取一点P
2、分别连接PA、PB、PC C的中点D、E、F 4、依次连接D、E、F
B
例题讲解
(二)经典例题
例2:利用位似中心作图将△ABC的三边放大为 A 原来的2倍. E
(2)、知识梳理 3、相似形 不一定 是位似形,但位似形一定是 相似图形 . (3)、预习自测 通过预习教材P88~P91的内容,试着完成下面各题。 1、在位似变换下,新图形与原图形的对应线段的比都等 于 相似比 ,并且 相似比 都等于位似比 。 2、利用位似变换将一个图形 放大 或 缩小 , 当位似比K>1时,这个图形 放大 为原来的K倍; 当位似比K<1时, 这个图形 缩小 为原来的K倍。
(1)、知识回眸 1、图形的变换有哪些种类?它们各有什么性质? 平移、旋转、轴反射、位似变换 (2)、知识梳理
优秀个人:
1、两个相似图形间可以看作是把其中一个图形 放大 或
缩小 而得到。 2、位似比是 经过位似变换的图形上的点到位似中心的距离 与 原图形 上的点到位似中心的距离之比。
(一)自主学习
(三)合作交流
1、已知五边形ABCDE与五边形FGHMN是位似 图形,且位似比是2,若五边形ABCDE的面积 是36cm2,周长是20cm那么五边形FGHMN的周长 是 18cm ,面积是 5cm2 。
第22章 22.4 图形的位似变换

与△DEF周长的比为2∶1;④△ABC与△DEF面积比为4∶1.
A.1个
B.2个
C.3个
D.4个
11.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA= 2AA′,S△ABC=8,则S△A′B′C′= 18 .
12.如图所示,按要求进行位似变换. 以O为位似中心,将△ABC放大,使新图形与原图形的位似比为2∶1.
为32,则 A′的坐标为( C )
A.(3,92)
B.(43,6)
C.(3,92)或(-3,-92)
D.(34,6)或(-43,-6)
10.按如下方法作图(如图):任取一点O,连接OA、OB、OC,并取它们的
中点D、E、F,连接DE、EF、DF,得到△DEF,则下列说法正确的有
(D) ①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC
【思路分析】 由题意得P′PQQ′=Q′QRR′=R′RPP′=12,得△P′Q′R′ 与△PQR的位似比为12,位似中心显然是点O.
平面直角坐标系中的位似变换 【例2】如图所示,△ABO缩小后变为△A′B′O,其中A、B的对应点分 别为A′、B′,点A、B、A′、B′均在图中格点上.若线段AB上有一点 P(m,n),则点P在A′B′上的对应点P′的坐标为( D )
1 周长与五边形A′B′C′D′E′的周长比值是 2 . 6.用直尺画出下面位似图形的位似中心.
解:作图略.
7.用作位似图形的方法,可以将一个图形放大或缩小,位似中心位置可选
在( D )
A.原图形的外部
B.原图形的内部
C.原图形的边上
D.任意位置
8.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为
《图形在平面直角坐标系中的位似变换》示范教学方案

第二十二章相似形22.4 图形的位似变换第2课时图形在平面直角坐标系中的位似变换一、教学目标1.巩固位似图形及其有关概念.2.会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.3.了解四种变换(平移、轴对称、旋转和位似)的异同,并能在复杂图形中找出这些变换.二、教学重点及难点重点:用图形的坐标的变化来表示图形的位似变换.难点:把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.三、教学用具多媒体课件四、相关资料《坐标系中的位似》动画、《平面直角坐标系中的位似》微课五、教学过程【情景引入】观察如图所示的坐标系中的几个图形,它们之间有什么联系?【探究新知】发布任务:1. 如下图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为31,把线段AB 缩小.观察对应点之间坐标的变化,你有什么发现?2. 如下图,△ABC 三个顶点坐标分别为A (2,3),B (2,1),C (6,2),以点O 为位似中心,相似比为2,将△ABC 放大,观察对应顶点坐标的变化,你有什么发现?总结:位似变换中对应点的坐标的变化规律:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或-k .此图片是动画缩略图,本资源为《坐标系中的位似》知识探究,通过交互式动画的方式,运用了本资源,可以吸引学生的学习兴趣,增加教学效果,适用于《坐标系中的位似》的教学.若需使用,请插入【数学探究】坐标系中的位似.【新知运用】在平面直角坐标系中,已知点E (-4,2),F (-2,-2),以原点O 为位似中心,相似比为12,把△EFO 缩小,则点E 的对应点E′的坐标是( )A .(2,-1)B .(-8,4)C .(-8,4)或(8,-4)D .(-2,1)或(2,-1)解析:根据题意画出相应的图形,找出点E 的对应点E′的坐标即可.答案:如图,△E′F′O 与△E″F″O 即为所求的位似图形,可求得点E 的对应点的坐标为(-2,1)或(2,-1).故选D.本图片是微课的首页截图,本微课资源讲解了图形在平面直角坐标系中的位似,并通过讲解实例巩固所学的知识点,有利于启发教师教学或学生预习或复习使用.若需使用,请插入微课【知识点解析】平面直角坐标系中的位似.【随堂检测】1. 如图,在平面直角坐标系中,A (1,2),B (2,4),C (4,5),D (3,1)围成四边形ABCD ,做出一个四边形ABCD 的位似图形,使得新图形与原图形对应线段的比为2∶1,位似中心是坐标原点.解:以坐标原点O为位似中心的两个位似图形,一种可能是位似图形在位似中心同侧,此时各顶点的坐标乘以2;另一种可能是位似图形在位似中心的两侧,此时各顶点的坐标乘以-2,此题做出一个即可.如图,利用位似变换中对应点的坐标的变化规律,分别取A′(2,4),B′(4,8),C′(8,10),D′(6,2),顺次连接A′B′,B′C′,C′D′,D′A′,则四边形A′B′C′D′就是四边形ABCD的一个位似图形.2. 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2).(1)请画出△ABC关于y轴对称的△A1B1C1;(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2.解析:(1)根据网格找到点A,B,C关于y轴的对称点A1,B1,C1的位置,然后顺次连接;(2)连接A1O并延长至A2,使A2O=2A1O.连接B1O并延长至B2,使B2O=2B1O.连接C1O并延长至C2,使C2O=2C1O,然后顺次连接即可.解:(1)△A1B1C1如图所示;(2)△A2B2C2如图所示.六、课堂小结这节课你学到了哪些新知识呢?在平面直角坐标系中,将一个多边形每个顶点的横、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,他们的相似比为|k|.设计意图:通过问题的设置将本节课所学的知识点进行集中的梳理,归纳总结出本节课的重点知识。
图形的位似变换PPT课件
OA OB OC OD
(4)连接A ' B ',B ' C ',C ' D ',D ' A '.
所得四边形A ' B ' C ' D'即为所求.
第5页/共18页
观察下述图形有什么共同特点?
C
C'
B' A'
O C'
A'
B'
B'
A
BA
第9页/共18页
探索:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心, 相似比为3:1,把线段AB缩小.
y
A′(2,1),B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现? 第10页/共18页
在平面直角坐标系中,有两点A(6,3),B(6,0),
以原点O为位似中心,相似比为1:3,把线段AB缩小.
y
A C
B
o
x
第14页/共18页
小结:
如果两个图形不仅形状相同,而且每组对应点所在的 直线都经过同一点,那么这样的两个图形叫做位似图 形, 这个点叫做位似中心. 在平面直角坐标系中,如果位似变换是以原点为位 似中心,相似比为k,那么位似图形对应点的坐标的 比等于k或-k.
第15页/共18页
布置作业
课堂作业:P97练习; 家庭作业 : (1)P99习题第2、3题; (2)预习下一节内容.
第16页/共18页
教学反思
第17页/共18页
感谢您的欣赏
第18页/共18页
y
A′(2,1),B′(2,0)
A〞(-2,-1), B〞 (-2,0)
224图形的位似变换

形. A
D
A
B
D
C
B
O
C'
O
D'
B'
C
A'
224图形的位似变换
在上图中所得的四边形A‘B’C‘D’∽四 边形ABCD,你能说明道理吗?
图中有多边形相似吗?如果有,那么这种相似 有什么特征?
O O
O
图中每幅图中的两个多边形不仅相似,而且 对应顶点的连线相交于一点。
概念与性质
1.位似图形的概念
一般地,如果一个图形上的点A,B,C,D, …,P和
相同的图形(全等变换),只是位置不同。
3.相似形具有这个特点吗? 下面请欣赏如下图形的变换
224图形的位似变换
B
D A C E
F
放映机
在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上 在照相馆里,摄影师通过照相机把实物的图象缩小在底片上 这样放大或缩小的图形,形状_相__同__,大小__不__同__,所以它们_相__似__.
A
B
D
A'
B'
D' C
C' O
探究
对于上面的问题,还有其他方法吗?如果在四
边形外任选一个点O,分别在OA、OB、OC、OD的
反向延长线上取A‘ ,B’ 、C‘ 、D’ ,
使得 O O'A AO O'B BO O'C C O O'D D 1 2呢?如果点O取 在四边形ABCD内部呢?分别画出这时得到的图
位似中心
位似比 相似图形的相似比 特征:
1、位似图形一定是相似形,反之不一定。 2、判断位似图形时要注意首先它们必须是相似形,
位似变换

分析:根据位似图形上任意一对对应点到位似中 心的距离之比等于位似比,我们只要连结位似中心
O和□ ABCD的各顶点,并把线段延长(或反向延长)
到原来的3倍,就得到所求作图形的各个顶点. 作法如下:
例题与练习
作法
作法如下:
1. 连结OA,OB,OC,OD.
2. 分别延长OA,OB,OC, OD至G,C,E,F,使
A'(-3,3)B'(-4,1)C'(-2,0)D'(-1,2) 或A'(3,-3)B'(4,-1)C'(2,0) D'(1,-2)
练习与拓展
课内练习:
1.如图,已知△ABC和点O.以O为位似中心,求作 △ABC的位似图形,并把△ABC的边长缩小到原来的一半.
练习与拓展
2.如图,在直角坐标系中,△ABC 的各个顶点的坐标为 A(-1,1), 2
25.4 位似变换
概念与性质
1.位似图形的概念
如果两个图形不仅形状相同,而且每组对应点所在的直线都经过 同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心. 如下面两个图形就是位似图形:
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
辨一辨
1. 判断下列各对图形哪些是位似图形,哪些不是. (1)五边形ABCDE与五边形A′B′C′D′E′;
似中心的位似图形?
在平面直角坐标系中, 如果位似变换是以原点为位似中心, 相似比为k, 那么位似图形对应点的坐标的比等于k或-k.
利用位似变换可以将图形放大或缩小,并且: 当位似比k>1时,一个图形被放大为原图形的k倍; 当位似比k<1时,一个图形被缩小为原图形的k倍.
【图形的位似变换】PPT课件

整合方法
同理∠OEH=∠OAD,∴∠HEF=∠DAB, 同理∠EFG=∠ABC,∠FGH=∠BCD,∠GHE=∠CDA. 又易得AEBF=FBGC=GCDH=HADE=12, ∴▱EFGH∽▱ABCD. 又∵它们的对应顶点的连线相交于点 O, ∴▱ABCD 与四边形 EFGH 是位似图形,O 为位似中心.
探究培优
12.如图,在矩形ABCD中,对角线AC,BD相交于点O. (1)过点O作OE⊥BC于点E,连接DE交OC于点F, 作FG⊥BC于点G,则△ABC与△FGC是位似图 形吗?若是,请写出位似中心,并求出相似比; 若不是,请说明理由.
探究培优
解:△ ABC 与△ FGC 是位似图形,位似中心是点 C.
整合方法
解:是.理由如下: ∵点 E,F 分别是 OA,OB 的中点,∴EF=12AB, EF∥AB.∵点 G,H 分别是 OC,OD 的中点, ∴HG=12CD,HG∥CD. ∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD. ∴EF=HG,EF∥HG.∴四边形EFGH是平行四边 形.∵EF∥AB,∴∠OEF=∠OAB.
此页为防盗标记页(下载后可删)
教师课堂用语在学科专业方面重在进行“引”与“导”,通过点拨、搭桥等方式让学生豁然开朗,得出结论,而不是和盘托 出,灌输告知。一般可分为:启发类、赏识类、表扬类、提醒类、劝诫类、鼓励类、反思类。
22.4图形的位似变换(第1课时)

基础导练
1.下列说法不正确的是( )
A. 位似图形一定是相似图形
B. 相似图形不一定是位似图形
C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比
D.位似图形中每组对应点所在的直线必相互平行
2.如图,五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形,
点A 和点A 1是一对对应点,P 是位似中心,且2 P A =3 P A 1, 则五边形ABCDE 和五边形A 1B 1C 1D 1E 1的相似比等于
( )
A.32
B.2
3 C.53 D.35 3.如果两个位似图形的对应线段长分别为3cm 和5cm.且较小图形周长为30cm,则较大图形周长为 .
能力提升
4.如图,已知△EFH 和△MNK 是位似图形,那么其位似中心是( )
A.点A
B.点B
C.点C
D.点D
5.如图,作出一个新图形,使新图形与原图形相似.且相似比为3
1 .
参考答案
1.D
2.B
3. 50cm
4.B
5.略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22.4图形的位似变换
第1课时位似图形
1.了解位似多边形及其有关概念,了解位似与相似的联系和区别;(重点)
2.掌握位似图形的性质,会画位似图形;(重点)
3.会利用位似将一个图形放大或缩小.(难点)
一、情境导入
生活中我们经常把自己好看的照片放大或缩小,由于没有改变图形的形状,我们得到的照片是真实的.观察图中有相似的多边形吗?如果有,那么这种相似有什么共同的特征?
二、合作探究
探究点一:位似图形的识别
观察图27.3-2图中有多边形相似吗?如果有,那么这种相似什么共同的特征?
图27.3-2
学生活动:学生通过观察了解到有一类相似图形,除具备相似的所有性质外,还有其特性,学生自己归纳出位似图形的概念:如果两个图形不仅是相似图形,而且是每组对应点连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.这个点叫做位似中心.这时的相似比又称为位似比.(位似中心可在形上、形外、形内.)每对位似对应点与位似中心共线;不经过位似中心的对应线段平行.
如图所示,指出下列图中两个图形是否是位似图形?
解:(1)(2)(4)三图中的两个图形都是位似图形.
方法总结:解决此类题的关键是首先要判断两个图形是不是相似图形,然后再找出对应点,作出几对对应点所在的直线,观察是否经过同一个点,若两个图形是相似图形,且所作的直线经过同一个点,则这两个图形是位似图形,据此可判断(1)(2)(4)是位似图形,(3)不是位似图形.
探究点二:位似图形的性质
如图所示,△ABC 与△A ′B ′C ′关于点O 位似,BO =3,B ′O =6.
(1)若AC =5,求A ′C ′的长;
(2)若△ABC 的面积为7,求△A ′B ′C ′的面积.
解:(1)∵△ABC 与△A ′B ′C ′是位似图形,位似比为OB ∶OB ′=3∶6=1∶2,
∴AC A ′C ′=12
,得A ′C ′=10; (2)根据题意,得S △ABC S △A ′B ′C ′=(AC A ′C ′
)2=14, 即7
S △A ′B ′C ′=14,所以S △A ′B ′C ′=7×4=28. 方法总结:位似图形是一种特殊的相似图形,图形上任意一对对应点到位似中心的距离之比都等于相似比,可利用相似三角形的性质解决有关问题.
探究点三:位似图形的画法
(1)如图甲,在位似中心O 的异侧,作出已知四边形ABCD 的位似图形A ′B ′C ′D ′,使四边形A ′B ′C ′D ′与四边形ABCD 的相似比为2∶3;
(2)如图乙,已知五边形ABCDE ,在位似中心O 的同侧作五边形ABCDE 的位似图形A ′B ′C ′D ′E ′,使五边形A ′B ′C ′D ′E ′与五边形ABCDE 的相似比为1∶3.
解:(1)画法如下:
①分别连接OA ,OB ,OC ,OD 并反向延长;
②分别在AO ,BO ,CO ,DO 的延长线上截取OA ′,OB ′,OC ′,OD ′,使OA ′OA =OB ′OB =OC ′OC
=OD ′OD =23
; ③顺次连接A ′B ′,B ′C ′,C ′D ′,D ′A ′.
四边形A ′B ′C ′D ′就是所求作的四边形;
(2)画法如下:
①分别连接OA ,OB ,OC ,OD ,OE ;
②分别在AO ,BO ,CO ,DO ,EO 上截取OA ′,OB ′,OC ′,OD ′,OE ′使OA ′OA =OB ′OB =OC ′OC
=OD ′OD =OE ′OE =13
; ③顺次连接A ′B ′,B ′C ′,C ′D ′,D ′E ′,E ′A ′.
五边形A ′B ′C ′D ′E ′就是所求作的五边形.
方法总结:(1)画位似图形时,要注意相似比,即分清楚是已知原图与新图的相似比,还是新图与原图的相似比;(2)画位似图形的关键是画出图形中顶点的对应点,画图的方法大致有两种:一是每对对应点都在位似中心的同侧;二是每对对应点都在位似中心的两侧;
(3)若没有指定位似中心,则画图时位似中心的取法有多种,对画图而言,以多边形的一个顶点为位似中心时,画图最简便.
三、小结:谈谈你这节课学习的收获.
四、板书设计
位似图形及其性质⎩⎪⎪⎪⎨⎪⎪⎪⎧定义:如果两个相似多边形任意一组对应顶点
P ,P ′所在的直线都经过同一点O ,且有 OP ′=k ·OP (k ≠0),那么这样的两个图
形叫做位似图形性质:⎩⎪⎨⎪⎧①两个图形相似②对应点的连线相交于一点,对应边互 相平行或在同一条直线上
③任意一对对应点到位似中心的距离
之比等于相似比作位似图形:关键是确定位似中心、相似比和 找关键点的对应点
五、作业:
• 1、必做题:自己任意画一三角形,将它放大2倍。
• 2、合作题:(部分学生)
如图:有一边长为30m 的正五边形草地ABCDE,想在草地中间搞一个边长为5m
的正五边形花圃,请你利用位似把图形画出来。
六、教学反思:
位似是相似图形的延伸和深化.经历位似图形的探索过程,进一步发展学生的探究、交流能力,培养学生动手操作的能力,体验学习的乐趣.位似图形在实际生产和生活中有着广泛的应用,通过现实情境,进一步发展学生从数学角度提出问题、分析问题、解决问题的能力,培养学生的数学应用意识,体会数学与自然、社会的联系.。
