清华理论力学课后答案9
理论力学课后答案9
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
w.
kh
a ,方向向上。 2
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
9.9 图示一凸轮导板机构。半径为 r 的偏心圆轮 O 以匀角速度 绕轴 O 转动,偏 心距 OO e ,导板 AB 重 FW 。当导板在最低位置时,弹簧的压缩量为 。要使 导板在运动过程中始终不离开轮轴,试求弹簧的刚度系数。
魏
泳
涛
m
课
后
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
ww
w.
kh
而 A 点坐标为 xA 2l cos S y A 2l sin 化简后 y2 ( x A l cos ) 2 A l 2 4
da
w.
co
解: 由于在水平方向上质心运动守恒。由于系统初始静止,因此系统质心位置始 终保持不变。 由图知 xC l cos l cos S
魏
泳
涛
m
ae 即为 AB 的加速度。
当 0 时, AB 处于最高位置,其加速度为 2e 。弹簧的压缩量为 2e 。 AB 受力图如下。
课
后
答
案
网
ww
T FW N k ( 2e) FW N
要保持接触,则应该有
理论力学课后习题答案

理论力学课后习题答案理论力学课后习题答案引言:理论力学是物理学的基础课程之一,对于理解和应用物理学的原理和方法具有重要意义。
在学习理论力学的过程中,课后习题是巩固知识、提高能力的重要途径。
本文将针对理论力学课后习题进行解答,帮助读者更好地理解和掌握这门课程。
第一章:牛顿力学1. 一个物体以初速度v0沿直线运动,加速度为a,求物体的位移与时间的关系。
答:根据牛顿第二定律F=ma,可得物体所受合力F=ma=mv/t,其中m为物体的质量,v为物体的速度,t为时间。
由此可得物体的位移s=vt+1/2at^2。
2. 一个质点在重力作用下自由下落,求它在t时刻的速度和位移。
答:在重力作用下,质点的加速度为g,即a=g。
根据牛顿第二定律F=ma,可得质点所受合力F=mg。
根据牛顿第一定律,质点的速度随时间的变化率为v=g*t,位移随时间的变化率为s=1/2gt^2。
第二章:拉格朗日力学1. 一个质点沿半径为R的圆周运动,求它的动能和势能。
答:质点的动能由动能定理可得,即K=1/2mv^2,其中m为质点的质量,v为质点的速度。
质点的势能由引力势能可得,即U=-GmM/R,其中G为引力常数,M为圆周的质量。
2. 一个质点在势能为U(r)的力场中运动,求它的运动方程。
答:根据拉格朗日方程可得,质点的运动方程为d/dt(dL/dv)-dL/dr=0,其中L=T-U,T为质点的动能,U为质点的势能。
第三章:哈密顿力学1. 一个质点在势能为U(x)的力场中运动,求它的哈密顿量和哈密顿运动方程。
答:质点的哈密顿量由哈密顿定理可得,即H=T+U,其中T为质点的动能,U为质点的势能。
质点的哈密顿运动方程为dp/dt=-dH/dx,其中p为质点的动量。
2. 一个质点在势能为U(x)的力场中运动,求它的哈密顿正则方程。
答:质点的哈密顿正则方程为dx/dt=dH/dp,dp/dt=-dH/dx,其中x为质点的位置,p为质点的动量。
结论:通过对理论力学课后习题的解答,我们可以更深入地理解和应用物理学的原理和方法。
理论力学习题解答第九章

理论力学习题解答第九章题9-2图9-2 如图所示,均质圆盘半径为R,质量为m ,不计质量的细杆长,绕轴O转动,角速度为,求下列三种情况下圆盘对固定轴的动量矩:(a)圆盘固结于杆;(b)圆盘绕A轴转动,相对于杆OA的角速度为;(c)圆盘绕A轴转动,相对于杆OA的角速度为。
(a);(b);(c)9-3水平圆盘可绕铅直轴转动,如图所示,其对轴的转动惯量为。
一质量为m的质点,在圆盘上作匀速圆周运动,质点的速度为,圆的半径为r,圆心到盘中心的距离为。
开始运动时,质点在位置,圆盘角速度为零。
求圆盘角速度与角间的关系,轴承摩擦不计。
9-4如图所示,质量为m的滑块A,可以在水平光滑槽中运动,具有刚性系数为k的弹簧一端与滑块相连接,另一端固定。
杆AB长度为l,质量忽略不计,A端与滑块A铰接,B端装有质量,在铅直平面内可绕点A旋转。
设在力偶M作用下转动角速度为常数。
求滑块A的运动微分方程。
9-5质量为m ,半径为R的均质圆盘,置于质量为M的平板上,沿平板加一常力F。
设平板与地面间摩擦系数为f,平板与圆盘间的接触是足够粗糙的,求圆盘中心A点的加速度。
9-6均质实心圆柱体A和薄铁环B的质量均为m,半径都等于r,两者用杆AB铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为,如图所示。
如杆的质量忽略不计,求杆AB的加速度和杆的内力。
;9-7均质圆柱体A和B的质量均为m,半径为r,一绳缠在绕固定轴O转动的圆柱A上,绳的另一端绕在圆柱B上,如图所示。
摩擦不计。
求:(1)圆柱体B下落时质心的加速度;(2)若在圆柱体A上作用一逆时针转向,矩为M 的力偶,试问在什么条件下圆柱体B的质心加速度将向上。
9-8平面机构由两匀质杆AB,BO组成,两杆的质量均为m,长度均为l,在铅垂平面内运动。
在杆AB上作用一不变的力偶矩M,从图示位置由静止开始运动。
不计摩擦,试求当A即将碰到铰支座O时A 端的速度。
9-9长为l、质量为m的均质杆OA以球铰链O固定,并以等角速度绕铅直线转动,如图所示。
理论力学答案完整版(清华大学出版社)9

F1 = F1(sinϑ i − cosϑ j) , F2 = F2i
点 A 和 B 的坐标及其变分为
rA = −(l1 − l2 )cosϑ i + (l1 + l2 )sinϑ j
,
rB = −2l1 cosϑ i
δrA = (l1 − l2 )sinϑ ⋅δϑ i + (l1 + l2 )cosϑ ⋅δϑ j ,
Fδ re − G1δ ra = 0 按速度合成定理,虚位移存在如下关系:δ ra = δ re tan β ,于是
(a)
题 9-9 图
导出 F = G1 tan β .
(2)水平面有摩擦时,当水平力 F 较小,斜面 D 有向左运动趋势,此时摩擦力方向向右,
临界平衡时,虚功方程为
(F + ) Fmax δ re − G1δ ra = 0 , 其中 Fmax = (G1 + G2 ) f 。求得: F ≥ G1 tan β − (G1 + G2 ) f .
i =1
解题要领 1) 对于自由度不为零的系统,求其平衡时主动力满足的关系可用虚功原理. 2) 对于自由度为零的系统,为求其约束力,可以依次解除一个约束,使自由度为 1,即将
此约束力作为主动力应用虚功原理. 3) 独立的坐标变分个数与系统的自由度相同,可以用解析或虚速度的方法建立不独立的坐
标变分满足的关系.
三 广义坐标表示的虚位移原理
广义坐标:确定质点系位形的独立坐标。
虚功原理的广义坐标表述:受理想约束的质点系,其平衡的充分必要条件是系统所有与广义
坐标对应的广义力为零
Qj = 0 ( j = 1,2,L, m)
∑ 其中
Qj
=
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
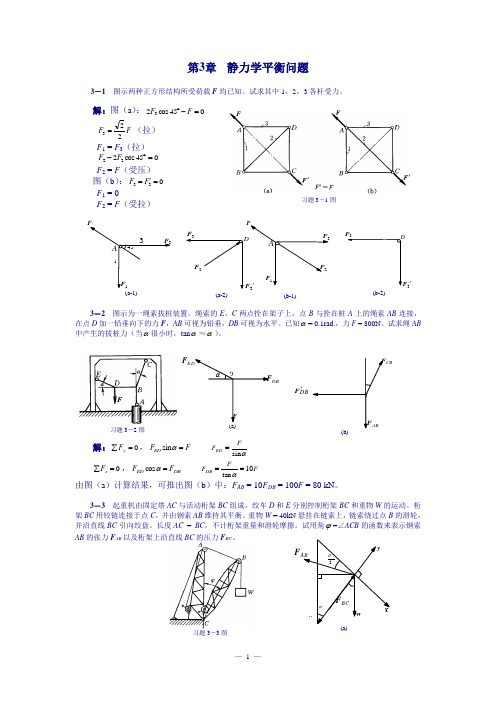
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
清华大学版理论力学课后习题答案大全

第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕc o s )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
(完整word版)理论力学课后习题及答案解析.docx

理论力学教科书课后习题及解析第一章偶,大小是260Nm,转向是逆时针。
习题 4- 1.求图示平面力系的合成结果,长度单位为m。
习题 4- 3.求下列各图中平行分布力的合力和对于 A 点之矩。
解: (1) 平行力系对 A 点的矩是:解: (1) 取 O 点为简化中心,求平面力系的主矢:取 B 点为简化中心,平行力系的主矢是:求平面力系对O 点的主矩:平行力系对 B 点的主矩是:(2)合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;向 A 点简化的结果是一个力R A和一个力偶M A,且:如图所示;将 R B向下平移一段距离d,使满足:最后简化为一个力R ,大小等于R B。
其几何意义是: R 的大小等于载荷分布的将 R A向右平移一段距离d,使满足:矩形面积,作用点通过矩形的形心。
(2)取 A 点为简化中心,平行力系的主矢是:最后简化为一个力R,大小等于R A。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
平行力系对 A 点的主矩是:列平衡方程:习题 4-4 .求下列各梁和刚架的支座反力,长度单位为m。
解方程组:反力的实际方向如图示。
校核:解: (1) 研究 AB 杆,受力分析,画受力图:结果正确。
(2) 研究 AB 杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:(3) 研究 ABC ,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:列平衡方程:反力的实际方向如图示。
校核:解方程组:结果正确。
反力的实际方向如图示。
校核:结果正确。
习题 4-5 .重物悬挂如图,已知G=1.8kN ,其他重量不计;求铰链 A 的约束反力和杆 BC 所受的力。
列平衡方程:解方程组:解: (1) 研究整体,受力分析(BC 是二力杆),画受力图:反力的实际方向如图示。
列平衡方程:习题 4-8 .图示钻井架,G=177kN ,铅垂荷载P=1350kN ,风荷载 q=1.5kN/m ,水平力 F=50kN ;求支座 A 的约束反力和撑杆CD 所受的力。
理论力学解答清华版

第一章 静力学基本概念1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2FB.2F - 1FC.1F +2F图1-18 图1-191-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体;B. 变形体;C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.-F/31-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21第二章力系的简化2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A指向B的力F,在z轴上投影为,对z轴的矩的大小为。
答:F/2;62F/5。
2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b,c,则力F在轴z和y上的投影:Fz= ;Fy= ;F对轴x的矩M x(F)= 。
答:Fz=F·sinφ;Fy=-F·cosφ·cosφ;Mx(F)=F(b·sinφ+c·cosφ·cosθ)图2-40 图2-412-3.力通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力在x轴上的投影为,对x轴的矩为。
理论力学课后答案9

魏
泳
涛
m
1 (1). ml 2 (2). me
课
后
解:
答
案
网
(3).动量水平分量: m1v m2 (v
m2l sin 2 v (4).圆轮角速度: 2r 圆轮轮心速度 v轮 0.5v
动量铅垂分量:
总动量: m1v m2 0.5v 2 (m1 m2 )v
课
后
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
ww
w.
l m l ,动量: 1 ,方向垂直于 OC 向上 2 2 滑 块 A 、 B 以 及 杆 AB 组 成 的 系 统 的 质 心 为 C , 速 度 为 l , 动 量 : 2(m1 m2 )l ,方向垂直于 OC 向上 l 总动量: (5m1 4m2 )l ,方向垂直于 OC 向上 2
魏
泳
涛
m
课
后
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
ww
w.
kh
1 OA 杆动量: ml1 2 AB 杆瞬时平动,动量: ml1 轮 B 质心速度为 l1 ,动量: ml1 5 因此系统总动量为: ml1 2
da
w.
co
解:
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
9.8 质量为 m , 长为 2l 的均质杆 OA 绕定轴 O 转动, 设在图示瞬时的角速度为 , 角加速度为 ,求此时轴 O 对杆的约束力。
理论力学第九章习题
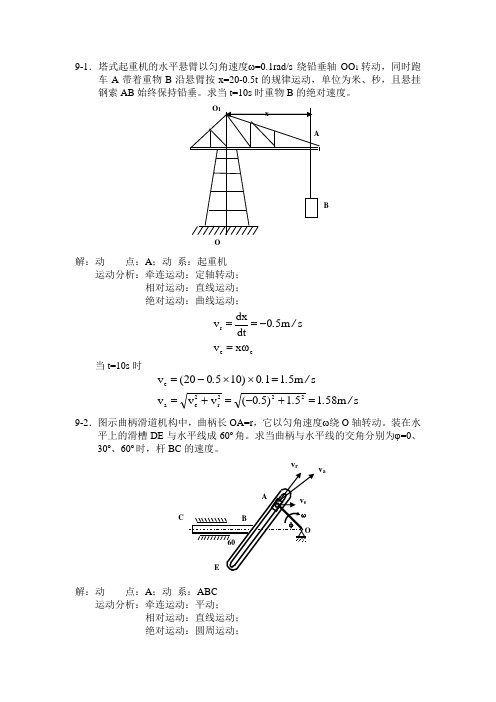
9-1.塔式起重机的水平悬臂以匀角速度ω=0.1rad/s 绕铅垂轴OO 1转动,同时跑车A 带着重物B 沿悬臂按x=20-0.5t 的规律运动,单位为米、秒,且悬挂钢索AB 始终保持铅垂。
求当t=10s 时重物B 的绝对速度。
解:动 点:A ;动 系:起重机运动分析:牵连运动:定轴转动; 相对运动:直线运动; 绝对运动:曲线运动;ee r ωx v sm 50dtdx v =-==/.当t=10s 时sm 58151)50(v v v s m 5110)105020(v 222r 2e a e /.../...=+-=+==⨯⨯-=9-2.图示曲柄滑道机构中,曲柄长OA=r ,它以匀角速度ω绕O 轴转动。
装在水平上的滑槽DE 与水平线成60o 角。
求当曲柄与水平线的交角分别为ϕ=0、30o 、60o 时,杆BC 的速度。
解:动 点:A ;动 系:ABC 运动分析:牵连运动:平动; 相对运动:直线运动; 绝对运动:圆周运动;OBC v rv a由正弦定理得:()()()12030φv v φ90v 30φv 120v ae rea sin sin sin sin sin -=-=-=当ϕ=0o 时, ωr 33v e -=当ϕ=30o 时, 0v e = 当ϕ=60o 时, ωr 33v e =9-3.图示曲柄滑道机构中,杆BC 为水平,而杆DE 保持铅垂。
曲柄长OA=10cm ,以匀角速度ω=20rad/s 绕O 轴转动,通过滑块A 使杆BC 作往复运动。
求当曲柄与水平线的交角分别为ϕ=0、30o 、90o 时,杆BC 的速度。
解:动 点:A ;动 系:BDC 运动分析:牵连运动:平动;相对运动:直线运动; 绝对运动:圆周运动;φv v s cm 200ωr v a e a sin /===当ϕ=0o 时, 0v e =;当ϕ=30o 时, s cm 100v e /=; 当ϕ=90o 时, s cm 200v e /=9-4.矿砂从传送带A 落到另一传送带B 的绝对速度为v 1=4m/s ,其方向与铅垂线成30o 角。
清华大学-理论力学-习题解答-9-09

! sin ϕ − z ! cos ϕ ) x = 2ω ( y !! !! ! y = −2ω x sin ϕ !! ! cos ϕ z = − g + 2ω x
! (0) = 0,y ! (0) = v0 cos α,z ! (0) = v0 sin α 。 初始条件为: x(0) = y (0) = z (0) = 0;x
(1)
将 ω = 0 代入(1)式,得到零次近似项:
x0 = 0 !! y0 = 0 !! !! z0 = − g !0 (0) = 0,y ! 0 (0) = v0 cos α,z !0 (0) = v0 sin α 得: 积分上式,并由初始条件 x0 (0) = y0 (0) = z0 (0) = 0;x !0 = 0 x ! 0 = v0 cos α y z !0 = − gt + v0 sin α !! ! 将上式代入公式 r 1 = − gk − 2ω × r0 ,可得第一次近似项: !! r1 = − gk + 2ω (v0 sin ϕ cos α − v0 cos ϕ sin α + gt cos ϕ )i
1 x1 = ω (v0 sin ϕ cos பைடு நூலகம் − v0 cos ϕ sin α )t 2 + ω gt 3 cos ϕ 3
故经过时间 t 后,炮弹偏东的距离为 ω v0 t 2 sin(ϕ − α ) + ω gt 3 cos ϕ 。
理论力学解答清华版

第一章 静力学基本概念1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2FB.2F - 1FC.1F +2F图1-18 图1-191-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体;B. 变形体;C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.-F/31-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21第二章 力系的简化2-1.通过A (3,0,0),B (0,4,5)两点(长度单位为米),且由A 指向B 的力F ,在z 轴上投影为 ,对z 轴的矩的大小为 。
答:F /2;62F /5。
2-2.已知力F 的大小,角度φ和θ,以及长方体的边长a ,b ,c ,则力F 在轴z 和y 上的投影:Fz= ;Fy= ;F 对轴x 的矩M x ()= 。
答:Fz=F ·sin φ;Fy=-F ·cos φ·cos φ;Mx (F )=F (b ·sin φ+c ·cos φ·cos θ)图2-40 图2-412-3.力通过A (3,4、0),B (0,4,4)两点(长度单位为米),若F=100N ,则该力在x 轴上的投影为 ,对x 轴的矩为 。
理论力学课后习题答案_清华大学出版社_2004年版_范钦珊,刘燕,王琪 编著
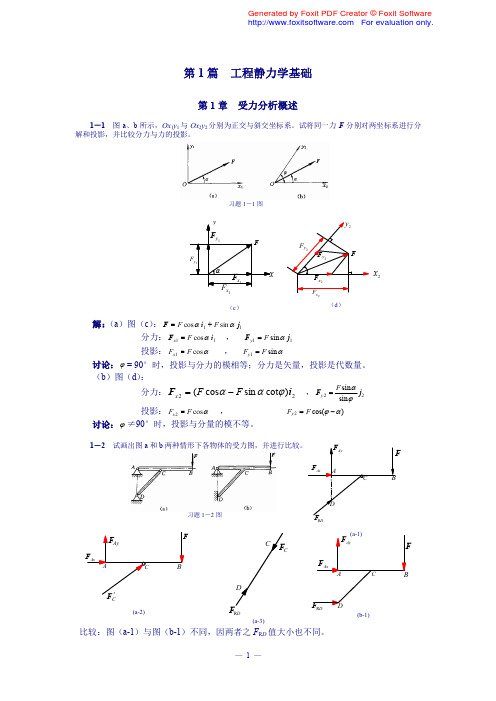
习题 1-1 图
y
y2
F
F y1
F y1
F y2 F y2
F
Fx1 Fx1
(c)
x
F x2
Fx 2
x2
(d)
解: (a)图(c) : F F cos i1 F sin j1 分力: F x1 F cos i1 投影: Fx1 F cos , ,
F y1 F sin j1 Fy1 F sin
讨论: = 90°时,投影与分力的模相等;分力是矢量,投影是代数量。 (b)图(d) : 分力: F x 2 ( F cos F sin cot ) i 2 投影: Fx 2 F cos , 讨论: ≠90°时,投影与分量的模不等。
1-2 试画出图 a 和 b 两种情形下各物体的受力图,并进行比较。
F Ax
, Fy 2
F sin j2 sin
Fy 2 F cos( )
FAy
A
C
F
B
D
习题 1-2 图
FRD
FAy
F Ax
A
C
F
C
FC
F Ax
FAy
(a-1)
F
C
B
A
B
D
' FC
(a-2)
FRD
(a-3)
FRD
D
(b-1)
比较:图(a-1)与图(b-1)不同,因两者之 FRD 值大小也不同。
解: 图(a) : 2F3 cos 45 F 0
F3 2 F (拉) 2
F1 = F3(拉)
F2 2 F3 cos 45 0
F2 = F(受压) 图(b) : F3 F3 0 F1 = 0 F2 = F(受拉)
清华大学版理论力学课后习题答案大全(免费下载)(第9章动量矩

清华大学版理论力学课后习题答案大全(免费下载)(第9章动量矩第9章动量矩定理及其应用9-1在下列条件下计算系统的动量矩。
1.圆盘以ω的角速度绕o轴转动,质量为m的小球m可沿圆盘的径向凹槽运动,图示瞬时小球以相对于圆盘的速度vr运动到om=s处(图a);求小球对o点的动量矩。
2.图中质量为m的偏心轮在水平面上作平面运动。
车轮中心为a,质心为C,AC=E;车轮半径为R,车轮中心a的惯性矩为JA;c、 a点和B点位于同一铅垂线上(图B)。
(1)当车轮仅滚动而不滑动时,如果VA已知,则计算车轮的动量和到B点的动量矩;(2)当车轮滚动和滑动时,如果VAω已知,求车轮的动量和B点的动量矩。
解:1。
瞧?MS2(逆)2,(1)vrωmoωab(a)crvaep?mvc?m(va??e)?mva(1?)(逆)rv(r?e)2lb?mvc(r?e)?jc??mva?(ja?me2)arr(b)(2)p?mvc?m(va??e)图9-1lb?mvc(r?e)?jc??m(va??e)(r?e)?(ja?me2)??m(r?e)va?(ja?mer)?9-2在图中所示的系统中,已知滚筒绕O轴旋转的角速度ω,其大半径和小半径分别为R和R,相对于O轴的惯性矩为Jo;a区和B区的质量分别为ma和MB;试着找出系统相对于O轴的动量矩。
ω或解:Rlo?(jo?mar2?mbr2)?练习a的图9-2bθ9-3图中所示的均质细杆OA和EC的质量分别为50kg和100kg,它们在a点焊接在一起。
如果结构在图中所示的位置从静态状态下释放,计算刚释放时杆的角加速度和铰链o处的约束力。
没有铰链摩擦。
解:令m=moa=50kg,则mec=2m质心d位置:(设l=1m)d?od?l255l?m66foxfoymgd2mg刚体作定轴转动,初瞬时ω=0jo??mg??2mg?ljo?ml2?即3ml2??131?2m?(2l)2?2ml2?3ml212习题20-3图D习题20-3解图5mgl2??5g?8.17rad/2s6l525tad?lg636由质心运动定理:3m?ad?3mg?foyt2511g?mg?449n(↑)3612n?0,福克斯?0,阿德福?3毫克?3米-1-9-4绞车机构如图所示,能绕固定轴旋转的B轮和C轮的半径分别为R和R,各自旋转轴的惯性矩分别为J1和J2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
及其变分
答 1
yC1 = 2 l sinϑ1 ,
1 δyC1 = 2 l cosϑ1 ⋅ δϑ1 ;
1
1
后 yC2 = l sinϑ1 + 2 l sinϑ2 , δyC2 = l cosϑ1 ⋅δϑ1 + 2 l cosϑ2 ⋅δϑ2 。
G1 tan β − (G1 + G2 ) f ≤ F ≤ G1 tan β + (G1 + G2 ) f 。
(b) 解:本体与上题在于ϑ 是变量,只要将上题中的 β 表示成 h 的
函数即可。易见ϑ = 90� − β , tan β = cotϑ =
上式结果,分别得到(1) F =
R2 − h
h2
.khdaw.co 题 9-13 图
题 9-13 图(a)
www 任一虚位移:AB 杆绕 A 的虚转动 δϑ ,BC 杆的瞬时虚平移 δrB = hδϑ = δrC ,CD 杆绕 D
的虚转动 δϕ = δrC 2h 。列出虚功方程:
网 Mδϑ − F1δrB − F2hδϕ = 0 ,解得: M A = (F1 + F2 / 2)h 。
题 9-11 图(a) 其中, δrD = hδr l 。
解得: FAy = F1 − F2h / l 。
9-12 水平力 F1 和 F2 分别作用于杆 BC 和杆 CD 的中点,如图示。不计`杆重,试计算固
定端 A 的约束力偶 MA。
m 解:解除固定端的转动约束而成为固定铰链,并代之以约束力偶,如图( a)所示。给机构
G1
,
R2 − h2
,代入
h
(b)
题 9-9 图
(2)
R2 − h2 h
G1
− (G1
+ G2 )f
≤F
≤
R2 − h
h2
G1
−
(G1
+
G2 )f
。
om 9-10 不计梁的自重,求图示水平梁在支座 B 和 C 处的约束力。 .c (a)解:图示组合梁的自由度为零。为用虚功原理求解, w 须解除一个约束,使之成为自由度为 1 的系统。 a 先解除滑动铰链 C,将约束力 FC 当作主动力。给系 d 统任一虚位移δϑ ,列出虚功方程 h FCδ rC − Mδϑ = 0 .k 虚位移的关系为δ rC = lδϑ ,代入上式,导出 wFC = M /l ww 其次解除滑动铰链 B,同理列出虚功方程
.k W = G(sinϑ − f cosϑ)s − 1 ks2 2
w 在弹簧压缩 s 再回弹 λ 的过程中,所有力的功为 [ ww] W = G(− sinϑ − f cosϑ)λ + 1 k s2 − (s − λ)2 。
2
题 9-2 图
网 9-3 弹簧原长 l,刚度系数为 k,一端固定在 O 点,此
−ϑ
)⎥⎦⎤δϕ
;
a yC = 2l cosϕ sinϑ , δyC = −2l sinϕ sinϑ ⋅δϕ .
d 按虚功原理,有
kh ∑ Fi ⋅δ ri = 0 ,
i
P1δyC1 + P1δyC2 + P2δyC = 0 ,
www. 解得:
tan ϕ
=
P1
2(P1 +
P2 ) cotϑ
。
9-6 两相同的匀质杆,长度为 l ,重为 G,其上作用有如图之力偶 M ,
= lδϑ , δra
=
δre cos 60�
=
2l δϑ
kh DC 杆的虚角位移为δϕ = δra ,(顺时针)。 l
. 列出平衡方程
w F ⋅ 2lδϑ − Mδϕ = 0
ww 解得: M = Fl 。
2 −1 kl 2 。
题 9-3 图
9-4 图示机构在力 F1 和 F2 作用下在图示位置平
衡,不计各构件自重和各处摩擦,OD=BD=l1,AD=l2。
求 F1/F2 的值。
解:用解析法解题。
F1 = F1(sinϑ i − cosϑ j) , F2 = F2i
点 A 和 B 的坐标及其变分为
rA = −(l1 − l2 )cosϑ i + (l1 + l2 )sinϑ j
为δϕ ,列出虚功方程 Mδϕ − Fδ rD = 0 ,
网
(a)
AB 杆和 BD 杆的虚位移瞬心为 CAB ,CBD ,存在如下关系
案 ( ) δ rA = aδϕ, δ rA cosϑ = δ rB cos 2ϑ ,δ rB cos 90� − 2ϑ = δ rD cosϑ . 答 代入式(a),解得
,
rB = −2l1 cosϑ i
δrA = (l1 − l2 )sinϑ ⋅δϑ i + (l1 + l2 )cosϑ ⋅δϑ j ,
1
δrB = 2l1 sinϑ ⋅δϑ i 。
按虚功原理,有
∑ Fi ⋅ δ ri = 0 , F1 ⋅ δ rA + F2 ⋅ δ rB = 0 ,
i
即
[ ] F1 sin2 ϑ(l1 − l2 ) − cos2 ϑ(l1 + l2 ) + 2F2l1 sinϑ = 0 ,
解:解除固定端 A 的铅垂方向的约束,并代之以
约束反力 FAy ,系统的自由度为 1。给系统任一虚位
移:AC 杆为虚平移 δr ,B 点为水平虚位移 δrB 。找
得 BC 折杆的瞬心 CCB ,如图(a)所示。列出虚功
方程:
( ) FAy − F1 ⋅ δr + F2 ⋅ δrD = 0 ,
题 9-11 图
案 点在半径为 r= l 的圆周上。如弹簧的另一端由图示的 B 点
拉至 A 点,求弹簧力所做的功。AC⊥BC,OA 为直径。
答 ( ) 解:在 B 点弹簧的变形为 λ1 = 2 −1 l ,
后 在 A 点弹簧的变形为 λ2 = l 。弹簧力所做的功为
课( ) ( ) W
=
1k 2
λ12
− λ22
=−
+
FBlδϑ
=
0
,
解得:
FB
=
⎛ ⎜
F1
⎝
+
F2 2
−
M l
⎞ ⎟ ⎠
再解除滑动铰链 C,给系统任一虚位移 δϑ ,列出
虚功方程:
−
F1lδϑ
+
M
2δϑ
+
F2
l 2
2δϑ
−
FC l 2δϑ
=
0
解得:
FC
=
1
⎛ ⎜
−
2⎝
F1
+
F2
+
2M l
⎞ ⎟ ⎠
4 题 9-10 图(b)
9-11 不计杆重,求图示结构固定端 A 处约束力的铅垂分量。
案
答 9-13 三根相同的匀质杆用铰链连接后,一端用铰链固定,一端有水平力作用如图示。 后 设杆重 G,求平衡时的角ϑ 值。
解:本题为 3 自由度系统。总势能为
课
例 9-13 图
受力图
V = −Gl(5cosϑ + cosϑ1 + cosϑ2 )
力 F 作用点的 x 坐标为
x = −2l(sinϑ + sinϑ1 + sinϑ2 ),
后 F = M cot 2ϑ . a
课 9-9 重为 G1 的杆 AB 铅垂放置,一端 A 搁在水平放置的斜面
D 上平衡。若 D 的重量为 G2,试求(1)不计所有摩擦,水平力
F 的大小;(2)水平面有摩擦,摩擦因数为 f,水平力 F 的范围。
(a)解:在系统的虚位移中,AB 杆上的 A 点作合成运动,如图示。
( ) F1
F2
=
l2
+
2l1 sinϑ l1 1 − 2sin
2
ϑ
。
本题也可以用虚速度方法计算 A 点和 B 点的虚位移关系。
9-5 图示机构中曲柄 AB 和连 BC 为匀质杆,长度相同,重量
均为 P1。滑块 C 的重量为 P2,可沿倾角为ϑ 的导轨滑动。设约
束都是理想的,求机构在铅垂面内的平衡位置。
(1)不计所有摩擦时,列出虚功方程
Fδ re − G1δ ra = 0 按速度合成定理,虚位移存在如下关系:δ ra = δ re tan β ,于是
(a)
题 9-9 图
导出 F = G1 tan β .
(2)水平面有摩擦时,当水平力 F 较小,斜面 D 有向左运动趋势,此时摩擦力方向向右,
临界平衡时-1 质量为 3 kg 的质点以 5 m/s 的速度沿水平直线向左运动。今对其施以水平向右的的 常力,此力的作用经 30 s 而停止,这时质点的速度水平向右,大小为 55 m/s。求此力的大 小及其所做的功。 解:取质点 m 为研究对象。由质点动量定理;
Ft = m(v2 − v1) : Ft = m(v2 + v1) ,
平衡方程为
5
∂V ∂ϑ
= Qϑ
其中, Qϑ
=
−F
∂x ∂ϑ
。即
5Gl sinϑ = 2Fl cosϑ ,
2F 解得: ϑ = arctan 。
5G
9-14 计算图示机构在图示平衡位置时主动力之间的关系。不计各构件自重和各处摩擦。
(a)解:图示机构的自由度为 1,选ϑ 位广义坐标,给机构任一虚位移 δϑ ,列出平衡方程
δW = GδyC1 + Mδϑ2 + GδyC2
