归纳:圆外一点求切线长的方法
切线长定理(2)全面版

2
A
P
O
B
C
再见
只要我们坚持了,就没有克服不了的困难。或许,为了将来,为了自己的发展,我们会把一件事情想得非常透彻,对自己越来越严,要求越来越高,对任何机会都不曾错过,其 目的也只不过是不让自己随时陷入逆境与失去那种面对困难不曾屈服的精神。但有时,“千里之行,始于足下。”我们更需要用时间持久的用心去做一件事情,让自己其中那小 小的浅浅的进步,来击破打破突破自己那本以为可以高枕无忧十分舒适的区域,强迫逼迫自己一刻不停的马不停蹄的一直向前走,向前看,向前进。所有的未来,都是靠脚步去 丈量。没有走,怎么知道,不可能;没有去努力,又怎么知道不能实现?幸福都是奋斗出来的。那不如,生活中、工作中,就让这“幸福都是奋斗出来的”完完全全彻彻底底的 渗入我们的心灵,着心、心平气和的去体验、去察觉这一种灵魂深处的安详,侧耳聆听这仅属于我们自己生命最原始最动人的节奏。但,这种聆听,它绝不是仅限于、执着于 “我”,而是观察一种生命状态能够扩展和超脱到什么程度,也就是那“幸福都是奋斗出来的”深处又会是如何?生命不止,奋斗不息!又或者,对于很多优秀的人来说,我们 奋斗了一辈子,拼搏了一辈子,也只是人家的起点。可是,这微不足道的进步,对于我们来说,却是幸福的,也是知足的,因为我们清清楚楚的知道自己需要的是什么,隐隐约 约的感觉到自己的人生正把握在自己手中,并且这一切还是通过我们自己勤勤恳恳努力,去积极争取的!“宝剑锋从磨砺出,梅花香自苦寒来。”当我们坦然接受这人生的终局, 或许,这无所皈依的心灵就有了归宿,这生命中觅寻处那真正的幸福、真正的清香也就从此真正的灿烂了我们的人生。一生有多少属于我们的时光?陌上的花,落了又开了,开 了又落了。无数个岁月就这样在悄无声息的时光里静静的流逝。童年的玩伴,曾经的天真,只能在梦里回味,每回梦醒时分,总是多了很多伤感。不知不觉中,走过了青春年少, 走过了人世间风风雨雨。爱过了,恨过了,哭过了,笑过了,才渐渐明白,酸甜苦辣咸才是人生的真味!生老病死是自然规律。所以,面对生活中经历的一切顺境和逆境都学会 了坦然承受,面对突然而至的灾难多了一份从容和冷静。这世上没有什么不能承受的,只要你有足够的坚强!这世上没有什么不能放下的,只要你有足够的胸襟! 一生有多少 属于我们的时光?当你为今天的落日而感伤流泪的时候,你也将错过了明日的旭日东升;当你为过去的遗憾郁郁寡欢,患得患失的时候,你也将忽略了沿途美丽的风景,淡漠了 对未来美好生活的憧憬。没有十全十美的生活,没有一帆风顺的旅途。波平浪静的人生太乏味,抑郁忧伤的人生少欢乐,风雨过后的彩虹最绚丽,历经磨砺的生命才丰盈而深刻。 见过了各样的人生:有的轻浮,有的踏实;有的喧哗,有的落寞;有的激扬,有的低回。肉体凡胎的我们之所以苦恼或喜悦,大都是缘于生活里的际遇沉浮,走不出个人心里的 藩篱。也许我们能挺得过物质生活的匮乏,却不能抵挡住内心的种种纠结。其实幸福和欢乐大多时候是对人对事对生活的一种态度,一花一世界,一树一菩提,就是一粒小小的 沙子,也有自己精彩的乾坤。如果想到我们终有一天会灰飞烟灭,一切象风一样无影亦无踪,还去争个什么?还去抱怨什么?还要烦恼什么?未曾生我谁是我?生我之时我是谁? 长大成人方是我,合眼朦胧又是谁?一生真的没有多少时光,何必要和生活过不去,和自己过不去呢。你在与不在,太阳每天都会照常升起;你愁与不愁,生活都将要继续。时
3.5 直线和圆的位置关系(3)切线长定理--

1、观察下图中哪些线段的长是切线长? 已知:AB、BC、AC切圆0于点D、E、F
点A到圆的切线长是
点B到圆的切线长是
A
点C到圆的切线长是
2、猜想:AD与
AF;BD与BE;
D
CE与CF的关系? B
为什么?
F C
E
挑战自我
• 1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切
线,A,B是切点.请你观察猜想,PA,PB有怎样的关系?
A 镇 商 业 区D
.M F
CE
B
镇工业区
如图:从⊙O外的定点P作⊙O 的两条切线,分别切⊙O于点A和B,
P
在弧AB上任取一点C,过 点C作⊙O的切线,分别交PA、 PB于点D、E。
DA
C
O
EB
试证:⑴ △PDE的周长是定值; PA+PB ⑵ ∠DOE的大小是定值. ∠AOB
2
若∠P=40°,你能说出∠DOE的度数吗?
L
B
即 AB+ CD = AD+BC
圆的外切四边形的两组对边的和相等(可做定理用)
定理:圆的外切四边形的两组对边和相等。
比较圆的内接四边形的性质:
圆的内接四边形:角的关系 圆的外切四边形:边的关系
练习、已知圆外切四边形 ABCD中,AB:BC:CD=4: 3:2,它的周长为24cm。则
AB= 8cm ,BC= 6cm ;
九年级数学(下)第三章 圆
5.直线和圆的位置关系(3)切线长定理
什么叫圆的切线?如何判定一条直线是 圆的切线?
(1)和圆有唯一公共点的直线是圆的切线; (2)和圆心的距离等于半径的直线是圆的切线; (3)经过半径的外端且垂直于这条半径的直线 是圆的切线.
第24章圆《切线长定理》课件人教版数学九年级上册

如图:PA、PB是⊙O的两条切线,A、B为切点。 B
思考:由切线长定理
O。 C
P
可以得出哪些结论?
A
A
c b
r.
r = a+b-c
2
你能推出 这个公式吗?
C
B
a
例:直角三角形的两直角边分别是5cm, 12cm 则其内切圆的半径为
__2_c_m__。
活动三:例题讲解
想一想
A D
1.如图⊙O是△ABC的内切圆。
C
E
o
60°
D
AB
课后作业: 教材 P101-102 习题24.2 ,第6、11、14题
早/起/的/鸟/儿/有/虫/吃
两切线的夹角。
思考:切线与切线长 有何区别?
B
P O
A
PA、PB分别切⊙O于A、B
PA = PB ∠OPA=∠OPB
三、教材P99 1、三角形内切圆圆心有何性质?
2、如何确定三角形内切圆的圆心? 3、画出△ABC的内切圆
三角形内心:三角形内切圆的圆心、三条角形平 分线的交点、内心到三边的距离相等。
切线长定理
教
了解切线长定理,掌握切线长定理并能用它解决
有关的证明或计算问题;
学
培养学生操作、观察、交流讨论、合作探究能力,
目
养成积极主动的良好学习习惯;
渗透数形结合思想,提高综合运用知识分析新问
标
题,解决问题的能力。
教学重难点
重点:理解切线长定理
难点:与切线长有关的证明 或计算问题,三角形的内切 圆计算问题
B O
A
1、什么叫做圆外一点到圆 的切线长? 2、切线长定理的内容是什么? 3、这个定理是怎样证明的?
九年级上册数学精品课件: 切线长定理

课堂小结
切线长 切线长 定理
三角形 内切圆
原理 作用
辅助线
有关概念 应用
图形的轴对称性
提供了证线段和 角相等的新方法
① 分别连接圆心和切点; ② 连接两切点; ③ 连接圆心和圆外一点.
内心概念及性质
运用切线长定理,将相等线段 转化集中到某条边上,从而建 立方程.
谢谢观看
证明:∵PA切☉O于点A,
O.
P
∴ OA⊥PA.
B
同理可得OB⊥PB.
∵OA=OB,OP=OP, ∴Rt△OAP≌Rt△OBP, ∴PA=PB,∠APO=∠BPO.
想一想:若连结两切点A、B,AB交
A
OP于点M.你又能得出什么新的结论? O. M
并给出证明.
P
OP垂直平分AB.
B
证明:∵PA,PB是⊙O的切线,点A,B是切点 ∴PA = PB ,∠OPA=∠OPB ∴△PAB是等腰三角形,PM为顶角的平分线 ∴OP垂直平分AB.
在Rt△OPA中,PA=5,∠POA=30°,
OP=5 3cm.
即铁环的半径为 5 3cm.
练一练
PA、PB是☉O的两条切线,A,B是切点,OA=3. (1)若AP=4,则OP=5 ; (2)若∠BPA=60 °,则OP= 6 .
A
O
P
B
二 三角形的内切圆及作法
互动探究
小明在一家木料厂上班,工作之余想对厂里的三 角形废料进行加工:裁下一块圆形用料,怎样才能 使裁下的圆的面积尽可能大呢?
BF=BD=AB-AF=13x(由cmB).D+CD=BC,可得
F E
O
(13-x)+(9-x)=14, C
D
切线长定理

沪科版《数学》九年级(下)小结升切线长定理这节课你学到了什么知识? 在解题的过程中你有什么解题的心得? 在和同学交流的过程中,你有什么体会?
马鞍山当涂县姑溪初中 袁正千
沪科版《数学》九年级(下)
教材41页9、10两题
分层作业
必做题
选做题
如图,PA、PB、QC分别与⊙O相切于点A、
B、C,CQ、BP的延长线交于点M ,当点A 在弧BC上运动时,△MQP的周长会发生变 化吗?请说明理由.
①QO与OP的位置关系,并证明;
②QO与AB的位置关系,并证明.
马鞍山当涂县姑溪初中 袁正千
沪科版《数学》九年级(下)
应用延伸
切线长定理
思考题
如图,PA、PB、QC分别与⊙O相切于点A、B、C,
当点A在弧BC上运动时,∠QOP的度数会发生变化 吗?请说明理由.
CQ
A O
几何画板文档
B
P
马鞍山当涂县姑溪初中 袁正千
安徽省2019年度“一师一优课、一课一名师”大赛
沪科版九年级下册24.4.4
马鞍山市当涂县姑溪初中 袁正千
人教版《数学》九年级(上)
马鞍山当涂县姑溪初中 袁正千
沪科版《数学》九年级(下)
情境引入
经过圆外一点的圆的切线上,这点和切点之间 的线段的长,叫切线长.
马鞍山当涂县姑溪初中 袁正千
沪科版《数学》九年级(下)
自主探索
经过圆外一点的圆的切线上,这点和切点之间 的线段的长,叫切线长.
切线长定理: 从圆外一点可以引圆的两条切线,它们的 切线长相等,这一点和圆心的连线平分两条切 线的夹角.
∵ PA、PB分别与⊙O相切于点A、B
∴ PA=PB, ∠APO=∠BPO
初中数学知识归纳圆的切线与切线定理的计算方法

初中数学知识归纳圆的切线与切线定理的计算方法圆是初中数学中非常重要的一个几何概念,而切线与切线定理也是与圆密切相关的概念和定理。
在本文中,我们将对圆的切线和切线定理进行归纳并介绍计算方法。
一、圆的切线圆的切线是指与圆只有一个公共点的直线。
切线的特点是与圆相切于切点,并且切点在切线上。
根据切线的定义,我们可以得出切线具有以下性质:1. 切线与半径垂直在圆的任意切点处,切线与通过该点的半径垂直相交。
这是切线与圆的一个重要性质,在计算切线时会用到。
2. 切线的切点切线与圆相切于切点,而切点位于切线上。
这也是切线的定义之一,切点的坐标可以通过计算得出。
二、切线定理的计算方法切线定理是描述切线与半径之间的关系的一组定理。
我们将介绍几个常用的切线定理及其计算方法。
1. 切线长定理切线长定理描述了切线和半径之间的关系。
对于与圆相切的切线来说,切线上的两个切点到圆心的距离乘积等于这两个切点分别到圆心的距离的平方。
具体计算方法如下:假设切线与圆相切于点A和点B,圆的半径为r,圆的圆心为O。
则有以下关系成立:AO × BO = AC² = BC²其中,AO和BO分别表示点A和点B到圆心O的距离,AC和BC分别表示点A和点B到圆心O的距离。
2. 外切线定理外切线定理指出,如果一条直线同时与两个相交圆的外切,那么它们的切点与连接圆心的直线构成一个等边三角形。
具体计算方法如下:对于与两个圆相切的外切线来说,它的两个切点与两个圆心之间形成的三角形是等边三角形。
设两个圆的半径分别为r₁和r₂,切点之间的距离为d,则有以下关系成立:d = r₁ + r₂其中,d表示切点之间的距离,r₁和r₂表示两个圆的半径。
三、圆的切线与切线定理的应用举例为了更好地理解切线和切线定理的计算方法,我们举例说明。
例题1:已知一个圆的半径为3 cm,点A是这个圆上的一个切点,连接点A和圆心O的线段OA与圆相交于一点B。
圆的切线长定理28页PPT文档

(2)如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,F;如
果AF=2cm,BD=7cm,CE=4cm,则BC= cm,A1C1= AB= 6cm
9cm
A
2 F
E 4
7
C
B
D
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB
于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
M I
B
D
C
与三角形各边都相切的角形的 内心
这个三角形叫做圆的外切三角形
A
D
三角形的内心就是三角形的三个内角角 F 平分线的交点
I
三角形的内心到三角形的三边的距离
相等
B
┐ E
C
归纳
三角形的内切圆可以作出一个,因为三角形 三个内角的平分线交于一点,这点即为圆心,这 点到三角形三边的距离相等,这个距离为半径, 圆心和半径都确定的圆只有一个.并且只能作出 一个,这个圆叫做三角形的内切圆(inscribed circle of triangle).
内切圆的圆心是三角形三条角平分线的交点, 叫做三角形的内心(incenter).
读一读P119 10
四边形与圆的位置关系
• 如果四边形的四条边都与一个圆相 A 切,这圆叫做四边形的内切圆.这个 四边形叫做圆的外切四边形.
B
D ●O
C
n我们可以证明圆外切四边的一个重要性质: n1.圆外切四边形两组对边的和相等.
已知:△ABC中,∠ABC=50º,∠ACB=70º,点 O是内心,求∠BOC的度数。
A
O
B
C
例2、圆的外切四边形ABCD,四边与圆的切点分别为E、F、G、H
切线长定理(用)

∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
则有
x+r=b y+r=a x+y=c
解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
解得
r=
a+b-c
2
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的 内切圆的半径 r= 或r=
拓展应用
练习5.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC的延长线于点D,试判断△AED的 形状,并说明理由.
拓展应用
练习5.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC的延长线于点D,试判断△AED的 形状,并说明理由.
Oቤተ መጻሕፍቲ ባይዱ
1
。
2
A
3
B
C
例1
已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C. (1)写出图中所有的垂直关系; (2)写出图中所有的全等三角形. (3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.
A
O
C
D
P
B
E
解:
(1) OA⊥PA , OB⊥PB , OP⊥AB
M
试一试
A
P
O
。
B
若延长PO交⊙O于点C,连结CA、CB,你又能得出什么新的结论?并给出证明.
CA=CB
证明:∵PA,PB是⊙O的切线,点A,B是切点 ∴PA = PB ∠OPA=∠OPB ∴PC=PC ∴ △PCA ≌ △PCB ∴AC=BC
切线长定理与圆内切三角形

N Q
O
A
P
B
2.如图,一圆内切于四边形ABCD,且AB=16, CD=10,则四边形的周长为( ) (A)50 (B) 52 (C)54 (D) 56
C D
A
B
携手共进,齐创精品工程
Thank You
世界触手可及
医学资料
• 仅供参考,用药方面谨遵医嘱
∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB ∠OPA=∠OPB
试用文字语言 叙述你所发现 的结论
若连结两切点A、B,AB交OP于点M.你又能得 出什么新的结论并给出证明.
内切圆的半径 r=
a+b-c
2
或r=
ab
a+b+c
例3.已知:如图,△ABC的面积为S,三边长分 别为a,b,c.求内切圆⊙O的半径r.
A
D
F
O
●
┓
B
E
C
四.课后作业
1.边长为3、4、5的三角形的内切圆的半径为__
2.边长为5、5、6的三角形的内切圆的半径为___
3.已知:△ABC的面积S=4cm,周长等于 10cm.则
AD
A
O
C
P
P
B
E B
六.课后作业
1.如图,过半径为6cm的⊙O外一点P作圆的切线PA、
PB,连结PO交⊙O于F,过F作⊙O切线分别交PA、PB
于D、E,如果PO=10cm, 求△PED的周长。
2.如图,AC为⊙O的直径,PA、PB分别切⊙O于点A、
B,OP交⊙O于点M,连结BC。
过圆外一点求圆的切线方程公式

过圆外一点求圆的切线方程公式切线方程是解析几何中的重要内容,它描述了一个圆外一点到圆的切线的位置关系。
在学习切线方程的过程中,我们需要了解圆的基本性质,学习如何求解圆的切线方程,以及掌握应用切线方程的能力。
本文将从这三个方面展开,详细介绍圆的切线方程相关知识。
一、圆的基本性质圆是平面上到一个定点距离恒定的点的轨迹。
圆的基本性质包括圆的半径、直径、圆心、弧长、扇形面积等,这些性质都对于计算切线方程很重要。
1.圆的半径和直径:圆的半径是圆心到圆上任意一点的距离,用r表示。
圆的直径是穿过圆心并且两端点都在圆上的线段,直径的长度是半径的两倍,即直径d=2r。
2.圆的圆心:圆的圆心是到圆上任意一点的距离恒定的点,用O表示。
3.圆的弧长和扇形面积:圆的弧长是圆心周围一部分圆的长度,用l表示。
圆的扇形面积是由两条半径和围成弧的线段所围成的部分,扇形面积S = (1/2)rl。
以上是圆的一些基本性质,后面的内容将涉及到这些性质的运用。
二、求解圆的切线方程在解决圆的切线方程时,首先需要确定给定点到圆的位置关系,然后使用几何和代数的方法进行求解。
1.给定圆和外点的位置关系:首先,给定一个圆和一点P,我们需要判断这个点与圆的位置关系。
如果点P到圆的圆心的距离等于圆的半径,即OP = r,那么点P在圆上;如果OP < r,点P在圆内;如果OP > r,点P在圆外。
2.求解切线方程的一般步骤:(1)确定圆心O、圆的半径r和外点P的坐标;(2)计算圆心O到外点P的距离OP;(3)根据距离OP与半径r的关系,判断P与圆的位置关系;(4)分析切线的几何性质,求解切线斜率和切点;(5)写出切线方程的一般形式。
3.以圆心为原点的情况:当圆的圆心O为原点时,圆的方程为x^2 + y^2 = r^2。
假设给定外点P的坐标为(x1, y1),根据距离公式,点到圆心的距离为OP = sqrt(x1^2 + y1^2),然后根据P与圆的位置关系进行求解。
切线长定理课件 (上课)

问题1、经过平面上一个已知点,作已知 圆的切线会有怎样的情形?
P· · O
P·
· O
P·
· O
问题2、经过圆外一点P,如何作已知⊙O的 切线?
问题2、经过圆外一点P,如何作已知⊙O的 切线? A
。
P
O
B
一、切线长定义 经过圆外一点做圆的切线,这点和切点之间的 线段的长叫做这点到圆的切线长。
A D P E ·O
C B
选做题:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
C E C
E
D
D
A · O
F
B
A
· O
B
练一练
已知:两个同心圆PA、PB是大圆的两条切线, PC、PD是小圆的两条切线,A、B、C、D为切点。 求证:AC=BD
A
O·
P
切线与切线长的区 别与联系:
B
(1)切线是一条与圆相切的直线; (2)切线长是指切线上某一点与切点间的线段的长。
若从⊙O外的一点引两条切线PA,PB,切点 分别是A、B,连结OA、OB、OP,你能发现什么结 论?并证明你所发现的结论。
B
PA = PB
∠OPA=∠OPB
。
P A
O
已知PA、PB是⊙O的两条切线,A、B为切点,
归纳:在解决有
关圆的切线长的问 题时,往往需要我 们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点 (3)连结圆心和圆外一点
A
。
O
P B
例2.如图所示PA、PB分别切圆O于A、B, 并与圆O的切线分别相交于C、D,• 已知 PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD的度数
2020年中考数学提优专题:《圆:切线长定理》(含答案)

《圆:切线长定理》知识梳理:(1)圆的切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.(2)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.(3)注意:切线和切线长是两个不同的概念,切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.(4)切线长定理包含着一些隐含结论:①垂直关系三处;②全等关系三对;③弧相等关系两对,在一些证明求解问题中经常用到.综合练习:一.选择题1.如图,已知AB为⊙O的直径,CB切⊙O于B,CD切⊙O于D,交BA的延长线于E,若AB=3,ED=2,则BC的长为()A.2 B.3 C.3.5 D.42.既有外接圆,又有内切圆的平行四边形是()A.矩形B.菱形C.正方形D.矩形或菱形3.如图所示,已知PA、PB切⊙O于A、B两点,C是上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=()A.56°B.60°C.62°D.不可求4.已知四边形ABCD是梯形,且AD∥BC,AD<BC,又⊙O与AB、AD、CD分别相切于点E、F、G,圆心O在BC上,则AB+CD与BC的大小关系是()A.大于B.等于C.小于D.不能确定5.如图,在平行四边形ABCD中,AB=15,过点D作一圆与AB、BC分别相切于G、H,与边AD、CD相交于点E、F,且5AE=4DE,8CF=DF,则BH等于()A.5 B.6 C.7 D.86.如图,PA,PB分别切⊙O于点A和点B,C是上任一点,过C的切线分别交PA,PB于D,E.若⊙O的半径为6,PO=10,则△PDE的周长是()A.16 B.14 C.12 D.107.如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为()A.B.C.D.8.PA、PB、CD分别切⊙O于A、B、E,∠APB=54°,则∠COD=()A.36°B.63°C.126°D.46°9.如图,P A、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为()A.35°B.45°C.60°D.70°10.已知:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O 于点E,AE的延长线交BC于点F,连接AD、BD.以下结论:①AD∥OC;②点E为△CDB的内心;③FC=FE;④CE•FB=AB•CF.其中正确的只有()A.①②B.②③④C.①③④D.①②④二.填空题11.如图,PA,PB分别为⊙O的切线,切点分别为A、B,PA=6,在劣弧AB上任取一点C,过C作⊙O的切线,分别交PA,PB于D,E,则△PDE的周长是.12.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE=.13.如图,四边形ABCD是正方形,以BC边为直径在正方形内作半圆O,再过顶点A作半圆O的切线(切点为F)交CD边于E,则sin∠DAE=.14.如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,AB=6,PA=5.则⊙O的半径.15.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为.16.如图,PA、PB、EF分别切⊙O于A、B、D,若PA=10cm,则△PEF的周长是cm,若∠P=35°,则∠AOB=(度),∠EOF=(度).17.如图,正方形ABCD的边长为4,以AB为直径向正方形内作半圆,CE与DF是半圆的切线,M,N为切点,CE,DF交于点P.则AE=,△PMN的面积是.三.解答题18.如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.(1)求△PDE的周长;(2)求∠DOE的度数.19.如图,P是半径为cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB =3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.(1)求△PDE的周长;(2)若DE=cm,求图中阴影部分的面积.20.已知:AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于E,⊙O的半径为,AD=2.①求BC的长;②延长AE交BC的延长线于G点,求EG的长.参考答案一.选择题1.解:由切割线定理,得DE2=EA•EB,∵AB=3,ED=2,∴4=AE(AE+3),解得AE=1或﹣4(舍去),∵CB切⊙O于B,∴∠B=90°,∴根据勾股定理得,BC2+42=(BC+2)2,∴BC=3.故选:B.2.解:A、矩形只有外接圆,没有内切圆,故本选项不符合题意;B、菱形只有内切圆,没有外接圆,故本选项不符合题意;C、正方形既有外接圆,也有内切圆,故本选项符合题意;D、矩形只有外接圆,没有内切圆,菱形只有内切圆,没有外接圆,故本选项不符合题意;故选:C.3.解:∠PMN+∠PNM=180°﹣∠P=124°,∠AMN+∠BNM=360°﹣124°=236°,∵MA、MC是⊙O的切线,∴∠AMO=∠CMO,∵NB、NC是⊙O的切线,∴∠BNO=∠CNO,∴∠CMO+∠CNO=(∠AMN+∠BNM)=118°,∴∠MON=180°﹣118°=62°,故选:C.4.解:连接OF,OA,OE,作AH⊥BC于H.∵AD是切线,∴OF⊥AD,易证四边形AHOF是矩形,∴AH=OF=OE,∵S△AOB=•OB•AH=•AB•OE,∴OB=AB,同理可证:CD=CO,∴AB+CD=BC,故选:B.5.解:由8CF=DF,得CF=15×=,则CH2=CF×DC,故CH=5,设BC=x,则BH=x﹣5=BG,故AG=20﹣x,又∵5AE=4DE,∴DE=x,AE=x,则AG2=AE×AD,则(20﹣x)2=x2,解得:x=12,故BH=BC﹣CH=7.故选:C.6.解:连接OA,∵PA切⊙O于A,∴∠OAP=90°,∴在Rt△OAP中,OP=10,OA=6,由勾股定理得:PA=8,∵PA,PB分别切⊙O于点A和点B,DE切⊙O于C,∴PA=PB=8,DA=DC,EB=EC,∴△PDE的周长是:PD+DE+PE=PD+DC+CE+PE=PD+DA+EB+PE=PA+PB=8+8=16,故选:A.7.解:连接OA,OB.则OA⊥AP,OB⊥PB,∴在四边形APBO中,∠P+∠AOB=180°,又∵∠AOB=2∠ACB,∠ABC=2∠P,设∠ACB=180°﹣2∠ABC=180°﹣4∠P,∴∠AOB=360°﹣8∠P,∴∠P+∠AOB=∠P+(360°﹣8∠P)=180°,∴∠P=,∴∠ACB=180﹣4×=,∴∠ACB的弧度数为.故选:A.8.解:如图,连接OA,OB,OE,∵PA、PB、CD分别切⊙O于A、B、E,∴∠AOC=∠EOC,同理∠BOD=∠DOE,∴∠COD=∠COE+∠DOE=∠AOB,∵∠APB=54°,∴∠AOB=126°,∴∠COD=63°.故选:B.9.解:根据切线的性质定理得∠PAC=90°,∴∠PAB=90°﹣∠BAC=90°﹣35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.故选:D.10.解:连接OD,DE,EB,CD与BC是⊙O的切线,∠ODC=∠OBC=90°,OD=OB,∵OC=OC∴Rt△CDO≌Rt△CBO,∴∠COD=∠COB,∴∠COB=∠DAB=∠DOB,∴AD∥OC,故①正确;∵CD是⊙O的切线,∴∠CDE=∠DOE,而∠BDE=∠BOE,∴∠CDE=∠BDE,即DE是∠CDB的角平分线,同理可证得BE是∠CBD的平分线,因此E为△CBD的内心,故②正确;若FC=FE,则应有∠OCB=∠CEF,应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA,∴弧AD=弧BE,而弧AD与弧BE不一定相等,故③不正确;设AE、BD交于点G,由②可知∠EBG=∠EBF,又∵BE⊥GF,∴FB=GB,由切线的性质可得,点E是弧BD的中点,∠DCE=∠BCE,又∵∠MDA=∠DCE(平行线的性质)=∠DBA,∴∠BCE=∠GBA,而∠CFE=∠ABF+∠FAB,∠DGE=∠ADB+∠DAG,∠DAG=∠FAB(等弧所对的圆周角相等),∴∠AGB=∠CFE,∴△ABG∽△CEF,∴CE•GB=AB•CF,又∵FB=GB,∴CE•FB=AB•CF故④正确.因此正确的结论有:①②④.故选:D.二.填空题(共7小题)11.解:∵PA,PB分别为⊙O的切线,∴PA=PB,同理,DA=DC,EB=EC.∴△PDE的周长=PD+DE+PE=PD+DC+CE+PE=PD+AD+PE+BE=PA+PB=2PA=2×6=12.故答案是:12.12.解:∵CD、CE分别与⊙O相切于点D、E,∴CD=CE,∵∠DAC=∠DCA,∴AD=CD,∴AD=CE,∵AD=2,∴CE=2.故答案为:2.13.解:设正方形ABCD的边长为4a,EC=x,∵AF为半圆O的切线,∴AF=AB=4a,EC=EF=x,在Rt△ADE中,DE=4a﹣x,AE=4a+x,∴AE2=AD2+DE2,即(4a+x)2=(4a)2+(4a﹣x)2,解得x=a,∴AE=5a,DE=3a,在Rt△ADE中,sin∠DAE===.故答案为.14.解:连接OP,OB,∵AP为⊙O切线,PB为⊙O切线,∴PA=PB,∵∠APO=∠BPO,PG=PG,∴△APG≌△BPG,∴∠PGA=90°,∵△APO为直角三角形,∠APG=∠APG,∴△PGA∽△PAO,根据垂径定理,得到AG=GB,在R t△PAG中,PG==4,∵△PGA∽△AGO,∴=,∴=,∴AO=.故答案为:.15.解:∵OA=OB,∴∠OAB=∠OBA,∵∠BAC=35°,∴∠AOB=110°,∵PA,PB分别是⊙O的切线,∴∠PAO=∠PBO=90°,∵∠P+∠AOB+∠PAO+∠PBO=360°,∴∠P=70°.故答案为:70°.16.解:∵PA、PB、EF分别切⊙O于A、B、D,∴PA=PB=10cm,ED=EA,FD=DB,∴PE+EF+PF=PE+ED+PF+FD=PA+PB=20(cm);∵PA、PB为⊙O的切线,∴∠PAO=∠PBO=90°,而∠P=35°,∴∠AOB=360°﹣90°﹣90°﹣35°=145°;连OD,如图,∴∠ODE=∠ODF=90°,易证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠AOB=72.5°,∠EOF=72.5°.故答案为20;145;72.5.17.解:(1)由切线长定理知:AE=EM,CM=CB;∵CD=CB,∴CM=CD=4.设AE=EM=x,则DE=4﹣x,CE=CM+EM=4+x;在Rt△CDE中,由勾股定理得:(4﹣x)2+42=(4+x)2,解得x=1;故AE=1.(2)同(1)可求得BF=FN=1,则DF=CE=5,DE=CF=3;则可证得Rt△CDE≌Rt△DCF;∴∠DCP=∠CDP,即DP=CP,∴PM=PN;故△DPC∽△NPM,且MN∥CD;设MN所在直线与AD、BC的交点为R、T,则MR⊥AD,NT⊥BC;在Rt△MRE中,ME=1,则ER=ME•cos∠DEC=,MR=ME•sin∠DEC=;过P作PG⊥MN于G,则RG=GT=2,MG=2﹣RM=;易知RE∥PG,则△REM∽△GPM,∴=()2=;∵S△REM=MR•RE=××=,∴S△PMG=×=,故S△PMN=2S△PMG=.三.解答题(共3小题)18.解:(1)∵PA、PB、DE都为⊙O的切线,∴DA=DF,EB=EF,PA=PB=6,∴DE=DA+EB,∴PE+PD+DE=PA+PB=12,即△PDE的周长为12;(2)连接OF,∵PA、PB、DE分别切⊙O于A、B、F三点,∴OB⊥PB,OA⊥PA,∠BOE=∠FOE=∠BOF,∠FOD=∠AOD=∠AOF,∵∠APB=52°,∴∠AOB=360°﹣90°﹣90°﹣52°=128°,∴∠DOE=∠FOE+∠FOD=(∠BOF+∠AOF)=∠BOA=64°.19.解:(1)∵PA、PB、DE是⊙O的切线,∴PA=PB=3cm,CE=BE,AD=DC,∴△PDE的周长=PE+DE+PD=PE+CE+CD+PD=PE+BE+AD+PD=PA+PB=3cm+3cm=6cm;(2)连接OB、OA、OE,OD,如图,∵PA、PB、OC是⊙O的切线,∴OB⊥PB,OA⊥PA,OC⊥DE,∴∠OBP=∠OPA=90°,∵∠APB=60°,∴∠BOA=120°,∵BE=CE,DC=DA,∴S△OCE=S△OBE,S△OCD=S△ODA,∴S五边AOBED=2S△ODE=2×××=4,∴图中阴影部分的面积=S五边AOBED﹣S扇形AOB=4﹣=(4﹣π)cm2.20.解:①过点D作DF⊥BC于点F,∵AB为⊙O的直径,∠A=∠B=90°,∴四边形ABFD是矩形,AD与BC是⊙O的切线,∴DF=AB=2,BF=AD=2,∵DE与⊙O相切,∴DE=AD=2,CE=BC,设BC=x,则CF=BC﹣BF=x﹣2,DC=DE+CE=2+x,在Rt△DCF中,DC2=CF2+DF2,即(2+x)2=(x﹣2)2+(2)2,解得:x=,即BC=;②∵AB为⊙O的直径,∠A=∠B=90°,∴AD∥BC,∴△ADE∽△GCE,∴AD:CG=DE:CE,AE:EG=AD:CG,∵AD=DE=2,∴CG=CE=BC=,∴BG=BC+CG=5,∴AE:EG=4:5,在Rt△ABG中,AG==3,∴EG=AG=.。
九年级数学切线长定理与三角形内切圆知识点讲解及练习

九年级数学切线长定理与三角形内切圆知识点讲解及练习【知识点精讲】(一)知识要点----切线长定理1.切线长:经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长。
如图,PA,PB即为P点到圆的切线长。
2.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
(二)知识要点----三角形内切圆1.三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心。
练习1.已知:如图,AB 为⊙O 的直径,PA 、PC 是⊙O 的切线,A 、C 为切点,∠BAC =30. (1)求∠P 的大小;(2)若AB =6,求PA 的长.【总结】切线长定理包括线段相等和角相等两个结论,利用切线长定理可以证明线段相等、角相等、弧相等以及垂直关系等。
2.如图,已知AB 是⊙O 的直径,点P 在BA 的延长线上,PD 切⊙O 于点D ,过点B 作BE ⊥PD ,交PD 的延长线于点C ,连接AD 并延长,交BE 于点E .(1)求证:AB=BE ;(2)连结OC ,如果PD=∠ABC=,求OC 的长.603.如图,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于D,过C 作CG∥AE交BA的延长线于点G.(1)求证:CG是⊙O的切线;4.如图,在平面直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,∠OAB=90°.⊙P1是△OAB的内切圆,且P1的坐标为(3,1).(1)OA的长为__________,OB的长为__________;(2)点C在OA的延长线上,CD∥AB交x轴于点D.将⊙P1沿水平方向向右平移2个单位得到⊙P2,将⊙P2沿水平方向向右平移2个单位得到⊙P3,按照同样的方法继续操作,依次得到⊙P4,…⊙Pn.若⊙P1,⊙P2,…⊙Pn均在△OCD的内部,且⊙Pn恰好与CD相切,则此时OD的长为__________.(用含n的式子表示)【总结】三角形内切圆的圆心是三角形三条角平分线的交点,它到三角形三条边的距离都相等。
精选掌握求两圆内外公切线长的方法

9.若⊙O1与⊙O2外离,A、B是一条内公切线与两条外公切线的交点,则 AB的长( )
A.等于一条外公切的长。
B.等于内公切线长与外公切线长的平均数。
C.等于内公切线长与外公切线长的比例中项。
D.当且仅当两圆为等圆时等于一条外公切线的长。
10.已知:如图,两圆外切于P,直线MN与两圆分别切于M、N,过P作一直 线交两圆于A、B,
如图,作O1E∥AB交O2B的延长线于E,
两圆外离时,有两条内公切线、由圆的对称性可知这两条内公切线的长相等,且两公切线的交点在连心线上,连心线平分两内公切线的夹角。如图(1)所示:内公切线 AB =CD,AB与CD的交点P在连心线O1O2上,∠APO1=∠CPO2 .
E
构成Rt△O1EO2,
A.一条外公切线长的二倍。
B.两条内公切线长的和。
C.一条外公切线长和一条内公切线长的和。
D.两条内公切线长和一条外公切长的和的一半。
9.设相离的半径分别为4cm和2cm,且它们的两条内公切线互相垂直,则内公切线的长为_______cm。
10.若两外切,内公切线和一条外公切线相交成60°的角,则小圆半径与大圆半径之比为_______ 。
解:
∴O1C=AB=6cm,O1A=BC
∴O2C=O2B+BC=O2B+O1A=8cm
分析:
例3 如图5,已知⊙O1和⊙O2的内公切线CD和外公切线AB分别与连心线O1O2相交于P、Q,
直接证明这个比例式较困难,
注意CD为内公切线,
连O1C、O2D可得O1C∥O2D,
连O1B、O2A可得O1B∥O2A,
1.两圆半径分别为8和5,若两圆共有三条公切线,那么圆心距d为( )
A.d=3 B.3<d<13 C.d=13 D.d>13
7 切线长定理

A P B
B
若从⊙O外的一点引两条切 线PA,PB,切点分别是点 A、点B,连接OA,OB, OP,你能发现什么结论? 证明你所发现的结论. PA = PB ∠OPA=∠OPB
。
O
P A
证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB, 即∠OAP=∠OBP=90°. ∵ OA=OB,OP=OP, ∴ Rt△AOP≌Rt△BOP(HL). ∴ PA = PB,∠OPA=∠OPB.
¤ 切线长定理
过圆外一点所画的圆的两条
A
切线,它们的切线长相等.
O
P
¤ 几何语言
∵PA,PB分别切⊙ O于A,B
∴PA = PB,∠OPA=∠OPB.
B
★切线长定理为证明线段相等、角相等提供了新的方法.
问题: PA,PB是⊙ O的两条切线,A,B为切点,直线OP交
⊙ O于点D,E,交AB于C. (1)写出图中所有的垂直关系: OA⊥PA,OB ⊥PB,AB ⊥OP. (2)写出图中与∠OAC相等的角: ∠OAC=∠OBC=∠APC=∠BPC. (3)写出图中所有的全等三角形: △AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP. (4)写出图中所有的等腰三角形: △ABP , AOB. A
如下左图,借助三角板,我们可以画出PA是⊙O的切线.
2.这样的切线能画出几条? 3.如果∠P=50°,求∠AOB的度数.
A
O
130°
B
P
50°
一 切线长的定义
讲授新课
A O. B
线段PA,PB是点P到 ⊙O的切线长.
¤ 切线长的定义
过圆外一点画圆的切线,这 点和切点之间的线段长叫作
5.切线长定理
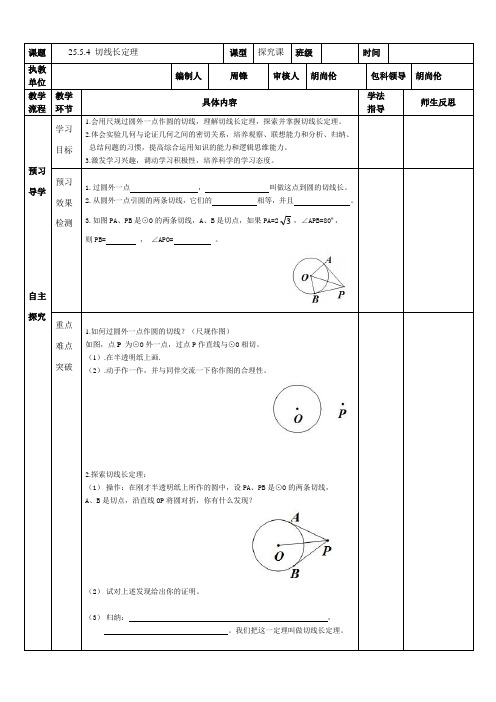
(1).在半透明纸上画.
(2).动手作一作,并与同伴交流一下你作图的合理性。
2.探索切线长定理:
(1)操作:在刚才半透明纸上所作的圆中,设PA、PB是⊙O的两条切线,
A、B是切点,沿直线OP将圆对折,你有么发现?(2)试对上述发现给出你的证明。
(3)归纳:,
第(1)题第(2)题第(3)题
总结评价
课堂
总结
本节课我们收获了哪些知识?你对自己的表现感觉怎样?以后还需要在哪些方面改进?
学生姓名:
_____________
自评得分:
_____________
课题
25.5.4切线长定理
课型
探究课
班级
时间
执教单位
编制人
周锋
审核人
胡尚伦
包科领导
胡尚伦
教学
流程
教学
环节
具体内容
学法
指导
师生反思
预习导学
自主探究
学习
目标
1.会用尺规过圆外一点作圆的切线,理解切线长定理,探索并掌握切线长定理。
2.体会实验几何与论证几何之间的密切关系,培养观察、联想能力和分析、归纳、
总结问题的习惯,提高综合运用知识的能力和逻辑思维能力。
3.激发学习兴趣,调动学习积极性,培养科学的学习态度。
预习
效果
检测
1.过圆外一点,叫做这点到圆的切线长。
2.从圆外一点引圆的两条切线,它们的相等,并且。
3.如图PA、PB是⊙O的两条切线,A、B是切点,如果PA=2 ,∠APB=80º,
则PB=,∠APO=。
重点
难点
突破
1.如何过圆外一点作圆的切线?(尺规作图)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一步:将圆的方程配成点斜式,求得圆心坐标与半径,并判断
点()00,y x M 与圆的位置关系:
若点
M 在圆上,则过点M 作圆的切线只存在一条,此时利用过
圆上一点求切线方程的公式即可求得切线方程。
若点M 在圆外,则过点M 作圆的切线一定能够作出两条。
第二步:假设点M 在圆外,并假设过点M 作圆的切线的斜率存
在,设其为k ,利用直线的点斜式方程可得方程为()00x x k y y -=-。
第三步:由于圆心C 到这条直线的距离等于半径,那根据点到直
线的距离公式可将斜率k 求出来:
若求得的k 值有两个,则将其代入该直线的方程即可求得两条切
线的方程;
若求得的k 值只有一个,那么另一条切线的斜率一定不存在,这
时,可通过画图观察得到另一条切线的方程。
