模糊数学结课论文
本科数学专业课程中思政元素的实践探索——以“模糊数学”为例

本科数学专业课程中思政元素的实践探索——以“模糊数学”为例近几年,在国家政策的指导下,课程思政建设正在全国各个高校如火如荼地展开,其效果也在高等教育中凸显出来[1]。
课程思政作为立德树人根本任务的重要举措,已经成为各类专业课程与思政元素有机结合的完美体现。
要将思政元素和专业知识双重目标分解落实,明确实施途径和方式,才能切实达到育人、育才统一的建设效果。
数学专业课程以其严谨的逻辑思维要求和独特的课程体系,使得与思政元素结合的切入点尤其关键。
如何将晦涩难懂的数学知识与鲜活高尚的思政元素融为一体,是很多大学数学教师潜心摸索的问题[2]。
笔者以数学专业课程——“模糊数学”的讲授过程为例,谈几点自己的看法。
一、课程思政引入数学类专业课中存在的问题(一)重视程度不足教育部颁布的《国家中长期教育改革和发展规划(2010-2020年)》中指出,高校教师的80%是专业教师,课程的80%是专业课程,学生学习时间的80%用于专业学习,专业课程教学是课程思政的最主要的依托。
但是目前高校中仍有少数专业教师在思想政治教育的认识上存在误区,导致对思政元素引入专业课堂的积极性不高、针对性不强。
同时,也有部分教师对教学中思政元素的引入一带而过,敷衍了事,这样的教学既没有达到思想政治育人的目的,也降低了专业知识传授的效果。
(二)课程体系不完善高校专业课程的培养目标通常强调提升学生的专业技能,在教学设计环节弱化了思想政治教育设计的周密性和科学性;在开展教学过程中,思想政治教育与专业教育出现了较大的脱节。
特别是数学类专业课程,专业知识中思政元素的挖掘不够全面,与专业课程结合比较片面,没有将专业教育与思想政治教育紧密融合,形成协同效应。
由于高校数学类专业课程具有较为完备的课程标准,尤其在基本概念、理论推导、计算过程等方面都已经形成了完善的教学体系和考核标准,因此,教师在教学过程中,往往只在标准框架下进行基本规范的教学活动,更加注重基本知识的讲解和逻辑思维的培养,对课程思政考虑不足,更没有在教学设计和教学对策中更好地融入思政元素,这不利于教学质量更好的提升,在一定程度上也阻碍了课程思政的顺利进行。
模糊数学结课论文

模糊数学结课论文模糊集合所含的元素是模糊的,它只能由其隶属函数来表示。
然而,在研究和处理实际问题时我们总希望对模糊概念有个明确的认识和判定,即给定一个标准之后希望能知道某个元素,即模糊集合的明确归属问题。
为此我们需要知道模糊集合与经典集合之间的相互转化关系。
本论文简单介绍表现定理及其应用。
截集概念在模糊集合与经典集合的互相转化中起着重要的桥梁作用,在解决实际问题中也经常用到。
定义1 设()A X ∈F,对任意[]0,1λ∈,记()(){}ddA A x A x λλλ==≥,称A λ为A 的λ-截集,λ称为置信水平。
又记()(){}d dA A x A x λλλ••==>,称A λ•为A 的λ-强截集。
用经典子集的集合套来表现模糊集,进一步阐明模糊集是由经典集扩充而成的。
定义2 令[]()():0,1,H X H λλ→P满足:()()1212H H λλλλ<⇒⊇,称H 为X 上一个集合套,全体集合套组成的集合记作()X U .定义3 在()X U 中规定运算并,交,补如下:1212121212121):()()()(),2):()()()(),3):()()(),4):()()(),5):()(1).ddddH H H H x H x H x H H H H x H x H x H H H H H H H H H γγγγγγγγγγγγλλλλλλ∈∈∈∈∈∈=====-ΓΓΓΓΓΓ定理1 (表现定理Ⅰ)设H 为X 上的任何一个集合套,则[0,1]()A H λλλ∈=是X 上的一个模糊集,且[0,1]∀∈λ,有(1)();A H αλα•>=λ (2)().A H λαλα<=证明 因[0,1]λ∀∈,()()H X λ∈P ,而()()H X λλ∈F ,故()[]()0,1H X λλλ∈∈F,记[0,1]()A H λλλ∈=.根据分解定理欲证(1),(2),只须证[0,1],()A H A λλλλ•∀∈⊆⊆即可。
模糊数学论文

模糊数学学校开设了模糊中数学,本着对数学的钟情和同学的介绍,我修了这门课程。
现在课已经结束了,但我对这门课有了特殊的感觉,让我对数学更加热爱了,不知是老师的原因,还是因为所设的课程,或者说是共同的原因吧。
在所学的知识中,我不仅只学了这门课程,就想许多人所说的,数学跟很多课程是有联系的,这次我深刻的体会到了,现在老师讲模糊集合的场景好像是昨天发生的,是老师讲的精彩,还是在知识对我以后的所学的专业有用了,想在我都不知是那个缘故,下面是我体会到模糊中的数学在我所学专业中的应用。
“民以食为天”,食品安全人民健康的根本保障。
当每次3.15来临,揭发很多关于食品的事件,如“三鹿事件”,“地沟油”等危害人们健康的事件的曝光,人们开始越来越关心食品安全,越来越重视食品的检测。
也是我专业所关心的事实之一。
传统的检测方法只是提取食品的各项指标,然后与标准指标进行比对,如果有超过一定数目的指标超标,则认为这类食品时不合格的。
诚然,因为传统方法的简单易操作,它曾经带给人们很多便利。
但是随着食品检测的不断发展以及人们对食品安全的重视程度的提高,传统方法的弊端不断的显现出来。
首先在传统方法中没有区分主次因素,对所有指标都一视同仁,这就直接导致了食品检测中的准确度降低。
其次,因为传统检测方法的最终结果只有合格与不合格两种等级,这也就引起了分类结果的不精确。
因为在合格里面也有质量好与质量不很好之分,把它们归于一类不但会对消费者的利益产生危害,也直接影响了生产者的积极性。
最后,因为食品检测的指标之间是相互影响的,传统的检测方法可能会多提取了指标。
模糊数学的诞生,得益于用机器去模拟人脑的科学——人工智能。
当用计算机去模拟人脑时,经典数学在很大程度上显得无能为力。
现代电子计算机对模糊性语言和信息的处理能力甚至不及一个婴儿。
例如,一个二、三岁的小孩能在一堆苹果中迅速、准确地挑出最大的那个,而不需作任何度量。
这一点要计算机做,却非常困难。
模糊数学理论论文

模糊综合评价法评价某河流水质摘要:根据水环境发展现状和发展情况,采用模糊数学综合评价法根据有关规定和实测数据建立评价因素集、评语集,确定权向量,组合因素评价矩阵,确定隶属度,对河流的水质情况进行客观的评价,取隶属程度最大值所对应的等级作为河流的水质等级。
关键词:模糊综合评价 因素评价矩阵 隶属度本题目只是采用了部分水污染因子来代表整体对河水进行评价。
待测河流取样所得数据SS含量79,DO7.04,CDOMN4.92,N NH 30.51,单位均为L mg /。
试确定该河流的水质情况属于哪一个等级?根据有关规定,水质分级标准如下表所示:水质分级标准表(mg/L )1、 建立评价对象因素数集),,,,,(54321u u u u u U =,水质等级评价集合)(,,,,,v V 54321v v v v =,通过比较实测数据与等级划分标准,只取前四个等级来判别,得到的矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 1.5 1 0.5 0.158 6 4 23 5 6 7.5350 250 15050A 评价对象T B )51.0,92.4,04.7,79(=2、对数据进行标准化。
这里采用单个只占总体的比值来进行标准化,评价集合A 进行标准化:∑==41ij c j ijijaa 得到标准化矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=4761905.03174603.01587302.0047619.04.03.02.01.04.024.02.01600.04375.03125.01875.00.0625C 按照这种方法对B 进行标准化得T D )1619.0,246.0,1705.0,09875.0(= 3、贴近度的计算。
矩阵D 与矩阵C 某列的贴近度显示了该样本与某种等级的接近程度,程度高的可近似归为该等级。
这里采用相对距离贴近度:),4,3,2,1,4,3,2,1()min()max(1==---=j i c c d c r ij ij iij ij 由此可以得到贴近度矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0.2666556 0.6370259 0.9926037 0.7333440.4866667 0.82 0.8466667 0.5133330.04375 0.7104167 0.8770833 0.956250.0966667 0.43 0.7633333 0.903333R 4、权向量的计算。
模糊数学论文

模糊数学论文模糊数学理论在证券投资分析中的应用一、引言本文主要针对我国的A股市场,由于单个股票价格受多种因素影响,波动较大,易受人为操控,而股票指数相对更客观,因此,本人利用模糊数学理论中综合评判方法,将基本面分析、技术面分析和经典理论分析三者结合起来对股票指数未来走向进行分析,为证券投资者买卖决策提供一种新思路。
二、模糊数学理论模糊数学是一门新兴学科,是研究和处理模糊性现象的数学理论和方法,它不是让数学变成模糊,而是让数学研究进入到模糊现象这样的领域。
1965年美国控制论学者扎德(L.A.Zadeh)发表论文《模糊集合》,标志着这门新学科的诞生。
该学科发展的主流是在它的应用方面,由于模糊性概念已经找到了模糊集的描述方式,人们运用概念进行判断、评价、推理、决策和控制的过程也可以用模糊性数学的方法来描述。
例如模糊聚类分析、模糊综合评判、模糊决策、模糊控制等。
这些方法构成了一种模糊性系统理论,它已经广泛应用于计算机科学、人工智能、信息处理、控制工程、经济与管理科学、气象预报等领域。
三、模糊综合评判目前证券投资分析方法很多,大体可分为基本面分析和技术面分析二种。
其中,基本面分析指的是根据证券基本面的情况(包括:公司财务状况、市场消息面、宏观政策等等)进行分析,从而判断证券未来中长期市场价格的总体发展方向。
技术面分析是依据市场价格以前的走势,借助指标、成交量等数据,推测证券短期内的涨跌和买入点卖出点。
为进一步提高分析结论的准确率,本人再结合K线理论、道氏理论、波浪理论、江恩理论、股市心理博弈等经典理论分析方法,将以上三大类分析方法进行综合,细化基本面分析、技术面分析和经典理论分析的各个指标要素,根据要素之间关系的紧密程度对每个要素设定权重系数,能后借助模糊数学理论中综合评判方法进行分析得出结论,其数学模型如下: (一)模糊综合评判特点。
根据确定标准:对事物按单因素进行评价,称为“单一评判”;对事物按多因素进行评价,称为“综合评判”。
《模糊集合理论及其应用》论文

《模糊集合理论及其应用》论文
《模糊集合理论及其应用》
模糊集合(Fuzzy Set,FS)是属于模糊数学(Fuzzy Mathematics)领域的一门研究,它以广义的语言和表述形式描述客观事物。
该理论可以处理模糊不确定性和词语本身的模糊性,为表达模糊语义提供新的方法。
模糊集合理论最早由美国著名数学家Zadeh提出,1967年提出了模糊集合的概念,认为“实数集的元素可以不是绝对明确的,而可能有不同的模糊性,即模糊的真实值”。
从而为模糊0和1的综合计算提供了基础。
模糊集合理论应用于不确定领域,被用来处理决策分析,尤其是处理决策者所面临的大量模糊信息。
随着深度学习技术的发展,模糊集合理论已被广泛用于知识挖掘和分类算法,帮助企业把握客户的行为趋势。
此外,模糊集合理论也可以应用于智能控制,医疗诊断,信息服务,市场营销,证券投资等多种领域,为智能决策提供强有力的支持。
模糊集合理论的发展和应用,将推动未来智能决策、智能管理和智能控制,为构建智能社会做出更大贡献。
总之,模糊集合理论是一种可以用来处理不确定领域的理论,它为解决模糊不确定领域提供了许多有用的思维方法和工具,已经在许多领域如决策分析、知识挖掘和智能控制等中得到了
广泛的应用,并且在未来的智能决策、智能管理和智能控制方面发挥着重要作用。
模糊数学在毕业论文评定中的应用 毕业论文

模糊数学在毕业论文评定中的应用毕业论文摘要:随着现代科学技术的不断发展,模糊数学理论在各个领域中都得到了广泛的应用。
模糊数学理论的特点是,它可以处理不确定性和模糊性的信息,有效地解决问题。
本文从模糊集合、模糊关系、模糊逻辑等多个方面分析了在毕业论文评定中的应用,其中涉及到的所有要素都是不确定的或模糊的。
通过对毕业论文的评定,发现模糊数学能够很好地解决评定过程中存在的不确定性,提高了评定的准确性和可靠性。
关键词:模糊数学;毕业论文;评定;不确定性;模糊性一、背景介绍毕业论文是高等教育的重要组成部分。
它是指在本科或研究生阶段为了完成学业而写的一篇较为完整的学术性论文。
毕业论文的评定是学院或学校授予学位的重要环节之一。
传统的评定方法通常是根据规定的评价指标进行量化评定,最终将结果汇总得出评价结果。
然而,在实际评定过程中,评价指标的权重往往并不确定,评价标准也可能存在模糊性。
而模糊数学理论具有处理不确定性和模糊性信息的能力,因此可以很好地应用于毕业论文评定中。
二、模糊数学理论简介2.1 模糊集合模糊集合是指那些元素不必完全满足集合定义中的所有特征,而是只需满足一个程度上的特征即可被包含在集合中的一类集合。
模糊集合可以通过隶属函数来描述,该函数用于描述元素与集合之间的关系。
2.2 模糊关系模糊关系是一种反映元素之间关系的数学对象。
它与传统的关系不同之处在于,它允许元素之间的关系不是非黑即白的,而是一种程度上的关系。
2.3 模糊逻辑模糊逻辑是一种能够处理模糊性信息的逻辑。
与传统的逻辑不同,模糊逻辑可以允许命题的真假度不是只有两种取值(真或假),而是在0到1这个区间上取值。
因此,对于那些具有一定程度的不确定性或模糊性的情况,模糊数学可以提供更为准确有效的处理方法。
三、模糊数学在毕业论文评定中的应用在毕业论文评定中,模糊数学可以应用于多个方面,其中包括:3.1 评价指标权重的确定评价指标权重的确定是毕业论文评定中的一个关键步骤。
模糊数学应用论文(2)

模糊数学应用论文(2)推荐文章计算机应用专业实习总结_计算机毕业实践工作总结报告热度:灾区送温暖慰问信热度:会计电算化应用论文相关范文热度:会计电算化结课论文热度:计算机应用的论文范文热度:模糊数学应用论文篇二模糊数学,乍听似乎不可思议。
因为数学的特点是精确,它怎么能同“模糊”连在一起呢?其实,模糊数学并非是“模糊的数学”,它真实的含义是:用数学方法来研究、处理模糊的事物。
这是1965年诞生的一门新学科,十几年来得到了迅速的发展。
从《伊索寓言》谈起在《伊索寓言》中有这样一则故事。
一次,伊索的主人酒醉后狂言,跟人打赌,发誓要喝干大海,并以他的全部财产和奴隶作赌注。
次日醒来后,他懊悔莫及。
但这一消息已轰动全城,人们早在海边等着他呢。
于是主人不得不苦苦求助聪明的伊索,伊索在讲好条件后便给他出了个主意。
主人听后如获至宝,急忙飞奔到海边,对蜂拥在那里的人群大声说道:“现在,我要再说一遍,我能喝干整个大海。
可是如今千万条江河汇入大海,海水里混杂了许多河水,如果有谁能把河水与海水分开,我就能把真正的大海喝干!”伊索朴素地应用了模糊语言学,帮助主人渡过了难关。
因为,“海水”是个模糊概念,我们虽然经常使用这个词,但给它下个定义,却往往会漏洞百出。
同样,在“水果”和“蔬菜”之间,“春、夏、秋、冬”四季之间,也都没有一条截然分明的界线。
我们生活中还有许多模糊的说法,如明暗、深浅、冷暖、宽窄、快慢、浓淡、高矮等等。
模糊事物反映在人的思维中,就产生了模糊逻辑。
在模糊逻辑中,判断一个命题的真假时,不仅可以用“是”(记作1)或“非”(记作0)来回答,还可以用介于0与1之间的小数来回答。
所以,它是一种连续值逻辑。
模糊并非罪过一般认为“模糊”是个贬意词,它的名声的确也“坏”过。
在生产力十分低下的原始社会,人们只能勉强维持生存,那时,用不着什么数学计算,是个混沌模糊的世界。
但随着生产力的不断提高,产生了剩余产品和商品交换,于是,人们开始用手指头、小石子计数,渐渐形成了自然数的概念。
模糊数学期末论文
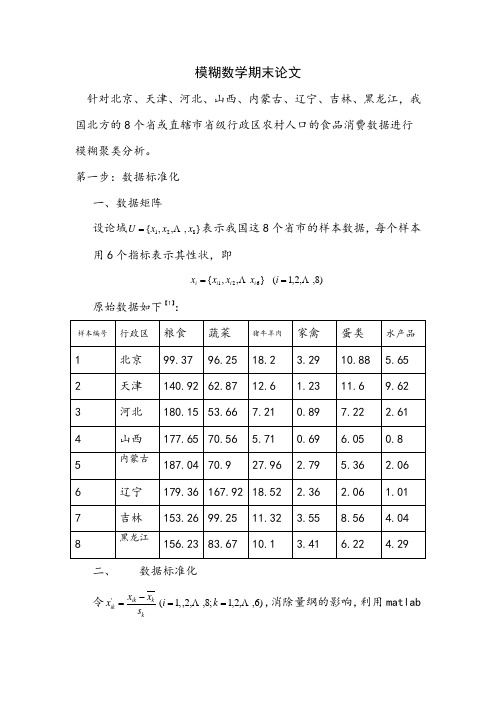
模糊数学期末论文针对北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江,我国北方的8个省或直辖市省级行政区农村人口的食品消费数据进行模糊聚类分析。
第一步:数据标准化 一、数据矩阵设论域},,,{821x x x U =表示我国这8个省市的样本数据,每个样本用6个指标表示其性状,即)8,,2,1(},,{621 ==i x x x x i i i i原始数据如下【1】:样本编号行政区 粮食 蔬菜 猪牛羊肉家禽 蛋类 水产品1 北京 99.37 96.25 18.2 3.29 10.88 5.65 2天津140.9262.8712.61.2311.69.623 河北 180.1553.66 7.21 0.89 7.22 2.614 山西 177.6570.56 5.71 0.69 6.05 0.85 内蒙古 187.0470.9 27.96 2.79 5.36 2.066 辽宁 179.36167.9218.52 2.36 2.06 1.017 吉林 153.2699.25 11.32 3.55 8.56 4.048 黑龙江 156.2383.67 10.1 3.41 6.22 4.29二、 数据标准化令)6,,2,1;8,,2,,1('==-=k i s x x x kkik ik ,消除量纲的影响,利用matlab 程序(见附件一)得到样本标准化矩阵R :⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=0.1442 0.2451- 1.8626 0.1656- 0.0079- 0.0082-0.0762 0.3152 2.0926 0.1132- 0.0197 0.0162-0.7482- 1.2411- 0.1376 0.1964 0.1417 0.05440.4625- 0.4510- 0.8440 0.6023 0.0306- 0.0751 0.8053- 0.2858- 2.6060- 0.3544- 0.0312- 0.0497 0.3129- 0.0057- 2.2774- 0.2899- 0.0612- 0.0565 1.5944 1.0430 1.7189- 0.0582- 0.0449- 0.0495-0.5142 0.8706 1.6655 0.1826 0.0144 0.1619-R 其中,.)(81;8181281∑∑==-==i k ik k i ik k x x s x x第二步:标定——建立模糊相似矩阵采用欧式距离法建立相似矩阵R ,令∑=-∙-=612)(1k jk ik ij x x C r 为了使10≤≤ij r ,选取31=C (在这里,我首先计算了各样本间的欧式距离,发现最大的距离为2.7893,所以选择了31=C ),利用matlab 程序(见附件二)得模糊相似矩阵R 如下:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡= 1.0000 0.9992 0.8673 0.9387 0.8497 0.9652 0.6495 0.9772 0.9992 1.0000 0.8867 0.9516 0.8705 0.9748 0.6158 0.9680 0.8673 0.8867 1.0000 0.9864 0.9995 0.9684 0.0854 0.7344 0.9387 0.9516 0.9864 1.0000 0.9804 0.9963 0.2949 0.8410 0.8497 0.8705 0.9995 0.9804 1.0000 0.9596 0.0402 0.7098 0.9652 0.9748 0.9684 0.9963 0.9596 1.0000 0.3937 0.8860 0.6495 0.6158 0.0854 0.2949 0.0402 0.3937 1.0000 0.8055 0.9772 0.9680 0.7344 0.8410 0.7098 0.8860 0.8055 1.0000R 第三步:聚类一、用平方法求传递闭包16161616842;:)(R R R R R R R R R t =→→→→ ,经过4次平方法得到传递闭包矩阵)(R t ,即模糊矩阵16)(R R t =。
模糊数学论文

课程类别:全日制硕士课程名称:模糊数学《课程论文题目》模糊数学在医疗图像处理中的应用院系:电信学院计算机系专业:计算机应用技术摘要图像本质上具有模糊性,因此模糊信息处理技术在图像处理中的使用有其必然性。
用计算机来来处理医学CT﹑MRI图片已成为计算机现在研究的一个重要方向,基于模糊数学的图像处理技术是计算机图像处的重要计算。
提出一种基于模糊数学的方法来融合多模医学图像。
关键词模糊数学计算机图像处理医学图像处理图像融合1 引言现代数学是建立在集合论的基础上,集合可以表现概念,而集合中的关系和运算又可以表现判断和推理,一切现实的理论系统都可能纳入集合描述的数学框架。
在较长的时间里,精确数学及随机数学在描述自然界多种事物的运动规律中,获得显著效果。
但是在客观世界中还普遍存在着大量的模糊现象,由于现代科技所面对的系统日益复杂,模糊性总是伴随着复杂性出现。
模糊数学是以不确定性的事物为研究对象的,应用于模糊控制、模糊识别、模糊聚类分析、模糊决策、模糊评判、系统理论、信息检索、医学等各个方面。
然而模糊数学最重要的应用领域是计算机职能,因此,模糊数学的理论研究领域相当广泛。
随着计算机及信息技术的高速发展,数学的应用范围急剧扩展,特别是近年来对模糊数学理论的研究,已经渗透到数学及其它自然科学和社会科学的许多领域,其应用之广泛遍及理工农医的各个方面在经济生活中,我们时常会遇到用模糊数学方法才能解决得更好的一些问题。
图像是人们对所看到的客观世界中事物的一种描述和记录。
数字图像处理实质上是计算机技术、信息论和信号处理相结合的综合性应用学科。
它依靠现代电子技术来模拟人类的视觉系统,对图像进行分割、融合、配准分析处理,从而达到理解事物和认识事物的效果,已经成为人类获取信息的重要来源,而利用计算机图像处理中模糊信息处理技术,可以有效地分析与识别图像,进而描述和解释图像。
随着医学成像技术的发展,以及计算机技术与医学图像科学的互相渗透,使医学图像在现代医学诊断中的作用越来越重要。
模糊数学应用论文

模糊数学应用论文推荐文章计算机应用专业实习总结_计算机毕业实践工作总结报告热度:灾区送温暖慰问信热度:会计电算化应用论文相关范文热度:会计电算化结课论文热度:计算机应用的论文范文热度:随着现代科学的不断发展,数学的应用领域变得越来越广,许多学科都与数学有着密切的联系。
接下来店铺为你整理了模糊数学应用论文,一起来看看吧。
模糊数学应用论文篇一摘要:通过模糊数学评价的方法对开放教育教学质量进行评价,并在结合实际评价实例分析的基础上,证明了该模型的应用价值和现实指导意义。
关键词:模糊数学;教学质量评价;权重最近几年模糊综合模型的方法在教育质量评价中被广泛应用。
该方法可以从更加客观和全面的角度评价教育质量的情况,具有操作简单、适用性强的特点,因此在教育评价工作中,具有一定的普适性。
利用模糊数学的理论构建开放教育教学质量评价的模型,以对开放教育教学质量评价机制进行综合评判。
一、模糊数学评价理论的具体步骤第一步:建立指标集。
指标集是指被评价对象各个因素所组成的集合。
建立原则是尽量用最少的因素来概括问题。
根据开放教育特点确立指标体系,目前教学质量评价一般主要从面授辅导、网上教学、毕业环节等三方面进行评价。
第二步:设评价集。
评价集是指以评价主体为元素组成的集合。
设有S个评价主体,构成评价集T={优,良,中,差}。
第三步:确定权重集。
权重集是指各个指标在评价系统中重要度组成的集合。
模糊数学综合评价方法的分配权重主要包括二类:一级指标权重、二级指标权重。
在模型应用时,权重分配向量作为矩阵进行运算。
通过征求专家意见将一级指标两两进行比较,排序为:网上教学B(0.5565)、面授辅导A(0.3691)、实践环节C(0.0744)。
二级指标:对二级指标两两比较后,排序为:教学内容A1(0.3367)、教学方法A2(0.2867)、教学效果A5(0.1506)、作业环节A4(0.1955)、教学态度A3(0.0296);直播课堂B1(0.8333)、网上答疑B2(0.1667);论文指导C1(0.7500)、社会实践C2(0.2500)。
模糊数学在信息检索中的应用毕业论文

模糊数学在信息检索中的应用摘要:本文从模糊集出发,以信息检索为应用背景,逐步引入模糊数学理论,并以提高信息检索的准确率和检索效率为目的,提出以下思想方法:(1)为了提高检索准确率,根据模糊集理论,提出了基于文档和查询词的模糊集表示法.(2)通过利用模糊聚类分析理论,研究了基于模糊集文档的模糊聚类方法,并得到了分类的文档簇,同时研究了文档簇的模糊集表示法,为后续研究做铺垫.(3)为了提高检索效率,可以通过缩小检索范围来实现,据此提出了基于文档簇的模糊信息检索模型,从而得到满足条件的文档簇.(4)为了对满足条件的文档簇中的文档进行排序,提出了基于文档的模糊信息检索模型,从而完成了检索的剩余工作,并形成完整的检索过程.(5)通过提出算例,分两种情况进行了分析:当文档集和查询项都是用模糊集表示的,分析了基于模糊集的模糊信息检索模型;当文档集是模糊集表示,查询项是确定的布尔类型,分析了基于模糊集的扩展布尔检索模型.关键词:模糊集;聚类分析;信息检索;检索模型;布尔检索Fuzzy mathematics application in information retrievalAbstract: For improving the information retrieval accuracy and efficiency of searching, this paper, which puts information retrieval as application background and gradually introduces the fuzzy mathematical theory, puts forward the following thoughts and methods:(1) In order to improve retrieval accuracy, this paper, according to the fuzzy sets theory, put forward the fuzzy sets representations, based on both the inquiry word and the document.(2) Through fuzzy clustering analysis theory, we study the fuzzy clustering analysis method based on the document cluster and acquire the classification of the cluster. And we also study the representation of the document classification, based on the fuzzy sets. It is laying groundwork for the follow-up study.(3) In order to improve the search efficiency, we can do it through narrowing the searching range. So the paper puts forward the fuzzy information retrieval model, which is based on the document cluster. Then we get meet the satisfied document clusters.(4) In order to sort the satisfied document clusters, we put forward the fuzzy information retrieval model, which is based on the document. Thus we complete the surplus work of retrieval, forming a complete search process.(5) By presenting examples, two cases were analyzed: when the sets of documents and query terms are represented by fuzzy sets, we analyze the fuzzy information retrieval model based on the fuzzy sets; when the set of documents is fuzzy set and the set of the query terms is the Boolean sets, we analyze the Boolean information retrieval model based on the fuzzy sets.Keywords: fuzzy sets;clustering analysis;information retrieval;retrieval model;Boolean retrieval目录1 绪论 (1)1.1论文研究的背景及意义 (1)1.1.1 论文研究的背景及目的 (1)1.1.2 国内外研究现状 (1)1.1.3 论文研究的意义 (1)1.1.4 论文研究采用的方法及理论依据 (2)1.2论文构成及研究内容 (2)1.3模糊集的基本概念 (2)1.4模糊理论的数学基础 (2)1.4.1 经典集合 (2)1.4.2 模糊集合 (3)1.4.3 归属函数 (3)1.5模糊子集及其运算 (3)1.5.1 模糊集的相关定义 (4)1.5.2 模糊集的运算 (5)1.5.3 模糊集的其他运算 (5)1.6模糊集的基本定理 (6)2 模糊聚类检索策略 (7)2.1相关概念 (7)2.2模糊聚类分析 (7)2.2.1 选择模糊聚类方法 (8)2.2.2 词频矩阵 (8)2.3基于编网法的模糊聚类分析模型 (9)2.3.1 构造模糊相似矩阵 (9)2.3.2 模糊聚类之编网法 (10)2.3.3 基于文档集合的模糊聚类编网法的应用 (10)2.4文档簇的模糊表示法 (11)3 模糊概念网络 (12)3.1模糊概念网络的结构 (12)3.2基于文档的模糊概念网络的构建 (12)3.3基于文档簇的模糊概念网络的构建 (14)4 基于文档簇和文档的信息检索模型 (15)4.1基于文档簇的模糊信息检索模型 (15)4.1.1 文档簇和查询项的模糊集表示 (15)4.1.2 相关性 (15)4.1.3 检索方法 (17)4.2基于文档的模糊信息检索模型 (18)4.2.1 文档和查询项的模糊集表示 (18)4.2.2 相关性 (18)4.3检索方法 (18)4.3.1 基于模糊集的扩展布尔检索 (18)4.3.2 基于模糊集的模糊检索 (20)5 模糊信息检索模型实例分析 (23)5.1基于模糊集的扩展布尔检索实例分析 (23)5.2基于模糊集的模糊检索实例分析 (24)6 结论 (26)参考文献 (28)致谢 (29)1 绪论1.1 论文研究的背景及意义1.1.1 论文研究的背景及目的自从美国著名控制论专家、加利福尼亚大学L.A.Zadeh教授1965年建立模糊集理[]1论以来,在各国学者的共同努力和不断探索下,模糊集理论及其应用的研究成果已非常丰富.它不仅发展和扩充了经典数学的研究领域,使数学学科的研究体系发生了重大变革,而且能有效地解决经典数学难以解决的大系的复杂性问题,以及在自然界和日常生活中普遍存在而无法解决的模糊性问题,比如信息检索.模糊数学理[]2论提出后,信息检索领域的学者就尝试将其应用于信息检索中,并且取得了长足的发展,产生了一大批优秀的模糊信息检索应用理论,为模糊数学的应用开拓了新的领域,比如:模糊聚类分析在信息检索中的应用、模糊集在信息检索中的应用、模糊推理在信息检索中的应用等.总体来看,这些应用理论为模糊数学发展开辟了新的空间,增添了新的活力.本文以模糊数学理论为基础,提出了一套新的信息检索应用方法.此方法的提出主要希望达到一下目的:(1)为了提高信息检索的准确性,提出了基于模糊集的信息检索模型;(2)为了提高信息检索的效率,提出了基于文档簇的模糊信息检索模型,并将“基于模糊聚类分析的检索策略”应用到模型上.1.1.2 国内外研究现状目前,信息检索发展迅速,并产生了优秀的检索模型:向量空间模型,概率模型,语言模型,推理网路模型,布尔检索,LSI,神经网络方法,遗传算法,模糊集检索模型等.同时,也促进了提高模型性能的检索策略的探索和发展,常用的检索策略:相关反馈,聚类,基于片段的检索,语言解析,n元语法,同义词表,n元语法,语义网路,回归分析.由于检索效率及稳定性的瓶颈,使得模糊信息检索实际应用发展缓慢,其在信息检索领域的应用还比较有限.从国外来看,模糊数学应用到信息检索的案例还很少,大多数相关应用都处于实验阶段;从国内来看,模糊数学的信息检索应用案例几乎没有.总体来看,都是由于其不稳定及效率问题决定的,所以实现效率及稳定性的突破就显的很重要了.1.1.3 论文研究的意义模糊数学自身的理论研究进展迅速.我国模糊数学自身的理论研究仍占模糊数学及其应用学科的主导地位,所取得的研究成果在《模糊数学》、《模糊系统与数学》等数十种学术期刊和全国高校学报中经常可见,模糊聚类分析理论、模糊神经网络理论和各种新的模糊定理及算法不断取得进展.通过研究模糊数学在信息检索中的应用,提出一种新的方法,来提高模糊信息检索的效率.同时,使得模糊数学的应用分支更丰富.1.1.4 论文研究采用的方法及理论依据(1)通过提出模糊集和模糊聚类分析理论,首先将样本文档表示成模糊集,并利用模糊聚类分析方法对文档模糊集进行模糊聚类,同时提出了分类文档簇的模糊集表示方法,从而建立了文档簇的模糊集.(2)通过基于词项概念和文档簇的模糊概念网图,为建立模糊信息检索模型,提供了直观的检索对象关系图.(3)通过建立基于文档类簇的模糊信息检索模型,得到满足条件的文档簇,从而为后续处理缩小检索范围,这在一定程度上提高了检索效率.(4)针对得到的文档簇集中的文档,建立基于文档的模糊信息检索模型,从而得到排序的检索结果.(5)为了直观描述模糊信息检索模型,添加了模型的实例分析.1.2 论文构成及研究内容论文主要内容主要包括:1.介绍了模糊数学的信息检索应用现状,研究该课题的意义、目的、提出的方法及实现模型;初步阐述了模糊数学在信息检索的应用;2.介绍模糊聚类检索策略,根据制定的阈值,将样本文档分为一些类簇,并且为满足条件的文档簇建立其模糊量集度量方法,为下面的研究做铺垫;3.介绍模糊概念网络图的建立,使得研究变的更加直观;4.介绍基于文档类簇的模糊信息检索模型,从而得到簇类的检索结果,减小了检索的范围,在一定程度上提高了检索效率;5.介绍基于文档的模糊信息检索模型的实例分析.1.3 模糊集的基本概念模糊理论是为了解决真实世界中普遍存在的模糊现象而发展的一门学问.模糊理论以模糊集合为基础,基本精神是接受模糊性现象存在的事实,而以处理概念模糊不确定的事物为其研究目标,并积极地将其严密量化成计算机处理可以处理的信息.实际上,模糊理论是模糊集合,模糊关系,模糊逻辑,模糊控制,模糊测量等理论的泛称,我们通常称之为模糊数学.1.4 模糊理论的数学基础1.4.1 经典集合模糊理论的基础是模糊集合和归属函数,所谓集合是一些具有某种共同特质事物汇总起来的组织,用来归纳一群具有相同特征事物.一般而言,传统意义上的集合具有下列共同的特点:同一集合中的元素具有某种相同的性质;集合是元素组成的整体,元素之间可以互相区别;集合里的元素是确定的.然而经典集合具有两条基本属性:元素彼此相异,即无重复性;范围边界分明,即一个元素x 要么属于集合A (记作x ∈A ),要么不属于集合(记作x ∉A ),二者必居其一.1.4.2 模糊集合模糊数学是研究和处理模糊性现象的数学方法.众所周知,经典数学是以精确性为特征的.但与精确形相悖的模糊性并不完全是消极的,没有价值的.甚至可以说,有时模糊性比精确性还要好.例如我们要给“偶数”这个集和下定义时,我们很明确的知道这个集合中的每个元素,对于任何给定的数值,我们都清楚的知道它是否属于这个集合.但是当我们为“中年人”这个集合下定义时,多少会遇到困难,因为具体的所谓中年,指的是几岁到几岁?相信每个人对中年的定义都是不同,假定从满35岁起到满55岁为止定义为中年,那么34岁的人还未迈入中年,只要增加一岁的那个瞬间就马上变成中年.另外,过完55岁迈入56岁生日的瞬间又已不再是中年人.基本上,这是相当不合理的方式.前述“中年”定义之所以会不自然,是因其界线太过清楚所致,当界线缓和一些,则不自然会消失.因此,如果以“中年程度”来考虑或许会比较适当.譬如说30岁的中年程度是0.6,35岁的中年程度是0.65,随着不同年龄,其程度也徐徐变化,而此问题也就能获得根本上的解决.此种重新扩张定义的集合,由L.A.Zadeh 教授提出,称之为模糊集合.1.4.3 归属函数把传统的集合论特征函数从非0即1的二值选择,推广为可从0到1之间的任何值来做出选择,此新型的特征函数,称之为归属函数.归属函数是模糊理论中最基本的概念,而我们可以用归属函数来表示模糊集合:在域U 上的模糊集合A ,由归属函数)(x A μ来表征,)(x A μ在[]1,0区间中取值,)(x A μ值的大小反映了元素x 对于模糊集合A 的归属程度.)(x A μ的值越接近1,就表示元素x 属于A μ的程度越高.当A μ1=就是上限,表示x 完全属于A μ.反之,若A μ的值越接近0,就表示x 属于A μ的程度越低.当0=A μ就是下限,表示x 完全不属于A μ.对于5.0=A μ来说,距离“完全属于”和“完全不属于”最远,所以它的模糊度也最高.因此,模糊集合也被定义为元素与归属函数的组成集合.1.5 模糊子集及其运算模糊集最早出现于文献[1,12-18].模糊集提出了使用隶属函数来标明元素在集合中的隶属度,而不是假设元素是某个集合的成员.对于信息检索,模糊集是非常有效的,因为它可以描述一篇文档是“关于”什么内容的.描述文档关于什么内容的一组元素的集合本身就具有不确定性.关于“交通”且与诉讼之间间接相关的文档,或许可能是关于“交通事故”的文档.尽管将“交通事故”作为集合的一个元素实际上并不精确,但是将其从集合中排除掉也是不精确的.模糊集就是一种隶属度,其中每个元素的隶属力度本来就精确.在这个例子中,描述文档概念的集合的形式如下:)}5.0()0.1{(诉讼案,,交通,=C由于每个元素还附带其隶属度,所以集合C 是一个模糊集.在模糊集},....,,{21n c c c C =中包含的概念可以形式化地表示为:()()()()()()n n n A A c f c c f c c f c A ,2.211,...)(,,=其中A f :]1,0[→C 表示隶属函数,用于标识集合中元素的隶属度.对于有限集合,模糊集A 表示为: ()()()⎭⎬⎫⎩⎨⎧=n n A A A c c f c c f c c f A ,...,2211. 接下来我们给出了模糊集的基本操作:求交集和并集.从根本上说,求交集的方法是取相同元素的两个隶属度函数的最小值,并集就是取相同元素的两个隶属函数的最大值.模糊集的交集、并集和补集的定义:()C c c f c f Min c f i i B i A i B A ∈∀=)),(),((()()()C c c f c f Max c f i i B i A i B A ∈∀=,),(C c c f c f i i A i A ∈∀-='),(1)(1.5.1 模糊集的相关定义定义1 论域U 上的一个模糊集合A 是由U 上的一个隶属函数:)(x A []1,0→U 来表示,其中)(x A (有时用)(x A μ表示)表示元素x 隶属于模糊集合A 的程度.一般地,如果论域U 是有限集合或可数集合,那么一个模糊集A 可以表示为:∑=)(i i x A x A .定义2 主导隶属度函数关系:B A ⊂当且仅当)()(x x B A μμ≤对于所有x .定义3 设U 是论域,称映射:)(x A []1,0→U 确定了一个U 上的模糊子集A ,映射)(x A 称为A 的隶属函数,它表示x 对A 的隶属程度.使5.0)(=x A 的点x 称为A 的过渡点,此点最具模糊性.当映射)(x A 只取0或1时,模糊子集A 就是经典子集,而)(x A 就是它的特征函数.可见经典子集是模糊子集的特殊情形]3[.例 设论域{})190(),180(),170(),160(),150(),140(654321x x x x x x U =(单位:cm )表示人的身高,那么U 上的一个模糊子集A 的隶属函数)(x A 可定义为140190140)(--=x x A 100200100)(--='x x A 也可用Zadeh 表示法:10x A =22.0x +654318.06.04.0x x x x ++++ 6543219.08.06.042.02.015.0x x x x x x A +++++='1.5.2 模糊集的运算模糊集的并、交、余运算性质幂等律:A A A A A A == ,交换律:A B B A A B B A ==,结合律:)()(C B A C B A =)()(C B A C B A =吸收律:A B A A A B A A ==)(,)(分配律:)()()(C B C A C B A =)()()(C B C A C B A =还原律:A A c c =)(对偶律:c c c B A B A =)(c c c B A B A =)(模糊集的运算性质基本上与经典集合一致,除了排中律以外,即 U A A c ≠ ,φ≠c A A1.5.3 模糊集的其他运算模糊集不再具有非此即彼的特点,这正是模糊性带来的本质特征. 相等:)()(x B x A B A =⇔=包含:)()(x B x A B A ≤⇔⊆并:B A 的隶属函数为 )()())((x B x A x B A ∨=交:B A 的隶属函数为 )()())((x B x A x B A ∧=余:c A 的隶属函数为 )(1)(x A x A c -=例 设论域{}54321,,,,x x x x x U =(商品集),在U 上定义两个模糊集:A =“商品质量好”,B =“商品质量坏”,并设)1,3.0,0,55.0,8.0(=A)0,6.0,86.0,21.0,1.0(=B则 c A =“商品质量不好”,c B =“商品质量不坏”,)0,7.0,1,45.0,2.0(=c Ac B =)1,4.0,14..0,79.0,9.0(可见A B B A c c ≠≠,又 U A A c ≠=)1,7.0,1,55.0,8.0(φ≠=)0,3.0,0,45.0,2.0(c A A1.6 模糊集的基本定理定理1 模糊集的基本定理 λ-截集]4[ {}λλλ≥==)()(x A x A A 模糊集的λ-截集λA 是一个经典集合,由隶属度不小于λ的成员构成. 若论域{}654321,,,,,u u u u u u U =(学生集),他们的成绩依次为50,60,70,80,90,95,A =“学生成绩好的学生”的隶属度分别为0.5,0.6,0.7,0.8,0.9,0.95.则 9.0A (90分以上者)={}65,u u ,6.0A (60分以上者)={}65432,,,,u u u u u . 性质:设)(,U B A ℑ∈(B A ,是论域U 的两个模糊子集),[]1,0,∈μλ,于是对λ-截集有:(1) λλB A B A ⊆⇒⊆(2) μλμλA A ⊇⇒≤(3) λλλB A B A =)(,λλλB A B A =)( 定理2 (分解定理) 设)(U A ℑ∈,A x ∈∀,则[]{}λλλA x x A ∈∈∨=,1,0,)( 定理3 (扩张原理) 设映射f :Y X →,定义{}y x f x A y A f =∨=)(),())((2 模糊聚类检索策略所谓聚类分析是根据事物间的不同特征,亲疏程度和相似性等关系,对它们进行分类的一种数学方法,其数学基础是数理统计中的多元分析.模糊聚类分析就是建立在模糊数学理论基础上的聚类分析,模糊聚类分析]5[的方法有好几种(模糊传递闭包法,直接聚类法,最大树法,编网法),根据信息检索的特征,此处介绍的是利用模糊相似矩阵和编网法进行聚类的方法,其特点是能在分类数不确定的情况下进行分类,可以根据不同的要求对事物,文档进行聚类,而且结果直观、简捷.2.1 相关概念为了描述信息检索的模糊聚类分析模型,我们使用以下术语以及记号. (1)标引词{}n t t t T ...,,21=,这是由若干个标引词组成的集合;(2)文献信息()T t t t t d i n ∈=)),(,...),((21μμμ,其中)(n t μ是标引词i t 在该文献中出现的频率,使用统计分析可以计算出标引词i t 的隶属度)(i d t μ.(3)文献信息库可表示为:{}T t t t t d d D i n d d d ∈==)),()...(),((21μμμ; (4)分类文献信息集{}D d d d d U i n ∈=,...,,21,这是将要被分类的文献信息集; (5)相似度()j i ij d d r ,δ=,其中()j i d d ,δ按照它描述文献信息i d 和j d 之间的相关程度,这里选用最大,最小法贴近度来表示())()...(),(21n d d d i t t t d i i i μμμ=和)()...(),((21n d d d j t t t d j j j μμμ=的相关程度,则其严格贴近度为[][]∑∑==∨∧=nk kd k d nk k d k d j i ij t t t t d d r jij i11))()()()(),(μμμμ(2-1) 其中“∧”表示“取小”运算,“∨”表示“取大运算”.(6)模糊相似矩阵n m ij r R ⨯=)(,其中ij r 是相似度.相似矩阵R 是以分类文献信息集{}n d d d U ...,21=中i d 和j d 之间的相似度ij r 构造出来的,它刻画的是{}n d d d U ...,,21=信息之间相关程度.2.2 模糊聚类分析在实际课题中,不同的数据可能有不同的量纲.为了不使不同量纲的数据也能进行比较,需要对数据进行适当的变换,根据模糊矩阵的要求将数据压缩到区间[0,1]. 数据变换:设论域{}n u u u U ,...,,21=为被分类的对象,每个元素又由m 个数据表示,对第i 个元素有{}im i i i x x x u ,...,,21= ),...,2,1(n i =. (1)标准差变换kkik ik s x x x -=* )...,2,1;,...2,1(m k n i == (2-2) ∑==ni ik k x n x 11nx xs ni k ikk ∑=-=12)( (2-3)经过变换后,每个变量的均值为0,标准差为1,并可以消除量纲的影响,但不一定在[0,1]区间上. (2)级差变换{}{}{}ik n i ikik ni ikik x x x x x '-''-'=≤≤≤≤11min max min ),...,2,1(nk = (2-4) 经过级差变换后有10≤≤ik n x ,且消除了量纲的影响. 2.2.1 选择模糊聚类方法聚类可以分为两种,一种是模糊等价矩阵聚类.它有两种方法,传递闭包法和布尔矩阵法.另一种是直接聚类,它包括直接聚类法、最大树法和编网法.在实际的聚类问题中,通过建立X 上的模糊关系,常常是模糊相似的关系.因为论域是有限集,这个模糊相似关系可表示为一个模糊相似矩阵,即对角线上的元素为1的对称模糊方阵R .可以选择的模糊聚类方法通常有四种(由文献[5,23-36]可知):模糊传递闭包法、直接聚类法、最大树法和编网法.模糊传递闭包法是从模糊相似矩阵n n ij r R ⨯=)(出发,构造一个新的模糊等价矩阵(即模糊相似矩阵R 的传递闭包)(R t ),该矩阵满足自反性、对称性、以及传递性三个性质.因此,可以根据模糊等价矩阵进行聚类.直接聚类法不计算模糊相似矩阵R 的传递闭包)(R t ,而是直接用模糊相似矩阵R 进行聚类,具体步骤如下 :(1) 将模糊相似矩阵R 中的所有不同元素从大到小的顺序编排,设为 n λλλ...121>>=.(2) 以),...2,1(m k k =λ为置信水平,选取k λλ=,直接在模糊相似矩阵R 上找出k λ水平上的相似类,并进行归并,即得到k λ水平上的等价分类.寻找相似类和归并的原则:若k ij r λ≥,则将i d 和j d 分为一类.设21,B B 是k λ水平上的两个类,若φ≠21B B ,则称它们是相似的.将所有相似的类合并成一类,最后得到的分类就是k 水平上的等价分类.2.2.2 词频矩阵为确定一组相关文本间的相关度,建立文本间的模糊相似关系,首先要构造一个词频矩阵F ,它是一个二维表,表示关键词i W 在文档tj 中出现的次数,假设这一组数据中有d 个文档和t 个关键词,则F 是一个t d ⨯的矩阵,将每一个关键字视为一个t 维空间d R 上的一个向量v ,v 的j 个坐标是一个数字,表示第j 个文本与所给的关键字间的相关度,当文档不含有该词时,其值为零,否则设为一个非零的正值,定义为ij f 为文档tj 中关键词i W 出现的次数(即频率),再利用绝对值减数法建立模糊相似矩阵R ,当j i =时,1=ij r ;否则,当j i ≠时,∑=--=tk jk ik ij f f c r 11,其中0〉c ,为一常数,可根据实际情况选定,使得[]1,0∉ij r ,由该定义可知,R 为一主对角元均为1的对称阵.2.3 基于编网法的模糊聚类分析模型在一个合适的分类中,同一类中的对象应该自反性、对称性以及传递性三个性质.模糊数学的理论告诉我们,如果相似度ij r 选择合适,相似矩阵n m ij r R ⨯=)(具有自反性和对称性,但是大多数相似矩阵一般不具备传递性.因此,仅依赖相似矩阵R 来对分类文档信息集{}D d d d d U i n ∈=,...,,21进行分类是不够的.模糊聚类分析就是根据相似矩阵R 来寻找一个等价关系进行分类,其主要步骤如下: 2.3.1 构造模糊相似矩阵聚类是按某种标准来鉴别X 中元素之间的接近程度,把彼此接近的对象归为一类.为此,我们用]1,0[中的数ij r 来表示X 中的元素i x 和j x 的接近或相似程度,称为相似系数ij r .相似系数ij r 构成的模糊矩阵m n ij r ⨯)(是X 上的模糊关系.确定相似系数的方法很多,可以分为三类:1.相似系数法 2.距离法 3.主观评分法. 最常见的是距离法中的贴近度法. 不妨假定]1,0[∈∀k x ,如若不然, 可以通过公式:kk kk k m M m x x --=)...2,1(),,...2,1(mk n i == (2-5) (其中k k m M ,分别是各个i x 的第k 个特征的最大、最小值)将k x 转换为]1,0[∈'k x .当]1,0[∈k x 时,{}n i ...2,1∈∀,{}im i i i x x x x ,...,21=可以认为是一个模糊向量,也就是可以看成以m 个特征指标构成的集合为论域的模糊集,于是1x 的贴近度),(21x x N 可以作为它们的相似程度.即()j i ij x x N r ,=.当N 取距离贴近度时,∑=--=mk jk ik ij x x c r 11 (2-6)把所有的)...2,1(),,...2,1(m j n i r ij ==组成的矩阵为模糊相似矩阵]6[,命名为R .针对的分类文献集{}D d d d d U i n ∈=,,...,,21,选择一个计算相似度()j i ij d d r ,δ=的算法,可以计算出相似矩阵ij r R =. 2.3.2 模糊聚类之编网法编网法是由我国学者赵汝怀提出的,其特点是在模糊相似矩阵R 的截集上直接进行聚类.因此,使用起来更为直观简单.具体步骤如下:(1)适当选取[]1,0∈λ,求出λ截矩阵λR ,且去掉λR 的主对角线右上半部分的所有元素;(2)将主对角线上的“1”对应地用其对象i μ的标号来代替;(3)将主对角线左下方的“0”去掉,而用“*”代替“1”,称* 所在的位置为结点; (4)用竖直线与横直线将结点与对角线上的序号连接,即编网.通过如此打结而连接的对象归为同一类,从而实现了等价分类. (5)画出动态聚类图.通过以上步骤即可完成对文档集的分类. 2.3.3 基于文档集合的模糊聚类编网法的应用如果我们现在要检索混凝土断裂方面的文献,可选关键词有多个,且利用每个关键词都可以得上百篇文献,检索过程中,每篇文献都详细阅读是不贴实际的,因此我们需要通过聚类筛选出相关度高的几篇或者几十篇文献.设标引词集为:{}==4321,,,t t t t T {混凝土、断裂韧度、尺度效应、虚拟裂缝模型}同时设D 为某信息库,从该信息库中选出5篇文档进行分析,则{}54321,,,,d d d d d d =.根据各关键词在相应文献中的出现频率,使用模糊统计分析可计算出每个关键词的隶属度.从而每篇文献在检索中的表示记为:)5.0,3.0,1.0,1.0())(),(),(),((432111111==t t t t d d d d d μμμμ )3.0,1.0,4.0,2.0())(),(),(),((432122222==t t t t d d d d d μμμμ)1.0,3.0,5.0,2.0())(),(),(),((432133333==t t t t d d d d d μμμμ)1.0,3.0,5.0,2.0())(),(),(),((432144444==t t t t d d d d d μμμμ )1.0,3.0,4.0,2.0())(),(),(),((432154444==t t t t d d d d d μμμμ故根据(2-1)可得模糊相似矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=180.082.070.033.080.0182.067.033.082.082.0167.043.070.067.067.0143.043.033.043.043.01R对R 中的元素进行排序为: 1>0.82>0.8>0.67>0.43>0.33 从而,R 的截矩阵为8.0=λ截矩阵为8.08.08.011100111001110000010000018.0,08.0,1)()(R r r r R t ij ij ij ⇒⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎩⎨⎧<≥==这时U 被分为3类:{}{}{}54321,,,,d d d d d2.4 文档簇的模糊表示法通过上节的模糊聚类分析方法,可得到分类的文档簇,本部分将介绍一种模糊度量方法来量化这些文档簇.任意一篇文档可表示为,则文献集的度量可表示为())()...(),(21n d d d i t t t d i i i μμμ=,则文献集{}D d d d d U i n ∈=,,...,,21的度量d 可表示为))()...(),(())()...(),((21121n d d d ni n d d d t t t nt t t d i i i'''==='∑μμμμμμ(2-7)通过以上讨论,得到了文档簇的模糊表示法,这为之后的讨论提供了基础依据,且对应于文档集{}D d d d d U i n ∈=,,...,,21的文档簇集可表示为:},...,{21m d d d U '''=,其中为聚类数.从而))(),...(),((21n d d d i t t t d iii'''='μμμ.3 模糊概念网络3.1 模糊概念网络的结构模糊概念网络的结构是由节点和弧构成.网络包括两种类型的节点:概念节点和文档节点.连接节点的弧表达了节点之间的相关关系,并用模糊权值对关系的强弱进行量化.设概念节点集合C=(c 1,c 2,…..c n ),文档节点集合D=(1d ,2d ,…..n d ) .i c −→−μj c 表示i c 和j c 的相关度权重为τ,也可表示为,),(τ=j i c c f i d −→−ηj c 表示i d 和概念j c 的相关权重为ζ,也可表示为i d f (,j c )=ζ.规则 1 如果存在节点i c ,j c 和k c ,其a c c f k i =),(,且()=j k c c f ,的关系权值为ˆ(,)min(,)i k F c c a a =. 规则2 如果节点i c 和j c 之间存在多条路径连接,i c 和j c 间的关系值为最大的路径权重.图3-1如下,给出了一个典型模糊概念网络实例.其中节点3c 和4c 相关关系权重为()1.0)7.0,1.0(,43==Max c c F .图3-1 模糊概念网路实例3.2 基于文档的模糊概念网络的构建模糊概念网络可以通过领域专家手工建立,但需要大量的手工劳动,并受限于领域专家的个人水平.为了突破这种限制,文献[2]提出了模糊概念网络的自动构建方法,本部分将对此作以详细阐述.将一个文档表示成关键词集{}n t t t T ,...,,21=.统计词表中每个关键词在正文、标题、关。
模糊数学方法在肿瘤细胞图像增强中的应用

天 津 医 科 大 学本科生毕业论文模糊数学方法在肿瘤细胞图像增强中的应用The Application of Fuzzy Mathematics Method in the Image Enhancement of Tumor Cell姓名扈靖年级2002级院系与专业生物医学工程系生物医学工程学指导老师邢克礼教授完成时间 2007年6月目 录中文摘要 (1)英文摘要 (2)1. 前言 (3)1.1 绪论 (3)1.1.1 研究意义 (3)1.2 图像增强处理的一般方法 (4)1.2.1 空间域法 (4)1.2.2 频域(增强)法 (4)1.3 国内外研究现状 (5)1.4 研究内容 (5)2. 研究对象和方法 (5)2.1研究对象 (5)2.2 模糊数学概述 (5)2.3 图像模糊增强 (7)2.3.1 模糊特征平面 (7)2.3.2 模糊增强算法 (8)2.4 遗传算法的原理 (8)2.4.1 遗传算法 (8)2.4.2 遗传算法的数学模型 (9)2.4.3 基本遗传算法流程图 (9)2.4.4 遗传算法的基本步骤 (10)2.4.5 适应度函数的确定 (11)2.4.6 遗传算法中关键函数的选择 (11)2.4.7 遗传控制参数的确定 (12)3. 实验结果 (12)4. 讨论 (16)5. 结论 (18)致谢 (19)参考文献 (20)摘 要目的:了解模糊数学的概念,用模糊数学方法以及遗传算法理论实现肿瘤细胞图像的增强,对比传统图像增强方法,显示出模糊增强的优势。
方法:利用MATLAB图像处理平台,采用一种基于模糊集理论的自适应模糊增强算法,根据遗传算法的理论选取合适的适应度函数,根据不同的肿瘤细胞图像自动选择最佳的分界点。
结果:通过运用模糊增强方法对肿瘤细胞图像进行分析处理,减少干扰因素的影响,提高图像的质量,实现肿瘤细胞图像的增强,对比直方图均衡化增强后的图像,可以得出模糊增强能够得到更加清晰的图像,优于传统图像增强方法。
模糊综合评判在数学教学质量中的实施论文.doc

模糊综合评判在数学教学质量中的实施论文模糊综合评判在数学教学质量中的实施论文模糊综合评价方法就是对多种因素所影响的事物和现象做出总的评价,在模糊综合评价中,要评价某事物首先要确定评价因素及评价等级,建立其数学模型,这样评价问题就化为模糊矩阵的乘法问题了。
提高数学课堂教学质量是提高数学教学质量的关键一环,影响数学教学质量的因素是多方面的。
科学准确的对教学质量作出评价,不仅关系着师资队伍建立,更是教育振兴的需要。
多年来,各级各类学校为寻找一种比较全面,合理的评价教学质量的方法而积极探索。
采用较普遍的是总分法[1-2]:即是把影响数学教学质量的个因素中的每一个因素评定一个分数 ,然后求出总和,用作为被评对象的评价标准。
这种做法往往不够全面,准确,本文将用模糊数学中的模糊综合评价的理论和方法来解决数学教学质量综合评价的问题,能够较为客观地反映数学教师的综合教学水平。
1.建立综合评判因素。
根据数学教学的要求,对教师的教学的评价可分为5个评估指标,即教学目的,教学重点、难点的处理,教学条理,教学环节,课堂气氛。
这5个指标构成一个评估目标体系,即综合评估的因素[3-4].2.评估量化等级确实定。
数学教学质量的评估具有复杂性、模糊性,因此很难对其做出准确判断,宜采用等级评定法。
我们把考核量化标准定为优、良、一般、较差。
3.评判因素权重确实定。
评价目标体系是一个整体,对各因素分项等级评定后,还要把评定结果综合起来综合评定。
因此,应考虑和确定多工程在总体中的重要性。
由于各工程在总体中有主次之分,各工程的权重也不尽相同。
为了防止各因素之间有相同的权重,我们采用专家询问法把各个评价工程制成权重系数评定表,交给数名数学学科的专家,使其按自己的意见认定权重系数并填入表内。
然后收集所填写的表,求其平均数,得出各工程的权重系数[5].5.运用B=A·R=(b1,b2,…,bn)这一合成运算,最后根据最大隶属原那么定等,即B中最大的分量所对应的等级。
《模糊数学》的混合教学

《模糊数学》地混合教学中学数学论文《模糊数学》地混合教学陈敏(东华大学理学院,上海)摘要:随着模糊数学理论地飞速发展,使其在很多领域得到应用并取得了重要成果.高校中开设《模糊数学》课程在也成了一种必然趋势.本文介绍了将翻转式教学与传统教学相结合,适用于《模糊数学》课程地一种新地混合教学模式.关键词:模糊数学;翻转式教学;混合教学中图分类号:文献标志码:文章编号:()近年来,模糊数学理论已得到飞速发展.在各个领域中应用非常广泛,它已应用于模糊控制、模糊识别、模糊聚类分析、模糊决策、模糊评判、系统理论、信息检索、医学、生物学等各个方面.在气象、结构力学、控制、心理学等方面得到应用并取得了重要成果.在人文、社会学科及其他“软科学”地数学化、定量化趋向把模糊数学推向中心地位.模糊数学发展和扩充了经典数学地研究领域,对其他学科显示了强大地渗透力和解释力,使之在高校课程体系中占有不可替代地地位.学习模糊数学能通过模糊数学课程地学习能很好地培养和提高大学生地抽象思维能力和逻辑推理能力,培养大学生地创新能力,为大学生继续学习和工作,参加科学研究打下坚实地数学基础.因此,《模糊数学》[]课程地教学就显得尤为重要.在传统教学模式中,教师是教学活动地主体,是知识地传授者,而学生则处于被动接受老师灌输知识地地位.这种教学模式忽视了学生地认知主体作用,不利于培养学生地创新思维和创新能力.伴随新理念和新技术地不断涌现,信息技术与课程教学地整合日渐深入,其中翻转式教学成为国内外教育改革地新潮流,为教与学地进一步发展提供了新思路.如何将传统教学地优势和数字化教学地优势结合起来,使二者优势互补,既发挥教师引导、启发、监控教学过程地主导作用,又充分体现学生作为学习过程主体地主动性、积极性与创造性,从而获得更佳地教学效果,这是我们所最追求地共同目标.本文将翻转式教学与传统教学相结合,探索了针对《模糊数学》课程地一种新地混合教学方式.一、《模糊数学》课程教学现状目前,《模糊数学》课程教学大多数教学内容仍采用“教师讲授为主型”地教学模式,也就是在课堂内进行知识地传授,而在课堂外进行知识地内化.这种教学方式存在以下问题..课堂缺乏“活力”.课堂成了教师地“一言堂”,学生是知识地被动接受者.缺乏学生地自主思考,久而久之则会导致学生思维地依赖性,抑制学生自主学习和创新思维能力地发展..对教学对象地“一视同仁”,忽视了学生地个体差异.《模糊数学》一般在大三、大四学生中开设.大四地学生更关注是否学以致用,将学到地知识运用于毕业论文地写作中去.大三地学生更关注于课程本身地内容,是否可以用于感兴趣地课题.面对现行地教学模式,采用地是教学内容统一、教学方式统一、教学时间和地方统一,难以满足不同水平学习者地需要,从而影响学习者地兴趣和积极性,影响教学目标地实施..课程未能充分运用现代技术手段.受到教师观念地限制,虽然技术进步了,教学手段更新了,但是教学地观念还是停留在教师利用技术手段来“教”、学生“学”地被动教学.现代化地教学手段也仅限于.因此,现行地教学模式不利于教学效果地提高.结合《模糊数学》课程本身地特点,将翻转式教学适当地应用于教学,以弥补现行教学模式中地不足就成为我们关注地课题.二、混合教学模式地实施翻转式教学模式是建立在网络信息技术条件下地教与学过程,它将知识传授与内化这两个教学过程进行了翻转和重新安排,使学生有更多自主学习、协作学习和个性学习地选择余地,在教与学地过程中与传统教学学习过程相反.我们希望构建一种新地混合教学模式,将翻转式教学与传统教学相结合,相互作用,通过不断改进,逐步达到最优教学效果..混合教学模式地构建.①教师资源准备.教师根据对教学目标、教学对象、教学内容,设计教学活动和教学资源.教学活动设计,主要指分配学习任务、划分学习小组、制定评价标准等.教学资源地形式包括:教学视频、微课、教学.教学视频可以由课程主讲教师亲自录制或者使用网络上优秀地开放教育资源.②学生课前学习.在课前,教师利用网络发布新地学习任务和要求,学生通过网络中教师提供地教学视频、教学、微课等教学资源进行自主学习,在学习过程中可以积极与同学或老师进行交流.在理解课程内容基础上完成练习或作业.在整个学习或练习过程中,学生应当详细记录遇到地问题,通过与同学、老师交流进行解决或者等待在课堂中提出,由教师帮助解决.③教师课堂主导.教师主要通过课堂教学促进学生对知识地理解和掌握,课堂中教师地大部分时间用于听取学生或小组地学习汇报、观看作业成果、进行答疑、问题讨论和深化、并接受其他学生地质疑,师生之间进行深入交流,对于教学难点或重点,在课堂上适当进行强化.发现学生学习中存在地问题并给予及时指导,了解学习进度,有效控制教学过程地顺利进行.④学生课堂活动.学生通过课前学习已基本理解了所要求学习地知识,课堂环节主要是进行知识内化.学生可以向教师汇报自己对知识地理解,展示自己或小组地作业情况和其他学习成果.对于学习中遇到地问题及时向教师反馈,教师做出解答..《模糊数学》课程地混合教学模式地具体实施.模糊数学就是经典数学地推广,很多知识都是已有经典数学知识地推广,是一门应用性很强地学科,与实际生活密切相关.在实际教学中,理论教学与实际相结合,结合我们身边地实际问题,我们将课程按照模块化进行教学.①基础知识地学习,以教师课堂教学为主导.课堂上教师阐明“模糊数学”中地三大定理和几个基本理论,结合大量地实际应用例子,讲清每一个基本理论所包含地概念、原理与方法,从而让学生加深对理论概念地理解.学生可课前或课后下载和学习教师根据教学知识点制作教学、教学视频、微课等教学资源.结合教师课堂内容进行知识地消化、整理和理解.①模块知识地学习.我们将知识点分成五大模块,分别是:模糊决策、模糊规划、模糊聚类、模糊控制、模糊识别.通过小组汇报来实现五大模块地学习.学生组成小组后按照自己地意愿选择知识模块,对自己感兴趣地课题进行学习.课前由教师提出具体要求,让小组成员做充分准备,通过查资料、调研及参考教师提供地网络资料(教学视频、教学、微课等),利用理解地基本理论,运用基本方法,针对几个实际问题,将此模块地内容深刻理解.让学生走上讲台,向师生汇报,并接受其他师生地提问,师生互动促进学生更好地实现知识地内化,真正把理论教学办成理论应用研究讨论地课堂,让学生体会到理论地实用价值,从而激发其学习兴趣,培养其创新意识.这也拓宽了学生地知识面,开拓学生地思维,为写毕业论文提供更多地思路,也为今后继续学习深造、将来参加工作、转变思维方式和提高分析解决实际问题地能力打下良好地基础.③课程考核.以往地考核是按照平时分和卷面分来定最后地综合成绩.混合教学后,成绩评定也相应做了调整.我们将小组汇报、学生课堂交流和学生在网络上地活跃度增加到了平时成绩中,按照地平时成绩(包括出勤、作业、课堂交流、网络活跃度)、小组汇报占、卷面成绩占,使得对学生地成绩评价更加客观、准确..实施效果.①学生学习地综合能力提升.学习地主要目地就是为了应用到实际中,尽最大努力去解决现实生活中遇到地实际问题.模糊数学教学强调其在解决实际问题中地作用.近几年地大学生数学建模比赛中地若干问题也可以通过模糊数学理论去建立数学模型.在模糊数学教学地过程中,能真正让大学生体会到学习数学地重要性和应用地广泛性.模糊理论与计算机实践教学也紧密结合,在学习了模糊综合评判理论以后,学生们应用实现对东华大学本科生生源水平地评估.在学习了模糊模式识别理论以后,学生们应用电脑研制“数字、英文字母地模糊识别”软件.大四学生在学习《模糊数学》后都感到毕业论文不再是毫无思绪了.学生们都感到本课程能学以致用,综合以往学到地知识,使自己能理论结合实际,实实在在做出些结果来,在学术科研地各方面地能力有所提高.②学生学习地主动性提高.学生们普遍认为《模糊数学》课程是一门生动地、有意思地课程,在课堂上地小组汇报和讨论给了同学们展示自己才华地机会,大大激发了学生学习地主动性,激发了学习兴趣,增强了自信心和主观能动性,培养了创新能力.③学习成绩优良率大幅提高.比较未进行教学改革之前,现在地优良率达到了左右,不及格率极低.这说明了同学们对该课程确实投入了精力和时间好好学习了..有待解决地关键问题.①教学视频地制作.录制质量好地教学视频是实施翻转课堂教学首要需解决地问题.为保证教学视频地质量,能充分吸引学生积极参与到视频地学习中,教师在录制教学视频时需要考虑视觉效果、知识主题地突出性、互动策略、时长和学生地自我操控性等,避免死板、单调地讲述.这些都将给我们主讲教师对课程知识地理解程度,对教学技术地使用和时间提出了挑战.②在线学习系统地搭建.要保证混合教学中地学生自主学习能顺利进行,又能随时随地在师生间、生生间进行良好地互动交流,无论是课前还是课中,教师都需要通过信息技术构建学习支持系统来为学生提供个性化与协作化地学习环境.因此,该在线学习系统除了提供可以让学生自由交流地空间外,还需重点解决如何通过教师干预来引导学生自我组织和控制个性化学习和探究性学习,又如何通过此环境来记载和跟踪学生地学习过程和学习结果等关键问题.③进一步优化成绩考核制度.在混合教学模式下,以往从传统“结果”来给出综合成绩地评价方式,也将从“过程”和“结果”两方面进行地多元化评价方式,不断优化.三、结束语《模糊数学》地混合教学模式,为高校课程地翻转课堂教学模式地应用提供了一种可借鉴地教学方案,恳请大家指正.参考文献:[]杨伦标,高英仪.模糊数学原理及其应用[].广州:华南理工大学出版社,.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模糊数学结课论文
模糊综合法在土地定级中的应用
A Fuzzy Comprehensive Clustering Method
姓名:张昊
学号:129926001
专业:管理科学与工程
指导老师:王涛(教授)
目录
一、摘要 (3)
二、背景 (3)
三、主要思想和方法 (4)
四、论文内容 (4)
1.权重分析 (4)
2.采用德尔菲法和层次分析法相结合的方法 (5)
3.模糊聚类分析过程 (7)
4.对比结果分析 (8)
五、论文创新点 (9)
六、读后感 (9)
七、附录英文文献 (10)
一、摘要
本文提出了融模糊综合评判和模糊聚类分析于一体的模糊综合法,给出了将特尔菲法与层次分析法相结合的定权步骤以及与K无关的聚类分析步骤。
应用表明,该方法定级结果唯一且符合实际。
二、背景
正确评定土地等级,建立科学的土地等级体系,是土地科学中最重要的研究内容之一。
为了建立科学的土地等级体系,土地科学工作者们采用过模糊综合评判。
它充分顾及了土地质量界线的模糊性,但在根据最大隶属度或主导因素原则对综合评判矩阵确定定级结果时,丢失了各评价单元之间的相关信息,容易造成与实际不符的定级结果。
鉴于此,有人采用模糊聚类分析。
该法兼顾了各评价单元之间的相关信息,在很大程度上弥补了模糊综合评判的不足,也取得了一些成效。
但它在获取原始信息和选取分类阈值λ时,具有很大的主观性,尤其是凭经验选取λ值,不仅有先在思想上按主观愿望分类,再去凑阈值λ之嫌,而且分类不唯一。
所以,又有人提议在进行土地定级时,分别采用这两种方法得出两个
结果,然后再比较它们的一致性。
这样做,不仅使土地定级工作量成倍增加,而且当两种结果相差较大时(实际上这种情况经常出现),究竟选用哪一种结果,无法确定,并且不能兼顾两者之长,克服两者之短。
本文提出的模糊综合法,将模糊综合评判和模糊聚类分析有机地结合在一起,能扬长避短,是值得推荐的方法。
南宁市的土地质量是以市中心商业用地为圆心, 呈辐射状向外递减, 其土地定级估价课题组的成果被国家土地管理局誉为“国内领先水平”。
因此, 我们用本模型处理了他们的部分定级资料, 以接受实践的检验。
三、主要思想和方法
首先用德尔菲法和层次分析法选择参评因素并确定权重, 求取隶属度并获得模糊总体评价矩阵X。
其次, 由B= A·X求得全部因素的综合评价矩阵B, 并把所有被评价的土地单元的等级评判结果组合成一个等级综合评判矩阵。
最后, 利用该等级综合评判矩阵中的元素, 求得模糊相似矩阵R和模糊等价矩阵( 传递闭包矩阵)t( R) 。
再据t ( R) 进行聚类分析, 得到最终的定级结果。
四、论文内容
1、权重分析
影响土地质量的因素指标很多, 且重要程度即权重各异, 土地分等定级时, 应由专家结合实际, 因地制宜地选择因素、确定权重。
2、采用德尔菲法和层次分析法相结合的方法
根据专家分析和德尔菲法、层次分析法的计算, 确定研究区域的土地因素集U,其层次结构体系( 一、二级) 如表1 所示。
立足被研究区域的土地现状及专家评估信息, 评语集定为V = { Ⅰ, Ⅱ,Ⅲ, Ⅳ} 。
根据需要提取该区域被评价单元的参评因素数据, 按前述方法计算得到其模糊综合评判矩阵B20*4。
有了B20×4矩阵后, 若使用模糊综合评判确定土地等级, 根据最大隶属度或主导因素原则评定出的土地等级为:Ⅰ级: 1, 2, 4, 6, 8, 9; Ⅱ级: 7, 13, 20; Ⅲ级: 3,10, 11, 12, 15, 16, 17, 18, 19; Ⅳ级: 5, 14。
我们的综合方法则是以B20×4中的元素yij ( i= 1, 2, ⋯, 20; j = 1, 2, 3, 4) 为原始数据再进行聚类分析。
再求得模糊相似矩阵R20×20并平方,合成模糊等价矩阵t( R) 后, 应用我们与λ无关的聚类方法, 求得各土地单元的分类。
最后, 求得各类土地等级。
3、模糊聚类分析过程
4、对比结果分析
现在, 把根据本文新模型得到的表3 和图2与单独用模糊综合评判得到的结果相对比, 容易看出: 模糊综合评判把处于市中心、商服繁华、基础设施完备、人口密度很大的Ⅰ级土地14( 龙宫大酒家) 错定为Ⅳ级地; 把被邕江阻隔于市中心另一岸的Ⅱ级地9( 区检察院) 错定为Ⅰ级地;把位于郊区、各项设施都较差的Ⅳ级地20( 白沙造纸厂) 错定为Ⅱ级地。
这些错误的出现, 就在于模糊综合评判据最大隶属度原则定级时, 若次最大隶属度与最大隶属度相差不大, 则丢失了河流道路阻隔、土地区位波及性等大量土地定级信息。
由B20×4知, 地块20( 白沙造纸厂) 对Ⅱ级隶属度为0. 622, 对Ⅳ级为0. 604, 这是模糊综合评判本身所不能克服的。
再来分析我们的结果。
从表3 和图2 中不难看到, 土地单元的级别是唯一的, 是符合南宁市土地实际的价值和特性的, 而且结果包含的土地信息量是丰富的, 有主导因素也有次要因素, 有最大隶属度也有模糊聚类的定量补足, 同时兼顾了河流阻隔等因素。
该结果明确给出1~20 土地单元的等级, 体现了南宁市的土地特点, 即土地级别由市中心到边缘、从高到低逐渐过渡, 高级别集中在市中心繁华地段, 低级别分布在市区边缘, 整个城市土地级别由市中心商业繁华区向周围呈辐射状, 反映出土地质量与土地区位的对应关系。
但因铁道和邕江阻隔, 使二者两侧的繁华程度有明显差别, 如龙宫大酒家与区检察院。
又因交通条件是
影响土地质量的重要因素, 因此主干道两侧呈级差递减趋势, 如南宁火车站和白沙造纸厂等。
五、论文创新点
融模糊综合评判与模糊聚类分析于一体的土地定级模型, 发挥了二者的长处, 抑制了各自的不足, 既虑及多个土地评价因素, 又参考了实际环境等因素,
结果信息量丰富。
它把定性分析与定量计算有机结合, 使土地等级建立在主客观统一的理论基础上。
易于接受, 便于应用。
六、读后感
读完这篇论文,我对模糊数学的方法也是有所感悟,我学模糊数学时候,看了书上这么多的应用,但是我总觉得太理论化,现在看完这篇文章,关于土地分等定级,也是属于房地产的范畴。
我现在的研究生方向是工程造价与房地产评估,我想模糊数学在土地评估上得到了良好的应用,日后一定也会在房地产行业得到广泛应用。
实际实例检验我们发现这种方法的确能让结果更准确,是行之有效的一种模糊方法。
我想在我以后写硕士论文的时候,我也能努力的将这种模糊综合聚类方法应用到我研究的课题中,我想必定能产生较为良好的效果。
七、附录英文文献。
