悬臂梁有限元模拟分析步骤
专业课设,悬臂梁有限元分析
1研究目的与问题阐述1.1 基本研究目的(1) 掌握ANSYS软件的基本几何形体构造、网格划分、边界条件施加等方法。
(2) 熟悉有限元建模、求解及结果分析步骤和方法。
(3) 利用ANSYS软件对梁结构进行有限元计算。
(4) 研究不同泊松比对同一位置应力的影响。
1.2 基本问题提出图1.1 模型示意图如图1.1所示，当EX=3.01e6，F=5000N，悬臂梁杆一端固定，另一端为自由端。
当悬臂梁的泊松比u为：0.2、0.25、0.3、0.35、0.4时，确定同一位置的应力分布，得出分布云图。
二维模型，3*0.09m。
2 软件的介绍与使用2.1 ANSYS 简介ANSYS程序是一个功能强大的灵活的设计分析及优化、融结构、流体、电场、磁场、声场分析于一体的大型通用有限元商用分析软件，可广泛应用于核工业、铁道、石油化工、航空航天、机械制造、能源、汽车交通、国防军工、电子、土木工程、造船、生物医学、轻工、地矿、水利、日用家电等一般工业及科学研究。
该软件提供了一个不断改进的功能清单，集体包括：结构高度非线性分析、电磁分析、计算流体动力分析、设计优化、接触分析、自适应网格划分、大应变/有限转动工功能一接利用ANSYS参数设计的扩展宏命令功能。
ANSYS由世界上最大的有限元分析软件公司之一的美国ANSYS开发，它能与多数系统下生成的集合数据传入ANSYS,如Pro/Engineer, NASTRAN, Alogor, I－DEAS, AutoCAD等，并通过必要的修补可准确地在该模型上划分网格并求解。
2.2 ANSYS软件的功能介绍ANSYS软件含有多种有限元分析的能力，包括从简单线性静态分析到复杂非线性动态分析。
一个典型的ANSYS分析过程可分为以下三个步骤：创建有限元模型；施加载荷进行求解；查看分析结果；在有限元的分析过程中，程序通常使用以下三个部分：前处理模块，分析求解模块和后处理模块。
前处理模块提供了一个强大的实体建模及网格划分工具，通过这个模块用户可以建立自己想要的工程有限模型。
《现代设计方法》有限元实验报告
《现代设计方法》有限元实验报告班级：XX机设（X）班姓名：XXX 学号：XXXXXXXXXX 实验地点：A1楼机房实验时间：XXXX.XX.XX 教师：XXX实验题目:中心开孔悬臂梁有限元分析1、实验目的：（1）了解有限元分析阶段（建立有限元模型，完成单元网格划分，采集处理分析结果）（2）掌握如何运用有限元分析解决实际问题2、问题描述：某一悬臂梁长800宽200厚20在其几何中心处开有直径D=100通孔，试有有限元法求解其位移，应力。
3、实验步骤：（1）建立有限元模型①打开我的电脑C盘→el文件夹→BIN文件夹→ELCUT.exe运行程序②选择File→选择New→命名236.pbm③选择Edit→选择默认平面应力问题→236.pbm④按键盘上的Esc键→选择Edit→选择Geometry→选择Model→选择Add Vertex→回车→用键盘上Tab键切换设X=200，Y=500，继续设点（200，500），（400，500），（900，500），（1000，500）（600，450），（600，350），（200，300），（1000，300），⑤按键盘上的Esc键→选择Add Edge→选择Arc angle→填0→建立悬臂梁的四条边平面图⑥按键盘上的Esc键→选择Add Edge→选择Arc angle→填180→建立悬臂梁中心的开孔平面图（2）完成单元网格划分①选择Edit→选择Mesh→选择Set Spacing→用定在界面上的光标选定所建模型的最左端左上角端点（轴两端弯矩大）→设置Spacing=30→同样用定在界面上的光标选定所建模型的最左端左下角端点（轴两端弯矩大）→设置Spacing=30→光标选定圆的最上点和最下点（孔周边应力大）→设置Spacing=25→光标选定所建模型的最右端右上角端点（轴两端弯矩大）→设置Spacing=40→光标选定所建模型的最右端右下角端点（轴两端弯矩大）→设置Spacing=50（受弯矩和应力）②按键盘上的Esc键→选择Build All→显示网格的划分③按键盘上的Esc键→选择Remove Mesh→光标选定悬臂梁中心的开孔（删掉多余的网格划分）④按键盘上的Esc键（两次）→选择Label Blocks→回车→命名为B1→回车⑤按键盘上的Esc键→选择Label Edges→光标选定悬臂梁平面图的位于左边的那条边→命名为e1→回车⑥按键盘上的Esc键→选择Label Edges→光标选定悬臂梁平面图位于上边均布载荷的那段→命名为e1→回车⑦按键盘上的Esc键→选择Label Vertices→光标选定悬臂梁平面图右上角点→命名为V1→回车⑧按键盘上的Esc键→选择Find Label（查看命名是否齐全）⑨按键盘上的Esc键（两次）→选择Save→选择yes(3)采集处理分析结果A:①选择Edit→选择Data→选择OK→选定Label B1→设置相应参数Ex=2.06e11,Ey=2.06e11,Ez=2.06e11→回车②按键盘上的Esc键→选定Label e1→用键盘上Tab键切换，按键盘上空格键设置相关参数。
悬 臂 梁 的 有 限 元 分 析
悬臂梁的有限元分析
1 几何模型
在部件中新建一个几何模型，类型为可变性，形状为实体，类型为拉伸，模型空间为三维。
在网格线中画一个5ⅹ5的正方形，进行拉伸，拉伸长度为47。
图1.1 几何建模过程图
如图所示，模块创立好
图1.2 几何建模图
2 材料属性
1)在模块列表中选择属性功能模块，按照步骤，先创建材料（材料类型为钢）。
2)材料行为选择为弹性，同时弹性模量为200e3MPa，泊松比为0.3
3)创建截面属性，保持默认参数不变，点击继续
4)给部件赋予截面属性
图2.1 材料属性
3定义装配件
在左上角的模块列表中选择装配功能模块，点击默认参数。
4设置分析步
选择分析步模块，取名为step-1，分析步类型为静力，通用。
其余默认-点击继续
图4.1 分析步
5.载荷与边界
1)施加载荷点击创建载荷，将分析步载荷类型设置为压强，其余参数为默认，点击继续，
选择平板上平面，压强大小为0.188
2)选择长方体做平面制定约束
图5.1 载荷与边界
6划分网格
在模块列表中选择网格功能模块，注意划分网格是为部件划分，而不是为装配件划分。
如图，单元类型为CPS4R:四结点双线性平面应力四边形单元，
如图，单元数为1175，结点总数为1728
7分析结果
7.1应力变形云图
7.2位移变形云图
8分析结果
如图所示，Smax=3.82e1<113根据第四强度理论，该平板不会发生断裂。
用有限元法对悬臂梁分析的算例算例
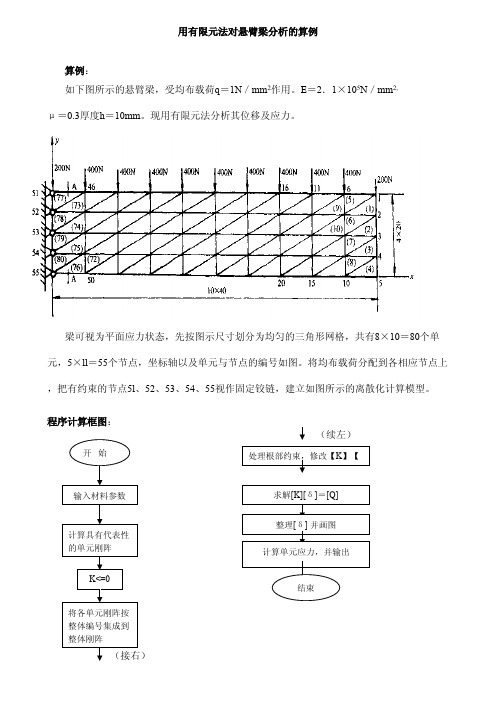
用有限元法对悬臂梁分析的算例算例：如下图所示的悬臂梁，受均布载荷q ＝1N ／mm 2作用。
E ＝2．1×105N ／mm 2,μ＝0.3厚度h ＝10mm 。
现用有限元法分析其位移及应力。
梁可视为平面应力状态，先按图示尺寸划分为均匀的三角形网格，共有8×10＝80个单元，5×ll ＝55个节点，坐标轴以及单元与节点的编号如图。
将均布载荷分配到各相应节点上，把有约束的节点5l 、52、53、54、55视作固定铰链，建立如图所示的离散化计算模型。
程序计算框图：（续左）程序中的函数功能介绍及源代码1.LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)――该函数用于计算平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)、第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)时的线性三角形元的单元刚度矩阵.该函数返回6×6的单位刚度矩阵k.2.LinearTriangleAssemble(K,k,i,j,m)――该函数将连接节点i,j,m的线性三角形元的单元刚度矩阵k集成到整体刚度矩阵K。
每集成一个单元，该函数都将返回2N×2N的整体刚度矩阵K.3.LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)-- 该函数计算在平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi, yi)第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)以及单元位移矢量为u时的单元应力。
该函数返回单元应力矢量。
函数源代码：function y = LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;%三角形单元面积，单元节点应该按逆时针排序，保证每个三角形单元的面积都为正值（也可作为一个小函数：LinearTriangleElementArea）betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);%B为应变矩阵，其中betai=yi-ym,betaj=ym-yi,betam=yi-yj.gammai=xm-xj, gammaj=xi-xm, gammam=xj-xi.D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%D为弹性矩阵，分为平面应力问题和平面应变问题对于平面应力问题D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];对于平面应变问题E1=E/（1-NU*NU），NU1=NU/（1-NU）y = t*A*B'*D*B;%单元刚度矩阵function y = LinearTriangleAssemble(K,k,i,j,m)K(2*i-1,2*i-1) = K(2*i-1,2*i-1) + k(1,1); K(2*i-1,2*i) = K(2*i-1,2*i) + k(1,2);K(2*i-1,2*j-1) = K(2*i-1,2*j-1) + k(1,3); K(2*i-1,2*j) = K(2*i-1,2*j) + k(1,4);K(2*i-1,2*m-1) = K(2*i-1,2*m-1) + k(1,5); K(2*i-1,2*m) = K(2*i-1,2*m) + k(1,6);K(2*i,2*i-1) = K(2*i,2*i-1) + k(2,1); K(2*i,2*i) = K(2*i,2*i) + k(2,2);K(2*i,2*j-1) = K(2*i,2*j-1) + k(2,3); K(2*i,2*j) = K(2*i,2*j) + k(2,4);K(2*i,2*m-1) = K(2*i,2*m-1) + k(2,5); K(2*i,2*m) = K(2*i,2*m) + k(2,6);K(2*j-1,2*i-1) = K(2*j-1,2*i-1) + k(3,1); K(2*j-1,2*i) = K(2*j-1,2*i) + k(3,2);K(2*j-1,2*j-1) = K(2*j-1,2*j-1) + k(3,3); K(2*j-1,2*j) = K(2*j-1,2*j) + k(3,4);K(2*j-1,2*m-1) = K(2*j-1,2*m-1) + k(3,5); K(2*j-1,2*m) = K(2*j-1,2*m) + k(3,6);K(2*j,2*i-1) = K(2*j,2*i-1) + k(4,1); K(2*j,2*i) = K(2*j,2*i) + k(4,2);K(2*j,2*j-1) = K(2*j,2*j-1) + k(4,3); K(2*j,2*j) = K(2*j,2*j) + k(4,4);K(2*j,2*m-1) = K(2*j,2*m-1) + k(4,5); K(2*j,2*m) = K(2*j,2*m) + k(4,6);K(2*m-1,2*i-1) = K(2*m-1,2*i-1) + k(5,1); K(2*m-1,2*i) = K(2*m-1,2*i) + k(5,2);K(2*m-1,2*j-1) = K(2*m-1,2*j-1) + k(5,3); K(2*m-1,2*j) = K(2*m-1,2*j) + k(5,4);K(2*m-1,2*m-1) = K(2*m-1,2*m-1) + k(5,5); K(2*m-1,2*m) = K(2*m-1,2*m) + k(5,6);K(2*m,2*i-1) = K(2*m,2*i-1) + k(6,1); K(2*m,2*i) = K(2*m,2*i) + k(6,2);K(2*m,2*j-1) = K(2*m,2*j-1) + k(6,3); K(2*m,2*j) = K(2*m,2*j) + k(6,4);K(2*m,2*m-1) = K(2*m,2*m-1) + k(6,5); K(2*m,2*m) = K(2*m,2*m) + k(6,6);K;%对号入座，如前所述，每集成一次都将返回2N×2N的整体刚度矩阵K.此题为110×110 function y = LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%平面应力和平面应变问题两种情况y = D*B*u;%单元应力计算主程序源代码E=21e7;NU=0.3;t=0.01;stifflike5=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.08,0.36,0.06,1) %选取2个基本单元，调用M文件stifflike1=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.06,0.4,0.06,1) K=sparse(110,110); %creat a xishu matrix for total stiff创建一个稀疏矩阵for i=1:49if rem(i,5)%模取余，bool型变量，非零即为真j=i;K=LinearTriangleAssemble(K,stifflike5,j,j+5,j+6);%节点编号K=LinearTriangleAssemble(K,stifflike1,j,j+6,j+1);endend%将每个单元刚度矩阵集成到总刚中K=full(K);%转化稀疏矩阵 k=K(1:100,1:100);k=[K,zeros(100,10);zeros(10,100),eye(10)];k=sparse(k);%利用边界条件简化基本方程Q=sparse(2:10:92,1,[-200,-400,-400,-400,-400,-400,-400,-400,-400,-400,],110,1);%外部荷载，此处不包括约束条件，通过形函数确定，是不是可以理解为梁的两端为中间的一半呢？d=k\Q;%高斯消元法，比克莱姆法则在计算速度上有绝对的优势！x=0:0.04:0.4;plot(x,d(106:-10:6))%基本绘图命令grid%带网格y=zeros(80,3);q=0;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.06;xn=0.4;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];xl=0.4;yl=0.06;xm=0.36;ym=0.04;xn=0.4;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.02;xn=0.4;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0;xn=0.4;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endendq=4;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.08;xn=0.36;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.06;xm=0.36;ym=0.06;xn=0.36;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.04;xn=0.36;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0.02;xn=0.36;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endend %y(i+q,:)这是实现什么的？没见过这种用法，算法上应该就是通过节点位移实现指定单元的内力，这部分本人看的也晕晕的，望高人指点N=y(73:80,1)结果图及数据输出悬臂梁轴线挠度图：一单元的单元刚阵1.0e+006 *0.8077 0 0 -0.4038 -0.8077 0.40380 2.3077 -0.3462 0 0.3462 -2.30770 -0.3462 0.5769 0 -0.5769 0.3462-0.4038 0 0 0.2019 0.4038 -0.2019-0.8077 0.3462 -0.5769 0.4038 1.3846 -0.75000.4038 -2.3077 0.3462 -0.2019 -0.7500 2.5096五单元的单元刚阵1.0e+006 *00.050.10.150.20.250.30.350.4x/m w /m0.5769 0 -0.5769 0.3462 0 -0.34620 0.2019 0.4038 -0.2019 -0.4038 0-0.5769 0.4038 1.3846 -0.7500 -0.8077 0.34620.3462 -0.2019 -0.7500 2.5096 0.4038 -2.30770 -0.4038 -0.8077 0.4038 0.8077 0-0.3462 0 0.3462 -2.3077 0 2.3077根部73-80各单元应力计算结果如下（n/m2）：1.0e+007 *2.1119 -0.0621 -2.2816 -4.8824 5.0479 2.4065 0.0352 -2.3753。
悬臂梁操作指导
（分析过程，包括前处理、求解、后处理，可以参考书中第74-81页装载机动臂的静力学有限元分析。尤其是前处理和后处理的内容）
1.
有一个如图1所示的悬臂梁（截面为10mm*10mm的矩形，长度100mm），受均布压力载荷10N/m2。试求出该悬臂梁的最大应力和最大挠度。
（它的解析解已经解完了，在图0的下面，挠度7.5e-6mm，应力0.003MPa，即3000Pa。）
图1悬臂梁的问题描述
2.
1）.启动CATIA，建立一个悬臂梁的3D模型，设置单位，加材料。（这一步已经做完了。）
2）.进入工程分析模块，加固定约束，加均布载荷，求解，查看结果。
3）.分析两次计算，第一次线性单元的边长为6mm，计算精度很低。第二次抛物线单元的边长为3mm，CATAI得到的挠度、应力与解析解基本一致。
3
1）.启动CATIA，打开xuanbiliang目录下的xuanbiliang.CATPart文件，在该文件中的几何模型中已经加好了材料（钢）。
2）.进入创成式零件有限元分析模块，如图1。之后点击“确定”，如图2。
图1
图2
3）.在零件的有限元模块中选择 工具条中的 按钮，按照如图3所示的方式选择梁的一个端面，点击“确定”，即可完成悬臂约束的施加。
18）.从图22的右侧可以看到挠度仅7.54e-6mmm，而理论上的挠度是7.5e-6mm，误差为0.53%。,精度足够了。
19）.选择 工具条中的 按钮，自动生成报告。参考图23，
在“output directory”中输入报告的存放位置。在title of the report中输入标题。
如果打算把查看过了图片都自动加到报告中，则把“add created image”选中。
悬臂梁—有限元ABAQUS线性静力学分析实例
线性静力学分析实例—-以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型，不涉及任何非线性(材料非线性、几何非线性、接触等）,也不考虑惯性及时间相关的材料属性。
在ABAQUS 中,该类问题通常采用静态通用（Ｓta ｔi ｃ,Gen ｅr ａｌ)分析步或静态线性摄动(Sta ｔi ｃ,Ｌi ｎear p ｅrturbation ）分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率，希望在获得较高精度的前提下尽量缩短计算时间，特别是大型模型。
这主要取决于网格的划分，包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子；若主要分析部位的网格没有大的扭曲,使用非协调单元（如CPS4I 、C3D8Ｉ）的性价比很高.对于复杂模型，可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐，用户可以采用精度较高的二次三角形/四面体单元进行网格划分。
悬臂梁的线性静力学分析1。
1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1—1所示,求梁受载后的Ｍises 应力、位移分布。
材料性质:弹性模量32e E =,泊松比3.0=ν均布载荷:Ｆ＝103N图1—1 悬臂梁受均布载荷图1.2 启动ＡB ＡQU Ｓ启动AB ＡＱUS 有两种方法,用户可以任选一种．（1）在Ｗin ｄow ｓ操作系统中单击“开始”—-“程序"——A ＢＡQU Ｓ 6.10-—AＢAQUS/ＣＡE。
（2）在操作系统的DOS窗口中输入命令:aｂaqｕs cａｅ。
启动ＡＢAQＵS／CAE后,在出现的Staｒt Sｅctioｎ（开始任务)对话框中选择Crｅate ModeｌDataｂａse。
1。
３创建部件在AＢAQUＳ／ＣAＥ顶部的环境栏中，可以看到模块列表：Module：Pａrt，这表示当前处在Part（部件)模块,在这个模块中可以定义模型各部分的几何形体。
悬臂梁有限元优化分析
悬臂梁优化分析班级：姓名：学号：指导老师：目录一、条件分析 (1)二、分析步骤 (1)（一）前处理阶段: (1)（二）求解阶段 (3)（三）后处理阶段 (4)（四）优化阶段 (9)三、优化结果 (13)（一）读取优化结果列表 (13)（二）选择优化结果 (13)（三）代入结果分析 (14)四、整理命令流 (14)参考文献 (17)一、条件分析由题可知：悬臂梁中的平均应力小于MPa 30，且梁的挠度小于1厘米。
而且横截面积约束条件为：cm X cm 2.1651≤≤，cm X cm 2.41202≤≤。
（考虑学号系数），连杆的材料属性为：杨氏模量Pa E 91012.30⨯=,泊松比为0.3。
由于梁的长度一定，若要使梁的重量最小，则要求体积最小，进而可知要求横截面积，所以可确定体积是所求目标，因此可确定：设计变量cm X cm 2.1651≤≤ cm X cm 2.41202≤≤状态变量平均应力MPa 30≤σ 挠度cm 1<δ目标函数体积V二、分析步骤1. 定义工作文件名和工作标题(1) 执行[Utility Menu]\File\change Jobname 。
弹出对话框，输入panjiafeng12，并选择复选框，单击“OK ”按钮。
(2) 执行[Utility Menu]\File\Change Title 。
弹出的对话框，输入panjiafeng12，单击“OK ”按钮。
（一）前处理阶段:1. 初始化设计变量执行[Utility Menu]\File\Parameters\Scalar Parameter,弹出对话框，输入X1=0.1cm ，X2=0.3cm 。
2.定义单元类型，面积，转动惯量执行[Utility Menu]\Preprocessor\Element Type\Add\Edit\Delete 弹出对话框，选择Structural Beam 中的2D elastic 3 单击“OK ”单击“Close ”。
悬臂梁有限元分析
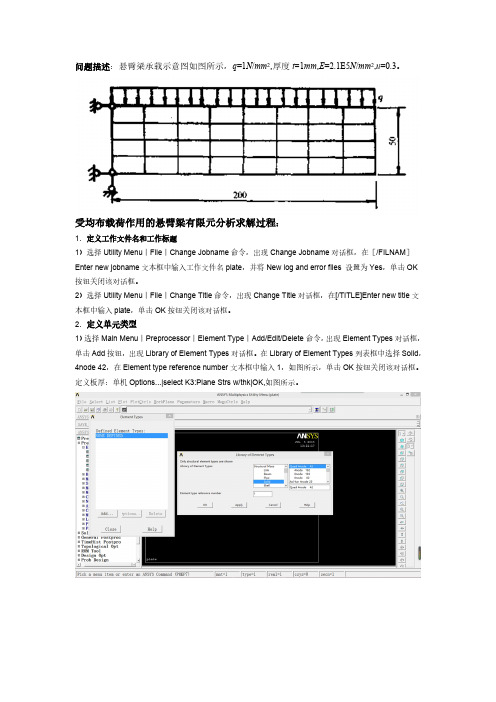
问题描述：悬臂梁承载示意图如图所示，q=1N/mm2,厚度t=1mm,E=2.1E5N/mm2,u=0.3。
受均布载荷作用的悬臂梁有限元分析求解过程：1．定义工作文件名和工作标题1）选择Utility Menu︱File︱Change Jobname命令，出现Change Jobname对话框，在［/FILNAM］Enter new jobname文本框中输入工作文件名plate，并将New log and error files 设置为Yes，单击OK 按钮关闭该对话框。
2）选择Utility Menu︱File︱Change Title命令，出现Change Title对话框，在[/TITLE]Enter new title文本框中输入plate，单击OK按钮关闭该对话框。
2．定义单元类型1）选择Main Menu︱Preprocessor︱Element Type︱Add/Edit/Delete命令，出现Element Types对话框，单击Add按钮，出现Library of Element Types对话框。
在Library of Element Types列表框中选择Solid，4node 42，在Element type reference number文本框中输入1，如图所示，单击OK按钮关闭该对话框。
定义板厚：单机Options...|select K3:Plane Strs w/thk|OK,如图所示。
3．定义材料性能参数1）选择Main Menu︱Preprocessor︱Material Props︱Material Models命令，出现Define Material Model Behavior对话框。
2）在Material Models Available一栏中依次单击Structural、Linear、Elastic、Isotropic选项（如图3.5所示），出现Linear Isotropic Properties for Material Number 1对话框，在EX文本框中输入2.1E5，在PRXY文本框中输入0.3，如图所示，单击OK按钮关闭该对话框。
有限元作业：悬臂梁
例一：悬臂梁在循环加载作用下的弹塑性计算(GUI)一、问题描述：一个左端固定的悬臂梁见图1-1(a)，厚度为1cm,在它的右段中点上施加有一个集中力，该集中力为循环载荷见图1-1(b)，悬臂梁的材料为多线性弹性材料，材料的弹性模量为20000，实验获得的该材料的非线性应力-应变行为见表1-2，分析该悬臂梁在循环载荷作用下的观测点P的水平方向上的应力应变历程。
(a)悬臂梁以及加载位置(cm)(b)所受的循环载荷(N)图1-1一个悬臂梁以及加载历程表1-2 〉材料的应力-应变行为实验数据二、问题分析解答：为考察悬臂梁根部P点的应力-应变历程，采用2D的计算模型，使用平面单元PLANE42，材料采用多线性弹塑性模型(mkin)，进行循环加载过程的分析。
建模的要点如下：①设置几何以及材料参数，②输入材料的多线性弹塑性模型(包括：弹性模量、屈服极限)，见图1-3；③通过设置time来给出加载历程，每次加载都输入当时的状态载荷值，不是增量加载，每次加载后，必须进行计算，再进入下一步的计算；④在时间后处理中，通过设置几何位置来查询对应的P观测点的节点编号，并设置观测点的应力显示变量(2号变量)以及塑性应变为显示变量(3号变量)，最后将3号变量设置为横轴，画出2号变量随3号变量的变化曲线见图1-4，可以看出，该材料具有非常明显的Bauschinger效应(即正向屈服与反向屈服之和是单拉实验屈服极限的2倍)。
给出的基于图形界面(GUI)的交互式操作(step by step)过程如下：(1) 进入ANSYS（设定工作目录和工作文件）程序→ANSYS →ANSYS Interactive →Working directory（设置工作目录）→Initial jobname（设置工作文件名）: Beams →Run →OK(2) 设置计算类型ANSYS Main Menu：Preferences… →Structural →OK(3) 设定不显示时间ANSYS Utility Menu：PlotCtrls→Window Controls →Window Options… →DATE：No Date or Time →OK(4) 定义单元类型ANSYS Main Menu：Preprocessor →Element Type →Add/Edit/Delete... →Add…→Solid: Quad 4node 42 →OK（返回到Element Types窗口）→Close(5) 定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →输入EX: 2E4, PRXY: 0.3 (定义弹性模量及泊松比) →OK →返回Define Material ModelBehavior 窗口Structural →NonLinear→Inelastic →Rate Independent →Kinematic Hardening Plasticity →Mises Plasticity →Multilinear (Fixed table) →在Strain一行中对应1至4号点输入0.004、0.015、0.03、0.08 →在Curve1中对应1至4号点输入80、160、210、280 →点击右下角Graph→OK →Close（关闭材料定义窗口），见图1-3，观察窗口中的多线性弹塑性模型(6) 构造模型生成关键点ANSYS Main Menu：Preprocessor →Modeling →Create →Keypoints→In Active CS →Keypoints number：1，X，Y，Z Location in active CS：0，0，0 →Apply →同样依次输入其他三个关键点（100，0，0）、（100，10，0）与（0，10，0）→OKANSYS Main Menu：Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPs →用鼠标依次点击1、2、3、4关键点，生成面单元，见图1-5构造模型图(7) 网格划分ANSYS Main Menu：Preprocessor →Meshing →Mesher Opts →Mesher Type : Mapped →OK →2D Shape Key : Quad →OKANSYS Main Menu：Preprocessor →Meshing →size contrls→ManualSize→Lines →Picked Lines →选择上下两条横边线，Ok →NDIV 设置为20 →Apply →选择两条竖边线→Ok →NDIV设置为8 →OK ANSYS Main Menu：Preprocessor →Meshing →Mesh →Areas →Target Surf →点击生成面几何体的位置，显示矩形面被选中→OK，见图1-6网格划分图(8) 模型加约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement On Lines →选取左侧边线（L4）→OK →select Lab2: All DOF(施加全部约束) →OK，见图1-7模型加约束图(9)求解设置ANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Analysis Options 为Large Displacement Satic，Number of substeps: 8, Max no. of substeps :25Min no. Of substeps:2, Frequency 设置为Write N number of substeps Where N = 10 →OK(10)按照时间步施加循环载荷ANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep:1 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→OK →Lab：Fy，Value：-40 →OK，结果见图1-8ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-9ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 2 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→OK→Lab：Fy，Value：0 →OK，结果见图1-10ANSYS Main Menu：Solution →Solve →Current LS →OK，ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 3 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→OK →Lab：Fy，Value：40 →OK，结果见图1-11ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-12ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 4 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→Lab：Fy，Value：0 →OK，结果见图1-13ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-14ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 5 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→Lab：Fy，Value：-40 →OK，结果见图1-15ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-16ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 6 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→Lab：Fy，Value：0 →OK，结果见图1-17ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-18(11) 计算结果ANSYS Main Menu：General Postproc→Read Results →Last SetANSYS Main Menu：General Postproc→Plot Results →Deformed Shape →Def + Undeformed→OK，观察最后变形情况，见图1-19ANSYS Main Menu：General Postproc→Plot Results →Contour Plot →Element solu→PlasticStrain →Equivalent plastic strain →OK，观察累计的等效塑性应变，见图1-20ANSYS Main Menu：TimeHistPostpro→关闭弹出窗口→Define Variables →Add… →Element Results →OK 在方框中输入2 →OK 在方框中输入4 →OK →在Item，Comp Data item 中选择Stress, X-direction SX →OK返回Define Time-History Variables →Add… →Element Results →OK 在方框中输入2 →OK 在方框中输入4 →OK →在Item，Comp Data item 中选择Strain-plastic, X-dir’n EPPL X →OK →Close ANSYS Main Menu：TimeHistPostpro→关闭弹出窗口→Settings →Graph →Single Variable No. 输入3 →OKANSYS Main Menu：TimeHistPostpro→关闭弹出窗口→Graph Variables →Nvar1中输入2 →OK观察观测点P上的应力应变历程(SX)，见图1-4ANSYS Utility Menu：File →Exit →Save Everything →OK三、ANSYS分析结果：图1-3 多线性弹塑性模型图1-4 观测点P上的应力应变历程(SX)图1-5 构造模型图图1-6 网格划分图图1-7 模型加约束图图1-8图1-9 图1-10图1-11 图1-12图1-13 图1-14图1-15 图1-16图1-17图1-18图1-19 图1-20。
abaqus悬臂梁例题
abaqus悬臂梁例题
ABAQUS是一种常用的有限元分析软件，用于模拟和分析工程结构的行为。
下面是一个简单的ABAQUS悬臂梁的例题，以便说明如何进行有限元分析：
问题描述：
考虑一个简单的悬臂梁，长度为L，截面为矩形，要分析该梁的挠度和应力分布。
步骤：
1.建立模型：首先，在ABAQUS中建立一个新模型。
定义悬臂梁的几何参数，如长度L 和梁截面的宽度和高度。
2.创建网格：划分悬臂梁的几何形状，创建有限元网格。
可以选择合适的单元类型，如梁单元或壳单元，以模拟结构行为。
3.应用边界条件：定义悬臂梁的支持条件，通常悬臂梁的一端是固定支持，另一端是自由端。
在ABAQUS中，你可以定义这些支持条件。
4.施加载荷：定义悬臂梁所受的载荷，如集中力、分布载荷等。
5.设置材料属性：指定悬臂梁所用的材料属性，如弹性模量、泊松比等。
6.运行分析：运行有限元分析，ABAQUS将计算悬臂梁的挠度和应力分布。
7.分析结果：分析完成后，你可以查看和可视化分析结果，包括挠度云图、应力云图等，以了解悬臂梁的行为。
这只是一个简单的悬臂梁分析示例，ABAQUS提供了广泛的功能来进行复杂结构的有限元分析。
具体的模型参数和步骤可能会因实际情况而有所不同。
你可以根据你的具体问题和需求来调整和扩展这个示例。
需要在软件中具体设置和模拟这个问题，以获得详细的分析结果。
悬臂梁的有限元分析
工程地质数值模拟成绩考核——昆明理工大学本科生课程*****学院：国土资源工程学院科系：地科系专业：勘查111学号：************2014年11 月8 日悬臂梁的有限元分析1.问题概述。
悬臂梁为矩形截面的钢梁，长10m宽1m、高2m，不计梁的自重，弹性模量为220GPa，泊松比为0.2，在悬臂端作用一集中荷载P=1200kN。
试分析该悬臂梁的内力和变形情况。
2.启动ANSYS程序。
(1)在【开始】菜单中依次选取【所有程序】/【ANSYS8.0】/【ConfigureANSYSProducts】选项，打开【ANSYS8.0Launcher】对话框。
(2)选中【FileManagement】选项卡，输入目录名：“D:\ANSYSFX\zhang1\Exam01\ANSYSjs”，输入项目名：“Z101Beam”。
(3)单击按钮运行程序，进入ANSYS使用界面。
3.定义材料、实常数和单元类型。
(1)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】（前处理）/【ElementType】/【Add/Edit/Delete】选项，打开单元类型对话框。
单击按钮，打开单元类型库对话框，在右侧两个列表框中分别选取【Beam】选项和【2Delastic3】选项（简称为Beam3单元，以后叙述中记为【Beam】-【2Delastic3】单元，类似的情况记法相同），如图1-16所示。
单击按钮，再单击【ElementType】对话框中的按钮。
图1-16【LibraryofElementTypes】对话框(2)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】/【RealConstants】/【Add/Edit/Delete】选项，打开实常数对话框，如图1-17所示。
单击按钮，打开Beam3实常数对话框，按照提示输入相应的面积、惯性矩和梁高参数，如图1-18所示。
悬臂梁ansys有限元分析求最大挠度
悬臂梁ansys有限元分析求最大挠度（一） 悬臂梁ansys 有限元分析求最大挠度问题：悬臂梁长1000mm ，宽50mm ，高10mm ，左端固定，求其在自重作用下的最大挠度？解：弯矩方程：221)()(x l q x M --=微分方程： 221'')(x l q y EI z-=积分求解：DCx qx qlx x ql y EI Cqx qlx x ql y EI z z +++-=++-=4322322'2416125.0615.05.0由边界条件：0;0,0''====A A A y y x θ 得：C=0，D=0I=1/12*h^3*b,h 为梁截面的高，b 为梁截面的宽。
q=ρ*g*a*h*l材料力学公式求：Y=EI85gahl^ρ=5.733mmq EILANSYS 模拟求：Y=5.5392mm，详细见下步骤ANSYS 软件设置及其具体过程如下：步骤1：建立一个模型，在model下creat一个长1，宽0.05，高0.01的长方体实体。
（单位默认为m）步骤2：材料属性设置。
密度：7800，杨氏模量：2E11，泊松比0.3。
步骤3：划分网格。
设置网格单元为structure solid brick 8node 185，mesh tool中设置网格大小为0.002，HEX下点击mesh。
步骤4：施加载荷；在preprocessor中inertia中设置重力加速度Y方向为9.8。
在左面施加固定约束（三个方向固定）步骤5:：求解。
在solve下solve current LS。
步骤6：后处理查看。
在result中plot result，查看nodes displacement。
List查看文本，观察nodes的最大位移点。
二维悬臂梁有限元分析
二维悬臂梁有限元分析二维悬臂梁有限元分析是一种常用的工程结构分析方法，在工程设计和研究中具有重要的应用价值。
本文将从有限元分析的原理和步骤、模型建立、载荷及边界条件、材料特性、求解方案以及结果分析等方面进行论述，探讨二维悬臂梁有限元分析的相关内容。
首先，有限元分析是一种通过将工程结构离散化为有限个小单元，利用单元的力学性质和相邻单元之间的相互作用关系，以数值解的方式求解结构的力学行为的方法。
二维悬臂梁有限元分析的步骤包括建立有限元模型、施加载荷和边界条件、确定材料特性、选择求解方案以及分析结果。
其次，模型建立是有限元分析的关键步骤之一、对于二维悬臂梁，可以采用梁单元进行建模。
梁单元是一种可以描述梁的位移、应变和应力的基本单元，具有两个节点和四个自由度。
通过将悬臂梁划分为多个梁单元，并将其节点连接起来建立悬臂梁有限元模型。
接下来，需要施加适当的载荷和边界条件。
载荷是指在悬臂梁上施加的外部力或力矩，可以是均布载荷、集中力、集中力矩等形式。
边界条件是指限制悬臂梁位移的条件，例如支座的固定或约束。
在二维悬臂梁中，通常将一端固定，即将该节点的两个位移约束为零。
选取合适的求解方案对于二维悬臂梁有限元分析非常关键。
常见的求解方案包括静态分析和动态分析。
静态分析适用于悬臂梁在静力加载下的弯曲和变形分析，动态分析适用于悬臂梁在动力加载下的响应分析。
根据具体问题的需求，选择适当的求解方案进行计算。
最后，需要对计算结果进行分析和评估。
通过数值计算得到的位移、应变和应力等结果，可以用于评估悬臂梁的强度和刚度等性能指标。
同时，也可以通过对结果的灵敏度分析，确定影响悬臂梁性能的关键因素，为工程设计提供参考。
综上所述，二维悬臂梁有限元分析是一种重要的工程结构分析方法。
通过有限元分析，可以预测悬臂梁的力学行为，为工程设计和结构优化提供依据。
然而，为了保证分析结果的准确性，需要合理地选择模型、载荷和边界条件、材料特性，以及采用适当的求解方案，对计算结果进行合理的解释和评估。
悬臂梁的有限元建模与优化分析
书托架的有限元建模与优化分析1. 题目概况：考虑如图1所示的木制悬臂梁结构，该梁为矩形截面，承受如图所示的集中载荷。
为满足产品性能及安全性要求，书托架的平均应力不能超过30MPa，且最大变形必须小于1cm，另外由于空间上的约束，其截面尺寸必须满足如下限制条件：5cm《X1《15cm，20cm《X2《40cm，请设计书托架的横断面尺寸，并使梁的重量最小。
习题文件名: Bracket。
图1－1 悬臂梁的示意图2. 题目分析：根据目标函数建立模型：最小化W=ρgabL假设材料密度为常数，该问题就成为一个求最小体积的问题：最下化V=abL本题约束条件：σ《30MPaδ《1cm5cm《X1《15cm20cm《X2《40cm3. 前处理阶段3.1 进入ANSYS(版本ANSYS11.0)程序→Ansys 11.0 Product Launcher →jobname: Bracket→Run3.2 初始化设计变量(长宽面积关于Z轴的惯性矩)实用程序菜单：Parameter →Scalar Parameter →X1=0.05 X2=0.2 AREA=X1*X2 IZZ=(X1*(X2**3))/12 →Accept →Close3.3 定义单元的类型、材料属性与实常数主菜单: Preprocessor →Element Type →Add/Edit/Delete →BEAM3 →OK →Close主菜单: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:3.0e7 →OK →Close主菜单: Preprocessor →Real Constants →Add/Edit/Delete →Add→OK →AREA：AREA IZZ：IZZ HEIGHT：X2 →OK →Close3.4生成几何模型3.4.1生成特征点主菜单: Preprocessor →Modeling →Create →Nodes →On Working Plane →依次输入三个点的坐标：input:1(0,0),2(2.5,0),3(5,0) →OK3.4.2定义单元主菜单: Preprocessor →Modeling →Create →Elements →Auto Numbered →Thru Nodes →点击1(0,0),2(2.5,0) →Apply →点击2(2.5,0),3(5,0) →OK4. 求解阶段4.1定义边界条件主菜单: Solution →Define Loads →Apply →Structural →Displacement →On Nodes →pick the 点1（0，0）→OK →select ALL DOF →OK4.2定义负荷主菜单: Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →pick the 点2（2.5，0）→OK →select FY 500 →Apply →pick the 点3（5，0）→OK →select FY 500 →OK4.3 分析计算主菜单: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK5. 后处理阶段主菜单:General Postproc →List Results →Sorted Listing →Sort Nodes→UY →OK实用程序菜单:Parameters →Get Scalar Data →Result datas :Global measures →DOF USUM DELTAMAX MAX →OK主菜单:General Postproc →Element Table →Define Table →Geometry →VOLU :VOLU →OK主菜单:General Postproc →Element Table →Define Table →By sequence num :SMAX_I NMISC,1 →OK主菜单:General Postproc →Element Table →Define Table →By sequence num :SMAX_J NMISC,3 →OK主菜单:General Postproc →Element Table →Sum of Each etem →OK (结果如下)SUM ALL THE ACTIVE ENTRIES IN THE ELEMENT TABLETABLE LABEL TOTALVOLU 0.500000E-01SMAX_I 0.150000E+08SMAX_J 0.375000E+07实用程序菜单:Parameters →Get Scalar Data →Result datas : Elem table sums →OK →VOLU: VOLUME →OK主菜单:General Postproc →Element Table →List Results →Sorted Listing →Sort Elems →SMAX_I Yes→OK实用程序菜单:Parameters →Get Scalar Data →Result datas :Global measures →SMAX_I MAX →OK主菜单:General Postproc →Element Table →List Results →Sorted Listing →Sort Elems →SMAX_J Yes→OK实用程序菜单：Parameter →Scalar Parameter →SMAX=SMAX_I>SMAX_J→Accept →Close实用程序菜单:File →Write DB log file →opt.db →OK6. 优化阶段主菜单：Design opt →Analysis File →Assign →opt.db →OK主菜单：Design opt →Design variables →x1,0.05,0.15→OK主菜单：Design opt →Design variables →x2,0.2,0.4→OK主菜单：Design opt →State variables →DELTAMAX,0,0.01→OK主菜单：Design opt →State variables →SMAX,0,0.01→OK主菜单：Design opt →Objective →VOLUME→OK主菜单：Design opt →Objective →Method/tool→First-order →100 →OK主菜单：Design opt →run →OK(结果如下)SET 3(INFEASIBLE)DELTAMAX(SV) > 1.1393SMAX (SV) 0.93750E+06X1 (DV) 0.15000X2 (DV) 0.40000VOLUME (OBJ) 0.300007. 结果分析结果显示，在最大截面积时（X1=0.15，X2=0.4），应变仍大于题目要求，因此应加大截面积或减少荷载8. 退出系统实用程序菜单: File→Exit…→Save Everything→OK。
基于有限元方法的汽车悬臂内应力模拟分析
基于有限元方法的汽车悬臂内应力模拟分析
基于有限元方法的汽车悬臂内应力模拟分析是一种常用的工程分析方法。
该方法通过将汽车悬臂系统离散为多个小元素，利用数值计算方法对每个小元素的应力分布进行计算，最终得到整个悬臂系统的应力分布情况。
具体分析步骤包括：
1. 建立模型：根据实际的汽车悬臂结构，使用CAD软件建立三维模型，并将模型进行网格划分，形成有限元网格模型。
2. 材料属性：为各个网格单元指定材料属性，如弹性模量、泊松比和密度等。
3. 加载条件：确定悬臂模型所受的各种外部加载条件，如悬臂端点的支撑约束、悬臂尾部的载荷等。
4. 边界条件：设置模型的边界条件，例如固支约束、驱动加载等。
5. 求解运算：利用有限元软件进行模型求解，计算每个网格单元的应力和应变。
6. 结果分析与评价：分析求解结果，评价悬臂系统的受力情况，包括确定关键部位的最大应力值、应力集中情况和位移响应等。
通过上述分析，可以对汽车悬臂系统的内应力分布进行模拟和分析，为设计和优化提供参考依据。
有限元分析(共2张PPT)
s
3、试计算下列载荷的单元等效节点力。
1、=一1/3悬，臂梁梁的，厚载度荷为均t。匀分布在自由端截面上，合力为P，采用图示网格，求各节点位移及单元应力。
1、=一1/3悬，臂梁梁的，厚载度荷为均t。匀分布在自由端截面上，合力为P，采用图示网格，求各节点位移及单t。单元等效节点力。
3、=试1/3计，算梁下的列厚载度荷为的t。单元等效节点力。
31、试一计悬算臂下梁列，载荷的均单 匀元分等布效在节自点由力端。截面上①，合力为P，采用图3示网格，求各节点位移及单元应力。
=1/3，梁的厚度为t。
112、 、=一一将1/3悬悬上，臂臂题梁梁梁的的，，悬厚载载臂度荷荷梁为均均改t。匀 匀 用分分图布布示在在的自自四由由个端端单1截截元面面的上上网，，格合合进力力行为为计算PP，，，3采采用用图图示示网网格格，，求求各各节节5 点点位位移移及及单单元元应应力力。。
作业
1、一悬臂梁，载荷均匀分布在自由端截面上，合力为P，采用图示网
格，求各节点位移及单元应力。=1/3，梁的厚度为t。
。 。。4
。 P/2 3 ②
1m
P t
。 。。1 ①
2m
。 2 P/2
2、将上题的悬臂梁改用图示的四个单元的网格进行计算，
设 = 0，试求整体刚度矩阵。
3、=试1/3计，算梁下的列厚载度荷为的t。单元等效节点力。
1、==一11//33悬， ，臂梁梁梁的 的，厚 厚载度 度荷为 为均tt。 。匀分布在自由端2 截面上，合力为P，4采用图示网格，求各节6点位移及单元应力。
3、=试1/3计，算梁下的列厚载度荷为的t。单元等效节点力。
31、 、=试一1/3计悬，算臂梁下梁的列，厚载载度荷荷为的均t。单 匀元分等布效在节自点由力端。截面上，合力为② P，采用图示网格4，求各节点位移及单元应力。
ANSYS有限元分析实例
ANSYS有限元分析实例1.悬臂梁的结构分析悬臂梁是一种常见的结构，其呈直线形式，一端固定于支撑点，另一端自由悬挂。
在这个分析中，我们将使用ANSYS来确定悬臂梁的最大弯曲应力和挠度。
首先，我们需要创建悬臂梁的几何模型，并给出其材料属性和加载条件。
然后，在ANSYS中创建有限元模型，并进行网格划分。
接下来，进行力学分析，求解材料在给定加载下的应力和位移。
最后，通过对结果的后处理，得出最大弯曲应力和挠度。
2.螺旋桨的流体力学分析螺旋桨是一种能够产生推力的旋转装置，广泛应用于船舶、飞机等交通工具中。
螺旋桨的流体力学分析可以帮助我们确定其叶片的受力情况和推力性能。
在这个分析中，我们需要建立螺旋桨的几何模型，并给出流体的流速和压力条件。
然后，我们在ANSYS中创建螺旋桨的有限元模型，并进行网格划分。
通过求解流体场方程，计算叶片上的压力分布和受力情况。
最后，通过对结果的后处理，得出叶片的受力情况和推力性能。
3.散热片的热传导分析散热片是一种用于散热的装置，广泛应用于电子设备、电脑等领域。
散热片的热传导分析可以帮助我们确定散热片在给定热源条件下的温度分布和散热性能。
在这个分析中，我们需要建立散热片的几何模型，并给出材料的热导率和热源条件。
然后，我们在ANSYS中创建散热片的有限元模型，并进行网格划分。
通过求解热传导方程，计算散热片上各点的温度分布。
最后，通过对结果的后处理，得出散热片的温度分布和散热性能。
以上是三个ANSYS有限元分析的实例，分别涉及结构分析、流体力学分析和热传导分析。
通过这些实例，我们可以充分展示ANSYS在不同领域的应用，并帮助工程师和科研人员解决工程问题，提高设计效率和产品性能。
有限元法手算求解悬臂梁内力
题目信息：已知一悬臂梁，其受荷情况及尺寸如右图所示，72210/,0.25E kN m ν=⨯=，厚度100t mm =，试用有限单元法计算其应力分布，并将有限元结果与材料力学结果进行对比。
解析：手算八节点六单元模型1 结构离散化将悬臂梁划分成六个三角形单元，单元节点以铰接的方式互相连接，节点和单元编号如图1.1所示。
图1.1 节点和单元编号2 位移模式图1.1中单元①在局部坐标下的坐标如图1.2所示。
图1.2 单元①在局部坐标三节点单元索取的多项式位移模式为：123456............(1)u x yv x yαααααα=++⎧⎨=++⎩ 将3、2、1节点的坐标代入位移方程中，可解得：33312222211110101111101,11,10222001010u u u u u u u u u ααα===∆∆∆将1α、2α、3α代入式(1)中，可解得：()()()()()()3333222211113333222211111212u a b x c y u a b x c y u a b x c y u v a b x c y v a b x c y v a b x c y v ⎧=++++++++⎡⎤⎣⎦⎪⎪∆⎨⎪=++++++++⎡⎤⎣⎦⎪⎩∆ 其中23122131232111,,,(3,2,1),1122a x y x yb y yc x x m =-=-=-∆=⨯⨯= .因此，解得：3211232131200010101000a x y x yb y yc x x =-=⨯-⨯=⎧⎪=-=-=⎨⎪=-=-=⎩ 2133121323100100000101a x y x y b y y c x x =-=⨯-⨯=⎧⎪=-=-=⎨⎪=-=-=⎩ 1322313212311001011011a x y x yb y yc x x =-=⨯-⨯=⎧⎪=-=-=-⎨⎪=-=-=-⎩ 3 单元刚度矩阵单元的形函数为：()()()33332222111110021002112N a b x c y x x N a b x c y y y N a b x c y x y ⎧=++=++=⎪∆⎪⎪=++=++=⎨∆⎪⎪=++=--⎪∆⎩则应变矩阵为：[]333333333001010000201N x b N B c y c b N N yx ⎡⎤∂⎢⎥∂⎢⎥⎡⎤⎡⎤⎢⎥∂⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥∂∆⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥∂∂⎢⎥∂∂⎣⎦[]222222222000010001210N x b N B c y c b N N y x ⎡⎤∂⎢⎥∂⎢⎥⎡⎤⎡⎤⎢⎥∂⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥∂∆⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥∂∂⎢⎥∂∂⎣⎦[]111111*********001211N x b N B c y c b N N yx ⎡⎤∂⎢⎥∂⎢⎥-⎡⎤⎡⎤⎢⎥∂⎢⎥⎢⎥===-⎢⎥⎢⎥⎢⎥∂∆⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥∂∂⎢⎥∂∂⎣⎦弹性矩阵为：[]72110410321101010115413000028E D νννν⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⨯⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦应力矩阵为：[][][]()2,(1,2,3)211122i i i i i i i i b c ES D B b c i c b ννννν⎡⎤⎢⎥⎢⎥===⎢⎥-∆⎢⎥--⎢⎥⎣⎦即[]7731080321410010201541503308S ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=⨯=⨯⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦[]7721002432410011008151533008S ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=⨯=⨯⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦[]771114823214101102815415333388S ⎡⎤--⎢⎥--⎡⎤⎢⎥⎢⎥⎢⎥=⨯--=⨯--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎢⎥--⎢⎥⎣⎦求单元刚度矩阵：[][][]iiij im eT jijj jm mi mjmm k k k K B S t k k k k k k ⎡⎤⎢⎥=∆=⎢⎥⎢⎥⎣⎦其中：[][][]()21122,(,3,2,1)114122r s r s r s r s T rs r r r s r s r s r s b b c c b c c b Et k B S t r s c b b c c c b b ννννννν--⎡⎤++⎢⎥=∆==⎢⎥---∆⎢⎥++⎢⎥⎣⎦代入数据求得单元刚度矩阵为：[](1)68002820330330330332102008281583321152338511K --⎡⎤⎢⎥--⎢⎥⎢⎥--=⨯⎢⎥--⎢⎥⎢⎥----⎢⎥----⎣⎦同理可求得其他各单元的刚度矩阵均为：[]()6800282033033033033210(2,3,4,5,6)2008281583321152338511i K i --⎡⎤⎢⎥--⎢⎥⎢⎥--=⨯=⎢⎥--⎢⎥⎢⎥----⎢⎥----⎣⎦4 整体刚度矩阵将单元刚度矩阵（6阶方阵）扩大成16阶方阵，除原有9个子矩阵外，其它子矩阵各元素均为零。
悬臂梁的ANSYS典型分析过程
2 、定义参数 Utility Menu>Parameters>Scalar Parameters 文本框中输入“L=2”， “H=0.1”、 “B=0.05”、 “XSECT=H*B” “INERTIAZ=(B*H*3)/12”
3 、定义单元类型和梁的截面尺寸 Main Menu>Preprocessor>Element Type>Add／Edit／Delete 选择“Structural Beam”和“2D elastic 3”选项。
悬臂梁的ANSYS典型分析过程
5
• 如图所示为一个悬臂梁，在力P作用下求该梁A点的挠度。 其中长度L=2m，高度H=0.1m，宽度B=0.05m，作用力 P=10000N，弹性模量E=2×1011Pa（钢材），泊松比为 0.3。
P
A
4
悬臂梁受力
1 、定义工作文件名 Utility Menu>File>Change Jobname ：“Beam”， 选择【New log and error files】寸
Main Menu>Preprocessor>Real Constants>Add／Edit／Delete 选择“Type l BEAM3”选项。弹 出【Real constants for BEAM3】对话框。输入几何特性 “xsect”、“inertiaz”和 “h”，单击“OK”按钮。
10、显示变形结果 Main Menu>General Postproc>Plot Results>Deformed Shape 弹 出 【Plot Deformed Shape】 对 话 框 。 选 择 “Def+undeformed”，生成结果如图1-19所示。
悬臂梁的有限元建模与变形分析
悬臂梁的有限元建模与变形分析摘要：应用有限元软件对矩形截面的悬臂梁受均匀载荷时采用三种不同的模型进 行分析，并且比较其有限元结果与理论结果， 从而得之有限元分析需要进行合理 的分析，建立合适的模型，才可以得到正确的结果。
关键词：建模，有限元1计算分析模型如图1-1所示，左边完全约束，右边不约束。
图1-1梁的计算分析模型 梁截面分别采用以下三种截面（单位：m ）:NameH Profle-1 Shapes Rectangulara: 0.05匚 ancel图1-2矩形截面—P 1 1 1-----------+ -------------------------- 1 1 11in ■ab: 0.3OK I► 1图1-3圆形截面"TEcfftName: Profile-3ihape:]r: OJN日m电；Profrle-2Shape: CircularOK匚ancel2理论计算模型取右端研究OK Cancel图1-4圆形截面qx = 1 .0e5 X XaxW z2000000.05 =2.67 e8Pa 50000400000 12 El 3 El带入y m ax 8.5e - 3m3有限元计算结果u, U2 +0.000e+00 -721Se-Q4 -1.44^-03 -2.165e-O3*3.609e-03 -4 331e-03 •5 0S2e-O3 ”5 774e-C3 -6 4^e.€-O3-7.218e-03 -7 939e-C3图1-5矩形截面变形位移图沢0.36Uj U2+0.000e +00 -7.400e*04 -1.480e-03 -2.220e-03 -2.960e-03 -3,700e-03 -4.440e-03 -5.180e-03 --5,920103-6.660e-03 -7.400e-03 -S.140e-03 -8.e80e-039o±l：teb-i匹 5亡庄 J ： SwiThit-- 帚flcfWrU*■: LA Ji加■OWB 'LV : “ Otf^^KknSr-Jlc-I'KW'- -e.iSfltTfll图1-7 2D 四边形单元变形位移图M MwP.<rPt<.m LffW vnrxr ■Av 5 ^5%' 応 *Cil*+09lL.'3i+G^ 严” I*+1.1讥 7三七时用 jg+03 + I +' JH+ 匕已75(?+U' +< S08«+07 + A 汕2电+07 +二：打知+" + F 3y>+iM图1-6矩形截面应力图盂眾sst 盂srws 力聖匕一^-•、戈Wpr-KODB; Job-222.odb Abaqui/Etandard 6.t0-l Tiie Apr LO LG:53:04 GMT+OS:OD MOiN图1-9 2D 三角形单元变形位移图Sj MisesSNEGf (fraction ■ -1.0) (Avg; 75%)+2.2226+03 +203了e+OS 十 L.S52e+0S + 1.667e+03 + 1.432e40e + 1.2976+03 i-l.lL2e+0S 4-9.2656+07 +7.4-156+07 +5.564^4 07 +3.7136+07 ■i -L.S62e+07 4-1.1246+05益八\醸' %B o.8^-ao#.jt<i33/zci >DHM ,^DVIK -C.H]1 I K A II H CH1 dUm mz1 k::Cbii r hMO图1-8四边形单元应力图J 亠T- +0. OOOe+00L -6.538e-04--1.3006-03 -1.961 £-03 -2£i5e -03 -3.269e-03 -3.923e-03 -4.577e-03 -5.2316-03 -5.gS4e-03 -6.S33e-03 -7.192e-03 -7.S46e-03n戈c 冷心:绻3Y A GDB ： Job-333.odb Abaqus/S^andar(3 6J0-L Tue10 1 e ：55:43 GMT+OS ： 00 201；JUK 3KH i jrK>±iKR i：±CtJ*INt -- ij^d3tl«_W U =E ftta -^rap/; -P 3.9#9r-qiS, M JECSSNEG, (a-dcoon = -1.0) (Aifgi 7 5%) 3沪2则 197c+0e 99S 狂辺■&田趺+oe 芳口"OS 讶机*讯+9和+ 7.993e->07 FS.996e+07+X-. 001^*07 +4J|.4t*Ot图1-10 3D 单元应力图叫憑z、、2图1-9 2D 三角形单元应力图5, Mises(Avg ： 7S<^)■i -G.37Je+06 ■kS.S43e+06 4-S.312e!+06 4^4.7004+06 H.4.24^i+06 +3-7 lSe+06 +3. ia7e+0& +2.656e+0& 4-2. 125e+05 + 1.5环+06 41.062e+0& +5.3口e+05 + 1.7 盘 e+02—7+ !--n■Uj U214-0.000$+00-1.62Oe-O5-3.240e-05-4.050^-05-4.S60e-05-5.669e-05-6.479e-'O5-7.2S9e-O5 a-®.099e-05-e.909e-05-9.719e-05二、结论理论1D2D四边形2D三角形3D单元最大应力(Mpa26726022224063.74最大挠度(mm8.58.78.887.848.099e-3由上面可以看出理论计算值与1D和2D计算结果基本吻合，而与三维结果差异巨大。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Introduction to Simulation
I-DEAS Tutorials: Simulation Projects Simulation involves three major steps: Pre-processing (modeling, applying boundary conditions, meshing); solving the model; and post-processing (displaying the results).
Learn how to:
•create a finite element model
•apply boundary conditions
•mesh the FE model
•solve the FE model
•display the results
Before you begin...
Prerequisite tutorials:•Introducing the I-DEAS Interface Quick Tips to Using I-DEAS
–and–
Creating Parts
•Extruding and Revolving Features
If you didn’t start I-DEAS with a new (empty) model file, open a new one now and give it a unique name.
File
Open
Open Model File form
Model File name: any unique name
OK
Simulation
Master Modeler
Set your units to mm.
Options
Units
mm (milli newton)
What: Sketch this closed shape to the dimensions shown.
Hint
What: Extrude the wireframe using a value of 40mm. Hint
What: Name the part.
Hint
Name form
Name: Bracket
Save the model file.
File
Save
Warning!
If you are prompted by I-DEAS to save your model file, respond:
No
Save only when the tutorial instructions tell you to––not when I-DEAS prompts for a save.
Why:
If you make a mistake at any time between saves and can’t recover, you can reopen your model file to the last save and start over from that point.
Hint
To reopen your model file to the previous save, press Control-Z.
Create a finite element model 1 of 1 What: Create a finite element (FE) model to associate with the part. An FE model is always associated directly to a part.
How:Change the task to Boundary Conditions.
Boundary Conditions
FE Model Create form
FE Model Name: Static Analysis
Geometry Based Analysis Only
OK
Recovery Point
File
Save
What: Fully restrain the rear vertical surface. How:
pick surface
Done
Displacement Restraint on Surface form
OK
What: Create a pressure on the top surface. How:
pick top surface
Done
Pressure on Surface form
Pressure: 500
OK
Things to notice
Circles around the arrows mean the pressure is applied to the part geometry.
Recovery Point
File
Save
Mesh the FE model 1 of 2
I-DEAS Simulation includes manual and automatic meshing tools. Next, a mesh is automatically generated on the entire part.
What: Define the overall element mesh length for the volume.
How:Change the task to Meshing.
Meshing
Done
Define Mesh form
Element Length: 20
OK
What: Generate the solid mesh.
How:
Done
Yes
Things to notice
The elements are parabolic tetrahedral elements. These are more accurate than linear tetrahedral elements for structural analysis.
Recovery Point
File
Save
What: Create a solution set (accepting all defaults) and solve the model using linear statics for deflection and stress.
How:
Model Solution
Manage Solution Sets form
Create...
Solution Set form
OK
Dismiss
What: Solve the model.
How:
Recovery Point
File
Save
I-DEAS List.
When the solve is finished, the I-DEAS List region displays any warnings or errors.
What: When the solver finishes, start the Visualizer. How:
Things to notice
A new graphics window is displayed along with the Visualizer subpanel. Since there’s no display defined, the Create Display form is automatically displayed. Create Display form
OK
Things to notice The display shows the default set of displacement and stress results on the deformed geometry.
What: Use dynamic viewing to orient the display. Only the Visualizer icons work in the Visualizer graphics window.
Hint
F1, F2, and F3
Graphics window to establish focus.
What: Close the Visualizer subpanel.
Close
Tutorial wrap-up 1 of 1 You have completed the Introduction to Simulation tutorial.
Delete the part. It is not used in any other tutorial. To delete the part, first delete the finite element model. How:
Manage Bins form
Dismiss。