专业课设,悬臂梁有限元分析
专业课设,悬臂梁有限元分析
1研究目的与问题阐述1.1 基本研究目的(1) 掌握ANSYS软件的基本几何形体构造、网格划分、边界条件施加等方法。
(2) 熟悉有限元建模、求解及结果分析步骤和方法。
(3) 利用ANSYS软件对梁结构进行有限元计算。
(4) 研究不同泊松比对同一位置应力的影响。
1.2 基本问题提出图1.1 模型示意图如图1.1所示，当EX=3.01e6，F=5000N，悬臂梁杆一端固定，另一端为自由端。
当悬臂梁的泊松比u为：0.2、0.25、0.3、0.35、0.4时，确定同一位置的应力分布，得出分布云图。
二维模型，3*0.09m。
2 软件的介绍与使用2.1 ANSYS 简介ANSYS程序是一个功能强大的灵活的设计分析及优化、融结构、流体、电场、磁场、声场分析于一体的大型通用有限元商用分析软件，可广泛应用于核工业、铁道、石油化工、航空航天、机械制造、能源、汽车交通、国防军工、电子、土木工程、造船、生物医学、轻工、地矿、水利、日用家电等一般工业及科学研究。
该软件提供了一个不断改进的功能清单，集体包括：结构高度非线性分析、电磁分析、计算流体动力分析、设计优化、接触分析、自适应网格划分、大应变/有限转动工功能一接利用ANSYS参数设计的扩展宏命令功能。
ANSYS由世界上最大的有限元分析软件公司之一的美国ANSYS开发，它能与多数系统下生成的集合数据传入ANSYS,如Pro/Engineer, NASTRAN, Alogor, I－DEAS, AutoCAD等，并通过必要的修补可准确地在该模型上划分网格并求解。
2.2 ANSYS软件的功能介绍ANSYS软件含有多种有限元分析的能力，包括从简单线性静态分析到复杂非线性动态分析。
一个典型的ANSYS分析过程可分为以下三个步骤：创建有限元模型；施加载荷进行求解；查看分析结果；在有限元的分析过程中，程序通常使用以下三个部分：前处理模块，分析求解模块和后处理模块。
前处理模块提供了一个强大的实体建模及网格划分工具，通过这个模块用户可以建立自己想要的工程有限模型。
悬臂梁在均布荷载作用下有限元分析报告
悬臂梁承受集中荷载作用问题的弹塑性分析何方平邹里〔某某大学土木工程与力学学院，某某某某411105〕[摘要]本文针对曲杆在水平力作用下的受力性能，结合弹性力学根本方程和塑性力学中Mises屈服条件，得到了弹性阶段应力、位移之间的关系，以与材料发生塑性变形时，处于临界状态点的应力、应变值。
同时，利用有限元分析软件ABAQUS，进展了数值模拟，分析结果与理论值吻合较好，证明所建立的有限元模型是合理的。
关键词：悬臂梁；集中荷载THE ELASTIC-PLASTIC ANALYSIS OF THE CANTILEVER BEAM UNDERconcentrated loadHe Fang-Ping Zhou Li〔College of Civil Engineering & Mechanics, XiangTanUniversity, Xiangtan 411105, China〕【Abstract】This article in view of the force performanceofCANTILEVER BEAM UNDER concentrated load, bined with elastic mechanics basic equations and the plastic mechanics Mises yield conditions, obtained the elastic stage between stress and displacement, and the relationship between material happen plastic deformation, a critical state points of stress and strain value. At the same time, the finite element analysis software ABAQUS, the numerical simulation and analysis results and a good agreement with the theoretical value, show that the established finite element model is reasonable.Keywords: CANTILEVER BEAMconcentrated load题目：试考察应力函数)43(h2223y h xy F-=φ能满足相容方程，并求出应力分量〔不记体力〕，画出例题3-2图所示矩形体边界上的面力分布〔在次要边界上表示出面力的主矢量和主矩〕，指出该应力函数所能解决的问题。
用有限元法对悬臂梁分析的算例算例
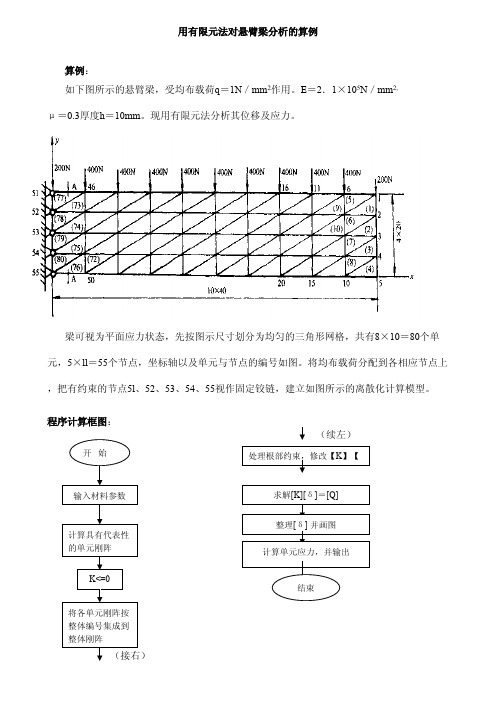
用有限元法对悬臂梁分析的算例算例：如下图所示的悬臂梁，受均布载荷q ＝1N ／mm 2作用。
E ＝2．1×105N ／mm 2,μ＝0.3厚度h ＝10mm 。
现用有限元法分析其位移及应力。
梁可视为平面应力状态，先按图示尺寸划分为均匀的三角形网格，共有8×10＝80个单元，5×ll ＝55个节点，坐标轴以及单元与节点的编号如图。
将均布载荷分配到各相应节点上，把有约束的节点5l 、52、53、54、55视作固定铰链，建立如图所示的离散化计算模型。
程序计算框图：（续左）程序中的函数功能介绍及源代码1.LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)――该函数用于计算平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)、第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)时的线性三角形元的单元刚度矩阵.该函数返回6×6的单位刚度矩阵k.2.LinearTriangleAssemble(K,k,i,j,m)――该函数将连接节点i,j,m的线性三角形元的单元刚度矩阵k集成到整体刚度矩阵K。
每集成一个单元，该函数都将返回2N×2N的整体刚度矩阵K.3.LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)-- 该函数计算在平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi, yi)第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)以及单元位移矢量为u时的单元应力。
该函数返回单元应力矢量。
函数源代码：function y = LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;%三角形单元面积，单元节点应该按逆时针排序，保证每个三角形单元的面积都为正值（也可作为一个小函数：LinearTriangleElementArea）betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);%B为应变矩阵，其中betai=yi-ym,betaj=ym-yi,betam=yi-yj.gammai=xm-xj, gammaj=xi-xm, gammam=xj-xi.D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%D为弹性矩阵，分为平面应力问题和平面应变问题对于平面应力问题D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];对于平面应变问题E1=E/（1-NU*NU），NU1=NU/（1-NU）y = t*A*B'*D*B;%单元刚度矩阵function y = LinearTriangleAssemble(K,k,i,j,m)K(2*i-1,2*i-1) = K(2*i-1,2*i-1) + k(1,1); K(2*i-1,2*i) = K(2*i-1,2*i) + k(1,2);K(2*i-1,2*j-1) = K(2*i-1,2*j-1) + k(1,3); K(2*i-1,2*j) = K(2*i-1,2*j) + k(1,4);K(2*i-1,2*m-1) = K(2*i-1,2*m-1) + k(1,5); K(2*i-1,2*m) = K(2*i-1,2*m) + k(1,6);K(2*i,2*i-1) = K(2*i,2*i-1) + k(2,1); K(2*i,2*i) = K(2*i,2*i) + k(2,2);K(2*i,2*j-1) = K(2*i,2*j-1) + k(2,3); K(2*i,2*j) = K(2*i,2*j) + k(2,4);K(2*i,2*m-1) = K(2*i,2*m-1) + k(2,5); K(2*i,2*m) = K(2*i,2*m) + k(2,6);K(2*j-1,2*i-1) = K(2*j-1,2*i-1) + k(3,1); K(2*j-1,2*i) = K(2*j-1,2*i) + k(3,2);K(2*j-1,2*j-1) = K(2*j-1,2*j-1) + k(3,3); K(2*j-1,2*j) = K(2*j-1,2*j) + k(3,4);K(2*j-1,2*m-1) = K(2*j-1,2*m-1) + k(3,5); K(2*j-1,2*m) = K(2*j-1,2*m) + k(3,6);K(2*j,2*i-1) = K(2*j,2*i-1) + k(4,1); K(2*j,2*i) = K(2*j,2*i) + k(4,2);K(2*j,2*j-1) = K(2*j,2*j-1) + k(4,3); K(2*j,2*j) = K(2*j,2*j) + k(4,4);K(2*j,2*m-1) = K(2*j,2*m-1) + k(4,5); K(2*j,2*m) = K(2*j,2*m) + k(4,6);K(2*m-1,2*i-1) = K(2*m-1,2*i-1) + k(5,1); K(2*m-1,2*i) = K(2*m-1,2*i) + k(5,2);K(2*m-1,2*j-1) = K(2*m-1,2*j-1) + k(5,3); K(2*m-1,2*j) = K(2*m-1,2*j) + k(5,4);K(2*m-1,2*m-1) = K(2*m-1,2*m-1) + k(5,5); K(2*m-1,2*m) = K(2*m-1,2*m) + k(5,6);K(2*m,2*i-1) = K(2*m,2*i-1) + k(6,1); K(2*m,2*i) = K(2*m,2*i) + k(6,2);K(2*m,2*j-1) = K(2*m,2*j-1) + k(6,3); K(2*m,2*j) = K(2*m,2*j) + k(6,4);K(2*m,2*m-1) = K(2*m,2*m-1) + k(6,5); K(2*m,2*m) = K(2*m,2*m) + k(6,6);K;%对号入座，如前所述，每集成一次都将返回2N×2N的整体刚度矩阵K.此题为110×110 function y = LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%平面应力和平面应变问题两种情况y = D*B*u;%单元应力计算主程序源代码E=21e7;NU=0.3;t=0.01;stifflike5=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.08,0.36,0.06,1) %选取2个基本单元，调用M文件stifflike1=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.06,0.4,0.06,1) K=sparse(110,110); %creat a xishu matrix for total stiff创建一个稀疏矩阵for i=1:49if rem(i,5)%模取余，bool型变量，非零即为真j=i;K=LinearTriangleAssemble(K,stifflike5,j,j+5,j+6);%节点编号K=LinearTriangleAssemble(K,stifflike1,j,j+6,j+1);endend%将每个单元刚度矩阵集成到总刚中K=full(K);%转化稀疏矩阵 k=K(1:100,1:100);k=[K,zeros(100,10);zeros(10,100),eye(10)];k=sparse(k);%利用边界条件简化基本方程Q=sparse(2:10:92,1,[-200,-400,-400,-400,-400,-400,-400,-400,-400,-400,],110,1);%外部荷载，此处不包括约束条件，通过形函数确定，是不是可以理解为梁的两端为中间的一半呢？d=k\Q;%高斯消元法，比克莱姆法则在计算速度上有绝对的优势！x=0:0.04:0.4;plot(x,d(106:-10:6))%基本绘图命令grid%带网格y=zeros(80,3);q=0;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.06;xn=0.4;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];xl=0.4;yl=0.06;xm=0.36;ym=0.04;xn=0.4;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.02;xn=0.4;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0;xn=0.4;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endendq=4;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.08;xn=0.36;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.06;xm=0.36;ym=0.06;xn=0.36;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.04;xn=0.36;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0.02;xn=0.36;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endend %y(i+q,:)这是实现什么的？没见过这种用法，算法上应该就是通过节点位移实现指定单元的内力，这部分本人看的也晕晕的，望高人指点N=y(73:80,1)结果图及数据输出悬臂梁轴线挠度图：一单元的单元刚阵1.0e+006 *0.8077 0 0 -0.4038 -0.8077 0.40380 2.3077 -0.3462 0 0.3462 -2.30770 -0.3462 0.5769 0 -0.5769 0.3462-0.4038 0 0 0.2019 0.4038 -0.2019-0.8077 0.3462 -0.5769 0.4038 1.3846 -0.75000.4038 -2.3077 0.3462 -0.2019 -0.7500 2.5096五单元的单元刚阵1.0e+006 *00.050.10.150.20.250.30.350.4x/m w /m0.5769 0 -0.5769 0.3462 0 -0.34620 0.2019 0.4038 -0.2019 -0.4038 0-0.5769 0.4038 1.3846 -0.7500 -0.8077 0.34620.3462 -0.2019 -0.7500 2.5096 0.4038 -2.30770 -0.4038 -0.8077 0.4038 0.8077 0-0.3462 0 0.3462 -2.3077 0 2.3077根部73-80各单元应力计算结果如下（n/m2）：1.0e+007 *2.1119 -0.0621 -2.2816 -4.8824 5.0479 2.4065 0.0352 -2.3753。
悬臂梁有限元分析验证
悬臂梁有限元分析验证XXX-XXX学年第二学期)XXX大学研究生课程论文课程论文题目：悬臂梁有限元分析验证课程名称有限元法课程类别□学位课□非学位课任课教师所在学院学科专业姓名学号提交日期注意事项：1、以上各项由研究生认真填写；2、研究生课程论文应符合一般学术规范，具有一定学术价值，严禁网上下载或抄袭；凡检查或抽查不合格者，一律取消该门课程成绩和学分，并按有关规定追究相关人员责任；3、论文得分由批阅教师填写（见封底），并签字确认；批阅教师应根据作业质量客观、公正的在文后签写批阅意见；4、原则上要求所有课程论文均须用A4纸打印，加装本封面封底，左侧装订；5、课程论文由各学院（部）统一保存，以备查用。
4、卷纸不够写，可另附纸。
摘要：本文通过有限元软件MSC.Patran建立悬臂梁模型，通过对悬臂梁的1D,2D,3D有限元受均布载荷时的应力云图与位移云图作比较，为有限元建模时对梁单元做简化提供验证依据。
关键词：悬臂梁应力位移一提出问题计算矩形截面梁在受均布载荷图1 1D模型应力云图图2 1D模型位移云图结果分析：通过结果云图可以看1D模型应力值在约束点最大值为1.33e7 Pa，最大位移在悬臂梁的自由端其最大值为4.33e-4 m。
计算结果与理论计算结果一致，证明了1D梁单元有限元模型计算的正确性。
2）应力分布由理论计算可得，最大应力为1.33e7Pa，由应力图可得最大应力为1.33e7 Pa，二者基本上相一致；由理论计算，最大挠度为0.423mm，由位移图可得最大桡度为0.433mm，二者基本上相一致。
2D模型分析运用Patran建立有限元模型，划分网格，对其进行约束与加载，并且定义其材料，定义属性，进行分析。
其结果应力云图，与位移云图如下：图4 2D 应力分布云图图5 2D位移云图结果分析：通过结果云图可以看2D模型应力值在约束点最大值为1.13e7 Pa，最大位移在悬臂梁的自由端其最大值为4.34e-4 m。
悬臂梁—有限元ABAQUS线性静力学分析报告实例
线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型，不涉及任何非线性（材料非线性、几何非线性、接触等），也不考虑惯性及时间相关的材料属性。
在ABAQUS 中，该类问题通常采用静态通用（Static ，General ）分析步或静态线性摄动（Static ，Linear perturbation ）分析步进行分析。
线性静力学问题很容易求解，往往用户更关系的是计算效率和求解效率，希望在获得较高精度的前提下尽量缩短计算时间，特别是大型模型。
这主要取决于网格的划分，包括种子的设置、网格控制和单元类型的选取。
在一般的分析中，应尽量选用精度和效率都较高的二次四边形/ 六面体单元，在主要的分析部位设置较密的种子；若主要分析部位的网格没有大的扭曲，使用非协调单元（如CPS4I、C3D8I）的性价比很高。
对于复杂模型，可以采用分割模型的方法划分二次四边形/ 六面体单元；有时分割过程过于繁琐，用户可以采用精度较高的二次三角形/ 四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束，右端自由，结构尺寸如图1-1 所示，求梁受载后的Mises 应力、位移分布。
材料性质：弹性模量 E 2e3 ，泊松比0.3均布载荷：F=103N图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法，用户可以任选一种1）在Windows 操作系统中单击“开始” -- “程序” --ABAQUS 6.10 -- ABAQUS/CA。
E（2）在操作系统的DOS窗口中输入命令：abaqus cae 。
启动ABAQUS/CA后E ，在出现的Start Section （开始任务）对话框中选择Create Model Database 。
1.3 创建部件在ABAQUS/CA顶E 部的环境栏中，可以看到模块列表：Module：Part ，这表示当前处在Part （部件）模块，在这个模块中可以定义模型各部分的几何形体。
悬臂梁有限元分析
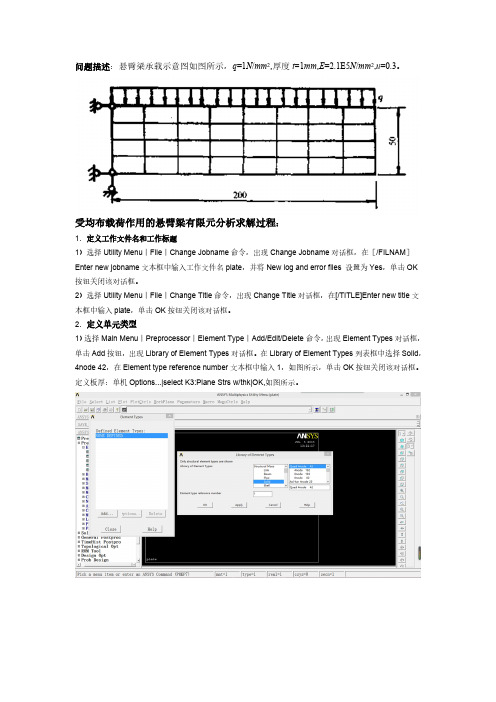
问题描述：悬臂梁承载示意图如图所示，q=1N/mm2,厚度t=1mm,E=2.1E5N/mm2,u=0.3。
受均布载荷作用的悬臂梁有限元分析求解过程：1．定义工作文件名和工作标题1）选择Utility Menu︱File︱Change Jobname命令，出现Change Jobname对话框，在［/FILNAM］Enter new jobname文本框中输入工作文件名plate，并将New log and error files 设置为Yes，单击OK 按钮关闭该对话框。
2）选择Utility Menu︱File︱Change Title命令，出现Change Title对话框，在[/TITLE]Enter new title文本框中输入plate，单击OK按钮关闭该对话框。
2．定义单元类型1）选择Main Menu︱Preprocessor︱Element Type︱Add/Edit/Delete命令，出现Element Types对话框，单击Add按钮，出现Library of Element Types对话框。
在Library of Element Types列表框中选择Solid，4node 42，在Element type reference number文本框中输入1，如图所示，单击OK按钮关闭该对话框。
定义板厚：单机Options...|select K3:Plane Strs w/thk|OK,如图所示。
3．定义材料性能参数1）选择Main Menu︱Preprocessor︱Material Props︱Material Models命令，出现Define Material Model Behavior对话框。
2）在Material Models Available一栏中依次单击Structural、Linear、Elastic、Isotropic选项（如图3.5所示），出现Linear Isotropic Properties for Material Number 1对话框，在EX文本框中输入2.1E5，在PRXY文本框中输入0.3，如图所示，单击OK按钮关闭该对话框。
悬臂梁的有限元分析
工程地质数值模拟成绩考核——昆明理工大学本科生课程*****学院：国土资源工程学院科系：地科系专业：勘查111学号：************2014年11 月8 日悬臂梁的有限元分析1.问题概述。
悬臂梁为矩形截面的钢梁，长10m宽1m、高2m，不计梁的自重，弹性模量为220GPa，泊松比为0.2，在悬臂端作用一集中荷载P=1200kN。
试分析该悬臂梁的内力和变形情况。
2.启动ANSYS程序。
(1)在【开始】菜单中依次选取【所有程序】/【ANSYS8.0】/【ConfigureANSYSProducts】选项，打开【ANSYS8.0Launcher】对话框。
(2)选中【FileManagement】选项卡，输入目录名：“D:\ANSYSFX\zhang1\Exam01\ANSYSjs”，输入项目名：“Z101Beam”。
(3)单击按钮运行程序，进入ANSYS使用界面。
3.定义材料、实常数和单元类型。
(1)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】（前处理）/【ElementType】/【Add/Edit/Delete】选项，打开单元类型对话框。
单击按钮，打开单元类型库对话框，在右侧两个列表框中分别选取【Beam】选项和【2Delastic3】选项（简称为Beam3单元，以后叙述中记为【Beam】-【2Delastic3】单元，类似的情况记法相同），如图1-16所示。
单击按钮，再单击【ElementType】对话框中的按钮。
图1-16【LibraryofElementTypes】对话框(2)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】/【RealConstants】/【Add/Edit/Delete】选项，打开实常数对话框，如图1-17所示。
单击按钮，打开Beam3实常数对话框，按照提示输入相应的面积、惯性矩和梁高参数，如图1-18所示。
悬臂梁的有限元分析
悬臂梁的有限元分析I. 内容综述悬臂梁的有限元分析是结构工程领域中的一个重要课题，它是一种数值计算方法，通过将连续的结构分解成许多小单元，然后对每个单元进行分析，最终得到整个结构的性能指标。
这种方法可以有效地模拟结构的变形和应力分布情况，为设计和优化提供可靠的依据。
在实际应用中，悬臂梁的有限元分析需要考虑多种因素，如材料属性、几何形状、载荷条件等。
因此在进行分析时，需要选择合适的模型和网格尺寸，并对边界条件进行合理设定。
此外由于悬臂梁的结构特点，其在不同位置的受力情况也有所不同，因此需要对各个部位进行分别分析。
悬臂梁的有限元分析是一项复杂而重要的工作，只有通过合理的建模和分析方法，才能得到准确的结果，并为实际工程提供有效的指导。
A. 研究背景和意义悬臂梁作为一种常见的结构形式，广泛应用于建筑、桥梁、机械等领域。
然而在实际应用过程中，由于各种因素的影响，悬臂梁的结构性能可能会发生退化，导致结构的安全性受到威胁。
因此对悬臂梁的有限元分析具有重要的研究意义。
有限元分析是一种基于数学模型的工程分析方法，通过将复杂的结构分解为若干个简单的单元，利用计算机模拟这些单元在受力作用下的变形和应力分布，从而预测结构的响应。
近年来随着计算机技术和数学方法的不断发展，有限元分析在工程领域中的应用越来越广泛，已经成为工程设计和施工的重要工具。
对于悬臂梁这种特殊结构，有限元分析不仅可以帮助我们了解其在不同工况下的性能表现，还可以为优化结构设计、提高结构强度和刚度提供理论依据。
此外通过对悬臂梁的有限元分析，我们还可以更好地了解其在使用过程中可能出现的缺陷和损伤，从而为预防事故、保障人员安全提供技术支持。
悬臂梁的有限元分析研究具有很高的实用价值和理论意义，对于推动工程技术的发展、提高人类生活质量具有重要作用。
B. 研究目的和方法本研究旨在通过有限元分析方法，对悬臂梁进行分析，以探究其在不同荷载下的应力分布情况。
我们将采用ANSYS软件进行模拟计算，并通过对计算结果的分析，得出悬臂梁的最大应力、最小应力以及平均应力等关键指标。
悬臂梁应力分析有限元程序设计
题目：悬臂梁应力分析有限元程序设计毕业设计（论文）外文摘要本科毕业设计（论文）第Ⅰ页共Ⅰ页目录1 引言 (1)2 有限元理论 (2)2.1 有限元法产生的动因分析 (2)2.2 有限元的发展历程 (3)2.3 有限元分析的研究特点 (4)2.4 有限元法的分析过程 (4)2.5 有限元的发展趋势 (6)3 悬臂梁应力分析有限元程序开发 (9)3.1 Matlab语言指南 (9)3.1.1 Matlab语言简介 (9)3.1.2 Matlab的优点 (10)3.2 悬臂梁应力分析程序设计 (11)3.2.1平面问题的4节点矩形单元描述 (11)3.2.2 平面问题4节点矩形单元的MATLAB程序 (16)3.2.3 悬臂梁应用举例 (20)结束语 (34)致谢 (35)参考文献 (36)1 引言悬臂梁在工程力学受力分析中，是一种比较典型的简化模型。
在实际工程分析中，大部分实际工程受力部件都可以简化为悬臂梁。
根据有限元法的基本原理和解决问题的基本思路，对悬臂梁所受的应力进行有限元分析有着重要的作用。
尽管目前已有不少从国外引进的大型通用程序，但由于这些程序通用性很强，语句多，要求计算内存大，在计算具体问题时往往占用机时多，计算成本高，在PC微机广泛普及的今天，编制一些便于推广应用的专用程序无论对于工业设计还是教学实践都是具有一定意义的。
目前，悬臂梁结构在实际工程中被得到广泛的应用，是一种较为常用的结构，尤其在机械设计、建筑设计中更是常见。
悬臂梁结构在实际的使用过程中，经常要承受各种集中载荷、分布载荷、弯矩和扭矩的作用，在梁的任意一处都有可能产生较大的应力和变形，从而使得悬臂梁结构破坏或失效。
悬臂梁的强度及刚度是否满足要求将关系到整个设备的安全使用[1]。
因此，在对悬臂梁结构设计的过程中，如何对悬臂梁的应力进行分析，具有工程实用价值和现实意义。
有限元分析是用来决定复杂机械结构中的应力和变形的一种非常有效的方法，当前用计算机进行的应力分析几乎全部都是以有限元理论为基础的。
悬臂梁ansys有限元分析求最大挠度
悬臂梁ansys有限元分析求最大挠度（一） 悬臂梁ansys 有限元分析求最大挠度问题：悬臂梁长1000mm ，宽50mm ，高10mm ，左端固定，求其在自重作用下的最大挠度？解：弯矩方程：221)()(x l q x M --=微分方程： 221'')(x l q y EI z-=积分求解：DCx qx qlx x ql y EI Cqx qlx x ql y EI z z +++-=++-=4322322'2416125.0615.05.0由边界条件：0;0,0''====A A A y y x θ 得：C=0，D=0I=1/12*h^3*b,h 为梁截面的高，b 为梁截面的宽。
q=ρ*g*a*h*l材料力学公式求：Y=EI85gahl^ρ=5.733mmq EILANSYS 模拟求：Y=5.5392mm，详细见下步骤ANSYS 软件设置及其具体过程如下：步骤1：建立一个模型，在model下creat一个长1，宽0.05，高0.01的长方体实体。
（单位默认为m）步骤2：材料属性设置。
密度：7800，杨氏模量：2E11，泊松比0.3。
步骤3：划分网格。
设置网格单元为structure solid brick 8node 185，mesh tool中设置网格大小为0.002，HEX下点击mesh。
步骤4：施加载荷；在preprocessor中inertia中设置重力加速度Y方向为9.8。
在左面施加固定约束（三个方向固定）步骤5:：求解。
在solve下solve current LS。
步骤6：后处理查看。
在result中plot result，查看nodes displacement。
List查看文本，观察nodes的最大位移点。
二维悬臂梁有限元分析
二维悬臂梁有限元分析二维悬臂梁有限元分析是一种常用的工程结构分析方法，在工程设计和研究中具有重要的应用价值。
本文将从有限元分析的原理和步骤、模型建立、载荷及边界条件、材料特性、求解方案以及结果分析等方面进行论述，探讨二维悬臂梁有限元分析的相关内容。
首先，有限元分析是一种通过将工程结构离散化为有限个小单元，利用单元的力学性质和相邻单元之间的相互作用关系，以数值解的方式求解结构的力学行为的方法。
二维悬臂梁有限元分析的步骤包括建立有限元模型、施加载荷和边界条件、确定材料特性、选择求解方案以及分析结果。
其次，模型建立是有限元分析的关键步骤之一、对于二维悬臂梁，可以采用梁单元进行建模。
梁单元是一种可以描述梁的位移、应变和应力的基本单元，具有两个节点和四个自由度。
通过将悬臂梁划分为多个梁单元，并将其节点连接起来建立悬臂梁有限元模型。
接下来，需要施加适当的载荷和边界条件。
载荷是指在悬臂梁上施加的外部力或力矩，可以是均布载荷、集中力、集中力矩等形式。
边界条件是指限制悬臂梁位移的条件，例如支座的固定或约束。
在二维悬臂梁中，通常将一端固定，即将该节点的两个位移约束为零。
选取合适的求解方案对于二维悬臂梁有限元分析非常关键。
常见的求解方案包括静态分析和动态分析。
静态分析适用于悬臂梁在静力加载下的弯曲和变形分析，动态分析适用于悬臂梁在动力加载下的响应分析。
根据具体问题的需求，选择适当的求解方案进行计算。
最后，需要对计算结果进行分析和评估。
通过数值计算得到的位移、应变和应力等结果，可以用于评估悬臂梁的强度和刚度等性能指标。
同时，也可以通过对结果的灵敏度分析，确定影响悬臂梁性能的关键因素，为工程设计提供参考。
综上所述，二维悬臂梁有限元分析是一种重要的工程结构分析方法。
通过有限元分析，可以预测悬臂梁的力学行为，为工程设计和结构优化提供依据。
然而，为了保证分析结果的准确性，需要合理地选择模型、载荷和边界条件、材料特性，以及采用适当的求解方案，对计算结果进行合理的解释和评估。
悬臂梁—有限元ABAQUS线性静力学分析实例
线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型，不涉及任何非线性（材料非线性、几何非线性、接触等），也不考虑惯性及时刻相关的材料属性。
在ABAQUS中，该类问题通常采纳静态通用（Static，General）分析步或静态线性摄动（Static，Linear perturbation）分析步进行分析。
线性静力学问题很容易求解，往往用户更关系的是计算效率和求解效率，希望在取得较高精度的前提下尽可能缩短计算时刻，专门是大型模型。
这要紧取决于网格的划分，包括种子的设置、网格操纵和单元类型的选取。
在一样的分析中，应尽可能选用精度和效率都较高的二次四边形/六面体单元，在要紧的分析部位设置较密的种子；假设要紧分析部位的网格没有大的扭曲，利用非和谐单元（如CPS4I、C3D8I）的性价比很高。
关于复杂模型，能够采纳分割模型的方式划分二次四边形/六面体单元；有时分割进程过于繁琐，用户能够采纳精度较高的二次三角形/四面体单元进行网格划分。
悬臂梁的线性静力学分析问题的描述一悬臂梁左端受固定约束，右端自由，结构尺寸如图1-1所示，求梁受载后的Mises应力、位移散布。
ν材料性质：弹性模量3E=，泊松比3.0=2e均布载荷：F=103N图1-1 悬臂梁受均布载荷图启动ABAQUS启动ABAQUS有两种方式，用户能够任选一种。
（1）在Windows操作系统中单击“开始”--“程序”--ABAQUS -- ABAQUS/CAE。
（2）在操作系统的DOS窗口中输入命令：abaqus cae。
启动ABAQUS/CAE后，在显现的Start Section（开始任务）对话框当选择Create Model Database。
创建部件在ABAQUS/CAE顶部的环境栏中，能够看到模块列表：Module：Part，这表示当前处在Part（部件）模块，在那个模块中能够概念模型各部份的几何形体。
能够参照下面步骤创建悬臂梁的几何模型。
悬臂梁的有限元建模与优化分析
书托架的有限元建模与优化分析1. 题目概况：考虑如图1所示的木制悬臂梁结构，该梁为矩形截面，承受如图所示的集中载荷。
为满足产品性能及安全性要求，书托架的平均应力不能超过30MPa，且最大变形必须小于1cm，另外由于空间上的约束，其截面尺寸必须满足如下限制条件：5cm《X1《15cm，20cm《X2《40cm，请设计书托架的横断面尺寸，并使梁的重量最小。
习题文件名: Bracket。
图1－1 悬臂梁的示意图2. 题目分析：根据目标函数建立模型：最小化W=ρgabL假设材料密度为常数，该问题就成为一个求最小体积的问题：最下化V=abL本题约束条件：σ《30MPaδ《1cm5cm《X1《15cm20cm《X2《40cm3. 前处理阶段3.1 进入ANSYS(版本ANSYS11.0)程序→Ansys 11.0 Product Launcher →jobname: Bracket→Run3.2 初始化设计变量(长宽面积关于Z轴的惯性矩)实用程序菜单：Parameter →Scalar Parameter →X1=0.05 X2=0.2 AREA=X1*X2 IZZ=(X1*(X2**3))/12 →Accept →Close3.3 定义单元的类型、材料属性与实常数主菜单: Preprocessor →Element Type →Add/Edit/Delete →BEAM3 →OK →Close主菜单: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:3.0e7 →OK →Close主菜单: Preprocessor →Real Constants →Add/Edit/Delete →Add→OK →AREA：AREA IZZ：IZZ HEIGHT：X2 →OK →Close3.4生成几何模型3.4.1生成特征点主菜单: Preprocessor →Modeling →Create →Nodes →On Working Plane →依次输入三个点的坐标：input:1(0,0),2(2.5,0),3(5,0) →OK3.4.2定义单元主菜单: Preprocessor →Modeling →Create →Elements →Auto Numbered →Thru Nodes →点击1(0,0),2(2.5,0) →Apply →点击2(2.5,0),3(5,0) →OK4. 求解阶段4.1定义边界条件主菜单: Solution →Define Loads →Apply →Structural →Displacement →On Nodes →pick the 点1（0，0）→OK →select ALL DOF →OK4.2定义负荷主菜单: Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →pick the 点2（2.5，0）→OK →select FY 500 →Apply →pick the 点3（5，0）→OK →select FY 500 →OK4.3 分析计算主菜单: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK5. 后处理阶段主菜单:General Postproc →List Results →Sorted Listing →Sort Nodes→UY →OK实用程序菜单:Parameters →Get Scalar Data →Result datas :Global measures →DOF USUM DELTAMAX MAX →OK主菜单:General Postproc →Element Table →Define Table →Geometry →VOLU :VOLU →OK主菜单:General Postproc →Element Table →Define Table →By sequence num :SMAX_I NMISC,1 →OK主菜单:General Postproc →Element Table →Define Table →By sequence num :SMAX_J NMISC,3 →OK主菜单:General Postproc →Element Table →Sum of Each etem →OK (结果如下)SUM ALL THE ACTIVE ENTRIES IN THE ELEMENT TABLETABLE LABEL TOTALVOLU 0.500000E-01SMAX_I 0.150000E+08SMAX_J 0.375000E+07实用程序菜单:Parameters →Get Scalar Data →Result datas : Elem table sums →OK →VOLU: VOLUME →OK主菜单:General Postproc →Element Table →List Results →Sorted Listing →Sort Elems →SMAX_I Yes→OK实用程序菜单:Parameters →Get Scalar Data →Result datas :Global measures →SMAX_I MAX →OK主菜单:General Postproc →Element Table →List Results →Sorted Listing →Sort Elems →SMAX_J Yes→OK实用程序菜单：Parameter →Scalar Parameter →SMAX=SMAX_I>SMAX_J→Accept →Close实用程序菜单:File →Write DB log file →opt.db →OK6. 优化阶段主菜单：Design opt →Analysis File →Assign →opt.db →OK主菜单：Design opt →Design variables →x1,0.05,0.15→OK主菜单：Design opt →Design variables →x2,0.2,0.4→OK主菜单：Design opt →State variables →DELTAMAX,0,0.01→OK主菜单：Design opt →State variables →SMAX,0,0.01→OK主菜单：Design opt →Objective →VOLUME→OK主菜单：Design opt →Objective →Method/tool→First-order →100 →OK主菜单：Design opt →run →OK(结果如下)SET 3(INFEASIBLE)DELTAMAX(SV) > 1.1393SMAX (SV) 0.93750E+06X1 (DV) 0.15000X2 (DV) 0.40000VOLUME (OBJ) 0.300007. 结果分析结果显示，在最大截面积时（X1=0.15，X2=0.4），应变仍大于题目要求，因此应加大截面积或减少荷载8. 退出系统实用程序菜单: File→Exit…→Save Everything→OK。
有限元分析(共2张PPT)
s
3、试计算下列载荷的单元等效节点力。
1、=一1/3悬，臂梁梁的，厚载度荷为均t。匀分布在自由端截面上，合力为P，采用图示网格，求各节点位移及单元应力。
1、=一1/3悬，臂梁梁的，厚载度荷为均t。匀分布在自由端截面上，合力为P，采用图示网格，求各节点位移及单t。单元等效节点力。
3、=试1/3计，算梁下的列厚载度荷为的t。单元等效节点力。
31、试一计悬算臂下梁列，载荷的均单 匀元分等布效在节自点由力端。截面上①，合力为P，采用图3示网格，求各节点位移及单元应力。
=1/3，梁的厚度为t。
112、 、=一一将1/3悬悬上，臂臂题梁梁梁的的，，悬厚载载臂度荷荷梁为均均改t。匀 匀 用分分图布布示在在的自自四由由个端端单1截截元面面的上上网，，格合合进力力行为为计算PP，，，3采采用用图图示示网网格格，，求求各各节节5 点点位位移移及及单单元元应应力力。。
作业
1、一悬臂梁，载荷均匀分布在自由端截面上，合力为P，采用图示网
格，求各节点位移及单元应力。=1/3，梁的厚度为t。
。 。。4
。 P/2 3 ②
1m
P t
。 。。1 ①
2m
。 2 P/2
2、将上题的悬臂梁改用图示的四个单元的网格进行计算，
设 = 0，试求整体刚度矩阵。
3、=试1/3计，算梁下的列厚载度荷为的t。单元等效节点力。
1、==一11//33悬， ，臂梁梁梁的 的，厚 厚载度 度荷为 为均tt。 。匀分布在自由端2 截面上，合力为P，4采用图示网格，求各节6点位移及单元应力。
3、=试1/3计，算梁下的列厚载度荷为的t。单元等效节点力。
31、 、=试一1/3计悬，算臂梁下梁的列，厚载载度荷荷为的均t。单 匀元分等布效在节自点由力端。截面上，合力为② P，采用图示网格4，求各节点位移及单元应力。
ANSYS有限元分析实例
ANSYS有限元分析实例1.悬臂梁的结构分析悬臂梁是一种常见的结构，其呈直线形式，一端固定于支撑点，另一端自由悬挂。
在这个分析中，我们将使用ANSYS来确定悬臂梁的最大弯曲应力和挠度。
首先，我们需要创建悬臂梁的几何模型，并给出其材料属性和加载条件。
然后，在ANSYS中创建有限元模型，并进行网格划分。
接下来，进行力学分析，求解材料在给定加载下的应力和位移。
最后，通过对结果的后处理，得出最大弯曲应力和挠度。
2.螺旋桨的流体力学分析螺旋桨是一种能够产生推力的旋转装置，广泛应用于船舶、飞机等交通工具中。
螺旋桨的流体力学分析可以帮助我们确定其叶片的受力情况和推力性能。
在这个分析中，我们需要建立螺旋桨的几何模型，并给出流体的流速和压力条件。
然后，我们在ANSYS中创建螺旋桨的有限元模型，并进行网格划分。
通过求解流体场方程，计算叶片上的压力分布和受力情况。
最后，通过对结果的后处理，得出叶片的受力情况和推力性能。
3.散热片的热传导分析散热片是一种用于散热的装置，广泛应用于电子设备、电脑等领域。
散热片的热传导分析可以帮助我们确定散热片在给定热源条件下的温度分布和散热性能。
在这个分析中，我们需要建立散热片的几何模型，并给出材料的热导率和热源条件。
然后，我们在ANSYS中创建散热片的有限元模型，并进行网格划分。
通过求解热传导方程，计算散热片上各点的温度分布。
最后，通过对结果的后处理，得出散热片的温度分布和散热性能。
以上是三个ANSYS有限元分析的实例，分别涉及结构分析、流体力学分析和热传导分析。
通过这些实例，我们可以充分展示ANSYS在不同领域的应用，并帮助工程师和科研人员解决工程问题，提高设计效率和产品性能。
有限元法手算求解悬臂梁内力
题目信息：已知一悬臂梁，其受荷情况及尺寸如右图所示，72210/,0.25E kN m ν=⨯=，厚度100t mm =，试用有限单元法计算其应力分布，并将有限元结果与材料力学结果进行对比。
解析：手算八节点六单元模型1 结构离散化将悬臂梁划分成六个三角形单元，单元节点以铰接的方式互相连接，节点和单元编号如图1.1所示。
图1.1 节点和单元编号2 位移模式图1.1中单元①在局部坐标下的坐标如图1.2所示。
图1.2 单元①在局部坐标三节点单元索取的多项式位移模式为：123456............(1)u x yv x yαααααα=++⎧⎨=++⎩ 将3、2、1节点的坐标代入位移方程中，可解得：33312222211110101111101,11,10222001010u u u u u u u u u ααα===∆∆∆将1α、2α、3α代入式(1)中，可解得：()()()()()()3333222211113333222211111212u a b x c y u a b x c y u a b x c y u v a b x c y v a b x c y v a b x c y v ⎧=++++++++⎡⎤⎣⎦⎪⎪∆⎨⎪=++++++++⎡⎤⎣⎦⎪⎩∆ 其中23122131232111,,,(3,2,1),1122a x y x yb y yc x x m =-=-=-∆=⨯⨯= .因此，解得：3211232131200010101000a x y x yb y yc x x =-=⨯-⨯=⎧⎪=-=-=⎨⎪=-=-=⎩ 2133121323100100000101a x y x y b y y c x x =-=⨯-⨯=⎧⎪=-=-=⎨⎪=-=-=⎩ 1322313212311001011011a x y x yb y yc x x =-=⨯-⨯=⎧⎪=-=-=-⎨⎪=-=-=-⎩ 3 单元刚度矩阵单元的形函数为：()()()33332222111110021002112N a b x c y x x N a b x c y y y N a b x c y x y ⎧=++=++=⎪∆⎪⎪=++=++=⎨∆⎪⎪=++=--⎪∆⎩则应变矩阵为：[]333333333001010000201N x b N B c y c b N N yx ⎡⎤∂⎢⎥∂⎢⎥⎡⎤⎡⎤⎢⎥∂⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥∂∆⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥∂∂⎢⎥∂∂⎣⎦[]222222222000010001210N x b N B c y c b N N y x ⎡⎤∂⎢⎥∂⎢⎥⎡⎤⎡⎤⎢⎥∂⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥∂∆⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥∂∂⎢⎥∂∂⎣⎦[]111111*********001211N x b N B c y c b N N yx ⎡⎤∂⎢⎥∂⎢⎥-⎡⎤⎡⎤⎢⎥∂⎢⎥⎢⎥===-⎢⎥⎢⎥⎢⎥∂∆⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥∂∂⎢⎥∂∂⎣⎦弹性矩阵为：[]72110410321101010115413000028E D νννν⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⨯⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦应力矩阵为：[][][]()2,(1,2,3)211122i i i i i i i i b c ES D B b c i c b ννννν⎡⎤⎢⎥⎢⎥===⎢⎥-∆⎢⎥--⎢⎥⎣⎦即[]7731080321410010201541503308S ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=⨯=⨯⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦[]7721002432410011008151533008S ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=⨯=⨯⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦[]771114823214101102815415333388S ⎡⎤--⎢⎥--⎡⎤⎢⎥⎢⎥⎢⎥=⨯--=⨯--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎢⎥--⎢⎥⎣⎦求单元刚度矩阵：[][][]iiij im eT jijj jm mi mjmm k k k K B S t k k k k k k ⎡⎤⎢⎥=∆=⎢⎥⎢⎥⎣⎦其中：[][][]()21122,(,3,2,1)114122r s r s r s r s T rs r r r s r s r s r s b b c c b c c b Et k B S t r s c b b c c c b b ννννννν--⎡⎤++⎢⎥=∆==⎢⎥---∆⎢⎥++⎢⎥⎣⎦代入数据求得单元刚度矩阵为：[](1)68002820330330330332102008281583321152338511K --⎡⎤⎢⎥--⎢⎥⎢⎥--=⨯⎢⎥--⎢⎥⎢⎥----⎢⎥----⎣⎦同理可求得其他各单元的刚度矩阵均为：[]()6800282033033033033210(2,3,4,5,6)2008281583321152338511i K i --⎡⎤⎢⎥--⎢⎥⎢⎥--=⨯=⎢⎥--⎢⎥⎢⎥----⎢⎥----⎣⎦4 整体刚度矩阵将单元刚度矩阵（6阶方阵）扩大成16阶方阵，除原有9个子矩阵外，其它子矩阵各元素均为零。
悬臂梁的有限元建模与变形分析
悬臂梁的有限元建模与变形分析摘要：应用有限元软件对矩形截面的悬臂梁受均匀载荷时采用三种不同的模型进 行分析，并且比较其有限元结果与理论结果， 从而得之有限元分析需要进行合理 的分析，建立合适的模型，才可以得到正确的结果。
关键词：建模，有限元1计算分析模型如图1-1所示，左边完全约束，右边不约束。
图1-1梁的计算分析模型 梁截面分别采用以下三种截面（单位：m ）:NameH Profle-1 Shapes Rectangulara: 0.05匚 ancel图1-2矩形截面—P 1 1 1-----------+ -------------------------- 1 1 11in ■ab: 0.3OK I► 1图1-3圆形截面"TEcfftName: Profile-3ihape:]r: OJN日m电；Profrle-2Shape: CircularOK匚ancel2理论计算模型取右端研究OK Cancel图1-4圆形截面qx = 1 .0e5 X XaxW z2000000.05 =2.67 e8Pa 50000400000 12 El 3 El带入y m ax 8.5e - 3m3有限元计算结果u, U2 +0.000e+00 -721Se-Q4 -1.44^-03 -2.165e-O3*3.609e-03 -4 331e-03 •5 0S2e-O3 ”5 774e-C3 -6 4^e.€-O3-7.218e-03 -7 939e-C3图1-5矩形截面变形位移图沢0.36Uj U2+0.000e +00 -7.400e*04 -1.480e-03 -2.220e-03 -2.960e-03 -3,700e-03 -4.440e-03 -5.180e-03 --5,920103-6.660e-03 -7.400e-03 -S.140e-03 -8.e80e-039o±l：teb-i匹 5亡庄 J ： SwiThit-- 帚flcfWrU*■: LA Ji加■OWB 'LV : “ Otf^^KknSr-Jlc-I'KW'- -e.iSfltTfll图1-7 2D 四边形单元变形位移图M MwP.<rPt<.m LffW vnrxr ■Av 5 ^5%' 応 *Cil*+09lL.'3i+G^ 严” I*+1.1讥 7三七时用 jg+03 + I +' JH+ 匕已75(?+U' +< S08«+07 + A 汕2电+07 +二：打知+" + F 3y>+iM图1-6矩形截面应力图盂眾sst 盂srws 力聖匕一^-•、戈Wpr-KODB; Job-222.odb Abaqui/Etandard 6.t0-l Tiie Apr LO LG:53:04 GMT+OS:OD MOiN图1-9 2D 三角形单元变形位移图Sj MisesSNEGf (fraction ■ -1.0) (Avg; 75%)+2.2226+03 +203了e+OS 十 L.S52e+0S + 1.667e+03 + 1.432e40e + 1.2976+03 i-l.lL2e+0S 4-9.2656+07 +7.4-156+07 +5.564^4 07 +3.7136+07 ■i -L.S62e+07 4-1.1246+05益八\醸' %B o.8^-ao#.jt<i33/zci >DHM ,^DVIK -C.H]1 I K A II H CH1 dUm mz1 k::Cbii r hMO图1-8四边形单元应力图J 亠T- +0. OOOe+00L -6.538e-04--1.3006-03 -1.961 £-03 -2£i5e -03 -3.269e-03 -3.923e-03 -4.577e-03 -5.2316-03 -5.gS4e-03 -6.S33e-03 -7.192e-03 -7.S46e-03n戈c 冷心:绻3Y A GDB ： Job-333.odb Abaqus/S^andar(3 6J0-L Tue10 1 e ：55:43 GMT+OS ： 00 201；JUK 3KH i jrK>±iKR i：±CtJ*INt -- ij^d3tl«_W U =E ftta -^rap/; -P 3.9#9r-qiS, M JECSSNEG, (a-dcoon = -1.0) (Aifgi 7 5%) 3沪2则 197c+0e 99S 狂辺■&田趺+oe 芳口"OS 讶机*讯+9和+ 7.993e->07 FS.996e+07+X-. 001^*07 +4J|.4t*Ot图1-10 3D 单元应力图叫憑z、、2图1-9 2D 三角形单元应力图5, Mises(Avg ： 7S<^)■i -G.37Je+06 ■kS.S43e+06 4-S.312e!+06 4^4.7004+06 H.4.24^i+06 +3-7 lSe+06 +3. ia7e+0& +2.656e+0& 4-2. 125e+05 + 1.5环+06 41.062e+0& +5.3口e+05 + 1.7 盘 e+02—7+ !--n■Uj U214-0.000$+00-1.62Oe-O5-3.240e-05-4.050^-05-4.S60e-05-5.669e-05-6.479e-'O5-7.2S9e-O5 a-®.099e-05-e.909e-05-9.719e-05二、结论理论1D2D四边形2D三角形3D单元最大应力(Mpa26726022224063.74最大挠度(mm8.58.78.887.848.099e-3由上面可以看出理论计算值与1D和2D计算结果基本吻合，而与三维结果差异巨大。
悬臂梁—有限元ABAQUS线性静力学分析实例
线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型，不涉及任何非线性（材料非线性、几何非线性、接触等），也不考虑惯性及时间相关的材料属性。
在ABAQUS中，该类问题通常采用静态通用（Static，General）分析步或静态线性摄动（Static，Linear perturbation）分析步进行分析。
线性静力学问题很容易求解，往往用户更关系的是计算效率和求解效率，希望在获得较高精度的前提下尽量缩短计算时间，特别是大型模型。
这主要取决于网格的划分，包括种子的设置、网格控制和单元类型的选取。
在一般的分析中，应尽量选用精度和效率都较高的二次四边形/六面体单元，在主要的分析部位设置较密的种子；若主要分析部位的网格没有大的扭曲，使用非协调单元（如CPS4I、C3D8I）的性价比很高。
对于复杂模型，可以采用分割模型的方法划分二次四边形/六面体单元；有时分割过程过于繁琐，用户可以采用精度较高的二次三角形/四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束，右端自由，结构尺寸如图1-1所示，求梁受载后的Mises应力、位移分布。
ν材料性质：弹性模量3=E=，泊松比3.02e均布载荷：F=103N图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法，用户可以任选一种。
（1）在Windows操作系统中单击“开始”--“程序”--ABAQUS 6.10 --ABAQUS/CAE。
（2）在操作系统的DOS窗口中输入命令：abaqus cae。
启动ABAQUS/CAE后，在出现的Start Section（开始任务）对话框中选择Create Model Database。
1.3 创建部件在ABAQUS/CAE顶部的环境栏中，可以看到模块列表：Module：Part，这表示当前处在Part（部件）模块，在这个模块中可以定义模型各部分的几何形体。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1研究目的与问题阐述1.1 基本研究目的(1) 掌握ANSYS软件的基本几何形体构造、网格划分、边界条件施加等方法。
(2) 熟悉有限元建模、求解及结果分析步骤和方法。
(3) 利用ANSYS软件对梁结构进行有限元计算。
(4) 研究不同泊松比对同一位置应力的影响。
1.2 基本问题提出图1.1 模型示意图如图1.1所示，当EX=3.01e6，F=5000N，悬臂梁杆一端固定，另一端为自由端。
当悬臂梁的泊松比u为：0.2、0.25、0.3、0.35、0.4时，确定同一位置的应力分布，得出分布云图。
二维模型，3*0.09m。
2 软件的介绍与使用2.1 ANSYS 简介ANSYS程序是一个功能强大的灵活的设计分析及优化、融结构、流体、电场、磁场、声场分析于一体的大型通用有限元商用分析软件，可广泛应用于核工业、铁道、石油化工、航空航天、机械制造、能源、汽车交通、国防军工、电子、土木工程、造船、生物医学、轻工、地矿、水利、日用家电等一般工业及科学研究。
该软件提供了一个不断改进的功能清单，集体包括：结构高度非线性分析、电磁分析、计算流体动力分析、设计优化、接触分析、自适应网格划分、大应变/有限转动工功能一接利用ANSYS参数设计的扩展宏命令功能。
ANSYS由世界上最大的有限元分析软件公司之一的美国ANSYS开发，它能与多数系统下生成的集合数据传入ANSYS,如Pro/Engineer, NASTRAN, Alogor, I－DEAS, AutoCAD等，并通过必要的修补可准确地在该模型上划分网格并求解。
2.2 ANSYS软件的功能介绍ANSYS软件含有多种有限元分析的能力，包括从简单线性静态分析到复杂非线性动态分析。
一个典型的ANSYS分析过程可分为以下三个步骤：创建有限元模型；施加载荷进行求解；查看分析结果；在有限元的分析过程中，程序通常使用以下三个部分：前处理模块，分析求解模块和后处理模块。
前处理模块提供了一个强大的实体建模及网格划分工具，通过这个模块用户可以建立自己想要的工程有限模型。
分析求解模块即是对已建立好的模型在一定的载荷和边界条件下进行有限元计算，求解平衡微分方程。
包括结构分析（可进行线性分析、非线性分析和高度非线性分析）、流体动力学分析、电磁场分析、声场分析、压电分析以及多物理场的耦合分析（热-应力耦合、流-固耦合以及电-磁-热-应力耦合）等，可模拟多种物理介质的相互作用，具有灵敏度分析及优化分析能力；后处理模块可将计算结果以彩色等值线显示、梯度显示、矢量显示、粒子流迹显示、立体切片显示、透明及半透明显示（可看到结构内部）等图形方式显示出来，也可将计算结果以图表、曲线形式显示或输出。
下面对ANSYS软件的三种模块的功能进行简要介绍：1.前处理模块ANSYS软件的前处理模块主要实现三种功能：参数定义、实体建模和网格划分。
（1）参数定义ANSYS程序在进行结构建模的过程中，首先要对所有被建模型的材料进行参数定义。
包括定义使用单位制，定义所有使用单元的类型，定义单元的实常数，定义材料的特性以及使用材料库文件等。
（2）实体建模在实体建模过程中，ANSYS程序提供了两种方法：从高级到低级的建模与从低级到高级的建模。
(3)网格划分ANSYS系统的网格划分功能十分强大，，使用起来十分便捷。
从使用选择的角度来讲，程序的网格划分可以分为系统智能划分和人工选择划分两种。
从网格划分的功能来讲，则包括四种划分：延伸划分、映像划分、自由划分和自适应划分。
2.求解模块在此阶段，用户可以定义分析类型、分析选项、载荷数据和载荷步选项。
（1）定义分析类型和分析选项用户可以根据所施加载荷条件和所要计算的响应来选择分析类型。
分析选项允许用户自定义分析类型。
（2）载荷一般所谓的载荷应该包括边界条件（结束、支承或边界场的参数）和其他外部或内部作用载荷。
在ANSYS程序中，载荷分为六类：DOF约束、力、表面分布载荷、体积载荷、惯性载荷、耦合场载荷。
（3）指定载荷步载荷步选项是用于改正载荷步的选项，如子步数、载荷步的结束时间和输出控制。
根据所作分析的类型，载荷步选项可有可无。
3.后处理模块ANSYS程序的后处理包含两个部分：通用后处理模块和时间历程后处理模块。
（1）通用后处理模块通用后处理模块可以用于查看整个模块或选定的部分模块在某一子步（时间步）的结果。
可获得等值线显示、变型形状以及检查和解释分析的结果和列表。
（2）时间历程后处理模块时间后处理模块可以用于查看模型的特定点在所有时间步内的结果。
可获得结果数据对时间（或频率）的关系的图形曲线以及列表。
软件提供了100种以上的单元类型，用来模拟工程中的各种结构和材料。
该软件有多种不同版本，可以运行在从个人机到大型机的多种计算机设备上，如PC，SGI，HP，SUN，DEC，IBM，CRAY等。
3.研究方法及过程3.1研究方法一介绍(1) Utility Menu→File→Clear&Start New(2) Utility Menu→File→Change Jobname（输入新的工作文件名为Cantilever）(3) Utility Menu→ File→ Change Title （输入Changing pressure on one point of a pole）(4) Main Menu→Preprocessor→Element Type→Add/Edit/Delete（选择单元类型Structural--Solid--Quad 4node 42）(5) Main Menu→Preprocessor→Material props→Material Models→Structural(机构）→Linear(线性）→Elastic(弹性）→Isotropic（各向同性）(6) Main Menu→Preprocessor→Modeling→Create→Areas→Rectangle→By Dimensions(7) Main Menu→Preprocessor→Meshing →MeshAttributes→All Areas(8) Main Menu→Preprocessor→Meshing →SizeCntrls→SmartSize→Basic(9) Main Menu→Preprocessor→Meshing →Mesh→Area→Free(10)Main Menu→Solution→Analysis Type→New Analysis(11)Main Menu→Solution→Define Load（定义载荷）→ Apply（加载）→Structural （结构）→Displacement（位移）→On Lines（在线上）(13) Main Menu→Solution→Define Load（定义载荷）→ Apply（加载）→Structural （结构）→Force/Moment（力/力矩）→On Keypoint （在关键点上）(14) Main Menu→ Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK(15) Main Menu→ General Postproc →Plot Results →Deformed Shape…→select Def + Undeformed →OK(16) Main Menu→General Postproc→Plot Results（绘制结果）→Contour Plot （绘制等值图）→Nodal Solu（节点解）→Nodal Solution（节点解）→Elastic Strain （弹性应变）→Y-Component of elastic strain（弹性应变Y分量）(17) Main Menu→ General Postproc → Query Results →Subgrid Solu →选择Stress → X-Component of stress →OK 在应力分布图中，选择一固定节点，点OK即可测出相应Y方向上应力。
3.2研究方法二介绍3.2.1过滤菜单（1) Main Menu: Preferences →select Structural → OK图3.1 过滤菜单3.3.2 实体建模(1) 建立方位点Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS →依次输入4个点的坐标：input:1(0,0,0)→Apply → 2(3000,0,0)→Apply →3(3000,90,0) →Apply → 4(0,90,0) →OK注：在实体建模中，建立四个方位点，首先建立点1，如图3.2所示，然后选用Apply应用，再依次输入点2、3、4方位。
图3.2 建立方位点(2) 由4个关键点组成面Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPs →依次拾取4个点→OK注：在拾取关键点是要按顺序依次拾取，拾取完点击OK即可3.3.3 划分网格(1) 定义单元类型Main Menu: Preprocessor →Element Type→Add/Edit/Delete →Add →select Solid Quad 4node 42 →OK (返回到the Element Types window) →Options→selelt K3: Plane Strsw/thk → Close (the Element Type window)此处选用Solid Quad 4node 42。
图 3.3 选择单元类型图 3.4（2) 定义实常数Main Menu: Preprocessor →Real Constants →Add →select Type 1→ OK→input THK:90 →OK →Close (the Real Constants Window)注：定义悬臂梁的厚度，即在THK框中输入90（mm）,如图3.5所示图 3.5 定义悬臂梁厚度(3) 定义材料（弹性模量，泊松比）Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:3.01e6, PRXY:0.2 → OK 注：定义材料弹性模量及泊松比，EX为弹性模量，PRXY为泊松比，在第一次定义时在PRXY框中输入0.2，以后同理，依次输入0.25、0.3、0.35、0.4，如图3.6所示。