图与网络模型实验
图与网络的运筹学实验报告

图与网络的运筹学实验报告图与网络的运筹学实验报告引言:图与网络是运筹学中的重要概念,它们在各个领域中都有广泛的应用。
本实验旨在通过实际案例,探讨图与网络在运筹学中的应用,并通过运筹学方法对问题进行求解和优化。
一、图与网络的基本概念1.1 图的定义与表示图是由节点和边组成的数学模型,它可以用来描述各种实际问题。
图可以用邻接矩阵或邻接表等方式进行表示。
1.2 网络的定义与分类网络是图的一种特殊形式,它的边具有权重或容量等属性。
根据边的属性不同,网络可以分为最短路径网络、最小生成树网络、最大流网络等。
二、图与网络在运筹学中的应用2.1 最短路径问题最短路径问题是图与网络中的经典问题之一。
通过运筹学方法,可以求解两点之间的最短路径,并找到最优解。
2.2 最小生成树问题最小生成树问题是在图中找到一棵包含所有节点的树,并使得树的边权重之和最小。
通过运筹学方法,可以有效地解决最小生成树问题。
2.3 最大流问题最大流问题是在网络中找到从源节点到汇节点的最大流量。
通过运筹学方法,可以确定网络中的最大流,并进行优化。
三、实际案例分析3.1 交通网络优化以城市交通网络为例,通过建立图模型,可以对交通流量进行优化调度,减少交通拥堵和能源消耗。
3.2 物流配送优化以物流配送为例,通过建立网络模型,可以优化货物运输路径,减少运输成本和时间。
3.3 电力网络优化以电力网络为例,通过建立图模型,可以优化电力输送路径,提高电网的稳定性和可靠性。
四、运筹学方法的求解4.1 最短路径求解算法常用的最短路径算法有Dijkstra算法和Floyd-Warshall算法,它们可以高效地求解最短路径问题。
4.2 最小生成树求解算法常用的最小生成树算法有Prim算法和Kruskal算法,它们可以高效地求解最小生成树问题。
4.3 最大流求解算法常用的最大流算法有Ford-Fulkerson算法和Edmonds-Karp算法,它们可以高效地求解最大流问题。
数学建模方法之图与网络模型

最小生成树问题就是指在一个赋权的连通的无向图G中找出一个生成 树,并使得这个生成树的所有边的权数之和为最小。
(a)
图11-12
(b)
(c)
11
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤: 1、在给定的赋权的连通图上任找一个圈。 2、在所找的圈中去掉一个权数最大的边(如果有两条或两条
1.给出点V1以标号(0,s) 2.找出已标号的点的集合I,没标号的点的集合J以及弧的集合
{(vi , v j ) | vi I , v j J}
3. 如果上述弧的集合是空集,则计算结束。如果vt已标号(lt,kt),则 vs 到vt的距离为lt,而从 vs到vt的最短路径,则可以从kt 反向追踪到起点 vs 而得到。如果vt 未标号,则可以断言不存在从 vs到vt的有向路。如果 上述的弧的集合不是空集,则转下一步。
e2
(v(v3) 李(v4)
周(v5)
图11-2
e5 吴(v6) 陈(v7)
3
如果我们把上面例子中的“相互认识”关系改为“认识”
的关系,那么只用两点之间的联线就很难刻画他们之间的关
系了,这是我们引入一个带箭头的联线,称为弧。图11-3就
是一个反映这七人“认识”关系的图。相互认识用两条反向
的弧表示。
a1 a2
(v2)钱
a7
a8
(赵v1)
a14 a15 a3
(v4) 李
a4
a9
(v3)孙
a5
a6
a12
a11
(v5) 周
a10
(v6)吴 a13
模型网络算法实验报告(3篇)

第1篇一、实验背景随着信息技术的飞速发展,模型网络算法在各个领域都得到了广泛应用。
为了深入了解模型网络算法的原理和应用,我们设计并完成了一次模型网络算法实验。
本次实验旨在通过构建一个简单的模型网络,学习并验证模型网络算法在数据处理和模式识别等方面的性能。
二、实验目的1. 理解模型网络算法的基本原理;2. 掌握模型网络算法的实现方法;3. 评估模型网络算法在不同数据集上的性能;4. 分析模型网络算法的优缺点。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 库:NumPy、Scikit-learn、Matplotlib4. 数据集:Iris数据集、MNIST数据集四、实验内容1. 模型网络算法概述模型网络算法是一种基于图论的算法,通过构建模型网络来模拟真实世界中的复杂关系。
模型网络由节点和边组成,节点代表实体,边代表实体之间的关系。
模型网络算法可以用于数据分析、模式识别、知识图谱构建等领域。
2. 模型网络算法实现本次实验采用Python编程语言实现模型网络算法。
具体步骤如下:(1)加载数据集:从Iris数据集和MNIST数据集中获取数据。
(2)构建模型网络:根据数据集的特征,构建模型网络。
例如,在Iris数据集中,可以按照花种类型构建节点,按照特征值构建边。
(3)模型网络算法:使用模型网络算法对数据进行处理。
例如,使用PageRank算法计算节点的权重,使用链接预测算法预测节点之间的关系。
(4)性能评估:使用准确率、召回率、F1值等指标评估模型网络算法在不同数据集上的性能。
3. 实验结果与分析(1)Iris数据集在Iris数据集上,我们使用PageRank算法计算节点的权重,并使用链接预测算法预测节点之间的关系。
实验结果显示,模型网络算法在Iris数据集上的准确率达到80%以上。
(2)MNIST数据集在MNIST数据集上,我们使用模型网络算法对图像进行分类。
实验结果显示,模型网络算法在MNIST数据集上的准确率达到90%以上。
图于网络分析实验报告

Inf Inf Inf Inf 300 Inf Inf Inf
Inf Inf Inf Inf Inf 100 Inf Inf
即最短路为12,24,34,46,56,57,68,她们构成一棵最小数,总长度为1400千米,如图:
五、分析与小结
end
end
ifnnz(mst)==(2*n-2)%|E|=|V|-1
input('The weight matrix of the Minimum Spanning Tree of the graph is:')
MST
else%|E|<|V|-1
input('The graph doesn"t include a Minimum Spanning Tree.')
end
实验结果:当起始点为1时,程序运行结果为
n =
8
W =
Inf 200 600 500 Inf Inf Inf Inf
200 Inf Inf 300 800 Inf 900 Inf
600 Inf Inf 100 Inf 400 Inf Inf
500 300 100 Inf 500 200 Inf Inf
Inf 800 Inf 500 Inf 200 300 Inf
Inf Inf 400 200 200 Inf 400 100
Inf 900 Inf Inf 300 400 Inf 500
Inf Inf Inf Inf Inf 100 500 Inf
The weight matrix of the Minimum Spanning Tree of the graph is:1
《运筹学》实验三__图与网络分析(学生版)
18
实验三 图与网络分析
一、实验目的
掌握不同问题的输入方法,求解网络模型,观察求解步骤,显示并读出结果。
二、实验平台和环境
WindowsXP 平台下,WinQSB V2.0版本已经安装在D:\WinQSB 中。
三、实验内容和要求
用WinQSB 软件求解最小支撑树,最短路及网络最大流等问题。
四、实验操作步骤
1、启动程序。
点击开始→程序→WinQSB →Network Modeling.
2、求最小支撑树:Minimal spanning tree ,输入节点数,沿编号从小到大顺次输入备树枝的长。
3、求最短路:Shortest path ,输入节点数,沿箭头方向输入各段弧上的数据。
4、求最大流:Maximal flow ,输入节点数,输入各段弧的容量。
五、分析讨论题
(一)应用求最小树子程序,求解下述问题的最小支撑树。
1、求以下问题的最小树
图3-39
2、求以下问题的最小树
图3-40
(二)应用求最短路子程序,求解下述问题从v 1到各点的最短路。
1、求v 1~v 7的最短路线及最短路长。
19
图3-41
2、求v 1~v 12的最短路线及最短路长。
图3-42
(三)应用求最大流的子程序,求解下述问题从v s 到v t 的网络最大流,图中弧旁数字为容量c ij 。
1、求以下网络的最大流
图3-43
2、求以下网络的最大流
图3-44
六、图论模型常用术语词汇及其含义
20。
图与网络模型
22
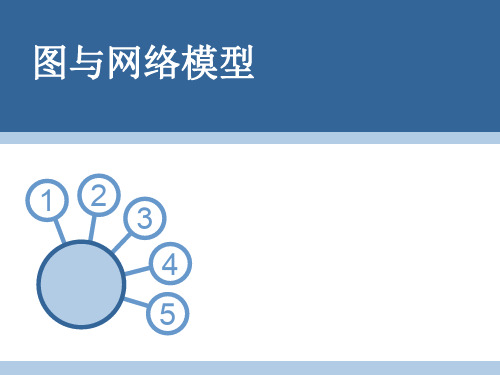
v6 3
v7
v3
2
5
1
2
v4
最小费用最大流问题
• 最小费用最大流问题:给了一个带收发点的 网络,对每一条边(vi, vj),除了给出容量cij 外,还给出了这条弧的单位流量的费用bij, 要求一个最大流F,并使得总运送费用最小。
• 主要目标:最大流 • 次要目标:最小费用 • 如反过来,即最小费用为主要目标,则只需
不运送即可。
最小费用最大流问题
• 例:由于输油管道的长短不一,所以在上个例子中
每段管道( vi, vj )除了有不同的流量限制cij外,还 有不同的单位流量的费用bij,cij的单位为万加仑/小 时,bij的单位为百元/万加仑。从采地 v1向销地 v7运 送石油,怎样运送才能运送最多的石油并使得总的
f14 f43 f46 f47 f23 f43 f35 f36 f25 f35 f57 f36 f46 f67 f57 f67 f47 f12 f14
fij cij , i 1, 2, , 6; j 1, 2, fij 0, i 1, 2, , 6; j 1, 2,
e5 (v6)吴
(v7)陈
图与网络的基本概念
• 一般情况下图中点的相对位置如何、点与点 之间联线的长短曲直,对于反映对象之间的 关系并不是重要的
• 无向图:边是无向的 • 有向图:边是有向的
– 如:将上述例子中“相互认识”关系改为“认 识”
– 如:family tree
• 一个图结构可记作G =(V,E)
• 生成树:如果图G的一个生成子图还是一个树,则 称这个生成子图为生成树
(a)
(b)
(c)
图与网络模型及方法 ppt课件

1
0
当G为无向图时,邻接矩阵为对称矩阵
最短轨道问题
给出了一个连接若干个城镇的铁路网络,在这个 网络的两个指定城镇间,找一条最短铁路线。
以各城镇为图G 的顶点,两城镇间的直通铁路为 图G 相应两顶点间的边,得图G 。对G 的每一边e, 赋以一个实数w(e)—直通铁路的长度,称为e的权, 得到赋权图G 。G 的子图的权是指子图的各边的 权和。
三.次(度)的性质
性质1:在图G=(V,E)中,所有点的次之和是边数m的两倍。 证明:由于每条边均与两个顶点关联,因此在计算顶点的次时
每条边都计算了两遍,所以顶点次数的总和等于边数的二倍。
性质2:在任何图G=(V,E)中,奇点的个数为偶数
证明:设V1,V2分别是图G中奇点和偶点的集合,则V1∪V2=V,
称矩阵A为图G的邻接矩阵。
例、写出下图的邻接矩阵
v2 •
v• 4
v1•
•v6
v3 •
• v5
v1 v2 v3 v4 v5 v6
v1 v2
0 0
1 0
1 1
0 0
0 0
0 0
A vvv 543 000
1 1 1
0 0 0
0 0 1
1 0 0
0 1 1
v6
0
0
0
0
问题就是求赋权图G 中指定的两个顶点u0 ,v0间的 具最小权的轨。这条轨叫做u0 ,v0间的最短路,它 的权叫做u0 ,v0间的距离,亦记作d(u0 ,v0)
最短轨道问题求法 ---Dijkstra算法
基本思想 是按距 u 0从近到远为顺序,依次求得u 0到G 的各顶点的最短路和距离,直至v 0 (或直 至G 的所有顶点),算法结束。为避免重 复并保留每一步的计算信息,采用了标号 算法。
图的应用及建立实验心得

图的应用及建立实验心得图是离散数学中的一种数学模型,在现实生活中有着广泛的应用。
图的应用包括社交网络分析、物流规划、路径优化、电路设计等等。
在进行图的应用研究时,我参与了一个实验项目,通过构建虚拟社交网络的图模型,来分析社交网络的特征以及推荐算法的效果。
在这个实验中,我积累了一些宝贵的心得体会。
首先,建立图模型需要明确目标和需求。
在实验之前,我们需要明确研究的问题和目标,并针对性地选择图的类型和构建方法。
比如,在社交网络分析中,我们可以选择无向图来表示社交关系,也可以选择有向图来表示信息传播。
根据实验的目标,我们可以选择使用邻接矩阵或邻接表来表示图的结构。
一个清晰的目标能够帮助我们更好地选择合适的图模型和算法。
其次,进行实验前,需要收集和处理数据。
在我们的实验中,我们使用了虚拟数据来构建社交网络图。
数据的质量和准确性对于实验结果的可靠性至关重要。
在收集数据时,我们要注意保护用户的隐私,确保数据的合法性。
在处理数据时,我们要进行必要的清洗和预处理,以保证数据的完整性和准确性。
这样才能够获得可靠的实验结果。
然后,需要选择合适的图算法来分析和处理图数据。
在我们的实验中,我们需要通过社交网络图来评估不同的推荐算法的效果。
因此,我们选择了一些经典的图算法,如最短路径算法和最小生成树算法。
这些算法能够帮助我们提取和分析图数据的特征。
在选择算法时,我们要充分考虑实验的目标和数据的特点,选择合适的算法来解决问题。
最后,需要对实验结果进行评估和反思。
在我们的实验中,我们通过比较不同推荐算法的效果,来评估它们的性能和可靠性。
并通过对实验结果的分析,我们可以对算法和模型的优化提出一些改进方案。
在反思过程中,我们还可以总结出一些经验和教训,以便今后的实验工作。
通过参与这个实验项目,我对图的应用有了更深入的理解,并积累了一些实践经验。
我认识到,在图的应用中,选择合适的图模型和算法非常重要,只有清晰地确定问题和目标,并选择合适的方法,才能取得良好的实验效果。
实验七图论模型

实验七图论模型一、实验目的掌握不同问题的输入方法,求解网络模型,观察求解步骤,显示并读出结果。
二、实验平台和环境Windows9X/ME/NT/2000/XP平台下,WinQSB V1.0版本已经安装在D:\WinQSB中。
三、实验内容和要求用WinQSB软件求解最小支撑树,最短路及网络最大流等问题。
四、实验操作步骤6.4.1启动程序。
点击开始→程序→WinQSB→Network Modeling.6.4.2求最小支撑树。
6.4.2.1分析例题。
点击File→Load Problem,打开文件,系统显示如图7-1所示的界面。
点击菜单栏Solve and Analyze或点击工具栏中的图标,观赏一下软件求解的过程。
图7-16.4.2.2实例操作。
例6.1某工厂内联结六个车间的道路网如图7-2所示。
已知每条道路的长,要求沿道路架设联结六个车间的电话线网,使电话线的总长最小。
1、启动程序。
点击开始→程序→WinQSB→Network Modeling,系统显示如图7-3所示的界面。
图7-32、建立新问题(点击File→New Problem),显示如图7-4所示的界面。
图7-4选择Minimal Spanning Tree,输入标题名、网络节点数,选择表格输入形式(spreadsheet matrix form),边弧权数转换(symmetric arc coefficients)可选可不选,如图7-5所示界面。
图7-53、输入数据。
在图7-5中输入各节点之间的权数,一般按照从小下标节点到大下标节点的原则输入权数,并且在输入过程中按Tab键或方向键即可输入下一个单元格。
如图7-6所示。
图7-64、修改参数。
1)修改标题名和节点名。
系统默认节点名称为node1,node2,……,noden。
如果对默认名不满意可以进行修改,点击菜单栏Edit,下拉菜单有两个修改选项:修改标题名(Problem Name)和节点名(Node Name)。
图与网络模型及方法

第五章 图与网络模型及方法§1 概论图论起源于18世纪。
第一篇图论论文是瑞士数学家欧拉于1736 年发表的“哥尼斯堡的七座桥”。
1847年,克希霍夫为了给出电网络方程而引进了“树”的概念。
1857年,凯莱在计数烷22 n n H C 的同分异构物时,也发现了“树”。
哈密尔顿于1859年提出“周游世界”游戏,用图论的术语,就是如何找出一个连通图中的生成圈,近几十年来,由于计算机技术和科学的飞速发展,大大地促进了图论研究和应用,图论的理论和方法已经渗透到物理、化学、通讯科学、建筑学、生物遗传学、心理学、经济学、社会学等学科中。
图论中所谓的“图”是指某类具体事物和这些事物之间的联系。
如果我们用点表示这些具体事物,用连接两点的线段(直的或曲的)表示两个事物的特定的联系,就得到了描述这个“图”的几何形象。
图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型,借助于图论的概念、理论和方法,可以对该模型求解。
哥尼斯堡七桥问题就是一个典型的例子。
在哥尼斯堡有七座桥将普莱格尔河中的两个岛及岛与河岸联结起来问题是要从这四块陆地中的任何一块开始通过每一座桥正好一次,再回到起点。
当然可以通过试验去尝试解决这个问题,但该城居民的任何尝试均未成功。
欧拉为了解决这个问题,采用了建立数学模型的方法。
他将每一块陆地用一个点来代替,将每一座桥用连接相应两点的一条线来代替,从而得到一个有四个“点”,七条“线”的“图”。
问题成为从任一点出发一笔画出七条线再回到起点。
欧拉考察了一般一笔画的结构特点,给出了一笔画的一个判定法则:这个图是连通的,且每个点都与偶数线相关联,将这个判定法则应用于七桥问题,得到了“不可能走通”的结果,不但彻底解决了这个问题,而且开创了图论研究的先河。
图与网络是运筹学(Operations Research )中的一个经典和重要的分支,所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。
数学实验 实验图与网络优化
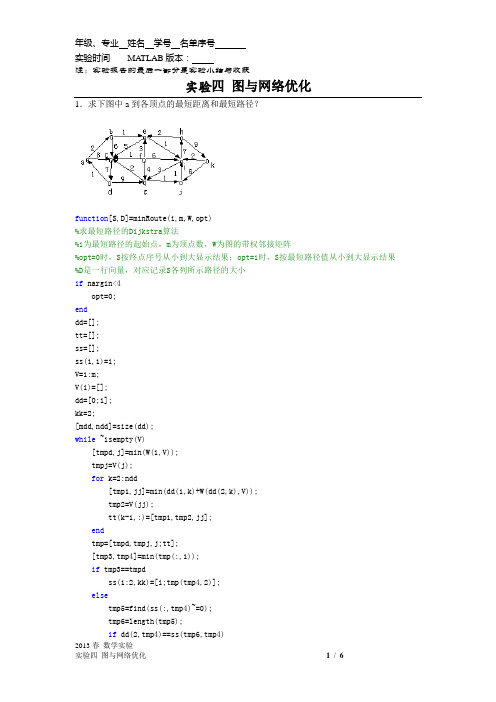
实验四图与网络优化1.求下图中a到各顶点的最短距离和最短路径?function[S,D]=minRoute(i,m,W,opt)%求最短路径的Dijkstra算法%i为最短路径的起始点,m为顶点数,W为图的带权邻接矩阵%opt=0时,S按终点序号从小到大显示结果;opt=1时,S按最短路径值从小到大显示结果%D是一行向量,对应记录S各列所示路径的大小if nargin<4opt=0;enddd=[];tt=[];ss=[];ss(1,1)=i;V=1:m;V(i)=[];dd=[0;i];kk=2;[mdd,ndd]=size(dd);while ~isempty(V)[tmpd,j]=min(W(i,V));tmpj=V(j);for k=2:ndd[tmp1,jj]=min(dd(1,k)+W(dd(2,k),V));tmp2=V(jj);tt(k-1,:)=[tmp1,tmp2,jj];endtmp=[tmpd,tmpj,j;tt];[tmp3,tmp4]=min(tmp(:,1));if tmp3==tmpdss(1:2,kk)=[i;tmp(tmp4,2)];elsetmp5=find(ss(:,tmp4)~=0);tmp6=length(tmp5);if dd(2,tmp4)==ss(tmp6,tmp4)实验四图与网络优化 ss(1:tmp6+1,kk)=[ss(tmp5,tmp4);tmp(tmp4,2)];elsess(1:3,kk)=[i;dd(2,tmp4);tmp(tmp4,2)];endenddd=[dd,[tmp3;tmp(tmp4,2)]];V(tmp(tmp4,3))=[];[mdd,ndd]=size(dd);kk=kk+1;endif opt==1[tmp,t]=sort(dd(2,:));S=ss(:,t);D=dd(1,t);elseS=ss;D=dd(1,:);end>> clear all>> w=inf*ones(11);>> w(1,[2,3])=[2,8];>> w(2,[3,5])=[6,1];>> w(3,[4])=[7];>> w(4,[1,7])=[1,9];>> w(5,[3,9])=[5,1];>> w(6,[3,5,7,9])=[1,3,4,6];>> w(7,[3,10])=[2,1];>> w(8,[5,11])=[2,9];>> w(9,[7,8])=[3,7];>> w(10,[9])=[1];实验四图与网络优化>> w(11,[9,10])=[2,6];>> [s,d]=minRoute(1,11,w)s =1 1 1 1 1 1 1 1 1 1 10 2 2 2 2 3 2 2 3 2 60 0 5 5 5 0 5 5 4 5 00 0 0 9 9 0 9 9 0 9 00 0 0 0 7 0 7 8 0 8 00 0 0 0 0 0 10 0 0 11 0d =0 2 3 4 7 8 8 11 15 20 Inf因此,按顶点序号a-b; a-b-e; a-b-e-i; a-b-e-i-g; a-c; a-b-e-i-g-j; a-b-e-i-h; a-c-d; a-b-e-i-h-k; a-f; 按上面次序最短距离分别是0 2 3 4 7 8 8 11 15 20 Inf2.一辆货车从水泥厂运水泥至某建筑工地。
数学建模图与网络模型

1 −1 A= 0 0
问题1:七桥问题
在哥尼斯堡有七座桥将普莱格尔河中的两个岛及岛与 河岸联结起来问题是要从这四块陆地中的任何一块开 始通过每一座桥正好一次,再回到起点。欧拉为了解 决这个问题,采用了建立数学模型的方法。他将每一 块陆地用一个点来代替,将每一座桥用连接相应两点 的一条线来代替,从而得到一个有四个“点”,七条 “线”的“图”。问题成为从任一点出发一笔画出七 条线再回到起点。
问题2(哈密顿环球旅行问题): 问题2(哈密顿环球旅行问题): 2(哈密顿环球旅行问题 十二面体的20个顶点代表世界上20个城市, 20个顶点代表世界上20个城市 十二面体的20个顶点代表世界上20个城市, 能否从某个城市出发在十二面体上依次经过每个 城市恰好一次最后回到出发点? 城市恰好一次最后回到出发点?
如果E的每一条边都是无向边 则称G为 如果 的每一条边都是无向边, 则称 为无向 的每一条边都是无向边 如图1) 如果E的每一条边都是有向边 1); 的每一条边都是有向边, 图(如图1) 如果 的每一条边都是有向边 则称 G为有向图(如图2) 否则 称G为混合图 2); 为有向图(如图2) 否则, 为混合图. 图 1 并且常记 V = {v1, v2, … , vn}, |V | = n ; E = {e1, e2, … , em}(ek=vivj ) , |E | = m. 称点v 为边v 端点. 在有向图中, 称点v 称点 i , vj为边 ivj的端点 在有向图中 称点 i , vj分 别为边v 始点和终点. 别为边 ivj的始点和终点 图 2
d(v1)= d(v3)= d(v4)=4, d(v2)=2.
我们今后只讨论有限简单图: 我们今后只讨论有限简单图: 有限简单图
顶点个数是有限的; (1) 顶点个数是有限的 (2) 任意一条边有且只有两个不同的点与它 相互关联; 相互关联 若是无向图, (3) 若是无向图, 则任意两个顶点最多只有 一条边与之相联结; 一条边与之相联结 若是有向图, (4) 若是有向图, 则任意两个顶点最多只有 两条边与之相联结. 两条边与之相联结. 当两个顶点有两条边与之相 联结时,这两条边的方向相反. 联结时,这两条边的方向相反. 如果某个有限图不满足(2)(3)(4),可在某条 如果某个有限图不满足(2)(3)(4),可在某条 (2)(3)(4), 边上增设顶点使之满足. 边上增设顶点使之满足.
2022年Python数学实验与建模-图与网络的基本概念

航空基础学院数学第教7研页室
数学建模算法与应用
第4章 图与网络模型及方法
图 4.1 中,边e2和e3为重边,e5为环,顶点v5为孤 立点。
v1• e1
•v 5
e5
e3
•v4 e4
v2•
e2
•v3
图 4.1 非简单图示例
航空基础学院数学第教8研页室
数学建模算法与应用
第4章 图与网络模型及方法
定义 4.4 无环且无重边的图称为简单图。 如果不特别申明,一般的图均指简单图。
航空基础学院数学第教27研页室
数学建模算法与应用
第4章 图与网络模型及方法
Naval Aeronautical University
02
MATLAB 工具箱简介
航空基础学院数学第教28研页室
数学建模算法与应用
第4章 图与网络模型及方法
1.图的生成
Graph:无向图(undirected Graph);
各边相异的道路称为迹(trail); 各顶点相异的道路称为轨道(path),记为 P(v0 ,vk ); 起点和终点重合的道路称为回路;
起点和终点重合的轨道称为圈,即对轨道 P(v0 ,vk ), 当v0 vk 时成为一个圈。
航空基础学院数学第教15研页室
数学建模算法与应用
第4章 图与网络模型及方法
3.定点的度
定义 4.7 (1)在无向图中,与顶点v 关联的边的 数目(环算两次)称为v 的度,记为d(v)。
(2)在有向图中,从顶点v 引出的弧的数目称为v 的出度,记为d (v),从顶点v 引入的弧的数目称为v 的入 度,记为d (v),d(v) d (v) d (v)称为v 的度。
在有向图 D中,如果对于任意两个顶点u和v ,从 u到v 和从v 到u都存在道路,则称图 D是强连通图。
第11章图与网络模型ppt课件
11.2 最小树问题 Minimal tree problem
1.树、支撑树、最小支撑树的概念 2.掌握求最小树的方法:
(1)破圈法 (2)加边法
02.08.2024
下一节:最短路问题
02.08.2024
11.3 最短路问题
Shortest Path Problem
11.3 最短路问题 Shortest Path Problem
(2)找出所有一端vi已标号另一端vj未标号的边集合 B={[i,j]}如 果这样的边不存在或vt已标号则计算结束;
(3)计算集合B中边标号:k[i,j]=b(i)+cij
(4)选一个点标号: 返回到第(2)步。
b (l) m j k [i,ijn ]|[i,j] B ,在v l处 端 b (l 标 点 )
A
C
D
B
欧拉证明了这是不可能的。
02.08.2024
在这一时期,还有许多游戏问题,诸如环球旅行、 迷宫问题、博奕问题等难题,吸引了许多学者, 这些问题看起来似乎是一些无足轻重的游戏, 但常常 是由于这些游戏引出了许多实用意义的 新问题,开辟了新学科。
图论在现实生活中很多,如各种通信网络的合理 架设,交通网络的合理分布,邮递员送信,怎 么走完他负责投递的全部街道,完成任务回到 邮局,使走的路线最短,电子商务物流配送中 的最佳运送路线的选择等,都属于图论问题。
支撑子图:G=(V,E),如果G’=(V’,E’),使V=V’及
E’ E,则G’为G的一个支撑子图.
02.08.2024
支撑子 图
有向图中: 路:如有(vi1,ai1,vi2,ai2,…..,v(ik-1),a(ik-1),vik)是D中一
条链,且有ait=(vit,v(it+1)),称从vi1→vik的一条路。 回路:若路中第一点和最后一点相同,则称为
南邮课内实验-运筹学-图与网络建模-第四次1

课内实验报告课程名:运筹学任课教师:邢光军专业:学号:姓名:/ 学年第学期南京邮电大学管理学院实验背景:求下图中v 1到v 6的最短路。
实验结果:一:问题分析和建立模型:用EXCEL 求解最短路的原理是:令最短路径变量为0或1.即如果最短路通过某弧,则该变量为1,否则为0,如最短路径为v1v2->v3v4->v4v6,那么最短路径变量v1v3=1,v3v4=1,v4v6=1,其余的为0.约束条件为起点的进出权数和为1,终点是-1。
除了起点和终点,其余每个中间节点的进出权数之和为0。
目标函数则为各弧的权数与对应的最短路径变量乘积之和。
于是可以转化规划求解最短路径。
二:计算过程:下面利用Spreadsheet 来求解该问题:在Excel2003版本中,单击“工具”栏中“加载宏”命令,在弹出的的“加载宏”对话框选择“规划求解”,在“工具”下拉菜单中会增加“规划求解”命令,这样就可以使用了。
利用EXCEL 求解题中v1到v6的最短路。
第一步,在Excel 上建立最短路模型,将所有的弧列出来,如图①中的A 和B 两列,所有弧的权数如C 列所示,并令最短路径变量的初始值为0,如D 列所示。
节点v1到v6的进出和如G 列所示。
(G2=D2+D3+D4.G3=D5-D2-D7,G4=D6-D3-D9,G5=D7+D8-D4-D6-D10,G6=D9+D10+D11,G7=-D5-D8-D11)。
目标函数为SUMPRODUCT (C2:C11,D2:D11)。
v 235 2 7 5 3 1 5 1 2v 1v 6v 5 v 3 v 4图①第二步,单击“规划求解”按钮,设置目标单元格为最小值,设置可变单元格为最短路径变量单元格,添加约束条件,如图②所示。
图②第三步,单击“求解”按钮,选择“保存规划求解结果”。
如图③。
图③三:结果分析:图③中D列为1的变量表示最短路径经过的弧,得到最短的路径为v1->v3->v4->v6,最短路长为8。
网络数学实验6图与网络分析-最短路问题

实验六:图与网络分析-最短路问题
一、实验目的:掌握不同问题的输入方法,求解网络模型,观察求解步骤,显示并读出结果。
二、内容和要求:用WinQSB软件求解最短路问题,并对结果进行简单分析。
例:求下图的最短路。
三、操作步骤:
1.“开始”菜单→“winQSB”→“Network Modeling”(网络模型)。
2.建立新问题:File→New Problem,出现下面界面。
选择Shortest Path Problem、Minimization、输入问题标题、节点的个数,然后单击“OK”。
3.修改节点名称:菜单“Edit”→“Node Names”,编辑完点“OK”,如下图。
4.按下图输入图的权矩阵,本例是无向图,每一条边必须输入两次。
5.菜单“Solve and Analyze”→“Solve the Problem”,出现以下对话框,
6.然后选择起点v1和终点v10,点“Solve”按键,出现下图:
从图中可以看到v1到v10的最短路径为v1→v3→v7→v10,总长为6,另外从v1到其他各点的最短距离也都计算了出来。
7.实例求解:有九个城市v1,v2…,v9,其公路网如下图,弧旁数字是该段公路的长度,有一批货物从v1运到v9,试用Dijkstra方法求出走哪条路最短?
自己先用标号法求出最短路,然后用winWSB软件进行验证。
8.思考题:教育部门打算在某新建城区建一所学校,让附近七个居民区的学生就近入学。
七个居民区之间的道路如下图所示,学校应建在哪个居民区,才能使大学都方便?(图中距离单位:百米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a=zeros(6); %邻接矩阵初始化 a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10; a(2,3)=15;a(2,4)=20;a(2,6)=25;a(3,4)=10;a(3,5)=20; a(4,5)=10;a(4,6)=25;a(5,6)=55; a=a; b=sparse(a)
2018/9/28 数学建模1
图与网络模型实验
1. 邻接矩阵表示法 邻接矩阵是表示顶点之间相邻关系的矩阵,邻接矩 阵记作W = ( wij )n´ n ,当G 为赋权图时 ì ï ï 权值,当vi 与v j 之间有边时, wij = í ï 0或¥ ,当vi 与v j 之间无边时. ï ï î 当G 为非赋权图时, ì ï ï 1,当vi 与v j 之间有边时, wij = í ï 0,当v i 与v j 之间无边时. ï ï î 采用邻接矩阵表示图,直观方便,通过查邻接矩阵元
v1
v2
v3
v4
v5
u5
2018/9/28
u4
u3
数学建模1
u2
u1
• 根据题意,人不在场时,狼要吃羊,羊要 吃菜,因此,人不在场时,不能将狼与羊, 羊与蔬菜留在河的任一岸。例如,状态(0, 1,1,0)表示人和菜在对岸,而狼和羊在 此岸,这时人不在场狼要吃羊,因此,这 个状态是不可行的。
• 通过穷举法将所有可行的状态列举出来,可行的状 态有(1,1,1,1),(1,1,1,0),(1,1, 0,1),(1,0,1,1),(1,0,1,0),(0, 1,0,1),(0,1,0,0),(0,0,1,0), (0,0,0,1),(0,0,0,0)可行状态共有十 种。每一次的渡河行为改变现有的状态。现构造赋 权图 ,其中顶点集合 中的顶点(按照上面的顺序 编号)分别表示上述十个可行状态,当且仅当对应 的两个可行状态之间存在一个可行转移时两顶点之 间才有边连接,并且对应的权重取为1,当两个顶 点之间不存在可行转移时,可以把相应的权重取为 inf 。
h = view(biograph(b,[],'ShowArrows','off','ShowWeights','off'))
2018/9/28
数学建模1
实验项目名称: 图论模型MATLAB软件预处理
• 实验目的与原理:掌握图与网络在计算机 中数据存取方法,将图与网络转化为领接 矩阵、稀疏矩阵等多种方法,矩阵的各种 读写方式。
赋权图G 之间的状态转移关系见图 4.8,最终求得的 状态转移顺序为 1 6 3 7 2 8 5 10 , 经过 7 次渡河就可以把狼,羊,蔬菜运过河,第一次运 羊过河,空船返回;第二次运菜过河,带羊返回;第三 次运狼过河,空船返回;第四次运羊过河。
Node 6 Node 7 Node 9 Node 8 Node 10
最短路问题软件求解
(1)用狄克斯屈拉算法写代码 (2)用逐次逼近法写代码 (3)用graphshortestpath() (4)0-1线性整数规划模型 x = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub,options) x = bintprog(f, A, b, Aeq, beq)
Node 1
Node 3
Node 2
Node 4
Node 5
图 4.8 可行状态之间的转移
clc, clear a=[1 1 1 1;1 1 1 0;1 1 0 1;1 0 1 1;1 0 1 0 0 1 0 1;0 1 0 0;0 0 1 0;0 0 0 1; 0 0 0 0]; %每一行是一个可行状态 b=[1 0 0 0;1 1 0 0;1 0 1 0;1 0 0 1]; %每一行是一个转移状态 w=zeros(10); %邻接矩阵初始化 for i=1:9 for j=i+1:10 for k=1:4 if findstr(mod(a(i,:)+b(k,:),2),a(j,:)) w(i,j)=1; end end end end w=w'; %变成下三角矩阵 [i,j,v]=find(w); %找非零元素 c=sparse(i,j,v,10,10) %构造稀疏矩阵 [x,y,z]=graphshortestpath(c,1,10,'Directed',false) % 该图是无向图 h = view(biograph(c,[],'ShowArrows','off','ShowWeights','off')); Edges = getedgesbynodeid(h); %提取句柄h中的边集 set(Edges,'LineColor',[0 0 0]); %为了将来打印清楚,边画成黑色 set(Edges,'LineWidth',1.5); %线型宽度设置为1.5
2018/9/28
数学建模1
• 定义: • 1)人—M(Man),狼—W(Wolf), 羊—G (Goat), 草—H(Hay) • 2) 点—— vi 表示河岸的状态 • 3) 边—— ek 表示由状态 vi 经一次渡河到状 态 vj • 4) 权——边 ek 上的权定为 1
我们可以得到下面的加权有向图
渡河游戏 • 一老汉带了一只狼、一只羊、一棵白菜想要 从南岸过河到北岸,河上只有一条独木舟, 每次除了人以外,只能带一样东西;另外, 如果人不在,狼就要吃羊,羊就要吃白菜, 问应该怎样安排渡河,才能做到既把所有东 西都运过河去,并且在河上来回次数最少? 这个问题就可以用求最短路方法解决。
实验内容与步骤:
• 因此问题变为在图 中寻找一条由初始状态(1, 1,1,1)出发,经最小次数转移达到最终状态 (0,0,0,0)的转移过程,即求从状态(1, 1,1,1)到状态(0,0,0,0)的最短路径。 这就将问题转化成了图论中的最短路问题。 • 该题的难点在于计算邻接矩阵,由于摆渡一次 就改变现有的状态,为此再引入一个四维状态 转移向量,用它来反映摆渡情况。用1表示过河, 0表示未过河。例如,(1,1,0,0)表示人带 狼过河。状态转移只有四种情况,用如下的向 量表示(1,0,0,0),(1,1,0,0),(1, 0,1,0),(1,0,0,1)。
素的值可以很容易地查找图中任两个顶点 v i 和 v j 之间有无 边,以及边上的权值。当图的边数 m 远小于顶点数 n 时, 邻接矩Байду номын сангаас表示法会造成很大的空间浪费。
4. 稀疏矩阵表示法 稀疏矩阵是指矩阵中零元素很多,非零元素很少的矩 阵。对于稀疏矩阵,只要存放非零元素的行标、列标、非零 元素的值即可,可以按如下方式存储(非零元素的行地址, 非零元素的列地址) ,非零元素的值。
最短路问题
2018/9/28
数学建模1
• 状态说明: • v1,u1 =( M,W,G,H ); v2,u2 =(M,W,G); v3,u3 =(M,W,H); 此游戏转化为在下面的二部图中求从 v 到 u 的最短路问题。 • v4,u4=(M,G,H); v5,u5 =(M,G)
1 1
最短路问题
在 Matlab 中无向图和有向图邻接矩阵的使用上有很 大差异。 对于有向图,只要写出邻接矩阵,直接使用 Matlab 的命令 sparse 命令, 就可以把邻接矩阵转化为稀疏矩阵的 表示方式。
对于无向图, 由于邻接矩阵是对称阵, Matlab 中只 需使用邻接矩阵的下三角元素,即 Matlab 只存储邻接 矩阵下三角元素中的非零元素。 稀疏矩阵只是一种存储格式。 Matlab 中, 普通矩阵 使用 sparse 命令变成稀疏矩阵, 稀疏矩阵使用 full 命令 变成普通矩阵。
= {v s , v1 ,L , v5 , vt } 中
?
8 3 0 .
clc, clear a=zeros(7); a(1,2)=4; a(1,3)=2; a(2,3)=3; a(2,4)=2; a(2,5)=6; a(3,4)=5; a(3,6)=4; a(4,5)=2; a(4,6)=7; a(5,6)=4; a(5,7)=8; a(6,7)=3; b=sparse(a); %构造稀疏矩阵,这里给出构造稀疏矩阵 的另一种方法 [x,y,z]=graphshortestpath(b,1,7,'Directed',true,'Method',' Dijkstra') % Directed是有向的 h=view(biograph(b,[],'ShowArrows','on','ShowWeights','o n'))
例 4.11 度。
求图 4.9 所示有向图中 v s 到 v t 的最短路径及长
v1
4
6
2
2
v4
8
vs
2
3
5
v3
4
4
7
vt
3
v2
v5
图 4.9 有向图的最短路
解 该赋权有向图中顶点集V 总共有 7 个顶点,邻接矩阵 轾 0 4 2 ゥ ゥ 犏 犏 ゥ 0 3 2 6 犏 犏 ゥ 0 5 ゥ 4 犏 W= 犏 ゥ ゥ 0 2 7 犏 犏 ゥ ゥ 0 4 犏 犏 ゥ ゥ ? 0 犏 犏 ゥ ゥ ゥ 臌
2018/9/28
数学建模1
S=[1 1 2 2 3 3 4 4 4 4 5 6 6 7 8]; %起始节点向量 E=[2 3 5 4 4 6 5 7 8 6 7 8 9 9 9]; %终止节点向量 W=[1 2 12 6 3 4 4 15 7 2 7 7 15 3 10]; %边权值向量,有向 图,G(9,9)=0; 9个节点 G=sparse(S,E,W); %关联矩阵的稀疏矩阵表示 G(9,9)=0; P=biograph(G,[],'ShowWeights','on');%建立有向图对象P H=view(P);%显示各个路径权值 [Dist,Path]=graphshortestpath(G,1,9,'Method','Dijkstra') % 求节点1到节点9的最短路径 set(H.Nodes(Path),'Color',[1 0.4 0.4]);%以下三条语句用红 色修饰最短路径 edges=getedgesbynodeid(H,get(H.Nodes(Path),'ID')); set(edges,'LineColor',[1 0 0]); set(edges,'LineWidth',2.0);
