chapt10(组合变形)材料力学ppt
合集下载
材料力学第七章 组合变形 PPT课件
7-2 斜弯曲
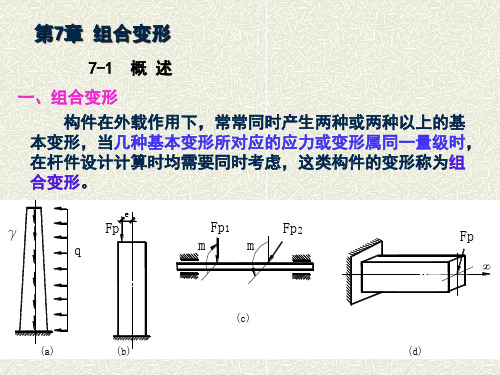
一、斜弯曲: 横向力通过梁横截面的弯心,不与形心主惯性轴重合或
平行,而是斜交,梁的挠曲线不再与荷载纵平面重合或平行。
例:下列图中给出几种常见截面,其中图(b)、(c)、
(d)、(f)是斜弯曲;图(a)是平面弯曲;图(e)
是斜弯曲与扭转的组合变形。
Fp
Fp
Fp
Fp
Fp Fp
弯心
(a)
(b)
三、组合变形下的变形计算 (1)外力分析:将载荷简化成符合各基本变形外力作用条件的 静力等效力系。 (2)变形(位移)计算:按各基本变形计算相应的变形(截面位 移)。对于不同变形性质的位移相互独 立,对于同一变形性质的位移进行叠加。
注:平面弯曲时, 剪力引起的最大剪应力值一般远小于正应力 值,也远小于扭矩引起的最大剪应力值,在组合变形的应 力计算中,由剪力引起的剪应力一般都忽略不计 。
故
h
5 21 z
34
yP
iz2 ay
0
zP
iy2 az
b2 12 b 2
b 6
2
1y
此同即理相可应得的与压中力性作轴用l2、点1l3的、坐l4标对。应的偏心力作用点图2、133.、154
的位置。但是通过角点 a 而与截面相切的中性轴有无穷多
个,由此法计算不简便。
解续
截面上中性轴上的点的坐标(y0,z0)与偏心压力作用点的坐
max A
I yc
100 103 500 103 55 800 7.27 105
P
12537.8162.8MPa
孔移至板中间时
A N 100103 631.9mm2 10(100 x)
材料力学组合变形 ppt课件

FN F
M 42 153 0FN.m
(3)立柱横截面的最大应力
t.max
Mz0 Iy
FN A
F 350
M FN
425103 F 0.075 5.31105
15
F 103
667F Pa
c.max
Mz1 Iy
FN A
t.max
c.max
425103 F 0.125 F
5.31105
15103
中性轴方程
x
PMzy0 A Iz
Myz0 Iy
0
对于偏心拉压问题
PPyPy0 PzPz0 0
A Iz
Iy
中性轴
危险点 (距中性轴最远的点)
1 yPy0 zPz0 0
A Iz
I Wy
m
a
x
PMz A Wz
My Wy
例题
铸铁压力机框架,立柱横截面尺寸如图所示,材料的许用 拉应力[t]=30MPa,许用压应力[c]=120MPa。试按立柱
1 242 0
22
25
M W
T Wt
1212 242
2 0
3212 242
第三强度理论:
r31 3
Wt 2W
r3 242[]
r3W 1 M2T2[]
26
M W
T Wt
1212 242
2 0
3212 242
第四强度理论:
r41 2 [(1 2)2 (2 3 )2 (3 1 )2]
r4 232[] r4W 1 M 20.7T 52[]
解:拉扭组合,危险点应力状态如图
F A
Me F
F 450 103 A 0.12
《材料力学组合变形》课件

这种变形通常发生在承受轴向力 和弯矩的杆件中,其变形特点是 杆件既有伸长或缩短,又有弯曲 。
拉伸与压缩组合变形的分析方法
01
02
03
弹性分析方法
基于弹性力学的基本原理 ,通过求解弹性方程来分 析杆件内部的应力和应变 分布。
塑性分析方法
在材料进入塑性阶段后, 采用塑性力学的基本理论 来分析杆件的承载能力和 变形行为。
材料力学在组合变形中的应用实例
01
02
03
04
桥梁工程
桥梁的受力分析、桥墩的稳定 性分析等。
建筑结构
高层建筑、大跨度结构的受力 分析、抗震设计等。
机械工程
机械零件的强度、刚度和稳定 性分析,如轴、轴承、齿轮等
。
航空航天
飞机和航天器的结构分析、材 料选择和制造工艺等。
材料力学在组合变形中的发展趋势
特点
剪切与扭转组合变形具有复杂性和多样性,其变形行为受到多种因素的影响,如 材料的性质、杆件的长度和截面尺寸、剪切和扭转的相对大小等。
剪切与扭转组合变形的分析方法
1 2 3
工程近似法
在分析剪切与扭转组合变形时,通常采用工程近 似法,通过简化模型和假设来计算杆件的应力和 变形。
有限元法
有限元法是一种数值分析方法,可以模拟杆件在 剪切与扭转组合变形中的真实行为,提供更精确 的结果。
弯曲组合变形的分析方法
叠加法
刚度矩阵法
叠加法是分析弯曲组合变形的基本方 法之一。该方法基于线性弹性力学理 论,认为各种基本变形的应力、应变 分量可以分别计算,然后按照线性叠 加原理得到最终的应力、应变分布。
刚度矩阵法是通过建立物体内任意一 点的应力、应变与外力之间的关系, 来求解复杂变形问题的一种方法。对 于弯曲组合变形,可以通过构建系统 的刚度矩阵来求解。
拉伸与压缩组合变形的分析方法
01
02
03
弹性分析方法
基于弹性力学的基本原理 ,通过求解弹性方程来分 析杆件内部的应力和应变 分布。
塑性分析方法
在材料进入塑性阶段后, 采用塑性力学的基本理论 来分析杆件的承载能力和 变形行为。
材料力学在组合变形中的应用实例
01
02
03
04
桥梁工程
桥梁的受力分析、桥墩的稳定 性分析等。
建筑结构
高层建筑、大跨度结构的受力 分析、抗震设计等。
机械工程
机械零件的强度、刚度和稳定 性分析,如轴、轴承、齿轮等
。
航空航天
飞机和航天器的结构分析、材 料选择和制造工艺等。
材料力学在组合变形中的发展趋势
特点
剪切与扭转组合变形具有复杂性和多样性,其变形行为受到多种因素的影响,如 材料的性质、杆件的长度和截面尺寸、剪切和扭转的相对大小等。
剪切与扭转组合变形的分析方法
1 2 3
工程近似法
在分析剪切与扭转组合变形时,通常采用工程近 似法,通过简化模型和假设来计算杆件的应力和 变形。
有限元法
有限元法是一种数值分析方法,可以模拟杆件在 剪切与扭转组合变形中的真实行为,提供更精确 的结果。
弯曲组合变形的分析方法
叠加法
刚度矩阵法
叠加法是分析弯曲组合变形的基本方 法之一。该方法基于线性弹性力学理 论,认为各种基本变形的应力、应变 分量可以分别计算,然后按照线性叠 加原理得到最终的应力、应变分布。
刚度矩阵法是通过建立物体内任意一 点的应力、应变与外力之间的关系, 来求解复杂变形问题的一种方法。对 于弯曲组合变形,可以通过构建系统 的刚度矩阵来求解。
材料力学2-第八章-组合变形PPT课件

x
z
xቤተ መጻሕፍቲ ባይዱ
m Pz
Py
y
LP
Pz
zj
Py P
y
② 应力
My引起的应力:
MyzMzcojs
Iy
Iy
M z引起的应力:
MzyMysijn
Iz
Iz
合应力: M(zcoj sysijn)
Iy
Iz
m
x
z
x
m Pz
Py
y
LP
Pz
zj
Py P
y
③ 中性轴方程 M(z0cojsy0sijn)0 中性轴
Iy
Iz
D2
tg y0 Iz ctgj
均布力作用, []=12MPa,许可挠度为L/200 ,E=9GPa,试选
择截面尺寸并校核刚度。
解:① 外力分析—分解q
yq
z
26°34´
q
A
B
L
qyqsin 80 0.0 44 375 N8/m
q z q co 8 s 0 0 .8 0 9 74 N 15 /m
Mzmaxqy8L235838240N 3m Myma xqz8L271 83 5280N4m
az
中性轴
1 yP y0 zPz0 0
iz2
iy2
ay
截面核心
已知 ay, az 后 ,
z
1
yPa y
i
2 z
0
1
z
Pa
i
2 y
z
0
P(zP,yP)
可求 P力的一个作用点 (zP,yP)
y
利用以上关系可确定截面核心的边界
例3 分别确定圆截面与矩形截面的截面核心.
材料力学10组合变形PPT课件

0McIozsy0sIiynz0
中性轴方程
cos
Iz y0
sIiynz0
0
( y0,z0 )
z
α φ
(1)中性轴是一条过截面形心 F 的直线;
y 中性轴
斜率 tany0 Iz tan
29
z0 Iy
10.1 斜弯曲
tan Iz tan
Iy
(2) 当Iz≠Iy,α ≠ φ,中性
轴与荷载线不垂直。
z
F
17
三、组合变形下的计算
分析方法:叠加法 前提条件:小变形
基本解法:
①外力分解或简化:使每一组力只产生一个方向的一种 基本变形; ②分别计算各基本变形下的内力及应力;
④对危险点进行应力分析; ⑤用强度理论进行强度计算。
18
思考题
1. 分析组合变形时,先分后合的依据是什么? 2.叠加原理的适用条件是什么? 能否应用于 大变形情况?
F
Fy
Fx B P
压弯组合变形
10
压弯组合变形
11
12
偏心压缩
拉弯组合变形
13
q
弯扭组合变形
14
F
弯扭组合变形
15
双向弯曲与扭转组合变形
16
组合变形的形式有很多种,本章学习四种典型形式。 1. 斜弯曲; 2. 拉伸(压缩)与弯曲组合; 3. 弯曲与扭转组合; 4. 偏心拉伸与压缩。
应注意通过这四种典型组合变形的学习,学会一般 组合变形的计算原理和方法。
A
B
C
22
10.1 斜弯曲
二、斜弯曲的研究方法
1.分解 将外力沿横截面的两个形心主轴分解,得到两个正 交的平面弯曲。
材料力学组合变形完整ppt文档

200
F
F
组合变形/拉压与弯曲的组合
思路分析:
根据受力情况判断立柱的 变形组合类型
拉伸和弯曲的组合
200 F F
拉伸: 求轴力,绘制轴力图 弯曲: 求弯矩,绘制弯矩图
判断危险截面,应力叠加,并进行校核(如下)
200 F F
任意横截面上拉伸正应力: 任意横截面上弯曲正应力:
同一个方向上的正应力可以根据分布情 况直接叠加,叠加后仍为单向应力状态,直 接校核强度。
1. 分解 竖直xy面:
水平xz面:
2. 分别求两个面内的弯矩,绘制弯矩图
竖直xy面:
水平矩图确定可能的危险截面
竖直xy面:
FL
水平xz面:
2FL
FL
结论: 危险截面可 能是中点或 固定端。
4. 通过叠加求危险截面的最大正应力
z
z
y
y
Mxy Mxz Wz Wy
Mx
2 y
Mx
2 z
W
y
竖直xy面:
FL
Z
水平xz面:
2FL FL
求中点处的最大正应力:
FL FL
Wz Wy
求固定端的最大正应力:
0 2FL
Wz Wy
5. 强度校核
2FL
固定端的最大正应力: max
y
Wy
[σ]=20FL/bh
2
m ax[]
梁满足强度要求
组合变形/扭转与弯曲的组合
§8.4 扭转与弯曲的组合
3.确定危险截面,求基本变形的应力
拉伸
N
FN A
(均布 ),
弯曲
Mm
a x Mm a Wz
x(线性 )
材料力学课件(组合变形)

截面核心是以O为中心,半径d/8的圆围成的 区域
(2)矩形截面 解:截面形心为点O 主惯性轴y、z 当中性轴切于边AB时
z A中性轴
b
12 o
y
C
B
h
截距
a y1
h 2
,a
z1
核心边界点1
yF1
iz2 a y1
h 6
,z
F1
i
2 y
az1
0
(iy
b 12
,iz
h) 12
类似地,可定点2
y F2
八、组合变形 (Combined deformation)
杆件有两种或两种以上基本变形的应力分量相当 两种基本变形组合的类型:
拉(压)+扭;拉(压)+弯;扭+弯;平面弯+平面弯
分析方法(线弹性、小变形假设下): 按基本变形分解外力与内力 计算各基本变形的应力与 变形分量 根据叠加原理综合各基本变形的结果 确定组合变形的危险截面与危险点的应力状态
(1
zF z
i
2 y
yF iz2
y
)
在截面上线性分布
中性轴
1
zF z
i
2 y
z0
yF y iz2
y0
0
——不过形心C的直线
截矩
ay
iz2 yF
,az
iy2 zF
距离中性轴最远点:D1——tmax, D2——cmax
横截面外周边具有棱角时,最大正应力在角点上
最大正应力点处于单向应力状态,强度条件 max [ ] 截面形心的位移 w wy2 wz2 x2
练习: P288习题8-16
M I
(2)矩形截面 解:截面形心为点O 主惯性轴y、z 当中性轴切于边AB时
z A中性轴
b
12 o
y
C
B
h
截距
a y1
h 2
,a
z1
核心边界点1
yF1
iz2 a y1
h 6
,z
F1
i
2 y
az1
0
(iy
b 12
,iz
h) 12
类似地,可定点2
y F2
八、组合变形 (Combined deformation)
杆件有两种或两种以上基本变形的应力分量相当 两种基本变形组合的类型:
拉(压)+扭;拉(压)+弯;扭+弯;平面弯+平面弯
分析方法(线弹性、小变形假设下): 按基本变形分解外力与内力 计算各基本变形的应力与 变形分量 根据叠加原理综合各基本变形的结果 确定组合变形的危险截面与危险点的应力状态
(1
zF z
i
2 y
yF iz2
y
)
在截面上线性分布
中性轴
1
zF z
i
2 y
z0
yF y iz2
y0
0
——不过形心C的直线
截矩
ay
iz2 yF
,az
iy2 zF
距离中性轴最远点:D1——tmax, D2——cmax
横截面外周边具有棱角时,最大正应力在角点上
最大正应力点处于单向应力状态,强度条件 max [ ] 截面形心的位移 w wy2 wz2 x2
练习: P288习题8-16
M I
材料力学 第十章组合变形(123)PPT课件

MPa。
18
例题 8-1
解:1. 将集中荷载F 沿梁横截面的两个对称轴y、z分解为
F y F c4 o o 0 s q 2 ca 4 o o 0 s 0 .3q 8 a 3
F z F s4 io n 0 q 2sa 4 io n 0 0 .3q 2 a 1
19
例题 8-1
2. 梁的计算简图如图b所示,并分别作水平弯曲和 竖直弯曲的弯矩My图和Mz 图(图c ,d)。
纵向对称面:梁的轴线与横截面纵向对称轴所构成的平面
平面弯曲:当作用在梁上的载荷和支反力均
位于纵向对称面内时,梁的轴线由直线弯成
一条位于纵向对称面内的曲线。 F'
F'
F
F'
纵向对称面?
轴线
7
CL7TU1
一.定义:斜弯曲—荷载不作用在构件的纵向对称 面内,梁的轴线变形后不在位于外力所在平面内。
一.力的分解
Fy Fcos
Fz Fsin
z
C
(y, z)
Fz
Fy
Fy
8
CL11TU3
Mz Fy(l x)以z为中性轴弯曲
My Fz(l x)以y为中性轴弯曲
Mz Fcos(lx)Mcos My Fsin(lx)Msin
二.基本变形分析
1.应力计算
z
M
的应力
z
Mz yMycos
Iz
Iz
y
9
M
的应力
y
Myz Mzsin
21
例题 8-1 z
(e)
MyA
z
D1 z
MzA
D2
y
yyBiblioteka (m )A a x M W y y A M W z zA 0 3 .6 .5 q 1 4 1 (1 6 2 2 0 ) 0 .2 2 q 3 6 1 ( 1 6 7 2 6 0 ) (2.1 5130)q
18
例题 8-1
解:1. 将集中荷载F 沿梁横截面的两个对称轴y、z分解为
F y F c4 o o 0 s q 2 ca 4 o o 0 s 0 .3q 8 a 3
F z F s4 io n 0 q 2sa 4 io n 0 0 .3q 2 a 1
19
例题 8-1
2. 梁的计算简图如图b所示,并分别作水平弯曲和 竖直弯曲的弯矩My图和Mz 图(图c ,d)。
纵向对称面:梁的轴线与横截面纵向对称轴所构成的平面
平面弯曲:当作用在梁上的载荷和支反力均
位于纵向对称面内时,梁的轴线由直线弯成
一条位于纵向对称面内的曲线。 F'
F'
F
F'
纵向对称面?
轴线
7
CL7TU1
一.定义:斜弯曲—荷载不作用在构件的纵向对称 面内,梁的轴线变形后不在位于外力所在平面内。
一.力的分解
Fy Fcos
Fz Fsin
z
C
(y, z)
Fz
Fy
Fy
8
CL11TU3
Mz Fy(l x)以z为中性轴弯曲
My Fz(l x)以y为中性轴弯曲
Mz Fcos(lx)Mcos My Fsin(lx)Msin
二.基本变形分析
1.应力计算
z
M
的应力
z
Mz yMycos
Iz
Iz
y
9
M
的应力
y
Myz Mzsin
21
例题 8-1 z
(e)
MyA
z
D1 z
MzA
D2
y
yyBiblioteka (m )A a x M W y y A M W z zA 0 3 .6 .5 q 1 4 1 (1 6 2 2 0 ) 0 .2 2 q 3 6 1 ( 1 6 7 2 6 0 ) (2.1 5130)q
《组合变形》PPT课件

0.266q (12 ) 237 106
(21.5103) q
( max )D
M yD Wy
M zD Wz
0.444q (12 ) 31.5 106
0.456q (12 ) 237 106
(16.02 103) q
危险点在A截面上的外棱角D1和D2处
z
MyA
y
z
MzA
y
D1 z D2
y
32
l 几何参数
A 15103 m2 , zo 7.5 cm, I y 5310 cm4
l 求内力(作用于截面形心)
取研究对象如图
FN P kN,
M y 42.5 102 P kN.m
l 危险截面
各截面相同
l 应力分布
350
FN
33
l 危险截面
各截面相同
l 应力分布
l FN引起的应力
FN P MPa
u 拉伸、压缩
l 组合变形 有两种或两种以上的 基本变形同时发生。
u 剪切
l 求解组合变形的方法
将载荷分为几组分别产生 基本变形的载荷,然后应 用叠加原理。
u 扭转
u 弯曲
3
2 叠加原理 如果内力、应力、变形等与外力成线性关系, 则复杂受力情况下组合变形构件的内力、应 力、变形等可以由几组产生基本变形的载荷 单独作用下的内力、应力、变形等的叠加而 得到,且与各组载荷的加载次序无关。
'' My z Mz y
Iy
Iz
中性轴的方程:
My F1l
F2 (l a)
Mz
My Iy
z0
Mz Iz
y0
0
5
中性轴的方程:
材料力学第八章组合变形 PPT

m Fr 1020 Nm
(1) 连杆轴颈得强度计算
l 危险截面
连杆轴颈得中点
l 计算内力
取左半部分
M z R1 L / 2 (C C1) l / 2 1170 N m
M y H1 L / 2 553 Nm
My Qy T
Mz Qz
M
M
2 z
M
2 y
1290
Nm
T H1 r 510 Nm
Qz
B点得应力状态如图。
r4 2 3 2 96.7 MPa [ ] 安全
50
例题5 F1=0、5kN,F2=1kN,[]=160MPa、
(1)用第三强度理论计算 AB 得直径 (2)若AB杆得直径 d = 40mm,并在B端加一水平力
F3 = 20kN,校核AB杆得强度、
400
400
B
求:校核轴得强度。
解:
l 求外力
u 力偶矩
m 9549 N n
21.7 Nm
u 皮带张力
(F f ) D m 又 F f 600
2
F 465 N, f 135 N
u 齿轮作用力
Pn
cos 20
d1 2
m
Pn 925 N
l 将各力向轴线简化
P 870 N, Pr 316 N, m m, Fy f y 542 N, Fx fx 257 N
示例1 示例2
F1 产生弯曲变形 F2 产生拉伸变形 Fy 产生弯曲变形 Fx 产生拉伸变形
F2
F1
F2
Fy
F
Fx
三、内力分析
横截面上内力
1、拉(压) :轴力 FN
弯矩 Mz
2、弯曲 剪力Fs
(1) 连杆轴颈得强度计算
l 危险截面
连杆轴颈得中点
l 计算内力
取左半部分
M z R1 L / 2 (C C1) l / 2 1170 N m
M y H1 L / 2 553 Nm
My Qy T
Mz Qz
M
M
2 z
M
2 y
1290
Nm
T H1 r 510 Nm
Qz
B点得应力状态如图。
r4 2 3 2 96.7 MPa [ ] 安全
50
例题5 F1=0、5kN,F2=1kN,[]=160MPa、
(1)用第三强度理论计算 AB 得直径 (2)若AB杆得直径 d = 40mm,并在B端加一水平力
F3 = 20kN,校核AB杆得强度、
400
400
B
求:校核轴得强度。
解:
l 求外力
u 力偶矩
m 9549 N n
21.7 Nm
u 皮带张力
(F f ) D m 又 F f 600
2
F 465 N, f 135 N
u 齿轮作用力
Pn
cos 20
d1 2
m
Pn 925 N
l 将各力向轴线简化
P 870 N, Pr 316 N, m m, Fy f y 542 N, Fx fx 257 N
示例1 示例2
F1 产生弯曲变形 F2 产生拉伸变形 Fy 产生弯曲变形 Fx 产生拉伸变形
F2
F1
F2
Fy
F
Fx
三、内力分析
横截面上内力
1、拉(压) :轴力 FN
弯矩 Mz
2、弯曲 剪力Fs
材力第8章组合变形PPT课件

已知: 皮带张力 F1=3.9kN, F2=1.5kN,两带轮直径均为
600mm,轴的[]=80MPa,
试:按第三第四强度理论选 择轴的直径。
解:1. 画计算简图
FDF CF 1F 25.4kN
2m . D 计算m C 支座F 1 反力F 2D 2 轮 0.7k2N m
FAy3.6kN FB,y1.8kN
叠加法: “先分后合”——将外力进行分解简化,得到
几种基本变形,分别计算应力变形,再进行叠加。
叠加法应用条件: 1)线弹性范围;2)小变形。
§8.2 拉伸(或压缩)与弯曲的组合
返回目录
一、外力分析
Fx Fcos ——拉
Fy Fsin ——弯
二、内力分析
固定端为危险面
轴力: FN Fx
弯矩: MmaxFyl
Fx 0
FAx40kN
Fy 0
FAy 4.8kN
FAx40kN,FAy 4.8kN
Fx 40kN, Fy 12.8kN
解: 2. 作内力图
C为危险截面 3. 分析C截面应力
max压maxFANM W max
查型钢表得16号工字钢
W141cm3, A26.13cm2
max10.40MPa
[]10M 0 Pa
r4W 1 MD 2合0.7T 5D 2 3d23 1.63kNm
d59.2mm
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
拉 ma x拉 max
600mm,轴的[]=80MPa,
试:按第三第四强度理论选 择轴的直径。
解:1. 画计算简图
FDF CF 1F 25.4kN
2m . D 计算m C 支座F 1 反力F 2D 2 轮 0.7k2N m
FAy3.6kN FB,y1.8kN
叠加法: “先分后合”——将外力进行分解简化,得到
几种基本变形,分别计算应力变形,再进行叠加。
叠加法应用条件: 1)线弹性范围;2)小变形。
§8.2 拉伸(或压缩)与弯曲的组合
返回目录
一、外力分析
Fx Fcos ——拉
Fy Fsin ——弯
二、内力分析
固定端为危险面
轴力: FN Fx
弯矩: MmaxFyl
Fx 0
FAx40kN
Fy 0
FAy 4.8kN
FAx40kN,FAy 4.8kN
Fx 40kN, Fy 12.8kN
解: 2. 作内力图
C为危险截面 3. 分析C截面应力
max压maxFANM W max
查型钢表得16号工字钢
W141cm3, A26.13cm2
max10.40MPa
[]10M 0 Pa
r4W 1 MD 2合0.7T 5D 2 3d23 1.63kNm
d59.2mm
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
拉 ma x拉 max
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①外力向形心简化(建立计算模型):
②作弯矩、扭矩图(找危险截面):
由弯矩图知:A截面|M|→max;全梁Mn处处相同,
∴A截面为危险截面:
|TMn A
| PL Pa
③危险截面的危险点:A截面K1、K2点,t、s数值均为最大,
∴K1、K2点均为危险点:
K1点:
s
s
tmax
|MA Wz
|
t Mn Wn
K2点:s
例题11-1 20 a号工字钢悬臂梁受集度为q的均布荷载和集中力P=qa/2作
用,如图所示。已知钢的许用弯曲正应力[o]=160MPa,a=1m。试求此梁 的许可荷载集度[q]。
解:将自由端B截面上的集中 力沿两主轴分解,并分别绘出 两个主轴平面内的弯矩图。
由型钢表查得20a号工字钢的抗弯 截面系数Wz和Wy值分别为:
二、双向弯曲和扭转强度计算(基本步骤与前相同)
例 115 图 示 皮 带 轮 传 动 轴 , 传 递 功 率 N=7kW , 转 速 n=200r/min。皮带轮重量Q=1.8kN。左端齿轮上啮合力Pn与齿 轮 节 圆 切 线 的 夹 角 ( 压 力 角 ) 为 20o 。 轴 材 料 的 许 用 应 力 [s]=80MPa,试按第三强度理论设计轴的直径。
解:由图可见,载荷P偏离立柱轴线,其偏心距为: e=yc+500=200+500=700mm。
在偏心拉力P作用下横截面上的内力及各自产生的应力如图:最大组合正应 力发生在截面内、外侧边缘a、b处,其值分别为
s s
a b
P A
P A
Pey
Iz Pey
Iz
c 2
32.3MPa 53.5MPa
可见,立柱符合强度要求。
zD1
a 2
cos
34.9mm;yD1
d 2
sin
72.0mm
绘出了此粱分别以z轴和y轴为中
性轴对称弯曲时的正应力变化规律,
可以看出,D1点均处于拉应力而D2点 均处于压应力。因此,按两个对称弯
曲叠加后的D1点即为该截面上的最大 拉应力点,而D2点为最大压应力点。
s max
s D1
M ymax Iy
二、基本解法(叠加法)
1.叠加原理:在线弹性、小变形下,每一组载荷引起
的变形和内力不受彼此影响,可采用代数相加;
2.基本解法: ①外力分解或简化:使每一组力只产生一个方向 的一种基本变形
②分别计算各基本变形下的内力及应力
③将各基本变形应力进行叠加(主要对危险截面危险点) ④对危险点进行应力分析(s1≥s2≥s3)
第十一章 组合变形时的强度计算
§11-1 概述
一、组合变形的概念
1.组合变形:构件同时存在两种以上基本变形
2.分类------①两个平面弯曲的组合(斜弯曲) ②拉伸(或压缩)与弯曲的组合,以及偏心拉、压 ③扭转与弯曲或扭转与拉伸(压缩)及弯曲的组合
3.一般不考虑剪切变形;含弯曲组合变形,一般以弯曲为主, 其危险截面主要依据Mmax,一般不考虑弯曲剪应力。
y0 M y I z I z
式中角度φ是横截面上合成弯矩M矢量与y轴间的夹角。一 般情况下,由于截面的Iy不等于Iz ,因而中性轴与合成弯矩M所 在的平面并不相互垂直。并由于截面的挠度垂直于中性轴,所
以挠曲线将不在合成弯矩所在的平面内。故这种弯曲称为斜弯 曲。
在确定中性轴的位置后,作平行于中性
轴的两直线,分别与横截面周边相切于D1、 D2两点,该两点即分别为横截面上拉应力和 压应力为最大的点。 将两点的坐标(y,z)分 别代人,就可得到横截面上的最大拉、压应 对于工程中常力用。的矩形、工字形等
Py
P cos400
qa 2
cos400
0.383qa
Pz
P sin
400
qa 2
sin
400
0.321qa
Wz 237106 m3,Wy 31.5106 m3
根据工字钢截面Wz不等 于Wy 的特点并结合内力图情 (s max)A 况,可按叠加原理分别算出A
M yA Wy
M zA WZ
0.642q 12 31.5 106
0.266q 12 237 106
21.5103 q
截面及D截面上的最大拉伸应 力,即:
(s
m
ax)
D
M yD WyM zD源自WZ0.444q 12 31.5 106
0.456q 12 237 106
16.02103 q
由此可见,该梁的危险点在固定端A截面的棱角处。由于危险点处是单
轴应力状态,故可将最大弯曲正应力与许用弯曲正应力相比较来建立强度
s
cmax
|M A Wz
|
tMn Wn
y
A d
z
L
Tn
_
PL
M
_
P C
B a x
P Pa
K1
st Pa
K1 A
t s
s K2 t
K2
ss t
s
④对危险点进行应力分析:(从K1、K2点取单元体,因它们的 s、t数值分别相同,危险程度也相同,不妨取K1点研究):
s1
s
2
s
2
2
t
2
,s2
0,s3
1.5m
RA
HA A
A 2m
M
C
B
1m P
N
T
Ty
Tx C
B
12kN·m
P
_
_
24kN
例114 图示压力机,最大压力P=1400kN,机架用铸铁作成,许用拉
应力[sL]=35MPa,许用压应力[sy]=140MPa,试校核该压力机立柱部分的 强度。立柱截面的几何性质如下:yc=200mm,h=700mm,A=1.8×105mm2, Iz=8.0×109mm4。
W Mmax 12106 120cm3 [s] 100
(4)查型钢表,选取W=141cm3的16号工字梁,然后按压弯组合变形进行 校核。易知,在C截面下缘的压应力最大,且有:
s max
N Mmax AW
24103 26.1102
12106 141103
94.3M Pa
最大压应力略小于许用应力,说明选取16号工字 梁是合适的。
二、注意事项:
1.如果材料许用拉应力和许用压应力不同,且截面部分区域受 拉,部分区域受压,应分别计算出最大拉应力和最大压应力,并 分别按拉伸、压缩进行强度计算。
2.如果横向力产生的挠度与横截面尺寸相比不能忽略,则轴向力 在横截面上引起附加弯矩DM=Py亦不能忽略,这时叠加法不能使用, 应考虑横向力与轴向力之间的相互影响。
⑤用强度准则进行强度计算
§11-2 两相互垂直平面内的弯曲
平面弯曲:对于横截面具有对称轴的梁,当横向外力或
外力偶作用在梁的纵向对称面内时,梁发生对称弯曲。这时, 梁变形后的轴线是一条位于外力所在平面内的平面曲线。
斜弯曲:双对称截面梁在水平和垂直两纵向对称平面内
同时承受横向外力作用的情况,这时梁分别在水平纵对称面
M zmax 9.35kN m, M ymax 5.40kN m
由于该梁横截面无外棱角,要求得危险截面上的最大拉应力和最大压
应力,须确定中性轴和位置
由Iz 2440104 mm4, 得:tg M z I y 2.06;则: 64.110
I y 2903104 mm4
M yIz
作平行于中性轴的两条直线分别与横截面周边相切于D1和D2,该两点即 为斜弯曲时横截面上最大拉应力和最大压应力点。
条件,即:
s max (s max) A 21.5103 q s 160 106
解得: q 160 103 7.44 103 N/m 7.44kN/m
21.5
例题11-2 一铸铁悬臂梁受集度为q=15kN/m的均布荷载作用,如图所 示。已知铸铁的许用拉应力[σ]=40MPa,许用压应力[σc]=160MPa,梁的截 面尺寸为d=160mm,b=70mm,h=110mm。试核核此梁的强度,并绘出危 险截面上的正应力变化图。
P P 500
z yc
c
y
h
e
M=Pe sMN=Pe
N=NP =Psa sa'
b
ca P
sb
sb' y2 yc
s
N
P A
s
a
'
Pey Iz
c
s
b
'
Pe I
y
z
2
s
a
s
N
s
a
'
P A
Pey Iz
c
s
b
s
N
s
b
'
P A
Pe I
y
z
2
§114弯曲与扭转组合变形
一、单向弯曲与扭转组合变形
1.引例:以钢制摇臂轴为例。
zD1
M zmax Iz
yD1
34.1MPa s
该梁能满足正应力强度条件
§113 拉伸(压缩)与弯曲组合变形
弯曲与拉伸(压缩)组合变形:当杆上的外力除横向力外,
还受有轴向拉(压)力时,所发生的组合变形。
q
P
P
y
一、计算方法:
x
1.分别计算轴向力引起的正应力和横向力引起的正应力;
2.按叠加原理求正应力的代数和,即可。
4.012 kN
F1=2F2 y
300 D2 500 D1
A
C
D
B
200
400
y Tn
Pz Py 0.446kN·m
My
